Assessing receiver noise using GPS short baseline time series

Abstract

In this contribution, we focus on both the functional and stochastic models of GPS short baseline time series. Biases in the observations can be interpreted as due to an incomplete functional model. Multipath, as a major part of errors, is believed to induce periodic effects on the carrier-phase observations over short time spans (a few minutes). Here, we employ a harmonic estimation method to include a set of harmonic functions in the functional model. Such sinusoidal functions are introduced to compensate for periodic systematic effects in GPS short baselines time series. This guarantees the property of unbiasedness of the least-squares estimators. On the other hand, the covariance matrix of observables is, in practice, generally based on the supposition of uncorrelated observables. A realistic description of the measurement noise characteristics, through the observation covariance matrix, is required to yield minimum variance (best) estimators. We will use least-squares variance component estimation to assess time-correlated noise of GPS receivers. Receiver noise characteristics are traditionally assessed through special zero baseline measurements. With the technique introduced in this paper we demonstrate that we can reach the same conclusions using (ordinary) short baseline measurements.

Introduction

In this contribution, we assess and compare the performance of high-end GPS receivers. For this purpose, traditionally, both a zero baseline and a short baseline are measured in the field. In the zero baseline test, the goal is to examine the performance of the receiver itself and to get an impression of the measurements’ noise characteristics. On the other hand, the short baseline test is conducted to examine the performance of the full system, i.e., antenna, cabling and receiver working together. This test gives an impression of the measurement noise plus multipath effects.

From previous work, it became clear that the suitable measurement to assess the intrinsic noise characteristics of GPS receivers is the zero baseline in which two receivers of the same type are connected to the same antenna and low-noise amplifier (LNA). In the single difference model for this configuration with fixed known coordinates, common external error sources such as atmospheric errors, satellite-dependent errors and multipath are absent. Also the common internal errors due to LNA noise cancel in the baseline processing to a large extent (Gourevitch 1996). We can therefore assess only the noise of the receivers themselves (too optimistic results). On the other hand, realistic and practically meaningful noise characteristics can only be obtained from a short baseline for which each receiver is connected to its own antenna (and amplifier). This underlines the relevance of using short baseline measurements to assess the noise characteristics of GPS observations. In previous testing procedures, although short baseline measurements were also carried out, the results could not be dealt with easily since the observations were affected by multipath. Our objective here is to study the stochastic characteristics of the observations of GPS receivers, from both zero and short baseline results. After handling unmodeled multipath effects on the short baseline, the findings based on the zero and short baseline measurements will be compared.

Components of the observables’ covariance matrix are estimated using least squares. We investigate the common assumption with data processing that measurements (carrier-phase observations) possess only white noise. In other words, they are not correlated from one epoch to the next. Also the correlation coefficient between observation types is estimated. A significant correlation between the observations on the two GPS frequencies can be expected, e.g., between L1 and L2 carrier phases. Least-squares variance component estimation (LS-VCE) with emphasis on time correlation is outlined in the next section. It is well known that multipath plays the main role in the unmodeled effects on short baseline results. The multipath effect on a single satellite’s measurements is, however, supposed to have a periodic behavior. We, therefore, assume that there exist harmonic functions able to capture multipath. However, the periods (or frequencies) of these harmonic functions are generally unknown. The problem of identifying these periods is the task of harmonic estimation. Here, least-squares harmonic estimation is used to identify and, hence, remove harmonic functions from the time series of GPS coordinates. The harmonic estimation method is explained in a later section. After removing the harmonic functions, to compensate for multipath effects, the receiver noise can be retrieved. Preprocessing of GPS data to obtain time series of baseline components and measurement residuals using a single difference phase observation model is presented in Data preprocessing. The results of the above test and analysis procedure, using GPS receivers in three different field experiments, is shown and discussed in Results and discussion.

Time-correlation estimation

In GPS data processing, one usually starts by formulating a system of observation equations consisting of two models: the functional model and the stochastic model. This section deals with the stochastic model. The covariance matrix of observations is generally based on the supposition of uncorrelated observables. However, this turns out not to be the case all the time. For example, time correlation might be present in a data series (e.g., a time series of baseline components or of measurement residuals) as well as correlation between L1 and L2 phase observations. The reader is referred to Tiberius and Kenselaar (2000), Bona (2000) and Amiri-Simkooei and Tiberius (2004) for more information. The problem of estimating unknown (co)variance components of a covariance matrix, Q _y , is often referred to as variance component estimation. The theory of LS-VCE was developed by Teunissen (1988). For a review see Teunissen and Amiri-Simkooei (2006).

In the following, we evaluate a special case that can be used for estimating time correlation. In Results and discussion, we apply the method to time series of both baseline coordinates and measurement residuals. Let us now consider the linear(ized) model of observation equations:

$$E\{ \underline{y} \} = Ax,\quad Q_{y} = Q_{0} + {\sum\limits_{k = 1}^p {\sigma _{k} Q_{k} } },$$

(1)

where A is the m × n design matrix, Q _y the m × m covariance matrix of the m-vector of observables $\underline{y},$ x the n-vector of unknown parameters, Q ₀ the known part of the covariance matrix and Q _k s the known cofactor matrices. The (co)variance components σ _k are estimated using LS-VCE.

We consider a stationary noise process and employ a side-diagonal structure for the covariance matrix Q _y . When our (co)variance component model is split into an unknown variance factor and m − 1 covariance factors, the covariance matrix can then be written as a linear combination of m cofactor matrices

$$Q_{y} = \sigma ^{2} I + {\sum\limits_{\tau = 1}^{m - 1} {\sigma _{\tau } Q_{\tau } } }$$

(2)

with

$$Q_{\tau } = {\sum\limits_{i = 1}^{m - \tau } {c_{i} c_{{i + \tau }}^{\rm T} + c_{{i + \tau }} c_{i}^{\rm T} }, }\quad \tau = 1, \ldots, m - 1,$$

(3)

where $c_{i} =\left[ {\begin{array}{*{20}l} 0 & \cdots & 0 & 1 & 0 & \cdots & 0 \\ \end{array} } \right]^{\rm T}$ is the canonical unit vector containing zeros except for a one at position i. This implies that the correlation between time series observations is only a function of the time-lag τ=|t _j − t _i |.

We can now apply the least-squares approach to estimate the components describing the time correlation in the time series. Consider the case that we measure m times a functionally known quantity. It can be shown that the variance of the noise process is simply estimated as (Teunissen and Amiri-Simkooei 2006)

$$\underline{{\hat{\sigma }}} ^{2} = \frac{{{\sum\nolimits_{i = 1}^m {\underline{{\hat{e}}} _{i} \underline{{\hat{e}}} _{i} } }}}{m},$$

(4)

where $\underline{{\hat{e}}} _{i}$ is the least-squares residual. Accordingly, the covariance elements are given as

$$\underline{{\hat{\sigma }}} _{\tau } = \frac{{{\sum\nolimits_{i = 1}^{m - \tau } {\underline{{\hat{e}}} _{i} \underline{{\hat{e}}} _{{i + \tau }} } }}}{{m - \tau }},\quad\tau = 1,2, \ldots, m - 1.$$

(5)

Because the method is based on the least-squares principle, it is possible to derive the covariance matrix of the estimators. An approximation for the variance of the (co)variance estimators is then

$$\sigma ^{2}_{{\hat{\sigma}^{2}}} \approx \frac{{2\sigma ^{4} }}{m},\quad\sigma ^{2}_{{\hat{\sigma}_{\tau } }} \approx \frac{{\sigma ^{4} }}{{m - \tau }},\quad \tau = 1,2, \ldots, m - 1.$$

(6)

From the estimated variance and covariance components, it is possible to obtain the correlation coefficients that, together, represent the empirical autocorrelation function (ACF):

$$\underline{{\hat{\rho }}} _{\tau } = \frac{{\underline{{\hat{\sigma }}} _{\tau } }}{{\underline{{\hat{\sigma }}} ^{2} }},\quad \tau = 1,2, \ldots, m - 1.$$

(7)

After linearization, application of the error propagation law to the preceding equation yields an approximation for the variance of the correlation coefficients:

$$\sigma ^{2}_{{\hat{\rho }_{\tau } }} \approx \frac{1}{{m - \tau }} + \frac{{2\rho ^{2}_{\tau } }}{m},\quad \tau = 1,2, \ldots, m - 1.$$

(8)

This shows that with increasing time-lag, the precision of the estimated time correlation gets poorer. This makes sense as the number of estimated residuals used for estimating the covariance σ_τ gets reduced to m − τ.

In this section, only a very simple application of the LS-VCE estimation was explained using some restrictive assumptions. The LS-VCE method is generally applicable. More general models of observation equations can be used, as well as other structures to capture different aspects of the observables’ noise. For precise GPS positioning, one could think of elevation dependence and cross correlation between observations. The reader is referred to Teunissen and Amiri-Simkooei (2006), in particular, for issues such as formulation of the model, iteration and precision of the (co)variance component estimators.

Harmonic estimation

This section deals with the functional model. If left undetected in the data, unmodeled effects can, for instance, be mistakenly interpreted as a time correlation. We will use the least-squares harmonic estimation to identify and compensate for unmodeled periodic effects in the functional model.

Consider the model of observation equations $E\{ \underline{y} \} = {\rm A}x.$ When dealing with a time series y=[y ₁, y ₂, ..., y _m ]^T, we are, in practice, very often involved in the following problem: given a data series y defined on R ^m, with R ^m an m-dimensional vector space, we assume that y can be expressed as the sum of q individual trigonometric terms, i.e., $y_{i} = {\sum\nolimits_{k = 1}^q {a_{k} \cos \omega _{k} t_{i} + } }b_{k} \sin \omega_{k} t_{i}.$ In matrix notation, when we also include the functional part Ax, we obtain

$$E\{ \underline{y} \} = Ax + {\sum\limits_{k = 1}^q {A_{k} x_{k},\quad D\{ \underline{y} \} } } = Q_{y},$$

(9)

where the matrix A _k contains two columns corresponding to frequency ω _k of the sinusoidal function:

$$A_{k} = {\left[ {\begin{array}{*{20}c} {{\cos \omega_{k} t_{1} }} & {{\sin \omega_{k} t_{1} }} \\ {{\cos \omega_{k} t_{2} }} & {{\sin \omega_{k} t_{2} }} \\ { \vdots } & { \vdots } \\ {{\cos \omega _{k} t_{m} }} & {{\sin \omega _{k} t_{m} }} \\ \end{array} } \right]},\; x_{k} = {\left[ {\begin{array}{*{20}c} {{a_{k} }} \\ {{b_{k} }} \\ \end{array} } \right]},$$

(10)

with a _k , b _k and ω _k being real numbers. If the frequencies ω _k are known, one is dealing with the common (linear) least-squares problem of estimating amplitudes a _k and b _k , for k=1, ..., q. However, if the frequencies ω _k are also unknown, the problem of finding all these unknown parameters, which is the case here, is the task of harmonic estimation. For this purpose, the following null and alternative hypotheses are put forward (to start, set i=1):

$$H_{0} : E\{ \underline{y} \} = Ax + {\sum\limits_{k = 1}^{i - 1} {A_{k} x_{k} } }$$

(11)

versus

$$H_{\rm a} : E\{ \underline{y} \} = Ax + {\sum\limits_{k = 1}^i {A_{k} x_{k} } }.$$

(12)

The identification and testing of the frequency ω _k=i is completed through the following two steps:

Step I: The goal is to identify the frequencies ω _i (and correspondingly A _i ) by solving the following minimization problem:

$$\omega _{{k = i}} = \arg {\mathop {\min }\limits_{\omega _{j} } }{\left|\left|{P^{ \bot }_{ \left[\begin{array}{*{20}l} \overline{A} & A_{j} \end{array}\right]} \underline{y} }\right|\right|}^{2}_{{Q^{{ - 1}}_{y} }} = \arg {\mathop {\min }\limits_{\omega _{j} } }{\left|\left|{\underline{{\hat{e}}} _{a} }\right|\right|}^{2}_{{Q^{{ - 1}}_{y} }}$$

(13)

with $\overline{A} = \left[ \begin{array}{*{20}l} A & {A_1 } & \cdots & {A_{i - 1} } \\ \end{array}\right]$ and $\underline{{\hat{e}}} _{a}$ the least-squares residuals under the alternative hypothesis. The matrix A _j has the same structure as A _k in Eq. 10. The matrix A _j which minimizes the preceding criterion is the desired A _i . The above minimization problem is equivalent to the following maximization problem (Teunissen 2000):

$$\omega _{{k = i}} = \arg {\mathop {\max }\limits_{\omega _{j} } }\left|\left|P_{{\overline{A} _{j} }} \underline{y}\right|\right|^{2}_{{Q^{{ - 1}}_{y} }} \hbox{ with }\overline{A} _{j} = P^{ \bot }_{{\overline{A} }} A_{j}$$

(14)

with $P_{{\overline{A} _{j} }} = \overline{A} _{j} (\overline{A}_{j}^{\rm T} Q_{y}^{{ - 1}} \overline{A} _{j})^{{ - 1}} \overline{A}_{j}^{\rm T} Q^{{ - 1}}_{y},$ an orthogonal projector. The preceding equation simplifies to

$$\omega _{{k = i}} = \arg {\mathop {\max }\limits_{\omega _{j} } }\underline{{\hat{e}}}_{0}^{\rm T} Q_{y}^{{ - 1}} A_{j} (A_{j}^{\rm T} Q_{y}^{{ - 1}} P_{{\overline{A} }}^{ \bot } A_{j})^{{ - 1}} A_{j}^{\rm T} Q_{y}^{{ - 1}} \underline{{\hat{e}}} _{0}$$

(15)

with $\underline{{\hat{e}}} _{0} = P_{{\overline{A} }}^{ \bot } \underline{y},$ the least-squares residuals under the null hypothesis. When the time series contains only white noise, namely Q _y =σ² I, it follows that

$$\omega _{{k = i}} = \arg {\mathop {\max }\limits_{\omega _{j} } }\underline{{\hat{e}}}_{0}^{\rm T} A_{j} (A_{j}^{\rm T} P_{{\overline{A} }}^{ \bot } A_{j})^{{ - 1}} A_{j}^{\rm T} \underline{{\hat{e}}} _{0}.$$

(16)

Analytical evaluation of the above maximization problem is very complicated. In practice, one has to be satisfied with numerical evaluation. A plot of spectral values $\left|\left|P_{{\overline{A} _{j} }} \underline{y} \right|\right|^{2}_{{Q^{{ - 1}}_{y} }}$ versus a set of discrete values for ω _j can be used as a tool for investigation of the contributions of different frequencies in the construction of the original data series y. In other words, we can compute the spectral values for different frequencies ω _j using Eq. 15 or 16. The frequency at which $\left|\left|P_{{\overline{A} _{j} }} \underline{y} \right|\right|^{2}_{{Q^{{ - 1}}_{y} }}$ achieves its maximum value is considered to be the frequency ω _i that we are looking for. Based on this frequency we can construct A _k=i .

Step II: To test H ₀ in Eq. 11 against H _a, we consider that Q _y =σ² I with unknown variance. The following test statistic can be used (Teunissen et al. 2005):

$$\underline{T} _{2} = \frac{{\left|\left|P_{{\overline{A} _{j} }} \underline{y}\right|\right|^{2}_{{Q^{{ - 1}}_{y} }} }}{{2\underline{{\hat{\sigma }}} ^{2}_{a} }} = \frac{{\underline{{\hat{e}}} ^{\rm T}_{0} A_{j} (A^{\rm T}_{j} P^{ \bot }_{{\overline{A} }} A_{j})^{{ - 1}} A^{\rm T}_{j} \underline{{\hat{e}}} _{0} }}{{2\underline{{\hat{\sigma }}} ^{2}_{a} }},$$

(17)

where $\overline{A} _{i} = P^{ \bot }_{{\overline{A} }} A_{i}$ and the estimator for the variance, $\underline{{\hat{\sigma }}} ^{2}_{a},$ has to be computed under the alternative hypothesis. The factor 2 originates from the fact that each harmonic has two components. Under H ₀, the test statistic has a central Fisher distribution:

$${\underline{T} _{2}} \sim F(2,m - n - 2i).$$

(18)

The test of the above hypothesis is, in fact, the parameter significance test because the test statistic $\underline{T} _{2}$ can also be expressed in terms of $\underline{{\hat{x}}} _{{k = i}}$ and its covariance matrix (see Teunissen et al. 2005). If the null hypothesis is rejected, we can increase i by one step and perform the same procedure to find yet another frequency.

Our application of harmonic estimation, after finding different harmonic functions and including them in the functional model of short baseline time series, is to assess the remaining noise characteristics of the data series. In this paper, multipath will be represented by the harmonic functions. Once we compensate for these effects in the functional model, the remaining noise (whether it is white noise or colored noise) of the series is found to be comparable to that obtained from the corresponding zero baseline result. Later, we elaborate on the time correlation of GPS receivers using the zero baseline time series and arrive at the same conclusions from short baseline results once multipath effects are captured by harmonic functions.

Finally, a practical comment on the numerical search for the frequency components is in order. The step size used for the periods, T _j =2π /ω _j (do not confuse it with the test statistic $\underline{T} _{2}$), is small at high frequencies and gets larger at lower frequencies. In this paper we have used the following recursive relation:

$$T_{{j + 1}} = T_{j} {\left({1 + \frac{{\alpha T_{j} }}{T}} \right)},\quad \alpha = 0.1,\quad j = 1,2, \ldots$$

(19)

with a starting period of T ₁=2 s (Nyquist period) and T being the total time span (1 h for most time series). For each time series, the lowest frequency that we will check is ω_min=2π /T, i.e., one cycle over the total time span. To avoid a $A_{j}^{\rm T} P_{{\overline{A} }}^{ \bot } A_{j}$ singularity in Eq. 16, one needs to exclude the previously detected frequencies ω₁, ..., ω _{i - 1} in the spectrum when finding ω _i .

Data preprocessing

Experiment description

For the purpose of demonstration and verification of the proposed method, we have used data from three (stationary) field experiments. Three receiver pairs were used, all from the same manufacturer, namely Trimble. The pairs consisted of two 4000SSI, 4700 and R7 dual-frequency receivers. The 4000SSI has 9 channels; the other receivers have 12 channels. Each time, a zero and a short (10 m) baseline were measured in the same open field, just outside the built-up area of Delft (Delfland). Table 1 lists the equipment and the experiments. The data were collected and processed at a 1 s interval with an elevation cut-off angle of 5°. Data files in Rinex format formed the starting point for the processing and analysis.

Table 1 Zero and short baseline measured on two consecutive days, same geometry, 1 h duration, except for 4700 zero baseline which was measured on the same day and only for 35 min

These data were selected to demonstrate the proposed analysis method, not to compare hardware or for any other purpose. One can efficiently evaluate and compare the performance of different receivers, even from different manufacturers, by carrying out a simultaneous measurement campaign. These data clearly show different receiver noise and multipath behavior. In particular, it will be shown that receiver-induced noise characteristics can be retrieved from short baseline data, and that they are similar to those obtained from zero baseline measurements. When comparing the results of the three receiver (and antennas) pairs, one should keep in mind that the measurements were not taken simultaneously, although all experiments took place using a similar set up in the same field.

Baseline processing

To process the baselines, the single difference phase observation equation is employed. All sessions of the two configurations in our experiment were static but we have first processed the data using a single epoch kinematic model (see De Jong 1999). Baseline components and differential receiver clock biases along with double difference ambiguities were estimated by least squares. The integer double difference ambiguities are determined by the LAMBDA method. These estimates are very reliable and can subsequently be introduced in the model. Furthermore, if the coordinates of the second receiver with respect to those of the reference receiver are known, either very precisely from a long survey or even exactly for a zero baseline, we can introduce them in the model. This is referred to as the position and ambiguity-constrained model. Note that, per baseline, both L1 and L2 data were used in one straight combined processing. Since all further results pertain to ambiguity-fixed solutions, the pseudo-range code observations do not play a role. We focus, in the sequel, on the dual-frequency carrier-phase observations. Therefore, we present the time series of baseline components from every epoch (with 1 s interval) of the kinematic solutions and the least-squares single difference measurement residuals from the constrained model. These are considered as input for further assessment. For more information refer to Tiberius and Kenselaar (2000).

Figure 1 displays the time series of kinematic positioning results for the 4000SSI, 4700 and R7 pairs on the zero and short baselines. Whereas the zero baselines show coordinate time series apparently with constant, zero means, some small but systematic variations (low frequency harmonics) are evident in all the time series of the short baselines. Table 2 displays the standard deviations of zero and short baseline components. At first sight, it appears that the oldest receiver, namely the 4000SSI, produces better results than the newer ones! There is still one thing to remember and that is time correlation. We will refer to this important issue in the following section.

Fig. 1

Time series of three coordinate components on zero (left) and short (right) baselines; top 4000SSI, middle 4700, bottom R7; offset by their individual averages for short baseline

Table 2 Estimated standard deviation for six sessions (two configurations) in local north, east and up components

Results and discussions

Introduction

To simplify data processing, most GPS users assume that the observations possess only white noise, i.e., that they are not correlated from epoch to epoch. To verify this assumption, we examine correlograms of time series of baseline components shown here using Eq. 7. A correlogram displays the estimated autocorrelation coefficient versus lag (the time interval between two samples). The coefficient at lag zero equals one by definition. If a white noise process can describe the time series, then all other coefficients should be approximately zero because the observation at one epoch is not correlated with the observation at any other epoch. Actually, the variations around zero imply that they are not deterministic values but random variables. Equation 8 expresses the precision of this estimated autocorrelation function. In graphs of the estimated autocorrelation coefficients shown here, we indicate the 95% confidence intervals. Recall that for large lags, the precision gets poorer because the autocorrelation estimates are based on less data.

Two aspects may cause time correlation in GPS coordinate time series or least-squares observation residuals. One is that the observations are noisy (e.g., because of the anti-spoofing encryption) so that some smoothing or filtering has been applied, on purpose, to bring down the noise level. The other is that some time-correlation error sources, such as multipath effects and atmospheric delays, remain in the time series after data processing. The external causes can generally be ruled out on zero baseline data. Tiberius and Borre (2000) give an overview of assessing time correlation in GPS data. Later on, in this paper, we will try to model and hence remove the external systematic effects, which are believed to be mainly due to multipath, by introducing harmonic functions and subsequently retrieve and assess the receiver noise. Once removed, it becomes possible to see the time correlation and the correlation between observation types (i.e., between L1 and L2 phases) due to the receiver measurement process itself on short baselines. The method also has the advantage that the harmonic functions give an indication of multipath effects in the short baseline test.

Time correlation

Figure 2 gives the correlograms of the time series of the zero baseline components for 4000SSI and R7. The correlograms obtained for the 4700 are very similar to those obtained for the R7; therefore, we will not show them here. The dashed lines indicate the 95% confidence levels of the autocorrelation functions (see Eq. 8). The figures on the left and right show the same results, but, for the sake of clarity, we have used different scales for the vertical and horizontal axes. The figures on the right ”zoom in” on the first part of the figures on the left, i.e., they are the correlogram for the first 100 s. It appears that the R7 and 4700 (similar to the R7 and so not included here) seem to be free from time correlation. In other words, the receiver noise of the 4700 and R7 is all white noise (at least at 1 s interval). However, this is not the case for the 4000SSI. The 4000SSI results show time correlation over a few (10–20) seconds. This can, for instance, be caused by the smoothing of the observations. Smoothing can bring down the noise level at the price of time correlation. This can be a reason for the standard deviations of the 4000SSI being better than those of the 4700 and R7 (see Table 2). On other time-lags, one can still see small irregular variations for the 4000SSI compared to the 4700 and R7. This is most likely due to the use of Eq. 8 as an approximation for the variance of the autocorrelation function. This expression holds exactly only for a white noise process. The noise of the 4000SSI receiver is clearly not white. Note that these results belong to the zero baselines and therefore they do not display external effects such as multipath. Thus, these autocorrelations must be a receiver effect.

Fig. 2

Autocorrelation coefficients (solid line) for time series of zero baseline components; top 4000SSI and bottom R7; left over the whole period, right over the first 100 epochs (zoom in); dashed line the 95% confidence interval

Figure 3 gives the correlograms of the time series of the short baseline components. It is quite obvious that there are positive correlations in time in the first 100 s lag intervals for both receivers (graphs on the right). On the other hand, over the full period (graphs on the left), the autocorrelation function behaves periodically. The correlograms are clearly different from those of the zero baselines (Fig. 3 vs. Fig. 2) and the low(er) frequency effects are thought to be caused by multipath. Recall this is supported by the periodic behavior evident in the short baseline plots (Fig. 1, graphs on the right).

Fig. 3

Autocorrelation coefficients (solid line) for time series of short baseline components; top 4000SSI and bottom R7; left over the whole period, right over the first 100 epochs (zoom in); dashed line the 95% confidence interval

Harmonic estimation

Harmonic estimation, the method introduced earlier, was used to remove the sinusoidal periodic effects from these results. For this purpose 10 harmonic functions were estimated. The step size used for discrete periods T _j (corresponding to frequencies ω _j ) is small at high frequencies and gets larger at lower frequencies (see Eq. 19). Recall that to avoid singularity, one needs to exclude the detected frequencies from the spectrum when finding a new frequency. Also recall that multipath is one of the few external error sources which can affect short baselines, such as those used here, and will be assumed to be the source of the sinusoidal signal seen in these results. Multipath is not a random error but a systematic effect over a short time span (a few seconds) and a periodic effect over a longer time span (a few minutes).

Figure 4 illustrates the least-squares spectra for finding the frequency of the first harmonic function (left column of graphs), the first 10 test statistic values given by Eq. 17 (middle column), and the combination of 10 harmonic functions which were ultimately removed from the data (right column). It becomes clear, from the graphs on the left, that most of the spectral power belongs to periods larger than 300 s. This means that multipath has a period of at least 5 min. It can also be seen (graphs in the middle) that the value of the test statistic levels off quickly. With 5–10 harmonic functions it gets close to the critical value (dashed line). Therefore, in all subsequent results, the number of harmonic functions q in Eq. 9 was set to 10. The amount by which the time series is corrected for is an indication of the multipath effect in the short baseline components (graphs on the right). The smallest value is obtained for the 4000SSI. The newest receiver, R7, shows better results compared to its older version, 4700. As they both have no correlation in time, such a comparison is fair. Note that the “thick” appearance of the lines representing the 10 harmonic function combinations obtained for the R7 (bottom right column) is because of the presence of (very) high frequency periodic effects (though their amplitudes are not very significant).

Fig. 4

Estimated spectral values for finding the frequency of the first harmonic function (left column); the first 10 test statistic values (solid line with circle) obtained from Eq. 17 as well as its critical values (dashed line, middle column); and combination of 10 harmonic functions (external effects) as removed from original north, east, and up component time series (right column); top 4000SSI, middle 4700, bottom R7

Given the periods (frequencies ω _i ) of the harmonic functions, one can estimate the coefficients of those functions (using the ordinary least-squares approach) and subsequently ‘detrend’ the data. The detrended data should then behave similar to the zero baseline results. Figure 5 shows the detrended data (left) and the autocorrelation functions (right) for the short baseline components after including the harmonic functions. Note that the estimated autocorrelation functions of the detrended data are very similar to those obtained for the zero baselines (see Fig. 2 at the right). For example, again, the 4000SSI shows time correlation over 10–20 s and the 4700 and R7 seem to be free from any time correlation.

Fig. 5

Time series of three components on short baseline after removing 10 harmonic functions from original data (left); autocorrelation coefficients (solid line) for time series of short baseline components after removing harmonic functions (right); top 4000SSI, middle 4700, bottom R7; dashed line the 95% confidence interval

Accordingly, we can define three standard deviations for a time series, namely the standard deviation of the original data, the standard deviation of the detrended data and the standard deviation of the harmonic functions (multipath effects). Table 3 gives these results. The smallest values were obtained for the 4000SSI receiver. The R7 receiver shows significant improvement compared to the 4700 (especially for multipath effects).

Table 3 Estimated standard deviation of the time series of short baseline components for different receivers

LS measurement residuals

Time correlation

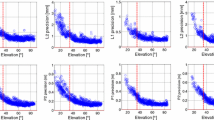
We will now turn our attention to the least-squares residuals of constrained model to see whether similar results as to those obtained for the baseline components can be found. Because the results of the 4700 are very similar to those of the R7, they are again omitted. For this purpose we consider both a high-elevation and a low-elevation satellite. Figure 6 shows the time series (in each subfigure a, b, c, or d, graphs at the top) and the autocorrelation functions (graphs at the bottom) of the phase residuals of the zero baselines, each time for a high-elevation satellite (a and c) and a low-elevation satellite (b and d). It is clear that the residuals of the 4000SSI are less noisy than those of the R7 for both L1 and L2. Except for the L2 phase of the 4000SSI, the other phase observations seem to possess only white noise, though the autocorrelation function of the L1 phase for the 4000SSI seems to stay at a small positive value. This may imply that there is a small (constant) systematic error (bias) in the residuals. There is no significant difference between the autocorrelation functions of a high-elevation satellite and a low-elevation satellite.

Fig. 6

Time series of least-squares residuals on zero baseline as well as their autocorrelation coefficients for a high- and a low-elevation satellite measured by receiver 4000SSI (a and b, respectively) and by receiver R7 (c and d, respectively). In each subfigure, graphs at the top are least-squares residuals (L1, left and L2, right) and graphs at the bottom are their corresponding autocorrelation coefficients (dashed line 95% confidence interval)

Figure 7 shows the time series of the phase residuals (in each subfigure a, b, c, or d, graphs at the top) of the short baseline tests for a high-elevation satellite (a and c) and a low-elevation satellite (b and d). Similar results to those from the zero baselines are obtained; namely, the residuals of the 4000SSI are less noisy than those of the R7, both for L1 and L2. The measurement residuals for the low-elevation satellite are noisier (by a factor of 2) than those for the high-elevation satellite (note that the range of the vertical axis has been doubled). The figure (graphs at the top) also show the combination of 10 harmonic functions included in the functional model (lighter line). The graphs at the bottom show the detrended residuals (corrected for the harmonic functions).

Fig. 7

Original and corrected time series of least-squares residuals on short baseline for a high- and a low-elevation satellite measured by receiver 4000SSI (a and b, respectively) and by receiver R7 (c and d, respectively). In each subfigure, graphs at the top show original least-squares residuals (L1, left and L2, right) and graphs at the bottom show their corresponding detrended ones; top graphs also show combination of 10 harmonic functions (light solid line) which were removed from the original time series

Figure 8 shows the estimated autocorrelation functions for the original data (in each subfigure a, b, c, or d, graphs at the top) and the detrended data (graphs at the bottom). The correlograms of the original short baseline data are clearly different from those of the corresponding zero baselines (see Fig. 6). In this case, all phase observations are positively correlated (at least over the first 100 s). The correlation of the 4000SSI is larger than that of the R7 (at least for the high-elevation satellite). The graphs at the bottom show the estimated autocorrelation functions after removing 10 harmonic functions from the least-squares residuals. Note that the estimated autocorrelation coefficients of the detrended residuals, to a large extent, are similar to those obtained on the zero baselines (again, see Fig. 6)). The slightly different result for the autocorrelation function of the 4000SSI (L1 phase) is likely due to the presence of remaining effects not captured by limiting the number of harmonic functions to 10.

Fig. 8

Autocorrelation coefficients of original time series and detrended time series of least-squares residuals for a high- and a low-elevation satellite measured by receiver 4000SSI (a and b, respectively) and by receiver R7 (c and d, respectively). In each subfigure, graphs at the top show autocorrelation coefficients of original residuals (L1, left and L2, right) and graphs at the bottom show their corresponding autocorrelation coefficients of detrended residuals (in all graphs dashed lines are 95% confidence interval)

As a final comment on the time-correlation analysis, it should be noted that all observations were taken at a 1 s sampling interval. The tracking loops in the receivers are expected to operate internally at (much) higher rates and the newer receivers (e.g., the R7) are, in fact, able to output observations at rates higher than 1 Hz. The current conclusions on the presence or, in particular, absence of time correlation hold only from the 1 s boundary onward. To assess time correlations below the 1 s interval, data collected at higher rates are needed.

Cross correlation

Neglecting the time correlation, we focus, here, on the elements of the single difference observations’ covariance matrix of only one satellite. The diagonal elements of the covariance matrix are the variances of the L1 and L2 phase observations, and the off-diagonal element is the covariance between those observations. Table 4 gives the estimated standard deviations of the phase observations and the corresponding correlation coefficients, for a high-elevation satellite from the zero baseline (ZB) and short baseline original (SB1), and detrended (SB2) observations. Correspondingly, Table 5 gives the results for a low-elevation satellite. There exists significant (positive) correlation, induced by the receivers, between the observations on the two frequencies, i.e., between the L1 and L2 phases for all receivers (see ZB). The correlation for the 4000SSI is smaller (0.32 and 0.17 for a high- and a low-elevation satellite, respectively) than those for the 4700 and R7. However, note that a single correlation coefficient between two time series can be easily computed only when the noise processes of both time series are the same (e.g., when both are white noise). Because of the L2 phase time correlation of this receiver, the correlation coefficient will be underestimated.

Table 4 Estimated standard deviation of L1 and L2 phase observations as well as their correlation coefficient for a high-elevation satellite

Table 5 Estimated standard deviation of L1 and L2 phase observations as well as their correlation coefficient for a low-elevation satellite

If we now try to estimate these correlation coefficients using the short baseline residuals (i.e., SB1), we can see a significant difference with those obtained from the zero baseline. The difference gets larger when we use, for instance, the residuals of a low-elevation satellite (see Table 5, the R7, ρ_ϕ1,ϕ2=− 0.01). However, by the strategy we suggested, i.e., removing harmonic functions from the residuals, it is possible to largely compensate for the unmodeled effects (e.g., multipath) and retrieve the correlation coefficients of phase observations (see SB2 and compare with ZB).

Tables 4 and 5 also give the estimated standard deviations of the L1 and L2 phase observations. The standard deviations for the short baseline are always larger than those obtained for the zero baseline (even for detrended data, SB2; see also Table 2). This is most likely due to the fact that, for a zero baseline, the two receivers are connected to the same antenna and LNA (see Gourevitch 1996). In this case we can only assess the noise of the receivers themselves. Common errors due to multipath cancel in the baseline processing and so does the LNA noise to a large extent. Realistic and practically meaningful noise values (standard deviations) can only be obtained from a short baseline for which each receiver is connected to its own antenna (and amplifier). This underlines the relevance of using short baseline measurements to assess the noise characteristics of GPS observations, including correlation.

Concluding remarks

This contribution presents a method for assessing the receiver-induced measurement noise and multipath effects for GPS baselines using harmonic functions. The relevance lies first on the ability to account for the remaining unmodeled functional effects in GPS data and second to come up through LS-VCE with an appropriate stochastic model that realistically describes the observables’ noise characteristics. This model is of direct importance to guarantee the optimality of the estimators for the unknown parameters of interest, for carrier-phase ambiguity resolution and for GPS data quality control.

Up to now, most efforts to assess the GPS receiver noise characteristics focused on zero baseline results. When using a short baseline, the receiver noise is contaminated with external effects of which the main source is believed to be multipath. Multipath is not a random error but a systematic effect over a short time span (a few seconds) and periodic over a longer time span (a few minutes). The period of a multipath error, however, differs from site to site and from time to time as it depends on the azimuth and elevation of the satellite and local geometry. To compensate for multipath, harmonic (sinusoidal) functions were introduced. The problem of finding the frequencies (or periods) of these functions is the task of the harmonic estimation.

To illustrate the proposed method, three receiver pairs were employed, namely, 4000SSI, 4700 and R7, all from the same manufacturer. The measurements used for this paper were collected out in the field under rather favorable, but realistic practical circumstances. For all receivers, the precision of the baseline components and phase observations is at the millimeter level. From the results of single epoch precise positioning, the standard deviation of the 4000SSI baseline components turns out to be better than those for the other two receivers, both for zero and short baseline. In other words, the time series of zero and short baseline components as well as the L1 and L2 phase residuals for the 4000SSI turn out to be less noisy than those for the 4700 and R7. On the other hand, the 4700 and R7 receivers seem to be free from time correlation (from a 1 s sampling interval and slower). The receiver noise of the 4700 and R7 is all white. However, this is not the case for the 4000SSI. The 4000SSI results show time correlation over some 10–20 s. Also, the carrier-phase observations on L1 and L2 are positively correlated for all receivers. The time correlation on the L2 phase for the 4000SSI will cause underestimation of this positive correlation.

It is important to note that the above conclusions were drawn from zero baseline tests. However, with the proposed method, it is now possible to arrive at the same conclusions from short baseline results. It is based on removing periodic systematic effects from the data using harmonic functions. A lucid example is the retrieval of time correlation induced by the receiver, from time series (either baseline components or measurement residuals) of a short baseline.

The proposed method has been demonstrated here on a series of receivers of only one manufacturer. The method is, however, generally applicable and can be used as an important measure to assess and compare, in an objective and quantitative manner, the performance of different receivers from the same or different manufacturers.