Integer ambiguity validation in high accuracy GNSS positioning

Abstract

Carrier phase observations are required for high-accuracy positioning with Global Navigation Satellite Systems. This requires that the correct number of whole carrier cycles in each observation (integer ambiguity) is determined. The existing methods have been shown to perform differently depending on the observables. Subsequently, the ratio test used for ambiguity validation was developed further including combining it with the integer aperture concept. The key challenges in using the ratio test are the existence of biases in float solutions and stochastic dependence between the two elements of the ratio. The current methods either make assumptions of independence and nonexistence of biases or use simulations together with the bias-free assumption. We propose a new method taking into account both challenges which result in an unknown distribution of the ratio test statistic. A doubly non-central F distribution (DNCF) is proposed for the determination of threshold. The cumulative distribution function (CDF) of DNCF over-bounds the CDF of ratio test statistic distribution in case there is a bias in the float solution and a correlation between the two elements of the ratio. The Precise Point Positioning (PPP) method with products from CNES and measurement data from 10 NOAA stations are used to verify the proposed method. The test results show that the proposed method improves the performance of ambiguity resolution achieving a lower rate of wrong fixing than current state of the art.

Introduction

Carrier phase measurements are required for high-accuracy positioning with Global Navigation Satellite Systems (GNSS) such as GPS. Different observables can be derived from the measurements to support different positioning concepts including the conventional approach for dynamic positioning referred to as Real Time Kinematic (RTK) and the more recent Precise Point Positioning (PPP). In order to exploit the excellent accuracy potential of carrier phase measurements, the correct whole number of carrier cycles (integer ambiguity) must be determined to facilitate the integrity of positioning solutions (Feng et al. 2009). A three-stage process is usually invoked to determine the correct integer ambiguities. The first involves the computation of the float ambiguities. The second stage employs a search method to find the candidate integer ambiguities. The third stage tests all or selected sets of candidates and determines whether any should be accepted. The well-known Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) method addresses the first and second stages including a transformation to reduce the search space (Teunissen 1995), while the third stage, referred to as ambiguity validation, continues to attract significant research effort. A number of approaches have been developed for ambiguity validation. These approaches usually involve the construction of test statistics, characterization of their distribution, and determination of thresholds. Examples of these tests include ratio, F-ratio (Verhagen 2004), W-ratio (Wang et al. 2000), and other tests constructed from residuals and/or their differences. It has been shown that none of these tests are based on a sound theoretical basis (Verhagen 2004) and that there is no single method that can be used in all situations. Specifically, the conventional ratio test uses the ratio between the residuals of the second best and best ambiguity candidates as the test statistic and adopts a fixed threshold. Because the use of a fixed threshold does not capture the major factors that impact the level of confidence (or success rate) associated with the resolved ambiguities, research has explored the use of ratio-based methods without the direct use of a fixed threshold. One example is the combination of the simulation approach with the integer aperture (IA) method (Verhagen 2004; Teunissen and Verhagen 2004, 2009a, 2009b). This requires the simulation of a large number of normally distributed independent samples of float ambiguities. However, the bias-free float ambiguity solution may not be achieved in practice. Furthermore, the need for significant computational resources for the online simulation of large samples (>100,000) (Teunissen and Verhagen 2004) and computation of the success/fail rates precludes the use of IA in real time. Moreover, this method does not link the simulation effort to the feasibility of acquiring integer ambiguities. For example, if it is unlikely to determine the integer ambiguity due to weak conditions, there is no need to waste resources to perform the simulation. For the ratio test with fixed fail rate, look-up tables can be created off-line to reduce computational resources required in real time (Verhagen and Teunissen 2013). The weaknesses of using fixed threshold were addressed in Feng et al. (2012), in which a new distribution doubly noncentral F distribution (DNCF) is used for real-time applications based on the assumption that the two elements in the ratio are independent.

To address the key challenges in using the ratio test, the existence of biases in float solutions and stochastic dependence between the two elements of the ratio, we propose a new over-bounding theory to determine the threshold for the ratio test. The next section summarizes the mixed integer least-squares method for ambiguity resolution and the formation of ratio test. The justification of using the DNCF for the determination of the threshold for ratio test is addressed. This is followed with the details of test data, algorithm and results, and conclusions.

Ambiguity resolution and ratio test

Carrier phase ambiguity resolution is the key to high-precision positioning with GNSS. Reliable ambiguity resolution is a function of several factors, the main ones being the types of measurements, formation of observable, residual error of observables, geometry and algorithmic formulation. To resolve ambiguity reliably, the observations must be pre-processed to mitigate errors. Due to the integer nature of ambiguities, the model used for GNSS positioning is an equation with mixed integer and real unknowns. A mixed integer least-squares (MILS) method is normally used to estimate ambiguities and positioning errors.

Mixed integer least-squares (MILS) for ambiguity resolution

The general MILS can be expressed as:

$$\hbox{min} \left\| y - Ax - Bz\right\|_{2}^{2}$$

(1)

where $x \in R^{k}$ is a vector of real unknowns, $z \in Z^{n}$, is a vector of integer unknowns, $A \in R^{m \times k}$ (known), $B \in R^{m \times n}$ (known), $y \in R^{m}$ is a vector of the observation (known), and $\left\| {} \right\|_{2}$ denotes the Euclidean norm.

Typically, MILS is translated to integer least-squares (ILS) and a real least-squares (RLS) by orthogonal transformations.

$$\left\| y - Ax - Bz\right\|_{2}^{2} = \left\|\left[ {\begin{array}{*{20}c} {Q_{A}^{T} } \\ {\bar{Q}_{A}^{T} } \\ \end{array} } \right]y - \left[ {\begin{array}{*{20}c} {R_{A} } \\ 0 \\ \end{array} } \right]x - \left[ {\begin{array}{*{20}c} {Q_{A}^{T} B} \\ {\bar{Q}_{A}^{T} B} \\ \end{array} } \right]z\right\|_{2}^{2}$$

(2)

Expression (1) can therefore be rewritten as:

$$\hbox{min} \left\|y - Ax - Bz\right\|_{2}^{2} = \hbox{min}\left\| \bar{Q}_{Z}^{T} y - \bar{Q}_{A}^{T} Bz\right\|_{2}^{2} + \hbox{min} \left\|Q_{A}^{T} y - R_{A} x - Q_{A}^{T} Bz\right\|_{2}^{2}$$

(3)

where $A = \left[ {\begin{array}{*{20}c} {Q_{A} } & {\bar{Q}_{A} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {R_{A} } & 0 \\ \end{array} } \right]^{T}$, $\left[ {\begin{array}{*{20}c} {Q_{A} } & {\bar{Q}_{A} } \\ \end{array} } \right]$ is orthogonal and $R_{A}$ is non-singular upper triangular.

The first part of (3) is an ILS. As long as the z in the first part is solved, the second part becomes a RLS which can be solved easily. The resolution of ILS is not straightforward. It normally involves two steps: (1) treat ILS as RLS to get float (real) solutions; (2) search all possible integers around the float solutions to find the integer. In the second step, a transformation maybe needed to reduce the search space for integer solutions. The well-known Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) is a typical MILS method in GNSS positioning.

Ratio test for ambiguity validation

In order to validate whether the integer solution is correct, a validation process using the information from LAMBDA is needed. The available information includes measurements and ambiguity residuals. A number of tests can be constructed such as ratio test, F-ratio and W-ratio with the ratio test being the most popular. There are also variations of the ratio test such as ratio test integer aperture estimator. The basic ratio test is based on the ambiguity residuals:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon }_{i} = \hat{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i}$$

(4)

where the real (float) ambiguity vector is denoted as $\hat{a}$, the estimate of integer values is denoted as $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i}$, and the order of a candidate ambiguity is denoted as i. If the float ambiguities follow a normal distribution, the ambiguity residuals follow a normal distribution subject to certain conditions (Verhagen and Teunissen 2006). For each ambiguity vector searched, an ambiguity residual vector is produced from which the sum of the squared errors (SSE), denoted as R, is generated. Searching through the specified space, a number of SSEs, denoted as $R_{i}$, are calculated as:

$$R_{i} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon }_{{_{i} }}^{T} G_{{\hat{a}}}^{ - 1} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon }_{i} = (\hat{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i} )^{T} G_{{\hat{a}}}^{ - 1} (\hat{a} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i} )$$

(5)

where $G_{{\hat{a}}}$ is ambiguity variance matrix. If the value of the variance factor (σ) is known and the probability density function (PDF) of $\hat{a}$ is sufficiently peaked (Verhagen and Teunissen 2006), then

$$X_{i} = \frac{{R_{i} }}{{\sigma^{2} }}\sim\chi^{2} (n,\delta_{i} )$$

(6)

where, $\delta_{i}$ is the non-central parameter (NCP) of the Chi-square distribution. If $R_{i}$ is sorted in ascending order, i.e., $R_{i} < R_{i + 1}$ for any $i \in \left[ {1, \left. n \right)} \right.$, the ratio test is therefore, defined as:

$$T = \frac{{R_{2} }}{{R_{1} }} > k$$

(7)

where, k is the threshold. If $T > k$, the best ambiguity vector is accepted.

The use of tests based on the best and second best ambiguity vector enables all cases to be covered, as they represent the smallest values, i.e., $R_{2} /R_{1} < R_{i} /R_{1}$ for any $i > 2$. The problem in using this test lies in the choice of the critical value k. This is because of the difficulty in defining the distribution of the ratio of two non-central Chi square distributions. Three simplified methods have been used in the past. The first assumes that the SSE of the residuals from the best ambiguity vector is bias free and R ₂ and R ₁ are independent. Therefore, the denominator in expression (7) ($R_{1}$) follows the Chi-square distribution ($\delta_{1} = 0$). This results in $\tfrac{{R_{2} }}{{R_{1} }}$ following an F distribution. However, the denominator is not necessarily bias free. In addition, R ₂ and R ₁ are highly correlated because the same float solution vector is used for both. Therefore, using the F distribution to describe the ratio is incorrect. The second method uses a constant value for k derived empirically. For example, the values of 1.5 and 3 have been used by Wei and Schwarz (1995) and Leick (2015), respectively. The third method approximates the threshold k by using the ratio of non-central parameters of the F distribution expressed as (Euler and Schaffrin 1991)

$$k = \frac{{\lambda_{2} (\gamma ,\beta_{2} )}}{{\lambda_{1} (\gamma ,\beta_{1} )}}$$

(8)

where γ is the false alarm rate when the float solution is correct but rejected, $\beta_{i}$ is the probability of incorrectly accepting the float solution while the ith set of ambiguities is true, $\lambda_{i}$ is the non-central parameter of an F distribution. The relationship between $\gamma$, $\beta_{i}$ and $\lambda_{i}$ is given by

$$\beta_{i} = \int\limits_{0}^{{F_{\gamma } (n,m - n - p,0)}} {F(x|n,m - n - p,\lambda_{i} )} {\text{d}}x$$

(9)

The third threshold determination method is not theoretically justifiable because the potential variations of the F distribution sample are ignored by only taking into account the non-central parameter of the F distribution. In addition, the calculation of the non-central parameter is complicated. In summary, all the simplified methods used are not theoretically justifiable. The simulation approach is adopted in the Ratio Test Integer Aperture (RTIA) method (Verhagen 2004; Teunissen and Verhagen 2009a). The IA method defines a region of acceptable ambiguities. Note that the conventional ratio test has been shown theoretically to be the IA because its reciprocal reflects the rate of success/fail of ambiguity resolution (Teunissen and Verhagen 2004, 2009b). However, instead of using the fixed threshold (as in the conventional ratio test), simulation is used to determine the success/fail rate for each reciprocal of the conventional ratio at the current epoch. This requires the simulation of a large number of normally distributed independent samples (>100,000) (Teunissen and Verhagen 2004) of float ambiguities. The main steps for validation are:

• to generate N samples of zero mean normally distributed float ambiguities

• to determine the ILS solutions (best and second best candidates) and ratio for each simulated sample

• to count and calculate fail rate

• to decide whether the best candidate should be accepted.

In order to reduce the computation load for the ratio test with fixed fail rate, look-up tables can be created offline (Verhagen and Teunissen 2013). The key assumption in the RTIA method is that float ambiguities follow a normal distribution which is widely accepted. Any biases in the float ambiguities should be corrected because the ratio test is not designed to test for the presence of biases (Verhagen and Teunissen 2013). It is suggested that standard hypothesis testing should always be applied before proceeding with ambiguity resolution to test for inconsistencies in the data and/or model, in order to prevent certain biases propagating into the ambiguity solution. Whether biases can be detected and corrected depends on the nature and size of the biases. Therefore, it is not possible to guarantee that the float ambiguities are bias-free. Hence, the potential existence of residual biases should be taken into account in ambiguity validation. In addition, the correlation between the two elements of the ratio should be considered also.

Distribution of ratio test

The distribution of the ratio test is the key to the determination of threshold which should also reflect the confidence level of the decision whether the best ambiguity vector is acceptable. From (4), it can be seen that all the ambiguity residual vectors ($\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon }_{i}$) are based on the same float ambiguity vector ($\hat{a}$). It has been proved in theory that the probability density function (PDF) of each ambiguity residual vector has the same probability distribution as the float ambiguities but translated over $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i}$ if the float ambiguity vector ($\hat{a}$) follows a normal distribution (Verhagen and Teunissen 2006). Therefore, all the SSEs of the ambiguity residuals ($R_{i}$) are highly correlated. Consequently, the numerator and denominator of the ratio test statistic are highly correlated. Therefore, it is difficult to analytically derive the distribution of the ratio test on which the threshold determination can be based.

With the same test statistic as that is used in conventional ratio testing (expression 4), the method by Euler and Schaffrin (1991) (expression 8) was developed further by Feng et al. (2012) taking into account the potential for a bias in the float solution resulting in a bias in both the numerator and denominator of the ratio test. In order to determine the confidence level of the ratio test, the distribution of $(R_{2} /R_{1} )$ is required. Thus (7) can be rewritten as:

$$T = \frac{{R_{2} }}{{R_{1} }} = \frac{{R_{2} /(n\sigma^{2} )}}{{R_{1} /(n\sigma^{2} )}} = \frac{{X_{2} }}{{X_{1} }}$$

(10)

As can be seen from (10), although the variance factor (σ) is not known, it is cancelled by the ratio operation. On the right side both the numerator and denominator follow a non-central $\chi^{2}$ distribution. Therefore, if $R_{1}$ and $R_{2}$ are assumed to be independent, $(R_{2} /R_{1} )$ has a doubly non-central F distribution (DNCF) (Bulgren 1971).

As discussed above, the assumption of independence is not true. However, the threshold determined from the assumption of independence can over-bound the actual dependent case. From (4), it can be seen that the ambiguity residual consists of two parts: constant (integer) and uncertainty, if the float ambiguity follows a normal distribution, which is an assumption for most of the other methods. Looking into (4) further, the uncertain part of the ambiguity residual vectors are the same for $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon }_{1}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon }_{2}$. The differences are in the integer part which is considered a translation over different constant values ($\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i}$). Therefore, the values of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon }_{1}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon }_{2}$ will increase or decrease simultaneously due to a change in the common uncertain part. This feature propagates to the SSE of the ambiguity residual ($R_{i}$). Therefore, expression (10) can be rewritten as:

$$T = \frac{{X_{2} }}{{X_{1} }} = \frac{c + u}{d + u}$$

(11)

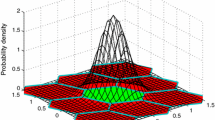
where c and d are the constant part, while u is the uncertainty part which is from the common float candidates. It can be seen from (11) that X ₁ and X ₂ increase or decrease at the same time when u changes. However, any change in T also depends on the value of c and d. Therefore, the distribution of ratio test T (10) is less spread than in the case where R ₁ and R ₂ are independent. To demonstrate the impact of the correlation between R ₁ and R ₂ on the ratio test, two simulation cases were run. In the first case, 1 million normally distributed ambiguity vectors (u in expression 11) were generated to simulate the float ambiguity vectors. Two constant vectors (c and d in expression 10) were then added to the normally distributed vectors. The corresponding SSEs were calculated to simulate R ₁ and R ₂. The discrete probability of the ratio test distribution based on a resolution of 0.1 is shown in Fig. 1. In the second case, 2 sets of 1 million normally distributed vectors for each size (e.g., 6) were generated. The constant vectors used in the first case were added to the two sets of the normally distributed vectors, respectively. The corresponding SSEs were then calculated to simulate R ₁ and R ₂. In the second case, R ₁ and R ₂ are independent. The discrete probability of independent ratio based on a resolution of 0.1 (X axis) is shown in Fig. 2.

Fig. 1

Distribution of correlated ratio

Fig. 2

Distribution of independent ratio

Figures 1 and 2 show that the distributions of correlated ratios are captured within a relatively narrow band, whereas the distributions of independent ratios have a wider spread for the same number of ambiguities (N). The corresponding cumulative distribution functions (CDF) of the two cases are shown in Figs. 3 and 4.

Fig. 3

CDF of correlated ratio

Fig. 4

CDF of independent ratio

Comparing Figs. 3 and 4, the CDF in Fig. 4 over-bounds that in Fig. 3 for each N when CDFs larger than 0.6 are considered. For instance, if a threshold of 3 is used, the CDF in Fig. 4 is 0.72 (N = 4), while the CDF in Fig. 3 is 0.95 (N = 4). This means that the confidence level is higher for the actual ratio test than determined from the assumed independent case. Therefore, the threshold determined from the doubly non-central F distribution is a conservative solution for use with the ratio test. The level of conservativeness depends on the level of correlation between R ₁ and R ₂, i.e., the higher the correlation, the more conservative the threshold. In other words, although the ratio $(R_{2} /R_{1} )$ does not strictly follow the DNCF distribution, a conservative threshold can be determined from it:

$$T \sim \,F(n,n,\delta_{2} ,\delta_{1} )$$

(12)

where n is the number of ambiguity residuals forming R ₁ (the same for R ₂); $\delta_{1}$ and $\delta_{2}$ are the non-central parameters which can be determined using the traditional failure detection scheme with a probability of false alarm (P _FA) and a probability of missed detection (P _MD) (Feng et al. 2006). Similar to expression (8), the probability of false alarm is the chance that the float solution is correct but rejected. The probability of missed detection is the chance of incorrectly accepting a float solution, while the integer ambiguities are true. The P _MD corresponding to each non-central parameter is

$$P_{{{\text{MD}}i}} = \int\limits_{0}^{{\chi_{{P_{\text{FA}} }}^{2} (n,0)}} {\chi^{2} (x|n,\delta_{i} )} {\text{d}}x \quad (i = 1,2)$$

(13)

Similar to expression (8), there are two probabilities of missed detection (P _MD1 and P _MD2) for the best and second best SSE, $R_{i} (i = 1,2)$. The non-central parameters $\delta_{1}$ and $\delta_{2}$ can then be derived from the above expression.

Realization of ratio test using doubly non-central F distribution

The analytical method for the solution of the confidence level $p_{c}$ is not straightforward, requiring the application of numerical methods using series representation. The CDF of the DNCF distribution can be written as (Bulgren 1971),

$$p_{c} = \int\limits_{0}^{{\tfrac{{R_{2} }}{{R_{1} }}}} {F(x|n_{2} ,n_{1} ;\delta_{2} ,} \delta_{1} ){\text{d}}x = \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {C_{i} D_{j} I(u,\tfrac{{n_{2} }}{2}} } + i,\tfrac{{n_{1} }}{2} + j)$$

(14)

where $C_{i} = (\delta_{2} /2)^{i} {\text{e}}^{{ - \delta_{2} /2}} /\varGamma (i + 1)$ and $D_{j} = (\delta_{1} /2)^{i} e^{{ - \delta_{1} /2}} /\varGamma (j + 1)$ are the probabilities of Poisson distribution, $\varGamma ( \, )$ is Gamma function, $I(u,a,b) = \int_{0}^{u} {t^{a - 1} (1 - t)^{b - 1} } {\text{d}}t/B(a,b)$ is the CDF of Beta distribution with $u = n_{2} x/(n_{2} x + n_{1} )$ and $x \ge 0$, and $B(a,b) = \int_{0}^{1} {t^{a - 1} (1 - t)^{b - 1} {\text{d}}t}$ is the Beta function with $a > 0$ and $b > 0$. For a practical implementation of the algorithm, the two infinite series are truncated when the higher orders are not needed to reach a specified accuracy.

For a given confidence level ($p_{c}$), the threshold T can be determined by

$$p_{c} = \int\limits_{0}^{T} {F(x|n_{2} ,n_{1} ;\delta_{2} ,} \delta_{1} ){\text{d}}x = \sum\limits_{i = 0}^{\infty } {\sum\limits_{j = 0}^{\infty } {C_{i} D_{j} I(u,\tfrac{{n_{2} }}{2}} } + i,\tfrac{{n_{1} }}{2} + j)$$

(15)

Following the execution of LAMBDA-type algorithms, the method here takes the outputs of carrier phase ambiguity resolution (R ₁, R ₂ and n) together with pre-defined PFA and PMD to generate in online computations the confidence levels for the candidate ambiguities at each epoch. Given a threshold, the confidence levels can be used to accept or reject the best set of candidate ambiguities. Some users may be more concerned with the confidence level satisfying the requirements rather than the confidence level itself. In this case, in order to reduce the processing resources consumed by online computations, it is possible to carry out offline calculations for the threshold of (R ₂/R ₁ ) to reflect the required confidence levels. Therefore, a look-up table could be calculated off-line taking into account all possible cases including a selected range of confidence levels and degrees of freedom. This is especially useful for embedded systems where computational power is low.

Results

In order to test the performance of the algorithm proposed, it is important that the true ambiguity is known. However, the true ambiguities may not be known in practice. However, the position errors at points of known position can give an indication of correctly resolving ambiguities. It is crucial that the test scheme minimizes the impact of various errors including ephemeris, tropospheric and ionospheric delays, cycle slips and multipath. A Precise Point Positioning (PPP) algorithm is implemented to demonstrate the proposed method.

Test data and algorithm

The PPP algorithms need products generated from a network of receivers and raw measurements from a receiver used for positioning. There are a number of organizations that provide products containing satellite position, clock, and ionospheric error corrections. For example, high-quality products are provided by the International GNSS service (IGS). The IGS combines products provided by the different service providers including the Centre National d’Etudes Spatiales (CNES) and Center for Orbit Determination in Europe (CODE). Conventionally, the raw data from a receiver at an IGS station are used because the true position of the station is known, enabling error analysis and performance characterization. However, the selected station should not be used to generate the products. Therefore, the CNES products were selected for this test, and the raw data used were from reference stations in the network of the National Oceanic and Atmospheric Administration (NOAA). Data from 10 NOAA stations were used. The features of these stations are given in Table 1. The data of 96 one-hour time periods for each station were used.

Table 1 Information of stations used for providing raw measurement

The PPP algorithm requires that errors are corrected as much as possible before position calculation is carried out. The satellite position and clock related errors are corrected by using products from CNES. The ionospheric effect is mitigated by using the ionospheric-free combination. The tropospheric errors are corrected by employing existing models and mapping function. The site-displacement effects are corrected using site-displacement models to estimate correction terms and adding these to position estimates. The antenna offsets and variations are corrected using corrections in the Antenna Exchange Format. The satellite antenna phase wind-up corrections are calculated based on the phase center coordinates of the receiver and satellite antennae. The receiver clock error is cancelled by using between-satellite difference (BSD) GPS observations. The key factor that affects conventional PPP is the fractional cycle biases (FCB) or uncalibrated phase delay (UPD). The PPP algorithm used here forms narrow lane observations to minimize the impact of UPD (Jokinen et al. 2013). The positioning algorithm uses an extended Kalman filter (EKF) and was implemented in C++. The data for tests were from monitoring stations; therefore, zero position process noise was used in the EKF.

Test results

For comparison purposes, three different ratio test based ambiguity validation methods were tested.

• Integer least-squares using constant threshold (CT) for ratio test. The threshold used was 3.0.

• Integer least-squares using fixed fail rate with simulation (FFS) for ratio test. This is based on the method presented in (Verhagen and Teunissen 2013). The allowed fail rate in the tests was 0.1 %.

• Integer least-squares using doubly non-central F distribution (DNCF) based threshold determination for ratio test. The confidence level with DNCF was 99.9 % in the test.

Table 2 shows the results. Among the 960 intended test periods, only 907 datasets were available due to data gaps. The statistics include the number of datasets where ambiguities were fixed, average epochs for ambiguity fixing, and three-dimensional position errors after ambiguities were validated in five bins. The errors of position estimates were analyzed by comparing them to the known ITRF 2008 coordinates of the stations provided by NOAA. The accuracy of the reference coordinates are at the millimeter level.

Table 2 Comparison of three validation methods

In this test with real data, the true ambiguities were not known. However, the position errors can give an indication of which method is better. It is difficult to justify that integer ambiguities have been fixed correctly if a solution has a 3D error bigger than 20 cm. Although the DNCF has the highest percentage of ambiguities not being fixed, it has the highest percentage of position errors smaller than 5 cm as shown in Fig. 5.

Fig. 5

Percentage of relative small 3D position errors

There is no significant difference in the percentage of position errors smaller than 10.7 cm between the CT and DNCF methods. However, the DNCF has the lowest percentage of 3D position errors larger than 10.7 (wavelength of narrow lane), 15 and 20 cm as shown in Fig. 6.

Fig. 6

Percentage of relative big 3D position errors

If the wrong ambiguity fixing is assessed in terms of the impact in the positioning domain, e.g., 10, 15 or 20 cm, then the DNCF has a significantly lower wrong ambiguity fixing rate than the other two methods. Comparing Figs. 5, 6 and Table 2, the lower ambiguity fixing rate of the DNCF method has no impact on the percentage of 3D position errors being less than 5 and 10.7 cm. However, it has significantly reduced the percentage of 3D position errors lager than 10.7, 15 and 20 cm.

Conclusions

Carrier phase ambiguity validation has been an open problem for many years. The popular ratio test and its variations including combination of simulation with the integer aperture (RTIA) method have not resolved the two critical issues, the existence of bias in float ambiguity estimates and the correlation of the two elements of the ratio test statistic. These two issues have been addressed in this research by using doubly non-central F distribution (DNCF) to determine the threshold for conventional ratio test statistic. The threshold determined over-bounds the actual threshold needed for the ratio test in terms of confidence levels. This approach is therefore a more objective method compared to the existing approaches.

The test results with Precise Point Positioning (PPP) algorithm using real data show that the proposed DNCF ambiguity validation method has a better performance than other methods in terms of percentage of 3D position errors being less than 5 and 10.7 cm. In theory, the over-bounding based on the independence of the two elements and the potential of bias in the denominator of the ratio test statistic may be overly conservative especially when there is no bias in the float ambiguity estimates. However, the results with PPP show that the rejection rate is higher than other methods while it is significantly better than the other methods in terms of wrong ambiguity fixing. A possible explanation is that the residual errors in the products used by PPP result in relatively large residual errors in observations. Further studies will be carried out on the application of this method to conventional Real Time Kinematic (RTK) positioning.