Theoretical analysis of the multi-GNSS contribution to partial ambiguity estimation and R-ratio test-based ambiguity validation

Abstract

The fast and high-precision positioning with multiple Global Navigation Satellite Systems (multi-GNSS) has been challenging for decades. Although the single-frequency single system (SF-SS), satellite selection for multi-GNSS, and multi-GNSS-based partial ambiguity resolution (PAR) can achieve rapid positioning, the varying theoretical bases of them result in different fixed reliability of ambiguities. Hence, we provide the theory analyzing the ambiguity resolution capabilities of the named systems. By adding satellite observations, the equations giving the variance–covariance matrix variation of the original float parameters are derived. Then, the relationship between the ambiguity dilution of precision (ADOP) values of the original ambiguity vector (OAV) before and after adding observations is obtained. This is followed by the analyses of the changing trends in the OAV’s probability density function, integer least-squares pull-in region, and the R-ratio test-based integer aperture pull-in region. In terms of precision, ADOP, and R-ratio test-based fixed reliability of ambiguities, the analyses indicate that the multi-GNSS can improve the partial ambiguity estimation and validation. Besides, compared to satellite selection and SF-SS, the PAR is optimal. The BeiDou Navigation Satellite System (BDS) and the Global Positioning System (GPS)-based single-epoch positioning experiments showed that both BDS B1 and B1-based PAR outperform GPS L1 and L1-based PAR in terms of ADOP and R-ratio test-based fixed reliability. The ADOP of the former is smaller than 0.14, and both the R-ratio test-based acceptance and success rates are up to 99.64%. Finally, the false alarm, failure, and detection rates are reduced to 0.34%, 0.0%, and 0.02%, respectively.

Introduction

The Global Navigation Satellite System (GNSS) has several advantages, such as weather independence, autonomy in operation, and no requirement for inter-visibility between stations. Hence, the GNSS-based instantaneous (single-epoch) positioning technology has been widely applied to many fields, including deformation monitoring, geological disasters monitoring, and unmanned driving technique (Yi et al. 2013). The applications of these fields require fast and high-precision positioning, and the key to achieving that is the ambiguities being correctly fast resolved (Li et al. 2015). The single-frequency single system (SF-SS) can achieve instantaneous positioning thanks to a small number of observations. However, the fixed success rate (SR) of ambiguity it has is not high enough, which is around 80.0% for the Global Positioning System (GPS) L1 with a baseline length of 1.0 km (Odolinski et al. 2015). To improve SR, some factors, such as baseline length and vector, have been taken into account (Li and Shen 2009; Tang et al. 2013). However, this made SR highly dependent on external constraints.

In the last decade, the GPS, Global Navigation Satellite System (GLONASS), Galileo, and BeiDou Navigation Satellite System (BDS) have made tremendous progress. The well-developed GPS has 31 operational satellites as of April 2020 (https://www.glonass-iac.ru/en/GPS/index.php). The GLONASS was commissioned in October 2011, and currently has 24 satellites offering global services (https://www.glonass-iac.ru/en/GLONASS/index.php). Similarly, there are 26 Galileo satellites in orbit, but only 22 of them are available for service (https://www.gsc-europa.eu/system-service-status/constellation-information). As of November 2020, there are 15 regional and 29 global BDS satellites up and running (https://www.glonass-iac.ru/en/BEIDOU/index.php).

With the development of multiple GNSSs (multi-GNSS), the single-epoch positioning based on single-frequency multi-GNSS has become feasible. The SR of this newly developed system can reach 100.0% for short baselines since more satellites can be observed (Liu et al. 2019; Odolinski et al. 2014, 2015; Odolinski and Teunissen 2016; Teunissen et al. 2014). However, the time it spends during positioning by the standard least squares and the least-squares ambiguity decorrelation adjustment (LAMBDA) increases rapidly with the increasing number of visible satellites (Li et al. 2015). In Liu et al. (2019), the average time consumption of single-epoch single-frequency positioning with 24 BDS/GPS/Galileo satellites was larger than 107 ms, which was not fast enough to apply to bridge deformation monitoring with vibration frequency higher than 10 Hz (Yi et al. 2013). Hence, the computational efficiency of multi-GNSS will limit its applications in many fields requiring fast positioning, which will also increase the power consumption of the equipment.

Both the satellite selection and the partial ambiguity resolution (PAR) can improve the multi-GNSS efficiency. However, their theoretical bases are different, which is mainly due to their way of calculating the float ambiguity vector. The satellite selection only uses the selected partial satellites of the multi-GNSS for positioning, and the SF-SS can be considered as a specific case of the satellite selection (Duangduen and Hassan A 2009). The PAR performs positioning by selecting the partial ambiguities from the float ambiguity vector that is calculated based on all observations (Brack 2017; Teunissen et al. 1999).

The multi-GNSS can improve the geometric strength of the GNSS model, the probability of correct ambiguity estimation, and the positioning accuracy and reliability of the system (He et al. 2014; Li et al. 2015; Yang et al. 2011). Hence, the PAR can reflect the advantages of the multi-GNSS better than the satellite selection, which will make their precision, fixed SR, and fixed reliability of the float ambiguity vector different. However, there is a lack of theoretical investigation in current literature analyzing the difference between PAR and satellite selection or SF-SS in ambiguity resolution. Furthermore, with the multi-GNSS development, the theoretical analysis investigating the effect of more observed satellites on the ambiguity resolution of the above methods needs more attention.

In this work, we first present the theoretical analysis. After adding satellite observations, the equations giving the variance–covariance (VC) matrix variation of the floating baseline and the original ambiguity vectors are derived. The relationship between the ambiguity dilution of precision (ADOP) values of the original ambiguity vector (OAV) before and after adding satellite observations is procured. The changing trends of the OAV’s probability density function (PDF), the integer least-squares (ILS) pull-in regions, and the R-ratio test-based integer aperture (RTIA) pull-in regions are analyzed. In terms of precision, fixed SR, and R-ratio test-based fixed reliability of ambiguities, the results of the theoretical analyses reveal that the multi-GNSS can improve the partial ambiguity estimation and the R-ratio test-based validation. Furthermore, compared to satellite selection and SF-SS, the PAR is optimal. The single-epoch relative positioning experiments of PAR and SF-SS based on the BDS and GPS show that from ADOP, empirical SR, and R-ratio test-based ambiguity reliability, both BDS B1 and B1-based PAR outperform the GPS L1 and L1-based PAR models.

Single-epoch ambiguity estimation

Let us assume that m > 3 satellites are observed, and n double-difference (DD) ambiguities are formed. The DD function and the stochastic models can be given by (Teunissen et al. 2014):

$$\varvec{E}\left[ {\begin{array}{*{20}c} {\varvec{p}_{1} } \\ {\emptyset _{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{B}_{1} } \\ {\varvec{B}_{1} } \\ \end{array} } & {\begin{array}{*{20}c} {\mathbf{0}} \\ {\varvec{B}_{{1,\;\lambda }} } \\ \end{array} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} \varvec{b} \\ {\varvec{a}^{1} } \\ \end{array} } \right]$$

(1)

$$\varvec {D}\left[ {\begin{array}{*{20}c} {\varvec {p}_{1} } \\ {\emptyset _{1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{Q}_{{p_{1} }} } & {\mathbf{0}} \\ \end{array} } \\ {\begin{array}{*{20}c} {\mathbf{0}} & {\varvec {Q}_{{\emptyset _{1} }} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sigma _{p}^{2} \varvec{Q}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {\sigma _{\emptyset }^{2} \varvec{Q}_{1} } \\ \end{array} } \right],\; \varvec {D}^{{ - 1}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec {p}_{1} /\sigma _{p}^{2} } & {\mathbf{0}} \\ \end{array} } \\ {\begin{array}{*{20}c} {\mathbf{0}} & {\varvec {p}_{1} /\sigma _{\emptyset }^{2} } \\ \end{array} } \\ \end{array} } \right],\;\varvec {p}_{1} = \varvec {Q}_{1}^{{ - 1}}$$

(2)

where ${\varvec {E}}\left[ \cdot \right]$ and ${\varvec {D}}\left[ \cdot \right]$, respectively, are the expectation and dispersion operators, ${\varvec {b}}$ and ${\varvec {a}}^{{\text{1}}}$, respectively, are the baseline and the DD ambiguity vectors, ${\varvec {B}}_{{1,\lambda }} = \lambda \cdot {\varvec I}_{{n \times n}}$ with rank $\left( {{\varvec {B}}_{{1,\lambda }} } \right) = n$, in which $\lambda$ is the carrier wavelength, ${\varvec {B}}_{{\text{1}}}$ is an n x 3-order matrix with rank $\left( {\varvec{B}_{1} } \right) = 3$, $\varvec{Q}_{{\text{1}}}$ is the covariance matrix of the DD observations, and lastly,$\sigma_{p}$ and $\sigma_{\emptyset }$ are, respectively, the standard deviations of the undifferenced code and the phase. It should be noted that $\varvec{Q}_{1}$, $\varvec{P}_{1}$, D, and $\varvec{D}^{{{ - }{\text{1}}}}$ are symmetrical positive definite matrices. The float solutions $\varvec{\hat{b}}$ and $\varvec{\hat{a}}^{1}$ together with the VC matrices can be obtained based on the standard least-squares method as (Teunissen et al. 2014):

$$\begin{array}{*{20}c} {\varvec{\hat{b}} = \varvec{Q}_{{\hat{b}\hat{b}}} \varvec{B}_{1}^{T} \varvec{Q}_{{p_{1} }}^{{ - 1}} \varvec{p}_{1} ,~~\varvec{Q}_{{\hat{b}\hat{b}}} = \left( {\varvec{B}_{1}^{T} \varvec{Q}_{{p_{1} }}^{{ - 1}} \varvec{B}_{1} } \right)^{{ - 1}} } \\ {\varvec{\hat{a}}^{1} = \varvec{B}_{{1,\;\lambda }}^{{ - 1}} \left( {\emptyset _{1} - \varvec{B}_{1} \hat{\varvec{b}}} \right),~~\varvec{Q}_{{\hat{a}^{1} \hat{a}^{1} }} = \varvec{B}_{{1,\;\lambda }}^{{ - 1}} (\sigma _{\emptyset }^{2} \varvec{Q}_{1} + \varvec{B}_{1} \varvec{Q}_{{\hat{b}\hat{b}}} \varvec{B}_{1}^{T} )\varvec{B}_{{1,\lambda }}^{{ - 1}} ~} \\ \end{array}$$

(3)

where $\varvec{Q}_{{\hat{b}\hat{b}}}$ and $\varvec{Q}_{{\hat{a}^{1} \hat{a}^{1} }}$ are also symmetrical positive definite matrices. The LAMBDA can be used to obtain the integer solutions $\varvec{\check{a}}^{1}$ and $\varvec{\check{b}}$ in (3) (Teunissen 1995).

R-ratio test-based ambiguity validation

The ambiguity validation deciding whether to accept the integer solution $\varvec{\check{a}}^{1}$ is a non-trivial procedure for achieving high-precision positioning. The ratio test with an empirical threshold has been widely used for ambiguity validation (Wang et al. 2017). The most common method is the R-ratio test, which can be defined as (Verhagen and Teunissen 2006a, 2013):

$$\frac{{\left( {\varvec{\hat{a}}^{1} - \varvec{\check {a}}_{2}^{1} } \right)^{T} \varvec{Q}_{{\hat{a}^{1} \hat {a}^{1} }}^{{ - 1}} \left( {\varvec{\hat{a}}^{1} - \varvec{\check {a}}_{2}^{1} } \right)}}{{\left( {\varvec{\hat{a}}^{1} - \varvec{\check {a}}_{1}^{1} } \right)^{T} \varvec{Q}_{{\hat{a}^{1} \hat {a}^{1} }}^{{ - 1}} \left( {\varvec{\hat{a}}^{1} - \varvec{\check{a}}_{1}^{1} } \right)}} = \frac{{R_{2} }}{{R_{1} }} \ge \mu$$

(4)

where $\mu$ is the tolerance value, $R_{i}$ is the quadratic form of the ambiguity residuals of the best (i = 1) and the second-best (i = 2) integer solutions, i.e., $\varvec{\check{a}}_{1}^{1}$ and $\varvec{\check{a}}_{2}^{1}$, respectively. Only when the ratio in (4) is large enough, the decision of whether to accept $\varvec{\check{a}}_{1}^{1}$ as the integer solution can be made (Verhagen and Teunissen 2013).

Single-epoch ADOP theory

The ADOP, first introduced in Teunissen (1997), is an easy-to-compute scalar diagnostic for measuring the intrinsic precision of ambiguities and the model strength for successful ambiguity resolution. The ADOP can be defined as:

$${\text{ADOP = }}\left| {{\varvec Q}_{{{{\hat{a}}}^{{\text{1}}} {{\hat{a}}}^{{\text{1}}} }} } \right|^{{\frac{{\text{1}}}{{{{2n}}}}}} ~~{\text{ (cycle)}}$$

(5)

The approximate ADOP for the geometry-based single-epoch single-baseline mode can be given as (Odijk and Teunissen 2008):

$${\text{ADOP}} \approx \frac{{\sqrt 2 \left| {\bar{\sigma }_{\phi } } \right|}}{{\bar{\lambda }}} \cdot \left[ {\frac{{\mathop \sum \nolimits_{{s = 1}}^{m} w_{s} }}{{\mathop \prod \nolimits_{{s = 1}}^{m} w_{s} }}} \right]^{{\frac{1}{{2n}}}} \cdot \left[ {~\frac{{\bar{\sigma }_{p} }}{{\bar{\sigma }_{\emptyset } }}} \right]^{{\frac{3}{n}}} = ~f_{1} \cdot f_{2} \cdot f_{3}$$

(6)

where $\left| \cdot \right|$ denotes the determinant, $\overline{\lambda } = \mathop \prod \nolimits_{i = 1}^{r} \lambda_{i}^{1/r}$, in which r is the number of frequencies, $\overline{\sigma }_{\phi } = \frac{{\sigma_{\phi 1} + \cdots + \sigma_{\phi r} }}{r}$, $\overline{\sigma }_{p} = \frac{{\sigma_{p1} + \cdots + \sigma_{pr} }}{r}$, and w denotes the satellite elevation-dependent weight. The ADOP also provides a good approximation to the ILS ambiguity SR ($P_{{s,{\text {ILS}}}}$), which can be expressed as (Odijk and Teunissen 2008; Verhagen 2003):

$$P_{{s,{\text{IB}}}} \le P_{{s,{\text{ILS}}}} \approx P_{{s,{\text{ADOP}}}} = \left[ {2\Phi \left( {\frac{1}{{{\text{2ADOP}}}}} \right) - 1} \right]^{n}$$

(7)

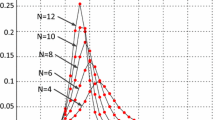
where $P_{{s,{\text{ADOP}}}}$ and $P_{{s,{\text{IB}}}}$, respectively, represent the ADOP-based and integer bootstrapping SR, and $\Phi \left( \cdot \right)$ denotes the standard normal cumulative distribution function. With the increase in ADOP, the $P_{{s,{\text{ADOP}}}}$ and $P_{{s,{\text {ILS}}}}$ decrease. The more ambiguities are involved, the steeper the decrease will be (Odijk and Teunissen 2008).

Theoretical analysis of the multi-GNSS contribution to the PAR

This section studies the multi-GNSS contribution to the PAR. Furthermore, the difference in ambiguity resolution between PAR and satellite selection or SF-SS is assessed by analyzing how satellite observations affect the precision, ADOP, and R-ratio test-based fixed reliability of the float OAV.

Effect of adding satellite observations on the precision of original float parameters

In this section, the rigorous precision variation formulas of the original float parameters with added satellite observations are derived theoretically. Hence, Eqs. (1) and (2) can be rewritten by adding ${m}^{^{\prime}}$ satellite observations as:

$$\varvec {E}\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{p}_{1} } \\ {\varvec{p}_{2} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\emptyset _{1} } \\ {\emptyset _{2} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{B}_{1} } \\ {\varvec{B}_{2} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\varvec{B}_{1} } \\ {\varvec{B}_{2} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \varvec{0} \\ \varvec{0} \\ \end{array} } \\ {\begin{array}{*{20}c} {\varvec{B}_{{1,\lambda }} } \\ \varvec{0} \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \varvec{0} \\ \varvec{0} \\ \end{array} } \\ {\begin{array}{*{20}c} \varvec{0} \\ {\varvec{B}_{{2,\lambda }} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} \varvec{b} \\ {\varvec{a}^{1} } \\ {\varvec{a}^{2} } \\ \end{array} } \right],\;\varvec{D}\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{p}_{1} } \\ {\varvec{p}_{2} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\emptyset _{1} } \\ {\emptyset _{2} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sigma _{p}^{2} \varvec{\tilde{Q}}_{1} } & \varvec{0} \\ \varvec{0} & {\sigma _{\emptyset }^{2} \varvec{\tilde{Q}}_{1} } \\ \end{array} } \right]$$

(8)

$$\varvec{\tilde{Q}}_{1} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{Q}_{1} } & {\varvec{Q}_{{12}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\varvec{Q}_{{21}} } & {\varvec{Q}_{2} } \\ \end{array} } \\ \end{array} } \right],\;\varvec{\tilde{P}}_{1} = \varvec{\tilde{Q}}_{1}^{{ - 1}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varvec{Q}_{1}^{{ - 1}} + \varvec{Q}_{1}^{{ - 1}} \varvec{Q}_{{12}} \varvec{P}_{2} \varvec{Q}_{{21}} \varvec{Q}_{1}^{{ - 1}} } \\ { - \varvec{P}_{2} \varvec{Q}_{{21}} \varvec{Q}_{1}^{{ - 1}} } \\ \end{array} } & {\begin{array}{*{20}c} { - \varvec{Q}_{1}^{{ - 1}} \varvec{Q}_{{12}} \varvec{P}_{2} } \\ {\varvec{P}_{2} } \\ \end{array} } \\ \end{array} } \right]$$

(9)

where ${\varvec{p}}_{*}$, $\emptyset_{*}$, $\varvec{B}_{*}$, $\varvec{B}_{{*,\lambda }}$, ${a}^{*}$, ${Q}_{*}$, and ‘*’ = 1, 2 (with 2 representing the added observations), are the same as the previous parameters in (1) and (2); $\varvec{Q}_{{12}} = \varvec{Q}_{{21}}^{T}$ refers to the covariance matrix, $\varvec{P}_{2} = (\varvec{Q}_{2} - \varvec{Q}_{{21}} \varvec{Q}_{1}^{{ - 1}} \varvec{Q}_{{12}} )^{{ - 1}}$, and $\varvec{B}_{{2,\lambda }} = \lambda \cdot \varvec{I}_{{n^{\prime} \times n^{\prime}}}$, in which ${n}^{^{\prime}}$ denotes the DD ambiguity dimension corresponding to the added observations. Here, $\varvec{\tilde{Q}}_{1}$, $\varvec{\tilde {P}}_{1}$, $\varvec{P}_{2}$, and $\varvec{ P}_{2}^{ - 1}$ are all symmetrical positive definite matrices (Horn and Johnson 1999). Using the standard least-squares method and the matrix inversion, the following equation can be obtained:

$$\left\{ {\begin{array}{*{20}c} {\varvec{\tilde{Q}}_{{\tilde{b}\tilde{b}}} ~ = ~\varvec{Q}_{{\hat{b}\hat{b}}} - \varvec{A}_{1} } \\ {\varvec{\tilde{Q}}_{{\tilde{a}^{1} \tilde{a}^{1} }} ~ = ~\varvec{Q}_{{\hat{a}^{1} \hat{a}^{1} }} - \varvec{A}_{2} } \\ \end{array} } \right.$$

(10)

where $\varvec{\tilde{Q}}_{{\tilde{b}\tilde{b}}}$ and $\varvec{\tilde{Q}}_{{\tilde{a}^{1} \tilde{a}^{1} }}$ are, respectively, the positive definite VC matrices of the float baseline vector $\varvec{\tilde{b}}$ and the float OAV $\varvec{\tilde{a}}^{{\text{1}}}$ after observations added; $\varvec{A}_{1} = \varvec{Q}_{{\hat{b}\hat{b}}} \varvec{A}_{3}^{T} \left( {\varvec{P}_{2}^{{ - 1}} + \varvec{A}_{3} \varvec{Q}_{{\hat{b}\hat{b}}} \varvec{A}_{3}^{T} } \right)^{{ - 1}} \varvec{A}_{3} \varvec{Q}_{{\hat{b}\hat{b}}}$, $\varvec{A}_{2} = \varvec{B}_{{1,\lambda }}^{{ - 1}} \varvec{B}_{1} \varvec{A}_{1} \varvec{B}_{1}^{T} \varvec{B}_{{1,\lambda }}^{{ - 1}}$, and $\varvec{A}_{3} = \frac{1}{{\sigma _{p} }}\left( {\varvec{Q}_{{21}} \varvec{Q}_{1}^{{ - 1}} \varvec{B}_{1} - \varvec{B}_{2} } \right)$, which is an n′ x 3 matrix. A₁ is either a positive semidefinite or a positive definite matrix and A₂ is a positive semidefinite matrix, the proofs of which are given in Appendix A. Equation (10) highlights that the change in the precision of the original float parameters is not due to the added phase observations, but the code observations. Hence, Eq. (10) and the above-given analysis provide the rigorous and intuitive theoretical proof and the basis for Conclusion (a): when the code observations are added, both the accuracy of $\varvec{\hat{b}}$ and the precision of $\varvec{\hat{a}}^{1}$ are improved. These results become more obvious with more observations added.

Effect of adding satellite observations on the ADOP of the OAV

Since the ADOP represents a scalar measure of ambiguity resolution SR, we analyze the relationship between the ADOP values of $\varvec{\hat{a}}^{1}$ (${\text{ADOP}}_{{\hat{a}^{1} \hat{a}^{1} }}$) and $\varvec{\tilde{a}}^{{1}}$ (${\text{ADOP}}_{{\tilde{a}^{1} \tilde{a}^{1} }}$). The increasing ambiguity precision decreases ADOP, i.e., ${\text{ADOP}}_{{\tilde{a}^{1} \tilde{a}^{1} }} \le {\text{ADOP}}_{{\hat{a}^{1} \hat{a}^{1} }}$ holds, but it lacks rigorous theoretical proof. Hence, this section provides a deeper theoretical investigation of the above result from the perspective of matrix analysis.

For the positive definite matrices $\varvec{Q}_{{\hat{a}^{1} \hat{a}^{1} }}$ and $\tilde{\varvec{Q}}_{{\tilde{a}^{1} \tilde{a}^{1} }}$, we assume that $\hat{\eta }_{i} > 0$ and $\tilde{\eta }_{i} > 0$ with, $i = 1,2, \ldots ,n$ are their eigenvalues sorted in ascending order, respectively. Based on (10), positive semi definiteness of A₂, and the Weyl Theorem (Lancaster and Tismenetsky 1985), the following expressions can be written:

$$\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\tilde{\eta }_{i} ~ \le ~\hat{\eta }_{i} ,~i = 1,2, \ldots ,n} \\ {\left| {\varvec{\tilde{Q}}_{{\tilde{a}^{1} \tilde{a}^{1} }} } \right| = \mathop \prod \limits_{{i = 1}}^{n} \tilde{\eta }_{i} \le \left| {\varvec{Q}_{{\hat{a}^{1} \hat{a}^{1} }} } \right| = \mathop \prod \limits_{{i = 1}}^{n} \hat{\eta }_{i} } \\ \end{array} } \\ {{\text{ADOP}}_{{\tilde{a}^{1} \tilde{a}^{1} }} = \left| {\varvec{\tilde{Q}}_{{\tilde{a}^{1} \tilde{a}^{1} }} } \right|^{{\frac{1}{{2n}}}} \le {\text{ADOP}}_{{\hat{a}^{1} \hat{a}^{1} }} = \left| {\varvec{Q}_{{\hat{a}^{1} \hat{a}^{1} }} } \right|^{{\frac{1}{{2n}}}} } \\ \end{array} } \right.$$

(11)

where the equal sign only holds when $\varvec{A}_{2} = 0$, which has a low probability. Hence, Eqs. (7), (10), and (11) provide a strict theoretical derivation and the basis for Conclusion (b): when the code observations are added, the $\varvec{\tilde{a}}^{{\text{1}}}$ with higher precision has a smaller ADOP and a larger ${P}_{\text{s,ADOP}}$ compared to $\varvec{\hat{a}}^{1}$. These results become more obvious with more code observations added.

Effect of adding satellite observations on the R-ratio test of the OAV

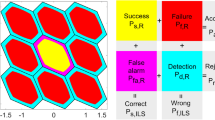
The improved precision of $\varvec{\hat{a}}^{1}$ means that $\varvec{\hat{a}}^{1}$ is closer to its nearest integer vector, where the closeness is tested by the relative distance defined by (4) (Teunissen and Verhagen 2009). Hence, adding code observations will make the R-ratio test result of the OAV different. The R-ratio test-based rates of acceptance (${P}_{{a,R}}$), success (${P}_{{s,R}}$), failure (${P}_{{f,R}}$), false alarm (${P}_{{fa,R}}$), and detection (${P}_{{d,R}}$) are equal to the integrals of the float ambiguity vector PDF over the corresponding pull-in regions shown in Fig. 1. Hence, this section studies the changing trends of the PDF, the ILS pull-in region, and the RTIA pull-in region of the OAV to assess the effect of added observations on the R-ratio test-based ambiguity validation. The normal PDFs of $\varvec{\hat{a}}^{1}$ and $\varvec{\tilde{a}}^{1}$ with mean $\varvec{a}^{{\text{1}}}$ can be expressed as (Verhagen and Teunissen 2006b):

$$\left\{ {\begin{array}{*{20}c} {f_{{\hat{a}^{1} }} \left( \varvec{x} \right) = \frac{1}{{\left( {2\pi } \right)^{{\frac{n}{{2}}}} {\text{ADOP}}_{{\hat{a}^{1} \hat{a}^{1} }}^{{n}} }}\exp ^{{\left\{ { - \frac{1}{2}\left( {\varvec{x} - \varvec{a}^{1} } \right)^{T} \varvec{Q}_{{\hat{a}^{1} \hat{a}^{1} }}^{{ - 1}} \left( {\varvec{x} - \varvec{a}^{1} } \right)} \right\}}} } \\ {f_{{\tilde{a}^{1} }} \left( \varvec{x} \right) = \frac{1}{{\left( {2\pi } \right)^{{\frac{n}{{2}}}} {\text{ADOP}}_{{\tilde{a}^{1} \tilde{a}^{1} }}^{{n}} }}\exp ^{{\left\{ { - \frac{1}{2}\left( {\varvec{x} - \varvec{a}^{1} } \right)^{T} \varvec{\tilde{Q}}_{{\tilde{a}^{1} \tilde{a}^{1} }}^{{ - 1}} \left( {\varvec{x} - \varvec{a}^{1} } \right)} \right\}}} } \\ \end{array} } \right.$$

(12)

Fig. 1

ILS and RTIA pull-in regions in the two-dimensional (2D) space (left) with meanings and relationships of the colored areas (right). The hexagons represent the ILS pull-in regions and colored areas denote the RTIA pull-in regions

We utilize $\varvec{a}^{{\text{1}}} {\text{ = }}\left[ {\begin{array}{*{20}c} {\text{0}} \\ {\text{0}} \\ \end{array} } \right]$ as well as the decorrelated VC matrices $\varvec{Q}_{{\hat{a}^{1} \hat{a}^{1} }} = \left[ {\begin{array}{*{20}c} {0.0865} & { - 0.0364} \\ { - 0.0364} & {0.0847} \\ \end{array} } \right]$ and ${\varvec{\tilde{Q}}}_{{\tilde{a}^{1} \tilde{a}^{1} }} = \left[ {\begin{array}{*{20}c} {0.0465} & { - 0.0160} \\ { - 0.0160} & {0.0447} \\ \end{array} } \right]$, in the following analyses.

When $\mu = 1.0$, the pull-in region of the RTIA is equal to that of the ILS; hence, $P_{{s,{\text{ILS}}}} = P_{s,R}$, ${P}_{{f,\text {ILS}}} { = P}_{{f,R}}$, and ${P}_{\text{fa},{R}} { = P}_{{d,R}} { = 0}$ hold, where ${P}_{{f, {\text {ILS}}}}$ denotes the ILS failure rate (Teunissen and Verhagen 2009). In this case, the changing trends of ${P}_{{s,R}}$ and ${P}_{{f,R}}$ can be assessed by analyzing ${P}_{{s, {\text {ILS}}}}$ and ${P}_{{f, {\text {ILS}}}}$. According to Fig. 2, the curve of ${f}_{{{\tilde{a}}^{{1}} }} \left( \varvec{x} \right)$ is steeper than that of ${f}_{{{\hat{a}}^{{1}} }} \left( \varvec{x} \right)$, which is consistent with Conclusions (a) and (b). Furthermore, ${P}_{{s, {\text {ILS}}}}$ and ${P}_{{f,{\text{ILS}}}}$ of $\varvec{\tilde{a}}^{{\text{1}}}$ is larger and smaller than the corresponding results of $\varvec{\hat{a}}^{{\text{1}}}$, respectively. Therefore, when $\mu = 1.0$, adding code observations can improve ${P}_{{s,R}}$, while reducing the ${P}_{{f,R}}$ of the OAV.

Fig. 2

Normal PDF and ILS pull-in regions of the 2D ambiguity vector (left), and the corresponding probability mass function (right). The blue parts represent the results of $\varvec{\hat{a}}^{{\text{1}}}$, and the green ones stand for $\varvec{\tilde{a}}^{{\text{1}}}$

As shown in Fig. 1, when $\mu > 1$, the pull-in region of the RTIA is smaller than that of the ILS. We next set $\mu$ to 2.0 (Teunissen and Verhagen 2009) and used the 2D float ambiguity vector $\varvec{\bar{a}}^{{\text{1}}}$ and its decorrelated VC matrix $\varvec{\tilde{Q}}_{{\bar{a}^{1} \bar{a}^{1} }} = \left[ {\begin{array}{*{20}c} {0.0337} & { - 0.0160} \\ { - 0.0160} & {0.0320} \\ \end{array} } \right]$ whose leading diagonal elements are further reduced compared to $\varvec{\tilde{Q}}_{{\tilde{a}^{1} \tilde{a}^{1} }}$. Based on the pull-in regions of $\varvec{\hat{a}}^{{\text{1}}}$, $\varvec{\tilde{a}}^{{\text{1}}}$, and $\varvec{\bar{a}}^{{\text{1}}}$ in Figs. 3 and 4, the pull-in regions of both RTIA and ILS vary with different VC matrices. However, the change in the shape of the ILS pull-in region is consistent with that of the RTIA. Besides, their RTIA pull-in regions have similar shapes and area sizes, which also holds for the ILS pull-in regions. The area sizes of the successful RTIA pull-in region of $\varvec{\hat{a}}^{{\text{1}}}$, $\varvec{\tilde{a}}^{{\text{1}}}$, and $\varvec{\bar{a}}^{{\text{1}}}$ are 0.664, 0.661, and 0.665, respectively. Thus, considering the unit area of the ILS pull-in region, the magenta regions in Fig. 3 are also similar in size. Observing the PDF projection on the pull-in regions in Fig. 5, two conclusions can be made: (i) the shape of the PDF changes with different VC matrices, but it is consistent with the pull-in regions of RTIA and ILS; (ii) the higher the float ambiguity vector precision is, the steeper the PDF curve inside the successful RTIA pull-in region will be. However, it acts adversely outside the successful RTIA pull-in region. With the improved precision of the float ambiguity vector, ${P}_{{s,R}}$ increases while ${P}_{{f,R}}$, ${P}_{{fa,R}}$, and ${P}_{{d,R}}$ decrease. This also refers to that ${P}_{{a,R}}$ increases based on Fig. 1. As a result, Conclusion (c) can be drawn: adding code observations can improve ${P}_{{a,R}}$ and SR (${P}_{{s}\text{,ILS}}$ and ${P}_{{s,R}}$) of the OAV and reduce its ${P}_{{f,R}}$, ${P}_{{fa,R}}$, and ${P}_{{d,R}}$.

Fig. 3

Successful RTIA and ILS pull-in regions of the 2D ambiguity vectors $\varvec{\hat{a}}^{{\text{1}}}$ (left), $\varvec{\tilde{a}}^{{\text{1}}}$ (middle), and $\varvec{\bar{a}}^{{\text{1}}}$ (right) for $\mu = 2$

Fig. 4

Overlapping successful ILS and IA pull-in regions of $\varvec{\hat{a}}^{{\text{1}}}$ (blue), $\varvec{\tilde{a}}^{{\text{1}}}$ (green), and $\varvec{\bar{a}}^{{\text{1}}}$ (brown) for $\mu = 2$

Fig. 5

PDF projections of the normal distribution of the 2D ambiguity vectors $\varvec{\hat{a}}^{{\text{1}}}$ (left), $\varvec{\tilde{a}}^{{\text{1}}}$ (middle), and $\varvec{\bar{a}}^{{\text{1}}}$ (right) on the pull-in regions of RTIA and ILS for $\mu = 2$

Both satellite selection and SF-SS belong to the algorithm with no added satellite observations, while PAR refers to the algorithm positioning by the OAV after adding satellite observations. Conclusions (a)–(c) denote that the multi-GNSS can improve the partial ambiguity estimation and its R-ratio test-based validation in terms of precision, SR, and fixed reliability of the float ambiguity vector. Besides, the multi-GNSS-based PAR is optimal compared to satellite selection and SF-SS.

Single-epoch positioning experiments

The single-epoch positioning experiments were conducted to verify the Conclusions (a)–(c) in terms of positioning performance and fixed reliability of the OAV. A Leica GR25 receiver collected the 24-h BDS/GPS data of a 5-km baseline from the Hong Kong Base Station with a sampling interval of 1 s. It should be noted that the positioning was based on epoch-by-epoch processing without any relationship between epochs. The baseline vector obtained using the precise coordinates of the Hong Kong Base Station was accepted as the ground truth, and the baseline vector error maps were obtained by subtracting the corresponding true values from the calculated baseline vectors. The empirical SR (${P}_{{s,E}}$) was calculated as (Odolinski and Teunissen 2016):

$$P_{s,E} \; = \text {Number}\; \text {of}\; \text {successfully}\; \text {fixed} \;\text {epochs} \, / \;\text {Total} \;\text {number} \;\text {of}\; \text {epochs}$$

(13)

The successfully fixed epochs met the following criteria: (i) the fixed ambiguity vector estimated was the same as the reference determined by the multiple-frequency multi-GNSS with master and rover stations of known coordinates; (ii) the baseline vector deviations were all within certain ranges in the directions of East (E), North (N), and Up (U), the values of which were 10, 10, and 20 cm, respectively. The value for U direction was largely due to the poor positioning accuracy alongside it.

In our analyses, the phase- and code-standard deviations of BDS B1 and B2 were used as ${\upsigma }_{\emptyset }^{{{B1}}} { = 0}{\text{.28 cm}}$, ${\upsigma }_{{\text{p}}}^{{{B1}}} { = 33}{\text{.0 cm}}$, ${\upsigma }_{\emptyset }^{{{B2}}} { = 0}{\text{.31 cm}}$, and ${\upsigma }_{{p}}^{{{B2}}} { = 25}{\text{.0 cm}}$, respectively. For GPS L1 and L2, these deviations were ${\upsigma }_{\emptyset }^{{{L1}}} { = 0}{\text{.315 cm}}$, ${\upsigma }_{{p}}^{{{L1}}} { = 30}{\text{.0 cm}}$, ${\upsigma }_{\emptyset }^{{{L2}}} { = 0}{\text{.351 cm}}$, and ${\upsigma }_{{p}}^{{{L2}}} { = 27}{\text{.0 cm}}$. These values were calculated with the method proposed by Odolinski et al. (2013), using the data that were independent of those used in the following experiments.

GPS L1-based positioning experiments

The GPS L1-based positioning experiments include: i) the positioning performance evaluation on the positioning accuracy, ADOP, and fixed SR; ii) the R-ratio test-based fixed reliability evaluation of ambiguities. The positioning models utilized the single-frequency (L1), dual-frequency (L1/L2), dual-frequency dual-system (L1/L2/B1/B2), and L1-based PAR (L1–L1/L2, L1–L1/L2/B1/B2) models with a cutoff elevation angle of $10^\circ$. For the float ambiguity vector calculated by multiple frequencies using (8) and (9), only the ambiguity vector corresponding to L1 was used for positioning, which was called the L1-based PAR.

GPS L1-based positioning performance

The GPS L1-based positioning performance results are provided in Table 1 and Figs. 6–8, in which SR refers to P_s,E. As shown in Table 1 and Fig. 7, the ADOP values of L1, L1–L1/L2, and L1–L1/L2/B1/B2 decreased in turn, while P_s,E, ${P}_{{s, {\text {IB}}}}$, and float positioning accuracy of models increased one by one. Hence, according to Fig. 6, the float ambiguity vector precision, float positioning accuracy, and P_s,E of L1 were improved when satellite observations were added. These improvements become larger with more observations added. The maximum reduction in ADOP of L1 was about 0.1, and the maximum improvements in P_s,E and float positioning accuracy were about 32.9% and 0.5 m, respectively. However, the ADOP and P_s,E could only reach the values of 0.229 and 78.15%.

Table 1 Positioning results of different GPS L1 models

Fig. 6

Number of satellites of different models

Fig. 7

ADOP (left) and P_s,IB (right) of different models

According to Table 1 and the left panel of Fig. 7, although the ADOP and P_s,E of L1 were improved with more observations added, they were still lower than those of L1/L2 and L1/L2/B1/B2. Meanwhile, the ADOP and P_s,E of L1/L2/B1/B2 were better than those of L1/L2. Hence, the high-dimension ambiguity vector in this section had higher precision, larger P_s,E, and smaller ADOP compared to the corresponding low-dimension ambiguity vector.

Figure 8 reveals that L1 and L1-based PAR models had similar fixed baseline vector accuracies, which made their fixed positioning accuracies also similar, as shown in Table 1. In specific, the fixed positioning accuracy of both was close to that of L1/L2 but 0.6 cm lower than that of L1/L2/B1/B2. This difference was occurred due to the larger volume of L1/L2/B1/B2, compared to that of L1, composed of the receiver and observed satellites.

Fig. 8

ENU deviations of L1 (left), L1–L1/L2 (middle), and L1–L1/L2/B1/B2 (right)

As a result, in terms of ADOP, P_s,E, float ambiguity vector precision, and float positioning accuracy of single-epoch positioning, the L1-based PAR outperformed the L1 model with satellite observations added, which was consistent with Conclusions (a) and (b).

R-ratio test-based ambiguity validation of the GPS L1

For the analyses in this section, we set $\mu$ to 1.5, 2.0, 2.5, and 3.0, respectively (Verhagen and Teunissen 2013). Table 2 provides the obtained statistical results, and Fig. 9 shows the ratio, the best quadratic form (BQF), and the second-best quadratic form (SQF). According to Fig. 1, P_a,R, P_f,R, and P_d,R are defined as the number of epochs falling into the corresponding color regions divided by 86,400, for the given $\mu$. Here, P_fa,R is defined as the number of epochs falling into the magenta region divided by the number of successfully fixed epochs defined in (13). The successfully fixed rate P_sf,R is defined as the ratio of the number of epochs falling into the yellow region to the number of accepted epochs (Teunissen and Verhagen 2009). For this section, SR refers to ${P}_{{s,R}}$, which is equal to P_sf,R·P_a,R.

Table 2 R-ratio test results of different GPS L1-based models

Fig. 9

Ratio (left), BQF (middle), and SQF (right) of L1, L1–L1/L2, and L1–L1/L2/B1/B2

The results in Fig. 9 illustrate that the time-series ratio values of L1, L1–L1/L2, and L1–L1/L2/B1/B2 had an increasing tendency, which was mainly due to the SQF. That means the float ambiguity vector of L1 became closer to its nearest integer solution with the added observations, which made the R-ratio test result different. According to Table 2, with a certain $\mu$, both P_a,R and ${P}_{{sf,R}}$ values of L1, L1–L1/L2, and L1–L1/L2/B1/B2 increased, while their ${P}_{{d,R}}$, ${P}_{{f,R}}$, and ${P}_{{fa,R}}$ decreased. Hence, adding observations can improve P_a,R and ${P}_{{sf,R}}$ of L1 and reduce its ${P}_{{d,R}}$, ${P}_{{f,R}}$, and ${P}_{{fa,R}}$. The maximum improvements in P_a,R and ${P}_{{sf,R}}$ of L1 were about 27.2% and 22.2%, respectively, while its P_a,R could be only up to 64.9%. The maximum reductions in ${P}_{{d,R}}$, ${P}_{{f,R}}$, and ${P}_{{fa,R}}$ were about 32.6%, 6.2%, and 22.2%, respectively.

According to Fig. 1, the improvement in P_a,R and the reduction in ${P}_{{f,R}}$ indicated the increase in ${P}_{{s,R}}$. Based on the relation of P_s,R = P_a,R·P_sf,R, the maximum improvement in ${P}_{{s,R}}$ of L1 was about 32.8%, and its ${P}_{{s,R}}$ was up to 59.33%. For $\mu = 1.0$, ${P}_{{s,E}}$ in Table 1 can be considered as ${P}_{{s,R}}$. The improvement in ${P}_{{s,E}}$ and the reduction in ${P}_{{fa,R}}$ of L1 denote that adding observations made the more float ambiguity vectors of L1 fall into the successful region in Fig. 1, and closer to their correct integer solutions increased.

To summarize, when the satellite observations were added, the L1-based PAR outperformed the L1 model in terms of R-ratio test-based fixed reliability of single-epoch positioning, which was consistent with Conclusion (c).

BDS B1-based positioning experiments

Similar to GPS, the BDS B1-based positioning experiments also have two parts and the positioning models utilize the B1, B1/B2, B1/B2/L1/L2, and B1-based PAR (B1–B1/B2, B1–B1/B2/L1/L2) models.

BDS B1-based positioning performance

In this section, SR refers to ${P}_{{s,E}}$. According to the results of ADOP, ${P}_{{s,E}}$, $P_{{s,{\text{IB}}}}$, float and fixed positioning accuracies of B1 provided in Table 3 and Figs. 11–12, the relationships between B1, B1–B1/B2, and B1–B1/B2/L1/L2 were the same as those of GPS L1 models provided in the previous section. Hence, based on Fig. 10, the conclusion of L1 drawn in the previous section was still valid for B1 in the above aspects. However, there were some discrepancies. For example, when B2/L1/L2 observations were added, the maximum reduction in the ADOP of B1 was 0.03. Furthermore, the maximum improvements in ${P}_{{s,E}}$ and float positioning accuracy were 0.48% and 0.58 m, respectively. However, its ADOP and ${P}_{{s,E}}$ could reach the values of 0.108 and 99.99%.

Table 3 Positioning results of different BDS B1 models

Fig. 10

Number of satellites of different models

Although the above improvements were lower than the corresponding results of the GPS L1, ADOP values of different B1 models were all smaller than 0.14, much smaller than those of L1-based models. Furthermore, ${P}_{{s,E}}$ values were all higher than 99.5%. Hence, they were close to those of B1/B2 and L1/L2/B1/B2, but much larger than those of L1-based models.

The average ADOP of L1/L2/B1/B2 given in Table 1 was smaller than that of B1/B2 in Table 3. However, as shown in the left panel of Fig. 11, the ADOP values of L1/L2/B1/B2 were larger than those of B1/B2 at a low number of epochs. The main reasons for this result are as follows. Adding L1/L2 to B1/B2 made f₁ larger, slowed down the decrease in ${1}/{{n}}$, and rapidly increased $\left( {\mathop \sum \limits_{s = 1}^{m} w_{s} } \right)/\left( {\mathop \prod \limits_{s = 1}^{m} w_{s} } \right)$, which made the increase in $f_{1} \cdot f_{2}$ larger than the decrease in f₃based on (6). Therefore, in some cases, the precision of the low-dimension ambiguity vector is higher than that of the high-dimension ambiguity vector.

Fig. 11

ADOP (left) and P_s,IB (right) of different models

Fig. 12

ENU deviations of B1 (left), B1–B1/B2 (middle), and B1–B1/B2/L1/L2 (right)

As can be seen in Tables 1 and 3, the fixed positioning accuracies of L1/L2/B1/B2, B1/B2, and B1 were improved. These were related not only to the volume composed of the receiver and the observed satellites but also to the phase-standard deviation. The average phase-standard deviations were 0.31, 0.29, and 0.27 cm, which can be named as the main reason for the above-given result.

Hence, same as the previous GPS experiments, the B1-based PAR outperformed the B1 model in terms of ADOP, ${P}_{{s,E}}$, float ambiguity vector precision, and float positioning accuracy of single-epoch positioning.

R-ratio test-based ambiguity validation of the BDS B1

In this section, we used the same values for $\mu$ as in the GPS experiment, and here, SR refers to ${P}_{{s,R}}$. Table 4 and Fig. 13 show that the changing trends in the ratio values, BQF, SQF, and R-ratio test-based rates between B1, B1–B1/B2, and B1–B1/B2/L1/L2 were similar to those of different GPS L1 models. Hence, the same conclusions of GPS L1 were obtained for BDS B1, but with certain changes. When observations were added, the maximum improvement in ${P}_{{a,R}}$ of B1 was about 11.0% and its maximum reductions in ${P}_{{d,R}}$ and ${P}_{{fa,R}}$ were 0.47% and 10.61%, respectively.

Table 4 R-ratio test results of different BDS B1-based models

Fig. 13

Ratio (left), BQF (middle), and SQF (right) of B1, B1–B1/B2, and B1–B1/B2/L1/L2

Although the above improvements were smaller than those of L1, the R-ratio test-based rates of different B1 models outperformed the L1 models. In specific, their ${P}_{{a,R}}$ and ${P}_{{sf,R}}$ values were larger than 83.5% and 99.95%, and were up to 99.64% and 100.0%, respectively. ${P}_{{d,R}}$, ${P}_{{f,R}}$, and ${P}_{{fa,R}}$ values were smaller than 0.5%, 0.06%, and 16.1%, and could be reduced to 0.02%, 0.0%, and 0.34%, respectively. Based on the relation of $P_{s,R} = P_{a,R} \cdot P_{sf,R}$ and the results presented in Table 4, the same conclusion of B1 ${P}_{{a,R}}$ could be obtained for ${P}_{{s,R}}$.

Therefore, same as the previous GPS experiments, the B1-based PAR could achieve better results than the B1 model in terms of R-ratio test-based fixed reliability of single-epoch positioning.

Finally, considering the above-given results, both BDS B1 and B1-based PAR outperform the GPS L1 and L1-based PAR models in terms of ${P}_{{s,E}}$, ADOP, and the R-ratio test-based fixed reliability of ambiguities.

Conclusions

Although the multi-GNSS can improve SR and the reliability of single-epoch positioning, its positioning time rapidly increases with the increasing number of visible satellites. The SF-SS, satellite selection, and PAR can all provide fast positioning, but the variety in theories that they are based on makes their ambiguity estimation and validation different. However, there has been no proper investigation of this theory yet, which motivates this research to provide the necessary theoretical analyses. With satellite observations added, the VC matrix variation formulas of the float parameters are derived. The relationship between the ADOP values of the OAV before and after the added observations is obtained. The changing trends in the R-ratio test-based fixed reliability of the OAV are analyzed. The results of precision, fixed SR, and fixed reliability of float OAV indicate that the multi-GNSS can improve the partial ambiguity estimation and validation. Furthermore, compared to satellite selection and SF-SS, the multi-GNSS-based PAR is optimal. The GPS and BDS-based single-epoch positioning results of PAR, SF-SS, and dual-frequency single- or multi-GNSS show the following:

(a) Compared to SF-SS, the multi-GNSS can improve the float positioning accuracy, float ambiguity vector precision, and ${P}_{{s,E}}$ of the L1- or B1-based PAR and reduce ADOP. It can also improve the R-ratio test-based fixed reliability of the ambiguities of the PAR. In other terms, the multi-GNSS can improve the acceptance and success rates of the PAR and reduce the failure, false alarm, and detection rates. These changes become more obvious when more satellite observations are added.

(b) From ${P}_{{s,E}}$, ADOP, and R-ratio test-based fixed reliability of ambiguities, both BDS B1 and B1-based PAR perform much better than the GPS L1 and L1-based PAR models. In specific, ${P}_{{s,E}}$ of the former is larger than 99.5%, its ADOP is smaller than 0.14, the acceptance and success rates are up to 99.64%, and the false alarm, failure, and detection rates are reduced to 0.34%, 0.0%, and 0.02%, respectively.

In the future, the GPS, BDS, GLONASS, and Galileo will provide much more visible satellites, which will further improve the positioning performance of the PAR. Considering that, in our next study, we will investigate how to quickly determine the optimal ambiguity subset of PAR to achieve instantaneous and high-precision positioning with high SR.

Appendix A: The proof of positive definiteness of matrices A 1 and A 2 in (10)

For the symmetrical positive definite matrix ${\varvec Q}_{{{{\hat{b}\hat{b}}}}}$, there is a 3-order real invertible matrix ${\varvec S}_{{\text{1}}}$ making $\varvec{Q}_{{\hat{b} \hat{b}}} = \varvec{S}_{1}^{ {T}} \cdot \varvec{S}_{1}$ (Horn and Johnson 1999). Hence, considering the positive definite matrix ${\varvec P}_{{\text{2}}}^{{{\text{ - 1}}}}$, $\forall {\varvec{x}} \ne {\bf{0}}$, it holds that $\varvec{x}^{T} \left( {\varvec{P}_{2}^{{ - 1}} + \varvec{A}_{3} \varvec{Q}_{{\hat{b}\hat{b}}} \varvec{A}_{3}^{T} } \right)\varvec{x}\, > \;0$. Thus, $\varvec{P}_{2}^{{ - 1}} \; + \;\varvec{A}_{3} \varvec{Q}_{{\hat{b}\hat{b}}} \varvec{A}_{3}^{T}$ is a symmetrical positive definite matrix. Similarly, there is a real invertible matrix S₂ making $\left( {\varvec{P}_{2}^{{ - 1}} + \varvec{A}_{3} \varvec{Q}_{{\hat{b}\hat{b}}} \varvec{A}_{3}^{T} } \right)^{{ - 1}} = \varvec{S}_{2}^{T} \cdot \varvec{S}_{2}$ and $\varvec{A}_{1} = \left( {\varvec{S}_{2} \varvec{A}_{3} \varvec{Q}_{{\hat{b}\hat{b}}} } \right)^{T} \cdot \varvec{S}_{2} \varvec{A}_{3} \varvec{Q}_{{\hat{b}\hat{b}}}$, and it holds that rank$\left( {\varvec{S}_{2} \varvec{A}_{3} \varvec{Q}_{{\hat{b}\hat{b}}} } \right)$ = rank (A₃) and rank (A₃)≤ 3. When rank (A₃) = 3, A₁ is a positive definite matrix, and for rank (A₃) < 3, A₁ is a positive semidefinite matrix.

Hence, there is a 3-order real matrix S₃ making $\varvec{A}_{1} = \varvec{S}_{3}^{T} \cdot \varvec{S}_{3}$ and $\varvec{A}_{2} = \left( {\varvec{S}_{3} \varvec{B}_{1}^{T} \varvec{B}_{{1,\;\lambda }}^{{ - 1}} } \right)^{T} \cdot \varvec{S}_{3} \varvec{B}_{1}^{T} \varvec{B}_{{1,\;\lambda }}^{{ - 1}}$. For the 3 x n-order matrix ${\varvec{S}}_{3} {\varvec{B}}_{1}^{T} {\varvec{B}}_{{1,\;\lambda }}^{{ - 1}}$, it holds that rank $\left( {\varvec{S}_{3} \varvec{B}_{1}^{T} \varvec{B}_{{1,\;\lambda }}^{{ - 1}} } \right) \le \min ~\left\{ {rank\left( {\varvec{S}_{3} } \right),\;rank\left( {\varvec{B}_{1}^{T} } \right)} \right\} < n$. Therefore, A₂ is a positive semidefinite matrix.

End of Proof.