Biaxial mechanical properties of swine uterosacral and cardinal ligaments

Abstract

Mechanical alterations to pelvic floor ligaments may contribute to the development and progression of pelvic floor disorders. In this study, the first biaxial elastic and viscoelastic properties were determined for uterosacral ligament (USL) and cardinal ligament (CL) complexes harvested from adult female swine. Biaxial stress–stretch data revealed that the ligaments undergo large strains. They are orthotropic, being typically stiffer along their main physiological loading direction (i.e., normal to the upper vaginal wall). Biaxial stress relaxation data showed that the ligaments relax equally in both loading directions and more when they are less stretched. In order to describe the experimental findings, a three-dimensional constitutive law based on the Pipkin–Rogers integral series was formulated. The model accounts for incompressibility, large deformations, nonlinear elasticity, orthotropy, and stretch-dependent stress relaxation. This combined theoretical and experimental study provides new knowledge about the mechanical properties of USLs and CLs that could lead to the development of new preventive and treatment methods for pelvic floor disorders.

1 Introduction

The number of American women with pelvic floor disorders, including fecal incontinence, urinary incontinence, and pelvic organ prolapse, are projected to increase from 28.1 million in 2010 to 43.8 million in 2050 (Wu et al. 2009). Epidemiological studies have suggested that, for pelvic organ prolapse alone, approximately 11 % of women will undergo surgery in their lifetime and that around 30 % of these women will require additional procedures due to recurrence (Olsen et al. 1997). Although the etiology of pelvic floor disorders is not completely understood, mechanical alterations to pelvic floor ligaments appear to contribute to their development and progression (Nygaard et al. 2008). In particular, pelvic floor disorders may result from damage to the cardinal ligament (CL) and uterosacral ligament (USL) (DeLancey 1992; Miklos et al. 2002). The CL and USL are visceral ligaments that connect the upper vagina/cervix to the pelvic sidewall. They form a thin, membrane-like complex that is composed of smooth muscle, blood vessels, nerve fibers, collagen, and elastin. The relative amount of these components and their organization remain unknown (Ramanah et al. 2012). These visceral ligaments can provide support to the pelvic organs while also accommodating highly mobile organs such as the uterus, owing to their structure and composition (Ramanah et al. 2012). The loading experienced by these ligamentous membranes is likely biaxial in vivo, with larger forces occurring along the axis normal to the upper vagina/cervix.

To date, there are no experimental studies on the mechanical properties of the CL, and only a few have described the uniaxial mechanical properties of the USL (Vardy et al. 2005; Shahryarinejad et al. 2010; Martins et al. 2013). The viscoelastic behavior of the USL has been characterized in the cynomolgus monkey (Macaca fascicularis) via incremental relaxation tests (Vardy et al. 2005; Shahryarinejad et al. 2010). In these studies, the effect of strain history on the stress relaxation behavior of the USL has been overlooked. During incremental relaxation tests, the specimens are subjected to constant strains that incrementally increase or decrease over time. Both the ascending and descending order in which the strains are applied and the recovery time between relaxation tests are likely to affect the viscoelastic properties of these tissues and thus must be taken into account (van Dommelen et al. 2006). Moreover, the possible dependency of the rate of stress relaxation on strain, as reported for other soft tissues (Provenzano et al. 2001; Hingorani et al. 2004; Davis and De Vita 2012), has not been investigated for the USL (and CL).

Tensile properties, such as elastic modulus and ultimate tensile strength, of the USL in female cadavers have been quantified only recently (Martins et al. 2013). Despite the limitations in the strain measurement (i.e, use of grip-to-grip displacement and engineering strain), the experimental study by Martins et al. (2013) confirms the earlier findings by Vardy et al. (2005) showing that the USL undergoes large deformations. However, the mechanical properties of the CL and USL should be determined by using a planar biaxial testing system together with accurate strain measurement techniques, as done for other soft tissues (Harris et al. 2003; Wells et al. 2005; Grashow et al. 2006; Nagatomi et al. 2008; Zou and Zhang 2011), in order to better emulate their complex in vivo loading conditions.

To the authors’ knowledge, no attempt has been made to model the constitutive behavior of the CL and USL. Constitutive laws for these ligaments must not only capture their viscoelastic behavior but also the more physiologically relevant biaxial loading conditions. The quasi-linear viscoelastic (QLV) theory proposed by Fung (1993) has been widely used in biomechanics. It has also been extended to describe the biaxial stress relaxation of several biological tissues such as, for example, the epicardium (Baek et al. 2005) and the aortic elastin (Zou and Zhang 2011). However, the QLV theory is based on the assumption that the rate of stress relaxation (or rate of creep) is independent of strain (or stress). As already pointed out, the extent to which such assumption is plausible for the CL and USL remains unknown.

Constitutive theories such as nonlinear superposition (Findley et al. 1976) and Schapery theory (Schapery 1969) have been successfully employed to describe the one-dimensional dependency of the stress relaxation rate (or creep rate) on strain (or stress) in articular ligaments and tendons (Provenzano et al. 2002; Hingorani et al. 2004; Duenwald et al. 2009, 2010). QLV generalizations have been also presented to capture such dependency in collagen (Pryse et al. 2003; Nekouzadeh et al. 2007). More recently, Rajagopal and Wineman (2009) have proposed the use of the Pipkin–Rogers theory for transversely isotropic and orthotropic nonlinear viscoelastic materials. Following their approach, Davis and De Vita (2014) have presented a three-dimensional constitutive equation for articular ligaments. This constitutive law has been validated by considering different boundary value problems with published experimental data. In this study, the first planar biaxial stress–stretch and stress relaxation data of swine CLs and USLs are presented. Nonlinearities and material symmetry of the elastic and viscoelastic response of these ligaments are investigated. Based on the findings of the biaxial tests, a new three-dimensional constitutive model is formulated within the theoretical framework set forth by Pipkin and Rogers (1968).

2 Methods

2.1 Specimen preparation

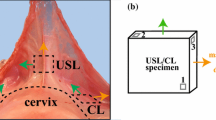
All animal protocols were approved by the Institutional Animal Care and Use Committee (IACUC) at Virginia Polytechnic Institute and State University. Four adult female, domestic swine (Sus scrofa domesticus) that were obtained from a slaughterhouse were used for this study. No information about the health history, parity, and litter’s size of the swine was available. However, the swine were 3–4 years old and had a weight of $\sim$450 lb. The swine was selected as animal model since the CL and USL in the swine are histologically similar to those in humans (Gruber et al. 2011). The CL and USL were carefully cleaned of extraneous fat and muscle tissue, cut into approximately $3 \times 3\,\hbox {cm}^{2}$ as shown in Fig. 1a. The specimens were then hydrated in phosphate-buffered saline (PBS, 0.5 M, pH 7.4) and frozen at $-20\,^{\circ }\hbox {C}$ for 1–4 months. Previous research has shown that the proper freezing of similar soft tissues has little effect on their mechanical properties (Rubod et al. 2007). Then, prior to testing, the specimens were thawed at room temperature (20–25$\,^{\circ }\hbox {C})$. The length and width of each specimen were determined optically by analyzing pictures taken with a CMOS camera (DCC1645C, Thor Labs). The thickness of each specimen was calculated by averaging four thickness measurements made with calipers containing a force gauge (accuracy $\pm$0.05 mm, Mitutoyo Absolute Low Force Calipers Series 573, Japan) by applying a 50-g compressive load. Such thickness ($\hbox {mean}\pm \hbox {SD}$) was found to be $0.26\pm 0.07\hbox { mm}$.

Fig. 1

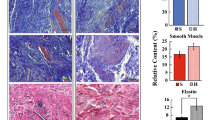
a Specimen position and orientation within the swine USL/CL complex. The black dots denote the location of the poppy seeds that were attached to the specimen surface. Note that $\mathbf{E}_1$ and $\mathbf{E}_2$ are orthogonal unit vectors in the undeformed configuration and $\mathbf{E}_1$ is perpendicular to the upper vaginal (or cervical) wall. b Bath of the planar biaxial testing system with load cells, actuator arms, and specimen. c Histology of a planar section of the swine USL in Masson Trichrome (blue collagen, red muscle and cytoplasm). d Scanning electron microscopy of a cross section of the swine USL showing the collagen fiber orientation

2.2 Biaxial testing and strain measurement

Four bent safety pins connected to fishing line (4 lb Extra Tough Trilene, Berkley Fishing Company, USA) were inserted into each side of each specimen. The specimens were then mounted into a planar biaxial tensile testing device (Instron, Norwood, MA, USA), partially shown in Fig. 1b, by wrapping the fishing line around four custom grips. These grips consisted of two pulleys and a bearing of negligible friction that could rotate to ensure that the tension in each of the four lines, each attached to one side of the specimen, was equal. During testing, the specimens were submerged in a bath containing PBS at $37\,^{\circ }\hbox {C}$. Load was recorded with four 20-N load cells (accuracy of at least $0.25\,\%$) simultaneously during mechanical testing. The load along each axis was taken as the average of the loads recorded by the two load cells located along such axis. Nominal stress was calculated by dividing the average load measured along each axis by the undeformed cross-sectional area of the sample that was perpendicular to such axis. Normalized stress at any time was obtained by dividing the stress at such time by its initial value during a relaxation test.

Prior to testing, four poppy seeds were glued to the surface of the ligaments to produce suitable contrast for non-contact strain measurements (Fig. 1a). Images were captured with a CMOS camera (DCC1645C, Thor Labs) and a 25-mm fixed focal length lens (25 mm compact fixed focal length lens, TECHSPEC, Edmund Optics Inc., USA). The displacements of the poppy seeds were tracked with ProAnalyst Software (Xcitex Inc. Woburn, MA, USA). The displacement gradient, $\nabla _\mathbf{X}{\mathbf{u}}$ where $\mathbf{u}$ is the displacement vector and $\mathbf{X}$ is the position vector of the undeformed configuration, was estimated using an interpolation method implemented in Matlab (MATLAB version 7.10.0, Natick, MA: The MathWorks Inc., 2010). This method was originally introduced by Humphrey (Humphrey et al. 1987) and later used by other researchers (Sacks 2000). From the displacement gradient, the deformation gradient tensor, F, and the right Cauchy–Green deformation tensor, C, were calculated as follows:

$$\begin{aligned} \mathbf{F}&= \nabla _\mathbf{X}{\mathbf{u}}+\mathbf{I},\end{aligned}$$

(1)

$$\begin{aligned} {\mathbf{C}}&= {\mathbf{F}}^{\text{ T }}{\mathbf{F}}, \end{aligned}$$

(2)

where $\mathbf{I}$ is the identity tensor. Note that ${\mathbf{F}}$ was assumed to be a plane deformation as discussed in detail by Humphrey (2002, pp. 171–177).

2.3 Test protocol

The biaxial tests were performed in displacement control mode. The displacements of the four actuators of the biaxial tensile testing device were set to be equal along the two loading axes for each test. However, the optically measured stretches of the specimens along such axes could not be controlled to be equal during testing. For this reason, equi-biaxial extension was not truly achieved.

A schematic of the testing protocol that was simultaneously used along the two loading axes is presented in Fig. 2. All specimens ($n=22$ from four different sows) were preloaded to 0.04 N and then preconditioned by loading them from 0.1 to 0.6 N for 10 cycles at a displacement rate of 0.1 mm/s. This displacement rate was selected to ensure quasi-static loading conditions of the specimens. Similar displacement rates have been employed by others for biaxial relaxation tests on soft tissues (Baek et al. 2005). Following preconditioning, each specimen was unloaded to 0.04 N and then loaded with the same displacement rate (0.1 mm/s).

Fig. 2

Testing protocol used simultaneously along each loading direction ($\mathbf{E}_1$ and $\mathbf{E}_2$) during biaxial tests. Note that the displacement was controlled and was set to be equal along the two loading directions

Each specimen was stretched until the load along one of the two loading axes reached a preset value between 2 and 12 N. More specifically, $n=9$ specimens were stretched up to a load between 2 and 4.9 N, $n=7$ specimens were stretched up to a load between 5 and 7.9 N, and $n=6$ specimens were stretched up to a load between 8 and 12 N. These loads are comparable to the tensile loads that were safely used in a recent in vivo mechanical study by Luo et al. (2014). By loading the specimens up to a range of loads from 2 to 12 N, a range of corresponding stretches of the specimens were obtained. The specimens were then held at these constant stretches for 50 min and allowed to relax while the load and time data were recorded.

The stress–stretch data that were collected during the ramp displacement portion of this protocol were used to determine the elastic properties of the specimens (Fig. 2). The stress–time data that were collected when the specimens were subjected to constant stretches were employed to determine the stress relaxation properties and dependence of the stress relaxation rate on stretch.

Single stress relaxation tests were conducted on 15 of the 22 specimens. These specimens were held at a single constant stretch, and the load was observed to decrease over 50 min. Three consecutive relaxation tests were performed on 7 of the 22 specimens (Fig. 2). For these specimens, a first relaxation test was performed as described above. This test was then followed by two additional relaxation tests. More specifically, for $n=4$ specimens, three constant displacements in an ascending order were applied (e.g., displacement value at 3-N load, displacement value at 6-N load, displacement value at 9-N load), and for $n=3$ specimens three constant displacements in a descending order were applied (e.g., displacement at 9-N load, displacement at 6-N load, displacement at 3-N load).

The resting time between consecutive relaxation tests at an ascending order of applied displacements was varied to be 0 h ($n=2$ specimens), 1 h ($n=1$ specimen), 12 h ($n=1$ specimen). Similarly, for relaxation tests with a descending order of applied displacements, this time was varied to be 0 h ($n=1$ specimen), 1 h ($n=1$ specimen), 12 h ($n=1$ specimen). The order in which the constant displacements were applied and the resting time during three consecutive relaxation tests were varied to investigate their effects on the stress relaxation response of the CL and USL.

3 Theoretical formulation

The CL and USL are assumed to be incompressible orthotropic materials. The incompressibility assumption is justified by the high water content, while the assumption on the material symmetry is due to the presence of fibrous components (collagen and nerve fibers) in the ligaments (Gruber et al. 2011).

3.1 Constitutive model

The integral series formulation introduced by Pipkin and Rogers (1968) is employed to model the three-dimensional stress relaxation behavior of CLs and USLs. Only the first term of the integral series is used, resulting in a first Piola–Kirchhoff stress tensor, $\mathbf{P}(\hbox {t})$, of the form (Rajagopal and Wineman 2009):

$$\begin{aligned} \mathbf{P}(t)&= -p(t)\mathbf{F}^{-T}(t)+\mathbf{F}(t)\nonumber \\&\quad \times \Big (\mathbf{R}[\mathbf{C}(t),0]+\displaystyle \int _{-\infty }^t \frac{\displaystyle \partial \mathbf R [\mathbf C (\tau ),t-\tau ]}{\displaystyle \partial (t-\tau )}\Big ), \end{aligned}$$

(3)

where $t$ denotes the time, $\mathbf{F}(t)$ is the deformation gradient tensor, $\mathbf{C}(t)$ is the right Cauchy–Green deformation tensor, $\mathbf{R}[\mathbf{C}(\tau ),t-\tau ]$ is the tensorial relaxation function and $p(t)$ is the Lagrange multiplier that accounts for incompressibility.

For simplicity, the relaxation function is assumed to have the following form:

$$\begin{aligned} \mathbf{R}[\mathbf{C}(\tau ),t-\tau ]&= \mathbf{R}_{m}[\mathbf{C}(\tau ),t-\tau ]+\mathbf{R}_{f_n}[\mathbf{C}(\tau ),t-\tau ]\nonumber \\&+\,\mathbf{R}_{f_t}[\mathbf{C}(\tau ),t-\tau ], \end{aligned}$$

(4)

where $\mathbf{R}_{m}$ is the tensorial relaxation function that accounts for the contribution of the (isotropic) matrix, $\mathbf{R}_{f_n}$ is the tensorial relaxation function associated with one family of fibers and $\mathbf{R}_{f_t}$ is the tensorial relaxation function associated with another family of fibers. Let $\mathbf M$ and $\mathbf N$ be the unit vectors that define the orientation of these two families of fibers within the USL/CL complex. These tensorial functions are selected to have one of the simplest forms for an orthotropic material (Holzapfel et al. 2000; Holzapfel and Ogden 2009):

$$\begin{aligned} \mathbf{R}_{m} = c_1\mathbf{1},\quad \mathbf{R}_{f_n} = f_n\mathbf{M}\otimes \mathbf{M},\quad \mathbf{R}_{f_t} = f_t\mathbf{N}\otimes \mathbf{N} \end{aligned}$$

(5)

where $f_n$ and $f_t$ are constitutive functions defined as

$$\begin{aligned}&f_n(I_1(\tau ),I_4(\tau ),t-\tau ) \nonumber \\&\quad = {\left\{ \begin{array}{ll} c_2(e^{c_3(I_4(\tau )-1)}-1)r_1(I_1(\tau ),t-\tau ), &{} I_4(\tau )>1\\ 0, &{} I_4(\tau )\le 1 \end{array}\right. } \end{aligned}$$

(6)

$$\begin{aligned}&f_t(I_1(\tau ),I_6(\tau ),t-\tau ) \nonumber \\&\quad = {\left\{ \begin{array}{ll} c_4(e^{c_5(I_6(\tau )-1)}-1)r_1(I_1(\tau ),t-\tau ), &{} I_6(\tau )>1\\ 0, &{} I_6(\tau )\le 1 \end{array}\right. } \end{aligned}$$

(7)

where $I_1(\tau ) = \text {tr}(\mathbf{C}(\tau ))$, $I_4(\tau ) = \mathbf{M}\cdot \mathbf{C}(\tau )\mathbf{M}$, $I_6(\tau ) = \mathbf{N}\cdot \mathbf{C}(\tau )\mathbf{N}$ are invariants of $\mathbf C$ and $c_1$, $c_2$, $c_3$, $c_4$ and $c_5$ are constant parameters. It must be noted that in the definition of $f_n$ and $f_t$, the fibrous components are assumed not to support compressive loads. The relaxation function, $r_1$, is selected to be

$$\begin{aligned}&r_1(I_1(\tau ),t-\tau )\nonumber \\&\quad =\frac{1+\alpha _1(I_1(\tau ))e^{-(t-\tau )\beta _1}+\alpha _2(I_1(\tau ))e^{-(t-\tau )\beta _2}}{1+\alpha _1(I_1(\tau ))+\alpha _2(I_1(\tau ))}, \end{aligned}$$

(8)

where $\alpha _1$ and $\alpha _2$ are functions of the first invariant of $\mathbf C$, $I_1$, and $\beta _1$ and $\beta _2$ are constant parameters. Note that $r_1$ goes to 1 when $t=\tau$. As discussed later (Sect. 3.3), the functions $\alpha _1(I_1(\tau ))$ and $\alpha _2(I_1(\tau ))$ can be determined from experimental data or defined a priori as:

$$\begin{aligned} \alpha _1(I_1(\tau ))&= a_1 e^{-a_2 (I_1(\tau )-3)}, \end{aligned}$$

(9)

$$\begin{aligned} \alpha _2(I_1(\tau ))&= a_3 e^{-a_4 (I_1(\tau )-3)}, \end{aligned}$$

(10)

where $a_1$, $a_2$, $a_3$, and $a_4$ are constant parameters.

3.2 Biaxial extension

Let $\{\mathbf{E}_1,\,\mathbf{E}_2,\,\mathbf{E}_3\}$ and $\{\mathbf{e}_1, \,\mathbf{e}_2,\,\mathbf{e}_3\}$ be two sets of unit vectors that define orthonormal bases in the reference and deformed configurations, respectively. The ligaments are assumed to contain two families of fibers that are parallel to $\mathbf{E}_1$ and $\mathbf{E}_2$ in the reference configuration so that ${\mathbf{M}}={\mathbf{E}}_1$ and $\mathbf{N}=\mathbf{{E}}_2$ as illustrated in Fig. 1. Note that this assumption is made to simplify and test the proposed model and must be validated by means of histological studies. The USL and CL are assumed to undergo an isochoric deformation described by

$$\begin{aligned} x_1 = \lambda _1(t) X_1, \quad x_2 = \lambda _2(t) X_2, \quad x_3 = \frac{1}{\lambda _1(t) \lambda _2(t)} X_3, \nonumber \\ \end{aligned}$$

(11)

where $(X_1,\,X_2,\,X_3)$ and $(x_1,\,x_2,\,x_3)$ represent the Cartesian coordinates of a generic point in the reference and deformed configurations, respectively, and $\lambda _1(t)$ and $\lambda _2(t)$ are the axial stretches that act along the directions of the two families of fibers. It follows that the deformation gradient tensor, $\mathbf{F}(t)$, and the right Cauchy–Green strain tensor, $\mathbf{C}(t)$, are given by:

$$\begin{aligned} \mathbf{F}(t)&= \lambda _1(t) \mathbf{e}_1\otimes \mathbf{E}_1+ \lambda _2(t) \mathbf{e}_2\otimes \mathbf{E}_2\nonumber \\&\quad +\frac{1}{\lambda _1(t) \lambda _2(t)} \mathbf{e}_3\otimes \mathbf{E}_3, \end{aligned}$$

(12)

$$\begin{aligned} \mathbf{C}(t)&= \lambda _1(t)^2 \mathbf{E}_1\otimes \mathbf{E}_1+ \lambda _2(t)^2 \mathbf{E}_2\otimes \mathbf{E}_2\nonumber \\&\quad +\frac{1}{\lambda _1(t)^2 \lambda _2(t)^2} \mathbf{E}_3\otimes \mathbf{E}_3. \end{aligned}$$

(13)

This deformation is selected because for the plane deformation F that was computed experimentally (see Sect. 2.2) $F_{11}$ and $F_{22}$ were found to be generally much larger than $F_{12}$ and $F_{21}$. This suggests that extension was much greater than shear. The magnitude of $F_{12}$ and $F_{21}$ typically fell below 0.025.

To derive the first Piola–Kirchhoff stress tensor that defines the instantaneous elastic response, Eq. 3 is evaluated at $t=\tau$ with the tensorial relaxation function defined in Eqs. 5–8 and the deformation tensors in Eqs. 12–13. The surface of the ligament that is normal to $\mathbf{E}_3$ is assumed to be traction-free so that $P_{33}=0$. By enforcing this boundary condition, the Lagrange multiplier, $p$, can be computed. Then, the only nonzero components of the first Piola–Kirchhoff stress tensors, $P_{11}$ and $P_{22}$, are found to be:

$$\begin{aligned} P_{11}&= c_2 \left( -1 + e^{c_3 (\lambda _1^2 -1)}\right) \lambda _1+c_1 \left( \lambda _1-\frac{1}{\lambda _1^3 \lambda _2^2}\right) , \end{aligned}$$

(14)

$$\begin{aligned} P_{22}&= c_4 \left( -1 + e^{c_5 (\lambda _2^2 -1)}\right) \lambda _2+c_1 \left( \lambda _2-\frac{1}{\lambda _2^3 \lambda _1^2}\right) . \end{aligned}$$

(15)

These components of the stress are in terms of five parameters, $c_1$, $c_2$, $c_3$, $c_4$, and $c_5$. These parameters can be computed from experimental data as described in Sect. 3.3.

The nonzero components of the first Piola–Kirchhoff that describes the biaxial stress relaxation response can be found from Eq. 3 with Eqs. 5–8 and Eqs. 12–13 with constant stretches, $\lambda _1 (t) = \lambda _1$ and $\lambda _2 (t) = \lambda _2$, and by setting $P_{33}=0$ to compute the Lagrange multiplier, $p$. These components have the form:

$$\begin{aligned} P_{11}&= c_1 \left( \lambda _1-\frac{1}{\lambda _1^3 \lambda _2^2}\right) + c_2 \lambda _1 \left( -1 + e^{c_3 (\lambda _1^2 -1)}\right) \nonumber \\&\quad \times \,r_1(I_1(\tau ),t-\tau ) \end{aligned}$$

(16)

$$\begin{aligned} P_{22}&= c_1 \left( \lambda _2-\frac{1}{\lambda _2^3 \lambda _1^2}\right) + c_4 \lambda _2 \left( -1 + e^{c_5 (\lambda _2^2 -1)}\right) \nonumber \\&\quad \times \, r_1(I_1(\tau ),t-\tau ) \end{aligned}$$

(17)

where the relaxation function $r_1$ is defined in Eq. 8 in terms of $\beta _1$, $\beta _2$, $\alpha _1$ and $\alpha _2$. The seven parameters, $c_1$, $c_2$, $c_3$, $c_4$, $c_5$, $\beta _1$, and $\beta _2$, and two functions, $\alpha _1$, and $\alpha _2$, in Eqs. 16–17 can be determined from experimental data as described in Sect. 3.3.

3.3 Identification of model parameters

A built in minimization function in Matlab,   fmincon, was utilized to fit the proposed constitutive model to the collected experimental data. Overall, a total of 44 sets of biaxial elastic data (22 sets of stress–stretch data for each of the two loading axes) and 44 sets of normalized stress relaxation data (22 sets of normalized stress–time data for each of the two loading axes) were used. It must be noted that, for the $n=7$ specimens subjected to three consecutive stress relaxation tests, the data collected after the first stress relaxation test were not considered when fitting the constitutive model.

More specifically, the model parameters were computed by minimizing the sum of the squared differences between the stresses computed via Eqs. 14 and 15 (or Eqs. 16 and 17) and the biaxial elastic data (or normalized stress relaxation data). During the minimization process, the model parameters were constrained to be nonnegative.

The five elastic parameters $c_1$, $c_2$, $c_3$, $c_4$, and $c_5$ were determined by simultaneously fitting Eqs. 14 and 15 to 22 sets of biaxial stress data that were obtained from the ramp displacement portion of the experiments, prior to any relaxation test (Fig. 2). Once determined, the elastic parameters were fixed in Eqs. 16 and 17 to compute the viscoelastic parameters $\beta _1$ and $\beta _2$ and the viscoelastic functions $\alpha _1$ and $\alpha _2$. Two different approaches were employed to compute these quantities.

Firstly, $\beta _1$, $\beta _2$, $\alpha _1$, and $\alpha _2$ were computed by fitting Eqs. 16 and 17 to one representative set of normalized stress relaxation data. This set was obtained by taking the average of the normalized stress relaxation data in the two loading directions. These data were collected from a specimen that was held at a constant displacement that was approximately equal to the average of the constant displacements used during the relaxation tests (or first relaxation tests for $n=7$ specimens subject to three consecutive relaxation tests).

The parameters $\beta _1$ and $\beta _2$ were then fixed to the values computed by fitting such representative data, while $\alpha _1$ and $\alpha _2$, which depend on the first invariant of strain $I_1$, were computed by fitting Eqs. 16 and 17 to the remaining normalized stress relaxation data. These data were again the average data over the two loading directions. This procedure led to values for $\alpha _1$ and $\alpha _2$ for different values of the first constant strain invariants that were associated with the constant displacements/stretches used during the relaxation tests. The parameters $a_1$, $a_2$, $a_3$, and $a_4$ were then computed by fitting Eqs. 9 and 10 to these generated $\alpha _1$ and $\alpha _2$ versus $I_1$ data.

An alternative approach for determining $\beta _1$, $\beta _2$, $a_1$, $a_2$, $a_3$, and $a_4$ in Eqs. 16–17 was also considered. In this case, the relaxation function given in Eq. 8 and appearing in Eqs. 16–17 was defined a priori in terms of $\beta _1$, $\beta _2$, $a_1$, $a_2$, $a_3$, and $a_4$. These constants were computed by simultaneously fitting Eqs. 16 and 17 to 44 sets of normalized stress relaxation data.

4 Results

4.1 Biaxial elastic properties

The USL and the CL exhibited a nonlinear elastic mechanical behavior and experienced large strains (as high as 75 %) when subjected to biaxial quasi-static loading conditions. Representative stress–stretch data collected on $n=9$ specimens isolated from a single sow during the ramp portion of the biaxial tests are presented in Fig. 3a for maximum stress levels up to $\sim$1 MPa and Fig. 3c for maximum stress levels up to $\sim$2.7 MPa. In Fig. 4a, c, e, data collected on a smaller number of specimens ($n=4$, $n=5$, and $n=4$, respectively) from the other three sows are reported together with the model fit. The anatomical location of each specimen within the USL/CL complex is reported in the inset of each figure.

Fig. 3

a, c Stress–stretch curves with (b), (d) corresponding normalized stress relaxation curves for $n=9$ specimens isolated from a single sow. The stress–stretch curves and stress relaxation curves obtained by testing the same specimens are presented using the same colors. Note that the filled symbols represent $P_{11}$ versus $\lambda _1$ data which are collected along ${\mathbf{E}}_1$, that is normal to the upper vagina/cervix, while the unfilled symbols denote $P_{22}$ versus $\lambda _2$ data which are collected along ${\mathbf{E}}_2$, that is transverse to the upper vagina/cervix as indicated in Fig. 1a. The specimen location within the USL/CL complex and relative to the vagina and rectum is presented in the insets. (Note that the model was fit to these data too but the results are not shown here)

Fig. 4

a, c, e Stress–stretch data with model fit and (b), (d), (f) corresponding normalized stress relaxation data with models fit for a total of $n=13$ specimens isolated from three sows. The stress–stretch curves and stress relaxation curves obtained by testing the same specimens are presented using the same colors. Note that the filled symbols represent $P_{11}$ versus $\lambda _1$ data which are collected along ${\mathbf{E}}_1$, that is normal to the upper vagina/cervix, while the unfilled symbols denote $P_{22}$ versus $\lambda _2$ data which are collected along ${\mathbf{E}}_2$, that is transverse to the upper vagina/cervix as indicated in Fig. 1a. The specimen location within the USL/CL complex and relative to the vagina and rectum is presented in the insets

A large amount of variability in the experimental data was observed, even when the specimens were isolated from the same sow as shown in Fig. 3a, c. The experimental results suggests that the mechanical behavior of the ligaments may be location dependent and orthotropic. In particular, it appears that USL specimens and specimens located closer to the USL within the USL/CL complex are stiffer in the direction normal to the upper vagina/cervix than the specimens further from the USL are in the same direction. Almost all the specimens were stiffer in ${\mathbf{E}}_1$-direction (normal to the upper vagina/cervix) than in the ${\mathbf{E}}_2$-direction.

The proposed model was able to capture the experimentally observed elastic behavior of the ligaments as shown in Fig. 4a, c, e. The mean and standard deviation of the elastic parameters, $c_1$, $c_2$, $c_3$, $c_4$, and $c_5$ in Eqs. 14–15, computed by fitting $n=22$ biaxial data sets are presented in Table 1. The $R^2$ values for these fittings range from 0.893 to 0.995. For many specimens, the elastic constant $c_1$, which represents the contribution of the (isotropic) ground substance, approached zero. This indicates that the ground substance had a relatively small mechanical contribution when compared with the fibrous components of the tissues. The elastic constants $c_2$ and $c_3$, which account for the contribution of the fibers normal to the upper vagina/cervix, were typically larger than the constants $c_4$ and $c_5$, which account for the contribution of the fibers transverse to the upper vagina/cervix. This is a result of the specimens being stiffer in the direction normal to the upper vagina/cervix.

Table 1 Mean and standard deviation of the parameters computed by fitting data collected from $n=22$ specimens

4.2 Biaxial viscoelastic properties

Three consecutive relaxation tests were performed on seven specimens. For each specimen, the greatest decrease in stress over time always occurred during the first relaxation test, regardless of whether the highest or lowest stretches were applied first (Fig. 5). Similar results were observed when the resting time between relaxation tests was 0, 1, or 12 h. These tests revealed that the number of stretches that were applied during three consecutive stress relaxation tests significantly affected the stress relaxation behavior of the CL and USL. Therefore, the data collected from the second and third tests on these specimens were not used to characterize the stress relaxation behavior of these ligaments.

Fig. 5

Stress relaxation response for $n=2$ specimens that were subjected to three consecutive biaxial relaxation tests. The resting period between relaxation tests was 1 h. It must be noted that the normalized stress relaxation data that are collected in two different directions, $\mathbf{E}_1$ and $\mathbf{E}_2$, at comparable stretches are, in most cases, almost identical. For this reason, the normalized stress relaxation data in these two directions cannot be distinguished: the data collected at a constant $\lambda _1$ in the $\mathbf{E}_1$-direction overlap with the data collected at a constant $\lambda _2$ in the $\mathbf{E}_2$-direction. a The specimen was subjected to three constant displacements in an ascending order. b The specimen was subjected to three constant displacements in a descending order

After considering only the data from the first relaxation tests on $n=7$ specimens tested three times and the data from single relaxation tests on $n=15$ specimens, a total of $n=22$ stress relaxation curves were obtained. Stress relaxation data for $n=9$ specimens isolated from one sow are presented in Fig. 3b, d. These data were collected after collecting the elastic data presented in Fig. 3a, c, respectively. In other words, each relaxation test was conducted at the constant axial displacements that generated the maximum axial stretches reported in Fig. 3a, c. For example, the maximum axial stretches for the stress–stretch curves represented in green squares in Fig. 3a were $\lambda _1 = 1.08$ and $\lambda _2 = 1.14$. These were the constant stretches used for the biaxial relaxation test represented with green squares in Fig. 3b.

Substantial stress relaxation was observed in all specimens tested. In general, the stress decreased very fast for the first few hundred seconds but then slowly until the end of the test. The stress relaxation behavior varied among specimens. For example, some specimens retained about 65 % of the initial stress at 3,000 s (curve represented with red squared symbols in Fig. 3d), while others maintained as little as 20 % of the initial stress at 3,000 s (curve represented with green squared symbols in Fig. 3b). The observed differences in relaxation rate and percent relaxation were dependent on the magnitude of the axial stretches applied to the specimens. In general, the stress relaxation was higher for specimens stretched to lower stretch levels when compared with specimens stretched to higher stretch levels. Interestingly, for all tested specimens, the normalized stress relaxation was identical in both axial directions even if the elastic behavior was different. This can be appreciated in Fig. 3b, d, where the stress relaxation curves in the two different axial directions, $\mathbf{E}_1$ and $\mathbf{E}_2$, overlap (i.e., curve represented with filled purple triangle symbols overlap with curve represented with unfilled purple triangle symbols in Fig. 3b).

The constitutive model was able to fit the stress relaxation data as shown in Fig. 4b, d, f with $\beta _1=0.0306$ and $\beta _2=0.0008$. The values of $\alpha _1$ and $\alpha _2$ computed by fitting the average stress relaxation data over the two axial directions are presented in Fig. 6 versus $I_1$ for each specimen. The $R^2$ values for these fittings range from 0.950 to 0.995. In general, the values of $\alpha _1$ and $\alpha _2$ were higher for lower values of $I_1$ which correspond to lower values of the axial stretch. The dependency of $\alpha _1$ on $I_1$ can be described by Eq. 9 with $a_1=1.078$ and $a_2= 2.303$ $(R^2=0.234)$ and the dependency of $\alpha _2$ can be described by Eq. 10 with $a_3= 2.175$ and $a_4= 4.915$ $(R^2=0.386)$.

Fig. 6

a Dependency of $\alpha _1$ on $I_1$ and b dependency of $\alpha _2$ on $I_1$. Recall that $I_1$ is the first invariant of strain and $\alpha _1$ and $\alpha _2$ are measures of the percent stress relaxation of the specimens. The continuous lines in (a) and (b) represent the functions $\alpha _1(I_1(\tau ))=1.078 e^{-2.303(I_1-3)}$ and $\alpha _2(I_1(\tau ))=2.175 e^{-4.915 (I_1-3)}$, respectively

When the relaxation function given in Eq. 8 was defined a priori in terms of $a_1$, $a_2$, $a_3$, $a_4$, $\beta _1$, and $\beta _2$ and Eqs. 16 and 17 were simultaneously fitted to the entire set of biaxial stress relaxation data, the model predicted the general trend in the stress relaxation behavior with $a_1 = 0.906$, $a_2 = 2.86$, $a_3 = 1.59$, $a_4 = 4.08$, $\beta _1 = 0.0469$, and $\beta _2 = 0.00117$ $(R^2=0.742)$. The predicted stress relaxation behavior of ligaments stretched to different initial stretches is presented in Fig. 7.

Fig. 7

Model predictions of the stress relaxation of ligaments that are subjected to equi-biaxial extensions (Eq. 11 with $\lambda _1=\lambda _2$) at different axial stretches levels. The predictions were made using the proposed constitutive model with parameters that were computed by fitting $n=22$ sets of biaxial normalized stress relaxation data simultaneously

5 Discussion

The swine CL and USL exhibited an orthotropic nonlinear elastic response and undergo large deformations when stretched biaxially (Figs. 3a, b, 4a, c, e). Not surprisingly, these membraneous ligaments were found to be in general stiffer along their main physiological loading direction that is normal to the upper vagina/cervix (${\mathbf{E}}_1$ in Fig. 1a). The large deformations are also to be expected since the ligaments support internal organs such as the uterus that are quite mobile within the pelvis.

Under constant biaxial stretches, the stresses in the swine CL and USL were found to significantly decrease over time (Figs. 3c, d, 4b, d, f). Our results are comparable to those by Vardy et al. (2005) on the USL in cynomolgus monkey where, after multiple relaxation tests along a single axis, the stress decreased by about 70 % over a 2,000 s time interval. Our biaxial data showed that, even though the elastic behavior of the ligaments is orthotropic, the normalized stress relaxation response is similar along the two loading axes (${\mathbf{E}}_1$ and ${\mathbf{E}}_2$ in Fig. 1a). The micro-structural origins of the planar anisotropic elasticity and isotropic viscoelasticity are unknown. It is likely that there are more collagen fibers aligned along the physiological loading direction of the ligaments. The different amount of collagen fibers could lead to different elastic properties in the two loading directions. However, if the stress relaxation behavior is determined mainly by the collagen fibers, as previously speculated by some researchers (Purslow et al. 1998), the normalized stress relaxation will be equal in the two loading directions. Indeed, the normalized stress relaxation data do not account for differences in the amount of collagen fibers. This difference will only influence the initial stress.

It is quite possible that the isotropic matrix and the other tissue’s components, rather than the collagen fibers, govern the stress relaxation behavior of the CL and USL. This appears to be, however, less likely since the collagen fibers are stiffer than the matrix and the other tissue’s components and are subjected to larger stresses. We speculate that the decrease in stress over time, which was recorded to be at least $20\,\%$, is too large to be attributed solely to the isotropic matrix.

In order to determine the dependency of stress relaxation on stretch, we completed three consecutive relaxation tests on $n=7$ specimens. By performing these tests on the same specimen, we attempted to limit possible inter-specimen variability that makes difficult the interpretation of our data. Constant stretches during these tests were applied in both ascending and descending orders (Fig. 5), allowing the specimens to rest for 0, 1, and 12 h between consecutive tests. Independently of such order and resting period, the specimens always relaxed more during the first relaxation test. These preliminary experiments revealed that the effects of strain history need to be carefully considered when studying the dependency of stress relaxation on stretch via multiple relaxation tests (van Dommelen et al. 2006). The increased level of hydration of the ligaments during these tests is also likely to alter their viscoelastic properties.

For the reasons mentioned above, we decided to consider only data collected during the first relaxation tests for the $n=7$ specimens subjected to three consecutive relaxation tests and performed single relaxation tests on $n=15$ specimens. Our findings revealed that the rate of stress relaxation depends on stretch: the ligaments relax less as the stretch increases (Figs. 3c, d, 4b, d, f). This trend was also observed in previous uniaxial studies on medial collateral ligaments (Hingorani et al. 2004; Provenzano et al. 2001). In these studies, the decrease in stress relaxation with increased stretch has been attributed to the loss of water that occurs as the ligaments are stretched out. However, this trend may have to do with the molecular reorganization that occurs within individual collagen fibers during stress relaxation.

We formulated a new constitutive law by assuming that the ligaments are composed of an isotropic matrix and two families of fibers. The model was successfully fitted to the biaxial elastic data although a large amount of variation was observed in the values of the elastic parameters $c_1$, $c_2$, $c_3$, $c_4$, and $c_5$ (Table 1). The large standard deviations in the values of these parameters are due to the significant differences in the shape of the stress–stretch curves. For all but three specimens, $c_1$ was much less than 1 implying that the $c_1$-term, representing the isotropic matrix, did not play an important role in determining the elastic properties of the CL and USL. For the three specimens with $c_1$ greater than one, the $c_1$-term played a slightly more important role. However, the contribution of the isotropic matrix was still inferior than the contribution of the fibrous components. The average values of $c_2$ and $c_3$ were comparable to $c_4$, and $c_5$, thus suggesting that the two family of fibers are equally contributing to the elasticity of the ligaments.

The relaxation function $r_1$ was selected to depend only on the first invariant of strain $I_1$ and not the fourth invariant of strain $I_4$ or fifth invariant of strain $I_5$ which would indicate direction-dependent stress relaxation. One must note that, if the function $\alpha _1$ and $\alpha _2$ presented in Eqs. 9 and 10, respectively, are taken to be constant, the proposed model collapses to the QLV model. Furthermore, a reduction of our three-dimensional model to a one-dimensional model will lead to a nonlinear viscoelastic model that is similar to the one proposed by Pryse and colleagues (Pryse et al. 2003; Nekouzadeh et al. 2007). By expressing the relaxation function in Eq. 8 in terms of the parameters $a_1$, $a_2$, $a_3$ and $a_4$ (Eqs. 9–10) and $\beta _1$, $\beta _2$, which are all independent of strain, we were able to compute these parameters by simultaneously fitting the biaxial stress relaxation data collected from $n=22$ specimens (Fig. 7). The model with these parameters predicts the general trend of decreasing stress relaxation with increasing stretch. But, due to the large variation in the experimental data, the model cannot reproduce very well the stress relaxation response for each specimen. This variation is likely due to differences in the locations of the specimens relative the vagina and rectum and differences among the sows.

Planar biaxial tests are useful for characterizing the mechanical behavior of membraneous ligaments such as the swine CL and USL. However, the development and validation of an orthotropic three-dimensional constitutive model require additional data such as, for example, through-thickness mechanical data (Holzapfel and Ogden 2009) that are currently unavailable. Ideally, the arrangement of the collagen fibers and other constituents (i.e., nerve fibers and smooth muscle cells) during elastic and viscoelastic planar biaxial tests should be quantified so that their contributions can be considered in the development of constitutive models. In the proposed constitutive law, we assumed the existence of two families of fibers that are oriented perpendicularly to each other. This assumption was primarily made to select the simplest orthotropic tensorial relaxation function. Although some of our preliminary histological and SEM studies (Fig. 1c, d) demonstrated the existence of these fibers’ families on some excised regions of the swine USL and CL complex, a more in depth analysis of the structure of these ligaments is needed.

Many researchers have noted that significant structural remodeling takes place in the CL and USL under pathological conditions. For example, CL specimens from women affected by uterine prolapse have been reported to have more sparsely distributed and thicker collagen fibers than healthy women (Salman et al. 2010). Other studies have reported that a decrease in collagen and elastin levels is associated with the development of prolapse and urinary incontinence (Campeau et al. 2011). This structural remodeling will likely alter the mechanical properties of the pelvic ligaments and compromise their ability to support pelvic organs. Additional experimental and theoretical studies are thus necessary to understand how the mechanical properties of the CL and USL are altered by pelvic disorders so as to develop new preventive and treatment strategies.

5.1 Conclusions

This study presents the first planar biaxial elastic and viscoelastic experimental data on the CL and USL. The results revealed that the specimens are orthotropic and stiffer in the direction normal to the upper vagina/cervix. The normalized relaxation behavior was similar in both loading axes, and the amount of relaxation was dependent on the applied stretch: specimens subjected to lower constant stretches relaxed more than specimens subjected to higher constant stretches. A novel nonlinear three-dimensional constitutive model was formulated by assuming that the ligaments are composed of two families of fibers embedded in an isotropic matrix. The model was able to capture the elastic orthotropy, finite strain, and stretch-dependent stress relaxation of the CL and USL. This research advances our limited knowledge about the mechanics of the CL and USL that is needed to understand the etiology of pelvic floor disorders and develop new preventive and treatment methods.