A Nonlinear Constitutive Model for Stress Relaxation in Ligaments and Tendons

Abstract

A novel constitutive model that describes stress relaxation in transversely isotropic soft collagenous tissues such as ligaments and tendons is presented. The model is formulated within the nonlinear integral representation framework proposed by Pipkin and Rogers (J. Mech. Phys. Solids. 16:59–72, 1968). It represents a departure from existing models in biomechanics since it describes not only the strain dependent stress relaxation behavior of collagenous tissues but also their finite strains and transverse isotropy. Axial stress–stretch data and stress relaxation data at different axial stretches are collected on rat tail tendon fascicles in order to compute the model parameters. Toward this end, the rat tail tendon fascicles are assumed to be incompressible and undergo an isochoric axisymmetric deformation. A comparison with the experimental data proves that, unlike the quasi-linear viscoelastic model (Fung, Biomechanics: Mechanics of Living Tissues. Springer, New York, 1993) the constitutive law can capture the observed nonlinearities in the stress relaxation response of rat tail tendon fascicles.

Introduction

Ligaments and tendons are dense fibrous soft connective tissues: ligaments connect bone to bone and support internal organs while tendons connect muscle and bone. They are primarily composed of collagen and elastin fibers embedded in a ground substance of water, proteoglycans, and glycoproteins, all of which are produced and organized by the resident cells. Collagen is the primary load bearing component and the most abundant protein constituting 65–80% of the tissues’ dry weight. It has a well-known hierarchical organization: collagen molecules are packed together to form collagen fibrils, collagen fibrils aggregate to form collagen fibers, and collagen fibers are arranged in distinct, parallel, wavy bundles known as fascicles.1

As many collagenous tissues, ligaments and tendons exhibit long-term viscoelastic behavior: they relax when held at a constant displacement and creep when subjected to a constant load. The origin of their long-term viscoelasticity is still unknown but has been recently attributed to collagen.31 In order to study the intrinsic viscoelastic properties of collagen, fascicles found in rat tail tendons are often tested. This is due their high content of collagen: 90–95% of the dry weight of rat tail tendon fascicles is comprised of collagen.13 In an early study by Rigby et al.,28 for example, fascicles isolated from rat tail tendons were used to determine the effect of temperature on stress relaxation. More recently, rat tail tendons have been mechanically tested to understand the role of proteoglycans15 and collagen fiber sliding17,30 in stress relaxation. In these studies incremental stress relaxation tests or stress relaxation tests at a single strain level were performed. However, none of these investigations focused on characterizing the strain dependent stress relaxation response of these fascicles.

Investigating the strain dependent stress relaxation of ligaments and tendons is essential for designing replacement grafts with mechanical properties similar to native tissues and establishing surgical reconstruction methods and post-operative rehabilitation protocols. For example, during reconstructive surgeries, ligaments, tendons, and their replacement grafts are often strained in an ad-hoc manner by the surgeons to achieve a desired tension. However, this tension decreases over time due to the viscoelasticity of the tissues depending on the applied strain. An excessive decrease in tension can have detrimental effects: it causes laxity in the tissues that predisposes one to the recurrence of injuries and leads to other musculoskeletal disorders such as osteoarthritis.4 Thus, the dependence of stress relaxation on the applied strain in ligaments, tendons, and their replacement grafts must be accurately characterized to establish guidelines in surgical procedures and enhance their outcome.

The most popular viscoelastic model employed for soft collagenous tissues is the quasi-linear viscoelastic (QLV) model proposed by Fung.16 The QLV model for stress relaxation is the following:

$$ \sigma(\varepsilon, t) = \int\limits_0^t { {\partial R(\varepsilon, t - \tau)}\over {\partial \varepsilon}} \frac{d \varepsilon}{d \tau}d\tau = \int\limits_0^t G(t - \tau) \frac{d \sigma^{e}(\varepsilon)}{d \varepsilon}\frac{d \varepsilon}{d \tau}d\tau $$

(1)

where $\sigma(\varepsilon, t)$ is the stress, $\varepsilon$ is the strain, t is the time, $R(\varepsilon, t-\tau)$ is the relaxation function, G(t − τ) is the normalized relaxation function and $\sigma^e=\sigma^e(\varepsilon)$ is the instantaneous elastic response. In the QLV model in Eq. (1), the relaxation function, $R(\varepsilon, t),$ is assumed to be a separable function of time and strain and thus takes the form $R(\varepsilon, t) = G(t) \sigma^e(\varepsilon).$ This assumption requires the time dependent relaxation behavior defined by G(t) to be the same for any strain $\varepsilon.$ The QLV model is attractive due to the ease of implementation: quasi-static tensile tests and stress relaxation tests at a single strain level are sufficient to compute its parameters. Some issues associated with the numerical determination of the parameters and predictive capabilities of the QLV model have been looked upon over the past few years.2,7 However, recent experimental evidence demonstrated that stress relaxation in ligaments and tendons is strain dependent and, hence, cannot be modeled using a separable relaxation function of time and strain.12,18,24,32

Nonlinear superposition and Schapery’s theory have been proposed as alternatives to the QLV theory in order to describe the strain dependent stress relaxation exhibited by these tissues.11,12,18,25 The proposed viscoelastic models are, however, one-dimensional and valid only when the tissues are subjected to small strains. Finite strains experienced by ligaments and tendons have been considered in a three-dimensional viscoelastic model proposed by Johnson et al. 20 This model has been derived within Pipkin and Rogers’s nonlinear integral representation23 but has then been tested by assuming that the tensorial relaxation function is a separable function of time and strain. This assumption leads to a finite strain form of the QLV model thus contradicting current experimental findings. Furthermore, in the model proposed by Johnson et al. 20 ligaments and tendons are erroneously assumed to be isotropic. While the above cited models capture the long-term viscoelasticity of ligaments and tendons, a robust three-dimensional constitutive model that accounts for the strain dependent stress relaxation behavior, transverse isotropy, finite strains experienced by these tissues needs to be developed.

In this manuscript, a nonlinear viscoelastic constitutive model that describes the stress relaxation behavior of parallel-fibered collagenous tissues is presented. The model is derived within the nonlinear integral series representation developed by Pipkin and Rogers23 and recently proposed for anisotropic materials by Rajagopal and Wineman.27 In order to account for the tissues’ nonlinearities and transverse isotropy, a tensorial relaxation function is proposed that is assumed to be a non-separable function of the strain invariants and time. Tensile axial stress–stretch data and stress relaxation data collected at multiple axial stretches from rat tail tendon fascicles are used to compute the model parameters. Moreover, a comparison of the proposed model with the predictions of the QLV model is also presented. To the authors’ knowledge, the constitutive model represents the first fully nonlinear, finite strain, transversely isotropic model for stress relaxation applied to parallel-fibered collagenous tissues.

Theoretical Formulation

An incompressible transversely isotropic nonlinear viscoelastic constitutive model is proposed for the description of stress relaxation in soft collagenous tissues having collagen fibers aligned mainly along one physiological loading direction such as ligaments and tendons. The model is formulated within the nonlinear viscoelastic framework set forth by Pipkin and Rogers23 by considering recent theoretical developments by Rajagopal and Wineman27 for anisotropic materials. Most importantly, the model can capture the dependence of stress relaxation on strain, which has been experimentally observed in ligaments and tendons.11,12,18,24

Constitutive Model

In order to describe the nonlinear viscoelastic behavior of soft collagenous tissues, the integral series representation proposed by Pipkin and Rogers23 is considered. As previously done by other investigators,20,27,29 only the first term of the integral series, which is a single integral with a nonlinear integrand, is used. It must be noted that this single integral representation is equivalent for small strain to the nonlinear superposition model used for ligaments and tendons.11,12,18,24

The first Piola-Kirchhoff stress tensor, ${\mathbf{P}}(t),$ at any time t has the form27:

$$ {{\mathbf{P}}}(t) = -p{{\mathbf{F}}}^{-\hbox {T}}(t) + {{\mathbf{F}}}(t) \left ( {{\mathbf{R}}}[{{\mathbf{C}}}(t), 0] + \int\limits_0^t \frac{\partial {{\mathbf{R}}}[{{\mathbf{C}}}(\tau), t-\tau]}{\partial (t-\tau)} d\tau \right ) $$

(2)

where ${\mathbf{F}}(t)$ is the deformation gradient tensor, ${\mathbf{C}}(t)={\mathbf{F}}(t)\!^{\hbox {T}} {\mathbf{F}}(t)$ is the right Cauchy-Green deformation tensor, ${\mathbf{R}}[{\mathbf{C}}(\tau), t - \tau]$ is the tensorial relaxation function, and p is the Lagrange multiplier that accounts for incompressibility. In Eq. (2) no deformation is assumed to occur prior to time t = 0 and the term ${\mathbf{F}}(t) {\mathbf{R}}[{\mathbf{C}}(t), 0]$ represents the instantaneous elastic contribution to the total stress at time t.

The use of the right Cauchy-Green deformation tensor, ${\mathbf{C}}(t),$ as a strain measure guarantees that the principle of material frame indifference is satisfied.33 In order to meet fading memory requirements, the tensorial relaxation function must be a monotonically decreasing function of time: the partial derivative of ${\mathbf{R}}[{\mathbf{C}}(\tau), t - \tau]$ with respect to t − τ must be always negative. One must note that the reference configuration is assumed to be a stress-free configuration so that in the absence of deformation, the tensorial relaxation function is identically zero. Finally, in absence of explicit time dependence in the tensorial relaxation function, Eq. (2) yields the general nonlinear elastic constitutive equation with ${\mathbf{R}}[{\mathbf{C}}(\tau)] = 2\frac{\partial W}{\partial {\mathbf{C}}}$ where W is the so-called strain energy density function.

Ligaments and tendons are assumed to be transversely isotropic and incompressible so that the tensorial relaxation function can be defined in terms of a scalar potential density function, $\tilde{W},$ as done by Rajagopal and Wineman27:

$$ {{\mathbf{R}}}[{{\mathbf{C}}}(\tau), t-\tau] = 2\frac{\partial \tilde{W}(I_1(\tau), I_2(\tau), I_4(\tau), I_5(\tau), t-\tau)}{\partial {{\mathbf{C}}}} $$

(3)

where I ₁(τ), I ₂(τ), I ₄(τ), and I ₅(τ) are the strain invariants defined as follows33

$$ I_1(\tau) = \hbox{tr}({{\mathbf{C}}}(\tau)), \quad I_2(\tau) = \frac{1}{2} (I_1^2(\tau) - \hbox {tr}({{\mathbf{C}}}^2(\tau)), \quad I_4 (\tau)= {{\mathbf{m}}}\cdot {{\mathbf{C}}}(\tau){{\mathbf{m}}}, \quad I_5 (\tau)= {{\mathbf{m}}}\cdot {{\mathbf{C}}}^2(\tau){{\mathbf{m}}}$$

(4)

and ${\mathbf{m}}$ is a unit vector that defines the axis of transverse isotropy in the reference configuration. The scalar potential density function does not depend on $I_3(\tau)=\det {\mathbf{C}}(\tau)$ since the strain invariant is identically equal to 1 due to the incompressibility assumption.

The tensorial relaxation function ${\mathbf{R}}[{\mathbf{C}}, t - \tau]$ presented in Eq. (3) can be alternatively written as

$$ {{\mathbf{R}}}[{{\mathbf{C}}}, t - \tau] = a_{1}{{\mathbf{1}}} + a_{2} {{\mathbf{C}}} + a_{3}{{\mathbf{m}}} \otimes {{\mathbf{m}}} + a_{4} \left[{{\mathbf{m}}} \otimes ({{\mathbf{Cm}}}) + ({{\mathbf{Cm}}}) \otimes {{\mathbf{m}}} \right] $$

(5)

where a ₁, a ₂, a ₃ and a ₄ are functions of the strain invariants I ₁ (τ), I ₂ (τ), I ₄ (τ), I ₅ (τ) and t − τ defined as

$$ a_1 = 2\left(\frac{\partial \tilde{W}}{\partial I_{1}} + I_{1} \frac{\partial \tilde{W}}{\partial I_{2}}\right), \quad a_2 = -2\frac{\partial \tilde{W}}{\partial I_{2}},\quad a_3 = 2\frac{\partial \tilde{W}}{\partial I_{4}},\quad a_4 = 2\frac{\partial \tilde{W}}{\partial I_{5}}. $$

(6)

Note that, for ease of notation, the dependence on the strain invariants and time has been dropped in Eqs. (5)–(6).

In this study, the tensorial relaxation function ${\mathbf{R}}[{\mathbf{C}}, t - \tau]$ is selected to depend only on the strain invariant I ₄ and is defined only in the direction ${\mathbf{m}}$ of the axis of material symmetry. Thus the functions a ₁, a ₂ and a ₄ are assumed to be identically zero thus limiting the types of finite deformations that can be described.26 Specifically, the tensorial relaxation function is chosen to be

$$ \begin{aligned} {{\mathbf{R}}}[I_4(\tau), t-\tau] &=a_3 (I_4(\tau), t-\tau) {{\mathbf{m}}} \otimes {{\mathbf{m}}}\\ & =\left\{ c_{1} \left[ e^{c_{2} (I_{4}(\tau) -1)} -1 \right] \right\}\left[ \left( 1- \alpha(I_4(\tau)) \right) e^{{-(t-\tau)} \beta(I_4 (\tau))} + \alpha(I_4(\tau)) \right] {{\mathbf{m}}} \otimes {{\mathbf{m}}} \end{aligned} $$

(7)

where c ₁ and c ₂ are non-negative constants and α(I ₄(τ)) and β(I ₄(τ)) are functions of the strain invariant I ₄(τ). In Eq. (7), the function of I ₄(τ) in the first curly brackets is used to describe the strain stiffening elastic behavior of soft collagenous tissues.16,19,22 Specifically, the parameter c ₁ represents the initial elastic modulus while the parameter c ₂ defines the strain stiffening of the tissues. The function in the second square brackets is used to describe the normalized relaxation behavior.29 The function α(I ₄(τ)) describes the ratio of the equilibrium stress to the initial stress and is referred to the elastic fraction while the function β(I ₄(τ)) defines the strain dependent relaxation rate. It must be noted that a finite strain form of the QLV model for stress relaxation is recovered when α and β are constants (not functions of I ₄(τ)).

Model Implementation

Uniaxial Deformation

The proposed model is tested with experimental data collected by loading rat tail tendon fascicles along their long axis. The fascicle is assumed to undergo an isochoric homogeneous axisymmetric deformation schematically presented in Fig. 1 and defined by

$$ r = {\lambda(t)}^{-1/2} R, \quad \theta = \Uptheta, \quad z = \lambda(t) Z $$

(8)

where ($R, \Uptheta, Z$) and (r, θ, z) represent the coordinates of a generic point in the reference and deformed configurations, respectively, and λ = λ(t) is the axial stretch. The orthonormal bases $\{{\mathbf{E}}_R, {\mathbf{{E}}}_{\Uptheta}, {\mathbf{E}}_Z\}$ and $\{{\mathbf{e}}_r, {\mathbf{e}}_{\theta}, {\mathbf{e}}_z\}$ in the reference and current configurations, respectively, are defined such that ${\mathbf{E}}_Z$ and ${\mathbf{e}}_z$ are unit vectors parallel to the direction of loading. Moreover, the collagen fibers are assumed to be aligned along ${\mathbf{E}}_Z$ in the reference configuration so that ${\mathbf{m}}={{\mathbf{E}}}_Z$ (Fig. 1).

Figure 1

Schematic of the rat tail tendon fascicle’s deformation. Note that the axis of transverse isotropy in the reference configuration, ${\mathbf{m}},$ is equal to ${\mathbf{E}}_{Z}$

It follows that the deformation gradient tensor, ${\mathbf{F}}(t),$ and the right Cauchy-Green deformation tensor, ${\mathbf{C}}(t),$ are given by

$$ \begin{aligned} {{\mathbf{F}}}(t) &=\frac{1}{\sqrt{\lambda (t)}} {{\mathbf{e}}}_r \otimes{{\mathbf{E}}}_R + \frac{1}{\sqrt{\lambda (t)}} {{\mathbf{e}}}_\theta \otimes{{\mathbf{E}}}_\Uptheta +\lambda (t) {{\mathbf{e}}}_z \otimes{{\mathbf{E}}}_Z,\\ {{\mathbf{C}}}(t)&=\frac{1}{\lambda (t)} {{\mathbf{E}}}_R \otimes{{\mathbf{E}}}_R + \frac{1}{\lambda (t)} {{\mathbf{E}}}_{\Uptheta} \otimes{{\mathbf{E}}}_{\Uptheta} +\lambda^2 (t) {{\mathbf{E}}}_Z \otimes{{\mathbf{E}}}_Z. \end{aligned} $$

(9)

The first Piola-Kirchhoff stress tensor that defines the instantaneous elastic stress can be computed by substituting Eq. (7) at time t = τ and Eq. (9) into Eq. (2). Assuming a traction-free boundary condition on the lateral surface of the tested fascicles leads to p = 0 in Eq. (2). Then the only non-zero component of the first Piola-Kirchhoff stress tensor has the form

$$ P_{zZ}(t) = {\lambda(t)} c_1\left[ e^{c_{2} ( \lambda^2(t) -1 )} - 1\right]\;. $$

(10)

Stress relaxation can be modeled using Eqs. (2), (7) and (9) by assuming that λ(t) = λ is constant. Then, the only non-zero component of the first Piola-Kirchhoff stress tensor that defines stress relaxation is

$$P_{zZ}(t) = \lambda c_1 \left[e^{c_{2}(\lambda^2 -1)}-1 \right]\left[\left(1-\alpha(\lambda^2)\right)e^{{-t} \beta(\lambda^2)} + \alpha(\lambda^2) \right]. $$

(11)

In summary, for a parallel-fibered collagenous tissue subjected to a uni-axial isochoric axisymmetric deformation, two parameters, c ₁ and c ₂, need to be determined to characterize the instantaneous elastic behavior while the same parameters, c ₁ and c ₂, and two functions, α(λ²) and β(λ²), need to be found to characterize the stress relaxation behavior.

Experimental Methods

Twenty-six rat tail tendon fascicles were subjected to tensile tests followed by stress relaxation tests. Two male Sprague Dawley rats were used in this study: one rat (rat A) weighed 235 g and the other rat (rat B) weighed 236 g. The animals were acquired from a different study, which did not affect the musculoskeletal system or collagen development, in accordance with an approved Virginia Tech IACUC protocol. Immediately after sacrifice, the tails were isolated from the rats and their skin was removed using a wire stripper. Group of fascicles were then teased out from the proximal end of the tails with fine tipped tweezers under a stereomicroscope (Stereoscope Stemi 2000C, Zeiss). The least amount of force necessary to free the fascicles was used to minimize their stretching. The fascicles were then separated, wrapped in paper towels soaked in phosphate buffered saline solution, and stored frozen (−20 °C). Twelve to twenty-four hours before testing, the fascicles were placed in a refrigerator at 2 °C and before testing they were allowed to come to room temperature for 1 h.

The fascicles were trimmed to a uniform length chosen to be 77 mm based on experimental results by Legerlotz et al. 21 Images of each fascicle were collected using the stereomicroscope. The width of each fascicle was measured at six locations from the images using ImageJ (ImageJ v. 1.44, National Institutes of Health). The value of the width ranged from 0.153 to 0.496 mm. The cross-sectional area was calculated using the average of the six measured values of the width and assuming a circular cross-section. The computed values of the area varied from 0.019 to 0.194 mm². Black ink was then sprayed on the surface of the fascicles using an airbrush (Professional 150, Badger Airbrush Co.) in order to produce marks with suitable contrast for strain calculation (Fig. 2a). The two ends of each fascicle were fixed to a piece of gridded plastic template using cyanoacrylate glue (Fig. 2b) to ensure their straight alignment during mounting on a custom built micro-tensile testing device. The main components of the micro-tensile testing device used to perform the mechanical experiments are shown in Fig. 2c. A 8.9 N (2 lb) load cell (LSB 200, Futek) with a resolution of ±0.002 N was used to measure the load and a micro-scale linear actuator (T-NA Series, Zaber Technologies) with a ± 8 μm accuracy was employed to stretch the specimens. Screw down grips and a bath for the testing device were custom made primarily of polycarbonate.

Figure 2

Preparation of rat tail tendon fascicle and custom designed micro-tensile testing device

For each test, the two ends of the fascicle attached to the gridded plastic template, were secured to the grips. The plastic template, cured glue, and screw down clamps contributed to gripping the fascicle and prevented its slippage. The portion of the plastic template not secured to the grips was cut with a pair of scissors and removed. The fascicle was then immersed in the bath that was filled with phosphate buffered saline solution. It was pre-loaded to 0.01 N and then preconditioned at 6 mm/min to 0.4 mm for 5 cycles followed by a 5 min recovery period. Preconditioning was performed to establish a consistent strain history for all samples.28 The configuration assumed by the fascicle following recovery was taken as the reference configuration. The 26 fascicles were stretched at 6 mm/min to different displacement values corresponding to 0.75 mm (n = 7), 1.25 mm (n = 7), 1.75 mm (n = 7) or 2.25 mm (n = 5) and subsequently held for 10 min for stress relaxation testing.

The load and displacement data were simultaneously recorded at 20 Hz using LabVIEW software (LabVIEW 2009, National Instruments). The axial nominal stress, P _zZ, was computed by dividing the current load by the initial cross-sectional area. A charge coupled device (CCD) camera (Stingray F-080B, Allied Vision) was used along with a stereomicroscope (Wild M3Z, Heerbrugg) to record images of the fascicle for the duration of the tests. A center region of the fascicle was selected for strain analysis and the displacement of the ink marks was measured using a digital image correlation method implemented in MATLAB (MATLAB v. 7.10, MathWorks).14 The right Cauchy-Green deformation tensor, ${\mathbf{C}},$ and, hence, the axial stretch λ were calculated from the measured displacements by assuming that the fascicle undergoes the deformation presented in Eq. (8). For comparison purpose, the Green-St. Venant strain tensor ${\mathbf{E}}$ related to ${\mathbf{C}}$ by ${\mathbf{E}} =\frac{1}{2} ({\mathbf{C}}-{\mathbf{1}})$ was also computed. Specifically, the component E _ZZ of the Green-St. Venant strain ${\mathbf{E}}$ related to the axial stretch λ by E$_{ZZ}=\frac{1}{2}(\lambda^2-1)$ was reported.

Results

Elastic Response

Axial stress–stretch data were obtained from 26 rat tail tendon fascicles by performing tensile tests as previously described. These data were collected by stretching the fascicles along their long axis up to the displacements that were then held constant during the stress relaxation experiments. These displacements were found to correspond to axial stretch values lower than 1.0566 (E _ZZ  = 5.82%) and the experimental data obtained fell within the toe-region or linear region of the stress–strain curves.21,28 A representative axial stress–stretch curve for a fascicle, which was subsequently tested for stress relaxation at an axial stretch of 1.0199 (E _ZZ  = 2.00%), is shown in Fig. 3. It can be clearly seen that the fascicle exhibits the typical nonlinear elastic strain-stiffening behavior of soft collagenous tissues.

Figure 3

Typical tensile axial stress–stretch curve collected from one rat tail tendon fascicle and model fit to data with c ₁ = 20.27 MPa and c ₂ = 14.15 (R ² = 0.99)

The axial stress–stretch data were used to compute the model parameters c ₁ and c ₂ that define the instantaneous elastic response of the fascicle. Toward this end, Eq. (10) was fit to these data by employing a nonlinear least squares algorithm implemented in MATLAB and imposing that the model parameters were non-negative. The least squares function and its gradient were supplied to a built-in minimization function called fmincon and the trust-region reflective algorithm was utilized.5

The proposed model for the instantaneous elastic response of the fascicle could fit the axial stress–stretch data well with 0.86 <R ² < 0.99. In Fig. 3, the model fit to the representative axial stress–stretch data is presented. For this data set, the parameters were found to be c ₁ = 20.27 and c ₂ = 14.15 (R ² = 0.99). The values of the parameters c ₁ and c ₂ obtained by fitting the axial stress–stretch data collected from each rat tail tendon fascicle are plotted vs. the maximum axial stretches in Fig. 4. They are represented with the same symbol and color when they are computed by fitting data from fascicles stretched up to an equal displacement. Note that the maximum axial stretch is the axial stretch held constant during the subsequent stress relaxation experiment. The values of the parameter c ₁, the initial elastic modulus, ranged from 1.424 to 331 MPa and the values of the parameter c ₂, the strain stiffening parameter, varied between 0.77 and 69.27.

Figure 4

Initial elastic modulus, c ₁, (a), and strain stiffening parameter, c ₂, (b), as a function of the axial stretch, λ, determined by the displacement, d, kept constant during stress relaxation experiments

Stress Relaxation Response

Stress relaxation data were collected by subjecting rat tail tendon fascicles to constant displacements ranging from 0.75 to 2.25 mm. Due to inter-specimen variability, an equal displacement applied to different fascicles was found to induce different axial stretches. The displacements used during stress relaxation experiments produced axial stretches in the fascicles that varied from 1.0098 (E _ZZ  = 0.98%) to 1.0566 (E _ZZ  = 5.82%). The stress relaxation data normalized by the initial stress value are presented in Fig. 5 for five representative fascicles. From Fig. 5, one can see that the shape of the stress relaxation curve changes with axial stretch (or strain). These results suggest that the QLV theory cannot be employed to describe the stress relaxation behavior of rat tail tendon fascicles. According to the QLV model, the normalized stress relaxation function, G(t) in Eq. (1), is independent of strain and thus should be identical regardless of the strain level considered.

Figure 5

Normalized stress relaxation curves at axial stretches, λ, equal to 1.0112, 1.0162, 1.0204, 1.0264 and 1.0349 which correspond to axial strain, E _ZZ , equal to 1.13, 1.65, 2.06, 2.67 and 3.55%, respectively. The axial stress, P _zZ , is normalized by the axial stress at t = 0, P _zZ (0)

The stress relaxation data collected at different axial stretches were used to determine the values of α(I ₄) and β(I ₄) in Eq. (11) with I ₄ = λ². As described above, a nonlinear least squares algorithm was implemented in MATLAB with α(I ₄) constrained to be between 0 and 1 and β(I ₄) constrained to be non-negative. Note that when curve fitting Eq. (11) to each set of stress relaxation data, the values of the parameters c ₁ and c ₂ were fixed to those previously computed by fitting the corresponding set of axial stress–stretch data.

The proposed model was able to capture the strain dependent stress relaxation behavior well (0.80 < R ² < 0.99). In Fig. 6 the value α(I ₄) and β(I ₄) are plotted vs. I ₄ = λ². These values are represented with the same symbol and color when they are computed by fitting stress relaxation data obtained from fascicles stretched up to the same displacement. As I ₄ increased, α(I ₄) tended to decrease (Fig. 6a) while β(I ₄) was found to increase (Fig. 6b). However, as seen in Fig. 6, there was significant variability in the values of α(I ₄) and β(I ₄). A function of the form $\alpha(I_{4}) = c_{3}e^{c_{4}(I_{4}-1)}$ was then fit to the α(I ₄) vs. I ₄ data with c ₃ = 0.7318 and c ₄ =  −14.69 (R ² = 0.68) and a function of the form β(I ₄) = c ₅(I ₄ − 1) was fit to the β(I ₄) vs. I ₄ data with c ₅ = 0.2084 (R ² = 0.30). These curve fits were performed in an attempt to suggest the form of the functions that characterize the stress relaxation response of the fascicles.

Figure 6

Elastic fraction, α(I ₄), (a) and strain dependent relaxation rate, β(I ₄), (b) as functions of the strain invariant I ₄ = λ². The values of α(I ₄) and β(I ₄) are computed by fitting Eq. (11) to stress relaxation data collected at different axial stretches that are determined by different displacements, d, as indicated in the legend. The curves obtained by plotting the values of α(I ₄) and β(I ₄) vs. I ₄ are then fit to $\alpha(I_{4})= c_{3}e^{c_{4}(I_{4}-1)}$ where c ₃ = 0.7318, c ₄ =  −14.69 (R ² = 0.68) and β(I ₄) = c ₅(I ₄ − 1) where c ₅ = 0.2084 (R ² = 0.30), respectively (solid line)

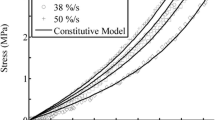
Stress relaxation data sets at three additional axial stretches are shown on a log–log plot in Fig. 7 along with model fits obtained with the proposed model and model predictions from the QLV. The QLV model used is given by Eq. (11) with α(I ₄) = α and β(I ₄) = β constant and independent of strain. Because the parameters α and β are independent of strain, they were computed by fitting stress relaxation data collected at one axial stretch level, chosen to be 1.0098 (E _ZZ  = 0.98%). The values of these parameters were found to be α = 0.7537 and β = 5.649 × 10⁻³. For each stress relaxation curve, the parameters c ₁ and c ₂ in the QLV model were set equal to the values computed by fitting the corresponding axial stress–stretch data. As expected the QLV and proposed models coincide at the axial stretch used for the fitting. However, it can be observed that the QLV model can capture the stress relaxation response at the other two axial stretches only for the first 5–10 s of the tests.

Figure 7

Experimental stress relaxation curves (symbols) for rat tail tendon fascicles at axial stretches λ = 1.0098, 1.0199, and 1.0323 which correspond to axial strains E _ZZ  = 0.98, 2.00 and 3.28%, respectively, proposed model fit to data (solid line), and comparison to QLV model (dashed line). The parameters in the QLV model are obtained by fitting data collected at E _ZZ  = 0.98% and predicts the same shape for the normalized stress relaxation curves regardless of the axial strain

Discussion

In this study, a novel constitutive law was formulated for the description of stress relaxation in transversely isotropic soft collagenous tissues such as ligaments and tendons. The model was derived within the nonlinear integral representation proposed by Pipkin and Rogers23 and recently extended to anisotropic materials by Rajagopal and Wineman.27 The tensorial relaxation function, which appears in this representation, was assumed to be a non-separable function of the strain invariants and time. In order to compute the model parameters, tensile tests and stress relaxation tests at four different displacement values on rat tail tendon fascicles were conducted. The experimental results confirmed previous findings on the nonlinear viscoelasticity of ligaments and tendons.11,12,18,25 They showed that the widely used QLV theory is inadequate to describe the strain dependent stress relaxation behavior of soft collagenous tissues. The proposed model was then successfully fit to the experimental data by assuming that the fascicle undergoes an isochoric axisymmetric deformation. Unlike previous constitutive models, the proposed model accounts for finite strain, tissue anisotropy, and strain dependent stress relaxation that are typical of soft collagenous tissues such as ligaments and tendons.

The elastic behavior of rat tail tendon fascicles was found to be nonlinear as expected21,28 (Fig. 3). However, the initial nonlinear region of the axial stress–strain curve, the so-called toe region, was observed within axial stretch values that correspond to strain values smaller than the 3–5% strain values reported by other authors.21,28 This difference may be due to difference in the experimental methods and protocols (e.g., preconditioning) and the longer length (77 mm) of the specimens used in this study. Indeed, in rat tail tendon fascicles the strain to failure decreases while the modulus increases as their length increases.21 As a consequence, the extent of the toe region is also expected to decrease.

The axial stress–stretch data were used to find the parameters c ₁ and c ₂ that determine the instantaneous elastic response of fascicles (Fig. 4). Some of the scatter in the data can be attributed due to the variability of the cross-sectional area of the tested fascicles.3,21 The length of the specimens used in this study was controlled and varied less than 1% but their cross-section area ranged from 0.02 to 0.1 mm². One could note that the value of the strain stiffening parameter, c ₂, tended to decrease with the maximum axial stretch (Fig. 4b) but no clear trend was found for the initial elastic modulus, c ₁ (Fig. 4a).

The rat tail tendon fascicles displayed the strain dependent stress relaxation behavior also observed in other soft collagenous tissues.11,12,18,24,32 Overall as the axial stretch increased the amount of relaxed stress increased. However, due to the inherent variability of the specimens, this trend was not always observed. For example, in Fig. 5 the specimen pulled to an axial stretch of 1.0180 (E _ZZ  = 1.82%) relaxed 65% of its initial stress while the specimen pulled to an axial stretch of 1.0204 (E _ZZ  = 2.06%) relaxed 59% of its initial stress. Similar results were reported by Screen et al. 30 when conducting incremental stress relaxation tests on rat tail tendon fascicles at strains less than 4%.

There are two major differences between the experimental protocol employed here and those employed in previous studies.17,18,24,30 First, direct stress relaxation tests, each conducted at a single axial stretch, were preferred over incremental stress relaxation tests. Direct stress relaxation tests likely provide more accurate information about the effect of strain on stress relaxation. The stress relaxation behavior studied by incremental stress relaxation tests may be affected by the history of incremental strains used during testing. Differences in the amount of stress relaxation measured from incremental and direct relaxation tests of rat tail tendon fascicles have been detected and quantified by Screen et al. 30 Secondly, unlike previous experimental studies,17,18,24,30 this study included preconditioning to the experimental protocol. Great care was taken in isolating the fascicles from the rat tail tendons and in handling and preparing the specimens for mechanical testing. However, the fascicles may have been stretched before mechanical testing. Thus, in an attempt to provide a more consistent strain history and reference state, the fascicles were preconditioned. Preconditioning has been reported to shorten or eliminate the toe region of the elastic response8 and alter the elastic modulus of spinal cord tissue6 while its effect on the stress relaxation still needs to be investigated.

The QLV model is unable to capture the nonlinear viscoelastic behavior of rat tail tendons. In Fig. 5, one can note that the normalized stress relaxation response depends on the axial stretch employed during testing. This behavior suggests that a separable relaxation function is not adequate to model stress relaxation in rat tail tendon fascicles. Several investigators have shown that the stress relaxation behavior of other soft collagenous tissues cannot be modeled using a separable relaxation function.11,12,18,24,32 In Fig. 7, the QLV model is compared with the proposed model using the same methodology employed by Provenzano et al. 24 However, we must note that in both cases, here and in the cited paper, the predictions of the QLV model are compared with model fits. Fitting the QLV model to stress relaxation data, each collected at different axial stretches, would provide a very good fit too. The purpose of the comparison in Fig. 7 is to show that QLV model is unable to capture the stress relaxation behavior at multiple axial stretches using one set of material parameters assumed to be independent of strain.

One limitation of this study was the inability to determine the functions α(I ₄) and β(I ₄) that could fit well the data generated by the computed α(I ₄) values vs. I ₄ and β(I ₄) values vs. I ₄ due to scatter in the experimental data (Fig. 6). The elastic fraction, α(I ₄), which represents the ratio of the equilibrium stress to the initial stress, was found to decrease with increasing axial stretch and was curve fit by an exponential function (Fig. 6a). Other investigators have either not measured the elastic fraction12,18,24 or have reported similar scatter in the data.17,30 The function β(I ₄), which represents the relaxation rate, was chosen to be a linear function of I ₄ to best fit the computed β(I ₄) values vs. I ₄ (Fig. 6b). This choice is consistent with the formulation by Roberts and Green29 and the results of several experimental studies.12,24,30

Future studies will be conducted to validate the proposed modeling framework using three-dimensional experimental data collected on collagenous tissues that undergo large strains such as the utero-sacral ligaments.34 For these complex tissues, the definition of the tensorial relaxation function given in Eq. (7) will need to be modified so as to consider the contribution of other tissue components (e.g., elastin). This function will likely need to depend not only on I ₄ but also on other strain invariants26 to describe physiological modes of deformations. Finally, the tensorial relaxation function will be re-formulated to account for the structural changes that occur during stress relaxation at the fiber32 and fibril17 levels including damage. Indeed, the strain applied during stress relaxation can cause damage which needs to be addressed by future constitutive models. This can be accomplished using an approach similar to the ones outlined by one of the authors elsewhere.9,10