Mechanistic micro-structural theory of soft tissues growth and remodeling: tissues with unidirectional fibers

Abstract

A new mechanistic theory was developed for soft tissues growth and remodeling (G&R). The theory considers tissues with unidirectional fibers. It is based on the loading-dependent local turnover events of each constituent and on the resulting evolution of the tissue micro-structure, the tissue dimensions and its mechanical properties. The theory incorporates the specific mechanical properties and turnover kinetics of each constituent, thereby establishing a general framework which can serve for future integration of additional mechanisms involved in G&R. The feasibility of the theory was examined by considering a specific realization of tissues with one fibrous constituent (collagen fibers), assuming a specific loading-dependent first-order fiber’s turnover kinetics and the fiber’s deposition characteristics. The tissue was subjected to a continuous constant rate growth. Model parameters were adopted from available data. The resulting predictions show qualitative agreement with a number of well-known features of tissues including the fibers’ non-uniform recruitment density distribution, the associated tissue convex nonlinear stress–stretch relationship, and the development of tissue pre-stretch and pre-stress states. These results show that mechanistic micro-structural modeling of soft tissue G&R based on first principles can successfully capture the evolution of observed tissues’ structure and size, and of their associated mechanical properties.

1 Introduction

Biological tissues adapt to altered mechanical environment by changing their size, structure and mechanical properties. Adaptation continues throughout life, not only during growth period but also at maturity where tissues remodel due, for instance, to changes in physical activity. Tissue growth and remodeling (G&R) involve processes occurring in at least four structural levels: intra-cellular, cellular, tissue space, and global tissue and organ. Humoral factors (e.g., hormones, growth factors and cytokines) are involved as well. There exists now a large accumulated body of evidence which suggests that in order to survive and proliferate, cells need to maintain a homeostatic mechanical environment (which is cell specific), both the intra- as well as extra-cellular one (Grinnell 1994). To that end, when faced with altered mechanical loading, cells strive to maintain homeostatic mechanical environment either by adapting their extracellular matrix (ECM) by means of production (by anabolic processes) or removal (by catabolic processes) of ECM constituents, and/or by altering their own cytoskeleton to adjust their length in order to maintain homeostatic stretch. As examples, fibrocytes utilize the former strategy while the latter is used by smooth muscle cells (SMC) (Martinez-Lemus et al. 2004). Tissue G&R results from these turnover events. The manifestation of G&R in the tissue level in the case of arteries, for example, is that they remodel to restore their homeostatic wall strain and luminal fluid shear stress (Jackson et al. 2002; Kamiya and Togawa 1980; Langille et al. 1989; Wayman et al. 2008).

Modeling G&R can be of great value. Models can potentially unify a collection of seemingly un-related facts into a general scientific framework, thus providing insight into the processes involved and allowing for hypotheses testing as to the role and significance of candidate G&R mechanisms. In practical applications, models serve for quantitative prediction and design. An important example is tissue engineering where it was found that mechanical conditioning not only stimulates matrix production, but plays a key role in the evolution of the vascular constructs toward targeted micro-structure and mechanical properties (Jockenhoevel et al. 2002; Nerem and Seliktar 2001; Niklason et al. 2010). Few excellent reviews have been published on the multi-scale processes involved in G&R and on their modeling, including the fundamental mechanical issues involved (Ambrosi et al. 2011; Cowin 2004; Humphrey and Holzapfel 2012; Taber 1995).

The present paper focuses on structural modeling of interstitial (volumetric) G&R of soft tissues. Structural features which may be altered by G&R are the constituents’ mass, their stress-free configuration and their orientation. Tozeren and Skalak G&R model (Tozern and Skalak 1988) seems to be the first structural model for soft tissues. It is based on the structural theory for tissue mechanics (Lanir 1979, 1983), modified to incorporate G&R via ad hoc assumptions on the (load-independent) kinetic evolution of the fiber’s structure. Most subsequent structural G&R models incorporated load dependence of tissue constituents’ turnover. In arteries, evolution of constituents’ mass (collagen, elastin and smooth muscle cells (SMC)) was analyzed by Gleason and co-workers (Gleason and Humphrey 2004, 2005) in the frame of the constrained mixture approach (Humphrey and Rajagopal 2002), under changing pressure, flow and axial stretch. A similar approach was used in a number of other studies on the effects of variation in constituents volume fractions between the wall layers (Alford et al. 2008), and on the effect of SMC vasoactivity in basilar arteries on their responses to axial stretch (Valentin and Humphrey 2009), to sustained alterations in trans-mural pressure, and to blood flow (Valentin et al. 2009). Evolution of collagen mass and orientation distribution in the aortic valve was modeled (Boerboom et al. 2003; Driessen et al. 2003) by assuming that collagen content in each of a fixed number of orientations increased with the fiber stretch in that direction. The same framework was applied to model G&R in the aortic valve (Driessen et al. 2005) and in articular cartilage (Wilson et al. 2006). In another study on artery and aortic valve (Driessen et al. 2008), remodeling of the orientation distribution was integrated with a semi-structural constitutive model (fibers embedded in a Neo-Hookean matrix) by assuming first-order evolution kinetics of the orientation distribution mean and dispersion. This approach was extended (Machyshyn et al. 2010) by incorporating in addition, remodeling of the collagen fiber’s undulation and by considering strain-dependent synthesis and degradation of collagen and matrix. Remodeling of collagen undulation was considered (Watton et al. 2004) via the evolution of a recruitment constant. Structure-based models have also been developed for aneurysm growth (due to elastin degradation) in both ascending aorta and cerebral arteries (Humphrey and Holzapfel 2012). They considered a thin-walled aneurysm, employing the concept of evolving constrained mixtures (Humphrey and Rajagopal 2002). Structure-based G&R models were proposed for the heart (Arts et al. 1994; Kerckhoffs et al. 2012) and for the lamina cribrosa under glaucoma-induced elevation of the intraocular pressure (Grytz et al. 2012).

Thanks to these G&R studies, significant insights have been gained into diverse aspects of tissues’ structural and functional adaptations to loading. Here, an attempt is made to build upon the knowledge gained to extend and generalize G&R modeling by relaxing the need for ad hoc assumptions regarding the consequence and phenomenology of structural G&R manifestation, as commonly used in previous models. Since tissue properties are derived from their constituents, ideally one would like to analyze G&R relying on the fundamental processes involved (the mechanistic approach, (Cowin 2004)), based on first principles and on the evolving tissue microstructure, while considering the specific mechanical and turnover kinetics of each constituent. The goal of this report is to present the theoretical framework of the new approach and to demonstrate its utility and potential via a specific realization. For clarity’s sake, the tissue is taken to consist of unidirectional bundle of fibers (e.g., collagen in tendons and ligaments), thus allowing the focus to be on the inherent interplay between mechanical and turnover events, free of the added complexity of a three-dimensional finite-deformation formulation. The paper considers first tissues with one type of fibers, followed by generalization to tissues with multiple types of fibers.

2 Methods

2.1 Theoretical framework

The present evolving structural G&R theory is based on a number of general assumptions relating to both the constituents mechanics and micro-structure response to deformation (“m” assumptions), and to their turnover kinetics (“k” assumptions). The former are: m1) soft tissues consist of fibers (collagen and elastin) and cells (e.g., muscle cells) embedded in a matrix of fluid ground substance. The tissue global response to loading equals the sum contributions of its solid constituents and of the osmotic-derived matrix hydrostatic pressure. m2) There are no voids in the tissue space. m3) All constituents are incompressible, and so is the tissue as a whole at each time point along the G&R process. m4) The fibers and muscle contributions are functions of their axial deformation. Being thin and long, the fibers buckle under contraction thereby losing their stiffness. m5) The nominal fiber bundle stretch equals the tissue stretch. Assumptions on the turnover kinetics are: k1) The characteristic time of tissue loading (on the order of seconds to hours) is several orders of magnitude shorter than the characteristic time of the biological G&R process (typically weeks to months (Cowin 2004)). Hence, at any time, the tissue response to short loading can be regarded as stable and analyzed independent of ongoing G&R process. k2) G&R of fibrous constituents results from fibers turnover where some are removed by degradation and new ones are synthesized (Langberg et al. 2001).¹ k3) Based on a large body of in vivo and in vitro evidence suggesting that the rate of fibers mass degradation depends on their loading (Carver et al. 1991; Curwin et al. 1988; Hannafin et al. 1995; Hansson et al. 1988; Hayashi et al. 1996; Matsumoto and Hayashi 1994; Minns and Steven 1980; Nabeshima et al. 1996; Nissen et al. 1978; Ruberti and Hallab 2005; Tipton et al. 1986; Willett et al. 2007, 2008; Wyatt et al. 2009; Yamamoto et al. 2002, 2003, 1993), strain is taken to be the stimulus of tissue G&R. k4) in addition to the deformation-dependent mass degradation there may be (depending on the constituent) a continuous deformation-independent one. k5) in parallel to degradation, the rate of fibers mass production has both a deformation-dependent and deformation-independent components (Carver et al. 1991; Curwin et al. 1988; Hannafin et al. 1995; Hansson et al. 1988; Hayashi et al. 1996; Matsumoto and Hayashi 1994; Minns and Steven 1980; Nabeshima et al. 1996; Nissen et al. 1978; Ruberti and Hallab 2005; Tipton et al. 1986; Willett et al. 2007, 2008; Wyatt et al. 2009; Yamamoto et al. 2002, 2003, 1993). k6) newly produced fibers are deposited on extant fibers (Birk et al. 1989; Nimni 1990) (which serve as “scaffold”) under homeostatic deposition stretch which is tissue and fiber specific (Eastwood et al. 1996; Harris et al. 1981).

The utility of the new theory will be demonstrated by considering a specific realization of it based on the following assumptions, which are special cases of the general ones listed above: s1) The fibers are hyper-elastic with linear relationship between the fiber’s first Piola-Kirchoff stress and its true stretch. It will be shown, however, that the hyper-elastic formulation can be readily extended to incorporate fibers visco-elasticity and preconditioning (e.g., (Lokshin and Lanir 2009; Raz and Lanir 2009)), as well as active properties (e.g., (Nevo and Lanir 1989)). s2) The fibers and matrix volume fractions and their respective mass densities remain constant during G&R (Gleason and Humphrey 2005). s3) The reaction kinetics of both deformation-dependent and deformation-independent (basal) components of mass degradation is of first order. s4) The rate of deformation-dependent fiber degradation is lower in the homeostatic stretch range and higher elsewhere. s5) The rate of total fibers mass production is proportional to the corresponding rate of total fibers mass degradation. Hence, the production kinetics is also of first order (Langberg et al. 2001; Niedermuller et al. 1977).² s6) the fibers’ deposition stretch is normally distributed within their homeostatic stretch range. s7) Torn fibers degrade at the same rate as un-stretched ones.

2.1.1 Kinematics³

In a unidirectional fibrous tissue considered in the present study, the fiber bundle consists of all the tissue fibers (“Appendix 1”). The bundle is subjected to a growth (stretch) protocol whereby its length $L_{\mathrm{bun}} (t)$ increases with time. During growth, fibers continuously turnover. As fibers degrade and new ones are produced and deposited at new birth lengths, the fiber bundle reference (stress-free) length evolves. Let $L_{\mathrm{bun}}^{\mathrm{ref}} (t)$ be the time-evolving bundle reference length with $L_{\mathrm{bun}}^{\mathrm{ref}} (0)\equiv L_{\mathrm{bun}} (t=0)$ as the original (initial) bundle reference length. The associated bundle reference stretch ratio is $\Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t)=L_{\mathrm{bun}}^{\mathrm{ref}} (t)/L_{\mathrm{bun}}^{\mathrm{ref}} (0)$.

The bundle nominal stretch ratio and strain at time $t$ (referred to the initial reference length $L_{\mathrm{bun}}^{\mathrm{ref}} (0)$ are, respectively (assumption m5)

$$\begin{aligned}&\Lambda _{\mathrm{bun}}^{nom} (t) \equiv L_{\mathrm{bun}} (t)/L_{\mathrm{bun}}^{\mathrm{ref}} (0),\nonumber \\&\quad E_{\mathrm{bun}}^{\mathrm{nom}} (t) =((\Lambda _{\mathrm{bun}}^{\mathrm{nom}} (t))^{2}-1)/2 \end{aligned}$$

(2.1)

The bundle true stretch ratio and strain (relative to the bundle current reference length) at time $t$ are, respectively

$$\begin{aligned}&\Lambda _{\mathrm{bun}} (t) \equiv L_{\mathrm{bun}} (t)/L_{\mathrm{bun}}^{\mathrm{ref}} (t)=\Lambda _{\mathrm{bun}}^{\mathrm{nom}} (t)/\Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t), \nonumber \\&\quad E_{\mathrm{bun}} (t) =(\Lambda _{\mathrm{bun}}^2 (t)-1)/2 \end{aligned}$$

(2.2)

The bundle nominal stretch incorporates the combined effects of its growth and deformation. The true stretch specifies the bundle deformation. Although both nominal and true stretches do not specify the single fiber stretch, the latter is linked to them in a fiber-specific relationship via its birth length. Each fiber is characterized by its “birth” length $l_f^b$. This is consistent with Humphrey and Rajagopal (Humphrey and Rajagopal 2002) concept of “natural configuration.”

A single fiber nominal birth stretch ratio and nominal birth strain are, respectively:⁴

$$\begin{aligned} \lambda _f^b \equiv l_f^b /L_{\mathrm{bun}}^{\mathrm{ref}} (0), \quad e_f^b =((\lambda _f^b )^{2}-1)/2. \end{aligned}$$

(2.3)

A single fiber true stretch ratio and true strain at time $t$ are, respectively

$$\begin{aligned}&\lambda _f (\lambda _f^b , t)\equiv L_{\mathrm{bun}} (t)/l_f^b \nonumber \\&\quad =(L_{\mathrm{bun}} (t)/L_{\mathrm{bun}}^{\mathrm{ref}} (0))\cdot (L_{\mathrm{bun}}^{\mathrm{ref}} (0)/l_f^b )=\Lambda _{\mathrm{bun}}^{\mathrm{nom}} (t)/\lambda _f^b \nonumber \\&e_f (e_f^b , t)=(\lambda _f ^{2}-1 )/2 =(E_{\mathrm{bun}}^{\mathrm{nom}} (t)-e_f^b )/(1+2e_f^b )\nonumber \\ \end{aligned}$$

(2.4)

Fibers gradually recruit with increasing bundle stretch and become load bearing at distributed recruitment stretches. A single fiber recruitment (straightening) stretch is the ratio of its birth length $l_f^b$ to the current bundle reference length, so that $\lambda _{f,bun}^{\mathrm{rec}} \equiv l_f^b /L_{\mathrm{bun}}^{\mathrm{ref}} (t)$. Hence, the fiber-in-bundle recruitment stretch is

$$\begin{aligned} \lambda _{f,\mathrm{bun}}^{\mathrm{rec}} (\lambda _f^b ,t)=\lambda _f^b /\Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t) \end{aligned}$$

(2.5)

Since the bundle true stretch is $\Lambda _{\mathrm{bun}} \left( t \right) \equiv L_{\mathrm{bun}} \left( t \right) / L_{\mathrm{bun}}^0 \left( t \right)$, then the fiber’s true stretch ratio and true strain can alternatively be referred to the true bundle stretch as

$$\begin{aligned}&\lambda _f (\lambda _f^b ,t)=\Lambda _{\mathrm{bun}} \left( t \right) /\lambda _{f,\mathrm{bun}}^{\mathrm{rec}} (\lambda _f^b ,t) \nonumber \\&\quad =\Lambda _{\mathrm{bun}} \left( t \right) \cdot \Lambda _{\mathrm{bun}}^{\mathrm{ref}} \left( t \right) /\lambda _f^b \nonumber \\&e_f (\lambda _b ,t)=(E_{\mathrm{bun}} (t)-e_{f,\mathrm{bun}}^{\mathrm{rec}} )/(1+2e_{f,\mathrm{bun}}^{\mathrm{rec}} )\nonumber \\&\quad =(E_{\mathrm{bun}} (t)-e_{f,\mathrm{bun}}^{\mathrm{rec}} )/(\lambda _{f,\mathrm{bun}}^{\mathrm{rec}} (\lambda _b ,t))^{2} \end{aligned}$$

(2.6)

In the specific realization of the theory, the bundle is assumed to grow in length at a constant rate $A$ where

$$\begin{aligned} L_{\mathrm{bun}} (t)=(1+A)\cdot L_{\mathrm{bun}}^{\mathrm{ref}} (0) \end{aligned}$$

(2.7)

2.1.2 Volume, mass and area

The time-dependent fibers and ground substance matrix volume fractions ($\Phi _f (t)$ and $\Phi _{\mathrm{mat}} (t))$ and their volumes ($V_f (t)$ and $V_{\mathrm{mat}} (t))$ are interrelated by:

$$\begin{aligned} \begin{array}{l} \Phi _f (t)=V_f (t)/V(t),\quad V_f (t) =M_f (t)/\rho _f (t) \\ \Phi _{\mathrm{mat}} (t)=V_{\mathrm{mat}} (t)/V(t),\quad V_{\mathrm{mat}} (t) =M_{\mathrm{mat}} (t)/\rho _{\mathrm{mat}} (t) \\ \end{array} \end{aligned}$$

(2.8)

where the constituents’ $M(t), V(t),$ and $\rho (t)$ terms are respectively their time-dependent total mass, volume and constituent density of the fibers and ground substance, while $V(t)$ the total tissue volume.

There are no voids in the tissue space (assumption m2). Hence, the volume fractions $\Phi _f (t)$ and $\Phi _{\mathrm{mat}} (t)$ must fulfill the condition

$$\begin{aligned} \Phi _f (t)+\Phi _{\mathrm{mat}} (t)=1 \quad \forall \quad t\ge 0 \end{aligned}$$

(2.9)

As fibers are produced at different times, thus at different tissue lengths, the fiber population assumes distributed length $l_f^b$ and associated distributed nominal birth stretch ratio $\lambda _f^b$ (Eq. 2.3). The time-dependent mass density distribution (not normalized) over the tissue fibers $m_f (\lambda _f^b ,t)$ (with mass units) is defined as follows: at time $t$, the mass of fibers having a nominal birth stretch between $\lambda _f^b$ and $\lambda _f^b +\hbox {d}\lambda _f^b$ is given by $m_f (\lambda _f^b ,t)\cdot \hbox {d}\lambda _f^b$. Hence, $M_f (t)$ and $m_f (\lambda _f^b ,t)$ are interrelated by:

$$\begin{aligned} M_f (t)= \int \limits _{\lambda _f^b } {m_f (\lambda _f^b ,t)} \cdot \hbox {d}\lambda _f^b \end{aligned}$$

(2.10)

The time-dependent fiber volume distribution $v_f (\lambda _f^b ,t)$ is similarly defined, where

$$\begin{aligned} V_f (t)=\int \limits _{\lambda _f^b } {v_f (\lambda _f^b ,t)\cdot \hbox {d}\lambda _f^b } \end{aligned}$$

(2.11)

The fibers’ mass and volume are inter-related by

$$\begin{aligned} m_f (\lambda _f^b ,t)=\rho _f (t)\cdot v_f (\lambda _f^b ,t) \end{aligned}$$

(2.12)

which by Eq. (2.8)$_{2}$ yields

$$\begin{aligned} m_f (\lambda _f^b ,t)=M_f (t)\cdot v_f (\lambda _f^b ,t)/V_f (t) \end{aligned}$$

(2.13)

In the framework of the micro-structural approach, the evolving bundle reference length $L_{\mathrm{bun}}^{\mathrm{ref}} (t)$ is equal to the lowest length at which fibers recruit (become stretched), i.e., the straightening length of the shortest fiber.⁵ Hence,

$$\begin{aligned} L_{\mathrm{bun}}^{\mathrm{ref}} (t)=\mathop {\min }\limits _{l_f^b } (l_f^b (t)) \end{aligned}$$

(2.14)

The tissue stress-free cross-sectional area and volume at time $t$ are inter-related by:

$$\begin{aligned} A_{\mathrm{tiss}}^{\mathrm{ref}} (t)=A_f^{\mathrm{ref}} (t)+A_{\mathrm{mat}}^{\mathrm{ref}} (t)=V(t)/L_{\mathrm{tiss}}^{\mathrm{ref}} (t) \end{aligned}$$

(2.15)

where $A_f^{\mathrm{ref}} (t)$ and $A_{\mathrm{mat}}^{\mathrm{ref}} (t)$ are, respectively, the fibers and ground substance areas at the bundle reference length.: The tissue reference length is linked to the bundle one via the matrix pressure (Sect. 2.1.5). From Eqs. (2.8)–(2.9),

$$\begin{aligned} \begin{array}{l} V_f (t)/V_{\mathrm{mat}} (t) =\Phi _f (t)/\Phi _{\mathrm{mat}} (t) \\ {\text {Therefore}} \quad V(t)=V_f (t)+V_{\mathrm{mat}} (t)=V_f (t)/\Phi _f (t) \\ \end{array}\nonumber \\ \end{aligned}$$

(2.16)

Hence, from Eq. (2.8),

$$\begin{aligned} A_{\mathrm{tiss}}^{\mathrm{ref}} (t)=(1/L_{\mathrm{tiss}}^{\mathrm{ref}} (t))\cdot M_f (t)/[\rho _f (t)\cdot \Phi _f (t)] \end{aligned}$$

(2.17)

In the specific realization of the theory, by assumption s2, the fibers and matrix volume fraction remain constant. Combined with Eq. (2.9), this restriction yields

$$\begin{aligned} \begin{array}{llll} \Phi _f (t)=\Phi _f (0)\equiv \Phi _f^0 , &{}\Phi _{\mathrm{mat}} (t)=\Phi _{\mathrm{mat}} (0)\equiv \Phi _{\mathrm{mat}}^0 , \\ \rho _f (t)=\rho _f (0)\equiv \rho _f^0 , &{}\rho _{\mathrm{mat}} (t)=\rho _{\mathrm{mat}} (0)\equiv \rho _{\mathrm{mat}}^0 ,\\ &{}\forall \quad t\ge 0 \\ \end{array}\nonumber \\ \end{aligned}$$

(2.18)

2.1.3 Turnover kinetics

Tissue constituents are subjected to continuing processes of production and removal (assumption k2). In studying the constituents’ turnover kinetics, attention is given to when, at what rate, and at which configuration are fibers degraded and produced. The rate of total fibers mass change is the difference between their total production ($Q_f^{pt} )$ and total degradation ($Q_f^{\mathrm{d}t}$), i.e.,

$$\begin{aligned} \hbox {d}M_f /\hbox {d}t=Q_f^{pt} -Q_f^{\mathrm{d}t} \end{aligned}$$

(2.19)

Fibers degradation

By assumptions k3 and k4, the fiber mass degradation has two possible components, one depending on the deformation, the other independent of it (the basal one). Focusing on the $\lambda _f^b$ fibers, the total mass degradation rate of these fibers (superscript dt) is the sum of the basal (superscript db) and deformation-dependent (superscript dd) rates:

$$\begin{aligned} \partial ^{dt}m_f (\lambda _f^b ,t)/\partial t=\partial ^{db}m_f (\lambda _f^b ,t)/\partial t+\partial ^{dd}m_f (\lambda _f^b ,t)/\partial t\nonumber \\ \end{aligned}$$

(2.20)

The two components can depend in general on a variety of determinants such as the nature of the fibers and tissue, genetic and environmental factors, age, health, medications, level of routine physical activity, diet, the specific mass of the $\lambda _f^b$ fibers, and the turnover rates of other constituents. These array of degradation determinants (and other possible ones) are state variables designated collectively by the vector ${\varvec{\Theta } }^{d}$. The deformation-dependent component depends, in addition, on the history of the fiber deformation (designated by $\lambda _f (\lambda _f^b ,\mathop \tau \limits _0^t )$. At present, there is a dearth of information on the functional dependence of the two degradation rates on ${\varvec{\Theta } }^{d}$. In the general case, these relationships are designated by two (hitherto unknown) constitutive functions $D^{db}$ and $D^{dd}$ such that

$$\begin{aligned}&\partial ^{db}m_f (\lambda _f^b ,t)/\partial t=\hbox {D}^{db}({\varvec{\Theta } }^{d}), \nonumber \\&\quad \partial ^{dd}m_f (\lambda _f^b ,t)/\partial t=D^{dd}[\varvec{\Theta } ^{d},\lambda _f (\lambda _f^b ,\mathop \tau \limits _0^t )] \end{aligned}$$

(2.21)

The rate of total fibers mass degradation is derived from Eq. (2.20) as

$$\begin{aligned} Q_f^{dt} =\int \limits _{\lambda _f^b } {\partial ^{dt}m_f (\lambda _f^b ,t)/\partial t\cdot \hbox {d}\lambda _f^b } \end{aligned}$$

(2.22)

In the specific realization of the theory the functions $\hbox {D}^{db}(\varvec{\Theta } ^{d})$ and $D^{dd}[\varvec{\Theta } ^{d},\lambda _f (\lambda _f^b ,\mathop \tau \limits _0^t )]$ for $\lambda _f^b$ fibers are assumed to be proportional to the fiber mass (assumption s3), and the expressions for the deformation–dependent and deformation-independent components’ degradation rates are taken to be first-order reactions expressed by

$$\begin{aligned}&\partial ^{dd}\varvec{m}_f (\lambda _f^b ,t)/\partial t\nonumber \\&\quad =\left\{ {\begin{array}{ll} -B^{dd}(\lambda _f ) \cdot m(\lambda _f^b ,t) &{}\forall \quad \lambda _f^b <\lambda _{f, \mathrm{high}}^b (t) \\ 0 &{} {\text {Otherwise}} \\ \end{array}} \right. \end{aligned}$$

(2.23)

$$\begin{aligned}&\partial ^{db}\varvec{m}_f (\lambda _f^b ,t)/\partial t=-B^{db}\cdot m_f (\lambda _f^b ,t) \end{aligned}$$

(2.24)

where the function $B^{dd}[\lambda _f (\lambda _f^b ,t)]$ (with units 1/time) is the deformation-dependent reaction constant. $\lambda _{f, \mathrm{high}}^b (t)$ is the highest level of $\lambda _f^b$ reached hitherto during the growth protocol. The limit $\lambda _f^b <\lambda _{f, \mathrm{high}}^b (t)$ stems from the fact that at the current growth time $t$, fibers with $\lambda _f^b >\lambda _{f, \mathrm{{high}}}^b$ have not been hitherto produced. $B^{db}$ (with units 1/time) is the basal degradation reaction constant.

Fibers production

Based on assumption k5, the rate of fibers mass production has deformation-dependent and deformation-independent components such that,

$$\begin{aligned} \partial ^{pt}m_f (\lambda _f^b ,t)/\partial t&= \partial ^{pb}\varvec{m}_f (\lambda _f^b ,t)/\partial t\nonumber \\&+\partial ^{pd}\varvec{m}_f (\lambda _f^b ,t)/\partial t \end{aligned}$$

(2.25)

where the indices pt, pb and pd designate total, basal and deformation-dependent production, respectively.

The rates in Eq. (2.25) depend on an array of determinant state variables designated collectively by the vector ${\varvec{\Theta } }^{p}$. Hence, in parallel with Eq. (2.21),

$$\begin{aligned}&\partial ^{pb}\varvec{m}_f (\lambda _f^b ,t)/\partial t=\hbox {P}^{pb}({\varvec{\Theta } }^{p}), \nonumber \\&\quad \partial ^{pd}\varvec{m}_f (\lambda _f^b ,t)/\partial t=P^{pd}(\varvec{\Theta } ^{p},e_f (\mathop \tau \limits _0^t )) \end{aligned}$$

(2.26)

where the functions $\hbox {P}^{pb}({\varvec{\Theta } }^{p})$ and $\hbox {P}^{pd}(\varvec{\Theta } ^{p},e_f (\mathop \tau \limits _0^t ))$ are general (hitherto unknown) functions. The rate of total fibers mass production is derived from Eq. (2.25) as

$$\begin{aligned} Q_f^{pt} (t)=\int \limits _{\lambda _f^b } {\partial ^{pt}\varvec{m}_f (\lambda _f^b ,t)/\partial t\cdot \hbox {d}\lambda _f^b } \end{aligned}$$

(2.27)

In the specific realization, by assumption s5 the rate of total fibers mass synthesis $Q_f^s (t)$ is proportional to the rate of total fibers mass degradation $Q_f^{dt} (t)$ and is given by,

$$\begin{aligned} Q_f^{pt} (t)\equiv {d^{pt}M_f }/{\hbox {d}t=}{\text {SDR}}\cdot Q_f^{\mathrm{d}t} (t) \end{aligned}$$

(2.28)

where SDR is the synthesis-to-degradation ratio. It can be smaller, equal or greater than 1 depending on the phase of growth, disease, injury and mechanical loading (e.g., routine physical activity).

Fibers deposition length

A fiber produced at time $t$ assumes a deposition length $l_f^{\mathrm{dep}} (t)$ which depends on the bundle current length $L_{\mathrm{bun}} (t)$ and on the tension imposed on it during deposition by the synthesizing cells (Alberts et al. 2002) (assumption k6). From Eq. (2.4)$_{1}$, a fiber produced with a deposition stretch $\lambda _f^{\mathrm{dep}}$ has a nominal birth stretch given by $\lambda _f^b (t)=\Lambda _{\mathrm{bun}}^{\mathrm{nom}} (t)/\lambda _f^{\mathrm{dep}}$.

In depositing the fibers under stretch, cells seek to maintain a homeostatic mechanical environment. Since there is a range of homeostatic stretches, it is reasonable to assume that fibers are deposited under a range of homeostatic stretches.

In the specific realization of the theory, the fibers deposition stretches are assumed to be normally distributed within the homeostatic stretch range (assumption s6).

Matrix turnover

Water imbibes into the tissue space due to osmotic forces. Hence, the volume fraction of the fluid-like ground substance matrix (the tissue hydration) is determined by the concentration of osmotic active species in the tissue space, primarily that of the proteoglycans (PG) with their negatively charged glycosaminoglycan (GAG) side groups (Maroudas et al. 1991). PGs are synthesized by the tissue cells (e.g., fibrocytes, smooth muscle cells). The PGs concentration is determined by the nature of the tissue and by its loading (e.g., tension versus compression (Koob et al. 1992; Koob and Vogel 1987)) and location in the organ (e.g., (Azeloglu et al. 2008), in addition to age, health and gender. Quantitative data on the effects of loading on the matrix remodeling is at present scarce. In the future, such data can be incorporated into the formulation when it becomes available.

In the specific realization of the theory, assumption s2 implies that the fibers and matrix volume fractions remain constant (Eq. 2.18) during the G&R process. In other words, the matrix volume changes proportionally to the change of the fibers volume.

2.1.4 Fiber and bundle mechanics

At each point in time, the tissue mechanical response can be analyzed independent of the growth-induced turnover events (assumption k1). The mechanical response of tissue fibers under stretch may be time-dependent (Raz and Lanir 2009). Hence, a single fiber stress depends in general on the history of its strain $e_f (\mathop \tau \limits _0^t )$. Focusing on all fibers with nominal birth stretch $\lambda _f^b$, the contribution of their Cauchy stress $\sigma _f$ to the total tissue Cauchy stress $\Sigma _f$ is obtained by scaling the former by their volume fraction in the tissue. Hence,

$$\begin{aligned} d\Sigma _f (t)&= (v_f (\lambda _f^b ,t)/V(t))\cdot \sigma _f (\lambda _f^b ,t)\cdot \hbox {d}\lambda _f^b \nonumber \\&= \Phi _f (t)\cdot (m_f (\lambda _f^b ,t)/M_f (t))\cdot \sigma _f (\lambda _f^b ,t)\cdot \hbox {d}\lambda _f^b\nonumber \\ \end{aligned}$$

(2.29)

where by assumption m4, the fiber constitutive equation is represented (in terms of its Cauchy stress) by $\sigma _f (\lambda _f^b ,t)=\sigma _f [e_f (\mathop \tau \limits _0^t )]$. The second Eq. (2.29) results from Eqs. (2.13) and (2.16).

By assumption m1, the bundle Cauchy stress is given by summation of Eq. (2.29) over all fibers⁶

$$\begin{aligned} \Sigma _{\mathrm{bun}} (t)=(\Phi _f (t)/M_f (t))\cdot \int \limits _{\lambda _f^b } {m_f (\lambda _f^b ,t)\cdot \sigma _f (\lambda _f^b ,t)\cdot \hbox {d}\lambda _f^b }\nonumber \\ \end{aligned}$$

(2.30)

The tissue’ first Piola-Kirchoff fibers stress, expressed per unit tissue area in the current reference length $L_{\mathrm{bun}}^{\mathrm{ref}} (t)$ ($A_{\mathrm{tiss}}^{\mathrm{ref}} (t)$, Eq. 2.17), is related to its Cauchy stress by $T_{\mathrm{bun}} =\Sigma _{\mathrm{bun}} /\Lambda _{\mathrm{bun}}$.⁷ Substitution of this expression, together with Eq. (2.6) into Eq. (2.30), shows that the stress $T_{\mathrm{bun}}$ can be expressed in terms of the fiber’s first Piola-Kirchoff stress $(t_f =\sigma _f /\lambda _f )$ by the expression

$$\begin{aligned} T_{\mathrm{bun}} (t)&= \Phi _f (t)\cdot (\Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t)/M_f (t))\cdot \int \limits _{\lambda _f^b } m_f \ (\lambda _f^b ,t)/\lambda _f^b \nonumber \\&\cdot t_f (\lambda _f^b ,t)\cdot \hbox {d}\lambda _f^b \end{aligned}$$

(2.31)

The total tissue fiber force is $F_{\mathrm{bun}} (t)=T_{\mathrm{bun}} (t)\cdot A_{\mathrm{tiss}}^{\mathrm{ref}} (t)$.

In the specific realization of the theory, the fibers are taken to be hyper-elastic (assumption s1). Hence, the fibers strain energy per unit of their volume $w_f \left( {e_f } \right)$ depends only on their current true strain $e_f$ if $e_f >0$ and $w_f \left( {e_f } \right) =0$ for $e_f \le 0$ (assumption m4). The strain energy of the $\lambda _f^b$ fibers per unit tissue volume (fibers and matrix) $dw(e_f )$ is thus given by:

$$\begin{aligned} \hbox {d}w(e_f ,t)&= (v_f (\lambda _f^b ,t)/V(t))\cdot w_f (e_f )\cdot \hbox {d}\lambda _f^b \nonumber \\&= \Phi _f^0 \cdot (m_f (\lambda _f^b ,t)/M_f (t))\cdot w_f (e_f )\cdot \hbox {d}\lambda _f^b\nonumber \\ \end{aligned}$$

(2.32)

where the second equation results from Eqs. (2.13). The total fibers volume fraction $\Phi _f^0$ is introduced to transform the strain energy function expressed per unit fibers volume to its value per unit tissue volume. In the specific realization, the fibers volume fraction remains constant (assumption s2), i.e., $\Phi _f (t)=\Phi _f^0$. Hence, the strain energy per unit tissue volume of all fibers in the bundle is

$$\begin{aligned}&W_{\mathrm{bun}} (E_{\mathrm{bun}} ,t)=\int \limits _{\lambda _f^b } {\hbox {d}w(e_f ,t)} \nonumber \\&\quad =(\Phi _f^0 /M_f (t))\cdot \int \limits _{\lambda _f^b } {m_f (\lambda _f^b ,t)\cdot w_f (e_f )\cdot \hbox {d}} \lambda _f^b \end{aligned}$$

(2.33)

The bundle’ second Piola-Kirchoff stress is given by,

$$\begin{aligned}&S_{\mathrm{bun}} (E_{\mathrm{bun}} ,t)={\partial W_{\mathrm{bun}} (E_{\mathrm{bun}} )}/{\partial E_{\mathrm{bun}} } \nonumber \\&\quad ={(\Phi _f^0 }/{M_f (t))}\!\cdot \!\int \limits _{\lambda _f^b } {m_f (\lambda _f^b ,t)\!\cdot \!{dw_f }/{de_f \cdot }{\partial e_f }/{\partial E_{\mathrm{bun}} \!\cdot \!\hbox {d}}} \lambda _f^b\nonumber \\ \end{aligned}$$

(2.34)

By using Eq. 2.6 in the chain differentiation in Eq. (2.34), one gets

$$\begin{aligned}&S_{\mathrm{bun}} (E_{\mathrm{bun}} ,t)={(\Phi _f^0 \cdot (\Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t))^{2}}/{M_f (t))}\nonumber \\&\quad \cdot \int \limits _{\lambda _f^b } {m_f (\lambda _f^b ,t)/(\lambda _f^b )^{2}\cdot s_f (e_f )\cdot \hbox {d}} \lambda _f^b \end{aligned}$$

(2.35)

where $s_f (e_f )=dw_f /de_f$ is the fiber’s second Piola-Kirchoff stress. The bundle component of the tissue’ first Piola-Kirchoff stress $T_{\mathrm{bun}} =\Lambda _{\mathrm{bun}} \cdot S_{\mathrm{bun}}$ can be expressed in terms of the fibers’ first Piola-Kirchoff stress $t_f (t_f =\lambda _f \cdot s_f )$ by substituting $\lambda _f =\Lambda _{\mathrm{bun}} \cdot \Lambda _{\mathrm{bun}}^{\mathrm{ref}} /\lambda _f^b$ (Eq. 2.6) in Eq. (2.35) so that

$$\begin{aligned}&T_{\mathrm{bun}} (E_{\mathrm{bun}} ,t)=\Lambda _{\mathrm{bun}} (t)\cdot S_{\mathrm{bun}} (E_{\mathrm{bun}} ,t) \nonumber \\&\quad ={(\Phi _f^0 \cdot \Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t)}/{M_f (t))}\!\cdot \!\int \limits _{\lambda _f^b } {m_f (\lambda _f^b ,t)/\lambda _f^b \!\cdot \!t_f (\lambda _f )\!\cdot \! \hbox {d}} \lambda _f^b\nonumber \\ \end{aligned}$$

(2.36)

An expression for the bundle Cauchy stress can be derived in a similar way resulting in an expression equivalent to Eq. (2.30) except that here in the hyper-elastic case the fiber Cauchy stress depends only on the fiber current stretch (or strain).

A comparison between Eqs. (2.31) and (2.36) shows that subject to the assumed equality $\Phi _f (t)=\Phi _f^0$, they are of similar forms. Since Eq. (2.31) applies for any material properties of the fibers, this similarity implies that in the micro-structural constitutive formulation, the hyper-elastic fibers material law in Eq. (2.36) can be readily generalized to non-elastic fibers (such as fibers visco-elasticity, preconditioning, active response) by replacing the fiber hyper-elastic stress-strain law with the relevant non-elastic one (Himpel et al. 2008; Lokshin and Lanir 2009; Raz and Lanir 2009).

2.1.5 The matrix pressure

In tissues, the fluid-like ground substance matrix is under osmotic-derived hydrostatic pressure. This matrix pressure affects the tissue mechanical response in two ways. It swells the tissue from its stress-free configuration into its unloaded (but not stress-free) one. In addition, the matrix pressure affects the tissue mechanical response by adding a pressure term to the fibers stress. Hence, the bundle and tissue differ in their reference configuration and in their mechanical response, even in the absence of other types of fibers such as elastin. These differences are detailed in the following.

In the present uniaxial case, the osmotic pressure induces at equilibrium a stretch $\Lambda _{\mathrm{bun}}^{\mathrm{osm}} (t)$ to the fiber bundle under which the bundle Cauchy stress balances the matrix pressure. As a result of $\Lambda _{\mathrm{bun}}^{\mathrm{osm}} (t)$, the tissue reference length (the unloaded one) differs from the bundle one (the stress-free $L_{\mathrm{bun}}^{\mathrm{ref}} (t))$ and is given by $L_{\mathrm{tiss}}^{\mathrm{ref}} (t)=L_{\mathrm{bun}}^{\mathrm{ref}} (t)\cdot \Lambda _{\mathrm{bun}}^{\mathrm{osm}} (t)$. The tissue true and reference stretches are thus related to the corresponding bundle terms by

$$\begin{aligned}&\Lambda _{\mathrm{tiss}} (t)\equiv L_{\mathrm{bun}} (t)/L_{\mathrm{tiss}}^{\mathrm{ref}} (t)=\Lambda _{\mathrm{bun}} (t)/\Lambda _{\mathrm{bun}}^{\mathrm{osm}} (t), \nonumber \\&\quad E_{\mathrm{tiss}} (t)=(\Lambda _{\mathrm{tiss}}^2 (t)-1)/2 \nonumber \\&\Lambda _{\mathrm{tiss}}^{\mathrm{ref}} (t)\equiv L_{\mathrm{tiss}}^{\mathrm{ref}} (t)/L_{\mathrm{bun}}^{\mathrm{ref}} (0)=\Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t)\cdot \Lambda _{\mathrm{bun}}^{\mathrm{osm}} (t). \end{aligned}$$

(2.37)

During growth, the tissue is under experimentally measurable in situ pre-stretch $\Lambda _{\mathrm{tiss}}^{\mathrm{pre}} (t)$ and associated pre-stress. The tissue pre-stretch is equal to its growth-induced true stretch, i.e., $\Lambda _{\mathrm{tiss}}^{\mathrm{pre}} (t)\equiv \Lambda _{\mathrm{tiss}} (t)$.

The experimentally accessible fiber recruitment stretch is the one referred to the tissue unloaded reference configuration, namely $\lambda _{f,\mathrm{tiss}}^{\mathrm{rec}} \equiv l_f^b /L_{\mathrm{tiss}}^{\mathrm{ref}} (t)$. The corresponding recruitment stretch is thus

$$\begin{aligned} \lambda _{f,\mathrm{tiss}}^{\mathrm{rec}} (\lambda _b ,t)=\lambda _f^b /\Lambda _{\mathrm{tiss}}^{\mathrm{ref}} (t) \end{aligned}$$

(2.38)

The fiber stretch and strain can be expressed in terms of the tissue stretch and the fibers-in-tissue recruitment stretch $\lambda _{f, \mathrm{{tiss}}}^{\mathrm{rec}}$ to yield,

$$\begin{aligned}&\lambda _f (\lambda _f^b ,t)=\Lambda _{\mathrm{tiss}} \left( t \right) / \lambda _{f, \mathrm{{tiss}}}^{\mathrm{rec}} (\lambda _f^b ,t)\nonumber \\&\quad =\Lambda _{\mathrm{tiss}} \left( t \right) \cdot \Lambda _{\mathrm{tiss}}^{\mathrm{ref}} \left( t \right) /\lambda _f^b \nonumber \\&e_f (\lambda _f^b ,t)=(E_{\mathrm{tiss}} (t)-e_{f,\mathrm{{tiss}}}^{\mathrm{rec}} )/(\lambda _{f,\mathrm{{tiss}}}^{\mathrm{rec}} (\lambda _b ,t))^{2}\nonumber \\&\quad =(E_{\mathrm{tiss}} (t)-e_{f,\mathrm{{tiss}}}^{\mathrm{rec}} )\cdot (\Lambda _{\mathrm{tiss}}^{\mathrm{ref}} \left( t \right) /\lambda _f^b )^{2} \end{aligned}$$

(2.39)

Equation (2.39) indicates that the fiber true stretch and the tissue true stretch are uniquely interconnected by the fiber recruitment stretch.

The tissue total stress equals the sum of stresses in the fibers due to their deformation, and the matrix osmotic-driven hydrostatic pressure (assumption m4). Hence, the tissue first Piola-Kirchoff stress is

$$\begin{aligned} T_{\mathrm{tiss}} (E_{\mathrm{tiss}} ,t)=T_{\mathrm{bun}} (E_{\mathrm{bun}} ,t)-P_{\mathrm{mat}} /\Lambda _{\mathrm{tiss}} (t) \end{aligned}$$

(2.40)

where $E_{\mathrm{tiss}}$ and $E_{\mathrm{bun}}$ are inter-related via the osmotic stretch $\Lambda _{\mathrm{bun}}^{\mathrm{osm}} (t)$ (Eq. 2.37) and $P_{\mathrm{mat}}$ is the osmotic-driven matrix pressure.

Under equilibrium, the matrix pressure is equal to the PG-induced tissue osmotic pressure, the level of which depends on the PG concentration. In tissues with unidirectional fibers such as tendons, the concentration of PG is low, and so is the associated matrix pressure. Even if small, the matrix osmotic pressure may play a significant role in the tissue global response by affecting the tissue load-free length. In the common case of tissues with undulated fibers, the stress–strain response at low strain levels is flat, so that even a small matrix hydrostatic pressure may substantially increase the unloaded reference length thereby shifting the apparent stress–stretch curve to the left by a stretch ratio of $\Lambda _{\mathrm{bun}}^{\mathrm{osm}} (t)$ (Eq. 2.37, Fig. 4). Osmotic pressure plays even a more significant role in tissues with multi-directional fibers (Lanir et al. 1996; Lokshin and Lanir 2009), especially in tissues subjected to compressive loading such as the articular cartilage and the inter-vertebral disk (both characterized by high concentrations of PG). In these tissues, when under high compressive loading, the matrix pressure may become the major load bearing component.

2.1.6 The fibers recruitment stretch distribution

The fibers turnover with growth, induces changes in their mass distribution over their birth stretch $\lambda _f^b$. The normalized mass density distribution function (d.d.f.) is $m_f (\lambda _{\!f}^b ,t)\!/\!M_{\!f} (t)$. However, the fibers birth stretch is unknown. The only experimentally measurable distribution is that of the fiber-in-tissue recruitment stretch $D(\lambda _{f, \mathrm{{tiss}}}^{\mathrm{rec}} )$. In the micro-structural theories of tissue mechanics (Lanir 1979, 1983), $D(\lambda _{f, \mathrm{{tiss}}}^{\mathrm{rec}} )$ is a fundamental feature of soft tissues mechanics which is the underlying cause of its nonlinear mechanical response. It is defined as follows: the proportion of fibers which become straight (and load bearing) between the stretches $\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}}$ and $\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} +\hbox {d}\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}}$ equals $D(\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} )\cdot \lambda _{f, \mathrm{tiss}}^{\mathrm{rec}}$ It can be readily shown (“Appendix 2”) that $D(\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} )$ is related to the normalized mass density distribution by

$$\begin{aligned} D(\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} ,t)=\Lambda _{\mathrm{tiss}}^{\mathrm{ref}} \cdot m_f (\lambda _f^b ,t)/M_f (t) \end{aligned}$$

(2.41)

2.1.7 Evolution of the tissue mechanical properties

Growth and remodeling are manifested not only by changes in length, mass and mass distribution, but also by the evolving tissue mechanical response. The latter occurs due to changes in the fibers’ mass and cross-sectional area even though the fibers’ intrinsic properties are constant. The evolution in the tissue response can be monitored by imposing a test stretch protocol $\Lambda _{\mathrm{bun}}^{\mathrm{test}} (\tau )$ at selected time points $t^{*}$ along the G&R period where the test is short compared with $t^{*}$. By assumption k1, there is no G&R adaptation during this short protocol duration, so that the tissue structure is fixed and the stress response can be evaluated by an equation similar to Eq. (2.36), namely:

$$\begin{aligned}&T_{\mathrm{bun}}^{\mathrm{test}} (\hbox {t}^{*},\tau )=(\Phi _f (t^{*})\cdot \Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t^{*})/M_f (t^{*}))\cdot \nonumber \\&\quad \int \limits _{\lambda _f^b } {m_f (\lambda _f^b ,t)/\lambda _f^b \cdot t_f \cdot \hbox {d}} \lambda _f^b \end{aligned}$$

(2.42)

where $\tau$ is the time along the test protocol, $t_f =t_f (\lambda _f )$ and following Eq. (2.6)

$$\begin{aligned} \lambda _f =\Lambda _{\mathrm{bun}}^{\mathrm{test}} (\tau )\cdot \Lambda _{\mathrm{bun}}^{\mathrm{ref}} (t^{*})/\lambda _f^b \end{aligned}$$

(2.43)

The total force is then given by $F_{\mathrm{bun}}^*(t,\tau )=T_{\mathrm{bun}}^{\mathrm{test}} (t^{*},\tau )\cdot A_{\mathrm{tiss}}^{\mathrm{ref}} (t^{*})$. By assumption m1, the global tissue force (fibers and matrix is $F^{*}(t^{*},\tau )=A_{\mathrm{tiss}}^{\mathrm{ref}} (t^{*})\cdot [T_{\mathrm{bun}}^{\mathrm{test}} (t^{*},\tau )-P_{\mathrm{mat}} / \Lambda _{\mathrm{bun}}^{\mathrm{test}} (\tau )]$ where $P_{\mathrm{mat}}$ is the matrix pressure, and tissue incompressibility (assumption m3) was applied.

In the specific realization, the test protocol was a stretch at constant rate, and the hyper-elastic fiber first Piola-Kirchoff stress $t_f$ was taken to vary linearly with its true stretch and vanish under contraction ($\lambda _f <1)$. Hence,

$$\begin{aligned} t_f =\left\{ {\begin{array}{l@{\quad }l} K(\lambda _f -1) &{}\forall \quad \lambda _f \ge 1 \\ 0 &{} \mathrm{otherwise} \\ \end{array}} \right\} \end{aligned}$$

(2.44)

where $K$ is the fiber’s stiffness.

2.1.8 Effect of growth on the tissue pre-stress

Growth induces in situ pre-stretch to the tissue. In parallel with the pre-stretch, tissues manifest pre-stress. Both pre-stretch and pre-stress are observable in some tissues (e.g., skin, coronary and other blood vessels). They retract their dimensions when cut and removed from the organ. In the current case of unidirectional tissues, if the uniaxial pre-stretch of the fiber bundle is $\Lambda _{\mathrm{bun}}^\mathrm{pre}$, then the tissue Cauchy pre-stress is given by $\Sigma _{\mathrm{tiss}}^\mathrm{pre} (t)=\Sigma _{\mathrm{bun}} (\Lambda _{\mathrm{bun}}^\mathrm{pre} )-P_{\mathrm{mat}}$. Both $\Sigma _{\mathrm{tiss}}^\mathrm{pre} (t)$ and $\Sigma _{\mathrm{bun}} (t)$ are expressed per unit tissue area in the pre-stretched configuration.

2.2 Tissues with multiple types of unidirectional fibers

The theory presented here can be readily generalized to tissues with multiple types of unidirectional fibers. An example is a bundle of fibers between the lamellae of arterial media which is composed of roughly parallel aligned collagen, elastin and smooth muscle cells. Generalization of the theory is carried out by considering that each type of fiber (designated by the index $i)$ has its own specific mass $(\rho _{f, i} )$, turnover kinetics, mechanical properties, and deposition stretch $(\lambda _{f, i}^{\mathrm{dep}} )$. This implies that in formulating the appropriate theory, the equations are similar to those for tissues with a single type of fibers (presented in Sect. 2.1 above), but with constitutive parameters that are fiber specific (e.g., $\hbox {D}_i^{db}$ instead of $\hbox {D}^{db}, {\varvec{\Theta } }_i^d$ instead of ${\varvec{\Theta } }^{d}, \sigma _{f, i} (\lambda _{f, i}^b ,t)$ instead of $\sigma _f (\lambda _b ,t))$. Naturally, the formulation variables become also fiber specific (e.g., $l_{f, i}^b , \lambda _{f, i}^b , \lambda _{f, i} , \Phi _{f, i} (t), V_{f, i} (t), M_{f, i} (t), m _{f, i} (\lambda _{f, i}^b ,t), Q_{f, i}^{pt} , \Sigma _{f, i} , T_{f, i} )$. The equations must be supplemented by expressions relating each fiber variable to those of the total fibers population, i.e.,

$$\begin{aligned}&V_f (t)= \sum _i {V_{f, i} (t)},\quad \Phi _f (t)=\sum _i {\Phi _{f, i} (t)}, \nonumber \\&\quad M_f (t)=\sum _i {M_{f, i} (t)} \end{aligned}$$

(2.45)

and likewise for the tissue fiber stress (by application of the rule of mixtures),

$$\begin{aligned} \Sigma _f (t)=\sum _i {\Sigma _{f, i} (t), \quad T_f (t)=\sum _i {T_{f, i} (t)} } \end{aligned}$$

(2.46)

One equation that is assigned a slightly different form is Eq. (2.14) for the evolving tissue reference length:

$$\begin{aligned} L_{\mathrm{bun}}^{\mathrm{ref}} (t)=\mathop {\min }\limits _i&{}(\mathop {\min }\limits _{l_f^b } (l_{f, i}^b (t))) \end{aligned}$$

(2.47)

Since the formulation and equations for the multiple fiber types is of a very similar form to that of a single fiber, rather than repeating all of it, only few examples of the modified equations are presented.

The fibers volume fraction (Eq. 2.8),

$$\begin{aligned} V_f (t) =\sum _i {M_{f, i} (t)/\rho _{f, i} (t)} \end{aligned}$$

(2.48)

The space-filling condition (Eq. 2.9),

$$\begin{aligned} \sum _i {\Phi _{f, i} (t)} +\Phi _\mathrm{mat} (t)=1\quad \forall t\ge 0 \end{aligned}$$

(2.49)

The relationship between mass and volume distributions (Eq. 2.12),

$$\begin{aligned} m_{f, i} (\lambda _{f, i}^b ,t)=\rho _{f, i} (t)\cdot v_{f, i} (\lambda _{f, i}^b ,t) \end{aligned}$$

(2.50)

The tissue reference cross-sectional area (Eq. 2.17),

$$\begin{aligned} A_{\mathrm{tiss}}^{\mathrm{ref}} (t)=(1/L_{\mathrm{tiss}}^{\mathrm{ref}} (t))\cdot \sum _i {M_{f, i} (t)/[\cdot \rho _{f, i} (t)\cdot \Phi _{f, i} (t)]}\nonumber \\ \end{aligned}$$

(2.51)

The basal and deformation-dependent rate of fiber degradation (Eq. 2.21),

$$\begin{aligned}&\partial _i^{db} m_{f, i} (\lambda _{f, i}^b ,t)/\partial t=\hbox {D}_i^{db} ({\varvec{\Theta } }_i^d ), \nonumber \\&\partial _i^{dd} m_{f, i} (\lambda _{f, i}^b ,t)/\partial t=\hbox {D}_i^{dd} (\varvec{\Theta } _i^d ,e_f (\mathop \tau \limits _0^t )) \end{aligned}$$

(2.52)

The fiber nominal birth stretch is given by $\lambda _{f, i}^b (t)=\Lambda _{\mathrm{bun}} (t)/\lambda _{f, i}^{\mathrm{dep}}$.

The total Cauchy stress due to the $i$ type fiber bundle (Eq. 2.30) is given by,

$$\begin{aligned} \Sigma _{bun, i} (t)&= (\Phi _{f, i} (t)/M_{f, i} (t))\cdot \int \limits _{\lambda _{f, i}^b } m_{f, i} (\lambda _{f, i}^b ,t)\nonumber \\&\cdot \sigma _{f, i} (\lambda _{f, i}^b ,t)\cdot \hbox {d}\lambda _{f, i}^b \end{aligned}$$

(2.53)

and the total tissue Cauchy stress is

$$\begin{aligned} \Sigma _{\mathrm{tiss}} (t)=\sum _i {\Sigma _{\mathrm{bun},i} (t)-P_{\mathrm{mat}} } \end{aligned}$$

(2.54)

2.3 Specific realization of the theory

Analysis of a specific case of the new theory is presented with the goal of demonstrating its feasibility and utility. Its predictions and consequences will be contrasted against known structural features of soft tissues. In particular, it will be shown that the commonly observed distribution of the fibers recruitment stretch and the associated tissue convex nonlinear stress–strain response (Viidik 1972; Zhao et al. 2013) may well result from the mechano-biological interaction between growth-induced tissue stretch and kinetics of the fibers turnover.

Methods of the specific realization

The assumptions relevant to the specific realization have been listed in the Sect. 2. The associated equations of kinematics, turnover kinetics and mechanical consequences of these assumptions have been presented together with the related equations for the general theory. Together these constitute the theoretical framework of the specific realization considered here. It is supplemented in the present section by a list of the selected numerical parameters values. In view of the absence of established data on few of the model parameters, they were selected by trial and error, aimed to obtain biologically reasonable general response features. However, no systematic parametric investigation was carried out and parameters were not optimized. The rationale behind some choices is presented in the Sect. 3.

The homeostatic fiber stretch was assumed to span the range between $\lambda _f =\lambda _1 =1.03$ and $\lambda _f =\lambda _2 =1.08$. The homeostatic range is taken to be the stretch range at which the fibers are most stable and experience the lowest turnover rate. The fibers were assumed to tear at $\lambda _f =\lambda _3 =1.15$. The basal degradation rate constant (Eq. 2.24) was set to $B^{db}=2\cdot 10^{-7} (\hbox {s}^{-1})$. The values for the deformation-dependent degradation rate constant were as follows (following assumptions s4 and s7):

• $B^{dd}=8\cdot 10^{-7} (\hbox {s}^{-1})$ at $\lambda _f <\lambda _1$ (the hypo-homeostatic stretch range)

• $B^{dd}=3\cdot 10^{-7} (\hbox {s}^{-1})$ at $\lambda _1 <\lambda _f <\lambda _2$ (the homeostatic stretch range)

• $B^{dd}=20\cdot 10^{-7} (\hbox {s}^{-1})$ at $\lambda _2 <\lambda _f$ (the hyper-homeostatic stretch range)

• $B^{dd}=8\cdot 10^{-7} (\hbox {s}^{-1})$ at $\lambda _3 <\lambda _f$ (torn fibers)

The value of SDR (ratio of total fibers mass production to total mass degradation) was set to ${\text {SDR}}=1.05$.

Torn fibers do not resist any load but they occupy volume in the tissue space thereby affecting its stress levels. In addition, they are subjected to degradation (assumption s7) thereby participating in the fiber turnover kinetics.

The tissue was taken to have initial cross-sectional area of $1\hbox {mm}^{2}$ and reference length of 10 mm. The fibers occupy 10 % of the initial tissue volume and are all straight (but not stretched) at their initial reference configuration. The fibers density is $\rho _f^0 =1.034 {\text {gr}}/{\text {cm}}^{3}$, and their intrinsic stiffness (Eq. 2.43) is $K=100\,{\text {MPa}}$ when stretched and $K=0$ when buckled under contraction. The tissue osmotic pressure was taken to be $P_{\mathrm{mat}} =2.5 {\text {kPa}}$.

The tissue was assumed to grow at a constant rate $A$ (Eq. 2.7) of 0.5 cm/year (50 % of the initial length per year) for two years. This growth is preceded by a step stretch to the mid-point of the homeostatic range $(\lambda =1.055)$. The evolution of the tissue mechanical properties was investigated by carrying out short stretch tests of up to 10 % extension at selected time laps along the growth period.

Results of the specific realization

The simulation results are presented for two distinct cases. One relates to the fiber bundle, without osmotic effects of the charged matrix. The other case is that of a tissue in which the fibers are embedded in an osmotic active matrix.

The simulation inputs are the bundle growth stretch protocol and initial fibers mass density distribution (Figs. 1A,B, respectively). All fibers are assumed to be initially straight but un-stretched. Evolutions of the tissue global dimensions are presented in terms of its reference length (Fig. 1C), cross-sectional area (Fig. 1D) and of the total fiber mass (Fig. 1E), respectively. It is seen that under constant kinetic rate, the reference length seems to grow linearly while both area and fiber mass grow exponentially with growth time.

Fig. 1

Simulation Inputs: A The bundle stretch protocol. B The initial fibers mass density distribution (lengths of all fibers is equal to the initial bundle length). Simulation Predicted Global Outputs: C The tissue reference stretch. D The tissue cross-sectional area. E The tissue total fibers mass. Time units are $10^{4}$ h

The predicted micro-structural manifestation of the tissue growth is presented in terms of the fibers mass density distribution which evolves with growth time from a single common birth stretch of $\lambda _b =1.0$ to a distribution over a range of birth stretches (Fig. 2). Concurrently with spreading, the distribution ranges progressively move to the right toward higher $\lambda _b$ levels.

Fig. 2

Effect of growth time on the fibers mass density distribution across their birth stretch $\lambda _f^b$, starting from an initial Dirac-$\delta$ population at $\lambda _f^b =1$. Note the predicted emerging non-uniform bell-shaped density distribution, a pattern commonly observed in soft tissues. The symbol “tf” designates the total growth period duration

Importantly, the evolving fibers mass density distribution depicted in Fig. 2 as function of the fibers birth stretch $\lambda _b$ is not readily observable since the tissue length increases during growth (Fig. 1C). The mass dispersion can be experimentally observed via the fibers recruitment density distribution over the tissue stretch relative to its current unloaded (reference) length (Fig. 3). The general patterns of the distributions are similar to those at Fig. 2. The important difference is that here the distribution range remains closer to the tissue reference length (tissue stretch $=$ 1). Fibers with recruitment stretch lower than unity are stretched in the unloaded state thereby balancing the matrix osmotic pressure.

Fig. 3

Evolution of the normalized fibers recruitment stretch density distribution function. Tissue stretch of unity corresponds to the current tissue unloaded length. The difference in the numerical values of the $X$-axis between Figs. 3 and 2 reflects the growth and pressure-induced increase in length. Fibers with recruitment stretch higher than unity are wavy at the unloaded length. Fibers having recruitment stretch lower than unity are already stretched in the unloaded length thereby balancing the matrix osmotic pressure. The gradually fading discontinuity in the rising part of the distributions represents the effect of the assumed initial uniformity of the fibers lengths (Fig. 1B)

The functional manifestation of growth-induced change in the fibers mass density distribution is seen in the evolution of fiber bundle response (no matrix osmotic effects) to mutually identical short test protocols along the growth duration. Initially (growth time $t=0$), all fibers are straight and manifest linear stress–stretch relationship (Fig. 4A). Later on, as the fibers acquire distribution of recruitment stretch and their stress response to the test protocol reduces in magnitude becoming convexly nonlinear and seemingly stable after sufficient growth duration. In parallel, the stress–stretch curves move to the right toward higher stretch levels. The total force response follows initially a similar pattern to that of the stress, but deviates from it thereafter increasing in magnitude due to the increase in cross-sectional area (Fig. 4B).

Fig. 4

Effect of growth on the fiber bundle (no osmotic effects) global mechanical response, presented at selected time laps along the growth period. A The bundle first Piola-Kirchoff (PK1) stress as function of its stretch. B The corresponding bundle total force. Curves represent responses at growth times $t=0 (+)$, $t=0.05*\hbox {t}_{\mathrm{f}}$, $t=0.08*\hbox {t}_{\mathrm{f}}$, $t=0.20*\hbox {t}_{\mathrm{f}}, \hbox {t}=\hbox {t}_{\mathrm{f}}\, (\hbox {t}_{\mathrm{f}}$ being the duration of the simulated growth period). Note the shift to the right of the curves origins (by $\Lambda _{\mathrm{mat}}^{\mathrm{osm}} (t)$, Eq. 2.37) and the initial linear response (at growth time $t=0$) of the straight fibers, which gradually develops with growth to convexly nonlinear response commonly observed in tissues

The predicted responses to the test protocols in terms of the experimentally observable stress–stretch properties of the whole tissue (fibers and matrix) are shown in Fig. 5A. The convexly nonlinear patterns are similar to those of the bundle itself (Fig. 4A), yet there are differences. First, the origins of the tissue response curves remain at tissue stretch of unity along the entire growth duration (Fig. 5A). Second, the stress magnitudes at corresponding stretch levels are in general higher in the tissue than those of the bundle. Finally, although in common with the results of Fig. 4A there is an initial drop in the stress level (at growth time $t=0.05*tf$), here at later times the tissue stress (Fig. 5A) picks up to attain higher stress levels.

Fig. 5

Evolution of the tissue (fibers in osmotic active matrix) global mechanical properties at selected time laps along the growth period. A The tissue first Piola-Kirchoff stress as function of its stretch. B The corresponding tissue total force. Curves designations as in Fig. 4. The initial linear response (at $t=0$) of the uniformly straight fibers, develops gradually to convexly nonlinear ones along the growth period

Tissue pre-stress and associated pre-stretch are additional readily observable features. Their evolution with growth time is presented in Fig. 6A,B, respectively. The results suggest that both pre-stress and pre-stretch tend to approach asymptotically constant levels, and that the stable pre-stretch is close to the simulated highest homeostatic stretch (1.08).

Fig. 6

Growth-induced development of in situ tissue pre-stress (a) and tissue pre-stretch (b). Both pre-stress and pre-stretch are predicted to asymptotically approach constant levels

3 Discussion

A theory was developed for analyzing G&R based on fundamental mechano-biological turnover events occurring at the constituents’ level, and on the resulting evolution of the tissue structure and properties. The theory considers growth and remodeling adaptation that may occur following but excluding the process of morphogenesis. In other words, during G&R, tissues maintain their overall geometrical and structural nature (e.g., type of fibers, unidirectional versus multi-directional fibers networks, flat versus cylindrical geometry, lamellae structure in the arterial media). The features which can be changed by G&R are the quantities of tissue constituents and their attributes such as deposition stretch and orientation distribution. The theory presented here is a framework linking local fundamental mechano-kinetic events with macro manifestation of tissue G&R. As such, it is a mechanistic theory which relies on both the local basic turnover processes and on the associated micro-structural manifestation of them. Hence, although it may not include all the processes involved in tissue G&R, it is of sufficient generality to be able to incorporate additional processes which may prove to be of significance.

The main advantages of the present theory are that it is based on first principles and fundamental processes involved in the evolving tissue micro-structure, free of ad hoc assumptions regarding the consequence and phenomenology of structural G&R manifestation. The theory accounts for G&R features which have not been previously addressed, namely the evolutions of non-uniform fiber undulation and of the tissue pre-stretch and pre-stress.

The present theory considers tissue G&R as stemming from the sum of local G&R processes in the fiber level. An important advantage of this approach is that it circumvents a fundamental unresolved difficulty of defining finite growth (which includes mass change) in the framework of general continuum mechanics. In a number of previous G&R models, growth was prescribed by an associated deformation gradient (Rodriguez et al. 1994). However, as Cowin pointed out (Cowin 2010), finite growth cannot be prescribed by a deformation gradient since the associated motion is not bijective (one-to-one and onto). In bijective motion every element (e.g., fiber) in the tissue at time $t$ is mapped to by exactly one element in the tissue at the reference state, so that the motion of the element corresponds in a one-to-one link via the time-dependent deformation field. The motion in tissue G&R is not bijective since fibers are continuously degraded and new ones are produced. The present micro-structural formulation circumvents this difficulty of non-bijective G&R motion since each fiber is labeled by its birth length (or birth stretch) which links in a one-to-one correspondence between the fiber and tissue motions (Eqs. 2.38 and 2.39). Hence, the G&R motion in the current formulation is bijective-like, perhaps “pseudo bijective.”

Incidentally, the difficulty associated with tissue motion not being bijective, and the manner by which it can be circumvented have already been previously applied in the micro-structural theory of the mechanics of inert tissue (no G&R) (Lanir 1979, 1983). In that theory, although there is no fibers turnover, fibers are gradually recruited with increasing stretch to become active in load bearing. Hence, at each instant, fibers not recruited are not a part of the load bearing tissue mass and are thus effectively non-existent. Hence, the effective mass of the tissue increases with increasing stretch as fibers are recruited. Yet, during this recruiting process, each fiber recruitment length is known, so that the fiber and the tissue motions correspond one-to-one.

The rule of mixtures used here to evaluate the global tissue response finds its theoretical basis in general mixture theory (Truesdell 1962). In the context of soft tissues’ equilibrium response, the application of the rule of mixtures encompasses two implicit assumptions: (i) under equilibrium there is no mechanical interaction between existing tissue constituents; (ii) newly produced constituents do not affect the response of extant ones. These assumptions represent a special case and may not be valid in a general growing continuum.

The constrained mixture approach to G&R (Humphrey and Rajagopal 2002) is consistent with the present theory in two ways: first, in that the global tissue response is evaluated from its constituents’ responses by application of the rule of mixtures. Second, in incorporation of evolving constituents’ natural configurations. The main difference between the two approaches is that structure is not considered in the classical mixture theory, while it is a fundamental feature of the present one.

3.1 Assumptions of the general theory

The dependence of turnover rate on stress is excluded (assumption k3) since stress is an abstract man-created concept that cannot be directly measured (Cowin 2004). On the other hand, since a key element of the theory is the evolving fibers gauge length, there is no difficulty in defining each fiber true strain, thus avoiding the difficulty in adopting strain as a G&R stimulus, a difficulty which exists in non-structural G&R models. Dependence on strain rate (Cowin 1996) can be readily incorporated into the present theory in relevant cases.

The assumed dependence of degradation kinetics on the fibers deformation reflects observations of a number of previous studies. Mechano-enzymatic studies on both reconstituted bovine collagen (Huang and Yannas 1977) and on intact rabbit tendon (Nabeshima et al. 1996) reveal that under 4 % strain there is a reduction in the rate of enzymatic degradation and an associate increase in the tensile failure strain compared to unloaded control. Higher strain causes an increase in the degradation rate. In another study on uni-axially loaded cornea subjected to enzymatic degradation, it was found that in the same sample, loss of collagen fibers birefringence (i.e., cleaved fibers) occurred only in the fibers aligned normal to the stretch direction (therefore un-stretched) while stretched fibers maintained their fibrillar nature (Ruberti and Hallab 2005). At the other end of the strain range, in tensile tests of bovine tail tendon collagen stretched up to its damage region, it was found that over-stretch significantly enhanced the fibers proteolysis by the serine enzyme acetyltrypsin, and likewise but to a lesser degree by $\upalpha$-chymotrypsin (Willett et al. 2007). The authors attributed the over-stretch effect to observed (by previous X-ray studies) stretch-induced intra-fiber sliding at the inter-fibril and intermolecular levels which result in the exposure of susceptible domains to the enzyme. The latter is attributed to stretch-induced disruption of semicrystalline lattice structure of collagen fibers, thereby liberating individual molecules from restrictions (created by their nearest neighbors) on their thermal movement. When thus liberated to move, these molecules are allowed to achieve greater numbers of conformations, which translates into increased probability for protease binding and catalysis (Willett et al. 2007).

The quantitative aspect of tissue constituents’ participation in G&R turnover is at present insufficiently known. The turnover rate decreases significantly from the embryonic stage toward maturity. There are, however, significant differences between tissue constituents. For collagen type 1, the rate of turnover depends on species, tissue and age (Mays et al. 1991), and the kinetics seems to follow a multi-compartment first-order model (Kao et al. 1977; Niedermuller et al. 1977; Sodek and Ferrier 1988) with characteristic time at maturity of weeks to months. Elastin, on the other hand at maturity is extremely stable against enzymatic and thermal denaturation with characteristic turnover time of many years. SMC respond to growth in two different ways. These cells (including vascular SMC (Martinez-Lemus et al. 2004)) exhibit the property of length adaptation which results from the malleability of the muscle myofilament lattice. The malleability appears to stem from plastic rearrangement of contractile and cytoskeleton filaments in response to the muscle cell loading. This rearrangement allows the muscle to adapt to a wide range of cell lengths, yet maintain optimal tension and contractility (Kerckhoffs et al. 2012; Langille et al. 1989; Seow 2005). In addition to their plastic length adaptation, SMC participate in G&R also by increasing their number during growth [with estimated replication rate of 0.06 % per day (Schwartz et al. 1990)].

3.2 Assumptions of the specific realization

In view of the present scarcity of relevant data, the actual constituents turnover kinetics can be incorporated in future realizations of the present theory when data becomes available. The first-order rate kinetics (assumption s3) in the specific realization of the theory is a simplification which does not capture the full range of the turnover kinetics which involves a number of cellular compartments and processes (Kao et al. 1977). However, although a simplification, the assumed first-order kinetics is still valuable since it captures the nature and significance of the interplay between mechanical and biological processes during G&R.

The fibers and tissue hydrations result from their osmotic properties which are determined by the fibers internal environment and by the fixed charge density of the extra-fibrillar matrix proteoglycans (Maroudas et al. 1991). Both are tissue specific. They may change with age (Sivan et al. 2006), with sustained altered loading (Koob et al. 1992), and consequently with location in the organ (e.g., (Azeloglu et al. 2008)). Both fibers and proteoglycans are produced by the tissue cells in their attempt to maintain constant homeostatic physical environment. Hence, it is not unreasonable to expect that during the slow process of G&R, the tissue fixed charge density and thus its hydration are maintained at constant levels (Gleason and Humphrey 2005) (assumption s2).

Both degradation and production of matrix fibers are regulated by the tissue cells. For degradation, the cells (e.g., SMC and fibroblasts) secrete matrix metalloproteinases (MMPs) which are zinc-dependent peptide enzymes. In vitro studies have shown that increased mechanical loading promotes both the secretion of MMP-2 and MMP-9 by these cells (Kim et al. 2009), and the synthesis of new collagen (Arts et al. 2012; Carver et al. 1991; Li et al. 1998). Indeed, under in vivo, it was shown that exercise increases both the synthesis and degradation of collagen in human peritendinous region of Achiles tendon, but the anabolic process dominated ((Langberg et al. 2001)). There seems thus to be a link between fibers degradation and production. In the specific realization, this link is taken to be of proportionality form (assumption s4).

Fibrils are deposited under stretch. It appears that cells need to be under external tension of the ECM fibers in order to proliferate and maintain bioactivity (Grinnell 1994). Collagen fibrils acquire their deposition stretch by the action of their secretion cells (e.g., fibroblasts) which crawl over them and tugging on them (Alberts et al. 2002). A specific mechanism was proposed for fibroblasts whereby the cells lamellipodia extend along held collagen fibers, bind and retract them in a ’hand-over-hand’ cycle, involving $\alpha _2 \beta _1$ integrins (Meshel et al. 2005). There are tissue differences with respect to the collagen fibril arrangement and organization in the matrix, even for the same type of collagen (Alberts et al. 2002). In parallel, there are differences in deposition stretch between different types of tissues (Eastwood et al. 1996; Harris et al. 1981). Since the cells seek to maintain a favorable mechanical environment, it is not surprising that fibers tend to be deposited under homeostatic stretch (Ellsmere et al. 1999). But since there seems to be a range of homeostatic stretch, there is no a priori reason to favor a single level of homeostatic stretch. Hence, in the specific realization of the theory, it was assumed that the deposition stretch is normally distributed within the fibril homeostatic stretch range (assumption s6).

Selected levels of the model parameters

In the specific realization of the theory, the selected levels of the stretch-dependent degradation parameters (which include the stretch ranges of hypo-homeostatic, homeostatic and hyper- homeostatic regions and the corresponding rate constants) were motivated by mechano-enzymatic studies reviewed above. In addition, in a recent detailed quantitative study of the strain effect on collagen proteolysis (Wyatt et al. 2009), it was observed that increased strain reduces the rate of enzymatic cleavage of tendon collagen and that there are three distinct strain ranges: at strain $\upvarepsilon < 3\,\%$ (roughly within the stress–strain toe region), the cleavage rate is constant, but drops sharply by roughly 50 % at $\upvarepsilon = 3\,\%$ and remains at that level in the strain range $3<\upvarepsilon < 5\,\%$. In the strain range $5<\varepsilon < 10\,\%$ (corresponding to the range where the collagen molecule triple-helix is stretched), the cleavage rate was found to decline linearly with strain.

The collagen half-life can vary considerably with age and under pathological conditions. In normotensive rat arteries it was found to be about 60–70 days (Nissen et al. 1978). This implies degradation rate constants ($B^{dd}$ and $B^{db}$) in the order of between $10^{-7}$ and $10^{-6}\hbox {s}^{-1}$ which correspond to the levels used in the specific realization.

The chosen level of collagen stiffness (100 MPa) is within the range of measured tendon data (Butler et al. 1984). The selected collagen volume fraction (0.10) corresponds approximately to its dry volume fraction in the skin (0.09 (Lokshin and Lanir 2009)) and to its percentage per wet tissue weight in the cartilage (18 %), considering that water accounts for about 75 % of the tissue weight (Maroudas et al. 1980).

Osmotic pressure in unloaded articular cartilage is approximately 2.5 atmospheres. In other soft tissues (e.g., tendon, skin arterial wall), the proteoglycans fixed charge density (FCD) is approximately 10 % of its level in the cartilage (Azeloglu et al. 2008; Gaudette et al. 2004). Since the tissue osmotic pressure was found to increase with the square of its FCD (Basser et al. 1998; Urban and McMullin 1985), the level of $P_{\mathrm{mat}}$ was selected here to equal 1 % of that of the cartilage, namely 2500 Pa.

Analysis of the sensitivity of the model predictions to its parameters should consider both the highly nonlinear nature of the model, and the significant interactions which exist between parameters. The latter implies that sensitivity analysis via perturbations of a single parameter may result in misleading conclusions since this sensitivity depends critically on the levels of other ones. Hence, a realistic sensitivity analysis should consider the multi-dimensional “sensitivity regions,” similar to the concept of confidence regions (in contrast to confidence intervals) in the theory of parameter estimation. The highly nonlinear nature of the model implies that interactions between parameters may critically depend on their values. For these reasons, a reliable sensitivity analysis in the present formulation involves an extensive multi-faced analysis which warrants a special study. This is left for future work (with two exceptions detailed below). Some qualitative insights can, however, be gained based on the model physical nature. For example, both the fibers volume fraction $(\Phi _f^0 )$ and their stiffness $(K)$ are likely to have mutually similar effects on the bundle and tissue mechanical responses (Figs. 4, 5, 6B), but no effect on the kinetics-driven evolution of the bundle structure (Figs. 1, 2, 3). The homeostatic stretch range $([\lambda _1 , \lambda _2 ])$ and the degradation reaction constants $(B^{db}, B^{dd})$ determine the rate of fibers turnover. They are thus expected to have significant effects on the evolving tissue dimensions and mass (Figs. 1D,E), on the fibers bundle structure (Figs. 2, 3), and on the mechanical responses of the bundle and tissue (Figs. 4, 5). In addition, these four parameters interact significantly between themselves and with the tissue rate of growth.

The sensitivities to two parameters, SDR and $P_{\mathrm{mat}}$ are less obvious. In addition, their physiological levels are less clear compared with other parameters. There are no data on the synthesis-to-degradation ratio (SDR). The matrix osmotic-driven pressure $(P_{\mathrm{mat}} )$ is well known in tissues like the articular cartilage and intervertebral disk but may vary in other tissues depending on the nature and magnitude of their loadings. In view of these considerations, their specific sensitivities where studied (“Appendix 3”) for the case in which all other parameters were held constant at their selected reference levels. The results demonstrate that SDR has insignificant or no effects on the mass and recruitment density distributions and on the bundle stress–stretch relationships, and has very little effect on the tissue stress–stretch relationships and on the tissue pre-stretch and pre-stress (results not shown). On the other hand, SDR affects significantly the evolution of the cross-sectional area and mass (Fig. 8), thereby altering also the bundle and tissue force-stretch relationships (Fig. 9). The osmotic-driven matrix pressure $P_{\mathrm{mat}}$ was found to have no effect on attributes such as the evolutions of the mass and cross-sectional area and the mass recruitment densities (results not shown). Only under extremely high perturbations, $P_{\mathrm{mat}}$ was found to have small effects on the tissue stress–stretch and force–stretch relationships (Fig. 10) and on the tissue pre-stretch and pre-stress (Fig. 11).

3.3 Results of the specific realization

In attempting to test the feasibility of the new G&R theory and its specific realization, predictions were contrasted against soft tissues measured and observed response features. Most importantly, the results depicted in Fig. 3 are compatible with the hypothesis that mechano-biological interaction between growth-induced tissue stretch and kinetics of the fibers turnover result (after sufficient growth time) in the commonly observed distribution of the fibers recruitment stretch and in the associated tissue convex nonlinear stress-strain response (Viidik 1972; Zhao et al. 2013).

The results highlight a number of additional interesting points. Both predicted tissue cross-sectional area and fibers total mass are seen to increase exponentially with growth time (Fig. 1). These predictions are valid only under the assumed constant rates of both growth and turnover reaction constants throughout the growth period. In reality, the growth rate and turnover kinetics can change with age during growth.

The initial condition for the fibers mass density distribution was taken to be homogeneous with all fibers straight and un-stretched at the initial reference length. Hence, all fibers have initially the same birth stretch $\lambda _f^b =1.0$ (Fig. 1b). To check the effect of the initial distribution on the evolving fibers mass density distribution, the simulation was run with different initial mass distributions. It was found (results not shown) that the growth induced features are affected by the initial conditions only at times close to the onset of growth, but this fades quickly away with growth time so that after longer times ($t>0.05*tf$ in the present case) both the fibers recruitment density distribution and resulting tissue mechanical response are indistinguishable from those in Figs. 3 and 5.

The functional importance of osmotic pressure (even if of small magnitude) is seen when comparing the bundle with the tissue responses to the test protocols (Fig. 4 vs. 5). Simply stated, the osmotic-derived tissue hydrostatic pressure stretches the tissue until the bundle stress counter-balances the matrix pressure. The magnitude of this stretch is significant due to the flat nature of the bundle response at low stretches. This adjustment of the tissue reference length has important functional consequences. First, the long range of bundle stretch manifesting zero stress is absent in the tissue. In addition, the bundle is under residual stress at the load-free tissue reference configuration. From the structural point of view, the lowest stretch level of the fibers density distribution is lower than unity, implying that the initial slope of the tissue stress-strain relationship, although small, is not zero. Finally, the tissue exhibits an apparent stiffer response than that of the bundle at comparable stretches. This stems from the convexly nonlinear response of the bundle, so that when pre-stretched by the pressure toward higher stretch levels, the slope of the tissue stress-strain response (i.e., its stiffness) at apparently comparable stretches is higher than that of the bundle. Hence, the osmotic pressure seems to stiffen the tissue (Eastwood et al. 1996).

In the specific realization, the tissue pre-stress (and pre-stretch) following stabilization, approach asymptotic levels (Fig. 6). The reason being that if the pre-stretch exceeds the highest homeostatic stretch, fibers degrade at higher rate and are replaced by longer fibers deposited under homeostatic stretch. This raises the question of how tissues such as arteries sustain axial pre-stretch of up to 1.6 in the aorta (Han and Fung 1995) or 1.4 in the left anterior descending coronary artery (Lu et al. 2003) with blood pressure exceeding 100 mmHg? The results here suggest that collagen fibers with their comparatively high rate of turnover cannot sustain such levels of axial and radial stretching. It is therefore speculated that in tissues having elastin as a significant component (such as the arterial wall), it is the elastin, known for its very low rate of turnover with half time of many years, is the component which bears these levels of pre-loading without being replaced for long time periods.

The growth-induced fiber mass density distribution gives rise to buckling of some fibers and their resulting wavy (undulated) disposition when the tissue is at its unloaded length. This applies to fibers with recruitment (straightening) stretches higher than unity (Fig. 3). Upon tissue extension these fibers gradually recruit to become stretched and load bearing. The other fibers (i.e., whose straightening stretch is lower than unity) are already stretched at the tissue load-free reference and their combined tension balances the matrix osmotic pressure. The experimentally measurable fibers recruitment density distribution function (Eq. 2.41) can be derived from their mass density distribution and vice versa.

The dynamics of the growth-induced remodeling is determined by the characteristic times of the mechanisms involved. In the specific realization, the characteristic degradation time is $10^{6}$–$10^{7}$ s (the inverse of the $B'$s values in Eqs. 2.23 and 2.24). Hence, it is expected that the effect of the initial fibers birth stretch distribution on its evolution with time will fade away for growth times higher than $10^{6}-10^{7}$ seconds. The results depicted in Fig. 3 support this since at $t=0.2\cdot tf(=12{,}440{,}000$ s) the assumed initial sharp density distribution (Fig. 1B) can no longer be seen. The effect of the loading dynamics (e.g., routine daily activity, special physical training) was not included in the specific realization since its characteristic time (order of $1 {\text {day}}=86,440\,{\text {s}}$) is much shorter than the characteristic degradation time. Hence, the effect of loading dynamics is expected to be damped.

The specific realization has limitations. First, just one type of fiber (collagen) is considered. This is suitable for tendons and ligaments, but insufficient for other tissue having elastin or SMCs as components of their micro-structure. The choice to consider one type of fiber was done to facilitate clearer insight into the consequences of mechano-kinetic interaction, free of the added complexity of multi-component investigation. Integration of several types of fibers can be readily carried out, as outlined in the general theory (Sect. 2.2). Another limitation (rationalized above) is the assumed first-order kinetics of the fiber degradation (and production). It was previously suggested that collagen secretion involves at least two separate first-order processes (Kao et al. 1977). The assumed first-order kinetics is not expected to have significant effects on the study results and conclusions since the effects of kinetics order fade away after long growth period. The platform developed is sufficiently general to incorporate other types of turnover kinetics in future studies. Finally, growth induced changes in composition of the tissue have not been addressed in the realization of the theory, which considers collagen fibers and fluid-like matrix. Naturally, if elastin fibers and/or SMCs were included (along the guidelines of Sect. 2.2) then owing to the differences in turnover kinetics between constituents, the tissue composition would change with growth.

In summary, a mechanistic theory was developed for growth and remodeling of soft tissues with unidirectional fibers. It is based on the fibers fundamental mechano-kinetic turnover processes and predicts the resulting evolution of the tissue micro-structure, its size and its mechanical properties. The theory constitutes a general framework which can incorporate multiple types of fibers having different mechanical properties and turnover kinetics. The feasibility of the new theory was examined via a specific realization. The predictions support the notion that the commonly observed distribution of the fibers’ undulation and the associated tissues convex nonlinear stress stretch response result from interaction of the fibers’ turnover with their growth-induced stretching.

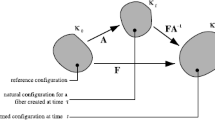
4 Appendix 1: A scheme of the tissue structure and its constituents stresses

Figure 7 depicts a scheme of the unidirectional tissue with one type of fibers (collagen). The fibers are non-uniformly undulated due to their distributed birth length. They thus recruit (become stretched and load bearing) at distributed tissue stretch. The total tissue stress is the sum of the fibers stresses and the fluid matrix pressure.

Fig. 7

A scheme of the simulated tissue structure and its constituents stresses

5 Appendix 2: Derivation of Eq. (2.41)

In classical tissue mechanics, the measurable strain and stress are referenced to the tissue unloaded reference configuration. In the structural theory for hyper-elastic soft tissues (Lanir 1979, 1983), the bundle strain energy is given by the weighted sum of the fibers strain energies,

$$\begin{aligned} W_{\mathrm{bun}} (E_{\mathrm{bun}} ,t)=\Phi _f^0 \cdot \int \limits _{\forall \lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} } {D(\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} ,\hbox {t})} \cdot w_f (e_f )\cdot \hbox {d}\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}}\nonumber \\ \end{aligned}$$

(5.1)

where $\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}}$ is the fiber-in-tissue recruitment stretch and $D(\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} )$ is the volume (or mass) density distribution such that the fraction of fibers with recruitment stretch between $\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}}$ and $\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} +\hbox {d}\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}}$ is $D(\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}} )\cdot \hbox {d}\lambda _{f, \mathrm{tiss}}^{\mathrm{rec}}$.

On the other hand, in the present G&R theory, the bundle strain energy expressed as a function of the tissue strain (instead of the bundle one) is

$$\begin{aligned} W_{\mathrm{bun}} (E_{\mathrm{bun}} ,t) =(\Phi _f^0 /M_f (t)) \cdot \! \int \limits _{\lambda _f^b } {m_f (\lambda _f^b ,t)\cdot w_f (e_f )\cdot {\text {d}}} \lambda _f^b\nonumber \\ \end{aligned}$$

(5.2)

The integration variable $\lambda _f^b$ in Eq. 5.2 can be replaced by $\lambda _{f,\mathrm{tiss}}^{\mathrm{rec}}$ of Eq. 5.1 by using Eq. 2.38 to yield

$$\begin{aligned} \hbox {d}\lambda _f^b =\Lambda _{\mathrm{tiss}}^{\mathrm{ref}} (t)\cdot \hbox {d}\lambda _{f,\mathrm{tiss}}^{\mathrm{rec}} \end{aligned}$$

(5.3)

By equating the two expressions for $W_{\mathrm{bun}}$ in Eqs. (5.1) and (5.2), the desired Eq. (2.41) is obtained.

6 Appendix 3: Sensitivity analysis

The analysis focuses on the effects of two parameters, the synthesis-to-degradation ratio (SDR) and the matrix pressure $(P_{\mathrm{mat}})$. The ratio SDR was found to affect solely the evolutions of the tissue cross-sectional area and mass. The magnitudes of these effects are most significant. Figure 8 shows that even small perturbations (3 %) in SDR from its reference level of 1.05 induce significant alterations in the evolution of the tissue cross-sectional area (A) and mass (B). These induce in turn equivalent large changes in the bundle and tissue force–stretch relationships (Fig. 9) but not in the stresses which are unaffected (results not shown).

Fig. 8

Effects of perturbations in the synthesis-to-degradation ratio (SDR) on the evolution of the tissue cross-sectional area (A) and mass (B). The SDR levels are 1.02, 1.05 and 1.08

Fig. 9

Effects of perturbations in the synthesis-to-degradation ratio (SDR) on the bundle’s (A) and the tissue’s (B) force-stretch relationships. Depicted are the corresponding responses at the end of the simulated growth period

The matrix pressure $P_{\mathrm{mat}}$ was found to have no effect on the model predictions with the exception of very small effects it has on the tissue stress–stretch and force–stretch relationships (Fig. 10). The tissue responses are seen to be mostly affected under 10-fold increase of the matrix pressure from 2,500 Pa at reference to 25,000 Pa, the latter figure being typical of the articular cartilage with its high concentration of osmotic active proteoglycans. The matrix pressure was found to have likewise a small effect on the evolution of the tissue pre-stretch and pre-stress (Fig. 11). These effects are small even under the large simulated perturbations in $P_{\mathrm{mat}}$.

Fig. 10

Effects of perturbations in the matrix pressure $P_{\mathrm{mat}}$ on the tissue stress–stretch (A) and force–stretch (B) relationships. Depicted are the corresponding relationships at the end of the simulated growth period. The $P_{\mathrm{mat}}$ levels are 250, 2,500, 25,000 Pa

Fig. 11

Effects of perturbations in the matrix pressure $P_{\mathrm{mat}}$ on the evolution of the tissue pre-stress (a) and pre-stretch (b)