Time-evolving collagen-like structural fibers in soft tissues: biaxial loading and spherical inflation

Abstract

This work considers a previously developed constitutive theory for the time dependent mechanical response of fibrous soft tissue resulting from the time dependent remodeling of a collagen fiber network that is embedded in a ground substance matrix. The matrix is taken to be an incompressible nonlinear elastic solid. The remodeling process consists of the continual dissolution of existing fibers and the creation of new fibers. Motivated by experimental reports on the enzyme degradation of collagen fibers, the remodeling is governed by first order chemical kinetics such that the dissolution rate is dependent upon the fiber stretch. The resulting time dependent mechanical response is sensitive to the natural configuration of the fibers when they are created, and different assumptions on the nature of the fiber’s stress free state are considered here. The response under biaxial loading, a type of loading that has particular significance for the characterization of biological materials, is studied. The inflation of a spherical membrane is then analyzed in terms of the equal biaxial stretch that occurs in the membrane approximation. Different assumptions on the natural configuration of the fibers, combined with their time dependent dissolution and reforming, are shown to emulate alternative forms of creep and relaxation response. This formal similarity to viscoelastic phenomena occurs even though the underlying mechanisms are fundamentally different from the mechanism of macromolecular reconfiguration that one typically associates with viscoelastic response.

1 Introduction

Biological soft tissues such as arteries (Holzapfel and Ogden 2010) and cervical tissues (Myers et al. 2015) consist of a mixture of a matrix material and collagen fibers. One of the aims of soft tissue biomechanics is to understand and to describe the mechanical properties of the resultant matrix–collagen fiber system as well as the interaction of the constituents. An important aspect of these biomaterial systems is that the tissue microstructure, and especially the fiber morphology, changes with time due to ongoing processes of growth and remodeling. These changes result from complex biochemical, mechanical, and thermodynamical processes that operate on a variety of length and time scales. To make this remodeling possible, the tissue’s solid phase constituents are infused with a liquid phase that facilitates local transport and provides for the necessary nutrition. This has been treated in the context of the theory of mixtures (Humphrey and Rajagopal 2002, and Myers and Ateshian 2014). The specific role of diffusion in such remodeling processes has been the object of both experimental and modeling studies (Stoffel et al. 2009 and Yi 2013).

The fiber remodeling processes involve the breakdown of existing fibers and their replacement by new fibers in a manner that is directly affected by stress and deformation. The orientation of newly deposited fibers appears to be particularly sensitive to these mechanical effects (Driessen et al. 2008; Karšaj et al. 2009; Shirazi et al. 2011). Recent experiments on the influence of cyclic stimulation on fiber remodeling are reported in Stoffel et al. (2011). Stress mediated fiber remodeling in intracranial saccular aneurysms and intracranial fusiform aneurysms was taken into account by Baek et al. (2005, 2006). As an example of the significance of deformation-dependent remodeling processes in tissue, Rodríguez and Merodio (2010) studied how a loss of strain-mediated stiffening processes leads to instability, i.e., the formation of aneurysms as a result of Marfan’s syndrome.

Degradation of collagen fibers in soft tissue is mediated by enzymes. Experiments indicate that the rate of fiber degradation and resorption is sensitive to the amount of fiber stretch. Specifically it is reported that increasing stretch tends to make the fibers more resistant to breakdown (Bhole et al. 2009; Robitaille et al. 2011). In order to describe this enzyme mediated breakdown, Hadi et al. (2012) represented the network of collagen fibers as rods in a three-dimensional truss-like structure. The rods were simultaneously axially loaded while their radii were subjected to a time dependent decrease that was modeled by a first order differential equation with stretch dependent coefficients.

Motivated by these works, and with the purpose of describing such processes within a broader continuum mechanics setting, Demirkoparan et al. (2013) developed a constitutive framework in which the matrix constituent is treated as an incompressible, isotropic and time-independent hyperelastic ground state matrix, while the fibrous constituent remodels within this matrix by an ongoing process of fiber creation and dissolution. This time-dependent process takes into account the influence of fiber stretch in a manner suggested by the above mentioned experiments. Fiber creation and dissolution are treated as separate processes and the continuum mechanical description of both are affected by the current state of tissue deformation. The state of deformation affects the fiber creation description because the specification of the stress-free (relaxed) state of each newly synthesized fiber would typically depend on the existing state of deformation when the fiber is made. The theory can accommodate different modeling hypotheses as regards the nature of this stress-free state. The state of deformation affects the degradation process by virtue of the already indicated stretch dependent enzymatic degradation rate.

In the theory presented here, all fiber directions are formally equivalent in their original process response. However, because load and deformation typically cause certain directions to stretch more than others, this quickly leads to directional dependence in fiber properties, which then confers anisotropy on the overall material properties. In any given direction, the overall effect is to give a first order chemical kinetics description for the expected lifetime of any individual fiber. This formally makes the material exhibit time-dependent mechanical affects in a manner that is not unlike that of other time-dependent materials. The mechanical response of the tissue therefore exhibits a pronounced rate effect which emerges naturally from the underlying physical description.

Specific time scales can be identified for both the creation and dissolution processes. If the external mechanical environment is held fixed, then these processes can come into balance leading to a steady state fiber morphology. This type of dynamic equilibrium between dissolution of aged fibers and the creation of new replacement fibers with identical properties is a necessary condition for tissue homeostasis. If the mechanical environment is not fixed, meaning that either load or deformation is changing, then there is one type of characteristic response if the boundary conditions change rapidly and a different type of characteristic response if the boundary conditions change slowly. As in other theories for time-dependent materials, such as either linear or nonlinear viscoelasticity, an idealized process with either an infinitely fast or an infinitely slow rate of loading is easily modeled because reduced mathematical models emerge easily from the overall framework under these specialized limits. Also, as in these other theories for time-dependent materials, mechanical processes that proceed at a finite nonzero rate require consideration of the more complicated full mathematical framework, although the specialized fast and slow limits can serve as useful bounds on the process description.

This paper describes how the collagen material model of Demirkoparan et al. (2013) generates such a time-dependent material response. Previous study of the present material constitutive model has focused attention on states of uniaxial loading and simple shearing (Topol et al. 2014, 2015; Topol and Demirkoparan 2014). Here we consider more general conditions of biaxial loading, a type of loading that has particular significance with respect to the characterization of biological materials (Sacks 2000). We also consider the mechanical response of a spherical membrane composed of such a material under symmetric inflation. In this case the material undergoes the same equal biaxial deformation history at each membrane location. The inflation response of even purely hyperelastic materials can be quite complicated (Holzapfel et al. 1996; Holzapfel 2000; Patil et al. 2014; Mangan and Destrade 2015). Specifically within the field of biomechanics the consideration of spherical inflation has a long history (see, e.g., Osborne (1909)). With regard to rate-dependent materials, Wineman (1977) has investigated spherical inflation for viscoelastic membranes. Myers and Wineman (2003) and Wineman (2009) have studied the spherical inflation response of an elastomeric membrane as it undergoes time-dependent processes of scission and formation of new molecular networks. It is therefore natural to study spherical inflation using the constitutive theory for materials undergoing the fiber remodeling processes considered here.

This work is organized as follows: Sect. 2 gives a summary of the material model. Section 3 discusses the time-dependent material response under the separate conditions of biaxial stretch-control and biaxial load-control. Of particular interest is the distinction between the instantaneous short time response and an asymptotic large time response. Using these results, Sect. 4 examines the inflation of a spherical membrane. The broader implications of this modeling are discussed in Sect. 5.

2 Summary of the material model

In view of the somewhat detailed technical development, some commentary on our notation convention is useful. A variety of different constants and functions enter into the treatment, all with various units. We shall often use a superscript ∗ to denote associated dimensionless quantities. This includes a dimensionless time $t^{*}$, dimensionless stress quantities (e.g., $T^{*}_{22}$ in (38)) and dimensionless elastic moduli (e.g., $\mu^{*}$ in (45)). Certain functions are naturally introduced as constitutive functions of specific variables (e.g., the fiber dissolution rate $\eta$ as a function of the stretch invariant $I_{4}$ in (9)), but then, in the context of a specific problem, those variables become a function of other quantities. This causes the original function to then become a direct function of the other quantities. We often use an overscript $\hat{(\cdot )}$ to identify this change in functional dependence (e.g., $\hat{\eta }$ in (29)). Finally, of significant interest is the material response when either load or displacement are suddenly changed. If this sudden change occurs at time $t=0$ then we use $t=0^{-}$ to describe the state of the system just before the sudden change and $t=0^{+}$ to describe the system just after the change.

We consider soft tissue constructs in which a collagen-fiber network permeates a ground substance matrix. When the tissue is deformed, the mechanical response of the matrix does not change with time, while the fibers undergo a time-dependent remodeling process involving destruction of existing fibers and creation of new fibers. These ongoing processes, which endow a time-dependence on the material mechanical response, are heavily influenced by the current state of deformation. The governing relations that seek to describe these processes are presented in this section.

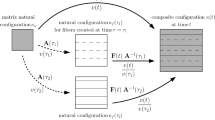
This mechanical response is described with respect to a configuration $\kappa_{0}$ which is the natural configuration for the matrix. The natural configuration for the fibers might be different from that of the matrix. The natural configuration for such fibers might also change so as to be dependent on their time of creation. This is especially to be expected if the fiber’s natural configuration is dependent on the state of deformation when it was created. Hence we introduce the natural configuration $\kappa_{f}(\tau )$ for fibers created at time $\tau$. A deformation gradient tensor $\mathbf{A}(\tau )=\mathbf{A} ^{(\kappa_{0}\rightarrow \kappa_{f}(\tau ))}$ is introduced to describe the mapping from $\kappa_{0}$ to $\kappa_{f}(\tau )$. For a deformation described by the deformation gradient tensor $\mathbf{F}=\mathbf{F}(t)$ from configuration $\kappa_{0}$ to configuration $\kappa (t)=\kappa$, the deformation gradient at time $t$ for the fiber created at time $\tau$ is therefore given by $\mathbf{F}(t) [ \mathbf{A}(\tau ) ] ^{-1}$. These configurations and deformation gradients are illustrated in Fig. 1.

Fig. 1

The different material configurations. The natural configuration of the matrix serves as the reference configuration

A significant question concerns the determination of $\mathbf {A}(\tau )$ because this is directly dependent on how collagen fibers are created by the tissue fibroblasts within the ground substance. We consider two hypothetical deposition processes and this motivates the consideration of two alternatives for the stipulation of $\mathbf {A}(\tau )$:

• If the fibers exhibit prestress when created so as to be in the same deformed state as the surrounding matrix then both the matrix and the fiber constituents share the same natural configuration, i.e., $\kappa_{0}=\kappa_{f}$. In this case $\mathbf {A}=\mathbf {I}$, where $\mathbf {I}$ is the identity tensor.

• If the fibers are undeformed at their time of creation $\tau$, then the fiber natural configuration is identical with the current deformation at time $\tau$, i.e., $\kappa_{f}(\tau )=\kappa (\tau )$. In this case $\mathbf {A}(\tau )= \mathbf {F}(\tau )$.

For any stipulation of $\mathbf {A}(\tau )$, a unit vector $\mathbf{N}= \mathbf{N}^{\kappa_{0}}$ along a line element in $\kappa_{0}$ deforms into $\mathbf{F}\mathbf{N}$ in $\kappa (t)$. Its stretch ratio is $\varLambda =\varLambda^{(\kappa_{0}\rightarrow \kappa )}=\sqrt{ \mathbf{F}\mathbf{N}\cdot \mathbf{F}\mathbf{N}}= \sqrt{\mathbf{N} \cdot \mathbf{C}\mathbf{N}}$, where $\mathbf{C}=\mathbf{C}^{(\kappa _{0}\rightarrow \kappa )}=\mathbf{F}^{T}\mathbf{F}$ is the right Cauchy–Green tensor for the deformation $\kappa_{0}\rightarrow \kappa (t)$. A unit vector $\mathbf{N}^{\kappa_{f}}$ in the fiber natural configuration $\kappa_{f}$ is related to the corresponding unit vector $\mathbf{N}=\mathbf{N}^{\kappa_{0}}$ in configuration $\kappa_{0}$ by

$$ \mathbf{N}^{\kappa_{f}}=\frac{\mathbf{A}\mathbf{N}}{\Vert \mathbf{A} \mathbf{N}\Vert }. $$

(1)

This unit vector deforms into

$$ \mathbf{F}(t)\mathbf{A}^{-1}\mathbf{N}^{\kappa_{f}}=\frac{\mathbf{F}(t) \mathbf{N}}{\Vert \mathbf{A}\mathbf{N}\Vert } $$

(2)

in configuration $\kappa (t)$, with stretch ratio $\hat{\varLambda }= \hat{\varLambda }^{(\kappa_{f}\to \kappa )}$ given by

$$ \hat{\varLambda }\bigl(\mathbf{C}(t),\mathbf{N},\mathbf{A}(\tau )\bigr)= \frac{\sqrt{ \mathbf{F}(t)\mathbf{N}\cdot \mathbf{F}(t)\mathbf{N}}}{\sqrt{ \mathbf{A}(\tau )\mathbf{N}\cdot \mathbf{A}(\tau )\mathbf{N}}} =\sqrt{\frac{ \mathbf{N}\cdot \mathbf{C}(t)\mathbf{N}}{\mathbf{A}(\tau )\mathbf{N} \cdot \mathbf{A}(\tau )\mathbf{N}}}. $$

(3)

As discussed by Holzapfel and Ogden (2010), many soft tissues can be treated as incompressible so that $\det \mathbf {F}=1$. At each instant of time, the body is assumed to respond as an anisotropic hyperelastic material whose Helmholtz free energy density is denoted by $W$. Each point $\mathbf{X}$ in the reference configuration is regarded as containing both fibrous and matrix components in the standard manner of continuum mechanics. In other words, the fiber and matrix components are not spatially resolved in this treatment; instead $W$ is a bulk averaged energy density that may be regarded as following from a suitable homogenization treatment of a finer scale representative volume element. In modeling fiber reinforced materials, $W$ is often decomposed into $W=W_{m}+W_{f}$, where $W_{m}$ represents the contribution from the matrix constituent and $W_{f}$ represents the contribution of the fibrous components. The constitutive relation for the Cauchy stress tensor $\mathbf {T}$ in such a hyperelastic model then has the form

$$ {\mathbf{T}}=-p\mathbf{I}+2\mathbf{F}\frac{\partial {W}}{\partial {\mathbf{C}}} \mathbf{F}^{T},\quad \mbox{where } W=W_{m}+W_{f}, $$

(4)

and $p$ is a scalar resulting from the incompressibility constraint. For the time-dependent fiber dissolution and reassembly process considered here, $W_{f}$ takes on a time dependence that is a reflection of this changing microstructure. The matrix contribution $W_{m}$ describes the ground substance which is assumed to be isotropic with $W_{m}=W_{m}(I_{1}, I_{2})$, where $I_{1}$ and $I_{2}$ are the invariants of $\mathbf {C}$ associated with isotropy. Any time dependence in this ground substance is taken to be negligible compared to that of the fiber constituent. In this paper, it is sufficient to describe this matrix constituent as a neo-Hookean material with

$$ W_{m}(I_{1})=\frac{\mu }{2} [ I_{1}-3 ] $$

(5)

where $\mu \geq 0$ is a material parameter.

In contrast, the Helmholtz free energy density function for the collagen fiber network reflects the time-dependent chemomechanical processes that govern the fiber dissolution and regeneration. These processes are continuously ongoing such that the current state of the fiber morphology is a consequence of deformation mediated events whose influence extends back in time. As discussed in Demirkoparan et al. (2013) and briefly recapitulated here, the consideration of these processes motivates a mathematical description of $W_{f}$ in the form

$$ W_{f} = \int_{\mathbf {N}} \int_{-\infty }^{t} \psi \bigl(I_{4}\bigl(\mathbf{C}(t), \mathbf {N}, \mathbf{A}(\tau )\bigr)\bigr)\zeta (t,\mathbf {N}, \tau ) \,\mathrm{d}\tau \,\mathrm{d}\mathbf {N}, $$

(6)

where $\int_{\mathbf {N}} \ldots \mathrm{d}\mathbf {N}$ is a notation for the integration over the unit sphere, and $\psi =\psi (I_{4}(\mathbf{C}(t), \mathbf {N}, \mathbf{A}(\tau )))$ is the Helmholtz free energy density function for a single fiber, a protofiber, with orientation $\mathbf {N}$.

The nature of this type of model is that each location $\mathbf {x}$ is regarded as containing both matrix and fiber constituents. Furthermore, each such continuum point is regarded as containing fibers in all directions. The integral with respect to $\mathbf {N}$ in (6) takes all such fibers into account. Thus the individual protofiber entities are not individually resolved. Instead the treatment makes use of the factor $\zeta =\zeta (t, \mathbf {N},\tau )$. This is the fiber survival kernel; it provides the density of fibers at time $t$ that were created at time $\tau$ with orientation $\mathbf{N}$.

The argument of $\psi$ in (6) is the invariant $I_{4}(\mathbf{C}(t), \mathbf{N},\mathbf{A}(\tau ))=I_{4}^{(\kappa _{f}\rightarrow \kappa )}$ for the fibrous constituent. Such a dependence is consistent with the notion that each protofiber is transversely isotropic in its natural configuration $\kappa_{f}$. For the deformation from $\kappa_{f}$ to $\kappa$ the invariant $I_{4}(\mathbf {C}(t), \mathbf {N}, \mathbf {A}(\tau ))=I_{4}^{(\kappa_{f}\rightarrow \kappa )}$ is

$$ I_{4}=I_{4}^{(\kappa_{f}\rightarrow \kappa )}= \frac{\mathbf {N}\cdot \mathbf {C}(t) \mathbf {N}}{\mathbf {A}(\tau )\mathbf {N}\cdot \mathbf {A}(\tau )\mathbf {N}}. $$

(7)

According to (3), $I_{4}^{(\kappa_{f}\rightarrow \kappa )}= [ \hat{\varLambda }( \mathbf{C}(t),\mathbf{N},\mathbf{A}(\tau )) ] ^{2}$ which represents the square of the fiber stretch. It will be assumed that $\psi$ is given by the relatively standard model form

$$ \psi =\frac{\gamma }{2} [ I_{4}-1 ] ^{2}, $$

(8)

where $\gamma$ is a material stiffness parameter (Qiu and Pence 1997). Other forms for $\psi$ such as those discussed in Holzapfel et al. (2000), Merodio and Ogden (2003), and Holzapfel and Ogden (2010) can be accommodated in the present framework.

The following expression for $\zeta (t,\mathbf{N}, \tau )$ is a consequence of a more fundamental development presented by Demirkoparan et al. (2013). On the basis of first order degradation kinetics, and motivated by the experimental evidence for stretch stabilized fiber dissolution (Bhole et al. 2009; Robitaille et al. 2011), Demirkoparan et al. (2013) developed the expression

$$ \zeta (t, \mathbf {N},\tau )=\chi_{c}\exp \biggl( - \int_{\tau }^{t} \eta \bigl(I _{4} \bigl( \mathbf{C}(s), \mathbf{N}, \mathbf{A}(\tau ) \bigr) \,\mathrm{d}s \biggr) , $$

(9)

where $\chi_{c}$ is a constant fiber creation rate, and $\eta =\eta ( I_{4})$ is the deformation dependent fiber dissolution rate. The fiber survival kernel also permits the determination of the fiber orientation density function

$$ R(t,\mathbf {N}) = \int_{-\infty }^{t} \zeta (t,\mathbf {N},\tau ) \,\mathrm{d} \tau = \chi_{c} \int_{-\infty }^{t} \exp \biggl( - \int_{\tau }^{t} \eta \bigl( I_{4}\bigl(\mathbf{C}(s),\mathbf {N}, \mathbf{A}(\tau )\bigr)\bigr)\,\mathrm{d}s \biggr) \,\mathrm{d}\tau . $$

(10)

A treatment based on (1)–(4), (6)–(7), (9), and (10) represents a rather general homogenized continuum. As developed in Demirkoparan et al. (2013), the various time integrals in (6), (9), and (10) arise from the solution of specific differential equations that describe the interplay of aged fiber dissolution and new replacement fiber creation. On the other hand, the stipulations (5) and (8) are particular modeling choices that are taken here on the basis of standard modeling practice. Another modeling choice is the form of $\eta$ in (9) and (10). Here we seek to model a stretch dependent fiber dissolution rate. For this purpose the form of $\eta$ is taken to be

$$ \eta (I_{4}) = k_{1} I_{4}^{-k_{2}}. $$

(11)

The coefficient $k_{1}$ is a positive constant that has the physical dimension of (time)⁻¹ and represents the reciprocal of a characteristic time for dissolution in the absence of fiber stretch ($I _{4}=1$). The exponent $k_{2}$ represents the influence of fiber stretch on dissolution. The larger the value of $k_{2}$ the smaller is the dissolution rate for a given fiber stretch. Constants $k_{1}$ and $k_{2}$ can be chosen to approximate known experimental results.

In order to obtain the Cauchy stress (4) from (6), we observe from (7) and (8) that

$$ \frac{\partial \psi }{\partial \mathbf {C}}\bigg|_{I_{4}=I_{4}( \mathbf{C},\mathbf {N}, \mathbf{A})}= \biggl\{ \frac{\partial \psi }{ \partial I_{4}}\frac{\partial I_{4}}{\partial \mathbf {C}} \biggr\} \bigg|_{I_{4}=I_{4}(\mathbf{C},\mathbf {N}, \mathbf{A})} = \gamma \frac{I_{4}( \mathbf{C},\mathbf {N}, \mathbf{A})-1}{\mathbf {A}\mathbf {N}\cdot \mathbf {A}\mathbf {N}} \mathbf {N} \otimes \mathbf {N}. $$

(12)

The Cauchy stress in (4) thus becomes

$$ \mathbf {T}=-p\mathbf {I}+\mu \mathbf {B}+2\mathbf {F}\mathbf {S}_{f} \mathbf {F}^{T}, $$

(13)

where $\mathbf {B}=\mathbf {F}\mathbf {F}^{T}$ is the left Cauchy–Green tensor, and

$$\begin{aligned} \mathbf {S}_{f} =& \gamma \chi_{c} \int_{\mathbf {N}} \int_{-\infty }^{t} \biggl\{ \frac{I_{4}(\mathbf{C}(t),\mathbf {N}, \mathbf{A}(\tau ))-1}{\mathbf {A}( \tau )\mathbf {N}\cdot \mathbf {A}(\tau )\mathbf {N}} \\ &{}\times \exp \biggl( - \int_{\tau }^{t} \eta \bigl( I_{4}\bigl( \mathbf{C}(s),\mathbf {N}, \mathbf{A}(\tau )\bigr)\bigr)\,\mathrm{d}s \biggr)\, \mathrm{d}\tau \biggr\} \mathbf {N}\otimes \mathbf {N}\, \mathrm{d}\mathbf {N}. \end{aligned}$$

(14)

Equations (14) and (10) connect the time dependence of the stress and the time dependence of the fiber orientation density.

2.1 Homeostatic initial conditions

Equations (13) and (14) show that the stress response at time $t$ is determined not only by the deformation state at time $t$, but also by the past deformation history, in principle extending $t$ to $-\infty$. Suppose, however, that the material has been held in a fixed state of deformation for a sufficiently long time with constant deformation gradient tensor $\mathbf{F}=\mathbf{F}_{0}$. Then $\mathbf {A}$ also remains constant for fibers created during this time period and so is described by a fixed $\mathbf{A}_{0}$. In the limit as the time period of constant $\mathbf{F}_{0}$ becomes arbitrary large, the fiber orientation density (10) approaches the limit

$$ R(t,\mathbf {N})= \chi_{c} \int_{-\infty }^{t} \exp \bigl( - \eta \bigl( I_{4}( \mathbf{C}_{0},\mathbf {N}, \mathbf{A}_{0})\bigr) [t - \tau ] \bigr) \,\mathrm{d} \tau = \frac{\chi_{c}}{\eta (I_{4}(\mathbf{C}_{0},\mathbf {N}, \mathbf{A}_{0}))}, $$

(15)

where $\mathbf {C}_{0}=\mathbf {F}_{0}^{T}\mathbf {F}_{0}$. The Cauchy stress as given by (13) then approaches the limit ${\mathbf {T}=-p\mathbf {I}+\mu \mathbf {B} _{0}+2\mathbf {F}_{0}\mathbf {S}_{f}\mathbf {F}_{0}^{T}}$ where $\mathbf {B}_{0}=\mathbf {F} _{0}\mathbf {F}_{0}^{T}$, and $\mathbf {S}_{f}$ as given by (14) tends to

$$ \mathbf {S}_{f}=\gamma \chi_{c} \int_{\mathbf {N}} \frac{ [I_{4}(\mathbf{C}_{0}, \mathbf {N}, \mathbf{A}_{0})-1]}{[\mathbf {A}_{0}\mathbf {N}\cdot \mathbf {A}_{0}\mathbf {N}] \eta ( I_{4}(\mathbf{C}_{0}, \mathbf {N}, \mathbf{A}_{0}))} \mathbf {N}\otimes \mathbf {N} \, \mathrm{d} \mathbf {N}. $$

(16)

Both $R$ and $\mathbf{T}$ approach constant values in time because the fiber creation and dissolution are now in balance. This process in which fiber remodeling is ongoing at the finer subcontinuum length scales while the overall properties of the biological material remain constant at the coarser continuum scale is denoted as homeostasis (see, e.g., Cowin and Doty 2007 and Bader et al. 2011). The evaluated limits in (15) and (16) show that homeostasis is a general feature of this model. The particular homeostatic states are determined by a fixed deformation $\mathbf {F}_{0}$ in terms of the fiber creation rate constant $\chi_{c}$ and the fiber dissolution function $\eta (I_{4})$.

If a condition of homeostasis prevails at time $t=0$ and this state is disrupted by some new loading for $t>0$ then the formulae (14) and (10) for $\mathbf {S}_{f}$ and $R$ are naturally analyzed by having their integrals with respect to $\tau$ decomposed into separate portions with $-\infty < \tau < 0$ and $0 < \tau < t$. The integrals over the domain $-\infty < \tau < 0$ can then be evaluated by the same type of procedures used to obtain (15) and (16). The result of this process is that the fiber orientation density (10) is given by

$$\begin{aligned} R(t,\mathbf {N}) =& \chi_{c} \biggl[ \frac{1}{\eta ( I_{4}(\mathbf{C}_{0},\mathbf {N}, \mathbf{A} _{0})) } \exp \biggl( - \int_{0}^{t} \eta \bigl( I_{4}\bigl( \mathbf{C}(s),\mathbf {N}, \mathbf{A}_{0}\bigr)\bigr) \,\mathrm{d}s \biggr) \\ &{} + \int_{0}^{t}\exp \biggl( - \int_{\tau }^{t} \eta \bigl( I_{4}\bigl( \mathbf{C}(s),\mathbf {N}, \mathbf{A}(\tau )\bigr)\bigr) \,\mathrm{d}s \biggr) \,\mathrm{d} \tau \biggr] \end{aligned}$$

(17)

and the Cauchy stress continues to be given by $\mathbf {T}=\displaystyle -p\mathbf {I}+ \mu \mathbf {B}+2\mathbf {F}\mathbf {S}_{f}\mathbf {F}^{T}$ where $\mathbf {S}_{f}=\mathbf {S}_{f}(t)$ as given by (14) now becomes

$$\begin{aligned} \mathbf {S}_{f}(t) =& \gamma \chi_{c} \int_{\mathbf {N}} \biggl\{ \frac{ [ I_{4}(\mathbf {C}(t),\mathbf {N}, \mathbf {A}_{0})-1 ] }{ \mathbf {A}_{0}\mathbf {N} \cdot \mathbf {A}_{0}\mathbf {N} } \frac{1}{\eta ( I_{4}(\mathbf{C}_{0},\mathbf {N}, \mathbf{A}_{0}))} \\ &{} \times \exp \biggl( - \int_{0}^{t}\eta \bigl(I_{4}\bigl( \mathbf {C}(s),\mathbf {N}, \mathbf {A} _{0}\bigr)\bigr)\,\mathrm{d}s \biggr) + \int_{0}^{t} \frac{ [I_{4}(\mathbf {C}(t), \mathbf {N},\mathbf {A}(\tau ))-1]}{\mathbf {A}( \tau )\mathbf {N}\cdot \mathbf {A}(\tau )\mathbf {N}} \\ &{} \times \exp \biggl( - \int_{\tau }^{t}\eta \bigl(I_{4}\bigl( \mathbf {C}(s),\mathbf {N}, \mathbf {A}(\tau )\bigr)\bigr)\,\mathrm{d}s \biggr) \,\mathrm{d}\tau \biggr\} \mathbf {N}\otimes \mathbf {N} \,\mathrm{d}\mathbf {N}. \end{aligned}$$

(18)

The essential point is that now, unlike (10) and (14), the tensors $\mathbf {F}$, $\mathbf {C}=\mathbf {F}^{T}\mathbf {F}$, and $\mathbf {A}$ are functions of time only for $t>0$. In particular, there is no longer a need to consider $t<0$ in the mathematical formulation.

We study this case in which homeostatic initial conditions at $t=0$ are disrupted by a new loading state for $t>0$. Specifically, we shall restrict attention to an undeformed homeostatic condition. Then (17) and (18) apply with both $\mathbf{F}_{0}=\mathbf{I}$ and $\mathbf{A}_{0}=\mathbf{I}$. Consequently, (17) and (18) simplify further to

$$\begin{aligned} R(t,\mathbf {N}) =& \chi_{c} \biggl\{ \frac{1}{\eta_{0} } \exp \biggl( - \int_{0}^{t} \eta \bigl( I_{4}\bigl( \mathbf{C}(s),\mathbf {N}, \mathbf{I}\bigr)\bigr) \,\mathrm{d}s \biggr) \\ &{} + \int_{0}^{t}\exp \biggl( - \int_{\tau }^{t} \eta \bigl( I_{4}\bigl( \mathbf{C}(s),\mathbf {N}, \mathbf{A}(\tau )\bigr)\bigr) \,\mathrm{d}s \biggr) \,\mathrm{d} \tau \biggr\} \end{aligned}$$

(19)

and

$$\begin{aligned} \mathbf {S}_{f}(t) =& \gamma \chi_{c} \int_{\mathbf {N}} \biggl\{ \frac{ [ I_{4}(\mathbf {C}(t),\mathbf {N}, \mathbf {I})-1 ] }{ \eta_{0} } \exp \biggl( - \int_{0}^{t}\eta \bigl(I_{4}\bigl( \mathbf {C}(s),\mathbf {N}, \mathbf {I}\bigr)\bigr)\,\mathrm{d}s \biggr) \\ & {}+ \int_{0}^{t} \frac{ [I_{4}(\mathbf {C}(t), \mathbf {N},\mathbf {A}(\tau ))-1]}{\mathbf {A}( \tau )\mathbf {N}\cdot \mathbf {A}(\tau )\mathbf {N}} \\ &{}\times \exp \biggl( - \int_{\tau }^{t}\eta \bigl(I_{4}\bigl( \mathbf {C}(s),\mathbf {N}, \mathbf {A}(\tau )\bigr)\bigr)\,\mathrm{d}s \biggr) \,\mathrm{d}\tau \biggr\} \mathbf {N}\otimes \mathbf {N} \,\mathrm{d}\mathbf {N}, \end{aligned}$$

(20)

where $\eta_{0}=\eta (I_{4}(\mathbf {I},\mathbf {N}, \mathbf {I}))=\eta (1)$ is the initial homeostatic dissolution rate which, because of (7), is now independent of fiber direction $\mathbf{N}$. For the model constitutive law (11), this is simply $\eta_{0}=k_{1}$.

The evolution of the fiber structure and the stress–deformation relation under the new loading ($t>0$) is then strongly influenced by the way that $\mathbf {A}$ is constitutively specified. Different specifications of the tensor $\mathbf {A}$ result in different expressions for the invariant $I_{4}$ in (19) and (20):

• The first case $\mathbf {A}=\mathbf {I}$ provides a model for a process where the fibers, at the time of their creation, are in the same deformation state as the surrounding matrix. In this case the invariant $I_{4}$ is given by

  $$ I_{4}\bigl({\mathbf {C}}(t),\mathbf {N}, \mathbf {I}\bigr) = \mathbf {N}\cdot {{ \mathbf {C}}(t)}\mathbf {N}. $$

  (21)

• The second case $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ provides a model for a process where the fibers are undeformed at the time of their creation $\tau$. In this case the invariant $I_{4}$ is given by

  $$ I_{4}\bigl({\mathbf {C}}(t),\mathbf {N}, {\mathbf {C}}(\tau )\bigr) = \frac{\mathbf {N}\cdot {{\mathbf {C}}(t)} \mathbf {N}}{\mathbf {N}\cdot {{\mathbf {C}}(\tau )}\mathbf {N}}. $$

  (22)

We now examine the separate mechanical loading consequences associated with these two separate cases.

3 Biaxial loading

We consider a Cartesian coordinate system represented by the unit vectors $\{ \mathbf {E}_{1}, \mathbf {E}_{2},\mathbf {E}_{3} \}$, and an initially undeformed cube of material in configuration $\kappa_{0}$ with edges parallel to these unit vectors. As indicated above, the initial state is one in which the material is undeformed and the fiber remodeling process is initially in homeostasis. This initial state is disrupted at $t=0$ by a biaxial loading for $t>0$ in which uniform normal tractions act on the surfaces normal to the $\mathbf {E}_{2}$ and $\mathbf {E}_{3}$ directions; the surface normal to $\mathbf {E}_{1}$ remains traction free. As shown in Fig. 2, the cube deforms into a rectangular parallelepiped along the coordinate directions. The Cauchy stress tensor $\mathbf{T}$ and the deformation gradient tensor $\mathbf {F}$ are then of the form

$$\begin{aligned} \mathbf {T} =&T_{22}\mathbf {E}_{2}\otimes \mathbf {E}_{2}+T_{33}\mathbf {E}_{3}\otimes \mathbf {E}_{3}, \end{aligned}$$

(23a)

$$\begin{aligned} \mathbf {F} =&\frac{1 }{\lambda _{2} \lambda _{3}}\mathbf {E}_{1}\otimes \mathbf {E}_{1}+\lambda_{2}\mathbf {E}_{2}\otimes \mathbf {E}_{2}+\lambda_{3} \mathbf {E}_{3}\otimes \mathbf {E}_{3}. \end{aligned}$$

(23b)

The components $T_{22}$, $T_{33}$, $\lambda_{2}$, and $\lambda_{3}$ are functions of time $t$. For displacement-control the pair $\lambda_{2}$ and $\lambda_{3}$ are specified and $T_{22}$ and $T_{33}$ are to be found. For load-control the total force on each loaded face is specified. This corresponds to specified values of the ratios $T_{22}/\lambda_{2}$ and $T_{33}/\lambda_{3}$. It is to be noted in all cases that the loading condition $T_{11}=0$ is easily satisfied by the appropriate choice of $p$.

Fig. 2

Elongation of the material in the $\mathbf {E}_{2}$ and $\mathbf {E}_{3}$ directions, contraction in the $\mathbf {E}_{1}$ direction. The surfaces normal to the $\mathbf {E}_{1}$ direction are traction free, while the surfaces perpendicular to the $\mathbf {E}_{2}$ and $\mathbf {E}_{3}$ directions are subject to the respective normal stresses $T_{22}$ and $T_{33}$. At each material point of the scale of this figure, the fibers are distributed in all directions as governed by $R$ in (19)

The tensor $\mathbf {A}$ is also necessarily of the general form

$$ \mathbf {A}= \frac{1}{a_{2} a_{3}} \mathbf {E}_{1}\otimes \mathbf {E}_{1}+ a_{2}\mathbf {E} _{2}\otimes \mathbf {E}_{2}+ a_{3}\mathbf {E}_{3}\otimes \mathbf {E}_{3}. $$

(24)

Both $a_{2}$ and $a_{3}$ are functions of time as determined by the constitutive rule for the determination of $\mathbf{A}$. For the options under consideration here the case $\mathbf {A}=\mathbf {I}$ yields $a_{2}=a_{3}=1$ and the case $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ yields $a_{2}(\tau )= \lambda_{2}(\tau )$ and $a_{3}(\tau )=\lambda_{3}(\tau )$.

With respect to the fixed unit vectors $\{ \mathbf {E}_{1}, \mathbf {E}_{2},\mathbf {E} _{3} \}$, one can always let the fiber orientation vectors $\mathbf{N}$ be represented using angles $\phi$ and $\theta$ in the following standard way

$$ \mathbf{N}=\cos {\theta }\mathbf{E}_{1}+\sin {\theta } \cos {\phi } \mathbf{E}_{2}+\sin {\theta }\sin {\phi } \mathbf{E}_{3},\quad 0\leq \phi \leq 2\pi,\ 0\leq \theta \leq \pi . $$

(25)

Then integrals such as (20) are evaluated by means of the replacement

$$ \int_{\mathbf {N}} \{ \dots \} \,\mathrm{d}\mathbf {N} \quad \longrightarrow \quad \int_{0}^{2\pi } \int_{0}^{ \pi } \{ \dots \} \sin \theta \, \mathrm{d} \theta \,\mathrm{d} \phi . $$

(26)

On combining the deformation gradient tensors (23b) and (24) with this representation for $\mathbf{N}$, the invariant $I_{4}$ in (7) becomes

$$ I_{4} =\frac{ [ \lambda_{2}\lambda_{3} ] ^{-2}\cos^{2}\theta + \lambda_{2}^{2}\sin^{2}\theta \cos^{2}\phi +\lambda_{3}^{2}\sin^{2} \theta \sin^{2}\phi }{ [ a_{2}a_{3} ] ^{-2}\cos^{2}\theta + a _{2}^{2}\sin^{2}\theta \cos^{2}\phi +a_{3}^{2}\sin^{2}\theta \sin^{2} \phi } \equiv \hat{I}_{4}( \lambda_{2}, \lambda_{3}, a_{2}, a_{3}, \theta , \phi ). $$

(27)

Observe in particular that the last step in the above equation defines a new function that will often replace $I_{4}(\mathbf {C},\mathbf {N},\mathbf {A})$ in subsequent expressions. We may further define

$$ {\tilde{I}_{4}}(t, \tau , \theta , \phi ) = \hat{I}_{4}\bigl(\lambda_{2}(t), \lambda_{3}(t), a_{2}(\tau ), a_{3}(\tau ), \theta , \phi \bigr) $$

(28)

and this will often serve to replace $I_{4}(\mathbf {C}(t),\mathbf {N},\mathbf {A}( \tau ))$. In a corresponding fashion, we define

$$ \hat{\eta }(\lambda_{2}, \lambda_{3}, a_{2}, a_{3}, \theta , \phi )= \eta \bigl( \hat{I}_{4}(\lambda_{2}, \lambda_{3}, a_{2}, a_{3}, \theta , \phi ) \bigr). $$

(29)

3.1 Application of a constant deformation

Let a step deformation be applied that has a step change at $t=0$ and which then remains constant for $t\ > 0$. Then the values $\lambda _{2}$, $\lambda_{3}$, $a_{2}$ and $a_{3}$ in the deformation gradients (23b) and (24) take on constant values which will be denoted by $\lambda_{2+}$, $\lambda_{3+}$, $a_{2+}$, and $a_{3+}$. The parameters $a_{2+}$ and $a_{3+}$ become $a_{2+}=a_{3+}=1$ for the $\mathbf {A}=\mathbf {I}$ treatment, whereas $a_{2+}=\lambda_{2+}$ and $a_{3+}=\lambda_{3+}$ in the $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ treatment. This step deformation results in values for the invariants $I_{1}$ and $I_{4}$ and the dissolution rate $\eta$ that do not vary with time although $I_{4}$ and $\eta$ do vary with direction.

For $t> 0$, the fiber orientation density function (19) takes the form $R=R(t, \theta , \phi , \lambda_{2+}, \lambda_{3+}, a_{2+}, a_{3+})$ where, suppressing some of the tedious argument structure,

$$ R(t, \theta , \phi )= \frac{\chi _{c} }{\eta _{0}} \exp {(- \eta_{+0} t)} + \frac{\chi _{c} }{\eta _{++}} \bigl[ 1- \exp {(- \eta_{++} t)} \bigr] . $$

(30)

Here $\eta_{0}$ continues to be given by $\eta_{0}=\eta (I_{4}(\mathbf {I},\mathbf {N}, \mathbf {I}))=\eta (1)$ and so is a directionally independent quantity. The new notations $\eta_{+0}$ and $\eta_{++}$ are shorthand for

$$ \eta_{+0}=\hat{\eta }(\lambda_{2+}, \lambda_{3+}, 1, 1, \theta , \phi ), \qquad \eta_{++}=\hat{ \eta }(\lambda_{2+}, \lambda_{3+}, a_{2+}, a_{3+}, \theta , \phi ). $$

(31)

These formulae apply to both the $\mathbf {A}=\mathbf {I}$ treatment and the $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ treatment. Unlike $\eta_{0}$, both $\eta_{+0}$ and $\eta_{++}$ are dependent on spatial direction. Observe as $t \to \infty$ that the above expression (30) approaches $\chi_{c} / \eta_{++}$ which, as seen by comparison with (15), is confirmation that a new condition of homeostasis is approached in the large time limit because of the fixed displacement.

The Cauchy stress components $T_{22}$ and $T_{33}$ for $t > 0$ are found by first determining $p$ from (13) using $T_{11}=0$ and then substituting from (20)–(25). Using $\mathbf {A}(\tau )\mathbf {N}\cdot \mathbf {A}(\tau )\mathbf {N}=\hat{I}_{4}(a_{2+}, a_{3+}, 1,1,\theta , \phi )$, this gives

$$\begin{aligned} {T}_{22} =&\mu \biggl[ \lambda_{2+}^{2}- \frac{1}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] +2\chi_{c}\gamma \int_{0}^{2\pi } \int_{0}^{ \pi } \biggl\{ \bigl[ \hat{I}_{4}( \lambda_{2+}, \lambda_{3+}, 1,1,\theta , \phi ) -1 \bigr] \\ &{}\times \frac{\exp ( - \eta_{+0} t ) }{\eta_{0}} + \biggl[ \frac{\hat{I}_{4}(\lambda_{2+}, \lambda_{3+}, a_{2+}, a_{3+},\theta , \phi ) -1}{\hat{I}_{4}(a_{2+}, a_{3+}, 1,1,\theta , \phi )} \biggr] \frac{1-\exp ( -\eta_{++}t ) }{ \eta_{++}} \biggr\} \\ & {}\times \biggl[ \lambda_{2+}^{2}\sin^{2} \theta \cos^{2}\phi - \frac{\cos^{2}{\theta }}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] \sin \theta \,\mathrm{d} \theta \,\mathrm{d} \phi , \end{aligned}$$

(32a)

$$\begin{aligned} {T}_{33} =& \mu \biggl[ \lambda_{3+}^{2}- \frac{1}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] +2\chi_{c}\gamma \int_{0}^{2\pi } \int_{0}^{ \pi } \biggl\{ \bigl[ \hat{I}_{4}( \lambda_{2+}, \lambda_{3+}, 1,1,\theta , \phi ) -1 \bigr] \\ &{} \times \frac{\exp ( - \eta_{+0} t ) }{\eta_{0}} + \biggl[ \frac{\hat{I}_{4}(\lambda_{2+}, \lambda_{3+}, a_{2+}, a_{3+},\theta , \phi ) -1}{\hat{I}_{4}(a_{2+}, a_{3+}, 1,1,\theta , \phi )} \biggr] \frac{1-\exp ( -\eta_{++}t ) }{ \eta_{++}} \biggr\} \\ &{} \times \biggl[ \lambda_{3+}^{2}\sin^{2} \theta \sin^{2}\phi - \frac{\cos^{2}{\theta }}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] \sin \theta \,\mathrm{d} \theta \,\mathrm{d} \phi . \end{aligned}$$

(32b)

Both the fiber orientation density (30) and the Cauchy stresses (32a), (32b) are seen to depend on the choice of $a_{2+}$ and $a_{3+}$.

Initial response

Consider the response immediately after application of the step deformation at $t=0$. It follows from (30) that the fiber orientation density through the step remains at $R=\chi_{c}/\eta _{0}$, which is independent of $\theta$ and $\phi$ and indicates a uniform distribution. The absence of a jump in $R$ is indicative of the finite time that it takes the microstructure to evolve in the present model. In contrast, the Cauchy stresses do exhibit a jump at $t=0$. Specifically, the $t=0^{+}$ Cauchy stresses obtained from Eqs. (32a), (32b) are

$$\begin{aligned} {T}_{22} =& \displaystyle \mu \biggl[ \lambda_{2+}^{2}- \frac{1}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] + \frac{8}{15}\frac{1}{\eta_{0}}\frac{\pi \gamma \chi_{c}}{\lambda_{2+}^{2}\lambda_{3+}^{2}} \bigl\{ 5\lambda_{2+}^{2}\lambda_{3+}^{2} \bigl[ 1-\lambda_{2+}^{4}\lambda_{3+}^{2} \bigr] \\ &{}\times 3 \bigl[ \lambda_{2+}^{8} \lambda_{3+}^{4}-1 \bigr] +\lambda_{2+}^{2} \lambda_{3+}^{4} \bigl[ \lambda_{2+}^{4} \lambda_{3+}^{2}-1 \bigr] \bigr\} , \end{aligned}$$

(33a)

$$\begin{aligned} {T}_{33} =& \displaystyle \mu \biggl[ \lambda_{3+}^{2}- \frac{1}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] + \frac{8}{15}\frac{1}{\eta_{0}}\frac{\pi \gamma \chi_{c}}{\lambda_{2+}^{2}\lambda_{3+}^{2}} \bigl\{ 5\lambda_{2+}^{2}\lambda_{3+}^{2} \bigl[ 1-\lambda_{2+}^{2}\lambda_{3+}^{4} \bigr] \\ &{}\times 3 \bigl[ \lambda_{2+}^{4} \lambda_{3+}^{8}-1 \bigr] +\lambda_{2+}^{4} \lambda_{3+}^{2} \bigl[ \lambda_{2+}^{2} \lambda_{3+}^{4}-1 \bigr] \bigr\} . \end{aligned}$$

(33b)

These values do not depend upon $a_{2+}$ and $a_{3+}$. This is because the fibrous component has not yet had time to undergo its $\mathbf {A}$-dependent remodeling process.

Asymptotic large time response

In the limit as $t\rightarrow \infty$, the fiber orientation density (30) approaches the limiting value

$$ R=\frac{\chi_{c}}{\eta_{++}} \quad (t \to \infty ). $$

(34)

The orientation distribution is no longer directionally uniform by virtue of the dependence of $\eta_{++}$ upon $\theta$ and $\phi$ as given in (31). The asymptotic Cauchy stresses are obtained from Eqs. (32a), (32b) as follows:

$$\begin{aligned} {T}_{22} =& \displaystyle \mu \biggl[ \lambda_{2+}^{2}- \frac{1}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] + 2\chi_{c}\gamma \int_{0}^{2\pi } \int_{0}^{ \pi } \frac{ [ \hat{I}_{4}(\lambda_{2+}, \lambda_{3+}, a_{2+}, a_{3+},\theta , \phi ) -1 ] }{\hat{I}_{4}(a_{2+}, a_{3+}, 1,1,\theta , \phi )} \\ &{}\times \displaystyle \frac{1}{\eta_{++}} \biggl[ \lambda_{2+}^{2} \sin^{2}\theta \cos^{2}\phi - \frac{\cos^{2}{\theta }}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] \sin \theta \,\mathrm{d} \theta \,\mathrm{d} \phi , \end{aligned}$$

(35a)

$$\begin{aligned} {T}_{33} =& \displaystyle \mu \biggl[ \lambda_{3+}^{2}- \frac{1}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] + 2\chi_{c}\gamma \int_{0}^{2\pi } \int_{0}^{ \pi } \frac{ [ \hat{I}_{4}(\lambda_{2+}, \lambda_{3+},a_{2+}, a_{3+}, \theta , \phi ) -1 ] }{\hat{I}_{4}(a_{2+}, a_{3+}, 1,1,\theta , \phi )} \\ &{}\times \displaystyle \frac{1}{\eta_{++}} \biggl[ \lambda_{3+}^{2} \sin^{2}\theta \sin^{2}\phi - \frac{\cos^{2}{\theta }}{ [ \lambda_{2+}\lambda_{3+} ] ^{2}} \biggr] \sin \theta \,\mathrm{d} \theta \,\mathrm{d} \phi . \end{aligned}$$

(35b)

Equations (34) and (35a), (35b) are specific cases of (13), (19), and (20) for biaxial deformation. They show that as $t\rightarrow \infty$ the limiting values for the fiber orientation density and the Cauchy stresses depend on the choice of $a_{2+}$ and $a_{3+}$ because of its effect on both the invariant $\hat{I}_{4}( \lambda_{2+}, \lambda_{3+}, a_{2+}, a_{3+},\theta , \phi )$ and the dissolution rate $\eta_{++}=\hat{\eta }(\lambda_{2+}, \lambda _{3+}, a_{2+}, a_{3+},\theta , \phi )$. In the case of $a_{2+}= \lambda_{2+}$ and $a_{3+}=\lambda_{3+}$, (27) shows that $\hat{I}_{4}(\lambda_{2+}, \lambda_{3+}, \lambda_{2+}, \lambda_{3+}, \theta , \phi )=1$, and consequently $\eta_{++}=k_{1}$. The limiting Cauchy stresses (35a), (35b) are in this case solely reduced to the matrix contribution.

Intermediate time response

The fiber orientation density function (30) evolves from the uniform distribution $R=\chi_{c}/\eta_{0}$ to the non-uniform distribution $R=\chi_{c}/\eta_{++}$ in a manner that depends on the model stipulation of $a_{2+}$ and $a_{3+}$.

• In the case of $a_{2+}=a_{3+}=1$, the dissolution rates $\hat{\eta }( \lambda_{2+}, \lambda_{3+}, 1, 1,\theta , \phi )$ and $\hat{\eta }( \lambda_{2+}, \lambda_{3+}, a_{2+}, a_{3+},\theta , \phi )$ are equal, and the fiber orientation density function approaches its limit as $t\rightarrow \infty$ monotonically at a rate that depends on $\theta$ and $\phi$.

• In the case of $a_{2+}=\lambda_{2+}$ and $a_{3+}=\lambda_{3+}$, (27) shows that $I_{4}(\lambda_{2+}, \lambda_{3+}, a_{2+}, a_{3+},\theta , \phi )=1$ and thus $\eta_{++}=k_{1}$. The distribution deviates from uniformity, reaches a maximum that depends on $\theta$ and $\phi$ and then returns to uniformity. This occurs because the fiber orientation density immediately increases after deformation due to the just-imposed stretch. The stretched fibers, which were created before the application of the deformation, dissolve and new undeformed fibers are created that remain undeformed. Hence the fiber orientation density approaches a local maximum and then decreases until it reapproaches the initial fiber density.

Both stress components $T_{22}$ and $T_{33}$ in (32a), (32b) evolve with time in a complex fashion because the exponentials in the integrand vary in a manner that depends on $\theta$ and $\phi$.

3.1.1 Influence of unequal biaxial stretch ratios on the fiber orientation density

Consider the deformation (23b) with (24) for $\lambda_{2+}=1.5$ and various values of $\lambda_{3+}$. The value $\lambda_{2+}=1.5$ is chosen so as to be well beyond a small strain regime while still being representative for a deformation in a biological tissue. Figure 3 shows the development of the fiber orientation density in the $(\mathbf {E}_{2},\mathbf {E}_{3})$-plane represented by the angles $\{ \theta =\frac{\pi }{2}, 0\leq \phi \leq 2\pi \}$. The $\mathbf {E}_{2}$-direction corresponds to $\{ \theta =\frac{\pi }{2}, \phi =0,\pi \}$, and the $\mathbf {E}_{3}$-direction corresponds to $\{ \theta =\frac{\pi }{2}, \phi =\frac{\pi }{2}, \frac{3\pi }{2} \}$. Results are shown for $\lambda_{3+}=2\lambda_{2+}$, corresponding to greater stretch along $\mathbf {E}_{3}$. The results depend on the stipulation of $\mathbf {A}$ as follows:

• The development of the fiber orientation density $R$ with time $t$ for the $\mathbf {A}=\mathbf {I}$ case is illustrated in the top panel of Fig. 3. The material is stretched in this plane and, as determined from (30), the fiber density increases monotonically as $t$ increases, so that

  $$ R|_{t=0}< R|_{t=1/k_{1}}< R|_{t=10/k_{1}}< \lim_{t \to \infty }R. $$

  (36)

  Fig. 3

  

  (Color figure online) Normalized fiber orientation density $R^{*}=R/\chi_{c}$ for $\lambda_{2+}=1.5$, $\lambda_{3+}=2\lambda_{2+}$, and different normalized times $t^{*}=k_{1}t$: (a) $\mathbf {A}=\mathbf {I}$; (b) $\mathbf {A}(\tau )=\mathbf {F}(\tau )$

• The development of $R$ with $t$ for $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ is illustrated in the bottom panel of Fig. 3. The diagram illustrates that

  $$ R|_{t=0}< \lim_{t \to \infty }R< R |_{t=10/k _{1}}< R|_{t=1/k_{1}}, $$

  (37)

  so that a local maximum has occurred for each $\theta$ and $\phi$.

Figure 4 presents the evolution of the fiber orientation density in the direction $\{ \theta =\phi =\frac{\pi }{2} \}$ ($\mathbf {E}_{3}$-direction) for $\lambda_{2+}=1.5$ and different values for $\lambda_{3+}$. The fiber orientation density becomes larger as $\lambda_{3+}$ increases.

Fig. 4

Evolution of the normalized fiber orientation density $R^{*}(\theta =\phi =\pi /2)=R/\chi_{c}$ with normalized time $t^{*}=k_{1}t$ for $\lambda_{2+}=1.5$ and different values for $\lambda_{3+}$. The upper curve in a line style correspond to $\mathbf {A}=\mathbf {I}$, and the lower curves to $\mathbf {A}(\tau )=\mathbf {F}(\tau )$. The direction $\theta =\phi =\pi /2$ corresponds to the direction of $\mathbf {E}_{3}$. Both panels present the same problem but for different ranges of $R^{*}$ and $t^{*}$

3.1.2 Influence of unequal biaxial stretch ratios on the stress distribution

An important feature of the constitutive theory is that the continuous time evolution of the fiber orientation density gives rise to a time evolution in the state of stress when the deformation is fixed. To show this, we continue with our example of a deformation given by (23b) with $\lambda_{2+}=1.5$. Figure 5 contrasts the evolution of the normalized Cauchy stresses,

$$ T^{*}_{22}=\frac{T_{22}k_{1}}{\gamma \chi_{c}}, \qquad T^{*}_{33}=\frac{T_{33}k_{1}}{\gamma \chi_{c}}, $$

(38)

for $\lambda_{3+}=1.0$ (no stretch in the $\mathbf {E}_{2}$-direction) and $\lambda_{3+}=2.0$ (larger stretch in the $\mathbf {E}_{3}$-direction) and for both cases $\mathbf {A}=\mathbf {I}$ and $\mathbf {A}(\tau )=\mathbf {F}(\tau )$.

Fig. 5

Normalized Cauchy stresses as a function of normalized time $t^{*}=k_{1}t$ for $\lambda_{2+}=1.5$ so as to contrast $\mathbf {A}=\mathbf {I}$ and $\mathbf {A}(\tau )=\mathbf {F}(\tau )$. For simplicity we have here taken $\mu =0$ (the matrix component is regarded as having negligible stiffness). The left panels illustrate $T^{*}_{22}$ (see (38)), the right panels illustrate $T^{*}_{33}$. The upper panels illustrate the stresses for $\lambda _{3+}=1$, the bottom panels illustrate the stresses for $\lambda_{3+}=2$

To discuss and interpret the results in Fig. 5, it is necessary to also consider the fiber density presented in Fig. 4. The Cauchy stresses at $t=0$ are independent of the choice for $\mathbf {A}$, as was shown in (32a), (32b). However, stresses for $t>0$ depend on the choice of $\mathbf {A}$:

• In the case of $\mathbf {A}=\mathbf {I,}$ the fiber orientation density increases and the material becomes stiffer so that a higher stress is needed to keep the material in the fixed deformation state.

• In the case of $\mathbf {A}(\tau )=\mathbf {F}(\tau )$, the fibers created at $\tau \geq 0$ are undeformed. Because the deformation of the material remains constant, less Cauchy stress is required to maintain material in the deformed state, so that the Cauchy stress decreases as $t\rightarrow \infty$.

3.1.3 Influence of the dissolution exponent on the stresses

The parameter $k_{2}$ in (11) determines the sensitivity of dissolution to fiber stretch and thus has an effect on the stresses. Figure 6 shows how different values of $k_{2}$ influence the development of the stresses. Results are presented for $\lambda_{2+}=1.5$ and $\lambda_{3+}=2.0$. The matrix influence is neglected so that $\mu =0$. The left panels illustrate $T^{*}_{22}$ (see (38)), the right panels illustrate $T^{*}_{33}$. The rising curves correspond to $\mathbf {A}=\mathbf {I}$, and the decreasing curves to $\mathbf {A}(\tau )=\mathbf {F}(\tau )$.

• In the case of $\mathbf {A}(\tau )=\mathbf {F}(\tau )$, the curves decrease faster with smaller values of $k_{2}$. In all cases the stress decreases to its matrix determined value as $t\rightarrow \infty$.

• In the case of $\mathbf {A}=\mathbf {I,}$ the curves increase faster with larger values of $k_{2}$. As $t\rightarrow \infty$, the stresses approach a finite limit value which also becomes larger with higher choices for $k_{2}$.

Fig. 6

Evolution of the normalized Cauchy stresses (38) as a function of normalized time $t^{*}=k_{1}t$ for $\lambda_{2+}=1.5$ and $\lambda_{3+}=2.0$ taking $\mu =0$. Panel (a) illustrates $T^{*}_{22}$, panel (b) illustrates $T^{*}_{33}$. The rising curves correspond to $\mathbf {A}=\mathbf {I}$, and the falling curves correspond to $\mathbf {A}(\tau )=\mathbf {F}(\tau )$

3.2 Application of constant forces

The situation considered in Sect. 3.1 involves displacement-control. We now turn to consider a situation of load-control. The material is again taken to be undeformed and in homeostasis for $t<0$. Its reference configuration is a cube with sides of length $\ell$. Biaxial forces $P_{2}$ and $P_{3}$ are suddenly applied to the surfaces of the cube at $t=0$ and then held fixed for $t>0$. The deformation process continues to be described by the Cauchy stress tensor (23a) and the deformation gradient tensors (23b) and (24). $P_{2}$ is a constant tensile force on the surfaces of the cube normal to the $\mathbf{E}_{2}$ direction, and $P_{3}$ is a constant tensile force on the surfaces of the cube normal to the $\mathbf{E}_{3}$ direction. The cube deforms into a rectangular cuboid. At time $t$, the edges parallel to the $\mathbf {E}_{i}$ direction have lengths $\ell_{i}=\ell_{i}(t)$, $i=1,2,3$, where $\ell_{i}= \ell \lambda_{i}$, and $\lambda_{1}= [ \lambda_{2}\lambda_{3} ] ^{-1}$. The forces $P_{2}$ and $P_{3}$ and the components $T_{22}(t)$ and $T_{33}(t)$ of the Cauchy stress tensor (23a) are related via

$$\begin{aligned} T_{22}(t) =& \textstyle\begin{cases} 0, & \mbox{for } t< 0,\\ P_{2}\lambda_{2}(t)/\ell^{2}, & \mbox{for } t\geq 0, \end{cases}\displaystyle \end{aligned}$$

(39a)

$$\begin{aligned} T_{33}(t) =& \textstyle\begin{cases} 0,& \mbox{for } t< 0,\\ P_{3}\lambda_{3}(t)/\ell^{2}, & \mbox{for } t\geq 0. \end{cases}\displaystyle \end{aligned}$$

(39b)

The relation between the forces $P_{2}$ and $P_{3}$ and the resulting deformation at $t\geq 0$ is obtained from Eqs. (23a)–(29), (39a), (39b), and reads

$$\begin{aligned} \frac{P_{2}}{\ell^{2}} =& \displaystyle \mu \biggl[ \lambda_{2}(t)-\frac{1}{\lambda_{2}^{3}(t)\lambda_{3}^{2}(t)} \biggr] +2\chi_{c}\gamma \int_{0}^{2\pi } \int_{0}^{ \pi } \biggl\{ \bigl[ \hat{I}_{4} \bigl(\lambda_{2}(t),\lambda_{3}(t),1,1,\theta ,\phi \bigr)-1 \bigr] \\ &{}\times \frac{1}{\eta_{0}}\exp \biggl( - \int_{0}^{t}\hat{\eta }\bigl(\lambda_{2}(s), \lambda_{3}(s),1,1,\theta ,\phi \bigr) \,\mathrm{d}s \biggr) \\ &{}+ \int_{0}^{t}\frac{\hat{I}_{4}(\lambda_{2}(t),\lambda_{3}(t), a_{2}(\tau ),a_{3}(\tau ),\theta ,\phi )-1}{\hat{I}_{4}(a_{2}(\tau ),a_{3}(\tau ),1,1,\theta ,\phi )} \\ &{}\times \exp \biggl( - \int_{\tau }^{t}\hat{\eta }\bigl(\lambda_{2}(s), \lambda_{3}(s), a_{2}(\tau ),a_{3}(\tau ),\theta , \phi \bigr) \,\mathrm{d}s \biggr) \,\mathrm{d}\tau \biggr\} \\ &{}\times \biggl[ \lambda_{2}(t)\sin^{2}\theta \cos^{2}\phi -\frac{\cos^{2}\theta }{\lambda_{2}^{3}(t)\lambda_{3}^{2}(t)} \biggr] \sin \theta \,\mathrm{d}\theta \,\mathrm{d}\phi , \end{aligned}$$

(40a)

$$\begin{aligned} \frac{P_{3}}{\ell^{2}} =& \displaystyle \mu \biggl[ \lambda_{3}(t)-\frac{1}{\lambda_{2}^{2}(t)\lambda_{3}^{3}(t)} \biggr] +2\chi_{c}\gamma \int_{0}^{2\pi } \int_{0}^{ \pi } \biggl\{ \bigl[ \hat{I}_{4} \bigl(\lambda_{2}(t),\lambda_{3}(t),1,1,\theta ,\phi \bigr)-1 \bigr] \\ &{}\times \frac{1}{\eta_{0}}\exp \biggl( - \int_{0}^{t}\hat{\eta }\bigl(\lambda_{2}(s), \lambda_{3}(s),1,1,\theta ,\phi \bigr) \,\mathrm{d}s \biggr) \\ &{}+ \int_{0}^{t}\frac{\hat{I}_{4}(\lambda_{2}(t),\lambda_{3}(t), a_{2}(\tau ),a_{3}(\tau ),\theta ,\phi )-1}{\hat{I}_{4}(a_{2}(\tau ),a_{3}(\tau ),1,1,\theta ,\phi )} \\ &{}\times \exp \biggl( - \int_{\tau }^{t}\hat{\eta }\bigl(\lambda_{2}(s), \lambda_{3}(s), a_{2}(\tau ),a_{3}(\tau ),\theta , \phi \bigr) \,\mathrm{d}s \biggr) \,\mathrm{d}\tau \biggr\} \\ &{}\times \biggl[ \lambda_{3}(t)\sin^{2}\theta \sin^{2}\phi -\frac{\cos^{2}\theta }{\lambda_{2}^{2}(t)\lambda_{3}^{3}(t)} \biggr] \sin \theta \,\mathrm{d}\theta \,\mathrm{d}\phi . \end{aligned}$$

(40b)

Initial response

The relation between the input forces $P_{2}$ and $P_{3}$ and the stretch ratios $\lambda_{2_{0}}=\lambda_{2}(0^{+})$ and $\lambda_{3_{0}}= \lambda_{3}(0^{+})$ at $t=0^{+}$ can be determined exactly. In this case Eqs. (40a), (40b) yield

$$\begin{aligned} \frac{P_{2}}{\ell^{2}} =&\displaystyle \mu \biggl[ \lambda_{2_{0}}-\frac{1}{\lambda_{2_{0}}^{3}\lambda_{3_{0}}^{2}} \biggr] + \frac{8}{15}\frac{1}{\eta_{0}}\frac{\pi \gamma \chi_{c}}{\lambda_{2_{0}}^{5}\lambda_{3_{0}}^{4}} \bigl\{ 5 \lambda_{2_{0}}^{2}\lambda_{3_{0}}^{2} \bigl[ 1 - \lambda_{2_{0}}^{4}\lambda_{3_{0}}^{2} \bigr] \\ &{}+3 \bigl[ \lambda_{2_{0}}^{8}\lambda_{3_{0}}^{4}-1 \bigr] +\lambda_{2_{0}}^{2}\lambda_{3_{0}}^{4} \bigl[ \lambda_{2_{0}}^{4}\lambda_{3_{0}}^{2} -1 \bigr] \bigr\} , \end{aligned}$$

(41a)

$$\begin{aligned} \frac{P_{3}}{\ell^{2}} =&\displaystyle \mu \biggl[ \lambda_{3_{0}}- \frac{1}{\lambda_{2_{0}}^{2}\lambda_{3_{0}}^{3}} \biggr] + \frac{8}{15}\frac{1}{\eta_{0}}\frac{\pi \gamma \chi_{c}}{\lambda_{2_{0}}^{5}\lambda_{3_{0}}^{4}} \bigl\{ 5\lambda_{2_{0}}^{2}\lambda_{3_{0}}^{2} \bigl[ 1 -\lambda_{2_{0}}^{2}\lambda_{3_{0}}^{4} \bigr] \\ &{}+3 \bigl[ \lambda_{2_{0}}^{4}\lambda_{3_{0}}^{8}-1 \bigr] +\lambda_{2_{0}}^{4}\lambda_{3_{0}}^{2} \bigl[ \lambda_{2_{0}}^{2}\lambda_{3_{0}}^{4} -1 \bigr] \bigr\} . \end{aligned}$$

(41b)

This relation between the input forces and the resulting deformation (41a), (41b) is independent of the choice of $\mathbf {A}$.

Asymptotic large time response

As $t\to \infty$ the exponentials in the various governing integrals impart a fading memory effect on the fiber creation process. Eventually all of the newly created fibers at time $\tau$ are formed in a state for which the material has substantially approached its limiting deformation. Consequently, the parameters $\lambda_{2}(t)$, $\lambda_{3}(t)$, $a_{2}(\tau )$, and $a_{3}(\tau )$ take the forms

$$\begin{aligned} \lim_{t\rightarrow \infty }\lambda_{2}(t) =& \lambda_{2_{ \infty }}, \qquad \lim_{\tau \rightarrow \infty }a_{2}(\tau )=a_{2_{ \infty }}, \end{aligned}$$

(42a)

$$\begin{aligned} \lim_{t\rightarrow \infty }\lambda_{3}(t) =&\lambda_{3_{\infty }}, \qquad \lim_{ \tau \rightarrow \infty }a_{3}(\tau )=a_{3_{\infty }}. \end{aligned}$$

(42b)

Here $a_{2_{\infty }}=a_{3_{\infty }}=1$ if $\mathbf {A}=\mathbf {I}$, and $a_{2_{\infty }}=\lambda_{2_{\infty }}$, $a_{3_{\infty }}= \lambda_{3_{\infty }}$ if $\mathbf {A}(\tau )=\mathbf {F}(\tau )$. Then (16) together with (40a), (40b) and (42a), (42b) gives the following relations for $t\rightarrow \infty$:

$$\begin{aligned} \frac{P_{2}}{\ell^{2}} =&\displaystyle \mu \biggl[ \lambda_{2_{\infty }}- \frac{1}{\lambda_{2_{\infty }}^{3}\lambda_{3_{ \infty }}^{2}} \biggr] + 2 \gamma \chi_{c} \int_{0}^{2\pi } \int_{0}^{ \pi } \frac{ [ \hat{I}_{4}(\lambda_{2_{\infty }},\lambda_{3_{ \infty }},a_{2_{\infty }},a_{3_{\infty }})-1 ] }{\hat{I}_{4}(a_{2_{ \infty }},a_{3_{\infty }},1,1)} \\ &{}\times \frac{1}{\hat{\eta }(\lambda_{2_{\infty }},\lambda_{3_{\infty }},a_{2_{\infty }},a_{3_{\infty }})} \biggl[ \lambda_{2_{\infty }}\sin^{2}\theta \cos^{2}\phi -\frac{\cos^{2}\theta }{\lambda_{2_{ \infty }}^{3}\lambda_{3_{\infty }}^{2}} \biggr] \sin \theta \,\mathrm{d}\theta \,\mathrm{d}\phi , \end{aligned}$$

(43a)

$$\begin{aligned} \frac{P_{3}}{\ell^{2}} =&\displaystyle \mu \biggl[ \lambda_{3_{\infty }}- \frac{1}{\lambda_{2_{\infty }}^{2}\lambda_{3_{ \infty }}^{3}} \biggr] + 2 \gamma \chi_{c} \int_{0}^{2\pi } \int_{0}^{ \pi } \frac{ [ \hat{I}_{4}(\lambda_{2_{\infty }},\lambda_{3_{ \infty }},a_{2_{\infty }},a_{3_{\infty }})-1 ] }{\hat{I}_{4}(a_{2_{ \infty }},a_{3_{\infty }},1,1)} \\ &{}\times \frac{1}{\hat{\eta }(\lambda_{2_{\infty }},\lambda_{3_{\infty }},a_{2_{\infty }},a_{3_{\infty }})} \biggl[ \lambda_{3_{\infty }}\sin^{2}\theta \sin^{2}\phi - \frac{\cos^{2}\theta }{\lambda_{2_{ \infty }}^{2}\lambda_{3_{\infty }}^{3}} \biggr] \sin \theta \,\mathrm{d}\theta \,\mathrm{d}\phi . \end{aligned}$$

(43b)

Intermediate time response

While (41a), (41b) gives the initial force–deformation relation exactly at $t=0^{+}$, the deformation process for $t>0^{+}$ requires a numerical treatment using time steps $\Delta t_{i}=t_{i+1}-t_{i}$, $i=1,2,\dots$. The integrals with respect to times $t$ and $\tau$ between $t_{0}$ and $t_{1}$ in (40a), (40b) are approximated by the trapezoidal rule (see Appendix A) and the displacements $\lambda_{2}(t_{i+1})$ and $\lambda_{3}(t_{i+1})$ are obtained by the Newton–Raphson method. Because the large time limit is known in advance from (43a), (43b), it is possible to directly gauge the severity of any error accumulation.

3.2.1 Influence of different force ratios on the deformation

We now consider the evolution of the stretch ratios $\lambda_{2}(t)$ and $\lambda_{3}(t)$ in response to the step forces $P_{2}$ and $P_{3}$ which are held fixed for $t\geq 0$. The initial stretch ratios at the moment of force application can be determined from (41a), (41b). It is convenient to introduce the normalization

$$ P^{*}=\frac{P_{2}k_{1}}{\gamma \chi_{c}\ell^{2}}. $$

(44)

The initial values for the deformation $\lambda_{2_{0}}$ and $\lambda_{3_{0}}$ for $P^{*}=100$, different force ratios $P_{3}/P _{2}$, and $k_{2}=1$ are illustrated in Fig. 7 on the range $0\leq \mu^{*}<200$, where

$$ \mu^{*}=\frac{\mu k_{1}}{\gamma \chi_{c}} $$

(45)

is the normalized shear modulus of the matrix. The initial values $\lambda_{2_{0}}$ and $\lambda_{3_{0}}$ do not depend upon the choice of $\mathbf {A}$.

Fig. 7

The initial values $\lambda_{2_{0}}$ and $\lambda_{3_{0}}$ for $P^{*}=100$, different force ratios $P_{3}/P_{2}$, and $k_{2}=1$ on the range $0\leq \mu^{*}<200$. These values do not depend on $\mathbf {A}$

The development of $\lambda_{2}$ and $\lambda_{3}$ with time $t$ are computed numerically as described above. Figure 8 shows the development of $\lambda_{2}(t)$ and $\lambda_{3}(t)$ with normalized time $t^{*}=k_{1}t$ due to the applied normalized force $P^{*}=100$, different force ratios $P_{2}/P_{3}$, and $k_{2}=1$ for both the $\mathbf {A}=\mathbf {I}$ treatment and the $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ treatment. The stiffness effect of the matrix component is again neglected for the purpose of this figure, i.e., $\mu =0$. Although the force $P_{2}$ in the $\mathbf {E}_{2}$ direction is the same in all panels, the elongation in this direction is influenced by the force $P_{3}$ in $\mathbf {E}_{3}$ direction. Specifically, an increasing force ratio $P_{3}/P_{2}$ leads to larger values of $\lambda_{3}$ and to smaller values for $\lambda_{2}$ in both cases $\mathbf {A}=\mathbf {I}$ and $\mathbf {A}(\tau )=\mathbf {F}(\tau )$.

Fig. 8

Evolution of the displacements $\lambda_{2}(t)$ and $\lambda_{3}(t)$ as a function of normalized time $t^{*}=k_{1}t$ for $P^{*}=100$, different force ratios $P_{3}/P_{2}$, and $k_{2}=1$. The matrix component is regarded as negligible so that $\mu =0$. The falling curves represent the $\mathbf {A}=\mathbf {I}$ treatment, and the rising curves represent the $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ treatment

The limiting values for $\lambda_{2}$ and $\lambda_{3}$ as $t\rightarrow \infty$ are determined from Eqs. (43a), (43b):

• In the case of $\mathbf {A}(\tau )=\mathbf {F}(\tau )$, the material undergoes a continuous process of fiber dissolution and creation of new undeformed fibers. This leads to increasing stretch under constant force, as shown in Fig. 8. If the matrix component is neglected so that $\mu =0$, then $\lambda_{2}\rightarrow \infty$ and $\lambda_{3} \rightarrow \infty$ as $t\rightarrow \infty$. If the matrix component is taken into consideration so that $\mu > 0$, then the limiting stress–deformation relation is solely governed by the properties of the matrix. The limiting values $\lambda_{2_{\infty }}$ and $\lambda_{3_{\infty }}$ for $P^{*}=100$, different force ratios $P_{3}/P_{2}$, and $k_{2}=1$ are illustrated in the upper panels of Fig. 9 on the range $0\leq \mu^{*}<200$.

  Fig. 9

  

  The limiting values $\lambda_{2_{\infty }}$ and $\lambda_{3_{\infty }}$ for $P^{*}=100$, different force ratios $P_{3}/P_{2}$, and $k_{2}=1$ on the range $0\leq \mu^{*}<200$. The upper panels treat $\mathbf {A}(\tau )=\mathbf {F}(\tau )$, the bottom panels treat $\mathbf {A}=\mathbf {I}$

• The choice of $\mathbf {A}=\mathbf {I}$ results in a stiffening of the material in the load direction. This stiffening leads to material contraction under constant force, as shown in Fig. 8. If matrix component is taken into consideration, so that $\mu > 0$, then the limiting stress–deformation relation is governed by the properties of both the matrix and the fibers. The limiting values $\lambda_{2_{ \infty }}$ and $\lambda_{3_{\infty }}$ for $P^{*}=100$ and different force ratios $P_{3}/P_{2}$ are illustrated in the bottom panels of Fig. 9 for the range $0\leq \mu^{*}<200$.

3.2.2 Influence of the dissolution exponent on the deformations

Consider the step load with $P^{*}=100$ and $P_{3}/P_{2}=10$. This example is also presented in panel (d) of Fig. 8 for $k_{2}=1$. Figure 10 shows how changing $k_{2}$ influences the evolution of the stretch ratios. Increasing $k_{2}$ leads to a slower dissolution rate. In the case of $\mathbf {A}(\tau )=\mathbf {F}(\tau )$, the elongations becomes slower as $k_{2}$ increases. In the case of $\mathbf {A}=\mathbf {I,}$ the shortening becomes faster, and the limiting values for $\lambda_{2}$ and $\lambda_{3}$ become smaller as $t\rightarrow \infty$. Panel (a) clearly shows an interaction between the biaxial loading: for $\mathbf {A}=\mathbf {I}$ the function $\lambda_{2}(t)$ has a local minimum, which does not occur in the uniaxial loading case (see Topol et al. 2015).

Fig. 10

Evolution of the displacements $\lambda_{2}(t)$ and $\lambda_{3}(t)$ as a function of normalized time $t^{*}=k_{1} t$ due to the applied normalized force $P^{*}=100$ and the force ratio $P_{3}/P_{2}=10$. The matrix stiffness is regarded as negligible so that $\mu =0$. The upper curve in a certain line style represents $\mathbf {A}(\tau )=\mathbf {F}(\tau )$, the lower curve $\mathbf {A}=\mathbf {I}$. Panel (a) is for $\lambda_{2}(t)$, and panel (b) for $\lambda_{3}(t)$

4 Inflation of a spherical membrane

We now turn to consider a spherical membrane that is composed of the same fiber reinforced material discussed in the previous sections. For $t<0$ the membrane is unpressurized with respect to the ambient external pressure. It is presumed to have been kept in this unpressurized state sufficiently long so that the fiber remodeling process is in homeostasis at $t=0^{-}$. At $t = 0^{+}$, the membrane is subjected to a uniform time-dependent pressure $P(t)$ over its inner surface,

$$ P_{i}= \textstyle\begin{cases} 0,&\mbox{for } t< 0, \\ P(t),&\mbox{for } t> 0. \end{cases} $$

(46)

This results in its time-dependent inflation, which is assumed to be spherically symmetric.

The reference configuration $\kappa_{0}$ and later configurations $\kappa (t)$ are described with respect to the spherical coordinate system defined by the unit vectors $\{ \mathbf {E}_{r}, \mathbf {E}_{\theta }, \mathbf {E}_{\phi } \}$. In its reference configuration $\kappa_{0}$, the mid-surface radius is $R$ and the membrane thickness is $H$. The usual membrane assumption $H/R\ll 1$ implies that the values of the stretch and stress at any point through the thickness of the membrane equals their values on the mid-surface to within $O(H/R)$ (Wineman 2009).

Each material particle moves radially during inflation and undergoes an equal biaxial stretch history in the directions $\{ \mathbf {E}_{ \theta }, \mathbf {E}_{\phi } \}$ tangent to the membrane mid-surface. Let $r(t)$ be the mid-surface radius, and $h(t)$ be the membrane thickness for $t> 0$ (see Fig. 11). Its deformation gradient tensor $\mathbf {F}=\mathbf {F}(t)$ has the form

$$ \mathbf {F}= \lambda_{r}\mathbf {E}_{r}\otimes \mathbf {E}_{r} +\lambda_{\theta }\mathbf {E}_{\theta }\otimes \mathbf {E}_{\theta }+\lambda_{\phi }\mathbf {E}_{ \phi }\otimes \mathbf {E}_{\phi }, $$

(47)

where

$$ \lambda_{r}=\lambda_{r}(t)= \frac{h(t)}{H},\qquad \lambda_{\theta }= \lambda_{\theta }(t)= \frac{r(t)}{R},\quad \text{and}\quad \lambda_{ \phi }=\lambda_{\phi }(t)= \frac{r(t)}{R}\equiv \lambda (t) $$

(48)

are the principal stretches in radial, circumferential, and azimuthal directions, respectively. Observe that we have let $\lambda (t)= \lambda =\lambda_{\theta }=\lambda_{\phi }$; the incompressibility condition $\lambda_{r}\lambda_{\theta }\lambda_{\phi }=1$ now results in

$$ \lambda_{r}={1}/{\lambda^{2}}. $$

(49)

The development in Sect. 3 applies locally with respect to the directions $\{ \mathbf {E}_{r}, \mathbf {E}_{\theta }, \mathbf {E}_{\phi } \}$. These directions also give a principal frame for both stress and stretch in the problem under consideration here. Hence

$$\begin{aligned} \mathbf {T} =& T [ \mathbf {E}_{\theta }\otimes \mathbf {E}_{ \theta }+ \mathbf {E}_{\phi }\otimes \mathbf {E}_{\phi } ] , \end{aligned}$$

(50a)

$$\begin{aligned} \mathbf {F} =&\frac{1}{\lambda^{2}}\mathbf {E}_{r}\otimes \mathbf {E}_{r} + \lambda [ \mathbf {E}_{ \theta }\otimes \mathbf {E}_{\theta }+\mathbf {E}_{\phi } \otimes \mathbf {E}_{\phi } ] , \end{aligned}$$

(50b)

$$\begin{aligned} \mathbf {A} =&\frac{1}{a^{2}}\mathbf {E}_{r}\otimes \mathbf {E}_{r} +a [ \mathbf {E}_{ \theta }\otimes \mathbf {E}_{\theta }+\mathbf {E}_{\phi }\otimes \mathbf {E}_{\phi } ] , \end{aligned}$$

(50c)

where $a=1$ in the case of $\mathbf {A}=\mathbf {I}$, and $a(\tau )=\lambda ( \tau )$ in the case of $\mathbf {A}(\tau )=\mathbf {F}(\tau )$.

Fig. 11

Inflation of a spherical membrane due to an inner pressure $P$

Echoing our previous considerations, each location within the spherical membrane contains a distribution of fibers with respect to all directions. Representations (16) and (17) for $R$ and $\mathbf {T}$ continue to hold upon taking the local representation of $\mathbf {N}$ in the form

$$ \mathbf{N}=\cos {\theta }\mathbf {E}_{r}+\sin {\theta }\cos {\phi }\mathbf {E} _{\theta }+\sin {\theta }\sin {\phi }\mathbf {E}_{\phi }. $$

(51)

The invariant $I_{4}=I_{4}(\mathbf {C},\mathbf {N},\mathbf {A})$ defined in (7) and the dissolution rate $\eta =\eta (I_{4})$ defined in (11) now give

$$ \hat{I}_{4}\bigl(\lambda (t),a(\tau ),\theta \bigr)= \frac{ \lambda^{-4}(t)\cos ^{2}\theta + \lambda^{2}(t)\sin^{2}\theta }{ a^{-4}(\tau )\cos^{2} \theta + a^{2}(\tau )\sin^{2}\theta } $$

(52)

and

$$ \hat{\eta }\bigl(\lambda (t),a(\tau ),\theta \bigr)= k_{1} \bigl[ \hat{I}_{4}\bigl( \lambda (t),a(\tau ),\theta \bigr) \bigr] ^{-k_{2}}, $$

(53)

making use of the notation introduced in (27) and (29).

Assuming the motion to be quasistatic, force balance implies (Wineman 2009) that the Cauchy stress $T$ and inflating pressure $P(t)$ are related via

$$ T(t)=\frac{1}{2}\frac{r(t)}{h(t)}P(t), $$

(54)

which with (48), (49), causes Eq. (54) to become

$$ T(t)=\frac{\lambda^{3}(t)}{2}\frac{R}{H}P(t). $$

(55)

The relation between the inflating pressure $P(t)$ and the stretch $\lambda (t)$ for $t\geq 0$ is obtained from (13) and (18) with the help of (50a)–(52), and (55) as

$$\begin{aligned} \displaystyle \frac{P(t)}{2}\frac{R}{H} =&\displaystyle \mu \biggl[ \frac{1}{\lambda (t)}-\frac{1}{\lambda^{7}(t)} \biggr] + 2 \pi \chi_{c}\gamma \int_{0}^{\pi } \biggl\{ \bigl[ \hat{I}_{4} \bigl(\lambda (t),1,\theta \bigr)-1 \bigr] \displaystyle \frac{1}{\eta_{0}} \\ &{}\times \exp \biggl( - \int_{0}^{t}\hat{\eta }\bigl(\lambda (s),1,\theta \bigr) \,\mathrm{d}s \biggr) + \int_{0}^{t}\frac{\hat{\eta }(\lambda (t),a( \tau ),\theta )-1}{\hat{I}_{4}(a(\tau ),1,\theta )} \\ &{}\times \exp \biggl( - \int_{0}^{t}\hat{\eta }\bigl(\lambda (s),a(\tau ), \theta \bigr) \,\mathrm{d}s \biggr) \,\mathrm{d}\tau \biggr\} \biggl[ \frac{\sin ^{3}{\theta }}{\lambda (t)}- \frac{2\sin {\theta }\cos^{2}{\theta }}{ \lambda^{7}(t)} \biggr] \,\mathrm{d}\theta , \end{aligned}$$

(56)

where $\eta_{0}=\eta (I_{4}(\mathbf {I},\mathbf {N},\mathbf {I}))=k_{1}$. Note that in (56) the integrations with respect to $\phi$ are already carried out, so that the presented equation is independent of $\phi$.

4.1 Inflation due to a constant pressure

Consider a constant and suddenly applied inflation pressure $P(t)=P>0$. The following examples investigate the inflation process represented by $\lambda (t)$, and show how the constitutive stipulation of the tensor $\mathbf {A}$ and the parameter $k_{2}$ influence both the deformation path and the limiting relations as $t\rightarrow \infty$. Note that $\lambda (t)=r(t)/R$ can be interpreted as a normalized radius in the deformed configuration at time $t$.

Initial response

The relation between $P$ and the initial response inflation $\lambda_{0}=\lambda (0^{+})$ at $t=0^{+}$ can be determined from (56) by setting $t=0$ and $\lambda (t)=\lambda _{0}$. Evaluation of the resulting integrals then gives

$$ \frac{PR}{2H}= \mu \biggl[ \frac{1}{\lambda_{0}}- \frac{1}{\lambda_{0} ^{7}} \biggr] +\frac{8\pi }{15}\frac{\chi_{c}\gamma }{k_{1}} \biggl[ 4 \lambda_{0}- \frac{5}{\lambda_{0}} - \frac{1}{\lambda_{0}^{5}} + \frac{5}{ \lambda_{0}^{7}} - \frac{3}{\lambda_{0}^{11}} \biggr] , $$

(57)

which is independent from $\mathbf {A}$ as in the initial response in the previously discussed biaxial cases. Applying the normalization

$$ {\bar{P}}=\frac{PR}{2H}\frac{k_{1}}{\chi_{c}\gamma }, $$

(58)

Figure 12 illustrates the relation between the initial displacements $\lambda_{0}$ and the applied normalized inner pressure ${\bar{P}}$ for different values of $\mu^{*}$, which continues to be given by (45). With larger values for $\mu^{*}$, the matrix properties dominate in the overall material response, and the relation between ${\bar{P}}$ and $\lambda_{0}$ shows a local maximum. Depending on the values of ${\bar{P}}$ and $\mu^{*}$ there may be one, two, or three associated values of $\lambda_{0}$. For example, when $\mu^{*}=200$, the value ${\bar{P}}=100$ yields three possible initial displacement values for $\lambda_{0}$; these are $\lambda_{0}= 1.149$, 2.235, and 12.663. The non-monotone dependence of inflation pressure on the deformed radius is a well-known feature of neo-Hookean material response (Müller and Strehlow 2004) and thus is retained here provided $\mu^{*}$ is sufficiently large. Conversely, the formation of a local extremum is not observed when only the fiber component is considered.

Fig. 12

Relation between the initial displacements $\lambda_{0}$ and the applied normalized inner pressure ${\bar{P}}$ (see Eq. (58)) for different values of $\mu^{*}$ (see Eq. (45)). This relation is independent of $\mathbf {A}$ and $k_{2}$

Asymptotic large time response

When $t\rightarrow \infty$ the material approaches a limiting deformation so that

$$ \lim_{t\rightarrow \infty }\lambda (t)=\lambda_{\infty }, \qquad \lim_{\tau \rightarrow \infty } a(\tau )=a_{\infty } $$

(59)

with $a_{\infty }=1$ if $\mathbf {A}=\mathbf {I}$ and $a_{\infty }=\lambda_{ \infty }$ if $\mathbf {A}(\tau )=\mathbf {F}(\tau )$. The limiting relation between $\lambda_{\infty }$, $a_{\infty }$, and $P$ follows from (56) by taking $t\to \infty$ using (59). This gives

$$\begin{aligned} \displaystyle \frac{PR}{2H} =&\displaystyle \mu \biggl[ \frac{1}{\lambda_{\infty }}-\frac{1}{\lambda_{\infty }^{7}} \biggr] + 2\pi \gamma \chi_{c} \int_{0}^{\pi } \frac{\hat{I}_{4}(\lambda_{ \infty },a_{\infty },\theta )-1}{\hat{I}_{4}(a_{\infty },1,\theta ) \hat{\eta }(\lambda_{\infty },a_{\infty },\theta )} \\ &{}\times \biggl[ \frac{\sin^{3}{\theta }}{\lambda_{\infty }} - \frac{2 \sin {\theta }\cos^{2}{\theta }}{\lambda_{\infty }^{7}} \biggr] \, \mathrm{d} \theta , \end{aligned}$$

(60)

which depends upon the stipulation for $\mathbf {A}$.

• In the case of $\mathbf {A}=\mathbf {I}$, the relation between ${\bar{P}}$ and $\lambda_{\infty }$ depends both on the choice of $\mu^{*}$ and on the choice of $k_{2}$. Some results are presented in Fig. 13. If $k_{2}=0.0$, then (60) coincides with (57). This is why panel (a) in Fig. 13 coincides with Fig. 12. Depending on the values of $k_{2}$, $\mu^{*}$, and ${\bar{P}}$, there may be one, two, or three values of $\lambda_{\infty }$. For example, if ${\bar{P}}=180$ and $\mu^{*}=300$, then there are three such values when $k_{2}=0.5$ ($\lambda_{\infty }=1.25,\ 1.7,\mbox{ and }4.4$). However, for the same ${\bar{P}}$ and $\mu^{*}$ there is only such value if $k_{2}=1.5$ ($\lambda_{\infty }=1.24$). For sufficiently large $\lambda_{\infty }$, the ${\bar{P}}$ vs. $\lambda_{\infty }$ curves all increase monotonically and without bound as $\lambda_{\infty }$ increases. Thus, for all values of ${\bar{P}}$, there is at least one finite positive value of $\lambda_{\infty }$ for which the fiber remodeling is in homeostasis. While the choice of $\mu^{*}$ has a stronger influence for smaller values of $\lambda_{\infty }$, the choice of $k_{2}$ has a stronger influence in the relation between ${\bar{P}}$ and $\lambda_{\infty }$ as these values become larger.

  Fig. 13

  

  Relation between the large time displacements $\lambda_{\infty }$ and the applied pressure ${\bar{P}}$ (see Eq. (58)) using $\mathbf {A}=\mathbf {I}$ for different values of $\mu^{*}$ (see Eq. (45)) and different values of $k_{2}$

• In the case of $\mathbf {A}(\tau )=\mathbf {F}(\tau )$, the invariant $\hat{I}_{4}$ takes the form $\hat{I}_{4}(\lambda_{\infty },a_{\infty },\theta )= \hat{I}_{4}(\lambda_{\infty },\lambda_{\infty },\theta )= 1$, and the second term in (60) becomes zero. Consequently, the fibers do not contribute to the limiting relation between ${\bar{P}}$ and $\lambda_{\infty }$, i.e., this limiting relation is solely governed by the properties of the neo-Hookean model. The relation between ${\bar{P}}$ and $\lambda_{\infty }$ for different values of $\mu^{*}$ is presented in Fig. 14. For each value of $\mu^{*}\neq 0$ when ${\bar{P}}$ is sufficiently small a deformation state $\lambda_{\infty }$ with fiber remodeling in homeostasis can be found. If ${\bar{P}}$ exceeds the local maximum of the ${\bar{P}}$ vs. $\lambda_{\infty }$ curve, then a deformation limit $\lambda_{\infty }$ with fiber remodeling in homeostasis does not exist.

  Fig. 14

  

  Relation between the limiting displacements $\lambda_{ \infty }$ and the applied normalized inner pressure ${\bar{P}}$ (see Eq. (58)) for different values of $\mu^{*}$ (see Eq. (45)) using $\mathbf {A}(\tau )=\mathbf {F}(\tau )$. In this case the fibers have no effect upon this relation. Consequently, the large-time behavior is that of the base neo-Hookean matrix material

Intermediate time response

The intermediate values for $\lambda$ are computed numerically from (56) in a similar fashion as that described in Sect. 3.2. As a simple example consider $\mu^{*}=100$ and $k_{2}=0.1$. Figure 15 shows the initial time curve of ${\bar{P}}$ vs. $\lambda_{0}$ for the immediate inflation response after the application of the positive internal pressure. As already emphasized, this initial inflation response curve is common for all the different possibilities of specifying $\mathbf {A}$ and $k_{2}$. Figure 15 also shows the large time ${\bar{P}}$ vs. $\lambda_{\infty }$ curves for both the stipulation $\mathbf {A}=\mathbf {I}$ and the stipulation $\mathbf {A}(\tau )=\mathbf {F}( \tau )$. The former is above the initial inflation response curve, the latter is below the initial inflation response curve. The initial inflation response curve has a local maximum at $(\lambda_{0},{\bar{P}})=(1.43,65.7)$ and a local minimum at $(\lambda_{0},{\bar{P}})=(3.69,49.5)$. Thus if $49.5<{\bar{P}}<65.7$, then there are three possible values for $\lambda_{0}$. On the other hand, if either ${\bar{P}}<49.5$ or ${\bar{P}}>65.7$, then there is only one possible value for $\lambda_{0}$.

Fig. 15

Initial time curve of ${\bar{P}}$ vs. $\lambda_{0}$ at time $t=0^{+}$ and large time curves ${\bar{P}}$ vs. $\lambda_{\infty }$ curves for both the stipulation $\mathbf {A}=\mathbf {I}$ and the stipulation $\mathbf {A}(\tau )=\mathbf {F}(\tau )$. All curves are for $\mu^{*}=100$, and $k_{2}=0.1$. The horizontal lines define the interval $49.5<{\bar{P}}<65.7$ for which three values for $\lambda_{0}$ are possible

For simplicity of explanation, take ${\bar{P}}=48$ so that there is one possible value for $\lambda_{0}$, namely $\lambda_{0}=1.13268$. For the $\mathbf {A}=\mathbf {I}$ stipulation there is only one value for $\lambda_{\infty }$ associated with this ${\bar{P}}$, namely $\lambda_{\infty }=1.13262<1.13268$. For the $\mathbf {A}(\tau )=\mathbf {F}( \tau )$ stipulation there are two values for $\lambda_{\infty }$ associated with this ${\bar{P}}$, namely $\lambda_{\infty }=1.1415> \lambda_{0}$ and $\lambda_{\infty }=2.055>\lambda_{0}$. The first of these two values is on the ascending branch of the ${\bar{P}}$ vs. $\lambda_{\infty }$ curve for the $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ treatment, and the second value is on the descending branch of this curve. On the basis of a standard stability argument, one anticipates that the first is indeed a large time attractor but the second value is not (Müller and Strehlow 2004). Figure 16 provides a magnified view of Fig. 15 focusing on the first ascending branch of the ${\bar{P}}$ vs. $\lambda$ curves. This figure shows the development of the inflation $\lambda$ for a constant pressure ${\bar{P}}=48$. The orientations of the arrows illustrates the direction of this development with time. The left panel treats $\mathbf {A}=\mathbf {I}$, and the right panels treats $\mathbf {A}(\tau )=\mathbf {F}( \tau )$.

Fig. 16

Development of the inflation $\lambda$ for a constant pressure ${\bar{P}}=48$, $\mu^{*}=100$, and $k_{2}=0.1$. Panel (a) treats $\mathbf {A}=\mathbf {I}$, the panel (b) treats $\mathbf {A}(\tau )=\mathbf {F}( \tau )$. Panel (b) specifically identifies the inflation at $\lambda_{i}=\lambda|_{t^{*}=i}$ for $i=1$ and 2 where again $t^{*}=k_{1}t$

An interesting aspect of this development concerns the effect of the non-monotone nature of the ${\bar{P}}$ versus $\lambda$ curves. The consequences of such non-monotone curves, with two ascending branches and one descending branch, have been studied extensively in the classical theory of hyperelasticity. Sudden transitions at fixed ${\bar{P}}$ between these branches are associated with an abrupt increase or decrease in the inflation of the sphere. The example given for illustration here in Fig. 16 is specifically chosen in both the $\mathbf {A}=\mathbf {I}$ and $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ cases so as to avoid any such branch transitions. However, it is a relatively simple matter to obtain examples in which such branch transitions occur, either because a particular branch can no longer sustain the given value of ${\bar{P}}$ or for more involved reasons associated with branch stability. For example, there may be a particular value of time at which the most stable branch for the given value of ${\bar{P}}$ switches from the current branch to the other ascending branch. The specific value of such a time could then be determined by a systematic analysis that combines the stability criterion under consideration with the type of analysis developed in this paper. Such considerations, while very interesting, are not in the scope of the present work.

5 Summary and discussion

This article has investigated the time-dependent mechanical response of a nonlinear elastic fiber reinforced composite material that is a result of a time-dependent fiber remodeling process. This is a chemomechanical process in which the chemical kinetics of remodeling are regulated by fiber stretch. The constitutive framework connecting stress, deformation and fiber remodeling was presented by Demirkoparan et al. (2013) and recapped here in Sect. 2.

An important aspect of this theory is the role played by the notion of a reference configuration. The natural configuration of the matrix $\kappa_{0}$ acts as the reference configuration for the initial state of the matrix/fiber system. The theory allows for the possibility that a newly created fiber may have a different natural configuration $\kappa_{f}(\tau )$. This configuration is defined relative to configuration $\kappa_{0}$ by tensor $\mathbf{A}$. In this work, two choices for the fiber natural configuration are considered. Specification of the fiber natural configuration will depend on an understanding of the actual physiological process of fiber reforming. The mechanical response results presented here may be useful in guiding the choice.

As in any constitutive theory, there are a collection of constants and functions that must be specified in order to completely characterize the model. In the present modeling, there are five such specifications: the stored energy density of the matrix constituent $W_{m}(I_{1}, I_{2})$ in which $I_{1}$ and $I_{2}$ are measured from the fixed reference configuration, the stored energy of a single protofiber entity $\psi (I_{4})$ where $I_{4}$ is measured from the natural configuration of the fiber (which is in general different from the fixed reference configuration), the constant rate of fiber creation $\chi_{c}$, the stretch dependent rate of fiber dissolution $\eta (I_{4})$, and, finally, the rule that determines the natural state for a newly deposited fiber.

New results are obtained that illustrate the influence of the biaxial deformation. The time-dependent response does not arise from the mechanical properties of the matrix or the fibers, i.e., the viscoelasticity of the individual constituents, as these constituents are assumed to be elastic. The time-dependent response arises from two distinct modeling features. The first is a first order chemical kinetics process in which there is continuous dissolution and creation of the reinforcing fibers. The second is an assumption about the state in which the fibers are created. Two different ways for stipulating such states are examined in detail: $\mathbf {A}=\mathbf {I}$ which corresponds to a process where fibers are in the same deformed state as the surrounding matrix when created, and $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ which corresponds to a process where fibers are undeformed when created. As the chemical kinetics process is affected by the stretch of the fiber relative to the state in which it is created, the different modeling choices for the as-deposited fiber states generate different mechanical outcomes. Another significant factor that influences the stress and deformation response is the fiber dissolution rate. As one would expect, lower dissolution rates confer a higher stiffness.

An important feature of the constitutive framework occurs when the material is maintained at a fixed deformation for a long period of time. The material then approaches a state of homeostasis, in which the stress and stretch do not vary with time although the underlying processes of fiber dissolution and creation are ongoing but are in balance. This result is analogous to the long time limiting state observed in viscoelasticity when the relaxation process has reached completion.

This constitutive framework is formulated so as to be able to model diverse possibilities for both the fiber creation mechanics and the fiber resorption mechanics. Within this general framework the specific constitutive choices (5), (8), (11), and both $\mathbf {A}(\tau )=\mathbf {I}$ and $\mathbf {A}(\tau )=\mathbf {F}(\tau )$ are motivated by the current state of understanding on the basis of soft tissue experimental findings. As a deeper understanding is developed, the constitutive framework is sufficiently general so as to be able to accommodate a variety of modeling refinements. Some of these are: (i) alternative chemical processes and their modification by multiaxial deformation; (ii) alternative choices for stipulating the fiber natural configuration; (iii) direct fiber/matrix interactions; and (iv) influence of fiber dissolution and reassembly on the viscoelastic characteristics of either the fiber or matrix constituent.

Appendix A: Numerical treatment of the integrals in (40a), (40b)

Consider the integration of the continuous function $f(s)$ with respect to $s$ over the interval $[ t_{0}, t_{m} ]$. Dividing this interval into sufficiently small subintervals and applying the trapezoidal rule gives

$$ \int_{t_{0}}^{t_{m}}f(s)\,\mathrm{d}s=\sum _{i=0}^{m-1} \int_{t_{i}}^{t _{i+1}}f(s)\,\mathrm{d}s\approx \frac{\Delta t_{i}}{2} \bigl[ f(t_{i+1})+ f(t_{i}) \bigr] $$

(61)

where $\Delta t_{i}=t_{i+1}-t_{i}$. If the integral with respect to $s$ occurs in the argument of an exponential function, then (61) leads to

$$ \exp \biggl( - \int_{t_{0}}^{t_{m}}f(s)\,\mathrm{d}s \biggr) \approx \prod _{i=0}^{m-1}\exp \biggl( -\frac{\Delta t_{i}}{2} \bigl[ f(t_{i+1})+ f(t _{i}) \bigr] \biggr) . $$

(62)

In the framework of this paper, integrals in the form

$$ \int_{t_{0}}^{t_{m}}f_{I}(t_{m}, \tau ) \exp \biggl[ - \int_{\tau }^{t _{m}}f_{II}(s,\tau )\,\mathrm{d}s \biggr] \,\mathrm{d}\tau , $$

(63)

are treated. If (61) is applied to approximate the integration with respect to $\tau$, then (63) becomes

$$\begin{aligned} &\displaystyle \int_{t_{0}}^{t_{m}}f_{I}(t_{m}, \tau ) \exp \biggl( - \int_{ \tau }^{t_{m}}f_{II}(s,\tau )\,\mathrm{d}s \biggr) \,\mathrm{d}\tau \\ & \quad {}\approx \displaystyle \sum_{i=0}^{m-1} \frac{\Delta t_{i}}{2} \biggl\{ f_{I}(t_{m}, t_{i}) \exp \biggl( - \int_{t_{i}}^{t_{m}}f_{II}(s,t_{i})\, \mathrm{d}s \biggr) \\ &\qquad {}+f_{I}(t_{m}, t_{i+1})\exp \biggl( - \int_{t_{i+1}}^{t_{m}}f_{II}(s,t_{i+1})\, \mathrm{d}s \biggr) \biggr\} . \end{aligned}$$

(64)

Additionally, if now the integration with respect to $s$ is approximated by (62), then (64) becomes

$$\begin{aligned} &\displaystyle \int_{t_{0}}^{t_{m}}f_{I}(t_{m}, \tau ) \exp \biggl( - \int_{ \tau }^{t_{m}}f_{II}(s,\tau )\,\mathrm{d}s \biggr) \,\mathrm{d}\tau \\ & \quad {}\approx \displaystyle \sum_{i=0}^{m-1} \frac{\Delta t_{i}}{2} \Biggl\{ f_{I}(t_{m}, t_{i}) \prod _{j=i}^{m-1} \exp \biggl( -\frac{\Delta t_{j}}{2} \bigl[ f_{II}(t _{j},t_{i})+f_{II}(t_{j+1},t_{i}) \bigr] \biggr) \\ &\displaystyle \qquad {}+ f_{I}(t_{m}, t_{i+1}) \prod _{j=i+1}^{m-1}\exp \biggl( -\frac{\Delta t_{j}}{2} \bigl[ f_{II}(t _{j},t_{i+1})+f_{II}(t_{j+1},t_{i+1}) \bigr] \biggr) \Biggr\} . \end{aligned}$$

(65)