Introduction

Accurate estimation of aquifer properties such as hydraulic conductivity, transmissivity, and storativity is paramount to successful groundwater modeling. Field pumping tests with graphical matching are the widely used and most common techniques to determine these parameters. This approach, however, usually involves significant simplification such as idealized flow models and assuming constant parameters, e.g., homogeneous and isotropic aquifers (Zhou et al. 2014). In the last two decades, inverse groundwater modeling has often been advocated as an advanced, economical, feasible, and automatic technique, and has been gradually adopted as a valid mathematical approach to estimate aquifer parameters. Using inverse problems, distributed parameters are assigned to a mathematical model with known boundary conditions in such a way that it ensures error minimization between the observed and simulated state variables to obtain representative optimal aquifer parameters (Lakshmi Prasad and Rastogi 2001).

Simulation optimization (SO) is a mathematical approach to solving inverse groundwater problems. In general, head values from the simulator are fed to the optimization model and the goal is to minimize the objective function, which is an expression of the sum of the error between simulated and measured heads at different monitoring well locations. Mahinthakumar and Sayeed (2005) broadly classified the optimization methods based on their application in SO models as derivative-based and nonderivative-based. The nonderivative-based optimizations are population-based stochastic search methods that do not require an initial guess of the parameter to be estimated, e.g., genetic algorithms (GA; Harrouni et al. 1996), simulated annealing (SA; Zheng and Wang 1996), particle swarm optimization (PSO; Ch and Mathur 2012; Abril et al. 2022; De Jesus et al. 2022), ant colony optimization (ACO; Abbaspour et al. 2001), cat swarm optimization (CSO; Thomas et al. 2018) and differential evolution (DE; Rastogi et al. 2014; Chang et al. 2021). These optimizations are frequently applied to synthetic problems and a few real field problems are also attempted.

The estimation of aquifer parameters using the SO-based approach is a challenging task for most regional aquifers because: (1) SO models call the simulator frequently to correct its course towards optima, and if a mesh-based simulator is used then it takes a fairly large number of iterative runs (due to mesh-based approximation error which increases geometrically with each generation), leading to higher run time to reach the convergence criteria; (2) minimizing the error norm (difference between observed and simulated head) with higher precision for smaller groundwater head variation is difficult with existing global stochastic search algorithms as their diversity of producing new population weakens after certain generations and they are eventually unable to produce unique representative optimal parameter values; and (3) the accuracy of the most-often used global search optimization methods is highly dependent on their manually adjusted control parameters, which are problem-specific and their tuned values are obtained after numerous model runs, which is the main cause for their high computational cost.

Meshfree (Mfree) simulators are independent of a mesh and therefore not prone to mesh-induced approximation errors. When coupled with population-based stochastic optimization, lower objective function values are achieved and aquifer parameters are estimated quickly. Among different groundwater Mfree simulators, the multiquadric-based groundwater simulator by Patel and Rastogi (2017) for groundwater modeling is a promising option, particularly for parameter estimation applications, for a number of reasons: (1) it has straightforward discretization for flow equations and its computer code is implemented conveniently; (2) it is computationally efficient compared to conventional mesh-based simulators like FEM (Li et al. 2003); (3) it does not suffer from mesh inadequacy and is free from mesh-based approximation error; and (4) it estimates accurate groundwater head values using a fixed range of the dimensionless shape parameter, which is uncertain in other Mfree simulators.

The optimization model feeds the input to the simulation model in terms of aquifer parameters. For this study, the covariance matrix adaptation evolutionary strategy (CMA-ES) optimization was selected and coupled with the Mfree simulator. CMA-ES is a quasi-parameter-free global stochastic optimization algorithm, where population size is the only parameter needed to be tuned (Hansen and Ostermeier 2001). It can be a better alternative when compared with existing optimization algorithms for parameter estimation. Two main advantages of this optimization are as follows. First, there is no need to perform numerous model runs to calibrate the associated strategy parameters; hence, it is highly suitable for field problems. Second, it works well for high-dimensional problems, requiring significantly fewer model generations (Bayer and Finkel 2004). The CMA-ES optimization model has already proved its applicability to a variety of groundwater engineering problems such as contaminant source identification (Bayer and Finkel 2004), parameter estimation for gully erosion (Rengers et al. 2016), and aquifer parameter estimation (Elshall et al. 2015).

This paper describes the novel combination of the multiquadric Mfree method with CMA-ES optimization to estimate aquifer parameters. The new model is referred to here as Mfree-CMA-ES. Most of the past studies used the combination of a mesh-based simulator and manually tuned control-parameters-based optimization for aquifer parameter estimation. These algorithms were unable to produce the lowest value of the objective function (due to premature convergence), and they are time-consuming and costly options in terms of computational cost. Therefore, the Mfree-CMA-ES-based SO model is developed which is a powerful tool to obtain aquifer parameters with high precision, particularly for regional aquifer systems that have minimum temporal changes in groundwater head. The accuracy of Mfree simulators for calculating head values together with the ability of CMA-ES optimization to converge faster with a lower number of generations is highly advantageous and yields more precise values for aquifer parameters.

Inverse groundwater model

The mathematical formulation of Mfree-CMA-ES for solving inverse problems using the SO approach is explained in the upcoming subsections.

Groundwater simulation

Consider a flow model representing a transient, two-dimensional (2D), heterogeneous, anisotropic, and fully saturated confined aquifer. The governing equation is given by (Wang and Anderson 1995):

$$\frac{\partial }{\partial x}\left({T}_x\frac{\partial H}{\partial x}\right)+\frac{\partial }{\partial y}\left({T}_y\frac{\partial H}{\partial y}\right)=S\left(\frac{\partial H}{\partial t}\right)\pm {Q}_w\delta \left(x-{x}_{\mathrm{p}},y-{y}_{\mathrm{p}}\right)+R$$
(1)

where H is the piezometric head, S is storativity, Tx and Ty are the transmissivity values in the longitudinal (x) and lateral (y) directions, Qw represents source (+) or sink (-) terms located at the points (xp,yp), δ(x,y) is the 2D Dirac delta function, t is time and R is surface recharge. Mesh-based simulations require computationally demanding preprocessing (Liu 2003); hence, a global collocation-based meshfree groundwater simulation model, developed by Patel and Rastogi (2017), is selected in this study. In this model, spatial derivatives are approximated by a multiquadric approach (Kansa 1990a, b) and the temporal terms are discretized by the finite difference method (FDM) using a central difference implicit scheme (section S1 of electronic supplementary material (ESM). The final discretized form of governing Eq. (1) for an individual node, using a multiquadric radial basis function (MQ-RBF) and after neglecting insignificant terms, is rewritten as (Patel and Rastogi 2017):

$$\begin{array}{c}\left\{\frac{S_j}{\nabla t}\left[\sum_{j=1}^N\phi_j\left(x_i,y_i\right)\right]-T_{x_j}\left[\sum_{j=1}^N\frac{\partial^2\phi_j\left(x_i,y_i\right)}{\partial x^2}\right]-T_{y_j}\left[\sum_{j=1}^N\frac{\partial^2\phi_j\left(x_i,y_i\right)}{\partial y^2}\right]\right\}\times\left\{H_j\right\}^{t+1}\\=\left\{\frac{S_j}{\triangle t}\left[\phi_j\left(x_i,y_i\right)\right].\left\{H_j\right\}^t\right\}\pm Q_w\left(x-x_{\mathrm p},y-y_{\mathrm p}\right)+R_j\;\mathrm{where}\;i=1,2\dots N_I\end{array}$$
(2)

where [ϕ] is known as a radial basis function matrix.

Objective functions

The objective functions used in optimization methods for parameter estimation are typically nonlinear, noncontinuous, and cannot be expressed explicitly in terms of decision variables, i.e., aquifer parameters. Here, the objective function to be minimized is defined as the fitting error between the observed and the simulated aquifer head at monitoring well locations. This fitting error can be represented in three different ways: the sum of squared difference (SSD; Eq. 3), the sum of the mode of difference (SMD; Eq. 4), and the sum of the root mean squared error (SRMSE; Eq. 5). These can be expressed as:

$$E(P)={\gamma}_{b,t}\sum_{b=1}^L\sum_{t={t}_0}^{t_t}{\left[{h}_{b,t}^{\mathrm{obs}}-{h}_{b,t}^{\mathrm{sim}}(P)\right]}^2$$
(3)
$$E(P)={\gamma}_{b,t}\sum_{b=1}^L\sum_{t={t}_0}^{t_t}{\left|{h}_{b,t}^{\mathrm{obs}}-{h}_{b,t}^{\mathrm{sim}}(P)\right|}^2$$
(4)
$$E(P)={\gamma}_{b,t}\sum_{b=1}^L\sum_{t={t}_0}^{t_t}\sqrt{\frac{{\left[{h}_{b,t}^{\mathrm{obs}}-{h}_{b,t}^{\mathrm{sim}}(P)\right]}^2}{L}}$$
(5)
$${P}_i^{\mathrm{l}}\le {P}_i\le {P}_i^{\mathrm{u}}$$
(6)

where E represents the objective function to be minimized,\({h}_{b,t}^{\mathrm{sim}}\) is calculated groundwater head at observation well b at time t with parameter (P) as input,\({h}_{b,t}^{\mathrm{obs}}\) is observed groundwater head at observation well b at time t, Pi is the aquifer parameter at zone i, L is the total number of observation wells, t0 and tt are the beginning and end time of observations, superscripts l and u represent the lower and upper bounds of the parameters, and γb, t ∈ [0, 1] is the weighting coefficient representing a confidence value for the groundwater head measurement accuracy at monitoring well locations. In the field problem, it is assumed that measurement for each monitoring well is undertaken with precision; therefore, a uniform value of γb, t as unity is considered in the entire study.

Optimization model

In this study, the CMA-ES proposed by Hansen and Ostermeier (2001) is selected as an optimization model for inverse groundwater problems. It is part of a family of evolutionary algorithms. Detailed information on CMA-ES is presented in section S2 of the ESM.

Development of the proposed simulation-optimization model for aquifer parameter estimation

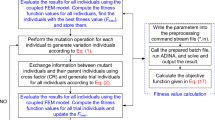
In this study, multiquadric-based Mfree simulation is coupled with CMA-ES optimization (for details, see section S1 of the ESM) to develop a SO model for aquifer parameter estimation. The detailed steps of the Mfree-CMA-ES model to estimate the aquifer parameters are as follows. It may be noted that all computations are performed using MATLAB 2015b on 4 GB RAM, Intel Core i5 processor with 3.20 GHz CPU speed (Source code at Patel 2022).

  1. Step 1.

    All input data, like observation well data, boundary conditions, storativity, zonation pattern, and other geological field data (obtained through field survey and hydrogeological investigation) are fed to the Mfree-CMA-ES-based SO model.

  2. Step 2.

    Similar to other evolutionary-based SO models, the upper and lower limits of parameters are predefined based on field experience and fed as input to the CMA-ES optimization model. This helps initialize a mean of the initial population using an assumed D-dimensional vector (according to the known zonation pattern) following predefined bounds. Values of different strategy parameters (i.e., ccov, μeff, cc, cσ, and dσ) are calculated based on empirical formulae suggested by Hansen and Ostermeier 2001). The covariance matrix (C) is initialized by a unit matrix for its further expected evolution with the progress of each generation. The global step size (σ) is initialized with the value 0.5 which is large enough to check the increment in σg. Population size (λ) is calculated via an empirical relation proposed by Hansen (2011), using the known dimension of the problem. This is necessary for creating an initial population (Pg = 0) using λ vectors in D-dimensional space.

  3. Step 3.

    The initial population is fed to the simulation model to obtain simulated head values at certain well locations (where field head values are known) and objective function values are calculated using Eq. (3). If the predefined convergence criterion is achieved then the mean values of D-dimensional λ vectors are the estimated aquifer parameters, otherwise, step 4 will be followed.

  4. Step 4.

    From the initially generated population, an updated weighted mean of μ selected vectors out of the λ vectors is calculated using Eq. S13 of the ESM. Next, the estimated strategy parameter covariance matrix and global step size are updated according to Eqs. S15 and S16 of the ESM, respectively. Therefore, a new population for the next generation is created according to Eq. S14 of the ESM.

  5. Step 5.

    This newly generated population is again fed to the simulation model to check the predefined convergence criteria. If the criterion is achieved then the iterative procedure is concluded and estimated aquifer parameters are reached, otherwise repeat steps 4 and 5 until a convergence criterion is met. The entire procedure of the indirect method of parameter estimation using the new Mfree-CMA-ES SO model is represented in a flow diagram (Fig. 1).

Fig. 1
figure 1

Flowchart of proposed Mfree-CMA-ES-based simulation-optimization (SO) model

Full size image

Application of the Mfree-CMA-ES model to a synthetic aquifer problem

Problem statement

The aquifer problem described in Cyriac and Rastogi (2016) is selected in order to test the applicability of the proposed algorithm on a synthetic aquifer mimicking a real field-like problem. This flow domain is irregular and occupies an area of around 40 km2, which extends to nearly 9 km in the longitudinal direction and 5 km in the transverse direction. It has a single confined stratum with a uniform thickness of 100 m. Two impervious granite formations are located on the southern and northern sides. A lake with a constant head of 98 m elevation is considered on the southeastern side. A Neumann boundary condition with an influx rate of 0.5 m2/day is considered along the eastern section and a river boundary on the western side has linearly varying groundwater head. The boundary conditions and zones are depicted in Fig. 2a.

Fig. 2
figure 2

Synthetic aquifer domain with a given zonation pattern and boundary conditions (e.g., Neumann and Dirichlet), b discretized domain using nonuniform collocation nodes showing pumping, recharge, and monitoring well locations, and c temporal variation in river head at upstream node number 40 throughout the year

Full size image

Ten nodes are taken to model the entire river length with a head difference of 2 m between the upstream- and downstream-most nodes. This results in an effective drop of 0.2 m head between two successive river nodes. To represent actual field conditions, the temporal change in the river head is considered to vary according to the Indian monsoon system, depicted in the histogram presented in Fig. 2c. For simplicity, a total simulation time of 360 days is considered, approximately equivalent to 1 year, and each month is represented uniformly by 30 days which are further divided into three segments of 10 days each.

In real field conditions, the aquifer parameters are generally continuously distributed, however, this is difficult to simulate mathematically. Therefore, parameters are often divided into a limited number of regions, a process known as parameterization (Zhou et al. 2014). In this study, the zonation method of parameterization is used to represent the aquifer geology. The selected synthetic problem contains five transmissivity zones that characterize the heterogeneous nature of the problem (see Fig. 2a). Detailed information on the assumed geological characteristics of each zone is presented in Table 1. The anisotropic nature of aquifers is also taken into account by assigning different values to the two components of transmissivity along the principal Cartesian x and y axes. Three pumping wells (P23, P76, P125 each with discharge rate of 2,000 m3/day) along with three recharge wells (R26, R80 and R122 with recharge of respectively 900, 1,000 and 1,000 m3/day) are considered in the domain, leading to dynamic variations in the aquifer. To model the flow, the entire aquifer domain is discretized using 146 nodes where the nodal distance varies from 500 to 620 m in both directions (Fig. 2b). Groundwater head values obtained using FEM simulation show insignificant fluctuations after 1 year and this is a condition that is analogous to aquifers in arid and semiarid regions.

Table 1 Zonal parameters—transmissivity (T) and storativity (S)—of the synthetic confined aquifer problem by Cyriac and Rastogi (2016)
Full size table

Parameter estimation for the synthetic aquifer problem

To solve the inverse problem, the multiquadric-based Mfree groundwater simulator requires calibration of two main parameters, i.e., nodal density (N) and shape parameter αs, prior to its application. The calibrated values of N and αs are 146 and 3, respectively, which are obtained after numerous trial runs using the suggested range as reported by Liu and Gu (2005). The values of other input parameters like time step size (Δt) and total simulation period are kept at 0.5 and 360 days, respectively (refer the study by Patel and Rastogi 2017 for more details).

In this study, ten transmissivity values (Table 1) representing five zones of the heterogeneous aquifer are considered to be unknown for testing the applicability of the proposed model. The objective here is to determine transmissivity values using known data like storativity, boundary conditions, and zonation pattern by minimizing the squared difference between observed and simulated groundwater head data at 50 distinct observation-well locations. Transmissivity values range from 500 m2/day (fine sand) to 2,000 m2/day (gravel). Since it is a synthetic aquifer problem, simulated groundwater head values at 50 observation-well locations are treated as observed data (known data) and are the input for the SO model to seek the 10 unknown transmissivity parameters.

The main strength of CMA-ES optimization lies in its ability to self-adapt with each generation (Bayer et al. 2009). Unlike precalibrated control parameters of other popular metaheuristic optimization methods, the strategy parameters of CMA-ES are calculated by certain empirical formulae. Some of these, like λ, μ, and cc, are functions of the dimension of the problem. The remaining strategy parameters, like ccov, cμ, and cσ, are a function of μeff, which varies with the weighting constant (wi). Since wi varies stochastically, the values of ccov, cμ and cσ will also change their values with each generation. This change will be adaptive and based on past experience obtained from evaluations of the generated candidate solution (section S2 of ESM). The calculated value of CMA-ES strategy parameters for the rectangular synthetic confined problem is presented in Table 2.

Table 2 Summary of the best-suited values of control parameters used in the CMA-ES model for the synthetic aquifer problem
Full size table

For comparison purposes, the different evolutionary algorithms, i.e., DE, PSO, and a hybrid version of DE and PSO, i.e. DE-PSO (Patel et al. 2020) are also investigated for the same synthetic problem. For DE and PSO, numerous model runs are performed to obtain the best configuration of control parameters and these are presented in Table 3. In the entire study, the possible range of DE and PSO control parameters are adopted based on the work of Price et al. (2005) and Kennedy and Eberhart (2010), respectively. For DE-PSO, the appropriate tuned control parameter values of both the individual heuristics are used directly. To compare the performance of the Mfree simulator in the inverse groundwater problems, a mesh-based FEM simulator is also coupled with DE, PSO, DE-PSO, and CMA-ES optimizations. Therefore, a total of eight SO models are developed and applied to the problems presented here, resulting from combinations of two simulators with four optimization algorithms.

Table 3 Summary of the best-suited values of control parameters used in the developed DE, PSO, and DE-PSO-based models for the synthetic aquifer problem
Full size table

Figure 3a presents the objective function values (i.e., SSD, Eq. 3) as a function of the generations for the eight different SO models considered here: FEM-DE, FEM-PSO, FEM-DE-PSO, FEM-CMA-ES, Mfree-DE, Mfree-PSO, Mfree-DE-PSO, and Mfree-CMA-ES. It is evident that the Mfree-CMA-ES model converged to the lowest objective function value (10–14), many orders of magnitude lower than the other models. In fact, the performance of MFree-CMA-ES surpassed the other models by attaining the lowest objective function value in the limited 300 iterations. These results affirm that Mfree-CMA-ES has better accuracy and higher robustness in comparison to other models.

Fig. 3
figure 3

The performance of different SO models for the synthetic aquifer problem based on a the objective function convergence graph and b a box-plot of the estimated transmissivity (T) using the last 50 generations from Mfree-CMA-ES (10% of total generations)

Full size image

To check the stability of all the estimated ten parameters using the new model, the populations of the last 50 generations are plotted in a box plot, presented in Fig. 3b. All the box plot attributes such as upper range, lower range, upper quartile, and lower quartile coincide with the median values for all 10 parameters. This shows the high stability of the solution. Although the number of iterations to reach convergence of all ten parameters using the Mfree-CMA-ES model is slightly higher when compared to other models, it is justifiable for two main reasons. First, it reaches a significantly higher degree of accuracy while arriving at a stable solution. This is particularly important for this arid-region aquifer which has low head variation. Second, its computational time to complete one generation is much lower (Fig. 4), therefore overall model run time to achieve 500 generations is significantly less compared to other models.

Fig. 4
figure 4

Bar chart showing the time required to perform one iteration using eight different SO models for the synthetic confined aquifer problem

Full size image

To further evaluate the performance of the eight models, the synthetic problem is also tested using two additional objective functions, other than SSD—these are SMD (Eq. 4) and SRMSE (Eq. 5). The results summarized in Table 4 reaffirm the superiority of Mfree-CMA-ES over its seven other counterparts. It can be seen that the new model produces the lowest fitness values which are many orders of magnitude smaller than the seven others and this is consistent for all three choices of objective functions.

Table 4 Performance of different algorithms based on objective function lowest values considering three different types of objective functions for the synthetic problem
Full size table

All the considered SO models are based on stochastic optimization algorithms, which are prone to some error due to the randomness of population generation. To reduce this effect, each SO calculation was conducted 10 times and its average value was taken to arrive at the final result. The average transmissivity value from all 10 runs using 8 distinct methods is presented in a bar chart in Fig. 5, along with the true values from Table 1. For all 10 values of transmissivity, the combination of Mfree with CMA-ES showed a higher degree of agreement with true transmissivity values when compared to other counterparts (Table 5). Here, it is emphasized that in Fig. 3a, the best performance among 10 trial SO runs for each method is presented, while Fig. 5 shows results for the average of 10 SO model runs; therefore, they are not directly associated with each other.

Fig. 5
figure 5

Average transmissivity over 10 model runs for eight different SO methods and their comparison with true values (dotted bar diagram) for the synthetic aquifer

Full size image
Table 5 Average transmissivity (T, m2/day) over 10 model runs for eight different SO methods and their comparison with true values for the synthetic aquifer
Full size table

The synthetic aquifer problems are free from field-measurement-related errors since simulated head values are directly considered as observed head values. In real field conditions, the head data acquired through measurement may contain errors. To check the impact of measurement error on the stability of the proposed model, observation head values are degenerated by incorporating normally distributed random noise at the 50 observation-well locations. Mathematically, the normally distributed random error is commonly denoted by N(μ, σ2) where μ represents the data mean and σ2 is the square of the standard deviation, i.e. variance. To represent measurement error, two sets of normal randomly distributed noises with N(0,0.1) and N(0,0.01) have been added to the original observation well data (dataset A) and are referred to as dataset B and dataset C, respectively. Using these two noisy data sets, two more model runs are performed and the results are presented in Table 6. Estimated parameters are shown to be stable as the projected model shows insignificant differences between the values of datasets A, B, and C, i.e., errors in estimated values are similar in all datasets. The obtained results again reaffirm the robustness of the proposed Mfree-CMA-ES and show promise for application to real field cases.

Table 6 Comparative assessment of transmissivity (T) with noisy and noiseless observation data
Full size table

The estimated parameters by the Mfree-CMA-ES model are subsequently fed as input to the forward model to obtain the groundwater head values after 360 days at 50 monitoring well locations. These estimated values are plotted in Fig. 6 and the maximum and minimum differences between observed and simulated heads are 138.77 and 1.49 × 10–8 mm, respectively. These differences are minuscule in comparison to the head values (less than 0.1%) and this is another result of the high accuracy of the new SO model.

Fig. 6
figure 6

Bar chart of head values at 50 monitoring well locations using true parameters and estimated parameters by the Mfree-CMA-ES-based SO model for the synthetic aquifer problem

Full size image

Field case study

The successful application of the proposed model to a synthetic problem leads to further evaluation considering a real field case study.

Study area

The Mahi Right Bank Canal (MRBC) aquifer region is a 2,798.5 km2 unconfined formation that is geographically located in the Kheda and Anand district of the Gujarat province of India. The study area receives nearly 823 mm normal annual rainfall, 90% of which falls during the monsoon season (June–September). The MRBC area exhibits characteristics of a semiarid region and hence it is selected for aquifer parameter estimation in this study. A geological survey and extensive field investigation of the MRBC command area have been previously carried out by the Gujarat Water Resources Development Corporation (GWRDC) and they estimated the applicable specific yield of the flow region as 15%.

The unconfined aquifer of MRBC command area represents a nearly triangular entity that is surrounded by known head boundaries from all three directions, i.e., Sedhi River on the northern side, Mahi River on the southern side, and the Alang drain on the west side, as shown in Fig. 7a. A large number of canals are spread across the aquifer, measuring a total length of 1,627 km. Six main canals comprise 539 km of the total length, while the remaining length is constituted by several branch canals and distributaries. A large volume of water is added to the aquifer by seepage from the lined (main and branch canals) and unlined distributaries. The rainfall recharge and canal seepage losses together with irrigation return flows are primarily responsible for the steady rise in the water table. The Department of Irrigation’s MRBC Project in Nadiad, Gujarat, provided the required meteorological, geomorphological, and hydrological data to understand the complete dynamics of groundwater flow in the region. These data are subsequently used to calculate the net annual recharge (NAR) of the year 2003 by following the recommendations of IARI (1983), which is then used to estimate groundwater head values with initial and boundary conditions as inputs to the simulator. The calculation of NAR is based on different hydrological input data which are presented in Appendix 1.

Fig. 7
figure 7

Real field case study, for the Mahi Right Bank Canal (MRBC) aquifer: a geographic map, b zone partitioning given by Lakshmi Prasad and Rastogi (2001), and c discretized domain using nonuniform collocation nodes with monitoring wells

Full size image

Model input parameter setting

Using the SO approach, the optimal hydraulic conductivity values are sought by least-squares-error-based data-fitting between observed and simulated head values. These observed head values were collected from the 44 different monitoring well locations while simulated values were obtained via the Mfree simulator using 117 nonuniformly distributed nodes (Fig. 7c). Using the known value of the aquifer area and a predefined number of nodes, the calculated value of ds is found to be 570.65 m. The numerous simulation trials on MRBC suggested the best-suited value of αs is equal to 3 (refer Patel and Rastogi (2017) for more details). To determine boundary head values, graphical interpolation is carried out using isobaths maps from the year 2003 (prepared by GWRDC). The initial head values are also extracted from the map to feed as input to the discretized form of unconfined flow, i.e., Eq. S12 of ESM. Collective well withdrawals are considered in the calculation of the NAR. To distribute the NAR value on each node, the recharge distribution coefficient (Rd) method proposed by Sondhi et al. (1989) is adopted in this study. It allocates the NAR value into each node in terms of actual nodal recharge (ANR), which is a product of average annual nodal recharge (AANR) and Rd for each specified nodal area. Here Rd values are obtained directly from the Rd contour map prepared by Sondhi et al. (1989) for the MRBC region, and AANR is defined as the nodal area-wise weighted distribution of NAR. After the incorporation of nodal recharge, each simulation is performed for 1 year of the simulation period for a time step size of one day.

Lakshmi Prasad and Rastogi (2001) used the FEM-GA-based SO model and identified optimal zonation patterns using structural identification for the MRBC region (Fig. 7b). The obtained parameter values are also verified by the hydraulic conductivity map prepared by GWRDC. It took nearly 600 generations with a population size of 75 to arrive at the convergence which can be considered costly in terms of the currently available computational resources. The possible reasons behind a poor convergence are, (1) mesh-based interpolation error and (2) application of GA for optimization, which requires a large population, a higher number of generation cycles and is highly dependent on the encoding scheme adopted. Therefore, the proposed Mfree-CMA-ES simulation-optimization model is expected to improve convergence.

Using the known zonation pattern of MRBC, 10 hydraulic conductivity values need to be identified. Therefore, in this case, the value of D will be 10. It also determines the estimated values of distinct strategy parameters which are presented in Table 7. The lower and upper bounds of hydraulic conductivity (decision variable) are kept as 15 and 150 m/day respectively. A uniform stopping criterion for solution convergence is taken to be 300 iterations for this problem.

Table 7 Summary of the strategy parameters used in the CMA-ES model for the MRBC aquifer problem based on the study of Hansen (2011)
Full size table

Following a similar procedure as described in the synthetic aquifer case, control parameters associated with DE, PSO, and DE-PSO for the MRBC region are fine-tuned and obtained after numerous model runs. The final values are presented in Table 8.

Table 8 Summary of control parameters used in DE, PSO, and DE-PSO-based SO models for MRBC aquifer problem
Full size table

Results and analysis

After strategy parameter values have been estimated, the Mfree-CMA-ES-based SO model can be applied to the MRBC problem. The other seven models that were used for comparison in the synthetic problem are also applied to the field case for comparison. Figure 8a presents results for the objective function values with each generation for all eight SO models. It is clear that the Mfree-CMA-ES model has the highest order of accuracy (lowest objective function value), many orders of magnitude smaller than the seven other models. The objective function of the Mfree-CMA-ES model shows oscillations due to the adaptation of σ and C. However, at the later stage, the objective function values become stable as the offspring population becomes uniform after certain generations. The multiquadric-based Mfree simulator is also proven to be effective since it is shown to be computationally efficient and accurate. Computational time to perform a single iteration of each SO model is presented in Fig. 9 showing that the CMA-ES-based models are the most computationally efficient, comparable only to FEM-CMA-ES. To check the convergence of the Mfree CMA-ES SO model in terms of hydraulic conductivity (K) values, the last 10% of the population is plotted in a box plot in Fig. 8b. Results verify the stability of all 10 estimated hydraulic conductivity values.

Fig. 8
figure 8

The performance of different SO models for the field aquifer problem based on a the objective function convergence graph and b a box-plot of the estimated hydraulic conductivity (K) values over 10 Mfree CMA-ES model runs using the last 50 generations (10% of total generations)

Full size image
Fig. 9
figure 9

Bar chart showing the time required to perform one iteration using eight different SO models for the MRBC unconfined aquifer problem

Full size image

To evaluate the impact of different objective functions on all eight models, SMD and SRSME are tested, replacing the SSD function. Results are presented in Table 9 in terms of the lowest value achieved by each algorithm. The Mfree-CMA-ES SO model is clearly shown to have a significantly lower objective function than its competitors for all three different types of functions.

Table 9 Performance of different algorithms based on objective-function lowest values considering three different types of objective functions for the MRBC aquifer problem
Full size table

Next, the average value of each estimated parameter from 10 model runs is taken as the final representative parameter value. The hydraulic conductivity results obtained through the different methods are presented in Fig. 10 as a bar chart. The final values of parameters are also presented in Table 10. For comparison, in addition to results from the seven SO models discussed previously, results of FEM-GA from Lakshmi Prasad and Rastogi (2001) are presented in Fig. 10 and Table 10. The new Mfree-CMA-ES shows the highest degree of agreement with the FEM-GA solution presented by Lakshmi Prasad and Rastogi (2001). Estimated values are also consistently in agreement with FEM-CMA-ES results. To check the accuracy of estimated parameters obtained by the new SO model, i.e., Mfree-CMA-ES, the parameter values are fed to the simulator to obtain groundwater head values. Results in the form of isobaths contour are presented in Fig. 11 alongside measured field data results from the year 2004. The results show good agreement between simulated and observed heads.

Fig. 10
figure 10

Average hydraulic conductivity over 10 model runs estimated by eight different SO methods and a comparison with values obtained by Lakshmi Prasad and Rastogi (2001) using the FEM-GA model for the MRBC aquifer

Full size image
Table 10 Results displayed in Fig. 8 for hydraulic conductivity (K, m/day) given here in tabulated form
Full size table
Fig. 11
figure 11

Isobath contours map of the head for the year 2004 using estimated hydraulic conductivity values by the Mfree-CMA-ES model and from real field values provided by Gujarat Water Resources Development Corporation (GWRDC) for the MRBC region

Full size image

A sensitivity analysis is carried out to evaluate the impact of head measurements on the parameter estimations. Low sensitivity of estimated parameters to observed heads may indicate unreliable estimations. Furthermore, the sensitivity of each parameter is tested separately, which allows for the determination of parameters that are estimated with higher confidence and others that may be inaccurate. The general sensitivity analysis is used to ascertain the mutual correlation and consistency of a specified model based on the effect of input aquifer parameters on output groundwater head values (Foglia et al. 2009). In this paper, the proposed inverse groundwater model for the field case is tested by two statistical measures, i.e. relative composite scaled sensitivity (RCSS) and coefficient of variation (CV). Details regarding these two sensitivity measures are given in Appendix 2.

The RCSS analysis indicates the sensitivity of each hydraulic conductivity estimation to the overall monitoring-well data. Results are plotted as a bar chart in Fig. 12 which generally shows that parameters K1, K2, K4, K7, and K9 are better-estimated using Mfree-CMA-ES due to their higher RCSS values as compared to the others, i.e., they are more sensitive to the information provided by monitoring well data. A general rule indicating unreliably estimated parameters is that the RCSS value of the specific parameter is less than 1% of the largest RCSS value (Poeter and Hill 1997). Since the RCSS values in this study are all in the range 0.1–1, which is significantly larger than 1% of the largest value, it indicates that even parameters with smaller RCSS (K3, K5, K6, K8, K10) can be estimated reliably using data from all 50 monitoring wells.

Fig. 12
figure 12

Bar-chart of relative composite scaled sensitivity (RCSS) for each K (hydraulic conductivity) estimated by the Mfree-CMA-ES based SO model for the MRBC aquifer

Full size image

Composite scaled sensitivity (CSS) and coefficient of variation (CV) are presented in Table 11. CSS values less than 1 indicate that the sensitivity contribution is less than the effect of observation error. It is seen that almost all estimated parameters have CSS well above 1, suggesting sufficient sensitivity, except three—K3, K8, and K10, with values of 0.5. CV is a measure to estimate the relative accuracy of estimated parameters. It is evident that all CV values in the table are small, suggesting that the Mfree-CMA-ES model is able to estimate fairly accurately values of all aquifer parameters for the MRBC region.

Table 11 Coefficient of variation (CV) and CSS values for each parameter (hydraulic conductivity) estimated by the Mfree-CMA-ES SO model for the MRBC aquifer
Full size table

Discussion

The main strength of the developed Mfree-CMA-ES model is its ability to explore the solution space thoroughly with significantly less computational time than other models. It was found that the model requires fewer generations with small populations to reach lower objective function values. For instance, Fig. 8a shows that the proposed model reaches an accuracy of about 0.001 after only 110 generations, while other models are unable to explore the solution space beyond the lowest value of 0.01. In addition to this, each generation requires less computational time. For example, Mfree-CMA-ES takes about 0.7 min to complete one iteration, while other models require 3.18, 0.7, 12, 2.4, 14.75, 4.2, and 2 min for FEM-DE, Mfree-DE, FEM-PSO, Mfree-PSO, FEM-DE-PSO, Mfree-DE-PSO, and FEM-CMA-ES, respectively. The Mfree-DE model is comparable in iteration time; however, it is unable to reach the same accuracy. The possible reason behind the faster convergence of CMA-ES based models is the adaptive nature of different search parameters, while PSO, DE, and DE-PSO have constant and predefined control parameters for a specified problem. Apart from this, the zonation pattern of the aquifer system is also assumed to be known and certain minimum number of collocation nodes are used to discretize the domain using the Mfree simulator. Considering these two assumptions, the new model can be successfully implemented in other real field problems.

Conclusions

After successful implementation of the proposed model the following conclusions can be drawn:

  • In the Mfree-CMA-ES SO model, strategy parameters control the direction of the optimal evolution path. However, unlike other heuristic-based models, there is no need to perform numerous model runs to calibrate these strategy parameters initially. Since they are estimated by different empirical formulae and are automatically updated with each generation, the developed model, therefore, is found to be more suited to field problems.

  • The Mfree-CMA-ES-based SO model is a better-performing algorithm in terms of convergence, minimization of the objective function, computational time, and accuracy. These positive results are very encouraging for the further application of the developed model in the areas of source identification, groundwater contaminant management, and other associated problems. To analyze the effect of measurement error on the observed head values, noise is introduced to the synthetic problem by adding normally distributed error to the monitoring wellhead values. The obtained results for Mfree-CMA-ES verify the stability of the model as no significant difference is observed between aquifer parameters obtained using noisy and error-free monitoring wellhead data.

  • A sensitivity analysis is performed for the real-field case to check the ability to estimate the aquifer parameters given the observation wellhead data. The RCSS value for each hydraulic conductivity estimation indicates that the values of all 10 zones are reliably estimated with available monitoring well data. The same is also confirmed by the evaluation of CV values.