Simulation–optimization Models for Aquifer Parameter Estimation

Abstract

An accurate estimation of aquifer parameters is important for effective groundwater management and future scenario prediction. These parameters are mostly obtained through different time-consuming and cumbersome field pumping tests. The inverse problem is a recently developed widely accepted mathematical approach to obtain the representative optimal aquifer parameters, particularly in large heterogeneous aquifer systems. For the inverse problem solution, the simulation–optimization (SO) model approach has been effectively used. The efficiency of these SO models depends mainly on two factors like, the accuracy of the simulation model and the ability of the optimization algorithm to explore the solution space. In this study, we selected the combination of two simulation models (i.e., FEM and Meshfree method) and four optimization algorithms (i.e., Particle Swarm Optimization (PSO), Differential Evolution (DE), a hybrid version of DE and PSO (DE-PSO) and Co-variance Matrix Adaptation Evolution Strategy (CMA-ES)) which resulted into the development of total eight number of SO models. These models are successfully applied to a synthetic confined aquifer problem. The obtained results showed the better performance of the Mfree-CMA-ES compared to its other counterparts like: FEM-DE, Mfree-DE, FEM-PSO, Mfree-PSO, FEM-CMA-ES and Mfree-DE-PSO in terms of convergence and a higher degree of unanimity with the known values of transmissivity and hydraulic conductivity.

1 Introduction

Groundwater is a significant natural resource in India, accounting for 45% of urban water supply, 85% of rural water supply, and 62% of irrigation demand (The Comptroller and Auditor General of India 2021). However, as a result of unchecked pumping, groundwater levels have recently plummeted in several parts of the world. The same trend can be seen in India, where a World Bank report predicted that in 15–20 years, 60% of Indian aquifers would be in unsafe conditions due to unchecked groundwater over-exploitation (The World Bank 2009). The best possible use of groundwater should thus be a priority for ensuring its sustainability, and strict adherence to groundwater management policies is required to achieve this goal.

Groundwater management policies are chosen in accordance with an anticipated future scenario for groundwater. The temporal variations in groundwater head are estimated by simulating groundwater governing flow equations with various numerical techniques such as the finite difference method (FDM), meshfree method (Mfree; Patel and Rastogi 2017) and the finite element method (FEM). These groundwater simulation models rely heavily on the accuracy of estimated aquifer parameters like hydraulic conductivity, transmissivity, and storage coefficient. As a result, accurate estimation of aquifer parameters is critical, which indirectly aids in the formulation of groundwater management policies (Thangarajan 2007). In-situ tests or graphical matching-based pumping tests are commonly used to estimate these aquifer parameters. The former tests are limited to homogeneous and isotropic aquifer domains and are based on governing equations with closed-form solutions (Theis, 1935). Aside from that, these pumping-based methods necessitate nearly 24–72 h of nonstop pumping in order to collect the data required for graphical matching, which is an inefficient and time-consuming solution (Michael 2009). As a result, researchers frequently employ a purely mathematical process known as inverse groundwater modelling. Simulation-optimization (SO) is a commonly used approach to solve these inverse problems. The SO approach assigns distributed parameters to a mathematical model with known boundary conditions in such a way that the error between observed and simulated state variables is minimised (Lakshmi Prasad and Rastogi 2001). This entire process is an optimization process in which aquifer parameters are decision variables, least square difference is the objective function, and possible parameter limits are the constraints.

According to Mahinthakumar and Sayeed (2005), the optimization methods used in the SO approach are broadly classified as derivative-based and non-derivative-based optimization. In the former, a derivative of the objective function improves the initial guess of parameters until the required objective function value is obtained. Previous research on inverse groundwater modelling demonstrated that the objective functions for parameter estimation problems are discrete, have multiple optima, and are non-convex. Because these objective function-related peculiarities cannot be addressed by derivative-based local optima methods and have a higher likelihood of becoming stuck in local minima, population-based stochastic search methods were introduced to inverse problems. These methods are non-derivative based optimization methods that do not require an initial guess of the parameter to be estimated. Global stochastic population-based metaheuristic optimizations have gradually replaced traditional numerical optimization methods in the SO approach due to their superior ability to handle discrete problems. By solving the inverse groundwater problem, these characteristics of metaheuristics-based optimization are successfully explored. Ant colony optimization (ACO; Abbaspour et al. 2001), Particle swarm optimization (PSO; Ch and Mathur 2012), differential evolution (DE; Rastogi et al. 2014), and, cat swarm optimization (CSO; Thomas et al. 2018), among others, are examples of this class of optimization that have been successfully applied to estimate aquifer parameters. However, these optimization methods have their own limitations. For example, DE explores the space with a higher multiplicity, making it more susceptible to unstable convergence (Wu et al. 2011); PSO typically becomes stuck to the previous best value (pbest), and eventually all remaining particles begin to follow it, resulting in a suboptimal solution (Jiang et al., 2010). Above all, the accuracy of the previously discussed heuristic-based global search methods is highly dependent on their manually adjusted control parameters. The control parameters of various popular and traditional metaheuristic algorithms are problem specific, and their tuned values are obtained after numerous model runs, which is the main reason for the higher model run cost. The Covariance Matrix Adaptation Evolutionary Strategy (CMA-ES) developed by Hansen (2006) is a quasi-parameter free global stochastic optimization algorithm in which population size is the only parameter that must be tuned. As a result, it may be a viable option to replace the existing optimization model with CMA-ES optimization in the parameter estimation problem.

In this paper, we proposed a novel approach to estimate aquifer parameters by combining the multiquadric-based Mfree approach with CMA-ES optimization. It is anticipated that this coupling will enhance the estimation of aquifer parameters, particularly in regional aquifer systems. Here, the Mfree is able to produce accurate head values (Patel et al. 2022), and CMA-ES optimization achieves objective function convergence faster with fewer generations, so this ultimate combination as a SO model yields accurate aquifer parameter values.

2 Materials and Methods

2.1 Mfree Based Groundwater Simulation Model

The groundwater flow governing equation for confined aquifer for the transient condition, including variabilities like anisotropy, non-homogeneity, areal recharge including pumping or draft or both is represented as Willis and Yeh (1987):

$$\frac{\partial }{\partial x}\left({T}_{x}\frac{\partial H}{\partial x}\right)+\frac{\partial }{\partial y}\left({T}_{y}\frac{\partial H}{\partial y}\right)=S\left(\frac{\partial H}{\partial t}\right)+{Q}_{w}\left(x-{x}_{p},y-{y}_{p}\right)-R$$

(1)

With an initial condition as:

$$H\left( {x,y,0} \right) = H_0 \left( {x,y} \right)\,\,\,x,y \in \Omega$$

(2)

The constant groundwater head (Dirichlet boundary) and boundary flux (Neumann boundary) are described as following:

$$H\left( {x,y,t} \right) = H_1 \left( {x,y,t} \right)\,\,x,y \in \partial \Omega_1$$

(3)

$$\left. {\begin{array}{*{20}c} {T\left( {\frac{\partial H}{{\partial n}}} \right)} \\ {or \left[ {T_x \left( {\frac{\partial H}{{\partial x}}} \right)} \right] + \left[ {T_y \left( {\frac{\partial H}{{\partial y}}} \right)} \right]} \\ \end{array} } \right\} = q_2 \left( {x,y,t} \right)\,\,\,\,x,y \in \partial \Omega_2$$

(4)

where $H(x,y,t)$ is the groundwater head (m); $T$, transmissivity (m²/day); ${T}_{x}$ and ${T}_{y}$ are transmissivity values along principal axes (m²/day); $S$, storativity (dimensionless); ${Q}_{w}$, source (−) or sink (+) term (m/day); $\left({x}_{p},{y}_{p}\right)$, ,coordinate for the well location (m); $\delta$, Dirac delta function with the property that if $x={x}_{p}$ and $y={y}_{p}$ then $\delta =1$ else $\delta =0$; $R$, areal- recharge (m/day); $t$, time (day); ${H}_{0}$, initial known groundwater head distribution (m); ${H}_{1}$, known groundwater head values at the boundary (m); ${q}_{2}$, known boundary flux (m³/day/m); $\left({l}_{x},{l}_{y}\right)$, direction cosine of the outward normal at certain node on Neumann boundary (dimensionless); $\Omega$, the computational domain; $\partial \Omega$, the boundary $\partial {\Omega }_{1}\cup \partial {\Omega }_{2}=\partial \Omega$ of computational domain; and $\left(\frac{\partial }{\partial n}\right)$, the normal derivative.

Using the global-collocation based Mfree method (Patel and Rastogi 2017) the governing groundwater flow Eq. (1) is approximated by scattered data interpolation, which is explained as follows:

$$\begin{gathered} \left[ {\frac{{S_{j} }}{{\ddot{A}t}}\left( {\mathop \sum \limits_{{j = 1}}^{N} \phi _{j} \left( {x_{i} ,y_{i} } \right)} \right) - T_{{x_{j} }} \left( {\mathop \sum \limits_{{j = 1}}^{N} \frac{{\partial ^{2} \phi _{j} \left( {x_{i} ,y_{i} } \right)}}{{\partial x^{2} }}} \right) - T_{{y_{j} }} \left( {\mathop \sum \limits_{{j = 1}}^{N} \frac{{\partial ^{2} \phi _{j} \left( {x_{i} ,y_{i} } \right)}}{{\partial y^{2} }}} \right)} \right] \hfill \\ \times \left\{ {h_{j} } \right\}^{{t + 1}} = \left[ {\frac{{S_{j} }}{{\Delta t}}\mathop \sum \limits_{{j = 1}}^{N} \phi _{j} \left( {x_{i} ,y_{i} } \right).\left\{ {h_{j} } \right\}^{t} } \right] \hfill \\ - Q_{w} \left( {x_{i} - x_{p} ,y_{i} - y_{p} } \right) + R_{j} {\text{~where~}}i = 1,2...N_{I} \hfill \\ \end{gathered}$$

(5)

where ${\phi }_{j}$ is a matrix of basis or shape function. Multiquadric is used as a shape function and can be express as (Hardy 1971) ${\phi }_{j}\left(x,y\right)=\sqrt{(x-{x}_{j}{)}^{2}+(y-{y}_{j}{)}^{2}+{C}_{s}^{2}}$; ${\left\{\left({x}_{j},{y}_{j}\right)\right\}}_{j=1}^{N}$ are coordinates of $N$ collocation nodes in $\Omega$. ${C}_{s}$ is a free parameter referred as shape parameter (Cheng et al. 2003) given as ${C}_{s}={\alpha }_{s}{d}_{s}$, where ${\alpha }_{s}$ is support size for radial basis function (dimensionless) and ${d}_{s}$ is the nodal spacing. Nodal spacing (Liu and Gu 2005) for two- dimensional case is computed as: ${d}_{s}=\frac{\sqrt{A}}{\left(\sqrt{N}-1\right)}$ (where $A$, is an area of the whole computational domain and $N$ is the total number of nodes distributed over the domain). The optimum value of ${\alpha }_{s}$ is known by performing numerous simulation on different benchmark problems. Liu and Gu (2005) suggested that the value between 2–3 is giving good results for a variety of problems.

2.2 Inverse Groundwater Modelling: As an Optimization Problem Using SO Approach

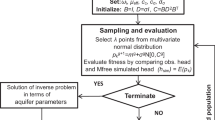
The inverse model generates initial natural guesses of upper and lower bounds of aquifer parameters based on random numbers. These values are used as input for the simulation model, which calculates the aquifer state variables. To calculate the objective function, the observed values are compared to the calculated values at the observation well location. If the termination criteria is met, the initial guess will be the optimum aquifer parameters; if not, the optimization model will modify previous input parameter values until the required termination criteria is met, and the corresponding modified input parameter will be the optimum aquifer parameters. Minimizing the fitting error between observed and simulated aquifer state variables at specific monitoring well locations yields the representative optimal parameter values. Because the fitting error-based objective function is nonlinear (NL) and non-continuous, it cannot be expressed explicitly in terms of decision variables (i.e. aquifer parameters). This study's objective function is the sum of squared differences (SSD), which can be expressed as:

$$Min\, E(P)={\beta }_{l,t}{{\sum }_{l=1}^{L}{\sum }_{t={t}_{0}}^{{t}_{t}}\left[{H}_{l,t}^{obs}-{H}_{l,t}^{sim}(P)\right]}^{2}$$

(6)

Subjected to:

$${P}_{i}^{lb}\le {P}_{i}\le {P}_{i}^{ub}$$

(7)

where E(P) represents objective function to be minimized; ${H}_{l,t}^{sim}$ is calculated groundwater head at observation well l at time t with parameter (P) as input [L]; ${H}_{l,t}^{obs}$ is observed groundwater head at observation well l at time t [L]; ${P}_{i}$ is aquifer parameter at zone i; L is total number of observation wells; t₀ and t_t are beginning and ending time of observations [day]; l_b and u_b are the superscripts representing the lower and upper bounds on the parameters and ${\beta }_{l,t}\in \left[\mathrm{0,1}\right]$ is the weighing coefficient whose value is chosen according to confidence on measured groundwater head at a certain observation well location.

3 Optimization Models

A number of population-based global metaheuristic optimizations (i.e., DE, PSO and CMA-ES) have been successfully applied to the varieties of groundwater problems such as aquifer parameter estimation, groundwater management problems, pollutant source detection, and many others. Since DE and PSO are commonly used in this class of problems, they are not discussed in depth; however, CMA-ES optimization, which is relatively new, has been extensively discussed.

3.1 Working of CMA-ES Optimization

CMA-ES belongs to the family of evolutionary algorithm, like GA and mimics the characteristics of Darwin's evolution theory. To generate new candidate solutions, a typical CMA-ES employs initialization, evaluation, and mutation (selection with recombination) operators. Like other stochastic search methods in the evolutionary strategy (ES), the possible solution is known as individuals. Mutation is a main step to generate the new individuals by adding the random vector from multivariate random distribution to parent vector. In CMA-ES, the possible solution moves with in the fitness landscape by rotating and scaling of the covariance matrix. This whole procedure is controlled by different strategy parameters which also evolve with each generation (Bayer and Finkel 2007) and hence there is no need to pre-calibrate them as they update themselves by utilizing the internal mechanism of CMA-ES. Eventually this iterative updation of covariance matrix leads the individual towards the convergence at an optimum value. Here it is noteworthy that CMA-ES uses the information of number of previous generations (called as evolution path) instead of only the last one (Bayer and Finkel 2004).

4 Initialization

In CMA-ES, new search points within the fitness landscape is produced by multivariate normal distribution. The equation to produce the sampling point is represented as (Hansen 2006):

$${p}_{k}^{g+1}\sim {\mathbb{N}}\left[{m}^{g},{\left({\sigma }^{g}\right)}^{2},{C}^{g}\right] \, where\, k=\mathrm{1,2}...\lambda$$

(8)

The equation further simplified as:

$${p}_{k}^{g+1}\sim {m}^{g}+{\sigma }^{g}{\mathbb{N}}\left[0,{C}^{g}\right] \sim {m}^{g}+{\sigma }^{g}{B}^{g}{D}^{g}{\mathbb{N}}\left[0,I\right]$$

(9)

where λ represent population size or total number of search points generated by multivariate distribution; g is generation number; ${p}_{k}^{g+1}\in {\mathbb{R}}^{n}$ is kth member of population from g + 1 generation; ${m}^{g}\in {\mathbb{R}}^{n}$ is mean value of ${p}^{g}$; ${\sigma }^{g}\in {\mathbb{R}}_{+}$ is overall standard deviation or step size at generation g; ${C}^{g}\in {\mathbb{R}}^{n\times n}$ is covariance matrix at generation g; ${B}^{g}\in {\mathbb{R}}^{n}$ represents eigenvectors of ${C}^{g}$ and ${D}^{g}\in {\mathbb{R}}^{n\times n}$ is diagonal matrix of eigenvalues of ${C}^{g}$.

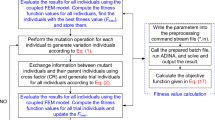
4.1 Selection and Recombination for Calculation of Mean Vector

After generation, all λ vectors (population) are evaluated based on the problem specific objective function. Subsequently, µ (≤λ) numbers of best parental vectors are selected from total λ vectors. This selection may be random or based on evaluated fitness value of each vector. Later these selected µ vectors recombined together and its weighted (based on fitness) mean vector is calculated using weighted recombination (represented by µ_w, λ-CMA-ES). This operation keeps the mean vector nearer to better individuals. This entire procedure is mathematically expressed as (Hansen 2006):

$${m}^{g+1}=\frac{{\sum }_{i=1}^{\mu }{w}_{i}{p}_{i}^{g+1}}{{\sum }_{i=1}^{\mu }{w}_{i}}$$

(10)

where ${w}_{i=1:\mu }\left({=}{\mathit{ln}}\left(\mu +1\right)-\mathit{ln}\left({\sum }_{i=1}^{\mu }i\right)\right)$ represents weight coefficient for recombination of µ selected vectors; µ (≤ λ) is size of parent population and calculated as $\frac{\uplambda }{2}$ where $\lambda =4+3\mathit{log}D$ (here D is number of parameter or dimension of the problem); ${p}_{i}^{g+1}$ is ith individual out of ${p}_{1}^{g+1}....{p}_{\uplambda }^{g+1}$; $i:\lambda$ denotes the index of ith ranked individual with $E\left({p}_{1:\uplambda }^{g+1}\right)\prec E\left({p}_{2:\uplambda }^{g+1}\right)\prec ......E\left({p}_{\uplambda :\uplambda }^{g+1}\right)$ where E is objective function to minimize.

Equation (10) implements recombination by taking weighted sum of µ individuals and selection by choosing µ ≤ λ and assigning different weights w_i.

4.2 Adapting the Covariance Matrix

According to Eq. (9), covariance matrix and step size are the other terms which are need to be estimated. Initially, the covariance matrix is estimated from single population and one generation. This matrix further needs to be modified because it is considered as unreliable due to its small population size by adaptation procedure. Further inclusion of successive step size also enhances the estimation of covariance matrix.

4.3 Estimating Covariance Matrix

According to the assumption by Hansen (2006), population contains enough information to estimate a covariance matrix. The covariance matrix can be estimated using generated sample population, ${p}_{1}^{g+1},{p}_{2}^{g+1}.......{p}_{\uplambda }^{g+1}$ as:

$${C}_{emp}^{g+1}=\frac{1}{\uplambda -1}{\sum }_{i=1}^{\uplambda }\left({p}_{i}^{g+1}-\frac{1}{\ddot{e} }{\sum }_{j=1}^{\uplambda }{p}_{j}^{g+1}\right){\left({p}_{i}^{g+1}-\frac{1}{\ddot{e} }{\sum }_{j=1}^{\uplambda }{p}_{j}^{g+1}\right)}^{T}$$

(11)

Here ${C}^{g+1}$ is unbiased estimator of covariance matrix by assuming ${p}_{i}^{g+1}$ is randomly distributed using normal distribution. Since it is based on the population of single generation we will try to further modify it to include the effect of previous generation as:

$${C}_{\uplambda }^{g+1}=\frac{1}{\uplambda }{\sum }_{i=1}^{\uplambda }\left({p}_{i}^{g+1}-{m}^{g}\right){\left({p}_{i}^{g+1}-{m}^{g}\right)}^{T}$$

(12)

The above equation represents an unbiased maximum likelihood estimator of covariance matrix. Here we can see the difference between Eqs. (11) and (12) in terms of mean value. In first one the mean value is calculated from actually realized sample while in second it is true mean value of gth population distribution. Subsequently, Eq. (11) represents the deviation within the sampled points while in Eq. (12) it is within the sampled steps. Hence Eq. (12) is more prominent representation of adapted covariance matrix.

For further improvement in Eq. (12) weightage (similar as mean) can be given to better to more successful µ vectors and can be represented as:

$$C_\mu^{g + 1} = \mathop \sum \limits_{i = 1}^\mu w_i \left( {p_{i:{\uplambda }}^{g + 1} - m^g } \right)\left( {p_{i:{\uplambda }}^{g + 1} - m^g } \right)^T$$

(13)

To maintain a reliable estimation of covariance matrix, variance effective selection mass ${\mu }_{eff}\left({=}{\left[{\sum }_{i=1}^{\mu }{{w}_{i}}^{2}\right]}^{-1}\right)$ should be large enough get condition smaller than 10. To avoid this restriction the upcoming next step modification is essential.

4.4 Rank-μ Update

Large population helps to estimate reliable values of covariance matrix but it will also increase the number of generation to achieve convergence criteria. As current form of Eq. (13) is not capable to estimate C^g+1 value, therefore as a remedy, information from previous generation is added. Mathematically, it can be presented as:

$${C}^{g+1}=\frac{1}{g+1}{\sum }_{i=0}^{g}\frac{1}{{\left({\sigma }^{i}\right)}^{2}}{C}_{\mu }^{i+1}$$

(14)

It is further modified by assigning different weight to different generation which is known as learning rate. Then C^g+1 reads:

$$\begin{aligned} {C}^{g+1}&=\left(1-{c}_{cov}\right){C}^{g}+{c}_{cov}\frac{1}{{\left({\sigma }^{g}\right)}^{2}}{C}^{g+1}\\&=(1-{c}_{cov}){C}^{g}+{c}_{cov}{\sum }_{i=1}^{\mu }{w}_{i}OP\left(\frac{{p}_{i:\uplambda }^{g+1}-{m}^{g}}{{\sigma }^{g}}\right) \end{aligned}$$

(15)

where $c\left(\in \left[\mathrm{0,1}\right]\right)$ is learning rate for updating the covariance matrix. If ${c}_{cov}$ is 1 then no information from previous generation will be incorporated and it is zero then learning take place; OP denotes the outer product of a vector by itself. Here it is noteworthy that covariance matrix is initiated as identity matrix (i.e. C⁰ = I).

As sum of the outer product in Eq. (14) is of rank µ, therefore, this modification for covariance is called as rank-µ-update.

The value of ${c}_{cov}$ is very crucial for rank-µ-updation. Small value of ${c}_{cov}$ leads towards slow convergence, while large value leads to premature convergence. Hansen (2006) applied CMA-ES on different classical optimization problem and found that ${c}_{cov}$ is only dependent on dimension of the problem and suggested an approximated value as ${\mu }_{eff}/D$.

4.5 Cummulation: Utilizing the Evolution Path

In Eq. (15) a term of outer product doesn’t use sign information, as $OP(x)=x{x}^{T}=OP(-x)$. Therefore, a concept of evolution path in which represents sequence of steps and the strategy over number of generation is introduced. It is expressed in terms of sum of consecutive steps and its summation is called as cummulation. For example, an evolution path of three steps can be constructed by the sum as:

$$\frac{{m}^{g+1}-{m}^{g}}{{\sigma }^{g}}+\frac{{m}^{g}-{m}^{g-1}}{{\sigma }^{g-1}}+\frac{{m}^{g-1}-{m}^{g-2}}{{\sigma }^{g-2}}$$

(16)

Similar as Eq. (15) using the exponential smoothing Eq. (16) can be utilized to write an expression for evolution path of generation (g + 1) for covariance matrix as (Hansen 2006):

$${p}_{c}^{g+1}=\left(1-{c}_{c}\right){p}_{c}^{g}+\sqrt{{c}_{c}(2-{c}_{c}){\mu }_{eff}}\frac{{m}^{g+1}-{m}^{g}}{{\acute{o} }^{g}}$$

(17)

where ${p}_{c}^{g}\in {\mathbb{R}}^{n}$ is evolution path at gth generation; $\sqrt{{c}_{c}(2-{c}_{c}){\mu }_{eff}}$ is a normalize constant for ${p}_{c}^{g}$

If ${c}_{c}=1$ and ${\mu }_{eff}=1$, then ${p}_{c}^{g+1}=\frac{{p}_{1:\lambda }^{g+1}-{m}^{g}}{{\sigma }^{g}}$

$${p}_{c}^{g+1}\sim {\mathbb{N}}\left(0,C\right)$$

(18)

If

$${p}_{c}^{g+1}\sim \frac{{p}_{1:\lambda }^{g+1}-{m}^{g}}{{\sigma }^{g}}\sim {\mathbb{N}}\left(0,C\right)\text{ for all \,i\,=\,1,2...,}\mu$$

(19)

In Eq. (17)

$$\begin{gathered} \left( {1 - c_c } \right)^2 + \sqrt {c_c \left( {2 - c_c } \right)\mu_{eff} }^2 = 1 \hfill \\ \mathop \sum \limits_{i = 1}^\mu w_i \rm{\mathbb{N}}\left( {0,C} \right) \sim \frac{1}{{\sqrt {\mu_{eff} } }}\rm{\mathbb{N}}\left( {0,C} \right) \hfill \\ \end{gathered}$$

(20)

Now utilizing the concept of evolution of path in Eq. (15) the ultimate equation can be read as:

$${C}^{g+1}=\left(1-{c}_{cov}\right){C}^{g}+{c}_{cov}{p}_{c}^{g+1}{p}_{c}^{{g+1}^{T}}$$

(21)

Empirical value of learning rate for rank-1-update of C, $({c}_{cov})$ and time cummulation of C (c_c) are respectively $\frac{2}{{D}^{2}}$ and $\frac{4}{D}$ provides optimal value of covariance matrix.

4.6 Combining Rank-µ Update and Commulation

Now by combining Eqs. (15) and (16) the ultimate equation for covariance matrix is:

$$\begin{gathered} C^{g + 1} = \left( {1 - c_{\text{cov}} } \right)C^g + \frac{{c_{\text{cov}} }}{{\mu_{\text{cov}} }}\underbrace {p_c^{g + 1} p_c^{g + 1^T } }_{rank - 1\,update} + c_{\text{cov}} \left( {1 - \frac{1}{{\mu_{\text{cov}} }}} \right) \hfill \\ \times \underbrace {\sum_{i = 1}^\mu {W_i \left( {\frac{{p_{i:\lambda }^{g + 1} - m^g }}{\sigma^g }} \right)\left( {\frac{{p_{i:\lambda }^{g + 1} - m^g }}{\sigma^g }} \right)^T } }_{rank - \mu \,update} \hfill \\ \end{gathered}$$

(22)

Where $\mu_{\text{cov}} \ge 1\,\,{\text{and}}\,\,\mu_{\text{cov}} = \mu_{eff} .$

The rank-one-update part of Eq. (22) uses the information of correlation between generations using evolution path while rank-µ-update uses the information within the population to reach optimal value of covariance matrix.

4.7 Step Size Control

Similar to covariance matrix, step size also utilizes an evolution path (sum of successive steps). To define the length of step size as ‘long’ or ‘short’, the length of evolution path is compared with its expected length under selection.

The conjugate evolution path for step size is defined as (based on exponentially smoothed sum):

$${p}_{\sigma }^{g+1}=\left(1-{c}_{\sigma }\right){p}_{c}^{g}+\sqrt{{c}_{\sigma }\left(2-{c}_{\sigma }\right){\mu }_{eff}}{C}^{{g}^{\frac{-1}{2}}}\frac{{m}^{g+1}-{m}^{g}}{{\sigma }^{g}}$$

(23)

The updation of step size based on the comparison of $\Vert {p}_{\sigma }^{g+1}\Vert$ with its expected length $E\Vert {\mathbb{N}}(0,I)\Vert$, and can be represented mathematically as:

$${\sigma }^{\text{g+1}}={\sigma }^{g}\mathit{exp}\left(\frac{{c}_{\sigma }}{{d}_{\sigma }}\left(\frac{\Vert {p}_{\sigma }^{g+1}\Vert }{E\Vert {\mathbb{N}}(0,I)\Vert }-1\right)\right)$$

(24)

where ${\sigma }^{\text{g+1}}$ is global step size; $E\Vert {\mathbb{N}}(0,I)\Vert$ is expectation of Euclidean norm of a ${\mathbb{N}}(0,I)$ distributed random vector $\left({=}\sqrt{D}\left(1-\frac{1}{4D}+\frac{1}{21{D}^{2}}\right)\right)$; ${d}_{\sigma }$ is damping parameter $\left({=}\frac{4}{D}\right)$ and ${C}_{\sigma }$ is backward time horizon of evolution path $\left({=}1+\sqrt{\frac{{\mu }_{eff}}{D}}\right)$.

5 Results and Discussion

5.1 Problem Description: Synthetic Confined Rectangular Problem

A confined hypothetic problem (6 km × 6 km) similar to Carrera and Neuman (1986) is selected in this study as shown in Fig. 1. Here, the assumed distance between two consecutive nodes is 1000 malong X and Y-directions. This rectangular confined region has an area of 36 sq. km. which is bounded by two impervious, a constant head and one inflow boundaries. The northern part of the aquifer is getting areal recharge at the rate of 0.15 × 10^–3 m/d (AR-1) and 0.25 × 10^–3 m/d (AR-2) through two distinct aquitard-layers. This aquifer is assumed to have three zones of known transmissivity values varying within the range of 5 to 150 m²/d. An inflow rate of 0.25 m3/d/m across the western boundary is also considered. A uniform storage coefficient value for entire aquifer region is assumed as 0.001.

Fig. 1

Synthetic confined aquifer domain showing zonation pattern (indexed in red), boundary conditions and two areal recharge regions

5.2 Model Input

For testing of all the developed SO models, the known transmissivity values of selected rectangular confined synthetic problem are considered to be unknown. The objective here is to determine the transmissivity values using known data i.e. storativity, boundary conditions and zonation pattern by minimizing the error between observed and simulated head values at certain monitoring well locations. The inputs in terms of predefined upper and lower limits of unknown aquifer parameters are kept between 1 to 150 m²/day.

FEM and Mfree simulators are used to estimate the head values by discretizing entire domain using uniformly distributed 49 nodes and 72 triangular elements. In case of FEM simulator, the coordinates of distributed nodes and elemental area are used to form various element-based coefficient matrices which are further assembled to form a global coefficient of matrix. On the other hand, the estimated value of average nodal distance (d_s) and shape parameter value (α_s) are utilized to calculate the elements of shape parameter which eventually forms a coefficient matrix in Mfee simulator Eq. (5). In this synthetic problem, the estimated value of d_s is 1000 m. Since Mfree model is successfully applied on different synthetic problems with α_s as 3, the same is adopted for present case also. Total 49 nodes as shown in Fig. 1 are used. Flux vector contains the known values like inflow flux and constant groundwater head values. Using both the simulators (i.e. FEM and Mfree) model runs are performed for 25 days as total simulation period with 1 day as time-step size.

5.3 Parameter Setting for Developed SO Models

In the developed SO models, the population evolution guides the ultimate algorithm towards the optima. This navigation is controlled by certain problem dependent parameters allied to that specific optimization models. These problem specific parameters are needed to be tuned or estimate empirically which are discussed in the upcoming sub-sections.

5.4 DE, PSO and DE-PSO Based Model Setting

The heuristic algorithms are dependent on various weighting factors for their best performance, which are commonly known as control parameters. These control parameters are fine-tuned to extract the best performance prior to their application. In the whole study, the possible range of DE based control parameters is investigated based on the literature of Storn and Price (1997) and Price et al. (2005). Similarly for PSO parameters, the range proposed by Eberhart and Kennedy (1995) and Kennedy and Eberhart (2010) are explored for their optimum values. For DE-PSO, the appropriate tuned control parameter values of both the individual heuristic are used directly. The optimum values of these control parameters for DE, PSO and DE-PSO are presented in Table 1.

Table 1 The range and calibrated values of control parameters used in the DE, PSO and DE-PSO based SO models for synthetic aquifer problem

5.5 CMA-ES Based Model Setting

The main strength of CMA-ES optimization lies on the capacity of self-adaption with each generation (Bayer et al. 2009). Unlike pre-calibrated control parameters of prior discussed metaheuristics, the strategy parameters of CMA-ES are calculated by certain empirical formulae. These parameters are obtained by researchers after numerous past experiments on different classical benchmark problems. Some of these like λ, µ and c_c are function of dimension of the problem. Remaining parameters like c_cov, c_µ and c_σ adapt their values based on rank- µ-update with cummulation, and vary with the progress of each generation. The calculated value of CMA-ES strategy parameters for rectangular synthetic confined problem is presented in Table 2.

Table 2 The empirical equation and estimated values of control parameters used in the CMA-ES based SO models for synthetic aquifer problem

5.6 Comparative Performance of Results Obtained Through the Developed SO Models

Using the prior-tuned values of optimization specific parameters, all the developed SO models i.e. FEM-DE, FEM-PSO, FEM-DE-PSO, FEM-CMA-ES, Mfree-DE, Mfree-PSO, Mfree-DE-PSO and Mfree-CMA-ES are applied to selected rectangular synthetic problem. The obtained results are presented in terms of a convergence graph as shown in Fig. 2. It is visible that Mfree-CMA-ES produces best convergence with lowest value of objective function as compared to others. It takes nearly 153 generations to get steady global convergence of all 4 transmissivity values. The second-best performer is Mfree-DE-PSO which tries to explore the solution space intensely by switching between DE and PSO phases hence at initial stage some oscillation is observed in the fitness function (Fig. 2). It can be seen in convergence graph that individual versions of selected optimizations i.e. DE and PSO lagged behind their hybrid version due to lack of multiplicity after certain generations. Use of MQ based Mfree simulator with different optimizations also strengthened the solution-space exploration capacity of a SO model due to its higher accuracy compared to conventional FEM simulator. It also compels the specific SO model to explore the solution space faster with less number of generations.

Fig. 2

The variation of objective function with iteration using eight different SO models for synthetic confined aquifer problem

Apart from functional evaluation, computational time is also an important criterion to judge the performance of a SO model. The time required to perform one iteration of all the developed models is presented in Table 3. It concludes that Mfree-CMA-ES is a better performing algorithm due self-adaptive internal mechanism. On the contrary, DE-PSO model consumes slightly higher time as population generated on each iteration is passed to DE and PSO phase in series manner for objective function evaluation.

Table 3 Time needed to complete one iteration of the synthetic confined aquifer problem utilising eight developed SO models

In above described discussion, for all the analysis the SSD (Eq. 6) is used as an objective function. The results obtained are presented in Table 4 and reaffirms the superiority of Mfree-CMA-ES over other seven models.

Table 4 Best solution obtained through eight different SO models based on SSD as an objective function on synthetic confined aquifer problem

As all these SO models are random number based stochastic search methods therefore each model run is performed 10 times and its mean value is taken as representative zonal transmissivity value as shown in Fig. 3 and Table 5. It was showed greater agreement with real value in all the developed eight models.

Fig. 3

Average values of each parameter after 10 times model run by 8 different methods and their comparison with the known value

Table 5 Average values of each parameter after 10 times model run by 8 different methods

It is clearly evident from present study that all the developed models are able to estimate the aquifer parameter values. This selected problem is relatively small in dimension where parameter estimation using different SO models is fairly accurate and easy to implement.

6 Conclusions

In this study eight different SO models are tested on a synthetic confined aquifer problem with known solution and found efficient and robust. Following are the conclusions that can be drawn from the present study:

• 1. DE, PSO and DEPSO based SO models require tuning of control parameters before its application to the problems while CMA-ES based models are free from such a limitation. Therefore, the CMA-ES is more efficient and robust algorithm and highly suitable to field problems.

• 2. Eight different combinations of SO models are applied to a synthetic confined aquifer problem. The obtain results proved that the developed CMA-ES based models are able to estimate the aquifer parameter values with the lowest value of objective function.

• 3. In terms of objective function evaluation, the accuracy-wise general pattern is CMA-ES > DE-PSO > DE > PSO and for time consumption criteria the general sequence is CMA-ES < DE < PSO < DE < DE-PSO.