1 Introduction

Estimation of confined and unconfined aquifer parameters using field methods is an enormous endeavour and entails a huge amount of expense and efforts; for instance, confined aquifer requires nearly 24 to 40 h continuous pumping to estimate transmissivity values (Michael 2009). These aquifer parameters are normally heterogeneous and anisotropic in nature and suffer from an inbuilt complexity for their spatial characterization. The inverse problem is a well-established computational model to assess aquifer parameters by minimizing the calibration error between the observed and simulated state variables, (Elshall et al. 2015). Apart from hydraulic conductivity estimation (Yao and Guo 2014), inverse problem is successfully applied to a wide variety of other groundwater problems such as contaminant source identification (Aral et al. 2001), transport parameter estimation (Keidser and Rosbjerg 1991), storage coefficient estimation (Gehman et al. 2009) and coupled problem (Sun and Yeh 1990) solution.

With growing computational power, numerous advanced techniques have been developed to solve inverse groundwater problem. Sun (1999) classified these methods into two categories based on their solution strategies i.e. direct and indirect methods. The direct method depends on a large number of observation well data for its accuracy which is not possible practically and is confined to a limited number of problems (Zhou et al. 2014). This inadequacy is overcome by the introduction of the indirect method which works efficiently with less number of observation data. The indirect method yields the solution by minimizing the squared sum of the difference between the observed and simulated state variables at the monitoring well locations based on the provided aquifer parameters. Two types of optimization approaches utilized to solve the inverse problem using indirect method are gradient-based and non-gradient-based optimization (Mahinthakumar and Sayeed 2005). In gradient-based approach, the initial guess of solution improves based on the objective function gradient; hence the significance of the proper choice of the initial guess is highly critical. Mostly inverse groundwater related problems have discrete objective function and multiple- minima, which encourage the solution to get stuck in local minima and is not considered to be suitable for the inverse groundwater problem (Yao and Guo 2014). The next approach is a non-gradient-based method which tries to improve the randomly generated candidate solution (population) by certain logical algorithms, usually inspired by social behaviour of colony based species (birds, ants, fish, termites, bee) and the theory of evolution. GA (Jha and Sahoo 2015), ant colony optimization (ACO) (He and Liu 2009), DE (Chiu 2014) are some methods which are explored extensively for a wide range of problems. These methods are found to be suitable for parameter estimation, since (1) the objective function is discrete in nature, (2) objective function is non-differentiable with respect to decision space, (3) they can operate with discrete, integer and continuous constraints and (4) they have inbuilt metaheuristics to avoid local optima. However, there are certain limitations to these methods individually, such as GA exhibits very slow convergence and is highly dependent on the encoding scheme (Yao and Guo 2014). Similarly, PSO works on particle velocity and if one particle (candidate solution) gets stuck into local minima, then other particles will also follow the same pattern and eventually algorithm will fall into sub-optimal solution (Jiang et al. 2010). Likewise, DE with its strong searching characteristic leads to an unstable convergence (Wu et al. 2011).

The synergy of two or more heuristics to exploit complementary attribute of different optimization can be a good response to the aforementioned problems. The hybrid form of two or more heuristic methods is commonly known as hybrid-metaheuristic optimization. In the recent past, various hybrid models have been successfully applied to groundwater management problems such as groundwater parameter identification (Yao and Guo 2014), groundwater source identification (Mahinthakumar and Sayeed 2005) and bioremediation problem (Kumar et al. 2015) etc.

DE searches the solution space effectively, but produces unstable convergence while PSO is easier to implement but often falls into sub-optimal solution due to a lack of diversity in the population. Therefore the complementary characteristics of these two methods are explored by their combination using different hybridization approaches. Kannan et al. (2004), and Wu et al. (2011) presented their hybrid approaches to solve several benchmark problems for combinatorial optimization.

Earlier literature suggests that most of the individual global optimization methods were employed to solve the inverse problem associated with synthetic, regular shape, linear (confined) aquifer cases. But in some specific class of real field problems, aquifer region observes the meagre temporal groundwater head fluctuation throughout the year and it is hard to reach a precise minimum value of error norm using an individual metaheuristic method. To overcome these limitations, in this paper a SO model based on the hybrid metaheuristic method is proposed and applied to obtain the groundwater parameter in real-field aquifer problem. The present study carries the comparative performance between existing evolutionary method and projected hybrid DE-PSO method in terms of improvement in fitness function and accuracy in estimated parameters.

2 Methodology

2.1 Inverse Groundwater Problem Formulation

The indirect method solves the inverse problem by formulating it as an optimization problem. Minimization of summation of the weighted squared difference between observed and simulated heads at a certain number of monitoring well locations is selected as an objective function in this study. Realistic possible upper and lower bounds of parameters are imposed as constraints to keep the solution under the limit. Inverse problem formulation mathematically can be described as (Sun 1999):

$$ E{(P)}_{\mathrm{min}}=\sum \limits_{l=1}^L\sum \limits_{t={t}_0}^{t_t}{\beta}_{l,t}{\left[{h}_{l,t}^{cal}(P)-{h}_{l,t}^{obs}\right]}^2 $$
(1)

Subjected to:

$$ {P}_i^l\le {P}_i\le {P}_i^u $$
(2)

where E represents an objective function; \( {\mathrm{h}}_{\mathrm{l},\mathrm{t}}^{\mathrm{cal}} \) is calculated groundwater head at the observation well l at time t as system response to various dynamic activities with parameter P at L; \( {\mathrm{h}}_{\mathrm{l},\mathrm{t}}^{\mathrm{obs}} \) is observed groundwater head at the observation well l at time t; Pi is an aquifer parameter at ith zone; L is the total number of observation wells; t0 and tt are beginning and ending time of observations; l and u are the subscripts for a plausible lower and upper bound to the parameters and βl, t is the weighting coefficient, which depends on the accuracy of the measured groundwater head at a specific monitoring well location. In real field problem, it is assumed that measurement of each monitoring well data are taken precisely, therefore, a uniform value ofβl, t as unity is considered throughout this study.

As most of the groundwater flow governing equations are complex to solve analytically, hence grid based numerical solution by finite element method (FEM) is adopted in this study. To get the intermediate head values spatial derivatives are approximated by Galerkin’s FEM and the temporal terms are discretized by a central difference implicit scheme of finite difference method (FDM) (Rastogi 2012).

2.2 Optimization Model Formulation

In this study, a hybrid version of DE and PSO is applied to estimate the optimal aquifer parameters. DE-PSO improves the population by sequentially passing it from DE to PSO to improve the objective function by profound exploration of the solution space that leads the candidate solution towards global optima. In this proposed method, DE evolves by using nearby solutions and their difference to get new position while PSO provides perturbation to the initial position of the solution based on its past experiences (memory characteristic).

2.2.1 DE Algorithm

DE is a recently developed evolutionary algorithm envisaged by Storn and Price (1997) to achieve the global optima. It follows the initialization, mutation, crossover and selection operations to improve the fitness.

Let us consider P as a vector (i.e. target vector) of D-dimensional aquifer parameters with Gth generation, i.e. \( {\mathrm{P}}_{\mathrm{i}}^{\mathrm{G}}={\mathrm{p}}_{1,\mathrm{i}}^{\mathrm{G}},{\mathrm{p}}_{2,\mathrm{i}}^{\mathrm{G}},{\mathrm{p}}_{3,\mathrm{i}}^{\mathrm{G}}..\dots \dots {\mathrm{p}}_{\mathrm{D},\mathrm{i}}^{\mathrm{G}} \) where i = 1, 2….Np and G = 0, 1…..Gmax. Np and Gmax represent the population size and maximum number of iterations respectively.

Therefore the optimization problem is mathematically framed as:

$$ {\displaystyle \begin{array}{c}\min E\left({p}_1,{p}_2,{p}_3.\dots \dots \dots {p}_D\right)\\ {}{p}_i\in \left({p}_i^l,{p}_i^u\right);i=1,2,3.\dots \dots D\end{array}} $$
(3)

where E represents the fitness function subjected to minimization and pil and piu are representations of upper and lower bounds of aquifer parameters respectively. Initialization starts with the generation of the initial random population based on a uniform probability distribution within the predefined upper and lower limits on p. This initial population is passed on to the mutation scheme to produce a newly generated population having characteristics of their parents. The offspring population is obtained by the addition of a randomly selected vector to the scaled difference between the other two different randomly selected vectors from parent population and the resultant vector commonly known as donor vector which can be given as:

$$ {\displaystyle \begin{array}{c} Donorvector{V}_i^G={P}_{r_1}^G+F.\left({P}_{r_2}^G-{P}_{r_3}^G\right)\\ {}{\mathsf{r}}_{\mathsf{1}},{\mathsf{r}}_{\mathsf{2}},{\mathsf{r}}_{\mathsf{3}}\in \left\{\mathsf{1},\mathsf{2}\dots \dots {\mathsf{N}}_{\mathsf{p}}\right\}\ \mathsf{and}\ {\mathsf{r}}_{\mathsf{1}}\ne {\mathsf{r}}_{\mathsf{2}}\ne {\mathsf{r}}_{\mathsf{3}}\ne \mathsf{i}\end{array}} $$
(4)

Where F is a constant scaling factor within the range of 0 to 1 and it scales the difference vector, r1, r2 and r3are indices for mutually exclusive integers from 1 to Np.

After mutation scheme, DE algorithm follows the crossover operation in which each element of the initial population is tested for their swapping with the mutation-based newly generated population by predefined crossover probability. This crossover operation mainly diversifies the existing population, with each vector known as a trial vector which can be represented mathematically as (Price et al. 2005):

$$ {\displaystyle \begin{array}{c} Trialvector{U}_{j,i}^G=\left\{\begin{array}{c}{V}_{j,i}^G if{R}_j\le Cr\\ {}{P}_{j,i}^G otherwise\end{array}\right\}j=1,2..\dots D\\ {} and{U}_i^G={U}_{j,i}^G={\left({U}_{1,i}^G,{U}_{2,i}^G\dots \dots \dots \dots {U}_{D,i}^G\right)}^T\\ {}{V}_i^G={V}_{j,i}^G={\left({V}_{1,i}^G,{V}_{2,i}^G\dots \dots \dots \dots {V}_{D,i}^G\right)}^T\\ {}{P}_i^G={P}_{j,i}^G={\left({P}_{1,i}^G,{P}_{2,i}^G\dots \dots \dots \dots {P}_{D,i}^G\right)}^T\end{array}} $$
(5)

Where Rj represents the uniformly distributed random number within the range of 0 to 1, Cr represents the crossover probability and controls the diversity in the population.

After crossover DE follows the selection operation which defines the fittest vector between trial and target vector in their respective location. It erects the fittest offspring compared to an initially generated population which is considered as initial population for the next generation. The procedure of selection can be represented as (Price et al. 2005):

$$ {P}_{j,i}^{G+1}=\left\{\begin{array}{c}{U}_i^{G+1} ifE\left({U}_i^{G+1}\right)\le E\left({P}_i^G\right)\\ {}{P}_i^G otherwise\end{array}\right. $$
(6)

Where (G + 1) represents the increment in the current iteration by 1.

2.2.2 PSO Algorithm

PSO is an established population-based stochastic search evolutionary technique which belongs to the family of swarm optimization. It is inspired by the social behaviour and moment dynamics of animals such as birds, sheep, insects, and fish (Du and Swamy 2016). In this approach potential candidate solution known as particles are randomly placed throughout the solution space and each particle in the swarm is represented by a randomized velocity and position. These particles try to search the new locations based on the best historical movement so far of the swarm and their own position. The individual best position is personal-best (pbest) while group-best (gbest) represents the best position of the whole swarm. The difference between the current location of an individual particle with pbest and gbest provides the perturbation to an individual particle towards their new position. Therefore the illustrative formulation of PSO to update the current position of a particle and velocity is presented as (Eberhart and Kennedy 1995):

$$ {\displaystyle \begin{array}{c}{V}_{j,i}^{G+1}=\omega \times {V}_{j,i}^G+{C}_1\times \mathit{\operatorname{ran}}{d}_1\times \left( pbes{t}_{j,i}^G-{P}_{j,i}^G\right)+{C}_2\times \mathit{\operatorname{ran}}{d}_2\times \left( gbes{t}_i^G-{P}_{j,i}^G\right)\\ {}{P}_{j,i}^{G+1}={P}_{j,i}^G+{V}_{j,i}^{G+1}\end{array}} $$
(7)

Where \( {P}_{j,i}^G \) represents the current location of an individual particle i in Gth generations [L]; \( {V}_{j,i}^G \) represents the velocity of particle at position at j dimensional space at current Gth generations [L]; \( pbes{t}_{j,i}^G \) represents the personal best performance of an individual particle till Gth generations [L]; \( gbes{t}_i^G \) represents the best performance of whole swarm till Gth generations [L]; \( {V}_{j,i}^{G+1} \) represents the velocity of a particle i at position at jth dimensional space after G + 1st generation [L]; ω is the inertia weight, which gives weight to the velocity of a particle at its previous position; C1 and C2 are the acceleration constants; rand1 and rand2 represent the random number between 0 and 1.

2.3 Development of DE-PSO Based Hybrid-Metaheuristic Optimization Model for Solution of Inverse Groundwater Problem for Aquifer Parameter Estimation

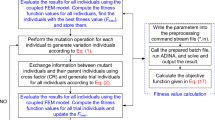
The projected hybrid SO model depends on field tests and surveys for hydrogeological data such as aquifer geology (storativity values), surrounding boundary conditions and prior groundwater head values as an input to finite element method (FEM) simulator. Global stochastic optimization algorithm feeds the varying input aquifer parameters in terms of population to FEM model which simulates the flow conditions and calculate the groundwater head as a simulated outcome. The indirect approach uses output least square criteria which try to minimize the error between observed and simulated head to get the best fitted optimal aquifer parameters. The entire procedure for groundwater parameter estimation is presented with a flowchart shown in Fig. 1. Hybrid DE-PSO optimization pursues the subsequent steps to search the solution space and generates the new population. The implemented steps are:

  1. 1.

    Initialization of optimization starts with DE phase which starts with the generation of a randomly produced population of candidate solution under the predefined solution space.

  2. 2.

    Evaluate the fitness function for the initially generated population.

  3. 3.

    Using mutation operation, a new vector is generated by summing up a randomly selected vector with the weighted difference vector presented in Eq. (4) called as donor vector \( \left({\mathrm{V}}_{\mathrm{i}}^{\mathrm{G}}\right) \) which relocates the initial candidate solution in the problem space.

  4. 4.

    The crossover operation produces trial vector \( \left({\mathrm{U}}_{\mathrm{j},\mathrm{i}}^{\mathrm{G}+1}\right) \) by selecting a vector from the initially generated population and mutated population from their respective locations based on the predefined crossover probability as Eq. (5).

  5. 5.

    Selection operation decides which vector is passed on to the next generation to form a new population. If updated population provides a better fitness, than the corresponding vector will be selected. Otherwise optimization model will enter into PSO phase. In this phase proposed algorithm generates a new particle \( \left({\mathrm{TP}}_{\mathrm{j},\mathrm{i}}^{\mathrm{G}+1}\right) \) according to Eq. (7) by giving perturbation to the initial population using pbest and gbest, which will also be checked for its fitness. If this new vector provides better fitness than corresponding initial population vector, then it will be selected, otherwise old population vector will be assimilated in a new generation.

  6. 6.

    The procedure to follow steps 2 to 5 will continue until a required stopping criterion is achieved.

    Fig. 1
    figure 1

    Flow-chart showing the functioning of simulation-optimization (SO) model for groundwater parameter identification

    Full size image

2.4 Sensitivity Analysis for Estimating Parameters

Sensitivity analysis is carried out to estimate the mutual correlation and reliability of the estimated parameters. The validity of the proposed inverse groundwater model is interpreted by various statistical parameters such as composite scaled sensitivity (CSS) and coefficient of variation (CV) which are discussed in the upcoming sections.2.4.1 Composite scaled sensitivity (CSS).

The CSS as a statistical measure depicts the total amount of information provided by the monitoring wellhead data for the assessment of one particular aquifer parameter (Hill and Tiedeman 2006). The CSS is often used relatively and the relatively higher value of CSS for a specific parameter indicates its better estimation in comparison to others. According to Hill (2000) CSS can be calculated as:

$$ \mathsf{Composite}\ \mathsf{scale}\ \mathsf{sensitivity}\ \left({C}_j\right)=\sum \limits_{i=1}^L\left\{\sqrt{\left[{\alpha}_i{\left(\frac{\partial {h}_i}{\partial {T}_j}\right)}^2{T_j}^2\right]/L}\right\}\ \mathsf{where}\ \mathsf{j}=\mathsf{1},\mathsf{2}.\dots \mathsf{M} $$
(8)

where αi represents the weighting coefficient (kept as unity); L is a number of observation wells in the domain; M depicts the number of estimated parameters and \( \left(\frac{\partial {h}_i}{\partial {T}_j}\right) \) is a sensitivity coefficient which can be calculated by the influence coefficient method as:

$$ \left(\frac{\partial {h}_i}{\partial {T}_j}\right)\approx \frac{h_i\left(T+\varDelta {T}_l{e}_l\right)-{h}_i(T)}{\varDelta {T}_l}\ \mathsf{where}\ \mathsf{j}=\mathsf{1},\mathsf{2}.\dots \mathsf{M} $$
(9)

where T is estimated parameter; ΔTl represents the small perturbation (5%) to the estimated parameter; el is lth unit vector and hi is simulated values of the aquifer state.

2.4.1 Coefficient of Variation (CV)

Variance-Covariance is a square matrix which represents the precision and correlation between each estimated parameter, especially in a nonlinear problem. Mathematically variance-covariance matrix can be represented as (Hill and Tiedeman 2006):

$$ {\left[\begin{array}{ccccc} Var(1)& Cov\left(1,2\right)& Cov\left(1,3\right)& .\dots & Cov\left(1,\mathsf{M}\right)\\ {} Cov\left(2,1\right)& Var(2)& Cov\left(2,3\right)& .\dots & Cov\left(2,M\right)\\ {} Cov\left(3,1\right)& Cov\left(3,2\right)& Var(3)& .\dots & Cov\left(3,M\right)\\ {}\begin{array}{c}.\\ {}.\end{array}& \begin{array}{c}.\\ {}.\end{array}& \begin{array}{c}.\\ {}.\end{array}& \begin{array}{c}.\\ {}.\end{array}& \begin{array}{c}.\\ {}.\end{array}\\ {} Cov\left(M,1\right)& Cov\left(M,1\right)& Cov\left(M,1\right)& .\dots & Var(M)\end{array}\right]}_{M\times M} $$
(10)

where M is a total number of estimated parameters.

The variance-covariance matrix contains two informative statistics, which are variance (diagonal elements) and covariance (off-diagonal elements). The square root of variance equals to the standard deviation which shows the amount of dispersion of the parameter. It can further be used to estimate the coefficient of variation (CV) which is a ratio of standard deviation to the parameter value and can be represented as:

$$ CoefficientofVariation(CV)=\left[\frac{\sqrt{\operatorname{var}\left({T}_e\right)}}{T_e}\right] $$
(11)

where var(Te) is a variation of an estimated parameter with true values. The coefficient of variation represents the relative accuracy of different estimated parameters.

3 Results and Discussion

The developed SO model is first tested on a synthetic aquifer domain and subsequently applied to a real-field problem for unconfined aquifer parameter estimation. In both the cases, the FEM groundwater model (Rastogi, 2012) is employed to estimate the intermediate aquifer state by its known initial state and boundary conditions. The performance of a hybrid version of metaheuristics is compared with their individual versions (DE and PSO) in the upcoming sections.

3.1 Testing of the Proposed Model on a Synthetic Problem

The projected inverse groundwater model is applied first to a synthetic confined aquifer problem presented by Cyriac and Rastogi (2016) to check its relevance for parameter estimation. The area occupied by the aquifer is around 40 km2 (Fig. 2) which is surrounded by a river with the variable head on the west side, the impervious granite formation on the northern and north-western side, and inflow boundary on the eastern side with influx as 0.5 m2/day. A reservoir with a constant head of 98 m is also considered on the south-eastern side. Western side River is flowing from north to south has spatial and temporal head variability. To simulate a real field like situation, a temporal variation on an upstream river node number 40 is considered which reflects the effect of a typical Indian monsoon cycle. For simplicity, here we consider a year represented by 360 days in each month equal to 30 days and further each month is subdivided into 3 sections of 10 days. To simulate spatial river head variation a linearly decreasing groundwater head relationship between nodes 40 to 12 is assumed where 0.2 m drop between every two consecutive river nodes is considered.

Fig. 2
figure 2

(a) Synthetic aquifer showing boundary conditions with location of monitoring, pumping and recharge well. (b) Bar-chart showing transient fluctuation in river head at node no. 40. (c) Zonation pattern of synthetic aquifer. (d) True values of aquifer parameters

Full size image

In the present study, continuous aquifer parameters are assumed to be distributed in different zones called as parameterization (Sun 1999). The entire synthetic aquifer domain is divided into five transmissivity zones using zonation method (Fig. 2) and each T is attributed with two components along the principal Cartesian axis, which represents true transmissivity values. Since we want to test the efficiency and robustness of the proposed inverse model, 10 representative values (=5 zones × 2 components of T i. e. Tx and Ty) of transmissivity are considered to be unknown. Other than T values, remaining characteristics such as zonation pattern, storage coefficient and boundary influx are known. The thickness of subsurface strata of the aquifer is considered as 100 m. For simulating the groundwater head values, FEM method is adopted and the representative irregular domain is discretized using 146 nodes and 252 linear- triangular elements as shown in Fig. 2. Three pumping (P-23 = P-76 = P-125 = 2000 m3/day) and three recharge wells (R-26 = 900 m3/day, R-80 = 1000 m3/day, and R-122 = 1000 m3/day) are considered in the problem to demonstrate the effect on the groundwater table after 360 days of the simulation period (time step size = 0.5 days) with pumping and recharge activities. All the parameters required to simulate the transient groundwater flow in the synthetic problem is presented in Fig. 2. The FEM-based simulation model is employed to calculate the monitoring wellhead values which eventually are used as known monitoring wellhead (reference head) data.

Before applying the proposed hybrid DE-PSO algorithm to synthetic problem, certain governing parameters are assessed to achieve optimal convergence. These control parameters are population size (Np), scaling factor (F), crossover probability (Cr), inertia weight (ω) and acceleration constants (C1 and C2) which have already been discussed in Eq. (4), (5) and (7). Based on the past research on DE (Price et al. 2005) and PSO (Eberhart and Kennedy 1995) sensitivity analysis is performed by assigning a suggested range to these problem-specific control parameters such as Np ∈ [20, 30], F ∈ [0.3,0.5], Cr ∈ [0.8,1], C1 = C2 ∈ [1.5,2] and ω ∈ [0.8, 0.3] to obtain the best-suited configuration. For the synthetic case, estimating transmissivity values are kept in the range of 500 to 2000 m2/day and a maximum number of generations (= 500) is decided based upon the initial tuning phase. The objective function is calculated with the help of 50 assumed monitoring wells distributed over the entire aquifer region as shown in Fig. 2. After performing several numerical experiment proficient values for Np, F, Cr, C1 = C2 and ω were found as 25, 0.3, 0.8, 1.9 and (0.8 to 0.3 linearly decreasing) respectively. For comparison purpose, the synthetic problem is also tried with an independent form of heuristic methods i.e. DE and PSO respectively.

Proposed simulation-optimization model is implemented on the test problem with above-recommended parameter settings using the hybrid DE-PSO. Figure 3 shows the minimum fitness value achieved by the DE-PSO as compared to the other three counterparts. It takes nearly 153 generations to get steady global convergence for all 10 transmissivity values. The proposed hybrid-optimization tries to explore the solution space intensely by switching between DE and PSO optimizations; hence at the initial stage, some oscillation is observed in the fitness function (Fig. 3). The parameter values obtained through hybrid DE-PSO shows greater agreement with the true values and reaffirms its accuracy as depicted in Fig. 3 in terms of a bar- chart and Table 1. It was also found that the individual DE and PSO lagged behind hybrid method due to the lack of multiplicity and eventually fall prey to sub-optimality. Presently simulated head data with known T values are used as known monitoring wellhead, therefore, the system will be free from equation error. However, in the real field condition, personal and instrumentation error in the field data is inevitable. Hence, to check the stability of the proposed model, it is tested by incorporating two types of normally distributed noise in the monitoring well reference head. The first error introduced is with zero mean and 0.1 as standard deviation is called as model-II data set while the second error introduced is with zero mean and 0.01 as standard deviation is called as model-III data set. For both these data set, the estimated parameters of the hybrid model showed a higher degree of unanimity with true values as compared to the other two SO models (Table 2).

Fig. 3
figure 3

(a) Convergence graph using DE, PSO and DE-PSO for parameter estimation in synthetic problem. (b) Bar-chart showing estimated values of transmissivity values using DE-PSO method

Full size image
Table 1 Estimated aquifer transmissivity using different optimization methods for the synthetic problem
Full size table
Table 2 Comparison of model accuracy by assimilation of noise in the aquifer state
Full size table

3.2 Application to Real-Field Problem

Subsequent to the successful testing of the proposed hybrid model on a synthetic problem for different data sets, it is further applied to a real field aquifer. For this, an unconfined aquifer situated in the MRBC area is selected to assess the hydraulic conductivity distribution in defined aquifer zones. The chosen aquifer is spread over Kheda and Anand districts of Gujarat province of India and encompasses an area of 0.28 million hectares (Rastogi and Huggi 2009). It is positioned between 22° 26’N to 22° 55’N latitude and 72° 49′E to 73° 23′ E longitude. Central Groundwater Board (CGWB) identified the soil type in this area as heavy black in the south-eastern region that becomes coarser (sand and silt) towards the north. The entire MRBC aquifer is surrounded by water bodies such as Mahi River on the eastern side, Shedi River on the northern side and a canal named as Alang drain on the western boundary connecting both the rivers as shown in Fig. 4. The recorded average precipitation for the chosen year 2003 is 823 mm which occurs mostly during the monsoon season, and the area represents arid and semi-arid climatic conditions. To irrigate the whole area, a large number of canals with a total length of 1627 km are constructed by the irrigation department of Gujarat state. The length of 539 km is covered by the lined main canal whereas the remaining belongs to six lined branch canals and a number of unlined distributaries.

Fig. 4
figure 4

(a) Mahi Right Bank Canal (MRBC) aquifer location map. (b) Monitoring well configuration in MRBC domain. (c) Optimized zonation pattern identified by Lakshmi Prasad and Rastogi (2001) for MRBC region

Full size image

Groundwater flow in the entire aquifer is estimated by FEM discretization using 117 nodes and 189 linear triangular elements as shown in Fig. 4. An available water-table contour map of the year 2003 prepared by Gujarat Water Resources Development Corporation (GWRDC) is used to assign the boundary conditions using graphical interpolation on 43 boundary nodes surrounding the aquifer domain. FEM simulation is performed to get the groundwater head in the MRBC flow domain after one year (i.e. the year 2004) using a time step size of 1 day which is compared with the available groundwater table map of the year 2004. Geological survey and exploration defined the specific yield as 15% for the study area. Although there is no recharge well in the aquifer, but observations well data show a continuous rise in the groundwater head, due to rainfall infiltration, seepage from the canal and return flow of irrigation, which are important to account for the recharge contribution in the unconfined aquifer. To assimilate the recharge values in each node, recharge distribution coefficient (Rd) method proposed by Sondhi et al. (1989) is adopted and different hydrological data which represent inflow and outflow to the aquifer are calculated based on the suggestions of IARI Research Bulletin-42 (1983).

Lakshmi Prasad and Rastogi (2001) identified an optimal zonation pattern (10 hydraulic conductivity zones) for MRBC as shown in Fig. 4. Their results followed an available hydraulic conductivity contour map of the region, which was prepared by GWRDC after extensive field investigation. Their SO model using GA took nearly 600 generation with a population size of 75 to reach the convergence which can be considered costly in terms of available computational resources. Now, the MATLAB coded hybrid DE-PSO is applied to estimate the aquifer parameters in the MRBC aquifer. Earlier hybrid model has also been tested for its accuracy, robustness, and cost-effectiveness on the synthetic problem as discussed in the last section. To extract the best performance of SO model, different ranges of suggested control parameters in research papers such as Np ∈ [20, 40], F ∈ [0.2,0.6], Cr ∈ [0.8,1], C = C1 = C2 ∈ [1.8,2]and ω ∈ [0.8, 0.3] are tested. The limit of upper and lower bound on the decision variable is kept between 15 to 150 m/day with 300 generations stopping limit based upon initial tuning. For fitness calculation, four configurations of monitoring wells, i.e. 40, 57, 72 and 99 are adopted. After a certain number of experiments, the final tuned values for different parameters are picked up as 25, 0.3, 0.6, and 1.9 corresponding to Np, F, Cr, and C respectively. For ω linearly decreasing values from 0.8 to 0.3 with each generation, was found most suitable. Eventually, 40 monitoring wells spread throughout the aquifer (Fig. 4) are selected as the most appropriate strategy for inverse modelling for MRBC region.

After feeding above described settings, the hybrid model is run to minimize the value of the objective function. For this problem, DE and PSO methods are also applied individually to compare the efficiency of these three techniques. The variation in the fitness function with each generation established the accuracy of the projected model as it delivered the lowest fitness values as compared to the other two methods (Fig. 5). It takes nearly 90 generations for the hybrid DE–PSO to reach convergence for optimal parameters compared to DE with 136 and PSO with 205 generations. Aquifer parameters (Fig. 5) represent the average value of obtained parameters corresponding to a minimum objective function value. Since these three global optimization methods are stochastic in nature, each model run is repeated 6 times and their average values are considered as representative parameter values. The calculated value of the coefficient of determination (R2) using different methods such as DE-PSO, DE and PSO are 0.9992, 0.9957 and 0.9859 respectively, which demonstrates the high accuracy of the hybrid method over others. The values of R2 do not show significant difference with the other two methods due to very small change in the head values over one year of the simulation period. However, it is noteworthy that the hybrid method converges faster with less number of generations as depicted in Fig. 5. The comparative accuracy in terms of estimated parameters is also presented by a bar chart. The parameter values obtained by the SO model are fed to the forward problem to get the groundwater head distribution values for a simulation period of one year. This analysis is executed to check the comparative performance of the estimated parameter as input to simulation model which showed a greater unanimity with the field contour (Fig. 6).

Fig. 5
figure 5

(a) Convergence graph for parameter estimation in MRBC flow region using DE, PSO and DE-PSO. (b) Estimated values of zonal hydraulic conductivity using hybrid DE-PSO method and its comparison with other methods for MRBC area. (c) Numerical values of hydraulic for MRBC (10 zones)

Full size image
Fig. 6
figure 6

Groundwater contours using the parameters obtained by hybrid DE-PSO

Full size image

To check the possibility of estimation of aquifer parameters using hybrid DE-PSO model, different sensitivity statistics (e.g. CSS and coefficient of variation) are calculated for MRBC region. CSS values are depicted in Fig. 7 which conveys K1, K4 and K9 are better-estimated parameters as representing higher values compared to others, because more information is obtained from these regions via monitoring wells data. The variance-covariance matrix (VCM) is a measure of the reliability and correlation between estimated parameters. The values of variance and covariance obtained by VCM are utilized to calculate the more informative measure i.e. coefficient of variation. Table 3 shows that estimated hydraulic conductivity obtained for zone 1, 4, 9 and 10 are estimated accurately as depicting lower values of CV. It shows the unanimity with results obtained by CSS analysis that K1, K4, and K9 are estimated more accurately compared to others after the non-linear regression.

Fig. 7
figure 7

Composite scaled sensitivity (CSS) for MRBC system

Full size image
Table 3 Coefficient of variation using hybrid DEPSO for MRBC region
Full size table

3.3 Discussion

The proposed SO model based on hybrid-metaheuristic (DE-PSO) optimization is able to reach the desired minimum value of error norm and finally helps the model to estimate the stable and precise aquifer parameters. The applications of DE-PSO model on two different problems is presented in the last section which demonstrates that (1) the projected model works efficiently with less number of population size, (2) the PSO phase diversifies the population generated by DE phase, which enables the hybrid algorithm to reach the convergence faster with less number of generations. On the other hand hybrid model requires the tuning of control parameters associated with both DE and PSO algorithms before its application to a certain problem. It is considered as a limitation of the present model. However the successful application of the hybrid model reduces the computational cost, which encourages the researchers to apply it to solve the inverse groundwater problems.

4 Conclusions

In this study, a hybrid-metaheuristic method DE-PSO is proposed to estimate the aquifer parameters. It utilized the advantages of both DE and PSO; DE has a greater ability to exploit the solution space while PSO uses the local and global past experience for exploration. These two characteristics are assisting each other and their combination compels the algorithm to reach a rapid optimal solution. The objective function is evolved from engaging FEM simulated head values which guide the algorithm towards the optima. In the present study, a hybrid SO model is presented and tested first on a synthetic 2D heterogeneous anisotropic confined aquifer problem with a considered set of transmissivity values. The performance of hybrid method depends upon a suitable configuration of control parameters such as F, Cr, C, and ω, which need tuning to ascertain their most appropriate problem specific values. The DE and PSO methods are also applied to the synthetic problem to analyse the comparative performance. To counter the argument of stability of proposed model, two different sets of normally distributed noise is assimilated in monitoring wellhead data to corrupt its values. The optimal solution suggested the superiority of hybrid optimization model over individual DE and PSO applications. Subsequently, a large MRBC unconfined aquifer region is selected for the real field application of the proposed hybrid model. The optimal assessment via DE-PSO are compared with the single DE, PSO and available GA optimization. The hybrid method demonstrated a higher degree of precision in terms of estimated hydraulic conductivity and fitness function values. The sensitivity analysis based on CSS and CV is also carried out to check the reliability and accuracy of estimated parameters. Existing global solution methods such as DE, GA, and PSO follow their unilateral strategy and this study found that if solution falls in local optima, it is hard to come back and needs additional iterations. From the present study, it can be concluded that a hybrid version of metaheuristics enhances the search characteristic of optimization algorithm which eventually helps the inverse model to achieve highly accurate values of the aquifer parameters.