1 Introduction

Magnetic resonance imaging (MRI) is an amazing noninvasive diagnostic imaging modality that is used for the assessment of soft tissues in the human body without the risk of ionizing radiation. MRI provides a large number of flexible contrast parameters for excellent soft tissue classification. The data acquisition time in MRI is inherently a slow process which increases linearly with the number of samples taken in the frequency domain (k-space). This long data acquisition process may lead to patient discomfort and results in artifacts in the image [1].

CS [2, 3] has been recently applied to speed up the acquisition of MRI data. In CS, the number of sample values acquired is usually much smaller than the samples normally defining the signal. The signals in CS can be potentially reconstructed with great accuracy using highly under-sampled values by a nonlinear reconstruction algorithm. The fundamental requirements for a successful application of CS are: (1) the desired image has a sparse representation in a known transform domain or the image should be inherently sparse, (2) the aliasing artifacts due to under-sampling be incoherent in a specified domain and (3) a nonlinear recovery algorithm be used to enforce data sparsity and data consistency with the acquired data [2].

The possibility of MR images to be sparse in certain transform domain (wavelets, contourlets, curvelets, finite-differences, etc.) and the Fourier-encoded nature of the MRI acquisition make the MR imaging a suitable candidate for the application of CS. The incoherent artifacts requirement of CS can be achieved by acquiring data in a variable density sampling pattern [3]. In variable density sampling scheme, the data are fully sampled (as per Nyquist criteria) at the center of the k-space and are under-sampled in the outer k-space. The data acquired in this way have the advantage that most of the energy of the signals is preserved at the center of the k-space with overall reduction in the scan time [3].

The third and the most important element of CS is the use of an efficient and robust reconstruction algorithm to recover original MR image from the under-sampled dataset. Until recently, many optimization algorithms ranging from steepest descent, conjugate gradient (CG), basis pursuit (BP) and interior-point methods have been proposed [4–6]. A review of the CS algorithms for MRI reconstruction can be found in [7, 8] and the references therein. However, all these general purpose algorithms are often inefficient, requiring too many computations and/or iterations to reach the final solution. This is especially true for high-dimensional images, as often encountered in medical image processing. Mathematically, the optimization problem encountered in CS can be modeled using Lagrangian expression [9].

$$J(x) = \left\| {y - Hx} \right\|_{2}^{2}\,+\,\lambda \left\| x \right\|_{1} .$$
(1)

This is called an l 1-norm regularized linear inverse problem. In this notation, x defines the sparse signal/image to be recovered, H is the sensing matrix, y is the measurement vector obtained through the random projections. The second term in Eq. (1) is a regularization term that controls the norm of the solution. The regularization parameter λ > 0 provides a trade-off between fidelity to the measurements and noise sensitivity.

In recent years, a new family of iterative-shrinkage algorithms based on POCS has been built addressing the above optimization problem efficiently [5, 10, 11]. POCS is a mathematical tool utilizing projection operator for the reconstruction of the under-sampled data. Well-known applications of POCS in MRI include image reconstruction from variable density k-space sampling [3, 12]. POCS in conjunction with iterative-shrinkage algorithms can be utilized to achieve improved image quality.

In this paper, we propose a new method for image reconstruction from highly under-sampled data in k-space. The new technique is based on the POCS formalism with g-Factor as a regularization parameter (λ). The g-Factor is simply a ratio of the signal-to-noise ratio (SNR) of an unaccelerated optimal image to an accelerated image multiplied with the square root of the acceleration factor [13, 14]. The g-Factor can be expressed as given in Eq. (2)

$$g = \frac{\text{SNRunaccelerated}}{{{\text{SNRaccelerated}} \cdot \sqrt R }}.$$
(2)

The proposed algorithm is applied to recover both the simulated as well as in vivo images from the compressively sampled measurements.

The remaining paper is organized as follows. Section 2 describes the g-Factor as regularization parameter. Section 3 discusses the POCS application for CS recovery. Section 4 presents the proposed g-Factor-based iterative-shrinkage algorithm. Section 5 introduces the datasets used in this paper. Section 6 contains the experimental results and discussion and finally, Sect. 7 concludes the paper.

2 g-Factor as a Regularization Parameter

In MRI, the scan time is reduced by decreasing the number of k-space lines in the data acquisition process. The acquired data contains noise which originates because of the coil geometry imperfections and also due to the receiver electronics and the sample itself [13]. Many Parallel MRI (PMRI) [13, 15, 16] algorithms utilize sensitivity maps of the receiver coils and samples in the k-space [1, 2, 13] to recover fully sampled data. In these methods, aliasing in the reconstructed image occurs because of under-sampling which can be mitigated with the help of sensitivity maps [13, 17, 18]. The sensitivity maps amplify noise during the image reconstruction process because of the ill-conditioning of the encoding matrix [1, 13]. The ill-conditioning can be partially resolved by conditioning the encoding matrix [4, 19]. The price of this conditioning is a decreased reconstruction accuracy that may appear in the final image in the form of aliasing artifacts. Another way of avoiding the effects of ill-conditioning is using the g-Factor map as a priori information for image reconstruction as proposed by [14, 15].

The noise amplification in MRI due to ill-conditioning is quantified by the g-Factor. The g-Factor can be used as a regularization parameter in linear inverse problems [14, 17]. The g-Factor map calculation has been proposed by Pruessmann et al. [13] using the following equation:

$$g_{p} = \sqrt {\left[ {\left( {C^{H} \psi^{ - 1} C} \right)^{ - 1} } \right]}_{p,p} \sqrt {\left[ {\left( {C^{H} \psi^{ - 1} C} \right)} \right]}_{p,p} ,$$
(3)

where ψ is N c XN c noise correlation matrix where the diagonal elements represent the noise variance in a single coil and off-diagonal elements represent the cross-correlation between any two coils, C is sensitivity encoding matrix derived from the sensitivity maps of the receiver coils and the subscript p refers to the aliased replicate number for a specific pixel in the aliased image.

A g-Factor value of 1 shows no noise amplification at a particular pixel location in the image and a higher g-Factor value indicates greater noise amplification. It is quite logical to use g-Factor as a regularization parameter because if the value of g-Factor is close to 1 at a pixel location, it is better to rely on the data consistency term, i.e., \(\left\| {y - Hx} \right\|_{2}^{2}\) to have good reconstruction results. On the other hand, if the g-Factor value is higher at a pixel location, it is wise to rely on the prior information, i.e., \(\left\| x \right\|_{1}\) about the image [15, 17]. In this way, the g-Factor can potentially be used as regularization parameter rather than a heuristically chosen value or through other search methods, e.g., l-curve, generalized cross-validation and discrepancy principle [6, 14].

3 Projection onto Convex Sets (POCS) Algorithm

POCS method can be used to include a priori information efficiently into the image reconstruction problem in CS. It is a powerful mathematical tool for the reconstruction of l 1 − l 2 convex optimization problems, Eq. (4), from an incomplete dataset by projecting the data between the convex sets. In POCS [5, 20], the data in k-space is transformed to image domain where soft-thresholding is applied followed by data consistency constraint in k-space. The POCS algorithm has been successfully applied in different fields including MRI and seismic data analysis and reconstruction [2, 5, 11, 20, 21]. In MRI, POCS has been utilized to remedy motion artifacts and also for the correction of ghosting artifacts in EPI images [21]. Another promising technique called, POCSENSE [21], is based on POCS and provides an algorithmically efficient way to incorporate various linear and nonlinear constraints in image reconstruction [5, 20]. The detailed steps involved for CS-MRI reconstruction using POCS are explained in an overcomplete dictionary [22, 23].

4 Proposed Algorithm

The proposed algorithm solves the convex optimization problem as given in Eq. (4) by incorporating g-Factor as a regularization parameter into the well-known iterative-shrinkage-thresholding algorithm [4]. Mathematically, the basic optimization problem with regularization term can be shown as:

$$\hbox{min} J(x) = \frac{1}{2}\left\| {y - F_{u} x} \right\| + \lambda R(x).$$
(4)

In Eq. (4), the penalty term R(x) is the regularization function and λ is the regularization parameter. The optimal choice of λ is crucial for an accurate solution of the optimization problem. The optimal choice of λ rationalizes the trade-off between data consistency and sparsity priors. The proposed algorithm is shown in Table 1. The modified form of Eq. (4) for MR image recovery problem with sparsity constraint can be given as:

Table 1 Proposed g-factor-based algorithm for CS-MRI reconstruction
Full size table
$$J(x)\,=\,\frac{1}{2}\left\| {F_{u} x - y} \right\|_{2}^{2}\,+\, \lambda \left\| {\psi x} \right\|_{1}^{1} .$$
(5)

The algorithm starts with an initial guess which is the inverse Fourier transform of the acquired data (with zero-filling of the non-acquired data points) obtained from the scanner. In each iteration, the missing k-space values are estimated using g-Factor-based soft-thresholding and back-projection. Many MR images are not sparse in the image domain, so the images are first transformed into a sparsifying domain using wavelet transform for shrinkage operation. To complete a single iteration, the solution is updated by transforming the data back into the k-space and performing the data consistency operation. The data consistency is like a projection which keeps the originally acquired Fourier samples intact.

The main feature in the proposed method is that the regularization parameter is not fixed (unlike the conventional shrinkage algorithms) but calculated based on the image characteristics and noise analysis of the receiver coils (i.e., g-Factor). Both the back-projected error and the shrinkage operation are performed based on the g-Factor map.

The stopping criterion of the proposed algorithm (outlined in Table 1) can be a predefined number of iterations or can be a desired number of fitness values. We have used the fitness value for stopping the algorithm and this value can be calculated using the expression, i.e., \(\left\| {F_{u} x_{j} - y_{ 2} } \right\|_{2}^{2}\).

5 Materials and Methods

The algorithm presented in Table 1 describes the sequence of operations in the proposed method. This includes the zero-filled data as an initial estimate to be reconstructed and the observed under-sampled data from the scanner. In the subsequent steps, iterative-thresholding is performed based on g-Factor in the sparsifying domain followed by data consistency in the Fourier domain. The same process is repeated until the stopping criteria based on the fitness value are achieved.

In this paper, fully sampled data have been acquired using 1.5T and 3T MRI machines. The under-sampling is performed on this fully sampled data to simulate the accelerated data acquisitions for different acceleration factors. The proposed method is tested on a phantom image obtained using 1.5T GE scanner and two in vivo images of human head which are acquired from two different volunteers using 1.5T GE and 3T GE MRI scanners, respectively. The data are obtained in all cases with an eight-channel receiver coil wrapped round the phantom and the head. Imaging experiments were performed at St. Mary’s Hospital London by applying gradient echo sequence with the following parameters: TE = 10 ms, TR = 500 ms, FOV = 20 cm, bandwidth = 31.25 kHz, slice thickness = 3 mm, flip angle 50o, matrix size = 256 × 256.

The metrics used to evaluate the performance of the proposed algorithm include artifact power (AP) and peak signal-to-noise ratio (PSNR). AP is the square difference error which can be computed as:

$${\text{AP}} = \frac{{\mathop \sum \nolimits_{j} \left| {x_{j} - \hat{x}_{j} } \right|^{2} }}{{\mathop \sum \nolimits_{j} \left| {x_{j} } \right|^{2} }}.$$
(6)

In Eq. (6) \(\hat{x}_{j}\) is the reconstructed image whereas x j is the reference image. Mathematical expression for calculating PSNR is given as [19]:

$${\text{PSNR}} = 10 \cdot \log_{10} \left\{ {\frac{{{\text{MAX}}_{f} }}{\text{MSE}}} \right\}.$$
(7)

6 Results and Discussion

This paper presents a modified POCS algorithm which uses g-Factor map as a regularization parameter for CS-based recovery of MR images from the under-sampled data. The reconstruction method utilizes iterative-shrinkage algorithm followed by data consistency in the k-space. During each iteration, a thresholding step is applied in the sparsifying domain for noise suppression and minimizing the objective function. The effectiveness of the proposed method has been validated by successfully recovering both the phantom and human head under-sampled data for different acceleration factors (AF), i.e., 2×, 3×, 4×, 5×, 8×, and 10×.

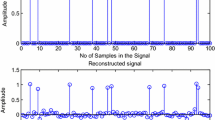
Figure 1 shows the reconstruction results for different datasets. The results show that in standard POCS, there are noisy effects which are successfully removed using the proposed technique. Table 2 shows the results of AP of the human head images obtained from 1.5T scanner for different acceleration factors for both the standard POCS and the proposed method. The results exhibit a significant improvement in AP for the proposed g-Factor-based reconstruction technique. Figures 2 and 3 show the graphs of AP against AF for the human head data (1.5T and 3T). It can be seen that AP is lower for the proposed method as compared to standard POCS, as desired. Moreover, the graphs also indicate that AP increases with an increase in the AF for both the algorithms. Table 3 shows a comparison of the proposed method with standard POCS in terms of PSNR and different AF for phantom and human head images. The results show that the performance of the proposed algorithm is better as compared to the standard POCS for phantom image. For human head image, the PSNR at low AF is slightly better than POCS but for higher AF both algorithms exhibit the same results.

Fig. 1
figure 1

Reconstruction results using the proposed algorithm and standard POCS (AF = 2). a Shepp–Logan phantom, b Phantom 1.5T and (c and d) human head data (1.5T and 3T)

Full size image
Table 2 AP for the 1.5T human head image reconstructed by the proposed method and standard POCS
Full size table
Fig. 2
figure 2

Comparison of the proposed algorithm with POCS when applied on human head (1.5T) in terms of AP and different AF

Full size image
Fig. 3
figure 3

Comparison of the proposed algorithm with standard POCS when applied on human head (3T) in terms of AP and different AF

Full size image
Table 3 Comparison of the proposed algorithm with standard POCS when applied on (a) phantom and (b) human head (3T) in terms of PSNR and AF
Full size table

The results show a considerable improvement in the quality of the reconstructed images by the proposed method than the standard POCS algorithm. The proposed method outperforms standard POCS in terms of AP and visual quality for phantom images, while PSNR at low AF is slightly better than POCS but for higher AF both algorithms show the same results.

7 Conclusion

A method based on using the g-factor as a regularization parameter in iterative-shrinkage-based POCS algorithm is proposed. The results show a considerable improvement in the quality of the reconstructed images than the standard soft-threshold-based POCS methods. It has been shown that g-Factor map effectively acts as an adaptive regularization parameter by providing quality image reconstructions. Future work includes the application and testing of the proposed algorithm for non-Cartesian k-space sampling trajectories (spiral and radial).