1 Introduction

Magnetic resonance imaging (MRI) is a useful medical imaging modality for an excellent soft-tissue characterization and because of its non-ionizing property. However, the fundamental limitation of MRI is the long data acquisition time which may lead to patient discomfort and results in artifacts in the image [1, 2]. To alleviate this problem many researchers have come up with different solutions including efficient data acquisition as well as reconstruction techniques. In the first place some researchers focused on fast data acquisition using different non-Cartesian trajectories with under-sampled data acquisition, followed by efficient reconstruction algorithms. For instance, parallel MRI (PMRI) [1] is a fast imaging method, which uses an array of radio frequency coils to acquire multiple sets of under-sampled k-space data simultaneously. In PMRI different reconstruction techniques can be applied in both the image domain and k-space [3, 4]. PMRI can accelerate data acquisition, but with some degradation in the reconstructed image and hence reduce the signal-to-noise ratio (SNR). The reduction in SNR is due to the reduction factor, g-factor and slice position [5]. This degradation can be improved by incorporating a regularization term in the reconstruction techniques [6–8].

Recently a new theory of applied mathematics called compressed sensing (CS) [9] has been extensively utilized in the data acquisition and reconstruction in MRI [2]. In CS, the number of the acquired sample values is usually much smaller than the samples normally defining the signal, i.e., the traditional Nyquist Shannon principle [10, 11]. The signals in CS can be potentially reconstructed with great accuracy using highly under-sampled values by a nonlinear reconstruction algorithm. The fundamental requirements for a successful application of CS are: (1) the desired image has a sparse representation in a known transform domain or the image should be inherently sparse, (2) the aliasing artifacts due to under-sampling be incoherent in a specified domain, (3) a non-linear recovery algorithm be used to enforce data sparsity and data consistency with the acquired data [2].

The possibility of MR images to be sparse in certain transform domain (Wavelets, Contourlets, Curvelets, finite-differences, etc.) and the Fourier-encoded nature of the MRI acquisition make the MR imaging a suitable candidate for the application of CS. The incoherent artifacts as required for successful implementation of CS can be achieved by acquiring data in a variable density sampling pattern [10]. In variable density sampling scheme, the data are fully sampled (as per Nyquist criteria) at the center of the k-space and are under-sampled in the outer k-space. The data acquired in this way has the advantage that most of the energy of the signals is preserved at the center of the k-space with overall reduction in MRI scan time [10].

The third and the most important element of CS is the use of an efficient and robust reconstruction algorithm to recover the fully sampled MR image from the under-sampled dataset. Until recently many optimization algorithms ranging from steepest descent, conjugate gradient (CG), basis pursuit (BP), split bregman (SB), two-step iterative shrinkage/thresholding algorithm (TwIST), alternating direction augmented lagrangian (ADAL), fast iterative shrinkage/thresholding algorithm (FISTA), and interior-point methods have been proposed recently [12–16]. A review of the CS algorithms for MRI reconstruction can be found in [17–19] and the references therein. However, all these general purpose algorithms are often inefficient, requiring too many computations and/or iterations to reach the final solution. This is especially true for high-dimensional images, as often encountered in medical image processing.

In this paper, we propose a new method for image reconstruction from highly under-sampled data in k-space. The new technique is based on the family of gradient-based adaptive algorithms called tangent-vector-based gradient method ‘with unit-norm constraint’ within the parameter space that are specified by \(\left\| X \right\| = 1\), where \(\left\| \cdot \right\|\) is any vector norm [20].

2 General Form of the Optimization Problem

The general form of the basic linear inverse problem arising in wide range of applications such as image restoration, deblurring, denoising, inpainting, source-separation, and CS can be modeled as solving a set of linear equations as given:

$$Ax = b + \eta$$
(1)

where in Eq. (1) \(A \in {\mathbb{R}}^{mxn}\), \(b \in {\mathbb{R}}^{m}\) are known, \(\eta\) is unknown noise vector, and \(x\) is the unknown signal/image to be estimated. The classical approach to the problem in Eq. (1) is the least-squares approach as given below:

$$\hat{x} = \mathop {\text{argmin}}\limits_{\text{x}} \left\| {Ax - b} \right\|_{2}^{2}$$
(2)

In many applications if the operator or function \(A\) is ill-conditioned [1] then a regularization method is required to stabilize the solution. The most popular choice that has attracted a revived interest in the signal and image processing literature is the \(l_{1}\)-norm regularization in which one seeks to find the solution of \(l_{1} - l_{2}\) expression of the form:

$$\hbox{min} J(x) \equiv \left\| {Ax - b} \right\|^{2} + \lambda \left\| x \right\|_{1}$$
(3)

where \(\left\| x \right\|_{1}\) stands for the sum of the absolute values of the components of \(x\) and \(\lambda\) is the regularization parameter.

More specifically for the gradient-based adaptive algorithms, the expression \(J(X) = \left\| {AX - b} \right\|_{2}^{2}\) is called the cost function for the parameter vector \(X = \left[ {x_{1} ,x_{2} \ldots x_{n} } \right]^{\text{T}}\). The general form of the problem formulation of Eq. (3) can be given as:

$$\begin{aligned} \hbox{min} J(X) \hfill \\ {\text{s}} . {\text{t }}\;\left\| X \right\|_{p}^{p} = c \hfill \\ \end{aligned}$$
(4)

Equation (4) imposes a geometric structure to the parameter space and expression \(\left\| X \right\|_{p} = \left( {\sum\nolimits_{i = 1}^{n} {\left| {X_{i} } \right|}^{p} } \right)^{1/p}\) is the \(l_{p}\)-norm of \(X\), where \(1 \le p \le 2\) and defines different geometric structures depending upon the values of \(p\). Another important parameter in Eq. (4), is how the constraint \(c\) is imposed. Throughout the paper, without loss of generality we choose \(c = 1\) and present tangent-vector-based gradient method [20] for the solution of the problem posed in Eq. (4).

To proceed further we define some important parameters of the tangent-vector-based gradient algorithm:

$$g(k) = \mu (k)\frac{{\partial J\left( {{\text{X}}(k)} \right)}}{\partial X}\, = \mu (k)\left[ {\frac{\partial J (x )}{{\partial x_{1} }} \cdots \frac{\partial J (x )}{{\partial x_{n} }}} \right]_{X = X(k)}^{\text{T}}$$
(5)
$$\begin{aligned} h_{g} (k) & = \left( {{\text{I}} - \frac{{V(k)V^{\text{T}} (k)}}{{\left\| {V(k)} \right\|_{2}^{2} }}} \right)g(k) \\ V(k) & = \left[ {\frac{\partial \left\| X \right\|}{\partial X}} \right]_{X = X(k)} \\ \end{aligned}$$
(6)

Geometrically, \(h_{g} (k)\) is tangent to the surface \(\left\| X \right\|_{p}^{p} = 1\) and is called the tangent gradient of \(J(x)\) in the constraint space.

3 Proposed Method

The proposed algorithm solves the convex optimization problem as given in Eq. (4) using tangent-vector-based gradient method [20]. The objective here is to mitigate the interference and noise from the under-sampled data and reconstructing the full resolution data without any artifacts. The flow chart of the proposed algorithm is shown in Table 1.

Table 1 Flow chart of the proposed algorithm for CS-MRI Reconstruction
Full size table

Now we can change the constraint problem of Eq. (4) to an unconstrained form using Lagrangian expression as:

$$\hat{J}(X,\lambda ) = J(X) + \lambda (\left\| X \right\|_{p} )$$
(7)

In Eq. (7) \(J(X) = \left\| {F_{\text{u}} X - Y} \right\|_{2}^{2}\) is the cost function and \(\left\| X \right\|_{p} = \left\| {\psi X} \right\|_{1}\) is the \(l_{1}\)-norm constraint in any sparse domain. The solution of Eq. (7) can be written as:

$$X(k + 1) = X(k) + \left( {{\text{I}} - \frac{{V(k)V(k)^{\text{T}} }}{{\left\| {V(k)} \right\|_{2}^{2} }}} \right)g(k)$$
(8)

In Eq. (8) \(g(k) = \mu (k)\frac{\partial J(X(k))}{\partial X}\) and \(V(k) = \left[ {\frac{\partial \left\| X \right\|}{\partial X}} \right]_{X = X(k)}\)

For illustration purpose 1-D sparse signal is reconstructed using the proposed tangent-vector-based gradient algorithm. As is evident from Fig. 1 that the resulting reconstructed coefficients are often slightly smaller than the original signal. This coefficient shrinkage can be improved if the reconstruction consistency in the cost function can be made smaller.

Fig. 1
figure 1

Reconstruction of the sparse 1-D signal using the proposed method

Full size image

Proof

The mathematical derivation of the final updated vector can be calculated using projections as shown in Fig. 2. From Fig. 2 the updated vector is given as:

$$X(k + 1) = X(k) + g_{\text{T}} (k)$$
(9)
Fig. 2
figure 2

Geometrical interpretation of the updated vector using projections

Full size image

where \(g_{\text{T}} (k)\) is the component of \(g(k)\) which is tangential to the surface \(\left\| X \right\|_{p}^{p} = C\) and the component of \(g(k)\) or \(g(t)\) in the direction of \(v(t)\) or \(v(k)\) which is perpendicular to the tangential vector \(\frac{\text{d}}{{{\text{d}}t}}X(t)\) and can be obtained using projections as given in Eq. (10):

$$\begin{aligned} g_{v} (k) & = \left\| g \right\|\cos \theta \frac{v(k)}{{\left\| {v(k)} \right\|}} \\ & & { = }\left\| g \right\|\frac{{g(k)^{\text{T}} v(k)}}{\left\| g \right\|\left\| v \right\|}\frac{v(k)}{{\left\| {v(k)} \right\|}} \\ & { = }\left( {\frac{{g(k)^{\text{T}} v(k)}}{{\left\| {v(k)} \right\|^{2} }}} \right)v(k) \\ \end{aligned}$$
(10)

Now using the fact that, \(g(k) = g_{v} (k) + g_{\text{T}} (k)\) and substituting the expression from Eq. (10) into Eq. (9) we get the following updated expression:

$$\begin{aligned} X(k + 1) & = X(k) + g_{\text{T}} (k) \\ \, & = X(k) + g(k) - g_{v} (k) \\ \, & = X(k) + g(k) - \left( {\frac{{g(k)^{\text{T}} v(k)}}{{\left\| {v(k)} \right\|^{2} }}} \right)v(k) \\ \, & = X(k) + g(k) - \left( {\frac{{v(k)v(k)^{\text{T}} }}{{\left\| {v(k)} \right\|^{2} }}} \right)g(k) \\ & X(k + 1) = X(k) + \left( {{\text{I}} - \frac{{V(k)V(k)^{\text{T}} }}{{\left\| {V(k)} \right\|_{2}^{2} }}} \right)g(k) \\ \end{aligned} .$$
(11)

The proposed tangent-vector-based gradient method is an iterative method in the parameter space for obtaining the desired solution. In each iteration, the algorithm estimates the missing \(k\)-space values until a satisfactory solution has been found. The input to the proposed algorithm is the under-sampled \(k\)-space data which is directly obtained from the MRI scanner. The algorithm starts (step 1) with an initial guess which is the inverse Fourier transform of the acquired data (with zero-filling of the non-acquired data points) obtained from the scanner. The gradient of the cost function (step 2) is calculated at each iteration as given below:

$$\nabla J(X) = 2F_{\text{u}}^{\text{T}} (F_{\text{u}} X - Y)$$
(12)

The right hand side of Eq. (12) tells how the gradient of the cost function plays its role in the reconstruction process. At every step of the algorithm, the actual image estimate \(X\) is transformed into the frequency domain using the Fourier transform operator \(F_{\text{u}}\) [10]. These transformed data are then compared with the measured data \(Y\) by calculating the difference. If the difference is small, then the estimate best fits the measured data, otherwise the residuum contains significant values. If the residuum is large, then the algorithm needs to know how to modify the image estimate to the best estimate in the frequency domain. This information is obtained by transforming the \(k\)-space data back to the image domain using inverse Fourier transform operator \(F_{\text{u}}^{\text{T}}\). The \(l_{1}\)-norm minimization of the regularization term in the wavelet domain is performed (step 3) which promotes sparsity. The final updated vector is calculated in step 4.

The stopping criterion of the proposed algorithm (outlined in Table 1) can be a predefined number of iterations or can be a desired fitness value. In this paper, the fitness value approach at \(j\)th iteration has been used for stopping criterion which is calculated through \(\left\| {F_{\text{u}} X_{j} - Y} \right\|_{2}^{2}\).

4 Materials and Methods

The proposed tangent-vector-based gradient method is outlined in Table 1 showing the basic operations involved in the method. The under-sampled k-space data after zero-filling are used as an initial estimate. In the subsequent steps the solution image is continuously updated until the stopping criterion is achieved.

The proposed method was evaluated on different datasets, i.e., simulated data, phantom data, and in vivo human head datasets. All the reconstruction results were obtained in MATLAB (Math works, Natick, MA) on a workstation with 3-GB random-access memory and 2.33 GHz central processing unit. The performance of the proposed algorithm is quantitatively evaluated using artifact power (AP), normalized mean square error (NMSE), and peak signal-to-noise ratio (PSNR) between the reconstructed and the reference images. AP, NMSE, and PSNR provide a combined metric for image artifacts, noise, and loss of resolution.

In this paper, a numerical phantom (256 × 256) was constructed to evaluate the performance of the proposed method. The phantom is piecewise smooth, i.e., most coefficients are exactly zero. Moreover, the simulation is used to show how the algorithm performs with different under-sampling factors and noise. For in vivo images, fully sampled data have been acquired using 1.5 T and 3 T MRI machines. The under-sampling is performed retrospectively on this fully sampled data to simulate the accelerated data acquisitions for different acceleration factors. The proposed method is tested on a scanned phantom image obtained using 1.5 T GE scanner and in vivo images of human head which are acquired from two different volunteers using 1.5 T GE and 3T GE MRI scanners, respectively. The data sets are acquired in all cases with an eight-channel receiver coil wrapped round the phantom and the head. Imaging experiments were performed at St. Mary’s Hospital London by applying Gradient Echo sequence with the following parameters: TE = 10 ms, TR = 500 ms, FOV = 20 cm, bandwidth = 31.25 kHz, slice thickness = 3 mm, flip angle 50°, matrix size = 256 × 256. The datasets used for the reconstructions are shown in Fig. 3.

Fig. 3
figure 3

Shepp-Logan phantom (left), phantom (middle), and human head (right) MR images used in the experiments

Full size image

In the simulation we have used the sampling mask shown in the Fig. 4 (left). Based on the CS requirements and the analysis in the sparse MRI, we have used variable density random under-sampling with denser sampling closer to the center of the \(k\)-space. This has the advantage that it fulfills the incoherent artifact requirement of CS and that the artifacts introduced due to this random under-sampling are noise like. The quantifying metrics used to evaluate the performance of the proposed algorithm include artifact power (AP), normalized mean square error (NMSE), and peak signal-to-noise ratio (PSNR). AP is the square difference error which can be computed as:

Fig. 4
figure 4

Sampling mask (left), under-sampled Shepp-Logan phantom (middle), and reconstructed phantom (right) using the proposed method

Full size image
$${\text{AP}} = \frac{{\mathop \sum \nolimits_{j} \left| {x_{j} - \hat{x}_{j} } \right|^{2} }}{{\mathop \sum \nolimits_{j} \left| {x_{j} } \right|^{2} }}$$
(13)

In Eq. (13) \(\hat{x}_{j}\) is the reconstructed image whereas \(x_{j}\) is the reference image. Mathematical expression for calculating PSNR is given as [19, 21]:

$${\text{PSNR}} = 10.\log_{10} \left\{ {\frac{{{\text{MAX}}_{\text{f}} }}{\text{MSE}}} \right\}$$
(14)

where in Eq. (14) \({\text{MSE}} = \frac{1}{{{\text{M}}x{\text{N}}}}\sum\nolimits_{i = 0}^{M - 1} {\sum\nolimits_{j = 0}^{N - 1} {\left( {\hat{x}(i,j) - x(i,j)} \right)} }^{2}\).

5 Results and Discussion

This paper presents a tangent-vector-based gradient method for CS based recovery of MR images from the under-sampled data. This method calculates the gradient of the cost function which consists of data consistency and sparsity priors. The effectiveness of the proposed method has been validated by successfully recovering the numerical phantom, scanned phantom as well as human head under-sampled datasets for different acceleration factors (AF), i.e., 2×, 3×, 4×, 5×, 8×, and 10×.

Table 2 and Fig. 5 show the reconstruction results for different noise levels at AF = 2 for Shepp-Logan phantom. The proposed method has been validated for higher acceleration factors on scanned phantom and in vivo datasets with different quantifying parameters.

Table 2 Reconstruction results in terms of AP (a) and NMSE (b) for different levels of noise variance for the Shepp-Logan phantom
Full size table
Fig. 5
figure 5

Reconstruction results from a set of simulated eight-channel Shepp-Logan phantom with different level of noise variance (NV) for AF = 2. Left column (NV = 0.00), center column (NV = 0.05), and right column (NV = 0.1). The first row shows the results of the proposed method and the second row shows the results of the standard CG

Full size image

The reconstruction results for the Shepp-Logan phantom are shown in Fig. 5 for different levels of noise added to the measurements for AF = 2. A visual inspection of the results indicates that at all the noise levels, the proposed method and CG both well preserve the fine structures in the image with random noise added on the structures.

Moreover, Table 2a, b provide a quantitative measure for the error in the reconstructed image in terms of AP and NMSE. As expected, both the methods perform better at low noise levels and the results deteriorate gracefully as the noise variance increases at the same acceleration factor (AF = 2). Similarly Table 2 a shows the reconstruction results for both the proposed and CG methods in terms of AP of the Shepp-Logan phantom for different levels of noise variance at AF = 2. The results show that both the methods perform equally well for different noise levels with a slight improvement in terms of NMSE and AP in the proposed method.

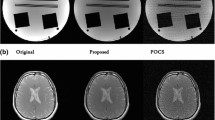
Figure 6 shows the reconstructions from the scanned phantom, axial, and sagittal human head datasets at AF = 2. The results show that both the methods perform equally well in reconstructing the images from the under-sampled data for low acceleration factors (AF = 2). Similarly Fig. 7 shows the performance of the proposed method as compared to CG for different datasets (phantom, axial, and sagittal).

Fig. 6
figure 6

Reconstruction results using the proposed algorithm and standard CG (AF = 2). Left column (original image), center column (proposed algorithm), and right column (standard CG). First row (phantom), second row [axial human head (1.5T)], third row [axial human head (3T)], Fourth row [sagittal human head (3T)]

Full size image
Fig. 7
figure 7

Reconstruction results using the proposed method and standard CG for different datasets in terms of AP with different 1/AF for a phantom, b axial human head (1.5T), c axial human head (3T), and d sagittal human head (3T)

Full size image

Table 3 provides a comparison of the proposed method with standard CG in terms of PSNR and different AF for the phantom and human head images. The results show that the performance of the proposed algorithm is better as compared to the standard CG for both the phantom as well as human head (3T) images.

Table 3 Comparison of the proposed algorithm with standard CG when applied on (a) phantom and (b) human head (3T) in terms of PSNR and AF
Full size table

6 Conclusion

A method based on using the unit-norm constraint in the parameter space is proposed. The results (Tables 2, 3; Fig. 7) show a considerable improvement in the quality of the reconstructed images than the standard non-linear CG method. It has been shown that the proposed tangent-vector-based gradient method acts as an adaptive algorithm providing quality image reconstructions. Future work includes the application and testing of the proposed algorithm for non-Cartesian \(k\)-space sampling trajectories (spiral and radial).