1 Introduction

MRI is a preferable clinical diagnostic imaging technique due to its high-resolution images and high-quality soft-tissue contrast. MRI does not employ ionization radiations which is good for patient’s health. The problem with MR imaging is that its acquisition process is slow, which results in discomfort for the patients. Long scanning time may also degrade the image due to motion during the scanning process.

MRI scanning time is linearly proportional to the number of samples taken in k-space. Compressed sensing is a novel data acquisition technique that exploits sparsity in signals to reconstruct it from a reduced number of samples [1, 2]. MRI naturally fits in as a potential application of CS due to its sparsity either directly or after transformation in well-defined domains, e.g. Finite-Difference domain and Wavelet domain. In compressive sampled, MRI acquisition process, non-Cartesian sampling techniques provide better reconstruction due to its low coherence with the sparsifying domain [3].

Reconstructing high-quality MRI image efficiently from its partially sampled k-space data is the most challenging part in CS. There are several reconstruction algorithms that can be used to recover MRI from under-sampled k-space data, which have been briefly reviewed in [4–6].

Recently, iterative shrinkage thresholding (IST) [7] and fast IST [8] algorithms have proved to be very effective in minimizing the mixed \(l_{1} - l_{2}\) cost function of the form:

$${\hat{\mathbf{x}}} = {\mathbf{arg}}_{\varvec{x}} {\mathbf{min}}\left( {\frac{1}{2}||{\mathbf{y}} - {\mathbf{\varPhi x}}||_{2}^{2} + \beta || {\mathbf{x}}||_{{_{1} }} } \right).$$
(1)

The parameter \(\beta \ge 0\) is used as regularizer that defines the sparsity in the estimated solution. \(\varvec{\varPhi}\) is the measurement matrix, \({\mathbf{x}}\) is the sparse signal, and \({\mathbf{y}}\) is the observation vector acquired from random projections. \({\hat{\mathbf{x}}}\) is the estimated signal and operators, \(\varvec{||z||}_{{_{1} }}\) and \(\varvec{||z||}_{{_{2} }}\) are the \(l_{1}\) and \(l_{2}\) norms of vector \(\varvec{z}\), respectively.

This study presents a novel technique to recover MRI from its partial k-space data using the iterative-reweighted least square method [9] with additional data consistency constraint. The proposed method was applied on Shepp–Logan phantom image and original human brain MR image, by exploiting their sparsity in the finite-difference domain and wavelet domain, respectively [10]. The performance of non-Cartesian under-sampling schemes, such as radial lines and variable density random sampling, were also compared.

2 Application of CS on Rapid MRI

There are several methods that can be found in the literature to reduce MRI scanning time. One such method is to provide a high gradient amplitude with rapid switching, which results in an undesirable nerve stimulation [11]. Other methods exploit the redundancy in MRI data, such as: multiple receiver coils that reduce the number of acquisitions per scan 0. Scan time can also be reduced by skipping some of the phase encoding lines, which results in a small field of view (FOV) that decreases the signal-to-noise ratio (SNR) [13].

The time taken for MRI scan is linearly proportional to the number of samples acquired during scanning. Compressed sensing is a novel data acquisition technique that exploits sparsity in MRI. CS allows a near perfect recovery of MR image even from lesser number of samples that reduces the scan time significantly. MRI is a suitable application for CS, because MRI scanning involves sampling in k-space rather than pixel-by-pixel data acquisition. For the accurate recovery of the signal using CS, signal has to be sparse in some domain. This condition is fulfilled by MRI as it is sparse either directly or in well-defined domains, i.e., finite-difference domain and wavelet transform domain.

The sampling patterns of MRI can be Cartesian or non-Cartesian. Cartesian sampling scheme is conventionally used in MRI, where samples are taken in equispaced lines and a simple inverse Fast Fourier transform (IFFT) can be used to reconstruct the fully sampled MR image. Unlike Cartesian sampling, non-Cartesian sampling techniques provide freedom to choose from several sampling patterns, such as radial lines, spirals, and variable density random sampling. Non-Cartesian sampling techniques are particularly useful for CS due to less coherence with sparsifying transform [3, 13], which directly impact the least number of samples required for accurate reconstruction. Low coherence means that a few samples are required for accurate reconstruction of MR image. In radial sampling scheme, the samples are taken along the uniformly angular spaced lines, passing through the origin of k-space. In variable density sampling scheme, nearly, all the samples are taken near the origin in k-space, while sampling sparsely away from the origin as most energy of the image is concentrated closer to the origin in k-space [3].

3 Recovery Methods

Several recovery techniques can be utilized for recovery of MRI from partial k-space data. These methods vary in terms of either their specific sampling pattern or recovery technique.

3.1 Linear Reconstruction Techniques

Zero Filling (ZF) is a simple MRI recovery method that gives freedom to choose any sampling pattern for under-sampling in k-space, while missing k-space data are filled with zeros. The image is simply reconstructed using inverse fast Fourier transform.

Low Resolution (LR) is another under-sampling technique with fixed sampling pattern. Only centric k-space data are acquired, leaving the rest of the space unsampled, and then, image is reconstructed using IFFT. This technique recovers smooth region in the image accurately, but sharp edges in the image are not recovered properly.

3.2 Project onto Convex Set Algorithm

Project onto Convex Set (POCS) is an iterative algorithm to recover MR image from under-sampled k-space data [12] (Fig. 1). In POCS method, all the constraints onto an image recovery problem can be mapped on convex sets in a Hilbert space consisting of all possible images. To reconstruct an image, all we need to do is to find a point of intersection of all the convex sets in a Hilbert space defined by a priori information. POCS is very effective in solving mixed \(l_{1} - l_{2}\) convex optimization problem in the following equation:

$${\hat{\mathbf{x}}} = \mathop {{\mathbf{arg}}_{\varvec{x}} {\mathbf{min}}}\limits_{{}} ||{\varvec{\Psi}}\varvec{x||}_{1} \varvec{ }\quad {\text{subject }}\;{\text{to }}\quad ||\varvec{F}_{\varvec{u}} \varvec{x} - \varvec{y||}_{2}^{2} < v ,$$
(2)

where \({\varvec{\Psi}}\) represents the sparsifying transform, e.g,. wavelet transform, \(\varvec{F}_{\varvec{u}}\) is the partial Fourier transform, and \(\varvec{x}\) represents the recovered image. The parameter \(v\) is set subject to the noise level and \(\varvec{||z||}_{1} = \mathop \sum \limits_{\varvec{j}} |z_{j} |\) is the \(l_{1}\) norm of vector \(\varvec{z}\) that tends to promote sparsity. A modified POCS has also been proposed for MRI recovery in [14].

Fig. 1
figure 1

POCS algorithm for MRI recovery from partial Fourier data

Full size image

3.3 Separable Surrogate Functional

Separable Surrogate Functional (SSF) algorithm belongs to the family of iterative shrinkage algorithms. IST algorithms are simple in structure but highly effective in recovering sparse signals by minimizing the mixed \(l_{1} - l_{2}\) objective function in the following [13]:

$$f\left( \varvec{x} \right) = \frac{1}{2}||\varvec{F}_{\varvec{u}} \varvec{x} - \varvec{y||}_{2}^{2} + \beta ||{\varvec{\Psi}}\varvec{x}\text{||}_{1} \text{ }\text{.}$$
(3)

Iterative shrinkage algorithms use shrinkage function \(\varvec{x}_{\text{opt}} = \varvec{S}_{\varvec{\beta}} (\varvec{\alpha})\), which maps the input α to output \(\varvec{x}_{\text{opt}}\). The values below the threshold T are mapped to zero (\(\text{(}\varvec{S}_{\varvec{\beta}} \left(\varvec{\alpha}\right) = 0\varvec{ }\quad {\text{for}}\quad \varvec{ }\left|\varvec{\alpha}\right| < T)\) and those values which are outside this threshold T are shrunk [15]. Each iteration includes a shrinkage step and multiplication by sensing matrix \(\varvec{F}_{\varvec{u}}\) and its transpose \((\varvec{F}_{\varvec{u}}^{\varvec{T}} )\). Iterative shrinkage algorithms are known for their simplicity, yet highly effective in minimizing the problem in Eq. (1) [16]. Separable surrogate functional (SSF) [17], Fast IST algorithm (FISTA) [18], Parallel Coordinate Descent (PCD) [15], and Iterative-Reweighted Least Squares (IRLS) algorithm [10] are some of the iterative shrinkage algorithms. Recently, PCD and SSF have been used with the genetic algorithm (GA) [19] and differential evolution (DE) to speed up the convergence of the sparse reconstruction problem [20].

The SSF algorithm was developed by Daubechies et al. [17] by adding the following function to objective function in Eq. (3)

$$d\left( {\varvec{x},\varvec{x}_{0} } \right) = \frac{c}{2}\varvec{||x} - \varvec{x}_{0} ||_{2}^{2} - \frac{1}{2}||\varvec{F}_{\varvec{u}} \varvec{x} - \varvec{F}_{\varvec{u}} \varvec{x}_{0} ||_{2}^{2} ,$$
(4)

where \(c\) is chosen to make function \(d (.)\) strictly convex; thereby, its Hessian should be positive-definite, i.e., \(c{\mathbf{I}} - \varvec{F}_{\varvec{u}}^{{\mathbf{T}}} \varvec{F}_{\varvec{u}} > 0\), which can be satisfied, if \(c > ||\varvec{F}_{\varvec{u}}^{\varvec{T}} \varvec{F}_{\varvec{u}} ||_{2} = \beta_{ \hbox{max} } (\varvec{F}_{\varvec{u}}^{{\mathbf{T}}} \varvec{F}_{\varvec{u}} )\). Recently, Combettes and Wajs [21] have proved that \(c > 0.5\beta_{ \hbox{max} } (\varvec{F}_{\varvec{u}}^{{\mathbf{T}}} \varvec{F}_{\varvec{u}} )\) for guaranteed convergence of SSF algorithm.

The optimal solution can be found by following shrinkage function:

$$\varvec{x}_{\text{opt}} = \varvec{S}\left( {\varvec{u}_{0} } \right) = \varvec{S}\left( {\frac{1}{c}\varvec{F}_{\varvec{u}}^{\varvec{T}} \left( {\varvec{y} - \varvec{F}_{\varvec{u}} \varvec{x}_{0} } \right) + \varvec{x}_{0} } \right).$$
(5)

Surrogate function is used to achieve minimization of cost function in Eq. (3) iteratively. The sequence of solutions that is produced iteratively is proved convergence to the local minima of objective function in Eq. (3). The resulting iterative process can be written as follows:

$$\varvec{x}_{k + 1} = \varvec{S}\left( {\frac{1}{c}\varvec{F}_{\varvec{u}}^{\varvec{T}} \left( {\varvec{x} - \varvec{F}_{\varvec{u}} \varvec{x}_{\varvec{k}} } \right) + \varvec{x}_{\varvec{k}} } \right).$$
(6)

The above-mentioned method can be described as proximal-point algorithm in optimization theory. The function \(d\left( {\varvec{x},\varvec{x}_{0} } \right)\) calculates the difference from previous solution. The directions \(\varvec{x} - \varvec{x}_{0}\)that are near null-space of \(\varvec{F}_{\varvec{u}}\), the distance is nearly Euclidean, \(0.5 c||\varvec{x} - \varvec{x}_{0} ||_{2}^{2}\) and those directions that are spanned by \(\varvec{F}_{\varvec{u}}\), the distance become closer to zero. Therefore, the function \(d\left( {\varvec{x},\varvec{x}_{0} } \right)\) limits the solutions in a range, which help us in achieving our goal of minimizing the objective function in Eq. (3) [15]. Figure 2 shows the SSF algorithm in detail.

Fig. 2
figure 2

Separable surrogate functional algorithm description

Full size image

3.4 Iterative-Reweighted Least Square

Iterative-reweighted least square (IRLS) is one of the algorithms that belong to iterative shrinkage thresholding (IST) algorithms family of algorithms. IST algorithms are simple in structure but highly effective in recovering sparse signals by minimizing the mixed \(l_{1} - l_{2}\) objective function in Eq. (3) [13]. Figure 3 shows the IRLS method in detail.

Fig. 3
figure 3

Brief description of iterative-reweighted least square

Full size image

3.5 Algorithms Performance Measures

The performance of various algorithms based on the recovered image and the original image can be measured using various methods. Structural Similarity (SSIM) index was proposed by Wang et al. [23]. SSIM index closer to one means two images are closely matched, whereas SSIM index closer to zero means that the recovered image is poorly matched.

Artifact Power (AP) is another performance measure to judge the accuracy of the recovered image. It is derived from square difference error, which can be calculated using Eq. (7). Smaller AP means better image recovery

$${\text{AP = }}\frac{{\sum\nolimits_{i} {|x(i) - \hat{x}(i)|^{2} } }}{{\sum\nolimits_{i} {|x(i)|^{2} } }}.$$
(7)

Improved signal-to-noise ratio (ISNR) is another parameter for measuring the recovered image quality [15]. ISNR can be evaluated using Eq. (8). Higher value of ISNR means that the recovered image is of better quality

$${\text{ISNR}} = 10 \cdot \log_{10} \left\{ {\frac{{\varvec{||x} - |\varvec{F}_{\varvec{u}} \varvec{x}|||_{2}^{2} }}{{\hat{\varvec{x}} - \varvec{x}_{2}^{2} }}} \right\} [{\text{dB}}].$$
(8)

Peak signal-to-noise ratio (PSNR) is the ratio between the maximum pixel value of an image and the power of the recovered image [24]. It is a popular metric used to measure the fidelity of the image. Higher value means better image recovery. It can be calculated using the following equation:

$${\text{PSNR}} = 20 \cdot \log_{10} \left\{ {{\text{Max}}(\varvec{X})} \right\} - 10 \cdot \log_{10} \left\{ {\frac{1}{mn}\mathop \sum \limits_{i} \mathop \sum \limits_{j} (\varvec{X}(i,j) - \hat{\varvec{X}}(i,j))^{2} } \right\}\; [{\text{dBs}}].$$
(9)

Fitness is another parameter that can be used to evaluate the recovered image. Fitness at each iteration can be calculated by \(||\varvec{F}_{\varvec{u}} \varvec{x}_{\varvec{i}} - \varvec{y||}_{2}^{2}\) or \(||\varvec{x}_{\varvec{i}} - \varvec{x}_{{\varvec{i} - 1}} ||_{2}^{2}\). Smaller value of fitness means better quality of the recovered image. Correlation is a statistical parameter to show the relationship between the original image and the recovered image. Correlation value closer to 1 means the two images are closely matched. It can be found using equation \(\rho_{X,Y} = \frac{{{\text{cov}}(X,Y)}}{{\sigma_{X} \sigma_{Y} }}\), where \({\text{cov}}\left( {X, Y} \right)\) is the covariance between \(X\) and \(Y\), and \(\sigma_{X} , \sigma_{Y}\) are the standard deviations of the images X and Y, respectively.

4 The Proposed Algorithm

The proposed algorithm is inspired by the Iterative-Reweighted Least Square (IRLS) method and the data consistency constraint in POCS algorithm. The IRLS algorithm is used frequently in convex optimization problems. IRLS has proved its utility in finding the maximum likelihood functions of generalized linear model. IRLS minimizes a weighted residual rather than minimizing the l 2 norm [16]. Non-l 2 norms are converted into l 2 ones using weighting by IRLS [22]. In Eq. (1), \(||x||_{1}\) is replaced by \(0.5\varvec{x}^{T} \varvec{W}^{ - 1} \left( \varvec{x} \right)\varvec{x}\), where \(\varvec{W}(\varvec{x})\) is a diagonal matrix, comprising of \(\varvec{W}\left[ {k,k} \right] = 0.5\varvec{x}\left[ k \right]^{2} /||\varvec{x}||_{1}\) values in its diagonal. The objective function in Eq. (1) can be rewritten as:

$$f\left( \varvec{x} \right) = 0.5||\varvec{y} - \varvec{F}_{\varvec{u}} \varvec{x||}_{2}^{2} + 0.5\beta \varvec{x}^{T} \varvec{W}^{ - 1} \left( \varvec{x} \right)\varvec{x}\text{.}$$
(10)

The solution \(\varvec{x}_{0}\) is updated, by assuming fixed W to minimize the quadratic function:

$$\nabla f\left( \varvec{x} \right) = - \varvec{F}_{\varvec{u}}^{{\mathbf{T}}} \left( {{\mathbf{y}} - \varvec{F}_{\varvec{u}} {\mathbf{x}}} \right) + \beta \varvec{x}^{T} \varvec{W}^{ - 1} \left( \varvec{x} \right)\varvec{x} = 0,$$
(11)

where x is updated by taking inverse of matrix: \({\mathbf{F}}_{\varvec{u}}^{{\mathbf{T}}} {\mathbf{F}}_{\varvec{u}} + \beta {\mathbf{W}}^{ - 1}\), then \(\varvec{W}\) is updated using the new solution.

IRLS performed poorly for large images [15]. To overcome this drawback, the above-mentioned algorithm was modified by Adeyemi and Davies [10] resulting in another iterative shrinkage algorithm by adding and subtracting c x from Eq. (13). The resulting iterative shrinkage update equation is given below:

$$\varvec{x}_{k + 1} = \left( {\frac{\beta }{c}\varvec{W}^{ - 1} (\varvec{x}_{k} ) + \varvec{I}} \right)^{ - 1} \left( {\frac{1}{c}\varvec{F}_{\varvec{u}}^{{\mathbf{T}}} {\mathbf{y}} - \frac{1}{c}(\varvec{F}_{\varvec{u}}^{{\mathbf{T}}} \varvec{F}_{\varvec{u}} - {\text{c}}{\mathbf{I}}){\mathbf{x}}_{{\mathbf{k}}} } \right)\; = \;\varvec{S}. \left( {\frac{1}{c}\varvec{F}_{\varvec{u}}^{{\mathbf{T}}} ({\mathbf{y}} - \varvec{F}_{\varvec{u}} {\mathbf{x}}_{{\mathbf{k}}} ) + {\mathbf{x}}_{{\mathbf{k}}} } \right),$$
(12)

where diagonal matrix \(\varvec{S} = \left( {\frac{\beta }{c}\varvec{W}^{ - 1} (\varvec{x}_{k} ) + \varvec{I}} \right)^{ - 1} = \left( {\frac{\beta }{c}\varvec{I} + \varvec{W}(\varvec{x}_{k} )} \right)^{ - 1} \varvec{W}(\varvec{x}_{\varvec{k}} )\) plays the role of shrinkage on the values of \(\frac{1}{c}\varvec{F}_{\varvec{u}}^{{\mathbf{T}}} ({\mathbf{y}} - \varvec{F}_{\varvec{u}} {\mathbf{x}}_{{\mathbf{k}}} ) + {\mathbf{x}}_{{\mathbf{k}}}\). Each entry is multiplied by a scalar value \(\frac{{0.5x_{k} [i]^{2} /x_{1} }}{{\frac{\beta }{c} + 0.5x_{k} [i]^{2} /x_{1} }} = \frac{{x_{k} [i]^{2} }}{{\frac{2\beta }{c}x_{1} + x_{k} [i]^{2} .}}\)

When the value of \(x_{k} [i]\) is large, the above factor becomes one, and for small values of \(x_{k} [i]\), its value approaches zero, similar to the way shrinkage works. The relaxation constant \(c \ge 1\) should be chosen as \(c > \lambda_{ \hbox{max} } (\varvec{\varPhi}^{\varvec{T}}\varvec{\varPhi})/2\) to ensure convergence of matrix S, where \(\lambda_{ \hbox{max} }\) is the maximum eigenvalue of the matrix.

The proposed algorithm is initialized by zero filling the missing k-space data. Then, the missing k-space data are synthesized by back-projection and soft-thresholding iteratively. As human brain MR image is sparse in wavelet domain, shrinkage operation is performed in wavelet domain. To reconstruct the MRI accurately, the proposed algorithm efficiently minimizes the objective function in Eq. (13). Figure 4 shows the proposed algorithm in detail

$$f\left( \varvec{x} \right) = \frac{1}{2}||\varvec{F}_{\varvec{u}} \varvec{x} - \varvec{y||}_{2}^{2} + \beta ||{\varvec{\Psi}}\varvec{x||}_{1} .$$
(13)
Fig. 4
figure 4

Brief description of the proposed algorithm for MRI recovery

Full size image

5 Simulation Results and Discussion

The performance of the proposed algorithm was validated by nearly perfect recovery of Shepp–Logan phantom image and the original human brain MR data. The human brain data were acquired using 1.5 Tesla GE HDxt MRI scanner with a gradient echo sequence and eight-channel head coil with the following parameters: \({\text{FOV}} = 20\; {\text{cm}}\), \({\text{TR}} = 55\), \({\text{TE}} = 10\; {\text{ms}}\), \({\text{bandwidth}} = 31.25 \;{\text{KHz}}\), \({\text{slice }}\;{\text{thickness}} = 3\; {\text{mm,}}\) \({\text{flip }}\;{\text{angle}} = 90{^\circ }\), \({\text{matrix}}\; {\text{size}} = 256\; \times \;256\) at St. Mary’s Hospital London. The size of the Shepp–Logan phantom image is \(256\; \times \;256\).

Both the data sets were fully sampled at the time of data acquisition and are under-sampled later by taking only 25 % of the samples in k-space using variable density random sampling as well as radial lines sampling schemes. The performance of the variable density random sampling and radial lines schemes performance are compared, keeping the same number of samples. The proposed IRLS with data consistency constraint algorithm exploits the sparsity of MR image in wavelet domain and the sparsity of the phantom image in finite-difference domain to apply shrinkage operation.

The proposed algorithm was compared with ZF, LR, POCS, IRLS, and SSF. The parameters set for comparison are fixed number of iterations = 10, IRLS parameter \(c = 100\), and the thresholding shrinkage operator β that was tuned to optimize the performance of POCS and the proposed algorithm.

Figure 5 shows the recovery of the phantom image when under-sampled using variable density random sampling scheme. Figure 5 a shows the recovery of the phantom image using ZF, LR, IRLS, POCS, and the proposed method. The image recovered by the proposed method subjectively looks better than other recovered images. Figure 5b shows the sampling pattern for each algorithm. LR has centric ordered data in k-space, while other algorithms have variable density random sampling scheme. Figure 5c shows the magnified difference between original image and recovered images. ZF performed poorly, while LR was not able to extract edges accurately. The simple IRLS and SSF algorithms are inefficient compared with the proposed algorithm. The error in the proposed method is far less as compared with POCS.

Fig. 5
figure 5

Recovery of the phantom image using various reconstruction methods

Full size image

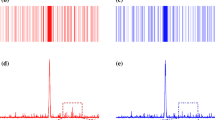
Figure 6 shows the efficiency of the proposed method graphically as compared with POCS when applied on phantom image. The under-sampling has been performed using variable density random sampling scheme. Figure 6a shows the ISNR of POCS and the proposed algorithm. The results show that an improvement in ISNR has been achieved using the proposed method. Figure 6b shows the improvement in PSNR when the proposed method is used. Figure 6c shows an increase in SSIM of the recovered image using the proposed algorithm. Figure 6d shows a decrease in the fitness using the proposed method.

Fig. 6
figure 6

Performance comparison of the proposed algorithm and POCS for phantom image

Full size image

Figure 7 shows the recovery of the real human brain MR image using variable density random sampling. Figure 7a shows the MRI reconstruction using different algorithms like ZF, LR, POCS, IRLS, SSF, and the proposed method. Figure 7b exhibits the corresponding sampling patterns of different algorithms. Figure 7c elaborates the difference between the original MRI and the recovered MR images. The results show that ZF performs poorly, LR fails to recover edges accurately in the reconstructed image, and the proposed algorithm has far less error compared with POCS.

Fig. 7
figure 7

Comparison of recovered MRI using different algorithms

Full size image

Figure 8 compares the performance of the proposed algorithm with POCS quantitatively, when applied on under-sampled MR data. The under-sampling has been performed using variable density random sampling pattern. Figure 8a shows the improvement in ISNR achieved by the proposed algorithm. Figure 8b shows the increase in PSNR when compared with POCS. Figure 8c shows an increase in SSIM index by the proposed algorithm when compared with POCS. Figure 8d shows the decrease in fitness of the recovered MR image by the proposed algorithm.

Fig. 8
figure 8

Comparison of the proposed algorithm and POCS in recovering MR image

Full size image

Figure 9 demonstrates the recovery of the MR image using the proposed algorithm for variable density random sampling and radial lines sampling schemes. The quality of the recovered images from both schemes shows the superiority of the variable density random sampling scheme over uniformly angular spaced radial lines sampling technique.

Fig. 9
figure 9

Comparison of the recovered MR image using variable density random sampling and radial sampling schemes

Full size image

Tables 1 and 2 summarize the performance of the different algorithms based on AP and the correlation between recovered and original for the phantom image and the MR image, respectively. The recovered images by the proposed algorithm better accomplish the minimum AP and maximum correlation with the original phantom image and the original MRI data. The value of β is tuned for the optimal performance of POCS and the proposed algorithm.

Table 1 Comparison of various recovery techniques applied on phantom image
Full size table
Table 2 Comparison of the recovery algorithms when applied on human brain MR data
Full size table

6 Conclusion

This study presents a novel method for the reconstruction of MR image from its partial Fourier data based on CS. The recovery technique is based on the IRLS algorithm with additional data consistency constraints in the k-space. The proposed method applies shrinkage in sparsifying domain iteratively, to minimize the cost function. The missing k-space data, due to under-sampling, are synthesized by soft-thresholding and back-projection. The experimental results demonstrate that the proposed algorithm can faithfully recover the phantom as well as human brain MR data from compressively sampled k-space data. The experimental results prove the superiority of IRLS-based MRI reconstruction method over LR, ZF, IRLS, SSF, and POCS recovery techniques in terms of performance metrics, i.e., PSNR, ISNR, fitness, SSIM, AP, and correlation.