Kinematic Shakedown Analysis for Strain-Hardening Plates with the C¹ Nodal Natural Element Method

Abstract

This paper proposes a novel numerical solution approach for the kinematic shakedown analysis of strain-hardening thin plates using the C¹ nodal natural element method (C¹ nodal NEM). Based on Koiter’s theorem and the von Mises and two-surface yield criteria, a nonlinear mathematical programming formulation is constructed for the kinematic shakedown analysis of strain-hardening thin plates, and the C¹ nodal NEM is adopted for discretization. Additionally, König’s theory is used to deal with time integration by treating the generalized plastic strain increment at each load vertex. A direct iterative method is developed to linearize and solve this formulation by modifying the relevant objective function and equality constraints at each iteration. Kinematic shakedown load factors are directly calculated in a monotonically converging manner. Numerical examples validate the accuracy and convergence of the developed method and illustrate the influences of limited and unlimited strain-hardening models on the kinematic shakedown load factors of thin square and circular plates.

1 Introduction

Thin plate structures are widely used in aerospace, aviation, nuclear energy, shipbuilding and other engineering fields. The precise and reliable computation of the plastic limit-bearing capacity is a very important issue for optimizing the design and safety assessment of thin plate structures under cyclic loading. Compared to traditional linear elastic methods, applying plastic theory to evaluate the bearing capacity of plates not only fully utilizes materials’ plastic properties, but also has important theoretical research and practical application value in terms of reducing costs and saving resources. Shakedown analysis is a significant branch of plastic mechanics that provides a direct and effective method for investigating the structural plastic failure load under repeated loading, without involving the load change history needed in elastic–plastic incremental analysis, and is just connected to the applied external load and structure’s material characteristics. Koiter’s theorem [1] (kinematic or upper bound theorem) and Melan’s theorem [2] (static or lower bound theorem) are two fundamental theories of shakedown analysis, where the kinematically admissible strain field is modified to solve the minimum shakedown load in the former, and the statically admissible residual stress field is optimized to calculate the maximum shakedown load in the latter. The obtained shakedown loads are important parameters that truly reflect the safety margin of structures and have already been used in many design codes and regulations of engineering structures [3].

Up to now, theoretical researches and engineering applications of shakedown analysis have progressed significantly. However, investigations of shakedown analysis for thin plates remain relatively scarce compared to their limit analysis. Theoretical and experimental works have been limited by structural geometry, boundary conditions, loading characteristics, etc., and few achievements have been reported. Notable studies include those by Li et al. [4], Chinh [5, 6], and Yu et al. [7]. With the rapid development of computer technologies and numerical calculation methods, some scholars have combined mature numerical methods with mathematical programming theorems of shakedown analysis, focused on developing highly efficient optimization algorithms and excellent numerical solution procedures, and published some interesting and remarkable findings. Such works include investigations by Qian and Wang [8], Atkociunas et al. [9], Tran [10], Zheng et al. [11], Blazevicius et al. [12], and Zhou et al. [13]. However, these studies have not considered the strain-hardening of materials in the shakedown analysis for plates. In fact, many metals and alloys exhibit obvious strain-hardening properties. The shakedown load is sometimes influenced by taking into account the material’s strain-hardening effect, and the conservative shakedown load may be obtained when ignoring strain-hardening. Relevant studies include those of Feng and Liu [14], Zhang [15], Xu [16], Simon [17], Ma et al. [18] and Peng et al. [19]. Thus, it is necessary to further develop excellent solution algorithms using accurate and efficient numerical methods and adopt them to study the influence of material’s strain-hardening on the shakedown failure loads of plates.

The C¹ natural element method (C¹ NEM) [20] is a unique and fascinating meshless method derived from the natural element method (NEM) [21], which does not require complex matrix operations, only relies on scattered nodal information without nodal mesh data or artificial parameters and has been successfully applied to study the limit and shakedown analyses of thin plates [13, 22, 23]. While the background integration carried out over each Delaunay triangle in the NEM and C¹ NEM provides high accuracy and stability, it also carries the drawbacks of a tremendous amount of computation and inconvenient post-processing, so it is considered to be far from the optimal selection. The stabilized conforming nodal integration (SCNI) with strain smoothing stabilization proposed by Chen et al. [24] effectively overcomes the shortcomings of background integration used in the NEM, and Zhou [25] adopted the nodal NEM [26] with SCNI and Sibson interpolation to obtain accurate upper bound shakedown load multipliers for elastic-perfectly plastic plane structures. Base on the sub-domain stabilized conforming integration (SSCI) developed from SCNI by Wang and Chen [27] for numerical analysis of thin plates, Zhou [28] further proposed the triangular sub-domain stabilized conforming nodal integration (TSNI) scheme and applied the numerical method named C¹ nodal NEM combining advantages of TSNI and C¹ shape functions to study linear elastic analysis of thin plates. The exact numerical results obtained imply that the C¹ nodal NEM is also ideal for kinematic shakedown analysis of strain-hardening thin plates.

This paper proposes an innovative numerical solution method using the C¹ nodal NEM for kinematic shakedown analysis of strain-hardening thin plates. Based on Koiter’s theorem and the von Mises and two-surface yield criteria, the associated mathematical programming formulation is established. The C¹ nodal NEM is used to discretize this formulation, in which the C¹ shape functions are utilized to approximate the trail function of residual displacement increment, and the TSNI scheme is adopted for numerical integration. Time integration involves treating the generalized plastic strain increment at each load vertex, and the nonlinear mathematical programming formulation is linearized and solved directly by revising the objective function and equality constraints iteratively. Ultimately, the accuracy and convergence of the proposed method are demonstrated through numerical examples, and the influences of limited and unlimited strain-hardening models on the kinematic shakedown load factors of thin square and circular plates are illustrated.

2 Kinematic Shakedown Analysis Based on the Two-Surface Yield Criterion

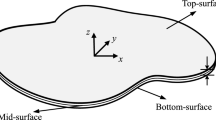
Suppose the studied thin plate described with problem domain $\varOmega = S \times h_{0}$ and displacement boundary $\varGamma_\text{u}$ satisfies the Kirchhoff assumption, where the mid-plane $S$ is set to coincide with the $xy$-plane and perpendicular to the $z$-axis, and $h_{0}$ stands for the thickness of plate. The classic kinematic shakedown theorem (Koiter’s theorem) is expressed as [3, 13, 25]: If there exists a kinematically admissible strain rate cycle that causes the external work rate from imposed loads to exceed the structural plastic dissipation work rate, shakedown does not occur. Accordingly, this paper establishes the following mathematical programming formulation for the kinematic shakedown analysis of strain-hardening plates [13, 28]:

$$ s = \mathop {\min }\limits_{{\dot{\varvec{\kappa }}^{\rm{p}} }} \int_{0}^{T} {\int_{\varOmega } {D\left( {\dot{\varvec{\kappa }}^{\rm{p}} } \right){\text{d}}\varOmega } } {\text{d}}t $$

(1)

$$ \int_{0}^{T} {\int_{\varOmega } {\varvec{\rm M}^{{\rm{eT}}} \dot{\varvec{\kappa }}^{\rm{p}} {\text{d}}\varOmega } } {\text{d}}t = {1} $$

(2)

$$\Delta {\varvec{\kappa}}^{\rm{p}} = \int_{0}^{T} {\dot{\varvec{\kappa }}^{\rm{p}} {\text{d}}t} = \tilde{\varvec{B}}\left( {\Delta {\varvec{a}}} \right)\;\;\;\;{\text{in}}\quad \varOmega $$

(3)

$$\Delta {\varvec{a}} = \int_{0}^{T} {\dot{\varvec{a}}{\text{d}}t} \quad {\text{in}}\quad \varOmega $$

(4)

$$\Delta {\varvec{a}} = 0\quad {\text{on}}\quad \varGamma_{{\text{u}}} $$

(5)

where $s$ is the kinematic shakedown load factor, $T$ means the loading cycle time, $\dot{\varvec{\kappa }}^{\rm{p}}$ represents the vector of generalized plastic strain rate, and $D\left( {\dot{\varvec{\kappa }}^{\rm{p}} } \right)$ denotes the plastic dissipation work rate. According to the von Mises yield criterion, and using the two-surface yield criterion to control the yield surface and the movement of its center, $D\left( {\dot{\varvec{\kappa }}^{\rm{p}} } \right)$ can be written as [15, 16]:

$$ D\left( {\dot{\varvec{\kappa }}^{\rm{p}} } \right) = M_{{\text{P}}} \sqrt {\left( {\dot{\varvec{\kappa }}^{\rm{p}} } \right)^{\rm{T}} {\varvec{Q}}^{ - 1} \dot{\varvec{\kappa }}^{\rm{p}} } + h_{{\text{P}}} \sqrt {\left( {\Delta {\varvec{\kappa}}^{{\text{p}}} } \right)^{\rm{T}} {\varvec{Q}}^{ - 1} \left( {\Delta {\varvec{\kappa}}^{{\text{p}}} } \right)} $$

(6)

In Eqs. (1)–(6), $\varvec{\rm M}^{\rm{e}}$ stands for the vector of virtual generalized pure elastic stress field produced by the independently variable external applied load ${{\varvec{P}}}$, $\Delta {\varvec{\kappa}}^{{\text{p}}}$ and $\Delta {\varvec{a}}$, respectively, represent the vectors of generalized plastic strain increment and residual displacement increment generated after one loading cycle during the time interval $t \in \left[ {0, \, T} \right]$, $\tilde{\varvec{B}}$ denotes the generalized strain–displacement relationship matrix, $\dot{\varvec{a}} = \left\{ {\begin{array}{*{20}c} {\dot{w}} & {\dot{\theta }_{x} } & {\dot{\theta }_{y} } \\ \end{array} } \right\}^{\rm{T}}$ stands for the vector of kinematically admissible displacement velocity field, and $\dot{w}$, $\dot{\theta }_{x} = \dot{w}_{{,x}}$ and $\dot{\theta }_{y} = \dot{w}_{{,y}}$, respectively, mean the rate of deflection, and the rates of rotation in the $x$- and $y$-directions. $M_{{\text{P}}} = Yh_{0}^{2} /4$ represents the plastic limit bending moment and $h_{{\text{P}}} = \tilde{h}h_{0}^{2} /4$, $Y$ denotes the yield stress of material, $\tilde{h}$ is the material’s hardening limit, ${\varvec{Q}}$ means a positive-definite symmetric constant matrix, and its inverse matrix is ${\varvec{Q}}^{ - 1} = 2{\varvec{D}}\rm{/}3$, where ${\varvec{D}}$ denotes a constant matrix introduced to deal with the plastic incompressibility condition [13, 22].

Equation (1) defines the objective function of this nonlinear minimization problem with time integration, which satisfies the equality constraints named normalization, geometric compatibility, cumulative displacement and displacement boundary conditions in Eqs. (2)–(5), respectively. In Eqs. (1)–(5), the classic assumptions of small deformation, constant elastic modulus and quasi-static loading are adopted.

3 C¹ Nodal Natural Element Method

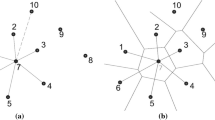
The C¹ nodal natural element method (C¹ nodal NEM) proposed and named by Zhou [28] is a recent variant of the C¹ NEM [20]. This novel numerical method is also based on the Voronoi diagram and Delaunay triangulation of scattered nodes, adopts the Galerkin method to discretize the global system equation, applies a transformation of the C¹ natural neighbor interpolation to approximate the C¹ shape functions and utilizes the TSCI scheme to perform numerical integration. This paper will firstly present the C¹ shape functions and TSCI scheme.

3.1 C¹ Shape Functions

$\textit{NP}$ scattered nodes are used to discretize the mid-plane $S$ of the studied thin plate, and $n$ nodes are searched as the natural neighbor nodes of point ${\varvec{x}} \in {\mathbb{R}}^{2}$ situated on $S$ using the empty circumcircle criterion adopted in the Sibson interpolation [21]. The obtained Sibson shape functions of these $n$ nodes are described as $\begin{array}{*{20}c} {\phi_{1} \left( {\varvec{x}} \right),\phi_{2} \left( {\varvec{x}} \right)}, & \cdots & ,{\phi_{n} \left( {\varvec{x}} \right)} \\ \end{array}$, and ${{\varvec{\Phi} = }}\left( {\begin{array}{*{20}c} {\phi_{1} \left( {\varvec{x}} \right),\phi_{2} \left( {\varvec{x}} \right)} , \cdots , {\phi_{n} \left( {\varvec{x}} \right)} \\ \end{array} } \right)$ is assumed as the natural neighbor coordinate of point ${\varvec{x}}$. Embedding ${{\varvec{\Phi}}}$ in the Bernstein–Bézier representation of a cubic simplex to approximate the C¹ shape functions ${\varvec{\varPsi}}\left( {{\varvec{\Phi}}} \right)$ obtained from the C¹ natural neighbor interpolation, the trial function for deflection $\hat{w}\left( {{\varvec{\Phi}}} \right)$ of the thin plate can be written in the following matrix form [20]:

$$ \hat{w}\left( {{\varvec{\Phi}}} \right) = \sum\limits_{I = 1}^{n} {{\varvec{\varPsi}}_{I} \left( {{\varvec{\Phi}}} \right){\varvec{a}}_{I} } ={\varvec{\varPsi}}^{\rm{T}} \left( {{\varvec{\Phi}}} \right){\varvec{a}} $$

(7)

with the following defined vectors:

$${\varvec{\varPsi}}^{\rm{T}} \left( {{\varvec{\Phi}}} \right) = {\varvec{B}}^{\rm{T}} \left( {{\varvec{\Phi}}} \right){\varvec{T}} $$

(8)

$$ {\varvec{a}} = \left[ {\begin{array}{*{20}c} {w_{1} } & {\theta_{1x} } & {\theta_{1y} } & \cdots & {w_{n} } & {\theta_{nx} } & {\theta_{ny} } \\ \end{array} } \right]^{\rm{T}} $$

(9)

$$\begin{aligned}&{\varvec{\varPsi}}^{\rm{T}} \left( {{\varvec{\varPsi}}} \right) = \left[ {\varPsi_{1} \left( {{\varvec{\Phi}}} \right)}\, {\varPsi_{2} \left( {{\varvec{\Phi}}} \right)}\, {\varPsi_{3} \left( {{\varvec{\Phi}}} \right)\,} \cdots\right.\\ &\quad \left.{\varPsi_{{{3}n - 2}} \left( {{\varvec{\Phi}}} \right)\,} {\varPsi_{3n - 1} \left( {{\varvec{\Phi}}} \right)}\, {\varPsi_{3n}\, \left( {{\varvec{\Phi}}} \right)} \right] \end{aligned}$$

(10)

where ${\varvec{B}}\left( {{\varvec{\Phi}}} \right)$ is the column vector of Bernstein–Bézier basis function. ${\varvec{T}}$ stands for the relationship matrix relating the column vector of Bézier ordinates ${\varvec{b}}$ and nodal degrees of freedom ${\varvec{a}}$, and ${\varvec{b}} = {\varvec{Ta}}$. $w_{n} = w\left( {{\varvec{x}}_{n} } \right)$, $\theta_{nx} = w_{{,x}} \left( {{\varvec{x}}_{n} } \right)$, and $\theta_{ny} = w_{{,y}} \left( {{\varvec{x}}_{n} } \right)$, respectively, are the displacement and rotations of node $n$. $\varPsi_{{{3}n - 2}} \left( {{\varvec{\Phi}}} \right)$, $\varPsi_{3n - 1} \left( {{\varvec{\Phi}}} \right)$ and $\varPsi_{3n} \left( {{\varvec{\Phi}}} \right)$, respectively, represent the C¹ shape functions for nodal displacement $w_{n}$, and rotations $\theta_{nx}$ and $\theta_{ny}$ of node $n$.

To evaluate the generalized strain–displacement relationship matrix $\tilde{\varvec{B}}$ in Sect. 3.2, the first-order derivative ${\varvec{\varPsi}}_{{,\alpha }}^{\rm{T}} \left( {{\varvec{\Phi}}} \right)$$\left( {\alpha = x,y} \right)$ of C¹ shape functions ${\varvec{\varPsi}}^{\rm{T}} \left( {{\varvec{\Phi}}} \right)$ is simply required to be calculated, which can be expressed as [20]:

$${\varvec{\varPsi}}_{{,\alpha }}^{\rm{T}} \left( {{\varvec{\Phi}}} \right) = {\varvec{B}}_{{,\alpha }}^{\rm{T}} \left( {{\varvec{\Phi}}} \right){\varvec{T}} $$

(11)

where ${\varvec{B}}_{{,\alpha }} \left( {{\varvec{\Phi}}} \right)$ denotes the first-order derivative of the Bernstein–Bézier basis function ${\varvec{B}}\left( {{\varvec{\Phi}}} \right)$. Further details on calculating and introducing the C¹ shape functions were provided by Sukumar and Moran [20]. The obtained C¹ shape functions possess the Kronecker delta property of nodal function and nodal rotation values, allowing displacement boundary conditions in the C¹ nodal NEM to be treated as easily and precisely as in the finite element method (FEM).

3.2 TSCI Scheme

Based on the principle of Voronoi diagram, the mid-plane $S$ discretized by ${\textit{NP}}$ scattered nodes can be divided into a series of domains $S_{r} \left( {S=\bigcup\nolimits_{r = 1}^{\textit{NP}} {S_{r} } } \right)$, with each $S_{r}$ relating to a node ${\varvec{x}}_{r}$. To ensure numerical precision and stability for the numerical solution problems of thin plates with high-order partial differential equations, each domain $S_{r}$ is further divided into RS nonoverlapping triangular sub-domains $S_{{rs}} \left( {S=\bigcup\nolimits_{r = 1}^{\textit{NP}} {S_{r} } = \bigcup\nolimits_{r = 1}^{\textit{NP}} {\bigcup\nolimits_{s = 1}^{\textit{RS}}} {S_{{rs}} } } \right)$ around node ${\varvec{x}}_{r}$, with each $S_{{rs}}$ relating to a virtual node ${\varvec{x}}_{{rs}}$. The smoothed generalized strain $\tilde{\kappa }_{ij} \left( {{\varvec{x}}_{{rs}} } \right)$ of virtual node ${\varvec{x}}_{{rs}}$ can be written as [27]:

$$ \begin{aligned} \tilde{\kappa }_{ij} \left( {{\varvec{x}}_{{rs}} } \right) & =\frac{1}{{{A}_{{rs}} }}\int_{{S_{{rs}} }} {\kappa_{ij} \left( {{\varvec{x}}_{{rs}} } \right){\text{d}}S} \\ & =\frac{1}{{2{A}_{{rs}} }}\int_{{S_{{rs}} }} {\left\{ {w_{,ij} + w_{,ji} } \right\}{\text{d}}S} \\ & =\frac{1}{{2{A}_{{rs}} }}\int_{{\varGamma_{{rs}} }} {\left\{ {w_{,i} n_{j} + w_{,j} n_{i} } \right\}{\text{d}}\varGamma } \\ \end{aligned} $$

(12)

where $i,j = \left\{ {x,y} \right\}$; $\varGamma_{{rs}}$ and ${A}_{{rs}}$ stand for the boundary and area of triangular sub-domain $S_{{rs}}$, respectively, and $n_{i}$ denotes the unit outward normal of boundary $\varGamma_{{rs}}$.

Substituting the trial function of deflection $\hat{w}\left( {{\varvec{\Phi}}} \right)$ in Eq. (7) into Eq. (12), the vector of smoothed generalized strain $\tilde{\varvec{\kappa }} \left( {{\varvec{x}}_{{rs}} } \right)$ can be calculated as:

$$ \tilde{\varvec{\kappa }} \left( {{\varvec{x}}_{{rs}} } \right) = \sum\limits_{I = 1}^{{\overline{np} }} {\tilde{\varvec{B}}_{I} \left( {{\varvec{x}}_{{rs}} } \right)} \varvec{ a}_{I} $$

(13)

$$ \tilde{\varvec{\kappa }} \left( {{\varvec{x}}_{{rs}} } \right)=\left[ {\begin{array}{*{20}c} {\tilde{\kappa }_{x} \left( {{\varvec{x}}_{{rs}} } \right)} & {\tilde{\kappa }_{y} \left( {{\varvec{x}}_{{rs}} } \right)} & {{2}\tilde{\kappa }_{xy} \left( {{\varvec{x}}_{{rs}} } \right)} \\ \end{array} } \right]^{\rm{T}} $$

(14)

$$ \begin{aligned} & \tilde{\varvec{B}}_{I} \left( {{\varvec{x}}_{{rs}} } \right) \hfill \\ &\quad= - \frac{1}{{{A}_{{rs}} }}\int_{{\varGamma_{{rs}} }} {\left[ {\begin{array}{*{20}c} {\psi_{{{3}I - \rm{2,}}x} \left( {{\varvec{x}}_{{rs}} } \right)n_{1} } & {\psi_{{{3}I - 1,x}} \left( {{\varvec{x}}_{{rs}} } \right)n_{1} } & {\psi_{{{3}I,x}} \left( {{\varvec{x}}_{{rs}} } \right)n_{1} } \\ {\psi_{{{3}I - \rm{2,}}y} \left( {{\varvec{x}}_{{rs}} } \right)n_{2} } & {\psi_{{{3}I - 1,y}} \left( {{\varvec{x}}_{{rs}} } \right)n_{2} } & {\psi_{{{3}I,y}} \left( {{\varvec{x}}_{{rs}} } \right)n_{2} } \\ {\psi_{{{3}I - \rm{2,}}x} \left( {{\varvec{x}}_{{rs}} } \right)n_{2} + \psi_{{{3}I - \rm{2,}}y} \left( {{\varvec{x}}_{{rs}} } \right)n_{1} } & {\psi_{{{3}I - 1,x}} \left( {{\varvec{x}}_{{rs}} } \right)n_{2} + \psi_{{{3}I - 1,y}} \left( {{\varvec{x}}_{{rs}} } \right)n_{1} } & {\psi_{{{3}I,x}} \left( {{\varvec{x}}_{{rs}} } \right)n_{2} + \psi_{{{3}I,y}} \left( {{\varvec{x}}_{{rs}} } \right)n_{1} } \\ \end{array} } \right]{\text{d}}\varGamma }\end{aligned} $$

(15)

where $\overline{np}$ is the number of natural neighbor nodes for integral points on the boundary $\varGamma_{{rs}}$ of triangular sub-domain $S_{{rs}}$. It is important to point out that the C¹ shape functions cannot be directly calculated when integral points are located on the Delaunay triangle boundaries. Zhou [28] proposed a strategy to slightly offset the coordinate of each Voronoi diagram vertex and properly set the offset factor $\gamma$ to guarantee computational accuracy and overcome C¹ shape function calculation difficulties.

Compared to the C¹ NEM using background integration, the C¹ nodal NEM adopting the TSCI scheme has obvious advantages in the following aspects [28]: (a) In evaluating the generalized strain–displacement relationship matrix $\tilde{\varvec{B}}_{I} \left( {{\varvec{x}}_{{rs}} } \right)$ in Eq. (15), only the unit outward normals of boundaries and the first-order derivatives of C¹ shape functions are needed, and the second-order derivatives of C¹ shape functions are not required. (b) The TSCI scheme adopted in the C¹ nodal NEM is beneficial to the construction of generalized plastic strain increment with high precision and good stability for kinematic shakedown analysis of plates. (c) By using the C¹ nodal NEM, the nodal values, such as generalized plastic strain increment and generalized dissipation work rate, can be directly obtained through simple algebraic calculation, eliminating the need to derive these values from the relevant values at integral points with approximation techniques as in the C¹ NEM and FEM [13, 29], and leading to much simpler post-processing of numerical results.

4 Kinematic Shakedown Analysis of Strain-Hardening Plates

4.1 Discretized Formulation

Building upon the above-mentioned fascinating properties and advantages, the C¹ nodal NEM is utilized to discretize the objective function, normalization condition and geometric compatibility in Eqs. (1)–(3). The corresponding discrete expressions are as follows:

$$\begin{aligned} s &= \mathop {\min }\limits_{{\varvec{\dot{\tilde{\kappa }}}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right)}} \int_{0}^{T} \sum\limits_{r = 1}^{\textit{NP}} \sum\limits_{s = 1}^{\textit{RS}} A_{{rs}} \left\{ M_{{\text{P}}} \sqrt {\left[ {\varvec{\dot{\tilde{\kappa }}}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\varvec{\dot{\tilde{\kappa }}}^{\text{p}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} \right.\\ &\quad\left. + h_{{\text{P}}} \sqrt {\left[ {\Delta \tilde{\varvec{\kappa }}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\Delta \tilde{\varvec{\kappa }}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} \right\} {\rm{d}}t \end{aligned}$$

(16)

$$ \int_{0}^{T} {\sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} \left[ {\varvec{\tilde{\rm M}}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\varvec{\dot{\tilde{\kappa }}}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} } } \text{d}t = \rm{1} $$

(17)

$$\Delta \tilde{\varvec{\kappa }} \left( {{\varvec{x}}_{{rs}} } \right) = \int_{0}^{T} {\varvec{\dot{\tilde{\kappa }}}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right){\text{d}}t} = \tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)\left( {\Delta {\varvec{a}}} \right) $$

(18)

König’s theory [30] is used to deal with the time integration in Eqs. (16)–(18). The smoothed generalized plastic strain increment $\Delta \tilde{\varvec{\kappa }} \left( {{\varvec{x}}_{{rs}} } \right)$ produced during one loading cycle is calculated as the sum of smoothed generalized plastic strain sub-increments $\tilde{\varvec{\kappa }}_{k}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right)$ generated by load vertices ${\varvec{P}}_{k}$$\left( {k = 1,2, \ldots ,l} \right)$, where $l = 2^{v}$ denotes the total number of load vertices ${\varvec{P}}_{k}$$\left( {k = 1,2, \ldots ,l} \right)$, with $v$ being the number of basis loads applied to the structure. Finally, the discrete mathematical programming formulation for kinematic shakedown analysis of strain-hardening plates can be written as:

$$ \begin{aligned} s &= \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } \sum\limits_{{k = \rm{1}}}^{l} {M_{{\text{P}}} \sqrt {\left[ {\tilde{\varvec{\kappa }}_{k}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{\kappa }}_{k}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} } \hfill \\ &\quad\, + \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } h_{{\text{P}}} \sqrt {\left[ {\Delta \tilde{\varvec{\kappa }}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\Delta \tilde{\varvec{\kappa }}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]}\end{aligned} $$

(19)

$$ \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } \sum\limits_{k = 1}^{l} {\left[ {\varvec{\tilde{\rm M}}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\tilde{\varvec{\kappa }}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} = \rm{1} $$

(20)

$$ \Delta \tilde{\varvec{\kappa }}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right) = \sum\limits_{k = 1}^{l} {\tilde{\varvec{\kappa }}_{k}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right)} = \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {\Delta {\varvec{a}}} \right)\quad {\text{in}}\quad \varOmega $$

(21)

$$\Delta {\varvec{a}} = 0\quad {\text{on}}\quad \varGamma_\text{u} $$

(22)

4.2 Iterative Algorithm

Using the Lagrange multipliers $\lambda$ and ${\varvec{L}}_{{rs}}$ to substitute Eqs. (20)–(21) into Eq. (19), respectively, the following improved objective function can be obtained:

$$ \begin{aligned} & L\left( {\tilde{\varvec{\kappa }}_{k}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right),\Delta {\varvec{a}},\lambda ,{\varvec{L}}_{{rs}} } \right) \\ &\quad = \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{{RS}} {{A}_{{rs}} } } \left\{ {\sum\limits_{{k = \rm{1}}}^{l} {M_{{\text{P}}} \sqrt {\left[ {\tilde{\varvec{\kappa }}_{k}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{\kappa }}_{k}^{\rm{p}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} } } \right\} \hfill \\ &\qquad{ + }\sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{{RS}} {{A}_{{rs}} } } \left\{ {h_{{\text{P}}} \sqrt {\left( {\Delta {\varvec{a}}} \right)^{\rm{T}} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {\Delta {\varvec{a}}} \right)} } \right\} \hfill \\ &\qquad{ + }\lambda \left\{ {1 - \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{{RS}} {{A}_{{rs}} } } \sum\limits_{{k = \rm{1}}}^{l} {\left[ {\varvec{\tilde{\rm M}}_{k}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\tilde{\varvec{\kappa }}_{k}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} } \right\} \hfill \\ &\qquad{ + }\sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{{RS}} {{\varvec{L}}_{{rs}}^{{\text{T}}} \left\{ {\sum\limits_{{k = \rm{1}}}^{l} {\tilde{\varvec{\kappa }}_{k}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right)} - \left[ {\tilde{\varvec{B}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {\Delta {\varvec{a}}} \right)} \right\}} }\end{aligned} $$

(23)

According to the minimization condition of Eq. (23), let $\partial L/\partial \tilde{\varvec{\kappa }}_{k}^{{\text{p}}} \left( {{\varvec{x}}_{{rs}} } \right) = {\mathbf{0}}$, $\partial L/\partial \left( {\Delta {\varvec{a}}} \right) = {\mathbf{0}}$, $\partial L/\partial \lambda = {\mathbf{0}}$, and $\partial L/\partial {\varvec{L}}_{{rs}} = {\mathbf{0}}$. The solution expression for the $h$-th iteration can be constructed as:

$$ \frac{{{A}_{{rs}} M_{{\text{P}}} }}{{\mu_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right)}}{\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{\kappa }}_{k}^{{\rm{p}}h} \left( {{\varvec{x}}_{{rs}} } \right)} \right] - \lambda^{h} {A}_{{rs}} \left[ {\varvec{\tilde{\rm M}}_{k}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right] + {\varvec{L}}_{{rs}}^{h} = 0 $$

(24)

$$ \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {\frac{{{A}_{{rs}} \widetilde{h}_{\text{{P}}} }}{{\mu^{h} \left( {{\varvec{x}}_{{rs}} } \right)}}\left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {\Delta {\varvec{a}}} \right)^{h} } } - \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {\left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{{\text{T}}} {\varvec{L}}_{{rs}}^{h} } } = 0 $$

(25)

$$ \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } \sum\limits_{{k = \rm{1}}}^{l} {\left[ {\varvec{\tilde{\rm M}}_{k}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\tilde{\varvec{\kappa }}_{k}^{{{\text{p}}h}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} = 1 $$

(26)

$$ \sum\limits_{{k = \rm{1}}}^{l} {\tilde{\varvec{\kappa }}_{k}^{{{\text{p}}h}} \left( {{\varvec{x}}_{{rs}} } \right)} = \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {{{\Delta}}{\varvec{a}}} \right)^{h} $$

(27)

with the following defined intermediate variables:

$$ \mu_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \sqrt {\left[ {\tilde{\varvec{\kappa }}_{k}^{{{\rm{p}}\left( {h - 1} \right)}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{\kappa }}_{k}^{{{\rm{p}}\left( {h - 1} \right)}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} $$

(28)

$$ \mu^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \sqrt {\left[ {\left( {\Delta {\varvec{a}}} \right)^{h - 1} } \right]^{\rm{T}} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {\Delta {\varvec{a}}} \right)^{h - 1} } $$

(29)

In Eqs. (24)–(27), the vectors of smoothed generalized plastic strain sub-increment $\tilde{\varvec{\kappa }}_{k}^{{\rm{p}}\left( {h - 1} \right)} \left( {{\varvec{x}}_{{rs}} } \right)$ and residual displacement increment $\left( {\Delta {\varvec{a}}} \right)^{h - 1}$ are obtained at the $\left( {h - 1} \right)$-th iteration with known values. This iterative solution expression forms a series of linear equations about the unknowns of smoothed generalized plastic strain sub-increment $\tilde{\varvec{\kappa }}_{k}^{{{\text{p}}h}} \left( {{\varvec{x}}_{{rs}} } \right)$, residual displacement increment $\left( {{{\Delta}}{\varvec{a}}} \right)^{h}$ and Lagrange multipliers $\lambda^{h}$ and ${\varvec{L}}_{{rs}}^{h}$.

The iterative formula in Eqs. (24)–(27) can be implemented meaningfully and smoothly under the condition that the intermediate variables $\mu_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right)$ and $\mu^{h} \left( {{\varvec{x}}_{{rs}} } \right)$ defined in Eqs. (28)–(29) are nonzero in each iteration. Thus, it is necessary to check the values of $\mu_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right)$ and $\mu^{h} \left( {{\varvec{x}}_{{rs}} } \right)$ before proceeding with each iteration. In the initial iteration ($h = 0$), the entire thin plate is assumed to be in a fully nonyielding state, with $\hat{\mu }_{k}^{0} \left( {{\varvec{x}}_{{rs}} } \right) = \mu_{k}^{0} \left( {{\varvec{x}}_{{rs}} } \right) = 1$ and $\hat{\mu }^{0} \left( {{\varvec{x}}_{{rs}} } \right) = \mu^{0} \left( {{\varvec{x}}_{{rs}} } \right) = l$ ($k = 1,2, \ldots l,$$r = 1,2, \ldots {\textit{NP}}, \,$ $s = 1,2, \ldots {\textit{RS}}$). For the $h$-th iteration, the following definitions are adopted:

$$ \hat{\mu }_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \left\{ \begin{aligned} & \mu_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right),\mu_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right) > \beta_{1} \hfill \\ &\quad\beta_{1} , \, \mu_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right) \le \beta_{1}\end{aligned} \right. $$

(30)

$$ \hat{\mu }^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \left\{ \begin{aligned} & \mu^{h} \left( {{\varvec{x}}_{{rs}} } \right),\mu^{h} \left( {{\varvec{x}}_{{rs}} } \right) > \beta_{2} \hfill \\ &\quad\beta_{2} , \, \mu^{h} \left( {{\varvec{x}}_{{rs}} } \right) \le \beta_{2}\end{aligned} \right. $$

(31)

In Eqs. (30)–(31), the positive decimals $\beta_{1}$ and $\beta_{2}$ are significantly smaller than the integer 1 and are typically defined as:

$$\begin{aligned} \beta_{1} & = \left( {10^{ - 5} \sim 10^{ - 8} } \right) \\ & \quad \times \sum\limits_{k = 1}^{l} {\sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {\mu_{k}^{1} \left( {{\varvec{x}}_{{rs}} } \right)/(l{ \times }{\textit{NP}}{ \times }{\textit{RS}})} } }\end{aligned} $$

(32)

$$ \mu_{k}^{1} \left( {{\varvec{x}}_{{rs}} } \right) = \sqrt {\left[ {\tilde{\varvec{\kappa }}_{k}^{{\rm{p}0}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{\kappa }}_{k}^{{\rm{p}0}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} $$

(33)

$$ \beta_{2} = \left( {10^{ - 5} \sim 10^{ - 8} } \right) \times \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {\mu^{1} \left( {{\varvec{x}}_{{rs}} } \right)/({\textit{NP}}{ \times }RS)} } $$

(34)

$$ \mu^{1} \left( {{\varvec{x}}_{{rs}} } \right) = \sqrt {\left[ {\left( {\Delta {\varvec{a}}} \right)^{0} } \right]^{\rm{T}} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {\Delta {\varvec{a}}} \right)^{0} } $$

(35)

Referring to the series of transformations and eliminations described by Zhou et al. [13, 25], Eqs. (24)–(27) can be further simplified into the following linear equations involving $\tilde{\varvec{\kappa }}_{k}^{{{\text{p}}h}} \left( {{\varvec{x}}_{{rs}} } \right)$, $\left( {{{\Delta}}{\varvec{a}}} \right)^{h}$, and $\lambda^{h}$:

$$ \begin{aligned} & \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\hat{\varvec{E}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]\left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {\Delta {\varvec{a}}} \right)^{h} \hfill \\ &\quad =\quad\sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} \lambda^{h} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\hat{\varvec{A}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]\left[ {\hat{\varvec{B}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} }\end{aligned} $$

(36)

$$ \begin{aligned} & \tilde{\varvec{\kappa }}_{k}^{{\rm{p}}h} \left( {{\varvec{x}}_{{rs}} } \right) =\left[ {\tilde{\varvec{H}}_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{ - 1} \left[ {\hat{\varvec{A}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]\left\{ \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {{{\Delta}}{\varvec{a}}} \right)^{h} - \lambda^{h} \right.\\ &\quad \left.\left\{ {\left[ {\hat{\varvec{B}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]{ - }\left[ {\hat{\varvec{A}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{ - 1} \left[ {\varvec{\tilde{\rm M}}_{k}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} \right\} \right\}\end{aligned} $$

(37)

$$ \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } \sum\limits_{{k = \rm{1}}}^{l} {\left[ {\varvec{\tilde{\rm M}}_{k}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\tilde{\varvec{\kappa }}_{k}^{{{\text{p}}h}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} = 1 $$

(38)

with the intermediate matrices defined as follows:

$$ \tilde{\varvec{H}}_{m}^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \frac{{M_{{\text{P}}} }}{{\hat{\mu }_{m}^{h} \left( {{\varvec{x}}_{{rs}} } \right)}}{\varvec{Q}}^{ - 1} $$

(39)

$$ \hat{\varvec{A}}^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \left\{ {\sum\limits_{m = 1}^{l} {\left[ {\tilde{\varvec{H}}_{m}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{ - 1} } } \right\}^{ - 1} $$

(40)

$$ \hat{\varvec{B}}^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \sum\limits_{m = 1}^{l} {\left[ {\tilde{\varvec{H}}_{m}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{ - 1} \left[ {\varvec{\tilde{\rm M}}_{m}^{\text{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} = \left\{ {\sum\limits_{m = 1}^{l} {\left[ {\varvec{\tilde{\rm M}}_{m}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\tilde{\varvec{H}}_{m}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{ - 1} } } \right\}^{\rm{T}} $$

(41)

$$ \hat{\varvec{E}}^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \frac{{\widetilde{h}_{\text{{P}}} }}{{\hat{\mu }^{h} \left( {{\varvec{x}}_{{rs}} } \right)}}{\varvec{Q}}^{ - 1} + \left\{ {\sum\limits_{m = 1}^{l} {\left[ {\tilde{\varvec{H}}_{m}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{ - 1} } } \right\}^{ - 1} = \frac{{\widetilde{h}_{{\text{P}}} }}{{\hat{\mu }^{h} \left( {{\varvec{x}}_{{rs}} } \right)}}{\varvec{Q}}^{ - 1} + \hat{\varvec{A}}^{h} \left( {{\varvec{x}}_{{rs}} } \right) $$

(42)

To solve Eqs. (36)–(38), we define the residual displacement increment $\left( {{{\Delta}}{\varvec{a}}} \right)^{h}$ at the $h$-th iteration as:

$$ \left( {{{\Delta}}{\varvec{a}}} \right)^{h} = \lambda^{h} \left( {{{\Delta}}{\varvec{a}}_{1} } \right)^{h} $$

(43)

By substituting Eq. (43) into Eq. (36), we can obtain the following linear control equation:

$$ {\varvec{K}}^{h} \left( {{{\Delta}}{\varvec{a}}_{1} } \right)^{h} = {\varvec{F}}^{h} $$

(44)

where

$$ {\varvec{K}}^{h} = \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\hat{\varvec{E}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]\left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right] $$

(45)

$$ {\varvec{F}}^{h} = \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} \left[ {\hat{\varvec{A}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]\left[ {\hat{\varvec{B}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right] $$

(46)

By introducing the displacement boundary condition of Eq. (22) to modify the matrix ${\varvec{K}}^{h}$ and column vector ${\varvec{F}}^{h}$ in Eqs. (45)–(46), and solving Eq. (44), we can obtain the intermediate vector of residual displacement increment $\left( {{{\Delta}}{\varvec{a}}_{1} } \right)^{h}$. Then, substituting Eq. (43) into Eq. (37), the smoothed generalized plastic strain sub-increment $\tilde{\varvec{\kappa }}_{k}^{{\text{p}h}} \left( {{\varvec{x}}_{{rs}} } \right)$ at iteration step $h$ can be calculated as:

$$ \tilde{\varvec{\kappa }}_{k}^{{\text{p}h}} \left( {{\varvec{x}}_{{rs}} } \right) = \lambda^{h} \left[ {\tilde{\varvec{H}}_{k}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{ - 1} \left[ {\hat{\varvec{C}}^{h} \left( {{\varvec{x}}_{{rs}} } \right) + \varvec{\tilde{\rm M}}_{k}^{\rm{e}} \left( {{\varvec{x}}_{{rs}} } \right)} \right] $$

(47)

where

$$ \hat{\varvec{C}}^{h} \left( {{\varvec{x}}_{{rs}} } \right) = \left[ {\hat{\varvec{A}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]\left\{ {\left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {{{\Delta}}{\varvec{a}}_{1} } \right)^{h} - \hat{\varvec{B}}^{h} \left( {{\varvec{x}}_{{rs}} } \right)} \right\} $$

(48)

By substituting $\tilde{\varvec{\kappa }}_{k}^{{\text{p}}h} \left( {{\varvec{x}}_{{rs}} } \right)$ in Eq. (47) into Eq. (38), we can derive the Lagrange multiplier $\lambda^{h}$ as:

$$\begin{aligned}& {\lambda ^h} =\frac{1}{{\sum_{r = 1}^{\textit{NP}} {\sum\nolimits_{s = 1}^{\textit{RS}} {{{A}_{rs}}} } \left\{ {{{\left[ {\hat {\varvec{B}}^h\left( {{\varvec{x}}_{{rs}} } \right)} \right]}^{\rm T}}\left[ {\hat {\varvec{C}}^h\left( {{\varvec{x}}_{{rs}} } \right)} \right] + \left\{ {\sum\nolimits_{k = 1}^l {{{\left[ {\tilde {\varvec{M}}_k^{\rm e}\left( {{\varvec{x}}_{{rs}} } \right)} \right]}^{\rm T}}{{\left[ {\tilde {\varvec{H}}_k^h\left( {{\varvec{x}}_{{rs}} } \right)} \right]}^{ - 1}}\left[ {\tilde {\varvec{M}}_{k}^{\rm e}\left( {{\varvec{x}}_{{rs}} }\right)} \right]} } \right\}} \right\}}}\end{aligned}$$

(49)

Substituting the obtained $\left( {{{\Delta}}{\varvec{a}}_{1} } \right)^{h}$ and $\lambda^{h}$ back into Eqs. (43) and (47)–(48), the residual displacement increment $\left( {{{\Delta}}{\varvec{a}}} \right)^{h}$ and the smoothed generalized plastic strain sub-increment $\tilde{\varvec{\kappa }}_{k}^{{{\text{p}}h}} \left( {{\varvec{x}}_{{rs}} } \right)$ can be obtained. According to Eqs. (28)–(31), the following intermediate variables can be further calculated as:

$$ \mu_{k}^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right) = \sqrt {\left[ {\tilde{\varvec{\kappa }}_{k}^{{\rm{p}}h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{\kappa }}_{k}^{{\rm{p}}h} \left( {{\varvec{x}}_{{rs}} } \right)} \right]} $$

(50)

$$ \mu^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right) = \sqrt {\left[ {\left( {\Delta {\varvec{a}}} \right)^{h} } \right]^{\rm{T}} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]^{\rm{T}} {\varvec{Q}}^{ - 1} \left[ {\tilde{\varvec{B}}\left( {{\varvec{x}}_{{rs}} } \right)} \right]\left( {\Delta {\varvec{a}}} \right)^{h} } $$

(51)

$$ \hat{\mu }_{k}^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right) = \left\{ \begin{aligned} & \mu_{k}^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right),\mu_{k}^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right) > \beta_{1} \hfill \\ &\quad\beta_{1} \, ,\mu_{k}^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right) \le \beta_{1}\end{aligned} \right. $$

(52)

$$ \hat{\mu }^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right) = \left\{ \begin{aligned} & \mu^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right),\mu^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right) > \beta_{2} \hfill \\ &\quad\beta_{2} \, ,\mu^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right) \le \beta_{2}\end{aligned} \right. $$

(53)

Finally, the shakedown load factor $s^{h}$ at iteration step $h$ can be written as:

$$ s^{h} = \sum\limits_{r = 1}^{\textit{NP}} {\sum\limits_{s = 1}^{\textit{RS}} {{A}_{{rs}} } } \left[ {\sum\limits_{{k = \rm{1}}}^{l} {M_{{\text{P}}} \hat{\mu }_{k}^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right)} + h_{{\text{P}}} \hat{\mu }^{h + 1} \left( {{\varvec{x}}_{{rs}} } \right)} \right] $$

(54)

According to the anticipated computational accuracy, two error tolerances,$\rm{vol}{1}$ and $\rm{vol}2$, are set in the iterative solution program, and the iteration will be terminated when the following convergence conditions are achieved:

$$ \left\| {\left( {\Delta {\varvec{a}}} \right)^{h} - \left( {\Delta {\varvec{a}}} \right)^{h - 1} } \right\| / \left\| {\left( {\Delta {\varvec{a}}} \right)^{h - 1} } \right\| \le {\rm{vol}}1, \quad \left|{{s^{h} - s^{h - 1} } }\right| / {{s^{h - 1} }}\le \text{vol}2$$

(55)

5 Numerical Examples

In this section, computer codes are developed based on the iterative algorithm proposed above with C¹ nodal NEM for the kinematic shakedown analysis of thin square and circular plates. The perfectly elasto-plastic ($\tilde{h} = 0$), limited kinematic hardening ($\tilde{h} = 0.05Y, \, 0.40Y, \, 0.75Y, \, 1.25Y$) and unlimited kinematic hardening ($\tilde{h} = + \, \infty$) material models are considered. The numerical results and computational times obtained using the C¹ NEM and the rectangular nonconforming plate element ACM [31, 32] are also provided for comparison. A two-point quadrature scheme is employed on each boundary line of the triangle sub-domain in the C¹ nodal NEM, a three-point quadrature rule is adopted over each Delaunay triangle in the C¹ NEM, and a 3 × 3 quadrature rule is used over each finite element in the ACM. The computational times listed below are counted from the same Lenovo computer (Intel(R) Core(TM)2 @ 3.0 GHz). In the numerical calculation, the relevant parameters are set as follows: offset factor $\gamma = 1.0 \times 10^{ - 5}$ [28], yield stress $Y = 200{\text{ MPa}}$, Young’s modulus $E = 2.1 \times 10^{5} {\text{ MPa}}$, Poisson’s ratio $v = 0.3$ and error tolerances $\rm{vol}1 = \rm{vol}2 = 1.0 \times 10^{ - 4}$. Two loading cases $0 \le q \le q^{\max }$ and $- q^{\max } \le q \le q^{\max }$ involving repeated uniform transverse pressure $q$ are considered, where $q^{\max }$ denotes a specific maximum magnitude of pressure $q$, and the reference value of pressure $q$ is set as $1.0 \, \rm{N/m}^{\rm{2}}$.

5.1 Square Plate

The clamped ($\dot{w} = \partial \dot{w}/\partial x = \partial \dot{w}/\partial y = 0$) and simply supported ($\dot{w} = 0$) thin square plates under the repeated uniform pressure $q$ are studied as the first example. The model sketch is displayed in Fig. 1a, where the length $2a = 1{\text{ m}}$ and the thickness $h_{0} = 0.01{\text{ m }}$, and the 441 regular nodes displayed in Fig. 1b are adopted for the numerical calculation. The obtained numerical results and the computational times using the C¹ nodal NEM, C¹ NEM and ACM are listed in Tables 1 and 2, respectively.

Fig. 1

Model sketch and nodal arrangement of a square plate: a simply supported boundary with repeated uniform pressure q; b 441 regular nodes [13]

Table 1 Comparison of kinematic shakedown load factors and computational times for a clamped square plate under different loading cases and material models

Table 2 Comparison of kinematic shakedown load factors and computational times for a simply supported square plate under different loading cases and material models

It can be seen that: (1) In various loading cases and material models, the kinematic shakedown load factors obtained using the C¹ nodal NEM agree well with those from the C¹ NEM and ACM under the same condition, with minimal differences. (2) In the cumulative loading case $0 \le q \le q^{\max }$, the limited and unlimited strain-hardening models tend to increase the kinematic shakedown load factors compared to the perfectly elasto-plastic model. For instance, using the C¹ nodal NEM, the load factors for the clamped square plate increase by 0.072% and 0.092% for $\tilde{h} = 0.05Y$ and $\tilde{h} = 0.40Y, \, 0.75Y, \, 1.25Y, \, + \infty$, respectively, and for the simply supported square plate, they increase by 4.999%, 40.010%, 43.815%, and 43.831% for $\tilde{h} = 0.05Y$, $\tilde{h} = 0.40Y$, $\tilde{h} = 0.75Y, \, 1.25Y$, and $\tilde{h} = + \infty$, respectively. (3) In the alternating loading case $- q^{\max } \le q \le q^{\max }$, the load factors obtained for the limited and unlimited kinematic hardening models are equal to those of the perfectly elasto-plastic model under the same condition. (4) In general, the computational times using the C¹ nodal NEM are comparable to those using the C¹ NEM and ACM. As per Zhou et al. [25], the costs of the nodal NEM in shakedown analysis of plane structures are approximately one-ninth to one-third of those of the NEM. However, owing to more triangular sub-domain partitions and numerical integrations on the boundary lines in each triangular sub-domain in the C¹ nodal NEM compared to the nodal NEM, the computational efficiency of the C¹ nodal NEM remains relatively unchanged from that of the C¹ NEM.

Figure 2 displays the iterative convergence processes of kinematic shakedown load factors for some loading cases and material models using the C¹ nodal NEM, C¹ NEM and ACM, which indicates that the proposed iterative algorithm ensures rapid and monotonic convergence of obtained kinematic shakedown load factors to stable minima after 19–103 iterations.

Fig. 2

Iterative convergence processes of kinematic shakedown load factors for a square plate: a clamped; b simply supported

As mentioned in Sect. 3.2, the nodal generalized plastic dissipation work rates in the kinematic shakedown analysis of plates can be directly obtained using the C¹ nodal NEM, and the C¹ nodal NEM offers obvious advantages in numerical result post-processing compared to the C¹ NEM and ACM. Figure 3 shows the distributions of plastic dissipation work rates obtained directly through the C¹ nodal NEM for a thin square plate under different loading cases and material models, which visually illustrates the cumulative and alternating plastic damage modes of the square plate at shakedown limit states.

Fig. 3

Distributions of plastic dissipation work rates for a square plate at shakedown limit states ($10^{6} \;\rm{N}\;\rm{m}$): a clamped, $\tilde{h} = 0$, $0 \le q \le q^{\max }$; b clamped, $\tilde{h} = 1.25Y$, $0 \le q \le q^{\max }$; c clamped, $\tilde{h} = 0$ and $\tilde{h} = 1.25Y$, $- q^{\max } \le q \le q^{\max }$; d simply supported, $\tilde{h} = 0$, $0 \le q \le q^{\max }$; e simply supported, $\tilde{h} = 1.25Y$, $0 \le q \le q^{\max }$; f simply supported, $\tilde{h} = 0$ and $\tilde{h} = 1.25Y$, $- q^{\max } \le q \le q^{\max }$

5.2 Circular Plate

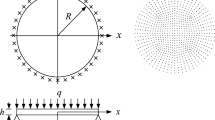
A clamped thin circular plate with the radius $R = 1{\text{ m}}$ and the thickness $h_{0} = 0.01{\text{ m }}$ under the repeated uniform pressure $q$ is examined as the second example. The model sketch and 801 regular nodal arrangement adopted in the numerical calculation are displayed in Fig. 4. By adopting the perfectly elasto-plastic model, Yu et al. [7] employed the unified yield criterion to deduce the analytical solution under the loading case $0 \le q \le q^{\max }$, while Zhou et al. [13] utilized the C¹ NEM to solve the numerical results under the loading cases $0 \le q \le q^{\max }$ and $- q^{\max } \le q \le q^{\max }$. This paper uses the proposed method with the C¹ nodal NEM and C¹ NEM to concurrently determine the kinematic shakedown load factors of this plate, with the results summarized in Table 3.

Fig. 4

A clamped circular plate: a under uniform pressure $q$; b 801 nodes [13]

Table 3 Comparison of kinematic shakedown load factors for a clamped circular plate under different loading cases and material models

It shows that: (1) The kinematic shakedown load factor obtained by the C¹ nodal NEM is closer to the analytical solution of Yu et al. [7] than that obtained by the C¹ NEM, which is in good agreement with the conclusion of Zhou [28] that the C¹ nodal NEM has better computational accuracy than the C¹ NEM in the linear elastic analysis of plates. The results obtained by the C¹ nodal NEM and C¹ NEM match well with each other under the same condition, indicating the proposed method in this paper has high computational accuracy. (2) In the cumulative loading case $0 \le q \le q^{\max }$, the load factors using the C¹ nodal NEM increase by 5.003%, 22.248%, and 22.371% for $\tilde{h} = 0.05Y$, $\tilde{h} = 0.40Y$, and $\tilde{h} = 0.75Y, \, 1.25Y, \, + \infty$, respectively, compared to the perfectly elasto-plastic model. This suggests that the shakedown load obtained may be conservative when the material’s strain-hardening effect is disregarded. (3) In the alternating loading case $- q^{\max } \le q \le q^{\max }$, the results for limited and unlimited kinematic hardening models align with the perfectly elasto-plastic model.

Figure 5 displays the distributions of plastic dissipation work rates obtained using the C¹ nodal NEM, which are symmetrical and reasonable, revealing the plastic failure modes of this clamped circular plate at shakedown limit states.

Fig. 5

Distributions of plastic dissipation work rates for a clamped circular plate at shakedown limit states ($10^{6} \;\rm{N}\;\rm{m}$): a $\tilde{h} = 0$, $0 \le q \le q^{\max }$; b $\tilde{h} = 1.25Y$, $0 \le q \le q^{\max }$; c $\tilde{h} = 0$ and $\tilde{h} = 1.25Y$, $- q^{\max } \le q \le q^{\max }$

6 Conclusions

This paper proposes a novel numerical approach using the C¹ nodal NEM to evaluate the kinematic shakedown load factors of strain-hardening plates based on the von Mises and two-surface yield criteria and adopts it to implement kinematic shakedown analysis of thin square and circular plates with perfectly elasto-plastic, limited kinematic hardening and unlimited kinematic hardening material models. The numerical results for kinematic shakedown load factors align closely with theoretical solution and numerical values obtained using the C¹ NEM and ACM. Compared to the perfectly elasto-plastic model, the limited and unlimited kinematic hardening models somewhat increase the obtained load factors of thin square and circular plates in cumulative loading cases, but have no impact in alternating loading cases. The distributions of plastic dissipation work rates effectively illustrate the cumulative and alternating plastic failure modes of thin square and circular plates at shakedown limit states. Numerical examples demonstrate the proposed numerical method’s benefits of high accuracy, rapid convergence and convenient post-processing capabilities.