1 Introduction

Different researchers have developed interest in obtaining both exact and approximate solutions of relativistic and nonrelativistic wave equations with various potential models. This is because all the information describing a quantum system can be obtained comfortably from these models [1,2,3,4,5,6,7]. These solutions are highly applicable to different areas of physics including chemical physics [8,9,10,11,12]. Different approximation schemes and formalisms have been employed to obtain the solutions of these wave equations [13,14,15,16,17,18,19,20,21,22,23]. Worth mentioning is the most recently proposed formalism called the Nikiforov-Uvarov-functional-analysis (NUFA) method [24,25,26,27]. This method is known to be very elegant and simple to use. Klein–Gordon equation (KGE) is one of the relativistic wave equation which has been widely studied [28]. The KGE is known to be a basic relativistic wave equation that describes the motion of spin zero particles [29, 30]. In recent times, the studies of KGE have been extended to higher dimensions with different potential models by some authors [31,32,33,34,35,36,37,38]. For instance, the functional analysis approach has been employed to obtain the solution of the KGE with generalized hyperbolic potential model in higher dimensions [39]. Many researchers have been involved in proffering solutions to scattering state problems with different potential models [40,41,42,43,44]. The bound and scattering states solutions of the relativistic spinless particles with multiparameter potential have been obtained by Tas and Havare [45]. In addition, the bound and scattering state solutions of position dependent mass KGE with Hulthen plus deformed-type hyperbolic potential has been obtained in higher dimensions [46]. Most recently, Okorie and his collaborators [47] employed the functional analysis approach (FAA) to obtain the bound and scattering states solutions of the Klein–Gordon equation with generalized Mobius square potential in higher dimensions for nitrogen monoiodide (NI) diatomic molecule. It has been observed that a study on the scattering states of KGE with potential model for diatomic molecular systems carried out by Okorie [47] is the first to the best of our knowledge. It is hoped that this study will extend the research trend in this direction. The aim of this paper is to obtain the bound and scattering states solutions of the KGE with Deng–Fan potential model for LiH and HCl diatomic molecules in higher dimensions. The Deng–Fan potential is defined as [48, 49]

$$\begin{aligned} V_{DFP} (r)=d_{e} \left[ {1\,\,-\,\,\,\frac{g\,e^{-\,\,\delta \,r}}{\left( {1\,\,-\,e^{-\,\,\delta \,r}} \right) }} \right] ^{\,2}\,;\,\,g\,\,=\,\,e^{\delta \,r_{e} }\,-\,1 , \end{aligned}$$
(1)

where \(\delta \) is the screening parameter,g is the potential parameter and \(d_{e} \,\,\text{ and }\,\,r_{e} \) represent the dissociation energy and equilibrium bond length of the molecular system, respectively. It is well known that molecular Deng–Fan is a modified form of Morse potential. This potential finds applications in the study of motion of nucleons in the mean field exerted by the interaction between nuclei and in describing diatomic energy spectra. Recent studies show that Deng–Fan potential is consistent with quantum requirement which can be used to study molecular systems besides the coulomb or linear terms [50].

The organization of this work is as follows: Sect. 2 gives the bound state solutions of the KGE with Deng–Fan potential in higher dimensions. The scattering state solutions of the Deng–Fan potential in higher dimensions are contained in Sect. 3. Section 4 contains the numerical and graphical results and obtained in this work and their necessary discussion. The concluding remarks of this work are given Sect. 5.

2 Bound State Solutions of the KGE with Deng–Fan Potential in Higher Dimensions

The KGE for spherically symmetric potential in higher dimensions is defined as [51]

$$\begin{aligned} -\,\,{\hbar }^{2}c^{2}\Delta _{D} \psi _{n,\,l,\,m} \left( {r,\,\Omega _{\,\,D} } \right) \,\,=\,\,\left\{ {\left( {E_{n,\,l_{D} } \,-\,V\left( r \right) } \right) ^{2}\,-\,\left( {\mu c^{2}\,+\,S\left( r \right) } \right) ^{2}} \right\} \psi _{n,\,l,\,m} \left( {r,\,\Omega _{\,\,D} } \right) , \end{aligned}$$
(2)

with \(E_{n,\,l_{D} } \) being the relativistic energy eigenvalues in higher dimensions, \(\mu \) is the reduced mass, \(V\left( r \right) \,\,\text{ and }\,\,S\left( r \right) \) are the vector potential and scalar potential , respectively. Also, the parameter \(\Delta _{\,D} \) is given as

$$\begin{aligned} \Delta _{D} \,\,\equiv \,\,\nabla _{D}^{2} \,\,=\,\,\frac{1}{r^{D\,-\,1}}\frac{\partial }{\partial r}\left( {r^{D\,-\,1}\frac{\partial }{\partial r}} \right) \,\,-\,\,\frac{\Lambda _{D}^{2} \left( {\Omega _{\,D} } \right) }{r^{2}}, \end{aligned}$$
(3)

where \(\Lambda _{D}^{2} \left( {\Omega _{\,D} } \right) \) defines the generalization of the centrifugal term for the higher dimensional space and \(\nabla _{D}^{2} \) is the Laplace operator in higher dimensions.

The total wave function in higher dimensions is defined as

$$\begin{aligned} \psi _{n,\,l,\,m} \left( {r,\,\Omega _{\,\,D} } \right) \,\,=\,\,F_{n,\,l_{D} } \left( r \right) Y_{l_{D} }^{m} \left( {\Omega _{\,\,D} } \right) , \end{aligned}$$
(4)

with the energy eigenvalues of \(\Lambda _{D}^{2} \left( {\Omega _{\,D} } \right) \) being given as

$$\begin{aligned} \Lambda _{D}^{2} \left( {\Omega _{\,D} } \right) Y_{l_{D} }^{m} \left( {\Omega _{\,\,D} } \right) \,\,=\,\,l_{D} \left( {l_{D} \,+\,D\,-\,2} \right) Y_{l_{D} }^{m} \left( {\Omega _{\,\,D} } \right) . \end{aligned}$$
(5)

Here, \(Y_{l_{D} }^{m} \left( {\Omega _{\,\,D} } \right) \) is the hyperspherical harmonics and \(l_{D} \) is the total angular momentum quantum number, both in higher dimensions.

Substituting ansatz of the form \(F_{n,\,l_{D} } \left( r \right) \,\,=\,\,r^{\,\frac{-\,\,\left( {D\,-\,1} \right) }{2}}G_{\,n,\,l_{D} } \left( r \right) \) for the wave function into Eq. (4) gives

$$\begin{aligned}&\left\{ {{\hbar }^{2}c^{2}\frac{d^{2}}{dr^{2}}\,+\,\left( {E_{n,\,l_{D} } \,-\,V\left( r \right) } \right) ^{2}\,-\,\,\left( {\mu c^{2}\,+\,S\left( r \right) } \right) ^{2}\,-\,\frac{\left( {D\,+\,2l_{D} \,-\,1} \right) \left( {D\,+\,2l_{D} \,-\,3} \right) {\hbar }^{2}c^{2}}{4r^{2}}} \right\} \nonumber \\&\qquad G_{\,n,\,l_{D} } \left( r \right) \,\,=\,\,0 , \end{aligned}$$
(6)

where \(G_{\,n,\,l_{D} } \left( r \right) \) is the hyper-radial wave function in higher dimensions.

In order to make the potential V(r) and not 2V(r) in the nonrelativistic limit, one proposed for equal vector potential and scalar potential, that is\(V(r)=S(r)=\frac{V(r)}{2}=\frac{S(r)}{2}\) for the simplicity of the Klein-Equation ,then Eq. (6) reduces to

$$\begin{aligned} \left\{ {{\hbar }^{2}c^{2}\frac{d^{2}}{dr^{2}}\,+\,\left( {E_{n,\,l_{D} }^{2} \,-\,\mu ^{2}c^{4}} \right) \,-\,\,\left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) V\left( r \right) \,\,-\,\,\frac{K\left( {K\,+\,1} \right) \,{\hbar }^{2}c^{2}}{r^{2}}} \right\} G_{\,n,\,l_{D} } \left( r \right) \,\,=\,\,0, \end{aligned}$$
(7)

where

$$\begin{aligned} K\,\,=\,\,l_{D} \,\,+\,\,\frac{1}{2}\left( {D\,-\,3} \right) . \end{aligned}$$
(8)

Substituting Eqs. (1) into (7) gives

$$\begin{aligned}&\left\{ {\frac{d^{2}}{dr^{2}}\,+\frac{\,\left( {E_{n,\,l_{D} }^{2} \,-\,\mu ^{2}c^{4}} \right) }{{\hbar }^{2}c^{2}}\,-\,\,\frac{\left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}c^{2}}d_{e} \left[ {1\,\,-\,\,\,\frac{g\,e^{-\,\,\delta \,r}}{\left( {1\,\,-\,e^{-\,\,\delta \,r}} \right) }} \right] ^{\,2}\,\,-\,\,\frac{K\left( {K\,+\,1} \right) }{r^{2}}} \right\} \nonumber \\&\qquad G_{\,n,\,l_{D} } \left( r \right) \,\,=\,\,0. \end{aligned}$$
(9)

Due to the presence of the centrifugal term, Eq. (9) cannot be solved exactly for \(l_{D} \,=\,\,0.\) Hence the improved Pekeris-type approximation scheme is employed to handle the centrifugal term, reason being that it is suitable for both bound and scattering state problems. The improved Pekeris-type approximation scheme used here is defined as [52]

$$\begin{aligned} \frac{1}{r^{2}}\,\,\approx \,\,\delta ^{2}\left[ {d_{0} \,\,+\,\,\frac{e^{\delta \,r}}{\left( {1\,\,-\,\,e^{\delta \,r}} \right) ^{2}}} \right] \,;\,\,\,d_{0} \,=\,\,\frac{1}{12}. \end{aligned}$$
(10)

Inserting Eqs. (10) into (9) and defining a new variable such as \(z=e^{-\,\,\delta \,r}\)with the following dimensionless parameters;

$$\begin{aligned} \left. {\begin{array}{l} \varepsilon _{n,\,l_{D} }^{2} =\,\,-\left( {\,\frac{\,\left( {E_{n,\,l_{D} }^{2} \,-\,\mu ^{2}c^{4}} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,\,-\,\,\frac{d_{e} \left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) \left( {1\,\,+\,\,g} \right) ^{2}}{{\hbar }^{2}\delta ^{2}c^{2}}\,\,-\,\,d_{0} K\left( {K\,\,+\,\,1} \right) } \right) ;\,\, \\ P=\,\,\,-\,\,\,\left( {\frac{\,2\left( {E_{n,\,l_{D} }^{2} \,-\,\mu ^{2}c^{4}} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}-\,\,\frac{2d_{e} \left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) \left( {1\,\,+\,\,g} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,-\,\,\,K\left( {K\,\,+\,\,1} \right) \left( {2d_{0} \,\,-\,\,1} \right) } \right) \,\,\,;\,\, \\ Q=\,\,-\left( {\,\frac{\,\left( {E_{n,\,l_{D} }^{2} \,-\,\mu ^{2}c^{4}} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,\,-\,\,\frac{d_{e} \left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,-\,\,d_{0} K\left( {K\,\,+\,\,1} \right) } \right) \\ \end{array}} \right] , \end{aligned}$$
(11)

Equation (9) becomes

$$\begin{aligned} \frac{d^{2}G_{\,n,\,l_{D} } \left( z \right) }{dz^{2}}+\frac{\left( {1-z} \right) }{z\left( {1-z} \right) }\frac{dG_{\,n,\,l_{D} } \left( z \right) }{dz}+\frac{\left[ {-\,\varepsilon _{n,\,l_{D} }^{2} z^{2}+P\,z-Q} \right] G_{\,n,\,l_{D} } \left( z \right) }{z^{2}\left( {1-z} \right) ^{2}}=0. \end{aligned}$$
(12)

By employing the Nikiforov-Uvarov-Functional-Analysis (NUFA) method [53, 54] and proposing a wave function of the form

$$\begin{aligned} G_{\,n,\,l_{D} } \left( z \right) \,\,=\,\,z^{\chi }\left( {1\,-\,z} \right) ^{\upsilon }f_{\,n,\,l_{D} } \left( z \right) , \end{aligned}$$
(13)

where

$$\begin{aligned} \left. {\begin{array}{l} \chi \,\,=\,\,\sqrt{-\left( {\,\frac{\,\left( {E_{n,\,l_{D} }^{2} \,-\,\mu ^{2}c^{4}} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,\,-\,\,\frac{d_{e} \left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,-\,\,d_{0} K\left( {K\,\,+\,\,1} \right) } \right) \,} \,\,; \\ \upsilon \,\,=\,\,\frac{1}{2}\left[ {1\,+\,\sqrt{1\,\,+\,\,4\left( {\frac{d_{e} g^{2}\left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,+K\left( {K\,\,+\,\,1} \right) } \right) } } \right] \\ \end{array}} \right] \end{aligned}$$
(14)

it is worthy to mention here that the term under the square root signed in Eq. (14) must always be positive for bound state solutions. The relativistic energy spectra of the Deng–Fan potential in higher dimensions is obtained as

$$\begin{aligned} E_{n,\,l_{D} }^{2} \,-\,\mu ^{2}c^{4}\,\,= & {} \,\,d_{e} \left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) \,\,+\,\,\,d_{0} K\left( {K\,\,+\,\,1} \right) {\hbar }^{2}\delta ^{2}c^{2}\,\,-\,\,{\hbar }^{2}\delta ^{2}c^{2}\nonumber \\&\left[ {\frac{d_{e} \left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) \left( {g^{2}\,+\,2g} \right) }{2\left( {n\,\,+\,\,\upsilon } \right) }\,\,-\,\,\frac{\left( {n\,\,+\,\,\upsilon } \right) }{2}\,} \right] ^{\,2}\, \end{aligned}$$
(15)

By making use of the following mapping structure, \(E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,\,\rightarrow \,\,2\mu c^{2}\) and \(E_{n,\,l_{D} } \,-\,\,\mu c^{2}\rightarrow \,\,E_{n,\,l_{D} } \), the nonrelativistic energy spectra of the Deng–Fan potential in higher dimensions is obtained as

$$\begin{aligned} E_{n,\,l_{D} } \,\,=\,\,d_{e} \,\,+\,\,\,\frac{{\hbar }^{2}\delta ^{2}}{2\mu }d_{0} K\left( {K\,+\,1} \right) \,\,-\,\,\frac{{\hbar }^{2}\delta ^{2}}{2\mu }\left[ {\frac{\frac{2\mu \,d_{e} }{{\hbar }^{2}\delta ^{2}}\left( {g^{2}\,+\,2g} \right) }{2\left( {n\,\,+\,\,{\upsilon }'} \right) }\,\,-\,\,\frac{\left( {n\,\,+\,\,{\upsilon }'} \right) }{2}\,} \right] ^{\,2}, \end{aligned}$$
(16)

where

$$\begin{aligned} {\upsilon }'\,\,=\,\,\frac{1}{2}\left[ {1\,+\,\sqrt{1\,\,+\,\,4\left( {\frac{2\mu \,d_{e} g^{2}}{{\hbar }^{2}\delta ^{2}}\,\,+K\left( {K\,\,+\,\,1} \right) } \right) } } \right] . \end{aligned}$$
(17)

3 Scattering State Solutions of the KGE with Deng–Fan Potential in Higher Dimensions

By employing a new transformation scheme \(\xi \,\,=\,\,1\,\,-\,\,e^{-\,\,\delta \,r}\)and the improved Pekeris-type approximation scheme of Eqs. (10), (9) becomes

$$\begin{aligned} \xi (1-\xi )\frac{d^{2}G_{\,n,\,l_{D} } \left( \xi \right) }{d\xi ^{2}}-\xi \frac{dG_{\,n,\,l_{D} } \left( \xi \right) }{d\xi }+\frac{\left[ {\Delta _{1} +\Delta _{2} \xi +\Delta _{3} \xi ^{2}} \right] }{\xi (1-\xi )}G_{\,n,\,l_{D} } \left( \xi \right) =0 , \end{aligned}$$
(18)

where

$$\begin{aligned} \left. {\begin{array}{l} \Delta _{1} \,\,=\,\,-\,\,\left( {\,\frac{d_{e} g^{2}\left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,+\,\,\,K\left( {K\,\,+\,\,1} \right) } \right) ; \\ \Delta _{2} \,\,=\,\frac{2\,d_{e} \,g\left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,+\,\,\frac{2\,d_{e} \,g^{2}\left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,+\,\,\,K\left( {K\,\,+\,\,1} \right) ; \\ \Delta _{3} \,\,=\,\,\,\frac{\,\left( {E_{n,\,l_{D} }^{2} \,-\,\mu ^{2}c^{4}} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,\,-\,\,\frac{d_{e} \left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,-\,\,\frac{2\,d_{e} \,g\left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}\,\,-\,\,\frac{d_{e} g^{2}\left( {E_{n,\,l_{D} } \,+\,\,\mu c^{2}\,} \right) }{{\hbar }^{2}\delta ^{2}c^{2}}-\,\,d_{0} K\left( {K\,\,+\,\,1} \right) \\ \end{array}} \right] .\nonumber \\ \end{aligned}$$
(19)

To find the regular solution of scattering states, the wave function is defined as

$$\begin{aligned} G_{\,n,\,l_{D} } \left( \xi \right) =\xi ^{\lambda }\,\left( {1-\xi } \right) ^{-\,\,\frac{ik}{\delta }}\,\gamma _{\,n,\,l_{D} } (\xi ), \end{aligned}$$
(20)

where

$$\begin{aligned} \lambda =\frac{1}{2}\left( {1\pm \sqrt{1\,\,-\,\,4\Delta _{1} } } \right) ;\,\,k=\delta \sqrt{\Delta _{1} +\Delta _{2} +\Delta _{3} } . \end{aligned}$$
(21)

Substituting Eqs. (21) into (18) gives the hypergeometric Gauss differential equation of the form

$$\begin{aligned}&\xi (1-\xi )\frac{d^{2}\gamma _{\,n,\,l_{D} } \left( \xi \right) }{d\xi ^{2}}+\left[ {2\lambda -\left( {1\,\,-\,\,\frac{2ik}{\delta }\,\,+\,\,2\lambda } \right) \,\,\xi } \right] \,\frac{d\gamma _{\,n,\,l_{D} } \left( \xi \right) }{d\xi }-\left( {\lambda -\,\,\frac{ik}{\delta }\,\,+\,\,H} \right) \left( {\lambda -\,\,\frac{ik}{\delta }\,\,-H} \right) \,\nonumber \\&\qquad \gamma _{\,n,\,l_{D} } \left( \xi \right) =0, \end{aligned}$$
(22)

where

$$\begin{aligned} H\,\,=\,\,\sqrt{-\,\,\Delta _{3} } . \end{aligned}$$
(23)

As noted before, the quantities in the square root of Eqs. (21) and (23) can either be positive/negative for bound/scattering states. If for instance, the term in the square root sign become negative then resonance phenomena will occur. The solutions of Eq. (22) is the hypergeometric function given as

$$\begin{aligned} \gamma _{\,n,\,l_{D} } \left( \xi \right) ={ }_{2}F_{1} ({\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} ,\,\,\,\xi ). \end{aligned}$$
(24)

Here, the following definitions are obtained:

$$\begin{aligned} {\phi }_{1} \,\,=\,\,\lambda -\frac{ik}{\delta }\,\,+H;\,\,\,{\phi }_{2} \,\,=\,\,\lambda -\,\,\frac{ik}{\delta }\,\,-\,\,H;\,\,\,{\phi }_{3} \,\,=\,\,2\lambda . \end{aligned}$$
(25)

The general solution of the wave function is obtained as

$$\begin{aligned} G_{\,n,\,l_{D} } \left( r \right) =\mathrm{N}_{n,\,l_{D} } \left( {1\,\,-\,\,e^{-\,\delta \,r}} \right) ^{\frac{1}{2}\left( {1\pm \sqrt{1\,\,-\,\,4\Delta _{1} } } \right) }\,\left( {e^{-\,\delta \,r}} \right) ^{-\,\,i\,\,\sqrt{\Delta _{1} +\Delta _{2} +\Delta _{3} } }\,{ }_{2}F_{1} \left( {{\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} ,\,\,1\,\,-\,\,e^{-\,\delta \,r}} \right) .\nonumber \\ \end{aligned}$$
(26)

The scattering state for relativistic energy greater than zero in three dimensions can be defined as [42]

$$\begin{aligned} \left. {\begin{array}{l} U\left( r \right) \rightarrow \,\,0,\,\,r\rightarrow \,\,0; \\ U\left( r \right) \rightarrow \,\,2\sin \left[ {kr\,+\,\,\varpi \,-\,\frac{l\pi }{2}\,} \right] ,\,\,r\rightarrow \,\,\infty \\ \end{array}} \right] . \end{aligned}$$
(27)

For higher dimensions, it can be expressed as [42]

$$\begin{aligned} \left. {\begin{array}{l} U\left( r \right) \rightarrow \,\,0,\,\,r\rightarrow \,\,0; \\ U\left( r \right) \rightarrow \,\,2\sin \left[ {kr\,+\,\,\varpi _{l_{D} } \,-\,\frac{\pi }{2}\left( {l_{D} \,+\,\frac{\left( {D\,-\,3} \right) }{2}} \right) \,} \right] ,\,\,r\rightarrow \,\,\infty \\ \end{array}} \right] , \end{aligned}$$
(28)

where \(\varpi ,\,\varpi _{l_{D} } \) and U(r)are the scattering phase shifts in three dimension, higher dimension and wave functions, respectively. From Eq. (26), the scattering phase shift and its corresponding normalization constant can be obtained for large values of r in higher dimensions. Hence,

$$\begin{aligned} \left. {\begin{array}{l} {\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} \,\,=\,\,\frac{2ik}{\delta }\,\,=\,\,\left( {{\phi }_{1} \,\,+\,\,{\phi }_{2} \,\,-\,\,{\phi }_{3} } \right) ^{*}; \\ {\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,=\,\,\lambda \,\,+\,\,\frac{ik}{\delta }\,\,-\,\,H=\,\,{\phi }_{2}^{*} ; \\ {\phi }_{3} \,\,-\,\,{\phi }_{2} \,\,=\,\,\lambda \,\,+\,\,\frac{ik}{\delta }\,\,+\,\,H=\,\,{\phi }_{1}^{*} \\ \end{array}} \right] . \end{aligned}$$
(29)

Employing the transformation properties for the hypergeometric function [55],

$$\begin{aligned}&{ }_{2}F_{1} ({\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} ,\,\,\,0)\,\,=\,\,1, \end{aligned}$$
(30)
$$\begin{aligned}&\begin{array}{l} { }_{2}F_{1} \left( {{\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} ,\,\,\,\xi } \right) \,\,=\,\,\frac{\Gamma \left( {{\phi }_{3} } \right) \Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} } \right) }{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} } \right) \Gamma \left( {{\phi }_{3} \,-\,\,{\phi }_{2} } \right) }{ }_{2}F_{1} \left( {{\phi }_{3} ;\,\,\,{\phi }_{2} ;\,\,\,{\phi }_{1} \,\,+\,\,{\phi }_{2} \,\,-\,\,{\phi }_{3} \,\,+\,\,1;\,1\,\,-\,\,\xi } \right) \, \\ \,+\,\,\left( {1\,\,-\,\,\xi } \right) ^{\,\left( {{\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} } \right) }\frac{\Gamma \left( {{\phi }_{3} } \right) \Gamma \left( {{\phi }_{1} \,\,+\,\,{\phi }_{1} \,\,-\,\,{\phi }_{3} } \right) }{\Gamma \left( {{\phi }_{1} } \right) \Gamma \left( {{\phi }_{2} } \right) }{ }_{2}F_{1} \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} ;\,\,\,{\phi }_{3} \,\,-\,\,{\phi }_{2} ;\,\,\,{\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} \,\,+\,\,1;\,1\,\,-\,\,\xi } \right) \, \\ \end{array}. \end{aligned}$$
(31)

Also, the term \({ }_{2}F_{1} \left( {{\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} ,\,\,1\,\,-\,\,e^{-\,\,\delta \,r}} \right) \) in Eq. (26) can be expanded as

$$\begin{aligned} { }_{2}F_{1} \left( {{\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} ,\,\,1\,\,-\,\,e^{-\,\,\delta \,r}} \right) \,\,= & {} \,\,\Gamma \left( {{\phi }_{3} } \right) \left[ \frac{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} } \right) }{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} } \right) \Gamma \left( {{\phi }_{3} \,-\,\,{\phi }_{2} } \right) }\,\,\right. \nonumber \\&+\,\,\left. \left[ {\frac{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} } \right) }{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} } \right) \Gamma \left( {{\phi }_{3} \,-\,\,{\phi }_{2} } \right) }} \right] ^{\,*}e^{-\,\,\delta \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} } \right) \,\,r} \right] . \end{aligned}$$
(32)

As \(r\rightarrow \infty \), Eq. (32) becomes

$$\begin{aligned} { }_{2}F_{1} \left( {{\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} ,\,\,1\,\,-\,\,e^{-\,\,\delta \,r}} \right) \,\,=\,\,\Gamma \left( {{\phi }_{3} } \right) \left[ {\frac{\Gamma \left( {\frac{2ik}{\delta }} \right) }{\Gamma \left( {{\phi }_{2}^{*} } \right) \Gamma \left( {{\phi }_{1}^{*} } \right) }\,\,+\,\,\left[ {\frac{\Gamma \left( {\frac{2ik}{\delta }} \right) }{\Gamma \left( {{\phi }_{2}^{*} } \right) \Gamma \left( {{\phi }_{1}^{*} } \right) }} \right] ^{\,*}e^{-\,2ik\,r}} \right] . \end{aligned}$$
(33)

By using the relation

$$\begin{aligned} \frac{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} } \right) }{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} } \right) \Gamma \left( {{\phi }_{3} \,-\,\,{\phi }_{2} } \right) }\,\,\,=\,\,\left| {\frac{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} } \right) }{\Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} } \right) \Gamma \left( {{\phi }_{3} \,-\,\,{\phi }_{2} } \right) }} \right| e^{i\,\varpi }, \end{aligned}$$
(34)

Equation (33) becomes

$$\begin{aligned} \left. {\begin{array}{l} { }_{2}F_{1} \left( {{\phi }_{1} ,\,\,\,{\phi }_{2} ,\,\,\,{\phi }_{3} ,\,\,1\,\,-\,\,e^{-\,\,\delta \,r}} \right) \,\,=\,\,\Gamma \left( {{\phi }_{3} } \right) \left| {\frac{\Gamma \left( {\frac{2ik}{\delta }} \right) }{\Gamma \left( {{\phi }_{2}^{*} } \right) \Gamma \left( {{\phi }_{1}^{*} } \right) }} \right| \left[ {e^{\,i\,\,\varpi }\,+\,\,e^{-\,2ik\,r}\times \,\,e^{-\,i\,\varpi }} \right] \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\,\,\Gamma \left( {{\phi }_{3} } \right) \left| {\frac{\Gamma \left( {\frac{2ik}{\delta }} \right) }{\Gamma \left( {{\phi }_{2}^{*} } \right) \Gamma \left( {{\phi }_{1}^{*} } \right) }} \right| e^{-\,i\,k\,r}\left[ {e^{i\,\left( {\varpi \,\,-\,\,\frac{k\,\ln 2}{\delta }\;+\,k\,r} \right) \,}\,+\,\,\,e^{-\,i\,\,\left( {\varpi \,\,-\,\,\frac{k\,\ln 2}{\delta }\;+\,k\,r} \right) }} \right] \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,=\,\,\Gamma \left( {{\phi }_{3} } \right) \left| {\frac{\Gamma \left( {\frac{2ik}{\delta }} \right) }{\Gamma \left( {{\phi }_{2}^{*} } \right) \Gamma \left( {{\phi }_{1}^{*} } \right) }} \right| e^{-\,i\,k\,r}\sin \left( {k\,r\,\,+\,\,\varpi \,\,-\,\,\frac{k\,\ln 2}{\delta }\,\,+\,\,\frac{\pi }{2}\left[ {l_{D} \,\,+\,\,\frac{\left( {D\,\,-\,\,3} \right) }{2}} \right] \,\,+\,\,\frac{\pi }{2}\left[ {l_{D} \,\,+\,\,\frac{\left( {D\,\,-\,\,1} \right) }{2}} \right] } \right) \\ \end{array}} \right] .\nonumber \\ \end{aligned}$$
(35)

The asymptotic form of Eq. (26) becomes

$$\begin{aligned} G_{n,\,l_{D} } \left( r \right) \,\,= & {} \,\,2\mathrm{N}_{n,\,\,l_{D} } \,\Gamma \left( {{\phi }_{3} } \right) \left| {\frac{\Gamma \left( {\frac{2ik}{\delta }} \right) }{\Gamma \left( {{\phi }_{2}^{*} } \right) \Gamma \left( {{\phi }_{1}^{*} } \right) }} \right| e^{-\,i\,k\,r}\sin \left( k\,r\,\,+\,\,\varpi \,\,-\,\,\frac{k\,\ln 2}{\delta }\,\,+\,\,\frac{\pi }{2}\left[ {l_{D} \,\,+\,\,\frac{\left( {D\,\,-\,\,3} \right) }{2}} \right] \,\,\right. \nonumber \\&\left. +\,\,\frac{\pi }{2}\left[ {l_{D} \,\,+\,\,\frac{\left( {D\,\,-\,\,1} \right) }{2}} \right] \right) . \end{aligned}$$
(36)

Comparing Eq. (36) with the boundary conditions [56],

\(r\rightarrow \,\infty \,\,\Rightarrow \,R\left( \infty \right) \rightarrow \,\,2\sin \,\left( {k\,r\,\,+\,\,\varpi _{l_{D} } \,\,-\,\,\frac{\pi }{2}\left[ {l_{D} \,\,+\,\,\frac{\left( {D\,\,-\,\,3} \right) }{2}} \right] } \right) .\) Hence, the scattering phase shift relation for the Deng–Fan potential in higher dimension becomes

$$\begin{aligned} \varpi _{l_{D} } \,\,= & {} \,\,\frac{\pi }{2}\left[ {l_{D} \,\,+\,\,\frac{\left( {D\,\,-\,\,1} \right) }{2}} \right] \,\,-\,\,\frac{k\,\ln 2}{\delta }\,\,+\,\,\arg \Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} \,\,-\,\,{\phi }_{2} } \right) \,\,-\,\,\arg \Gamma \left( {{\phi }_{3} \,\,-\,\,{\phi }_{1} } \right) \,\,\nonumber \\&-\,\,\arg \Gamma \left( {{\phi }_{3} \,-\,\,{\phi }_{2} } \right) . \end{aligned}$$
(37)

Its corresponding normalization constant gives

$$\begin{aligned} \mathrm{N}_{n,\,\,l_{D} } \,\,=\,\,\frac{1}{\Gamma \left( {{\phi }_{3} } \right) }\,\left| {\frac{\Gamma \left( {{\phi }_{2}^{*} } \right) \Gamma \left( {{\phi }_{1}^{*} } \right) }{\Gamma \left( {\frac{2ik}{\delta }} \right) }} \right| . \end{aligned}$$
(38)
Table 1 Spectroscopic data for LiH and HCl diatomic molecules [49]
Full size table
Table 2 Bound state energy eigenvalues (in eV) of the Deng–Fan potential for LiH at different quantum states in higher dimensions
Full size table
Table 3 Bound state energy eigenvalues (in eV) of the Deng–Fan potential for HCl at different quantum states in higher dimensions
Full size table

4 Results and Discussion

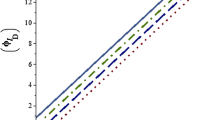
In this work, the hydrogen chloride (HCl) and the lithium hydride (LiH) diatomic molecules are considered. The molecular constants of the selected molecular systems are taken from Ref. [49], as presented in Table 1. The relativistic energy spectra and the corresponding nonrelativistic energy spectra of Deng–Fan potential are presented in Eqs. (15) and (16), respectively in higher dimensions. The bound state energies of the Deng–Fan potential for LiH and HCl diatomic molecules at different quantum states are presented in Tables 2 and 3, respectively at different dimensions. It is seen that the bound state energies increase with increase in the vibrational quantum number, n. For a particular vibrational quantum number, the bound state energies increase with increase in the rotational quantum number, l. In addition, there exists a slow increase in the bound state energies for each quantum state considered, as the dimension increases. This shows that the energy spectra of the diatomic molecules are more bounded at higher dimensions. Our results in Table 4 show that the computed results agree perfectly with the results obtained in Ref. [49] in three dimensions. In all the computation given in Tables 2, 3 and 4, the dissociation energy \(d_{e} \) has been used as reference level for the bound states solutions. The scattering state phase shift relation of the Deng–Fan potential in higher dimension is presented in Eq. (37) and its corresponding normalization constant is given in Eq. (38). The numerical results of the scattering state phase shift of the Deng–Fan potential for LiH and HCl diatomic molecules for different dimensions are given in Tables 5 and 6 respectively and the phrase shifts are expressed in radian. It is observed that the scattering phase shift of Deng–Fan potential increases with increase in rotational quantum number, for each dimension. Also, the scattering state phase shift of Deng–Fan potential increases slightly as the dimension increases, for each rotational quantum number. This shows that the diatomic molecules are easily scattered at higher dimensions than at lower dimensions. In addition, inter-dimensional degeneracy symmetry \(\left( {\varpi _{l}^{\,D} \,\,=\,\,\varpi _{l\,-\,1}^{\,D\,+\,2} } \right) \) is observed in the results for both the bound state energies and scattering state phase shift of the Deng–Fan potential for LiH and HCl diatomic molecules. Hence, the bound state energies and the scattering state phase shift of the Deng–Fan potential for LiH and HCl diatomic molecules are invariant under a transformation of an increase in the higher dimension by two \(\left( {D\,\,\rightarrow \,\,D\,+\,2} \right) \) and a decrease in the rotational quantum number by one \(\left( {l\,\,\rightarrow \,\,l\,\,-\,1} \right) \) which implies that there exists an inter-dimensional degeneracy symmetry for the D-dimensional relativistic rotation-vibration energy spectra of the Deng–Fan potential .The variations of the scattering state phase shift with rotational quantum numbers, at different dimensions for LiH and HCl diatomic molecules are presented in Figs. 1 and 2, respectively. Figure 1 shows a direct increase in the scattering state phase shift of Deng–Fan potential for LiH diatomic molecule as the rotational quantum number increases, for the different dimensions considered. In Fig. 2, the scattering state phase shift of the Deng–Fan potential for HCl diatomic molecule increases to a peak value as the rotational quantum number increases for each dimension. Beyond a specific value of the rotational quantum number, the scattering state phase shift begins to decrease and later increases as the rotational quantum number increases. It can be deduced that the scattering state phase shift of Deng–Fan potential for LiH and HCl diatomic molecules largely depend on the rotational quantum number for the dimensions considered. This is because nuclear and molecular potentials model are state dependent [57,58,59] and are characterised by the strength and range parameters which have many applications for obtaining the p- and d-wave scattering phase factor [60].

Table 4 Bound state energy eigenvalues (in eV) of the Deng–Fan potential for LiH and HCl at different quantum states in three dimensions
Full size table
Table 5 Scattering Phase Shift of LiH diatomic molecules at different dimensions
Full size table
Table 6 Scattering Phase Shift of HCl diatomic molecules at different dimensions
Full size table
Fig. 1
figure 1

Variation of Scattering phase shift with rotational quantum number of LiH for various dimensions

Full size image
Fig. 2
figure 2

Variation of Scattering phase shift with rotational quantum number of HCl for various dimensions

Full size image

5 Concluding Remarks

This study is devoted to the study of the bound state solutions, the scattering phase shift factor and the normalization constant of the Klein–Gordon equation (KGE) with the Deng–Fan potential in higher dimensions using the framework of Nikiforov-Uvarov-Functional Analysis (NUFA) method. Numerical results of the bound state energies and the scattering states phase shift were obtained for lithium hydride (LiH) and hydrogen chloride (HCl) diatomic molecules for various dimensions. In addition, the variations of the bound state energies and scattering state phase shift with rotational and vibrational quantum numbers have been discussed extensively. We have shown that the bound state energies and the scattering state phase shift of the Deng–Fan potential model depend on the angular momentum quantum numbers for the diatomic molecule systems considered. In our study, inter-dimensional degeneracy symmetry was seen to occur in the various bound state energy and scattering phase shift results for the LiH and HCl diatomic molecules at higher dimensions. This study will be very relevant in many areas of physics where the concepts of scattering and dimensional scaling are of great importance [61,62,63]. It is worthy to note that it has been shown by Jia et al. [64] that the behavior of the D-dimensional relativistic vibrational energies remains similar to that of the three dimensional non-relativistic system. Finally, the concepts of D-dimensional scaling techniques has been recently employed in physics and chemistry to study multiparticles systems in molecular quantum mechanics, even though the study of the D-dimensional scaling is restricted to ground and first excited energies of quantum system [65]. It will be a good task for researchers to investigate this present work using D-dimensional scaling techniques.