1 Introduction

Many years ago, the Morse potential model was proposed to describe the molecular vibrations of diatomic and polyatomic molecules [1,2,3]. This potential model has been employed to obtain solutions of the relativistic and nonrelativistic quantum mechanical problems in physics and chemistry. Its importance spans through different areas of study, including atomic and molecular physics [4, 5]. The Klein–Gordon equation is a relativistic wave equation that has been used to describe dynamic spin zero particles in the relativistic quantum mechanics [6]. Researchers over the years have carried out investigations to obtain the exact or approximate solutions of KGE with different potential models [7,8,9,10,11,12,13,14,15,16] using different analytical techniques [17,18,19,20,21,22,23,24,25,26,27,28,29,30] within the framework of relativistic and nonrelativistic quantum mechanics [31,32,33,34,35,36,37]. By employing the exact quantization rule, Qiang and Dong [38] studied the radial Schrodinger equation for the rotating Morse potential using the Pekeris approximation [39, 40]. In the study, the authors obtained the energy levels for some certain diatomic molecules and also compared their results with the results obtained by other researchers using other techniques. Bayrak et al. [41] studied the bound state solutions of the Klein–Gordon equation for equal scalar and vector Morse potentials, using the asymptotic iteration method. Sun [42] also studied the one-dimensional Klein–Gordon equation with the Morse potential, using the exact quantization rule. By employing the parametric Nikiforov–Uvarov (pNU) method and the Pekeris approximation scheme, Ikhdair [43] considered the spatially dependent mass Schrodinger equation of diatomic molecules for the generalized q-deformed Morse potential. Within the framework of Dirac equation, Agboola [44] presented the solutions of the rotation vibrational motion of diatomic molecules with position-dependent mass for repulsive vector and attractive scalar q-deformed Morse potential. Also, using the supersymmetric and shape invariance approach, Jia and Cao [45] solved the Klein–Gordon equation with the Morse potential energy model. The authors obtained both the bound state energies and the relativistic vibrational transition frequency for the scandium iodide (ScI) diatomic molecule. Their results agreed with the experimental results in literature. In a similar development, Ortakaya [46] obtained the approximate analytical solution of the Klein–Gordon equation with equal scalar and vector q-deformed Morse potential for arbitrary l-states, using the Laplace integral transform. Recently, a numerical algorithm to determine the solution of the time-dependent fractional Schrodinger equation for Morse potential has been developed, using the method of numerical integration and Riemann–Liouville definition [47]. The authors also obtained the numerical results of the wave function and the probability functions of the Morse potential for hydrogen chloride and hydrogen fluoride. Before now, different authors have employed various potential functions to study the thermodynamic properties of different systems, using numerous techniques [48,49,50,51,52,53,54,55,56]. Recently, Boumali [57] presented the closed-form expressions of the vibrational partition function and other related thermodynamic functions for the one-dimensional q-deformed Morse potential energy model, using the Euler–Maclaurin method [58]. Also, the thermal properties of three-dimensional Morse potential for some selected diatomic molecules were obtained [59] using Euler–Maclaurin method. In addition, quantum information theory has been studied with the Morse potential system [60, 61]. In this study, the generalized Morse potential (GMP) is proposed to be

$$V\left( r \right)\,\, = \,\,D_{0} \left( {1 - e^{{ - \alpha \left( {r - r_{e} } \right)}} } \right)^{2} + D_{1} \left( {q - e^{{ - \alpha \left( {r - r_{e} } \right)}} } \right)^{2} ,$$
(1)

where \(D_{0}\) and \(D_{1}\) describe the depths of the generalized Morse potential, \(r_{e}\) represents the equilibrium bond length or the distance at which the Morse potential equals zero, \(\alpha\) represents the range of the generalized Morse potential, and \(q\) is the deformation parameter, \(\left( {q\,\, > \,\,0} \right)\). The aim of the present study is to study the Klein–Gordon equation with the generalized Morse potential model of Eq. 1 using the Nikiforov–Uvarov-functional analysis (NUFA) method and also to investigate the effects of the \(q\) parameters on the energy spectra of the system and the thermodynamic functions of the system at the nonrelativistic limit.

This study is organized as follows: In Sect. 2, we review the theory of NUFA method for solving central potentials and Sect. 3 is devoted to the solutions of the Klein–Gordon equation with generalized Morse potential using NUFA method. In Sect. 4, the thermodynamic properties of the generalized Morse potential are evaluated. Section 5 is given to results and discussion. Finally, a brief conclusion is given in Sect. 6.

2 Nikiforov-Functional Analysis (NUFA) Method

Recently, the NUFA method [62] was proposed for solving exponential type potential using the concepts of NU method [18], parametric NU method [21], and the functional analysis method [63]. Here, a new version of NUFA method is proposed for solving central potentials which leads to confluent hypergeometric function. Now considering the parametric form of NU proposed by Tezcan and Sever [21] of the form

$$\psi^{\prime\prime} + \frac{{\alpha_{1} - \alpha_{2} s}}{{s\left( {1 - \alpha_{3} s} \right)}}\psi^{\prime} + \frac{1}{{s^{2} \left( {1 - \alpha_{3} s} \right)^{2} }}\left[ { - \xi_{1} s^{2} + \xi_{2} s - \xi_{3} } \right]\,\,\psi (s) = 0,$$
(2)

where \(\alpha_{i}\) and \(\xi_{i} (i = 1,\;2,\;3)\) are all parameters. It can be observed in Eq. 2 that the differential equation has two singularities at \(s \to 0\) and \(s \to \frac{1}{{\alpha_{3} }}\), and this solution has been reported in the NUFA method [62]. However, the intention here is to develop a simple and elegant method for solving Eq. 2 when \(\alpha_{3} \to 0\). Therefore, as \(\alpha_{3} \to 0\), Eq. 2 becomes

$$\psi (s) = e^{ - \mu s} s^{\nu } f(s).$$
(3)

Substituting Eq. 3 into Eq. 2 leads to the following equation:

$$\begin{aligned} sf^{\prime\prime}(s) + \left[ {\alpha_{1} + 2\nu - \left( {2\mu + \alpha_{2} } \right)s} \right]f^{\prime}(s) - \left( {2\mu \nu + \alpha_{1} \mu + \alpha_{2} \nu - \xi_{2} } \right)f(s) \hfill \\ \quad + \left[ {\frac{{\nu \left( {\nu - 1} \right) + \alpha_{1} \nu - \xi_{3} }}{s}} \right]f(s) + \left[ {\mu^{2} + \alpha_{2} \mu - \xi_{1} } \right]sf(s) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{aligned}$$
(4a)

Equation 4a can be reduced to a confluent hypergeometric equation if we set \(y = \left( {2\mu + \alpha_{2} } \right)s\) and we get

$$\begin{aligned} yf^{\prime\prime}(y) + \left[ {\alpha_{1} + 2\nu - y} \right]f^{\prime}(y) - \frac{{\left( {2\mu \nu + \alpha_{1} \mu + \alpha_{2} \nu - \xi_{2} } \right)}}{{2\mu + \alpha_{2} }}f(y) \hfill \\ + \left[ {\frac{{\nu \left( {\nu - 1} \right) + \alpha_{1} \nu - \xi_{3} }}{y}} \right]f(s) + \left[ {\frac{{\mu^{2} + \alpha_{2} \mu - \xi_{1} }}{{\left( {2\mu + \alpha_{2} } \right)^{2} }}} \right]yf(y) = 0\,\,\,\,\,\,\,\, \hfill \\ \end{aligned}$$
(4b)

Equation 4b becomes confluent hypergeomtric function, if and only if the last two terms in \(\frac{1}{y}\) and \(y\) vanished. That is,

$$\nu \left( {\nu - 1} \right) + \alpha_{1} \nu - \xi_{3} = 0,$$
(5)
$$\left[ {\frac{{\mu^{2} + \alpha_{2} \mu - \xi_{1} }}{{\left( {2\mu + \alpha_{2} } \right)^{2} }}} \right] = 0.$$
(6)

Therefore, Eq. 4b can now be written as

$$yf^{\prime\prime}(y) + \left[ {\alpha_{1} + 2\nu - y} \right]f^{\prime}(y) - \frac{{\left( {2\mu \nu + \alpha_{1} \mu + \alpha_{2} \nu - \xi_{2} } \right)}}{{2\mu + \alpha_{2} }}f(y) = 0.$$
(7)

The values of \(\mu\) and \(\nu\) can be obtained by solving Eqs. 6 and 7 explicitly as

$$\mu = \frac{{ - \alpha_{2} \pm \sqrt {\alpha_{2}^{2} + 4\xi_{1} } }}{2}\,$$
(8)
$$\nu = \frac{{ - \left( {\alpha_{1} - 1} \right) \pm \sqrt {\left( {\alpha_{1} - 1} \right)^{2} + 4\xi_{3} } }}{2}$$
(9)

Equation 7 is the confluent hypergeometric equation type of the form [63],

$$xf^{\prime\prime}(x) + \left[ {c - x} \right]f^{\prime}(x) - af(x) = 0,$$
(10)

which has a regular singularity at \(x = 0\) and irregular singularity at \(x = \infty\). The energy eigenvalues is defined from Eq. 7 as \(\frac{{\left( {2\mu \nu + \alpha_{1} \mu + \alpha_{2} \nu - \xi_{2} } \right)}}{{2\mu + \alpha_{2} }} = - n\) which can be expressed explicitly as

$$\left( {2\mu \nu + \alpha_{1} \mu + \alpha_{2} \nu - \xi_{2} } \right) + n\left( {2\mu + \alpha_{2} } \right) = 0.$$
(11)

The corresponding wave function is given by [63]

$$f(y) = {}_{1}F_{1} \left( {a;c;s} \right) = 1 + \frac{a}{c}\frac{y}{1!} + \frac{a(a + 1)}{c(c + 1)}\frac{{y^{2} }}{2!} + \cdots .$$
(12)

Thus, the total wave function is written as

$$\psi (s) = Ne^{ - \mu s} s^{\nu } {}_{1}F_{1} \left( { - n,\left( {\alpha_{1} + 2\nu } \right);\left( {\alpha_{2} + 2\mu } \right)s} \right).$$
(13)

With Eqs. 8, 9, 11, and 12, one can determine the energy spectra and the corresponding wave function for any central potential. This analysis is the new version of the NUFA method for solving Schrödinger, Klein-Gordon, and Dirac equations with central potentials. In the next section, the new version of the NUFA will be used to calculate the energy spectra and the corresponding wave function of the Klein–Gordon equation with generalized Morse potential.

3 Solutions of Klein–Gordon Equation for Generalized Morse Potential (GMP)

In this section, the energy spectra and the wave function of the Klein–Gordon equation for equal vector and scalar GMP will be calculated using the new version of the NUFA method. The Klein–Gordon equation in spherical coordinate for spin zero particles is defined as [64]

$$\left[ {\frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} \frac{\partial }{\partial r}} \right) + \frac{1}{{r^{2} \sin \theta }}\frac{\partial }{\partial \theta }\left( {\sin \theta \frac{\partial }{\partial }} \right) + \frac{1}{{r^{2} \sin^{2} \theta }}\frac{{\partial^{2} }}{{\partial \varphi^{2} }} - \left( {\frac{{E + mc^{2} }}{{\hbar^{2} c^{2} }}} \right)V(r) + \left( {\frac{{E^{2} - m^{2} c^{4} }}{{\hbar^{2} c^{2} }}} \right)} \right]\psi \left( {r,\theta ,\varphi } \right) = 0$$
(14)

where m is the mass of the particles, \(\hbar = \frac{h}{2\pi }\) is the reduced Planck’s constant, \(E\) is the energy level of the system, c is the speed of light, \(V(r)\) is the interacting potential function, and \(\psi \left( {r,\theta ,\phi } \right)\) is the a corresponding wave function. The spherical symmetric of Eq. 14 allows us to write the wave function as

$$\psi_{nlm} (r,\theta ,\phi ) = \frac{{R_{nl} (r)Y_{lm} (\theta ,\phi )}}{r},$$
(15)

where \(Y_{lm} (\theta ,\phi )\) is the spherical harmonics and defined as

$$Y_{lm} (\theta ,\phi ) = \frac{1}{{\sqrt {2\pi } }}e^{{im_{l} \phi }} P_{l}^{m} \left( {\cos \theta } \right),$$
(16)

where \(m_{l}\) is the magnetic quantum number and \(P_{l}^{m} (\cos \theta )\) is the associate Legendre polynomial. Substituting Eqs. 1 and 15 into Eq. 14 results in the Klein–Gordon equation with equal vector and scalar generalized Morse potential given as

$$\frac{{d^{2} R_{nl} (r)}}{{dr^{2} }} + \left[ {\frac{{E^{2} - m^{2} c^{4} }}{{\hbar^{2} c^{2} }} - \frac{{\left( {E + mc^{2} } \right)}}{{\hbar^{2} c^{2} }}\left\{ {D_{0} \left( {1 - e^{{ - \alpha \left( {r - r_{e} } \right)}} } \right)^{2} + D_{1} \left( {q - e^{{ - \alpha \left( {r - r_{e} } \right)}} } \right)^{2} } \right\} - \frac{{l\left( {l + 1} \right)}}{{r^{2} }}} \right]R_{nl} (r) = 0\,$$
(17)

Now let \(x = \frac{{r - r_{e} }}{{r_{e} }},\alpha = ar_{e}\) with the following abbreviations:

$$\varepsilon^{2} = \left( {\frac{{E^{2} - m^{2} c^{4} }}{{\hbar^{2} c^{2} }}} \right)r_{e}^{2} ,\,$$
(18a)
$$\lambda = \frac{{\left( {E + mc^{2} } \right)D_{0} r_{e}^{2} }}{{\hbar^{2} c^{2} }},\,$$
(18b)
$$\sigma = \frac{{\left( {E + mc^{2} } \right)D_{1} r_{e}^{2} }}{{\hbar^{2} c^{2} }}\,$$
(18c)

then Eq. 17 becomes

$$\frac{{d^{2} R_{nl} (x)}}{{dx^{2} }} + \left[ {\varepsilon^{2} - \lambda \left( {1 - e^{ - \alpha x} } \right)^{2} - \sigma \left( {q - e^{ - \alpha x} } \right)^{2} - \frac{{l\left( {l + 1} \right)r_{e}^{2} }}{{r^{2} }}} \right]R_{nl} (x) = 0\,$$
(19)

It is well known that Eq. 19 cannot be solved exactly because of the centrifugal barrier term \(\frac{{l(l + 1)r_{e}^{2} }}{{r^{2} }}\). In order to over this difficulty, a Pekeris approximation scheme [39] is employed to overcome the centrifugal term. Pekeris [39] expressed the centrifugal term around \(x = 0\) as

$$\frac{{l\left( {l + 1} \right)r_{e}^{2} }}{{r^{2} }} \approx \frac{{l\left( {l + 1} \right)}}{{\left( {1 + x} \right)^{2} }} \approx l\left( {l + 1} \right)\left( {1 - 2x + 3x^{2} - {\rm O}\left( {x^{3} } \right)} \right).$$
(20)

Subsequently, the centrifugal term can also be expressed in terms of the exponential term up to second order as follows:

$$\frac{{l\left( {l + 1} \right)r_{e}^{2} }}{{r^{2} }} \approx l\left( {l + 1} \right)\left( {C_{0} + C_{1} e^{ - \alpha x} + C_{2} e^{ - 2\alpha x} } \right).$$
(21)

Now expanding the exponential terms in Eq. 21 up to second order and comparing with Eq. 20, the expressions for the coefficients \(C_{0} ,C_{1}\), and \(C_{2}\) becomes

$$C_{0} = 1 - \frac{3}{\alpha } + \frac{3}{{\alpha^{2} }},\,\,C_{1} = \frac{4}{\alpha } - \frac{6}{{\alpha^{2} }},\,\,C_{2} = \frac{3}{{\alpha^{2} }} - \frac{1}{\alpha }.$$
(22)

By substitution of Eq. 21 into Eq. 19 with a new coordinate transformation, \(z = e^{ - \alpha x}\), the radial Klein–Gordon equation with the generalized Morse potential becomes

$$\begin{aligned}& R^{\prime\prime}_{nl} + \frac{1}{z}R^{\prime}_{nl} \hfill \\& + \frac{1}{{z^{2} }}\left[ { - \left( {\frac{{\lambda + \sigma + l(l + 1)C_{2} }}{{\alpha^{2} }}} \right)z^{2} + \left( {\frac{{2\lambda + 2q\sigma - l(l + 1)C_{1} }}{{\alpha^{2} }}} \right)z - \left( {\frac{{\lambda + q^{2} \sigma + l(l + 1)C_{0} - \varepsilon^{2} }}{{\alpha^{2} }}} \right)} \right]R_{nl} = 0\, \hfill \\ \end{aligned}$$
(23)

Equation 23 can now be solved with the new version of the NUFA method. Comparing Eq. 23 with Eq. 2 results in the following expressions:

$$\begin{aligned} \alpha_{1} = 1,\,\,\alpha_{2} = \alpha_{3} = 0,\,\,\xi_{1} = \left( {\frac{{\lambda + \sigma + l(l + 1)C_{2} }}{{\alpha^{2} }}} \right), \hfill \\ \xi_{2} = \left( {\frac{{2\lambda + 2q\sigma - l(l + 1)C_{1} }}{{\alpha^{2} }}} \right),\,\,\xi_{3} = \left( {\frac{{\lambda + q^{2} \sigma + l(l + 1)C_{0} - \varepsilon^{2} }}{{\alpha^{2} }}} \right). \hfill \\ \end{aligned}$$
(24)

With Eqs. 8 and 9, \(\mu\) and \(\nu\) can be obtained as follows:

$$\mu = \frac{1}{\alpha }\sqrt {\lambda + \sigma + l\left( {l + 1} \right)C_{2} } \,\,;\,\,\,\nu = \pm \frac{1}{\alpha }\sqrt {\lambda + q^{2} \sigma + l(l + 1)C_{0} - \varepsilon^{2} }$$
(25)

The energy eigenvalues and the corresponding wave function are now obtained using Eqs. 11 and 13 as

$$E^{2} - m^{2} c^{4} = \frac{{\hbar^{2} c^{2} }}{{r_{e}^{2} }}\left( {\lambda + q^{2} \sigma + l(l + 1)C_{0} } \right) - \frac{{\hbar^{2} c^{2} \alpha^{2} }}{{r_{e}^{2} }}\left[ {\frac{{\left( {2\lambda + 2q\sigma - l(l + 1)C_{0} } \right)}}{{\alpha \sqrt {\lambda + \sigma + l\left( {l + 1} \right)C_{0} } }} - \left( {n + \frac{1}{2}} \right)} \right]^{2}$$
(26)
$$R_{nl} (z) = Ne^{ - \mu z} z^{\nu } {}_{1}F_{1} \left( { - n,\left( {1 + 2\nu } \right)\,;\,\,z} \right),$$
(27)

where N is the normalization constant. The confluent hypergeometric function in Eq. 27 can be written in terms of Laquerre’s polynomial whose property is defined as

$$_{1} F_{1} \left( { - n,p + 1,s} \right) = \frac{{n\varGamma \left( {\left( {n + p + 1} \right)} \right)}}{{\varGamma \left( {p + 1} \right)}}L_{n}^{p} (s),$$
(28)

where \(L_{n}^{p} (s)\) is the Laguerre polynomial. With Eq. 28, the wave function in Eq. 27 becomes

$$R_{nl} (z) = Ne^{ - \mu z} z^{\nu } L_{n}^{2\nu } \left( {2\mu z} \right).$$
(29)

4 Euler–Maclaurin Method and the Thermal Properties of Generalized Morse Potential Model at the Nonrelativistic Limit

In this section, the obtained energy spectra will be used at the nonrelativistic limits to study the thermodynamic properties of the systems using Euler–Maclaurin method. Now mapping \(E_{nl} + mc^{2} \to 2mc^{2} ,E - mc^{2} \to E_{nl}\), the solution of the Klein–Gordon equation with generalized Morse potential in the nonrelativistic limit becomes

$$E_{nl} = \,\,G_{1} \,\, - \,\,H\left[ {\frac{{G_{2} }}{{G_{3} }} - \left( {n + \frac{1}{2}} \right)} \right]^{2} ,$$
(30)

where

$$\begin{aligned} H\,\, = \,\,\frac{{\hbar^{2} \alpha^{2} }}{{2mr_{e}^{2} }}\,;\,\,\lambda^{\prime} = \frac{{2mD_{0} r_{e}^{2} }}{{\hbar^{2} }};\,\,\,\sigma^{\prime} = \frac{{2mD_{1} r_{e}^{2} }}{{\hbar^{2} }}\,\,\,;\,\,G_{1} \,\, = \,\,\frac{{\hbar^{2} }}{{2mr_{e}^{2} }}\left( {\lambda^{\prime} + q^{2} \sigma^{\prime} + l(l + 1)C_{0} } \right)\,;\,\,\,\,\, \hfill \\ G_{2} \,\, = \,\,\left( {2\lambda^{\prime} + 2q\sigma^{\prime} - l(l + 1)C_{0} } \right)\,;\,\,G_{3} \,\, = \,\,\alpha^{2} \left( {1 + \sqrt {1 + \frac{{4\left( {\lambda^{\prime} + \sigma^{\prime} + l(l + 1)C_{2} } \right)}}{{\alpha^{2} }}} } \right)\, \hfill \\ \end{aligned}$$
(31)

In order to calculate the thermal properties of the system, it is necessary to calculate first its partition function. The partition function in statistical physics which is a function of temperature is usually regarded as the distribution function, and once it is known, then other thermal properties can be obtained from it, such as entropy, internal energy, specific heat capacity, and Helmholtz free energy. These thermal properties of the system can either be calculated theoretically or experimentally [65,66,67,68]. The bound state contributions to the vibrational partition function of any system at a given temperature T is given as [69]

$$Z\left( {\beta ,N_{\text{max} } } \right) = \sum\limits_{n = 0}^{{N_{\text{max} } }} {e^{{ - \beta \left( {E_{n} \, - \,E_{0} } \right)}} } ,\,\,\beta = \left( {k_{B} T} \right)^{ - 1} ,$$
(32)

where \(k_{B}\) is the Boltzmann’s constant, \(N_{\text{max} }\) is the upper bound quantum number which is obtained using the expression \(\frac{{dE_{n} }}{dn}\,\, = \,\,0\), \(E_{n}\) is the vibrational energy eigenvalues of the generalized potential, and \(E_{0}\) is the ground state energy. The vibrational partition function can be evaluated using the Euler–Maclaurin formula, as defined as [57,58,59]

$$\sum\limits_{n\, = \,0}^{\infty } {f\left( x \right)\,\, = \,\,\frac{1}{2}f\left( 0 \right)\,\, + \,\,\int\limits_{0}^{\infty } {f\left( x \right)dx\,\, - \,\,\sum\limits_{p\, = \,1}^{\infty } {\frac{{B_{2p} }}{{\left( {2p} \right)!}}f^{{\left( {2p\, - \,1} \right)}} \left( 0 \right)} } }$$
(33)

Here, \(B_{2p}\) are the Bernoulli numbers, \(f^{{\left( {2p\, - \,1} \right)}}\) is the derivative of order \(\left( {2p\, - \,1} \right)\). Taking \(p\) up to \(3\), we have

$$Z\left( {\beta ,\,N_{\text{max} } } \right)\,\, = \,\,\frac{1}{2}\,\, + \,\,\int\limits_{0}^{{N_{\text{max} } }} {f\left( n \right)dn\,\, - \,\,\sum\limits_{p\, = \,1}^{\infty } {\frac{{B_{2p} }}{{\left( {2p} \right)!}}f^{{\left( {2p\, - \,1} \right)}} \left( 0 \right)} }$$
(34)

where \(f\left( n \right)\,\, = \,\,e^{{ - \,\beta \left( {E_{n\ell } \,\, - \,\,E_{0\ell } } \right)}}\), \(B_{2} \,\, = \,\,\frac{1}{6}\), and \(B_{4} \,\, = \,\, - \frac{1}{30}\). Using the Mathematica software and the Euler–Maclaurin formula, the expression for the vibrational partition function of the generalized Morse potential is obtained as follows:

$$Z\left( {\beta ,\,N_{\text{max} } } \right)\,\, = \,\,\frac{1}{2}\,\, + \,\,\frac{{e^{{\left( {E_{0l} \,\, - \,\,G_{1} } \right)\beta }} \sqrt \pi \left( { - \,Erfi\left[ {\left( {\frac{1}{2}\, - \,\frac{{G_{2} }}{{G_{3} }}} \right)\sqrt {H\beta } } \right]\,\, + \,\,Erfi\left[ {\sqrt {H\beta } \left( {\frac{1}{2}\, - \,\frac{{G_{2} }}{{G_{3} }}\, + \,\,N_{\text{max} } } \right)} \right]} \right)}}{{2\sqrt {H\beta } }}\,\, + \,\,\frac{H\beta }{6}\left( {\frac{1}{2}\, - \,\frac{{G_{2} }}{{G_{3} }}} \right),$$
(35)

where the \(Erfi\left( z \right)\) is the imaginary error function defined as [69]

$$Erfi\left( z \right)\, = \,iErf\left( z \right)\, = \,\frac{2}{\sqrt \pi }\int\limits_{0}^{z} {e^{{u^{2} }} du}$$
(36)

Other thermodynamic functions, such as vibrational free energy \(F\left( {\beta ,\,\,N_{\text{max} } } \right)\), vibrational internal energy \(U\left( {\beta ,\,\,N_{\text{max} } } \right)\), vibrational entropy \(S\left( {\beta ,\,\,N_{\text{max} } } \right)\), and vibrational specific heat capacity \(C_{v} \left( {\beta ,\,\,N_{\text{max} } } \right)\) can be obtained from the vibrational partition function as follows:

$$\begin{aligned} F\left( {\beta ,\,\,N_{\text{max} } } \right) = - \,\,\frac{1}{\beta }\ln Z\left( {\beta ,\,\,N_{\text{max} } } \right);\,\,\,U\left( {\beta ,\,\,N_{\text{max} } } \right) = - \,\,\frac{{\partial \left( {\ln Z\left( {\beta ,\,\,N_{\text{max} } } \right)} \right)}}{\partial \beta }; \hfill \\ S\left( {\beta ,\,\,N_{\text{max} } } \right)\,\, = \,\, - \,\,k_{B} \frac{{\partial F\left( {\beta ,\,\,N_{\text{max} } } \right)}}{\partial \beta };\,\,\,C_{v} \left( {\beta ,\,\,N_{\text{max} } } \right)\,\, = \,\,k_{B} \frac{{\partial U\left( {\beta ,\,\,N_{\text{max} } } \right)}}{\partial \beta } \hfill \\ \end{aligned}$$
(37)

5 Results and Discussion

In this study, the following parameters have been employed throughout our analysis:

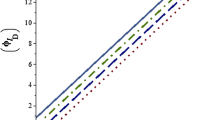
\(m\,\, = \,\,\hbar \, = \,\,k_{B} \, = \,\,1\,;\,\,n\,\, = \,\,2;\,\,l\,\, = \,\,0\,;\,\,D_{0} \, = \,\,3\,;\,\,D_{1} \, = \,\,2\,;\,\,r_{e} \,\, = \,\,1.5\,\,\,{\text{and}}\,\,\alpha \,\, = \,\,0.1\). First, the plots of the nonrelativistic energy spectra of the generalized Morse potential as a function of the potential parameters and quantum numbers are presented in Fig. 1a–f. It was observed there exists a monotonous increase in the energy eigenvalues as \(D_{0}\) and \(D_{1}\) get increased, as shown in Fig. 1a and b, respectively. In Fig. 1c, the energy eigenvalues increase to a peak value for each deformation parameter when \(r_{e} \, \simeq \,\,0\). As \(r_{e}\) increases to about \(1\), there exists a monotonous decrease in energy eigenvalues to a specific value for each deformation parameter. As \(r_{e}\) is further increased, constant values of the energy eigenvalues for each deformation parameter were obtained. The energy eigenvalues of the generalized Morse potential are seen to increase to a certain value and then decrease, as \(\alpha\) and \(n\) increase for the deformation parameters considered. This is demonstrated in Fig. 1d and e, respectively. In Fig. 1f, there exists a direct increase in the energy eigenvalues as \(l\) increases. In addition, it was observed that the energy eigenvalues of the generalized Morse potential increase as the deformation parameter increases. The effects of the deformation parameter on the thermodynamic properties of the generalized Morse potential as a function of temperature are analyzed as shown in Fig. 2a–e. Here, a monotonous increase in vibrational partition function, vibrational internal energy, and vibrational entropy is observed as temperature increases, as shown in Fig. 2a, c and d, respectively. In Fig. 2b, the vibrational free energy decreases as temperature is increased. Also, a monotonous decrease in vibrational specific heat capacity to the origin is observed as temperature is increased. As the temperature is further enhanced beyond \(50\,{\text{K}}\), the vibrational specific heat capacity remains constant at the origin for the selected deformation parameters. The effects of deformation parameter on the thermodynamic properties of the generalized Morse potential as a function of the upper bound vibration quantum number are shown in Fig. 3a–e. The vibrational partition function, vibrational internal energy, and vibrational entropy increase monotonously as \(N_{\text{max} }\) increases, as shown in Fig. 3a, c, and d, respectively. Figure 3b shows a monotonous decrease in vibrational free energy as \(N_{\text{max} }\) increases. In Fig. 3e, the vibrational specific heat capacity increases sharply at \(N_{\text{max} } \, \simeq \,\,0\) to a particular value, for all the deformation parameter considered. As \(N_{\text{max} }\) is increased beyond the origin, a unique decrease and increase phenomenon of the vibrational specific heat capacity for each of the deformation parameter is observed. The plots of the wave function of the generalized Morse potential as a function of position for the ground, first, and second excited states corresponding to \(n = \,\,0,\,\,1\), and 2 for various deformation parameters \(q = \,\,1,\,\,2,\,\,3\), and \(4\), respectively, are displayed in Fig. 4a–c. It is also known that the information of a particle is given by the probability density \(\rho \,\,\left( r \right) = \,\,\left| {\psi_{nlm} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} )} \right|^{2} .\) In Fig. 4d–f, the probability densities of the generalized Morse potential for the three states corresponding to the ground, first, and second excited states for various deformation parameters \(q = 1,\,\,2,\,\,3\), and \(4\), respectively, are plotted.

Fig. 1
figure 1

(a) Variation of the nonrelativistic energy eigenvalues of generalized Morse potential with \(D_{0}\) for various deformation parameters; (b) Variation of the nonrelativistic energy eigenvalues of generalized Morse potential with \(D_{1}\) for various deformation parameters; (c) Variation of the nonrelativistic energy eigenvalues of generalized Morse potential with \(r_{e}\) for various deformation parameters; (d) Variation of the nonrelativistic energy eigenvalues of generalized Morse potential with \(\alpha\) for various deformation parameters; (e) Variation of the nonrelativistic energy eigenvalues of generalized Morse potential with \(n\) for various deformation parameters; (f) Variation of the nonrelativistic energy eigenvalues of generalized Morse potential with \(l\) for various deformation parameters

Full size image
Fig. 2
figure 2

(a) Variation of the vibrational partition function of generalized Morse potential with temperature for various deformation parameters; (b) Variation of the vibrational free energy of generalized Morse potential with temperature for various deformation parameters; (c) Variation of the vibrational internal energy of generalized Morse potential with temperature for various deformation parameters; (d) Variation of the vibrational entropy of generalized Morse potential with temperature for various deformation parameters; (e) Variation of the vibrational specific heat capacity of generalized Morse potential with temperature for various deformation parameters

Full size image
Fig. 3
figure 3

(a) Variation of the vibrational partition function of generalized Morse potential with upper bound vibration quantum number for various deformation parameters; (b) Variation of the vibrational free energy of generalized Morse potential with upper bound vibration quantum number for various deformation parameters; (c) Variation of the vibrational internal energy of generalized Morse potential with upper bound vibration quantum number for various deformation parameters; (d) Variation of the vibrational entropy of generalized Morse potential with upper bound vibration quantum number for various deformation parameters; (e) Variation of the vibrational specific heat capacity of generalized Morse potential with upper bound vibration quantum number for various deformation parameters

Full size image
Fig. 4
figure 4

(a) Variation of the wave function of generalized Morse potential with position at the ground state for various deformation parameters; (b) Variation of the wave function of generalized Morse potential with position at the first excited state for various deformation parameters; (c) Variation of the wave function of generalized Morse potential with position at the second excited state for various deformation parameters; (d) Variation of the probability density of generalized Morse potential with position at the ground state for various deformation parameters; (e) Variation of the probability density of generalized Morse potential with position at the first excited state for various deformation parameters; (f) Variation of the probability density of generalized Morse potential with position at the second excited state for various deformation parameters

Full size image

6 Conclusion

In this study, the generalized Morse potential (GMP) was proposed and its analytical solutions of the Klein–Gordon equation were obtained using the Nikiforov–Uvarov-functional analysis (NUFA) method, for solving central potentials. The effects of the GMP parameters on the energy eigenvalues obtained have been discussed in details for different arbitrary deformation parameters. In addition, plots of the wave function and the probability density as functions of position, corresponding to the ground state, first, and second excited states for the selected deformation parameters have been presented.

By employing the energy eigenvalues of GMP in the nonrelativistic regime, the effects of both temperature and upper bound vibrational quantum number have been graphically illustrated for various deformation parameters, using Euler–Maclaurin formula.

It is seen from our discussion that the deformation parameter has a strong influence on the energy eigenvalues variation and thermodynamic functions of any system considered. Our results are new and they are very promising to be applicable to different fields of study, including chemical physics, atomic, and molecular physics.