1 Introduction

Industry has been looking for a low-cost sensor for many years. The high cost of inertial sensors has hampered their use in medicine, robotics, and automotive applications. Therefore, MEMS gyroscopes have been designed for use in many different applications because of their small size and low-cost. MEMS gyroscope usually use vibrating mechanical element as a sensing element in order to detect the angular velocity (Passaro et al. 2017). Control of a MEMS gyroscope can be taken into consideration when applied in a system. MEMS gyroscopes are constantly subjected to external perturbations and quadrature errors, therefore, a robust control method needs to be used in MEMS gyroscopes in order to suppress these external disturbances.

Many researchers have used the sliding mode controller in MEMS gyroscope applications. Fei and Yuan (2013) considered dynamic sliding mode control for the state tracking of MEMS gyroscopes. The novel switching function is proposed via the method of differentiating the conventional sliding mode surface. Batur et al. (2006) used sliding mode control to ensure the stability of a MEMS gyroscope. The numerical simulations demonstrated that the sliding mode controller appropriately estimated the unknown angular velocity. However, sliding mode control is not applicable in the control of a MEMS gyroscope as it creates a chattering phenomenon, as well as causing low tracking performance and accuracy. In order to solve those problems, researchers have used different techniques in addition to the sliding mode control.

An important tool to be taken into consideration for this difficulty is the Neural network. Zhang et al. (2018) proposed the sliding mode control with composite learning for MEMS gyroscopes in order to improve the system tracking performance, stability, and accuracy. Yang and Fei (2013), proposed an adaptive sliding mode control using a radial basis function (RBF) network in order to estimate the unknown system dynamics for MEMS gyroscopes. Fei and Chu (2016) proposed a new global PID sliding mode controller for MEMS gyroscopes. The main drawbacks of the PID sliding mode controller is the creation of a chattering phenomenon. Therefore, by using a RBF neural network, the chattering phenomenon is eliminated. The neural network has some disadvantages such as long training times, requiring a large amount of training data, and the necessity of fine tuning the network architectures to achieve the best performance. As a result of these problems, scientists have been using another tool for improving control of the MEMS gyroscope.

Fei and Xin (2015) proposed an adaptive fuzzy sliding mode control scheme in order to deal with nonlinearity terms, parameter uncertainties, and external perturbations of MEMS gyroscopes. In order to estimate both the switching control term and the equivalent control term, the adaptive fuzzy control is used. Fang et al. (2015) proposed a Lyapunov based H-infinity control method in order to eliminate the effect of different external disturbances. Fei et al. (2013) proposed an adaptive fuzzy sliding mode control law with bound approximation in order to control the position of a MEMS gyroscope in the presence of external perturbations and model uncertainties. Fuzzy control has been widely used by scholars (Ren et al. 2016; Fang et al. 2014; Fei and Xin 2012), but implementation of such a controller is difficult and needs expert experience of how to choose the fuzzy logic rules.

Additionally, other researchers have pursued the inclusion of new control methods. A new robust compound fractional order integral terminal sliding mode control and proportional-derivative control is proposed for MEMS gyroscopes. The proposed compound controller is free from chattering and has high tracking performance (Rahmani 2018). Rahmani et al. (2018a) proposed a new PID sliding mode control and super-twisting control based on bat algorithm for control of a MEMS gyroscope. Fang et al. (2018) proposed a new adaptive backstepping controller for a MEMS gyroscope. The simulation results validated the suggested control law by showing excellent tracking performance and guaranteed asymptotic stability.

Based on the results of previous studies, a new control method should be designed for control of MEMS gyroscopes. The proposed control method is new, and has not yet been deployed in a MEMS gyroscope.

In particular, a new adaptive fractional sliding mode control is proposed for control of MEMS gyroscopes. The main contributions of the proposed control method, which are novel in comparison to previous studies are:

  1. 1.

    MEMS gyroscope have continuously encountered external perturbations and model uncertainties. A novel fractional integral sliding mode control method is designed to suppress external disturbances.

  2. 2.

    A new robust control method is proposed in order to suppress these external disturbances, the main drawback of this proposed control method is that it is not able track the desired trajectory suitably. Therefore, a new adaptive law is applied to improve tracking performance and accuracy.

  3. 3.

    The stability of the proposed control method is verified via Lyapunov theory.

The rest of this paper is organized as follows. In Sect. 2, the summary has described the dynamic equation of the MEMS gyroscope. In Sect. 3, the new fractional integral sliding mode control is included. In Sect. 4, new adaptive fractional integral sliding mode control has been delineated. Section 5: presents simulation results and provide the conclusion and contributions of the work.

2 Dynamics of MEMS gyroscope

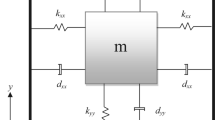
A MEMS z-axis MEMS gyroscope is illustrated in Fig. 1. The dynamics of a MEMS gyroscope has been widely used in different studies.

Fig. 1
figure 1

Structure of a MEMS gyroscope (Rahmani 2018)

Full size image

The main equation of the MEMS gyroscope dynamic model can be denoted as follows (Rahmani 2018):

$$\ddot{q} = - \, \left( {D + 2\varOmega } \right)\dot{q} - K_{b} q + u + E$$
(1)

The Eq. (1) parameters can be shown as below (Rahmani 2018):

$$\begin{aligned} & q = \left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right],\quad u = \left[ {\begin{array}{*{20}c} {u_{x} } \\ {u_{y} } \\ \end{array} } \right],\quad \varOmega = \left[ {\begin{array}{*{20}c} 0 & { - \,\varOmega_{z} } \\ {\varOmega_{z} } & 0 \\ \end{array} } \right] \hfill \\ \hfill \\ & D = \left[ {\begin{array}{*{20}c} {d_{xx} } & {d_{xy} } \\ {d_{xy} } & {d_{yy} } \\ \end{array} } \right],\quad K_{b} = \left[ {\begin{array}{*{20}c} {\omega_{x}^{2} } & {\omega_{xy} } \\ {\omega_{xy} } & {\omega_{y}^{2} } \\ \end{array} } \right], \hfill \\ \end{aligned}$$
(2)

where E is external disturbance. From Eq. (1), the dynamic equations for a MEMS gyroscope becomes (Rahmani 2018):

$$\ddot{q} = - \,Y\dot{q} - \,Pq + u + E,$$
(3)

where Y = (D + 2Ω) and P = Kb. ΔY and ΔP determine some uncertainties of the parameter variations. The Eq. (3) can be denoted as Rahmani (2018):

$$\ddot{q} = - \,(Y + \Delta Y)\dot{q} - (P + \Delta P)q + u(t) + E.$$
(4)

The uncertainties can be described in terms of l and u as lower and upper uncertainty values as shown below:

$$\Delta Y_{l} < \left| {\Delta Y} \right| < \Delta Y_{u} \quad {\text{and}}\quad \Delta P_{l} < \left| {\Delta P} \right| < \Delta P_{u} .$$

3 New fractional integral sliding mode control

Fractional calculus is a conventional method which can be used in different structures (Rahmani et al. 2016a). It is an imortant topic in control system engineering. Fractional order operators can be applied to a sliding mode controller as an effective method to improve its robustness and tracking performance. In addition, choosing a fractional sliding mode surface is the main part of fractional sliding mode control process. If the fractional sliding mode surface is selected appropriately, an excellent control surface can be obtained. The new proposed fractional sliding mode surface can be defined as:

$$s(t) = \dot{e}(t) + \alpha D^{\mu - 2} (e(t)) + \gamma \int_{0}^{t} {(sign(e(\tau )) + sign(\dot{e}(\tau ))} )d\tau ,$$
(5)

where α and γ are positive constants. D = d/dt is fractional order operator.

Where tracking error can be shown as:

$$e(t) = q_{d} - q,$$
(6)

where qd is desired tracking performance. The fractional order operator type is Grunwald–Letnikov (Rahmani and Ghanbari 2016). The reasons why that fractional sliding mode surface is selected are below:

  1. 1.

    \(\dot{e}(t)\) improves tracking performance of the proposed control method.

  2. 2.

    \(\alpha D^{\mu - 2} (e(t))\) improves the robustness of the fractional sliding mode controller.

  3. 3.

    \(\gamma \int_{0}^{t} {(sign(e(\tau )) + sign(\dot{e}(\tau ))} )d\tau\) improves the stability of the proposed control method.

The control input can be defined as follows:

$$u(t) = u_{eq} (t) + u_{r} (t)$$
(7)

where \(u_{eq} (t)\) is the equivalent control and \(u_{r} (t)\) is the reaching control law. In order to obtain the equivalent control scheme, \(s(t)\) need to be equal to zero (\(\dot{s}(t) = 0\)) as shown below:

$$\dot{s}(t) = \ddot{e}(t) + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t))).$$
(8)

Double derivation from Eq. (6) and substitution into Eq. (8) generates:

$$\dot{s}(t) = \ddot{q}_{d} - \ddot{q} + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t))).$$
(9)

By forcing Eq. (9) to be zero, it can be illustrated as:

$$\ddot{q}_{d} - \ddot{q} + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t))) = 0.$$
(10)

Substituting Eq. (3) into Eq. (10) generates:

$$\ddot{q}_{d} + Y\dot{q} + Pq - u - E + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t))) = 0.$$
(11)

The equivalent control method can be shown as:

$$u_{eq} (t) = \ddot{q}_{d} + Y\dot{q} + Pq - E + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t))).$$
(12)

The equivalent control law cannot solely be robust against external perturbations and model uncertainties. In order to solve this problem, a reaching control law can be defined, which improves the robustness of the control method. The reaching control law can be obtained through Lyapunov theory as Rahmani et al. (2016b, 2018b), Rahmani and Ghanbari 2016):

$$L(t) = \frac{1}{2}s^{T} (t)s(t).$$
(13)

The condition for stability can be defined as:

$$\dot{L}(t) = s^{T} (t)\dot{s}(t) < 0,\quad s(t) \ne 0.$$
(14)

Substituting Eq. (9) in Eq. (14) produces:

$$\dot{L}(t) = s^{T} (t)(\ddot{q}_{d} - \ddot{q} + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t)))).$$
(15)

Substituting Eqs. (4) and (7) into Eq. (15) generates:

$$\begin{aligned} \dot{L}(t) & = s^{T} (t)(\ddot{q}_{d} + (Y + \Delta Y)\dot{q} + (P + \Delta P)q - u_{eq} (t) - u_{r} (t) \\ & - \,E + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t)))). \\ \end{aligned}$$
(16)

Substituting Eq. (12) into Eq. (16) produces:

$$\begin{aligned} \dot{L}(t) & = s^{T} (t)(\ddot{q}_{d} + (Y + \Delta Y)\dot{q} + (P + \Delta P)q - \ddot{q}_{d} - Y\dot{q} - Pq + E \\ & - \,(\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t))) - u_{r} (t) \\ & - \,E + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t)))). \\ \end{aligned}$$
(17)

By simplifying Eq. (17), it can be shown as:

$$\begin{aligned} \dot{L}(t) & = s^{T} (t)(\Delta Y\dot{q} + \Delta Pq - u_{r} (t)) \\ & \le \,s^{T} (t)(\left| {\Delta Y} \right|\left| {\dot{q}} \right| + \left| {\Delta P} \right|\left| q \right| - u_{r} (t)). \\ \end{aligned}$$
(18)

The reaching control law need to be chosen in order to guarantee that Eq. (18) is less than zero as shown below:

$$u_{r} (t) = \left| {\Delta Y_{u} } \right|\left| {\dot{q}} \right| + \left| {\Delta P_{u} } \right|\left| q \right|.$$
(19)

Substitution of Eq. (19) into Eq. (18) generates:

$$\dot{L}(t) \le s^{T} (t)((\left| {\Delta Y} \right| - \left| {\Delta Y_{u} } \right|)\left| {\dot{q}} \right| + (\left| {\Delta P} \right| - \left| {\Delta P_{u} } \right|)\left| q \right|).$$
(20)

The Eq. (20) shows that \(\dot{L}(t) \le 0\), which can be taken into consideration when determining that the proposed control method is stable. Therefore, the reaching control law can be defined as follows:

$$u_{r} (t) = K_{r} s(t),$$
(21)

where Kr is reaching control gain.

4 New adaptive fractional integral sliding mode control

Adaptive fractional sliding mode control can improve tracking performance and accuracy. The adaptive law decreases the gain inside and increases the gain outside a vicinity of the sliding surface (Liao et al. 2018). The new adaptive control law can be defined as follows:

$$\dot{\alpha } = \dot{\gamma } = - \,k_{i} sign(s_{i} ) - k_{i} s_{i} ,\quad i = 1,2,3,4,$$
(22)

where ki (i = 1, 2, ….,n) are positive adaptive law gains. The new fractional integral sliding mode control block diagram is shown in Fig. 2.

Fig. 2
figure 2

Block diagram of the proposed fractional integral sliding mode control

Full size image

The Lyapunov theory for the proposed fractional integral sliding mode control can be defined as follows:

$$L(t) = \frac{1}{2}s^{T} (t)s(t) + \frac{1}{{2k_{i} }}\alpha^{2} + \frac{1}{{2k_{i} }}\gamma^{2} .$$
(23)

Derivation from Eq. (23) produces:

$$\dot{L}(t) = s^{T} (t)\dot{s}(t) + \frac{1}{{k_{i} }}\alpha \dot{\alpha } + \frac{1}{{k_{i} }}\gamma \dot{\gamma }.$$
(24)

Substituting Eqs. (4) and (7) into Eq. (24) generates:

$$\begin{aligned} \dot{L}(t) & = s^{T} (t)(\ddot{q}_{d} + (Y + \Delta Y)\dot{q} + (P + \Delta P)q - u_{eq} (t) - u_{r} (t) \\ & - \,E + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t)))) \\ & + \,\frac{1}{{k_{i} }}\alpha \dot{\alpha } + \frac{1}{{k_{i} }}\gamma \dot{\gamma }. \\ \end{aligned}$$
(25)

Substituting Eq. (12) into Eq. (25) produces:

$$\begin{aligned} \dot{L}(t) = \, & s^{T} (t)(\ddot{q}_{d} + (Y + \Delta Y)\dot{q} + (P + \Delta P)q - \ddot{q}_{d} - Y\dot{q} - Pq + E \\ & - \,(\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t))) - u_{r} (t) \\ & - \,E + (\mu - 2)\alpha D^{\mu - 1} (e(t)) + \gamma (sign(e(t)) + sign(\dot{e}(t)))) \\ & + \,\frac{1}{{k_{i} }}\alpha \dot{\alpha } + \frac{1}{{k_{i} }}\gamma \dot{\gamma }. \\ \end{aligned}$$
(26)

By simplifying Eq. (17), and substituting Eq. (22) into Eq. (26), it can be shown as:

$$\begin{aligned} \dot{L}(t) & = s^{T} (t)(\Delta Y\dot{q} + \Delta Pq - u_{r} (t)) - \alpha (sign(s_{i} ) + s_{i} ) - \gamma (sign(s_{i} ) + s_{i} ) \\ & \le \,s^{T} (t)(\left| {\Delta Y} \right|\left| {\dot{q}} \right| + \left| {\Delta P} \right|\left| q \right| - u_{r} (t)) - \left| \alpha \right|\left| {sign(s_{i} ) + s_{i} } \right| - \left| \gamma \right|\left| {sign(s_{i} ) + s_{i} } \right|. \\ \end{aligned}$$
(27)

Substituting Eq. (19) into Eq. (27) generates:

$$\dot{L}(t) \le s^{T} (t)((\left| {\Delta Y} \right| - \left| {\Delta Y_{u} } \right|)\left| {\dot{q}} \right| + (\left| {\Delta P} \right| - \left| {\Delta P_{u} } \right|)\left| q \right|) - \left| \alpha \right|\left| {sign(s_{i} ) + s_{i} } \right| - \left| \gamma \right|\left| {sign(s_{i} ) + s_{i} } \right|.$$
(28)

The Eq. (28) illustrates that \(\dot{L}(t) \le 0\), which can be taken into consideration when evaluating if the proposed control method is stable. As a result of this, the reaching control law can be shown as follows:

$$\begin{aligned} u_{r} (t) = K_{r} s(t), \hfill \\ \hfill \\ \end{aligned}$$
(29)

where Kr is reaching control gain.

5 Simulation results

This research developed a new adaptive fractional integral sliding mode control of MEMS gyroscope. The effectiveness of the proposed control method is validated by numerical simulation in MATLAB Software via ODE45 order.

The new fractional integral sliding mode control parameters are chosen as μ = 1.5, α = 0.75, γ = 0.75, and Kr = 7. The new adaptive fractional integral sliding mode surface parameters are selected as k1 = k2 = k3 = k4 = 0.75.

The desired motion trajectory is determined by qd1 = sin(4.17t) and qd2 = 1.2sin(5.11t).The initial values of the system are selected as \(q_{1} (0) = 0.4,\,q_{2} (0) = 0.6,\,\dot{q}_{1} (0) = 0\,{\text{and}}\,\dot{q}_{2} (0) = 0.\)

The parameters of the MEMS gyroscope are selected as Rahmani (2018):

$$\begin{aligned} & m = 1.8 \times 10^{ - 7} \,{\text{kg}}\quad k_{xy} = 12.779\,{\text{N/m}}\quad d_{xy} = 3.6 \times 10^{ - 7} \,{\text{Ns/m}} \\ & k_{xx} = 63.955\,{\text{N/m}}\quad d_{xx} = 1.8 \times 10^{ - 6} \,{\text{Ns/m}} \\ & k_{yy} 95.92\,{\text{N/m}}\quad d_{yy} 1.8 \times 10^{ - 6} \,{\text{Ns/m}}. \\ \end{aligned}$$

The conventional natural frequency of each axis of a MEMS gyroscope is in the kHz range, so, ω0 is chosen as 1 kHz. It is suitable to choose 1 μm as the reference length q0 when the displacement rang of the MEMS gyroscope in each axis is sub-micrometer level. The unknown angular velocity is assumed Ωz = 100 rad/s. Therefore, the non- dimensional values of the MEMS gyroscope parameters are chosen as Rahmani (2018):

$$\omega_{x}^{2} = 355.3,\;\omega_{y}^{2} = 532.9,\,\omega_{xy} = 70.99,\,d_{xx} = 0.01,\,d_{yy} = 0.01,\,d_{xy} = 0.002,\,\varOmega_{z} = 0.1.$$

Figure 3 shows position tracking of the x-axis and y-axis using the new fractional integral sliding mode control and adaptive fractional integral sliding mode control. The proposed control method tracks the desired trajectory suitably. It demonstrates that the tracking performance of the new adaptive fractional integral sliding mode control is better than in the fractional integral sliding mode control. Figure 4 shows position tracking error of x-axis and y-axis under the new fractional integral sliding mode control as well as the new adaptive fractional integral sliding mode control. The value of the position tracking error in the x-axis under fractional integral sliding mode control is 0.033, which cannot track zero values during the 10 s interval. In contrast, the value of position tracking error of the x-axis under the new adaptive fractional integral sliding mode control is equal to zero after 2 s. Therefore, it can be inferred that by using this new adaptive law, the position tracking error will converge to zero. Similarly, the value of position tracking error of the y-axis under the new fractional integral sliding mode control is equal to 0.047 during the 10 s sample time, which shows position tracking error cannot converge to zero in that period of time. However, the value of position tracking error of the y-axis under the new adaptive fractional integral sliding mode control is equal to zero after 1.7 s. Considering these results, the new adaptive fractional integral sliding mode control has high tracking performance and zero tracking error performance in comparision to the new fractional integral sliding mode control. Figure 5 shows the velocity in the x-axis and y-axis under the new fractional integral sliding mode control and the new adaptive fractional integral sliding mode control. Figure 6 illustrates the control input of x-axis and y-axis under the new fractional integral sliding mode control and the new adaptive fractional integral sliding mode control.

Fig. 3
figure 3

Position tracking of x-axis and y-axis under new fractional integral sliding mode control (FOISMC) and new adaptive fractional integral sliding mode control (AFOISMC)

Full size image
Fig. 4
figure 4

Position tracking error of x-axis and y-axis under new fractional integral sliding mode control (FOISMC) and new adaptive fractional integral sliding mode control (AFOISMC)

Full size image
Fig. 5
figure 5

Velocity of x-axis and y-axis under new fractional integral sliding mode control (FOISMC) and new adaptive fractional integral sliding mode control (AFOISMC)

Full size image
Fig. 6
figure 6

Control input of x-axis and y-axis under new fractional integral sliding mode control (FOISMC) and new adaptive fractional integral sliding mode control (AFOISMC)

Full size image

The robustness of the proposed control method is evaluated by applying a random noise function (d(t) = 0.5*randn(1,1)). Figure 7 shows that the adaptive fractional integral sliding mode control is robust against external disturbances and is able to suppress the applied noise effectively.

Fig. 7
figure 7

Robustness verification of new fractional integral sliding mode control (FOISMC) and new adaptive fractional integral sliding mode control (AFOISMC) under random noise application

Full size image

6 Conclusion

In this study, a new adaptive fractional integral sliding mode control for MEMS gyroscopes was proposed. The proposed control method is robust against external perturbations and model uncertainties. The robustness of the new fractional integral sliding mode control and new adaptive fractional sliding mode control is validated by the application of random noise. It shows that by using the adaptive law, the control method proposed will suppress the external disturbances more effectively in comparison with the new fractional integral sliding mode control. Moreover, the effectiveness of the proposed control method is considered in terms of trajectory tracking and accuracy, where the adaptive fractional integral sliding mode control had better performance than the fractional integral sliding mode control. Simulation results verified the effectiveness of the proposed control law.