1 Introduction

The Micro-Electro-Mechanical Systems (MEMS) are penetrating more and more into measurement and control problems because of their small size, low cost, and low power consumption. The vibrating gyroscope is one of the MEMS devices that commonly used for measuring angular velocity. MEMS gyroscopes are widely applied in the area of aviation, navigation, automotive, biomedicine, military affairs, and consumer electronics. The performance of the MEMS gyroscopes is deteriorated by the effects of time varying parameters, environment variations, quadrature errors, and external disturbances. Therefore, advanced control such as adaptive control, sliding mode control, and intelligent control are necessary to be used to control the MEMS gyroscope and improve its performance and stability.

In the last few years, some control approaches have been proposed to control the MEMS gyroscope. Increasing attention has been given to the adaptive tracking control of MEMS gyroscope. Adaptive control is a technique of applying system identification method to obtain a model of the process with its environment and using this model to design a real-time controller. Therefore, adaptive control can effectively solve the robustness problem in the presence of unknown model parameters and external disturbances. Park [1] and Leland [2] presented an adaptive controller for a MEMS gyroscope, which drives both axes of vibration and controls the entire operation of the gyroscope. John et al. [3] extends the park’s method [1] and presents an adaptive controller for triaxial angular sensors. Batur et al. [4] developed a sliding mode control for a MEMS gyroscope. Sung et al. [5] derived a phase-domain design approach to study the mode-matched control of gyroscope. Park et al. [6] developed adaptive control and trajectory-switching algorithm for a MEMS Gyroscope. Adaptive sliding mode control has the advantages of combining the robustness of variable structure methods with the tracking capability of adaptive control strategies. An adaptive sliding mode controller with upper bound estimation has been developed to control the vibration of MEMS gyroscope [7]. System nonlinearities are inevitable in actual engineering and require the controller to be either adaptive or robust to these model uncertainties. Intelligent control approaches such as neural network and fuzzy control do not require mathematical models and have ability to approximate nonlinear systems. Neural network technologies have been applied into the nonlinear control system [8–10]. Wang [11] proposed universal approximation theorem and demonstrated that the arbitrary function of a certain set of functions can be approximated with arbitrary accuracy using fuzzy system on a compact domain. Therefore, fuzzy logic system which can approximate arbitrary nonlinear functions makes it a useful tool for adaptive application. Guo et al. [12] proposed adaptive fuzzy sliding mode controller for robot manipulator. Yoo et al. [13] developed adaptive controller for robot manipulator using fuzzy compensator. Wai et al. [14, 15] presented adaptive fuzzy sliding-mode control with application to electrical servo drive. Chen et al. [16] derived adaptive fuzzy output tracking control of MIMO nonlinear uncertain systems. Ren et al. [17] investigated a fuzzy adaptive high-gain-based observer backstepping control for SISO nonlinear systems with dynamical uncertainties. Cetin et al. [18] developed a new semi-active nonlinear adaptive controller for structures using MR damper. Li et al. [19] derived an adaptive fuzzy controller for uncertain MIMO nonlinear systems in block-triangular forms. Wen et al. [20] designed an adaptive fuzzy-neural tracking controller for uncertain nonlinear discrete-time systems in the NARMAX form.

In this paper, the study of AFSMC is extended from two axial angular sensors to triaxial angular sensors. The contribution of this paper is the integration of the adaptive sliding mode control and the nonlinear approximation of AFSMC. Consider the MEMS triaxial gyroscope with parameter uncertainties and external disturbances, a novel adaptive identification approach based on the sliding mode control that can identify angular velocity and other system parameters is developed. As we know, the sliding mode control requires the upper bound of uncertainties and disturbances to specify the sliding mode gain to satisfy the requirement of stability and robustness. However, the bound of the uncertainties is difficult to measure in advance for practical applications and high sliding mode gain will cause large chattering. Therefore, an AFSMC is designed to approximate the upper bound of the uncertainties and external disturbances. Thus, the chattering in control efforts is reduced greatly. The proposed adaptive fuzzy sliding mode controller can guarantee the stability of the closed loop system and improve the robustness for external disturbances and model uncertainties.

The main motivations in the paper are highlighted as follows:

  1. 1.

    The adaptive fuzzy control method has been extended to the control of MEMS gyroscope in this paper. An adaptive fuzzy sliding mode control is adopted to approximate the unknown upper bound of the uncertainties and external disturbances. The advantage of using adaptive fuzzy sliding mode control is that we need not know the upper bound of uncertainties and disturbances in advance. It will be convenient for us to control the MEMS gyroscope since the upper bound of the uncertainties and external disturbances can be adaptively tuned. This is the most important feature of the proposed control as compared with the existing work.

  2. 2.

    An adaptive fuzzy control is incorporated into the MEMS control system to strengthen the robustness of the control system. An adaptive sliding mode controller is derived to identify angular velocity and other system parameters of MEMS triaxial gyroscopes and an adaptive fuzzy control method based on the sliding-mode control is developed to estimate the optimal upper bound of uncertainties and disturbance. This is the successfully application example using fuzzy control with the MEMS gyroscope. Both of these features are the innovative developments of intelligent adaptive control approach incorporated into conventional adaptive control for the MEMS gyroscope.

The organization of this paper is as follows: In Sect. 2, the dynamics of MEMS triaxial gyroscope is described through nondimensional transformation. In Sect. 3, an adaptive sliding mode control strategy is derived to identify angular velocity and other system parameters of MEMS triaxial gyroscopes. In Sect. 4, an adaptive fuzzy control method based on the sliding-mode control is developed to estimate the optimal upper bound of uncertainties and disturbance. Simulation results are presented in Sect. 5 to verify the effectiveness of the proposed adaptive fuzzy sliding mode control. Finally, conclusions are given in Sect. 6.

2 Dynamics of MEMS triaxial gyroscope

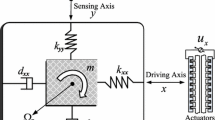
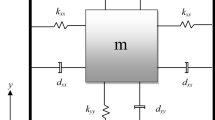
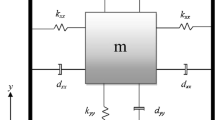
This section describes the dynamics of MEMS triaxial gyroscope. We assume that the gyroscope is moving with a constant linear speed. The gyroscope is rotating at a constant angular velocity. The centrifugal forces are assumed negligible because of small displacements. The gyroscope undergoes rotations along x, y, and z axis.

Referring to [6], the dynamics of triaxial gyroscope becomes

$$ \begin{array}{@{}l} m\ddot{x} + d_{xx}\dot{x} + d_{xy}\dot{y} + d_{xz}\dot{z} + k_{xx}x + k_{xy}y + k_{xz}z\\[2mm] \quad{}= u_{x} + 2m\varOmega_{z}\dot{y} - 2m\varOmega_{y}\dot{z} \\[2mm] m\ddot{y} + d_{xy}\dot{x} + d_{yy}\dot{y} + d_{yz}\dot{z} + k_{xy}x + k_{yy}y + k_{yz}z \\[2mm] \quad{}= u_{y} - 2m\varOmega_{z}\dot{x} + 2m\varOmega_{x}\dot{z} \\[2mm] m\ddot{z} + d_{xz}\dot{x} + d_{yz}\dot{y} + d_{zz}\dot{z} + k_{xz}x + k_{yz}y + k_{zz}z\\[2mm] \quad{} = u_{z} + 2m\varOmega_{y}\dot{x} - 2m\varOmega_{x}\dot{y} \end{array} $$
(1)

where m is the mass of proof mass. Fabrication imperfections contribute mainly to the asymmetric spring terms k xy , k xz , and k yz and asymmetric damping terms d xy , d xz , and d yz . The spring terms in the x, y and z direction are k xx , k yy , and k zz , respectively. The damping terms in the x, y, and z direction are d xx , d yy , and d zz .

Ω x , Ω y , and Ω z are angular velocities in the x, y, and z direction, respectively. u x , u y , and u z are the control forces in the x, y, and z direction, respectively.

Dividing Eq. (1) by the reference mass and rewriting the dynamics in vector forms result in

$$ \ddot{q} + \frac{D}{m}\dot{q} + \frac{K_{a}}{m}q = \frac{u}{m} - 2\varOmega\dot{q} $$
(2)

where

$$\varOmega= \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & - \varOmega_{z} & \varOmega_{y} \\[0.5mm] \varOmega_{z} & 0 & - \varOmega_{x} \\[0.5mm] - \varOmega_{y} & \varOmega_{x} & 0 \end{array} \right] $$

Using nondimensional time t ∗=w 0 t, and dividing both sides of equation by reference length \(w_{0}^{2}\) and the reference length q 0 give the final form of the nondimensional equation of motion as

$$ \frac{\ddot{q}}{q_{0}} + \frac{D}{mw_{0}}\frac{\dot{q}}{q_{0}} + \frac{K}{mw_{0}^{2}}\frac{q}{q_{0}} = \frac{u}{mw_{0}^{2}q_{0}} - 2\frac{\varOmega}{w_{0}}\frac{\dot{q}}{q_{0}} $$
(3)

We define the new parameters as follows:

Ignoring the superscript (∗) for notational clarity, the nondimensional representation of (1) and (2) is

$$ \ddot{q} + D\dot{q} + K_{b}q = u - 2\varOmega\dot{q} $$
(4)

where

$$K_{b} = \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} w^{2}_{x} & w_{xy} & w_{xz} \\[0.5mm] w_{xy} & w^{2}_{y} & w_{yz} \\[0.5mm] w_{xz} & w_{yz} & w^{2}_{z} \end{array} \right] $$

3 Angular velocity estimation based on adaptive sliding mode control

In this section, we consider the parameter uncertainties and external disturbances, an adaptive sliding mode control strategy is presented to identify angular velocity and other system parameters of MEMS triaxial gyroscopes.

Rewriting the gyroscope model in state-space equation as

$$ \dot{X} = AX + Bu $$
(5)

where

The reference models are chosen at the given different frequency and amplitude:

The state-space equation of reference model can be rewritten as

$$ \dot{X}_{m} = A_{m}X_{m} $$
(6)

where

Referring Eq. (5), we consider the system with parameter uncertainties and external disturbances as

$$ \dot{X} = (A + \Delta A)X + Bu + f(t) $$
(7)

where ΔA is the unknown parameter uncertainties of the matrix A, f(t) is the external disturbances.

To ensure the achievement of the control objective, we make the following assumptions.

Assumption 1

(Matching condition)

There exists unknown matrix functions of appropriate dimensions D(t) and G(t) such that

$$ \Delta A(t) = BD(t),\qquad f(t) = BG(t) $$
(8)

where BD(t) is the matched uncertainty and BG(t) is the matched disturbance

Under the assumption of matching condition, (7) can be rewritten as follows:

(9)

where Bf m represents the lumped matched parameter uncertainties and external disturbances, which is given by

$$ f_{m} = DX + G $$
(10)

Assumption 2

(Matching condition)

There exists a constant matrix K ∗ such that the following matching condition A+BK ∗T=A m can be always satisfied, where

$$K^{*\mathrm{T}} = \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \omega_{x}^{2} - \omega_{1}^{2} & d_{xx} & \omega_{xy} & d_{xy} - 2\varOmega_{z} & \omega_{xz} & d_{xz} + 2\varOmega_{y} \\[0.5mm] \omega_{xy} & d_{xy} + 2\varOmega_{z} & \omega_{y}^{2} - \omega_{2}^{2} & d_{yy} & \omega_{yz} & d_{yz} - 2\varOmega_{x} \\[0.5mm] \omega_{xz} & d_{xz} - 2\varOmega_{y} & \omega_{yz} & (d_{yz} + 2\varOmega_{x}) & \omega_{z}^{2} - \omega_{3}^{2} & d_{zz} \end{array} \right]. $$

Assumption 3

(Bounded condition)

There exists a positive definite matrix f=diag[f 1 f 2 f 3] such that the bounded condition |f mi |<f i (i=1,2,3) can always be satisfied.

Define the tracking error as follows:

$$ e = X - X_{m} $$
(11)

Then the derivative of tracking error is

(12)

Define the sliding surface as follows:

$$ S = Ce $$
(13)

where S=[s 1 s 2 s 3]T, C is a constant matrix.

Then the derivative of sliding surface is

(14)

Setting \(\dot{S} = 0\), we get the equivalent control u eq as

$$ u_{\mathrm{eq}} = K^{*\mathrm{T}}X - (CB)^{ - 1}CA_{m}e - f_{m} $$
(15)

Consider the system parameters of A may be unknown, namely K ∗ is unknown, the control law u eq cannot be implemented in practical applications. Therefore, an adaptive version of control algorithm is proposed as

(16)

where K is the estimate of K ∗, the last component \(u_{n} = - f\operatorname{sgn} (S)\) is designed to compensate the uncertainties and disturbances f m to guarantee that the sliding mode reaching condition can be always satisfied.

Substituting (16) into (14), we get

$$ \dot{S} = C\dot{e} = CB\tilde{K}^{\mathrm{T}}X + CBf_{m} - CBf\operatorname{sgn} (S) $$
(17)

where \(\tilde{K} = K - K^{*}\).

Define a Lyapunov function as

$$ V_{1} = \frac{1}{2}S^{\mathrm{T}}S + \frac{1}{2} \operatorname{tr}\bigl[\tilde{K}M^{ - 1} \tilde{K}^{\mathrm{T}}\bigr] $$
(18)

where M=M T>0, M is a positive definite matrix, \(\operatorname{tr}[M]\) denoting the trace of M.

Differentiating V 1 with respect to time yields

(19)

To make \(\dot{V}_{1} \le0\), we choose the adaptive laws as

$$ \dot{\tilde{K}}{}^{\mathrm{T}}(t) = \dot{K}^{\mathrm{T}}(t) = - MB^{\mathrm{T}}C^{\mathrm{T}}SX^{\mathrm{T}} $$
(20)

Substituting \(\dot{\tilde{K}}{}^{\mathrm{T}}(t)\) into (19)

(21)

This implies that the trajectory reaches the sliding surface in finite time and remains on the sliding surface. Furthermore, it can be proved that the controller parametersK will converge to their true values K ∗ if ω 1≠ω 2≠ω 3, \(\lim_{t \to\infty} \tilde{K} \to0\). Then from Assumption 3, we get

(22)

The parameters of MEMS gyroscope can be obtained as follows:

4 Adaptive fuzzy sliding mode control design

In conventional sliding mode control, the upper bound f of uncertainties, which includes parameter variations and external disturbances, must be available. However, the bound of the uncertainties is difficult to measure in advance for practical applications. If f is chosen to be too small, it may not compensate the uncertainties and disturbances f m to guarantee reaching condition of sliding mode, so the control system may be unstable. If f is chosen to be too large, the control effort will have large chattering. Therefore, an adaptive fuzzy control method based on the sliding-mode control is proposed to estimate the optimal upper bound of f m in this section.

Replacing f by \(\hat{f}\) in (16), the new version of control algorithm can be obtained:

(23)

where \(\hat{f}\) is the estimate of f, \(\hat{f} = \operatorname{diag}[ \hat{f}_{1}\ \hat{f}_{2}\ \hat{f}_{3}]\).

The dynamics of sliding surface (17) can be rewritten as

$$ \dot{S} = C\dot{e} = CB\tilde{K}^{\mathrm{T}}X + CBf_{m} - CB\hat{f}\operatorname{sgn}(S) $$
(24)

According to the universal approximation theorem, there exists an optimal fuzzy control system f ∗ such that

$$ f^{*} = f + \varepsilon=\boldsymbol{\alpha} _{i}^{*\mathrm{T}}\boldsymbol{\xi}_{i} $$
(25)

where ε is the approximation error and satisfying |ε|<E.

Employing an adaptive fuzzy control system\(\hat{f}\) to approximate f. By using the strategy of singleton fuzzification, product inference and center-average defuzzification, the output of adaptive fuzzy system is

$$ \hat{f}_{i} = \frac{\sum_{j = 1}^{m} \alpha_{ij} \mu _{A}(s_{i})}{\sum_{j = 1}^{m} \mu_{A}(s_{i})} = \hat{\boldsymbol{\alpha}} _{i}^{\mathrm{T}}\boldsymbol{\xi} _{i} $$
(26)

where \(\hat{\boldsymbol{\alpha}} _{i}\) is the estimate of \(\boldsymbol{\alpha} ^{*}_{i}\), which is an adjustable parameter vector. \(\hat{\boldsymbol{\alpha}}_{i} = [\hat{\alpha}_{i1},\hat{\alpha} _{i2},\ldots,\hat{\alpha} _{im}]^{\mathrm{T}}\), ξ i =[ξ i1,ξ i2,…,ξ im ]T.

Define a Lyapunov function as

$$ V = \frac{1}{2}S^{\mathrm{T}}S + \frac{1}{2} \operatorname{tr}\bigl[\tilde{K}M^{ - 1}\tilde{K}^{\mathrm{T}}\bigr] + \frac{1}{2\eta} \sum_{i = 1}^{3} \tilde{ \boldsymbol{\alpha}}_{i}^{\mathrm{T}}\tilde{\boldsymbol{ \alpha}}_{i} $$
(27)

where M=M T>0, M is a positive definite matrix, \(\operatorname{tr}[M]\) denoting the trace of M, η is a positive constant, \(\tilde{\boldsymbol{\alpha}} _{i} = \hat{\boldsymbol{\alpha}} _{i} - \boldsymbol{\alpha}^{*}_{i}\).

Differentiating V with respect to time yields

(28)

To make \(\dot{V} \le0\), the adaptive law is designed as

$$ \dot{\tilde{\boldsymbol{\alpha}}}_{i} = \dot{\hat{\boldsymbol{\alpha}}}_{i} = \eta\lambda_{i}| s_{i} |\boldsymbol{\xi}_{i} $$
(29)

Then (28) becomes

$$ \dot{V} \le- \sum_{i = 1}^{3} \lambda_{i}| s_{i} | \bigl(f_{i} + \varepsilon_{i} - | f_{mi} |\bigr) \le0 $$
(30)

This implies that \(\dot{V}\) is a negative semi-definite function. \(\dot{V}\) becomes negative semi-definite implying that the trajectory reaches the sliding surface in finite time and remains on the sliding surface and \(S,\tilde{K},\tilde{\boldsymbol{\alpha}}_{i}\) are all bounded.

Furthermore, we have \(\int_{0}^{t} \dot{V}(\tau)\,d\tau = V(t) - V(0) \le- \int_{0}^{t} \sum_{i = 1}^{3} \lambda_{i}| s_{i} | (f_{i} + \varepsilon_{i} - | f_{mi} |)\,d\tau\), that is \(V(t) + \int_{0}^{t} \sum_{i = 1}^{3} \lambda_{i}| s_{i} | (f_{i} + \varepsilon_{i} - | f_{mi} |)\,d\tau\le V(0)\). Since V(0) is bounded and V(t) is nonincreasing bounded function, \(\lim_{t \to \infty} \int_{0}^{t} \sum_{i = 1}^{3} \lambda_{i}| s_{i} | (f_{i} + \varepsilon_{i} - | f_{mi} |) \,d\tau< \infty\). According to the Barbalat lemma, it can be concluded that \(\lim_{t \to\infty} \sum_{i = 1}^{3} \lambda_{i}| s_{i} | (f_{i} + \varepsilon_{i} - | f_{mi} |) = 0\), which means lim t→∞ s i (t)=0. Consequently, e(t) also converges to zero asymptotically.

5 Simulation analysis

According to the proposed adaptive fuzzy sliding mode control approach, the simulation is performed in MATLAB/Simulink software. The control objective is design an adaptive fuzzy sliding mode controller so that the position q can track the reference model q m and the unknown angular velocity can be estimated. The parameters of the MEMS triaxial gyroscope are as follows:

The unknown angular velocity is assumed Ω x =3 rad/s, Ω y =2 rad/s, Ω z =5 rad/s. Through non-dimensional transformation, angular velocity can be obtained:

$$\varOmega_{x} = 0.001,\qquad\varOmega_{y} = 0.000667,\qquad\varOmega_{z} = 0.00167 $$

The reference inputs are x m =sin(6.71t), y m =1.2sin(5.11t), z m =1.5sin(4.17t).

The initial state condition are x 0=[0 0 0 0 0 0], the initial value of K is K(0)=0.95K ∗, the true value of K are

$$K^{*\mathrm{T}} = \left[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1533.5 & 0.0251 & 97.4659 & - 0.00083 & 116.9591 & 0.0054 \\ 97.4659 & 0.0059 & 1370 & 0.0402 & 136.4522 & 0.0032 \\ 116.9591 & 0.0027 & 136.4522 & 0.0072 & 1171.1 & 0.0523 \end{array} \right], $$

the external disturbance is f m (t)=[10sin(6t)10cos(5t) 10cos(4t)]T. The upper bound of gain is \(f = \operatorname{diag}[ 100\ 100\ 100]\).

In (20) and (29), the parameters are chosen as

The membership functions for sliding surface s are chosen as

Figures 1 and 2 show the position tracking and tracking error of X, Y, and Z axis of the AFSMC system, respectively. It can be found that the position of X, Y, and Z axis can effectively track the desired trajectory in the presence of the external disturbances and the tracking error can converge to zero in very short time. It can be concluded from Fig. 1 and Fig. 2 that the MEMS triaxial gyroscope can maintain the proof mass to oscillate in the X, Y, and Z direction at given frequency and amplitude. Figure 3 depicts that the sliding surface converge to zero asymptotically in a short time, demonstrating the control system will get into sliding surface and remain along with it. Figure 5 plots the adaptation of the controller parameters K. It can be shown that the estimation of controller parameters K converge to their true values with persistent excitation signals.

Fig. 1
figure 1

Position tracking of X, Y, Z axis

Full size image
Fig. 2
figure 2

Tracking errors of X, Y, Z axis

Full size image
Fig. 3
figure 3

Convergence of the sliding surface s

Full size image

Figure 4 draws the adaptation of angular velocity. It can be observed that the angular velocity Ω x , Ω y , Ω z converge to their true values after computation of dimensionless. Figure 6 shows the adaptation of \(\hat{\boldsymbol{\alpha}} _{i}\). It can be found that the adjustable parameter \(\hat{\boldsymbol{\alpha}}_{i}\) converge to constant values. Figure 7 and Fig. 8 compare the control efforts between AFSMC system with adaptive sliding gain using adaptive fuzzy approach and the conventional adaptive sliding control system with fixed sliding gain. It is obvious that the control input in Fig. 7 is better than that of Fig. 8 and the chattering is reduced greatly when using AFSMC to estimate the upper bound of system disturbances.

Fig. 4
figure 4

Adaptation of angular velocity Ω x , Ω y , Ω z

Full size image
Fig. 5
figure 5

Adaptation of the controller parameters K

Full size image
Fig. 6
figure 6

Adaptation of \(\hat{\boldsymbol{\alpha}}_{i}\)

Full size image
Fig. 7
figure 7

Control efforts with AFSMC

Full size image
Fig. 8
figure 8

Control efforts with fixed gain

Full size image

6 Conclusion

This paper investigates an adaptive algorithm based the sliding mode control to identify the unknown angular velocity and an AFSMC strategy to estimate the upper bound of the uncertainties and external disturbances. The stability of the closed-loop system can be guaranteed with the proposed AFSMC strategy. The simulation results demonstrate the proposed AFSMC method has better robustness and favorable tracking performance. At the same time, the unknown angular velocity can be estimated correctly when the persistent excitation condition is satisfied and the chattering is reduced greatly with the upper bound estimation of the model uncertainties and external disturbances.