1 Introduction

One of the useful tools to measure angular velocity is the MEMS gyroscope. By measuring the x- and y-direction movement of the MEMS gyroscope, the angular velocity will be obtained. This device is used in many industries such as the automotive industry and medicine. The most important part of using the MEMS gyroscope is how to control this device appropriately. Several control methods are used to control the MEMS gyroscope such as proportional integral derivative (PID) controller [1], sliding mode control (SMC) [2], and some other controllers [3, 4]. However, the mentioned controllers were applied on a linear MEMS gyroscope. There are a few researchers who worked on the nonlinear dynamic model of MEMS gyroscope and controlled it in comparison with linear MEMS gyroscope [5].

Linearization of the nonlinear dynamic model will give better information on the behavior of the systems. This will provide some detail to better analyze the system. Koopman's theory is one of the strong approaches to linearizing the nonlinear dynamic model [6,7,8,9]. Koopman operators have infinite dimensions and capture nonlinear dynamics in a lifted global linear way. A class of linear predictors is produced by the finite data-driven approximation of Koopman operators, which helps create linear control of nonlinear dynamical systems with minimal computing complexity [8]. The main part of applying Koopman's theory on nonlinear dynamic equations is how to approximate the Koopman operator. The DMD method is one of the most prevalent methods in estimating the Koopman operator [10,11,12]. Nathan et al. [13] investigate using Koopman theory to solve data-driven spatiotemporal systems and nonlinear partial differential equations. They show that an appropriate approximation to the nonlinear dynamics depends on the observables selected for building the Koopman operator. The DMD technique may be used to compute a finite-dimensional approximation of the Koopman operator, together with its eigenfunctions, eigenvalues, and Koopman modes, if such observables can be discovered.

Several control methods are used to control the linearized dynamic model by Koopman theory such as linear quadratic regulator (LQR) [14, 15] and model predictive controller (MPC) [16, 17]. The LQR and MPC controllers have suitable performances, but the main drawbacks of those controllers are not robust against external disturbances. The FOSMC is a strong robust control method that can suppress external perturbations. The reason that makes this controller a strong control approach is that the fractional order used in the sliding mode surface provides the ability to select the fraction power of error. This issue provides excellent flexibility to select the best sliding mode surface. Therefore, the dynamic states of the linearized dynamics model can suitably slide close to the normal behavior of the system. It causes to provide the better control performance in terms of high tracking performance, low tracking error, and robustness.

Most of the previous works related to MEMS gyroscopes were about the control of linear dynamics of MEMS gyroscopes by FOSMC. However, the FOSMC was used in combination with the other controller to benefit from the advantages of other controllers like reducing the chattering phenomenon [18, 19] and improving tracking performance [20]. Based on high-gain and disturbance observers, a dynamic backstepping sliding mode controller with a fractional order sliding surface and a fuzzy boundary layer is created to regulate the operation of a MEMS gyroscope [21]. A combination of sliding mode and a reliable nonlinear backstepping controller is applied to suppress the system uncertainties. The sliding surface in this model is chosen to be of fractional order to improve the degree of freedom of the controller. In addition to the initial sliding surface, a new dynamic sliding surface is utilized to considerably minimize the chattering phenomena in the control signal. Fuzzy control theory is also used to regulate the boundary layer. Wang and Fei [22] proposed the use of a trajectory tracking control system with a neural network estimator to sustain the vibrations of the gyroscope-proof mass. A recurrent Chebyshev fuzzy neural network with a self-evolving mechanism and a fractional controller based on the terminal sliding mode are both included in the suggested control system. A self-evolving recurrent Chebyshev fuzzy neural network is presented to reduce the need for nonlinear functional certainty, and the fractional-order terminal sliding mode control may guarantee the tracking error is exponentially stable.

This paper proposes a data-driven method to control a nonlinear MEMS gyroscope. The Koopman theory is applied to linearize the nonlinear model of the MEMS gyroscope. The DMD method is used to approximate the Koopman operator. The model uncertainty and unmodeled dynamics are unknown parameters in a nonlinear dynamic model. Therefore, the data-driven Koopman method will provide a high-fidelity model by linearization of nonlinear dynamics models. A FOSMC is applied to the nonlinear dynamic model and linear dynamic model by the Koopman theory to verify the better performance of the control system after linearization in terms of high trajectory tracking, low tracking error, and low control input signals. A new compound control method is applied to improve the control method of the FOSMC such as reducing the control efforts.

The rest of this paper is organized as: Sect. 2 introduces the nonlinear MEMS gyroscope dynamic model. Section 3 explains the FOSMC. Section 4 discusses the Koopman theory. Section 5 describes the DMD method. Section 6 proposes Koopman-FOSMC. Section 7 produces the new compound proposed controller. Section 8 demonstrates the simulation results. Section 9 describes the conclusion.

2 Nonlinear MEMS gyroscope dynamic model

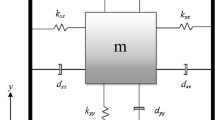
The MEMS gyroscope is a small device that can measure angular velocity. This device has been used in many applications such as automotive and medicine [2, 23, 24]. Most of the research considered the linear model of the MEMS gyroscope, but we provide a nonlinear dynamic model of the MEMS gyroscope. Figure 1 depicts a typical z-axis MEMS gyroscope construction.

Fig. 1
figure 1

MEMS gyroscope structure [21]

Full size image

A proof mass supported by springs, sensor mechanisms, and an electrostatic actuation system are all components of a typical MEMS gyroscope design [2]. The oscillatory motion created by the electrostatic actuation system may be used to determine the location and speed of the proof mass. The gyroscope rotates at a gradually increasing angular velocity \({\Omega }_{z}\) while the proof mass is mounted on a frame that moves with a constant linear velocity. Due to the small displacements x and y, it is anticipated that the centrifugal forces \(m{\Omega }_{z}^{2}x\) and \(m{\Omega }_{z}^{2}y\) will be negligible. The \(2m{\Omega }_{z}^{*}\dot{y}\) and \(2m{\Omega }_{z}^{*}\dot{x}\), Coriolis forces develop parallel to the driving and rotational axes. The following equations describe the gyroscope's dynamics:

$$m\ddot{x}+{d}_{xx}^{*}\dot{x}+{d}_{xy}^{*}\dot{y}+{k}_{xx}^{*}x+{k}_{xy}^{*}y+\beta {x}^{3}={u}_{x}^{*}+2m{\Omega }_{z}^{*}\dot{y}$$
(1)
$$m\ddot{y}+{d}_{xy}^{*}\dot{y}+{d}_{yy}^{*}\dot{y}+{k}_{xy}^{*}x+{k}_{yy}^{*}y+\beta {y}^{3}={u}_{y}^{*}-2m{\Omega }_{z}^{*}\dot{x}$$
(2)

Since there is no external force acting on the system, the origin of the coordinates in Eqs. 1 and 2 is located in the middle of the proof mass. The asymmetric spring and damping coefficients are represented by the constants \({k}_{xy}^{*}\) and \({d}_{xy}^{*}\), respectively. The control forces in the x- and y-direction, \({u}_{x}^{*}\) and \({u}_{y}^{*}\), are often accepted despite the potential of modest unknown deviations from their nominal values. The damping rates, \({d}_{xx}^{*}\) and \({d}_{yy}^{*}\), and the spring constants of springs interacting in the x- and y-directions, \({k}_{xx}^{*}\) and \({k}_{yy}^{*}\), are also often described. Consequently, the terms \(\beta {x}^{3}\) and \(\beta {y}^{3}\) will be introduced by the positive constants "electromechanical" and "mechanical" nonlinearity. Equations 1 and 2 might be expressed using the vector form shown below:

$$\frac{{\ddot{q}}^{*}}{{q}_{0}}+\frac{{D}^{*}}{m{\omega }_{0}}\frac{{\dot{q}}^{*}}{{q}_{0}}+\frac{{K}_{a}}{m{\omega }_{0}^{2}}\frac{{q}^{*}}{{q}_{0}}+\beta \frac{{q}^{{*}^{3}}}{{q}_{0}}=\frac{{u}^{*}}{m{\omega }_{0}^{2}{q}_{0}}-2\frac{{\Omega }^{*}}{{\omega }_{0}}\frac{{\dot{q}}^{*}}{{q}_{0}}$$
(3)

where \(q^{*} = \left[ {\begin{array}{*{20}c} {x^{*} } \\ {y^{*} } \\ \end{array} } \right],u = \left[ {\begin{array}{*{20}c} {u_{x}^{*} } \\ {u_{y}^{*} } \\ \end{array} } \right],\Omega^{*} = \left[ {\begin{array}{*{20}c} 0 & { - \Omega_{z}^{*} } \\ {\Omega_{z}^{*} } & 0 \\ \end{array} } \right],D^{*} = \left[ {\begin{array}{*{20}c} {d_{xx}^{*} } & {d_{xy}^{*} } \\ {d_{xy}^{*} } & {d_{yy}^{*} } \\ \end{array} } \right],K_{a} = \left[ {\begin{array}{*{20}c} {k_{xx}^{*} } & {k_{xy}^{*} } \\ {k_{xy}^{*} } & {k_{yy}^{*} } \\ \end{array} } \right],\) and nondimensional parameters as follows:

$$ q = \frac{{q^{*} }}{{q_{0} }}\quad d_{xy} = \frac{{d_{xy}^{*} }}{{m\omega_{0} }}\quad \Omega_{z} = \frac{{\Omega_{z}^{*} }}{{\omega_{0} }} $$
(4)
$$ u_{x} = \frac{{u_{x}^{*} }}{{m\omega_{0}^{2} q_{0} }}\quad u_{y} = \frac{{u_{y}^{*} }}{{m\omega_{0}^{2} q_{0} }} $$
(5)
$$ \omega_{x} = \sqrt {\frac{{k_{xx} }}{{m\omega_{0}^{2} }}} \quad \omega_{y} = \sqrt {\frac{{k_{yy} }}{{m\omega_{0}^{2} }}} \quad \omega_{xy} = \frac{{k_{xy} }}{{m\omega_{0}^{2} }} $$
(6)

Since the reference length is q0, the natural frequency of each axis is \({\omega }_{0}\). The MEMS gyroscope's dynamic equations are listed below:

$$\ddot{q}=-\left(D+2\Omega \right)\dot{q}-{K}_{b}q-\beta {q}^{3}+u+E$$
(7)

A possible model for an external disturbance, E, is:

$$\ddot{q}=-Y\dot{q}-Pq-\beta {q}^{3}+u+E$$
(8)

\(P= {K}_{b}\), and \(Y = (D+2\Omega )\) determine certain parameter variation uncertainties. As a result, Eq. (8) might be written as:

$$\ddot{q}=-\left(Y+\Delta Y\right)\dot{q}-\left(P+\Delta P\right)q-\beta {q}^{3}+u+E$$
(9)

where

$$ q = \left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right],\;u = \left[ {\begin{array}{*{20}c} {u_{x} } \\ {u_{y} } \\ \end{array} } \right],\;\Omega = \left[ {\begin{array}{*{20}c} 0 & { - \Omega_{z} } \\ {\Omega_{z} } & 0 \\ \end{array} } \right],\;D = \left[ {\begin{array}{*{20}c} {d_{xx} } & {d_{xy} } \\ {d_{xy} } & {d_{yy} } \\ \end{array} } \right],\;K_{b} = \left[ {\begin{array}{*{20}c} {\omega_{x}^{2} } & {\omega_{xy} } \\ {\omega_{xy} } & {\omega_{y}^{2} } \\ \end{array} } \right] $$

Equation (9) can be shown in a variety of ways:

$$\ddot{q}=-Y\dot{q}-Pq-\beta {q}^{3}+u(t)+D(t)$$
(10)

D(t) is defined as:

$$D\left(t\right)=-\Delta Y\dot{q}-\Delta Pq+E$$
(11)

The x- and y-directions of Eq. (10)'s equation are as follows:

$$ \begin{aligned} \left[ {\begin{array}{*{20}c} {\ddot{x}} \\ {\ddot{y}} \\ \end{array} } \right] & = - \left( {\left[ {\begin{array}{*{20}c} {d_{xx} } & {d_{xy} } \\ {d_{xy} } & {d_{yy} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & { - 2\Omega_{z} } \\ {2\Omega_{z} } & 0 \\ \end{array} } \right]} \right)\left[ {\begin{array}{*{20}c} {\dot{x}} \\ {\dot{y}} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {\omega_{x}^{2} } & {\omega_{xy} } \\ {\omega_{xy} } & {\omega_{y}^{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} \beta & 0 \\ 0 & \beta \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x^{3} } \\ {y^{3} } \\ \end{array} } \right] \\ & \quad + \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{x} } \\ {u_{y} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {D\left( t \right)_{x} } \\ {D\left( t \right)_{y} } \\ \end{array} } \right] \\ \end{aligned} $$
(12)

The following parameters will be used to convert Eq. (12) into first-order dynamic equations:

$$\left\{\begin{array}{c}x={z}_{1}\\ \dot{x}={z}_{2}\\ \begin{array}{c}y={z}_{3}\\ \dot{y}={z}_{4}\end{array}\end{array}\right.$$

There is also:

$$ \left\{ {\begin{array}{*{20}l} {\dot{z}_{1} = z_{2} } \hfill \\ {\begin{array}{*{20}c} {\dot{z}_{2} = - \omega_{x}^{2} z_{1} - \beta z_{1}^{3} - d_{xx} z_{2} - \omega_{xy} z_{3} + \left( {2\Omega_{z} - d_{xy} } \right)z_{4} + u_{{z_{1} }} + D_{{z_{1} }} } \\ {\begin{array}{*{20}l} {\dot{z}_{3} = z_{4} } \hfill \\ {\dot{z}_{4} = - \omega_{xy} z_{1} - \left( {d_{xy} + 2\Omega_{z} } \right)z_{2} - \omega_{y}^{2} z_{3} - \beta z_{3}^{3} - d_{yy} z_{4} + u_{{z_{3} }} + D_{{z_{3} }} } \hfill \\ \end{array} } \\ \end{array} } \hfill \\ \end{array} } \right. $$
(13)

Equation (13) demonstrates:

$$\dot{z}=A\left(z\right)+Bu$$
(14)

The following is how Eq. (14) can be stated in its original form:

$$\frac{d}{dt}z\left(t\right)=f\left(z\right)$$
(15)

3 Fractional sliding mode control

The FOSMC is a robust control method that can suppress external perturbations. This control method is a flexible method that can provide fraction derivative power of error [25,26,27]. This issue will provide the opportunity for choosing the suitable sliding mode surface that is the most important part of designing FOSMC. The fractional sliding mode surface defines as:

$$s\left(t\right)=\dot{e}\left(t\right)+\alpha {D}^{\mu }e(t)$$
(16)

where \(e\left(t\right)={q}_{d}-q\) and D is fractional operator defines as \(D=\frac{d}{dt}\) and μ is fractional order.

The FOSMC contains two control sections: equivalent control law and reaching control law. The equivalent control can be obtained by \(\dot{s}\left(t\right)=0\). Taking derivative from Eq. (16) produces:

$$ \dot{s}\left( t \right) = \ddot{e}\left( t \right) + \alpha \mu D^{\mu + 1} e\left( t \right) = \ddot{q}_{d} - \ddot{q} + \alpha \mu D^{\mu + 1} e\left( t \right) $$
(17)

Equation (10) is substituted into Eq. (17) to produce.

$$ \dot{s}\left( t \right) = \ddot{q}_{d} + Y\dot{q} + Pq + \beta q^{3} - u\left( t \right) - D\left( t \right) + \alpha \mu D^{\mu + 1} e\left( t \right) $$
(18)

The ueq(t) can be described by \(\dot{s}\left(t\right)=0\) as

$$ u_{eq} \left( t \right) = \ddot{q}_{d} + Y\dot{q} + Pq + \beta q^{3} - D\left( t \right) + \alpha \mu D^{\mu + 1} e\left( t \right) $$
(19)

The reaching control law introduces as

$${u}_{r}(t)={K}_{r}s(t)$$
(20)

where Kr is positive constant. Therefore, the control input is defined as

$${{u}_{\mathrm{FOSMC}}\left(t\right)={u}_{eq}\left(t\right)+u}_{r}(t)$$
(21)

A powerful technique for demonstrating the stability of the FOSMC is the Lyapunov theory [1]. It is characterized as:

$$V\left(t\right)=\frac{1}{2}s(t){s}^{T}(t)$$
(22)

Taking derivative from Eq. (22) describes:

$$\dot{V}\left(t\right)={s}^{T}(t)\dot{s}(t)$$
(23)

The outcome of putting Eq. (18) into Eq. (23):

$$ \dot{V}\left( t \right) = s^{T} \left( t \right)(\ddot{q}_{d} + Y\dot{q} + Pq + \beta q^{3} - u\left( t \right) - D\left( t \right) + \alpha \mu D^{\mu + 1} e\left( t \right)) $$
(24)

Substituting Eq. (21) into Eq. (24) produces:

$$ \dot{V}\left( t \right) = s^{T} \left( t \right)(\ddot{q}_{d} + Y\dot{q} + Pq + \beta q^{3} - u_{eq} \left( t \right) - u_{r} \left( t \right) - D\left( t \right) + \alpha \mu D^{\mu + 1} e\left( t \right)) $$
(25)

Equation (19) used into Eq. (25) results in:

$$ \begin{aligned} \dot{V}\left( t \right) & = s^{T} \left( t \right)(\ddot{q}_{d} + Y\dot{q} + Pq + \beta q^{3} - \ddot{q}_{d} - Y\dot{q} - Pq - \beta q^{3} \\ & \quad + D\left( t \right) - \alpha \mu D^{\mu + 1} e\left( t \right) - u_{r} \left( t \right) - D\left( t \right) \\ & \quad + \alpha \mu D^{\mu + 1} e\left( t \right)) \\ \end{aligned} $$
(26)

Simplifying Eq. (26) produces:

$$\dot{V}\left(t\right)={s}^{T}(t)({-u}_{r}(t))$$
(27)

Substituting Eqs. (20) into (27) describes:

$$\dot{V}\left(t\right)={s}^{T}(t)({-K}_{r}s(t))$$
(28)

Equation (28) shows that the \(\dot{V}\left(t\right)<0\). Therefore, the proposed controller is stable.

In this study, we employ the Grunwald–Letnikov fractional type [28]. The Grunwald–Letnikov fractional derivative of the function e(t) with respect to t is given:

$${D}_{t}^{\mu }e\left(t\right)={lim}_{h\to 0}{h}^{-\mu }\sum_{k=0}^{n}{(-1)}^{k}\left(\begin{array}{c}\mu \\ k\end{array}\right)f\left(e\left(t\right)-kh\right),$$
(29)

where

$$\left(\begin{array}{c}\mu \\ k\end{array}\right)=\frac{\mu \left(\mu -1\right)\left(\mu -2\right)\dots (\mu -k+1)}{k!}=\frac{\Gamma \left(\mu +1\right)}{k!\Gamma \left(\mu -k+1\right)}$$

The detailed explanation about the Grunwald–Letnikov method can be found in [28]. The proposed control method block diagram is shown in Fig. 2.

Fig. 2
figure 2

The proposed controller block diagram

Full size image

4 Koopman theory

The Koopman operator theory states that to successfully solve a nonlinear dynamical system, the nonlinear system's initial form must be converted into an infinite-dimensional state space, resulting in a linear system [29]. The discrete time definition of a dynamic is [29]:

$${z}_{k+1}=F\left({z}_{k}\right)$$
(30)

where F is indicated by

$$F\left(z\left({t}_{0}\right)\right)=z\left({t}_{0}\right)+{\int }_{{t}_{0}}^{{t}_{0}+t}f\left(z\left(\tau \right)\right)d\tau $$
(31)

The dynamics of the original system becomes linear when the dynamics of a finite-dimensional nonlinear system is transferred to an infinite-dimensional function space. The measurement function and observable g is a real-valued scalar in an infinite-dimensional Hilbert space. Based on this observable, the Koopman operator generates as follows:

$$Kg=g\circ F$$
(32)

Using a continuous system, smooth dynamics may be constructed.

$$\frac{d}{dt}g\left(z\right)=Kg\left(z\right)=\nabla g\left(z\right).f\left(z\right)$$
(33)

where K is the Koopman operator. Due to the Koopman operator's infinite dimensions, which is important yet troublesome for operation and representation. Applied Koopman analysis approximates the evolution on a subspace covered by a limited number of measurement functions rather than detailing the development of all measurement functions in a Hilbert space. By restricting the operator to an invariant subspace, the Koopman operator may be represented as a finite-dimensional matrix. Any combination of the Koopman operator's eigenfunctions will cover a Koopman invariant subspace. When the Koopman model's eigenfunction \(\varphi \left(z\right)\) fulfills eigenvalue:

$$\lambda \varphi \left(z\right)=\varphi \left(F\left(z\right)\right)$$
(34)

A Koopman eigenfunction (z) is defined in continuous time:

$$\frac{d}{dt}\varphi \left(z\right)=\lambda \varphi \left(z\right)$$
(35)

The Koopman operator must be approximated from the application side using a finite-dimensional approximation. One method that can estimate the Koopman operator is the DMD method.

5 DMD method

DMD uses a robust numerical technique to approximate the Koopman operator.

$${Z}^{\prime}\approx AZ$$
(36)

where \({Z}^{\prime}\) is time shifted of matrix Z as:

$$Z=\left[\begin{array}{ccc}{z}_{1}& {z}_{2}& \dots \dots .\end{array}\right]$$

The A may be determined as follows using Eq. (36):

$$A={Z}{\prime}{Z}^{+}$$
(37)

where the Moore–Penrose pseudoinverse is represented by + . Because a normal calculation utilizing A would necessitate a substantial amount of computation due to its enormous n, we may utilize Singular Value Decomposition (SVD) on the snapshots to identify the dominant characteristics of the pseudoinverse of Z [30].

$$Z\approx U\Sigma {V}^{*}$$
(38)

where \( U\epsilon R^{{n \times r}} \),\(\Sigma \epsilon {R}^{r \times r}\), \(V \epsilon {R}^{n \times r}\), and * demonstrates the conjugate transpose. SVD's reduced rank for approximating Z is r. The eigenvectors can be defined as:

$$\upphi = {Z}{\prime}V{\Sigma }^{-1}\mathtt{W}$$
(39)

where W is a set of dynamic full rank system eigenvectors.

Let λ be eigenfunction, then we will have:

$$KW=\lambda W$$
(40)

where K is the Koopman operator.

The demonstration of the linearized dynamic model is as follows:

$$\frac{d}{dt}y=Ky+Bu$$
(41)

6 Koopman fractional sliding mode control

The fractional sliding mode surface can be defined as:

$$s\left(t\right)=e\left(t\right)+\alpha {D}^{\mu }e(t)$$
(42)

where \(e\left(t\right)={y}_{d}-y\). Taking derivative from Eq. (42) produce:

$$\dot{s}\left(t\right)=\dot{e}\left(t\right)+\alpha \mu {D}^{\mu +1}e\left(t\right)={\dot{y}}_{d}-\dot{y}+\alpha \mu {D}^{\mu +1}e\left(t\right)$$
(43)

Substituting Eqs. (41) into (43) provides

$$\dot{s}\left(t\right)={\dot{y}}_{d}-Ky-Bu+\alpha \mu {D}^{\mu +1}e\left(t\right)$$
(44)

The equivalent control can be demonstrated by \(\dot{s}=0\) as:

$${u}_{eq}(t)={B}^{-1}({\dot{y}}_{d}-Ky+\alpha \mu {D}^{\mu +1}e\left(t\right))$$
(45)

The reaching control law defines as:

$${u}_{r}(t)={K}_{r}s(t)$$
(46)

The Koopman-FOSMC can be demonstrated as:

$${u}_{\mathrm{Koopman}-\mathrm{FOSMC}}\left(t\right)={u}_{\mathrm{eq}}\left(t\right)+{u}_{r}\left(t\right)$$
(47)

The stability of the Koopman-FOSMC controller can be proved by using the Lyapunov theory as:

$$V\left(t\right)=\frac{1}{2}s(t){s}^{T}(t)$$
(48)

Taking derivative from Eq. (48) results,

$$\dot{V}\left(t\right)={s}^{T}(t)\dot{s}(t)$$
(49)

Substituting Eqs. (44) into (49) provides:

$$\dot{V}\left(t\right)={s}^{T}(t)({\dot{y}}_{d}-Ky-Bu+\alpha \mu {D}^{\mu +1}e\left(t\right))$$
(50)

Equation (47) is substituted into Eq. (50) to produce:

$$\dot{V}\left(t\right)={s}^{T}(t)({\dot{y}}_{d}-Ky-B{u}_{eq}\left(t\right)-B{u}_{r}\left(t\right)+\alpha \mu {D}^{\mu +1}e\left(t\right))$$
(51)

Substituting Eqs. (45) into (51) provides:

$$\dot{V}\left(t\right)={s}^{T}(t)({\dot{y}}_{d}-Ky-B({B}^{-1}({\dot{y}}_{d}-Ky+\alpha \mu {D}^{\mu +1}e\left(t\right)))-B{u}_{r}\left(t\right)+\alpha \mu {D}^{\mu +1}e\left(t\right))$$
(52)

Simplifying Eq. (52) produces:

$$\dot{V}\left(t\right)={s}^{T}(t)(-B{u}_{r}\left(t\right))$$
(53)

Substituting Eqs. (46) into (53) provides

$$\dot{V}\left(t\right)={s}^{T}(t)(-B{K}_{r}s(t))$$
(54)

The \(\dot{V}\left(t\right)<0\) according to Eq. (54). The suggested controller is hence stable.

7 The proposed control method

Most of the controllers have some disadvantages. The Koopman-FOSMC controller provides robustness and FOPID has high tracking performance. By combining the Koopman-FOSMC and FOPID controllers, the new compound controller will be obtained which benefits the advantages of both controllers. The proposed control method defines as:

$${u}_{\mathrm{Koopman}-\mathrm{CFOPIDSMC}}\left(t\right)={u}_{\mathrm{Koopman}-\mathrm{FOSMC}}\left(t\right)-{u}_{\mathrm{FOPID}}\left(t\right)$$
(55)

where \({u}_{\mathrm{FOPID}}\left(t\right)\) can be defined as:

$${u}_{\mathrm{FOPID}}\left(t\right)={K}_{p}e\left(t\right)+{K}_{i}{D}^{-\mu }e\left(t\right)+{K}_{d}{D}^{\mu }e\left(t\right)$$
(56)

where are the \({K}_{p}, {K}_{i}\) and \({K}_{d}\) are the FOPID controller’s gains.

8 Simulation results

This research applies a new compound control method to control nonlinear MEMS gyroscope dynamics. The simulations are done in MATLAB software. The proposed controller parameters are as follows:

$$ \begin{array}{*{20}l} {\alpha = diag\left\{ {10,10} \right\}} \hfill & {\mu = 0.75} \hfill & {K_{r} = diag\left\{ {10,10} \right\}} \hfill \\ {K_{p} = diag\left\{ {100,100} \right\}} \hfill & {K_{i} = diag\left\{ {40,40} \right\}} \hfill & {K_{d} = diag\left\{ {70,70} \right\}} \hfill \\ \end{array} $$

The initial values of position are \({q}_{0x}=0.4\) and \({q}_{0y}=0.6\). Also, the initial velocity values are as \({\dot{q}}_{0x}=0\) and \({\dot{q}}_{0y}=0\). The desired trajectory tracking for x-axis is \({q}_{dx}=\mathrm{sin}(4.17t)\) and y-axis is \({q}_{dy}=1.2\mathrm{sin}(5.11t).\)

Figure 3 shows the position tracking of x-axis and y-axis under FOSMC, Koopman-FOSMC and Koopman-CFOPIDSMC. The conventional FOSMC controller has a low tracking trajectory in comparison with two other controllers such as the Koopman-FOSMC and Koopman-CFOPIDSMC. It illustrates that the data-driven Koopman method affects highly improving tracking performance. Figure 4 illustrates the position tracking error of the x- and y-axis under FOSMC, Koopman-FOSMC and Koopman-CFOPIDSMC. The proposed controller has a low tracking error in comparison with the FOSMC and Koopman-FOSMC. Figure 5 shows the velocity of the x- and y-axis under the proposed controllers. Figure 6 shows the input control efforts under the FOSMC, Koopman-FOSMC and Koopman-CFOPIDSMC controllers. The control input under conventional FOSMC reached 200 (N.m) in some cases. When the Koopman method was used, the control inputs were significantly reduced. Also, the main benefit of the compound controller (Koopman-CFOPIDSMC) is reducing the control input signals. A small part of the figures was magnified to show the reduction of the control input by implementing the Koopman-CFOPIDSMC controller.

Fig. 3
figure 3

The position tracking of x- and y-directions under the proposed controllers

Full size image
Fig. 4
figure 4

The position tracking error of x- and y-direction under the proposed controllers

Full size image
Fig. 5
figure 5

Velocity of x- and y-axis under the proposed controllers

Full size image
Fig. 6
figure 6

Control input of x- and y-direction under the proposed controllers

Full size image

9 Conclusions

This paper proposed a compound controller based on the data-driven Koopman method. First, a conventional FOSMC is applied on a nonlinear MEMS gyroscope dynamic model. Then, the Koopman theory is used to linearize the nonlinear dynamic model of the MEMS gyroscope. The main problem with using the Koopman theory is how to obtain the Koopman operator. The DMD method was used to obtain the Koopman operator. When the model was linearized by the Koopman method, the FOSMC was used to control the x- and y-axis of the linearized model of the MEMS gyroscope. The results illustrated that using the Koopman method will significantly improve the controller performance. Finally, a compound controller is proposed to improve trajectory tracking and reduce the control inputs. Simulation results verified the performance of the Koopman-CFOPIDSMC was better than the FOSMC and Koopman-FOSMC.