Chaotic dynamics of a non-autonomous nonlinear system for a smart composite shell subjected to the hygro-thermal environment

Abstract

In this research, nonlinear dynamic behaviors of multiscale composites doubly curved shells have been investigated by employing multiple scales Perturbation Method. Three-phase composites shells with polymer/Carbon nanotube/fiber (PCF) according to Halpin–Tsai model have been assumed. The displacement- strain of nonlinear vibration of multiscale laminated doubly curved shells via higher order shear deformation (HSDT) theory and using Green–Lagrange nonlinear shell theory is obtained. The governing equations of composite doubly curved shell have been derived by implementing Hamilton’s principle and shell considered to be simply supported. For investigating correctness and accuracy, this paper is validated by other previous researches. Finally, bifurcation diagram, phase portraits and Poincare maps are investigated. The results indicate different dimensionless force; curvature ratio and kind of distribution pattern have strong influence on nonlinear vibration control of the composite multiscale doubly curved shell.

1 Introduction

The composite material individual including stiff reinforcement fibers and matrix employ in the aerospace and other industries, are Carbone nanotube—reinforced, Graphene platelet- reinforced (CNTF and GPLF respectively) which are strong and stiff (for their density). A composite material with most or all of the useful (stiffness, low density, high strength and toughness) is achieved with few or none of the especially weaknesses of the component materials. In order to, multiscale models are used for micromechanics and atomic simulations to investigate the constitutive properties of diffrent functionalized nanotube materials (Odegard et al. 2005; Gao and Li 2005). The mechanical response in a single polymer-CNT using FE analysis is investigated by Chen et al. (2003). The nonlinear statics and dynamics behavior of composite structure investigated in significant previous research that are presented some of them.

The nonlinear vibration of composite shells in hygrothermal environments is investigated by Naidu and Sinha (2007). In frame work first-order shear deformation theory and Green–Lagrange type nonlinear displacement and strain have been obtained. The results analyzed by finite element method. The effects of thin cylindrical shell panel in hygrothermal environment and curvature radios are investigated in this research. Large amplitude vibration analysis of doubly curved composite spherical shell via higher order shear deformation theory is presented by Panda and Singh (2008). They studied different parameters such as aspect ratio, hygrothermal loading, curvature ratio, stacking sequences, boundary conditions and side to thickness ratio. Yazdi (2013) presented the nonlinear vibration behavior of doubly curved cross-ply shell. The displacements-strains have been obtained via by Donnell’s shell theory and von-Karman type nonlinearity and by HPM method have been solved. Singh and Panda (2014) investigated nonlinear vibration behavior of doubly curved composite shell panel based on higher order shear deformation theory. Finally, the influences of aspect ratio, curvature ratio, stacking sequence have been studied. Nonlinear vibration of cylindrical shell in frame work higher order shear deformation theory are presented by Amabili and Reddy (2010). They have been illustrated nonlinear term are significant role to predict the nonlinear response of composite shell. Alijani et al. (2011) studied primary and subharmonic responses of FGM shallow shell by multiple scales analytical method. Based on Donnell’s type nonlinear strain–displacement relationships have been obtained. They found that two-to-one internal resonance may be taken measure in doubly curved FGM shells by kind of the volume fraction exponent. Continued from previous work, large amplitude forced vibrations of rectangular plates Via higher order shear deformation theory have been investigated by Alijani and Amabili (2013). From the experimental and analytical method they are presented that nonlinear frequency result in important effect in nonlinear to linear response of plates. In order to, fundamental frequency of functionally graded material doubly curved shallow shell is studied by Chorfi and Houmat (2010). Based on FEM method they established their results. And they investigated the influence of thickness ratio, volume fraction versus nonlinear to linear vibration. The fundamental frequency of FGM doubly curved shell embedded in elastic foundation is presented by Shen et al. (2015). in frame work shear deformation theory and von-Karman nonlinear strain–displacement have been obtained. The inflence of volume fraction index, Pasternak foundation, curveture ratio and other parameter have been investigated. Singh and Panda (2015) presented large amplitude of composite single and doubly curved shell via the piezoelectric layer according to the higher-order shear deformation theory and Green–Lagrange nonlinearity. They studied different parameters such as aspect ratio, curvature ratio, stacking sequences, boundary conditions, side to thickness ratio and number of piezoelectric layers. Heydari et al. (2015) researched the nonlinear bending of functionally graded/CNT plates via first order shear deformation plate theory subjected to uniform pressure and embedded in elastomeric medium based on generalized differential quadrature method. The nonlinear bending of hybrid plates including CNTRC layers embedded in elastic foundations where influence of matrix cracks by Fan and Wang (2017). Shen et al. (2017) investigated the nonlinear vibration of composites functionally graded-Graphene reinforcement plates resting on elastic foundation in thermal environments. According to the FSDT thermally postbuckled plates is studied by Lee and Lee (1997). Wu et al. (2017) studied the nonlinear dynamic instability behavior of FG/polymer/GPL nanocomposite by using Timoshenko Beam theory. The vibration behavior of sandwich plates with composite face sheets was presented by Shiau and Kuo (2006). Recently, based on the nonlocal strain gradient theory Sahmani and Aghdam (2017) investigated the buckling and postbuckling of multilayer GPLRC nanoshell. Recently, large amplitude vibration of graphene- reinforced composite cylindrical shell subjected to thermal environment is investigated by Shen et al. (2017). In frame work Reddy’s third order shear deformation theory and von-Karman theory the linear and nonlinear relationship equations of displacement- strain have been obtained. The equations of motion are solved by perturbation method. Two end conditions movable and unmovable are assumed. They carried out the effect of several parameters such as temperature rising, different distribution pattern, end condition situation, stacking sequence. Mahapatra et al. (2015) investigated based on higher order shear deformation theory nonlinear vibration behavior of composite single/doubly curved shell subjected to hygrothermal environment. Influence of several parameters such as geometrical and material properties versus nonlinear frequency under hygrothermal environment are studied. The wave propagation behaviors of functionally graded plate subjected to the thermal environments have been investigated by Boukhari et al. (2016). Ahouel et al. (2016) investigated by the bending, buckling and vibration of functionally graded (FG) nanobeams in frame work nonlocal differential theories. The free vibration behaviors of functionally graded nano plates resting on elastic foundation have been presented by Bounouara et al. (2016). Large deflection of composite spherical shell subjected to the hygrothermal environment has been investigated by Mahapatra et al. (2016a, b). They studied different parameters such ad aspect ratio, hygrothermal loading, curvature ratio and side to thickness ratio. The vibration of composite structure subjected to the hygrothermal environment has been investigated by Mahapatra et al. (2016a, b). They studied different parameters such ad aspect ratio, hygrothermal loading, curvature ratio and side to thickness ratio. In continues Mahapatra et al. (2016a, b) analyzed deflection of composite cylindrical shell. This structure has been considered by Green–Lagrange nonlinearity via higher order shear deformation theory. The effects kind of parameters such as geometrical and material properties versus nonlinear frequency under hygrothermal environment is investigated. The nonlinear vibration of the functionally graded sandwich structure reinforcement by CNT subjected to the thermal environment based on higher-order shear deformation theory and Green–Lagrange geometrical nonlinear strains is investigated by Mehar et al. (2017a, b). Large amplitude of composite plate under hygrothermal environment has been investigated by Mahapatra et al. (2016a, b). They studied different parameters such as aspect ratio, hygrothermal loading, curvature ratio and side to thickness ratio. The bending and free vibration behavior of isotropic functionally graded sandwich composite plates according to the new hyperbolic shear deformation theory has been studied Mahi and Tounsi (2015). Bouafia et al. (2017) investigated bending and free flexural vibration response of functionally graded nanobeams in frame works of nonlocal quasi-3D theory. They presented several parameters such as the influence of the nonlocal parameter, the beam aspect ratio and material gradient index on the FG nanobeam. They discussed a lot of parameters in detailed in their researches. The bending and vibration behavior of functionally graded beams has been presented by Bourada et al. (2015). They investigated numerical results of their studied compared with other theories to show the effect of the inclusion of transverse normal strain on the deflections and stresses. Bousahla et al. (2016) the buckling behavior of functionally graded plates subjected to linear and non-linear temperature rises via four-variable refined plate theory. They studied the effects of influences kind of parameters such as ratio of thermal expansion, aspect ratio, side-to-thickness ratio and gradient index will be investigated on buckling response. The free vibration analysis of functionally graded (FG) plates by using a new simple higher-order shear deformation theory has been studied by Houari et al. (2016). They discussed a lot of parameters in detailed in their researches. The bending and dynamic response of functionally graded plates by using new first-order shear deformation theory is proposed by Bellifa et al. (2016). The hygro-thermo-mechanical bending behavior of functionally graded material plate subjected to variable two-parameter elastic foundations is presented by Beldjelili et al. (2016) by employing a four-variable refined plate theory. They studied influence of plate aspect ratio, power-law index, elastic foundation parameters, temperature rise and side-to-thickness ratio on the static behavior of FGM plates. Thermal stability of functionally graded sandwich plates by employing simple shear deformation theory has been studied by Bouderba et al. (2016). Bellifa et al. (2017a, b) presented the buckling behavior of functionally graded plates via a new displacement field which includes undetermined integral variables. El-Haina et al. (2017) studied thermal buckling of thick functionally graded sandwich plates based on stress function and sinusoidal shear deformation theory. They presented the influence of functionally graded layers thickness, power law index, loading type on the thermal buckling of sandwich plate. The thermal buckling behavior of functionally graded sandwich plates via higher shear deformation theories has been presented by Menasria (2017). According to the their researches the effects of material index, thickness and aspect ratios, loading and sandwich plate type on the critical buckling. The nonlinear postbuckling response of nanobeams based on nonlocal zeroth-order shear deformation has been investigated by Bellifa (2017a, b). They discussed a lot of parameters in detailed in their works. The free vibration characteristics of functionally graded nanobeams resting on elastic foundation subjected moisture and temperature on have been studied by Mouffoki et al. (2017). They discussed influence of power law index, hygro-thermal environments, nonlocality and elastic foundation on the free vibration analyzed of FG beams. The thermal buckling analysis of functionally graded sandwich by using stress function and sinusoidal shear deformation theory has been investigated by El-Haina et al. (2017). They investigated the effect of loading type, functionally graded layers thickness, power law index on the thermal buckling behavior of thick functionally graded sandwich. They studied influence of the porosity volume fraction and volume fraction distributions on wave propagation of functionally graded plate. Chikh et al. (2017) thermal buckling analysis laminated composite plates based on higher order shear deformation theory. They discussed a lot of parameters in detailed in their works. The buckling force behavior of FG nanoplates resting on an elastic Kerr foundation and subjected to hygrothermal environment is investigated by Shahsavari et al. (2018). They presented effects on the buckling of FG nanoplates of porosity amount, power-law index, geometry, moisture and elastic foundation. The wave propagation in FGM plate has been investigated via four variable refined plate theories and an efficient shear deformation theory has been proposed by Fourn et al. (2018). The stability response of plate in frame work a novel nonlocal refined theory for of orthotropic single-layer graphene sheet has been proposed by Yazid et al. (2018). Their research presented buckling response of embedded orthotropic nanoplates such as graphene by using a new refined plate theory and nonlocal theory. The dynamics analysis of nanobeam with surface effects has been presented by Youcef et al. (2018). Menasria et al. (2017) presented thermal buckling response of functionally graded (FG) sandwich plates via four variables of higher order shear order theory. They discussed effects of material index, aspect and thickness ratios, and loading type on the critical buckling. The buckling behavior of single layer graphene sheet by using novel shear deformation theory based on nonlocal elasticity theory has been proposed by Mokhtar et al. (2018). Karami et al. (2018a, b, c) investigated wave dispersion in anisotropic doubly-curved nanoshells is presented. They demonstrated that the nonlocal-strain gradient parameters, material properties and wave number effects on wave frequencies and phase velocities. The thermal buckling response of embedded FG nano plates via new nonlocal trigonometric shear deformation theory has been presented by Khetir et al. (2017). Besseghier et al. (2017) proposed free vibration behavior of functionally graded (FG) nanoplates resting on two-parameter elastic foundation is investigated based on a novel nonlocal refined trigonometric shear deformation theory. The mechanical analysis of anisotropic nanoparticles based on three dimensional elasticity theory in with nonlocal strain gradient theory has been investigated by Karami et al. (2018a, b, c). Karami et al. (2018a, b, c) presented the influence of triaxial magnetic field on the anisotropic nanoplates. Furthermore they proposed the nonlocal strain gradient elasticity theory and small scale effects. The wave dispersion behavior of FG nanoplates by employing a size-dependent quasi-3D model has been proposed by Karami et al. (2018a, b, c). Bellifa et al. (2017a, b) studied buckling response of functionally graded plates by using a new displacement field which includes undetermined integral variables. Belabed et al. (2018) presented vibration of functionally graded sandwich plate with new 3 unknown hyperbolic shear deformation theories. The thermal buckling response of functionally graded sandwich plates with various boundary conditions by using simple first-order shear deformation theory has been investigated by Kaci et al. (2018). Their numerical results prove that the present simple first-order shear deformation theory can achieve the same accuracy of the existing conventional first-order shear deformation theory which has more number of unknowns. Belabed et al. (2018) studied of sound transmission through corrugated core FGM sandwich plates filled with porous material via 3-unkonw hyperbolic shear deformation theory. Based on their studied the influence of the temperature and volume fraction distributions on wave propagation of functionally graded. Thermoelasic deflections of composite sandwich shell subjected to the thermo-mechanical loading are investigated by Mehar et al. (2018a). They studied different parameters such as flexural behavior and structural stiffness. The vibroacoustic behavior of laminated composite curved panels subjected to hygrothermal environment is studied in frame work a new higher-order finite-boundary element model is investigated by Sharma et al. (2018a, b). They studied different parameters such as geometry, modular ratio, aspect ratio, hygrothermal loading, curvature ratio and side to thickness ratio on the hygro- thermos- acoustic responses. Furthermore, Sharma et al. (2018a, b) investigated thermoacoustic responses of a new higher-order coupled finite-boundary element scheme of the composite panel. Influence of several parameters such as geometrical and material properties versus acoustic frequency are studied. The nonlinear deflection behavior carbon nanotube-reinforced polymer composite based on a novel higher order has been studied by Mehar et al. (2018b). They investigated several parameters and discussed about these effects. Finally, it can be mentioned that present article is presented the large amplitude dynamic behavior of multiscale composite doubly curved shell. The equations of motion are constructed in frame work HSDT and Green–Lagrange type geometric nonlinearity. Based on multiple scales Perturbation theory the equations of motion are solved. Bifurcation diagram, phase portraits and Poincare maps are investigated.

2 Theory and formulation multiscale composite

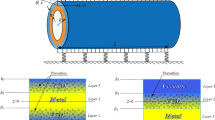
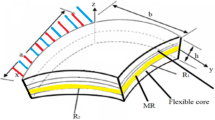
Figure 1 illustrated multiscale composite doubly curved shell with length of l, thickness of h and shell curvatures of ${\text{R}}_{1} ,{\text{R}}_{2}$. The shell is embedded in a distributed hygrothermal load, which is considered in the symmetry plane of the shell cross section, i.e. in the x–y plane.

Fig. 1

Geometry of doubly curved multiscale composite shell

2.1 Multiscale model

The effective constituent of the PCF multiscale composite can be presented via Halpin–Tsai model (Thostenson et al. 2002) and micromechanics approaches of scheme have been expressed by Shen (2009).

The properties of the PCF shell are concentrated to be orthotropic can be presented as (Shen 2009):

$$ E_{11} = V_{f} E_{11}^{F} + V_{mcn} , $$

(1)

$$ \frac{1}{{E_{22} }} = \frac{1}{{E_{11}^{F} }} + \frac{{V_{mcn} }}{{E_{mcn} }} - V_{f} V_{mnc} - \frac{{\frac{{V_{f}^{2} E_{mcn} }}{{E_{22}^{F} }} + \frac{{V_{mcn}^{2} E_{mcn} }}{{E^{mcn} }} - 2V_{f} V_{mcn} }}{{V_{f} E_{22}^{F} + V_{mcn} E_{mcn} }}, $$

(2)

$$ \frac{1}{{G_{12} }} = \frac{{V_{f} }}{{G_{11}^{F} }} + \frac{{V_{mcn} }}{{G_{mcn} }}, $$

(3)

$$ \rho = V_{f} \rho_{f} + V_{mcn } \rho_{mcn} , $$

(4)

$$ \vartheta_{12} = V_{f} v_{f} + V_{mcn} v_{mcn} , $$

(5)

where $E_{11}^{F} ,E_{22}^{F}$ are the Young’s modulus of CNT, $G_{12}$ shear modulus and $\rho$ is mass density, $\vartheta_{12}$ Poisson’s ratio of fibers, respectively, the corresponding properties of the isotropic matrixes of CNT composite presented with $E_{mcn} ,G_{mcn} ,\rho_{mcn}$ and $V_{mcn}$ and Volume fractions of the fiber presented by $V_{f}$.

Via Halpin–Tsai model, composites tensile modulus has been expressed (Kim et al. 2009):

$$ E_{mcn} = \frac{{E_{M} }}{8}\left[ {5\left( {\frac{{1 + 2\beta_{dd} V_{cn} }}{{1 - \beta_{dd} V_{cn} }}} \right) + 3\left( {\frac{{1 + 2\left( {\frac{{l_{cn} }}{{d_{cn} }}} \right)\beta_{ll} V_{cn} }}{{1 - \beta_{ll} V_{cn} }}} \right)} \right], $$

(6)

$$ \beta_{ll} = \frac{{\frac{{E_{11}^{cn} }}{{E_{M} }} - \left( {\frac{{d_{ccn} }}{{4t^{cn} }}} \right)}}{{\frac{{E_{11}^{cn} }}{{E_{M} }} + \left( {\frac{{l_{cn} }}{{2h^{cn/gpl} }}} \right)}}, $$

(7)

$$ \beta_{dd} = \frac{{\frac{{E_{11}^{cn} }}{{E_{M} }} - \left( {\frac{{d_{cn} }}{{4h^{cn} }}} \right)}}{{\frac{{E_{11}^{cn} }}{{E_{M} }} + \left( {\frac{{d_{cn} }}{{2h^{cn} }}} \right)}}, $$

(8)

where $E_{11}^{cn} ,$ refers to the Young’s modulus, $h^{cn} ,$$d_{cn, }$, $l_{cn}$ presented thickness, outer diameter, length and $V_{cn}$ are the volumes fraction of Carbon Nanotubes, respectively, and $V_{mcn}$ and $E_{mcn}$ are the volumes fraction of the matrixes and Young’s modulus, respectively.

For the different distribution multiscale composite shell, the weight fraction of CNT changes layerwise in accordance with the according distribution pattern such as U, X, A and O are studied. CNT volume fraction of n-th layer corresponding to each distribution pattern can be presented as (Feng et al. 2017):

$$ U :V_{cn}^{n} = V_{cn} , $$

(9a)

$$ X: V_{cn}^{n} = 2V_{cn} \left( {\frac{{\left| {2n - n_{t} - 1} \right|}}{{n_{t} }}} \right), $$

(9b)

$$ O:V_{cn}^{n} = 2V_{cn} \left( {1 - \frac{{\left| {2n - n_{t} - 1} \right|}}{{n_{t} }}} \right), $$

(9c)

$$ A:V_{cn}^{n} = V_{cn} \left( {\frac{{\left| {2n - 1} \right|}}{{n_{t} }}} \right), $$

(9d)

where the total number of layers can be expressed by $n_{t}$ and the total volumes fraction of CNT can be presented by (Rafiee et al. 2013):

$$ V_{cn} = \frac{{w_{cn} }}{{w_{cn} + \left( {\frac{{\rho_{cn} }}{{\rho_{m} }}} \right) - \left( {\frac{{\rho_{cn} }}{{\rho_{m} }}} \right)w_{cn} }}, $$

(10)

where $\rho_{cn/gpl}$ are the mass densities of the CNT L and $\rho_{m}$ is epoxy resin matrix, $w_{cn}$ are the mass fraction of the CNT, respectively.

The mass densities of CNT can be presented as:

$$ \rho_{mnc} = V_{cn} \rho_{cn} + v_{m} \rho_{m} , $$

(11)

$$ G_{mnc} = \frac{{E_{mnc} }}{{2(1 + v_{mcn} )}}, $$

(12)

$$ V_{mcn} = V_{m} , $$

(13)

where $v_{m}$$,v_{mcn}$ Poisson’s ratio of the matrix, CNT and $\alpha_{11}$ refer to the thermal expansion coefficients of longitudinal and $\alpha_{22}$ presented in transverse directions (Shen 2009). So $\alpha_{11}^{f}$ is the thermal expansion coefficient of longitudinal fiber and $\alpha_{22}$ presented in transverse directions of the fiber. $\alpha_{mcn}$ can be expressed as (Hu et al. 2013):

$$ \alpha_{11} = \frac{{V_{f} E_{11}^{f} \alpha_{11}^{f} + V_{mcn} E_{mcn} \alpha_{mcn} }}{{V_{f} E_{11}^{f} + V_{mcn} E_{mcn} }}, $$

(14)

$$ \alpha_{22} = \left( {1 + V_{f} )V_{f} \alpha_{22}^{f} + (1 + V_{mnc} } \right)V_{mcn} \alpha_{mcn} - v_{12} \alpha_{11} , $$

(15)

$$ \alpha_{mcn} = \frac{1}{2}\left\{ {\left( {\frac{{V_{cn} E_{cn} \alpha_{cn} + v_{m} E_{m} \alpha_{m} }}{{v_{cn} E_{cn} + v_{m} E_{m} }}} \right)} \right\}\left( {1 - v_{mcn} } \right) + (1 + v_{m} )\alpha_{m} V_{m} + (1 + v_{cn} )\alpha_{cn} V_{cn} , $$

(16)

where $\alpha_{mcn}$, $\beta_{mcn} ,$ are the thermal expansion and moisture coefficients of the epoxy resin CNT and GPL matrix and $\alpha_{cn}$ are the thermal expansion coefficients of the CNT.

$$ \beta_{11} = \frac{{V_{f} E_{11}^{f} + V_{mcn} E_{mcn} \beta_{m} }}{{V_{f} E_{11}^{f} + V_{mcn} E_{mcn} }}, $$

(17)

$$ \beta_{22} = \left( {1 + V_{mcn} } \right)V_{mcn} \beta_{m} - v_{12} \beta_{11} . $$

(18)

2.2 Kinematic relations

In frame work, higher-order shear deformable theory, the displacement fields at an arbitrary point in the composite shell can be expressed as:

$$ u = u_{0} + z\varphi_{x} + z^{2} \psi_{x} + z^{3} \theta_{x} , $$

(19a)

$$ v = v_{0} + z\varphi_{y} + z^{2} \psi_{y} + z^{3} \theta_{y} , $$

(19b)

$$ w = w_{0} . $$

(19c)

In these equations, $u_{0}$, $v_{0}$, and $w_{0}$ are the original displacements of the shell in the x, y directions; the rotations of transverse normal at the mid-plane in the x and y axes represented by $\varphi_{x}$ and $\varphi_{y}$.$\psi_{x}$$,\psi_{y} ,\theta_{x}$ and $\theta_{x} a$ re higher order terms of Taylor series expansion defined at the mid-plane.

The vanishing of the shear strains at the top and the bottom surfaces of the shell requires

$$ \gamma_{xz} |_{Z \pm h/2} = 0,\quad \gamma_{yz} |_{Z \pm h/2} = 0, $$

these equations give:

$$ \begin{aligned} \psi_{x} & = - \frac{4}{{3h^{2} }}z^{3} \left( {\varphi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right),\quad \psi_{y} = - \frac{4}{{3h^{2} }}z^{3} \left( {\varphi_{y} + \frac{{\partial w_{0} }}{\partial y}} \right) \\ \theta_{x} & = \frac{{\psi_{x} }}{{2R_{1} }},\quad \theta_{y} = \frac{{\psi_{y} }}{{2R_{1} }}, \\ \end{aligned} $$

$$ u = u_{0} + z\varphi_{x} - \frac{4}{{3h^{2} }}z^{3} \left( {\varphi_{x} + \frac{{\partial w_{0} }}{\partial x}} \right), $$

(20a)

$$ v = v_{0} + z\varphi_{y} - \frac{4}{{3h^{2} }}z^{3} \left( {\varphi_{y} + \frac{{\partial w_{0} }}{\partial y}} \right), $$

(20b)

$$ w = w_{0} , $$

(20c)

where the geometric imperfection $w_{0}$ in the normal direction has been introduced. Equation (20) represent the parabolic distribution of shear effects through the thickness and satisfy the zero shear boundary condition at both the top and bottom surfaces of the shell. This is the justification for the use of a third-order shear deformation theory.

Green–Lagrange type geometric nonlinearity, the strain components $\varepsilon_{xx}$, $\varepsilon_{yy}$ and $\gamma_{xy }$ can be shown as:

$$ \begin{aligned} & \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} \\ & \quad = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x} + \frac{{w_{0} }}{{R_{1} }}} \\ {\frac{{\partial v_{0} }}{\partial y} + \frac{{w_{0} }}{{R_{2} }}} \\ {\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial u_{0} }}{\partial x}} \\ {\frac{{\partial u_{0} }}{\partial x} + \left( {\frac{{\partial w_{0} }}{\partial x} - \frac{{u_{0} }}{{R_{1} }}} \right)} \\ {\frac{{\partial v_{0} }}{\partial y} + \left( {\frac{{\partial w_{0} }}{\partial y} - \frac{{v_{0} }}{{R_{2} }}} \right)} \\ \end{array} } \right\} \\ & \quad \quad + \frac{1}{2}\left\{ {\begin{array}{*{20}c} {\left[ {\left( {\frac{{\partial u_{0} }}{\partial x} + \frac{{w_{0} }}{{R_{1} }}} \right)^{2} + \left( {\frac{{\partial v_{0} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial w_{0} }}{\partial x} - \frac{{u_{0} }}{{R_{1} }}} \right)^{2} } \right]} \\ {\left[ {\left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} + \left( {\frac{{\partial v_{0} }}{\partial y} + \frac{{w_{0} }}{{R_{2} }}} \right)^{2} + \left( {\frac{{\partial w_{0} }}{\partial y} - \frac{{v_{0} }}{{R_{2} }}} \right)^{2} } \right]} \\ {2\left[ {\left( {\frac{{\partial u_{0} }}{\partial x} + \frac{{w_{0} }}{{R_{1} }}} \right)\frac{{\partial u_{0} }}{\partial y} + \frac{{\partial v_{0} }}{\partial x}\left( {\frac{{\partial v_{0} }}{\partial y} + \frac{{w_{0} }}{{R_{2} }}} \right) + \left( {\frac{{\partial w_{0} }}{\partial x} - \frac{{u_{0} }}{{R_{1} }}} \right)\left( {\frac{{\partial w_{0} }}{\partial y} - \frac{{v_{0} }}{{R_{2} }}} \right)} \right]} \\ {2\left[ {\left( {\frac{{\partial u_{0} }}{\partial x} + \frac{{w_{0} }}{{R_{1} }}} \right)\frac{{\partial u_{0} }}{\partial z} + \frac{{\partial v_{0} }}{\partial x}\frac{{\partial v_{0} }}{\partial z} + \left( {\frac{{\partial w_{0} }}{\partial x} - \frac{{u_{0} }}{{R_{1} }}} \right)\frac{{\partial w_{0} }}{\partial z}} \right]} \\ {2\left[ {\frac{{\partial u_{0} }}{\partial y}\frac{{\partial u_{0} }}{\partial z} + \left( {\frac{{\partial v_{0} }}{\partial y} + \frac{{w_{0} }}{{R_{2} }}} \right)\frac{{\partial v_{0} }}{\partial z} + \left( {\frac{{\partial w_{0} }}{\partial y} - \frac{{v_{0} }}{{R_{2} }}} \right)\frac{{\partial w_{0} }}{\partial z}} \right]} \\ \end{array} } \right\}. \\ \end{aligned} $$

(20a)

The constitutive relation of the composite doubly curved shell can be expressed as:

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ \end{array} } \\ {\tau_{yz} } \\ {\tau_{xy} } \\ {\tau_{xz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {Q_{11}^{n} } \\ {Q_{12}^{n} } \\ 0 \\ \end{array} } \\ 0 \\ { 0 } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {Q_{12}^{n} } \\ {Q_{22}^{n} } \\ 0 \\ \end{array} } \\ 0 \\ { 0 } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ {Q_{44}^{n} } \\ \end{array} } \\ 0 \\ { 0 } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ {Q_{55}^{n} } \\ { 0} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ { Q_{66}^{n} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{xx} - \alpha_{11} \left( {T\left( z \right) - T_{0} } \right)} \\ {\varepsilon_{yy} - \alpha_{22} \left( {T\left( z \right) - T_{0} } \right)} \\ \end{array} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ \end{array} } \right\}. $$

(21)

If the fiber angle with the geometric x axis is expressed by θ, the relation (31) can be transferred to the geometric coordinates as:

$$ \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ \end{array} } \\ {\tau_{yz} } \\ {\tau_{xy} } \\ {\tau_{xz} } \\ \end{array} } \right\}_{T} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\bar{Q}_{11}^{n} } \\ {\bar{Q}_{12}^{n} } \\ 0 \\ \end{array} } \\ 0 \\ { 0 } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} {\bar{Q}_{12}^{n} } \\ {\bar{Q}_{22}^{n} } \\ 0 \\ \end{array} } \\ 0 \\ { 0 } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ {\bar{Q}_{44}^{n} } \\ \end{array} } \\ 0 \\ { 0 } \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ {\bar{Q}_{55}^{n} } \\ { 0} \\ \end{array} \begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ 0 \\ { \bar{Q}_{66}^{n} } \\ \end{array} } \right]_{T} \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{xx} - \alpha_{11} \left( {T\left( z \right) - T_{0} } \right)} \\ {\varepsilon_{yy} - \alpha_{22} \left( {T\left( z \right) - T_{0} } \right)} \\ \end{array} } \\ {\gamma_{xz} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ \end{array} } \right\}_{T} . $$

(22)

The reduce stiffness modulus of composite doubly curved can be expressed by:

$$ Q_{11} = \frac{{E_{11} }}{{1 - \nu_{12} \nu_{21} }},\quad Q_{12} = \frac{{\nu_{12} E_{22} }}{{1 - \nu_{12} \nu_{21} }},\quad Q_{22} = \frac{{E_{22} }}{{1 - \nu_{12} \nu_{21} }},\quad Q_{44} = G_{23} ,\quad Q_{55} = G_{13} ,\quad Q_{66} = G_{12} . $$

(23)

Transformed shell principal coordinates are in expressed Appendix A.

Now via Hamilton’s principle can be written:

$$ \mathop \int \limits_{0}^{t} \delta (V + U - T)dt = 0, $$

(24)

where, $V$ is the work done by external energy, $U$ is strain energy, and $T$ is kinetic energy.

The strain energy is expressed as:

$$ \begin{aligned} U & = \frac{1}{2}\mathop \sum \limits_{n = 1}^{N} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \mathop \int \limits_{{h_{n - 1} }}^{{h_{n} }} \left[\left(\sigma_{xx} \varepsilon_{xx} + \sigma_{yy} \varepsilon_{yy} + \tau_{yz} \gamma_{yz} + \tau_{xz} \gamma_{xz} + \tau_{xy} \gamma_{xy} \right)\right] \\ & \quad \times \left( {1 + \frac{z}{{R_{1} }}} \right)\left( {1 + \frac{z}{{R_{2} }}} \right)dc_{1} dc_{2} dz. \\ \end{aligned} $$

(25)

The first variation can be obtained as:

$$ \begin{aligned} \delta U & = \mathop \sum \limits_{n = 1}^{N} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \left[ {\left( {N_{xx} \delta \varepsilon_{xx}^{0} + M_{xx} \delta k_{xx}^{0} + P_{xx} \delta k_{xx}^{2} + N_{yy} \delta \varepsilon_{yy}^{0} + M_{yy} \delta k_{yy}^{2} + P_{yy} \delta k_{yy}^{2} + N_{xy} \delta \varepsilon_{xy}^{0} } \right.} \right. \\ & \quad \left. {\left. { + M_{xy} \delta k_{xy}^{2} + P_{xy} \delta k_{xy}^{2} + K_{yy} \delta \gamma_{yz}^{0} + R_{yy} k_{yz}^{1} + K_{xx} \delta \gamma_{xz}^{0} + R_{xx} k_{xz}^{1} } \right)} \right] \\ & \quad \times \left( {1 + \frac{z}{{R_{1} }}} \right)\left( {1 + \frac{z}{{R_{2} }}} \right)dc_{1} dc_{2} , \\ \end{aligned} $$

(26)

where, for convenience a shell by rectangular base in dimension a and b in $c_{1}$ and $c_{2}$ directions, has been considered.

$q_{1}$, $q_{2}$ are the Lame coefficients of the shell can be expressed as $q_{1} = c_{1} \left( {1 + \frac{Z}{{R_{1} }}} \right), q_{2} = c._{2} \left( {1 + \frac{Z}{{R_{2} }}} \right)$.

$R_{1}$ and $R_{2}$ are the principal radii of curvature in $q_{1}$ and $q_{1}$ directions, respectively

The Kinetic energy can be presented as:

$$ T = \frac{1}{2}\rho^{n} \mathop \sum \limits_{n = 1}^{N} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \mathop \int \limits_{{h_{n - 1} }}^{{h_{n} }} (\dot{u}_{0}^{2} + \dot{v}_{0}^{2} + \dot{w}_{0}^{2} ) \times \left( {1 + \frac{z}{{R_{1} }}} \right)\left( {1 + \frac{z}{{R_{2} }}} \right)dc_{1} dc_{2} dz. $$

(27)

For simplified the kinetic energy relationship of composite shell can be obtained:

$$ \begin{aligned} T & = \frac{1}{2}\rho^{n} \mathop \sum \limits_{n = 1}^{N} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \left( {\dot{u}_{0}^{2} + \dot{v}_{0}^{2} + \dot{w}_{0}^{2} + h^{2} \left[ {\frac{17}{315}\left( {\dot{\varphi }_{x}^{2} + \dot{\varphi }_{y}^{2} } \right) + \dot{\varphi }_{x} \dot{u}_{0} \left( {\frac{41}{{120R_{1} }} + \frac{2}{{15R_{2} }}} \right)} \right.} \right. \\ & \quad + \dot{\varphi }_{y} \dot{v}_{0} \left( {\frac{41}{{120R_{2} }} + \frac{2}{{15R_{1} }}} \right) + \frac{1}{4}\left( {\frac{{\dot{u}_{0}^{2} }}{{R_{1} }} + \frac{{\dot{v}_{0}^{2} }}{{R_{2} }}} \right) + \frac{{\dot{w}_{0}^{2} }}{{12R_{1} R_{2} }} + \frac{{\partial \dot{w}_{0} }}{{q_{1} \partial c_{1} }}\left( {\frac{{\partial \dot{w}_{0} }}{{252q_{1} \partial c_{1} }} + \frac{{\dot{u}_{0} }}{{120R_{1} }} - \frac{{\dot{u}_{0} }}{{30R_{2} }} - 8\frac{{\dot{\varphi }_{x} }}{315}} \right) \\ & \quad \left. {\left. { + \frac{{\partial \dot{w}_{0} }}{{q_{2} \partial c_{2} }}\left( {\frac{{\partial \dot{w}_{0} }}{{252q_{2} \partial c_{1} }} + \frac{{\dot{v}_{0} }}{{120R_{2} }} - \frac{{\dot{v}_{0} }}{{30R_{1} }} - 8\frac{{\dot{\varphi }_{y} }}{315}} \right)} \right]} \right)dc_{1} dc_{2} . \\ \end{aligned} $$

(28)

The first variation of work can be expressed in the following form:

$$ \delta \varPi_{w} = \mathop \int \limits_{0}^{2\pi } \mathop \int \limits_{0}^{L} \left[ {\left( {q^{hyg} + q} \right)\frac{{\partial w_{0} }}{\partial x}\frac{{\partial \delta w_{0} }}{\partial x} - c_{d} \frac{{\partial w_{0} }}{\partial t}} \right]dc_{1} dc_{2} , $$

(29)

where $q^{hyg} ,q$ expressed by:

$$ \begin{gathered} q = q_{0} - q_{1} cos\Omega t, \hfill \\ q^{{hyg}} = N^{{T_{n} }} + N^{{H_{n} }} \hfill \\ \end{gathered} $$

$N^{{T_{n} }} \;and\; N^{{H_{n} }}$ are applied forces due to variation of temperature and moisture where are written as:

$$ N^{{T_{n} }} = \mathop \int \limits_{{h_{n - 1} }}^{{h_{n} }} \left[ {\bar{Q}_{11} \alpha_{11} + \bar{Q}_{12} \alpha_{12} } \right]({\text{T}} - {\text{T}}_{1} )dz, $$

(30)

$$ N^{{H_{n} }} = \mathop \int \limits_{{h_{n - 1} }}^{{h_{n} }} \left[ {\bar{Q}_{11} \beta_{11} + \bar{Q}_{12} \beta_{12} } \right](H - H_{1} )dz. $$

(31)

And $T - T_{1}$,$H - H_{1}$ are variation of temperature and moisture, T can be defined by sinusoidal temperature following as:

$$ T = T_{1} + \Delta T\,\left( {1 - \text{Cos} \frac{\pi }{2}\left( {\frac{1}{2} + \frac{z}{h}} \right)} \right). $$

(32)

By setting the coefficients of $\delta u$, $\delta v$,$\delta w$, $\delta \varphi_{x}$ and $\delta \varphi_{y}$ to zero and substituting Eqs. (25), (27), and (29) into Eq. (24) may be stated as:

$$ \frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = \bar{I}_{0} \left( {\frac{{\partial^{2} u_{0} }}{{\partial t^{2} }}} \right) - \bar{J}_{1} \left( {\frac{{\partial^{2} \varphi_{x} }}{{\partial t^{2} }}} \right) + s_{1} \bar{I}_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{\partial x}} \right), $$

(33a)

$$ \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{y} }}{\partial y} = \bar{I}_{0} \left( {\frac{{\partial^{2} v_{0} }}{{\partial t^{2} }}} \right) - \bar{J}_{1} \left( {\frac{{\partial^{2} \varphi_{y} }}{{\partial t^{2} }}} \right) + s_{1} \bar{I}_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{\partial y}} \right), $$

(33b)

$$ \begin{aligned} & \frac{{\partial \bar{K}_{x} }}{\partial x} + \frac{{\partial \bar{K}_{y} }}{\partial y} + \frac{\partial }{\partial x}\left[ {N_{x} \left( {\frac{{\partial w_{0} }}{\partial x} - \frac{{u_{0} }}{{R_{1} }}} \right) + N_{xy} \left( {\frac{{\partial w_{0} }}{\partial y} - \frac{{v_{0} }}{{R_{2} }}} \right)} \right] \\ & \quad \quad + \frac{\partial }{\partial y}\left[ {N_{xy} \left( {\frac{{\partial w_{0} }}{\partial x} - \frac{{u_{0} }}{{R_{1} }}} \right) + N_{y} \left( {\frac{{\partial w_{0} }}{\partial y} - \frac{{v_{0} }}{{R_{2} }}} \right)} \right] + s_{1} \left( {\frac{{\partial^{2} P_{y} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} P_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} P_{y} }}{{\partial y^{2} }}} \right) - \frac{{N_{x} }}{{R_{1} }} - \frac{{N_{y} }}{{R_{2} }} + q^{hyg} \\ & \quad = I_{0} \left( {\frac{{\partial^{2} w_{0} }}{{\partial t^{2} }}} \right) - s_{1}^{2} I_{6} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad \quad + s_{1} \left[ {I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial u_{0} }}{\partial x}} \right) + I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial v_{0} }}{\partial y}} \right) + J_{4} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial \varphi_{x} }}{\partial x} + \frac{{\partial^{2} \varphi_{y} }}{\partial y}} \right)} \right], \\ \end{aligned} $$

(33c)

$$ \frac{{\partial \bar{M}_{x} }}{\partial x} + \frac{{\partial \bar{M}_{xy} }}{\partial y} - \bar{K}_{x} = J_{1} \left( {\frac{{\partial^{2} u_{0} }}{{\partial t^{2} }}} \right) + k_{2} \left( {\frac{{\partial^{2} \varphi_{x} }}{{\partial t^{2} }}} \right) - s_{1} J_{4} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{\partial x}} \right), $$

(33d)

$$ \frac{{\partial \bar{M}_{xy} }}{\partial x} + \frac{{\partial \bar{M}_{y} }}{\partial y} - \bar{K}_{y} = J_{1} \left( {\frac{{\partial^{2} v_{0} }}{{\partial t^{2} }}} \right) + k_{2} \left( {\frac{{\partial^{2} \varphi_{y} }}{{\partial t^{2} }}} \right) - s_{1} J_{4} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{\partial y}} \right), $$

(33e)

where:

$$ \bar{M}_{i} = M_{i} - s_{1} P_{i} \left( {i = 1,2,6} \right),\quad s_{1} = \frac{4}{{3h^{2} }},\quad s_{2} = 3{\text{s}}_{1} . $$

(34a)

$$ \bar{K}_{j} = K_{j} - s_{2} R_{j} \quad (j = 1,2). $$

(34b)

Here, $N_{x} ,\;N_{y} ,\;N_{xy}\;and\;M_{x} ,\;M_{y} ,\;M_{xy}$ expressed the total in-plane forced and moment resultants and $P_{x} ,\;P_{y} ,\;P_{xy}$ and $R_{x},\;R_{y}$ are the third order stresses resultants can be written as:

$$ {\text{N}}_{x} ,{\text{M}}_{x} ,{\text{P}}_{x} = \mathop \int \limits_{ - h/2}^{h/2} \sigma_{x} (1,z,z^{3} )dz, $$

(35a)

$$ {\text{N}}_{y} ,{\text{M}}_{y} ,{\text{P}}_{y} = \mathop \int \limits_{ - h/2}^{h/2} \sigma_{y} (1,z,z^{3} )dz, $$

(35b)

$$ {\text{P}}_{x} ,{\text{R}}_{x} = \mathop \int \limits_{ - h/2}^{h/2} \tau_{xz} (1,z,z^{3} )dz, $$

(35c)

$$ {\text{P}}_{y} ,{\text{R}}_{y} = \mathop \int \limits_{ - h/2}^{h/2} \tau_{yz} (1,z,z^{3} )dz. $$

(35d)

The mass inertias of composite shell can be express in the following form:

$$ {\text{I}}_{i} = \mathop \sum \limits_{n = 1}^{N} \mathop \int \limits_{n}^{n + 1} \rho^{n} z_{i} dz,\quad (i = 0, \ldots ,6), $$

(36a)

$$ {\text{J}}_{i} = {\text{I}}_{i} - s_{1} {\text{I}}_{i + 2} ,\quad \left( {i = 1,4} \right), $$

(36b)

$$ \bar{K}_{2} = I_{2} - 2s_{1} {\text{I}}_{4} + s_{1}^{2} {\text{I}}_{6} , $$

(36c)

$$ {\bar{\text{I}}}_{0} = I_{0} + 2\frac{{s_{1} }}{{R_{1} }}I_{3} + \left( {\frac{{s_{1} }}{{R_{1} }}} \right)^{2} I_{6} , $$

(36d)

$$ {\bar{\text{J}}}_{1} = J_{1} + \frac{{s_{1} }}{{R_{1} }}I_{4} , $$

(36e)

$$ {\bar{\text{I}}}_{3} = I_{3} + \frac{{s_{1} }}{{R_{1} }}I_{5} . $$

(36f)

3 Solution procedure

The boundary conditions of the multiscale composite have been considered simply-supported (S–S):

$$ u_{0} (x,0,t) = u_{0} (x,b,t) = 0, $$

(37a)

$$ v_{0} (x,0,t) = v_{0} (x,b,t) = 0, $$

(37b)

$$ w_{0} (x,0,t) = w_{0} (x,b,t) = 0, $$

(37c)

$$ \varphi_{x} (x,0,t) = \varphi_{x} (x,b,t) = 0, $$

(37d)

$$ \varphi_{y} (0,y,t) = \varphi_{y} (a,y,t) = 0, $$

(37e)

$$ \mathop \int \limits_{0}^{b} N_{{x\left| {x = 0,a} \right.}} dy = \mathop \int \limits_{a}^{b} q_{0} - q_{1} cos\varOmega t, $$

(37f)

$$ N_{y} (0,y,t) = N_{y} (a,y,t) = 0, $$

(37g)

$$ \bar{M}_{x} (x,0,t) = \bar{M}_{x} (x,b,t) = 0, $$

(37h)

$$ \bar{M}_{y} (0,y,t) = \bar{M}_{y} (a,y,t) = 0. $$

(37i)

Furthermore for obtain the boundary conditions, the displacement of the composite shell are driven as:

$$ u_{0} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } U_{mn} (t){ \cos }\left( {\frac{n\pi x}{b}} \right){ \sin }(my), $$

(38a)

$$ v_{0} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } V_{mn} (t){ \cos }\left( {\frac{n\pi x}{b}} \right){ \sin }(my), $$

(38b)

$$ w_{0} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } W_{mn} (t){ \cos }\left( {\frac{n\pi x}{b}} \right){ \sin }(my), $$

(38c)

$$ \varphi_{x} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } \varphi_{xmn} (t)\cos \left( {\frac{n\pi x}{b}} \right)\sin (my), $$

(38d)

$$ \varphi_{y} \left( {x,y,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } \mathop \sum \limits_{m = 1}^{\infty } \varphi_{ymn} (t){ \cos }\left( {\frac{n\pi x}{b}} \right){ \sin }(my), $$

(38e)

where $U_{mn} \left( t \right),V_{mn} \left( t \right),W_{mn} \left( t \right), \varphi_{xmn} \left( t \right)\;and \; \varphi_{ymn} (t)$ refer to the unknown functions of the time; n and m are the number mode of frequency in the x and y directions, respectively.

Here, $\frac{n\pi x}{b} = l$ are assumed.

By substituting Eqs. (37a–37i) into Eqs. (33a–33e) and driving the Navier procedure, the following expressions can be expressed:

$$ a_{11} U_{mn} \left( t \right) + a_{12} V_{mn} \left( t \right) + a_{13} W_{mn} \left( t \right) + a_{14} \varphi_{xmn} \left( t \right) = M_{11} \ddot{U}_{mn} \left( t \right) + M_{13} \ddot{W}_{mn} + M_{14} \ddot{\varphi }_{xmn} \left( t \right), $$

(39a)

$$ a_{21} U_{mn} \left( t \right) + a_{22} V_{mn} \left( t \right) + a_{23} W_{mn} \left( t \right) + a_{24} \varphi_{xmn} \left( t \right) + a_{25} \varphi_{ymn} (t) = M_{22} \ddot{V}_{mn} (t) + M_{23} \ddot{W}_{mn} + M_{25} \ddot{\varphi }_{ymn} \left( t \right), $$

(39b)

$$ a_{31} U_{mn(t)} + a_{32} V_{mn} \left( t \right) + a_{33} W_{mn} \left( t \right) + a_{34} W_{mn}^{3} \left( t \right) + a_{35} \varphi_{xmn} \left( t \right) + a_{36} \varphi_{ymn} \left( t \right) = M_{33} \ddot{W}_{mn} + M_{34} \ddot{\varphi }_{xmn} \left( t \right) + M_{35} \ddot{\varphi }_{ymn} \left( t \right), $$

(39c)

$$ a_{41} U_{mn} \left( t \right) + a_{42} V_{mn} \left( t \right) + a_{43} W_{mn} \left( t \right) + a_{44} \varphi_{xmn} \left( t \right) + a_{45} \varphi_{ymn} (t) = M_{44} \ddot{\varphi }_{xmn} \left( t \right), $$

(39d)

$$ a_{51} U_{mn} \left( t \right) + a_{52} V_{mn} \left( t \right) + a_{53} W_{mn} \left( t \right) + a_{54} \varphi_{xmn} \left( t \right) + a_{55} \varphi_{ymn} (t) = M_{55} \ddot{\varphi }_{ymn} \left( t \right), $$

(39e)

where the coefficients $a_{ij}$ and $M_{ij}$ experssion stiffness matrix and mass matrix of sandwich composite shell that are defined in Appendix.

The nonlinear differential equation of nanocomposite can be driven as:

$$ \frac{{d^{2} W_{mn} \left( t \right)}}{{dt^{2} }} + \mu \dot{w} + P_{1} W_{mn} \left( t \right) + P_{2} W_{mn}^{2} \left( t \right) + P_{3} W_{mn}^{3} \left( t \right) = q cos\varOmega t, $$

(40)

where:

$$ P_{3} = - \frac{{M_{33} + M_{34} + M_{35} }}{{a_{34} }} . $$

(41)

And the linear frequency of the nanocomposite nanoshell is expressed by:

$$ \omega_{l} = \sqrt {p_{1} } $$

(42)

where initial conditions are illustrated by:

$$ W_{mn} \left( 0 \right) = \frac{{\bar{W}}}{h} ,\left. {\frac{{dW_{mn} \left( t \right)}}{dt}} \right|_{t = 0} = 0, $$

(43)

primary resonance:

For primary resonance case, it is considered that the frequency of excitation and linear frequency of the system $\omega_{0}$ are near together as $\varOmega = \omega_{0}$. So a detuning parameter σ is employing to illustrate the nearness $\varOmega$ of to $\omega_{0}$ as:

$$ \omega^{2} = \varOmega + \varepsilon \sigma , $$

(44)

where σ are the detuning parameters.

The uniformly approximate solutions of (50) are obtained as:

$$ w = w_{0} \left( {T_{0} ,T_{1} ,T_{2} , \ldots } \right) + \varepsilon w_{1} \left( {T_{0} ,T_{1} ,T_{2} , \ldots } \right) + \varepsilon^{2} w_{2} \left( {T_{0} ,T_{1} ,T_{2} , \ldots } \right), $$

(45)

where $T_{0}$ =  t and $T_{1}$ = .εt

The terms of $T_{0}$ and $T_{1}$ are expressed as:

$$ F\left( {\text{t}} \right) = \varepsilon \bar{q}cos(\omega_{0} T_{0} + \sigma T_{1} ), $$

(46)

the derivatives to yield:

$$ \frac{d}{dt} = D_{0} + \varepsilon D_{1} , $$

(47)

$$ \frac{d}{dt} = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \varepsilon^{2} (D_{1}^{2} + 2D_{0} D_{1} ). $$

(48)

Substituting (43), (44) and (45) into (40) and putting the coefficients of to zero yield the following differential equations:

$$ \varepsilon^{0} : D_{0}^{2} w_{0} + \varOmega^{2} w_{0} = 0, $$

(49)

$$ \varepsilon^{1} : D_{0}^{2} w_{1} + \varOmega^{2} w_{1} = - 2D_{0} D_{1} w_{0} - \mu D_{0} w_{0} - P_{3} w_{0}^{3} - kcos(\omega_{0} T_{0} + \sigma T_{1} ). $$

(50)

With this approach it generates to be simply to write the solution of Eq. (55) as:

$$ w_{0} \left( {T_{0} ,T_{1} ,T_{2} , \ldots } \right) = \exp \left( {iT_{0} } \right) + \bar{A}\exp \left( { - iT_{0} } \right), $$

(51)

where A is an unknown complex function and A is the complex conjugate of A. A governing equation are defined by requiring $w_{1}$ to be periodic in $T_{0}$ and extracting secular terms that are coefficients of $e^{{ \pm i\omega_{0} T_{0} }}$ the finding equation will be determined as:

$$ 2i\omega_{0} (A^{\prime } + \mu A) + 3P_{3} A^{2} {\bar{\text{A}}} - \frac{1}{2}k\exp \left( { - i{{\sigma }}T_{1} } \right) = 0. $$

(52)

Assumed A be in polar form:

$$ A = \frac{1}{2}a\exp \left( {i\gamma } \right), $$

(53)

where a and $\gamma$ are real parameters. Separating this terms parts of the derived equation, it cause

$$ a^{'} = - \mu a + \frac{1}{2}\frac{{\bar{q}}}{{\omega_{0} }}\sin \left( {\sigma T_{1} - \gamma } \right), $$

(54)

$$ a\gamma^{'} = \frac{3}{8}\frac{{P_{3} }}{{\omega_{0} }}a^{3} - \frac{1}{2}\frac{{\bar{q}}}{{\omega_{0} }}\cos \left( {\sigma T_{1} - \gamma } \right), $$

(55)

where:

$$ \theta = \sigma T_{1} - \gamma $$

(56)

and substituting Eqs. (59, 60) in Eq. (61) yield:

$$ a^{'} = - \mu a + \frac{1}{2}\frac{{\bar{q}}}{{\omega_{0} }}\sin \theta , $$

(57)

$$ a\gamma^{'} = \frac{3}{8}\frac{{P_{3} }}{{\omega_{0} }}a^{3} - \frac{1}{2}\frac{{\bar{q}}}{{\omega_{0} }}\cos \theta . $$

(58)

Singular point of this system at $a^{'} = 0$ and $\theta^{'} = 0$ illustrates the steady-state motion of the system. So, in steady-state condition can be expressed as:

$$ a = - \mu a + \frac{1}{2}\frac{{\bar{q}}}{{\omega_{0} }}\sin \theta , $$

(59)

$$ \sigma a - \frac{3}{8}\frac{{P_{3} }}{{\omega_{0} }}a^{3} = - \frac{1}{2}\frac{{\bar{q}}}{{\omega_{0} }}\cos \theta . $$

(60)

The fixed points of Eq. (57, 58) correspond to solutions with constant amplitude and phase. These solutions satisfy

$$ \mu a = \frac{1}{2}\frac{{\bar{q}}}{{\omega_{0} }}\sin \theta , $$

(61)

$$ \sigma - \frac{3}{8}\frac{{P_{3} }}{{\omega_{0} }}a^{2} = - \frac{1}{2}\frac{{\bar{q}}}{{\omega_{0} }}\cos \theta . $$

(62)

The equation of frequency response presented by:

$$ \left[ {\left( {\sigma - \frac{3}{8}\frac{{P_{3} }}{{\omega_{0} }}a^{2} } \right)^{2} + \mu^{2} } \right]a^{2} = \frac{{\bar{q}^{2} }}{{4\omega_{0}^{2} }}. $$

(63)

Substituting Eq. (66) into Eqs. (59–60) and substituting that result into Eqs. (61–61), can be obtained as:

$$ {\text{w}} = a\cos (\omega_{0} {\text{t}} + \varepsilon \sigma {\text{t}} - \theta ) + {\text{O}}(\varepsilon ). $$

(64)

With this, the amplitude response (magnification factor) can be obtained as:

$$ {\text{M}} = \frac{a}{{\left| {\bar{q}} \right|}} = \frac{1}{{2\omega_{0} \sqrt {(\sigma - \frac{3}{8}\frac{{P_{3} }}{{\omega_{0} }}a^{2} )^{2} + \mu^{2} } }}. $$

(65)

Similar to the case of the linear oscillator, the maximum value of the magnification factor can be found from

$$ \frac{dM}{d\varOmega } = 0, \frac{{d^{2} M}}{{d^{2} \varOmega }}. $$

(66)

Equation (65) with respect to $\varOmega$ yields:

$$ \frac{1}{32}a\left( {3P_{3} a^{2} - 8\varOmega - 8} \right)\left( {3P_{3} \frac{da}{d\varOmega } - 4} \right) + (\mu^{2} + \left( {\varOmega - 1 - 3P_{3} a^{2} )^{2} } \right)\frac{da}{d\varOmega } = 0, $$

(67)

which can be solved for $\frac{da}{d\varOmega }$ as:

$$ \frac{da}{d\varOmega } = \frac{{8a\left( {3P_{3} a^{2} - 8\varOmega - 8} \right)}}{{27P_{3}^{2} a^{4} - 96\left( {\varOmega - 1} \right)P_{3} a^{2} + 64(\mu^{2} + \left( {\varOmega - 1)^{2} } \right)}}. $$

(68)

This derivative vanishes (and so does $\frac{dM}{d\varOmega }$) when:

$$ \left( {3P_{3} a^{2} - 8\varOmega - 8} \right) = 0 \Rightarrow a_{p} = \sqrt {\frac{8(\varOmega - 1)}{{3P_{3} }}} . $$

(69)

To find the values of the critical points $\varOmega_{1}$ and $\varOmega_{2}$, these points correspond to vertical tangencies of the response curve; that is, where $\frac{d\varOmega }{dM} = 0$:

$$ 27P_{3}^{2} a^{4} - 96\left( {\varOmega - 1} \right)P_{3} a^{2} + 64(\mu^{2} + \left( {\varOmega - 1)^{2} } \right). $$

(70)

This condition can be found by equating the denominator of Eq. (70) to zero, which translates to This condition can be found by equating the whose roots provide:

$$ \varOmega_{1,2} = \frac{1}{8}(8 + 6P_{3} a^{2} - \sqrt {9P_{3}^{2} a^{4} - 64\mu^{2} } , $$

(71)

$$ a \ge \sqrt {\frac{8\mu }{{3P_{3} }}} . $$

(72)

The condition for the existence of real solutions is:

4 Results and discussion

Numerical results of the nonlinear vibration of doubly curved shell are presented in this section. The properties of multiscale composite shell are established in in Table 1, further more we assumed Elliptic paraboloid shell ($R_{1} \ne R_{2} )$. Carbon nanotube with effective thickness t_cnt= 0.0348 nm are selected as reinforcements and G₁₃ = G₂₃ = 0.5G₁₂ considered. The validity of the present study is proved by the means of comparing the dimensionless frequencies of this model by several previous researches. The correctness of the nonlinear to linear frequency of the doubly curved shell composite based on first shear deformable theory compared with Singh and Panda (2014) is presented in Table 2. As well as, it is brightly that the results of this comparison are similar. The geometric and material properties $\frac{{E_{1} }}{{E_{2} }} = 40,\;G_{12} = G_{12} = G_{13} = 0.6E_{2} , \;G_{23} = 0.5E_{2} ,\;\upsilon_{12} = \upsilon_{13} = \upsilon_{23} = 0.25$ are considered for compare results with Singh and Panda (2014). Table 3 illustrated the dimensionless frequency $\bar{\omega } = \omega \frac{{R^{2} }}{h}\sqrt {\frac{{\rho_{0} }}{E}}$ for U, A, X, O distribution pattern with $R_{1} = R_{2}$ (cylindrical shell) and $\frac{R}{h} = 10,h = 5\;{\text{nm}}\;@\;T = 300 K$ are assumed via first order shear deformation theory and verified by Ansari and Torabi (2016) and Shen (2017) results.

Table 1 The properties of multiscale composite shell (Shen et al. 2015; Sahmani and Aghdam 2017)

Table 2 Comparison of dimensionless frequencies for 4-layer cylindrical shell (a/b = 1, R/a = 5)

Table 3 Comparison of dimensionless frequencies for laminated cylindrical shell [a/h = 100 (m, n = 1, 2)]

The dimensionless parameters are adopted as:

$$ \begin{aligned} \bar{u}_{0} & = \pi \frac{{u_{0} }}{a},\;\;\bar{v}_{0} = \pi \frac{{v_{0} }}{b},\;\; \bar{w}_{0} = \frac{{w_{0} }}{R}, \;\;\bar{\varphi }_{x} = \varphi_{x} , \;\;\bar{\varphi }_{y} = \varphi_{y} , \;\; \bar{y} = \pi \frac{y}{b}, \;\;\bar{x} = \pi \frac{x}{a}, \;\;\bar{z} = \frac{z}{h}, \\ \bar{R}_{1} & = \frac{{R_{1} }}{R}, \;\;\bar{R}_{2} = \frac{{R_{2} }}{R}, \;\;\varOmega = \omega_{l} \frac{{R^{2} }}{h}\sqrt {\frac{{\rho_{0} }}{E}} ,\;\;\bar{q} = \frac{{(Rh^{)7/2} }}{{Eh^{7} }}q. \\ \end{aligned} $$

(73)

Numerical integration phase plots of doubly curved shell with different excitation force with U distribution pattern $\frac{a}{{R_{1} }} = 0.1, \frac{b}{{R_{2} }} = 0.05, c_{d} = 0.3$, h = 2 mm, T = 300, H = 1 and (m, n = 1, 1) on the (X, ${\dot{\text{X}}})$ plane are presented in Fig. 2. Stacking sequence is considered cross ply [$0/90$]_S. The systems have been shown regular chaotic motion or quasi-periodic motion. To reveal the dynamic behaviors for a given magnitude of different excitation force such as A, B, C and D which dimensionless force in theses Figs have been assumed 5, 10, 15, 20. It can be found Fig. A has two fixed points in the phase space, according to the periodic motion of the doubly curved shell. By increasing dimensionless force to 10, fixed points number has been taken leapt, but Fig. 2c has four fixed point in phase portrait and Fig. 2d similar to b mode have lots of fixed points.

Fig. 2

Numerical integration phase plots for different excitation force a$\bar{q} = 5,$b$\bar{q} = 10$, c$\bar{q} = 15$. d$\bar{q} = 20$ of doubly curved shell with $\frac{a}{{R_{1} }} = 0.1, \frac{b}{{R_{2} }} = 0.05, c_{d} = 0.3$, h = 2 mm, H = 1 and (m, n = 1, 1)

Figure 3 Investigated numerical integration Poincare sections for different excitation force (A) $\bar{q} = 5,$(B) $\bar{q} = 10$, (C) $\bar{q} = 15$. (D) $\bar{q} = 20)$ of doubly curved shell with U distribution pattern, $\frac{a}{{R_{1} }} = 0.1, \frac{b}{{R_{2} }} = 0.05, c_{d} = 0.3$, h = 2 mm, H = 1 and (m, n = 1, 1) on the (X, ${\dot{\text{X}}})$ plane. Also, stacking sequence is assumed cross ply [$0/90$]_S. It is known that the Poincare sections reveal the similar evolution of the dynamic analysis. It is significant express that the chaos retains until the other bifurcation yield to its invisibility.

Fig. 3

Numerical integration Poincare sections for different excitation force a$\bar{q} = 5,$b$\bar{q} = 10$, c$\bar{q} = 15$. d$\bar{q} = 20$ of doubly curved shell with $\frac{a}{{R_{1} }} = 0.1, \frac{b}{{R_{2} }} = 0.05, c_{d} = 0.3$, h = 2 mm, H = 1 and (m, n = 1, 1)

Numerical integration phase plots and Poincare sections of doubly curved shell with $\frac{a}{{R_{1} }} = 0.1,\;\; \frac{b}{{R_{2} }} = 0.05,\;\; c_{d} = 0.3,\;\;\bar{q} = 10$, h = 2 mm, T = 300, H = 1 and the cross ply [$0/90$]_S composite shell mode is considered (m, n = 1, 1) are investigated in Figs. 4 and 5. Different distribution pattern such as X, A, U, O are considered. Unlike linear frequency, it is observed that frequency of the O distribution is highest and X is the lowest value. Via the chaotic motion of the system, Fig. 4. presented different distribution pattern to describe the nonlinear frequency of the system. It can be shown that the Poincare sections in Fig. 5. reveal the similar evolution of the dynamic analysis. It is clear that increasing the value $\omega_{nl}$ makes the chaotic motion region are increased. It is because the stiffness of the dynamic system decreases.

Fig. 4

Numerical integration phase plots for different distributions pattern a$X ,$b U, c$A$, d$O$ of doubly curved shell with $\frac{a}{{R_{1} }} = 0.1, \frac{b}{{R_{2} }} = 0.05, c_{d} = 0.3,\bar{q} = 10$, h = 2 mm, H = 1 and (m, n = 1, 1)

Fig. 5

Numerical integration Poincare sections for different distributions pattern a${\text{X}} ,$b U, c$A$, d O of doubly curved shell with $\frac{a}{{R_{1} }} = 0.1, \frac{b}{{R_{2} }} = 0.05, c_{d} = 0.3,\bar{q} = 10$, h = 2 mm, H = 1 and (m, n = 1, 1)

Figures 6, 7. Investigated numerical integration phase plane and Poincare map under influence of hygrothermal environment with U distribution pattern, $\frac{a}{{R_{1} }} = 0.1, \frac{b}{{R_{2} }} = 0.05$, h = 2 mm, $\frac{a}{h} = 10, \frac{a}{b} = 1$, ∆H = 1, T = 300 and (m, n = 1, 1) is shown in Stacking sequence is considered cross ply [$0^{PCF} /90^{SMA}$]_S. It is brightly shown that the nonlinear frequency parameters increase by temperature and moisture rising. Based on the results of this numerical research, it is found that the rise of temperature and moisture coefficient could adjust the nonlinear vibration responses of the composite doubly curved shell. By increasing magnitude of rise temperature and moisture volume fraction inherent frequency of the system changes and dynamic behavior of chaotic motion is different in various modes of rise temperature and moisture. By the numerical results it is found that the Poincare sections reveal the similar evolution of the dynamic analysis and the chaos retains until the other bifurcation yield to its invisibility.

Fig. 6

Numerical integration phase plots for different temperature and moisture rise of doubly curved shell with ${\text{T}} = 300 ,$ T = 400, T = 500 and T = 600 $\frac{a}{{R_{1} }} = 0.1, \;\;\frac{b}{{R_{2} }} = 0.05,\;\; c_{d} = 0.25,\;\;\bar{F} = 10$, h = 2 mm and (m, n = 1, 1)

Fig. 7

Numerical integration Poincare sections for temperature and moisture rise of doubly curved shell with ${\text{T}} = 300 ,$ T = 400, T = 500 and T = 600 $\frac{a}{{R_{1} }} = 0.1,\;\; \frac{b}{{R_{2} }} = 0.05, \;\;c_{d} = 0.25,\;\;\bar{F} = 10$, h = 2 mm and (m, n = 1, 1)

Figure 8 investigated bifurcation diagram of doubly curved shell with $\frac{a}{{R_{1} }} = 0.1, \frac{b}{{R_{2} }} = 0.05$, h = 2 mm and (m, n = 1, 1),$c_{d} = 0.25$$V_{s} = 5\%$ and the cross ply [$0^{PCF} /90^{SMA}$]_S composite shell mode is considered (m, n = 1, 1). This diagram was constructed by splicing together intersections on the Poincare section corresponding to a chaotic motion with increasing values of $\bar{q}$ in the range [0.5–1.1].

Fig. 8

Bifurcation diagrams of doubly curved shell with $\frac{a}{{R_{1} }} = 0.1,\;\; \frac{b}{{R_{2} }} = 0.05,\;\; c_{d} = 0.25$, h = 2 mm, H = 1 and (m, n = 1, 1) for uniform distribution

5 Conclusion

In this research, nonlinear dynamics of smart multiscale composite doubly curved shell via Halpin–Tsai model is studied. The nonlinear model is obtained by Green–Lagrange-type geometric nonlinearity in frame work higher order shear deformation theory. Via Hamilton’s principle the governing equation are derived and solved numerically by using the multiple scales Perturbation method. For investigated the accuracy and correctness of present work, the numerical results has been verified by important pervious researches. Base on numerical study can be expressed significant resales as:

• The highest value of the nonlinear frequency for O distribution pattern and the lowest value for the X distribution pattern of nanoshell.

• The nonlinear frequency of composite doubly curved shell increases with decrease of decrease by increasing curvature ratio.

• By increasing rise of temperature and moisture rise nonlinear frequency increase.

• Increasing the value $\omega_{nl}$ yields the chaotic motion region are increased.

• The Poincare sections reveal the similar evolution of the dynamic analysis.

Appendix

Transformed shell principle coordinate can be expressed by:

$$ \begin{aligned} \bar{Q}_{{11}}^{n} &= Q_{{11}}^{n} cos^{4} \theta + 2\left( {Q_{{12}}^{n} + 2Q_{{66}}^{n} } \right)sin^{2} \theta cos^{2} \theta + Q_{{22}}^{n} sin^{4} \theta \hfill \\ \bar{Q}_{{12}}^{n} &= (Q_{{11}}^{n} + Q_{{22}}^{n} - 4Q_{{66}}^{n} )sin^{2} \theta cos^{2} \theta + Q_{{12}}^{n} (sin^{4} \theta + cos^{4} \theta ) \hfill \\ \bar{Q}_{{22}}^{n} &= Q_{{11}}^{n} sin^{4} \theta + 2(Q_{{12}}^{n} + 2Q_{{66}}^{n} )sin^{2} \theta cos^{2} \theta + Q_{{22}}^{n} cos^{4} \theta \hfill \\ \bar{Q}_{{66}}^{n} &= (Q_{{11}}^{n} + Q_{{22}}^{n} - 2Q_{{12}}^{n} - 2Q_{{66}}^{n} )sin^{2} \theta cos^{2} \theta + Q_{{66}}^{n} (sin^{4} \theta + cos^{4} \theta ) \hfill \\ \bar{Q}_{{44}}^{n} &= Q_{{44}}^{n} cos^{2} \theta + Q_{{55}}^{n} sin^{2} \theta \hfill \\ \end{aligned} $$

(74)

where ${\overline{Q}}_{ij} \left(i,j=\text{1,2},\text{3,4},\text{5,6}\right)$ presented the transformed reduce stiffness modulus.

Motions equations of multiscale composite shell can be expressed in terms of u, v, w, ${\phi }_{x}, {\phi }_{y}$ displacements are obtained by substituting Eqs. (19a–19c) into (33a–33d) yields:

$$ \begin{aligned} & A_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) + A_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{16}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) + B_{{11}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) + B_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad + B_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) - s_{1} E_{{11}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) \\ & \quad - s_{1} E_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{16}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{16}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + A_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + B_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}}} \right) + B_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) \\ & \quad + B_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }}} \right) - s_{1} E_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} E_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + \frac{1}{{R_{1} }}\left[ {\hat{A}_{{45}} \left( {\phi _{y} + \frac{{\partial w_{0} }}{{\partial y}} - \frac{{v_{0} }}{{R_{2} }}} \right) + \hat{A}_{{55}} \left( {\phi _{x} + \frac{{\partial w_{0} }}{{\partial x}} - \frac{{u_{0} }}{{R_{1} }}} \right)} \right]\\ & \quad + \frac{{s_{1} }}{{R_{1} }}\left[ {E_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + E_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right)} \right. \\ & \quad + E_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + E_{{16}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + F_{{11}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) + F_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + F16\left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{11}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) - s_{1} H_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{16}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + E_{{16}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) + E_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + E_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + F_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}}} \right) + F_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) + F_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }}} \right) \\ & \quad \left. { - s_{1} H_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right)} \right] \\ & \quad = \bar{I}_{0} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }}} \right) - \bar{J}_{1} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial t^{2} }}} \right) + s_{1} \bar{I}_{3} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right) \\ \end{aligned} $$

(75a)

$$ \begin{aligned} & A_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + A_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + B_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) \\ & \quad + B_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + B_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) - s_{1} E_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + A_{{12}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) + A_{{22}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + A_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + B_{{12}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}}} \right) + B_{{22}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) \\ & \quad + B_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }}} \right) - s_{1} E_{{12}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} E_{{22}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} E_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + \frac{1}{{R_{2} }}\left[ {\hat{A}_{{45}} \left( {\phi _{y} + \frac{{\partial w_{0} }}{{\partial y}} - \frac{{v_{0} }}{{R_{2} }}} \right) + \hat{A}_{{55}} \left( {\phi _{x} + \frac{{\partial w_{0} }}{{\partial x}} - \frac{{u_{0} }}{{R_{1} }}} \right)} \right] \\ & \quad + \frac{{s_{1} }}{{R_{1} }}\left[ {E_{{12}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right)} \right. + E_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + E_{{22}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) + E_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) \\ & \quad + F_{{12}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}}} \right) + F_{{22}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) + F_{{26}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{y} }}{{\partial \partial y^{2} }}} \right) \\ & \quad - s_{1} H_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) - s_{1} H_{{22}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }}} \right) \\ & \quad - s_{1} H_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + E_{{16}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + E_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + E_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + F_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) + F_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + F_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} H_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) - s_{1} H_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) \\ & \quad \left. { - s_{1} H_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right)} \right] \\ & \quad = \bar{I}_{0} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial t^{2} }}} \right) - \bar{J}_{1} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial t^{2} }}} \right) + s_{1} \bar{I}_{3} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right) \\ \end{aligned} $$

(75b)

$$ \begin{aligned} & \hat{A}_{{45}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial x}}} \right) + \hat{A}_{{55}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) \\ & \quad + \hat{A}_{{44}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right) + \hat{A}_{{45}} \left( {\frac{{\partial \phi _{x} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial y}}} \right) \\ & \quad + s_{1} \left[ {E_{{11}} \left( {\frac{{\partial ^{3} u_{0} }}{{\partial x^{3} }} + \frac{1}{{R_{1} }}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }}} \right)} \right. \\ & \quad + E_{{12}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial y\partial x^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}}} \right) \\ & \quad + E_{{16}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial x^{3} }} + \frac{{\partial ^{3} u_{0} }}{{\partial x^{2} \partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{3} w_{0} }}{{\partial x^{2} \partial y}}} \right) \\ & \quad + F_{{11}} \frac{{\partial ^{3} \phi _{x} }}{{\partial x^{3} }} \\ & \quad + F_{{12}} \frac{{\partial ^{3} \phi _{y} }}{{\partial x^{2} \partial y}} + F_{{16}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x^{3} }} + \frac{{\partial ^{3} \phi _{x} }}{{\partial x^{2} \partial y}}} \right) - s_{1} H_{{11}} \left( {\frac{{\partial ^{3} \phi _{x} }}{{\partial x^{3} }} + \frac{{\partial ^{4} w_{0} }}{{\partial x^{4} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial x^{3} }}} \right) \\ & \quad - s_{1} H_{{12}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x^{2} \partial y}} + \frac{{\partial ^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial y\partial x^{2} }}} \right) \\ & \quad - s_{1} H_{{16}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x^{3} }} + \frac{{\partial ^{3} \phi _{x} }}{{\partial x\partial y^{2} }} + 2\frac{{\partial ^{4} w_{0} }}{{\partial x^{3} \partial y}} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial x^{2} \partial y}}} \right) \\ & \quad + E_{{12}} \left( {\frac{{\partial ^{3} u_{0} }}{{\partial x\partial y^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}}} \right) \\ & \quad + E_{{22}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial y^{3} }} + \frac{1}{{R_{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{3} }}} \right) \\ & \quad + E_{{26}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }} + \frac{{\partial ^{3} u_{0} }}{{\partial y^{3} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{3} }}} \right) \\ & \quad + F_{{12}} \frac{{\partial ^{3} \phi _{x} }}{{\partial y^{2} \partial x}} + F_{{22}} \frac{{\partial ^{3} \phi _{y} }}{{\partial y^{3} }} + F_{{26}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial y^{2} \partial x}} + \frac{{\partial ^{3} \phi _{x} }}{{\partial y^{3} }}} \right) \\ & \quad - s_{1} H_{{12}} \left( {\frac{{\partial ^{3} \phi _{x} }}{{\partial y^{2} \partial x}} + \frac{{\partial ^{4} w_{0} }}{{\partial x^{2} \partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }}} \right) \\ & \quad - s_{1} H_{{26}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x\partial y^{2} }} + \frac{{\partial ^{3} \phi _{x} }}{{\partial y^{3} }} + 2\frac{{\partial ^{4} w_{0} }}{{\partial y^{3} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial y^{3} }}} \right) \\ & \quad + 2E_{{16}} \left( {\frac{{\partial ^{3} u_{0} }}{{\partial y\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}}} \right) \\ & \quad + 2E_{{66}} \left( {\frac{{\partial ^{3} v_{0} }}{{\partial y\partial x^{2} }} + \frac{{\partial ^{3} u_{0} }}{{\partial y^{2} \partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}}} \right) \\ & \quad + 2F_{{16}} \left( {\frac{{\partial ^{3} \phi _{x} }}{{\partial x^{2} \partial y}}} \right) + 2F_{{66}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial x^{2} \partial y}} + \frac{{\partial ^{3} \phi _{y} }}{{\partial y^{2} \partial x}}} \right) \\ & \quad - 2s_{1} H_{{16}} \left( {\frac{{\partial ^{3} \phi _{x} }}{{\partial x^{2} \partial y}} + \frac{{\partial ^{4} w_{0} }}{{\partial x^{3} \partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial y\partial x^{2} }}} \right) - 2s_{1} H_{{26}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial y^{2} \partial x}} + \frac{{\partial ^{4} w_{0} }}{{\partial x\partial y^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }}} \right) \\ & \quad \left. { - 2s_{1} H_{{66}} \left( {\frac{{\partial ^{3} \phi _{y} }}{{\partial y\partial x^{2} }} + \frac{{\partial ^{3} \phi _{x} }}{{\partial x\partial y^{2} }} + 2\frac{{\partial ^{4} w_{0} }}{{\partial y^{2} \partial x^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{3} v_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{3} u_{0} }}{{\partial x\partial y^{2} }}} \right)} \right] \\ \end{aligned} $$

$$ \begin{aligned} & \frac{\partial }{{\partial x}}\left( {\frac{{\partial w_{0} }}{{\partial x}}\left\{ {A_{{11}} \left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{w}{{R_{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right)} \right.} \right. + A_{{12}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{w}{{R_{2} }} + \left( {\frac{1}{2}\frac{{\partial w_{0} }}{{\partial y}})^{2} } \right)} \right) \\ & \quad + A_{{16}} \left( {\frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{11}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}}} \right) + B_{{12}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}}} \right) \\ & \quad + B_{{16}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) - s_{1} E_{{16}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) \\ & \quad - s_{1} E_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right) \\ & \quad \left. { - s_{1} E_{{66}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}} + 2\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}}} \right)} \right\} \\ & \quad + \frac{\partial }{{\partial y}}\left( {\frac{{\partial w_{0} }}{{\partial x}}\left\{ {A_{{16}} \left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{w}{{R_{1} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}^{2} } \right)} \right) + A_{{26}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{w}{{R_{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right)} \right.} \right. \\ & \quad + A_{{66}} \left( {\frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{16}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}}} \right) + B_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}}} \right) \\ & \quad + B_{{66}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) - s_{1} E_{{16}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) \\ & \quad - s_{1} E_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right)\left. { - s_{1} E_{{66}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + 2\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right)} \right\} \\ & \frac{\partial }{{\partial x}}\left( {\frac{{\partial w_{0} }}{{\partial y}}\left\{ {A_{{12}} \left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{w}{{R_{1} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right) + A_{{22}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{w}{{R_{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right)} \right.} \right. \\ & \quad + A_{{26}} \left( {\frac{{\partial v_{0} }}{{\partial x}} + \frac{{\partial u_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{12}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}}} \right) + B_{{22}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}}} \right) + B_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) \\ & \quad - s_{1} E_{{12}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) - s_{1} E_{{22}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right) \\ & \quad - s_{1} E_{{16}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}} + 2\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}}} \right) \\ & \quad - \frac{1}{{R_{2} }}\left\{ {A_{{12}} \left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{w}{{R_{1} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right)^{2} } \right) + A_{{22}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{w}{{R_{2} }} + \frac{1}{2}\left( {\frac{{\partial w_{0} }}{{\partial y}}} \right)^{2} } \right)} \right. \\ & \quad + A_{{26}} \left( {\frac{{\partial v_{0} }}{{\partial y}} + \frac{{\partial u_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial w_{0} }}{{\partial y}}} \right) + B_{{12}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}}} \right) + B_{{22}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}}} \right) + B_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) \\ & \quad - s_{1} E_{{12}} \left( {\frac{{\partial \phi _{x} }}{{\partial x}} + \frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial u_{0} }}{{\partial x}}} \right) - s_{1} E_{{22}} \left( {\frac{{\partial \phi _{y} }}{{\partial y}} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial v_{0} }}{{\partial y}}} \right) \\ & \quad \left. { - s_{1} E_{{26}} \left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}} + 2\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}} - \frac{1}{{R_{2} }}\frac{{\partial u_{0} }}{{\partial y}}} \right)} \right\} + q^{{hyg}} \\ & \quad = \bar{I}_{0} \left( {\frac{{\partial ^{2} w_{0} }}{{\partial t^{2} }}} \right) + s_{1}^{2} \bar{I}_{6} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) + s_{1} \left[ {\bar{I}_{3} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial u_{0} }}{{\partial x}} + \frac{{\partial v_{0} }}{{\partial y}}} \right)} \right] \\ & \quad - \bar{J}_{4} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial \phi _{y} }}{{\partial x}} + \frac{{\partial \phi _{x} }}{{\partial y}}} \right) \\ \end{aligned} $$

(75c)

$$ \begin{aligned} & \hat{B}_{{11}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + \hat{B}_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{16}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + \hat{D}_{{11}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) \\ & \quad + \hat{D}_{{12}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + \hat{B}_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial y^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} \hat{F}_{{16}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + \hat{B}_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ & \quad + \hat{D}_{{16}} \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \hat{D}_{{26}} \frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \hat{D}_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} \hat{F}_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial y\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial y^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - s_{1} \hat{F}_{{66}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }}} \right) \\ & \quad - \hat{A}_{{45}} \left( {\phi _{y} + \frac{{\partial w_{0} }}{{\partial y}} - \frac{{v_{0} }}{{R_{2} }}} \right) - \hat{A}_{{55}} \left( {\phi _{x} + \frac{{\partial w_{0} }}{{\partial x}} - \frac{{u_{0} }}{{R_{1} }}} \right) \\ & \quad = \bar{J}_{1} \frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }} + \bar{K}_{2} \frac{{\partial ^{2} \phi _{x} }}{{\partial t^{2} }} - s_{1} \bar{J}_{4} \frac{{\partial ^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial w_{0} }}{{\partial x}}} \right) \\ \end{aligned} $$

(75d)

$$ \begin{aligned} & \hat{B}_{{16}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + \hat{B}_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{2} }}\frac{{\partial w_{0} }}{{\partial x}} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x^{2} }}} \right) + \hat{D}_{{16}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }}} \right) \\ & \quad + \hat{D}_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) + \hat{D}_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{16}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x^{2} }} + \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }}} \right) \\ & \quad - s_{1} \hat{F}_{{26}} \left( {\frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + \frac{{\partial ^{3} w_{0} }}{{\partial x\partial y^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}}} \right) \\ & \quad - s_{1} \hat{F}_{{66}} \left( {\frac{{\partial ^{2} \phi _{x} }}{{\partial x^{2} }} + \frac{{\partial ^{2} \phi _{y} }}{{\partial x\partial y}} + 2\frac{{\partial ^{3} w_{0} }}{{\partial y^{2} \partial x}} - \frac{1}{{R_{2} }}\frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} - \frac{1}{{R_{1} }}\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{22}} \left( {\frac{{\partial ^{2} u_{0} }}{{\partial x\partial y}} + \frac{1}{{R_{1} }}\frac{{\partial w_{0} }}{{\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}}} \right) \\ & \quad + \hat{B}_{{26}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x\partial y}} + \frac{{\partial ^{2} u_{0} }}{{\partial y^{2} }} + \frac{{\partial w_{0} }}{{\partial y}}\frac{{\partial ^{2} w_{0} }}{{\partial x\partial y}} + \frac{{\partial w_{0} }}{{\partial x}}\frac{{\partial ^{2} w_{0} }}{{\partial y^{2} }}} \right) \\ \end{aligned} $$

(75e)