1 Introduction

Since the invention of carbon nanotubes (CNTs) in the 1990s [1], various nano-engineered devices were designed thanks to the outstanding properties of nanosize elements [2, 3]. In other words, the enhanced ultimate stiffness and strength, high slenderness ratio, light weight, and high thermal conductivity of CNTs [4] have made them key elements in the design of critical instruments. Therefore, implementation of CNTs for the purpose of reinforcing polymers can be an efficient means to design structural elements. Keeping this fact in mind, many studies can be addressed whose major concern is to monitor the reaction of CNT-reinforced (CNTR) nanocomposite structures, in different working conditions, to mechanical stimulations [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42]. Even though these studies provided rough data about the general behaviors of CNTR polymers, their findings seem to be engineering overestimations because of the fact that practical aspects of designing nanocomposites exist in none of them. In other words, all of the above studies were accomplished by assuming the CNTR polymer to be like a fiber-reinforced one. However, this ideal assumption cannot be satisfied in such polymer nanocomposites. This mismatch has several reasons, among them the wavy shape of CNTs (i.e., reported to originate from high slenderness ratio of the CNTs, their topological defect, and existing van der Waals (vdW) forces between them [43, 44]) is of high significance. To capture this issue while tracking the stress–strain curve of the CNTR polymers, a semi-empirical attempt was made in [45]. According to this study, a modified homogenization technique for accurate estimation of the Young’s modulus of CNTR polymers was attained. In addition to the waviness phenomenon, formation of CNT agglomerates in the microstructure of a CNTR polymer weakens the reinforcing power of such nanofillers. To cover this issue, a gradual distribution of the agglomerated CNTs across the thickness direction was introduced in another micromechanics-assisted study [46]. In this work, the entanglement of the CNTs inside the inclusions was kept in mind while the Young’s modulus of the CNTR nanocomposite was calculated. Recently, the effect of temporal degradation of the properties of polymer on the approximation of modulus in nanocomposites has been covered in another micromechanical investigation [47].

In the above-mentioned studies, bi-phase nanocomposites consisting of polymer and CNT were discussed. Recent studies, however, have shown that three-phase nanocomposites, referred to as multi-scale hybrid (MSH) nanocomposites, have potential to better match the design criteria in the field of structural mechanics. In these hybrid nanomaterials, the third phase belongs to macro-scale fibers such as glass or carbon fibers (GFs/CFs). In the middle 2010s, some researchers started to analyze static and dynamic behaviors of MSH nanocomposite structures. In one of the initial efforts in this area, first-order shear deformation theory (FSDT) was hired to probe nonlinear free vibration behaviors of rectangular sandwich plates made of smart piezoelectric MSH nanomaterials [48]. By means of a rheological solid element, the viscoelastically damped oscillations of sandwich beams consisting of MSH nanocomposites were tracked in [49]. Investigation of the nonlinear dynamic properties of MSH nanocomposite blades was done in [50] once the nanomaterial-made blade seemed to be rotating around its longitudinal axis. In another geometrically nonlinear study, finite element method (FEM) was employed in [51] to probe low-velocity impact features of MSH nanocomposite plates positioned in a hygrothermal environment. According to the classical theory of thin beams, nonlinear deflection, critical postbuckling temperature, and bifurcation properties of MSH nanocomposite beams were determined in [52] via simple Halpin–Tsai homogenization algorithm. Using the well-known Rayleigh–Ritz FE solution, the modal characteristics of MSH nanocomposite thick beams were studied in [53]. In another endeavor, the same authors surveyed the bi-axial buckling problem of rectangular plates consisting of MSH nanocomposites [54] in the framework of classical theory of thin plates. Lately, the destroying influence of the CNT agglomerates on the buckling-mode failure and oscillation frequency of MSH nanocomposite structures was covered in [55,56,57] and [58, 59], respectively.

Based on the above literature review, it can be easily realized that the impacts of wavy shape of the CNTs and time-varying modulus of the polymer on the dynamic characteristics of MSH nanocomposite structures have not been paid enough attention. In the solitary work in this field, the vibrational behaviors of viscoelastic three-phase nanocomposite plates were studied in [60]. To cover this lack in the literature and by recalling the broad application of nanocomposite shells as aerospace structures, structural devices, marine structures, energy storage devices, highly sensitive strain sensors, etc., we decided to probe the nonlinear vibration of MSH nanocomposite thin-walled shells subjected to a hard-type harmonic stimulation. In this regard, the viscoelastic properties of the matrix will be considered to be like that expressed in [47]. Afterward, the modified version of the Halpin–Tsai method will be implemented to consider the effect of curved shape of the nanofillers on the dynamic response of the continuous system. Next, the classical theory of thin cylindrical shells will be mixed with the nonlinear strain–displacement relations of von Kármán to derive the nonlinear governing equations of the system with the aid of an energy method. Finally, the problem will be solved analytically and both tabular and illustrative case studies will be depicted for reference.

2 Theory and formulation

2.1 Micromechanical homogenization

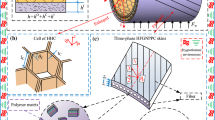
Here, the equivalent properties of MSH nanocomposite will be obtained. The schematic flowchart implemented for modeling the hybrid nanocomposite can be found in Fig. 1. The MSH nanocomposite is assumed to be hosted by a polymer whose time-varying properties are reported in the literature. Polymers promote viscoelastic behavior in various working conditions [61]. Thus, it is logical to consider the properties of such soft materials to be time varying [62]. In this study, an exponential temporal degradation for the polymer’s properties will be considered, in accordance with the well-known viscoelastic model of Maxwell [47, 63]. Based on this method, the modulus and Poisson’s ratio of the polymer can be calculated via [60]:

$$ E_{{{\text{PM}}}} (t) = E_{{{\text{PM}}}}^{{0}} \exp \left( { - \frac{t}{{\tau_{v} }}} \right)^{{\beta_{v} }} , $$
(1)
$$ \nu_{{{\text{PM}}}} (t) = 0.5 - (0.5 - \nu_{{{\text{PM}}}}^{0} )\exp \left( { - \frac{t}{{\tau_{v} }}} \right)^{{\beta_{v} }} , $$
(2)

where \(E_{{{\text{PM}}}}^{0}\) and \(\nu_{{{\text{PM}}}}^{0}\) are the instantaneous elastic modulus at the initial time and initial value of Poisson’s ratio, respectively. The parameters \(\beta_{v}\) and \(\tau_{v}\) are stretching exponent and characteristic relaxation time, respectively. It is worth mentioning that the mass density of the polymer does not vary with time and, thus, it can be stated that \(\rho_{{{\text{PM}}}} = \rho_{{{\text{PM}}}}^{{0}}\).

Fig. 1
figure 1

Schematic flowchart of modeling of the MSH polymer nanocomposites

Full size image

Next, the equivalent properties of CNTR polymer must be gathered. To this end and with regard to the important influence of the waviness phenomenon on the modulus determination in nanocomposites, the semi-empirical modified Halpin–Tsai method [45] is chosen. Prior to discussing about the homogenization method, it must be declared that the present modeling is based on the fact that a limited content of CNTs is utilized in the composition of the hybrid nanomaterial. If CNT loadings above 2 wt.% are purposed, the present model is not reliable. This issue does not seem important herein, because it is not logical to use CNT loadings of as high as 2 wt.% or more due to the high probability of aggregation phenomenon in such CNT loadings. Once CNTR polymers with low reinforcement content are studied, the present model can be trusted due to the excellent agreement between model predictions and those of experiments [45]. Following this algorithm, the Young’s modulus of the CNTR nanocomposite can be computed as:

$$ E_{{{\text{NCM}}}} = \frac{{1 + C\eta V_{{{\text{CNT}}}} }}{{1 - \eta V_{{{\text{CNT}}}} }}E_{{{\text{PM}}}} , $$
(3)

where

$$ \eta = \frac{{C_{w} \left[ {\alpha {{E_{{{\text{CNT}}}} } \mathord{\left/ {\vphantom {{E_{{{\text{CNT}}}} } {E_{{{\text{PM}}}} }}} \right. \kern-\nulldelimiterspace} {E_{{{\text{PM}}}} }}} \right] - 1}}{{C_{w} \left[ {\alpha {{E_{{{\text{CNT}}}} } \mathord{\left/ {\vphantom {{E_{{{\text{CNT}}}} } {E_{{{\text{PM}}}} }}} \right. \kern-\nulldelimiterspace} {E_{{{\text{PM}}}} }}} \right] + C}}, $$
(4)
$$ C = 2\frac{{l_{{{\text{CNT}}}} }}{{d_{{{\text{CNT}}}} }}, $$
(5)

in which α is the orientation factor that must be set to 1/6 due to very small dimensions of the CNTs in comparison with the entire thickness of the structure [64]. In addition, \(C\) is a geometry-based coefficient which is in charge of capturing the shape of nanofillers. Finally, the sign \(C_{w}\) stands for the waviness coefficient which is defined as \(C_{w} = 1 - {a \mathord{\left/ {\vphantom {a w}} \right. \kern-\nulldelimiterspace} w}\). In this definition, a and w are amplitude and range of the wave existing in the CNT, respectively. It is worth mentioning that the introduced waviness coefficient varies between zero and one where the CNTs are assumed to be like circle (fully curved CNTs) and string (ideal CNTs), respectively. Also, the mass density and Poisson’s ratio of the CNTR nanocomposite can be achieved using [60]:

$$ \rho_{{{\text{NCM}}}} = \rho_{{{\text{CNT}}}} V_{{{\text{CNT}}}} + \rho_{{{\text{PM}}}} V_{{{\text{PM}}}} , $$
(6)
$$ \nu_{{{\text{NCM}}}} = \nu_{{{\text{CNT}}}} V_{{{\text{CNT}}}} + \nu_{{{\text{PM}}}} V_{{{\text{PM}}}} . $$
(7)

Once Eqs. (3) and (7) are mixed, the shear modulus of the CNTR polymer will be obtained via \(G_{{{\text{NCM}}}} = {{E_{{{\text{NCM}}}} } \mathord{\left/ {\vphantom {{E_{{{\text{NCM}}}} } {2\left( {1 + \nu_{{{\text{NCM}}}} } \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {1 + \nu_{{{\text{NCM}}}} } \right)}}\). In Eqs. (3), (6), and (7), the volume fraction of the CNTs can be gathered by [60]:

$$ V_{{{\text{CNT}}}} = \left( {\frac{{\rho_{{{\text{CNT}}}} }}{{m_{r} \rho_{{{\text{PM}}}} }} - \frac{{\rho_{{{\text{CNT}}}} }}{{\rho_{{{\text{PM}}}} }} + 1} \right)^{ - 1} , $$
(8)

where \(\rho_{{{\text{CNT}}}}\) and \(\rho_{{{\text{PM}}}}\), respectively, correspond to the mass densities of CNTs and polymer. Also, \(m_{r}\) is the mass fraction of the nanofillers.

At this stage, we find the equivalent properties of the MSH nanomaterial. To do so, assume a fiber-reinforced composite whose matrix is the CNTR polymer. In this paper, GFs are employed as the reinforcing macro-scale fiber. If the Young’s modulus, shear modulus, and Poisson’s ratio of the GFs are, respectively, \(E_{F}\), \(G_{F}\), and \(\nu_{F}\), the effective properties of MSH nanocomposite can be achieved using [60]:

$$ E_{11} = E_{F} V_{F} + E_{{{\text{NCM}}}} V_{{{\text{PM}}}}^{*} , $$
(9)
$$ E_{22} = E_{33} = \frac{{E_{{{\text{NCM}}}} }}{{1 - V_{F} (1 - E_{{{\text{NCM}}}} /E_{F} )}}, $$
(10)
$$ G_{12} = G_{13} = G_{23} = \frac{{G_{{{\text{NCM}}}} }}{{1 - V_{F} (1 - G_{{{\text{NCM}}}} /G_{F} )}}, $$
(11)
$$ \nu_{12} = \nu_{13} = \nu_{F} V_{F} + \nu_{{{\text{NCM}}}} V_{{{\text{PM}}}}^{*} , $$
(12)
$$ \nu_{23} = \frac{{E_{22} }}{{2G_{23} }} - 1, $$
(13)

in which \(E_{11}\), \(E_{22}\), and \(E_{33}\) stand for Young’s modulus in the axial, transverse, and flexural directions, respectively. Besides, in- and out-of-plane shear modules are shown with \(G_{12}\), \(G_{13}\), and \(G_{23}\). The signs \(\nu_{12}\), \(\nu_{13}\), and \(\nu_{23}\) indicate the Poisson’s ratios in different planes. It is worth mentioning that in Eqs. (9)–(12), the GFs’ volume fraction \(V_{F}\) (i.e., identical to \(1 - V_{{{\text{PM}}}}^{*}\)) can be defined as [60]:

$$ V_{F} = \left( {\frac{{\rho_{F} }}{{m_{f} \rho_{{{\text{NCM}}}} }} - \frac{{\rho_{F} }}{{\rho_{{{\text{NCM}}}} }} + 1} \right)^{ - 1} . $$
(14)

In the above definition, \(m_{f}\) denotes GFs’ mass fraction.

2.2 Classical shell theory

The present section of this article is dedicated to derivation of the kinematic relations describing the problem. There exist different kinematic theories for mathematical description of structures’ motion in the solid mechanics. Generally, these theories can be categorized into three classical [65,66,67,68], first-order [69,70,71], and higher-order [72,73,74] theories whose main objective is to simulate thin, moderately thick, and thick structures, respectively. Due to the fact that shear deformation can be ignored in the investigation of thin structures [75, 76], classical theory of thin-walled cylindrical shells is selected in this study. By considering the axial displacement, circumferential one, and bending deformation shown by u, v, and w, respectively, and keeping the von Kármán-type geometrical nonlinearity in mind, the nonvanishing components of the strain tensor can be presented as [77]:

$$ \begin{gathered} \varepsilon_{xx} = \varepsilon_{x}^{0} - z\kappa_{x} , \hfill \\ \varepsilon_{yy} = \varepsilon_{y}^{0} - z\kappa_{y} , \hfill \\ \gamma_{xy} = \gamma_{xy}^{0} - 2z\kappa_{xy} . \hfill \\ \end{gathered} $$
(15)

In the above definitions, normal (\(\varepsilon_{x}^{0}\) and \(\varepsilon_{y}^{0}\)) and in-plane shear (\(\gamma_{xy}^{0}\)) strains are [77]:

$$ \begin{gathered} \varepsilon_{x}^{0} = \frac{\partial u}{{\partial x}} + \frac{1}{2}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} , \hfill \\ \varepsilon_{y}^{0} = \frac{\partial v}{{\partial y}} - \frac{w}{R} + \frac{1}{2}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} , \hfill \\ \gamma_{xy}^{0} = \frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}} + \frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}}. \hfill \\ \end{gathered} $$
(16)

Also, longitudinal (\(\kappa_{x}\)) and circumferential (\(\kappa_{y}\)) curvatures and the in-plane twist (\(\kappa_{xy}\)) are [77]:

$$ \begin{gathered} \kappa_{x} = \frac{{\partial^{2} w}}{{\partial x^{2} }}, \hfill \\ \kappa_{y} = \frac{1}{R}\frac{\partial v}{{\partial y}} + \frac{{\partial^{2} w}}{{\partial y^{2} }}, \hfill \\ \kappa_{xy} = \frac{1}{2R}\frac{\partial v}{{\partial x}} + \frac{{\partial^{2} w}}{\partial x\partial y}, \hfill \\ \end{gathered} $$
(17)

where \(y = R\theta\).

2.3 Constitutive equations

Herein, the Hook’s law for linearly elastic solids will be hired to find a suitable relationship between forces, moments, and displacement field components. According to this rule, the Cauchy stress and strain tensors can be related to each other via \(\sigma_{ij} = C_{ijkl} \varepsilon_{kl}\). In this identity, the corresponding arrays of Cauchy stress and strain tensors are shown with \(\sigma_{ij}\) and \(\varepsilon_{kl}\), respectively, whereas \(C_{ijkl}\) indicates the corresponding array of the elasticity tensor. If the plane stress condition is considered, the above-mentioned identity can be re-written as follows [78]:

$$ \left\{ \begin{gathered} \sigma_{xx} \hfill \\ \sigma_{yy} \hfill \\ \sigma_{xy} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon_{xx} \hfill \\ \varepsilon_{yy} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right\}, $$
(18)

where

$$ Q_{11} = \frac{{E_{11} }}{{1 - \nu_{12} \nu_{21} }},\,\,\,\,\,Q_{12} = \frac{{\nu_{12} E_{22} }}{{1 - \nu_{12} \nu_{21} }},\,\,\,\,\,Q_{22} = \frac{{E_{22} }}{{1 - \nu_{12} \nu_{21} }},\,\,\,\,\,Q_{66} = \frac{{E_{11} }}{{2(1 + \nu_{12} )}}. $$
(19)

Now, if the forces and moments are assumed to be defined in the following through-the-thickness form \((N_{ij} ,M_{ij} ) = \int\limits_{ - h/2}^{h/2} {(1,z)\sigma_{ij} dz} ,\,\,\,\,\,(i,j = x,y)\) and Eq. (18) is integrated over the thickness of the structure, the following expression can be attained:

$$ \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 \\ {A_{12} } & {A_{22} } & 0 & {B_{12} } & {B_{22} } & 0 \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 \\ {B_{12} } & {B_{22} } & 0 & {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {B_{66} } & 0 & 0 & {D_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ { - \kappa_{x} } \\ { - \kappa_{y} } \\ { - 2\kappa_{xy} } \\ \end{array} } \right\}. $$
(20)

In the above identity, through-the-thickness rigidities of the shell can be expressed as:

$$ [A_{n} ,B_{n} ,D_{n} ] = \int\limits_{ - h/2}^{h/2} {[1,z,} z^{2} ]Q_{n} (z)dz,\,\,\,\,\,\,n = (11,12,22,66). $$
(21)

2.4 Governing equations

Within this section, the energy method will be implemented for the goal of deriving the motion equations of thin-walled cylindrical shell. To this goal, the dynamic form of the principle of virtual work will be utilized. According to this principle, the variation of the continuous system’s Lagrangian, i.e., defined as \(L = U + V - T\) (U and T stand for strain and kinetic energies, respectively, and V denotes the work done on the system by external loadings), over any desired time interval must be set to zero [78, 79]. Following this principle as well as considering the kinematic relations of classical shells, the Euler–Lagrange equations can be derived [77]:

$$ \frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }}, $$
(22)
$$ \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{y} }}{\partial y} - \frac{1}{R}\left( {\frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{y} }}{\partial y}} \right) = I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }}, $$
(23)
$$ \begin{gathered} \frac{{\partial^{2} M_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} M_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} M_{y} }}{{\partial y^{2} }} - \frac{{N_{x} }}{R} + \frac{\partial }{\partial x}\left( {N_{x} \frac{\partial w}{{\partial x}} + N_{xy} \frac{\partial w}{{\partial y}}} \right) \hfill \\ + \frac{\partial }{\partial x}\left( {N_{xy} \frac{\partial w}{{\partial x}} + N_{y} \frac{\partial w}{{\partial y}}} \right) - ph\frac{{\partial^{2} w}}{{\partial x^{2} }} + q = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon I_{0} \frac{\partial w}{{\partial t}}. \hfill \\ \end{gathered} $$
(24)

In the above set of equations, the in-plane through-the-thickness inertia of the shell can be calculated via:

$$ I_{0} = \int\limits_{ - h/2}^{h/2} {\rho dz} . $$
(25)

In Eqs. (22)–(24), \(p\) and \(q\) are the axial compression and external distributed load, respectively. In addition, \(\varepsilon\) stands for the damping coefficient of the viscose damper below the structure. Now, the above motion equations must be presented in terms of the components of the displacement field to achieve the governing equations. To this purpose, substitution of Eq. (20) into Eqs. (22)–(24) yields:

$$ L_{11} (u) + L_{12} (v) + L_{13} (w) + P_{1} (w) = I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }}, $$
(26)
$$ L_{21} (u) + L_{22} (v) + L_{23} (w) + P_{2} (w) = I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }}, $$
(27)
$$ \begin{gathered} L_{31} (u) + L_{32} (v) + L_{33} (w) + P_{3} (w) + Q_{3} (u,w) + R_{3} (v,w) \hfill \\ - ph\frac{{\partial^{2} w}}{{\partial x^{2} }} + q = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon \frac{\partial w}{{\partial t}}, \hfill \\ \end{gathered} $$
(28)

where \(L_{ij} \left( . \right)\) linear operators can be expressed in the following form:

$$ \begin{gathered} L_{11} (u) = A_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + A_{66} \frac{{\partial^{2} u}}{{\partial y^{2} }}, \hfill \\ L_{12} (v) = \left( {A_{12} + A_{66} - \frac{{B_{12} + B_{66} }}{R}} \right)\frac{{\partial^{2} v}}{\partial x\partial y}, \hfill \\ L_{13} (w) = - \frac{{A_{12} }}{R}\frac{\partial w}{{\partial x}} - B_{11} \frac{{\partial^{3} w}}{{\partial x^{3} }} - (B_{12} + 2B_{66} )\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}, \hfill \\ L_{21} (u) = \left( {A_{12} + A_{66} - \frac{{B_{12} + B_{66} }}{R}} \right)\frac{{\partial^{2} u}}{\partial x\partial y}, \hfill \\ L_{22} (v) = \left( {A_{66} - \frac{{2B_{66} }}{R} + \frac{{D_{66} }}{{R^{2} }}} \right)\frac{{\partial^{2} v}}{{\partial x^{2} }} + \left( {A_{11} - \frac{{2B_{11} }}{R} + \frac{{D_{11} }}{{R^{2} }}} \right)\frac{{\partial^{2} v}}{{\partial y^{2} }}, \hfill \\ L_{23} (w) = - \left( {\frac{{A_{11} }}{R} - \frac{{B_{11} }}{{R^{2} }}} \right)\frac{\partial w}{{\partial y}} - \left( {B_{11} - \frac{{D_{11} }}{R}} \right)\frac{{\partial^{3} w}}{{\partial y^{3} }} - \left( {B_{12} + 2B_{66} - \frac{{D_{12} + 2D_{66} }}{R}} \right)\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}, \hfill \\ L_{31} (u) = \frac{{A_{21} }}{R}\frac{\partial u}{{\partial x}} + B_{11} \frac{{\partial^{3} u}}{{\partial x^{3} }} + (B_{12} + 2B_{66} )\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }}, \hfill \\ L_{32} (v) = \left( {\frac{{A_{11} }}{R} - \frac{{B_{11} }}{{R^{2} }}} \right)\frac{\partial v}{{\partial y}} + \left( {B_{11} - \frac{{D_{11} }}{R}} \right)\frac{{\partial^{3} v}}{{\partial y^{3} }} + \left( {B_{12} + 2B_{66} - \frac{{D_{12} + 2D_{66} }}{R}} \right)\frac{{\partial^{3} v}}{{\partial x^{2} \partial y}}, \hfill \\ L_{33} (w) = - \frac{{A_{11} }}{{R^{2} }}w - \frac{{2A_{12} }}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }} - \frac{{2B_{12} }}{R}\frac{{\partial^{2} w}}{{\partial y^{2} }} - D_{11} \left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) - 2(D_{12} + 2D_{66} )\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }}. \hfill \\ \end{gathered} $$
(29)

In addition, the nonlinear operators \(P_{i} \left( . \right)\), \(Q_{3} \left( . \right)\), and \(R_{3} \left( . \right)\) can be defined as:

$$ P_{1} (w) = A_{11} \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + (A_{12} + A_{66} )\frac{\partial w}{{\partial y}}\frac{{\partial^{2} w}}{\partial x\partial y} + A_{66} \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial y^{2} }}, $$
(30)
$$ P_{2} (w) = \left( {A_{66} - \frac{{B_{66} }}{R}} \right)\frac{\partial w}{{\partial y}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {A_{11} - \frac{{B_{11} }}{R}} \right)\frac{\partial w}{{\partial y}}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \left( {A_{12} + A_{66} - \frac{{B_{12} + B_{66} }}{R}} \right)\frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{\partial x\partial y}, $$
(31)
$$ \begin{gathered} P_{3} (w) = 2(A_{12} + 2A_{66} )\frac{\partial w}{{\partial x}}\frac{\partial w}{{\partial y}}\frac{{\partial^{2} w}}{\partial x\partial y} - \frac{w}{R}\left( {A_{12} \frac{{\partial^{2} w}}{{\partial x^{2} }} + A_{11} \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + 2(B_{66} - B_{12} )\frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2(B_{12} - B_{66} )\left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{A_{12} }}{2R}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} - \frac{{A_{11} }}{2R}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} + \frac{{3A_{11} }}{2}\left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{{\partial^{2} w}}{{\partial y^{2} }}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right] + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\frac{{A_{12} }}{2} + A_{66} } \right)\left[ {\frac{{\partial^{2} w}}{{\partial y^{2} }}\left( {\frac{\partial w}{{\partial x}}} \right)^{2} + \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{{\partial y}}} \right)^{2} } \right], \hfill \\ \end{gathered} $$
(32)
$$ \begin{gathered} Q_{3} (u,w) = \left( {\frac{\partial u}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial x^{2} }}\frac{\partial w}{{\partial x}}} \right) + A_{12} \frac{\partial u}{{\partial x}}\frac{{\partial^{2} w}}{{\partial y^{2} }} + A_{66} \frac{\partial w}{{\partial x}}\frac{{\partial^{2} u}}{{\partial y^{2} }} + (A_{12} + A_{66} )\frac{\partial w}{{\partial y}}\frac{{\partial^{2} u}}{\partial x\partial y} + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2A_{66} \frac{\partial u}{{\partial y}}\frac{{\partial^{2} w}}{\partial x\partial y}, \hfill \\ \end{gathered} $$
(33)
$$ \begin{gathered} R_{3} (v,w) = \left( {A_{12} - \frac{{B_{12} }}{R}} \right)\frac{\partial v}{{\partial y}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2\left( {A_{66} - \frac{{B_{66} }}{R}} \right)\frac{\partial v}{{\partial x}}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \left( {A_{11} - \frac{{B_{11} }}{R}} \right)\left( {\frac{\partial v}{{\partial y}}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{\partial w}{{\partial y}}\frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) + \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {A_{66} - \frac{{B_{66} }}{R}} \right)\frac{\partial w}{{\partial y}}\frac{{\partial^{2} v}}{{\partial x^{2} }} + \left( {A_{12} + A_{66} - \frac{{B_{12} + B_{66} }}{R}} \right)\frac{\partial w}{{\partial x}}\frac{{\partial^{2} v}}{\partial x\partial y}. \hfill \\ \end{gathered} $$
(34)

3 Analytical solution

Many types of analytical and numerical methods are presented in the open literature to obtain a solution for the dynamic problems of continuous systems [80,81,82,83,84,85,86]. In this section, an analytical framework will be introduced to solve the governing equations of the problem. In this method, i.e., founded on the basis of Galerkin’s technique, the displacement field components for a thin shell with both ends simply supported (S–S) will be considered as [77]:

$$ \begin{gathered} u = U(t)\cos \frac{m\pi x}{L}\sin \frac{ny}{R}, \hfill \\ v = V(t)\sin \frac{m\pi x}{L}\cos \frac{ny}{R}, \hfill \\ w = W(t)\sin \frac{m\pi x}{L}\sin \frac{ny}{R}, \hfill \\ \end{gathered} $$
(35)

in which \(U(t)\), \(V(t)\), and \(W(t)\) are the unknown Fourier coefficients regarding the oscillation amplitudes. Also, the longitudinal and circumferential half-mode numbers are shown with m and n, respectively. If Eq. (35) is inserted into Eqs. (26)–(28), one can reach:

$$ l_{11} U(t) + l_{12} V(t) + l_{13} W(t) + n_{1} W^{2} (t) = I_{0} \frac{{d^{2} U(t)}}{{dt^{2} }}, $$
(36)
$$ l_{21} U(t) + l_{22} V(t) + l_{23} W(t) + n_{2} W^{2} (t) = I_{0} \frac{{d^{2} V(t)}}{{dt^{2} }}, $$
(37)
$$ \begin{gathered} l_{31} U(t) + l_{32} V(t) + l_{33} W(t) + n_{3} W^{2} (t) + n_{4} W^{3} (t) + n_{5} U(t)W(t) \hfill \\ + n_{6} V(t)W(t) + \frac{16q}{{\pi^{2} mn}} = I_{0} \frac{{d^{2} W(t)}}{{dt^{2} }} + 2\varepsilon I_{0} \frac{dW(t)}{{dt}}, \hfill \\ \end{gathered} $$
(38)

where

$$ \begin{gathered} l_{11} = - A_{11} \frac{{\pi^{2} m^{2} }}{{L^{2} }} - A_{66} \frac{{n^{2} }}{{R^{2} }}, \hfill \\ l_{12} = l_{21} = \left( { - A_{12} - A_{66} + \frac{{B_{12} + B_{66} }}{R}} \right)\frac{\pi mn}{{LR}}, \hfill \\ l_{13} = l_{31} = - A_{12} \frac{\pi m}{{LR}} + B_{11} \frac{{\pi^{3} m^{3} }}{{L^{3} }} + (B_{12} + 2B_{66} )\frac{{\pi mn^{2} }}{{LR^{2} }}, \hfill \\ l_{22} = \left( { - A_{66} + \frac{{2B_{66} }}{R} - \frac{{D_{66} }}{{R^{2} }}} \right)\frac{{\pi^{2} m^{2} }}{{L^{2} }} + \left( { - A_{11} + \frac{{2B_{11} }}{R} - \frac{{D_{11} }}{{R^{2} }}} \right)\frac{{\pi^{2} m^{2} n}}{{L^{2} R}}, \hfill \\ l_{33} = 2B_{12} \frac{{\pi^{2} m^{2} }}{{L^{2} R}} + 2B_{11} \frac{{n^{2} }}{{R^{3} }} - D_{11} \frac{{\pi^{4} m^{4} }}{{L^{4} }} - D_{11} \frac{{n^{4} }}{{R^{4} }} - 2(D_{12} + 2D_{66} )\frac{{\pi^{2} m^{2} n}}{{L^{2} R^{2} }} - \frac{{A_{11} }}{{R^{2} }} + \frac{{ph\pi^{2} m^{2} }}{{L^{2} }}, \hfill \\ n_{1} = - 32A_{11} \frac{{\pi m^{2} }}{{9L^{3} n}} + 16( - A_{11} - A_{66} )\frac{n}{{9\pi LR^{2} }}, \hfill \\ n_{2} = \left( { - A_{66} + A_{12} + \frac{{B_{66} - B_{12} }}{R}} \right)\frac{16m}{{9L^{2} R}} + \left( { - A_{11} + \frac{{B_{11} }}{R}} \right)\frac{{32n^{2} }}{{9\pi^{2} R^{3} m}}, \hfill \\ n_{3} = 16A_{12} \frac{m}{{3L^{2} Rn}} + 16A_{11} \frac{n}{{3\pi^{2} R^{3} m}} + 32(B_{66} - B_{12} )\frac{mn}{{3L^{2} R^{2} }}, \hfill \\ n_{4} = - 9A_{11} \frac{{\pi^{4} m^{4} }}{{32L^{4} }} - (A_{12} + 2A_{66} )\frac{{\pi^{2} m^{2} n^{2} }}{{16L^{2} R^{2} }} - 9A_{11} \frac{{n^{4} }}{{32LR^{2} }}, \hfill \\ n_{5} = 32A_{11} \frac{{\pi m^{2} }}{{9L^{3} n}} + 32(A_{12} - A_{66} )\frac{n}{{9\pi LR^{2} }}, \hfill \\ n_{6} = \left( {A_{12} - A_{66} + \frac{{B_{66} - B_{12} }}{R}} \right)\frac{32m}{{9L^{2} R}} + \left( {A_{11} - \frac{{B_{11} }}{R}} \right)\frac{{32n^{2} }}{{9\pi^{2} R^{3} m}}. \hfill \\ \end{gathered} $$
(39)

In the nonlinear vibration problems with small oscillation amplitudes, it is logical to assume the in-plane inertia to be ignorable compared with the out-of-plane one [87]. Hence, Eqs. (36)–(38) can be re-written in the following form:

$$ l_{11} U(t) + l_{12} V(t) + l_{13} W(t) + n_{1} W^{2} (t) = 0, $$
(40)
$$ l_{21} U(t) + l_{22} V(t) + l_{23} W(t) + n_{2} W^{2} (t) = 0, $$
(41)
$$ \begin{gathered} l_{31} U(t) + l_{32} V(t) + l_{33} W(t) + n_{3} W^{2} (t) + n_{4} W^{3} (t) + n_{5} U(t)W(t) \hfill \\ + n_{6} V(t)W(t) + \frac{16q}{{\pi^{2} mn}} = I_{0} \frac{{d^{2} W(t)}}{{dt^{2} }} + 2\varepsilon I_{0} \frac{dW(t)}{{dt}}. \hfill \\ \end{gathered} $$
(42)

If \(U(t)\) and \(V(t)\) are extracted from simultaneous solution of Eqs. (40) and (41) in terms of \(W(t)\) and \(W^{2} (t)\) and thereafter substituted in Eq. (42), the following duffing equation will be achieved:

$$ I_{0} \frac{{d^{2} W(t)}}{{dt^{2} }} + 2\varepsilon I_{0} \frac{dW(t)}{{dt}} + a_{1} W(t) - a_{2} W^{2} (t) + a_{3} W^{3} (t) = \frac{16q}{{\pi^{2} mn}}, $$
(43)

in which

$$ \begin{gathered} a_{1} = - l_{33} - \frac{{l_{31} (l_{12} l_{23} - l_{22} l_{13} ) + l_{32} (l_{21} l_{13} - l_{11} l_{23} )}}{{l_{11} l_{22} - l_{12}^{2} }}, \hfill \\ a_{2} = n_{3} + \frac{{l_{31} (l_{12} n_{2} - l_{22} n_{1} ) + l_{32} (l_{12} n_{1} - l_{11} n_{2} ) + n_{5} (l_{12} l_{23} - l_{22} l_{13} ) + n_{6} (l_{12} l_{13} - l_{11} l_{23} )}}{{l_{11} l_{22} - l_{12}^{2} }}, \hfill \\ a_{3} = - n_{4} - \frac{{n_{5} (l_{12} n_{2} - l_{22} n_{1} ) + n_{6} (l_{12} n_{1} - l_{11} n_{2} )}}{{l_{11} l_{22} - l_{12}^{2} }}. \hfill \\ \end{gathered} $$
(44)

3.1 Linear frequency

It is possible to use Eqs. (36)–(38) to obtain linear natural frequency of the shell by ignoring nonlinear terms and the effect of the applied distributed load. The linear frequencies can be determined by solving the following eigenvalue system as [77]:

$$ \left| {\begin{array}{*{20}c} {l_{11} + I_{0} \omega^{2} } & {l_{12} } & {l_{13} } \\ {l_{21} } & {l_{22} + I_{0} \omega^{2} } & {l_{23} } \\ {l_{31} } & {l_{32} } & {l_{33} + I_{0} \omega^{2} } \\ \end{array} } \right| = 0. $$
(45)

Once the above identity is solved, the natural frequencies of the system will be attained. Among all of the triple frequencies, the smallest one will be the the fundamental frequency which is identical to \(\omega_{mn} = \sqrt {{{a_{1} } \mathord{\left/ {\vphantom {{a_{1} } {I_{0} }}} \right. \kern-\nulldelimiterspace} {I_{0} }}}\) that could be found earlier from Eq. (43).

3.2 Nonlinear forced vibration response

In this sub-section, it will be shown how to find the frequency–response relation of the present problem. In this work, a harmonic form will be considered for the distributed load applied on the edge of the shell. It is worth regarding that the harmonic excitation is presumed to be of the hard type. In other words, the load \(q\) is assumed to be \(q = Q\sin \Omega t\) so that \(\Omega\) denotes the excitation frequency. Once this type of dynamic stimulation is inserted into Eq. (43), the following expression can be achieved:

$$ \frac{{d^{2} W}}{{dt^{2} }} + 2\varepsilon \frac{dW}{{dt}} + \omega_{mn}^{2} (W - HW^{2} + KW^{3} ) = F\sin \Omega t, $$
(46)

in which

$$ F = \frac{16q}{{\pi^{2} mn}},\,\,\,\,\,\omega_{mn} = \sqrt {{{a_{1} } \mathord{\left/ {\vphantom {{a_{1} } {I_{0} }}} \right. \kern-\nulldelimiterspace} {I_{0} }}} ,\,\,\,\,\,H = \frac{{a_{2} }}{{a_{1} }},\,\,\,\,\,K = \frac{{a_{3} }}{{a_{1} }}. $$
(47)

To solve the problem, the method of harmonic balance will be utilized in this study. According to this method, the oscillation amplitude can be considered to be in a sinusoidal form as \(W = A\sin \Omega t\). If this definition is substituted in Eq. (46), the identity will be enhanced as [77]:

$$ \psi \equiv A(\omega_{mn}^{2} - \Omega^{2} )\sin \Omega t + 2\varepsilon A\Omega \cos \Omega t - \omega_{mn}^{2} HA^{2} \sin^{2} \Omega t + K\omega_{mn}^{2} A^{3} \sin^{3} \Omega t - F\sin \Omega t = 0. $$
(48)

Once the product of the above identity in \(\sin \Omega t\) is integrated with respect to time over a quarter of the oscillation period (\(\int\limits_{0}^{{{\pi \mathord{\left/ {\vphantom {\pi {2\Omega }}} \right. \kern-\nulldelimiterspace} {2\Omega }}}} {\psi \sin \Omega tdt} = 0\)), one can achieve:

$$ \Omega^{2} - \frac{4\varepsilon }{\pi }\Omega = \omega_{mn}^{2} \left( {1 - \frac{8}{3\pi }HA + \frac{3K}{4}A^{2} } \right) - \frac{F}{A}. $$
(49)

By defining \(\alpha^{2} = {{\Omega^{2} } \mathord{\left/ {\vphantom {{\Omega^{2} } {\omega_{mn}^{2} }}} \right. \kern-\nulldelimiterspace} {\omega_{mn}^{2} }},\) Eq. (49) can be re-written as:

$$ \alpha^{2} - \frac{4\varepsilon }{{\pi \omega_{mn} }}\alpha = 1 - \frac{8}{3\pi }HA + \frac{3K}{4}A^{2} - \frac{F}{{A\omega_{mn}^{2} }}. $$
(50)

The above relation is the frequency–response equation corresponding to the present system.

3.3 Nonlinear transient response

In this part of the solution, it will be tried to solve the problem in the time domain to reach the transient response of the MSH nanocomposite shell. To this purpose, Eq. (43) will be utilized. Once the fourth-order Runge–Kutta is applied to the mentioned relation and it is considered that the coefficients of the equation are functions of time due to the viscoelastic properties of the polymer, the time-varying expression for calculation of the dynamic deflection will be gathered.

4 Results and discussion

Present part deals with numerical case studies revealing the most important findings of this study. In the following cases, the radius-to-thickness ratio of the shell is assumed to be \({R \mathord{\left/ {\vphantom {R h}} \right. \kern-\nulldelimiterspace} h} = 500\), to satisfy the assumption of thin-walled being of the structure. The entire thickness is fixed \(h = 1\,\,{\text{mm}}\), whereas the length of the shell is assumed to be two times its radius (\({L \mathord{\left/ {\vphantom {L R}} \right. \kern-\nulldelimiterspace} R} = 2\)). It is noteworthy that the stretching component and relaxation time are fixed on \(\beta_{v} = 1\) and \(\tau_{v} = 120\,\,{\text{s}}\), respectively. Although the aforesaid inputs are considered in the following numerical cases, one can tailor the stretching component in the range of \(0 < \beta_{v} < 1\) if it is supposed to monitor the viscoelastic behaviors of MSH nanocomposite shells in different damping rates. In addition, the material properties of the polymer and GF can be found in Table 1, whereas those of the CNTs are shown in Table 2.

Table 1 Mechanical properties of the polymeric matrix and GFs [47]
Full size table
Table 2 Material properties of SWCNTs [51]
Full size table

4.1 Validation study

For the goal of being sure of the accuracy of the presented modeling, dynamic responses of cylindrical shells obtained from the present method are compared with those available in the literature. To this purpose, linear frequencies of metal foam shells reported in Refs. [88] and [89] are re-generated here. The results of this comparison can be found by referring to Table 3. Based on this comparison, the present method is able to approximate the vibrational characteristics of shell-type elements with a high precision. As another attempt toward validity check, the dimensionless frequencies of isotropic shells were calculated and are shown in Table 4. According to this table, our data are in an excellent agreement with those reported in Refs. [90,91,92,93].

Table 3 Comparison of the nondimensional linear natural frequencies of metal foam shells
Full size table
Table 4 Comparison of dimensionless frequencies \(\tilde{\omega } = \Omega (h/\pi )\sqrt {2(1 + \nu )\rho /E}\) of an isotropic cylindrical shell
Full size table

4.2 Frequency–response curves

In this section of numerical results, frequency–response curves of the oscillating MSH nanocomposite structure will be depicted in the framework of Figs. 2–6. Based on Fig. 2, it can be simply perceived that the utilization of wavy CNTs leads to having a wider range for the frequency ratio in constant values of the system’s deflection. This trend means that the system behaves in a more flexible manner whenever curved nanofillers are employed as reinforcing gadgets. This figure also denotes that compressive pre-loading results in a reduction in the frequency ratio of the MSH nanocomposite shell, which can be referred to as a mechanical constraint.

Fig. 2
figure 2

Frequency–response curve of MSH nanocomposite shells subjected to various compressive loadings while (a) straight and (b) wavy nanofillers are utilized for the goal of reinforcement (mr = 0.05, mf = 0.2)

Full size image

To be familiar with the effect of waviness coefficient on the frequency–response curve of the nanocomposite shell, Fig. 3 is presented while there exists no compressive pre-loading. Based on this illustration, it can be confirmed that if big values are assigned to the waviness coefficient, a wider range of frequency ratio will be achieved. This trend is physically due to the fact that in such cases, the reinforcing nanofillers will be closer to their ideal straight shape. In other words, the amplitude of the existing wave in the CNTs’ chord will be smaller, while the waviness coefficient increases. So, it is recommended to choose waviness coefficients between 0.3 and 0.4, while it is aimed to have a safe approximation from the system’s behavior according to the experiments [45]. This finding can be observed in Tables 5 and 6, too. In these tables, the impact of the waviness coefficient on the linear natural frequency of the MSH nanocomposite shell is presented. According to Table 5, higher natural frequencies correspond to bigger waviness coefficients. Besides, Table 6 reveals that adding the time leads to a reduction in the frequency of the system because of the fact that in longer times, the stiffness of the polymeric matrix will be attenuated continuously.

Fig. 3
figure 3

Frequency–response curve of MSH nanocomposite shells for different values of waviness coefficient (mr = 0.05, mf = 0.2, p = 0)

Full size image
Table 5 Effect of waviness coefficient \(C_{w}\) on natural frequencies (s−1) of MSH nanocomposite shell (p = 0, t = 0)
Full size table
Table 6 Effect of time and circumferential wave number n on natural frequencies (s−1) of MSH nanocomposite shell reinforced with both straight and wavy CNTs (p = 0)
Full size table

In Figs. 4 and 5, the main concentration is on the investigation of the influences of GFs’ and CNTs’ mass fraction on the frequency–response curves of MSH nanocomposite shells, respectively. According to Fig. 4, it can be realized that addition of the GFs’ mass fraction makes the frequency ratio wider, which might seem a little strange at the first glance. However, this effect is logical from physics viewpoint. In fact, a greater content of the macro-scale GFs corresponds with a reduction in the value of the nanofillers in the composition of the MSH nanomaterial. Hence, it is accurate to observe such a trend. In reverse, Fig. 5 indicates the positive role of the CNTs’ mass fraction on the frequency ratio of the vibrating nanocomposite structure. Based on this illustration, it can be figured out that the frequency ratio will be narrow if higher values are assigned to the mass fraction of the CNTs, thanks to the stiffness enhancement made in the nanomaterial.

Fig. 4
figure 4

Frequency–response curve of MSH nanocomposite shells reinforced with ideal (straight) CNTs for different values of GFs’ mass fraction (mr = 0.05, Cw = 1, p = 0)

Full size image
Fig. 5
figure 5

Frequency–response curve of MSH nanocomposite shells reinforced with non-ideal (wavy) CNTs for different values of CNTs’ mass fraction (mf = 0.2, Cw = 0.35, p = 0)

Full size image

As the final case study in this section, the combined effects of waviness phenomenon and excitation amplitude on the frequency–response curve of MSH nanocomposite shells are provided in Fig. 6. This diagram states that the deviation of the frequency–response curve from free oscillation case (\(F = 0\)) will be increased as the excitation amplitude is added. Also, it is clear that the tendency of the frequency–response curve of the system to the left side will be increased in the case of employing wavy CNTs for the purpose of manufacturing the hybrid nanomaterial. From our knowledge about nonlinear systems, it is obvious that this trend is a softening one that originated due to the destroying effect of the wavy shape of the nanofillers on the reinforcement mechanism in the nanocomposites. Hence, the resonance path of the fluctuating nanocomposite shell can be dramatically affected by the waviness phenomenon according to this diagram.

Fig. 6
figure 6

Frequency–response curve of MSH nanocomposite shells for different values of loading amplitude F while (a) straight and (b) wavy CNTs are utilized for the goal of reinforcement (mr = 0.05, mf = 0.2)

Full size image

4.3 Transient response monitoring

Within this part of this manuscript, Figs. 7–10 will be studied whose major concern is to analyze the transient response of the vibrating system. In the first example, i.e., Fig. 7, the long-term behavior of the system is monitored. According to this figure, it is obvious that the mean value of the deflection amplitude will be decreased as time exceeds. The reason for this trend is the decreasing influence of time on the total stiffness of the polymeric matrix because of the viscoelastic nature of the polymers. Also, this diagram shows another phenomenon. Indeed, it can be seen that over time, the variation of the deflection amplitude will be reduced because of the fact that the oscillator reaches its steady condition.

Fig. 7
figure 7

Transient response of MSH nanocomposite subjected to a harmonic excitation once wavy CNTs are utilized for the goal of reinforcement (Cw = 0.35, mr = 0.05, mf = 0.2, F = 1500, Ω = 600)

Full size image

On the other hand, variation of the transient response of the system in a limited time interval can be observed in Fig. 8 whenever ideal and non-ideal CNTs are utilized in the composition of the hybrid nanomaterial. Based on this diagram, it is clear that the MSH nanocomposite shell experiences a beating-type oscillation. The small and big amplitudes of the system’s beat are sensitive to the type of the reinforcing nanofillers. It is clear that if wavy CNTs are hired, the beating amplitude will be enlarged because of the negative impact of the waviness phenomenon on the stiffness of the three-phase nanomaterial. Also, the wavy shape of the nanofillers induces a delay in the beating of the system, so that the number of beating cycles decreases in a constant time period if non-straight nanofillers are implemented in the manufacturing procedure.

Fig. 8
figure 8

Qualitative effect of the waviness phenomenon on the transient response of MSH nanocomposite shells (mr = 0.1, mf = 0.2)

Full size image

Moreover, the effects of mass fraction of the macro- and nano-size reinforcing gadgets, namely GFs and CNTs, on the transient response of the MSH nanocomposite shells are shown in Figs. 9 and 10, respectively. According to these diagrams, it can be simply conceived that the addition of the GFs’ mass fraction intensifies the beating amplitude, whereas this parameter will be decreased if a greater content of the CNTs are hired in the fabrication procedure. The major reason of the first trend is that by adding the portion of the GFs in the hybrid nanomaterial, the content of the CNTs will be reduced because of the constant volume of the continua. Hence, it is natural to see such a softening behavior from physics point of view. Also, the observations of Fig. 10 can be physically justified by pointing out that addition of the content of the nanofillers stiffens the MSH nanocomposite.

Fig. 9
figure 9

Transient response of MSH nanocomposite shells reinforced via wavy CNTs for different values of GFs’ mass fraction (mr = 0.05, Cw = 0.35)

Full size image
Fig. 10
figure 10

Transient response of MSH nanocomposite shells reinforced via wavy CNTs for different values of CNTs’ mass fraction (mf = 0.2, Cw = 0.35)

Full size image

5 Conclusion

This manuscript was majorly written to account for the coupled influences of the polymer’s viscoelastic behavior and non-ideal shape of the CNTs on the nonlinear dynamic responses of thin-walled shells made from MSH nanocomposites. Herein, the most crucial highlights of this work will be reviewed in brief as below:

  • It was shown that the dynamic amplitude of the system’s beating diminished with increment of time. This trend physically appeared due to the viscoelastic features of the polymer.

  • It was demonstrated that the nonlinear behavior of the shell is softer than the ideal theoretical estimations. This difference originates from the destructive impact of the waviness phenomenon on the mechanism of reinforcement in the hybrid nanomaterial.

  • A limited rise in the mass fraction of the nanofillers is able to lessen the dynamic amplitude of deflection. The physical reason of this trend is enhancement of stiffness in MSH nanocomposites.

  • Addition of the GFs’ mass fraction resulted in a reduction in the equivalent stiffness of the MSH nanocomposite shell because it enforced the nanofillers’ content to be decreased.

  • It was illustrated that the existence of an axial compressive pre-load can lead to a wider range of nonlinear-to-linear frequency ratio in MSH nanocomposite shells through softening the structure.

  • According to the utilized methodology, nonlinear dynamic characteristics of MSH nanocomposite shells are easy to reach without being involved in complex algebraic operations available in the method of multiple time scales.

  • Finally, the presented micromechanical modeling makes it possible to estimate the mechanical properties of MSH nanocomposites, so that the guessed values are close to experimental data. Interestingly, this achievement is obtained with a very low-cost computational framework.

In addition to the above-mentioned positive aspects of this study, it is also crucial to point out the limitations of the present work. The effect of entanglement of CNTs in clusters on the Young’s modulus is not covered in this work. Furthermore, the presented results are generated based on the assumption of the essence of ideal bonding between the nanofillers and matrix.