Nonlinear low-velocity impact on damped and matrix-cracked hybrid laminated beams containing carbon nanotube reinforced composite layers

Abstract

This paper investigates the low-velocity impact response of a shear deformable laminated beam which contains both carbon nanotube reinforced composite (CNTRC) layers and carbon fiber reinforced composite (CFRC) layers. The effect of matrix cracks is considered, and a refined self-consistent model is selected to describe the degraded stiffness caused by the damage. The beam including damping effects rests on a two-parameter elastic foundation in thermal environments. Based on a higher-order shear deformation theory and von Kármán nonlinear strain–displacement relationships, the motion equations of the beam and impactor are established and solved by means of a two-step perturbation approach. The material properties of both CFRC layers and CNTRC layers are assumed to be temperature-dependent. To assess engineering application of this hybrid structure, two conditions for outer CNTRC layers and outer CFRC layers are compared. Besides, the effects of the crack density, volume fraction of carbon nanotube, temperature variation, the foundation stiffness and damping on the nonlinear low-velocity impact behavior of hybrid laminated beams are also discussed in detail.

1 Introduction

Carbon nanotubes (CNTs) possessing extraordinary mechanical and physical properties over traditional carbon fiber [1, 2] shows a great prospect on the aeronautical application. It has been reported that a small quantity of CNTs could significantly improve elastic moduli of polystyrene composites [3]. In other words, the composites using CNTs rather than carbon fibers as reinforcements can reduce the weight further. However, owing to the weak combination between carbon nanotube (CNT) and matrix, excess addition of CNT will degrade the mechanical properties, instead [4]. In this condition, Shen [5] firstly presented the novel conception of functionally graded (FG) carbon nanotube reinforced composite (CNTRC), which develops the most out of the effectiveness of reinforcement. Since then, many researchers have been focused on the mechanical behaviors of FG-CNTRC structures [6,7,8,9,10,11,12,13,14,15,16,17,18].

As an important mechanical property, low-velocity impact response always affects the engineering application of the structures. However, to the best of authors’ knowledge, the relevant literatures [19,20,21,22] which report the low-velocity impact of FG-CNTRC structures are lacked. Wang et al. [19] first investigated the low-velocity impact response of CNTRC plates and sandwiches. They built the motion equations of the plate based on a higher-order shear deformation theory and von Kármán nonlinearity. Two types of FG-CNTRC single layer plate, i.e., FG-X and FG-$\Lambda$, were considered, and uniformed distributed (UD) CNTRC plate was also included as a comparator. The results illustrated that the impact properties of CNTRC plate were significantly influenced by initial velocity of the impactor and initial stress of the plate as well as CNT volume fraction. Jam and Kiani [20] studied the response of FG-CNTRC beams subjected to the action of an impacting mass. In their analysis, Timoshenko beam theory (TBT) was employed and the results were obtained by Ritz method. They found that indentation, peak contact force and contact history time were all improved with the increase of the radius of projectile. An investigation of low-velocity impact on CNTRC skew plates was implemented by Malekzadeh and Dehbozorgi [21]. The equilibrium equations were formulated based on the first-order shear deformation theory and solved by finite element method (FEM). It was found that the peak contact force was increased, but the impact duration was reduced when the skew angle of CNTRC plate became larger. Song et al. [22] investigated the dynamic response of CNT reinforced FG composite plates subjected to impact loading. Besides FG-X distribution, FG-O was also taken into account. They found that increasing the stiffness near the surface of the plate could effectively reduce the deflection of the plate.

Although the relevant literatures about low-velocity impact of CNTRC beam are very little, we can still take the literatures about low-velocity impact of CFRC beam as reference. For example, a Ritz method for low-velocity impact analysis of CFRC laminated beam subjected to asynchronous/repeated multiple masses was presented by Sisi et al [23]. In their method, a higher-order shear deformation beam theory was employed and a modified Hertzian contact law was used to simulate the contact process. In their analysis, the arbitrary layups and various boundary conditions were both considered. Besides, Topac et al. [24] investigated CFRC beams under low-velocity impact both experimentally and numerically. They employed ABAQUS to simulate the experiments and observed the development of damage during the impact process.

Because of the limitation of manufacturing, it is difficult to produce a structure in large size by CNTRC. Presently, it seems to be feasible to replace some CFRC layers by CNTRC layers in a composite structure for the application. However, in a laminated structure, if all the single CNTRC layers are chosen to be the same FG type, the effect of FG distributed CNTs on structural behavior could be neglected [25,26,27]. Hence, we presented a novel CNT FG distribution for laminated structures, which has been proved to be efficiency for improving the mechanical properties in our previous works [16, 17]. In the present work, we pay our attention to the low-velocity impact response of damped hybrid laminated beams containing both CFRC layers and CNTRC layers resting on an elastic foundation. The dynamic equations of the beams are based on a higher-order shear deformation theory and von Kármán stress–strain relationship. The solutions are derived by a two-step perturbation technique [28]. The effect of matrix cracking is included and which is modeled by a refined self-consistent method (SCM). Furthermore, as CFRC and CNTRC are both assumed to be temperature-dependent, we also consider the influence of temperature variation. A modified Hertz model is proposed to describe the contact force and then the system of impactor and beam can be solved by a forth-order Runge–Kutta method. The numerical results show the effects of matrix cracks on contact force and center defection of hybrid beams under different conditions.

2 Governing equations

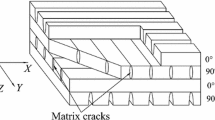
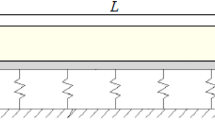
A hybrid laminated beam with length L and width b which consists of n plies is considered. Each ply has a constant thickness $h_\mathrm{p}$, and the total thickness of the beam is $h = n\times h_\mathrm{p}$. An impactor with mass $m^{i}$, initial velocity $\overline{{V}}_0$ and tip radius $R^{i}$ is impacted to the surface of the beam at the middle which is assumed to be simply supported and in-plane immovable. The schematic of the impactor and beam is shown in Fig. 1.

Fig. 1

Geometry and coordinate system of a hybrid laminated beam

2.1 Modified contact model

In the case of low-velocity impact, the Hertz contact law is simpler and more accurate than other contact theories [29]. Hence, the total contact force $F_\mathrm{c}$ is assumed to be related to the local contact indentation $\delta (t)$:

$$\begin{aligned} F_c (t)=K_c [\delta (t)]^{r} \end{aligned}$$

(1)

The local contact indentation $\delta (t)$ is defined as

$$\begin{aligned} \delta (t)=\overline{{W}}^{i}(t)-\overline{{W}}(t) \end{aligned}$$

(2)

where $\overline{{W}}^{i}(t)$ denotes the displacement of the impactor and $\overline{{W}}(t)$ represents the deflection of the beam at the impact location. According to Hertz contact law, the exponent r = 1.5 is considered for the contact between two homogeneous isotropic solids. However, it has been reported that $r = 1.5$ is also available for laminated composite targets [30]. $K_\mathrm{c}$ is contact stiffness and defined by

$$\begin{aligned} K_\mathrm{c} =\frac{4}{3}E^{{*}}\sqrt{R^{i}} \end{aligned}$$

(3)

where $R^{i}$ is the radius of the impactor tip, and

$$\begin{aligned} E^{{*}}=\left( {\frac{1-\nu ^{i}\nu ^{i}}{E^{i}}+\frac{1}{E_z }} \right) ^{-1} \end{aligned}$$

(4)

where $E^{i}$ and $\nu ^{i}$ are the Yong’s modulus and Poisson’s ratio of the impactor, respectively, and $E_{z}$ is the transverse Yong’s modulus at the surface of the beam, which can be approximated the same as the Yong’s modulus $E_{22}$. Since $E_{22 }$is variable in the thickness direction, we assume that $E_{z}$ is not a fixed value during impact process and is dependent on indentation. Based on that, a new definition of $E_{z}$ can be written as

$$\begin{aligned} E_z (t)=\frac{1}{\delta (t)}\int _{t_u }^{t_u +\delta (t)} {E_{22} (Z)\mathrm{d}Z} \end{aligned}$$

(5)

in which $Z=t_{u}$ is the top surface of the beam. During the unloading phase, the contact force $F_\mathrm{c}$ can be defined as

$$\begin{aligned} F_\mathrm{c} (t)=F_{\max } \left[ {\frac{\delta (t)-\delta _0 }{\delta _{\max } -\delta _0 }} \right] ^{s} \end{aligned}$$

(6)

where $F_\mathrm{max}$ and $\delta _\mathrm{max}$ are the maximum contact force and indentation. The local indentation $\delta _{0}$ equals to zero when $\delta _\mathrm{max}$ remains below a critical indentation during the loading phase [31]. It shows that exponent $s = 2.5$ provides a good fit to the experimental data [32].

2.2 Nonlinear dynamics

A two-dimensional coordinate system (X, Z) is used, in which X is in the length direction of the beam and Z is in the direction of the downward normal to the middle surface, as shown in Fig. 1. Let $\overline{{W}}$ be the deflection of the beam and $\overline{{\varPsi }}_x$ be the mid-plane rotation of the normal about the Y axis. The beam rests on a two-parameter elastic foundation. The foundation is assumed to be bonded well with the beam in the large deflection region and the load–displacement relationship of the foundation can be expressed by $p=\overline{{K}}_1 \overline{{W}}-\overline{{K}}_2 ({d^{2}\overline{{W}}}/{{d}X^{2}})$, where p is the force per unit area, $\overline{{K}}_1$ and $\overline{{K}}_2$ are, respectively, the Winkler foundation stiffness and the shearing layer stiffness of the foundation. The damping force $F_\mathrm{c}$ is assumed to be constituted by two parts [33], which are proportional to the speeds of lateral vibration and the bending slope separately, that is

$$\begin{aligned} F_\mathrm{c} =C_w \frac{\partial \overline{{W}}}{\partial \overline{{t}}}+C_\psi \frac{\partial \overline{{\varPsi }}_x }{\partial \overline{{t}}} \end{aligned}$$

(7)

in which $C_{w}$ and $C_{\psi }$ are damping coefficients per unit length corresponding to lateral and rotational speed, respectively. Based on a higher-order shear deformation beam theory and von-Kármán-type nonlinear strain–displacement relationships, the governing equations of a shear deformable laminated beam, which includes the beam–foundation interaction and thermal effect, can be expressed by

$$\begin{aligned}&s_{11} \frac{\partial ^{4}\overline{{W}}}{\partial X^{4}}+s_{12} \frac{\partial ^{3}\overline{{{\varPsi } }}_x }{\partial X^{3}}+\frac{\overline{{B}}_{11} }{\overline{{A}}_{11} }\frac{\partial ^{2}\overline{{N}}^{T}}{\partial X^{2}}+\frac{\partial ^{2}\overline{{M}}^{T}}{\partial X^{2}} \nonumber \\&\qquad +\,\overline{{N}}_x \frac{\partial ^{2}\overline{{W}}}{\partial X^{2}}+\left( {\overline{{K}}_1 \overline{{W}}-\overline{{K}}_2 \frac{\partial ^{2}\overline{{W}}}{\partial X^{2}}} \right) \nonumber \\&\quad =Q+I_1 \frac{\partial ^{2}\overline{{W}}}{\partial \overline{{t}}^{2}}+\hat{{I}}_5 \frac{\partial ^{3}\overline{{{\varPsi } }}_x }{\partial X\partial \overline{{t}}^{2}} \nonumber \\&\qquad -\frac{4}{3h^{2}}\hat{{I}}_7 \frac{\partial ^{4}\overline{{W}}}{\partial X^{2}\partial \overline{{t}}^{2}}-C_w \frac{\partial \overline{{W}}}{\partial \overline{t}} \end{aligned}$$

(8)

$$\begin{aligned}&s_{21} \frac{\partial ^{3}\overline{{W}}}{\partial X^{3}}+s_{22} \frac{\partial ^{2}\overline{{{\varPsi } }}_x }{\partial X^{2}}-s_{23} \left( {\overline{{{\varPsi } }}_x +\frac{\partial \overline{{W}}}{\partial X}} \right) \nonumber \\&\qquad -s_{26} \frac{\partial \overline{{N}}^{T}}{\partial X}+\frac{\partial \overline{{S}}^{T}}{\partial X} \nonumber \\&\quad =\tilde{I}_3 \frac{\partial ^{2}\overline{{{\varPsi } }}_x }{\partial \overline{{t}}^{2}}-\frac{4}{3h^{2}}\tilde{I}_5 \frac{\partial ^{3}\overline{{W}}}{\partial X\partial \overline{{t}}^{2}}-C_\psi \frac{\partial \overline{{{\varPsi } }}_x }{\partial \overline{{t}}} \end{aligned}$$

(9)

$$\begin{aligned}&\overline{{N}}_x =\frac{1}{L}\int _0^L \left[ \frac{\overline{{A}}_{11} }{2}\left( {\frac{\partial \overline{{W}}}{\partial X}} \right) ^{2}+\overline{{B}}_{11} \frac{\partial \overline{{{\varPsi } }}_x }{\partial X} \right. \nonumber \\&\qquad \left. -\frac{4}{3h^{2}}\overline{{E}}_{11} \left( {\frac{\partial \overline{{{\varPsi } }}_x }{\partial X}+\frac{\partial ^{2}\overline{{W}}}{\partial X^{2}}} \right) -\overline{{N}}^{T} \right] \mathrm{d}X \end{aligned}$$

(10)

where

$$\begin{aligned} s_{11}= & {} -\frac{4}{3h^{2}}\left( {\overline{{F}}_{11} -\frac{\overline{{B}}_{11} \overline{{E}}_{11} }{\overline{{A}}_{11} }} \right) \nonumber \\ s_{12}= & {} \overline{{D}}_{11} -\frac{4}{3h^{2}}\overline{{F}}_{11} -\frac{\overline{{B}}_{11} }{\overline{{A}}_{11} }\left( {\overline{{B}}_{11} -\frac{4}{3h^{2}}\overline{{E}}_{11} } \right) \nonumber \\ s_{21}= & {} -\frac{4}{3h^{2}}\overline{{F}}_{11} +\frac{16}{9h^{4}}\overline{{H}}_{11} \nonumber \\&+\frac{4\overline{{E}}_{11} }{3h^{2}\overline{{A}}_{11} }\left( {overline{{B}}_{11} -\frac{4}{3h^{2}}\overline{{E}}_{11} } \right) \nonumber \\ s_{22}= & {} \overline{{D}}_{11} -\frac{4}{3h^{2}}\overline{{F}}_{11} -\frac{4}{3h^{2}}\left( {\overline{{F}}_{11} -\frac{4}{3h^{2}}\overline{{H}}_{11} } \right) \nonumber \\&-\frac{1}{\overline{{A}}_{11} }\left( {\overline{{B}}_{11} -\frac{4}{3h^{2}}\overline{{E}}_{11} } \right) ^{2} \nonumber \\ s_{23}= & {} A_{55} -\frac{4}{h^{2}}D_{55} -\frac{4}{h^{2}}\left( {D_{55} -\frac{4}{h^{2}}F_{55} } \right) \nonumber \\ s_{26}= & {} \frac{\overline{{B}}_{11} }{\overline{{A}}_{11} }-\frac{4}{3h^{2}}\frac{\overline{{E}}_{11} }{\overline{{A}}_{11} } \end{aligned}$$

(11)

where $\overline{{A}}_{11}$, $\overline{{B}}_{11}$, etc., are the reduced stiffnesses of beam and they can be expressed by

$$\begin{aligned}&(\overline{{A}}_{11} ,\overline{{B}}_{11} ,\overline{{D}}_{11} ,\overline{{E}}_{11} ,\overline{{F}}_{11} ,\overline{{H}}_{11} ) \nonumber \\&\quad =b\sum _{k=1}^N {\int \limits _{h_{k-1} }^{h_k } {(\widetilde{Q}_{11} )_k (1,Z,Z^{2},Z^{3},Z^{4},Z^{6})\mathrm{d}Z} } \end{aligned}$$

(12)

$$\begin{aligned}&(\overline{{A}}_{55} ,\overline{{B}}_{55} ,\overline{{D}}_{55} ) \nonumber \\&\quad =b\sum _{k=1}^N {\int \limits _{h_{k-1} }^{h_k } {(\widetilde{Q}_{55} )_k (1,Z,Z^{2})\mathrm{d}Z} } \end{aligned}$$

(13)

in which $\widetilde{Q}_{11}$ and $\widetilde{Q}_{55}$ are the refined transformed elastic constants, defined by [34, 35]

$$\begin{aligned}&\widetilde{Q}_{11} =\overline{{Q}}_{11} \nonumber \\&\quad +\frac{(\overline{{Q}}_{16})^{2}\overline{{Q}}_{22} -2\overline{{Q}}_{12} \overline{{Q}}_{16} \overline{{Q}}_{26} +(\overline{{Q}}_{12} )^{2}\overline{{Q}}_{66} }{(\overline{{Q}}_{26} )^{2}-\overline{{Q}}_{22} \overline{{Q}}_{66} } \end{aligned}$$

(14)

$$\begin{aligned}&\widetilde{Q}_{55} =\overline{{Q}}_{55} -\frac{(\overline{{Q}}_{45} )^{2}}{\overline{{Q}}_{44} } \end{aligned}$$

(15)

In Eqs. (12) and (13), subscript $k\, (1\le k\le N)$ denotes the $k\hbox {th}$ ply in the laminate. In such a way, $h_{k}$ is the value of top surface of the $k\hbox {th}$ ply while $h_{0}$ is the value of bottom surface of the beam. The degraded stiffnesses $\overline{{Q}}_{ij}$ affected by matrix cracks will be detailed discussed in the next Section. In Eqs. (8) and (9), the inertias $I_{i}\, (i = 1,2,3,4,5,7)$ are defined by

$$\begin{aligned}&(I_1 ,I_2 ,I_3 ,I_4 ,I_5 ,I_7 ) \nonumber \\&\quad =b\sum _{k=1}^N {\int \limits _{h_{k-1} }^{h_k } {\rho _k (1,Z,Z^{2},Z^{3},Z^{4},Z^{6})\mathrm{d}Z} } \end{aligned}$$

(16)

where $\rho _{k}$ is the mass density of the $k\hbox {th}$ ply, and

$$\begin{aligned} \overline{{I}}_2= & {} I_2 -\frac{4}{3h^{2}}I_4 , \overline{{I}}_3 =I_3 -\frac{8}{3h^{2}}I_5 +\frac{16}{9h^{4}}I_7 , \nonumber \\ \tilde{I}_3= & {} \overline{{I}}_3 -\frac{\overline{{I}}_2 \overline{{I}}_2 }{I_1 }, \nonumber \\ \overline{{I}}_5= & {} I_5 -\frac{4}{3h^{2}}I_7 , \nonumber \\ \tilde{I}_5= & {} \overline{{I}}_5 -\frac{\overline{{I}}_2 I_4}{I_1 }, \nonumber \\ \hat{{I}}_5= & {} \tilde{I}_3 -\frac{4}{3h^{2}}\tilde{I}_5 , \tilde{I}_7 =I_7 -\frac{I_4 I_4 }{I_1 }, \hat{{I}}_7 \nonumber \\= & {} \tilde{I}_5 -\frac{4}{3h^{2}}\tilde{I}_7 \end{aligned}$$

(17)

In Eqs. (8)–(10), $\overline{{N}}^{T}$, $\overline{{M}}^{T}$and $\overline{{P}}^{T}$are force, moment and higher-order moment caused by temperature rise and defined by

$$\begin{aligned}&(\overline{{N}}^{T},\overline{{M}}^{T},\overline{{P}}^{T}) \nonumber \\&\quad =\sum _{k=1}^N{\int \limits _{h_{k-1} }^{h_k } {(A_x )_k (1,Z,Z^{3})} } \Delta TdZ \end{aligned}$$

(18)

$$\begin{aligned}&\overline{{S}}^{T}=\overline{{M}}^{T}-\frac{4}{3h^{2}}\overline{{P}}^{T} \end{aligned}$$

(19)

where $\Delta T=T-T_{0}$ is the temperature rise from the reference temperature $T_{0}$ at which there are no thermal strains and

$$\begin{aligned} A_x= & {} \overline{{Q}}_{11} (c^{2}\alpha _{11} +s^{2}\alpha _{22} )+\overline{{Q}}_{12} (s^{2}\alpha _{11} +c^{2}\alpha _{22} ) \nonumber \\&+2cs\overline{{Q}}_{16} (\alpha _{11} -\alpha _{22} ) \end{aligned}$$

(20)

in which, c and s denote cos $\theta$ and sin $\theta$, respectively, where $\theta$ is the lamination angle with respect to the X-axis. $\alpha _{11}$ and $\alpha _{22}$ are thermal expansion coefficients of a single layer in X and Y directions, respectively.

In the analysis, the longitudinal vibration of impactor can be neglected. Hence, the equation of motion of the impactor and the corresponding initial conditions can be written as

$$\begin{aligned} m^{i}\ddot{\overline{{W}}}^{i}(t)+F_c (t)=0, \overline{{W}}^{i}(0)=0, \dot{\overline{{W}}}^{i}(0)=\overline{{V}}_0 \end{aligned}$$

(21)

3 Micromechanical models

It is assumed that for both CFRC and CNTRC the matrix is the same. In microscale, the only difference for two materials is the reinforcement. From [5] and [36], the properties of CFRC and CNTRC can be gotten together and written as

$$\begin{aligned}&E_{11} =\eta _1 V_r E_{11}^r +V_m E^{m}, \nonumber \\&\frac{\eta _2 }{E_{22}}=\frac{V_r }{E_{22}^r }+\frac{V_m }{E^{m}} \nonumber \\&\quad -\,\eta _4 V_r V_m \frac{{V_r^2 E^{m}}/{E_{22}^r }+{V_m^2 E_{22}^r}/{E^{m}}-2v_r v_m }{V_r E_{22}^r +V_m E^{m}}, \nonumber \\&\frac{\eta _3 }{G_{12} }=\frac{V_r }{G_{12}^r }+\frac{V_m }{G^{m}}, \nonumber \\&\nu _{12} =V_r \nu _{\hbox {12}}^r +V_m \nu ^{m}, \end{aligned}$$

(22)

where $E_{11}$, $E_{22}$, $G_{12}$ and $\nu _{12}$ are elastic modulus, shear modulus and Poisson’s ratio, respectively. The superscript or subscript r denotes reinforcement, while m denotes matrix. V is the volume fraction of component (reinforcement or matrix) in materials, and the relationship $V_{r}+V_{m} =1$ is satisfied. It is worth noting that efficiency parameters $\eta _{i}\, (i=1, 2, 3, 4)$ depend on the type of material. For CFRC, $\eta _{1} = \eta _{2} = \eta _{3} = \eta _{4} = 1$; while for CNTRC, $\eta _{4} = 0$ and the values of $\eta _{1},\, \eta _{2}$ and $\eta _{3}$ will be detailed given in Sect. 5.

Usually, fibers are uniformly distributed in the thickness direction in CFRC and the volume fraction of fiber is independent on the value of Z, consequently. However, the condition is different for CNTs, which can be functionally graded distributed in the thickness direction. Hence, the CNT volume fraction is the function of Z. In the present study, two regular types of FG-CNTRC, i.e., FG-V and FG-$\Lambda$, are employed for a single layer. The volume fractions corresponding to those four types can be expressed as

$$\begin{aligned} V_\mathrm{CN}= & {} 2\left( {\frac{Z-t_0 }{t_1 -t_0 }} \right) V_\mathrm{CN}^{*} \qquad \qquad (\hbox {FG-V}) \end{aligned}$$

(23a)

$$\begin{aligned} V_\mathrm{CN}= & {} 2\left( {\frac{t_1 -Z}{t_1 -t_0 }} \right) V_\mathrm{CN}^{*} \qquad \qquad (\hbox {FG}-\Lambda ) \end{aligned}$$

(23b)

where the subscript CN denotes CNT. $\hbox {Z}=t_{1}$ and $Z=t_{0}$ are, respectively, the top surface and bottom surface of a CNTRC ply, and $V_\mathrm{CN}^*$ depends on the mass densities of CNTs and matrix, and can be written as

$$\begin{aligned} V_\mathrm{CN}^*=\frac{w_\mathrm{CN} }{w_\mathrm{CN} +\left( {{\rho ^{CN}}/{\rho ^{m}}} \right) -\left( {{\rho ^{CN}}/{\rho ^{m}}} \right) w_\mathrm{CN} } \end{aligned}$$

(24)

where $w_\mathrm{CN}$ is the mass fraction of CNTs. It is worth noting that for uniformly distributed CNTRC ply $V_\mathrm{CN} =\;V_\mathrm{CN}^*$.

The overall elastic moduli of the composite may change if matrix cracks arise. According to [37], the self-consistent estimates for the overall compliance matrices S of matrix-cracked composite can be expressed by

$$\begin{aligned} \mathbf{S}=\mathbf{S}_0 +\overline{{\rho }}_{crk} \varvec{\Lambda } \end{aligned}$$

(25)

where the subscript 0 denotes intact composite and the damage parameter $\overline{{\rho }}_{crk}$ can be written as

$$\begin{aligned} \overline{{\rho }}_{crk} =\frac{1}{4}\pi \rho _{crk} \end{aligned}$$

(26)

in which the detailed expression of the crack density parameter $\rho _{crk}$ is defined as [38]

$$\begin{aligned} \rho _{crk} =4\eta l^{2} \end{aligned}$$

(27)

where $\eta$ is the number of cracks per unite area and l is the half length of two adjacent cracks. It must be emphasized that the surface layer containing cracks may be regarded as half of a layer of the thickness. This means the crack density of a surface layer is twice as much as that of interior layer with the same angle-ply. The coordinate system presented in Fig. 1 is different from that used in [37], in which the fiber is aligned in the Z-direction, whereas in the present work the fiber is aligned in the X-direction. Accordingly, the $6\times 6$ matrix $\varvec{\Lambda }$ can be derived under present coordinate system. However, only three nonzero components can be obtained, and for the sake of convenience, they are expressed in terms of compliances $S_{ij}$ of effective medium as

$$\begin{aligned} \Lambda _{22}= & {} \frac{S_{11} S_{22} -S_{12}^2 }{S_{11} }\left( \sqrt{\alpha _1 }+\sqrt{\alpha _2 }\right) \end{aligned}$$

(28a)

$$\begin{aligned} \Lambda _{44}= & {} \frac{\sqrt{\left( S_{11} S_{22} -S_{12}^2 \right) \left( S_{11} S_{33} -S_{13}^2 \right) }}{S_{11}} \nonumber \\&\left( \sqrt{\alpha _1 }+\sqrt{\alpha _2 }\right) \end{aligned}$$

(28b)

$$\begin{aligned} \Lambda _{66}= & {} \sqrt{S_{55} S_{66} } \end{aligned}$$

(28c)

where $\alpha _{1}$ and $\alpha _{2}$ are roots of

$$\begin{aligned}&(S_{11} S_{22} -S_{12}^2 )\alpha ^{2}-[S_{11} S_{44} +2(S_{11} S_{23} -S_{12} S_{13} )]\alpha \nonumber \\&\quad +\,S_{11} S_{33} -S_{13}^2 =0 \end{aligned}$$

(29)

These results imply that only three compliance coefficients $S_{22}$, $S_{44}$ and $S_{66}$ are affected by the cracks. $S_{66}$ can be obtained directly from Eqs. (25) and (28c), while Eq. (29) can be solved by Newton–Raphson method as reported in [38]. The remaining unknowns $S_{22}$ and $S_{44}$ are then solved from Eqs. (28a) and (28b). Based on the laminated plate theory, the reduced compliance matrix $\overline{{\varvec{S}}}$ can be expressed as

$$\begin{aligned} \left[ {{\begin{array}{l} {\overline{{S}}_{11}} \\ {\overline{{S}}_{12}} \\ {\overline{{S}}_{22}} \\ {\overline{{S}}_{16}} \\ {\overline{{S}}_{26}} \\ {\overline{{S}}_{66}} \\ \end{array} }} \right]= & {} \left[ {{\begin{array}{cccc} {c^{4}}&{} {2s^{2}c^{2}}&{} {s^{4}}&{} {s^{2}c^{2}} \\ {s^{2}c^{2}}&{} {1-2s^{2}c^{2}}&{} {s^{2}c^{2}}&{} {-s^{2}c^{2}} \\ {s^{4}}&{} {2s^{2}c^{2}}&{} {c^{4}}&{} {s^{2}c^{2}} \\ {2sc^{3}}&{} {2sc(s^{2}-c^{2})}&{} {-2s^{3}c}&{} {sc(s^{2}-c^{2})} \\ {2s^{3}c}&{} {2sc(c^{2}-s^{2})}&{} {-2sc^{3}}&{} {sc(c^{2}-s^{2})} \\ {4s^{2}c^{2}}&{} {-8s^{2}c^{2}}&{} {4s^{2}c^{2}}&{} {1-4s^{2}c^{2}} \\ \end{array}}} \right] \nonumber \\&\left[ {{\begin{array}{l} {S_{11} } \\ {S_{12} } \\ {S_{22} } \\ {S_{66} } \\ \end{array} }} \right] \end{aligned}$$

(30)

The relationships between stiffness coefficients $Q_{ij}$ and compliance coefficients $S_{ij}$ are

$$\begin{aligned} Q_{11}= & {} \frac{S_{22} }{S_{11} S_{22} -S_{12}^2 }, \nonumber \\ Q_{12}= & {} -\frac{S_{12} }{S_{11} S_{22} -S_{12}^2 }, \nonumber \\ Q_{22}= & {} \frac{S_{11} }{S_{11} S_{22} -S_{12}^2 }, \nonumber \\ Q_{44}= & {} \frac{1}{S_{44} }, Q_{55} =\frac{1}{S_{55} }, Q_{66} =\frac{1}{S_{66} } \end{aligned}$$

(31)

4 Solution method

It has been reported that nonlinear problems can be solved by numerous methods [9, 11, 13, 15,16,17,18,19,20,21,22,23,24, 28, 39,40,41,42]. A two-step perturbation technique [28] is selected herein to solve the governing equations obtained in Sect. 2. For the sake of convenience, the following dimensionless parameters are introduced

$$\begin{aligned}&x=\pi \frac{X}{L}, W=\frac{\overline{{W}}}{L}, {\varPsi } _x =\frac{\overline{{{\varPsi } }}_x }{\pi }, N_x =\frac{L^{2}\overline{{N}}_x }{\pi ^{2}\overline{{D}}_{11} }, \\&(M_x ,P_x )=\frac{L^{2}}{\pi ^{2}h\overline{{D}}_{11} }\left( {\overline{{M}}_x ,\frac{4}{3h^{2}}\overline{{P}}_x } \right) , \\&(K_1 ,k_1 )=\overline{{K}}_1 \left( {\frac{L^{4}}{\pi ^{4}\overline{{D}}_{11} },\frac{L^{4}}{E_0 I}} \right) , \\&(K_2 ,k_2 )=\overline{{K}}_2 \left( {\frac{L^{2}}{\pi ^{2}\overline{{D}}_{11} },\frac{L^{2}}{E_0 I}} \right) \\&c_w =\frac{C_w bL^{3}}{\pi ^{3}\overline{{D}}_{11} }\sqrt{\frac{E_0 }{\rho _0 }}, c_\psi =\frac{C_\psi bL}{\pi \overline{{D}}_{11} }\sqrt{\frac{E_0 }{\rho _0 }} \\&(\gamma _{11} ,\gamma _{12} ,\gamma _{21} ,\gamma _{22} ) =\frac{1}{\overline{{D}}_{11} }(-s_{11} ,s_{12} ,-s_{21} ,s_{22} ), \\&\gamma _{23} =\frac{L^{2}}{\pi ^{2}\overline{{D}}_{11} }s_{23} , \gamma _{13} =\frac{L^{2}\overline{{A}}_{11} }{\pi ^{2}\overline{{D}}_{11} }, \\&(\gamma _{14} ,\gamma _{15} )=\frac{L}{\pi ^{2}\overline{{D}}{ }_{11}} \left( \overline{{B}}_{11} -\frac{4}{3h^{2}}\overline{{E}}_{11},\frac{4}{3h^{2}}\overline{{E}}_{11} \right) , \end{aligned}$$

$$\begin{aligned}&(\gamma _{16} ,\gamma _{26} )=\frac{1}{\overline{{A}}_{11} L}\left( {\overline{{B}}_{11} ,\overline{{B}}_{11} -\frac{4}{3h^{2}}\overline{{E}}_{11} } \right) , \nonumber \\&\gamma _{17} =-\frac{bI_1 E_0 L^{2}}{\pi ^{2}\rho _0 \overline{{D}}_{11} }, \nonumber \\&V_0 =\frac{\overline{{V}}_0 }{\pi }\sqrt{\frac{\rho _0 }{E_0 }}, \nonumber \\&(\gamma _{18} ,\gamma _{19} ,\gamma _{28} ,\gamma _{29} ) \nonumber \\&\quad =-\left( \hat{{I}}_5 ,-\frac{4}{3h^{2}}\hat{{I}}_7 ,\tilde{I}_3 ,-\frac{4}{3h^{2}}\tilde{I}_5 \right) \frac{E_0 }{\rho _0 \overline{{D}}_{11}}, \nonumber \\&t=\frac{\pi \overline{{t}}}{L}\sqrt{\frac{E_0 }{\rho _0 }}, \nonumber \\&\omega _L =\Omega _L \frac{L}{\pi }\sqrt{\frac{\rho _0 }{E_0 }}, \nonumber \\&\gamma _{T1} \Delta T=\frac{L^{2}A_x^T \Delta T}{\pi ^{2}\overline{{D}}_{11} }, \nonumber \\&(\gamma _{T3} ,\gamma _{T6} )\Delta T =\frac{L^{2}\Delta T}{\pi ^{2}h\overline{{D}}_{11} }\left( {D_x^T ,\frac{4}{3h^{2}}F_x^T } \right) , \nonumber \\&\lambda _q =\frac{F_c bL}{\pi ^{2}\overline{{D}}_{11} } \end{aligned}$$

(32)

in which $\rho _0$ and $E_{0}$ are herein the reference values of $\rho ^{m}$ and $E^{m}$ at the room temperature ($T_{0}=300\hbox { K}$).

By employing Eqs. (32), (8) and (9) may then be rewritten in the following dimensionless form

$$\begin{aligned}&\gamma _{11} \frac{\partial ^{4}W}{\partial x^{4}}-\gamma _{12} \frac{\partial ^{3}{\varPsi } _x }{\partial x^{3}} \nonumber \\&\qquad -\,\pi \left\{ {\int \limits _0^\pi {\left[ {\frac{\gamma _{13} }{2}\left( {\frac{\partial W}{\partial x}} \right) ^{2}+\gamma _{14} \frac{\partial {\varPsi } _x }{\partial x}-\gamma _{15} \frac{\partial ^{2}W}{\partial x^{2}}} \right] } \mathrm{d}x} \right\} \nonumber \\&\qquad \frac{\partial ^{2}W}{\partial x^{2}} +\gamma _{T1} \Delta T\frac{\partial ^{2}W}{\partial x^{2}}-\gamma _{16} \frac{\partial ^{2}N^{T}}{\partial x^{2}} \nonumber \\&\qquad -\,\gamma _{T3} \Delta T\frac{\partial ^{2}M^{T}}{\partial x^{2}} \nonumber \\&\qquad +\left( {K_1 W-K_2 \frac{\partial ^{2}W}{\partial x^{2}}} \right) \nonumber \\&\quad =\lambda _q -c_w \frac{\partial W}{\partial t}+\gamma _{17} \frac{\partial ^{2}W}{\partial t^{2}}+\gamma _{18} \frac{\partial ^{3}{\varPsi } _x }{\partial x\partial t^{2}} \nonumber \\&\qquad +\,\gamma _{19} \frac{\partial ^{4}W}{\partial x^{2}\partial t^{2}} \end{aligned}$$

(33)

$$\begin{aligned}&\gamma _{21} \frac{\partial ^{3}W}{\partial x^{3}}-\gamma _{22} \frac{\partial ^{2}{\varPsi } _x }{\partial x^{2}}+\gamma _{23} \left( {{\varPsi } _x +\frac{\partial W}{\partial x}} \right) \nonumber \\&\qquad -\,\gamma _{26} \frac{\partial N^{T}}{\partial x}-(\gamma _{T3} -\gamma _{T6} )\Delta T\frac{\partial ^{2}M^{T}}{\partial x^{2}} \nonumber \\&\quad =\,\gamma _{28} \frac{\partial ^{2}{\varPsi } _x }{\partial t^{2}}-c_\psi \frac{\partial {\varPsi } _x }{\partial t}+\gamma _{29} \frac{\partial ^{3}W}{\partial x\partial t^{2}} \end{aligned}$$

(34)

Since two ends of the beam ($x = 0,\, \pi$) are simply supported, the initial conditions may be written as

$$\begin{aligned} \left. W \right| _{t=0} =\left. {\frac{\partial W}{\partial \tau }} \right| _{t=0} =0, \left. {M_x } \right| _{t=0} =\left. {\frac{\partial M_x }{\partial \tau }} \right| _{t=0} =0\nonumber \\ \end{aligned}$$

(35)

The solutions of Eqs. (33) and (34) can be assumed and expanded by a two-step perturbation technique

$$\begin{aligned} W(x,t)= & {} W^{{*}}(x)+\widetilde{W}(x,t) \end{aligned}$$

(36a)

$$\begin{aligned} {\varPsi }_x (x,t)= & {} {\varPsi } _x^{*} (x)+\widetilde{{\varPsi }}_x (x,t) \end{aligned}$$

(36b)

in which $\widetilde{W}(x,t)$ is an additional deflection and $W^{*}(x)$ is an initial deflection due to initial thermal bending moment. $\widetilde{{\varPsi }}_x (x,t)$ and ${\varPsi }_x^{*} (x)$ are the mid-plane rotations corresponding to $\widetilde{W}(x,t)$ and $W^{*}(x)$, respectively. Note that $W^{*}(x)={\varPsi } _x^{*} (x) = 0$ at room temperature. In such a case, Eqs. (33) and (34) can be rewritten as

$$\begin{aligned}&\gamma _{11} \frac{\partial ^{4}\widetilde{W}}{\partial x^{4}}-\gamma _{12} \frac{\partial ^{3}\widetilde{{\varPsi } }_x }{\partial x^{3}} -\pi \left\{ \int \limits _0^\pi \left[ \frac{\gamma _{13} }{2}\left( {\frac{\partial \widetilde{W}}{\partial x}} \right) ^{2} \right. \right. \nonumber \\&\qquad \left. \left. +\gamma _{14} \frac{\partial \widetilde{{\varPsi } }_x }{\partial x}-\gamma _{15} \frac{\partial ^{2}\widetilde{W}}{\partial x^{2}} \right] \mathrm{d}x \right\} \left( \frac{\partial ^{2}\widetilde{W}}{\partial x^{2}}+\frac{\partial ^{2}W^{{*}}}{\partial x^{2}} \right) \nonumber \\&\quad -\pi \left\{ \int \limits _0^\pi \left[ \frac{\gamma _{13} }{2}\left( {2\frac{\partial \widetilde{W}}{\partial x}\frac{\partial W^{{*}}}{\partial x}+\left( {\frac{\partial W^{{*}}}{\partial x}} \right) ^{2}} \right) \right. \right. \nonumber \\&\quad \left. \left. +\gamma _{14} \frac{\partial {\varPsi } _x^{*} }{\partial x}-\gamma _{15} \frac{\partial ^{2}W^{{*}}}{\partial x^{2}} \right] \mathrm{d}x \right\} \frac{\partial ^{2}\widetilde{W}}{\partial x^{2}} \nonumber \\&\quad =\lambda _q -\left( {K_1 \widetilde{W}-K_2 \frac{\partial ^{2}\widetilde{W}}{\partial x^{2}}} \right) -\varepsilon \left( {c_w \frac{\partial \widetilde{W}}{\partial \tau }} \right) \nonumber \\&\quad +\varepsilon ^{2}\left( {\gamma _{17} \frac{\partial ^{2}\widetilde{W}}{\partial \tau ^{2}}+\gamma _{18} \frac{\partial ^{3}\widetilde{{\varPsi } }_x }{\partial x\partial \tau ^{2}}+\gamma _{19} \frac{\partial ^{4}\widetilde{W}}{\partial x^{2}\partial \tau ^{2}}} \right) \end{aligned}$$

(37)

$$\begin{aligned}&\gamma _{21} \frac{\partial ^{3}\widetilde{W}}{\partial x^{3}}-\gamma _{22} \frac{\partial ^{2}\widetilde{{\varPsi } }_x }{\partial x^{2}}+\gamma _{23} \left( {\widetilde{{\varPsi } }_x +\frac{\partial \widetilde{W}}{\partial x}} \right) \nonumber \\&\quad =-\varepsilon \left( {c_\psi \frac{\partial \widetilde{{\varPsi } }_x }{\partial \tau }} \right) \nonumber \\&\quad +\varepsilon ^{2}\left( {\gamma _{28} \frac{\partial ^{2}\widetilde{{\varPsi }}_x }{\partial \tau ^{2}}+\gamma _{29} \frac{\partial ^{3}\widetilde{W}}{\partial X\partial \tau ^{2}}} \right) \end{aligned}$$

(38)

Using a two-step perturbation technique, the solutions can be written in the following forms

$$\begin{aligned}&\widetilde{W}\left( {x,\tau ,\varepsilon } \right) =\sum _{j=1} {\varepsilon ^{j}w_j \left( {x,\tau } \right) } , \nonumber \\&\quad \widetilde{{\varPsi } }_x \left( {x,\tau ,\varepsilon } \right) =\sum _{j=1} {\varepsilon ^{j}\psi _{xj} \left( {x,\tau } \right) } , \nonumber \\&\quad \lambda _q \left( {x,\tau ,\varepsilon } \right) =\sum _{j=1} {\varepsilon ^{j}\lambda _j \left( {x,\tau } \right) } \end{aligned}$$

(39)

Table 1 Temperature-dependent material properties for (10, 10) SWCNT [44]

where $\varepsilon$ is a small perturbation parameter without any physical meaning and $\tau = \varepsilon t$ is introduced to improve perturbation procedure for solving nonlinear vibration problem. Using Eqs. (37)–(39), a set of perturbation equations for the different order of $\varepsilon$ can be obtained and solved order by order. We obtain the asymptotic solutions

$$\begin{aligned}&W=\varepsilon A_{10}^{(1)} \sin mx+O\left( {\varepsilon ^{4}} \right) \end{aligned}$$

(40a)

$$\begin{aligned}&{\varPsi } _x =\varepsilon B_{10}^{(1)} \cos mx+\varepsilon ^{2}B_{10}^{(2)} \cos mx \nonumber \\&\quad \qquad +\,\varepsilon ^{3}B_{10}^{(3)} \cos mx+O(\varepsilon ^{4}) \end{aligned}$$

(40b)

$$\begin{aligned}&\lambda _q =\left[ g_{30} \varepsilon \ddot{A}_{10}^{(1)} +g_{31} \varepsilon A_{10}^{(1)} \right] \sin mx \nonumber \\&\quad \qquad +\left[ \left( {\varepsilon A_{10}^{(1)} } \right) ^{2}g_{321} \!+\!\left( {\varepsilon A_{10}^{(1)} } \right) \left( {\varepsilon A_{10}^{*}} \right) g_{322} \right] \sin mx \nonumber \\&\quad \qquad +\left[ \left( {\varepsilon A_{10}^{(1)} } \right) ^{3}g_{331} +\left( {\varepsilon A_{10}^{(1)} } \right) ^{2}\varepsilon A_{10}^{*} g_{332} \right] \nonumber \\&\quad \qquad \sin mx+O(\varepsilon ^{4}) \end{aligned}$$

(40c)

We take $x=\pi /2$, which is the impact point. The second perturbation parameter $\left( {\varepsilon A_{10}^{(1)} } \right)$ in Eq. (40c) can be replaced by the maximum dimensionless deflection of the beam $W_{m}$ through Eq. (40a). Applying Galerkin process, Eq. (41) can be rewritten as

$$\begin{aligned}&g_{30} \frac{d^{2}\left( {W_m } \right) }{d\tau ^{2}}+g_c \frac{d\left( {W_m } \right) }{d\tau } +g_{31} \left( {W_m } \right) +g_{32} \left( {W_m } \right) ^{2} \nonumber \\&\quad +\,g_{33} \left( {W_m } \right) ^{3}=g_q (W^{i}-W_m )^{\frac{3}{2}} \end{aligned}$$

(41)

After the process of non-dimension, Eq. (21) can be rewritten as

$$\begin{aligned} \ddot{W}^{i}=g_i (W^{i}-W_m )^{3/2} \end{aligned}$$

(42)

A forth-order Runge–Kutta numerical method is appropriate to solve Eqs (41) and (42). All symbols used in Eqs. (41) and (42) will be detailed described in “Appendix.”

Table 2 Linear frequencies and nonlinear to linear frequency ratios comparison for laminated beams with both ends simply supported

5 Numerical studies and discussion

In this section, the numerical results of low-velocity impact on hybrid beams with various parameters are presented. The beam with $b=h = 1\hbox { mm}$ and $L = 30\hbox { mm}$ is simply supported. As is mentioned before, the CFRC and CNTRC have the same matrix material, whose mechanical properties are assumed to be $\nu ^{m} = 0.34$, $\alpha ^{m} = 45(1+0.0005\Delta T)\times 10^{-6}\hbox { K}^{-1}$, $E^{m} = (3.52-0.0034T)$ GPa and $\rho ^{m} = 1150 \hbox { kg}/\hbox {m}^{3}$. For CFRC, the volume fraction of carbon fiber is fixed at 0.6 and the detailed material properties of the fiber are [43]: $E_{11}^f = 233.05\hbox { GPa}$, $E_{22}^f = 23.1\hbox { GPa}$, $G_{12}^f = 8.96\hbox { GPa}$, $\nu ^{f} = 0.2,\, \rho ^{f} = 1750 \hbox { kg}/\hbox {m}^{3}$, $\alpha _{11}^f = -0.54\times 10^{-6}\hbox {K}^{-1}$, and $\alpha _{22}^f =10.08\times 10^{-6}\hbox { K}^{-1}$. While for CNTRC, the (10, 10) single-walled carbon nanotubes (SWCNTs) are selected to be reinforcements and the temperature-dependent material properties are listed in Table 1 [44]. In computation, three volume fractions ($V_\mathrm{CN}^*=0.12, 0.17$ and 0.28) of CNTs are considered and the corresponding efficiency parameters are given by

$$\begin{aligned} V_\mathrm{CN}^*= & {} 0.12:\! \quad \eta _1 =0.137,\! \quad \eta _2 =1.022, \eta _3 = 0.715, \\ V_\mathrm{CN}^*= & {} 0.17:\! \quad \eta _1 =0.142,\! \quad \eta _2 =1.626, \eta _3 =1.138, \\ V_\mathrm{CN}^*= & {} 0.28:\! \quad \eta _1 =0.141,\! \quad \eta _2 =1.585, \eta _3 =1.109. \end{aligned}$$

In addition, we assume that out-plane shear moduli $G_{13}=G_{12}$ and $G_{23} = 1.2G_{12}$. It has been proved in our previous work [14, 15] that FG-1 grading profile could significantly improve the mechanical properties of beams or plates. Hence, we only take FG-1 into account. For FG-1, the FG-V CNTRC layers are used above the middle plane, while below the middle plane, FG-$\Lambda$ CNTRC layers are used. It is assumed that the matrix cracks occur only in CFRC layer. Unless otherwise statement, the properties of materials constituted of the hybrid beam and assumptions mentioned above are used in the following examples.

Fig. 2

Comparisons of impact response for CNTRC beams with both ends simply supported: a contact force history and b indention

Fig. 3

Effects of different materials used in outer layers on low-velocity impact response of hybrid beams with both ends simply supported: a contact force history and b deflection of beam

Fig. 4

Effects of matrix cracks used in outer layers on low-velocity impact response of hybrid beams with both ends simply supported: a contact force history and b deflection of beam

The impactor is made from steel with the mechanical properties: $E^{i} = 207\hbox { GPa}$, $\nu ^{i} = 0.3$ and $\rho ^{i} = 7960 \hbox { kg}/\hbox {m}^{3}$. The geometry of the impactor is spherical with radius $R^{i} = 1\hbox {mm}$. Unless otherwise statement, the initial velocity of the impactor is taken to be 1m/s.

5.1 Comparison studies

Before carrying out the parametric studies, we have to test the effectiveness and accuracy of the present method. Eq. (42) can be degraded to be used to analyze the nonlinear free vibration of beam, when $g_{q}$ is taken to be zero. The comparison of both linear and nonlinear frequencies of the composite laminated beams with four layups ($[0]_{6},\, [0/90/90]_{s},\, [90/90/0]_{s}$ and $[90]_{6}$) between the results of Gunda et al. [45] and present results is shown in Table 2. The geometry of the beam is $0.25\hbox {m}\times 0.01\hbox {m}\times 0.001\hbox {m}$ and the material properties of a single layer are $E_{1} = 155\hbox { GPa}$, $E_{2} = 12.1 \hbox { GPa}$, $\nu _{12} = 0.248,\, G_{12} = 4.4\hbox { GPa}$ and $\rho = 1570\hbox { kg}/\hbox {m}^{3}$. In Table 2, Gunda et al. [45] employed two methods, Rayleigh–Ritz (R–R) and finite element method (FEM), to analyze this vibration problem. It is shown that the present results have good agreements with the both R–R and FEM results obtained by Gunda et al. [45].

Another validated example of low-velocity impact on a CNTRC beam with both ends simply supported is given. The material for impactor is the same as we used here, but the radius is 10 mm and the initial velocity is 3 m/s. The beam has square cross section with $b=h = 10\hbox { mm}$ and the ratio of length to thickness is 30. The volume fraction of CNT is taken to be 0.28 and two FG distributions of CNTRC, i.e., FG-X and FG-$\Lambda$, are considered. The curves of contact force and indention vs. time are calculated and plotted in Fig. 2. It is shown that the peak contact forces obtained from the present method are slightly lower than those of Jam and Kiani [20], and the indentions are also lower than those of Jam and Kiani [20]. The TBT is employed by Jam and Kiani [20], and the difference between the present results and the results of Jam and Kiani may be caused by the different beam theories.

Fig. 5

Effects of CNT volume fraction on low-velocity impact response of hybrid beams with both ends simply supported: a contact force history and b deflection of beam

Fig. 6

Effects of temperature variation on low-velocity impact response of hybrid beams with both ends simply supported: a contact force history and b deflection of beam

Fig. 7

Effects of initial velocity on low-velocity impact response of hybrid beams with both ends simply supported: a contact force history and b deflection of beam

Fig. 8

Effects of elastic foundation on low-velocity impact response of hybrid beams with both ends simply supported: a contact force history and b deflection of beam

Fig. 9

Damping effects on low-velocity impact response of hybrid beams with both ends simply supported: a contact force history and b deflection of beam

5.2 Parametric studies

To compare the effect of the material for the outer layers on low-velocity impact response of the hybrid beam, two stack sequences $[0^{C}/90^{F}/90^{F}/0^{C}]$ and $[0^{F}/90^{C}/90^{C}/0^{F}]$, where superscripts C and F, respectively, represent CNTRC and CFRC, are both taken into account as shown in Fig. 3. It is clearly observed that the beam with $[0^{C}/90^{F}/90^{F}/0^{C}]$, where the FG-1 distribution for CNTs is used, has the largest contact force but the lowest deflection. This is because FG-1 CNTRC layer provides the highest contact stiffness and the higher overall stiffness. When outer layers are CFRC, the influence of CNT FG distribution may be ignored. The beam with $[0^{C}/90^{F}/90^{F}/0^{C}]$ layup and FG-1 grading profile layers is only considered in the following examples, due to its best behavior.

The effect of matrix cracking on contact force and deflection of the hybrid beam is illustrated in Fig. 4. Two matrix crack densities (0.2 and 0.5) are chosen, and the CNT volume fraction is 0.12. It can be found that the presence of matrix cracks can slightly increase the deflection but has almost no effect on the contact force. It is because the transverse matrix cracks only appear in the interior FRC layers, the contact stiffness between the impactor and the beam is affected hardly, but the overall stiffness of the beam is still degraded slightly.

Figure 5 presents the effect of CNT volume fraction on low-velocity impact response of the hybrid beam. Obviously, the stiffness of CNTRC layers will be increased with higher volume fraction of CNT reinforcements. As seen from this figure, the contact force is increased with improving the CNT volume fraction. However, under the same condition, the curve of deflection of the beam declines. Figure 6 shows the effect of temperature changes on low-velocity impact response of the hybrid beam. In fact, the increase of temperature will cause the stiffness degradation of both the matrix and CNT. That means the stiffness of each layer in the beam is reduced and it can be seen from Fig. 6 that increasing the temperature may reduce both contact force and plate deflection. The effect of various initial velocities on contact force and deflection of the hybrid beam is analyzed in Fig. 7. As expected, the larger velocity may cause the greater contact force and higher curve of deflection.

Figures 8, 9 demonstrate the effect of foundation stiffness and damping on low-velocity impact response of the hybrid beam, respectively. In Fig. 8, the foundation stiffness are $(k_{1},\, k_{2})=(1000, 100)$ for the Pasternak elastic foundation, $(k_{1},\, k_{2})=(1000, 0)$ for the Winkler elastic foundation and $(k_{1},\, k_{2})=(0, 0)$ for the beam without an elastic foundation. In Fig. 9, the dimensionless damping coefficients $c_{w}$ and $c_{\psi }$ defined in Eq. (32) are determined according to [31] and the relative Rayleigh damping coefficient is taken to be 0.09 [46]. The damping coefficients are $(c_{w},\, c_{\psi })=(0.157, 0)$ for only considering the effect of lateral speed, $(c_{w},\, c_{\psi })=(0.157, 1.57)$ for considering both the effect of lateral and rotational speed and $(c_{w},\, c_{\psi })=(0,\, 0)$ for without considering damping effect. From Fig. 8a, it can be observed that the peak value of the contact force is almost invariable, due to no effect of the foundation on contact stiffness. As seen from Fig. 8b, the deflection of the beam drops with the increase of elastic foundation. The similar conclusion can be obtained from Fig. 9b, but the damping effect is tiny. Moreover, neither damping effect nor elastic foundation can affect the contact force.

6 Conclusions

The nonlinear low-velocity impact response of damped and matrix-cracked hybrid beams containing both CFRC layers and CNTRC layers is investigated in this paper. The matrix cracking is modeled by a refined SCM, and a modified Hertz model is utilized to describe the contact force between the impactor and the beam. The numerical results show the following main conclusions:

• 1. The results illustrate that the FG-1 distribution of CNTRC layers for hybrid laminated beams has a significant influence on the low-velocity impact response. Obviously, the beam possesses a lower deflection when the outer layers are CNTRC.

• 2. The peak value of deflection for the beam is increased slightly when the matrix cracking is occurred. However, the presence of matrix cracks plays little or no role on the contact force.

• 3. The effect of damping on the low-velocity impact response of the beam is the same as that of elastic foundation. The reduction of center deflection due to elastic foundation is more significant than that caused by damping.

Based on the above points, it is advised that the surface layers of the hybrid laminated beam applied in engineering is selected to be CNTRC.

Appendix

In Eqs. (41) and (42)

$$\begin{aligned} g_{30}= & {} -\gamma _{17} +m^{2}\left( {\gamma _{18} +\gamma _{19} } \right) \frac{\gamma _{21} m^{2}-\gamma _{23} }{\gamma _{22} m^{2}+\gamma _{23} } \nonumber \\&-\left( {\gamma _{29} +\gamma _{28} \frac{\gamma _{21} m^{2}-\gamma _{23} }{\gamma _{22} m^{2}+\gamma _{23} }} \right) \frac{\gamma _{12} m^{4}}{\gamma _{22} m^{2}+\gamma _{23} } \end{aligned}$$

(43)

$$\begin{aligned} g_{31}= & {} m^{4}\left[ {\gamma _{11} -\gamma _{12} \frac{\gamma _{21} m^{2}-\gamma _{23} }{\gamma _{22} m^{2}+\gamma _{23} }} \right] +(K_1 +K_2 m^{2}) \nonumber \\&+\,2m^{2}\pi \left[ {\gamma _{15} -\gamma _{14} \frac{\gamma _{21} -\gamma _{23} }{\gamma _{22} +\gamma _{23} }} \right] {\varPhi } \nonumber \\&+\,2\pi C_1 \left[ {\gamma _{15} -\gamma _{14} \frac{\gamma _{21} m^{2}-\gamma _{23} }{\gamma _{22} m^{2}+\gamma _{23} }} \right] {\varPhi } \end{aligned}$$

(44)

$$\begin{aligned} g_{32}= & {} 2m^{3}\pi \left[ {\gamma _{15} -\gamma _{14} \frac{\gamma _{21} m^{2}-\gamma _{23} }{\gamma _{22} m^{2}+\gamma _{23} }} \right] \nonumber \\&+\,\frac{3}{4}\pi ^{2}C_2 \gamma _{13} {\varPhi } \end{aligned}$$

(45)

$$\begin{aligned} g_{33}= & {} \frac{m^{4}\pi ^{2}}{4}\gamma _{13} \end{aligned}$$

(46)

$$\begin{aligned} g_c= & {} c_w +c_\psi \frac{m^{4}\gamma _{12} (\gamma _{21} m^{2}-\gamma _{23} )}{(\gamma _{22} m^{2}+\gamma _{23} )^{2}} \end{aligned}$$

(47)

$$\begin{aligned} g_q= & {} \frac{\hbox {2}k_c bL^{5/2}}{\pi ^{3}\overline{{D}}_{11} }\sin \frac{m}{2}\pi \end{aligned}$$

(48)

$$\begin{aligned} g_i= & {} -\frac{k_c \rho _0 L^{5/2}}{\pi ^{2}ME_0 } \end{aligned}$$

(49)

In Eqs. (44) and (45), $C_{1}$ and $C_{2}$ is dependent on the value of m. When m = 1, $C_{1}$ and $C_{2}$ are both equaled to be 1. In other case, $C_{1}=C_{2} = 0$.