Influence of magnetic field on generalized piezo-thermoelastic rotating medium with two relaxation times

Abstract

In the present paper, the two different theories (coupled theory and Green–Lindsay theory with two relaxation times) are applied to study the deformation of a generalized piezo-thermoelastic rotating medium under the influence of magnetic field. The normal mode analysis is used to obtain the expressions for the displacement components, the temperature, the stress, the strain components, the electric potential and the electric displacements. Numerical results for the field quantities are given in the physical domain and illustrated graphically. Comparisons are made with the results predicted by coupled and Green–Lindsay theories in the presence and absence of rotation as well as magnetic field.

1 Introduction

The brothers Curie and Curie (1880) was discovered the piezoelectricity when electric charges were created by mechanical stress on the surface of tourmaline crystals. The first application of piezoelectric materials was used as resonators for ultrasound sources in sonar devices. The better type’s piezoelectric materials such as Barium Titanate are obtained by the development of the materials. Recently, breakthrough in single crystal growth technique has led to the development of high strain and high electric breakdown piezoceramics by Tichy et al. (2010). Mindlin (1961) discussed first the theory of thermo-piezoelectricity. Nowachi (1978, 1983) investigated the physical laws for the thermo-piezo-electric materials. Chandrasekharaiah (1984, 1988) studied the generalized linear thermoelasticity theory for piezoelectric media. He et al. (2002a, b) investigated two dimensional generalized thermal shock problem of a thick piezo-electric plate of infinite extent. They deduced that the generalized thermoelasticity theory, heat propagated as a wave with finite velocity. The propagation of Rayleigh waves in transversely isotropic piezo-thermoelastic materials are investigated by Sharma et al. (2005).

Youssef and Bassiouny (2008) discussed the two temperature generalized thermo-piezoelasticity for one dimensional problem with the state-space approach. They solved the governing equations in the Laplace transform domain by using the state-space approach of the modern control theory. Othman and Ahmed (2016) studied the influence of the gravitational field on piezo-thermoelastic rotating medium with G–L theory. Qin and Yang (2008) suggested the effective properties of thermo-piezoelectricity. Said (2016) studied the influence of gravity on generalized magneto-thermoelastic medium for three-phase-lag model. Othman and Kumar (2009) and Othman (2005) suggested the generalized electro-magneto-thermoelastic wave under different theories. El-Naggar and Abd-Alla (1989) studied Rayleigh waves in magneto-thermoelastic half-space under initial stress. Othman and Abbas (2014) studied the effect of rotation on plane waves in generalized thermo-microstretch elastic solid comparison of different theories using finite element method. Sharma and Kumar (2000) investigated the plane harmonic waves in piezo-thermoelastic materials. Schoenberg and Censor (1973) studied elastic waves in rotating media. Othman and Elmaklizi (2013) studied the 2-D problem of generalized magneto-thermoelastic diffusion with the temperature dependent elastic medium. Othman (2002) investigated Lord–Shulman theory under the dependence of the modulus of elasticity on the reference temperature in two-dimensional generalized thermoelasticity. Othman et al. (2014) studied the effect of rotation on micropolar generalized thermoelasticity with two-temperature using a dual-phase-lag model. Othman et al. (2013) studied the influence of the gravity field and rotation on a generalized thermoelastic medium using a dual-phase-lag model. Othman and Abbas (2015) used the finite element method to study the effect of rotation on a magneto-thermoelastic hollow cylinder with energy dissipation using.

Piezo-thermoelastic materials take into account the coupling effect of elastic, thermal and electric fields simultaneously. These materials can be used as sensors and actuators in smart structural systems undergoing thermomechanical excitation. The usefulness of piezoelectric devices in such systems stems from the coupling that exists between the thermoelastic and electric fields. In sensor applications, thermomechanical disturbances can be determined from measurements of the induced electric potential differences (direct piezoelectric effect); in actuator applications, deformation and/or stress are controlled through the introduction of an appropriate electric field (converse piezo effect) (Ashida et al. 1994). Sensors made of these materials can be used in automatic fire control systems. In regards to aerospace applications, these structures are generally light and flexible enough to induce large deformation. In living bodies’ bones, cartilage, tendons, ligaments, and nerve tissues are pyroelectric substances. PVF2 polymer is used in hydrophones that are used at great ocean depth. Piezo-thermo-elastic or thermo-piezoelectric sensors are also used in automatic fire control system.

The present work deals with the effect of rotation and magnetic field in a generalized piezo-thermoelastic. The normal mode analysis is used to obtain the exact expressions for the considered variables. The distributions of the considered variables are presented graphically. Numerical results for the field quantities are given and illustrated graphically in the presence and absence of the magnetic field and rotation.

2 Formulation of the problem

2.1 Basic equations

The basic governing field equations of generalized hexagonal piezo-thermoelastic for two-dimensional motion in x–z plane are (2000)

2.2 Strain–displacement-relation

$$ \varepsilon_{ij} = \frac{1}{2}(u_{i,\,\,j} + u_{j,\,\,i} ) $$

(1)

• Stress–strain-temperature:

  $$ \sigma_{ij} = C_{ijkl} \varepsilon_{kl} - \,\,e_{kij} E_{k} - \beta_{ij} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)\,T\delta_{ij} , $$

  (2)

  where $i,j,k,l = 1,2,3.$

2.3 Gauss equation and electric field relation

$$ D_{i,\,\,i} = 0, $$

(3)

$$ D_{i} = \;\,e_{ijk} \varepsilon_{jk} + \in_{ij} E_{j} + p_{i} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)T, $$

(4)

where $E_{i} = - \;\varphi_{,\,\,i} .$

2.4 Heat conduction equation

$$ K_{ij} T_{,\,\,ij} = \rho \,C_{e} \left( {1 + t_{0} \frac{\partial }{\partial \,t}} \right)\dot{T} + T_{0} [\beta_{ij} \,\dot{u}_{i,\,j} - p_{i} \dot{\varphi }_{,\,\,i} ]. $$

(5)

2.5 Equation of motion

Since the medium is rotating uniformly with an angular velocity ${\varvec{\Omega}} = \varOmega \,{\mathbf{n}}$ where ${\mathbf{n}}$ is a unit vector representing the direction of the axis of the rotation, the equation of motion in the rotating frame of reference has two additional terms (Schoenberg and Censor 1973): centripetal acceleration ${\varvec{\Omega}} \wedge \text{(}{\varvec{\Omega}} \wedge {\mathbf{u}}\text{)}$ due to time-varying motion only and Corioli’s acceleration $2\,{\varvec{\Omega}} \wedge {\dot{\mathbf{u}}}\text{, }$ then the equation of motion in a rotating frame of reference and with body force is

$$ \rho [\ddot{u}_{i} + \{ {\varvec{\Omega}} \wedge ({\varvec{\Omega}} \wedge {\mathbf{u}})\}_{i} + (2{\varvec{\Omega}} \wedge {\dot{\mathbf{u}}})_{i} ] = \sigma_{ij,j} + F_{i} , $$

(6)

where $F_{i}$ is the Lorentz force and is given by:

$$ F_{i} = \mu_{0} \,(\varvec{J} \times \varvec{H})_{\text{i}} . $$

(7)

The variation of the magnetic and electric fields are perfectly conducting slowly moving medium and are given by Maxwell’s equations:

$$ \text{curl }{\mathbf{h}} = {\mathbf{J}}\text{ + }\varepsilon_{\text{0}} \,{\dot{\mathbf{E}}}, $$

(8)

$$ \text{curl }{\mathbf{E}} = - \;\mu_{\text{0}} \,{\dot{\mathbf{h}}}, $$

(9)

$$ {\mathbf{E}}\text{ = } - \;\mu_{\text{0}} \;\text{(}{\dot{\mathbf{u}}}{ \times }{\mathbf{H}}\,\text{),} $$

(10)

$$ \text{div }{\mathbf{h}} = 0. $$

(11)

Expressing components of the vector ${\mathbf{J}}\text{ = (}J_{\text{1}} ,J_{\text{2}} ,J_{\text{3}} )$ in terms of the displacement by eliminating the quantities ${\mathbf{h}}$ and ${\mathbf{E}}$ from Eq. (8), thus yields

$$ J_{\text{1}} \text{ = } - h_{{\text{,z}}} \text{ + }\varepsilon_{\text{0}} \mu_{\text{0}} H_{\text{0}} \,\ddot{w}\text{,}\quad J_{\text{2}} \text{ = 0,}\quad J_{\text{3}} \text{ = }h_{{\text{,x}}} \text{ + }\varepsilon_{\text{0}} \mu_{\text{0}} H_{\text{0}} {\ddot{u}}. $$

(12)

From Eqs. (8)–(11), it can be concluded that:

$$ h\text{ = } - \,H_{\text{0}} \,e. $$

(13)

Substituting from Eq. (12) in Eq. (7), one can get

$$ \varvec{F}\text{ = (}F_{x} \text{,}F_{y} \text{,}F_{z} \text{) = }\left( {\mu_{\text{0}} \,H_{\text{0}}^{\text{2}} \,e_{{\text{,x}}} - \;\varepsilon_{\text{0}} \,\mu_{\text{0}}^{\text{2}} \,H_{\text{0}}^{\text{2}} \,\ddot{u}\text{,}\;\text{0}\,\text{,}\;\mu_{\text{0}} \,H_{\text{0}}^{\text{2}} \,e_{{\text{,z}}} - \;\varepsilon_{\text{0}} \,\mu_{\text{0}}^{\text{2}} \,H_{\text{0}}^{\text{2}} \,\ddot{w}} \right). $$

(14)

The constitutive relation and electric displacement of the hexagonal (6 mm) crystal symmetry are given by

$$ \sigma_{xx} = \,\;C_{11} \varepsilon_{xx} + \;C_{13} \varepsilon_{zz} - \;e_{31} E_{z} - \beta_{1} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)T, $$

(15)

$$ \sigma_{zz} = \;\,C_{13} \varepsilon_{xx} + \;C_{33} \varepsilon_{zz} - \;e_{33} E_{z} - \beta_{3} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)T, $$

(16)

$$ \sigma_{xz} = 2\,C_{44} \,\varepsilon_{zx} - \;e_{15} E_{x} , $$

(17)

$$ D_{\text{x}} = e_{15} (u_{,z} + w_{,x} )\, + \in_{11} E_{x} , $$

(18)

$$ D_{\text{z}} = e_{31} {\kern 1pt} u_{,x} + \,\,e_{33} w_{,z} + \,\, \in_{33} E_{z} + p_{3} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)T. $$

(19)

3 The boundary conditions:

• 1. A mechanical boundary condition

  $$ \sigma_{zz} (x,0,t) = - f_{1} (x,0,t) = - f_{1}^{*} \exp (ia(x - ct)),\quad \sigma_{xz} (x,0,t) = 0,\quad \frac{\partial \varphi }{\partial z} = 0. $$

  (20)

• 2. A thermal boundary condition that the surface of the half-space subjected to thermal shock

  $$ T(x,0,t) = f_{2} (x,0,t) = f_{2}^{*} \exp (ia(x - ct)), $$

  (21)

  where $f_{1} (x,t)$ and $f_{2} (x,t)$ are arbitrary functions of $x,t$ and $f_{1}^{*} ,$ $f_{2}^{*}$ are constant.

We consider a homogeneous, anisotropic, piezo-thermoelastic half-space of hexagonal type. The basic governing Eqs. (3)–(6) for the temperature change $T(x,z,t),$ displacement vector $\varvec{u}(x,z,t) = (u,0,w),$ and electric potential $\varphi \,(x,z,t),$ under the effect of rotation and magnetic field are given by,

$$ \begin{aligned} & C_{11} \,u_{,xx} + C_{44} \,u_{,zz} + (C_{13} + C_{44} )\,\,w_{,xz} + (e_{31} + e_{15} )\,\,\varphi_{,xz} - \beta_{1} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)T_{,x} + \mu_{0} H_{0}^{2} e_{,x} \\ & \quad - \;\varepsilon_{0} \mu_{0}^{2} H_{0}^{2} \ddot{u} = \rho \,\left( {\ddot{u} - \varOmega^{2} u + 2\varOmega \dot{w}} \right), \\ \end{aligned} $$

(22)

$$ \begin{aligned} & (C_{44} + C_{13} )\;u_{,xz} + C_{44} \,w_{,xx} + C_{33} \,w_{,zz} + e_{15} \,\varphi_{,xx} + e_{33} \,\varphi_{,zz} - \beta_{3} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)\,T_{,z} + \,\mu_{0} H_{0}^{2} e_{,z} \\ & \quad - \,\varepsilon_{0} \mu_{0}^{2} H_{0}^{2} \,\ddot{w} = \rho \,\left( {\ddot{w} - \varOmega^{2} w - 2\varOmega \dot{u}} \right), \\ \end{aligned} $$

(23)

$$ \left( {e_{15} + \,e_{31} } \right)\,u_{,xz} + \;\,e_{15} \,w_{,xx} + \,\;e_{33} \,w_{,zz} - \,\; \in_{11} \varphi_{,xx} - \,\; \in_{33} \varphi_{,zz} + p_{3} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)\,T_{,z} = 0, $$

(24)

$$ K_{1} \;T_{,xx} + K_{3} \,T_{,zz} - \rho \,C_{e} \left( {1 + t_{0} \frac{\partial }{\partial t}} \right)\;\dot{T} = T_{0} \,[\beta_{1} \;\dot{u}_{,x} + \beta_{3} \,\dot{w}_{,z} - p_{3} \,\dot{\varphi }_{,z} ]. $$

(25)

To facilitate the solution, the following non-dimensional quantities are introduced

$$ x^{\prime } = \frac{{\omega^{*} }}{{v_{p} }}x,\quad z^{\prime } = \frac{{\omega^{*} }}{{v_{p} }}z,\quad u^{\prime } = \frac{{\rho \omega^{*} v_{p} }}{{\beta_{1} T_{0} }}u,\quad w^{\prime } = \frac{{\rho \omega^{*} v_{p} }}{{\beta_{1} T_{0} }}w,\quad T^{\prime } = \frac{T}{{T_{0} }},\quad \sigma_{ij}^{\prime } = \frac{{\sigma_{ij} }}{{\beta_{1} T_{0} }},\quad \varphi^{\prime } = \varepsilon_{p} \varphi , $$

$$ \{ t^{\prime } ,t_{1}^{\prime } ,t^{\prime}_{0} \} = \omega^{*} \{ t,t_{1} ,t_{0} \} ,\quad D_{i}^{\prime } = \frac{{D_{i} }}{e},\varOmega^{\prime } = \frac{\varOmega }{{\omega^{*} }}, $$

(26)

where $\omega^{*} = \frac{{C_{e} C_{11} }}{{K_{11} }},\quad \varepsilon_{p} = \frac{{\omega^{*} e_{33} }}{{v_{p} \beta_{1} \;T_{0} }},\quad \beta_{1} = (C_{11} + C_{12} ){\kern 1pt} \alpha_{1} + C_{13} {\kern 1pt} \alpha_{3} ,\quad \beta_{3} = 2C_{13} {\kern 1pt} \alpha_{1} + C_{33} {\kern 1pt} \alpha_{3} .$

In terms of the non-dimensional quantities defined in Eq. (26), the above governing Eqs. (22)–(25) take the form (dropping the primes over the non-dimensional variables for convenience)

$$ \delta_{1} u_{,xx} + \delta_{2} \,u_{,zz} + \delta_{3} \,w_{,xz} + \delta_{4} \,\varphi_{,xz} - \,\left( {1 + t_{1} \frac{\partial }{\partial t}} \right)T_{,x} = \delta_{5} \ddot{u} - \varOmega^{2} u + 2\varOmega \dot{w}, $$

(27)

$$ \delta_{3} \,u_{,xz} + \delta_{2} \;w_{,xx} + \delta_{6} \;w_{,zz} + \delta_{7} \;\varphi_{,xx} + \varphi_{,zz} + \delta_{8} \left( {1 + t_{1} \frac{\partial }{\partial t}} \right)T_{,z} = \,\delta_{5} \ddot{w} - \varOmega^{2} w - 2\varOmega \dot{u}, $$

(28)

$$ \delta_{9} \,u_{,xz} + \delta_{10} \,w_{,xx} + \delta_{11} \,w_{,zz} + \delta_{12} \;\varphi_{,xx} + \delta_{13} \;\varphi_{,zz} + \delta_{14} \;\left( {1 + t_{1} \frac{\partial }{\partial t}} \right)T_{,z} = 0, $$

(29)

$$ \delta_{15} \,T_{,xx} + \delta_{16} \,T_{,zz} - \left( {1 + t_{0} \frac{\partial }{\partial t}} \right)\dot{T} = [\delta_{17} \,\dot{u}_{,x} + \delta_{18} \,\dot{w}_{,z} + \delta_{19} \dot{\varphi }_{,z} ], $$

(30)

where $\delta_{j} ,\quad j = 1 - 19$ are given in “Appendix A”.

4 The solution of the problem

In this section, we applied the normal mode analysis, which gives exact solutions without any assumed restrictions on the displacement, stress distributions and temperature. It is applied to a wide range of problems in different branches (Othman (2002) and Othman et al. (2013, 2014, 2015)).

The solution of the considered physical quantities can be decomposed in terms of the normal mode in the following form:

$$ [u,w,\varphi ,T](x,z,t) = [u^{*} ,w^{*} ,\varphi^{*} ,T^{*} ]\;(z)\;\exp (ia(x - ct)). $$

(31)

where $\text{D = }\frac{\text{d}}{{\text{d}\,z}},$ $c = \frac{\omega }{a},$ $\omega$ is the complex time constant (frequency), $i$ is the imaginary unit, $a$ is the wave number in the $x$ direction, $u^{*} ,\;w^{*} ,\;\varphi^{*}$ and $T^{*}$ are the amplitudes of the functions $u,\;w,\;\varphi ,\;T.$

Subsisting from Eq. (31) in Eqs. (27)–(30), we get

$$ (\text{D}^{2} + A_{1} )\,u^{*} + (A_{2} \text{D} + A_{3} )\;w^{*} + A_{4} \text{D}\,\varphi^{*} + A_{5} T^{*} = 0, $$

(32)

$$ (A_{6} \text{D} + A_{7} )\;u^{*} + (\text{D}^{2} + A_{8} )\,w^{*} + (A_{9} \text{D}^{2} + A_{10} )\,\varphi^{*} + A_{11} \text{D}T^{*} = 0, $$

(33)

$$ A_{12} \text{D}\,u^{*} + (\text{D}^{2} + A_{13} )\,w^{*} + (A_{14} \text{D}^{2} + A_{15} )\,\varphi^{*} + A_{16} \text{D}T^{*} = 0, $$

(34)

$$ A_{17} \,u^{*} + A_{18} \text{D}\,w^{*} + A_{19} \text{D}\,\varphi^{*} + (\text{D}^{2} + A_{20} )T^{*} = 0, $$

(35)

where $A_{j} ,{\kern 1pt} \;j = 1 - 20$ are given in “Appendix A”.

Equations (32)–(35) have a non-trivial solution if the determinant coefficients of the physical quantities equal to zero, then we get

$$ \text{[D}^{8} - A\,\text{D}^{6} + B\,\text{D}^{4} - C\,\text{D}^{2} + E]\{ u^{*} (z),w^{*} (z),\varphi^{*} (z),T^{*} (z)\} = 0, $$

(36)

where $A,\;B,\;C,\;E$ are given in “Appendix A”.

Equation (36) can be factored as

$$ \left( {\text{D}^{2} - k_{1}^{2} } \right)\left( {\text{D}^{2} - k_{2}^{2} } \right)\left( {\text{D}^{2} - k_{3}^{2} } \right)\left( {\text{D}^{2} - k_{4}^{2} } \right)\,{\kern 1pt} \{ u^{*} (z),w^{*} (z),\varphi^{*} (z),T^{*} (z)\} = 0. $$

(37)

The solution of Eq. (37), bound as $z \to \infty ,$ is given by

$$ u^{*} = \sum\limits_{n = 1}^{4} {M_{n} \exp ( - k_{n} z)} , $$

(38)

$$ w^{*} = \sum\limits_{n = 1}^{4} {H_{1n} M_{n} \exp ( - k_{n} z)} , $$

(39)

$$ \varphi^{*} = \sum\limits_{n = 1}^{4} {H_{2n} M_{n} \exp ( - k_{n} z)} , $$

(40)

$$ T^{*} = \sum\limits_{n = 1}^{4} {H_{3n} M_{n} \exp ( - k_{n} z)} , $$

(41)

where $k_{n}^{2} (n = 1,2,3,4)$ are the roots of the characteristic equation of Eq. (37).

By taking a non-dimension and the normal mode to Eqs. (15)–(19) then substituting from Eqs. (38)–(41), we obtain

$$ \sigma_{xx}^{*} = \sum\limits_{n = 1}^{4} {H_{4n} M_{n} \exp ( - k_{n} z)} , $$

(42)

$$ \sigma_{zz}^{*} = \sum\limits_{n = 1}^{4} {H_{5n} M_{n} \exp ( - k_{n} z)} , $$

(43)

$$ \sigma_{xz}^{*} = \sum\limits_{n = 1}^{4} {H_{6n} M_{n} \exp ( - k_{n} z)} , $$

(44)

$$ D_{x}^{*} = \sum\limits_{n = 1}^{4} {H_{7n} M_{n} \exp ( - k_{n} z)} , $$

(45)

$$ D_{z}^{*} = \sum\limits_{n = 1}^{4} {H_{8n} M_{n} \exp ( - k_{n} z)} , $$

(46)

where $H_{jn} ,\;j = 1 - 8,\;n = 1,2,3,4$ are given in “Appendix B”.

By applying the boundary conditions (20) and (21) to determine $M_{n} (n = 1,2,3,4)$, we obtain

$$ \sum\limits_{n = 1}^{4} {H_{5n} M_{n} = - \;f_{1}^{*} ,} $$

(47)

$$ \sum\limits_{n = 1}^{4} {H_{6n} M_{n} = 0,} $$

(48)

$$ \sum\limits_{n = 1}^{4} {k_{n} H_{2n} M_{n} = 0,} $$

(49)

$$ \sum\limits_{n = 1}^{4} {H_{3n} M_{n} = f_{2}^{*} .} $$

(50)

By solving the above system of Eqs. (47)–(50), of $M_{n} \left( {n = 1,\,2\,,3,4\,} \right)$ by using the inverse of matrix method as follows:

$$ \left( \begin{aligned} M_{1} \hfill \\ M_{2} \hfill \\ M_{3} \hfill \\ M_{4} \hfill \\ \end{aligned} \right){\kern 1pt} = \left( {\begin{array}{*{20}c} {H_{51} } & {H_{52} } & {H_{53} } & {H_{54} } \\ {H_{61} } & {H_{62} } & {H_{63} } & {H_{64} } \\ {k_{1} H_{21} } & {k_{2} H_{22} } & {k_{3} H_{23} } & {k_{4} H_{24} } \\ {H_{31} } & {H_{32} } & {H_{33} } & {H_{34} } \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} { - f_{1}^{*} } \\ 0 \\ 0 \\ {f_{2}^{*} } \\ \end{array} } \right). $$

(51)

5 Numerical results and discussions

For study the effect of rotation and magnetic field, we will apply the numerical results. The material chosen for the purpose of numerical calculations is taken as Cadmium Selenide (CdSe) having hexagonal symmetry (6 mm class)

$\begin{aligned} C_{11} & = 7.41 \times 10^{10} \;{\text{Nm}}^{ - 2} ,\quad C_{12} = 4.52 \times 10^{10} \;{\text{Nm}}^{ - 2} ,\quad C_{13} = 3.93 \times 10^{10} \;{\text{Nm}}^{ - 2} ,\quad C_{33} = 8.36 \times 10^{10} \;{\text{Nm}}^{ - 2} , \\ C_{44} & = 1.32 \times 10^{10} \;{\text{Nm}}^{ - 2} ,\quad T_{0} = 298\;{\text{K}},\quad \rho = 5504\;{\text{Kg}}\,{\text{m}}^{ - 3} ,\quad e_{13} = - \;0.160\;{\text{Cm}}^{ - 2} ,\quad e_{33} = 0.347\;{\text{Cm}}^{ - 2} , \\ e_{15} & = - \;0.138\;{\text{Cm}}^{ - 2} ,\quad \beta_{1} = 0.621 \times 10^{6} \;{\text{Nk}}^{ - 1} \,{\text{m}}^{ - 2} ,\quad \beta_{3} = 0.551 \times 10^{6} \;{\text{NK}}^{ - 1} \,{\text{m}}^{ - 2} ,\quad p_{3} = - \;2.94 \times 10^{ - 6} \;{\text{CK}}^{ - 1} \,{\text{m}}^{ - 2} , \\ K_{1} & = K_{3} = 9\;{\text{Wm}}^{ - 1} \,{\text{K}}^{ - 1} ,\quad \in_{11} = 8.26 \times 10^{ - 11} \;{\text{C}}^{2} \,{\text{N}}^{ - 1} \,{\text{m}}^{ - 2} ,\quad \in_{33} = 9.03 \times 10^{ - 11} \;{\text{C}}^{2} \,{\text{N}}^{ - 1} \,{\text{m}}^{ - 2} ,\quad C_{e} = 260\;{\text{J}}\,{\text{Kg}}^{ - 1} \,{\text{K}}^{ - 1} . \\ \end{aligned}$ The numerical technique, outlined above, was used for the distribution of the real part of the displacement component $u,$ the temperature $T,$ the stress components $\sigma_{zz} ,$ $\sigma_{xz}$ the electric potential $\varphi$ and the electric displacement $D_{z}$ for the problem. Here, all variables are taken in non-dimensional form. The results are shown in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12; the graph shows four curves predicted by two theories of thermoelasticity. In these figures, the solid lines represent the solution in the coupled theory (CT) and the dashed lines represent the solution derived using (G–L) theory.

Fig. 1

Horizontal displacement distribution $u$ in the absence and presence of rotation

Fig. 2

Temperature distribution $T$ in the absence and presence of rotation

Fig. 3

Distribution of stress component $\sigma_{zz}$ in the absence and presence of rotation

Fig. 4

Distribution of stress component $\sigma_{xz}$ in the absence and presence of rotation

Fig. 5

Distribution of electric potential $\phi$ in the absence and presence of rotation

Fig. 6

Distribution of electric displacement component $D_{z}$ in the absence and presence of rotation

Fig. 7

Horizontal displacement distribution $u$ in the absence and presence of magnetic field

Fig. 8

Temperature distribution $T$ in the absence and presence of magnetic field

Fig. 9

Distribution of stress component $\sigma_{zz}$ in the absence and presence of magnetic field

Fig. 10

Distribution of stress component $\sigma_{xz}$ in the absence and presence of magnetic field

Fig. 11

Distribution of electric potential $\phi$ in the absence and presence of magnetic field

Fig. 12

Distribution of electric displacement component $D_{z}$ in the absence and presence of magnetic field

Figures 1, 2, 3, 4, 5 and 6 show the comparisons between the considered variables in the absence and presence of rotation (i.e. $\varOmega = 0,0.5$) at $H_{0} = 10^{8} .$ The computations are carried out for the non-dimensional time $t = 0.1$ on the surface plane $x = 1.5,$ $f_{1}^{*} = 10,$ $f_{2}^{*} = 10.$

Figure 1 depicts that the distribution of the horizontal displacement $u,$ in the context the (CT) and (G–L) theories, always begins from negative values for $\varOmega = 0,0.5.$ It shows that the values of $u$ based on the (CT) and (G–L) theories increase then decrease and converges to zero for $\varOmega = 0,0.5.$ Figure 2 demonstrates that the distribution of the temperature $T.$ In the context of the (CT) and (G–L) theories and in the absence and presence of a rotation (i.e. $\varOmega = 0,0.5$), the distribution of $T$ are increasing to the maximum value in the range $0 \le z \le 0.2$ then decreases and converges to zero. Figure 3 shows that the distribution of the stress components $\sigma_{zz} ,$ in the context of the (CT) theory the value of $\sigma_{zz}$ decreases in the range $0 \le z \le 0.2,$ then increases in the range $0.2 \le z \le 1.5,$ for $\varOmega = 0,0.5,$ while in the context of (G–L) theory, it is observed that the value of $\sigma_{zz}$ decreases in the range $0 \le z \le 0.2,$ then increase in the range $0.2 \le z \le 1,$ then decrease and finally converges to zero for $\varOmega = 0,0.5.$ Figure 4 clarifies that the distribution of the stress component $\sigma_{xz} ,$ in the context of the (CT) and (G–L) theories, begins from zero and satisfies the boundary conditions at $z = 0.$ In the context of the two theories, the values of $\sigma_{xz}$ decreases in the range $0 \le z \le 0.3,$ then increases for $\varOmega = 0,0.5.$ It is observed that the values of the stress components $\sigma_{xz}$ at $\varOmega = 0$ are higher than those at $\varOmega = 0.5.$ Figure 5 exhibits the distribution of the electric potential $\varphi ,$ in the context of the (CT) theory for $\varOmega = 0,0.5,$ the values of $\varphi$ decreases then increases and converges to zero. However, in the context of (G–L) theory the values of $\varphi$ increases, then decrease for $\varOmega = 0,0.5.$ It is observed that the values of the electric potential $\varphi ,$ in the context of the (G–L) for $\varOmega = 0,0.5,$ are higher than the values of the electric potential $\varphi ,$ in the context of the (CT) for $\varOmega = 0,0.5.$ Figure 6 depicts that the distribution of the electric displacement $D_{z} ,$ in the context the (CT) and (G–L) theories, always begins from positive values for $\varOmega = 0,0.5.$ It shows that the values of $D_{z} ,$ based on the (CT) and (G–L) theories decrease then increase and finally converges to zero for $\varOmega = 0,0.5.$

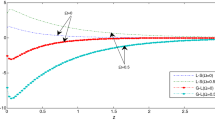
Figures 7, 8, 9, 10, 11 and 12 show the comparisons between the considered variables in the absence and presence of a magnetic field (i.e. $H_{0} = 0,10^{9}$) at $\varOmega = 0.5.$

Figure 7 shows that the distribution of the horizontal displacement $u,$ in the context of (CT) and (G–L) theories, the value of $u,$ increase in the range $0 \le z \le 0.5,$ then decreases in the range $0.5 \le z \le 3,$ for $H_{0} = 0.$ It is observed that in the case of absence of magnetic field the two curves of the (CT) and (G–L) theories are coincide, while for $H_{0} = 10^{9} ,$ it is observed that the value of $u,$ decreases then converges to zero. Figure 8 shows the distribution of temperature $T.$ For $H_{0} = 0,$ the value of $T$ increase to the maximum value in the range $0 \le z \le 0.2,$ then decrease in the range $0.2 \le z \le 1,$ then increase in the range $1 \le z \le 3.5,$ and finally converges to zero. For $H_{0} = 10^{9} ,$ the value of $T$ decreases, then increase and finally converge to zero in the context of the (CT) and (G–L) theories. Figure 9 represents the distribution of the stress component $\sigma_{zz} ,$ in the context of the (CT) and (G–L) theories, always begins from negative values for $H_{0} = 0,10^{9} .$ In the case of absence of the magnetic field the curve which represent (CT) theory decreases to the minimum value in the range $0 \le z \le 0.2,$ then increase and converge to zero at $z \ge 1.5,$ while the curve which represent the (G–L) theory decreases to the minimum value in the range $0 \le z \le 0.2,$ then increases in the range $0.2 \le z \le 1,$ then decrease and converge to zero at $z \ge 2.5$. However, in the case of the presence of a magnetic field the curve, which represents (CT) theory has increased then decreased while the curve, which represent (G–L) theory is an increase in the range $0 \le z \le 0.1,$ then decrease in the range $0.1 \le z \le 0.5,$ then increase and converge to zero at $z \ge 3.5.$ Figure 10 exhibits that the distribution of the stress component $\sigma_{xz}$ in the context of the (CT) and (G–L) theories, begins from zero and satisfies the boundary conditions at $z = 0$. In the context of the two theories, the values of $\sigma_{xz}$ decreases in the range $0 \le z \le 0.3,$ then increase for $H_{0} = 10^{9} .$ However, in the case of absence of the magnetic field the values of $\sigma_{xz}$ increases then decreases and converges to zero. It is observed that the values of the stress components $\sigma_{xz}$ at $H_{0} = 10^{9} ,$ are higher than those at $H_{0} = 0.$ Figure 11 represents the variations of the electric potential $\varphi ,$ in the context of the (CT) and (G–L) theories, the values of $\varphi ,$ decreases in the range $0 \le x \le 0.5,$ then increases for (CT) at $H_{0} = 0,$ and (G–L) at $H_{0} = 10^{9} ,$ while in the case of (CT) at $H_{0} = 10^{9} ,$ and (G–L) at $H_{0} = 0,$ it is observed that the value of $\varphi ,$ increases then decreases and converges to zero. Figure 12 shows that the distribution of the electric displacement $D_{z} ,$ in the context of (CT) and (G–L) theories, the value of $D_{z} ,$ decrease in the range $0 \le x \le 0.7,$ then increases for $H_{0} = 0,$ while for $H_{0} = 10^{9} ,$ it is observed that the value of $D_{z} ,$ increases then converges to zero.

3D curves Figs. 13, 14, 15, 16, 17 and 18 are representing the relation between the physical variables and both components of the distance, in the presence of rotation $\varOmega = 0.5$ and magnetic field ${\rm H}_{\text{0}} = 10^{8}$ in a generalized piezo-thermoelastic medium, in the context of (G–L). These figures are very important to study the dependence of these physical quantities on the vertical component of distance. The curves obtained are highly depending on the vertical distance and all the physical quantities are moving in wave propagation.

Fig. 13

(3D) Distribution of the displacement component u versus the components of distance based on (G–L) model at $\varOmega = 0.5$ and H₀ = 10⁸

Fig. 14

(3D) Distribution of the displacement component wversus the components of distance based on (G–L) model at $\varOmega = 0.5$ and H₀ = 10⁸

Fig. 15

(3D) Distribution of temperature Tversus the components of distance based on (G–L) model at $\varOmega = 0.5$ and H₀ = 10⁸

Fig. 16

(3D) Distribution of the stress component σ _xx versus the components of distance based on (G–L) model at $\varOmega = 0.5$ and H₀ = 10⁸

Fig. 17

(3D) Electric potential against both components of distance based on G–L model at $\varOmega = 0.5$ and H₀ = 10⁸

Fig. 18

(3D) Distribution of electric displacement D _z against both components of distance based on G–L model at $\varOmega = 0.5$ and H₀ = 10⁸

6 Conclusions

This study solves the mathematical model for studying the influence of rotation and magnetic field in anisotropic piezo-thermoelastic materials for two-dimensional propagation of plane harmonic waves. Recent interest in the piezoelectric materials stems from their potential applications in intelligent structural systems, and piezoelectric is currently enjoying a greatest resurgence in both fundamental research and technical applications. The thermoelasticity is concerned with the study of thermo-dynamics system of bodies in equilibrium, whose interactions with the surroundings are limited to mechanical work, heat exchange and external work. Comparing the figures which obtained under the two theories, important phenomena have observed that,

• Analytical solutions based upon normal mode analysis for thermoelastic problem in solids have been developed and used.

• The method which used in the present article is applicable to a wide range of problems in hydrodynamics and thermoelasticity.

• The value of all physical quantities converges to zero with an increase in distance $z$ and all functions are continuous. All the physical quantities satisfy the boundary conditions.

• Deformation of a body depends on the nature of forced applied as well as the type of boundary conditions.

• The comparisons of two theories of thermoelasticity, (CT) and (G–L) theories are carried out.

Appendices

Appendix A

$$ \begin{aligned} \delta_{1} & = \frac{{C_{11} + \mu_{0} H_{0}^{2} }}{{\rho \;v_{p}^{2} }},\quad \delta_{2} = \frac{{C_{44} }}{{\rho \;v_{p}^{2} }},\quad \delta_{3} = \frac{{C_{13} + C_{44} + \mu_{0} H_{0}^{2} }}{{\rho \;v_{p}^{2} }},\quad \delta_{4} = \frac{{(e_{31} + e_{15} )}}{{e_{33} }},\quad \delta_{5} = \left( {1 + \frac{{\varepsilon_{0} \mu_{0}^{2} H_{0}^{2} }}{\rho \;}} \right), \\ \delta_{6} & = \frac{{C_{33} + \mu_{0} H_{0}^{2} }}{{\rho \;v_{p}^{2} }},\quad \delta_{7} = \frac{{e_{15} }}{{e_{33} }},\quad \delta_{8} = - \frac{{\beta_{3} }}{{\beta_{1} }},\quad \delta_{9} = \frac{{(e_{15} + e_{31} )}}{{\rho \;v_{p}^{2} }},\quad \delta_{10} = \frac{{e_{15} }}{{\rho \;v_{p}^{2} }},\quad \delta_{11} = \frac{{e_{33} }}{{\rho \;v_{p}^{2} }}, \\ \delta_{12} & = - \frac{{ \in_{11} }}{{e_{33} }},\quad \delta_{13} = - \frac{{ \in_{33} }}{{e_{33} }},\quad \delta_{14} = \frac{{p_{3} }}{{\beta_{1} }},\quad \delta_{15} = \frac{{K_{1} \omega^{*} }}{{\rho \;C_{e} {\kern 1pt} v_{p}^{2} }},\quad \delta_{16} = \frac{{K_{3} \omega^{*} }}{{\rho \;C_{e} {\kern 1pt} v_{p}^{2} }},\quad \delta_{17} = \frac{{\beta_{1}^{2} {\kern 1pt} T_{0} }}{{\rho^{2} C_{e} {\kern 1pt} v_{p}^{2} }}, \\ \delta_{18} & = \frac{{\beta_{\,1} \;\beta_{\,3} \;T_{0} }}{{\rho^{2} C_{e} v_{p}^{2} }},\quad \delta_{19} = - \frac{{p_{3} \;\beta_{\,1} \;T_{0} }}{{\rho \,C_{e} e_{33} }}. \\ \end{aligned} $$

(52)

$$ \begin{aligned} A_{1} & = - \frac{{(a^{2} \delta_{1} - a^{2} c^{2} \delta_{5} - \varOmega^{2} )}}{{\delta_{2} }},\quad A_{2} = \frac{{ia\delta_{3} }}{{\delta_{2} }},\quad A_{3} = \frac{{2ia{\kern 1pt} c{\kern 1pt} \varOmega }}{{\delta_{2} }},\quad A_{4} = \frac{{ia\delta_{4} }}{{\delta_{2} }},\quad A_{5} = - \frac{{ia(1 - i{\kern 1pt} a{\kern 1pt} c{\kern 1pt} t_{1} )}}{{\delta_{2} }}, \\ A_{6} & = \frac{{ia\delta_{3} }}{{\delta_{6} }},\quad A_{7} = - \frac{{2ia{\kern 1pt} c{\kern 1pt} \varOmega }}{{\delta_{6} }},\quad A_{8} = - \frac{{(a^{2} \delta_{2} - a^{2} c^{2} \delta_{5} - \varOmega^{2} )}}{{\delta_{6} }},\quad A_{9} = \frac{1}{{\delta_{6} }},\quad A_{10} = - \frac{{a^{2} \delta_{7} }}{{\delta_{6} }}, \\ A_{11} & = \frac{{\delta_{8} (1 - ia{\kern 1pt} c{\kern 1pt} t_{1} )}}{{\delta_{6} }},\quad A_{12} = \frac{{ia\delta_{9} }}{{\delta_{11} }},\quad A_{13} = - \frac{{a^{2} \delta_{10} }}{{\delta_{11} }},\quad A_{14} = \frac{{\delta_{13} }}{{\delta_{11} }},\quad A_{15} = - \frac{{a^{2} \delta_{12} }}{{\delta_{11} }}, \\ A_{16} & = \frac{{\delta_{14} (1 - ia{\kern 1pt} c{\kern 1pt} t_{1} )}}{{\delta_{11} }},\quad A_{17} = - \frac{{a^{2} c{\kern 1pt} \delta_{17} }}{{\delta_{16} }},\quad A_{18} = \frac{{ia{\kern 1pt} c\delta_{18} }}{{\delta_{16} }},\quad A_{19} = \frac{{ia{\kern 1pt} c\delta_{19} }}{{\delta_{16} }},\quad A_{20} = - \frac{{(a^{2} \delta_{15} - ia{\kern 1pt} c - a^{2} c^{2} t_{0} )}}{{\delta_{16} }}. \\ \end{aligned} $$

(53)

$$ \begin{aligned} A & = - \left( {\frac{1}{{A_{14} - A_{9} }}} \right)(A_{14} A_{20} + A_{15} - A_{16} A_{19} + A_{8} A_{14} - A_{9} A_{13} - A_{9} A_{20} + A_{9} A_{16} A_{18} - A_{10} \\ & \quad + \;A_{11} A_{19} - A_{11} A_{14} A_{18} + A_{1} A_{14} - A_{1} A_{9} - A_{2} A_{6} A_{14} + A_{2} A_{9} A_{12} + A_{4} A_{6} - A_{4} A_{12} ) \\ \end{aligned} $$

(54)

$$ \begin{aligned} B & = \left( {\frac{1}{{A_{14} - A_{9} }}} \right)(A_{15} A_{20} + A_{8} A_{14} A_{20} + A_{8} A_{15} - A_{8} A_{16} A_{19} - A_{9} A_{13} A_{20} - A_{10} A_{13} - A_{10} A_{20} \\ & \quad + A_{10} A_{16} A_{18} + A_{11} A_{13} A_{19} - A_{11} A_{15} A_{18} + A_{1} A_{14} A_{20} + A_{1} A_{15} - A_{1} A_{16} A_{19} + A_{1} A_{8} A_{14} \\ & \quad - A_{1} A_{9} A_{13} - A_{1} A_{9} A_{20} + A_{1} A_{9} A_{16} A_{18} - A_{1} A_{10} + A_{1} A_{11} A_{19} - A_{1} A_{11} A_{14} A_{18} - A_{2} A_{6} A_{14} A_{20} \\ & \quad - A_{2} A_{6} A_{15} + A_{2} A_{6} A_{16} A_{19} + A_{2} A_{9} A_{12} A_{20} - A_{2} A_{9} A_{16} A_{17} + A_{2} A_{10} A_{12} - A_{2} A_{11} A_{12} A_{19} \\ & \quad + A_{2} A_{11} A_{14} A_{17} - A_{3} A_{7} A_{14} + A_{4} A_{6} A_{13} + A_{4} A_{6} A_{20} - A_{4} A_{6} A_{16} A_{18} - A_{4} A_{12} A_{20} + A_{4} A_{16} A_{17} \\ & \quad - A_{4} A_{8} A_{12} + A_{4} A_{11} A_{12} A_{18} - A_{4} A_{11} A_{17} - A_{5} A_{6} A_{19} + A_{5} A_{6} A_{14} A_{18} + A_{5} A_{12} A_{19} \\ & \quad - A_{5} A_{14} A_{17} - A_{5} A_{9} A_{12} A_{18} + A_{5} A_{9} A_{17} ). \\ \end{aligned} $$

(55)

$$ \begin{aligned} C & = - \left( {\frac{1}{{A_{14} - A_{9} }}} \right)(A_{8} A_{15} A_{20} - A_{10} A_{13} A_{20} + A_{1} A_{15} A_{20} + A_{1} A_{8} A_{14} A_{20} + A_{1} A_{8} A_{15} - A_{1} A_{8} A_{16} A_{19} \\ & \quad - A_{1} A_{9} A_{13} A_{20} - A_{1} A_{10} A_{13} - A_{1} A_{10} A_{20} + A_{1} A_{10} A_{16} A_{18} + A_{1} A_{11} A_{13} A_{19} - A_{1} A_{11} A_{15} A_{18} \\ & \quad - A_{2} A_{6} A_{15} A_{20} + A_{2} A_{10} A_{12} A_{20} - A_{2} A_{10} A_{16} A_{17} + A_{2} A_{11} A_{15} A_{17} - A_{3} A_{7} A_{14} A_{20} - A_{3} A_{7} A_{15} + A_{3} A_{7} A_{16} A_{19} \\ & \quad + A_{4} A_{6} A_{13} A_{20} - A_{4} A_{8} A_{12} A_{20} + A_{4} A_{8} A_{16} A_{17} - A_{4} A_{11} A_{13} A_{17} - A_{5} A_{6} A_{13} A_{19} + A_{5} A_{6} A_{15} A_{18} \\ & \quad - A_{5} A_{15} A_{17} + A_{5} A_{8} A_{12} A_{19} - A_{5} A_{8} A_{14} A_{17} + A_{5} A_{9} A_{13} A_{17} - A_{5} A_{10} A_{12} A_{18} + A_{5} A_{10} A_{17} ). \\ \end{aligned} $$

(56)

$$ E = \left( {\frac{1}{{A_{14} - A_{9} }}} \right)(A_{1} A_{8} A_{15} A_{20} - A_{1} A_{10} A_{13} A_{20} - A_{3} A_{7} A_{15} A_{20} - A_{5} A_{8} A_{15} A_{17} + A_{5} A_{10} A_{13} A_{17} ). $$

(57)

Appendix B

$$ \begin{aligned} H_{1n} & = - \frac{{s_{1n} }}{{s_{2n} }},\quad H_{2n} = - \frac{{(q_{1n} + q_{2n} H_{1n} )}}{{q_{3n} }},\quad H_{3n} = - \frac{1}{{A_{5} }}[(k_{n}^{2} + A_{1} ) + ( - A_{2} k_{n} + A_{3} )H_{1n} - A_{4} k_{n} H_{2n} ], \\ H_{4n} & = r_{1} - l_{2} k_{n} H_{1n} - l_{3} k_{n} H_{2n} + r_{2} H_{3n} ,\quad H_{5n} = r_{3} - l_{4} k_{n} H_{1n} - k_{n} H_{2n} + r_{4} H_{3n} , \\ H_{6n} & = - \;\delta_{2} k_{n} + r_{5} H_{1n} + r_{6} H_{2n} ,\quad H_{7n} = - \;l_{5} k_{n} + r_{7} H_{1n} + r_{8} H_{2n} , \\ H_{8n} & = r_{9} - l_{12} k_{n} H_{1n} - l_{9} k_{n} H_{2n} + r_{10} H_{3n} ,\quad {\text{n}} = { 1}, 2, 3, 4. \\ \end{aligned} $$

(58)

$$ \begin{aligned} q_{1n} & = A_{11} k_{n}^{3} + (A_{1} A_{11} - A_{5} A_{6} )k_{n} + A_{5} A_{7} ,\quad q_{2n} = ( - A_{2} A_{11} + A_{5} )k_{n}^{2} + A_{3} A_{11} k_{n} + A_{5} A_{8} , \\ q_{3n} & = ( - A_{4} A_{11} + A_{5} A_{9} )k_{n}^{2} + A_{5} A_{10} ,\quad q_{4n} = A_{16} k_{n}^{3} + (A_{1} A_{16} - A_{5} A_{12} )k_{n} , \\ q_{5n} & = (A_{5} - A_{2} A_{16} )k_{n}^{2} + A_{3} A_{16} k_{n} + A_{5} A_{13} ,\quad q_{6n} = (A_{5} A_{14} - A_{4} A_{16} )k_{n}^{2} + A_{5} A_{15} , \\ \end{aligned} $$

(59)

$$ \text{s}_{1n} = q_{1n} q_{6n} - q_{3n} q_{4n} ,\quad \text{s}_{2n} = q_{2n} q_{6n} - q_{3n} q_{5n} , $$

(60)

$$ \begin{aligned} l_{1} & = \frac{{C_{11} }}{{\rho \,v_{p}^{2} }},\quad l_{2} = \frac{{C_{13} }}{{\rho \,v_{p}^{2} }},\quad l_{3} = \frac{{e_{31} }}{{e_{33} }},\quad l_{4} = \frac{{C_{33} }}{{\rho \,v_{p}^{2} }},\quad l_{5} = \frac{{e_{15} \beta_{1} T_{0} }}{{e\rho \,v_{p}^{2} }},\quad l_{6} = - \frac{{ \in_{11} \beta_{1} T_{0} }}{{e_{33} e}}, \\ l_{7} & = \frac{{e_{31} \beta_{1} T_{0} }}{{e\rho \,v_{p}^{2} }},\quad l_{8} = \frac{{e_{33} \beta_{1} T_{0} }}{{e\rho \,v_{p}^{2} }},\quad l_{9} = - \frac{{ \in_{33} \beta_{1} T_{0} }}{{e_{33} e}},\quad l_{10} = \frac{{P_{3} T_{0} }}{e}, \\ \end{aligned} $$

(61)

$$ \begin{aligned} \{ r_{1} ,r_{3} ,r_{5} ,r_{6} ,r_{7} ,r_{8} ,r_{9} \} & = ia\{ l_{1} ,l_{2} ,\delta_{2} ,\delta_{7} ,l_{5} ,l_{6} ,l_{7} \} ,\quad r_{2} = - (1 - i{\kern 1pt} a{\kern 1pt} c{\kern 1pt} t_{1} ), \\ r_{4} & = \delta_{8} (1 - i{\kern 1pt} a{\kern 1pt} c{\kern 1pt} t_{1} ),\quad r_{10} = l_{10} (1 - i{\kern 1pt} a{\kern 1pt} c{\kern 1pt} t_{1} ). \\ \end{aligned} $$

(62)