1 Introduction

The design and construction of piezoelectric gyroscopes and other rotating sensors have important applications in technology. The study of the effects of rotation on the propagation of waves in piezo-thermoelastic media has been extensively studied in the past two decades.

The theory of thermo-piezo-electricity was first proposed by Mindlin (1974). Ahmed et al. (2019) applied dual-phase-lag model to study the effect of gravity on piezo-thermoelastic half-space medium by using normal mode analysis method. Othman and Ahmed (2015) investigated the effect of rotation of a piezo-thermoelastic medium based on three theories (CT, L–S, G–L). Othman and Ahmed (2016) used normal mode analysis method to investigate the influence of the gravitational field on a piezo-thermoelastic rotating medium with G–L Theory. Schoenberg and Censor (1973) investigated an elastic waves in rotating media. Alshaikh (2012) presented the mathematical modelling for studying the influence of the initial stresses and relaxation times on reflection and refraction waves in piezothermoelastic half-space. The effects of piezoelectricity and piezomagnetism on the surface wave velocity of magneto-electroelastic solids has been investigated by Li and Wei (2014). Othman (2004) studied the effect of rotation on plane waves in generalized thermoelasticity with two relaxation times. Othman et al. (2013) studied the influence of gravity field and rotation on a generalized thermoelastic medium using dual-phase-lag model. Kumar et al. (2018) discussed the reflection of plane waves at a free surface of orthotropic micropolar piezothermoelastic medium. Sharma and Kumar (2000) studied the plane harmonic waves in piezo-thermoelastic materials. Abbas and Zenkour (2014) used a finite element method to study dual-phase-lag model on thermoelastic interactions in a semi-infinite medium subjected to a ramp-type heating. Abou-Dina et al. (2017) studied the model of nonlinear thermo-electroelasticity in extended thermo-electroelasticity in extended thermoelasticity. Mahmoud (2016) presented an analytical solution for the effect of initial stress, rotation, magnetic field and periodic loading in a thermoviscoelastic medium with a spherical cavity. Othman et al. (2017) studied the influence of magnetic field on generalized piezo-thermoelastic rotating medium with two relaxation times. Quintanilla and Racke (2006) compared two different mathematical hyperbolic models in dual-phase-lag, heat conduction proposed by Tzou, and found the parameter regions where stability can be expected. The theory of thermoelasticity with dual phase-lag effects has been used by Roy Choudhuri (2007) to study the problem of one-dimensional disturbance in an elastic half-space with its plane boundary subjected to a constant step input of temperature and zero stress, or a constant step input of stress and zero temperature. Singh et al. (2017) solved the governing equations of transversely isotropic dual-phase-lag, two-temperature thermoelasticity for the surface waves. Ciesielski (2017) discussed the considerations concerning the analytical solution of DPL equation in the one-dimensional bounded domain. Hou and Leung (2009) studied three-dimensional Green’s functions for two-phase transversely isotropic piezothermoelastic media. The reflection and refraction of plane quasi-longitudinal waves at an interface of two piezoelectric media under initial stresses discussed by Abd-Alla and Alsheikh (2009). Othman et al. (2014) studied the effect of rotation on micro-polar generalized thermoelasticity with two-temperatures using a dual-phase-lag model.

In the present paper, the dual-phase-lag model is applied to study the effect of rotation on a half-space filled with a piezo-thermoelastic medium. The normal mode analysis is used to obtain an exact analytical solution for the displacement components, the stress, the strain components, the temperature, the electric potential and the electric displacement. Comparison of the results is carried out with those obtained from Lord and Shulman theory, to assess the effect of rotation on wave propagation. The present results may be of interest in the design and construction of different pyro/piezoelectric devices, such as sensors and gyroscopes involving piezoelectric components.

2 Problem formulation

2.1 Basic equations

Consider a homogeneous, generalized piezo-thermoelastic half-space \((x,y,z \ge 0)\), rotating uniformly with an angular velocity about a fixed axis in space with angular velocity \({\varvec{\Omega }}=\Omega \mathbf {n,}\) where \(\mathbf {n}\) is a unit vector Fig. 1. All considered functions depend on the time variable t and the spatial coordinates x and z. The equation of motion has two additional terms representing Coriolis force and the centripetal acceleration (Schoenberg and Censor 1973). In what follows, we consider a rotation about the y-axis, so that \({\varvec{\Omega }} =(0,\Omega ,0)\).

Fig. 1
figure 1

Geometry of the problem and direction of rotation

Full size image

The governing two-dimensional field equations for a homogeneous, generalized anisotropic piezo-thermoelastic solid belonging to a hexagonal crystallographic symmetry class are expressed as (see Sharma and Kumar 2000):

  1. 1.

    Strain-displacement relations

    $$\begin{aligned} \varepsilon _{i,j}=\frac{1}{2} \left( u_{i,j}+u_{j,i} \right) . \end{aligned}$$
    (1)
  2. 2.

    Generalized Hooke’s law

    $$\begin{aligned} \sigma _{ij}=C_{ijkl}\varepsilon _{kl}-e_{kij}E_{k}-\beta _{ij}T \end{aligned}$$
    (2)
  3. 3.

    Equation of motion

    $$\begin{aligned} \rho \{\overset{\cdot \cdot }{u}_{i}+{\varvec{\Omega }} \times ({\varvec{\Omega }} \times \mathbf{u })+(2{\varvec{\Omega }} \times \overset{\cdot }{\mathbf {u}})_{i}=\sigma _{ij,j} \end{aligned}$$
    (3)
  4. 4.

    Equation of electrostatics

    $$\begin{aligned} D_{i,i}=0, \end{aligned}$$
    (4)
  5. 5.

    Electric constitutive equation

    $$\begin{aligned} D_{i}=e_{ijk}\varepsilon _{jk}+\epsilon _{ij}E_{j}+p_{i}T \end{aligned}$$
    (5)

    with

    $$\begin{aligned} E_{i}=-\varphi _{,i}, \end{aligned}$$
    (6)

    \(\varphi\) being the electric potential.

  6. 6.

    Heat conduction equation in dual-phase-lag model for a piezoelectric material may be expressed as (see Tzou 1995, Aouadi 2006):

    $$\begin{aligned} \left( 1+\tau _{\theta }\frac{\partial }{\partial t}\right) k_{ij}T_{,ij}=\left( 1+\tau _{q} \frac{\partial }{\partial t}\right) [\rho C_{T}\dot{T}+T_{0}(\beta _{ij}\overset{ \cdot }{u}_{i,j}-P_{i}\overset{\cdot }{\varphi }_{,i})]. \end{aligned}$$
    (7)

In the following, we denote \(C_{1111}, C_{1133}, C_{3333}, C_{2323}\) by \(C_{11}, C_{13}, C_{33}, C_{44}\) respectively for simplicity.

For the hexagonal (6 mm) crystallographic class under consideration, the constitutive relations are given in components by (Sharma and Kumar 2000) as:

$$\begin{aligned} \sigma _{xx} = C_{11}\varepsilon _{xx}+C_{13}\varepsilon _{zz}-e_{31}E_{z}-\beta _{1}T, \end{aligned}$$
(8)
$$\begin{aligned} \sigma _{zz} = C_{13}\varepsilon _{xx}+C_{33}\varepsilon _{zz}-e_{33}E_{z}-\beta _{3}T, \end{aligned}$$
(9)
$$\begin{aligned} \sigma _{xz} = 2C_{44}\varepsilon _{xz}-e_{15}E_{x}, \end{aligned}$$
(10)
$$\begin{aligned} D_{x} = e_{15}(u_{,z}+w_{,x})+\epsilon _{11}E_{x}, \end{aligned}$$
(11)
$$\begin{aligned} D_{z} = e_{31}u_{,x}+e_{33}w_{,z}+\epsilon _{33}E_{z}+P_{3}T. \end{aligned}$$
(12)

2.2 Boundary conditions

The governing equations will be solved in a half-space \((x, y, z \ge 0)\) under the following boundary conditions:

  1. 1.

    Mechanical boundary conditions:

    $$\begin{aligned} \sigma _{zz}(x,0,t)=f_{1}(x,t)=-f_{1}^{*}e^{ia(x-ct)},\qquad \sigma _{xz}(x,0,t)=0, \end{aligned}$$
    (13)
  2. 2.

    Thermal boundary condition:

    $$\begin{aligned} T(x,0,t)=f_{2}(x,t)=f_{2}^{*}e^{ia(x-ct)}, \end{aligned}$$
    (14)

    where \(f_{1}(x,t)\) and \(f_{2}(x,t)\) are arbitrary functions of (x, t), \(f_{1}^{*},f_{2}^{*}\) are constants, a is the wave number in the x-direction and \(\omega =ac\) is the frequency.

  3. 3.

    Electrical boundary condition:

    $$\begin{aligned} \frac{\partial \varphi }{\partial z}(x,0,t) =0. \end{aligned}$$
    (15)

We consider a homogeneous, anisotropic, piezo-thermoelastic half-space of hexagonal type under the influence of the rotation.

The basic system of field equations (3), (4) and (7) for temperature change T(x, z, t),  displacement vector \(\mathbf {u }(x,z,t)=(u,0,w),\) and electric potential \(\varphi (x,z,t),\) is given by:

$$\begin{aligned}&C_{11}u_{,xx}+C_{44}u_{,zz}+(C_{13}+C_{44})w_{,xz}\nonumber \\&\qquad +(e_{31}+e_{15})\varphi _{,xz}-\beta _{1}T_{,x}\nonumber \\&\quad =\rho (\overset{\cdot \cdot }{u}-\Omega ^{2}u+2\Omega \overset{\cdot }{w}), \end{aligned}$$
(16)
$$\begin{aligned}&(C_{13}+C_{44})u_{,xz}+C_{44}w_{,xx}+C_{33}w_{,zz}+e_{15}\varphi _{,xx}+e_{33}\varphi _{,zz}\nonumber \\&\quad -\beta _{3}T_{,z}=\rho (\overset{\cdot \cdot }{w} -\Omega ^{2}w-2\Omega \overset{\cdot }{u}), \end{aligned}$$
(17)
$$\begin{aligned}&(e_{15}+e_{31})u,_{xz}+e_{15}w_{,xx}+e_{33}w_{,zz}-\epsilon _{11}\varphi _{,xx}\nonumber \\&\quad -\epsilon _{33}\varphi _{,zz}+P_{3}T_{,z}=0, \ \end{aligned}$$
(18)
$$\begin{aligned}&\left( 1+\tau _{\theta }\ \frac{\partial }{\partial t} \right) (k_{1}T_{,xx}+k_{3}T_{,zz}) =\left( 1+\tau _{q}\ \frac{\partial }{\partial t} \right) \nonumber \\&\quad [\rho C_{T}\overset{\cdot }{T}+T_{0}(\beta _{1}\overset{\cdot }{u_{,x}} +\beta _{3}\overset{\cdot }{w_{,z}}-P_{3}\overset{\cdot }{\varphi _{,z}})] \end{aligned}$$
(19)

The following non-dimensional quantities are introduced for convenience:

$$\begin{aligned}&x^\prime =\frac{\omega ^{*}}{v_{p}}x,\quad z^\prime =\frac{\omega ^{*}}{v_{p}}z,\quad u^\prime =\frac{\rho \omega ^{*}v_{p}}{\beta _{1}T_{o}}u,\quad w^\prime =\frac{\rho \omega ^{*}v_{p}}{\beta _{1}T_{o}}w, \\&T^\prime =\frac{T}{T_{o}},\quad \sigma _{ij}^\prime =\frac{\sigma _{ij} }{\beta _{1}T_{o}},\quad \varphi ^\prime =\varepsilon _{p}\varphi ,\quad \{t^\prime ,\tau ^\prime _{\theta },\tau ^\prime _{q}\}=\omega ^{*}\{t,\tau _{\theta },\tau _{q}\}, \\&D_{i}^\prime =\frac{D_{i}}{e},\quad \Omega ^\prime =\frac{\Omega }{ \omega ^{*}}, \end{aligned}$$

where

$$\begin{aligned}&\omega ^{*}=\frac{C_{T}C_{11}}{K_{11}},\quad \varepsilon _{p}=\frac{ \omega ^{*}e_{33}}{v_{p}}\beta _{1}T_{0}, \\&\beta _{1}=\left( C_{11}+C_{12}\right) \alpha _{1}+C_{13}\alpha _{3},\quad \beta _{3}=2C_{13}\alpha _{1}+C_{33}\alpha _{3}. \end{aligned}$$

Using the non-dimensional quantities, system (16)–(19) recasts in the following form after suppressing the primes

$$\begin{aligned}&\delta _{1}u_{,xx}+\delta _{2}u_{.zz}+\delta _{3}w_{,xz}\nonumber \\&\quad +\delta _{4}\varphi _{,xz}-T_{,x}=\overset{\cdot \cdot }{u}-\Omega ^{2}u+2\Omega \overset{\cdot }{w} \end{aligned}$$
(20)
$$\begin{aligned}&\delta _{3}u_{,xz}+\delta _{2}w_{.xx}+\delta _{5}w_{,zz}\nonumber \\&\quad +\delta _{6}\varphi _{,xx}+\varphi _{,zz}+\delta _{7}T_{,z}=\overset{\cdot \cdot }{w} -\Omega ^{2}w-2\Omega \overset{\cdot }{u} \end{aligned}$$
(21)
$$\begin{aligned}&\delta _{8}u_{,xz}+\delta _{9}w_{.xx}+\delta _{10}w_{,zz}+\delta _{11}\varphi _{,xx}\nonumber \\&\quad +\delta _{12}\varphi _{,zz}+\delta _{13}T_{,z}=0 \end{aligned}$$
(22)
$$\begin{aligned}&\left( 1+\tau _{\theta }\ \frac{\partial }{\partial t} \right) \left( \delta _{14}T_{,xx}+\delta _{15}T_{,zz} \right) \nonumber \\&\quad =\left( 1+\tau _{q}\ \frac{\partial }{\partial t} \right) \left( \overset{\cdot }{T}+\delta _{16}\overset{\cdot }{ u}_{,x}\nonumber \right. \\&\left. \quad \quad +\delta _{17}\overset{\cdot }{w}_{,z}-\delta _{18}\overset{\cdot }{ \varphi }_{,z}\right) \end{aligned}$$
(23)

3 Solution of the problem

The solution of the considered physical quantities can be decomposed in terms of normal modes in the following form

$$\begin{aligned}[u,w,\varphi ,T](x,z,t)=[u^{*},w^{*},\varphi ^{*},T^{*}](z)e^{ia(x-ct)}, \end{aligned}$$
(24)

where \(u^{*},w^{*},\varphi ^{*}\) and \(T^{*}\) are the amplitudes of the functions \(u,w,\varphi\) and T, respectively. Thus our solution represents progressive waves propagating parallel to the boundary of the half-space, with amplitude decaying in depth.

Substituting from Eq. (24) into Eqs. (20)–(23), and denoting \(D=\frac{d}{dz},\) we get

$$\begin{aligned}&(D^{2}+A_{1})u^{*}+(A_{2}D+A_{3})w^{*}\nonumber \\&\quad +A_{4}D\varphi ^{*}+A_{5}T^{*}=0, \end{aligned}$$
(25)
$$\begin{aligned}&(A_{6}D+A_{7})u^{*}+(D^{2}+A_{8})w^{*}+(A_{9}D^{2}\nonumber \\&\quad +A_{10})\varphi ^{*}+A_{11}DT^{*}=0, \end{aligned}$$
(26)
$$\begin{aligned}&A_{12}Du^{*}+(D^{2}+A_{13})w^{*}\nonumber \\&\quad +(A_{14}D^{2}+A_{15})\varphi ^{*}+A_{16}DT^{*}=0, \end{aligned}$$
(27)
$$\begin{aligned}&A_{17}u^{*}+A_{18}Dw^{*}\nonumber \\&\quad +A_{19}D\varphi ^{*}+(D^{2}+A_{20})T^{*}=0. \end{aligned}$$
(28)

where \(A_{j},\,\)\(j=1,2,\ldots ,20\) are given in Appendix A

Equations (25)–(28) have a non-trivial solution only if the determinant of the coefficients of the above linear system vanishes. Then

$$\begin{aligned}&(D^{8}-AD^{6}+BD^{4}-CD^{2}+E)\{u^{*}(z),w^{*}(z),\nonumber \\&\quad \varphi ^{*}(z),T^{*}(z)\}=0, \end{aligned}$$
(29)

where A,  B,  C and E are given in Appendix A.

Equation (29) can be factored as:

$$\begin{aligned}&(D^{2}-k_{1}^{2})(D^{2}-k_{2}^{2})(D^{2}-k_{3}^{2})(D^{2}-k_{4}^{2})\{u^{ *}(z),\nonumber \\&\quad w^{*}(z),\varphi ^{*}(z),T^{*}(z)\}=0. \end{aligned}$$
(30)

The solutions of equations (29), which are bounded as \(z\rightarrow \infty\) are given as:

$$\begin{aligned}&u^{*}=\underset{n=1}{\overset{4}{\sum }}M_{n}e^{-k_{n}z}, \end{aligned}$$
(31)
$$\begin{aligned}&w^{*}=\underset{n=1}{\overset{4}{\sum }}H_{1n}M_{n}e^{-k_{n}z}, \end{aligned}$$
(32)
$$\begin{aligned}&\varphi ^{*}=\underset{n=1}{\overset{4}{\sum }}H_{2n}M_{n}e^{-k_{n}z}, \end{aligned}$$
(33)
$$\begin{aligned}&T^{*}=\underset{n=1}{\overset{4}{\sum }}H_{3n}M_{n}e^{-k_{n}z}, \end{aligned}$$
(34)

where \(k_{n}^{2},(n=1,2,3,4)\) are the roots of the characteristic equation of Eq. (29).

Inserting Eqs. (31)–(34) into Eqs. (8)–(12), after making dimension analysis, in the frame of the normal mode method, one obtains

$$\begin{aligned}&\sigma _{xx}^{*}=\underset{n=1}{\overset{4}{\sum }} H_{4n}M_{n}e^{-k_{n}z}, \end{aligned}$$
(35)
$$\begin{aligned}&\sigma _{zz}^{*}=\underset{n=1}{\overset{4}{\sum }} H_{5n}M_{n}e^{-k_{n}z}, \end{aligned}$$
(36)
$$\begin{aligned}&T_{xz}^{*}=\underset{n=1}{\overset{4}{\sum }}H_{6n}M_{n}e^{-k_{n}z}, \end{aligned}$$
(37)
$$\begin{aligned}&D_{x}^{*}=\underset{n=1}{\overset{4}{\sum }}H_{7n}M_{n}e^{-k_{n}z}, \end{aligned}$$
(38)
$$\begin{aligned}&D_{z}^{*}=\underset{n=1}{\overset{4}{\sum }}H_{8n}M_{n}e^{-k_{n}z}, \end{aligned}$$
(39)

where \(H_{jn},j=1,...,8,n=1,2,3,4\) are given in Appendix B.

Applying the boundary conditions (13)–(15) to determine the coefficients \(M_{n}(n=1,2,3,4),\) we obtain

$$\begin{aligned}&\underset{n=1}{\overset{4}{\sum }}H_{5n}M_{n}=-f_{1}^{*}, \end{aligned}$$
(40)
$$\begin{aligned}&\underset{n=1}{\overset{4}{\sum }}H_{6n}M_{n}=0, \end{aligned}$$
(41)
$$\begin{aligned}&\underset{n=1}{\overset{4}{\sum }}H_{3n}M_{n}=f_{2}^{*}, \end{aligned}$$
(42)
$$\begin{aligned}&\underset{n=1}{\overset{4}{\sum }}k_{n}H_{2n}M_{n}=0. \end{aligned}$$
(43)

Solving Eqs. (40)–(43) for \(M_{n}(n=1,2,3,4)\) by the inverse matrix method as follows:

$$\begin{aligned} \left( \begin{array}{c} M_{1} \\ M_{2} \\ M_{3} \\ M_{4} \end{array} \right) =\left( \begin{array}{cccc} H_{51} & H_{52} & H_{53} & H_{54} \\ H_{61} & H_{62} & H_{63} & H_{64} \\ H_{31} & H_{32} & H_{33} & H_{34} \\ k_{1}H_{21} & k_{2}H_{22} & k_{3}H_{23} & k_{4}H_{24} \end{array} \right) ^{-1}\left( \begin{array}{c} -f_{1}^{*} \\ 0 \\ f_{2}^{*} \\ 0 \end{array} \right) \end{aligned}$$
(44)

Thus, we obtain an exact analytical formula for the displacement vector components, the stress and the strain tensors components, the temperature, the electric potential and the electric displacement.

4 Numerical results and discussion

To study the effect of rotation, we will carry out some numerical experiments. The material chosen for the purpose of the numerical calculations is taken as Cadmium Selenide (CdSe) having hexagonal symmetry (6 mm class). The following particular values for the parameters are chosen as:

$$\begin{aligned}&C_{11}=7.41\times 10^{10}\;{\text {Nm}}^{-2},\quad C_{12}=4.52\times 10^{10}\;{\text {Nm}}^{-2}, \\&C_{13}=3.93\times 10^{10}\;{\text {Nm}}^{-2},\quad C_{33}=8.36\times 10^{10}\;{\text {Nm}}^{-2}, \\&C_{44}=1.32\times 10^{10}\;{\text {Nm}}^{-2},\quad T_{0}=298\;{\text {K}}, \\&\rho =5504\;{\text {kg\;m}}^{-3},\quad C_{T}=260\;{\text {J\;kg}}^{-1}\;{\text {K}}^{-1}. \\&e_{13}=-0.160\,{\text {Cm}}^{-2},\quad e_{33}=0.347\,{\text {Cm}}^{-2},\\&\quad e_{15}=-0.138\,{\text {Cm}}^{-2}, \\&\beta _{1}=0.621\times 10^{6}\;{\text {Nk}}^{-1}\;{\text {m}}^{-2},\\&\quad \beta _{3}=0.551\times 10^{6}\;{\text {Nk}}^{-1}\;{\text {m}}^{-2}, \\&P_{3}=-2.94\times 10^{6}\;{\text {Ck}}^{-1}\;{\text {m}}^{-2},\\&\quad K_{1}=K_{3}=9\,{\text {Wm}}^{-1}\;{\text {K}}^{-1}, \\&\epsilon _{11}=8.26\times 10^{-11}{\text {C}}^{2}{\text {N}}^{-1}\;{\text {m}}^{-2},\\&\quad \epsilon _{33}=9.03\times 10^{-11}{\text {C}}^{2}{\text {N}}^{-1}\;{\text {m}}^{-2}. \\&\tau _q = 0.9342 \times 10^{-12} \, {\text {s}}, \quad \\&\tau _{\theta } = 0.37371 \times 10^{-12} \, {\text {s}}. \end{aligned}$$

For these values, the characteristic time

$$\begin{aligned} \frac{1}{\omega ^{*}} \simeq 0.4671 \times 10^{-12} \, {\text {s}} \end{aligned}$$

is in the range of picoseconds, while the characteristic length is

$$\begin{aligned} \frac{v_p}{\omega ^{*}} \simeq 0.1714 \times 10^{-8} \, {\text {m}}. \end{aligned}$$

In applying the numerical technique outlined above, we are interested in the real parts of the displacement vector components u, w, the temperature T , the stress tensor components \(\sigma _{xx},\sigma _{zz},\sigma _{xz},\) the electric potential \(\varphi\) and the electric displacement components \(D_{x},D_{z}\). Here all variables are taken in non-dimensional form. The results are shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10. The graphs exhibit the curves predicted by L–S theory and DPL model. In these figures, the solid lines represent the solution in the dual-phase-lag model and dashed lines represent the solution derived using the generalized Lord and Shulman theory.

Fig. 2
figure 2

Distribution of the horizontal component u of the displacement vector at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image
Fig. 3
figure 3

Distribution of the vertical component w of the displacement vector at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image
Fig. 4
figure 4

Temperature distribution T at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image
Fig. 5
figure 5

Distribution of the stress component \(\sigma _{xx}\) at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image
Fig. 6
figure 6

Distribution of the stress component \(\sigma _{zz}\) at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image
Fig. 7
figure 7

Distribution of the stress component \(\sigma _{xz}\) at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image
Fig. 8
figure 8

Distribution of the electric potential \(\varphi\) at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image
Fig. 9
figure 9

Distribution of the electric displacement component \(D_{x}\) at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image
Fig. 10
figure 10

Distribution of the electric displacement component \(D_{z}\) at \(x=0.1\), \(t=1.5\), in the absence or presence of rotation

Full size image

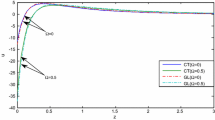
These figures show a comparison between the values assumed by the different functions of practical interest in the absence of rotation (\(\Omega =0\)) and for \(\Omega =0.4\). Comparison is also carried out between the results of DPL and those from L–S. The computations are carried out for the non-dimensional instant of time \(t=1.5\) at \(x=0.1\)with \(\ f_{1}^{*}=1\)and \(f_{2}^{*}=6\). It follows from the presented figures that all the physical quantities suffer appreciable variations only in a narrow slab \(0 \le z \le 1\), while all quantities practically vanish outside the slab \(0 \le z \le 2\).

Figure 2 depicts the distribution of the displacement u parallel to the boundary against z. It shows that this displacement component wealky depends on rotation, which amounts to adding a small positive displacement, and is for the most part opposite to the direction of propagation of the wave. The absolute value of this displacement component for L–S is monotonically decreasing, and exceeds that obtained from DPL.

Figure 3 illustrates the distribution of the in-depth displacement w against z. Here, the effect of rotation is appreciable, and amounts to adding a negative displacement. Moreover, the absolute values obtained for this displacement component are larger with DPL.

Figure 4 exhibits the behavior of temperature T against z. As expected, the effect of rotation here is negligible. The temperature for L–S is monotonic decreasing to zero, and is smaller than that obtained from DPL in the neighborhood of the boundary.

Figures 5, 6 and 7 show the distributions of the stress tensor components \(\sigma _{xx}, \sigma _{zz}, \sigma _{xz}\) with z. The effect of rotation is appreciable only for the last two components, while the fluctuations of the three stress components are more appreciable for DPL than for L–S.

Figures 8, 9 and 10 exhibit the distributions with z of the electrical potential \(\varphi\) and the two electric displacement components \(D_{x}\) and \(D_{z}\). The effect of rotation is appreciable only for \(\varphi\) and \(D_{x}\) within DPL, while it is negligible otherwise. Here again, the fluctuations within DPL are more pronounced for the first two functions as compared to the corresponding results of L–S.

Fig. 11
figure 11

The distribution of the horizontal component u of the displacement vector at \(t=1.5\)in the (x, z) plane calculated in the frame of the DPL model with \(\Omega =0.4\)

Full size image
Fig. 12
figure 12

Distribution of the vertical component w of the displacement vector at \(t=1.5\) in the (x, z) plane calculated in the frame of the DPL model with \(\Omega =0.4\)

Full size image
Fig. 13
figure 13

Distribution of the temperature T at \(t=1.5\)in the (x, z) plane calculated in the frame of the DPL model with \(\Omega =0.4\)

Full size image
Fig. 14
figure 14

Distribution of the stress component \(\sigma _{xx}\) at \(t=1.5\) in the (x, z)plane calculated in the frame of the DPL model with \(\Omega =0.4\)

Full size image
Fig. 15
figure 15

Distribution of the stress component \(\sigma _{zz}\) at \(t=1.5\) in the (x, z) plane calculated in the frame of the DPL model with \(\Omega =0.4\)

Full size image
Fig. 16
figure 16

Distribution of the stress component \(\sigma _{xz}\) at \(t=1.5\) in the (x, z) plane calculated in the frame of the DPL model with \(\Omega =0.4\)

Full size image
Fig. 17
figure 17

Distribution of the electric potential \(\varphi\) at \(t=1.5\)in the (x, z) plane calculated in the frame of the DPL model with \(\Omega =0.4\)

Full size image
Fig. 18
figure 18

Distribution of the electric displacement component \(D_{x}\) at \(t=1.5\)in the (x, z) plane calculated in the frame of the DPL model with \(\Omega =0.4\)

Full size image
Fig. 19
figure 19

Distribution of the electric displacement component \(D_{z}\) at \(t=2.0\)in the (x, z) plane calculated in the frame of the DPL model at \(t=1.5\) with \(\Omega =0.4\)

Full size image

Figures 11, 12, 13, 14, 15, 16, 17, 18 and 19 exhibit the 3D plots of the solution in the (x, z) plane at \(t=1.5\) for DPL, in the presence of rotation (\(\Omega =0.4\)).

5 Conclusions

The main purpose of the present work is to assess the effect of rotation on a piezo-thermoelastic medium within dual-phase-lag model. Comparison is carried out with the results obtained from L–S. Normal mode analysis is used for the solution of the mathematical problem, and the boundary conditions are particulary chosen to fit the requirements of such technique.

An exact analytical solution is obtained under these limitations. According to this solution, all the physical quantities tend to zero away from the boundary and all functions are continuous.

The performed calculations at particular locations of the half-space have revealed that the effect of rotation may differ from one physical quantity to the other, and that fluctuations of the different functions in the zone near the boundary are more pronounced within DPL, than those obtained from the L–S theory.

The presented results, in connection with experimental measurements, may be useful in calculating numerical values of different material parameters, and in assessing the efficiency of the two considered theories.

A numerical treatment of the general system of equations and conditions governing the phenomenon may be useful in getting rid of the limitations of the method of normal modes’ technique and this task is actually in progress.