Non-linear static stability of bi-layer carbon nanosheets resting on an elastic matrix under various types of in-plane shearing loads in thermo-elasticity using nonlocal continuum

Abstract

In this research, the shear and thermal buckling of bi-layer rectangular orthotropic carbon nanosheets embedded on an elastic matrix using the nonlocal elasticity theory and non-linear strains of Von-Karman was studied. The bi-layer carbon sheets was modeled as a double-layered plate, and van der Waals forces between layers were considered. The governing equations and boundary conditions were obtained using the first order shear deformation theory. For calculation of critical temperature and critical shear load, the equations were divided for two states via adjacent equilibrium criterion, pre-buckling and stability. The stability equations were discretized by differential quadrature method which is a high accurate numerical method. The equations were solved for various boundary conditions, such as free edges. Finally, the small scale parameter effect due to length to the width ratio, stiffness of elastic medium on the critical load was considered. The shear buckling results showed that the effect of type of shear loading on the nonlocal results is more than local results. Also, in thermal buckling analysis, the most important results being that whether the boundary conditions have more flexibility, by increasing the dimensions ratio, the results of critical temperature were tightly close together in nonlocal and local analysis.

1 Introduction

A Carbon nanosheets (CNSs) is a two-dimensional nanostructure with special form of carbon that’s an only single atom thick (Coleman et al. 2011; Shaojun and Shaojun 2011). CNSs consist of vertically aligned graphene layer stacks, one to multi-layers thick, which can attain micron-scale lengths (Geim 2009). Graphene layers have attracted great attention for energy storage applications. Especially, they have been widely used as catalyst supports or non-noble catalysts for fuel cells (Zhong et al. 2012).

Besides experimental efforts which may be formidable and expensive at the nano-scale, there are three main approaches for modeling of nanostructures: (a) atomistic modeling, (b) hybrid atomistic-continuum mechanics and (c) continuum mechanics (Arash and Wang 2012). Both atomistic and hybrid atomistic-continuum mechanics are computationally expensive and are not suitable for analyzing large scale systems. Continuum mechanics approach is less computationally expensive than the former two approaches. It has been found that continuum mechanics results are in good agreement with atomistic and hybrid approaches (Pradhan and Kumar 2011). In recent years various size dependent continuum theories such as couple stress theory (Mindlin and Tiersten 1962; Toupin 1962), modified couple stress theory (Akgöz and Civalek 2013; Akgöz and Civalek 2011), strain gradient elasticity theory (Arani et al. 2012; Eringen 2002), and nonlocal elasticity theory (Civalek et al. 2010; Mohammadi et al. 2014) are proposed. These theories are comprised of information about the inter-atomic forces and internal lengths. Among these theories, nonlocal elasticity theory of Eringen (Mohammadi et al. 2014a, b; Eringen and Edelen 1972; Xu and Liao 2001) has been widely applied because of its simplicity, high reliability and close agreement with molecular dynamic simulations for mechanical analysis of carbon nanotubes and graphene sheets (Eringen and Edelen 1972). The nonlocal elasticity theory assumes that the stress at a point is a function of strains at all points in the continuum.

In this way, in the field of nanosheets analysis via Eringen nonlocal elasticity theory, Mohammadi et al. (2013) studied the post-buckling analysis of multilayer graphene sheet under the biaxial compression. They proved that the nonlocal parameter reduced the post-buckling load effects. Murmu et al. (2013) conducted buckling analysis of bi-layer nano graphene in nonlocal theory under biaxial compression via analytical solution using the classical plate theory with linear strains. It also demonstrated that nonlocal critical load was always less than local critical load. Anjomshoa et al. (2014) derived mechanical buckling equations of multi-layers of rectangular graphene sheet placed on an elastic foundation using the classical plate theory and finite element numerical method. Radic et al. (2014) published a study on mechanical buckling of multi-layers rectangular graphene sheet based on an elastic foundation and found that the nonlocal effect had great influence on higher buckling modes. The exact solution for vibrations and biaxial buckling the multilayers graphene sheet based on the Winkler elastic foundation were investigated by Murmu et al. (2014). The presented equations utilized the classical plate theory and proved that the critical temperature and natural frequencies were further affected by reducing the Winkler coefficient in high modes.

Also, in the field of thermal buckling of nanoplates, Malekzadeh et al. (2011) considered the Small scale effect on the thermal buckling of orthotropic arbitrary straight-sided quadrilateral nanoplates embedded in an elastic medium via classical plate theory. Zenkour and Sobhy (2013) analyzed the thermal buckling of rectangular nano graphene sheet based on the Winkler-Pasternak foundation. The sine function and sinusoidal plate theory was used to derive the equations. Wang et al. (2013) investigated the thermal buckling of nanoscale plate via classical and Mindlin plate theory, using simply supported boundary condition. Malekzadeh and Alibeygi (2014) analyzed the thermal buckling of orthotropic single layer graphene sheet using nonlinear elastic foundation. The classical theory and differential quadrature method was used, together with the Winkler elastic foundation which was modeled with the nonlinear spring. This method serves as a bench mark for future research.

The comparisons were made with the results of single layer graphene sheet in other researches in order to verify the results. The results of shear buckling were compared with Mohammadi et al. (2014) that were studied the shear buckling of orthotropic rectangular single layer nanoplate in thermal environment by classical plate theory. They showed that the difference between the shear buckling load calculated by isotropic and orthotropic plates decreases with increasing nonlocal parameter. Bassily and Dickinson (1972) who used the Ritz approach for buckling and lateral vibration of rectangular plates subject to inplane shear loads. Budiansky and Connor (1948) studied the buckling stress of clamped rectangular flat plate in shear via Lagrangian multiplier method. Cook and Rockey (1963) were investigated the shear buckling of rectangular plates with mixed boundary conditions using the Ritz method. Smith et al. (1999) considered the elastic buckling of unilaterally constrained rectangular plates in pure shear. They have used the Rayleigh–Ritz method for solved equations. In all the comparison papers were used classical plate theory for derived equations.

In this study, the shear and thermal buckling analysis of bi-layer graphene sheets (BLGs) based on polymer matrix using the first order shear deformation theory and via the nonlinear strain of Von-Karman with regard to nonlocal elasticity theory of Eringen was investigated. The equations for buckling analysis was derived by adjacent equilibrium criterion. The obtained equations were discretizing by differential quadrature method (DQM) which is a highly accurate numerical method. The DQ method utilized the nonuniform distribution of Chebyshev-Gauss–Lobatto method. Finally, the results of critical load changes were considered with changes in various parameters, such as nonlocal parameter, the length of plate and elastic stiffness of foundation.

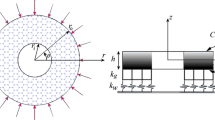
2 Governing equations

A rectangular graphene sheet is considered to have a thickness h, length L _x and width L _y as shown in Fig. 1. Most of the researches that have been conducted in field of graphene plate analysis via Eringen nonlocal theory are based on the classical plate theory (CLPT). This theory makes use of thin plate. In these plates, the ratio of thickness to the length is small, and the effects of transverse shear deformations being neglected. But this effect must be considered in the moderately thick plates and thick plates. To this end, the governing equations are derived based on the first order shear deformation theory (FSDT) and Von-Karman strains. According to the FSDT, the following displacement field can be expressed as:

Fig. 1

Schematic diagram of rectangular graphene sheet

$$U\left( {x,y,z} \right) = u\left( {x,y} \right) + z\varphi \left( {x,y} \right)$$

(1)

$$V\left( {x,y,z} \right) = v\left( {x,y} \right) + z\psi \left( {x,y} \right)$$

(2)

$$W\left( {x,y,z} \right) = w\left( {x,y} \right)$$

(3)

where u, v and w, are displacement components of mid-planes at x, y and z direction. $\varphi$ and $\psi$ are rotation components about of y and x axis. The properties of the plate considered to be orthotropic and are given as:

$$\left[ Q \right] = \left[ {\begin{array}{*{20}c} {\frac{{E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}} & {\frac{{\nu_{xy} E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}} & 0 & 0 & 0 \\ {\frac{{\nu_{yx} E_{x} }}{{1 - \nu_{xy} \nu_{yx} }}} & {\frac{{E_{y} }}{{1 - \nu_{xy} \nu_{yx} }}} & 0 & 0 & 0 \\ 0 & 0 & {G_{yz} } & 0 & 0 \\ 0 & 0 & 0 & {G_{xz} } & 0 \\ 0 & 0 & 0 & 0 & {G_{xy} } \\ \end{array} } \right]$$

(4)

$$\left[ {\sigma_{ij} } \right] = \left[ {Q_{ijkl} } \right].\left\{ {\varepsilon_{kl} } \right\}$$

(5)

In which $E_{x}$ and $E_{y}$ are the Young’s elasticity modulus along the x and y directions. $\nu_{xy} ,\nu_{yx}$ are the Poisson’s ratios and $G_{yz} ,G_{xz} ,G_{xy}$ are the shear modules. To consider, the von-Karman assumptions the nonlinear strains field are expressed as follows:

$$\varepsilon_{xx} = \frac{\partial u}{\partial x} + z\frac{\partial \varphi }{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - \alpha {}_{xx}\Delta T$$

(6)

$$\varepsilon_{yy} = \frac{\partial v}{\partial y} + z\frac{\partial \psi }{\partial y} + \frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} - \alpha {}_{yy}\Delta T$$

(7)

$$\gamma_{xz} = \frac{\partial w}{\partial x} + \varphi$$

(8)

$$\gamma_{yz} = \frac{\partial w}{\partial y} + \psi$$

(9)

$$\gamma_{xy} = \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right) + z\left( {\frac{\partial \varphi }{\partial y} + \frac{\partial \psi }{\partial x}} \right) + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}$$

(10)

In Eqs. (6) and (7) T _i is initial temperature [300 K = 27 °C (normal room temperature)] and the temperature can be uniformly raised to a final value is T _f (critical temperature).

According to Eringen theory, the local and nonlocal relations are defined as Eringen (2002)

$$\left( {1 - \mu \nabla^{2} } \right)\sigma_{ij}^{NonLocal} = \sigma_{ij}^{Local} {,}\quad\mu = (e_{0} a)^{2}$$

(11)

In Eq. (11), $\nabla^{2}$ is the Laplacian operator in Cartesian coordinates system:

$$\nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}$$

(12)

Here e ₀ is nonlocal elasticity constant proportionate with every material that is dependent on structure of nano materials. µ is a scale coefficient which describes the small scale effect for mechanical behavior of nanostructures [Value of e ₀ according to Eringen (1983) is 0.39 and Eringen (1972) is 0.31]. Also (a) is the connection length of two carbon atoms together (Narendar and Gopalakrishnan 2012). e ₀ a Coefficient taken from references is equal to $(0 < e_{0} a \le 2{\text{ nm)}}$ (Duan et al. 2007; Duan and Wang 2007).

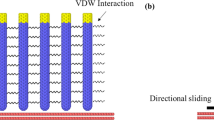
In Fig. 2 show BLGs on an elastic foundation. Using the principle of stationary total potential energy, the governing equations as well as the related boundary conditions along the edges of graphene plate can be derived. The equations of the total potential energy in case of non-local form are expressed as (Index 1 is for upper layer and index 2 is for lower layer):

Fig. 2

Schematic diagram of BLG sheets embedded on elastic matrix

$$\delta U_{k} = \iiint\limits_{v} {\sigma_{ij}^{NonLocal} \, \delta \, \varepsilon_{ij} dV\quad } \, i,j = x,y,z \, \left( {k = 1,2} \right)$$

(13)

$$\delta \varOmega_{1} = \int_{0}^{{L_{y} }} {\int_{0}^{{L_{x} }} {\left( {k_{o} \left( {w_{2} - w_{1} } \right)} \right)\delta w_{1} dxdy} }$$

(14)

$$\delta \varOmega_{2} = \int_{0}^{{L_{y} }} {\int_{0}^{{L_{x} }} {\left( { - k_{o} \left( {w_{2} - w_{1} } \right) + k_{G} \nabla^{2} w_{2} - k_{w} w_{2} } \right)\delta w_{2} dxdy} }$$

(15)

$$\frac{{\partial N_{x}^{NL} {\kern 1pt}_{i} }}{\partial x} + \frac{{\partial N_{xy}^{NL} {\kern 1pt}_{i} }}{\partial y} = 0 \, \left( {\text{i = 1, 2}} \right)$$

(16)

$$\frac{{\partial N_{y}^{NL} \;_{i} }}{\partial y} + \frac{{\partial N_{xy}^{NL} \;_{i} }}{\partial x} = 0 \, \left( {\text{i = 1, 2}} \right)$$

(17)

$$\frac{{\partial Q_{x}^{NL} \;_{1} }}{\partial x} + \frac{{\partial Q_{y}^{NL} \;_{1} }}{\partial y} + N_{x}^{NL} \;_{1} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} + 2 \times N_{xy}^{NL} \;_{1} \frac{{\partial^{2} w_{1} }}{\partial x\partial y} + N_{y}^{NL} \;_{ 1} {\kern 1pt} \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }} + k_{o} \left( {w_{2} - w_{1} } \right) = 0$$

(18)

$$\frac{{\partial Q_{x}^{NL} \;_{2} }}{\partial x} + \frac{{\partial Q_{y}^{NL} \;_{2} }}{\partial y} + N_{x}^{NL} \;_{2} \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + 2 \times N_{xy}^{NL} \;_{2} \frac{{\partial^{2} w_{2} }}{\partial x\partial y} + N_{y}^{NL} \;_{2} \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }} - k_{o} \left( {w_{2} - w_{1} } \right) + k_{G} \nabla^{2} w_{2} - k_{w} w_{2} = 0$$

(19)

$$\frac{{\partial M_{x}^{NL} \;_{i} }}{\partial x} + \frac{{\partial M_{xy}^{NL} \;_{i} }}{\partial y} - Q_{x}^{NL\;} \;_{i} = 0 \, \left( {\text{i = 1, 2}} \right)$$

(20)

$$\frac{{\partial M_{xy}^{NL} \;_{i} }}{\partial x} + \frac{{\partial M_{y}^{NL} \;_{i} }}{\partial y} - Q_{y}^{NL} \;_{i} \; = 0 \, \left( {\text{i = 1, 2}} \right)$$

(21)

$k_{w}$ and $k_{G}$ are the Winkler and Pasternak stiffness coefficient of elastic matrix and $k_{o}$ represents the van der Waals interaction bonds between the layers. Also N _i , M _i and Q _i (i = x, y, xy) are nonlocal stress resultants. Also subscript NL and L denotes the quantities in Nonlocal and Local, respectively. The stress resultants can be defined by the following relations:

$$(N_{x}^{L} ,N_{y}^{L} ,N_{xy}^{L} ) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\sigma_{x} ,\sigma_{y} ,\sigma_{xy} } \right)dz}$$

(22)

$$(M_{x}^{L} ,M_{y}^{L} ,M_{xy}^{L} ) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\sigma_{x} ,\sigma_{y} ,\sigma_{xy} } \right)zdz}$$

(23)

$$\left( {Q_{x}^{L} ,Q_{y}^{L} } \right) = k_{s} \times \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {\sigma_{xz} ,\sigma_{yz} } \right)} \, dz$$

(24)

In Eq. (24) k _s is the shear correction factor in the FSDT. The relations between stress resultants in local and nonlocal theories by using Eq. (11) are defined as below:

$$\left( {1 - \mu \nabla^{2} } \right)N_{j}^{NL} = N_{j}^{L} , \, j = x,y,xy$$

(25)

$$\left( {1 - \mu \nabla^{2} } \right)M_{j}^{NL} = M_{j}^{L} ,j = x,y,xy$$

(26)

$$\left( {1 - \mu \nabla^{2} } \right)Q_{j}^{NL} = Q_{j}^{L} ,j = x,y$$

(27)

For converting Eqs. (16)–(21) to local form using Eq. (25)–(27), the non-linear governing equations can be defined as (Dastjerdi et al. 2016):

$$\frac{{\partial N_{x \, }^{L} \;_{i} }}{\partial x} + \frac{{\partial N_{xy \, }^{L} \;_{i} }}{\partial y} = 0 \, \left( {\text{i = 1, 2}} \right)$$

(28)

$$\frac{{\partial N_{y}^{L} \;_{ \, i} }}{\partial y} + \frac{{\partial N_{xy}^{L} \;_{ \, i} }}{\partial x} = 0 \, \left( {\text{i = 1, 2}} \right)$$

(29)

$$\begin{aligned} \frac{{\partial Q_{x}^{L} \;_{1} }}{\partial x} + \frac{{\partial Q_{y}^{L} \;_{1} }}{\partial y} + \left( {1 - \mu \nabla^{2} } \right) \times \left( {N_{x}^{L} \;_{1} \frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} + 2N_{xy}^{L} \, _{1} \frac{{\partial^{2} w_{1} }}{\partial x\partial y} + N_{y}^{L} \;_{1} \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }}} \right) + \mu \left( {\left( {\nabla^{2} N_{x \, }^{L} \;_{1} } \right)\frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} + \left( {\nabla^{2} N_{y \, }^{L} \;_{1} } \right)\frac{{\partial^{2} w_{1} }}{{\partial y^{2} }}} \right. + \hfill \\ \left. {2\left( {\nabla^{2} N_{xy \, }^{L} \;_{1} } \right)\frac{{\partial^{2} w_{1} }}{\partial x\partial y}} \right) + \left( {1 - \mu \nabla^{2} } \right)k_{o} \left( {w_{2} - w_{1} } \right) = 0 \hfill \\ \end{aligned}$$

(30)

$$\begin{aligned} \frac{{\partial Q_{x}^{L} \;_{2} }}{\partial x} + \frac{{\partial Q_{y}^{L} \;_{2} }}{\partial y} + \left( {1 - \mu \nabla^{2} } \right) \times \left( {N_{x}^{L} \;_{2} \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + 2 \times N_{xy}^{L} \;_{2} \frac{{\partial^{2} w_{2} }}{\partial x\partial y} + N_{y}^{L} \;_{2} \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }}} \right) + \mu \left( {\left( {\nabla^{2} N_{x}^{L} \;_{2} } \right)\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + \left( {\nabla^{2} N_{y}^{L} \;_{2} } \right)\frac{{\partial^{2} w_{2} }}{{\partial y^{2} }}} \right. \hfill \\ \left. +{2\left( {\nabla^{2} N_{xy}^{L} \;_{2} } \right)\frac{{\partial^{2} w_{2} }}{\partial x\partial y}} \right) + \left( {1 - \mu \nabla^{2} } \right)\left( { - k_{o} \left( {w_{2} - w_{1} } \right) + k_{G} \nabla^{2} w_{2} - k_{w} w_{2} } \right) = 0 \hfill \\ \end{aligned}$$

(31)

$$\frac{{\partial M_{x}^{L} \;_{i} }}{\partial x} + \frac{{\partial M_{xy}^{L} \;_{\text{i}} }}{\partial y} - Q_{x}^{L} \;_{i} = 0 \, \left( {\text{i = 1, 2}} \right)$$

(32)

$$\frac{{\partial M_{xy}^{L} \;_{i} }}{\partial x} + \frac{{\partial M_{y}^{L} \;_{i} }}{\partial y} - Q_{y}^{L} \;_{i} = 0 \, \left( {\text{i = 1, 2}} \right)$$

(33)

The local stress resultant in Eqs. (28)–(33) with the help of Eqs. (22)–(24) are defined:

$$N_{xx} i = A_{11} \left( {\frac{\partial ui}{\partial x} + \frac{1}{2}\left( {\frac{\partial wi}{\partial x}} \right)^{2} } \right) + A_{12} \left( {\frac{\partial vi}{\partial y} + \frac{1}{2}\left( {\frac{\partial wi}{\partial y}} \right)^{2} } \right) - N_{xx}^{T} \, \left( {\text{i = 1,2}} \right)$$

(34)

$$N_{yy} i = A_{12} \left( {\frac{\partial ui}{\partial x} + \frac{1}{2}\left( {\frac{\partial wi}{\partial x}} \right)^{2} } \right) + A_{22} \left( {\frac{\partial vi}{\partial y} + \frac{1}{2}\left( {\frac{\partial wi}{\partial y}} \right)^{2} } \right) - N_{yy}^{T} \, \left( {\text{i = 1,2}} \right)$$

(35)

$$N_{xy} i = A_{66} \left( {\frac{\partial ui}{\partial y} + \frac{\partial vi}{\partial x} + \frac{\partial wi}{\partial y}\frac{\partial wi}{\partial x}} \right) \, \left( {\text{i = 1,2}} \right)$$

(36)

$$M_{xx} i = D_{11} \frac{\partial \varphi i}{\partial x} + D_{12} \frac{\partial \psi i}{\partial y} \, \left( {\text{i = 1,2}} \right)$$

(37)

$$M_{yy} i = D_{12} \frac{\partial \varphi i}{\partial x} + D_{22} \frac{\partial \psi i}{\partial y} \, \left( {\text{i = 1,2}} \right)$$

(38)

$$M_{xy} i = D_{66} \left( {\frac{\partial \varphi i}{\partial y} + \frac{\partial \psi i}{\partial x}} \right) \, \left( {\text{i = 1,2}} \right)$$

(39)

$$Q_{x} i = H_{55} \left( {\frac{\partial wi}{\partial x} + \varphi i} \right) \, \left( {\text{i = 1,2}} \right)$$

(40)

$$Q_{y} i = H_{55} \left( {\frac{\partial wi}{\partial y} + \psi i} \right) \, \left( {\text{i = 1,2}} \right)$$

(41)

Here, the quantities $N_{xx}^{T} , \, N_{yy}^{T}$ are the resultants due to the applied temperature. Constants A _ij (i, j = 1, 2, 6), D _ij (i, j = 1, 2, 6) and H ₄₄ , H ₅₅ in Eqs. (34)–(41) are defined by:

$$H_{44} = G_{yz} h \times k_{s} , \, H_{55} = G_{xz} h \times k_{s}$$

(42)

$$Q_{11} = \frac{{E_{x} }}{{1 - \upsilon_{xy} \upsilon_{yx} }}, \, Q_{22} = \frac{{E_{y} }}{{1 - \upsilon_{xy} \upsilon_{yx} }}, \, Q_{12} = \frac{{\upsilon_{yx} E_{x} }}{{1 - \upsilon_{xy} \upsilon_{yx} }}, \, Q_{66} = G_{xy}$$

(43)

$$\left( {A_{ij} ,D_{ij} } \right) = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {1,z^{2} } \right)} {\text{ Q}}_{\text{ij}} dz \, \left( {i,k = 1,2,6} \right)$$

(44)

The stability equations of the nanoplate are achieved using the adjacent equilibrium criterion. We assume u ⁰, v ⁰, w ⁰, ψ ⁰, φ ⁰, as the rotation and displacement components of the equilibrium state and u ¹, v ¹, w ¹, ψ ¹, φ ¹, as the virtual rotation and displacements corresponding to a neighboring state. The rotation and displacement components of the neighboring state are:

$$u = u^{0} + u^{1}$$

(45)

$$v = v^{0} + v^{1}$$

(46)

$$w = w^{0} + w^{1}$$

(47)

$$\varphi = \varphi^{0} + \varphi^{1}$$

(48)

$$\psi = \psi^{0} + \psi^{1}$$

(49)

The deflection and rotations in the pre-buckling configuration are w ⁰ = ψ ⁰ = φ ⁰ = 0. In addition, temperature at all zones of plate is constant, having no differential in two x and y directions ($T_{x} = T_{y} = T$), then $N_{xx,x}^{T} = N_{yy,y}^{T} = 0$. The prebuckling force can be

$$\begin{aligned}& N_{xx}^{0} = N_{xx}^{M0} + N_{xx}^{T0} \hfill \\& N_{yy}^{0} = N_{yy}^{M0} + N_{yy}^{T0} \hfill \\& N_{xy}^{0} = N_{xy}^{M0} \hfill \\ \end{aligned}$$

(50)

where $N_{xx}^{M0 \, } , \, N_{xx}^{T0}$ and $N_{xy}^{M0 \, }$ are mechanical, thermal and shear prebuckling forces (In this research for shear buckling analysis only considered shear forces and thermal effects are ignored $(\Delta T = 300k)$). By using the prebuckling equations, the thermal prebuckling forces are obtained as:

$$\begin{aligned} N_{xx}^{T0} = - \frac{{E_{x} h\Delta T}}{{1 - \upsilon_{xy} \upsilon_{yx} }}\left( {\alpha_{xx} + \upsilon_{yx} \alpha_{yy} } \right) \hfill \\ N_{yy}^{T0} = - \frac{{E_{y} h\Delta T}}{{1 - \upsilon_{xy} \upsilon_{yx} }}\left( {\alpha_{yy} + \upsilon_{xy} \alpha_{xx} } \right) \hfill \\ \end{aligned}$$

(51)

In the thermal buckling analysis, the shear in-plane forces $\left( {N_{xy}^{L} } \right)$ are ignored. Also, the following terms are:

$$\nabla^{2} N_{xx}^{L} = \nabla^{2} N_{yy}^{L} = \nabla^{2} N_{xy}^{L} = 0$$

(52)

Also, in shear buckling analysis, we consider the following relation for the shear prebuckling force (Mohammadi et al. 2014):

$$N_{xy}^{L} = p$$

(53)

For shear load on the edges of sheets, we define $p_{1}$ and ${\text{p}}_{ 2}$. The shear load apply on the upper layer edges is $p_{1}$, and likewise ${\text{p}}_{ 2}$ is apply on the lower layer edges. $k_{1} , \, k_{2}$ define the direction of shear load on sheets.

$$p_{1} = k_{1} \times p$$

(54)

$$p_{2} = k_{2} \times p$$

(55)

According to Fig. 3 the positive directions of the $p_{1} ,{\text{ p}}_{ 2}$ on the edges of every layer are shown (Bassily and Dickinson 1972). By substituting Eqs. (45)–(51) into Eqs. (28)–(33) the stability equations of thermal buckling based on displacement components are expressed as follows:

Fig. 3

Shear loading on bi-layer graphene nanoplate edges

$$\begin{aligned} H_{55} \left( {\frac{{\partial^{2} w_{1}^{1} }}{{\partial x^{2} }} + \frac{{\partial \varphi_{1}^{1} }}{\partial x}} \right) + H_{44} \left( {\frac{{\partial^{2} w_{1}^{1} }}{{\partial y^{2} }} + \frac{{\partial \psi_{1}^{1} }}{\partial y}} \right) - \mu \frac{{\partial^{4} w_{1}^{1} }}{{\partial x^{2} \partial y^{2} }}\left( {N_{xx}^{T0} + N_{yy}^{T0} } \right) + N_{xx}^{T0} \left( {\frac{{\partial^{2} w_{1}^{1} }}{{\partial x^{2} }}} \right.\left. { - \mu \frac{{\partial^{4} w_{1}^{1} }}{{\partial x^{4} }}} \right) + N_{yy}^{T0} \left( {\frac{{\partial^{2} w_{1}^{1} }}{{\partial y^{2} }} - \mu \frac{{\partial^{4} w_{1}^{1} }}{{\partial y^{4} }}} \right) \hfill \\ + \left( {1 - \mu \nabla^{2} } \right) \times \left( {k_{o} \left( {w_{2}^{1} - w_{1}^{1} } \right)} \right) = 0 \hfill \\ \end{aligned}$$

(56)

$$\begin{aligned} H_{55} \left( {\frac{{\partial^{2} w_{2}^{1} }}{{\partial x^{2} }} + \frac{{\partial \varphi_{2}^{1} }}{\partial x}} \right) + H_{44} \left( {\frac{{\partial^{2} w_{2}^{1} }}{{\partial y^{2} }} + \frac{{\partial \psi_{2}^{1} }}{\partial y}} \right) - \mu \frac{{\partial^{4} w_{2}^{1} }}{{\partial x^{2} \partial y^{2} }}\left( {N_{xx}^{T0} + N_{yy}^{T0} } \right) + N_{xx}^{T0} \left( {\frac{{\partial^{2} w_{2}^{1} }}{{\partial x^{2} }}} \right.\left. { - \mu \frac{{\partial^{4} w_{2}^{1} }}{{\partial x^{4} }}} \right) + N_{yy}^{T0} \left( {\frac{{\partial^{2} w_{2}^{1} }}{{\partial y^{2} }} - \mu \frac{{\partial^{4} w_{2}^{1} }}{{\partial y^{4} }}} \right) \hfill \\ + \left( {1 - \mu \nabla^{2} } \right)\left( { - k_{o} \left( {w_{2}^{1} - w_{1}^{1} } \right)} \right. + k_{G} \nabla^{2} w_{2}^{1} \left. { - k_{w} w_{2}^{1} } \right) = 0 \hfill \\ \end{aligned}$$

(57)

$$D_{11} \frac{{\partial^{2} \varphi^{1}_{i} }}{{\partial x^{2} }} + \left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \psi^{1}_{i} }}{\partial x\partial y} + D_{66} \frac{{\partial^{2} \varphi^{1}_{i} }}{{\partial y^{2} }} - H_{55} \left( {\frac{{\partial w^{1}_{i} }}{\partial x} + \varphi^{1}_{i} } \right) = 0 \, \left( {i = 1,2} \right)$$

(58)

$$D_{22} \frac{{\partial^{2} \psi^{1}_{i} }}{{\partial y^{2} }} + \left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \varphi^{1}_{i} }}{\partial x\partial y} + D_{66} \frac{{\partial^{2} \psi^{1}_{i} }}{{\partial x^{2} }} - H_{44} \left( {\frac{{\partial w^{1}_{i} }}{\partial y} + \psi^{1}_{i} } \right) = 0 \, \left( {i = 1,2} \right)$$

(59)

Also, by substituting Eqs. (45)–(50) and (58) into Eqs. (28)–(33) the stability equations of shear buckling based on displacement components can be obtained lead to Eqs. (60)–(63):

$$H_{55} \left( {\frac{{\partial^{2} w_{1}^{1} }}{{\partial x^{2} }} + \frac{{\partial \varphi_{1}^{1} }}{\partial x}} \right) + H_{44} \left( {\frac{{\partial^{2} w_{1}^{1} }}{{\partial y^{2} }} + \frac{{\partial \psi_{1}^{1} }}{\partial y}} \right) + 2 \times k_{1} \times p \times \left( {\frac{{\partial^{2} w_{1}^{1} }}{\partial x\partial y}} \right. - \mu \frac{{\partial^{4} w_{1}^{1} }}{{\partial x^{3} \partial y}}\left. { - \mu \frac{{\partial^{4} w_{1}^{1} }}{{\partial x\partial y^{3} }}} \right) + \left( {1 - \mu \nabla^{2} } \right)\left( {k_{o} \left( {w_{2}^{1} - w_{1}^{1} } \right)} \right) = 0$$

(60)

$$\begin{aligned} H_{55} \left( {\frac{{\partial^{2} w_{2}^{1} }}{{\partial x^{2} }} + \frac{{\partial \varphi_{2}^{1} }}{\partial x}} \right) + H_{44} \left( {\frac{{\partial^{2} w_{2}^{1} }}{{\partial y^{2} }} + \frac{{\partial \psi_{2}^{1} }}{\partial y}} \right) + 2 \times k_{2} \times p \times \left( {\frac{{\partial^{2} w_{2}^{1} }}{\partial x\partial y}} \right. - \mu \frac{{\partial^{4} w_{2}^{1} }}{{\partial x^{3} \partial y}} - \left. {\mu \frac{{\partial^{4} w_{2}^{1} }}{{\partial x\partial y^{3} }}} \right) - \left( {1 - \mu \nabla^{2} } \right) \times \left( {k_{o} \left( {w_{2}^{1} - w_{1}^{1} } \right)} \right. \hfill \\ - k_{G} \nabla^{2} w_{2}^{1} \left. { + k_{w} w_{2}^{1} } \right) = 0 \hfill \\ \end{aligned}$$

(61)

$$D_{11} \frac{{\partial^{2} \varphi^{1}_{i} }}{{\partial x^{2} }} + \left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \psi^{1}_{i} }}{\partial x\partial y} + D_{66} \frac{{\partial^{2} \varphi^{1}_{i} }}{{\partial y^{2} }} - H_{55} \left( {\frac{{\partial w^{1}_{i} }}{\partial x} + \varphi^{1}_{i} } \right) = 0 \, \left( {i = 1,2} \right)$$

(62)

$$D_{22} \frac{{\partial^{2} \psi^{1}_{i} }}{{\partial y^{2} }} + \left( {D_{12} + D_{66} } \right)\frac{{\partial^{2} \varphi^{1}_{i} }}{\partial x\partial y} + D_{66} \frac{{\partial^{2} \psi^{1}_{i} }}{{\partial x^{2} }} - H_{44} \left( {\frac{{\partial w^{1}_{i} }}{\partial y} + \psi^{1}_{i} } \right) = 0 \, \left( {i = 1,2} \right)$$

(63)

For numerical solution method especially for nanoscale problems, it is important to use dimensionless equations. By introducing the following non-dimensional parameters:

$$\begin{aligned} W^{1} = \frac{{w^{1} }}{{L_{x} }}, \, \alpha = \frac{{L_{x} }}{h}, \, \varPhi^{1} = \varphi^{1} , \, \varPsi^{1} = \psi^{1} , \, \xi = \frac{x}{{L_{x} }}, \, \eta = \frac{y}{{L_{y} }}, \, \beta = \frac{{L_{x} }}{{L_{y} }}, \, \varGamma = \frac{\mu }{{L_{x}^{2} }}, \, K_{G} = \frac{{k_{G} }}{{G_{xy} \times h}}, \, K_{W} = \frac{{k_{w} \times L_{x}^{2} }}{{G_{xy} \times h}}, \, \hfill \\ \lambda_{2} = \frac{{H_{44} \times L_{x}^{2} }}{{G_{xy} \times h^{3} }}, \, \delta_{1} = \frac{{D_{11} }}{{G_{xy} \times h^{3} }}, \, \delta_{2} = \frac{{D_{22} }}{{G_{xy} \times h^{3} }}, \, \delta_{3} = \frac{{D_{12} }}{{G_{xy} \times h^{3} }}, \, \delta_{4} = \frac{{D_{66} }}{{G_{xy} \times h^{3} }}, \, P_{1} = \frac{{p_{1} }}{{G_{xy} \times h}}, \, P_{2} = \frac{{p_{2} }}{{G_{xy} \times h}} \hfill \\ T_{\text{Cr}}^{ *} = 10^{3} \alpha_{xx} \Delta T_{cr} , \, N_{XX}^{T} \;^{0*} = \frac{{N_{xx}^{T0} }}{{G_{xy} \times h}}, \, N_{YY}^{T} \;^{0*} = \frac{{N_{yy}^{T0} }}{{G_{xy} \times h}}, \, K_{O} = \frac{{k_{o} \times L_{x}^{2} }}{{G_{xy} \times h}}, \, \lambda_{1} = \frac{{H_{55} \times L_{x}^{2} }}{{G_{xy} \times h^{3} }} \hfill \\ \end{aligned}$$

(64)

Equations (56)–(59) can be rewritten as the following non-dimensional form:

$$\begin{aligned} \frac{{\lambda_{1} }}{{\alpha^{2} }}\left( {\frac{{\partial^{2} W^{1}_{1} }}{{\partial \xi^{2} }} + \frac{{\partial \varPhi^{1}_{1} }}{\partial \xi }} \right) + \frac{{\lambda_{2} }}{{\alpha^{2} }}\left( {\beta^{2} \frac{{\partial^{2} W^{1}_{1} }}{{\partial \eta^{2} }} + \beta \frac{{\partial \varPsi^{1}_{1} }}{\partial \eta }} \right) - \varGamma \beta^{2} \times \frac{{\partial^{4} W^{1}_{1} }}{{\partial \xi^{2} \partial \eta^{2} }} \times \left( {N_{XX}^{T} \;^{0*} + N_{YY}^{T} \;^{0*} } \right) + N_{XX}^{T} \;^{0*} \left( {\frac{{\partial^{2} W^{1}_{1} }}{{\partial \xi^{2} }}} \right.\left. { - \varGamma \frac{{\partial^{4} W^{1}_{1} }}{{\partial \xi^{4} }}} \right) \hfill \\ + N_{YY}^{T} \;^{0*} \times \left( {\beta^{2} \frac{{\partial^{2} W^{1}_{1} }}{{\partial \eta^{2} }} - } \right.\left. {\varGamma \beta^{4} \frac{{\partial^{4} W^{1}_{1} }}{{\partial \eta^{4} }}} \right) + \left( {1 - \varGamma \left( {\frac{{\partial^{2} }}{{\partial \xi^{2} }} + \beta^{2} \frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right)} \right) \times K_{O} \left( {W^{1}_{2} - W^{1}_{1} } \right) = 0 \, \hfill \\ \end{aligned}$$

(65)

$$\frac{{\lambda _{1} }}{{\alpha ^{2} }}\left( {\frac{{\partial ^{2} W_{2}^{1} }}{{\partial \xi ^{2} }} + \frac{{\partial \Phi _{2}^{1} }}{{\partial \xi }}} \right) + \frac{{\lambda _{2} }}{{\alpha ^{2} }}\left( {\beta ^{2} \frac{{\partial ^{2} W_{2}^{1} }}{{\partial \eta ^{2} }} + \beta \frac{{\partial \Psi _{2}^{1} }}{{\partial \eta }}} \right) - \Gamma \beta ^{2} \times \frac{{\partial ^{4} W_{2}^{1} }}{{\partial \xi ^{2} \partial \eta ^{2} }} \times \left( {N_{{XX}}^{{T^{{0*}} }} + N_{{YY}}^{{T^{{0*}} }} } \right) + N_{{XX}}^{{T^{{0*}} }} \left( {\frac{{\partial ^{2} W_{2}^{1} }}{{\partial \xi ^{2} }}} \right.\left. { - \Gamma \frac{{\partial ^{4} W_{2}^{1} }}{{\partial \xi ^{4} }}} \right){\text{ }} + N_{{YY}}^{{T^{{0*}} }} \times \left( {\beta ^{2} \frac{{\partial ^{2} W_{2}^{1} }}{{\partial \eta ^{2} }} - } \right.\left. {\Gamma \beta ^{4} \frac{{\partial ^{4} W_{2}^{1} }}{{\partial \eta ^{4} }}} \right) - \left( {1 - \Gamma \left( {\frac{{\partial ^{2} }}{{\partial \xi ^{2} }} + \beta ^{2} \frac{{\partial ^{2} }}{{\partial \eta ^{2} }}} \right)} \right) \times K_{W} W_{2}^{1} - \left( {1 - \Gamma \left( {\frac{{\partial ^{2} }}{{\partial \xi ^{2} }} + \beta ^{2} \frac{{\partial ^{2} }}{{\partial \eta ^{2} }}} \right)} \right)K_{O} \left( {W_{2}^{1} - W_{1}^{1} } \right){\text{ }} + \left( {1 - \Gamma \left( {\frac{{\partial ^{2} }}{{\partial \xi ^{2} }} + \beta ^{2} \frac{{\partial ^{2} }}{{\partial \eta ^{2} }}} \right)} \right) \times \left( {\frac{{\partial ^{2} }}{{\partial \xi ^{2} }} + \beta ^{2} \frac{{\partial ^{2} }}{{\partial \eta ^{2} }}} \right)K_{G} W_{2}^{1} = 0{\text{ }}$$

(66)

$$\delta_{1} \frac{{\partial^{2} \varPhi^{1}_{i} }}{{\partial \xi^{2} }} + \left( {\delta_{3} + \delta_{4} } \right)\beta \frac{{\partial^{2} \varPsi^{1}_{i} }}{\partial \xi \partial \eta } + \delta_{4} \beta^{2} \frac{{\partial^{2} \varPhi^{1}_{i} }}{{\partial \eta^{2} }} - \lambda_{1} \left( {\frac{{\partial W^{1}_{i} }}{\partial \xi } + \varPhi^{1}_{i} } \right) = 0 \, \left( {i = 1,2} \right)$$

(67)

$$\delta_{2} \beta^{2} \frac{{\partial^{2} \varPsi^{1}_{i} }}{{\partial \eta^{2} }} + \left( {\delta_{3} + \delta_{4} } \right)\beta \frac{{\partial^{2} \varPhi^{1}_{i} }}{\partial \xi \partial \eta } + \delta_{4} \frac{{\partial^{2} \varPsi^{1}_{i} }}{{\partial \xi^{2} }} - \lambda_{2} \left( {\beta \frac{{\partial W^{1}_{i} }}{\partial \eta } + \varPsi^{1}_{i} } \right) = 0 \, \left( {i = 1,2} \right)$$

(68)

And, Eqs. (60)–(63) rewritten lead to Eqs. (69)–(72):

$$\begin{aligned} \frac{{\lambda_{1} }}{{\alpha^{2} }}\left( {\frac{{\partial^{2} W^{1} i}}{{\partial \xi^{2} }} + \frac{{\partial \varPhi^{1} i}}{\partial \xi }} \right) + \frac{{\lambda_{2} }}{{\alpha^{2} }}\left( {\beta^{2} \frac{{\partial^{2} W^{1} i}}{{\partial \eta^{2} }} + \beta \frac{{\partial \varPsi^{1} i}}{\partial \eta }} \right) + 2k_{1} P\beta \left( {\frac{{\partial^{2} W^{1} i}}{\partial \xi \partial \eta }} \right.\left. { - \varGamma \frac{{\partial^{4} W^{1} i}}{{\partial \xi^{3} \partial \eta }} - \beta^{2} \varGamma \frac{{\partial^{4} W^{1} i}}{{\partial \xi \partial \eta^{3} }}} \right) + \left( {1 - \varGamma \left( {\frac{{\partial^{2} }}{{\partial \xi^{2} }} + \beta^{2} \frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right)} \right) \times \hfill \\ K_{O} \left( {W^{1} 2 - W^{1} i} \right) = 0 \, \left( {i = 1} \right) \hfill \\ \end{aligned}$$

(69)

$$\begin{aligned} \frac{{\lambda_{1} }}{{\alpha^{2} }}\left( {\frac{{\partial^{2} W^{1} i}}{{\partial \xi^{2} }} + \frac{{\partial \varPhi^{1} i}}{\partial \xi }} \right) + \frac{{\lambda_{2} }}{{\alpha^{2} }}\left( {\beta^{2} \frac{{\partial^{2} W^{1} i}}{{\partial \eta^{2} }} + \beta \frac{{\partial \varPsi^{1} i}}{\partial \eta }} \right) + 2k_{2} P\beta \left( {\frac{{\partial^{2} W^{1} i}}{\partial \xi \partial \eta }} \right.\left. { - \varGamma \frac{{\partial^{4} W^{1} i}}{{\partial \xi^{3} \partial \eta }} - \beta^{2} \varGamma \frac{{\partial^{4} W^{1} i}}{{\partial \xi \partial \eta^{3} }}} \right) - \left( {1 - \varGamma \left( {\frac{{\partial^{2} }}{{\partial \xi^{2} }} + \beta^{2} \frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right)} \right) \times \hfill \\ K_{W} W^{1} i - \left( {1 - \varGamma \left( {\frac{{\partial^{2} }}{{\partial \xi^{2} }} + \beta^{2} \frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right)} \right) \times K_{O} \left( {W^{1} i - W^{1} 1} \right) + \left( {1 - \varGamma \left( {\frac{{\partial^{2} }}{{\partial \xi^{2} }} + \beta^{2} \frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right)} \right)\left( {\frac{{\partial^{2} }}{{\partial \xi^{2} }} + \beta^{2} \frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right)K_{G} W^{1} i = 0 \, \left( {i = 2} \right) \hfill \\ \end{aligned}$$

(70)

$$\delta_{1} \frac{{\partial^{2} \varPhi^{1} i}}{{\partial \xi^{2} }} + \left( {\delta_{3} + \delta_{4} } \right)\beta \frac{{\partial^{2} \varPsi^{1} i}}{\partial \xi \partial \eta } + \delta_{4} \beta^{2} \frac{{\partial^{2} \varPhi^{1} i}}{{\partial \eta^{2} }} - \lambda_{1} \left( {\frac{{\partial W^{1} i}}{\partial \xi } + \varPhi^{1} i} \right) = 0 \, \left( {i = 1,2} \right)$$

(71)

$$\delta_{2} \beta^{2} \frac{{\partial^{2} \varPsi^{1} i}}{{\partial \eta^{2} }} + \left( {\delta_{3} + \delta_{4} } \right)\beta \frac{{\partial^{2} \varPhi^{1} i}}{\partial \xi \partial \eta } + \delta_{4} \frac{{\partial^{2} \varPsi^{1} i}}{{\partial \xi^{2} }} - \lambda_{2} \left( {\beta \frac{{\partial W^{1} i}}{\partial \eta } + \varPsi^{1} i} \right) = 0 \, \left( {i = 1,2} \right)$$

(72)

3 Solving the stability equations

In this paper, in order to solve the equilibrium equations the differential quadrature method (DQM) was applied. Differential quadrature is a numerical method which was proposed for time by Bellman and Casti (1971). The DQ method is based on the approximation of partial derivative of a function at a point and is affected by the values of the function in the whole domain (Bellman et al. 1993). This method is highly accurate compared to many other numerical methods, such as Finite Difference method (FD), which is convenient in formulation when compared with Dynamic Relaxation method (DR), and compatible for solving the partial differential equations (Shu 2000). The method can easily and precisely apply a variety of boundary conditions (Dastjerdi and Jabbarzadeh 2015).

First, with implementation of DQM into the Eqs. (65)–(68), the upper layers equations can be obtained:

$$\frac{{\lambda _{1} }}{{\alpha ^{2} }}\left( {\sum\limits_{{k = 1}}^{N} {C_{{ik}}^{{(2)}} } W_{1}^{1} \left( {x_{k} ,y_{j} } \right) + \sum\limits_{{k = 1}}^{N} {C_{{ik}}^{{(1)}} } \Phi _{1}^{1} \left( {x_{k} ,y_{j} } \right)} \right) + \frac{{\lambda _{2} }}{{\alpha ^{2} }} \times \left( {\beta ^{2} \sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(2)}} } W_{1}^{1} \left( {x_{i} ,y_{r} } \right) + \beta \sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(1)}} } \Psi _{1}^{1} \left( {x_{i} ,y_{r} } \right)} \right) - K_{O}^{*} \Gamma \times {\text{ }}\left[ {\left( {\sum\limits_{{k = 1}}^{N} {C_{{ik}}^{{(2)}} } W_{2}^{1} \left( {x_{k} ,y_{j} } \right) + \beta ^{2} \sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(2)}} } W_{2}^{1} \left( {x_{i} ,y_{r} } \right)} \right)} \right. - \left. {\left( {\sum\limits_{{k = 1}}^{N} {C_{{ik}}^{{(2)}} } W_{1}^{1} \left( {x_{k} ,y_{j} } \right) + \beta ^{2} \sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(2)}} } W_{1}^{1} \left( {x_{i} ,y_{r} } \right)} \right)} \right] + K_{O}^{*} \times {\text{ }}\left( {W_{2}^{1} - W_{1}^{1} } \right) + N_{{XX}}^{{T^{{0*}} }} \sum\limits_{{k = 1}}^{N} {C_{{ik}}^{{(2)}} } W_{1}^{1} \left( {x_{k} ,y_{j} } \right) + \beta ^{2} \times N_{{YY}}^{{T^{{0*}} }} \times \sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(2)}} } W_{1}^{1} \left( {x_{i} ,y_{r} } \right) - \Gamma \times N_{{XX}}^{{T^{{0*}} }} \sum\limits_{{k = 1}}^{N} {C_{{ik}}^{{(4)}} } W_{1}^{1} \left( {x_{k} ,y_{j} } \right) - {\text{ }}\Gamma \beta ^{4} \times N_{{YY}}^{{T^{{0*}} }} \sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(4)}} } W_{1}^{1} \left( {x_{i} ,y_{r} } \right) - \Gamma \times \beta ^{2} \left( {N_{{XX}}^{{T^{{0*}} }} + N_{{YY}}^{{T^{{0*}} }} } \right) \times \sum\limits_{{k = 1}}^{N} {\sum\limits_{{r = 1}}^{M} {C_{{ik}}^{{(2)}} W_{1}^{1} \left( {x_{k} ,y_{r} } \right)} } C_{{jr}}^{{(2)}} = 0$$

(73)

$$\begin{aligned} \delta_{1} \sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } \varPhi^{1}_{1} \left( {x_{k} ,y_{j} } \right) + \left( {\delta_{3} + \delta_{4} } \right)\beta \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} \varPsi^{1}_{1} \left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} + \delta_{4} \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } \varPhi^{1}_{1} \left( {x_{i} ,y_{r} } \right) - \lambda_{1} \sum\limits_{k = 1}^{N} {C_{ik}^{(1)} } W^{1}_{1} \left( {x_{k} ,y_{j} } \right) - \hfill \\ \lambda_{1} \varPhi^{1}_{1} = 0 \hfill \\ \end{aligned}$$

(74)

$$\begin{aligned} \delta_{4} \sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } \varPsi^{1}_{1} \left( {x_{k} ,y_{j} } \right) + \delta_{2} \beta^{2} \sum\limits_{k = 1}^{M} {C_{jr}^{(2)} } \varPsi^{1}_{1} \left( {x_{i} ,y_{r} } \right) + \left( {\delta_{3} + \delta_{4} } \right)\beta \times \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} \varPhi^{1}_{1} \left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} - \lambda_{2} \beta \sum\limits_{k = 1}^{M} {C_{jr}^{(1)} } W^{1}_{1} \left( {x_{i} ,y_{r} } \right) \hfill \\ - \lambda_{2} \varPsi^{1}_{1} = 0 \hfill \\ \end{aligned}$$

(75)

Then, the lower layer equations will be displayed as follow:

$$\begin{aligned} \frac{{\lambda {}_{1}}}{{\alpha^{2} }}\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1}_{2} \left( {x_{k} ,y_{j} } \right) + \sum\limits_{k = 1}^{N} {C_{ik}^{(1)} } \varPhi^{1}_{2} \left( {x_{k} ,y_{j} } \right)} \right) + \frac{{\lambda {}_{2}}}{{\alpha^{2} }} \times \left( {\beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1}_{2} \left( {x_{i} ,y_{r} } \right) + \beta \sum\limits_{r = 1}^{M} {C_{jr}^{(1)} } \varPsi^{1}_{2} \left( {x_{i} ,y_{r} } \right)} \right) - K_{O}^{*} \hfill \\ \times\left( {W^{1}_{2} } \right.\left. { - W^{1}_{1} } \right) + K_{O}^{*} \varGamma \left[ {\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1}_{2} \left( {x_{k} ,y_{j} } \right) + } \right.} \right.\beta^{2} \times \left. {\sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1}_{2} \left( {x_{i} ,y_{r} } \right)} \right) - \left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1}_{1} \left( {x_{k} ,y_{j} } \right)} \right. + \beta^{2} \hfill \\ \times\left. {\left. {\sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1}_{1} \left( {x_{i} ,y_{r} } \right)} \right)} \right] - K_{W}^{*} W^{1}_{2} + K_{W}^{*} \varGamma \times \left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1}_{2} \left( {x_{k} ,y_{j} } \right)} \right.\left. { + \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1}_{2} \left( {x_{i} ,y_{r} } \right)} \right) + K_{G}^{*} \hfill \\ \times\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1}_{2} \left( {x_{k} ,y_{j} } \right) + } \right.\beta^{2} \times \left. {\sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1}_{2} \left( {x_{i} ,y_{r} } \right)} \right) - K_{G}^{*} \varGamma \times \left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(4)} } W^{1}_{2} \left( {x_{k} ,y_{j} } \right) + 2\beta^{2} } \right.\sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(2)} W^{1}_{2} \left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(2)} \hfill \\ + \beta ^{4} \left. {\sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(4)}} } W_{2}^{1} \left( {x_{i} ,y_{r} } \right)} \right) + N_{{XX}}^{{T^{{0*}} }} \times \sum\limits_{{k = 1}}^{N} {C_{{ik}}^{{(2)}} } W_{2}^{1} \left( {x_{k} ,y_{j} } \right) + \beta ^{2} \times N_{{YY}}^{{T^{{0*}} }} \sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(2)}} } W_{2}^{1} \left( {x_{i} ,y_{r} } \right) - \Gamma N_{{XX}}^{{T^{{0*}} }} \\ \times\sum\limits_{{k = 1}}^{N} {C_{{ik}}^{{(4)}} } W_{2}^{1} \left( {x_{k} ,y_{j} } \right) - \Gamma \beta ^{4} N_{{YY}}^{{T^{{0*}} }} \times \sum\limits_{{r = 1}}^{M} {C_{{jr}}^{{(4)}} } W_{2}^{1} \left( {x_{i} ,y_{r} } \right) - \Gamma \beta ^{2} \left( {N_{{XX}}^{{T^{{0*}} }} + N_{{YY}}^{{T^{{0*}} }} } \right) \times \sum\limits_{{k = 1}}^{N} {\sum\limits_{{r = 1}}^{M} {C_{{ik}}^{{(2)}} W_{2}^{1} \left( {x_{k} ,y_{r} } \right)} } C_{{jr}}^{{(2)}} = 0 \, \hfill \\ \end{aligned}$$

(76)

$$\begin{aligned} \delta_{1} \sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } \varPhi^{1}_{2} \left( {x_{k} ,y_{j} } \right) + \left( {\delta_{3} + \delta_{4} } \right)\beta \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} \varPsi^{1}_{2} \left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} + \delta_{4} \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } \varPhi^{1}_{2} \left( {x_{i} ,y_{r} } \right) - \lambda_{1} \sum\limits_{k = 1}^{N} {C_{ik}^{(1)} } W^{1}_{2} \left( {x_{k} ,y_{j} } \right) \hfill \\ - \lambda_{1} \varPhi^{1}_{2} = 0 \hfill \\ \end{aligned}$$

(77)

$$\begin{aligned} \delta_{4} \sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } \varPsi^{1}_{2} \left( {x_{k} ,y_{j} } \right) + \delta_{2} \beta^{2} \sum\limits_{k = 1}^{M} {C_{jr}^{(2)} } \varPsi^{1}_{2} \left( {x_{i} ,y_{r} } \right) + \left( {\delta_{3} + \delta_{4} } \right) \times \beta \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} \varPhi^{1}_{2} \left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} - \lambda_{2} \beta \sum\limits_{k = 1}^{M} {C_{jr}^{(1)} } W^{1}_{2} \left( {x_{i} ,y_{r} } \right) \hfill \\ - \lambda_{2} \varPsi^{1}_{2} = 0 \hfill \\ \end{aligned}$$

(78)

The shear buckling stability equations of BLGs, lead to Eqs. (69)–(72), the upper and lower layers equations can be obtained:

$$\begin{aligned} \frac{{\lambda_{1} }}{{\alpha^{2} }}\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1} i\left( {x_{k} ,y_{j} } \right) + \sum\limits_{k = 1}^{N} {C_{ik}^{(1)} } \varPhi^{1} i\left( {x_{k} ,y_{j} } \right)} \right) + \frac{{\lambda_{2} }}{{\alpha^{2} }}\left( {\beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1} i\left( {x_{i} ,y_{r} } \right) + \beta \sum\limits_{r = 1}^{M} {C_{jr}^{(1)} } \varPsi^{1} i\left( {x_{i} ,y_{r} } \right)} \right) - K_{O} \varGamma \hfill \\ \left[ {\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1} 2\left( {x_{k} ,y_{j} } \right) + \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1} 2\left( {x_{i} ,y_{r} } \right)} \right)} \right. - \left. {\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1} i\left( {x_{k} ,y_{j} } \right) + \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1} i\left( {x_{i} ,y_{r} } \right)} \right)} \right] + K_{O} \left( {W^{1} 2 - W^{1} i} \right) \hfill \\ + 2k_{1} P\beta \left( {\sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} W^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} - \varGamma \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(3)} W^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} - \varGamma \beta^{2} \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} W^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(3)} } \right) = 0 \, \left( {i = 1} \right) \hfill \\ \end{aligned}$$

(79)

$$\begin{aligned} \frac{{\lambda_{1} }}{{\alpha^{2} }}\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1} i\left( {x_{k} ,y_{j} } \right) + \sum\limits_{k = 1}^{N} {C_{ik}^{(1)} } \varPhi^{1} i\left( {x_{k} ,y_{j} } \right)} \right) + \frac{{\lambda_{2} }}{{\alpha^{2} }}\left( {\beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1} i\left( {x_{i} ,y_{r} } \right) + \beta \sum\limits_{r = 1}^{M} {C_{jr}^{(1)} } \varPsi^{1} i\left( {x_{i} ,y_{r} } \right)} \right) - K_{O} \left( {W^{1} i} \right.\left. { - W^{1} 1} \right) \hfill \\ + K_{O} \varGamma \left[ {\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1} i\left( {x_{k} ,y_{j} } \right) + \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1} i\left( {x_{i} ,y_{r} } \right)} \right)} \right. - \left. {\left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1} 1\left( {x_{k} ,y_{j} } \right) + \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1} 1\left( {x_{i} ,y_{r} } \right)} \right)} \right] - K_{W} W^{1} i \hfill \\ + K_{W} \varGamma \left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1} i\left( {x_{k} ,y_{j} } \right) + \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1} i\left( {x_{i} ,y_{r} } \right)} \right) + K_{G} \left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } W^{1} i\left( {x_{k} ,y_{j} } \right) + \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } W^{1} i\left( {x_{i} ,y_{r} } \right)} \right) - K_{G} \varGamma \hfill \\ \left( {\sum\limits_{k = 1}^{N} {C_{ik}^{(4)} } W^{1} i\left( {x_{k} ,y_{j} } \right) + 2\beta^{2} \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(2)} W^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(2)} + } \right.\beta^{4} \left. {\sum\limits_{r = 1}^{M} {C_{jr}^{(4)} } W^{1} i\left( {x_{i} ,y_{r} } \right)} \right) + 2k_{2} P\beta \hfill \\ \left( {\sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} W^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} - \varGamma \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(3)} W^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} - \varGamma \beta^{2} \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} W^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(3)} } \right) = 0 \, \left( {i = 2} \right) \hfill \\ \end{aligned}$$

(80)

$$\begin{aligned} \delta_{1} \sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } \varPhi^{1} i\left( {x_{k} ,y_{j} } \right) + \left( {\delta_{3} + \delta_{4} } \right)\beta \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} \varPsi^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} + \delta_{4} \beta^{2} \sum\limits_{r = 1}^{M} {C_{jr}^{(2)} } \varPhi^{1} i\left( {x_{i} ,y_{r} } \right) - \lambda_{1} \sum\limits_{k = 1}^{N} {C_{ik}^{(1)} } W^{1} i\left( {x_{k} ,y_{j} } \right) \hfill \\ -\lambda_{1} \varPhi^{1} i = 0 \, \left( {i = 1,2} \right) \hfill \\ \end{aligned}$$

(81)

$$\begin{aligned} \delta_{4} \sum\limits_{k = 1}^{N} {C_{ik}^{(2)} } \varPsi^{1} i\left( {x_{k} ,y_{j} } \right) + \delta_{2} \beta^{2} \sum\limits_{k = 1}^{M} {C_{jr}^{(2)} } \varPsi^{1} i\left( {x_{i} ,y_{r} } \right) + \left( {\delta_{3} + \delta_{4} } \right)\beta \sum\limits_{k = 1}^{N} {\sum\limits_{r = 1}^{M} {C_{ik}^{(1)} \varPhi^{1} i\left( {x_{k} ,y_{r} } \right)} } C_{jr}^{(1)} - \lambda_{2} \beta \sum\limits_{k = 1}^{M} {C_{jr}^{(1)} } W^{1} i\left( {x_{i} ,y_{r} } \right) \hfill \\ -\lambda_{2} \varPsi^{1} i = 0 \, \left( {i = 1,2} \right) \hfill \\ \end{aligned}$$

(82)

4 Boundary conditions

In order to complete the formulation, the stability equations should be accompanied by a set of boundary conditions. The following cases of boundary conditions are used in this study:

Simply supported (S):

$$\begin{aligned} W = 0, \, \varPsi = 0, \, M_{\xi } = 0{ : }\xi = 0,1 \hfill \\ W = 0, \, \varPhi = 0, \, M_{\eta } = 0{ : }\eta = 0,1 \hfill \\ \end{aligned}$$

(83)

Clamped (C):

$$\begin{aligned} W = 0, \, \varPsi = 0, \, \varPhi = 0{ : }\xi = 0,1 \hfill \\ W = 0, \, \varPsi = 0, \, \varPhi = 0{ : }\eta = 0,1 \hfill \\ \end{aligned}$$

(84)

Free edges (F):

$$\begin{aligned} {\text{Q}}_{\xi } { = 0, }M_{\xi } { = 0, }M_{\xi \eta } { = 0 : }\xi = 0,1 \hfill \\ {\text{Q}}_{\eta } { = 0, }M_{\eta } { = 0, }M_{\xi \eta } { = 0 : }\eta = 0,1 \hfill \\ \end{aligned}$$

(85)

5 Results of Shear buckling

First, in the survey of convergence of the grid points required on BLGs, the grid points changes are based on the critical shear load as shows in Fig. 4. As shown in the figure, with nine nodes in each direction, high accurate and suitable results are obtained.

Fig. 4

Critical shear load versus the number of grid points for DQM domain (k ₁ = 1, k ₂ = 1, e ₀ a = 2 nm, β = 1)

In order to validate the numerical results, the results was obtained using differential quadrature method to compare the convergence results for simply supported and clamped boundary conditions with Mohammadi et al. (2014) that is based on classical plate theory as shown in Table 1 (In this reference used DQ method). The results in Table 2 were compared with Bassily and Dickinson (1972), Budiansky and Connor (1948), Cook and Rockey (1963) and Smith et al. (1999) according to Tables 1 and 2 in Mohammadi et al. (2014a, b). It can be seen that the results herein are in agreement with the other results reported.

Table 1 Convergence study and minimum number of grid points (M = N) required to obtain accurate results for different boundary conditions (first mode number)

Table 2 Convergence and comparison of the buckling loads with increasing number of terms taken in the displacement series

In order to further clarify the convergence of the shear load, the numerical results in Table 3 were obtained for orthotropic single-layered graphene sheets (Mohammadi et al. 2014). Mohammadi et al. (2014) for obtained the governing equations used the CPLT and the equations were solved with DQ method. The numerical results (DQ and Galerkin method results) are listed in Table 3 for various nonlocal parameters.

Table 3 Comparison of the DQM results with those of the Galerkin method for nonlocal orthotropic plates

Geometrical and material properties of Graphene nanoplate, elastic foundation properties used in the parametric study as follow (Dastjerdi and Jabbarzadeh 2015; Golmakani and Rezatalab 2015):

Lx (nm)	Ly (nm)	Ex (Gpa)	Ey (Gpa)	k w (Gpa/nm)	k G (pa.m)	υ xy	υ yx	h (nm)
10.2	10.2	1765	1588	1.13	1.13	0.3	0.27	0.34

Also for shear correction factor used value 5/6 (Dastjerdi and Jabbarzadeh 2015; Golmakani and Rezatalab 2015), and vdW interaction coefficient taken are 45 Gpa/nm (Pradhan and Phadikar 2009; Farajpour et al. 2013).

Figure 5 shows the critical shear load based on μ parameter for several values of aspect ratio (β). As shown in the figure, the critical shear load decreases with increase in nonlocal parameter. Also, the results of the critical shear load in nanoplate with β greater than one was more than the nanoplate with β equal to one.

Fig. 5

The effects of length versus the nonlocal parameter (k ₁ = 1, k ₂ = 1, Ly = 10.2 nm)

Figure 6 shows the critical shear load based on the small scale effects of various boundary conditions. As shown in the figure, whenever there is an increase in the numbers of free edges adjacent to each other, the effect of nonlocal parameter on the boundary condition is reduced. Also in boundary conditions with less flexibility, the shear critical load increased.

Fig. 6

The effects of small scale parameter on various boundary conditions (k ₁ = 1, k ₂ = 1, β = 1)

In Fig. 7 the different types of shear loading on the edges for two boundary conditions is shown. It is obvious that, due to the behavior of the orthotropic material as a results of shift in the direction of the load, there was a change in the results. When the shear load on the edges of the two layers are in the opposite direction, shear critical load will reduce as compared with when the loads are in similar direction.

Fig. 7

Types of loading versus the small scale parameter changes (β = 1)

Figure 8 shows the effect of nonlocal parameter on the critical load in the three types of loading. Figure 8a plotted for BLGs on a weak elastic foundation. In the first case, only the top layer has the shear load, in the second case only the bottom layer and in the third case, both layers have the shear load. As demonstrated in the figure, when only the shear load is located on the edges of the bottom layer, the critical load becomes higher than other cases. It has been shown that, in the local analysis (μ = 0 nm²), the difference between the results of cases 1 and 2 is almost close. In study of the strong foundation (Fig. 8b), the results of the distances between the two cases were more than the initial state. But in considering the small scale effects, by increasing the nonlocal parameter, this difference increased further. Hence, results show that the change in loading direction, had little effect on the critical shear load in local analysis.

Fig. 8

a The effects of loading type on critical load changes (CCCC, β = 1). b The effects of loading type on critical load changes in various Winkler stiffness (CCCC, β = 1)

Figure 9 shows the nonlocal parameter versus dimensionless ratio (Lx/h) for clamped boundary condition. For this purpose, the length and width are equal and constant, but the thickness is variable. By increasing the thickness, the effect of nonlocal parameter on the results will increase. Figure 9b indicate the effect of thickness on the critical shear load in three types of loading. It can be concluded that, in the analysis of nonlocal graphene sheets with reduced thickness, the differences in the results of the three types of loading will increase further.

Fig. 9

a The effects of length to thickness ratio on critical shear load (k ₁ = 1, k ₂ = 1, Lx = Ly = 10.2 nm, CCCC). b The effects of length to thickness ratio on critical shear load (e ₀ a = 1 nm, Lx = Ly = 10.2 nm, CCCC)

For comparing nonlocal elasticity theory with local definition R parameter as a following:

$$R = \frac{{P{}_{critical} \, _{NL} }}{{P{}_{critical} \, _{L} }}$$

(86)

Figure 10 evaluates the results of nonlocal to local for the two boundary conditions. In this case the width of nanoplate is constant and the length is variable. As shown in the figure, when the boundary condition is less flexible, the difference between the nonlocal solutions to local becomes closer. Beside, by increasing the aspect ratio, the results of the two theories become close.

Fig. 10

Variations of R ratio versus β parameter (k ₁ = 1, k ₂ = 1, Ly = 10.2 nm, e ₀ a = 2 nm)

Figure 11 shows the critical shear load results versus Winkler stiffness for clamped boundary condition. It is clear that in the low stiffness value of elastic foundation, the changes in k _w had further effect on the critical load. Also, by increasing the stiffness of elastic foundation, the effects of μ on the critical load has decrease.

Fig. 11

Nonlocal parameter versus Winkler stiffness (CCCC, β = 1, k ₁ = 1, k ₂ = 1)

6 Results of thermal buckling

In considering the accuracy of thermal buckling results, the results with references Zenkour and Sobhy (2013) and Wang et al. (2013) were compared. Zenkour and Sobhy (2013) Solved the thermal buckling of single layer nanoplate resting on the elastic foundation using variety plate theory via nonlinear strains, and assumed that the graphene sheet was an isotropic plate (Table 4). Also Wang et al. (2013) solved the thermal buckling of single layer nanoplate via linear CLPT and FSDT without considering the elastic foundation, with the assumption that the graphene sheet was an isotropic plate. In order to obtain the results in Table 5, the governing equations in Wang et al. (2013) were solved.

Table 4 Comparison of dimensionless ratio of length to the width with Zenkour and Sobhy (2013)

Table 5 Comparison of ratio of nonlocal to the local with Wang et al. (2013)

The coefficient of thermal expansion are considered for orthotropic graphene sheet, α _yy  = α _xx /3 from Mohammadi et al. (2014) and Benzair et al. (2008) and are taken α _xx  = 1.1e-6 1/k from Mohammadi et al. (2014, Benzair et al. 2008) for room temperature.

Figure 12 shows the dimensionless critical temperature of buckling based on the nonlocal parameter expressed such that an increase in the nonlocal parameter resulted in a decrease in the critical temperature. Also, with more flexible boundary conditions, the critical temperature increased further. As can be seen, in all boundary conditions between local value (zero) and μ = 2 nm² the slope of the diagrams is steep and tend downward. But in larger values from μ = 2 nm², the slope of the diagrams is slower. Also, with increasing nonlocal parameter, the critical temperature values in variety of boundary conditions were almost similar.

Fig. 12

Effects of small scale parameter on dimensionless critical temperature changes (β = 1)

Figure 13 displays the dimensionless critical temperature changes in the dimensionless ratio (Lx/h) in variety of nonlocal parameter for clamped boundary condition. For this purpose, the length and width were equal and constant, but the thickness varied. By increasing the thickness, the critical temperature increased, and also with increasing thickness, the effect of nonlocal parameter on the critical temperature increased. In comparing nonlocal elasticity theory with local, the definition R _T parameter is as follows:

Fig. 13

Effects of length to the thickness ratio on dimensionless critical temperature changes (CCCC, β = 1)

$$R_{T} = \frac{{T_{Critical} NonLocal}}{{T_{Critical} Local}}$$

(87)

Figure 14 shows the changes in parameter R _T based on the parameter β (Lx/Ly).To this end, we hypothesized that plate length increased and its width was constant. It can be seen that with increasing β and also boundary condition being more flexible, the results of two theory were almost similar. It is noteworthy that in the field of small scale, due to use of nonlocal elasticity theory for the same aspect ratio (β) but different sizes, various results were achieved. For example, for β = 2 the results of critical temperature were not equal. Meaning that, if the length of plate is selected as 20.4 nm and its width as 10.2 nm and in other state the length as 10.2 nm and its width as 5.1 nm, various results for critical temperature will be obtained. This is due to the effects of dimensions on the results of nonlocal elasticity theory. In considering this issue, Fig. 15 is presented for SSSF boundary condition. In the same aspect ratio, the critical temperature of buckling increased with increasing plate dimensions.

Fig. 14

Influence of R _T on dimensionless critical temperature changes in rectangular plate (Ly = 10.2 nm = constant, e ₀ a = 2 nm)

Fig. 15

Influence of plate dimensions on R _T in rectangular plate (Ly = 10.2 nm = constant, SSSF)

The effects of coefficient of van der Waals on the results are investigated in Fig. 16. A discussion concerning two states of nanoplates buckling will be made here. In the first case, it is assumed that two nanoplates are bonded by an internal elastic medium (Murmu et al. 2014). In this state the nanoplates demonstrated buckling in opposite or same directions, implying that the system is double-nanoplate and has two single layer with behaviors independent of each other. In the other case, the buckling of nanoplates is only in the same direction, resulting in a synchronous buckling. In this case, two single layers are converted to a bi-layer sheets (Double-layer). Figure 16 indicates the critical temperature based on the vdW coefficient in the several of nonlocal parameter. The vdW coefficient from 30 Gpa/nm to the next had no effect on the critical temperature in clamped-free boundary conditions. Therefore, according to Fig. 16, it is obvious that the value of vdW coefficient in Pradhan and Phadikar (2009) and Farajpour et al. (2013) are suitable.

Fig. 16

Influence of nonlocal parameter on vdW interaction coefficient changes (β = 1, CCCF)

Figure 17 displays the plate in two cases, in first case, the plate is with a foundation and in the other case the plate is without foundation. In CCCC boundary condition, with elastic foundation, the difference between the results of two cases was more, whenever the flexibility of boundary condition increased, the difference of results reduced in the two cases.

Fig. 17

Comparison of dimensionless critical temperature on plate with foundation and without foundation (β = 1)

According to Fig. 18 when plate was on the foundation, the nonlocal results were closer to the local. Also, with stronger Winkler foundation, the difference between results in two states reduced. So in plates on the high strength foundation the small scale effects on the results were fewer. Hence, it is acceptable to use the local elasticity theory with a little difference from the real result.

Fig. 18

Effects of Winkler modulus nonlocal parameter (β = 1, CCCF)

Figures 19, 20 and 21 shows the buckling modes in several of boundary conditions (respectively SSSF, SSSS and CCCC). As is clear in boundary condition, with less flexibility the difference between modes number were smaller than other boundary conditions. In fact, in the boundary conditions, with more flexibility, the much more temperature is needed to attain the next mode.

Fig. 19

Effects of nonlocal parameter on dimensionless temperature modes (β = 1, SSSF)

Fig. 20

Effects of nonlocal parameter on dimensionless temperature modes (β = 1, SSSS)

Fig. 21

Effects of nonlocal parameter on dimensionless temperature modes (β = 1, CCCC)

In Fig. 22, the possibility of replacing the bi-layer nanoplates with Equivalent Single layer (ES layer) has been considered. The thickness of ES layer was 0.68 nm and the BLGs system had a thickness of 0.34 nm for every layer. It can be concluded that there are some difference between the results of ES layer versus bi-layer, and in the same thickness, it is advisable to use BLGs system in place of ES layer.

Fig. 22

Influence of nonlocal parameter on equivalent single layer (β = 1)

7 Conclusion

In this study, the shear and thermal buckling of bi-layer orthotropic rectangular nanoplate based on a Winkler-Pasternak foundation was investigated. Equilibrium equations were obtained using FSDT for orthotropic plate models, and the nonlocal elasticity theory was applied to consider the small scale parameter effect. The governing equations for different boundary conditions were solved using the DQ method such as free edges. Based on the results obtained in this study, the following conclusions have been drawn.

In shear buckling analysis:

• by increasing the thickness, the effect of nonlocal parameter on the critical shear load increases.

• With reduced length and increased of μ parameter, the effect of the boundary condition on the shear critical results are reduced.

• The effect of type of shear loading on the nonlocal results is more than local results.

• Effect of μ on the critical shear load in absence of elastic foundation is more than presence of elastic foundation.

• For the BLGs, based on the considering of elastic foundation, the most critical is when the shear load is only located at the bottom layer.

• In analysis of the BLGs, with reduced thickness, the type of shear loading will become more significant.

• Whenever there is an increase in the numbers of free edges adjacent to each other, the effect of nonlocal parameter on the boundary condition is reduced.

• When the stiffness values of elastic foundation is lower, it is not important that the shear load located on the upper layer or the lower layer edges.

• The type of loading found when the BLGs is on the low strength foundation in local analysis is not important.

In thermal buckling analysis:

• whatever the boundary conditions have more flexibility, by increasing the dimensions ratio, the results of critical temperature in nonlocal and local analysis is almost similar.

• According to references, the correct value of the van der Waals coefficient is 45 Gpa/nm, resulting in a synchronous buckling. If smaller values were considered, layers may be buckle asynchronous.

• When plate embedded on the foundation, the results of nonlocal analysis is tightly close to local and for plates on the foundation with high strength can use of local theory instead of nonlocal theory.

• Whatever the boundary conditions have more flexibility, the more temperature is needed to attain the next mode.

• By Comparing in results of bi-layer and equivalent single layer, different results are obtained and it is advisable to use bi-layer system in place of ES layer.

• Whatever the boundary conditions have more flexibility, the difference of results are smaller in two states (The plate on the elastic foundation and without foundation).