1 Introduction

Carbon nanotubes (CNTs) with a one-dimensional tubular geometry have excellent mechanical, thermal, optical, and electronic properties. They are widely used in nanoelectromechanical systems (NEMS) such as nano switches, nanosensors, and nanomotors (Bai et al. 2018, 2020; Dai 2002; Guo et al. 2011; Kim et al. 2001; Liu et al. 2017). When one-dimensional CNTs are extended to three-dimensional arrays, their excellent properties are also preserved while generating more application scenarios. Examples of such applications are bionic dry adhesive materials, thermal conductivity interfaces, and field emission devices (Aradhya et al. 2008; Buldum 2014; Jagtap et al. 2015; Qu et al. 2008). Therefore, the mechanical behaviors of single CNT, CNT bundles, and CNTs reinforced composites in static bending, buckling, free vibration, and crack sprouting in different application scenarios have received a lot of attention from researchers (Akbas 2020; Alimoradzadeh and Akbas 2021; Civalek et al. 2021; Lin and Xiang 2014; Yas and Samadi 2012).

CNTs are usually applied at the micro–nano scales, and the van der Waals (vdW) interaction is inevitable at these scales. For a single CNT, there exist vdW interactions between the tubes. For a vertically aligned carbon nanotube array (VACNT), vdW interaction exists between the inner tubes and the surface. The CNTs are constrained by the radial vdW interaction in the length direction, and this interaction affects their mechanical behavior (Buehler et al. 2004; Lu et al. 2009; Yuan et al. 2018). Girifalco et al. (2000) computed the potential energies of vdW interaction for two parallel CNTs per unit length using the Lennard–Jones (LJ) potential. Evgeny et al. obtained accurate algebraic expressions of the vdW potential and the force for two parallel and crossed CNTs (Pogorelov et al. 2012). Based on the results of Evgeny et al. Zhao et al. (2013, 2015) derived the binding energy of the vdW interaction between two parallel (and two crossed) single-walled (and multiwalled) CNTs.

The buckling behavior determines the stability of CNTs under axial load. Regardless of whether considering a single CNT or a VACNT array, the buckling behavior must be examined because it affects the NEMS/MEMS system's safety and reliability. For example, the compression deformation of the CNT leads to problems such as system collapse and contact instability at the interface. Ru (2000, 2001) indicated the first infinitesimal buckling of a double-walled CNT with intertube vdW forces based on an elastic double-shell model and the Winkler model. Huang et al. (2010) revealed the post-buckling morphologies and energetics of short, thick multiwalled CNTs (MWCNTs) under uniaxial compression and reported that the inner-shell vdW interactions increase the buckling strain of the outermost shells. Yao and Sun (2012) established the continuum shell theory-based finite element models of MWCNTs and studied the axial compression buckling behaviors of a single MWCNT subjected to the nonlinear vdW forces between the neighboring surfaces. Sun and Liew (2014) investigated the buckling behavior of SWCNTs based on the classical Bernoulli–Euler beam theory and the second-order deformation gradients. Shi et al. (2014) reported that because of the vdW interaction between the rolled layers of CNTs, buckling instability occurs easily in the outermost rolled layer of MWCNTs under hydrostatic pressure. Reddy and Pang (2008) analyzed the static bending, vibration, and buckling responses of CNTs using the nonlocal differential constitutive relations of Eringen's model. Yoshitaka et al. performed the atomistic structural instability analysis for the buckling of CNTs with different thicknesses (Umeno et al. 2017). Benguediab et al. (2014) examined the small-scale effects and chirality of the buckling behavior of a zigzag double-walled CNT using the Timoshenko beam and Eringen's nonlocal model. Semmah et al. (2015) calculated the critical buckling temperature of a zigzag SWCNT by adopting Eringen's nonlocal model and the continuum theory. Bensattalah et al. (2020) studied the buckling of triple-walled CNTs by the nonlocal Eringen's model and Timoshenko beam theory. Malikan et al. (2020) analyzed the axial buckling of nonconcentric double-walled CNTs with vdW interactions for the inner and outer tubes under clamped as well as hinged boundary conditions. Mohamed et al. (2020) illustrated the buckling and post-buckling behaviors of the armchair and zigzag CNTs using an energy-equivalent model under simply supported and doubly clamped boundary conditions.

The research on the buckling behavior of the VACNTs has focused chiefly on global methods. Cao et al. (2011) reported the buckling initiation and displacement dependence of the compression of the VACNTs and indicated the critical value for compressive strain. Li et al. (2015) experimentally analyzed the buckling behavior of VACNTs and compared their behavior with a compressive stress–strain response and plastic deformation. Liew et al. (2005) investigated the buckling behavior of CNT bundles under axial compression by molecular dynamics simulations and found that the vdW interactions improved the overall rigidity of the CNT bundles. Keivan calculated the lateral buckling of two- and three-dimensional ensembles of VACNTs using the nonlocal Rayleigh beam theory under simply supported-simply supported ends, and reported different boundary conditions requiring special treatments (Kiani 2014). Gangele et al. (2018) employed an atomic-scale finite element method to study the influence of VWD forces on the elastic and buckling characteristics of VACNTs constrained at the clamped–clamped ends and under axial displacement. Wittmaack et al. (2018) simulated the uniaxial compression of VACNTs with different densities and microstructures by using a coarse-grained mesoscopic model. Experiments have shown that the vdW interaction effects between neighboring CNTs in VACNT arrays are difficult to distinguish. On the one hand, it is challenging to prepare the VACNT arrays with good uniformity and orientation. On the other hand, measuring the influence of the vdW interaction in a VACNT array on buckling directly by using instruments such as the atomic force microscope and nano-indenter instrument is a challenging task. The influence can only be inferred from the global buckling of the array. In the current theoretical and simulation analyses, the buckling behavior is usually studied under four common boundary conditions (i.e., clamped–clamped, clamped-simply supported, simply supported-simply supported, and clamped-free). The sliding boundary conditions of the CNT and the contact interface are different from the common boundary conditions in the adhesion/contact application of the VACNT to the NEMS. The buckling behavior of the CNTs accompanied by surface vdW interactions have not been considered under the sliding boundary conditions.

Another way to study the CNT is to use several non-classical continuum mechanics involving the internal material length parameters, which are practical tools of significant interest for predicting scale effects. Among them, Eringen's nonlocal theory of size effects is one of the most popular theories and has been applied to many size-dependent structures (Akbas 2019; Ceballes and Abdelkefi 2020; Faroughi et al. 2020; Guo et al. 2021; Huang et al. 2019; Mohammadimehr et al. 2020) . However, this model has been proven to be ambiguous in higher-order boundary problems, and it is not entirely equivalent to the differential form. Further, it cannot show well-posed results under certain types of boundary conditions. The stress-driven nonlocal theory proposed recently can solve the aforementioned problems well (Barretta et al. 2018a; Barretta et al. 2019a, b; Romano et al. 2017; Zhang and Qing 2020; Zhang et al. 2020). In addition, based on Eringen’s nonlocal model, nanoscale material is usually softening trend. The softening effect conflicts with the hardening trend obtained from the part of the experiment, the stress-driven model can well represent the hardening tendency of the material with increasing scale effects (Zhang and Qing 2021a, b; Zhang et al. 2021).

With this understanding, the buckling behavior of the single CNT in the dry-adhesive material of the gecko-inspired VACNT array during pre-pressure adhesion will be considered. The size-affected buckling of CNT will be studied through the newly stress-driven Timoshenko nonlocal beam model (Barretta et al. 2018b; Jiang et al. 2020). The vdW forces of parallel per unit length CNTs are established. According to Hooke's law and surface spacing, the nonlinear vdW force is equivalent to the spring constant and applied to the Winkel model. Based on Hamilton's principle, the governing equations of the CNT buckling are derived. By using the Laplace transform technique, the axial buckling of the SWCNT with surface vdW interaction in the arrays is derived analytically and then compared with the results obtained without surface vdW interaction under pre-pressure adhesive processors. In numerical examples, the influence of the nonlocal elastic parameter, length-to-radii ratio, and type of the SWCNT on the critical buckling load is also discussed.

2 Assumptions and description of mathematical modeling

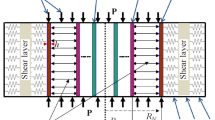
The preload adhesion process between the VACNTs and the contact interface (i.e. bilayer graphene) is shown in Fig. 1. vdW interactions between the SWCNTs are simulated using nonlinear spring elements based on the LJ potential. Consider the axially compressed buckling of an SWCNT with radius and thickness in order are represented by \(r\) and \(t\). For simplicity, the SWCNT is assumed to not undergo radial deformation during axial compression and the adjacent CNTs are assumed to be rigid bodies. The x-axis represents the axial direction of the CNT. Furthermore, the compression of the single SWCNT is assumed to not affect the deformation of the surrounding CNTs.

Fig. 1
figure 1

Schematic of the SWCNT geometry with vdW interactions under pre-pressure adhesion. a vertically aligned carbon nanotube arrays, b an SWCNT (yellow colour represents the fixed end of the CNT, blue colour represents the main body of the CNT, and red colour represents the double-layer graphene)

Full size image

2.1 vdW forces for the neighboring parallel SWCNTs

The energy of the vdW interactions is described by general LJ potential

$$V(R) = 4 \in \left( {\left( {\frac{\sigma }{R}} \right)^{12} - \left( {\frac{\sigma }{R}} \right)^{6} } \right),$$
(1)

where \(\in\) denotes the well depth parameter, \(\sigma\) denotes equilibrium distance; and \(R\) is the distance between two atoms.

By deriving the above-mentioned potential function, the vdW force between two carbon atoms can be obtained as

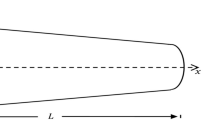
$$F(R) = 4 \in \left( {\frac{{12\sigma^{12} }}{{R^{13} }} - \frac{{6\sigma^{6} }}{{R^{7} }}} \right).$$
(2)

The vdW force with varying distances between two parallel infinite CNTs using the present analytical model. Figure 2 shows the coordinate system and a schematic diagram of the two parallel SWCNTs. The radii of the two SWCNTs were \(r_{1}\) and \(r_{2}\), respectively, \(h\) is the distance between the surfaces of SWCNTs. Without loss of generality, take one point \((r_{1} ,\alpha ,z)\) on the outer wall of one of the SWCNTs and one point \((a_{0} ,\beta ,0)\) on the outer wall of the other SWCNT. Analyzing the geometric relationship between adjacent SWCNTs, we obtain

$$\begin{aligned} a_{0} \cos \theta & = \left( {r_{1} + r_{2} + h} \right) + r_{2} \cos \beta \\ a_{0} \sin \theta & = r_{2} \sin \beta . \\ \end{aligned}$$
(3)
Fig. 2
figure 2

Schematic illustration of the continuum model for vdW analysis of VACNTs

Full size image

Based on Eq. (3), \(\alpha_{0}\) and \(\theta_{0}\) can be written as follows

$$\begin{aligned} a_{0} & = \sqrt {\left( {r_{1} + r_{2} + h} \right)^{2} + r_{2}^{2} + 2\left( {r_{1} + r_{2} + h} \right)r_{2} \cos \beta } \\ \theta_{0} & = \arccos \frac{{\left( {r_{1} + r_{2} + h} \right)^{2} + a_{0}^{2} - r_{2}^{2} }}{{2\left( {r_{1} + r_{2} + h} \right)a_{0} }}. \\ \end{aligned}$$
(4)

The distance between these two points on two adjacent SWCNTs is expressed as

$$r = \sqrt {\left( {a_{0} \cos \alpha - r_{1} \cos \theta } \right)^{2} + \left( {a_{0} \sin \alpha - r_{1} \sin \theta } \right)^{2} + z^{2} } = \sqrt {a^{2} + b^{2} + c^{2} } ,$$
(5)

where

$$\begin{aligned} a & = a_{0} \cos \alpha - r_{1} \cos \theta \\ b & = a_{0} \sin \alpha - r_{1} \sin \theta . \\ \end{aligned}$$
(6)

The vdW interactions force per unit length along the z-direction on the CNT can be expressed as

$$\begin{aligned} F_{VDW} {\kern 1pt} {\kern 1pt} & = \int_{0}^{2\pi } {\rho r_{2} } {\text{d}}\theta_{2} \int_{{A_{1} }}^{{}} {F(R)} \rho {\text{d}}A_{1} \\ & {\kern 1pt} = 4 \in \rho^{2} \int_{0}^{2\pi } {r_{2} } {\text{d}}\theta_{2} \int_{ - \infty }^{\infty } {F(R){\text{d}}z\int_{0}^{2\pi } {r_{1} } } {\text{d}}\theta \\ & = 4 \in \rho^{2} r_{1} r_{2} \int_{0}^{2\pi } {d\theta_{2} } \int_{0}^{2\pi } {\left( {\frac{{2048\sigma^{12} }}{{231(a^{2} + b^{2} )^{6} }} - \frac{{32\sigma^{6} }}{{5(a^{2} + b^{2} )^{3} }}} \right)} {\text{d}}\theta , \\ \end{aligned}$$
(7)

where \(\rho\) is the number of atoms per unit length. From C–C bond length,\(\rho = {4 \mathord{\left/ {\vphantom {4 {(3\sqrt 3 b^{2} )}}} \right. \kern-\nulldelimiterspace} {(3\sqrt 3 b^{2} )}}\).

Equation (7) can be entirely solved by the Gaussian quadrature method. To ensure the accuracy of the calculation results, [0,2π] is divided into 100 equal parts, and 10 Gaussian points integral is used in each part. According to Hooke's law, the vdW force of different intervals between two CNTs is equivalent to the corresponding spring constants.

2.2 Buckling of the SWCNTs under sliding boundary conditions

In the framework of the nonlocal Timoshenko beam theory, the displacement field of the SWCNT is defined as

$$\begin{aligned} u_{x} & = z\varphi (x) \\ u_{y} & = 0 \\ u_{z} & = w(x). \\ \end{aligned}$$
(8)

The strain–displacement relation of the SWCNT can be given as

$$\begin{aligned} \varepsilon_{{x{\text{x}}}} & = z\varphi^{\prime}(x) \\ \varepsilon_{{x{\text{z}}}} & { = }w^{\prime}(x){ + }\varphi (x). \\ \end{aligned}$$
(9)

The stress resultant moment \(M\) and the shear resultant \(V\) at the end of the SWCNT are given by

$$M = \int_{A} z \sigma_{xx} {\text{d}}A,$$
(10)
$$V = \int_{A} {\chi \sigma_{xz} } {\text{d}}A,$$
(11)

where \(\chi\) is the shear correction factor, and \(A\) is the cross-sectional area of SWCNT.

$$A = \pi (r^{2} - (r - t)^{2} ).$$
(12)

According to the stress-driven nonlocal elastic theory proposed by the Ref. (Romano et al. 2017), the integral constitutive relation of the SWCNT in the frame of the Timoshenko beam defined on a bounded interval [0, L] and adopting a bi-exponential kernel function can be expressed as

$$\tau_{ij} (x) = \frac{1}{2\kappa }\int_{0}^{L} {e^{{ - \frac{|x - \eta |}{\kappa }}} } \sigma_{ij} (\eta ){\text{d}}\eta .$$
(13)

Here, \(\kappa\) is utilized to regulate the amplitude of the area of nonlocal effect.

$$\kappa = \lambda L,$$
(14)

where \(\lambda\) is the nonlocal elastic parameter.

By combining Eqs. (9), (11), and (13), the nonlocal constitutive equations of the SWCNT can be expressed as

$$EI\varphi^{\prime}(x) = \frac{1}{2\kappa }\int_{0}^{L} {e^{{ - \frac{|x - \eta |}{\kappa }}} } M(\eta ){\text{d}}\eta ,$$
(15)
$$GA\chi (w^{\prime}(x) + \varphi (x)) = \frac{1}{2\kappa }\int_{0}^{L} {e^{{ - \frac{|x - \eta |}{\kappa }}} } V(\eta ){\text{d}}\eta ,$$
(16)

where \(I\) is the second moment of area about the z-axis for the SWCNT, and \(E\) is Young's modulus, \(G\) is the shear modulus.

$$I = \int_{A} {z^{2} dA} .$$
(17)

According to the equivalent form of the Fredholm integral equation of the first kind, one can obtain

$$f^{\prime \prime } (x) - \frac{1}{{\kappa^{2} }}f(x) = - \frac{1}{{\kappa^{2} }}\varphi (x).$$
(18)

Substituting Eq. (15) and (16) into (13), one can obtain

$$\kappa^{2} \varphi^{\prime\prime\prime} - \varphi^{\prime} = - \frac{M}{EI},$$
(19)
$$\kappa^{2} (w^{\prime\prime\prime} + \varphi^{\prime\prime}) - (w^{\prime} + \varphi ) = - \frac{V}{GA\chi }.$$
(20)

According to Hamilton's principle expressed as

$$\delta \int_{{t_{1} }}^{{t_{2} }} {\left( {U + U_{w} - W} \right)} {\text{d}}t = 0.$$
(21)

The virtual work done by external force can be written as

$$\delta W = N_{a} \int_{0}^{L} {w^{\prime}} \delta w^{\prime}{\text{d}}x = \left. {N_{a} w^{\prime}\delta w} \right|_{0}^{L} - N_{a} \int_{0}^{L} {w^{\prime\prime}} \delta w{\text{d}}x,$$
(22)

where \(N_{a}\) denotes the external load in the axial direction.

The total strain energy can be written as

$$\delta U = \left. {M\delta \varphi } \right|_{0}^{L} + \left. {V\delta w} \right|_{0}^{L} + \int_{0}^{L} {\left[ {\left( {V - M^{\prime}} \right)\delta \phi - V^{\prime}\delta w} \right]} {\text{d}}x.$$
(23)

Similar to Winkler elastic foundation model, the virtual work by vdW forces is denoted by

$$\delta U_{w} = \int_{0}^{L} {(k_{w1} w\delta w} + k_{w2} w\delta w){\text{d}}x.$$
(24)

Substituting Eqs. (22), (23), and (24) into (21), one may have

$$\left. {M\delta \varphi } \right|_{0}^{L} + \left. {(V - N_{a} w^{\prime})\delta w} \right|_{0}^{L} + \int_{0}^{L} {\left( {V - M^{\prime}} \right)\delta \phi {\text{d}}x + } \int_{0}^{L} {[N_{a} w^{\prime\prime}} - V^{\prime} + (k_{w1} + k_{w2} )w]\delta w{\text{d}}x = 0.$$
(25)

The governing equilibrium equations for global buckling of the SWCNT are expressed as

$$\begin{aligned} & V - M^{\prime} = 0 \\ & N_{a} w^{\prime\prime} - V^{\prime} + Kw = 0, \\ \end{aligned}$$
(26)

where \(K = k_{w1} + k_{w2}\), \(k_{w1}\) and \(k_{w2}\) are the vdW force equivalent spring constant of the middle SWCNT and the left and right adjacent SWCNT.

The corresponding boundary conditions are

$$\begin{gathered} \left. {M\delta \varphi } \right|_{0}^{L} = 0 \hfill \\ \left. {(V - N_{a} w^{\prime})\delta w} \right|_{0}^{L} = 0. \hfill \\ \end{gathered}$$
(27)

In this study, the buckling behavior of the SWCNT and the contact interface during the sliding process was examined. The bottom of the CNT was fixed on the substrate, and the boundary condition was clamped support (C). The sliding boundary of the CNT and the contact interface was assumed with the boundary as a guided end (G). The corresponding C–G boundary conditions are written as

$$\begin{aligned} C:w(0) & = 0,\varphi (0) = 0 \\ G:\varphi (L) & = 0,V(L) - N_{a} w^{\prime}(L) = 0. \\ \end{aligned}$$
(28)

So far only four boundary conditions have been obtained. According to the Refs. (Romano and Barretta 2017; Zhang et al. 2020), two constitutive boundary conditions can be derived from the first kind of Fredholm integral equations.

$$\left\{ {\begin{array}{*{20}l} {f^{\prime } (a) - \frac{1}{\kappa }f(a) = 0} \hfill \\ {f^{\prime } (b) + \frac{1}{\kappa }f(b) = 0} \hfill \\ \end{array} } \right..$$
(29)

By substituting (15) in (29), one gets

$$\left\{ {\begin{array}{*{20}l} {EI\varphi^{\prime\prime}(0) - \frac{1}{\kappa }EI\varphi^{\prime}(0){ = }0} \\ {EI\varphi^{\prime\prime}(L){ + }\frac{1}{\kappa }EI\varphi^{\prime}(L){ = }0} \\ \end{array} } \right..$$
(30)

By substituting (16) in (29), one gets

$$\left\{ {\begin{array}{*{20}l} {GA\chi (w^{\prime\prime}(0) + \varphi^{\prime}(0)) - \frac{1}{\kappa }GA\chi (w^{\prime}(0) + \varphi (0)) = 0} \\ {GA\chi (w^{\prime\prime}(L) + \varphi^{\prime}(L)) + \frac{1}{\kappa }GA\chi (w^{\prime}(L) + \varphi (L)) = 0} \\ \end{array} } \right..$$
(31)

2.3 Solution method for the carbon nanotube model

For this purpose, by applying the Laplace transform technique, the governing Eq. (26) and nonlocal constitutive Eqs. (15) and (16) can be written as

$$\left\{ \begin{gathered} {\mathcal{L}}\{ V\} - {\mathcal{L}}\{ M^{\prime}\} = 0 \hfill \\ N_{a} {\mathcal{L}}\{ w^{\prime\prime}\} - {\mathcal{L}}\{ V^{\prime}\} + K{\mathcal{L}}\{ w\} = 0 \hfill \\ \kappa^{2} {\mathcal{L}}\{ \varphi^{\prime\prime\prime}\} - {\mathcal{L}}\{ \varphi^{\prime}\} = - \frac{{{\mathcal{L}}\{ M\} }}{EI} \hfill \\ \kappa^{2} ({\mathcal{L}}\{ w^{\prime\prime\prime}\} + {\mathcal{L}}\{ \varphi^{\prime\prime}\} ) - ({\mathcal{L}}\{ w^{\prime}\} + {\mathcal{L}}\{ \varphi \} ) = - \frac{{{\mathcal{L}}\{ V\} }}{GA\chi } \hfill \\ \end{gathered} \right.,$$
(32)

where \({\mathcal{L}}\{ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{\} }}\) is Laplace operator.

The variables in Laplace domain can be defined as

$$\begin{aligned} {\mathcal{L}}\{ M^{\prime}\} & = s{\mathcal{L}}\{ M\} - C_{1} \\ {\mathcal{L}}\{ V^{\prime}\} & = s{\mathcal{L}}\{ V\} - C_{2} , \\ \end{aligned}$$
(33)

wherein the unknown parameters are given by

$$C_{1} = M(0);{\kern 1pt} C_{2} = V(0).$$
(34)

The variables in Laplace domain can be defined as

$$\begin{aligned} {\mathcal{L}}\{ w^{\prime}\} & = s{\mathcal{L}}\{ w\} - C_{3} \\ {\mathcal{L}}\{ w^{\prime\prime}\} & = s{\mathcal{L}}\{ w^{\prime}\} - C_{4} \\ {\mathcal{L}}\{ w^{\prime\prime\prime}\} & = s{\mathcal{L}}\{ w^{\prime\prime}\} - C_{5} , \\ \end{aligned}$$
(35)

where the unknown parameters are given by

$$C_{3} = w(0);C_{4} = w^{\prime}(0);C_{5} = w^{\prime\prime}(0).$$
(36)

Further, the variables in Laplace domain can be defined as

$$\begin{aligned} {\mathcal{L}}\{ \varphi^{\prime}\} & = s{\mathcal{L}}\{ \varphi \} - C_{6} \\ {\mathcal{L}}\{ \varphi^{\prime\prime}\} & = s{\mathcal{L}}\{ \varphi^{\prime}\} - C_{7} \\ {\mathcal{L}}\{ \varphi^{\prime\prime\prime}\} & = s{\mathcal{L}}\{ \varphi^{\prime\prime}\} - C_{8} , \\ \end{aligned}$$
(37)

and the unknown parameters are given by

$$C_{6} = \varphi (0);C_{7} = \varphi^{\prime}(0);C_{8} = \varphi^{\prime\prime}(0).$$
(38)

By substituting Eqs. (33)–(38) into Eq. (32), the explicit expressions of \({\mathcal{L}}\{ M{\text{\} }}\),\({\mathcal{L}}\{ V\}\),\({\mathcal{L}}\{ w{\text{\} }}\), and \({\mathcal{L}}\{ \varphi {\text{\} }}\) can be derived

$${\mathcal{L}}\{ M{\text{\} = }}\frac{{\left( \begin{gathered} GA\chi s^{5} \kappa^{2} C_{1} + GA\chi s^{4} \kappa^{2} C_{2} + \hfill \\ s^{3} \left( { - GA\chi C_{1} + N_{a} C_{1} + GA\chi K\kappa^{2} C_{3} + GA\chi N_{a} \kappa^{2} C_{5} } \right) + \hfill \\ s^{2} GA\chi \left( { - C_{2} + N_{a} C_{4} + K\kappa^{2} C_{4} + N_{a} C_{6} - N_{a} \kappa^{2} C_{8} } \right) + \hfill \\ s\left( {KC_{1} - GA\chi KC_{3} + GA\chi K\kappa^{2} C_{5} } \right) + \left( {GA\chi KC_{6} - GA\chi K\kappa^{2} C_{8} } \right) \hfill \\ \end{gathered} \right)}}{{GA\chi \kappa^{2} \left( {s^{2} - a^{2} } \right)\left( {s^{2} - b^{2} } \right)\left( {s^{2} - c^{2} } \right)}},$$
(39)
$${\mathcal{L}}\{ V\} { = }\frac{{\left( \begin{gathered} EIs^{5} \kappa^{2} C_{2} + EIs^{4} \left( {K\kappa^{2} C_{3} + N_{a} \kappa^{2} C_{5} } \right) + \hfill \\ EIs^{3} \left( { - C_{2} + N_{a} C_{4} + K\kappa^{2} C_{4} + N_{a} C_{6} - N_{a} \kappa^{2} C_{8} } \right) + \hfill \\ s^{2} \left( {N_{a} C_{1} - EIKC_{3} + EIK\kappa^{2} C_{5} } \right) + EIKs\left( {C_{6} - \kappa^{2} C_{8} } \right) + KC_{1} \hfill \\ \end{gathered} \right)}}{{EI\kappa^{2} \left( {s^{2} - a^{2} } \right)\left( {s^{2} - b^{2} } \right)\left( {s^{2} - c^{2} } \right)}},$$
(40)
$${\mathcal{L}}\{ w{\text{\} }} = \frac{{\left( \begin{gathered} EIGA\chi s^{5} \kappa^{2} C_{3} + EIGA\chi s^{4} \kappa^{2} C_{4} + EIs^{3} \left( {(N_{a} - GA\chi )C_{3} + GA\chi \kappa^{2} C_{5} } \right) + \hfill \\ EIs^{2} \left( { - C_{2} + N_{a} C_{4} + GA\chi C_{6} - GA\chi \kappa^{2} C_{8} } \right) + \hfill \\ GA\chi s\left( {C_{1} - N_{a} C_{3} } \right) + GA\chi (C_{2} - N_{a}C_{4} ) \hfill \\ \end{gathered} \right)}}{{EIGA\chi \kappa^{2} \left( {s^{2} - a^{2} } \right)\left( {s^{2} - b^{2} } \right)\left( {s^{2} - c^{2} } \right)}},$$
(41)
$${\mathcal{L}}\{ \varphi {\text{\} = }}\frac{{\left( \begin{gathered} s^{7} EIGA\chi \kappa^{4} C_{6} + s^{6} EIGA\chi \kappa^{4} C_{7} + s^{5} EI\left( { - 2GA\chi \kappa^{2} C_{6} + N_{a} \kappa^{2} C_{6} + GA\chi \kappa^{4} C_{8} } \right) + \hfill \\ s^{4} \left( { - GA\chi \kappa^{2} C_{1} + EI\kappa^{2} (N_{a} - GA\chi )C_{7} } \right) + \hfill \\ s^{3} \left( { - GA\chi \kappa^{2} C_{2} + (EI(GA\chi - N_{a} + K\kappa^{2} ) - GA\chi N_{a} \kappa^{2} )C_{6} + EI(N_{a} \kappa^{2} - GA\chi \kappa^{2} )C_{8} } \right) + \hfill \\ s^{2} \left( {(GA\chi - N_{a} )C_{1} - GA\chi K\kappa^{2} C_{3} - GA\chi N_{a} \kappa^{2} C_{5} + EIK\kappa^{2} C_{7} - GA\chi N_{a} \kappa^{2} C_{7} } \right) + \hfill \\ s\left( {GA\chi C_{2} - GA\chi (N_{a} + K\kappa^{2} )C_{4} - EIKC_{6} - GA\chi K\kappa^{2} C_{6} + EIK\kappa^{2} C_{8} } \right) + \hfill \\ GA\chi KC_{3} - GA\chi K\kappa^{2} C_{7} - GA\chi K\kappa^{2} C_{5} - KC_{1} \hfill \\ \end{gathered} \right)}}{{EIGA\chi \kappa^{4} \left( {s^{2} - a^{2} } \right)\left( {s^{2} - b^{2} } \right)\left( {s^{2} - c^{2} } \right)\left( {s^{2} - d^{2} } \right)}},$$
(42)

where

$$\begin{aligned} a & = \sqrt { - \frac{{\sqrt[3]{{\left( \frac{2}{3} \right)}}p}}{{\left( { - 9q + \sqrt 3 \sqrt {4p^{3} + 27q^{2} } } \right)^{1/3} }} - \frac{{m_{1} }}{3} + \frac{{\left( { - 9q + \sqrt 3 \sqrt {4p^{3} + 27q^{2} } } \right)^{1/3} }}{{\sqrt[3]{18}}}} \\ b & = \sqrt {\frac{{\left( {1 + {\text{I}}\sqrt 3 } \right)p}}{{\sqrt[3]{18}\left( { - 9q + \sqrt 3 \sqrt {4p^{3} + 27q^{2} } } \right)^{1/3} }} - \frac{{m_{1} }}{3} - \frac{{\left( {1 - {\text{I}}\sqrt 3 } \right)\left( { - 9q + \sqrt 3 \sqrt {4p^{3} + 27q^{2} } } \right)^{1/3} }}{{2\sqrt[3]{18}}}} \\ c & = \sqrt {\frac{{\left( {1 - {\text{I}}\sqrt 3 } \right)p}}{{\sqrt[3]{18}\left( { - 9q + \sqrt 3 \sqrt {4p^{3} + 27q^{2} } } \right)^{1/3} }} - \frac{{m_{1} }}{3} - \frac{{\left( {1 + {\text{I}}\sqrt 3 } \right)\left( { - 9q + \sqrt 3 \sqrt {4p^{3} + 27q^{2} } } \right)^{1/3} }}{{2\sqrt[3]{18}}}} \\ d & = \frac{1}{\kappa }, \\ \end{aligned}$$
(43)

in which,

$$\begin{aligned} p & = - \frac{{m_{1}^{2} }}{3} + m_{2} ;q = \frac{{2m_{1}^{3} }}{27} - \frac{{m_{1} m_{2} }}{3} + m_{3} ; \\ m_{1} & = \frac{{N_{a} - GA\chi }}{{GA\chi \kappa^{2} }};m_{2} = \frac{{EIK - GA\chi N_{a} }}{{EIGA\chi \kappa^{2} }};m_{3} = \frac{ - K}{{EI\kappa^{2} }}. \\ \end{aligned}$$
(44)

Finally, through the inverse transformation, one can directly obtain the exact expressions of the resultants \(M(x)\), \(w(x)\), \(V(x)\), and \(\varphi (x)\). can be directly obtained.

The exact solution for bending moment \(M(x)\) is expressed as

$$M = \frac{1}{{GA\chi \kappa^{2} }}\left( \begin{gathered} f_{5} (x)GA\chi \kappa^{2} C_{1} + f_{4} (x)GA\chi \kappa^{2} C_{2} + \hfill \\ f_{3} (x)\left( {(N_{a} - GA\chi )C_{1} + GA\chi K\kappa^{2} C_{3} + GA\chi N_{a} \kappa^{2} C_{5} } \right) + \hfill \\ f_{2} (x)\left( {GA\chi \left( { - C_{2} + (N_{a} + K\kappa^{2} )C_{4} + N_{a} C_{6} - N_{a} \kappa^{2} C_{8} } \right)} \right) + \hfill \\ f_{1} (x)K\left( {C_{1} - GA\chi C_{3} + GA\chi \kappa^{2} C_{5} } \right) + f_{0} (x)KGA\chi \left( {C_{6} - \kappa^{2} C_{8} } \right) \hfill \\ \end{gathered} \right).$$
(45)

The exact solution for deflection \(w(x)\) is expressed as

$$w = \frac{1}{{EIGA\chi \kappa^{2} }}\left( \begin{gathered} f_{5} (x)EIGA\chi \kappa^{2} C_{3} + f_{4} (x)EIGA\chi \kappa^{2} C_{4} + \hfill \\ f_{3} (x)EI\left( { - GA\chi C_{3} + N_{a} C_{3} + GA\chi \kappa^{2} C_{5} } \right) + \hfill \\ f_{2} (x)EI\left( { - C_{2} + N_{a} C_{4} + GA\chi C_{6} - GA\chi \kappa^{2} C_{8} } \right) + \hfill \\ f_{1} (x)GA\chi \left( {C_{1} - N_{a} C_{3} } \right){ + }f_{0} (x)GA\chi \left( {C_{2} - N_{a} C_{4} } \right) \hfill \\ \end{gathered} \right).$$
(46)

The exact solution for shear force \(V(x)\) is expressed as

$$V = \frac{1}{{EI\kappa^{2} }}\left( \begin{gathered} f_{5} (x)EI\kappa^{2} C_{2} + f_{4} (x)EI\left( {K\kappa^{2} C_{3} + N_{a} \kappa^{2} C_{5} } \right) + \hfill \\ f_{3} (x)EI\left( { - C_{2} + N_{a} C_{4} + K\kappa^{2} C_{4} + N_{a} C_{6} - N_{a} \kappa^{2} C_{8} } \right) + \hfill \\ f_{2} (x)\left( {N_{a} C_{1} - EIKC_{3} + EIK\kappa^{2} C_{5} } \right) + \hfill \\ f_{1} (x)EIK\left( {C_{6} - \kappa^{2} C_{8} } \right) + f_{0} (x)KC_{1} \hfill \\ \end{gathered} \right).$$
(47)

The exact solution for rotation \(\varphi (x)\) is expressed as

$$\varphi = \frac{1}{{EIGA\chi \kappa^{4} }}\left( \begin{gathered} g_{7} (x)EIGA\chi \kappa^{4} C_{6} + g_{6} (x)EIGA\chi \kappa^{4} C_{7} + \hfill \\ g_{5} (x)EI\left( {\kappa^{2} (N_{a} - 2GA\chi )C_{6} + GA\chi \kappa^{4} C_{8} } \right) + \hfill \\ g_{4} (x)\kappa^{2} \left( { - GA\chi C_{1} - EIGA\chi C_{7} + EIN_{a} C_{7} } \right) + \hfill \\ g_{3} (x)\left( { - GA\chi \kappa^{2} C_{2} + EI(GA\chi - N_{a} + K\kappa^{2} - GA\chi N_{a} \kappa^{2} )C_{6} + EI\kappa^{2} (N_{a} - GA\chi )C_{8} } \right) + \hfill \\ g_{2} (x)\left( {(GA\chi - N_{a} )C_{1} - GA\chi K\kappa^{2} C_{3} - GA\chi N_{a} \kappa^{2} C_{5} + \kappa^{2} (EIK - GA\chi N_{a} )C_{7} } \right) + \hfill \\ g_{1} (x)\left( {GA\chi (C_{2} - (N_{a} + K\kappa^{2} )C_{4} ) - K(EI + GA\chi \kappa^{2} )C_{6} + EIK\kappa^{2} C_{8} } \right) + \hfill \\ g_{0} (x)K\left( { - C_{1} + GA\chi (C_{3} - \kappa^{2} C_{5} - \kappa^{2} C_{7} )} \right) \hfill \\ \end{gathered} \right),$$
(48)

in which,

$$\left\{ \begin{gathered} f_{i} (x) = \begin{array}{*{20}l} {{\mathcal{L}}^{ - 1} \{ \frac{{s^{i} }}{{\left( {s^{2} - a^{2} } \right)\left( {s^{2} - b^{2} } \right)\left( {s^{2} - c^{2} } \right)}}\} ,} & {(i = 0,1,2,...,5)} \\ \end{array} \hfill \\ g_{i} (x) = \begin{array}{*{20}l} {{\mathcal{L}}^{ - 1} \{ \frac{{s^{i} }}{{\left( {s^{2} - a^{2} } \right)\left( {s^{2} - b^{2} } \right)\left( {s^{2} - c^{2} } \right)\left( {s^{2} - d^{2} } \right)}}\} ,} & {(i = 0,1,2,...,7)} \\ \end{array} \hfill \\ \end{gathered} \right..$$
(49)

The simplified expressions of \(f_{i} (x)\) and \(g_{i} (x)\) are listed in Appendix A.

To determine the critical buckling force, inserting (45–48) into (28), (30), and (31), summarizing the eight equations into a matrix form, a system of linear algebraic equations for unknown coefficient \(C_{i}\). The determinant of the coefficient matrix Cnm must be zero.

$$\left( {\begin{array}{*{20}l} {C_{11} } & {C_{12} } & \ldots & {C_{18} } \\ {C_{21} } & {C_{22} } & \ldots & {C_{28} } \\ \vdots & \vdots & \ddots & \vdots \\ {C_{31} } & {C_{32} } & \cdots & {C_{88} } \\ \end{array} } \right)\left( {\begin{array}{*{20}l} {C_{1} } \\ {C_{2} } \\ \vdots \\ {C_{8} } \\ \end{array} } \right) = 0.$$
(50)

The above tasks of deriving and solving the critical buckling force were implemented in Wolfram Mathematica 12.3 using built-in functions available in the Symbolic and Numeric computation boxes.

3 Results and discussion

In this section, the results of the surface vdW forces on the buckling behavior of the single SWCNT in the arrays with sliding boundary conditions under the pre-pressure adhesion process are given. The effect of the computational parameters such as aspect ratio, diameter, surface distance, and nonlocal elastic parameter to critical buckling load are illustrated.

Herein, The parameters of the pair carbon atoms of Lennard–Jones potential are taken to be \(\sigma {\kern 1pt} { = }{\kern 1pt} 3.4{\kern 1pt} \;{\text{\AA}}\) and \(\in {\kern 1pt} {\kern 1pt} { = }{\kern 1pt} {\kern 1pt} 2.8347{\kern 1pt} {\text{meV}}\), the following properties of the CNTs are applied: \(E{ = }120{\kern 1pt} {\kern 1pt} {\text{GPa}}\), \(\nu {\kern 1pt} { = }{\kern 1pt} {0}{\text{.19}}\), \(\chi {\kern 1pt} { = }{\kern 1pt} 0.877\) and \(t{\kern 1pt} = {\kern 1pt} 0.182{\kern 1pt} {\text{nm}}\), as suggested in the Refs. (Bai et al. 2020; Reddy and Pang 2008). The length of the CNT is \(L{\kern 1pt} = {\kern 1pt} 9.84{\kern 1pt} {\text{nm}}\), the bond length of the CNT is \({\text{b}}{\kern 1pt} { = }{\kern 1pt} 1.42{\kern 1pt} {\text{\AA}}\). The radii of different types of the SWCNTs used are summarized in Table 1.

Table 1 The radii for SWCNTs
Full size table

3.1 Verification

First, to verify the correctness of the proposed numerical solution, a comparison between the normalized critical buckling loads of stress-driven nonlocal Timoshenko beam model predicted by the present solution (\(K \to 0^{ + }\) and using the same parameters in the Ref. (Jiang et al. 2020)) and those from the Ref. (Jiang et al. 2020) is made in Table 2. The comparative results show that the present solution is valid.

Table 2 Comparison of the normalized critical buckling load \(\overline{P}_{cr} = P_{cr} /P_{cr} - CG - classical\) of Stress-driven nonlocal Timoshenko beam model between this work and results in Ref. (Jiang et al. 2020)
Full size table

3.2 Parametric analysis

To consider the influence of vdW force on the critical buckling load of the CNTs, firstly, the vdW interactions of the CNTs per unit length at different distances are determined. Figure 3 shows the vdW forces between two parallel CNTs. When \(F_{VDW} \ge 0\), the vdW force is repulsive; when \(F_{VDW} < 0\), the vdW force is attractive. The variation of vdW forces with distance for two parallel CNTs with the same diameter is shown in Fig. 3a. When the distance between two parallel CNTs is the same, the larger the diameter, the greater the vdW force. Because of the vdW interaction area has a larger interaction surface under the same distance. When the distance is around 0.36 nm, comparing the case of (30, 0)//(30, 0) and (10, 0)//(10, 0) systems, the vdW force of (30, 0)//(30, 0) system is significantly greater than that of (10, 0)//(10, 0) system. When the distance is around 1.0 nm, the difference of vdW forces is small between the case of (30, 0)//(30, 0) and (10, 0)//(10, 0) systems. This is in line with the law that vdW force decreases with increasing distance. In Fig. 3b, keeping the diameter of one of the CNTs (14, 0) constant, the diameter of the other parallel CNT gradually increases. When the distance is the same, as the diameter of one of them increases, the vdW force of the attraction area gradually increases.

Fig. 3
figure 3

vdW force with different distances between two parallel SWCNTs per unit length. a The same diameters of two SWNTs, b the different diameters of two SWCNTs

Full size image

Objects on the microscopic scale have a certain size effect, which will seriously affect the mechanical behavior of the CNT at the microscopic scale. Nonlocal elasticity parameters determine the effect of size effect, it is very important to choose the appropriate nonlocal parameters. Figure 4 describes the influence of nonlocal parameters on the critical buckling load of a single CNT under sliding boundary conditions. When \({\lambda \mathord{\left/ {\vphantom {\lambda {L{\kern 1pt} = {\kern 1pt} 0}}} \right. \kern-\nulldelimiterspace} {L{\kern 1pt} = {\kern 1pt} 0}}\), the nonlocal stress-driven model degenerates into the classic Timoshenko beam model. Compared with the gradual increase of the nonlocal elastic parameter, the nonlocal model parameters are normalized by the classical model. The results show that the increase of nonlocal parameters increases the critical buckling load of the single CNT. This means that the hardening behavior of the single CNT becomes stronger the increase of the nonlocal elastic parameters. The stress-driven model provides a good hardening prediction for the beams at the nanoscale. Similar to Ref. (Wang and Wang 2007), the relevant characteristic length \(\lambda {\kern 1pt} { = }{\kern 1pt} 1{\kern 1pt} {\kern 1pt} {\text{nm}}\) is chosen to discuss the buckling behavior of the single CNT in the array under the vdW interaction.

Fig. 4
figure 4

Effect of nonlocal elastic parameter λ on the critical buckling load for single SWCNT under C–G boundary conditions

Full size image

Figure 5 shows the influence of aspect ratio on the critical buckling load of the CNT in the classical and the stress-driven nonlocal models under sliding boundary conditions. The critical buckling load decreases with the increases of aspect ratio \({L \mathord{\left/ {\vphantom {L R}} \right. \kern-\nulldelimiterspace} R}\). The larger the \({L \mathord{\left/ {\vphantom {L R}} \right. \kern-\nulldelimiterspace} R}\) is, the smaller the critical buckling load is. In the stress-driven nonlocal model, the length of the CNT increases, and the nonlocal parameters will gradually change if the characteristic size of the CNT is unchanged. When the length of the CNT is longer, the nonlocal critical buckling will tend to the classic model. This result corresponds to the result in Fig. 4.

Fig. 5
figure 5

Effect of the SWCNT on the local and nonlocal critical buckling load for different aspect ratios

Full size image

Figure 6 shows the buckling behavior of CNTs in the array with and without vdW forces interaction, and the type of SWCNT is (10, 5). The range of distance is considered from 0.4 to 1.0 nm. When the vdW interaction is not considered, the buckling behavior of the SWCNT remains the same regardless of the value of the pitch. When the vdW force among the CNTs is used as lateral support, the critical buckling load shows the nonlinear relationship to the surface interval.

Fig. 6
figure 6

Comparison of the critical buckling load of SWCNTs with and without the presence of vdW interaction

Full size image

In the VACNTs, the critical buckling behavior of the single CNT affected by the vdW interaction of adjacent CNTs is discussed under the pre-compression-adhesion process. First, consider the situation where the diameters of the CNTs are the same in the array. Figure 7a shows a schematic diagram of the same diameter CNTs. Figure 7b–d represent the critical buckling load of different types of CNTs at a different distance. The types correspond to zigzag type (c) chiral type (d) armchair type. The results show that when the length of the CNT is the same, the critical buckling load is on an uptrend with increasing radii. It is worth noting that the critical buckling changes significantly when considering the vdW interaction between adjacent CNTs. The stronger the vdW force is, the more critical buckling of CNT of the same geometric size will increase. This means that during the pre-compression-adhesion process, a larger normal load needs to be provided. When the interval distance is about 0.425 nm, the vdW force begins to increase sharply, this results in the maximum value of the corresponding critical buckling load in the vdW force attraction area.

Fig. 7
figure 7

The variation of critical buckling load with different distances between adjacent SWCNTs of the same diameter. a Schematic diagram, b zigzag type, c chiral type, d armchair type

Full size image

For clarity, the case where the diameter of a single CNT in the array is different from that of the adjacent CNTs is discussed. Consider the case where the diameter of the middle SWCNT is unchanged, and the diameter of the adjacent CNT is from small to large, as shown in Fig. 8a. Corresponding to Fig. 8b–d, three types of the (14, 0), (14, 7) and (14, 14) SWCNTs are set as intermediate compressed CNTs. The diameters of (14, 0), (14, 7) and (14, 14) SWCNTs gradually increase. When the CNT spacing is the same and the diameter of adjacent CNTs gradually increases, the critical buckling load of the CNT under axial pressure will gradually increase. The vdW interaction effect on the buckling behavior of the single embedded CNT in the VACNTs with different diameters is similar to that of with the same diameter.

Fig. 8
figure 8

The variation of critical buckling load with different distances between adjacent SWCNTs of different diameters. a Schematic diagram, b zigzag type, c chiral type, d armchair type

Full size image

4 Conclusions

The surface vdW interaction plays a significant role in the mechanical behavior of the VACNTs. A clear understanding of the vdW interaction between the SWCNTs in the array is crucial for their mechanical behavior in nanoelectromechanical systems and dry adhesion applications. At the first step, using the general LJ potential and the continuum model, the vdW forces between different types of the SWCNTs are calculated. Then, based on the stress-driven nonlocal theory and Hamilton's principle, the buckling behavior of the SWCNTs constrained by vdW force is analyzed under the frame of Timoshenko beam. The closed-form nonlocal solutions for the single embedded SWCNT under the sliding boundary have been provided. The most important conclusions can be summarized as follows:

The vdW forces of two neighboring parallel SWCNTs in the arrays system depend on the diameters and distances. The larger the diameter of the SWCNT is, the larger the specific surface area of the vdW interaction will be, which will obviously enhance the vdW force. Based on the stress-driven nonlocal model, the increase of nonlocal elastic parameters leads to the raise of the critical buckling load of the SWCNT. When the characteristic length is fixed, the longer the length of the SWCNT, the smaller the influence of the scale effect on the critical buckling load. The nonlocal model degenerates into the local model. The critical buckling of the single SWCNT with vdW interaction is larger than that without vdW interaction. In the attraction region of vdW interaction, the critical buckling load increases with the decreased distance between two CNTs. For the VACNTs system with the same diameter, the larger the diameter of the single CNT, the greater the critical buckling load. For the VACNT system with a different diameter, the diameter change of the adjacent CNTs affects the critical buckling load as the diameter of the compressive CNT is constant.