I. INTRODUCTION

Carbon nanocones (CNCs) were first discovered by Ge and Sattler,1 and this synthesized carbon allotrope has gained popularity over the past 20 years. Its several potential applications, such as nanoscale probes,2 ultra-sensors,3 and absorbing materials,4 have been studied. Based on these potential applications, numerous studies have investigated the fundamental mechanical properties of SWCNCs which represent certain significant characteristics for practical applications. However, the understanding of their mechanical responses remains incomplete.

Several atomistic approaches are used to predict the mechanical behaviors of SWCNCs. Narjabadifam et al.5 adopted molecular dynamics (MD) simulations to predict the resonant frequencies and vibrational modes of bottom-fixed-SWCNCs and indicated that the frequencies and mode shapes highly depend on the structural parameters, especially the apex angle (see Fig. 1 for reference). Fakhrabadi et al.6 comprehensively studied the elastic properties and buckling behaviors of SWCNCs using molecular mechanics. The results revealed that Young’s moduli and critical forces under compression decrease as length and apex angle increase. Liew et al.7 compared the buckling behaviors of SWCNCs subjected to axial compression with those under in-planar compression via MD simulations. Using the same methodology, Jordan and Crespi8 examined the inversion of SWCNCs pressed using a spherical indenter. The main advantage of atomistic methods is that the physical responses of nanostructures can be described precisely, however, the computational efforts are time consuming. Therefore, this approach is limited to relatively small scale problems.

FIG. 1
figure 1

The rolling process from the planar fan-shaped graphene sheet to the undeformed SWCNC, θS denotes the sector angle of the fan-shaped graphene sheet, θA is the apex angle of the corresponding SWCNC, ξ1(T) and ξ2(T) are the structural relaxation parameters along the radial and circumferential directions in the fan-shaped graphene sheet, respectively: (a) the planar fan-shaped graphene sheet and (b) the undeformed SWCNC rolled from the planar fan-shaped graphene sheet.

Full size image

From this perspective, several continuum and quasi-continuum approaches are proposed for studying the mechanical properties of SWCNCs. Using the proposed spring-mass model, Ansari and Mahmoudinezhad9 investigated the mechanical properties of SWCNCs with the C–C covalent bond described by the rotational spring. The apex angle gives rise to an increasing effect on Young’s modulus. Recently, they indicated that the apex angle could increase the oscillation frequency of CNC inside the corresponding nanotube by analyzing continuum theory.10 Lee and Lee11 studied the vibration model of SWCNCs based on the finite element method using an elastic beam model for the C–C bond. Furthermore, on the basis of the higher order gradient quasi-continuum theory, Yan et al.12–14 systematically investigated the elastic properties and buckling behaviors of SWCNCs using the so-called higher order Cauchy–Born rule as the link between nanostructure deformation and the corresponding continuum level.

Temperature is among the critical factors affecting the mechanical characteristics of nanostructures. However, a few studies have been reported on this aspect. Tsai and Fang15 adopted MD simulations to predict the thermal stability of CNCs and revealed that the stability increases as the apex angle increases. Moreover, using MD simulations, Liao et al.16 studied the influence of temperature on the deformation behaviors of open-tip CNCs subjected to tensile and compressive loadings. The results showed that both tensile failure and compressive critical strains highly depend on the temperature variation. Later, the same author predicted the compressive buckling behaviors of SWCNCs at elevated temperatures within 300–700 K and found that the critical strain decreases as the temperature increases.17 Moreover, using the Helmholtz free energy as a thermodynamics potential, Wang et al.18 used the so-called temperature-dependent higher order Cauchy–Born (THCB) rule to deduce the quasi-continuum model to study the buckling and post-buckling behaviors of SWCNCs under compression at finite temperatures. The results also revealed that the temperature exerts a decreasing effect on the compressive critical strain.

Despite the numerous achievements on the subject, the understanding of the mechanical properties of SWCNCs has not matured. This paper aims to study the buckling behaviors of SWCNCs under bending at finite temperatures. To this end, a quasi-continuum model has been constructed using the THCB rule as the kinematic relationship of the atomic crystal lattice. The details of the interatomic interaction and the curvature effect of the atomic structure can be naturally incorporated into constitutive relationships. Moreover, the thermal effect of SWCNCs in finite temperature environments has been accurately described using the Helmholtz free energy as the thermodynamic potential. On this basis, the numerical simulations for predicting the bending buckling behaviors of SWCNCs at finite temperatures have been implemented via the developed meshless computational framework using the moving least-squares approximation as the interpolation function. The main advantages over MD simulations of the proposed method can be summarized as follows: First, the degree of freedom of the total atomic system can be reduced substantially while preserving numerical accuracy. The second advantage is the low requirement of computational resources and marked improvement of the computational efficiency. Subsequently, the effectiveness of the present approach is verified by comparing with present publications.

II. TRANSFORMATION MAPPING RELATIONSHIP OF SWCNCS

A single-walled carbon nanocone (SWCNC) can be envisioned as a curved carbon nanocrystalline sheet with a conical geometry formed by rolling up a fan-shaped graphene sheet seamlessly. The schematic of the rolling process is shown in Fig. 1. Due to the orthohexagonal crystalline lattice in the initial flawless graphene sheet, only five kinds of regular SWCNCs can be fabricated from the corresponding tailored graphene sheets with sector angles of 60°, 120°, 180°, 240°, and 300°, respectively. The apex angles of SWCNCs can be calculated by \({\theta _{{\rm{CNC}}}} = {{360\arcsin \left( {1 - {n \over 6}} \right)} \over \pi }\) with n = 1, 2, 3, 4, 5 and the five apex angles, accordingly, of this synthesized nanostructure are approximately of 19.2°, 38.9°, 60°, 83.6°, and 112.9°, respectively.

Chirality is one of the significant characteristics for most low-dimensional micro/nanoscale structures, including SWCNCs.12,18 As mentioned by Compernolle et al.,19 the chirality of a carbon atom in SWCNCs varies with the position. To simplify the study of the dependence of SWCNCs deformation behaviors on chirality, we defined the rotation angle of the cutting lines θ for the tailored graphene sheet, as shown in Fig. 2 which illustrates a strong correlation between chirality and the rotation angle θ.18 The dependency of the rotation angle θ on the buckling behaviors of SWCNCs was subsequently studied using the proposed approach.

FIG. 2
figure 2

Schematic illustration of clipping of the fan-shaped graphene sheet. The counter-clockwise direction is prescribed as the positive rotation direction, and the initial rotation angle θ of the cutting line OA/OB is defined as 0°.

Full size image

The whole transformation mapping of a SWCNC has two steps: the rolling of the tailored fan-shaped graphene sheet to the corresponding undeformed SWCNC, which is not rigid and the equilibrium configuration can be obtained using an energy minimization process using structural relaxation parameters (see Fig. 1 for reference), and the loading process of the undeformed SWCNC to the deformed counterpart. The total mapping relationship can be described as

$$\left\{ \matrix{ {x_1} = {{{\xi _1}\left( T \right)\sqrt {X_1^2 + X_2^2} \sqrt {4{\pi ^2} - \xi _2^2\theta _{\rm{s}}^2} } \over {2\pi }} + {u_1}\left( {{X_1},{X_2}} \right) \hfill \cr {x_2} = {{{\xi _1}\left( T \right){\xi _2}\left( T \right){\theta _{\rm{s}}}} \over {2\pi }}\sqrt {X_1^2 + X_2^2} \cos \left( {2\pi {{\arctan \left( {{{{X_1}} \over {{X_2}}}} \right)} \over {{\theta _{\rm{s}}}}}} \right) + {u_2}\left( {{X_1},{X_2}} \right) \hfill \cr {x_3} = {{{\xi _1}\left( T \right){\xi _2}\left( T \right){\theta _{\rm{s}}}} \over {2\pi }}\sqrt {X_1^2 + X_2^2} \sin \left( {2\pi {{\arctan \left( {{{{X_1}} \over {{X_2}}}} \right)} \over {{\theta _s}}}} \right) + {u_3}\left( {{X_1},{X_2}} \right) \hfill \cr} \right.\,\,\,\,\,\,\,\,\,\,\,\,,$$
(1)

where ξ1(T) and ξ2(T) denote the structural relaxation parameters along the radial and circumferential directions in the initial fan-shaped graphene sheet, respectively, which are used to preliminarily determine the equilibrium configuration of the undeformed SWCNC approximately at the prescribed temperature. X = (X1, X2)T is the coordinate of the fan-shaped graphene sheet and x = (x1, x2, x3)T is the image of X in the undeformed SWCNC. θs represents the sector angle of the tailored graphene sheet. u = (u1(X1, X2), u2(X1, X2), u3(X1, X2))T denotes the displacement between the undeformed and deformed configurations of the SWCNC, which is determined approximately in the initial equilibrium configuration.

III. TEMPERATURE-DEPENDENT HYPER-ELASTIC CONSTITUTIVE MODEL

In thermal environment, every atom among atomic systems vibrates irregularly around the thermal vibration center continuously. To simplify, a virtual smooth initial configuration for the graphene sheet, at a finite temperature, was developed by Guo et al. in the context of quasi-continuum theory.20 This configuration has been successfully used for studying the mechanical characteristics of carbon nanostructures, such as SWCNCs, single-walled carbon nanotubes (SWCNTs), and graphene sheets.18,20–23 To match the virtual geometrical model, Guo et al.20 proposed the THCB rule which links nanoscale and macroscale deformations and can be used to study the mechanical properties of graphene-based nanostructures. The effectiveness of the THCB rule is sufficiently verified by comparing atomistic simulations.18,20–23 Considering the noncentrosymmetrical details of the regular nanoscale crystalline lattice, an inner shifting vector η(T) defined in the initial reference configuration should be incorporated into the THCB rule to satisfy the requirement of the total system energy minimization. In this case, the THCB rule can be expressed as

$$\eqalign{ & {\bf{r}}\left( T \right) = {\bf{F}}\,{\rm{\cdot}}\,\left( {{\bf{R}}\left( T \right) + \eta \left( T \right)} \right) + {1 \over 2}{\bf{G}}: \cr & \,\,\,\,\,\,\,\,\,\left[ {\left( {{\bf{R}}\left( T \right) + \eta \left( T \right)} \right) \otimes \left( {{\bf{R}}\left( T \right) + \eta \left( T \right)} \right)} \right]\quad , \cr} $$
(2)

where r(T) and R(T) are the bond vectors between the vibration centers of the nearest neighboring atoms in the current configuration and the initial counterpart at the prescribed temperature T, respectively. \({\bf{F}} = {{\partial {\bf{x}}} \over {\partial {\bf{X}}}}{\rm{ }}\) and \({\bf{G}} = {\rm{ }}{{\partial {{\bf{x}}^{\bf{2}}}} \over {\partial {\bf{X}} \otimes \partial {\bf{X}}}}\) denote first- and second-order deformation gradient tensors, respectively, which can be determined using Eq. (1). The curvature effect of nanofilms, which should be considered, otherwise the numerical results become unphysical,24,25 can be presented using the THCB rule owing to the involved second-order deformation gradient. The THCB rule can only be used to develop the quasi-continuum model for CNCs with perfect lattice structures. The rule cannot be used to study the mechanical behavior of CNCs with defects in their original forms as well as those with breakage and recombination of C–C bonds of CNCs under large deformations. This issue can be addressed with use of the multiscale approach,26 in which the THCB rule can be used to develop the quasi-continuum model in the defect-free region while regions are subjected to severe deformation (defects are prone to be generated).

The constitutive model is constructed via homogenization of the free energy for the considered atomic system at finite temperatures. The carbon atom groups in the initial reference configuration, i.e., the virtual fan-shaped graphene sheet, with the central atom surrounded by the three nearest neighboring atoms and the six next nearest neighboring atoms connected by C–C bonds is chosen as the representative cell. The area occupied by the central atom can be calculated by

$${\Omega _{\rm{c}}} = {{3\sqrt 3 a_0^2\left( T \right)} \over 4}\quad ,$$
(3)

where a0(T) represents the equilibrium bond length between the two vibration centers of the corresponding adjacent carbon atoms in the graphene sheet at the considered temperature.

The surface free energy density of a SWCNC can be derived with homogenizing the free energy of the representative cell which can be described by

$${W_T}\,\left( {\left. {{\bf{r}}\left( {\bf{T}} \right)} \right) = {{{\bf{H}}\left( {{\bf{r}}\left( {\bf{T}} \right)} \right)} \over {{\Omega _{\rm{c}}}}}} \right.\quad ,$$
(4)

in which H(r(T)) is the simplified free energy based on the so-called local harmonic approximation (LHA) involved in the representative cell, which has been successfully used to study the mechanical responses of SWCNCs and SWCNTs at finite temperatures,18,20–22 with the expression

$$\eqalign{ & H\left( {{\bf{r}}\left( T \right)} \right) = {\phi _0}\left( {{\bf{r}}\left( T \right)} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {k_{\rm{B}}}T\sum\limits_{i = 1}^3 {\ln \left( {2\sinh \left( {{{\hbar {\omega _i}\left( {{\bf{r}}\left( T \right)} \right)} \over {2{k_{\rm{B}}}T}}} \right)} \right)} \quad , \cr} $$
(5)

where ϕ0(r(T)) denotes the potential energy of the representative cell which can be obtained by using the Tersoff–Brenner potential.30,31kB = 1.38 × 10−23 J/K is the Boltzmann constant, and ħ = 1.05 × 10−34 J s is Planck’s constant. ωi(r(T)) (i = 1, 2, 3) is the i-th order normal vibration frequency of the central atom. Supposing that only the central atom vibrates and all the surrounding atoms fixed, the value can be calculated by the following equation:

$$\left| {{1 \over {{m_{\rm{c}}}}}{{\left. {{{{\partial ^2}{\phi _0}\left( {{\bf{r}}\left( T \right)} \right)} \over {\partial {\bf{x}} \otimes \partial {\bf{x}}}}} \right|}_{x = {x^0}}} - {{\bf{I}}_{3 \times 3}}{{\left( {{\omega _i}\left( {{\bf{r}}\left( T \right)} \right)} \right)}^2}} \right| = 0\quad ,$$
(6)

where mc is the mass of the carbon atom. x0 denotes the vibration center of the central atom. I3×3 is the 3 × 3 identity matrix. According to Foiles,27 although the LHA may relatively underestimate the temperature effects, the approach can provide a good description of the temperature-dependence trend. Notably, the results are acceptable when the temperature is lower than the half of the melting point of the nanostructures. Najafabadi and Srolovitz28 studied the effect of LHA on the interatomic potentials. The LHA provides a reasonable compromise between accuracy and computational efforts. Jiang et al.29 used the LHA to investigate the temperature-dependence of specific heat and the coefficient of thermal expansion of carbon nanostructures. Moreover, the results verified the feasibility of LHA.

The first Piola–Kirchhoff stress tensor P and the second-order stress tensor Q, which are conjugated to F and G, respectively, can be expressed as

$${\bf{P}} = {{\partial {W_T}} \over {\partial {\bf{F}}}}\quad ,$$
(7)
$${\bf{Q}} = {{\partial {W_T}} \over {\partial {\bf{G}}}}\quad .$$
(8)

The tangent modulus tensors can be obtained by the second-order partial derivatives of the surface free energy density with respect to the deformation gradient tensors as

$${{\bf{M}}_{{\rm{FF}}}} = {{{\partial ^2}{W_T}} \over {\partial {\bf{F}} \otimes \partial {\bf{F}}}}\quad ,$$
(9)
$${{\bf{M}}_{{\rm{FG}}}} = {{{\partial ^2}{W_T}} \over {\partial {\bf{F}} \otimes \partial {\bf{G}}}}\quad ,$$
(10)
$${{\bf{M}}_{{\rm{GF}}}} = {{{\partial ^2}{W_T}} \over {\partial {\bf{G}} \otimes \partial {\bf{F}}}}\quad ,$$
(11)
$${{\bf{M}}_{{\rm{GG}}}} = {{{\partial ^2}{W_T}} \over {\partial {\bf{G}} \otimes \partial {\bf{G}}}}\quad .$$
(12)

IV. MESHLESS COMPUTATIONAL FRAMEWORK

In this section, a meshless computational framework, based on the temperature-dependent quasi-continuum model, is developed to simulate the deformation behaviors of SWCNCs under bending at finite temperatures. The core of the numerical simulation is to find the equilibrium configuration of a deformed SWCNC, in which the total free energy of the atomic system is minimized, at the prescribed external boundary and loading condition.

To fulfill the requirement of the higher order continuity of the proposed constitutive model, we adopted the moving least squares method32 to describe the approximate displacement field function from the undeformed configuration to the deformed counterpart (as mentioned in Sec. II) as

$${\bf{u}}\left( {\bf{X}} \right) = {\varphi _\alpha }\left( {\bf{X}} \right){\overline {\bf{u}} _\alpha }\quad ,$$
(13)

where the subscript α denotes the α-th node in the influence domain of the point X and the dummy implies the summation rule. \({\overline {\bf{u}} _\alpha }\) is the displacement parameter and φα(X) is the meshless shape function of the α-th node, calculated by33

$${\varphi _\alpha }\left( {\bf{X}} \right) = {\bf{p}}\left( {\bf{X}} \right)\,\,{\rm{\cdot}}\,\,{\left[ {{{\bf{A}}^{ - 1}}\left( {\bf{X}} \right)\,\,{\rm{\cdot}}\,\,{\bf{B}}\left( {\bf{X}} \right)} \right]_\alpha }\quad ,$$
(14)

where the basis p(X) is a full polynomial.

A(X) and B(X) in Eq. (14) are expressed, respectively, as

$${\bf{A}}\left( {\bf{X}} \right) = \sum\limits_{\alpha = 1}^n {\omega \left( {{\bf{X}} - {{\bf{X}}_\alpha }} \right){\bf{p}}\left( {{{\bf{X}}_\alpha }} \right)\,\,{\rm{\cdot}}\,{\bf{p}}\left( {{{\bf{X}}_\alpha }} \right)} \quad ,$$
(15)
$${\bf{B}}\left( {\bf{X}} \right) = \left[ {\omega \left( {{\bf{X}} - {{\bf{X}}_1}} \right){\bf{p}}\left( {{{\bf{X}}_1}} \right),\omega \left( {{\bf{X}} - {{\bf{X}}_2}} \right){\bf{p}}\left( {{{\bf{X}}_2}} \right), \ldots ,\omega \left( {{\bf{X}} - {{\bf{X}}_n}} \right){\bf{p}}\left( {{{\bf{X}}_n}} \right)} \right]\quad ,$$
(16)

where the weight function ω(X − Xα) can be described with the use of the cubic spline function and n is the total number of nodes in the influence domain.

The total energy functional of the boundary value problems, i.e., the finite deformation behaviors of SWCNCs under bending at finite temperatures, using the higher-order gradient continuum theory can be expressed exactly as

$$\eqalign{ & {\Pi _{{\rm{tot}}}}\left( {\bf{u}} \right) = \int_\Omega {{W_T}\left( {{\bf{F}}{\rm{,}}\,{\bf{G}}} \right){\rm{d}}V} - \int_\Omega {{\bf{u}}\,\,{\rm{\cdot}}\,\,{{\bf{b}}_0}\,{\rm{d}}V} \cr & - \int_{{\Gamma _{\rm{t}}}} {u\,\,{\rm{\cdot}}\,\,t_0^{\rm{P}}{\rm{d}}S} - \int_{{\Gamma _{\rm{t}}}} {{\nabla _{\rm{N}}}{\bf{u}}\,\,{\rm{\cdot}}\,\,{\bf{t}}_0^{\rm{Q}}\,{\rm{d}}S} \cr & + \int_{{\Gamma _{\rm{u}}}} {{1 \over 2}\left( {{\bf{u}} - {\bf{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over u} }}} \right)\lambda \left( {{\bf{u}} - {\bf{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over u} }}} \right){\rm{d}}S} \quad , \cr} $$
(17)

where b0 is the body force density, \(t_0^{\rm{P}}\) and \(t_0^{\rm{Q}}\) are the boundary traction and boundary couple, respectively, on the surface Γt. ∇N(∘) = ∇X(∘)·N, in which N is the outward normal vector. ŭ denotes the boundary displacement on the surface Γu and λ is the penalty factor.

Taking variation of Πtot with respect to u and setting it to zero, it yields the virtual work equation as

$$\eqalign{ & \delta {\Pi _{{\rm{tot}}}}\left( {{\bf{u}};\,\delta {\bf{u}}} \right) = \int_\Omega {\left( {\left( {{\bf{Q}}\,\,{\rm{\cdot}}\,\nabla \,\,{\rm{\cdot}}\,\nabla - {\bf{P}}\,{\rm{\cdot}}\nabla } \right) - {{\bf{b}}_0}} \right)} \,\,{\rm{\cdot}}\,\,\delta {\bf{u}}{\rm{d}}V \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \int_{{\Gamma _{\rm{t}}}} {\left( {\left( {{\bf{P}} - \left( {{\bf{Q}}\,\,{\rm{\cdot}}\,\nabla } \right)} \right)\,\,{\rm{\cdot}}\,{\bf{N}} - \left( {{\bf{K}}\left( {{\bf{Q}}\,\,{\rm{\cdot}}\,{\bf{N}}} \right)\,\,{\rm{\cdot}}\,{\bf{N}}} \right.} \right)} \cr & \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {\nabla _X}\left( {{\bf{Q}}\,\,{\rm{\cdot}}\,{\bf{N}}} \right):\overline {\bf{T}} } \right) - {\bf{t}}_0^{\rm{P}}{\rm{\cdot}}\delta {\bf{u}}{\rm{d}}S \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \int_{{\Gamma _{\rm{t}}}} {{\nabla _{\rm{N}}}\delta {\bf{u}}\,\,{\rm{\cdot}}\,\,\left( {\left( {{\bf{Q}}:{\bf{N}} \otimes {\bf{N}}} \right) - {\bf{t}}_0^{\rm{Q}}} \right){\rm{d}}S} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \int_{{\Gamma _{\rm{u}}}} {\lambda \delta {\bf{u}}\,\,{\rm{\cdot}}\,\,\left( {{\bf{u}} - {\bf{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over u} }}} \right){\rm{d}}S = 0} \quad , \cr} $$
(18)

where \(\overline {\bf{T}} = {\bf{I}} - {\bf{N}} \otimes {\bf{N}}\) and \({\bf{K}} = - {\nabla _X}{\bf{N}}:\overline {\bf{T}} \).

The incremental stiffness equation can be derived through the linearization of the virtual work equation (18),

$${\bf{K}}\,{\rm{\cdot}}\,{\bf{\Delta }}\overline {\bf{u}} = {\bf{f}}\quad ,$$
(19)

where \({\bf{\Delta }}\overline {\bf{u}} = {\overline {\bf{u}} _{i + 1}} - {\overline {\bf{u}} _i}\), in which \({\overline {\bf{u}} _i}\) and \({\overline {\bf{u}} _{i + 1}}\) are the displacement parameters at i-th and (i + 1)-th iteration steps, respectively. The global stiffness matrix \({\bf{K}} = {{\bf{K}}_0}\left( {{{\overline {\bf{u}} }_i}} \right) + {{\bf{K}}_\lambda }\), and the non-equilibrium force \({\bf{f}} = - {{\bf{P}}_0}\left( {{{\overline {\bf{u}} }_i}} \right) - \left( {{{\bf{K}}_\lambda }\,\cdot\,\,{{\overline {\bf{u}} }_i} - {{\bf{P}}_\lambda }} \right)\), in which K0, Kλ, P0, and Pλ can be calculated as follows:

$${{\bf{K}}_0} = \int_\Omega {{{\bf{M}}_{{\rm{FF}}}}} :{\nabla _X}{\varphi _\alpha } \otimes {\nabla _X}{\varphi _\beta } + {{\bf{M}}_{FG}} \vdots {\nabla _X}{\varphi _\alpha } \otimes {\nabla _{XX}}{\varphi _\beta } + {M_{{\rm{GF}}}} \vdots {\nabla _{XX}}{\varphi _\alpha } \otimes {\nabla _X}{\varphi _\beta } + {\nabla _{XX}}{\varphi _\alpha }:{{\bf{M}}_{{\rm{GG}}}}:{\nabla _{XX}}{\varphi _\beta }{\rm{d}}V\quad ,$$
(20)
$${{\bf{K}}_\lambda } = \int_{{\Gamma _{\rm{u}}}} {\lambda {\varphi _\alpha }{\varphi _\beta }\widetilde{\bf{1}}{\rm{d}}S} \quad ,$$
(21)
$$\eqalign{ & {{\bf{P}}_0} = \int_\Omega {{\bf{P}}\,\,{\rm{\cdot}}\,{\nabla _X}{\varphi _\alpha }} + {\bf{Q}}:{\nabla _{XX}}{\varphi _\alpha } - {{\bf{b}}_0}{\varphi _\alpha }{\rm{d}}V \cr & \,\,\,\,\,\,\,\,\,\, - \int_{{\Gamma _{\rm{t}}}} {{\bf{t}}_0^{\rm{P}}{\varphi _\alpha } + {\bf{t}}_0^{\rm{Q}}\left( {{\bf{N}}\,\,\cdot\,\,{\nabla _X}{\varphi _\alpha }} \right){\rm{d}}S} \quad , \cr} $$
(22)
$${{\bf{P}}_\lambda } = \int_{{\Gamma _{\bf{u}}}} {\lambda {\varphi _\alpha }{\bf{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over u} }}{\rm{d}}S} \quad ,$$
(23)

where \(\widetilde{\bf{1}}\) is the second-order identity tensor.

In this study, the phenomena involving bending deformation and buckling behaviors of SWCNCs at finite temperatures are simulated using the developed meshless computational scheme. The incremental stiffness equation in Eq. (19) can be solved iteratively using the Newton–Raphson method. However, the stiffness matrix K in Eq. (19) and the local dynamic matrix \({{{\partial ^2}{\phi _0}\left( {{\bf{r}}\left( T \right)} \right)} \over {\partial {\bf{x}} \otimes \partial {\bf{x}}}}\) in Eq. (6) usually become non-positive definite upon buckling, thereby resulting in failure on the iteration solution. From the numerical calculation perspective, this problem can be remedied by replacing of the original K with the revisional positive stiffness K0 + γI,18,20–22 where the stiffness matrix K0 is assembled by the sub-stiffness matrix without considering the thermal effect; moreover, I is the identity matrix, with the same order of K, and γ is a positive number which is slightly larger than the absolute value of the smallest negative eigenvalue of K0. The stiffness matrix K will restore the positive definite as the equilibrium configuration of the deformed SWCNC is found.

V. NUMERICAL EXAMPLES AND DISCUSSION

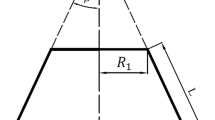
In this study, using the proposed meshless computational framework, the finite deformation and buckling behaviors of SWCNCs upon bending are simulated at finite temperatures. We systematically discuss the effect of the temperature, height, top radius, and rotation angles θ (see Sec. II) on the critical bending angle of SWCNCs. The loading process is isothermal and quasi-static. In the following study, the apex angle of the samples is prescribed as 19.2°.

A. Bent SWCNC

In this subsection, the effectiveness of the proposed meshless computational scheme is illustrated by studying the deformation behaviors for the SWCNC under bending at 300 K. The height, the top radius, and the rotation angle θ are of 9.41 nm, 0.8 nm, and 0°, respectively. During the bending process, the bending angle is imposed on the two ends in opposite directions, where 0.5° per step is for the initial stage of the deformation while 0.1° per step is for the buckling and post-buckling stages. Simultaneously, the radial and circumferential displacements of the nodes on the top and end cross-sections are constrained.

The variations of the average strain energy (eV/atom) with respect to the bending angle for the considered SWCNC are depicted in Fig. 3(a). Evidently, an energy jump occurred in the average strain energy curve upon buckling, but a slight energy jump can be observed at the post-buckling stage; this finding is consistent with those of Yan et al.14 The buckling and post-buckling patterns are presented in Figs. 3(b) and 3(c). At a bending angle of 3.7°, with the relatively large energy jump, a single pit is developed at the central part of the SWCNC, thereby forming a local buckling pattern as shown in Fig. 3(b). As the deformation increased, the second buckling occurred at the bending angle of approximately 10°, accompanied by a slight energy jump. Afterward, the mid-pit moved to the bottom; simultaneously, two smaller symmetrical pits appeared near the end below the largest pit [Fig. 3(c)]. The deformation process and buckling patterns of the SWCNC are in good agreement with those depicted by Yan et al.14 Therefore, the proposed meshless computational framework can effectively simulate the buckling behaviors of SWCNCs subjected to bending. Further studies are done in the following sections.

FIG. 3
figure 3

The buckling behavior of the SWCNC: (a) the average strain energy of the SWCNC versus bending angle, (b) the first buckling pattern at the bending angle of 3.7°, and (c) the post-buckling pattern at the bending angle of 10°.

Full size image

B. Effect of the temperature on the critical bending angle

The SWCNCs with the top radius from 0.5 to 0.7 nm, the height of 6.3 nm, and the rotation angle θ of 30° are selected as samples to discuss the effect of the temperature on the critical bending angle, corresponding to the appearance of buckling. Figure 4 shows the relationship between the critical bending angles of the SWCNCs and temperature. The critical bending angle of the SWCNC enlarges nonlinearly, as the temperature increases from 100 K to 900 K. The SWCNC showed a weak buckling resistance at low temperatures. However, as the temperature increased, the SWCNC resisted buckling at the same bending angle. Foiles27 pointed out that although LHA may somewhat underestimate the temperature dependence of atomic systems, it can provide a reasonably good description of the trend. From Fig. 4, the critical bending angle decreased as the top radius increased at the same temperature, and the influence of temperature on the critical bending angle decreased as the radius increased. This finding may be attributed to the fact that the mechanical properties of the SWCNC with a large radius approximate those of the graphene sheet. Moreover, ripples were found in the graphene sheet,34,35 which denoted weak anti-bending capacity.23 Therefore, as the top radius increases, the buckling of SWCNC becomes insensitive to temperature.

FIG. 4
figure 4

The variation of the critical bending angles of the SWCNC versus temperature.

Full size image

The results illustrated that the temperature induces a significant softening effect on SWCNCs with small top radii, which is rational from the physical perspective. This finding revealed that the temperature effect of SWCNCs can be considered using the proposed temperature-dependent constitutive model and the corresponding meshless computational framework.

C. Effect of height and radius on the critical bending angle

In this subsection, the SWCNCs with heights from 4.2 to 10.5 nm, of which the top radius is of 0.6 nm and θ is of 0°, were simulated at 300 K to exhibit the effects of height on the critical bending angle. The variations of the critical bending angles of the SWCNCs versus the heights are shown in Fig. 5. The curve demonstrated that the height caused a decreasing effect on the critical bending angle of SWCNCs. This outcome implied that the anti-buckling capacity decreases as the height of the SWCNC increases, whereas the apex angle and top radius are constant. This conclusion is in good accordance with that found by Yan et al.14

FIG. 5
figure 5

The relationship between critical bending angles of the SWCNCs and the heights.

Full size image

To study the effects of top radius on the buckling of SWCNCs, we selected samples with top radii of 0.6–3 nm, height of 7.2 nm, and θ of 0° at room temperature (300 K). The relationship between the critical bending angles and the top radii of the SWCNCs is presented in Fig. 6. Similar to height, the top radius exerted a decreasing effect on the critical bending angle of SWCNCs. The relationship between the critical bending angle and the top radius can be approximated by a hyperbola. The curvature of the cross section of SWCNC’s central part decreased almost hyperbolically as the top radius increased, and the bending stiffness of the SWCNC with a large radius/small curvature was close to that of the graphene sheet. Therefore, the effect of the top radius on the critical bending angle was considerable for the SWCNCs with smaller top radii, whereas the influence was low for SWCNCs with large top radii. This phenomenon is also consistent with that reported by Yan et al.14

FIG. 6
figure 6

The variation of the critical bending angles of the SWCNCs versus the top radii.

Full size image

These phenomena shown in Figs. 5 and 6 can be explained by the following simple mechanical model under bending (see Fig. 7 for reference). For ease of understanding, a long narrow stripe “tailored” from the SWCNC along the side edge. For the buckling point A, F1 denotes the resultant compressive stress experienced by the adjacent stripes in the cross-sectional plane, and F2 is the resultant compressive stress in the vertical section of the SWCNC. Before buckling, point A maintained a balance under F1 and F2. Evidently, with the increasing of either height or top radius, the circumferential/transverse curvature of the point A decreases and the stress F1 can be easily exceeded by F2 for SWCNCs under the same bending angle, thereby causing buckling. Therefore, the SWCNC with a large height or top radius is prone to buckling under bending compared with nanocones with a small height or top radius.

FIG. 7
figure 7

The force diagram for the buckling point of a SWCNC under bending.

Full size image

D. Effect of the rotation angle on the critical bending angle

Except for the height and the top radius, the rotation angle θ for the cutting lines of the fan-shaped graphene sheet influences the critical bending angle of SWCNCs. For ease of study, SWCNCs with 0.5–0.7 nm top radii and 5.94 nm height were selected for bending tests at room temperature, and θ varies from 0° to 60°. Figure 8 shows the variations of the rotation angle θ with respect to the critical bending angle of the SWCNCs. The curve is symmetrical at approximately θ = 30°. The critical bending angle at θ = 30° is larger than others, indicating the highest buckling resistance for SWCNCs at this rotation angle. As the rotation angle is larger or smaller than 30°, the critical bending angle decreases, i.e., the buckling resistance ability decreases, until θ reaches 0° or 60°.

FIG. 8
figure 8

The variation of the critical bending angle of the SWCNCs versus the rotation angle θ of the cutting lines.

Full size image

Shen et al.36 found that it is easier to change the length of the C–C bond than to change the bond angle of single layer of graphene sheets. As shown in Fig. 2, the number of C–C bonds along the longitudinal direction of the SWCNC rolled up by the corresponding tailored graphene sheet with the rotation angle of 30° is less than those obtained at other angles. By contrast, the SWCNC with a rotation angle of 0° or 60° presents the largest number of C–C bonds along the longitudinal direction. This finding may explain the strongest anti-buckling capacity of the SWCNC with the rotation angle of 30°.

As shown in Fig. 8, the influence of the rotation angle θ on the critical bending angle decreases with the top radius increasing; that is, as the top radius increases, the mechanics of SWCNCs tends toward that of graphene sheet and the bending stiffness decreases, therefore the effect of the rotation angle θ decreases with bending stiffness. The difference between the largest and smallest critical bending angles reaches approximately 5%, 4.8%, and 4.4% for SWCNCs with top radii of 0.5, 0.6, and 0.7 nm, respectively. Notably, in SWCNCs with small top radii, the effect of the rotation angle θ on the buckling of SWCNCs under bending should be considered.

VI. CONCLUDING REMARKS

In this study, a temperature-dependent multiscale quasi-continuum model and the corresponding meshless computational framework were developed to investigate the bending deformation and buckling phenomena of SWCNCs at finite temperatures. The details of the nanoscale geometry of SWCNCs can be considered naturally and were illustrated by studying the relationship between the rotation angle of the clipping line for the tailored graphene sheet and the critical bending angle for the corresponding SWCNC. Apparently, the SWCNCs with the rotation angle θ of 30° exhibited the highest buckling resistance capacity compared with other nanocones with the same height and top radius. The influence of temperature on the buckling of SWCNCs under bending can be simulated using this method. Moreover, as the temperature increases, the softening effect of SWCNCs can be captured. Furthermore, the decreasing effects of height and top radius on the critical bending angle of SWCNCs can be reproduced using the present approach.