1 Introduction

In most particular applications, especially in the field of engineering, to successfully solve the complex optimization problems with complicated constraints, we are looking for powerful global and more efficient Artificial Intelligent Optimization (AIO) methods. These Artificial Intelligence-based (AI) algorithms find the optimal in the low possible number of iterations; where optimal mean the best from all possibilities selected from a special point of view. Because, due to the complexity, nonlinearity and potentially high-dimensionality of the problems, traditional optimization techniques such as gradient-based methods cannot satisfy the optimization requirements and often stuck in too local/optimal minimum (Yang 2010, 2015). These problems can even be NP-hard, and thus require alternative solution methods (Yang 2010, 2015; Tao et al. 2015). Recently, soft computing techniques have attracted significant popularity in the solving of different and intricate optimization problems (Tavakoli et al. 2012; Mazinan and Sagharichiha 2015; Malekzadeh et al. 2016; Sharifi et al. 2017; Moeini and Babaei 2017). Although, due to their high applicability and effectiveness, these techniques have been a popular choice to solve modern optimization problems and apply them to a wide range of optimization problems in various applications (Melin and Castillo 2013; Balas et al. 2013; Páramo-Carranza et al. 2017; Mohammadi et al. 2015, 2017).

Digital filtering is one of the most important tools in Digital Signal Processing (DSP) systems (Chauhan and Arya 2013) and it is a powerful tool for system modeling and parameter estimation (Singh and Verma 2014). Digital filters have attracted increasing attention in recent years due to demands for improved performance in high-data-rate digital communication systems and in wideband image/video processing systems (Dai et al. 2010). Adaptive digital filters are computational modules that are trying to model the ratio of the two signals, in real-time and repeated. An adaptive filter plays an important role in linear prediction, equalization, echo and noise cancellation, system identification and modeling etc. for many different physical systems (Saha et al. 2014). The typical application of adaptive digital filter for identifying any unknown actual system mainly consists of two parts, digital filter and optimization technique. The optimization technique adjusts the coefficient values of the digital filter towards the minimization/optimization of error signal generated as the difference of outputs from the unknown actual system and the digital filter when the same input is applied to both (Saha et al. 2014). The digital filters are broadly classified into two types: Finite Impulse Response (FIR) and Infinite Impulse Response (IIR) filters (Vegte 2001). An IIR filter can provide a much better performance than the FIR filters having the same number of coefficients (Dai et al. 2010). However, in the IIR digital filter design, the error surface is generally multi-modal (Dai et al. 2010). Therefore, a reliable and optimal design method of adaptive IIR digital filters must be based on a powerful global search procedure. Genetic Algorithm (GA) (Goldberg 1989), Simulated Annealing (SA) (Kirkpatrick et al. 1983), Ant Colony Optimization (ACO) (Dorigo et al. 1996), and Particle Swarm Optimization (PSO) (Kennedy and Eberhart 1995) are four well-known classes of such global optimization methods. In overview, loosely speaking we can say that the current main intelligent optimization algorithms are based on the mode of population based iteration (Tao et al. 2015). Therefore, the effectiveness of such algorithms is significantly related to population size.

In this paper, we will focus on four of the AIO algorithms, namely: GA, PSO and Gravitational Search Algorithm (GSA) (Rashedi et al. 2009), accompanied by the Inclined Planes System Optimization (IPO) (Mozaffari et al. 2016). The IPO algorithm is a relatively new heuristic technique based on the dynamics of sliding motion along a frictionless inclined surface (Mozaffari et al. 2016). The proposed algorithms are selected based on the coverage of different types of artificial intelligence optimization methods. As GA is selected from the category of evolutionary methods and other three algorithms are heuristic search methods, PSO from swarm-based methods, and two GSA and IPO algorithms also are jointly chosen form the methods of population-based and based on Newton’s laws. This paper is an extended version of work published in (Mohammadi and Zahiri 2016b). The main approach of the paper is to evaluate performance, efficiency and efficacy of AIO methods in the adaptive IIR systems modeling based on the two new indicators, Indicator of Success (IoS) and Degree of Reliability (DoR), along with Mean Squared Error (MSE) and the simulation results will be investigated for the evaluation of the proposed algorithms in their categorization. The IoS index represents the persistence and continuity of an adaptive algorithm to convergence into an optimal model in the modeling process. This indicator is defined based on the number of successful trials in achieving the optimal solution than unsuccessful trials of an algorithm. The numerical value of the IoS index is calculated by dividing the number of successful trials into unsuccessful trials plus number one. The integer 1 in the denominator of IoS index is for two purposes: one to avoid the undefined response resulted via the convergence all trials to the optimal solution, and secondly to affect the value IoS index only for the high successful trials number (more than fifty percent). So that the unsuccessful less than fifty percent in the convergence to the optimal models will result a significant reduction in the amount of IoS and an undesirable success. On the other hand, the maximum value IoS index will obtain based on high success trials, and indicates the powerfulness, intelligence, usefulness and competence of the algorithm for applying in the solving of IIR system modeling problem. However, the user has the option of choosing and replacing a guaranteed optimal design approach than traditional and complex techniques to overcome the challenge of modeling and designing digital filtering systems. DoR criterion is also defined parametrically as a complement and conflation from the algorithm’s success rate estimation in continuous convergence to the optimal response and the desirability of optimal solutions. In such a way, a successful algorithm with a high numerical value and the best statistical values of fitness will get a high score DoR. This index is proposed to show the overall performance of the adaptive algorithms in the design of digital filters, so that the user can select the best method depending on the variation performance of each algorithm and the desirability of the IoS and MSE indexes.

The remaining of our paper is organized as follows. In Sect. 2, some recent works on the IIR system modeling using artificial intelligent optimization methods are reviewed. Also, we briefly describe the proposed AIO algorithms in Sect. 3. Section 4 presents the IIR digital filtering systems modeling problem along with how to use optimization algorithms for this purpose. In Sect. 5, the performance and efficiency of the proposed algorithms is investigated and results are evaluated. Finally, the conclusion and scope for future works are offered in Sect. 6.

2 Recent works on the IIR system modeling using AIO algorithms

Artificial intelligent optimization methods are widely used in solving IIR system modeling problem and IIR digital filter design (Mohammadi and Zahiri 2016a, 2017; Kumar et al. 2017; Lagos-Eulogio et al. 2017; Yang et al. 2017). In (Mohammadi and Zahiri 2016a), a design method based on IPO algorithm is introduced for the IIR system identification. The effectiveness of the proposed method verified in presence of the additive noise, and both same and reduced order identification of few benchmarked IIR plants carried out in the simulations (Mohammadi and Zahiri 2016a). Mohammadi and Zahiri (2017) introduced a modified version of IPO algorithm titled MIPO and applied it to the IIR model identification problem. Based on the results (Mohammadi and Zahiri 2017), MIPO shown the better performance and high stability and reliability for achieve the desirable solution with global convergence in compared to the other algorithms.

Kumar et al. (2017) used Interior Search Algorithm (ISA) with Lèvy flight as a new metaheuristic optimization method to estimate the optimal parameters of the IIR systems for the system modeling problem. The ISA algorithm has been adapted from the concepts of interior design and decoration (Kumar et al. 2017). In the proposed revision in (Kumar et al. 2017), called M-ISA, the concept of Lèvy flight used to improve the exploration and exploitation of the standard ISA. The results were compared to demonstrate the efficiency and effectiveness of the proposed method with the results of the standard ISA algorithm and several intelligent optimization algorithms (Kumar et al. 2017). In Lagos-Eulogio et al. (2017), for the optimal IIR filters design, an efficient hybrid optimization method proposed and it used for estimating the optimum values of filter coefficients with both equal and reduced order adaptive IIR system modeling. The proposed technique (Lagos-Eulogio et al. 2017) is based on combination two intelligent optimization algorithms, Cellular-PSO and Differential Evolution (CPSO-DE). In CPSO-DE, DE method applied as an evolution rule of the cellular part of CPSO, which performs a local search for improvement each particle of the swarm. The simulation results in compared to other evolutionary algorithms had been shown the success of the proposed approach in terms of convergence properties and MSE values (Lagos-Eulogio et al. 2017). In Yang et al. (2017), Yang and et al. introduced a novel bio-inspired intelligent optimization algorithm called the Opposition Based Hybrid Coral Reefs Optimization (OHCRO). The OHCRO proposed as a modified version of CRO algorithm, which inspired from the growing and evolution of coral reefs (Yang et al. 2017). In Yang et al. (2017), the adaptive IIR system modeling problem has been solved in the presence of noise for modeling with the same and reduced order in the form of the MSE fitness function. The overall estimation of the results for a limited numbers of trials the proposed algorithm and other methods indicated the superiority of OHCRO algorithm (Yang et al. 2017).

3 Artificial intelligent optimization methods

The description of proposed Artificial Intelligent Optimization (AIO) methods is briefly presented in this Section.

3.1 Genetic algorithm

The Genetic Algorithm (GA) developed by John Holland and his collaborators in the 1960s and 1970s (Holland 1975), and it is a model or abstraction of biological evolution based on Charles Darwin’s theory of natural selection (Yang 2010). Holland was the first to use the crossover and recombination, mutation, and selection in the study of adaptive and artificial systems. These genetic operators form the essential part of the genetic algorithm as a problem-solving strategy (Yang 2010). GA algorithm starts with the random initialization of a population of individuals, which are known as gene.

The procedure of GA is as follows (Saha et al. 2015):

  • Initializing a population of individuals (chromosome strings).

  • Decoding of the strings and evaluation of error fitness values.

  • Selection of elite strings to increase error fitness values from the minimum value.

  • Copying of the elite strings over the non-selected strings.

  • Crossover and mutation generate offspring.

  • Genetic cycle updating.

  • The iteration process stops when the maximum number of cycle is reached.

In GA, the choice of the important parameters such as the rate of mutation and crossover, and the selection criteria of new population should carefully be carried out (Yang 2010).

3.2 Particle swarm optimization

Particle Swarm Optimization (PSO) algorithm developed by Kennedy and Eberhart in 1995 (Kennedy and Eberhart 1995), based on swarm behavior such as fish and bird schooling in nature. PSO algorithm starts with the random initialization of a swarm of individuals, which are known as particles, in which each particle attempts to move toward the optimum solution and where next movement is influenced by the previously acquired knowledge of particle best and global best positions, once achieved, of the individuals and the entire swarm, respectively.

The basic steps of the PSO algorithm are as follows (Saha et al. 2015):

  • Initializing a swarm of individuals (particle strings).

  • Compute the error fitness value for the current position of each particle.

  • Each particle can remember its best position (pbest), which is known as cognitive information that is updated with each iteration.

  • Each particle can also remember the best position the swarm has ever attained (gbest), which is known as social information and updated with each iteration.

  • The velocity and position of each particle are updated according to Eqs. (1) and (2), respectively (Kennedy and Eberhart 1995).

$$v_{i}^{d}(t+1)=w(t)v_{i}^{d}(t)+{c_1}ran{d_{i1}}(pbest_{i}^{d} - p_{i}^{d}(t))+{c_2}ran{d_{i2}}(gbes{t^d} - p_{i}^{d}(t))$$
(1)
$$p_{i}^{d}(t+1)=p_{i}^{d}(t)+v_{i}^{d}(t+1)$$
(2)

Here, w(t) represents inertia weight, and it decreases linearly during the algorithm iteration process. \(v_{i}^{d}(t+1)\) and \(p_{i}^{d}(t+1)\) are, respectively, the dth velocity variable and the dth position variable of particle i at iteration t + 1. \(pbest_{i}^{d}\) denotes the dth variable of the personal best position of particle i, while \(gbes{t^d}\) signifies the dth variable of the global best position of the population. c1 is defined as cognitive factor, while c2 represents social factor. rand1 and rand2 are two random vectors, and each entry taking the values between 0 and 1 (Kennedy and Eberhart 1995; Saha et al. 2015). Also \(p_{i}^{d}(t)\) is the dth position variable of particle i at current iteration t.

  • The iteration process stops when the maximum number of iteration cycles is reached.

3.3 Gravitational search algorithm

The Gravitational Search Algorithm (GSA) proposed by Rashedi et al. in 2009 (Rashedi et al. 2009), and in it agents/solution vectors are considered as objects, and their performances are measured by their masses. All these objects attract each other via gravity forces, and these forces produce a global movement of all objects toward the objects with heavier masses. Thus, masses cooperate using a direct form of communication through gravitational forces. The heavier masses (which correspond to better solutions) move more slowly than lighter ones. This guarantees the exploitation step of the algorithm. GSA is similar to a small artificial world of masses obeying the Newtonian laws of gravitation and motion (Saha et al. 2015).

The different steps of the GSA are the followings (Rashedi et al. 2009):

  • Generate initial population of masses (agents)

  • Evaluate the fitness for each agent

  • Calculate Mi(t) for each agent

$${M_i}(t)=\frac{{fi{t_i}(t) - worst(t)}}{{\sum\nolimits_{{j=1}}^{{{N_p}}} {fi{t_j}(t) - worst(t)} }}$$
(3)

where Np, Mi(t) and fiti(t) are the population size, the mass, and the fitness value of the ith agent at iteration t, respectively, and worst(t) is the worst fitness of all agents at iteration t.

  • Update the acceleration, velocity and position of each agent.

$$\begin{array}{*{20}{c}} {a_{i}^{d}(t)=\sum\limits_{{j \in Kbest,j \ne i}}^{{{N_p}}} {ran{d_j} \times G(t)} \times \frac{{{M_j}(t)}}{{{R_{ij}}{{(t)}^{Rpower}}+\varepsilon }} \times (x_{j}^{d}(t) - x_{i}^{d}(t));}&{d=1,2,3, \ldots ,n} \end{array}$$
(4)
$$V_{i}^{d}(t+1)=ran{d_i} \times V_{i}^{d}(t)+a_{i}^{d}(t)$$
(5)
$$X_{i}^{d}(t+1)=X_{i}^{d}(t)+V_{i}^{d}(t+1)$$
(6)
$$\begin{array}{*{20}{c}} {G(t)=G({G_0},t),}&{G(t)={G_0}\exp ( - \alpha \frac{t}{{{t_{\text{max} }}}})} \end{array}$$
(7)
$${R_{ij}}(t)={\left\| {{X_i}(t),{X_j}(t)} \right\|_2}$$
(8)

where \(a_{i}^{d}(t)\), \(V_{i}^{d}(t)\) and \(X_{i}^{d}(t)\) present the acceleration, velocity and position of agent i in dimension d at iteration t, respectively. randi and randj are two uniformly distributed random numbers in the interval [0 1], ε is a small constant, n is the dimension of the search space, \({R_{ij}}(t)\) is the Euclidean distance between two agents, i and j, and Rpower is the power of distances. Kbest is the set of first K agents with the best fitness value and the heaviest mass, which is initialized to K0 and decreased with time (Rashedi et al. 2009). G(t) is the gravitational constant at iteration cycle t, which is set to G0 at the beginning and it will be reduced with time t (iteration cycle) to control the search accuracy, and α is a constant.

  • Repeat second step to previous until the stop criteria is reached.

3.4 Inclined planes system optimization

Inclined Planes System Optimization (IPO) algorithm introduced by Mozaffari et al. in 2016 (Mozaffari et al. 2016), and is inspired by the dynamic of sliding motion along frictionless inclined surfaces. In IPO algorithm, agents vectors are proposed as “tiny balls” and their performance are evaluated by their heights, regarding to their fitness. All these tiny balls interact with each other by the Newton’s second law and equations of motion, and these balls would like to miss their potential energy and to get the reference point. The point is the same the optimal solution that balls accelerate and search the problem space for it, iteratively (Mohammadi and Zahiri 2017). Each ball (agent) in IPO has three specifications: position, height, and angles made with other balls. The position of the ball corresponds to a feasible solution of the problem, and its angle is calculated by crossing straight line from center of ball to centers of other balls in the search space, and its height are determined using a fitness function value. The algorithm is conducted by properly adjusting the velocity and acceleration (Mohammadi and Zahiri 2017).

The procedure of IPO is as follows (Mozaffari et al. 2016):

  • Generate randomized population of balls (agents)

  • Evaluate the fitness (height) of each agent

  • Calculate angle, acceleration, and velocity of each agent

$$\begin{array}{*{20}{c}} {\varphi _{{ij}}^{d}(t)=\left( {{{\tan }^{ - 1}}\left( {\frac{{{f_j}(t) - {f_i}(t)}}{{r_{i}^{d}(t) - r_{j}^{d}(t)}}} \right)} \right),}&{for\,d=1, \ldots ,n\;and\;i,j=1,2, \ldots ,P,i \ne j} \end{array}$$
(9)
$$a_{i}^{d}(t)=\sum\limits_{{j=1,j \ne i}}^{P} {U({f_i}(t) - {f_j}(t)).\sin (\varphi _{{ij}}^{d}(t))}$$
(10)
$$U(g)=\left\{ {\begin{array}{*{20}{c}} {1\quad g \ge 0} \\ {0\quad g < 0} \end{array}} \right.$$
(11)
$$v_{i}^{d}(t)=\frac{{r_{{best}}^{d}(t) - r_{i}^{d}(t)}}{{\Delta t}}$$
(12)

where \(\varphi _{{ij}}^{d}(t)\), \(a_{i}^{d}(t)\), \(v_{i}^{d}(t)\), and fi(t) are the angle between the ith ball and jth ball, the value along with direction of acceleration, the velocity, and the fitness value of the ith ball in dimension d at iteration cycle t, respectively. Also, n is the dimension of the search space, and P is the population size of balls. Also \(r_{i}^{d}(t)\) is the position of ith agent in the dth dimension at iteration t and rbest is the best agent with lowest height among other agents in all iterations till current iteration cycle.

  • Update the position of each agent

$$r_{i}^{d}(t+1)={k_1}(t) \cdot {r_{i1}} \cdot a_{i}^{d}(t) \cdot \Delta {t^2}+{k_2}(t) \cdot {r_{i2}} \cdot v_{i}^{d}(t) \cdot \Delta t+r_{i}^{d}(t)$$
(13)

where \(r_{i}^{d}(t+1)\) is ith ball position in dimension d at time t + 1, and r1 and r2 denote the uniformly generated random numbers in the range [0 1]. The k1 and k2 are two changing constants with time for controlling exploration and exploitation of the algorithm search process.

  • Update values of exploration and exploitation tuners of the algorithm.

$${k_1}(t)=\frac{{c1}}{{(1+\exp ((t - shift1) \times scale1))}},$$
(14)
$${k_2}(t)=\frac{{c2}}{{(1+\exp ( - (t - shift2) \times scale2))}},$$
(15)

where c1, c2, shift1, shift2, scale1 and scale2 are experimentally determined constants based on each function/problem (Mozaffari et al. 2016).

  • Repeat second step to previous until meeting the stopping criteria.

4 IIR digital filtering systems modeling problem

In this section, firstly the IIR system modeling problem is introduced; and then proposed AIO algorithms are applied to the design of IIR digital filters for the purpose of adaptive system identification.

4.1 IIR system modeling

In system modeling (system identification configuration) based on IIR digital filtering, the coefficients an adaptive IIR model is repeatedly adjusted by an adaptive algorithm until the error between output of the IIR model and unknown actual system is minimized. The adequacy and accuracy of the resulting model depends on the structure IIR filter (filter transfer function), the intelligent/adaptive algorithm used, specifications of the measurement noise and the characteristics of the input signal. Here, all considerations have been made to achieve maximum accuracy of modeling. As proposed filter models are including two types of challenging IIR plants, powerful and new intelligent optimization algorithms instead of an adaptive algorithm, the measurement noise as the best candidate for unpredictable environmental noise and effective on the system with the capability covering all frequencies and the possibility generating different power from it, and the input signal also is considered a uniformly distributed noise with an effective amplitude to cover a wide variety of input states (commonly used in other studies in this area).

The input–output relation of IIR system is given by:

$$y(k)+\sum\limits_{{i=1}}^{N} {{a_i}y(k - i)=\sum\limits_{{i=0}}^{M} {{b_i}x(k - i)} }$$
(16)

In Eq. (16), x(k) and y(k) are kth input and output of the system, N and M are the order of numerator and denominator, respectively, \({a_i}\)’s and \({b_i}\)’s are IIR filtering system coefficients, and N(≥ M) is the filter order. It is assumed that the actual system is known, by considering some standard IIR plants. Hence, the transfer function of both systems is considered as similar. Also, we considered that all the coefficients are real valued. Assuming the value of coefficient \({a_0}=1\), the transfer function of the adaptive IIR digital filtering system is given as:

$$H(z)=\frac{{\sum\limits_{{i=0}}^{M} {{b_i}{z^{ - i}}} }}{{1+\sum\limits_{{i=1}}^{N} {{a_i}{z^{ - i}}} }}$$
(17)

Since digital filters are discrete-time systems whose input and output are discrete-time signals (Jackson 1999), the z transform is used to represent them. The transfer function H(z) is the z transform of the impulse response h(k) of the system in the z domain. The h(k) characterizes a system (e.g. a filter) and the coefficients represent the samples for an “infinite impulse response” or IIR filtering system. In implementations, a digital filter is designed using electronic circuits (Jackson 1999). They carry out the addition, multiplication, and delay operations (Jackson 1999; Shenoi 2005). Therefore, we need three arithmetic units adder, multiplier and delay to design a digital IIR filter. In the above equations, the numerical coefficients (\({a_i}\), \({b_i}\)) are multiplier coefficients of a digital filter (Jackson 1999). We change the transfer function of the IIR filter via changing the coefficients.

4.2 AIO methods and IIR system modeling

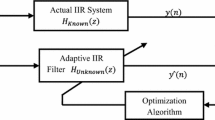
Configuration of IIR system modeling process using AIO algorithms is shown in Fig. 1. The objective is to find the optimal IIR filter coefficient vector [\({a_i}\), \({b_i}\)] such that the response of the estimated adaptive IIR filtering system approaches the actual system response. In this research, the IIR system modeling is implemented in form an optimization problem with the fitness function Jv given by the following:

Fig. 1
figure 1

IIR system modeling by AIO algorithms

Full size image
$$\hbox{min}\quad {J_v}\quad {\text{for}}\, v\in V,$$

where \(v=\left[ {{b_0}{b_1} \ldots {b_M}{a_1}{a_2} \ldots {a_N}} \right]\)is the filter coefficients vector, and V is coefficient space.

4.2.1 Search agents definition

In any AIO algorithm, each search agent in the population i (Vi=v) is encoded as a set of candidate solutions to the modeling problem. It means that each search agent is a D-dimensional vector containing the D filter coefficient variables. The coefficients values associated with each agent are used to evaluate the MSE criterion. Then, the agents move through the search space to find the optimum set of filter coefficients.

As a result, a matrix \(V={\left[ {{V_1},{V_2}, \ldots ,{V_{{N_p}}}} \right]^T}\) of order \({N_p} \times D\) is arranged where Np denotes the number of population size and D denotes the number of coefficients of the IIR model. The filter coefficients are encoded in the string form as shown in Fig. 2.

Fig. 2
figure 2

Representation scheme for a search agent structure (Vi) of design variables in the string form

Full size image

4.2.2 Fitness function definition

In this work, the fitness function is considered in the MSE form (as Eq. 18). Based on the definition of MSE in statistics, it measures the average of the squares of the errors; that is, the difference between the estimator and what is estimated. The MSE criterion has been also used in in many recently published papers (Rubio 2017a, b; Rong et al. 2018; Meza et al. 2017).

$${J_{MSE}}={J_v}(k)=\frac{1}{P}\sum\limits_{{k=1}}^{P} {{e^2}(k)} =\frac{1}{P}\sum\limits_{{k=1}}^{P} {{{(y(k) - \hat {y}(k))}^2}}$$
(18)

In Eq. (18), e(k) is the error signal, y(k) and \(\hat {y}(k)\) are the response of the unknown plant (desired response) and the estimated adaptive IIR filter (actual response) at sample time k, respectively, and P is the number of samples used for the fitness function calculation. Note also that the measurement noise is combined to the desired signal. The purpose of is that minimize the error fitness MSE by proper adjusting v iteratively. In this paper, the coefficients of IIR filtering system are iteratively adjusted by proposed adaptive AIO algorithms in such a manner that the error between adaptive IIR filtering system output and the actual system output is minimized.

Function Evaluation: \({J_{i,MSE}}\) = Evaluation (Vi, P, x)

where Vi denotes the elements of ith search agent (e.g. a chromosome, mass, particle or ball) of V as the current estimated coefficients of the IIR model, P denotes the input samples, x represents the input signal.

 Calculate the IIR filtering system output \(\hat {y}\) for all P input samples of x by using the current values Vi.

 Compute the actual system output y for all P input samples of x.

 Evaluate the fitness function MSE of the ith agent, \({J_{i,MSE}}\), according to Eq. (18).

The steps to solve the IIR system modeling problem using AIO methods are executed to obtain the optimal filter coefficients of the identified IIR model, in such a way that the values of MSE are minimized, approaching zero as much as possible. The complete process of IIR systems modeling by proposed AIO methods consists of eleven following steps:

Step I: Initialize the tuning parameters of the AIO algorithm (e.g. c1,c2 and the initial w, for PSO).

Step II: Generate a random input signal x(k), k = 1, 2, …, P.

Step III: Randomly generate an initial population containing Np agents of elements Vi with the search space dimension D (that is equal to number of design variables or filter coefficients) between lower and upper bounds.

Set the iteration counter t = 0.

Step IV: Identify the initial best values, agent and MSE.

Step V: While stopping criterion t < tmax is not satisfied, increase the iteration counter t; otherwise, go to Step XI.

Step VI: Update the control volumes and calculate their new values (e.g. Mi(t), G(t), Rij(t) and \(a_{i}^{d}(t)\), for GSA).

Step VII: Update the next condition for all agents and obtain a new matrix V (e.g. \(r_{i}^{d}(t+1)\), for IPO).

Step VIII: Perform Function Evaluation for each agent Vi and obtain the fitness value Ji,MSE(t) based on the new matrix V.

Step IX: Update the best values, agent and MSE.

Step X: If the stopping criterion (t > tmax) is met, then go to Step XI; Otherwise, go to Step V.

Step XI: Output the best solution that denotes the final and optimal filter coefficients of the adaptive IIR model.

5 Results and discussion

In the simulations, the system input x(k) is a uniformly distributed white sequence, taking values from (–0.5, 0.5). The measurement noise is a Gaussian white signal with variance 0.001. The data length used to calculate the MSE (Eq. 18) is P = 100. Simulation results, implemented by MATLAB, are presented to compare the performance of the proposed AIO algorithms that applied to adaptive IIR digital filtering systems modeling. Two different challenging benchmark IIR plants with high and low orders, which are already reported in the different and new papers (Mohammadi and Zahiri 2016a, 2017; Kumar et al. 2017; Lagos-Eulogio et al. 2017; Yang et al. 2017), have been considered in this work. The proposed plants are two IIR digital filters non-minimum phase and unstable, and are designed in the direct form structure. Note, the lower and upper bounds of the filter coefficients (design variable (v)) are considered − 2 and + 2, respectively.

The IIR modeling is assumed as constrained single optimization problem and is evaluated in the both the same and reduced order cases for each of Plants (A) and (B). Another aspect of the innovation of this article is that three important criteria called “Indicator of Success (IoS)” (as Eq. 19) and “Degree of Reliability (DoR)” along with MSE are also used to verify the performance correctness of AIO algorithms. Then, the results are verified in terms of the MSE, IoS and DoR. In each model, independent 100 trials are performed by employing all the algorithms for evaluating the statistical analysis of MSE values, IoS, and their DoR. Then, the values (results and curves) for the best trial of each algorithm are reported in this work. So that, the IoS value 100 represents a completely accurate and consummate modeling of the unknown actual system. The DoR, according to the results estimation of the MSE and IoS parameters, is expressed in parametric form. In addition, for revealing a ground of judgment of comparative performance for the proposed AIO algorithms, statistically analyzed results are presented.

The tuning values of the proposed AIO algorithms are given in Table 1. It is notable that all the algorithms appropriately had been tuned for suitable IIR system modeling. The population size value is selected based on the complete coverage multimodal space of the design problem. Also, the number of iterations is selected equal to 400 to allocate enough time to analyze the modeling problem by an algorithm. The control parameters settings of the algorithms are often adjusted by focusing on their exploration and exploitation concepts. So that the changes are finalized experimentally based on Eqs. (1), (7), (14), and (15) and from the settings presented in other similar studies. For clarity of how and the initial maneuvering of the convergence of algorithms, the horizontal axis of fitness curves is logarithmically and the best numerical results are also displayed in bold.

Table 1 Tuning values of the proposed artificial intelligent optimization algorithms
Full size table
$${\mathbf{IoS}}{\text{ }}= \frac{{\text{Trials leading to optimal model}}} {{\text{Trials leading to suboptimal model}}+1}$$
(19)

5.1 Plant (A): low-order IIR modeling

The transfer function of the unknown actual system is given by, (Saha et al. 2014; Kumar et al. 2017; Lagos-Eulogio et al. 2017)

$$H\left[ {{z^{ - 1}}} \right]=\frac{{ - 0.2 - 0.4{z^{ - 1}}+0.5{z^{ - 2}}}}{{1 - 0.6{z^{ - 1}}+0.25{z^{ - 2}} - 0.2{z^{ - 3}}}}$$
(20)

5.1.1 The first case: modeling with same order

In this case, the 3rd order system Eq. (20) is identified using a 3rd order IIR model. Hence the transfer function of the IIR filter is considered as

$$H\left[ {{z^{ - 1}}} \right]=\frac{{{b_0}+{b_1}{z^{ - 1}}+{b_2}{z^{ - 2}}}}{{1 - {a_1}{z^{ - 1}} - {a_2}{z^{ - 2}} - {a_3}{z^{ - 3}}}}$$
(21)

Figure 3 depicts the convergence of fitness function for first case of low-order IIR modeling [Plant (A)]. From Fig. 3, it is indicated that GSA and PSO algorithms have best convergences to achieve the optimal model with minimum number of iteration. Of course, IPO is successful in identifying the target system, and it has a continuum search process to convergence the optimal solution, based on its structural mechanism. But the convergence speed of GSA is not comparable to the other AIO algorithms. In this case of modeling, GA algorithm shown a relatively unfavorable convergence. However, as is shown in Fig. 3, the overall review of fitness curves is indicated a good performance. The estimated coefficients along with their graphical representation are shown in Fig. 4 and Table 2, respectively, for Plant (A). The statistical results are also reported in Table 3. The results indicate that three methods based on heuristic search of GSA, IPO and PSO perform much better than evolutionary algorithm GA. So that all three of the heuristic algorithms have found optimal models in over 50% trials. In fact, this successful is obtained by GA, PSO, GSA, and IPO with IoS values 0.51, 1.30, 2.06 and 6.77, respectively. In accordance with the estimated filter coefficients values in Table 2 and the minimum highlighted fitness value in Table 3 (Min.MSE), for this case of same order system modeling, the estimated filter coefficients for the GSA algorithm have the most accuracy and similarity to the coefficients of main IIR filter plant. Of course, the bolded values in the column of PSO also indicate the powerful of the algorithm in continuity of convergence to the best optimal response.

Fig. 3
figure 3

Fitness curves based on same order IIR system modeling for Plant (A), population = 60

Full size image
Fig. 4
figure 4

Graphical representation of estimated filter coefficients values for Plant (A), population = 60

Full size image
Table 2 Estimated filter coefficients based on same order IIR system modeling for Plant (A), population = 60
Full size table
Table 3 Results and statistical analysis based on same order IIR system modeling for Plant (A), population = 60
Full size table

In general, it can be admitted that the performance of AIO methods will result a significant DoR. Overall evaluation of the simulation results and statistical analysis of MSE and IoS values shown in Table 3 reveal that IPO and PSO provide a good performance, efficiency and efficacy in global optimization of IIR system modeling problem for IIR digital filters design. Although, with respect to IoS values, IPO and GSA have the highest values with 88% and 76% convergence to the optimal model respectively. So, we can assign an acceptable DoR to them, particularly for IPO algorithm. On the contrary, the performance of GA algorithm has been undesirable in this case, in terms of IoS, Min, Max, Variance, and Standard Deviation, it present the minimum DoR. It can be analyzed that the success of heuristic and metahuristic based optimization algorithms, in relation to evolutionary strategy, GA method, caused by the randomization mechanism and reliance on swarm intelligence. Despite the fact that crossover, mutation and selection operators are well suited to implement the genetic algorithm, the approach of the evolutionary method has been relatively unsuccessful, and random approaches and swarm intelligence have shown the great superiority and powerful. Therefore, it can be concluded that the success rate of an algorithm will improve via the more heuristic routine and pay attention to the intelligence of each search agent in the response space.

5.1.2 The second case: modeling with reduced order

The 3rd order system shown in Eq. (20) can be also identified using a 2nd order IIR filter. Hence the transfer function of the considered is as follows:

$$H^{\prime}\left[ {{z^{ - 1}}} \right]=\frac{{{{b^{\prime}}_0}+{{b^{\prime}}_1}{z^{ - 1}}}}{{1 - {{a^{\prime}}_1}{z^{ - 1}} - {{a^{\prime}}_2}{z^{ - 2}}}}$$
(22)

In Fig. 5, MSE fitness curves are plotted for the best trial for all four AIO algorithms. It should be noted that the performance of an adaptive approach to compete in the replacement as an adaptive algorithm, in order to overcome the challenge of optimal modeling of IIR systems, is more focused on this kind of modeling (with reduced orders). Therefore, it is deduced from the observation convergence curves resulting from the best trial of each proposed algorithm, which, based on the mechanism and speed of convergence, PSO alone has the best form in both aspects. Along with the PSO, the GSA, IPO and GA algorithms also have relative superiority to each other, respectively. Noteworthy, in Fig. 5, the convergence curve of the evolutionary algorithm GA has a continuous exploration procedure, even in the final iteration 400, which is a strong point in the multimodal space of IIR digital filtering system modeling problems, relative to the Gradient-based techniques. The results are listed in Table 4 for the trials with optimal models. Table 4 offers a statistical analysis on the performance of intelligent optimization algorithms in terms of MSE and IoS values.

Fig. 5
figure 5

Fitness curves based on reduced order IIR system modeling for Plant (A), population = 60

Full size image
Table 4 Results and statistical analysis based on reduced order IIR system modeling for Plant (A), population = 60
Full size table

The statistical superiority of the results of qualitative indicators, IoS and MSE, obtained from proposed adaptive algorithms, is evident in this complex modeling case. This advantage for IoS values of 0.25 (20%), 3.40 (78%), 4.05 (81%) and 10.22 (92%) are obtained using GA, GSA, PSO and IPO algorithm, respectively. The superiority for MSE values are also obtained, according to the bolded best values of MSE in Table 4, 20% (minimum fitness) by PSO, 40% (the best values of Max.MSE and Max.MSE) by IPO, and 40% (the best values of Variance.MSE and Std.MSE) by GSA algorithm. Comprehensive evaluation of the obtained values clearly indicates that AIO algorithms have competent and reliable performance in the IIR system modeling cases of Plant (A), especially heuristic search methods PSO, GSA, and IPO.

5.2 Plant (B): high-order IIR modeling

The transfer function of the unknown actual system is given by, (Saha et al. 2014; Lagos-Eulogio et al. 2017)

$$H\left[ {{z^{ - 1}}} \right]=\frac{{0.1084+0.5419{z^{ - 1}}+1.0837{z^{ - 2}}+1.0837{z^{ - 3}}+0.5419{z^{ - 4}}+0.1084{z^{ - 5}}}}{{1+0.9853{z^{ - 1}}+0.9738{z^{ - 2}}+0.3864{z^{ - 3}}+0.1112{z^{ - 4}}+0.0113{z^{ - 5}}}}$$
(23)

5.2.1 The first case: modeling with same order

In this case, the 5th order system Eq. (23) is identified using a 5th order IIR filter. Hence the transfer function of the IIR filter is considered as

$$H\left[ {{z^{ - 1}}} \right]=\frac{{{b_0}+{b_1}{z^{ - 1}}+{b_2}{z^{ - 2}}+{b_3}{z^{ - 3}}+{b_4}{z^{ - 4}}+{b_5}{z^{ - 5}}}}{{1 - {a_1}{z^{ - 1}} - {a_2}{z^{ - 2}} - {a_3}{z^{ - 3}} - {a_4}{z^{ - 4}} - {a_5}{z^{ - 5}}}}$$
(24)

For this case, fitness curves of all proposed AIO method are shown in Fig. 6. It can be seen from Fig. 6 that, GSA, PSO and IPO algorithms have the best convergences in achieve to the optimal model again. The difference is that, in this case of adaptive IIR modeling, GSA algorithm has been surpassed from the PSO in the convergence speed. Notice that, these conditions were been quite different for other trials. Due to the ongoing convergence mechanism of IPO algorithm in the desire to global minimum, curves of IPO and GA algorithms also show a good convergence along with a strong search process.

Fig. 6
figure 6

Fitness curves based on same order IIR system modeling for Plant (B), population = 60

Full size image

As are shown in Tables 5 and 6 and Fig. 7, the estimated coefficients using the GSA matches very well with the actual values. Also, they show that the average values and statistical analysis of MSE values obtained using the IPO are more desirable. There are two remarkable thing in this case; the high index of reliability of the PSO algorithm (IoS higher than other methods), and amounts of variance and standard deviation 0 for MSE values by GA. So, we cannot assign a proper DoR value to the proposed artificial intelligent optimization methods for the first case of adaptive IIR modeling problem. However, due to the high-order of IIR digital filter [Plant (B)] and as well as big challenges for optimal design of IIR digital filters with multi-modal error surface, this performance is acceptable and the poor DoR is negligible.

Table 5 Estimated filter coefficients based on same order IIR system modeling for Plant (B), population = 60
Full size table
Table 6 Results and Statistical Analysis based on same order IIR system modeling for Plant (B), population = 60
Full size table
Fig. 7
figure 7

Graphical representation of estimated filter coefficients values for Plant (B), population = 60

Full size image

5.2.2 The second case: modeling with reduced order

In this case, the 5th order system shown in Eq. (23) can be also identified using a fourth-order IIR recursive filter. Hence the transfer function of the considered is as follows:

$$H^{\prime}\left[ {{z^{ - 1}}} \right]=\frac{{{{b^{\prime}}_0}+{{b^{\prime}}_1}{z^{ - 1}}+{{b^{\prime}}_2}{z^{ - 2}}+{{b^{\prime}}_3}{z^{ - 3}}+{{b^{\prime}}_4}{z^{ - 4}}}}{{1 - {{a^{\prime}}_1}{z^{ - 1}} - {{a^{\prime}}_2}{z^{ - 2}} - {{a^{\prime}}_3}{z^{ - 3}} - {{a^{\prime}}_4}{z^{ - 4}}}}$$
(25)

Fitness curves based on reduced order IIR system modeling for Plant (B) with the population size 60 shown in Fig. 8. In Fig. 8, it is obvious that GA, GSA and IPO algorithm have the convergence properties better than PSO. In this plant, like the previous one [Plant (A)], GA converges to a minimum level with a lazy convergence speed again. The obvious superiority of convergence process of the GSA, compared to other heuristic-based algorithms, is due to the correct definition its exploration and exploitation concepts. The algorithm also employs more randomization mechanisms in its structure than two other swarm-based heuristic algorithms. Because, in solving problems with multidimensional error surface, the only way out of local optimization is to generate more randomized solutions and away from the local response area. Of course, this technique should be included in the structure of the algorithm in the best way, otherwise it will have an opposite and destructive function, which will escape the algorithm from the global solution and lose the optimal model.

Fig. 8
figure 8

Fitness curves based on reduced order IIR system modeling for Plant (B), population = 60

Full size image

A list of statistically analyzed results between trials with optimal/sub-optimal models reported in Table 7. According to the percentage of success of any algorithm in achieving optimal models over 100 trials, 6% with a IoS 0.06 for PSO, 8% with a IoS 0.09 for GA, 17% with a IoS 0.20 for GSA, and 23% with a IoS 0.30 for IPO, along with MSE statistical values, represents that the best performance is for IPO and undesirable performance directed toward PSO and GA algorithms. Although, given the mechanism embedded for exploring and exploiting the IPO algorithm, k1 and k2, this continuity is evident in looking for optimal response until the latest iteration and continuity in achieving optimal models. Because the mechanism of Eqs. (14) and (15) is such that to the correct tuning of the fixed parameter values can achive the best performance of algorithm.

Table 7 Results and Statistical Analysis based on reduced order IIR system modeling for Plant (B), population = 60
Full size table

5.3 The effect of reducing the population size on the performance of AIO algorithms [for the Plant (A)]

As stated in the first Section, population size is one of the factors influencing the performance and efficiency of the algorithms discussed in this study. So that a high population size will increase the runtime and delay of convergence and, conversely, a population size low will cause the probability of early convergence. Hence, a suitable population size can achieve optimal and desired results at a minimum runtime. This section checks the implementation results of the IIR system modeling problem for the first benchmark IIR sample (Plant (A) of 3rd order) for the equal and reduced order modeling for the population of 20.

Figure 9 presents the comparison of obtained fitness curves by the AIO algorithms for the recorded best solution in trials with optimal model. From Fig. 9, it is seen that the PSO and GSA algorithms can design an acceptable IIR digital filter only after 98 and 172 iterations, respectively. It is clear that the PSO and GSA need less time as compared with IPO and GA. From the Fig. 9, it is also clear that although IPO seems more quick in early iterations, it has a gradual procedure for the fine tuning of the parameters due to its ongoing search ability. For the this case of the low-order system modeling with a reduced population size, as expect, the executive process of the GA, GSA and IPO algorithms lasted more to design an acceptable filter. For the GA algorithm, it can be concluded that it often fails to achieve the global optimal model and needs more iterations for designing an adaptive IIR digital filter. The graphical representation of estimated filter coefficients values for this case is shown in Fig. 10. Also, results and statistical analysis of the performance parameters are shown in the Tables 8 and 9. Table 9 shows Mins, Means, Maxs, variances and standard deviations of MSE values along with numbers of trials with optimal/sub-optimal model for proposed AIO algorithms. The obtained simulation results in Table 9 indicate that both IPO and PSO algorithms obtained the best results. These algorithms have been successfully applied to solve IIR system modeling in this case, IoS values 0.74 and 0.94 respectively, so that we can assign a high DoR to them and a poor DoR to the GA and GSA algorithms for of their unfavorable efficiency. From Table 9, it is clear that IPO has the lowest Min.MSE and Max.MSE. This is because the meta-heuristic algorithm IPO has an ongoing search with the global minimal. Also, it can be concluded that when the population size decreases, it is possible that the performance and efficiency of AIO algorithms be dropped. Therefore, an appropriate value for population size should be assigned.

Fig. 9
figure 9

Fitness curves based on same order IIR system modeling for Plant (A), population = 20

Full size image
Fig. 10
figure 10

Graphical representation of estimated filter coefficients values for Plant (A), population = 20

Full size image
Table 8 Estimated filter coefficients based on same order IIR system modeling for Plant (A), population = 20
Full size table
Table 9 Results and Statistical Analysis of MSE Values based on same order IIR system modeling for Plant (A), population = 20
Full size table

Figure 11 depicts the convergences of the AIO algorithms for the second-order IIR digital filter design. As shown in Fig. 11, GA, PSO, GSA and IPO take about 20, 65, 145 and 120 iteration cycles to reach to their MSE surface, respectively. It can be concluded that the GA converges to the optimal model faster than other algorithms. So that, improvement is quite evident in the convergence speed of the GA algorithm as compared with the previous cases. Although at the beginning of the process, an IPO algorithm searches much faster and efficient, but after about 10 iteration cycles it became slower than the GA. Clearly, it is inferred that the performance of GSA algorithm is fallen to reduce the population size in the low-order IIR system modeling problems. So that GSA has a poor convergence properties compared to other algorithms. Also, it can be seen from Fig. 11 that the both the PSO and IPO have almost a similar convergence, with the exception that the PSO has a slightly faster convergence with a risky convergence mechanism.

Fig. 11
figure 11

Fitness curves based on reduced order IIR system modeling for Plant (A), population = 20

Full size image

Results and statistical analysis of MSE values for the low-order IIR modeling with reduced population size, 20, are shown in Table 10. It shows that the IPO and PSO algorithms provide the best results in terms of the MSE and IoS. So these are able to identify more accurately than GA and GSA algorithms. In this regard, IPO and PSO offer a high DoR value. In addition, due to the successive convergence of IPO algorithm to the optimal model and its capacity for locate the global optimal in a multi-modal error surface (the main challenge of IIR digital filters design); it is certainly one of the best choices for this type of IIR system modeling with reduced population size. It also governs the for the PSO algorithm. Overall evaluation of simulation results in this subsection, in the analysis of the effect of reducing the population size on the performance of the AIO algorithms, shows a proper DoR and stability of AIO algorithms for solving IIR systems modeling. However, it is obvious that the performance of GA algorithm has been improved. In general, the AIO algorithms have the advantages of finding the true global minimum of a multi-modal search space (error surface). Also notable is the fact that, based on all of the fitness curves for the proposed algorithms, the convergence characteristic of the algorithms is closely related to the number of iterations, and if a researcher selects a less iteration, the AIO algorithms gives roughly the same results without increasing the computational time.

Table 10 Results and statistical analysis of MSE values based on reduced order IIR system modeling for Plant (A), population = 20
Full size table

6 Conclusion

In this paper, we analyzed a category of AI-based techniques called AIO algorithms and evaluated their applicability in IIR system modeling problems. The applicability and efficiency of the proposed algorithms, in identifying an unknown actual system with both the same and reduced order cases of adaptive IIR filter for two different benchmark IIR plants with high and low orders, is proven by the evaluation of simulation results in terms of convergence properties, statistical analysis of MSE values, IoS and DoR parameter. It was shown that AIO algorithms have more chance to find the optimal set of coefficients and can find an acceptable estimate model, where in modeling process, the error surface be multi-modal and challenging. In general, the quality of obtained solution (optimal model), high convergence speed in the low iteration, the best average results of MSE values, IoS good values and high levels of DoR demonstrates the superiority and high efficiency of the proposed AIO algorithms for system modeling problems, preferably for PSO and IPO algorithms. Consequently, the AIO algorithms are undoubtedly a promising approach and a proper candidate to achieve the optimal model in the IIR system modeling and optimal digital filters design.

The identification/modeling approach used in this paper is an offline one based on AIO Algorithms. Future researches may concentrate on developing real-time identification or nonlinear systems modeling. Also, utilizing neural networks along with AIO algorithms to achieve an optimal network structure for more accurate IIR system modeling, applying multi-objective versions of proposed methods, the fuzzy selection of control parameters values of AIO algorithms to improve their convergence and optimal responses, the using of more qualitative indicators, such as evaluating the steps, impulse, amplitude and phase responses of obtained models with the actual plant to check the accuracy of modeling are other potential approaches in this area.