1 Introduction

Recently, adaptive filtering has gained much attention due to its wide area of applications in signal processing, control systems, image processing, biomedical engineering and communication systems [1,2,3,4]. Infinite impulse response (IIR) filter and finite impulse response (FIR) filter are the two types of adaptive filters. IIR filter output depends on the past input and output samples as compared to the FIR filter whose output depends only on the present and past input samples. IIR filter is mainly the choice of many researchers because it requires a lesser number of system parameters as compared to the FIR filter, for the same set of specifications [5].

The system identification problem aims at finding the optimal set of system coefficients by minimizing the objective function. The objective function is the mean square error (MSE) which is the difference between the outputs of the adaptive system and the unknown IIR system. The main focus of this work is to minimize the MSE value. The MSE is minimum when the output of both the systems matches closely. Many well-known gradient-based algorithms have been applied for system identification problem. However, these gradient-based algorithms yield the slow convergence profile and quickly fall into local minima for multimodal error surface.

These shortcomings of the above said algorithms lead to the significant increase in the use of metaheuristic algorithms. In addition, the problem of nonlinear and multimodal error functions in system identification can be easily solved by evolutionary and metaheuristic algorithms [8]. Recently, vector quantization algorithm [6] and neural dynamic programming inspired particle swarm search [7] have been applied to obtain the optimal model.

The evolutionary and metaheuristic algorithms [9] like genetic algorithm (GA) [10], real coded genetic algorithm (RGA) [11], particle swarm optimization (PSO) [12,13,14,15], quantum behaved PSO (QPSO) [16], cat swarm optimization (CSO) [17, 18], flower pollination algorithm (FPA) [19], differential evolution (DE) [20], cuckoo search algorithm (CSA) [21,22,23,24], seeker optimization algorithm (SOA) [25], bat algorithm (BAT) [26], artificial bee colony (ABC) algorithm [27], gravitational search algorithm (GSA) [28], harmony search (HS) algorithm [29], opposition based harmony search (OHS) [30], firefly algorithm (FFA) [31] have been successfully employed for system identification problem. Linear and non linear system coefficients have been estimated by Yao and Sethares by using GA [10]. Aggarwal et al. evaluated the optimal filter coefficients using RGA [11]. PSO was originally introduced by Kennedy and Eberhart [12] and thereafter applied for estimating the IIR filter coefficients and finding the suitable structure for IIR filter [13,14,15]. Many strategies have been utilized by different reaseachers to enhance the outcome of PSO in IIR system identification, such as QPSO and craziness based PSO (CRPSO) algorithm [16]. Panda et al. presented that optimal IIR system coefficients can be evaluated using CSO [17]. Saha et al. utilized the unique characteristic of a cat for the FIR filter designing [18]. Singh et al. presented that FPA estimates the best parameter values close to the actual values of the adaptive IIR system compared to the GA and PSO [19]. In addition, Karaboga et al. presented the numerical results of the IIR filter designed using DE [20]. CSA was proposed by Yang and Deb [21] and has found a lot of applications in the fields of filter designing and system identification. For an instance, Kumar and Rawat applied CSA in designing of the fractional order FIR filter [23, 24]. Next, Dai et al. evaluated the parameter values of IIR filter using SOA [25]. Further, Kumar et al. solved the problem of system identification by using BAT [26]. In addition, Karaboga et al. utilized a robust, flexible and simple technique called ABC for the IIR filter design [27]. Rashedi et al. obtained the optimal set of filter coefficients and proved that GSA is best-suited optimization algorithm for filter designing [28]. Saha et al. applied HS based algorithm for finding the minimum mean square error for system identification problem [29]. Upadhyay et al. presented the detailed comparison results with state of the art algorithms such as OHS, FFA, BAT, and CRPSO for the IIR system identification problem [30,31,32,33].

Mostly, the performance of a hybrid algorithm is always better as compared to an individual algorithm. So recently, Jiang et al. applied a hybrid algorithm combining PSO and GSA for finding the optimal set of the IIR system coefficients [34]. Also, Yang et al. utilized opposition based hybrid coral reefs optimization algorithm (OHCRO) and proved the efficiency of hybrid algorithm [35] for the system identification problem. Further, Eulogio et al. reported the numerical results obtained by hybrid cellular PSO and DE [36]. In recent literature, Mohammadi et al. have taken two performance measures “Indicator of Success” and “Degree of Reliability” for the optimal system modeling using GA, GSA, PSO and inclined planes optimization (IPO) algorithm [37]. In addition, Wenchao et al. applied a new hybrid technique called DE with hybrid mutation operator having self-adapting control parameters (HSDE) for global optimization problem [39].

Every algorithm has its importance and shortcomings. GA results in fast computation but quickly falls into local optimal solution in the multimodal surface. For complex optimization problems, PSO, DE and other optimization algorithms in literature undergo premature convergence. Also, these algorithms require many control parameters for obtaining the optimized set of coefficients which lead to the large computation time and slow convergence.

Till date, TLBO algorithm is not applied for system identification problem. It is a novel population-based algorithm, inspired by the teaching-learning process in the classroom [38]. Some key points of TLBO algorithms are as follows:

  • The employed technique is free from the algorithmic specific parameters as in the other optimization techniques, which are dependent on many control parameters.

  • Difference mean, which is the difference between the existing mean result of the class and the teacher, is calculated for each learner.

  • This difference mean is updated in each iteration and is responsible for maintaining the diversity of the applied technique.

  • Teacher phase and learner phase are responsible for the exploration and exploitation phase of optimization.

In order to prove the effectiveness of the applied algorithm, four different benchmark functions are used and a detailed comparison of results of GA, PSO, CSO, CSA, DEWM, CRPSO, FFA, BAT, HS, and OHS is reported for the same order and reduced order systems.

The rest of the paper is organized as follows: a comprehensive literature survey is described in Section 1, the formulation of system identification problem is explained in Section 2. In Section 3, overview of TLBO algorithm and its importance is described. Simulation and comparative results of four different benchmark functions are discussed and reported in Section 4. Finally, Section 5 concludes the paper.

2 Problem formulation

IIR system identification problem is based on minimizing the objective function such that the outputs of the adaptive IIR system and the unknown IIR system match closely when both systems are subjected to the same input.

Transfer function of an IIR system is given by

$$ H(z)= \frac {Y(z)}{X(z)}=\frac{b_{0}+b_{1}z^{-1}+...+b_{M}z^{-M}}{1+a_{1}z^{-1}+...+a_{N}z^{-N}}. $$
(1)

Where, Y (z) and X(z) are the output and input of the IIR system, respectively. b0,b1,...,bM and a1,a2,...,aN are the coefficients of the numerator and denominator polynomial, respectively. M and N are the order of the numerator and denominator polynomial, respectively. The difference equation in time domain for the IIR system is given as:

$$ y(n)+...+a_{N}y(n-N)=b_{0}x(n)+...+b_{M}x(n-M) $$
(2)

or,

$$ y(n)+\sum\limits_{j = 1}^{N} a_{j}y(n-j)= \sum\limits_{i = 0}^{M} b_{i}x(n-i) $$
(3)

which can be rewritten as:

$$ y(n)={\Theta}{\Phi}^{T}(n) $$
(4)

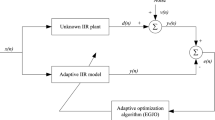
where, Θ = [−a1,−a2,...,−aN,b0,b1,...,bM] and Φ = [y(n − 1),...,y(n − N),x(n),x(n − 1),...,x(n − M)]. In order to obtain the desired output for the adaptive system, the coefficients of the Θ vector must be altered. Figure 1 shows the block diagram of an IIR system identification problem using TLBO algorithm. In Fig. 1, x(n) is the input of the adaptive IIR system and the unknown IIR system, d(n) is the output of the unknown IIR system and v(n) is the noise signal added with the output of unknown IIR system. The error objective function is given by

$$ E(\mathbf{a}_{j},\mathbf{b}_{i})=\frac{1}{L}\sum\limits_{n = 1}^{L} e^{2}(n)=\frac{1}{L}\sum\limits_{n = 1}^{L}(y(n)-\hat{y}(n))^{2}. $$
(5)
Fig. 1
figure 1

Block diagram of IIR system identification problem using TLBO algorithm

Full size image

Here, y(n) is the output of the unknown IIR system with noise and \(\hat {y}(n)\) is the output of the adaptive IIR system, e(n) is the error signal generated and L is the total number of input samples.

3 Teacher learner based optimization algorithm

Teacher-learner based optimization algorithm is a meta-heuristic algorithm, based on teaching-learning process of the classroom. It is a simple, dynamic population-based algorithm with no algorithm specific parameters, which makes this algorithm applicable to very vast and diverse fields. Whereas, other algorithms require careful selection of algorithm specific parameters which influence the solution immensely. According to TLBO algorithm, if we consider a classroom environment then there are two ways in which a student can learn, firstly, through a teacher (Teacher Phase), where a teacher deploys his or her knowledge to improve the performance of the student and secondly, through discussion with other fellow students (Learner Phase) [38]. The flow chart of TLBO algorithm is shown in Fig. 2.

Fig. 2
figure 2

Flow chart of TLBO algorithm

Full size image

3.1 Teacher phase

In this part of the algorithm, learners gain knowledge through the teacher. A teacher attempts to improve the overall performance of every student in the class. The improvement in overall result depends on the potential of the teacher. The teacher is someone who has adequate command over the subject thus the best solution among all the available solutions is considered to be the solution of the teacher.

Considering that m are number of design variables or number of subjects allocated to students, and n are the number of learners or population size. In our problem of system identification, we have taken a different order with IIR systems. Here, design variables are taken as the number of numerator and denominator coefficients of the unknown IIR system which is equivalent to the number of subjects allocated to the students in a class. Likewise, we initialize the population size equivalent to the number of learners. The result of learners is analogous to the fitness value for our system identification problem. Mean result is calculated for the whole population using a particular jth design variable (coefficient). At any iteration i, Mj, i is the mean result of the learners in a particular subject ‘j‘, where j = 1,2,…,m. X(total−kb),i is assumed to be the result of the best learner kb, that is, the teacher. Difference mean is calculated for each learner, which is the difference between the existing mean result of the class and the teacher, given by

$$ DM_{j,k,i}=r_{i}(X_{j,\text {kb},i}-T_{F}M_{j,i}). $$
(6)

where, Xj, kb, i is the result of the best learner in subject j, TF is the teaching factor, and ri is the random number in the range [0,1]. TF is selected randomly with value 1 or 2, given as:

$$ T_{F}=\text{round} [1+\text{rand}(0,1)\{2-1\}] $$
(7)

The existing difference mean is updated as

$$ X_{j,k,i}^{\prime} = X_{j,k,i} + DM_{j,k,i} $$
(8)

where, \(X_{j,k,i}^{\prime }\) is the updated value of Xj, k, i. If this updated value is better than the previous values, then these are saved. Further, these values become the input for the learner part.

3.2 Learner phase

In Learner phase, students reach out to one another in order to enhance or boost their knowledge. Students collaborate with each other to improve their overall performance. The intercommunication among the students is random. In the interaction of two students, a student with more knowledge will enhance the knowledge of the other student. Now, let A and B are the two randomly selected students, these two students have different results, that is, \(X_{total - A,i}^{\prime } \ne X_{total - B,i}^{\prime }\) where, \(X_{total - A,i}^{\prime }\) and \(X_{total - B,i}^{\prime }\) are the updated function values of Xtotal−A, i and Xtotal−A, i, respectively. In our problem also, two numbers are selected randomly out of the whole population and their solutions are updated in every iteration. These updated solutions are kept if it gives a better function value.

$$ X_{j,A,i}^{\prime\prime} = X_{j,A,i}^{\prime} + {r_{i}}(X_{j,A,i}^{\prime} - X_{j,B,i}^{\prime}),if X_{total - A,i}^{\prime} < X_{total - B,i}^{\prime} $$
(9)
$$ X_{j,A,i}^{\prime\prime} = X_{j,A,i}^{\prime} + {r_{i}}(X_{j,B,i}^{\prime} - X_{j,A,i}^{\prime}),if X_{total - B,i}^{\prime} < X_{total - A,i}^{\prime} $$
(10)

where, \(X_{j,A,i}^{\prime \prime }\) is the updated value of \(X_{j,A,i}^{\prime }\) and this value is accepted if it is better than the previous one.

4 Simulation results

The performance of TLBO algorithm for four benchmark IIR system functions is evaluated. Each unknown system is estimated by an adaptive IIR filter for two cases: (i) same order and (ii) reduced order system. The results obtained using TLBO algorithm are compared with the results obtained using GA, PSO, CSO, CSA, DEWM, FFA, BAT, CRPSO, HS and OHS algorithms. The control parameters for TLBO algorithm are reported in Table 1. MSE, computation time and percentage improvement are considered as the performance measures of the applied algorithm.

Table 1 Control parameters of TLBO algorithm for IIR system identification
Full size table

Example 1

Consider a second-order system whose transfer function is given by [16, 28, 35]

$$ H_{p}(z)=\frac{0.05-0.4z^{-1}}{1-1.314z^{-1}+ 0.25z^{-2}} $$
(11)

To test the superiority of the applied algorithm, Hp(z) is modeled using a same order system as described in Case 1 and reduced order system in Case 2.

Case 1

Transfer function of the second-order system used to approximate the same order system is given by

$$ H_{s}(z)=\frac{b_{0}+b_{1}z^{-1}}{1-a_{1}z^{-1}-a_{2}z^{-2}} $$
(12)

The estimated coefficient values for the same order system are listed in Table 2 and graphically represented in Fig. 3. The MSE values (normalized and dB) in terms of best, worst, average and standard deviation (SD) are reported in Table 3. The best MSE values obtained are 5.1425 × 10− 15, 9.8367 × 10− 13, 1.1687 × 10− 08, 4.9770 × 10− 06, 4.9770 × 10− 06, 1.6311 × 10− 11, 2.1569 × 10− 05, 2.6659 × 10− 06, 3.8000 × 10− 08, 6.3639 × 10− 05, 1.0116 × 10− 04, 1.0116 × 10− 04 and 2.6428 × 10− 04 for TLBO, OHS, HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA, respectively. Based on these observations, the applied algorithm can be ranked as TLBO> OHS > FFA > HS = CSA >CRPSO=DEWM> CSO > PSO>GA. The fitness values (MSE) are demonstrated in Fig. 4. It is verified from Fig. 4 that, TLBO gives a fitness value near to − 143 dB in 230 iterations, which is the minimum MSE value compared to the recently reported algorithms. OHS requires 176 iterations for the fitness value of − 130 dB, HS consumes 164 iterations for the MSE value of − 79 dB, CRPSO results in a fitness value of − 54 dB in 140 iterations, FFA requires 165 iterations to yield a fitness value of − 107 dB, BAT takes 100 iterations to converge a fitness near to − 47 dB, DEWM converges to − 56 dB in 185 iterations, CSA requires 175 iterations to obtain a fitness value of − 75 dB. CSO, PSO and GA approaches to a fitness value of − 42 dB, − 40 dB and − 36 dB in 52, 120 and 135 iterations, respectively. Finally, it can be concluded that the TLBO algorithm has faster convergence compared to the other reported algorithms.

Table 2 Optimized parameter values of second order IIR system for Example 1 in case of same order system
Full size table
Fig. 3
figure 3

Coefficient comparison for Example 1 optimized using TLBO, BAT, FFA, DEWM, CSA, CSO, PSO and GA

Full size image
Table 3 Statistical results of MSE (normalized and dB) for Example 1 in case of same order system
Full size table
Fig. 4
figure 4

Convergence plot for Example 1 in case of same order system using TLBO, OHS, HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA

Full size image

Case 2

Transfer function of a first-order system used to approximate the second-order system is given by

$$ H_{r}(z)=\frac{b_{0}}{1-a_{1}z^{-1}} $$
(13)

In this case, MSE and convergence profile are taken as the two performance measures. The statistical results are considered for evaluating the comparative performance of the applied algorithms. The MSE values in terms of best, worst, average and SD are listed in Table 4. The best MSE values obtained for TLBO, OHS, HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA are 1.6523 × 10− 03, 6.8000 × 10− 03, 9.5999 × 10− 03, 3.4000 × 10− 03, 7.9178 × 10− 03, 4.2000 × 10− 03, 1.1934 × 10− 02, 1.7515 × 10− 02, 1.7515 × 10− 02 and 2.7122 × 10− 02, respectively. The TLBO algorithm gives minimum MSE. Based on the above results the optimization algorithms can be ranked as TLBO> OHS > HS > CRPSO > FFA > BATT > DEWM > CSA > CSO = PSO >GA. The convergence profiles for different applied algorithms are demonstrated in Fig. 5. The TLBO algorithm converges quickly and reaches a minimum fitness value of − 27 dB in 145 iterations.

Table 4 Statistical results of MSE (normalized and dB) for Example 1 in case of reduced order system
Full size table
Fig. 5
figure 5

Convergence plot for Example 1 in case of reduced order system using TLBO, OHS, HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA

Full size image

The percentage improvement in the performance of TLBO over other applied algorithms is graphically represented in Fig. 6 for the same order and reduced order IIR system identification.

Fig. 6
figure 6

Percentage improvement in MSE value of Example 1 compared to other reported algorithm using same order and reduced order system

Full size image

Example 2

A third-order IIR system is considered, which is approximated using the same order and a reduced second-order system. The transfer function is given by [16, 28, 37]

$$ H_{p}(z)=\frac{-0.2-0.4z^{-1}+ 0.5z^{-2}}{1-0.6z^{-1}+ 0.25z^{-2}-0.2z^{-3}} $$
(14)

Case 1

Transfer function of the third order system is given by

$$ H_{s}(z)=\frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}}{1-a_{1}z^{-1}-a_{2}z^{-2}-a_{3}z^{-3}} $$
(15)

The optimal coefficient values are reported in Table 5 and illustrated in Fig. 7. The TLBO algorithm approximates the coefficients, near to the actual value. The normalized and dB values of MSE in terms of best, worst, average and SD are listed in Table 6. The best MSE values obtained for TLBO, HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA are 3.1287 × 10− 12,1.6516 × 10− 07, 2.1087 × 10− 06, 5.0709 × 10− 09, 2.3037 × 10− 05, 4.6051 × 10− 05, 4.3350 × 10− 08, 6.3520 × 10− 05, 6.3520 × 10− 05 and 7.3203 × 10− 04, respectively. The convergence profiles of the applied algorithms are shown in Fig. 8. A total of 300 iterations are used to demonstrate the efficiency of TLBO. The MSE value of − 115dB is attained by TLBO at 238th iteration, whereas, HS requires 170 iterations to attain a MSE value of − 82 dB. Fitness value of − 56 dB is prevailed by CRPSO in 151 iterations, FFA takes 153 iterations to reach a fitness of − 82 dB, BAT converges in 161 iterations to a fitness of − 35 dB; DEWM approaches to a fitness of − 44 dB in 183 iterations, CSA, CSO and PSO converges in 173, 116 and 114 iterations to obtain the fitness of − 75 dB, − 40 dB and − 41 dB, respectively. GA converges in 110 iterations to a minimum error value of − 31 dB. It can be deduced from these observations that least MSE value can be obtained using TLBO for the system identification problem.

Table 5 Optimal coefficient values of third order IIR system for Example 2 in case of reduce order system using TLBO, FFA, BAT, DEWM, CSA, CSO, PSO and GA
Full size table
Fig. 7
figure 7

Coefficient comparison for Example 2 optimized using TLBO, BAT, FFA, DEWM, CSA, CSO, PSO and GA

Full size image
Table 6 Statistical results of MSE (normalized and dB) for Example 2 in case of same order system
Full size table
Fig. 8
figure 8

Convergence plot for Example 2 in case of same order system using TLBO, OHS, HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA

Full size image

Case 2

The transfer function of a second-order system used to approximate the third-order system is given by

$$ H_{r}(z)=\frac{b_{0}+b_{1}z^{-1}}{1-a_{1}z^{-1}-a_{2}z^{-2}} $$
(16)

MSE values obtained using different reported algorithms are listed in Table 7. The best values of MSE for TLBO, HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA are 1.8004 × 10− 04, 6.4798 × 10− 04, 7.4848 × 10− 04, 2.8997 × 10− 04, 8.0205 × 10− 04, 8.3264 × 10− 04, 4.0182 × 10− 04, 2.3310 × 10− 03 1.3938 × 10− 03, 1.3938 × 10− 03 and 1.6505 × 10− 02, respectively. It can be seen from Table 7 that TLBO outperform HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA in terms of minimum MSE. Based on the performance, the applied and existing algorithms can be ordered as TLBO > CRPSO > DEWM > HS > FFA > BAT > CSO = PSO > CSA > GA. The convergence profiles of the applied algorithms are depicted in Fig. 9. It is clear from the convergence profiles that TLBO has a faster convergence rate as compared to the other applied algorithms. The minimum convergence value obtained using TLBO is − 37 dB in 62 iterations.

Table 7 Statistical results of MSE (normalized and dB) for Example 2 in case of reduced order system
Full size table
Fig. 9
figure 9

Convergence profile for Example 2 in case of reduced order system using TLBO, OHS, HS, CRPSO, FFA, BAT, DEWM, CSA, CSO, PSO and GA

Full size image

The enhancement in the performance of TLBO over other reported algorithms, for system identification using reduced order is depicted in Fig. 10.

Fig. 10
figure 10

Percentage improvement in MSE value of Example 2 compared to other reported algorithm using same order and reduced order system

Full size image

Example 3

Transfer function of the fourth-order IIR system is given by [33, 35]

$$ H_{p}(z)\!=\frac{1-0.9z^{-1}+ 0.81z^{-2}-0.729z^{-3}}{1 + 0.04z^{-1}+ 0.277z^{-2}-0.2101z^{-3}+ 0.14z^{-4}} $$
(17)

Case 1

In this case, the fourth-order system is approximated using the same order unknown IIR system whose transfer function is given by

$$ H_{s}(z)=\frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}+b_{3}z^{-3}}{1-a_{1}z^{-1}-a_{2}z^{-2}-a_{3}z^{-3}-a_{4}z^{-4}} $$
(18)

The optimized coefficients are listed in Table 8 and illustrated in Fig. 11. The MSE values computed in terms of best, worst, average and SD are reported in Table 9. The best MSE values reported in Table 9 for TLBO, OHS, HS, FFA, BAT, CRPSO, CSA, CSO, PSO and GA are 7.3906 × 10− 29, 2.3238 × 10− 14, 1.9175 × 10− 08, 2.2341 × 10− 14, 1.7315 × 10− 05, 1.8523 × 10− 07, 5.5540 × 10− 08, 5.9421 × 10− 05, 6.1146 × 10− 05 and 7.1586 × 10− 03, respectively. It can be noticed from Table 9, that results obtained using TLBO are best in terms of MSE as compared to the other reported algorithms. Based on the observations made from Table 9, the applied algorithms can be sequenced as TLBO> OHS > FFA > HS > CSA > CRPSO > BATT >CSO > PSO >GA. Convergence profiles are depicted in Fig. 12. It is apparent from Fig. 12 that TLBO converges to a fitness value near to − 281 dB in 65 iterations; whereas, OHS requires 145 iterations to a fitness value of − 136 dB, HS contributes to a fitness value of − 77 dB in 85 iterations; FFA converges in 126 iteration to a MSE value of − 136 dB; BAT obtains a fitness value of − 47 dB in 78 iterations; CRPSO approaches to a fitness value of − 67 dB in 75 iterations; 95 iterations are taken by CSA to converge to a fitness value of − 72 dB; CSO requires 104 iterations and converges to − 42 dB; PSO converges to a fitness value of − 43 dB in 112 iterations; GA obtains a fitness value of − 21 dB in 88 iterations. Based on these observations one can conclude that the convergence rate of TLBO is faster than other applied algorithms.

Table 8 Optimal coefficient values of fourth order IIR system for Example 3 in case of same order system estimated using TLBO, FFA, BAT, CSA, CSO, PSO and GA
Full size table
Fig. 11
figure 11

Coefficient comparison for Example 3 optimized using TLBO, BAT, FFA, DEWM, CSA, CSO, PSO and GA

Full size image
Table 9 Statistical results of MSE (normalized and dB) for Example 3 using same order system
Full size table
Fig. 12
figure 12

Convergence profile for Example 3 in case of same order system using TLBO, OHS, HS, CRPSO, FFA, BAT, CSA, CSO, PSO and GA

Full size image

Case 2

Transfer function of the reduced third-order system is given by

$$ H_{r}(z)=\frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}}{1-a_{1}z^{-1}-a_{2}z^{-2}-a_{3}z^{-3}} $$
(19)

The MSE values are reported in Table 10. The best MSE values reported are 6.1273 × 10− 04, 1.8999 × 10− 03, 2.9999 × 10− 03, 2.1000 × 10− 03, 3.2999 × 10− 03, 7.6325 × 10− 04, 6.5610 × 10− 03, 6.7051 × 10− 03, 6.7051 × 10− 03 and 1.9375 × 10− 02 for TLBO, OHS, HS, CRPSO, FFA, BAT, CSA, CSO, PSO and GA respectively. From these results, one can conclude that TLBO algorithm gives the best results for the system identification problem compared to other applied algorithms. Based on the numerical results stated in Table 10, the employed algorithms can be ranked as TLBO> BAT> OHS > CRPSO > HS > FFA > CSA > CSO = PSO >GA. The convergence plots of MSE values of different employed algorithms are shown in Fig. 13. It is apparent from Fig. 13 that TLBO converges to a minimum fitness value of − 32 dB in 62 iterations.

Table 10 Statistical results of MSE (normalized and dB) value for Example 3 using reduced order system
Full size table
Fig. 13
figure 13

Convergence profile for Example 3 in case of reduced order system using TLBO, OHS, HS, CRPSO, FFA, BAT, CSA, CSO, PSO and GA

Full size image

The percentage improvement of TLBO algorithm over the other algorithms for the same order and reduced order system is evaluated. This percentage is graphically illustrated in Fig. 14. The observed improvement using TLBO algorithm over all other employed algorithms is 99.99% for the same order. For reduced order system the percentage improvement of TLBO over OHS, HS, CRPSO, FFA, BATT, CSA, CSO, PSO and GA is 67.74%, 79.57%, 70.82%, 81.40%, 19.72%, 90.66%, 90.86%,90.86% and 96.83% respectively.

Fig. 14
figure 14

Percentage improvement in MSE value of Example 3 compared to other reported algorithm using same order and reduced order system

Full size image

Example 4

Transfer function Hp(z) of the fifth-order IIR system is given by [37]

$$ H_{p}(z)=\frac{0.1084 + 0.5419z^{-1}+ 1.0837z^{-2}+ 1.0837z^{-3}+ 0.5419z^{-4}+ 0.1084z^{-5}}{1 + 0.9853z^{-1}+ 0.9738z^{-2}+ 0.3864z^{-3}+ 0.1112z^{-4}+ 0.0113z^{-5}} $$
(20)

Case 1

In this case, the fifth-order IIR system is approximated using the same order unknown system whose transfer function is given by

$$ H_{s}(z)=\frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}+b_{3}z^{-3}+b_{4}z^{-4}+b_{5}z^{-5}}{1-a_{1}z^{-1}-a_{2}z^{-2}-a_{3}z^{-3}-a_{4}z^{-4}-a_{5}z^{-5}} $$
(21)

The optimal values of the coefficients are summarized in Table 11. It is apparent from Table 11 and Fig. 15 that TLBO algorithm is superior in optimizing the coefficients of the fifth-order system, among all the other applied algorithms. The statistical results of MSE values (normalized and dB) in terms of best, worst, average and SD are evaluated. These evaluated results are listed in Table 12. The best numerical values of MSE observed are 9.1905 × 10− 08, 3.1511 × 10− 06, 7.1407 × 10− 06, 4.9770 × 10− 06, 1.8737 × 10− 06, 5.4017 × 10− 05, 6.3551 × 10− 05, 7.2739 × 10− 05 and 1.3336 × 10− 02 for TLBO, OHS, HS, CRPSO, FFA, BAT, CSA, PSO and GA, respectively. These results reflect the efficiency of TLBO over the other present algorithms. The convergence behavior is depicted in Fig. 16. TLBO converges to − 70 dB in 117 iterations. OHS consumes 168 iterations to converge to a value of − 55 dB. Similarly, HS, CRPSO, FFA, BAT, CSA, PSO and GA converges to minimum fitness value of − 51 dB, − 53 dB, − 57 dB, − 42 dB, − 41 dB, − 41 dB and − 18 dB, respectively. It can be noticed from Fig. 16 that TLBO has a very high convergence rate as compared to the other reported algorithms. Based on the convergence plot, these algorithms can be sequenced as TLBO> FFA> OHS > CRPSO > HS > BAT > CSO > PSO >GA.

Table 11 Optimal coefficient values of fifth order IIR system for Example 4 in case of same order system estimated using TLBO, FFA, BAT, CSO, PSO and GA
Full size table
Fig. 15
figure 15

Coefficient comparison for Example 4 optimized using TLBO, BAT, FFA, CSO, PSO and GA

Full size image
Table 12 Statistical results of MSE (normalized and dB) value for Example 4 using same order system
Full size table
Fig. 16
figure 16

Convergence profile for Example 4 in case of same order system using TLBO, OHS, HS, CRPSO, FFA, BAT, CSO, PSO and GA

Full size image

Case 2

Transfer function of the reduced fourth-order system is given by

$$ H_{r}(z)=\frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}+b_{3}z^{-3}+b_{4}z^{-4}}{1-a_{1}z^{-1}-a_{2}z^{-2}-a_{3}z^{-3}-a_{4}z^{-4}} $$
(22)

Numerical values of MSE are given in Table 13. The best MSE values obtained for fifth order system modeled using fourth order system utilizing TLBO, OHS, HS, CRPSO, FFA, BAT, CSA, CSO, PSO and GA are 9.9913 × 10− 08, 2.3028 × 10− 06, 6.1214 × 10− 06, 6.1344 × 10− 06, 5.5835 × 10− 06, 2.6589 × 10− 05, 6.9475 × 10− 05, 6.9373 × 10− 05 and 8.4596 × 10− 02, respectively. It can be observed from the results that TLBO is superior among all the other applied algorithms. Further, the convergence profiles of TLBO and all other remaining algorithms are demonstrated in Fig. 17. It is evident from Fig. 17 that TLBO has a very fast convergence rate and it reaches a minimum value of − 70 dB in 128 iterations. By observing the results shown in Table 13, Figs. 16 and 17, the optimization algorithms can be ranked as TLBO> FFA > HS > CRPSO > BATT > PSO > CSO >GA.

Table 13 Statistical results of MSE (normalized and dB) value for Example 4 in case of reduced order system
Full size table
Fig. 17
figure 17

Convergence profile for Example 4 in case of reduced order system using TLBO, OHS, HS, CRPSO, FFA, BAT, CSO, PSO and GA

Full size image

The percentage improvement in the performance of TLBO algorithm over other algorithms, in terms of best MSE values for the same order and reduced order system is calculated and demonstrated in Fig. 18.

Fig. 18
figure 18

Percentage improvement in MSE value of Example 4 compared to other reported algorithm using same order and reduced order system

Full size image

4.1 Comparison analysis of elapsed time

Here, the performance of TLBO algorithm is reported in terms of the elapsed time and comparison is made with the other applied algorithms. The values of elapsed time (seconds) are listed in Table 14. The elapsed time reported using TLBO algorithm is 4.6839, 2.0365, 0.5255 and 1.6869 for modeling of the 2nd, 3rd, 4th and 5th order unknown IIR system, respectively. It is apparent from Table 14 that TLBO algorithm requires more elapsed time for Example 1 and Example 4 as compared to the FFA. However, it outperforms OHS, HS, FFA, CSO and PSO for 3rd and 4th order unknown IIR system. The elapsed times (seconds) of the reduced order system are summarized in Table 15. The elapsed times for 2nd, 3rd, 4th and 5th order unknown IIR system using TLBO are 2.7004, 2.3924, 1.2526 and 1.2300, respectively. Table 15 illustrates that TLBO algorithm requires more elapsed time as compared to the FFA for Example 2 and 3. However, it takes minimum elapsed time for Example 1 and 4. Tables 16 and 17 demonstrate the percentage improvement in elapsed time for the same order and reduced order systems, respectively.

Table 14 Comparison of elapsed times (seconds) in case of same order system
Full size table
Table 15 Comparison of elapsed times (seconds) in case of reduced order system
Full size table
Table 16 Percentage improvement in elapsed time obtained using TLBO over other employed algorithms in case of same order system
Full size table
Table 17 Percentage improvement in elapsed time obtained using TLBO over other employed algorithms in case of reduced order system
Full size table

4.2 Comparison of the proposed TLBO based system identification with the other existing algorithms

The efficiency of the applied TLBO algorithm for the system identification problem can be proved by comparing its results with the results of other applied algorithms. The detailed comparison of the MSE values is given in Table 18. It is observed that for the same order case, except HPSO-GSA and OHCRO the TLBO algorithm is efficient in terms of minimum MSE values for Example 1. In Example 2, TLBO outperforms all reported algorithms except OHCRO and OHS. However, TLBO algorithm outperforms the other reported algorithms for Example 3 and 4. In reduced order case, TLBO results are superior among the reported algorithms, shown in Table 18. The best MSE values measured for the same order case are 5.1425 × 10− 15, 3.1287 × 10− 12, 7.3906 × 10− 29 and 9.1905 × 10− 08, and for the reduced order 1.6523 × 10− 03, 1.8004 × 10− 04, 6.1273 × 10− 04 and 9.9913 × 10− 08, for Example 1, 2, 3 and 4 respectively.

Table 18 Comparison of MSE values of all Examples for different applied algorithms using same order and reduced order system
Full size table

These measured results show the ability of the proposed algorithm in obtaining satisfactory results in terms of system parameters, MSE value and elapsed time. Moreover, TLBO is free from algorithmic specific parameters, which controls the diversity of the algorithm. Also, Teacher-phase and Learner-phase assure the exploitation and exploration phase of the algorithm.

5 Conclusion

In this paper, a new population-based algorithm called TLBO, is introduced to estimate the coefficients of an unknown IIR system. The main advantage of this algorithm is that, it is free from algorithmic specific parameters. Hence, it is less complicated compared to the other state-of-the-art algorithms. The teacher and learner phase assure the exploitation and exploration of the algorithm. The optimal set of parameters and MSE values for the same order and reduced order unknown IIR system are evaluated. Results obtained using TLBO algorithm are compared with the existing algorithms like OHS, HS, FFA, BAT, DEWM, CSA, CSO, PSO and GA. It is evident from the results that the proposed method is superior to OHS, HS, FFA, BAT, DEWM, CSA, CSO, PSO and GA in terms of MSE and convergence speed. Further, this algorithm can be modified to solve the complex optimization problem such as nonlinear system identification.