1 Introduction

1.1 Background

Over the last few decades, 2D/3D images have become ubiquitous and increasingly important in many scientific domains such as manufacturing, molecular biology, medicine and computer vision [1,2,3,4]. At the same time, image moments and geometric invariance of moments have emerged as effective methods of feature extraction from images [5, 6]. Moment invariants have become a useful tool for describing objects regardless of their position, viewing angle and illumination. Due to their ability to represent global features of an image, moment invariants have found widely applications in image processing and pattern recognition [7,8,9]. Hu [10] is the first who introduced a set of seven invariants of geometric moments for pattern recognition. After this date, several applications of moments appeared in the literature such as image reconstruction [11, 12], image tattoo [13], medical image analysis [1, 14], image compression [15, 16], image watermarking [17] and image encryption [18]. Geometric moments are very sensitive to noise and are not orthogonal, which complicates the task of reconstructing the image because of the information redundancy. To overcome these two problems, the researchers proposed the continuous orthogonal moments that are defined from the bases of orthogonal polynomials such as the polynomials of: Legendre [16], Zernike [19], Pseudo-Zernike [20], Gegenbauer [21], Laguerre [22], Jacobi [23], Gaussian–Hermite [24] and Fourier–Mellin [5]. This set of orthogonal moments has received much attention in recent years because of their ability to represent images with minimal information redundancy and a high level of robustness to noise [25]. More recently, Mukundan et al. [26] introduced discrete orthogonal moments, based on Tchebichef discrete orthogonal polynomials, which have the property of being natively defined in discrete space. Consecutively, other discrete orthogonal moments, such as Krawtchouk [27], Charlier [12, 28], Mexnier [6, 29], Hahn [30], Racah [31] and dual-Hahn [32] were introduced in the field of image analysis. Zhu et al. [33] have defined a new type of moments called separable two-dimensional orthogonal continuous moments. These are defined from the separable bi-variable continuous orthogonal polynomials, which are obtained by the product of two continuous orthogonal polynomials of a single variable. It can be seen that all the aforementioned orthogonal moments are limited to an integer order, since their basic functions are represented by orthogonal integer polynomials.

1.2 Related works

Several works for image reconstruction and classification based on two-dimensional continuous of fractional-order orthogonal moments and moment invariants of fractional-order have been presented in the literature. In recent years, considerable attention has been given to find more accurate numerical solution of fractional differential equations using orthogonal polynomials. This has led to define the fractional-order type of some classical orthogonal polynomials [25, 33, 34], such as the shifted fractional-order Jacobi orthogonal functions (SFrJOFs) [35, 36], fractional-order Chebyshev polynomials (FrCPs) [37, 38] and fractional-order Legendre polynomials (FrLPs) [39, 40]. These orthogonal polynomials imply the introduction of a fractional parameter \(\lambda \succ 0\), in order to generalize the notion of integer order n with to a fractional order, where we can obtain the classical orthogonal polynomials by defining \(\lambda = 1\). In fact, fractional-order orthogonal polynomials can be used to represent the basic function of a new set of fractional-order orthogonal moments. In this context, Zhang et al. [5] introduced fractional-order orthogonal radial order Fourier–Mellin moments based on fractional-order Fourier–Mellin polynomials. Xiao et al. [40] have introduced two types of fractional-order orthogonal moments defined in polar and Cartesian coordinates, based, respectively, on the fractional-order Legendre radial polynomials and the shifted fractional-order Legendre polynomials. Benouini et al. [41] presented the orthogonal fractional-order Chebyshev moments (FrCMs) for image representation and pattern recognition. El Ogri, et al. [22] derived the Laguerre polynomials of fractional order and defined what is called fractional-order generalized Laguerre moment invariants (FrGLMs). Hosny et al. [21] defined the fractional-order shifted Gegenbauer moments for image analysis and recognition (FrSGMs). The fractional-order moments presented in the aforementioned studies [20] can easily become invariant in rotation due to the separable nature of their radial and angular components. However, their practical use was substantially limited for the extraction of rotational invariant features and image reconstruction, and no discussion regarding the computation of scale and translation invariants has yet to be found in these studies because it is difficult to extract a common scale and translational factors from the radial base function [7, 42, 43]. In addition, these fractional-order moments are very fast and computationally inexpensive which increase its applicability in wide range of real-time applications such as distributed clustering of linear bandits in peer to peer networks [44], the art of clustering bandits [45], collaborative filtering bandits [46], medicine rating prediction and recommendation in mobile social networks [2], fast distributed bandits for online recommendation systems [47].

1.3 Problem statement

Due to their strong image description ability, Jacobi moments (JMs) have been widely used in various fields of image processing in recent years. However, there is a numerical instability problem with JMs because they can only take integer orders, and this problem restricts the performance of JMs in the extraction of the regions of interest (ROI), image reconstruction and noise resistance. To address this problem, the concept of fractional order is introduced and incorporated into Jacobi moments (JMs) and fractional-order orthogonal Jacobi moments (FrOJMs) are proposed; then, the FrOJMs that are suitable for digital images and have better performance than JMs in noise resistance, image reconstruction, global and local feature extraction capability, invariability property and image classification performance on various databases images to the public. In this paper, we introduce a new set of fractional‐order moments, named fractional‐order orthogonal Jacobi moments (FrOJMs) for image reconstruction and pattern recognition. This set of moments is defined on the Cartesian coordinate system based on the Jacobi polynomials of fractional order. In addition, the proposed set of moments have the capability of being able to extract both global and local features, where the extraction of local features can be easily achieved by adjusting polynomials parameters associated with the gamma distribution. Also, we propose a new set of RST moment invariants, baptized fractional‐order Jacobi moment invariants (FrJMIs), based on using the algebraic relation between the FrOJMs and the fractional‐order geometric moments. What is more, we developed new recurrence relations for the computation of the polynomials coefficients, which can be used to efficiently reduce the numerical instability and computation cost of the proposed FrJMIs. Therefore, appropriate numerical experiments are performed to demonstrate the utility of our new feature descriptor on different databases. Motivated by the facts summarized above, the main contributions of this paper include the following points:

  1. (i)

    Introduce a new set of fractional-order orthogonal Jacobi moments for the images representation.

  2. (ii)

    Provide an accurate and fast computation algorithm to derive invariants of Jacobi fractional-order moments from the RST transformations. These invariant moments have the capacity to remain unchanged despite geometric transformations of rotation, scale and translation of grayscale images.

  3. (iii)

    To present an adaptive method for the extraction of invariant characteristics based on the capacity of the proposed moments to capture local information from the fractional parameters and parameters of the Jacobi polynomials for any position of the image.

  4. (iv)

    Propose a systematic method of parameter selection to select the appropriate parameter values to find the optimal values of the fractional parameters of FrJMIs, based on experimental studies.

  5. (v)

    The new fractional-order orthogonal Jacobi moments descriptors are robust to noise.

The rest of this article is organized as follows: In Sect. 2, we introduce the classical polynomials and moments of Jacobi. Section 3 is devoted to the definition of the proposed fractional-order Jacobi moments. Following Sect. 4, we present the theoretical framework for obtaining the fractional-order Jacobi moment invariants of rotation, scale and translation. The experimental results and discussions are carried out in Sect. 5. Finally, the final remarks and directions for future research are given in Sect. 6.

2 Classical orthogonal Jacobi moments

The Jacobi polynomials are widely used for approximating numerical functions and solving ordinary and partial differential equations. The polynomials of Legendre, Gegenbauer, Chebyshev of the first and second species are special cases of continuous orthogonal polynomials of Jacobi [33]. In the next section, we present the definition of continuous orthogonal polynomials of Jacobi and their methods of computation.

2.1 Orthogonal Jacobi polynomials

For \(\alpha , \, \beta \in {\mathbb{R}}\,;\,\alpha \succ - 1\,,\beta \succ - 1\), and a nonnegative integer n, we denote by \(J_{n}^{(\alpha ,\beta )} (x)\) the Jacobi polynomials, which comprises all the polynomial solutions to singular Sturm–Liouville problems on \(\left[ { - 1,1} \right]\).

The Jacobi polynomials, \(J_{n}^{(\alpha ,\beta )} (x)\), have the following Gauss hypergeometric representation [36]:

$$ J_{n}^{(\alpha ,\beta )} (x) = \frac{{(\alpha + 1)_{n} }}{n!}{}_{2}F_{1} \left( { - n,\,1 + \alpha + \beta + n\,,\alpha + 1\,;\,\frac{1 - x}{2}} \right) $$
(1)

where \((\alpha + 1)_{n}\) is Pochhammer’s symbol given by:

$$ (\alpha + 1)_{n} = (\alpha + 1)(\alpha + 2) \cdots (\alpha + n),\,\,\,\,n \ge 1\,\,\,\,{\text{and}}\,\,\,\,(\alpha + 1)_{0} = 1 $$
(2)

The function \({}_{2}F_{1}\) is the generalized hypergeometric which is defined as:

$$ {}_{2}F_{1} (a,b,c\,;x) = \sum\limits_{k = 0}^{\infty } {\frac{{(a)_{k} (b)_{k} }}{{(c)_{k} }}\frac{{x^{k} }}{k!}}. $$
(3)

In this case, the series for the hypergeometric function is finite, so we get the expression of the Jacobi polynomials \(J_{n}^{(\alpha ,\beta )} (x)\) of degree n is given by:

$$ J_{n}^{(\alpha ,\beta )} (x) = \sum\limits_{k = 0}^{n} {\chi_{k}^{(\alpha ,\beta ,n)} } x^{k} $$
(4)

where

$$ \chi_{k}^{(\alpha ,\beta ,n)} = ( - 1)^{n - k} \frac{\,\Gamma (n + \beta + 1)\Gamma (n + k + \alpha + \beta + 1)}{{\,\Gamma (k + \beta + 1)\Gamma (n + \alpha + \beta + 1)\,(n - k)!k!}}. $$
(5)

The direct calculation of Jacobi polynomials is very complex, requires computation time and causes numerical fluctuations especially for large orders. To overcome this problem, it is proposed to use the recursive form of Jacobi polynomials. The Jacobi polynomials are generated from the three-term recurrence relations [35]:

$$ J_{n + 1}^{(\alpha ,\beta )} (x)\, = (A_{n} x - B_{n} )J_{n}^{(\alpha ,\beta )} (x)\, - C_{n} J_{n - 1}^{(\alpha ,\beta )} (x)\,\,,\,\,\,n \ge 1\, $$
(6)

with

$$ J_{0}^{(\alpha ,\beta )} (x)\, = 1\,\,\,\,\,\,{\text{and}}\,\,\,\,J_{1}^{(\alpha ,\beta )} (x)\, = (\alpha + \beta + 2)x - (\beta + 1) $$
(7)

and

$$ \begin{gathered} A_{n} = \frac{(2n + \alpha + \beta + 1)(2n + \alpha + \beta + 2)}{{(n + 1)(n + \alpha + \beta + 1)}} \hfill \\ \hfill \\ B_{n} = \frac{{(2n + \alpha + \beta + 1)(2n^{2} + (1 + \beta )(\alpha + \beta ) + 2n(\alpha + \beta + 1))}}{(n + 1)(n + \alpha + \beta + 1)(2n + \alpha + \beta )} \hfill \\ \hfill \\ C_{n} = \frac{(2n + \alpha + \beta + 2)(n + \alpha )(n + \beta )}{{(n + 1)(n + \alpha + \beta + 1)(2n + \alpha + \beta )}}. \hfill \\ \end{gathered} $$
(8)

The Jacobi polynomials constitute an orthogonal system with respect to the weight function \(\omega_{{}}^{(\alpha ,\beta )} (x)\, = (1 + x)^{\alpha } (1 - x)^{\beta }\) over \(I = \left[ { - 1,1} \right]\), that is,

$$ \int_{ - 1}^{1} {J_{j}^{(\alpha ,\beta )} (x)\,J_{k}^{(\alpha ,\beta )} (x)\,\omega_{{}}^{(\alpha ,\beta )} (x)\,} dx = h_{k}^{(\alpha ,\beta )} \,\delta_{jk} $$
(9)

where \(\delta_{jk}\) is the Kronecker function and

$$ h_{k}^{(\alpha ,\beta )} = \frac{{2^{\alpha + \beta + 1} \,\Gamma (k + \alpha + 1)\Gamma (k + \beta + 1)}}{(2k + \alpha + \beta + 1)k!\,\Gamma (k + \alpha + \beta + 1)}. $$
(10)

The normalized Jacobi polynomials \(\tilde{J}_{n}^{(\alpha ,\beta )} (x)\,\) are defined as:

$$ \tilde{J}_{n}^{(\alpha ,\beta )} (x)\, = \sqrt {\frac{{\omega_{{}}^{(\alpha ,\beta )} (x)\,}}{{h_{k}^{(\alpha ,\beta )} }}} J_{n}^{(\alpha ,\beta )} (x)\, .$$
(11)

We can deduce that the orthogonality relation of the normalized Jacobi polynomials:

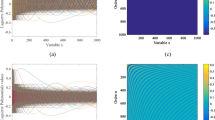
$$ \int_{ - 1}^{1} {\tilde{J}_{j}^{(\alpha ,\beta )} (x)\,\tilde{J}_{k}^{(\alpha ,\beta )} (x)\,\,} dx = \delta_{jk}. $$
(12)

Figure 1a presents the 2D plot of the matrix of Jacobi polynomial values for the first five hundred orders using the recursive relation with respect to the order n as defined in Eqs. (6) and (11) for \(N \, = 500\,{\text{and}}\, \, a = b = 1\). Note that the values of the polynomials are indefinite from the order 100. After an experimental study of the source of the problems of the numerical fluctuation of the polynomial values (Fig. 1), it has been found that the divergence comes from the parameters \(h_{k}^{(\alpha ,\beta )}\) because this parameter constitutes gamma function. To solve these problems, we propose to calculate the weighted parameters \(h_{k}^{(\alpha ,\beta )}\) by the formula of recurrence.

Fig. 1.
figure 1

2D plot of the coefficient matrix of Jacobi polynomials for orders n ranging from 0 to 500 and \(a = b = 1\) a: using Eq. (8) and b: using Eq. (13)

Full size image

Using the formula of Eq. (10) we find:

$$ h_{k + 1}^{(\alpha ,\beta )} = \frac{(2k + \alpha + \beta - 1)(k + \alpha )(k + \beta )}{{(2k + \alpha + \beta + 1)(k + \alpha + \beta )k}}h_{k}^{(\alpha ,\beta )} $$
(13)

with \(h_{0}^{(\alpha ,\beta )} = \frac{{2^{\alpha + \beta + 1} \Gamma (\alpha + 1)\Gamma (\beta + 1)}}{(\alpha + \beta + 1)\Gamma (\alpha + \beta + 1)}\).

The recurrence relation in Eq. (13) is independent of the power and the factorial, we could calculate the Jacobi values without numerical fluctuation up to order 1000. Figure 1b shows plots of polynomial values up to 500 without divergence.

2.2 Computation of classical orthogonal Jacobi moments

The classical Jacobi moments (CJMs) of order \((n + m)\) of any function \(f\left( {x,y} \right)\) defined on \(\left[ { - 1,1} \right] \times \left[ { - 1,1} \right]\) can be computed using continuous integrals as:

$$ {\text{CJM}}_{nm}^{(\alpha ,\beta )} = \int_{ - 1}^{1} {\int_{ - 1}^{1} {f(x,y)\tilde{J}_{n}^{(\alpha ,\beta )} (x)\,\tilde{J}_{m}^{(\alpha ,\beta )} (y)\,dxdy} } $$
(14)
$$ {\text{where }}\quad n,m = 0,1,2, \ldots N. $$

Therefore, the classical Jacobi moments \({\text{CJM}}_{nm}^{(\alpha ,\beta )}\) of a digital image function \(f\left( {x,y} \right)\) with the size \(M \times N\), mapped into the region \(\left[ { - 1,1} \right] \times \left[ { - 1,1} \right]\), can be computed using zeroth-order approximation (ZOA) method as [48]:

$$ {\text{CJM}}_{nm}^{(\alpha ,\beta )} = \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {f(i,j)\tilde{J}_{n}^{(\alpha ,\beta )} (x_{i} )\,\tilde{J}_{m}^{(\alpha ,\beta )} (y_{j} )\,\Delta x} } \Delta y $$
(15)

where

  • \(\tilde{J}_{n}^{(\alpha ,\beta )} (x)\) is the nth order orthonormal polynomials of Jacobi and \(\Delta x = x_{i} - x_{i - 1}\), \(\Delta y = y_{j} - y{}_{j - 1}\) are sampling intervals in the “x” and “y” directions, respectively, \(\left( {x_{i} ,y_{j} } \right)\) is the center of \(\left( {i,j} \right)\) pixel.

  • The image coordinates transform is defined as follows:

    $$ x_{i} = \left( {i + \frac{1}{2}} \right)\Delta x - 1\,\,,\,\,y_{j} = \left( {j + \frac{1}{2}} \right)\Delta y - 1 $$
    (16)

\({\text{with}}\,\)\(\,\Delta x = \frac{2}{N}\,\,\,\,,\,\,\,\,\Delta y = \frac{2}{M}\,\,\,\,,\,\,\,\,i = 0,1,2.....,N - 1\,\,\,\,{\text{and}}\,\,\,\,j = 0,1,2.....,M - 1\).

An approximation \(\tilde{f}\left( {x,y} \right)\) of the original image can be obtained by:

$$ \tilde{f}(i,j) = \sum\limits_{n = 0}^{{n_{\max } }} {\sum\limits_{m = 0}^{{m_{\max } }} {{\text{CJM}}_{nm}^{(\alpha ,\beta )} \,\tilde{J}_{n}^{(\alpha ,\beta )} (x_{i} )\,\tilde{J}_{m}^{(\alpha ,\beta )} (y_{j} )} }. $$
(17)

The classical Jacobi orthogonal moments above are defined only for integer orders. In the next section, we propose a new type of moments that are fractional-order orthogonal Jacobi moments. These are extended to orthogonal moments of real order (or fractional-order) using fractional-order orthogonal Jacobi polynomials.

3 Proposed fractional-order orthogonal Jacobi moments

In this section, we will initially review some general properties of the fractional-order orthogonal Jacobi polynomials (FrOJPs). In the following, we will provide the definition of the new FrOJMs.

3.1 Fractional-order orthogonal Jacobi polynomials

In this sub-section, we will define new orthogonal system of FrOJPs from classical Jacobi polynomials. Let \(\lambda\) be a rational positive number \(\lambda \ge 0\), for using these polynomials on \(\left[ {0,1} \right]\), we present the classical Jacobi polynomials by implementing the change of variable \(x = 2t^{\lambda } - 1\).

From the classical Jacobi polynomials of Eq. (4), we can define the fractional-order Jacobi polynomials \({\text{FrJ}}_{n}^{(\alpha ,\beta ,\lambda )} (t)\) as [35]:

$$ {\text{FrJ}}_{n}^{(\alpha ,\beta ,\lambda )} (t)\, = J_{n}^{(\alpha ,\beta )} (2t^{\lambda } - 1)\,\,\,{\text{with}}\,\,\,\,\,t \in \left[ {0,1} \right]. $$
(18)

Using Eqs. (4) and (5), we obtain:

$$ {\text{FrJ}}_{n}^{(\alpha ,\beta ,\lambda )} (t) = \sum\limits_{k = 0}^{n} {\chi_{k}^{(\alpha ,\beta ,n)} } t^{\lambda k} $$
(19)

with

$$ \chi_{k}^{(\alpha ,\beta ,n)} = ( - 1)^{n - k} \frac{\,\Gamma (n + \beta + 1)\Gamma (n + k + \alpha + \beta + 1)}{{\,\Gamma (k + \beta + 1)\Gamma (n + \alpha + \beta + 1)\,(n - k)!k!}}. $$
(20)

From Eq. (6), we find the following recurrence relations of fractional-order Jacobi polynomials \({\text{FrJ}}_{n}^{(\alpha ,\beta ,\lambda )} (t)\):

$$ {\text{FrJ}}_{n + 1}^{(\alpha ,\beta ,\lambda )} (t)\, = (A_{n} (2t^{\lambda } - 1) - B_{n} ){\text{FrJ}}_{n}^{(\alpha ,\beta ,\lambda )} (t)\, - C_{n} {\text{FrJ}}_{n - 1}^{(\alpha ,\beta ,\lambda )} (t)\,\,,\,\,\,n \ge 1\, $$
(21)

with \(A_{n} \,,B_{n} \,{\text{and}}\,C_{n}\) in the relations (8):

$$ {\text{FrJ}}_{0}^{(\alpha ,\beta ,\lambda )} (t)\, = 1,\,\,\,\,\,\,\,{\text{FrJ}}_{1}^{(\alpha ,\beta ,\lambda )} (t)\, = \frac{(\alpha + \beta + 2)}{2}(2t^{\lambda } - 1) + \frac{(\alpha - \beta )}{2}. $$
(22)

Let \(\omega_{{}}^{(\alpha ,\beta ,\lambda )} (t)\, = \lambda \,t^{(\beta + 1)\lambda - 1} (1 - t^{\lambda } )^{\alpha }\). Thanks to (12), the fractional-order Jacobi functions form a complete \(L_{{\omega_{{}}^{(\alpha ,\beta ,\lambda )} }}^{2} [0,1]\)-orthogonal system, that is:

$$ \int_{0}^{1} {{\text{FrJ}}_{j}^{(\alpha ,\beta ,\lambda )} (t)\,{\text{FrJ}}_{k}^{(\alpha ,\beta ,\lambda )} (t)\,\omega_{{}}^{(\alpha ,\beta ,\lambda )} (t)\,} {\text{d}}t = h_{k}^{(\alpha ,\beta )} \delta_{jk}. $$
(23)

We can define the normalized fractional-order Jacobi polynomials by:

$$ \widetilde{{{\text{FrJ}}}}_{n}^{(\alpha ,\beta ,\lambda )} (t)\, = \sqrt {\frac{{\omega_{{}}^{(\alpha ,\beta ,\lambda )} (t)\,}}{{h_{k}^{(\alpha ,\beta )} }}} {\text{FrJ}}_{n}^{(\alpha ,\beta ,\lambda )} (t)\, .$$
(24)

As a result, the recurrence relation of the normalized FrOJMs is given as follows:

$$ \widetilde{{{\text{FrJ}}}}_{n + 1}^{(\alpha ,\beta ,\lambda )} (t)\, = (A_{n} (2t^{\lambda } - 1) - B_{n} )\widetilde{{{\text{FrJ}}}}_{n}^{(\alpha ,\beta ,\lambda )} (t)\, - C_{n} \widetilde{{{\text{FrJ}}}}_{n - 1}^{(\alpha ,\beta ,\lambda )} (t)\,\,,\,\,\,n \ge 1\, $$
(25)

with

$$ \begin{gathered} \widetilde{FrJ}_{0}^{(\alpha ,\beta ,\lambda )} (t) = \sqrt {\frac{{\omega_{{}}^{(\alpha ,\beta ,\lambda )} (t)}}{{h_{k}^{(\alpha ,\beta )} }}} \hfill \\ \hfill \\ \widetilde{FrJ}_{1}^{(\alpha ,\beta ,\lambda )} (t) = \left( {\frac{{(\alpha + \beta + 2)(2t^{\lambda } - 1) + (\alpha - \beta )}}{2}} \right)\sqrt {\frac{{\omega_{{}}^{(\alpha ,\beta ,\lambda )} (t)}}{{h_{k}^{(\alpha ,\beta )} }}}. \hfill \\ \end{gathered} $$
(26)

It is easy to verify that the orthogonality condition becomes:

$$ \int_{0}^{1} {\widetilde{{{\text{FrJ}}}}_{j}^{(\alpha ,\beta ,\lambda )} (t)\,\widetilde{{{\text{FrJ}}}}_{k}^{(\alpha ,\beta ,\lambda )} (t)} {\text{d}}t = \delta_{jk}. $$
(27)

Finally, it is important to note that the FrOJPs inherit all the properties of the classical Jacobi polynomials, including their relation with the standard gamma distribution. What is more, the presented FrOJPs include a new fractional parameter \(\lambda \succ 0\), so as to generalize the notion of integer‐order \(n \in {\mathbb{N}}\) to fractional‐order \(\lambda n\), where we can recover the classical Jacobi polynomials as \({\text{FrJ}}_{n}^{(\alpha ,\beta ,1)} (x)\, = J_{n}^{(\alpha ,\beta )} (x)\) by setting \(\lambda\) to 1. In fact, this parameter can be also used for adjusting the distribution and the contraction of the polynomials zeros. Figure 2 clearly depicts the influence of the parameter \(\lambda\) on the graph of the FrOJPs.

Fig. 2
figure 2

Graphs of the first seven orders of the normalized FrOJPs for different values of \(\alpha ,\beta \,\,{\text{and}}\,\,\lambda\)

Full size image

Figure 3 presents the numerical results of the fractional-order Jacobi polynomials for the four first order \(n = 1, \, 2, \, 3, \, 4\) and different values of \(\lambda = 1, \, 1.25, \, 1.5, \, 1.75, \, 2, \, 2.25\).

Fig. 3
figure 3

Graph of the FrOJPs for the four first order \(n = 1, \, 2, \, 3, \, 4\) and various values of \(\lambda\)

Full size image

3.2 Fast and accurate computation of the fractional-order orthogonal Jacobi moments

The fractional-order orthogonal Jacobi moments (FrOJMs) of order \((n + m)\) of any function \(f\left( {x,y} \right)\) defined on \(\left[ {0,1} \right] \times \left[ {0,1} \right]\) can be computed using the continuous integrals as follows:

$$ {\text{FrJM}}_{nm}^{(\alpha ,\beta ,\lambda )} = \int_{0}^{1} {\int_{0}^{1} {f(x,y)\widetilde{{{\text{FrJ}}}}_{n}^{(\alpha ,\beta ,\lambda )} (x)\,\widetilde{{{\text{FrJ}}}}_{m}^{(\alpha ,\beta ,\lambda )} (y)\,{\text{d}}x{\text{d}}y} } $$
(28)
$$ {\text{where }}n,m = 0,1,2,....N. $$

Therefore, for a digital image intensity function \(f\left( {i,j} \right)\) of size \(M \times N\), the moments \({\text{FrJM}}_{nm}\) can be computed using zeroth-order approximation (ZOA) method as [48]:

$$ {\text{FrJM}}_{nm}^{(\alpha ,\beta ,\lambda )} = \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {f(i,j)\widetilde{FrJ}_{n}^{(\alpha ,\beta ,\lambda )} (x_{i} )\widetilde{FrJ}_{m}^{(\alpha ,\beta ,\lambda )} (y_{j} )\Delta x} } \Delta y $$
(29)

where the image coordinates transform is defined in Eq. (16).

An approximation \(\tilde{f}(i,j)\) of the original image can be reconstructed by:

$$ \tilde{f}(i,j) = \sum\limits_{n = 0}^{{n_{\max } }} {\sum\limits_{m = 0}^{{m_{\max } }} {{\text{FrJM}}_{nm} \widetilde{FrJ}_{n}^{(\alpha ,\beta ,\lambda )} (x_{i} )\,\widetilde{FrJ}_{m}^{(\alpha ,\beta ,\lambda )} (y_{j} )} }. $$
(30)

The calculation of the FrOJMs by the approximate method is limited by two problems: the very high computation time especially for the large orders and the errors of approximations which influence on the quality of the processed images. To solve these problems, we propose precise and rapid method for calculating Jacobi fractional-order moments. This method is based on the use of the separability property of the moment transform, which allows the computation of the 2D FrOJMs in two cascaded stages by successive calculation of the corresponding 1D FrOJMs for each line.

From Eq. (29), we obtained the following expression of the FrOJMs:

$$ {\text{FrJM}}_{nm}^{(\alpha ,\beta ,\lambda )} = \frac{4}{NM}\sum\limits_{i = 0}^{N - 1} {I_{Xn} (x_{i} )\left[ {\sum\limits_{j = 0}^{M - 1} {I_{Ym} (y_{j} )f(x_{i} ,y_{j} )} } \right]} = \frac{4}{NM}\sum\limits_{i = 0}^{N - 1} {I_{Xn} (x_{i} )} \,Y_{m}^{i} $$
(31)

where

$$ Y_{m}^{i} = \sum\limits_{j = 0}^{M - 1} {f(i,j)I_{Ym} (y_{j} )}. $$
(32)

In the first step, we successively calculate the corresponding 1D moments for each line by using the matrix form of FrOJMs

$$ Y_{m}^{i} = H_{1} \,f. $$
(33)

In the second step, we calculate \(M\) temporary matrices along y direction by using the matrix form of FrOJMs by successive computation of the corresponding 2D moments for a grayscale image:

$$ {\text{FrJM}}_{nm}^{(\alpha ,\beta ,\lambda )} = \left\{ {\left. {{\text{FrJM}}_{ij}^{(\alpha ,\beta ,\lambda )} } \right\}_{0 \le j \le m}^{0 \le i \le n} } \right. = H_{1} \,fH_{2}^{T} $$
(34)

where

$$ \begin{aligned}H_{1} &= \left\{ {\left. {I_{Xl} (x_{i} )} \right\}} \right._{{1 \le x_{i} \le N}}^{0 \le l \le n} \,\,\,;\,\,\,H_{2} = \left\{ {\left. {I_{Ys} (y_{j} )} \right\}} \right._{{1 \le y_{j} \le M}}^{0 \le s \le m} \\ f &= \left\{ {\left. {f(x_{i} ,y_{j} )} \right\}} \right._{{1 \le y_{j} \le M}}^{{1 \le x_{i} \le N}}. \end{aligned}$$
(35)

The FrOJMs of lower orders are used to describe the components of low spatial frequency images and higher-order moments store high spatial frequencies of images that correspond to rapid changes in pixel intensities. The position and distribution of the zeros correspond to the ability of the moments to extract image information, making the proposed moments more suitable for image reconstruction and classification of images. In fact, the region of interest can be shifted to different positions, for \(\lambda_{\,x} \prec 1\) the region shifted to the left and for \(\lambda_{\,x} \succ 1\) region shifted to the right, with respect to the x-axis. The region is moved up for \(\lambda_{\,y} \prec 1\) and down for \(\lambda_{\,y} \succ 1\), along the y-axis. Moments have become important and frequently used as form descriptors for classification and pattern recognition. The properties of these moments aroused the interest of finding their invariants in terms of translation, scale and rotation. In the next section, we will show how to obtain fractional-order Jacobi moment invariants with respect to translation and scaling and rotation using the invariants of the corresponding fractional-order geometric moment invariants.

4 Proposed generalized fractional-order Jacobi moment invariants

The FrOJMs are not precisely designed for pattern recognition, in the sense that FrOJMs are not invariants with respect to the geometric transformation, like rotation, scaling and translation. And therefore, it may be insufficient to use the FrOJMs for describing and recognizing deformed objects. For this, to obtain the rotation, scale and translation invariants of the FrOJMs, we first need to define the fractional-order geometric moment invariants (FrGMIs), which is a modified form of the traditional geometric moments invariants, by introducing two positive fractional parameters \(\lambda_{\,1} \,,\,\lambda_{\,2} \, \succ 0\) in the geometric basis function \((x^{{\lambda_{\,1} p}} y^{{\lambda_{\,2} \,q}} )\), with \(p,q \in N\). In the next step, we will establish the algebraic relationship between the fractional-order geometric moments and their invariants in order to obtain generalized Jacobi moment invariants.

4.1 Exact computation of the FrGMs

The FrGMs are defined as the projection of the image intensity function \(f(x,y)\) onto the nominal \(x^{{\lambda_{\,1} p}} y^{{\lambda_{\,2} \,q}}\). The FrGMs of order \((n + m)\) are defined as:

$$ FrGM_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }} = \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {f(i,j)} m_{pq} (x_{i} ,y_{j} )} $$
(36)

where

$$ m_{pq} (x_{i} ,y_{j} ) = \int_{{x_{i} - \frac{{\Delta x_{i} }}{2}}}^{{x_{i} + \frac{{\Delta x_{i} }}{2}}} {\int_{{y_{i} - \frac{{\Delta y_{j} }}{2}}}^{{y_{i} + \frac{{\Delta y_{j} }}{2}}} {x^{{\lambda_{\,1} p}} y^{{\lambda_{\,2} \,q}} dxdy} }. $$
(37)

Therefore, based on the separability property of the moments kernel function, we can write the double integral as follow:

$$ m_{pq} (x_{i} ,y_{j} ) = I_{p} (x_{i} )I_{q} (y_{j} ) $$
(38)

where

$$ \begin{gathered} I_{p} (x_{i} ){ = }\int_{{x_{i} - \frac{{\Delta x_{i} }}{2}}}^{{x_{i} + \frac{\Delta xi}{2}}} {x^{{\lambda_{\,1} p}} dx} = \frac{1}{{\lambda_{\,1} p + 1}}\left[ {U_{i + 1}^{{\lambda_{\,1} p + 1}} - U_{i}^{{\lambda_{\,1} p + 1}} } \right] \hfill \\ I_{q} (y_{j} ){ = }\int_{{y_{i} - \frac{{\Delta y_{j} }}{2}}}^{{y_{i} + \frac{{\Delta y_{j} }}{2}}} {y^{{\lambda_{\,2} \,q}} dy} = \frac{1}{{\lambda_{\,2} q + 1}}\left[ {V_{j + 1}^{{\lambda_{\,2} q + 1}} - V_{j}^{{\lambda_{\,2} q + 1}} } \right]. \hfill \\ \end{gathered} $$
(39)

Upper and lower limits of the integration in Eq. (39) will be expressed as follows:

$$ \begin{gathered} U_{i + 1} = x_{i} + \frac{{\Delta x_{i} }}{2}{ = }\,{(}i{ + 1)}\Delta x_{i} { ; }U_{i} = x_{i} - \frac{{\Delta x_{i} }}{2} = i\Delta x_{i} \hfill \\ \hfill \\ V_{j + 1} = y_{j} + \frac{{\Delta y_{i} }}{2}{ = }\,{(}j{ + 1)}\Delta y_{j} { ; }V_{j} = y_{j} - \frac{{\Delta y_{i} }}{2} = j\Delta y_{j} \hfill \\ \hfill \\ \end{gathered} $$
(40)

Substituting Eq. (38) into Eq. (36) yields a set of exact geometric moments.

$$ FrGM_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }} = \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {f(i,j)} \,I_{p} (x_{i} )\,I_{q} (y_{j} )} $$
(41)

with \(\lambda_{\,1}\) and \(\lambda_{\,2}\) are rational positive numbers.

The image centroid \(\left( {\hat{x},\hat{y}} \right)\) with \(\left( {\hat{x},\hat{y}} \right) \in \left[ {0,1} \right]^{2}\) is defined in terms of the first.

order moments as follows:

$$ \hat{x} = \frac{{FrGM_{10}^{{\lambda_{\,1} \,\lambda_{\,2} }} }}{{FrGM_{00}^{{\lambda_{\,1} \,\lambda_{\,2} }} }}\,\,\,,\,\,\,\hat{y} = \frac{{FrGM_{01}^{{\lambda_{\,1} \,\lambda_{\,2} }} }}{{FrGM_{00}^{{\lambda_{\,1} \,\lambda_{\,2} }} }} $$
(42)

with \(\lambda_{\,1} \, = \,\lambda_{\,2} \, = 1\).

4.2 Accurate fractional-order geometric moment invariants

After the definition of FrGMs as a function of the geometric moments, we will propose, in this sub-section, the exact computation of the fractional-order geometric moment invariants (FrGMIs) by the transformations of translation, scaling and rotation. For this, we will define the central moments of FrGMs noted \(FrU_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }}\) that are invariant to the translation as follows:

$$ FrU_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }} = \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {f(i,j)} \,u_{pq} (x_{i} ,y_{j} )} $$
(43)

where

$$ u_{pq} (x_{i} ,y_{j} ) = \int_{{x_{i} - \frac{{\Delta x_{i} }}{2}}}^{{x_{i} + \frac{{\Delta x_{i} }}{2}}} {\int_{{y_{i} - \frac{{\Delta y_{j} }}{2}}}^{{y_{i} + \frac{{\Delta y_{j} }}{2}}} {\left( {x - \hat{x}} \right)^{{\lambda_{\,1} p}} \left( {y - \hat{y}} \right)^{{\lambda_{\,2} \,q}} dxdy} }. $$
(44)

By applying the separability property of the moments of the principal function, we can write the double integral in Eq. (44) as follows:

$$ u_{pq} (x_{i} ,y_{j} ) = Iu_{p} (x_{i} )Iu_{q} (y_{j} ) $$
(45)

where

$$ \begin{gathered} Iu_{p} (x_{i} ){ = }\int_{{x_{i} - \frac{{\Delta x_{i} }}{2}}}^{{x_{i} + \frac{\Delta xi}{2}}} {\left( {x - \hat{x}} \right)^{{\lambda_{\,1} p}} dx} = \frac{1}{{\lambda_{\,1} p + 1}}\left[ {(U_{i + 1} - \hat{x})^{{\lambda_{\,1} p + 1}} - (U_{i} - \hat{x})^{{\lambda_{\,1} p + 1}} } \right] \hfill \\ Iu_{q} (y_{j} ){ = }\int_{{y_{i} - \frac{{\Delta y_{j} }}{2}}}^{{y_{i} + \frac{{\Delta y_{j} }}{2}}} {\left( {y - \hat{y}} \right)^{{\lambda_{\,2} \,q}} dy} = \frac{1}{{\lambda_{\,2} q + 1}}\left[ {(V_{j + 1} - \hat{y})^{{\lambda_{\,2} q + 1}} - (V_{j} - \hat{y})^{{\lambda_{\,2} q + 1}} } \right]. \hfill \\ \end{gathered} $$
(46)

The fractional-order geometric moment invariants (FrGMIs), denoted \(FrV_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }}\), by the transformations of translation, scaling and rotation are written as:

$$ FrV_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }} = \eta^{ - \gamma } \sum\limits_{i = 0}^{N - 1} {\sum\limits_{j = 0}^{M - 1} {f(i,j)} \,v_{pq} (x_{i} ,y_{j} )} $$
(47)

where

$$ v_{pq} (x_{i} ,y_{j} ) = \int_{{x_{i} - \frac{{\Delta x_{i} }}{2}}}^{{x_{i} + \frac{{\Delta x_{i} }}{2}}} {\int_{{y_{i} - \frac{{\Delta y_{j} }}{2}}}^{{y_{i} + \frac{{\Delta y_{j} }}{2}}} {\left[ {\begin{array}{*{20}c} {\left( {(x - \hat{x})\cos \theta + (y - \hat{y})\sin \theta } \right)^{{\lambda_{\,1} p}} } \\ { \times \left( {(y - \hat{y})\cos \theta - (x - \hat{x})\sin \theta } \right)^{{\lambda_{\,2} q}} } \\ \end{array} } \right]dxdy} }. $$
(48)

The appropriate values for the normalization parameters \(\gamma \,,\,\eta\), and the rotational invariants can be obtained by normalizing the transformed object, are already defined in the literature [33, 49, 50], by using the special case \(\lambda_{\,1} + \lambda_{\,2} = 1\) as follows:

$$\begin{aligned} \eta &= FrGM_{00}^{{\lambda_{\,1} \,\lambda_{\,2} }} \,\,\,,\,\,\,\gamma = \frac{{\lambda_{\,1} \,n + \lambda_{\,2} \,m + 2}}{2}\\ \theta &= \frac{1}{2}\tan^{ - 1} \left( {\frac{{2FrU_{11}^{{\lambda_{\,1} \,\lambda_{\,2} }} }}{{FrU_{20}^{{\lambda_{\,1} \,\lambda_{\,2} }} + FrU_{02}^{{\lambda_{\,1} \,\lambda_{\,2} }} }}} \right). \end{aligned} $$
(49)

4.3 Accurate computation of the FrJMIs

In this sub-section, we will propose an accurate method for the extraction of fractional-order Jacobi moment invariants based on fractional-order geometric moment invariants. For this, we will normalize the image function \(f\left( {x,y,z} \right)\) by the product of the weight functions \(\left( {\omega (x)\omega (y)\omega (z)} \right)^{ - 1/2}\). So, the FrJMs defined by Eq. (28) are written:

$$ {\text{FrJM}}_{nm} = \frac{1}{{\sqrt {h_{n}^{(\alpha ,\beta )} h_{m}^{(\alpha ,\beta )} } }}\int_{0}^{1} {\int_{0}^{1} {\tilde{f}(x,y)FrJ_{n}^{(\alpha ,\beta ,\lambda )} (x)\,FrJ_{m}^{(\alpha ,\beta ,\lambda )} (y)\,dxdy} }. $$
(50)

By Eqs. (19) and (29), we can express FrOJMs in terms of \(FrGM_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }}\), based on the relation between \(FrJ_{n}^{(\alpha ,\beta ,\lambda )} (t)\) and the polynomials of \(t^{\lambda k}\):

$$ {\text{FrJM}}_{nm} = \frac{1}{{\sqrt {h_{n}^{(\alpha ,\beta )} h_{m}^{(\alpha ,\beta )} } }}\sum\limits_{p = 0}^{n} {\sum\limits_{q = 0}^{m} {\chi_{p}^{(\alpha ,\beta ,n)} \chi_{q}^{(\alpha ,\beta ,m)} } } FrGM_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }}. $$
(51)

Replacing the \(FrGM_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }}\) in the right side of the previous equation with \(FrV_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }}\) defined in Eq. (51), we can obtain the invariants of rotation, scaling and translation of fractional-order Jacobi moment invariants, which will be designated by FrJMIs in this article:

$$ {\text{FrJMI}}_{nm} = \frac{1}{{\sqrt {h_{n}^{(\alpha ,\beta )} h_{m}^{(\alpha ,\beta )} } }}\sum\limits_{p = 0}^{n} {\sum\limits_{q = 0}^{m} {\chi_{p}^{(\alpha ,\beta ,n)} \chi_{q}^{(\alpha ,\beta ,m)} } } FrV_{pq}^{{\lambda_{\,1} \,\lambda_{\,2} }}. $$
(52)

The different stages of calculation fractional-order Jacobi moment invariants are summarized in Algorithm 1:

figure a

5 Experimental results and discussion

In this section, several experiments are provided to validate the performance and effectiveness of newly introduced FrOJMs and FrJMIs compared to existing fractional-order methods [21, 40, 41]. It is important to note that all the algorithms and the numerical experiments are implemented and executed in MATLAB R2016a under Microsoft Windows environment using a PC with Intel Core i5 CPU 2.4 GHz and 8 GB RAM. Through these experiments, we will test: (1) the ability to represent gray-level images by adjusting the fractional parameters and parameters of Jacobi polynomials, (2) the experiments evaluated the proposed FrOJMs on image reconstruction, ROI-feature extraction and the influence of different parameter conditions on image reconstruction, (3) invariance of fractional-order Jacobi invariant moments with respect to RST, (4) robustness to different kinds of noises, (5) classification performance on gray-level images and (6) computational CPU times for the proposed FrOJMs and FrJMIs.

5.1 Image representation capability

To demonstrate the capacity and the quality of the image representation by the fractional-order orthogonal Jacobi moments (FrOJMs) developed in this paper, we will make comparisons with moments that belongs to the same family of Jacobi moments as fractional-order Chebyshev moments (FrCMs) [41], fractional-order Gegenbauer moments (FrGegMs) [21] and fractional-order Legendre moments (FrLMs) [40]. As a comparison criterion, we will use the mean squared error (MSE) that measures the difference between the original image \(f(x,y)\) and the reconstructed image \(\hat{f}(x,y)\). The latter is defined as follows:

$$ {\text{MSE}} = \frac{1}{NM}\sum\limits_{x = 0}^{N - 1} {\sum\limits_{y = 0}^{M - 1} {\left[ {f(x,y) - \hat{f}(x,y)} \right]} }^{2}. $$
(53)

5.1.1 Choice of parameter of the FrOJPs

The Jacobi polynomials depend on the parameters \(\alpha\) and \(\beta\). Therefore, the choice of these parameters is essential for a better reconstruction of the images by fractional-order orthogonal Jacobi moments. To measure the appropriate parameter range \(\alpha\) and \(\beta\), we will reconstruct image “Lena” of size \(1000 \times 1000\). The reconstruction of this image is performed for different parameter values \(\alpha ,\beta\) and for several fractional orders \(\lambda\) for different orders of fractional-order orthogonal Jacobi moments. Figure 4 shows the MSE and PSNR curves for different parameter choices using the image “Lena” for fractional-order Jacobi moment orders ranging from 0 to 512. For parameters \(\alpha\) and \(\beta\) vary between \((10,10)\) and \((70,70)\), we notice that the MSE curves of the reconstructed images decrease and get closer to zero when the orders of the fractional-order Jacobi moments increase which shows the capacity of the Jacobi moments for image reconstruction to different values \(\alpha\) and \(\beta\). There is also a slight increase in the MSE with the increase in the parameters \(\alpha\) and \(\beta\). So, for better image reconstruction by fractional-order Jacobi moments, we choose parameters \(\alpha\) and \(\beta\) around \((10,10).\)

Fig. 4
figure 4

The MSE and PSNR values for the grayscale image of Lena for different parameter values of Jacobi polynomials

Full size image

In the second reconstruction test, the same image of the first test was used to perform their reconstructions by fractional-order Jacobi moments for \((\alpha ,\beta ) = (10,10)\) and for fractional-order values \(\lambda = 0.2\,,\, \, 0.8\,, \, 1, \, 1.2, \, 1.4, \, 1.8, \, 2.2\). Figure 5 shows the MSE curves for the different fractional-order parameters using the image “Lena” for fractional-order Jacobi moment orders ranging from 0 to 512. The results obtained experimentally are valid for different types of images and for different fractional orders \(\lambda\). We note that the best values of the fractional-order parameters \(\lambda\) are between 1.2 and 2.2.

Fig. 5
figure 5

The MSE values for the grayscale image of Lena: a The MSE of image for different parameter fractional-order \(\lambda\) values and b zoom for more clarification

Full size image

5.1.2 Digital image reconstruction

In this experiment, we will compare the image reconstruction capacity of proposed FrOJMs with the existing recent orthogonal moments [21, 40, 41]. For this fact, the reconstruction test is performed on image “Lena” of size \(1000 \times 1000 \, \) which is shown in Fig. 6, for fractional orders ranging between 0.8 and 1.4 to orders of moments ranging from 0 to 500.

Fig. 6
figure 6

The test images of size 1000 × 1000 pixels: a “Lena” image and b “IRM” medical images [51]

Full size image

Figure 7 shows the MSE and PSNR curves for the four types of fractional-order moments FrOJMs, FrLMs [40], FrCMs [41] and FrGegMs [21]. We then note that the MSE of the four moments decreases and tends toward zero with the increase in the orders of the moments, which shows the capacity of the latter for the reconstruction of the images for any fractional order knowing that for \(\lambda x = 1{\text{ and }}\lambda y = 1\), we find classical continuous orthogonal moments of Jacobi, Legendre, Chebyshev and Gegenbauer. We can still see from the curves that MSE of FrOJMs is smaller than MSE moments fractional-order moments of Legendre, Chebyshev and Gegenbauer, which shows the performance of the proposed fractional moments compared to other orthogonal moments [21, 40, 41].

Fig. 7
figure 7

a–h MSE and PSNR of the “Lena” image for different fractional-order parameters \(\lambda x\,{\text{and}}\,\lambda y\) of FrOJMs for different orders of moments

Full size image

Figures 8 and 9 illustrate a comparison of a set of reconstructed images by the FrOJMs, FrLMs [40], FrCMs [41] and FrGegMs [21] for orders \(n,m = 20, \, 60, \, 100, \, 500, \, 1000\) and for different fractional orders: (a) \(\lambda x = \lambda y = 0.8\), (b) \(\lambda x = \lambda y = 1\), (c) \(\lambda x = \lambda y = 1.4\), et (d) \(\lambda x = 1.4\,,\,\lambda y = 0.8\). From these Figs. 8 and 9, we clearly see the quality of reconstruction of the images reconstructed by the different types of fractional-order moments and that the reconstructed images are close to that of the original image with the increases of the orders of the fractional-order moments for the different fractional orders.

Fig. 8
figure 8

The reconstructed “Lena” images using the proposed FrOJMs and the fractional-order orthogonal moments [21, 40, 41] for different orders of moments \(n,m = 20, \, 60, \, 100, \, 500, \, 1000\)

Full size image
Fig. 9
figure 9

The reconstructed “IRM” medical images using the proposed FrOJMs and the fractional-order orthogonal moments [21, 40, 41] for different orders of moments \(n,m = 20, \, 60, \, 100, \, 500, \, 1000\)

Full size image

5.2 Effect of fractional parameters \(\lambda\) and \((\alpha ,\,\beta )\) on the extraction of image characteristics

In recent years, local feature extraction or ROI detection has presented new challenges for the existing orthogonal moments. The existing image moments, especially most of the orthogonal moments, extract only the global features, and cannot describe the local features. In this experiment, we will test the capacity of the proposed FrOJMs for ROI-feature extraction of image while adjusting the parameters \(\lambda \,,\,\alpha \,,\,\beta\) and study the influence these parameters on quality of the image reconstruction.

5.3 Effect of fractional-order parameter \(\lambda\)

In this subsection, we discuss the effect of the fractional parameters \(\lambda x{\text{ and }}\lambda y\) to extract the region of interest from the “Checkerboard” image during its reconstruction using fractional-order Jacobi moments. Knowing that, the region of interest can be shifted to different positions, for \(\lambda_{\,x} \prec 1\) the region shifted to the left and for \(\lambda_{\,x} \succ 1\) region shifted to the right, with respect to the x-axis. The region is moved up for \(\lambda_{\,y} \prec 1\) and down for \(\lambda_{\,y} \succ 1\), along the y-axis.

Figure 10 shows the result of reconstruction of the “Checkerboard” image using FrOJMs for different orders and for different values \(\lambda x\) and \(\lambda y\). This figure shows that the region of interest at the top left, bottom left, top right and bottom right are reconstructed by FrOJMs for {\(\lambda_{\,x} = 5\,,\,\lambda_{\,y} = 5\)}, {\(\,\lambda_{\,x} = 5\,,\,\lambda_{\,y} = 15\)}, {\(\,\lambda_{\,x} = 15\,\,,\lambda_{\,y} = 5\)} et {\(\,\lambda_{\,x} = 15\,\,,\lambda_{\,y} = 15\)}, respectively.

Fig. 10
figure 10

Region of interest feature extraction of the “checkerboard” image by FrOJMs with different choices of the fractional parameters \(\lambda_{\,x} \,{\text{and}}\,\lambda_{\,y}\), for increasing moments orders

Full size image

5.4 Effect of Jacobi parameters \(\alpha\) and \(\beta\) on feature extraction

In this subsection, we discuss the extraction of image interest regions by adjusting the parameters \(\,\alpha \,\,{\text{and}}\,\,\beta\) of Jacobi polynomials. The test image used (Fig. 11) consists of four images of the Butterflies. We first calculate the Jacobi moments of the image using different parameters \((\alpha_{1} ,\beta_{1} ,\alpha_{2} ,\beta_{2} )\) then we will reconstruct this image using Jacobi's moments for different orders \((n,m)\) Table 1 summarizes the different cases of parameters \((\alpha_{1} ,\beta_{1} ,\alpha_{2} ,\beta_{2} )\) and the regions of interest for each case.

Fig. 11
figure 11

a Global features \(\alpha_{1} = \beta_{1} = \alpha_{2} = \beta_{2} = 0\,\), local features. The parameters used are b \(\alpha_{1} = 0,\beta_{1} = 160,\alpha_{2} = 0,\beta_{2} = 160\), c \(\alpha_{1} = 160,\beta_{1} = 0,\alpha_{2} = 0,\beta_{2} = 160\), d \(\alpha_{1} = 0,\beta_{1} = 160,\alpha_{2} = 160,\beta_{2} = 0\) and e \(\alpha_{1} = 160,\beta_{1} = 0,\alpha_{2} = 160,\beta_{2} = 0,\,\,P = 300\) for all cases

Full size image
Table 1 Conditions and rules for controlling the features extracted by the Jacobi moments
Full size table

The set of fractional-order Jacobi moments can extract the global features of an image if (A)\(\alpha_{1} = \beta_{1} = \alpha_{2} = \beta_{2} = 0\) shows the reconstructed image under this parameter setting. The set of fractional-order Jacobi moments can extract the local features of an image if \(\,\alpha_{1} ,\beta_{1} ,\alpha_{2} ,\beta_{2}\) are set to values other than that mentioned in the previous section and by following Table 1. We show in Fig. 11 a set of reconstructed images for different parameters \(\,\alpha_{1} ,\beta_{1} ,\alpha_{2} ,\beta_{2}\). The interesting point of Jacobi moments is that, by defining the parameters \(\alpha \,{\text{and}}\,\beta\), one can extract the desired part in an image according to the requested information. Considering the above analysis, by using similar parameters settings for FrOJMs, as depicted in Figs. 10 and 11, we can obtain global or local FrOJMs according to the desired ROI. Finally, it is important to conclude that the proposed FrOJMs could have many important practical applications in the field of medical image analysis like tumor localization in brain magnetic resonance images. However, a remarkable topic to be discussed, is how to theoretically choose the optimal Jacobi parameters values with regard to different pattern recognition applications.

5.5 Optimal parameter selection

As presented previously, the proposed FrOJMs with determined translation parameters \(\alpha\) and \(\beta\) requires the proper selection of the fractional-order parameter \(\lambda\), because this parameter mainly affects the quality of the local image feature extraction and the detailed descriptions of the reconstructed image. Therefore, optimizing the parameter \(\lambda\) is the key requirement of image reconstruction and classification by the proposed FrOJMs. In addition, it is important to present a systematic selection method of the parameters \(\lambda x\) and \(\lambda y\), which could lead to desirable results with regard to quality of the image reconstruction and the accuracy of image classification.

To study the influence of the parameters \(\lambda x\) and \(\lambda y\) on the performance of the proposed FrOJMs, we employed ten images selected from two well-known database, COIL-20 [52] and ETHZ-53Obj [53], respectively. The selected images are shown in Fig. 12. Referring to the different image reconstructions, an approach for selecting the parameter optimization method is proposed in this subsection. To elucidate how image size affects the parameters \(\lambda x\) and \(\lambda y\), we have considered two different image sizes: 128 × 128 and 64 × 64 pixels for database COIL-20 [52] and 512 × 512 and 256 × 256 pixels for database ETHZ-53Obj [53].To determine the optimal parameters \(\lambda x\) and \(\lambda y\) in combination, this subsection computes the performance of the proposed FrOJMs by the average of mean squared error (AMSE), which is defined as follows:

$$ {\text{AMSE}}\left( {\alpha ,\beta ,\lambda x,\lambda y} \right) = \frac{1}{{N_{I} }}\sum\limits_{k = 1}^{{N_{I} }} {{\text{MSE}}(f,\hat{f}_{k} )}. $$
(54)

Here, the number of testing images \(N_{I}\) was 10, \(f\) is an original image, and \(\hat{f}\) is the reconstruction of that image. The MSE is the mean squared error function, defined in Eq. (53). Figure 13a–d shows, respectively, the grid search (or exhaustive search) corresponding to the different image reconstructions. Note that the search space is restricted to \(0.2 \le \lambda x,\lambda y \le 5\) with step 0.2, and the sections with minimum values (darkest color) represent the neighborhood of the best combinations of \(\lambda x\) and \(\lambda y\). In addition, the regions marked with red color for each of the search grids, are corresponding to the lowest AMSE values and hold the optimal combinations of the fractional parameters \(\lambda x\) and \(\lambda y\).

Fig. 12
figure 12

Search space of the optimal fractional parameters {\(\lambda x,\lambda y\)}, based on AMSE values, with respect to: a 128 × 128 pixels , b 64 × 64 pixels for database COIL-20 [52], c 512 × 512 pixels and d 256 × 256 pixels for database ETHZ-53Obj [53]

Full size image

In order to examine the effect of the parameters \(\alpha\) and \(\beta\) on the proposed FrOJMs, we employed ten images selected from COIL-20 database [52], shown in Fig. 12a. Referring to the different image reconstructions, an approach for test the best combinations of the parameters \(\alpha\) and \(\beta\). The cutting order \(N_{I}\) can find the optimal parameters for fractional-order moments to different fractional parameters \(\lambda x\) and \(\lambda y\).

Fig. 13
figure 13

Tµeach database: a COIL-20 [52] and b ETHZ-53Obj [53]

Full size image

Figure 14a–d shows, respectively, the grid search results corresponding to the different image reconstructions. It is important to note that the search interval is restricted to \(1 \le \alpha ,\beta \le 50\) with step 1, and the regions with the minimum values (marked with the darkest blue color) present the neighborhood of the best optimum parameter combinations of \(\alpha\) and \(\beta\). Finally, we can conclude that this experiment could considerably help in selecting the optimal parameters (\(\alpha \,,\,\beta\) and \(\lambda x\,,\,\lambda y\)) values for quality of the image reconstruction. In addition, these methods may find a local, rather than a global optimum, which could highly influence the ROI-feature extraction performance for image representation. As a conclusion, this experiment will help choosing the appropriate parameters values for the following sections, for the tasks of recognition of the proposed invariants and image classification.

Fig. 14
figure 14

Graphs of search grid results of the proposed FrOJMs based on AMSE values according to different combinations of \(\alpha\) and \(\beta\): a \(\lambda x = 2\,,\,\lambda y = 2\), b \(\lambda x = 1\,,\,\lambda y = 1\), c \(\lambda x = 0.2\,,\,\lambda y = 2\) and d \(\lambda x = 0.2\,,\,\lambda y = 0.2\)

Full size image

5.6 Invariance to RST

This experiment aims to verify the rotation, scaling and translation in variance of the proposed FrJMIs. We used the test image obj12__0 of size 128 × 128 pixels, selected from COIL-20 [52] database and shown in Fig. 15. The test image is first translated by a vector varying from (− 10, − 10) to (10, 10) with a step (1,1), then scaled by factors ranging from 0.6 to 1.3 with an interval of 0.05 and finally rotated by a rotation angle varying between 0◦ and 360◦ with a step equal to 10. The invariant moments of Jacobi are computed for five cases of fractional parameters: (a) \(\lambda x = \lambda y = 0.8\), (b) \(\lambda x = \lambda y = 1\), (c) \(\lambda x = \lambda y = 1.4\) and (d) \(\lambda x = 0.8\,,\,\lambda y = 1.4\). And as a comparison criterion, the relative error between the FrJMIs coefficients, up to the order \(\left( {n,m = 3} \right)\), of the original and transformed images is used. The latter is given by the following formula:

$$ RE\left( {f,f^{d} } \right) = \frac{{\left\| {FrJMI(f) - FrJMI(f^{d} )} \right\|}}{{\left\| {FrJMI(f)} \right\|}} $$
(55)
Fig. 15
figure 15

obj12__0 [52] image of size 128 × 128 pixels

Full size image

where || ||, \(f\) et \(f^{d}\) and, respectively, designate the Euclidean norm, the original images and the deformed images. It should be emphasized that a very small relative error leads to a good invariance.

The corresponding results of invariance to scale rotation and translation are illustrated, respectively, in Fig. 16a, b and c. These results ensure the high accuracy and the invariances of the proposed method FrJMIs with respect to rotation, scaling and translation. Generally, the results show that the relative error is very small and approaches zero (\(10^{ - 12}\)) for the three transformations (RST), and ensure the superiority of these proposed moments FrJMIs, over the existing fractional-order method FrLMIs [40], FrCMIs [41] and FrGegMIs [21] for grayscale images.

Fig. 16
figure 16

The relative error values of the grayscale images calculated for scaling invariance using the proposed FrJMIs and the recent fractional-order moments [21, 40, 41]

Full size image

5.7 Noise sensitivity

Three experiments were performed to assess the noise sensitivity of FrOJMs. Different levels of the noise, white Gaussian, speckle and “salt & peppers,” are added to the object obj12__0 [52]. First, affected by salt-and-pepper noise with a varying density from 0 to 5% with step 0.25%. Second, distorted by Gaussian noise with zero mean and standard deviation varying from 0 to 0.5 with step 0.05. Third, contaminated by speckle noise varying from 0 to 1 with step 0.05. Figure 17 shows the standard and contaminated images. Relative error values are computed using the proposed FrOJMs, four parameterization FrOJMs are considered in this experiment: (a) \(\lambda x = \lambda y = 0.8\), (b) \(\lambda x = \lambda y = 1,\) (c) \(\lambda x = \lambda y = 1.4\), (d) \(\lambda x = 0.8\,,\,\lambda y = 1.4\) and the orthogonal moments [21, 40, 41] for contaminated images and displayed in Fig. 18a, b, c.

Fig. 17
figure 17

Noisy grayscale image of obj12__0 [52] by “Salt & Peppers” (1% until 5%), “Gaussian” (mean = 0 and variance = 0.1% until variance = 0.5%) and “Speckle” (0.2% until 1%)

Full size image
Fig. 18
figure 18

c-scale images of obj12__0 [52] for FrOJMs and the recent fractional-order methods [21, 40, 41]: (a) salt-and-Pepper noise, (b) Gaussian noise and (c) Speckle noise

Full size image

The values of the relative errors are clearly seen to increase with the increase in the noise densities but they remain very low (\(10^{ - 10}\)) for all the fractional-order. FrOJMs are less sensitive to noise than the existing fractional-order moments, FrLMs [40], FrCMs [41] and FrGegMs [21]. Finally, these important results concerning the invariance of FrJMIs to geometric transformations and noise encourage us to use these as a characteristic descriptor for object recognition and images classification.

5.8 Image recognition using FrJMIs

The experimental study of the invariance to the geometric transformations, rotation, scaling and translation are attractive characteristics required by pattern recognition and computer vision applications. In this subsection, where three well-known databases are adopted: MPEG-7 [54], COIL-20 [52] and ETHZ-53Obj [53]. These grayscale images are resized to the unified size 128 × 128. Basically, this experiment is conducted on three testing sets, which have been created by selecting 20 images from the original databases. Each selected image will be affected by different transformations (8 translations + 8 scale + 8 rotations + 8 mixed transformations), in order to generate 640 objects per base. In addition, to illustrate the noise robustness of the proposed invariant descriptors, we will contaminate the selected images of each base by the noise salt and pepper with densities {1%, 2%, 3%, 4%, 5%}, for create five noisy test sets. In fact, the feature vector is constructed by fractional-order Jacobi moment invariants up to the third order. We used K-NN (K-Nearest Neighbors with k = 1) as a classifier with the fivefold cross-validation technique. Tables 2, 3 and 4, respectively, present the comparison results in terms of object recognition accuracy for the three bases between the proposed FrJMIs invariant moments and the classical geometric momentary invariants (GMIs) [49], the invariants fractional-order moments of Legendre (FrLMI) [40], Chebyshev (FrCMIs) [41], Gegenbauer (FrGegMIs) [21] and Gaussian–Hermite moments invariants GHMIs [42]. Finally, it is important to note that we used five fractional-order parameters when calculating the FrJMIs: (a) \(\lambda x = \lambda y = 0.8\), (b) \(\lambda x = \lambda y = 1\), (c) \(\lambda x = \lambda y = 1.4\) and (d) \(\lambda x = 0.8\,,\,\lambda y = 1.4\).

Table 2 Comparative analysis of object recognition accuracy (%) on MPEG-7 [54] database, by using FrJMIs, FrLMIs, FrCMIs, FrGegMIs, GHMIs and GMIs, with \(\lambda = 1.4\)
Full size table
Table 3 Comparative analysis of object recognition accuracy (%) on Columbia COIL-20 [52] database, by using FrJMIs, FrLMIs, FrCMIs, FrGegMIs, GHMIs and GMIs, with \(\lambda = 1.4\)
Full size table
Table 4 Comparative analysis of object recognition accuracy (%) on ETHZ-53Obj [53] database, by using FrJMIs, FrLMIs, FrCMIs, FrGegMIs, GHMIs and GMIs, with \(\lambda = 1.4\)
Full size table

The obtained results clearly show that the proposed FrJMIs moments outperform the exiting method [21, 40, 41] in terms of recognition rates. As a follow-up, the FrJMIs have better recognition performance for the three databases for (e) with (\(\lambda x = 0.8\,,\,\lambda y = 1.4\)). We can conclude that the newly introduced fractional-order invariants could be extremely useful for representing the characteristics of objects for pattern recognition and image classification.

5.9 Execution times

In this subsection, we aim to evaluate the computational efficiency of the proposed FrOJMs and FrJMIs in comparison with the existing fractional-order moment invariants. Experiments are performed to quantitatively estimate the computational time of the proposed FrOJMs and FrJMIs. In first experiment, we will evaluate the computational performance of the proposed fractional-order moments. These experiments are performed using three well-known datasets of grayscale images, MPEG-7 [54], COIL-20 [52] and ETHZ-53Obj [53], respectively. These datasets have different grayscale image’ sizes and numbers. Few images are randomly selected from these datasets and displayed in Fig. 19.

Fig. 19
figure 19

The selected images from each database: a MPEG-7 [54], b COIL-20 [52] and c ETHZ-53Obj [53]

Full size image

Figure 20 shows the elapsed CPU times in seconds for the moment’s computation of these grayscale images, by using the proposed method FrOJMs and the recent fractional-order methods [21, 40, 41], for an increasing maximum moments order from 0 to 60 with fixed increment 10. According to the results presented in Fig. 20, one can observe that the computation time taken by the proposed method is much faster than the existing fractional moments [21, 40, 41].

Fig. 20
figure 20

The average CPU times for computing the proposed FrOJMs and the existing fractional moments [21, 40, 41]

Full size image

In second experiment, we aim to evaluate the computational efficiency of the proposed FrJMIs in comparison with the existing fractional-order moment invariants. Therefore, this current experiment is conducted on the three well-known datasets of grayscale images, MPEG-7 [54], COIL-20 [52] and ETHZ-53Obj [53], respectively, where we record the elapsed CPU times for the generation of moment invariants with an increasing order from 0 to 60. The process of computing moments is repeated 10 times for each method and the average CPU times are computed and summarized in Tables 5, 6 and 7. The obtained results clearly show that the proposed FrJMIs are very fast and much faster than the FrLMIs [40], FrCMIs [41] and FrGegMIs [21].

Table 5 CPU times in seconds for MPEG-7 [54] grayscale images of size (256 × 256), with \(\lambda = 1.4\)
Full size table
Table 6 CPU times in seconds for COIL-20 [52] grayscale images of size (128 × 128), with \(\lambda = 1.4\)
Full size table
Table 7 CPU times in seconds for ETHZ-53Obj [53] grayscale images of size (512 × 512), with \(\lambda = 1.4\)
Full size table

6 Conclusion

In this paper, we have introduced a new set of fractional-order orthogonal Jacobi moments for the global and local representation of grayscale images which significantly improve their image reconstruction capabilities, these new moments are robust against the well-known kinds of noise. We also constructed a new series of fractional-order invariant moments to RST geometric transformations based on fractional-order Jacobi polynomials. New fast and accurate algorithm to compute the fractional-order moment invariants which accelerating the computation time and increase their pattern recognition capabilities. In addition, we proposed a new method for extracting adaptive local image characteristics by adjusting the fractional parameters of the proposed invariant moments. What is more, we have presented a systematic parameter selection method for choosing the appropriate parameter values for the FrOJMs, with respect to pattern recognition applications, by using the grid search approach. The experimental results showed the capacity of the proposed moments for the reconstruction and classification tasks of the grayscale images compared to the existing fractional-order moments. Finally, these fractional-order moments are very fast and computationally inexpensive which increase its applicability in wide range of real-time applications. In our future work, we will focus on exploring other types of moments and for other applications.