Solving Volterra’s population growth model of arbitrary order using the generalized fractional order of the Chebyshev functions

Abstract

Volterra’s model for population growth in a closed system includes an integral term to indicate accumulated toxicity in addition to the usual terms of the logistic equation, that occurs in ecology. In this paper, a new numerical approximation is introduced for solving this model of arbitrary (integer or fractional) order. The proposed numerical approach is based on the generalized fractional order Chebyshev orthogonal functions of the first kind and the collocation method. Accordingly, we employ a collocation approach, by computing through Volterra’s population model in the integro-differential form. This method reduces the solution of a problem to the solution of a nonlinear system of algebraic equations. To illustrate the reliability of this method, we compare the numerical results of the present method with some well-known results in order to show that the new method is efficient and applicable.

1 Introduction

In this section, Spectral methods and some basic definitions and theorems which are useful for our method have been introduced.

1.1 Spectral methods

Spectral methods have been developed rapidly in the past two decades. They have been successfully applied to numerical simulations in many fields, such as heat conduction, fluid dynamics, quantum mechanics etc. These methods are powerful tools to solve differential equations. The key components of their formulation are the trial functions and the test functions. The trial functions, which are the linear combinations of suitable trial basis functions, are used to provide an approximate representation of the solution. The test functions are used to ensure that the differential equation and perhaps some boundary conditions are satisfied as closely as possible by the truncated series expansion. This is achieved by minimizing the residual function that is produced by using the truncated expansion instead of the exact solution with respect to a suitable norm [1–10].

1.2 Basical definitions

In this section some basic definitions and theorems which are useful for our method have been introduced [11].

Definition 1

For any real function f(t), $t>0$, if there exists a real number $p>\mu$, such that $f(t)=t^p f_1(t)$, where $f_1(t) \in C(0,\infty )$, is said to be in space $C_\mu$, $\mu \in \mathfrak {R}$, and it is in the space $C_\mu ^n$ if and only if $f^n \in C_\mu ,~n \in N$.

Definition 2

The fractional derivative of f(t) in the Caputo sense by the Riemann–Liouville fractional integral operator of order $\alpha >0$ is defined as [12, 13]:

$$\begin{aligned} D^\alpha f(t)=\frac{1}{\Gamma (m-\alpha )} \int _0^t (t-s)^{m-\alpha -1} D^mf(s)ds,\quad \alpha >0, \end{aligned}$$

for $m-1<\alpha \le m,~ m \in N,~t>0$, m is the smallest integer greater than $\alpha$, and $f\in C_{-1}^m$.

Some properties of the operator $D^{\alpha }$ are as follows. For $f\in C_\mu$, $\mu \ge -1$, $\alpha , \beta \ge 0$, $\gamma \ge -1, N_0=\{0,1,2,\cdots \}$ and constant C:

$$\begin{aligned}&(i)~ D^\alpha C=0, \nonumber \\&(ii)~ D^\alpha D^\beta f(t)=D^{\alpha +\beta }f(t),\end{aligned}$$

(1)

$$\begin{aligned}&(iii)~ D^\alpha t^\gamma =\left\{ \begin{array}{l} {0~~~~~~~~~~~~~~~~~~~\qquad \quad \gamma \in N_0~ and ~ \gamma <\lceil \alpha \rceil ,} \\ {}\\ {\frac{\Gamma (\gamma +1)}{\Gamma (\gamma -\alpha +1)}t^{\gamma -\alpha },~\quad \gamma \in N_0~ and ~ \gamma \ge \lceil \alpha \rceil ~or~\gamma \notin N~ and ~ \gamma >\lfloor \alpha \rfloor .}\end{array}\right. \nonumber \\\end{aligned}$$

(2)

$$\begin{aligned}&(iv)~ D^\alpha ( \sum _{i=1}^n c_i f_i (t) ) = \sum _{i=1}^n c_i D^\alpha f_i (t),\quad where \quad c_i \in R. \end{aligned}$$

(3)

Definition 3

Suppose that $f, g \in C[0,\eta ]$ and w(t) is a weight function, then

$$\begin{aligned} \parallel f(t)\parallel _w^2= & {} \int _0^\eta f^2(t)w(t)dt,\nonumber \\ \langle f(t),g(t)\rangle _w= & {} \int _0^\eta f(t)g(t)w(t)dt.\nonumber \end{aligned}$$

Theorem 1

(Generalized Taylor’s formula) Suppose that $f(t) \in C[0,\eta ]$ and $D^{k \alpha }f(t) \in C[0,\eta ]$, where $k=0,1,\ldots ,m$, $0 < \alpha \le 1$ and $\eta >0$. Then we have

$$\begin{aligned} f(t) = \sum _{i=0}^{m-1} \frac{t^{i\alpha }}{\Gamma (i \alpha +1)}D^{i \alpha }f(0^+)+\frac{t^{m\alpha }}{\Gamma (m \alpha +1)}D^{m \alpha }f(\xi ), \end{aligned}$$

(4)

with $0<\xi \le t,~ \forall t\in [0,\eta ]$. And thus

$$\begin{aligned} | f(t) - \sum _{i=0}^{m-1} \frac{t^{i\alpha }}{\Gamma (i \alpha +1)}D^{i \alpha }f(0^+) | \le M_\alpha \frac{t^{m\alpha }}{\Gamma (m \alpha +1)}, \end{aligned}$$

(5)

where $M_\alpha \ge |D^{m \alpha }f(\xi )|$.

Proof

See Ref. [14].

In case of $\alpha =1$, the generalized Taylor’s formula (4) reduces to the classical Taylors formula. $\square$

Theorem 2

Suppose that $\{P_i(t)\}$ be a sequence of orthogonal polynomials, w(t) is weight function for $\{P_i(t)\}$, and q(t) is a polynomial of degree at most $n-1$, then for $p_n(t) \in \{P_i(t)\}$ we have: $\langle p_n(t),q(t)\rangle _w=0$.

Proof

See the Section 2.3 in Ref. [15].

The organization of paper is expressed as follows: in Sect. 2, we express the mathematical Preliminaries on Volterra’s population model of arbitrary (integer or fractional) order. In Sect. 3, we obtain the GFCFs and their properties. In Sect. 4, the proposed method is applied to the Volterra’s population model of arbitrary order. Results and discussion of the proposed method is shown in Sect. 5 and a comparison is made with the approximate solutions that were reported in other published works in the literature. Finally, we give a brief conclusion in the last section. $\square$

2 Mathematical preliminaries on Volterra’s population model

In this section, the mathematical preliminaries on Volterra’s population model of arbitrary (integer or fractional) order have been introduced.

2.1 Volterra’s population model of integer order

Attempts to explain the balance of nature through mathematics began to appear around the turn of the century. A simple set of differential equations to describe malaria epidemics was proposed by Ross [16]. Martini improved these equations by allowing for the immunity of individuals who had recovered from infection [17]. A further refinement, the incubation lag, was introduced by Lotka and Sharp [18]. In 1925, Lotka [19] published his Elements of Physical Biology. In this work, the interaction between two species is accounted for by a system of quadratic differential equations [19]

$$\begin{aligned} \frac{dp_1(t)}{dt}=(\varepsilon _1+\gamma _1p_2(t))p_1(t), \end{aligned}$$

(6)

$$\begin{aligned} \frac{dp_2(t)}{dt}=(\varepsilon _2+\gamma _2p_1(t))p_2(t), \end{aligned}$$

(7)

where the $\varepsilon$ are the coefficients of self-increase, the $\gamma$ account for the interactions, and the $p_1(t),~p_2(t)$ are population sizes.

This system can be represented by the integro-differential equation [20]

$$\begin{aligned} \frac{dp(t)}{dt}= & {} \left( \varepsilon -\lambda p(t) -\mu \int _0^tp(\tau )d\tau \right) p(t), \end{aligned}$$

(8)

$$\begin{aligned} p(0)= & {} p_0, \end{aligned}$$

(9)

where $\mu > 0$ is the toxicity coefficient and $p_0$ is the initial population.

This model includes the well-known terms of a logistic equation, and, in addition, it includes an integral term $\mu p(t) \int _0^t p(\tau )d\tau$ that characterizes the accumulated toxicity produced since time zero [21, 22]. A dimensionalization is under taken as follows:

$$\begin{aligned} t=\frac{t \mu }{\lambda },\quad u=\frac{p \mu }{\varepsilon }, \end{aligned}$$

to obtain the non-dimensional problem

$$\begin{aligned} \kappa \frac{du}{dt}= & {} u-u^2-u \int _0^t u(x)dx,\end{aligned}$$

(10)

$$\begin{aligned} u(0)= & {} u_0, \end{aligned}$$

(11)

where u(t) is the scaled population of the identical individuals at time t and $\kappa =\frac{\mu }{ \varepsilon \lambda }$ is a prescribed non-dimensional parameter. The equilibrium points are the trivial solution $u(t) = 0$ and the analytical solution of Eq. (10) [21]

$$\begin{aligned} u(t)=u_0exp\left( \frac{1}{\kappa } \int _0^t \left[ 1-u(\tau )-\int _0^{\tau }u(x)dx \right] d\tau \right) , \end{aligned}$$

shows that $u(t) > 0$ for all t if $u_0 > 0$.

Although a closed form solution has been achieved in [21, 22], it was formally shown that the closed form solution cannot lead to any insight into the behavior of the population evolution [23]. Therefore, the solution of Eq. (10) is one of considerable problems. Some researchers have worked on this problem; for example, Scudo [20] by the successive approximation method was offered. TeBeest [21] by three numerical algorithms, namely the Euler method, the modified Euler method and a fourth order Rung-Kutta method, have been used for Eq. (10). Recently, some researchers employed spectral methods to solve Volterra’s population model for example [24–29]; also, some researchers have used the analytical methods for approximating this problem, for example [30–33].

2.2 Volterra’s population model of fractional order

Volterra’s population growth model of fractional order has been introduced as follows

$$\begin{aligned} \kappa \frac{d^\alpha u}{dt^\alpha }= & {} u-u^2-u \int _0^t u(x)dx,\end{aligned}$$

(12)

$$\begin{aligned} u(0)= & {} u_0, \end{aligned}$$

(13)

where $0<\alpha \le 1$.

Some researchers have worked on this problem; for example, Erturk et al. [34] by the differential transform method and Pade approximates, Momani et al. [35] by Adomian decomposition method and Pade approximates, Yuzbasi [36] and Parand et al. [37] by the Bessel collocation method, Maleki et al. [38] by multi-domain pseudospectral method, and Khan et al. [39] and Ghasemi et al. [40] by homotopy method and Pade approximates.

In this paper, we attempt to introduce a new method, based on the generalized fractional order of the Chebyshev orthogonal functions (GFCFs) of the first kind for solving the Volterra’s model for population growth of arbitrary order in a closed system.

3 Generalized fractional order of the Chebyshev functions

In this section, first, the generalized fractional order of the Chebyshev functions (GFCF) have been defined, and then some properties and convergence of them for our method have been introduced.

3.1 The Chebyshev functions

The Chebyshev polynomials have been used in numerical analysis, frequently, including polynomial approximation, Gauss-quadrature integration, integral and differential equations and spectral methods. Chebyshev polynomials have many properties, for example orthogonal, recursive, simple real roots, complete for the space of polynomials. For these reasons, many researchers have employed these polynomials in their research [41–46].

The number of researchers using some transformations extended Chebyshev polynomials to semi-infinite or infinite domain, for example by using $x=\frac{t-L}{t+L}, L >0$ the rational functions introduced [47–52].

In proposed work, by transformation $z=1-2(\frac{t}{\eta })^\alpha$, $\alpha > 0$ on the Chebyshev polynomials of the first kind, the fractional order of the Chebyshev orthogonal functions in interval $[0,\eta ]$ have been introduced, that they can use to solve the Volterra’s population model of arbitrary (integer or fractional) order.

3.2 The GFCFs definition

The efficient methods have been used by many researchers to solve the differential equations (DE) is based on series expansion of the form $\sum _{i=0}^n c_i t^{i}$, such as Adomian decomposition method [53] and Homotopy perturbation method [54]. But exact solution of many DEs can’t be estimated by polynomials basis. Therefore we have defined a new basis for Spectral methods to solve them as follows:

$$\begin{aligned} \Phi _n(t)=\sum _{i=0}^n c_i t^{i\alpha }. \end{aligned}$$

Now by transformation $z=1-2(\frac{t}{\eta })^\alpha$, $\alpha ,\eta > 0$ on classical Chebyshev polynomials of the first kind, we defined the GFCFs in interval $[0,\eta ]$, that be denoted by $_\eta FT_n^\alpha (t)=T_n(1-2(\frac{t}{\eta })^\alpha )$.

By this definition the singular Sturm-Liouville differential equation of classical Chebyshev polynomials become:

$$\begin{aligned} \frac{\sqrt{\eta ^{\alpha }-t^\alpha }}{t^{\frac{\alpha }{2}-1}}\frac{d}{dt}\left[ \frac{\sqrt{\eta ^{\alpha }-t^\alpha }}{t^{\frac{\alpha }{2}-1}}\frac{d}{dt}\ _\eta FT_n^\alpha (t)\right] +n^2\alpha ^2\ _\eta FT_n^\alpha (t)=0,\quad t\in [0,\eta ]. \end{aligned}$$

(14)

The $_\eta FT_n^\alpha (t)$ can be obtained using recursive relation as follows ($n=1,2,\ldots$):

$$\begin{aligned}&_\eta FT_0^\alpha (t)=1,\quad _\eta FT_1^\alpha (t)=1-2(\frac{t}{\eta })^\alpha ,\\&_\eta FT_{n+1}^\alpha (t)=\left( 2-4\left( \frac{t}{\eta }\right) ^\alpha \right) ~_\eta FT_n^\alpha (t)-~_\eta FT_{n-1}^\alpha (t). \end{aligned}$$

The analytical form of $_\eta FT_n^\alpha (t)$ of degree $n\alpha$ given by

$$\begin{aligned} _\eta FT_n^\alpha (t)= & {} \sum _{k=0}^n(-1)^k\frac{n2^{2k}(n+k-1)!}{(n-k)!(2k)!} \left( \frac{t}{\eta }\right) ^{\alpha k} \nonumber \\= & {} \sum _{k=0}^n \beta _{n,k,\eta ,\alpha }.t^{\alpha k},\quad t\in [0,\eta ], \end{aligned}$$

(15)

where

$$\begin{aligned} \beta _{n,k,\eta ,\alpha }=(-1)^k \frac{n2^{2k}(n+k-1)!}{(n-k)!(2k)! \eta ^{\alpha k}}\quad and \quad \beta _{0,k,\eta ,\alpha }=1. \end{aligned}$$

Note that $_\eta FT_n^\alpha (0)=1$ and $_\eta FT_n^\alpha (\eta )=(-1)^n$.

The GFCFs are orthogonal with respect to the weight function $w(t)=\frac{t^{\frac{\alpha }{2}-1}}{\sqrt{\eta ^\alpha -t^\alpha }}$ in the interval $[0,\eta ]$:

$$\begin{aligned} \int _{0}^{\eta }~_\eta FT_n^\alpha (t)~_\eta FT_m^\alpha (t)w(t)dt=\frac{\pi }{2\alpha }c_n\delta _{mn}. \end{aligned}$$

(16)

where $\delta _{mn}$ is Kronecker delta, $c_0=2$, and $c_n=1$ for $n \ge 1$. Equation (16) is provable using properties of orthogonality in the Chebyshev polynomials.

The pictures in Fig. 1 shown graphs of GFCFs for various values of n and $\alpha$ and $\eta =5$.

Fig. 1

Graphs of the GFCFs for various values of n and $\alpha$. a Graph of the GFCFs with $\alpha = 0.25$ and various values of n. b Graph of the GFCFs with $n = 5$ and various values of $\alpha$

3.3 Approximation of functions

Any function y(t), $t\in [0,\eta ]$, can be expanded as the follows:

$$\begin{aligned} y(t)=\sum _{n=0}^\infty a_n ~_\eta FT_n^\alpha (t), \end{aligned}$$

where the coefficients $a_n$ obtain by inner product:

$$\begin{aligned} \left\langle y(t),\quad _\eta FT_n^\alpha (t) \right\rangle _w = \left\langle \sum _{n=0}^\infty a_n ~_\eta FT_n^\alpha (t),~_\eta FT_n^\alpha (t) \right\rangle _w \end{aligned}$$

and using property of orthogonality in the GFCFs:

$$\begin{aligned} a_n=\frac{2\alpha }{\pi c_n}\int _{0}^{\eta }~_\eta FT_n^\alpha (t)y(t)w(t)dt,\quad n=0,1,2,\ldots . \end{aligned}$$

In practice, we have to use first m-terms GFCFs and approximate y(t):

$$\begin{aligned} y(t)\simeq y_m(t)=\sum _{n=0}^{m-1} a_n ~_\eta FT_n^\alpha (t)=A^T\Phi (t), \end{aligned}$$

(17)

with

$$\begin{aligned} A= & {} \left[ a_0,a_1,\ldots ,a_{m-1}\right] ^T, \end{aligned}$$

(18)

$$\begin{aligned} \Phi (t)= & {} \left[ _\eta FT_0^\alpha (t),~_\eta FT_1^\alpha (t),\ldots ,~_\eta FT_{m-1}^\alpha (t)\right] ^T. \end{aligned}$$

(19)

3.4 Convergence of method

The following theorem shows that by increasing m, the approximation solution $f_m(t)$ is convergent to f(t) exponentially.

Theorem 3

Suppose that $D^{k\alpha }f(t)\in C[0,\eta ]$ for $k=0,1,...,m,$ and $_\eta F_m^\alpha$ is the subspace generated by $\{_\eta FT_0^\alpha (t),_\eta FT_1^\alpha (t),\ldots ,_\eta FT_{m-1}^\alpha (t)\}$. If $f_m=A^T\Phi$ (in Eq. (17)) is the best approximation to f(t) from $_\eta F_m^\alpha$, then the error bound is presented as follows

$$\begin{aligned} \parallel f(t)-f_m(t)\parallel _w \,\le \, \frac{ \eta ^{m\alpha } M_\alpha }{2^m\Gamma (m\alpha +1)}\sqrt{\frac{\pi }{\alpha .m!}}, \end{aligned}$$

where $M_\alpha \ge |D^{m\alpha }f(t)|, ~~t\in [0,\eta ].$

Proof

By theorem 1, $y= \sum _{i=0}^{m-1} \frac{t^{i\alpha }}{\Gamma (i \alpha +1)}D^{i \alpha }f(0^+)$ and

$$\begin{aligned} | f(t)-y(t) | \le M_\alpha \frac{ t^{m\alpha }}{\Gamma (m\alpha +1)}, \end{aligned}$$

since $A^T\Phi (t)$ is the best approximation to f(t) from $_\eta F_m^\alpha$, and $y\in ~_\eta F_m^\alpha$, one has

$$\begin{aligned} \parallel f(t)-f_m(t)\parallel _w^2\le & {} \parallel f(t)-y(t)\parallel _w^2 \nonumber \\\le & {} \frac{M_\alpha ^2}{\Gamma (m\alpha +1)^2}\int _0^\eta \frac{t^{\frac{\alpha }{2}+2m\alpha -1}}{\sqrt{\eta ^\alpha -t^\alpha }}dt \nonumber \\= & {} \frac{M_\alpha ^2}{\Gamma (m\alpha +1)^2}\frac{\eta ^{2m\alpha }\pi }{\alpha 2^{2m}m!}.\nonumber \end{aligned}$$

Now by taking the square roots, the theorem can be proved. $\square$

Theorem 4

The generalized fractional order of the Chebyshev function $_\eta FT_n^\alpha (t)$, has precisely n real zeros on interval $(0,\eta )$ in the form

$$\begin{aligned} t_k=\eta \left( \frac{1-\cos \left( \frac{(2k-1)\pi }{2n}\right) }{2}\right) ^\frac{1}{\alpha },\quad k=1,2,\ldots ,n. \end{aligned}$$

Moreover, $\frac{d}{dt} _\eta FT_n^\alpha (t)$ has precisely $n-1$ real zeros on interval $(0,\eta )$ in the following points:

$$\begin{aligned} t'_k=\eta \left( \frac{1-\cos (\frac{k\pi }{n})}{2}\right) ^\frac{1}{\alpha },\quad k=1,2,\ldots ,n-1. \end{aligned}$$

Proof

The Chebyshev polynomial $T_n(x)$ has n real zeros [55, 56]:

$$\begin{aligned} x_k=\cos \left( \frac{(2k-1)\pi }{2n}\right) ,\quad k=1,2,\ldots ,n, \end{aligned}$$

therefore $T_n(x)$ can be written as

$$\begin{aligned} T_n(x)=(x-x_1)(x-x_2)\cdots (x-x_n). \end{aligned}$$

Using transformation $x=1-2(\frac{t}{\eta })^\alpha$ yields to

$$\begin{aligned} FT_n^\alpha (t)= & {} \left( \left( 1-2\left( \frac{t}{\eta }\right) ^\alpha \right) -x_1\right) \left( \left( 1-2\left( \frac{t}{\eta }\right) ^\alpha \right) -x_2\right) \cdots \\&\left( \left( 1-2\left( \frac{t}{\eta }\right) ^\alpha \right) -x_n\right) , \end{aligned}$$

so, the real zeros of $_\eta FT_n^\alpha (t)$ are $t_k=\eta (\frac{1-x_k}{2})^{\frac{1}{\alpha }}$.

Also, the real zeros of $\frac{d}{dt}T_n(t)$ occurs in the following points [55]:

$$\begin{aligned} x'_k=\cos \left( \frac{k\pi }{n}\right) ,\quad k=1,2,\ldots ,n-1. \end{aligned}$$

Same as in previous, the absolute extremes of $_\eta FT_n^\alpha (t)$ are $t'_k=\eta (\frac{1-x'_k}{2})^{\frac{1}{\alpha }}$. $\square$

3.5 The fractional derivative operational matrix of GFCFs

In the next theorem, we generalize the operational matrix of the Caputo fractional derivative of order $\alpha > 0$ for GFCFs, which can be expressed by:

$$\begin{aligned} D^\alpha \Phi (t)= D^{(\alpha )} \Phi (t). \end{aligned}$$

(20)

Theorem 5

Let $\Phi (t)$ be GFCFs vector in Eq. (19), and $D^{(\alpha )}$ is an $m\times m$ operational matrix of the Caputo fractional derivatives of order $\alpha > 0$, then:

$$\begin{aligned} D_{i,j}^{(\alpha )}=\left\{ \begin{array}{l}{\frac{2}{\sqrt{\pi }c_j}\sum _{k=1}^i \sum _{s=0}^j \beta _{i,k,\eta ,\alpha } \beta _{j,s,\eta ,\alpha }\frac{\Gamma (\alpha k+1)\Gamma \left( s+ k-\frac{1}{2}\right) \eta ^{\alpha (k+s-1)}}{\Gamma (\alpha k-\alpha +1)\Gamma (s+ k)},\quad i>j}\\ {} \\ {0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \qquad \qquad \quad otherwise} \end{array} \right. \end{aligned}$$

(21)

for $i,j=0,1,\ldots ,m-1.$

Proof

Using Eq. (20)

$$\begin{aligned} \left[ \begin{array}{ccccc} D_{0,0} &{} \cdots &{} D_{0,j} &{} \cdots &{} D_{0,m-1} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ D_{i,0} &{} \cdots &{} D_{i,j} &{} \cdots &{} D_{i,m-1} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ D_{m-1,0} &{} \cdots &{} D_{m-1,j} &{} \cdots &{} D_{m,m-1} \\ \end{array} \right] \left[ \begin{array}{c} \Phi _0 \\ \vdots \\ \Phi _j \\ \vdots \\ \Phi _{m-1} \\ \end{array} \right] = \left[ \begin{array}{c} D^\alpha \Phi _0 \\ \vdots \\ D^\alpha \Phi _i \\ \vdots \\ D^\alpha \Phi _{m-1} \\ \end{array} \right] . \end{aligned}$$

By orthogonality property of the GFCFs, and the Eqs. (2) and (15), for $i,j=0,1,\ldots ,m-1$:

$$\begin{aligned} D_{i,j}^{(\alpha )}=\frac{2\alpha }{\pi c_j} \int _0^\eta D^\alpha \left( _\eta FT_i^\alpha (t)\right) \left( _\eta FT_j^\alpha (t)\right) w(t)dt. \nonumber \end{aligned}$$

Since $D^\alpha FT_0^\alpha (t) =0$, therefore $D_{0,j}^{(\alpha )}= \int _0^\eta D^\alpha FT_0^\alpha (t) FT_j^\alpha (t) w(t)dt=0$. And if $i\le j$ then $deg(D^\alpha (_\eta FT_i^\alpha (t)))<deg( _\eta FT_j^\alpha (t))$, therefore by theorem 2, $D_{i,j}^{(\alpha )}=0$ for any $i\le j$. Now for $i>j$ we have:

$$\begin{aligned} D_{i,j}^{(\alpha )}= & {} \frac{2\alpha }{\pi c_j}\int _0^\eta \sum _{k=1}^i \beta _{i,k,\eta ,\alpha } \frac{\Gamma (\alpha k+1)t^{\alpha k -\alpha }}{\Gamma (\alpha k-\alpha +1)} \sum _{s=0}^j \beta _{j,s,\eta ,\alpha }t^{\alpha s}\frac{t^{\frac{\alpha }{2}-1}}{\sqrt{\eta ^\alpha -t^\alpha }}dt\nonumber \\= & {} \frac{2\alpha }{\pi c_j}\sum _{k=1}^i \sum _{s=0}^j \beta _{i,k,\eta ,\alpha }\beta _{j,s,\eta ,\alpha }\frac{\Gamma (\alpha k+1)}{\Gamma (\alpha k-\alpha +1)}\int _0^\eta \frac{t^{\alpha (k+s-\frac{1}{2})-1}}{\sqrt{\eta ^\alpha -t^\alpha }}dt.\nonumber \end{aligned}$$

Now, by integration of above equation, the theorem can be proves. $\square$

Remark

The fractional derivative operational matrix of GFCFs is an lower-triangular matrix and for $\alpha =1,~\eta =1$ is same as shifted Chebyshev polynomials [57].

Table 1 Values of $u_{max}$ by the present method and comparison with exact values

Table 2 Values of $u_{max}$ by present method and [23, 26, 27], comparison with exact values

4 Application of the method

In this section, we apply the GFCFs collocation method to solve the Volterra’s population model of arbitrary order.

• 1. Volterra’s population model of integer order: for satisfying the boundary condition, we satisfy condition (11) by multiplying the operator (17) by t and adding it to $u_0$ as follows:

  $$\begin{aligned} \widehat{y_m}(t)=u_0+t~y_m(t), \end{aligned}$$

  (22)

  where $y_m(t)$ is defined in Eq. (17). Now, $\widehat{y_m}(t) = u_0$ when t tends to zero, so that the condition (11) is satisfied. To apply the collocation method, we construct the residual function by substituting $\widehat{y_m}(t)$ in Eq. (22) for u(t) in the Volterra’s population model Eq. (10):

  $$\begin{aligned} Res(t)=\kappa \frac{d\widehat{y_m(t)}}{dt}-\widehat{y_m(t)}+\widehat{y_m(t)}^2+\widehat{y_m(t)} \int _0^t \widehat{y_m(x)}(x)dx. \end{aligned}$$

  (23)

  The equations for obtaining the coefficient $\{a_i\}_{i=0}^{m-1}$ arise from equalizing Res(t) to zero on m collocation points:

  $$\begin{aligned} Res(t_i) = 0,\quad i = 0, 1, \ldots , m-1. \end{aligned}$$

• 2. Volterra’s population model of fractional order: to apply the collocation method, we construct the residual function by substituting $y_m(t)=A^T\Phi (t)$ in Eq. (17) for u(t) in the Volterra’s population model of fractional order Eq. (12):

  $$\begin{aligned} Res(t)=\kappa A^T D^{(\alpha )}\Phi (t)-A^T\Phi (t) +(A^T\Phi (t))^2 +A^T\Phi (t) \int _0^t A^T\Phi (x)dx,\nonumber \\ \end{aligned}$$

  (24)

  where $D^{(\alpha )}$ is defined in Eq. (20). The equations for obtaining the coefficient $\{a_i\}_{i=0}^{m-1}$ arise from equalizing Res(t) to zero on $m-1$ collocation points:

  $$\begin{aligned} Res(t_i) = 0,\quad i = 1, 2, \ldots , m-1, \end{aligned}$$

  and the initial condition

  $$\begin{aligned} A^T\Phi (0)=u_0. \end{aligned}$$

  In this study, we used the roots of the GFCFs in the interval $[0, \eta ]$ (Theorem 4), as collocation points. By solving the obtained set of equations, we have the approximating function $\widehat{y_m}(t)$. And also consider that all of the computations have been done by Maple 18 on a laptop with CPU Core i7, Windows 8.1 64bit, and 8GB of RAM.

Table 3 Convergence of the method with $\kappa = 0.70,~\kappa = 0.50$ and $\alpha =0.25$ by $u_{max}$

Table 4 Convergence of the method with $\kappa = 0.2,~\kappa = 0.02$ and $\alpha =0.50$ by $u_{max}$

Table 5 Convergence of the method with $\kappa = 0.10,~\kappa = 0.04$ and $\alpha =0.25$ by $u_{max}$

Fig. 2

Graphs of Volterra’s population model for various values $\kappa$ by the present method. a Integer order. b Fractional order for $\alpha = 0.50$

4.1 Tau-Collocation algorithm

To obtain the Spectral coefficients $\{a_i\}_{i=0}^{m-1}$ in the Eq. (17) and approximate of $y_m(t)$, we define the Tau-Collocation algorithm as follows:

BEGIN

• 1. Construct series in the Eq. (17).

• 2. If operator of L is integer order then we calculate the function $\widehat{y_m}(t)$ by the Eq. (22), else we calculate the operational matrix $D^{(\alpha )}$ by the Eq. (20).

• 3. Construct the residual function as follows: if operator of L is integer order then we calculate Res(t) using the Eq. (23) else using the Eq. (24). Now we have m unknown $\{a_i\}_{i=0}^{m-1}$. To obtain these unknown coefficients, we need m equations.

• 4. Choose m points $t_i, i = 0, 1, \ldots ,m-1$ in the domain of the problem as collocation points and substituting them in Res(t), and using the boundary conditions, we construct a system which contains m nonlinearly independent equations.

• 5. Solve this system of equations by a suitable method (e.g. Newton’s method) to find the $\{a_i\}_{i=0}^{m-1}$.

END.

In step 1, according to the Eq. (17), the order of complexity is O(m). In step 2, if operator of L is integer order then the order of complexity is O(1) else is $O(m^4)$. In step 3, according to the Eqs. (23) and (24), the order of complexity is $O(m^4)$. The order of complexity in step 4 is O(m). The order of complexity in step 5 is dependent on the method of choice. it is worthwhile to note that it is common to solve a system of nonlinear equations, is applying the Newton’s method. We used the command “fsolve” in the software Maple to solve this system of nonlinear equations, that this software uses the Newton’s method. Thus, the order of complexity in the above algorithm is at least $O(m^4)$.

Fig. 3

The logarithm absolute error for various values m, to express convergence of the present method. a $\kappa =0.20$. b $\kappa =0.70$. a The logarithm absolute error $\kappa =0.20$. b The logarithm absolute error $\kappa =0.70$

Table 6 Values of $u_{max}$ by the present method for Volterra’s model of fractional order

Table 7 Values of obtained $y_m(t)$ from solving Volterra’s population model of fractional order by the present method with $\kappa =0.01$ and $m=7$

Table 8 Values of obtained $y_m(t)$ from solving Volterra’s population model of fractional order by the present method with $\kappa =0.10$ and $m=7$

Table 9 Values of obtained $y_m(t)$ from solving Volterra’s population model of fractional order by the present method with $\kappa =0.50$ and $m=10$

Table 10 Values of obtained $y_m(t)$ from solving Volterra’s population model of fractional order by the present method with $\kappa =2.50$ and $m=10$

5 Results and discussion

In this section, we consider the obtained results with the present method for solving Volterra’s population models.

5.1 Volterra’s population model of integer order

We solve Eq. (10) with $u_0=0.1$ and $\kappa =0.02,~0.04,~0.1,~0.2,0.4,0.5$ and 0.7.

We obtain the approximation function $\widehat{y_m}(t)$. Then, we evaluate the important values $u_{max}$, that obtained by TeBeest [21]:

$$\begin{aligned} u_{max}=1+\kappa ln \left( \frac{\kappa }{1+\kappa +u_0}\right) . \end{aligned}$$

(25)

Table 1 represents the obtained values $u_{max}$ of the GFCF collocation method and it compares with $u_{max}$ exact values. We can see the approximate solution is in a very good accuracy with the exact solution.

Wazwaz [23] has calculated an analytical approximation by using the Adomian decomposition method, and Parand et al. [26, 27] have calculated the numerical approximations by using radial basis functions and the modified Bessel functions, respectively. Table 2 represents the obtained values $u_{max}$ of GFCF collocation method and obtained values by [23, 26, 27] and compare them with each other. In Refs. [23, 26, 27] the values for $\kappa =0.40$ and 0.70 have not been calculated. We can see that the obtained values by the present method have very good accuracy.

Tables 3, 4 and 5 represents the obtained values of $u_{max}$ and the absolute errors for various values of m to express convergence of the present method.

Figure 2a shows the graphs of solutions of Volterra’s population model of integer order for various values of $\kappa$.

Figure 3 shows the logarithm absolute error for various values of m and $\kappa$ to express convergence of the present method.

5.2 Volterra’s population model of fractional order

This model is studied with two different approaches by researchers: analytical methods and numerical methods. Erturk et al. [34], Momani et al. [35], Khan et al. [39], and Ghasemi et al. [40] have used analytical methods to solve this model, and Yuzbasi [36], Parand et al. [37], and Maleki et al. [38] have used numerical methods to solve this model. Now we solve this model by the GFCFs collocation method, with $u_0 = 0.1$ and $\kappa = 0.01,0.10,0.20,0.50,0.90$ and 2.5.

Table 6 represents the obtained values $u_{max}$ of the GFCF collocation method with $\alpha =0.50$ and various values of $\kappa$.

Fig. 4

Graphs of fractional order for $\kappa =0.01,~m=7$ and various values $\alpha$. a The approximate solutions. b The logarithm residual error functions

Fig. 5

Graphs of fractional order for $\kappa =0.10,~m=7$ and various values $\alpha$. a The approximate solutions. b The logarithm residual error functions

Fig. 6

Graphs of fractional order for $\kappa =0.20,~m=7$ and various values $\alpha$. a The approximate solutions. b The logarithm residual error functions

Fig. 7

Graphs of fractional order for $\kappa =0.50,~m=10$ and various values $\alpha$. a The approximate solutions. b The logarithm residual error functions

Fig. 8

Graphs of fractional order for $\kappa =0.90,~m=10$ and various values $\alpha$. a The approximate solutions. b The logarithm residual error functions

Fig. 9

Graphs of fractional order for $\kappa =2.50,~m=10$ and various values $\alpha$. a The approximate solutions. b The logarithm residual error functions

Tables 7, 8, 9 and 10 represents the obtained values of $y_m(t)$ and the residual error for various values of $\alpha ,~\kappa$ and t.

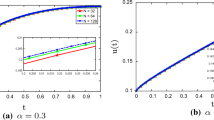
Figure 2b shows the graphs of solutions of Volterra’s population model of fractional order for $\alpha =0.50$ and various values of $\kappa$.

Figures 4, 5, 6, 7, 8 and 9 shows the graphs of solutions of Volterra’s population model of fractional order for various values of $\kappa$ and $\alpha$.

6 Conclusion

Attempts to explain the balance of nature through mathematics began to appear during the last two decades. Volterra’s model for population growth in a closed system includes an integral term to indicate the accumulated toxicity in addition to the usual terms of the logistic equation. This model has been considered by some mathematicians as mentioned before. The main goal of this paper was to introduce a new orthogonal basis, namely the generalized fractional order of the Chebyshev orthogonal functions (GFCFs) of the first kind to construct an approximation to the solution of Volterra’s population model of arbitrary order. For the first time, a fractional basis was used for solving an integro-differential equation, that it provided insight into an important issue. The present results show that the introduced basis for the collocation spectral method is efficient and applicable. Our results have better accuracy with lesser m, and the absolute error as compared to other results. A comparison was made of the exact solution, the numerical solutions of Parand et al. [26, 27], the analytical solution of Wazwaz [23] and the present method. It has been shown that the present work has provided an acceptable approach for solving Volterra’s population model of arbitrary order.