1 Introduction

In designing geotechnical constructions like tunnels, the rock tensile strength (TS) is a must to be determined accurately [1]. The literature consists of both direct and indirect approaches for this end. In case of the direct approach, researchers normally utilize the previously empirical equations suggested by others or gather some sample rock specimens to test them in laboratory, which is both costly and time-consuming [2,3,4]. On the other hand, the use of indirect approach has made it easier, faster, and cheaper through predicting the TS value by means of several rock index tests like the Schmidt hammer, density, point load, and p-wave velocity tests. The Brazilian tensile strength (BTS) which is the direct determination of TS in laboratory, was standardized by the international society for rock mechanics (ISRM) [5]. To predict the TS value, a large number of empirical relations can be found in the literature [6,7,8].

Kahraman et al. [9] attempted to find out the rock properties with the most significant effects on the percussive drills penetration rate. They made use of statistical analyses, e.g. regression analysis, to achieve their desired results for different rock types such as limestone, sandstone marl, metasandstone and dolomite. Their findings confirmed the significance of the following rock properties on the percussive drills penetration rate: the Schmidt hammer rebound number (Rn), p-wave velocity, density, the uniaxial compressive strength (UCS), point load strength, and BTS. They introduced various simple regressions for prediction of drilling penetration rate using BTS, density, p-wave velocity, UCS, elastic modulus, point load index, and Rn parameters. In another study, Mishra and Basu [10] conducted UCS, BTS, point load, and block punch tests on the three rock types (sandstone, granite and, schist) samples and then evaluated their results. For each rock type, they introduced empirical correlations between results of point load strength index (Is50) and BTS and UCS and separately between results of block punch test values and BTS and UCS. They evaluated performance prediction of their empirical equation with the use of coefficient of determination (R2) results.

Sheorey [11] confirmed a frequently-acknowledged statement claiming a correlation between BTS and UCS in rocks, and also maintained that the rock compressive strength is about ten times greater than the BTS values. He emphasized that the behaviours of the rocks are site-specific. Kahraman et al. [6], in another project, introduced several linear empirical relationships between UCS and indentation hardness index as independent variables and BTS as dependent variable in three rock groups of metamorphic, igneous, and sedimentary. The R2 ranges of 0.5–0.9 were proposed in their study which are acceptable for estimation of the BTS values. Heidari et al. [2] made a review of all methods previously proposed for point load tests and compared them in terms of their applicability to practical applications. They made use of three methods, i.e. diametric, axial, and irregular in the process of Is50 prediction. A comprehensive comparison was made on the obtained results and a number of equations were developed in a way to practically and economically estimate the BTS values. In terms of R2, they concluded that the irregular method was the best one in preliminary prediction of the BTS values. On the other hand, Perras and Diederichs [12] considered the rocks TS aiming at finding a relationship between BTS and direct TS. They reviewed the methods that had been already proposed for the measurement (BTS, direct TS, and alternative methods) and estimation of the rock TS. Their findings rejected the laboratory testing due to its difficulty in delivering an accurate prediction of the rock TS. In another research, Armaghani et al. [13] carried out a number of laboratory tests on a total of 87 granite rock samples in order to estimate the BTS value. However, as they stated in their paper, due to high expense and time required for such kind of tests, they finally made use of only simple and multiple regressions to achieve their above-noted objective. Their final results showed the superiority of the multiple regression models over the simple regression ones in terms of estimating the BTS value with a high precision. In another empirical work, Nazir et al. [8] conducted BTS and UCS tests on 20 limestone samples and made a correlation between them. They showed that UCS values are successfully able to predict BTS values through the implement of a power equation with a high accuracy level. Although empirical equations have been extensively proposed to estimate BTS of the rock, the accuracy level of these equations are in the range of low to moderate. Therefore, in order to provide a higher level of accuracy, there is a need to develop new techniques with the use of multiple inputs parameters such as intelligent predictive models.

Aside from empirical equations, the literature also consists of intelligent systems widely applied by different researchers to address the problems that may appear in the context of engineering (particularly the geotechnical engineering) and science fields [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. Furthermore, specific to the topic of the present paper, a number of significant studies have been carried out. For instance, using both artificial neural networks (ANNs) and statistical methods, Singh et al. [54] attempted to predict BTS of the schistose rock groups. They used various parameters as model inputs such as type of specific rock, grain size, and percentage of different minerals (such as quartz, feldspar and mica). According to their findings, ANNs are more successful in the prediction of BTS compared to traditional methods in terms of the accuracy level. In addition, they concluded that an ANN model is able to produce such results where statistical techniques fail to draw them. Baykasoğlu et al. [1] investigated the capability of several artificial intelligent (AI) methods, i.e. genetic programming (GP), gene expression programming and linear GP in predicting BTS values of soft limestone rock samples. In the modelling process, they used a database comprising of 118 sample sets where water absorption, dry density, saturated density, Bulk density and ultrasonic pulse velocity were selected to be used as model inputs. They finally introduced the high applicability of GP in predicting BTS of the rock compared to other implemented techniques. The hybrid ANN-based models, i.e. the imperialism competitive algorithm-ANN, the particle swarm optimization (PSO)-ANN, the invasive weed optimization (IWO)-ANN, and genetic algorithm (GA)-ANN were developed by Mahdiyar et al. [3] and Huang et al. [55] to forecast BTS of the granitic rock samples. These models were developed with the help of a database comprising of 80 sample sets where results of density, Is50 and Schmidt hammer tests were utilized as independent variables. They concluded that all of these models are able to approximate BTS of the rock samples with high accuracy level.

The aim of this study is to create a new hybrid neural network by combining fuzzy logic concepts with group method of data handling (GMDH) framework in each partial description (PD’s) optimized by the gravitational search algorithm (GSA) metaheuristic optimization which leads to developing fuzzy-GMDH-GSA model for estimating BTS of the rock materials. In addition to the creation of fuzzy-GMDH-GSA, other predictive models such as conventional GMDH model and complex fuzzy C-mean-based fuzzy inference system (CFCM-FIS) models are also constructed and proposed for BTS prediction. Then, the performance of these models is evaluated to select the best predictive model among all for BTS estimation. For the purpose of the research presented herein, a suitable database from a water transfer tunnel (operated in Malaysia) was considered and used. Different rock index tests, i.e. the Rn, the dry density (DD), Is50, as well as BTS were conducted in order to perform modelling and required analyses. In the following sections, principles of the intelligence techniques used in this study are described. Then, after description of data source and laboratory tests, model developments will be explained in details. Eventually, the best predictive intelligence technique in predicting BTS of the rock material will be selected and introduced.

2 Principles of the artificial intelligence (AI) models

This section first describes the complex fuzzy C-means-fuzzy inference system (CFCM-FIS) model; then, introduces the GMDH structure. As noted earlier, the present paper establishes an innovative hybrid fuzzy-GMDH optimized by GSA, which is called the fuzzy-GMDH-GSA algorithm, in order to compare with the other mentioned models.

2.1 Framework of CFCM-FIS algorithm

The modelling systems based on fuzzy rule have been recently applied to different fields like the construction of geophysical, engineering, and biological systems. The fuzzy expert system is indeed constructed by combining the rules and membership function (MF), which is produced by CFCM clustering or some other clustering techniques. In the present research, the technique of collaborative fuzzy clustering is applied to the generation of several rules and computation of the MF. Benzek et al. [56] introduced CFCM clustering which has been modified for several times and utilized in a variety of applications in various real-life problems. Recently, a large number of modifications and a number of popular clustering methods have been introduced to the literature applicable to FIS systems [57,58,59], and time series prediction models [60, 61]. Fuzzy clustering is mainly used to reassure to works on data and, at the same time, attempts to take advantages of different knowledge sources coming from a variety of patterns of accessible data when addressing a certain problem [62].

2.1.1 Complex fuzzy C-means (CFCM)

In 1981, Bezdek et al. [63] pioneered the complex fuzzy C-means (CFCM). This is a technique of data clustering through which each data point is allowed to belong to one or multiple clusters determined using a MF. FCM conducts the clustering operation on the basis of minimizing the objective function offered by Eq. (1):

$$J_{m} = \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{C} {u_{ij}^{m} \,\left\| {x_{i} - c_{j} } \right\|}^{2} }$$
(1)

where \(m\) signifies any real number that is greater than 1, \(u_{ij}\) stands for the membership degree of \(x_{i}\) within cluster \(j\), \(x_{i}\) represents the ith of d-dimension data, \(c_{j}\) denotes the d-dimension of the cluster and \(\left\| * \right\|\) represents any norm that expresses similarity between the centre and any measured data. The fuzzy partitioning is performed through iteratively optimizing the objective function presented in Eq. (1) with updating of membership \(u_{ij}\) and the cluster centre \(c_{j}\), which are given by Eqs. (2) and (3), respectively,

$$u_{ij} = \frac{1}{{\sum\nolimits_{k = 1}^{C} {\left( {\frac{{\left\| {x_{i} - c_{j} } \right\|}}{{\left\| {x_{i} - c_{k} } \right\|}}} \right)^{{\frac{2}{m - 1}}} } }}$$
(2)
$$c = \frac{{\sum\nolimits_{i = 1}^{N} {u_{ij}^{m} {\mkern 1mu} x_{i} } }}{{\sum\nolimits_{i = 1}^{N} {u_{ij}^{m} } }}.$$
(3)

This iteration that consists of Eqs. (2) and (3) stops once:

$$\max_{ij} \left\{ {\left| {u_{ij}^{(k + 1)} - u_{ij}^{(k)} } \right|} \right\} < \varepsilon$$
(4)

where \(\varepsilon\) stands for a stopping criterion between 0 and 1, and \(k\) denotes the iteration steps. Such process is converged to a local minimum or a saddle point of \(J_{m}\). Table 1 demonstrates the FCM procedure.

Table 1 CFCM procedures
Full size table

2.1.2 Fuzzy inference system (FIS)-Mamdani type

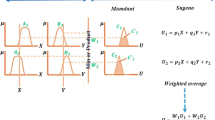
The fuzzy inference system (FIS) makes use of the fuzzy set theory for the purpose of mapping the inputs (features) to outputs (classes). FIS has been offered under two titles: Mamdani [64] and the Sugeno [65], among which the former is discussed in the previous researches (see Fig. 1).

Fig. 1
figure 1

The fuzzy inference system description [66]

Full size image

To calculate the output of this FIS given the inputs, the following six steps are needed to be followed (see Table 2).

Table 2 Steps involved in FIS development
Full size table

2.2 Framework of GMDH type neural network

Ivahnenko [67] firstly developed the self-organizing GMDH algorithm. Its structure is generally based on self-organized systems. This AI-based model is capable of generating quadratic polynomials in any neuron known as partial descriptions (PD’s), in order to select neurons with the best fit values for filtering PD’s (or neurons), as well as generating error criteria in order to terminate training phase and form a tree-like structure used to solve highly complex problems [68,69,70]. According to previous studies carried out in this field, the GMDH is a flexible AI approach that can be integrated effectively into other evolutionary algorithms such as PSO [71, 72], GP [73, 74], GA [75, 76], and back propagations [77, 78]. For the exploration of a precise solution to system identification problems, a function of \(\hat{f}\) can be used as a replacement for the actual function \(f\) in a way to predict the final output of a complex system, \(\hat{y}\), for a given model input \(X = \left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right)\) in such a way that it can be as close as possible to its output y. As a result, in case of a certain \(n\) observations of multi-variable, an output variable is shown as:

$$y_{i} = f\left( {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} } \right),\quad \left( {i = 1,2,3, \ldots ,M} \right)$$
(5)

In current status, the model of GMDH can be well-constructed to predict the final values of output, \(\hat{y}_{i}\), in case of each given input vector \(X = \left( {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} } \right)\). Indeed, the function presented below is considered for defining a relationship that can connect the final output to the inputs as [79]:

$$\hat{y}_{i} = \hat{f}\left( {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} } \right)\quad (i = 1,2,3, \ldots ,M)$$
(6)

The following equation expresses the error values offered by the measured (observed) values and the predicted model outputs:

$$\sum\limits_{i = 1}^{M} {\left[ {\hat{f}\left( {x_{i1} ,x_{i2} ,x_{i3} , \ldots ,x_{in} } \right) - y_{i} } \right]}^{2} \Rightarrow \hbox{min}$$
(7)

The GMDH model proposes a relationship between dependent and independent parameters by the following equation:

$$y = w_{0} + \sum\limits_{i = 1}^{n} {w_{i} \,x_{i} } + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {w_{ij} \,x_{i} \,x_{j} + \sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {w_{ijk} \,x_{i} \,x_{j} \,x_{k} + \cdots ,} } } } }$$
(8)

Moreover, Eq. (8) is proposed as the Kolmogorov–Gabor polynomial [80,81,82]. The literature over the last decades indicated that the use of quadratic polynomial are able to provide a relatively lower rate of error compared to other types of polynomials [68, 69].

$${\text{Quadratic:}}\quad \hat{y} = G(x_{i} ,\,x_{j} ) = w_{0} + w_{1} \,x_{i} + w_{2} \,x_{j} + w_{3} \,x_{i} \,x_{j} + w_{4} \,x_{i}^{2} + w_{5} \,x_{j}^{2}$$
(9)

Weighting coefficients in relation to Eq. (9) are calculated using least square technique. Therefore, the error value between actual value,\(y\), and the predicted model output, \(\hat{y}\), for each pair of \(x_{i}\) and \(x_{j}\), as input variables, should be minimized. In addition, this error function is able to compute the performance of quadratic polynomial, \(G_{i}\), using least-square method to optimally remove a number of neurons (nodes) in every layer, is expressed as follows:

$$E = \frac{{\sum\nolimits_{i = 1}^{M} {\left( {y_{i} - G_{i} ()} \right)^{2} } }}{M} \to \hbox{min} .$$
(10)

In GMDH, all possibilities of two independent variables (or inputs) out of total \(n\) input variables are taken into account in building the regression quadratic polynomial in the form of Eq. (9). In this equation, the weighting coefficients have been derived from a least square method. Essentially, in each (or current) layer, the nodes number can be calculated as follows: \(C_{n}^{2} = n(n - 1)/2\) where n stands for the inputs numbers of the former layer. However, the partial descriptions will be produced in the initial layer from observations \(\left\{ {(y_{i} ,x_{ip} ,x_{iq} );\,(i = 1,2, \ldots ,M)} \right\}\) for different pairs of \(p, \, q \in \left\{ {1,2, \ldots ,n} \right\}\). In other words, M triples \(\left\{ {(y_{i} ,x_{ip} ,x_{iq} );\,(i = 1,2, \ldots ,M)} \right\}\) could be formed as inputs–output systems, from \(n\) observations using \(p, \, q \in \left\{ {1,2, \ldots ,n} \right\}\), expressed as follows [83]:

$$\left[ {\begin{array}{*{20}c} {x_{1p} } & {x_{1q} } & {y_{1} } \\ {x_{2p} } & {x_{2q} } & {y_{2} } \\ {\begin{array}{*{20}c} . \\ {x_{mp} } \\ \end{array} } & {\begin{array}{*{20}c} . \\ {x_{mq} } \\ \end{array} } & {\begin{array}{*{20}c} . \\ {y_{m} } \\ \end{array} } \\ \end{array} } \right]$$
(11)

The application of quadratic polynomial, for a row of M (Eq. 10), may result in the formation of a mathematical matrix equation as follows:

$$AW = Y$$
(12)

where \(W\) is the vector, which includes six coefficients of weighting of the quadratic polynomial as:

$$W = \left\{ {w_{0} ,w_{1} ,w_{2} ,w_{3} ,w_{4} ,w_{5} } \right\}^{\text{Tr}}$$
(13)

The superscript \(T\) signifies of matrix transpose. In addition, the vector of output is attained as follows:

$$Y = \left\{ {y_{1} ,y_{2} ,y_{3} , \ldots ,y_{M} } \right\}^{\text{Tr}}$$
(14)

In Eq. (12), A matrix denotes a combined form of 2 inputs being created. As a result, A can be derived as follows:

$$\left[ {\begin{array}{*{20}c} 1 & {x_{1p} } & {\begin{array}{*{20}c} {x_{1q} } & {x_{1p} \cdot x_{1q} } & {\begin{array}{*{20}c} {x_{1p}^{2} } & {x_{1q}^{2} } \\ \end{array} } \\ \end{array} } \\ 1 & {x_{2p} } & {\begin{array}{*{20}c} {x_{2q} } & {x_{2p} \cdot x_{2q} } & {\begin{array}{*{20}c} {x_{2p}^{2} } & {x_{2q}^{2} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} \cdot \\ 1 \\ \end{array} } & {\begin{array}{*{20}c} \cdot \\ {x_{mp} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdot \\ {x_{mq} } \\ \end{array} } & {\begin{array}{*{20}c} \cdot \\ {x_{mp} \cdot x_{mq} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdot \\ {x_{mp}^{2} } \\ \end{array} } & {\begin{array}{*{20}c} \cdot \\ {x_{mq}^{2} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(15)

As expressed in Eq. (16), the coefficients vector is presented using the least-squares approach as follows:

$$W = \left( {A^{\text{Tr}} A} \right)^{ - 1} A^{\text{Tr}} Y$$
(16)

This is believable that method of GMDH is iterated for each node of the subsequent layers. For more description regarding the conventional GMDH model, other studies in the literature can be found [68, 75]. The conventional GMDH structure is shown in Fig. 2 briefly.

Fig. 2
figure 2

The construction of GMDH type neural network

Full size image

2.3 Framework of fuzzy-GMDH-GSA algorithm

2.3.1 Hybrid fuzzy-GMDH structure development

The GMDH-based network indeed acts a tool of machine learning in regard to problems pertaining to classification and decision-making processes. This is a type of ANN that uses a polynomial activation function. The model is converged into a termination criterion subsequent to an adequate quantity of epochs by means of series of embedded operations [84]. This network has been extended to new versions by different researchers (e.g. [85]). Among all, a popular one is fuzzy-GMDH (FGMDH) automatically formed by a self-organized algorithm. The FGMDH algorithm is highly flexible; thus, the evolutionary algorithms can be effortlessly adapted with that. Moreover, the GMDH network can be enhanced using a basic fuzzy reasoning rule like “If \(x_{1}\) equals \(F_{k1}\) and \(x_{2}\) equals \(F_{k2}\), output \(y\) equals \(w_{k}\)” [86]. The Gaussian MF is used in respect to \(F_{kJ}\) accompanied with the kth fuzzy rules in the extent of the jth input values \(x_{j}\) (Eq. 17):

$$F_{kj} (x_{j} ) = \exp \left( { - \frac{{(x_{j} - a_{kj} )^{2} }}{{b_{kj} }}} \right)$$
(17)

where \(a_{kj}\) and \(b_{kj}\) stand for the constant values for each fuzzy rule. In addition, the parameter of \(y\) is determined as an output, as presented in Eqs. (18) and (19):

$$y = \sum\limits_{k = 1}^{K} {u_{k} \,w_{k} }$$
(18)
$$u_{k} = \prod\limits_{j} {F_{kj} (x_{j} )}$$
(19)

where \(w_{k}\) signifies the real value for the kth rules [85, 87, 88].

It is noted that each neuron in the FGMDH model possesses two input variables and one output variable. Each neuron’s output will be a layer that is linked directly to the next layer’s input entry. To attain the final output, there is a need to compute the average of the outputs of the last layer. From the mth model and pth layer, the input variables are the output ones of \((m - 1){\text{th}}\) and mth model in the \((p - 1){\text{th}}\) layer. Equations (20) and (21) represent the mathematical functions for the calculation of \(y^{pm}\) as follow:

$$y^{pm} = f\left( {y^{p - 1,m - 1} ,\,y^{p - 1,m} } \right) = \sum\limits_{k = 1}^{K} {\mu_{k}^{pm} \cdot w_{k}^{pm} }$$
(20)
$$\mu_{k}^{pm} = \exp \left\{ { - \frac{{\left( {y^{p - 1.m - 1} - a_{k,1}^{pm} } \right)^{2} }}{{b_{k,1}^{pm} }} - \frac{{\left( {y^{p - 1,m} - a_{k,2}^{pm} } \right)^{2} }}{{b_{k,2}^{pm} }}} \right\}$$
(21)

where \(\mu_{k}^{pm}\) signifies the kth Gaussian function and \(w_{k}^{pm}\) stands for its corresponding weight parameter, which have relation with mth model at the pth layer. Additionally, \(a_{k}^{pm}\) and \(b_{k}^{pm}\) act the role of Gaussian factors applied to the ith model input from mth model and pth layer. Furthermore, Eq. (22) represents the output variable as follows:

$$y = \frac{1}{M}\,\sum\limits_{m = 1}^{M} {y^{pm} }$$
(22)

Training feed-forward FGMDH is an iterative process performed in order to solve the systems having high complexity. In each iteration step, Eq. (23) is used to compute the error parameter as follows:

$$E = \frac{1}{2}\,\left( {y^{*} - y} \right)^{2}$$
(23)

where \(y^{ * }\) stands for the predicted value. Figure 3 shows the FGMDH structure.

Fig. 3
figure 3

The hybrid structure of FGMDH algorithm

Full size image

2.3.2 Improvement in fuzzy-GMDH topology by GSA

Among various swarm intelligence algorithms introduced in the literature, a metaheuristic optimization algorithm, i.e. GSA, is designed in such a way that it can explore within a multi-dimensional search space to find the extremum values of the target function. Optimization process in this algorithm is done based on the gravity rule and the movements within a simulated system with discrete time coordinates [89, 90]. In GSA, a group of masses are given the role of search agents, in such a way that each mass can identify the situation of the other masses. As a result, the gravitational force is applied to transferring information between various masses. When dealing with a minimization problem with GSA, each agent’s mass will be calculated following the computation of the current population fitness [91, 92] by (Eqs. 24, 25):

$$q_{i} (t) = \frac{{fit_{i} (t) - worst(t)}}{best(t) - worst(t)}$$
(24)
$$M_{i} (t) = \frac{{q_{i} (t)}}{{\sum\nolimits_{j = 1}^{s} {q_{j} (t)} }}$$
(25)

where \(fit_{i} (t)\) and \(M_{i} (t)\) signify the fitness and mass values, respectively, of agent \(i\) at time \(t\); and \(S\) stands for the population size. In addition, when addressing a minimization problem, \(worst(t)\) and \(best(t)\) are expressed using Eqs. (26) and (27):

$$best(t) = \mathop {\hbox{min} }\limits_{{j \in \{ 1, \ldots ,s\} }} fit_{j} (t)$$
(26)
$$worst(t) = \mathop {\hbox{max} }\limits_{{j \in \{ 1, \ldots ,s\} }} fit_{j} (t)$$
(27)

For calculation acceleration of agents, there is a need to have total forces (from a set of agents) with highest masses according to gravity laws (Eq. 28)

$$F_{i}^{d} (t) = \sum\limits_{j \in kbest,j \ne i}^{{}} {rand_{j} } G(t)\frac{{M_{j} (t)M_{i} (t)}}{{R_{ij} (t) + \varepsilon }}\left( {x_{j}^{d} (t) - x_{i}^{d} (t)} \right).$$
(28)

To measure an agent’s acceleration, all forces from heavier masses implemented to it, need to be calculated through taking into account the law of gravity and the second law of Newton on motion (Eq. 29), at the same time [89]. Then, an agent’s updated velocity is attained as a fraction of its current velocity added to its own acceleration (Eq. 30). Afterwards, Eq. (31) can be used to determine its situation as follows:

$$a_{i}^{d} (t) = \frac{{F_{i}^{d} (t)}}{{M_{i} (t)}} = \sum\limits_{j \in kbest,j \ne i}^{{}} {rand_{j} } G(t)\frac{{M_{j} (t)}}{{R_{ij} (t) + \varepsilon }}\left( {x_{j}^{d} (t) - x_{i}^{d} (t)} \right)$$
(29)
$$v_{i}^{d} (t + 1) = rand_{i} \times v_{i}^{d} (t) + a_{i}^{d} (t)$$
(30)
$$x_{i}^{d} (t + 1) = x_{i}^{d} (t) + v_{i}^{d} (t + 1)$$
(31)

where \(x_{i}^{d}\), \(v_{i}^{d}\) and \(a_{i}^{d}\) are the position, velocity, and acceleration of agent \(i\) in dimension \(d\), respectively, \(rand_{i}\) and \(rand_{j}\) represent two uniform random at the range of \([0,\,1]\), \(\varepsilon\) signifies a small value, \(d\) shows the dimension of the search space, and \(R_{ij} (t)\) denotes the Euclidean distance that exists between two agents \(i\) and \(j\) that are defined as \(R_{ij} (t) = \left\| {x_{i} (t) - x_{j} (t)} \right\|_{2}\). Remember that \(X_{i} = \left( {x_{i}^{1} ,x_{i}^{2} , \ldots ,x_{i}^{d} } \right)\) shows the ith agent position within the search space. The \(kbest\) represents the set of first \(K\) agents having the optimum fitness values and the largest masses, which can be initialized as \(K_{0}\) in the starting time. In this study, \(K_{0}\) is set for total number of agents \((N)\) and it is reduced linearly to value of 1. Also gravitational constant, \(G\), parameter is a time descending function; initially, it is set as \(G_{0}\), then it reduces exponentially with passing time as expressed in Eq. (32):

$$G(t) = G(G_{0} ,t) = G(t) = G_{0} e^{{ - \alpha \frac{t}{T}}}$$
(32)

During optimization process, based on previous investigations in terms of trial–error and convergence rate, the values of \(\alpha\) and \(G_{0}\) are suggested as 20 and 100, respectively, while the maximum number of iteration is set as 100 and the number of agents are fixed at 50 in order to achieve best performance on developed hybrid model [89, 91, 93]. in order to optimize and tuning fuzzy MFs parameters parallel to achieving optimal weighting coefficients associated to Partial Descriptions (PDs) in GMDH type neural network over complex topology of fuzzy-GMDH model. The flowchart of this hybrid process is displayed in Fig. 4.

Fig. 4
figure 4

Workflow flowchart of hybrid fuzzy-GMDH algorithm improved by GSA optimization method

Full size image

3 Case study and testing procedure

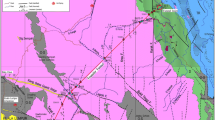
The Pahang Selangor raw water tunnel (PSRWT) is responsible for transferring raw water from Pahang to Selangor states, Malaysia. More specifically, from the Semantan River, it transfers 1890 million L/day of water for domestic and industrial purposes. This huge project involved excavation by means of three tunnel boring machines (TBMs) as well as four traditional machines of drilling and blasting. The TBMs of the size of 5.23 m in diameter were utilized to work under a variety of ground conditions. Figure 5 displays the tunnel location in Malaysia. This research involved the collection of 100 granitic block samples from the location of the tunnel and transferring them to laboratory to be exposed to different rock index tests. The tests conducted on the samples were Rn, DD, Is50, and BTS. All tests were carried out in accordance with the ISRM standards [94]. In order to have a better understanding about conducted tests and their procedures, Fig. 6a–d shows procedure of coring rock samples, conducting Schmidt hammer test, conducting Brazilian tensile test, and point load test, respectively.

Fig. 5
figure 5

Location of the PSRWT project

Full size image
Fig. 6
figure 6

Conducted tests and their procedures; a procedure of coring rock samples, b conducting Schmidt hammer test, c conducting Brazilian tensile test, d point load test

Full size image

In this section, through the use of simple regression analysis, the relationships between input (Rn, DD, Is50) and output (BTS) parameters have been identified. Different simple equations types were evaluated in order to investigate the most accurate one among all for each input parameter. These evaluations were based on R2 results (where the best R2 for the perfect model is equal to 1). The best equations selected for the prediction of BTS, as well as their scatter graphs and R2 results, are displayed in Fig. 7. R2 values of 0.6976, 0.6735, and 0.6761 were obtained for Rn, Is50, and DD parameters, respectively. The obtained results were found significant; however, in order to have higher performance for BTS estimation, a new hybrid intelligence system is introduced in this study. It should be noted that in order to have a better understanding regarding modelling and analysis, all 80 datasets (input and output parameters) are shown in Table 3.

Fig. 7
figure 7

The selected scatter graphs together with their equations in predicting BTS: a Rn, b Is50, c DD

Full size image
Table 3 The datasets used in this study
Full size table

4 Predictive model development

4.1 Developing CFCM-FIS model for BTS prediction

As illustrated in Fig. 8, the proposed CFCM-FIS model falls into two main parts; the first part contains the CFCM procedure and the second one comprises the Mamdani-based FIS. The model proposed here provides a vigorous and dependable modelling system through making an efficient combination of the CFCM capability in representing knowledge and the reasoning capacities of the Mamdani-based FIS. First, the available input data is divided into two or more equal sub-datasets; after that, FCM is applied to each sub-dataset in order to compute the prototypes and partition matrix for each dataset. In the next step, all partition matrix and prototype are updated by CFCM through having a collaboration with each of them, then CFCM extracts their common features and makes available the extracted features to the knowledge-base sub-system of FIS. Knowledge base refers to the rule base and the database conjointly. A rule base is consisted of several fuzzy IF–THEN rules, whereas a database outlines the fuzzy sets MFs used in the fuzzy system. The fuzzy knowledge base transfers its own information into the inference engine wherein the fuzzy input is converted into fuzzy output by means of the fuzzy IF–THEN rules. By means of the MFs that exist within the fuzzy knowledge base, the crisp input is converted into a linguistic variable by the fuzzifier. In the inference engine, the fuzzy input is converted into the fuzzy output by means of the IF–THEN type fuzzy rules. On the other hand, it is the task of the defuzzier part to convert the fuzzy output extracted from fuzzy inference engine to crisp output. A FIS is produced by Genfis (generate fuzzy inference system) through applying FCM clustering to inputs–output datasets. This is done by deriving a set of rules modelling the data behaviours. The first step of the rule extraction method is the use of the FCM function aiming at the determination of the number of rules and MFs for consequents and antecedent’s parts. Figure 9 shows the surfaces derived during the FIS process for all input parameters together with system output. It is worth mentioning that, a MATLAB function called Genfis was applied in order to construct and predict BTS of the rock samples.

Fig. 8
figure 8

Flowchart diagram of FCM-FIS model [95]

Full size image
Fig. 9
figure 9

The surfaces derived during the FIS process to predict BTS of the rock samples

Full size image

4.2 Development of GMDH model for BTS prediction

GMDH indeed belongs to the inductive algorithm’s category, which can be implemented in a variety of problems pertaining to pattern recognition and data mining. GMDH has a self-organizing and inductive nature; accordingly, it can automatically find the optimum structure of its network. GMDH operates on the basis of gradually sorting out the complex models and choosing optimal solutions through the use of an external criterion. This is on the basis of a multilayer network of the second-order polynomials. In such polynomials, the single output of each quadratic neuron with two inputs \((X_{i} ,\,X_{j} )\) is computed as follows:

$$z_{ij} = C_{1} + C_{2} X_{i} + C_{3} X_{j} + C_{4} X_{i}^{2} + C_{5} X_{j}^{2} + C_{6} X_{i} X_{j}$$
(33)

Tuning the quadratic neurons weights is done in the course of process of learning. If \(X\) is \(n \times m\) matrix of input data, which is consisted of n number of training sets offered by m features, then the GMDH model will create all probable mixtures of inputs from m variables within the first hidden layer. After that, each one of the quadratic neurons is trained using the least-squares method. The criterion for selecting neurons is used in each layer on the basis of the natural selection process in order to preserve a feasible network complexity. For that reason, the precision of classification in case of each quadratic neuron is calculated through making a comparison between the polynomial model output and the target. The neurons whose polynomial model fitness function is less than a preset level of error will be kept and the others are removed. The definition of selection error criterion \(\left( {e_{\text{c}} } \right)\) is as follows:

$$e_{\text{c}} = \alpha {\mkern 1mu} e_{ \hbox{min} } + (1 - \alpha ){\mkern 1mu} e_{ \hbox{max} }$$
(34)

where \(e_{ \hbox{max} }\) and \(e_{ \hbox{min} }\) stand for the maximum and minimum errors attained within each one of the existing layers, respectively, and \(\alpha \,(0 < \alpha < 1)\) denotes the selection pressure. Figure 10 illustrates the structure of a GMDH model with four inputs. This is clearly observable that the neurons that exist within each layer whose polynomial model error exceeds \(e_{\text{c}}\) are removed and the remaining ones are applied to the construction of the next hidden layer. It is noted that a selection pressure of 0.6 was set for the purpose of the current study. In each of the layers, a limitation can be set for maximum node and layer numbers in order to adjust the network complication level. As a result, within each layer, the maximum node numbers and layers were fixed at 50 and 30, respectively, in a way to gain a full control on the evolutionary structure of the network.

Fig. 10
figure 10

GMDH model structure with four inputs

Full size image

4.3 Development of FGMDH-GSA for BTS prediction

In this section, the topology of fuzzy-GMDH structure was combined and improved in a parallel process through applying GSA optimization method. In developing fuzzy-GMDH-GSA model, network structure was established using three layers and were constructed based on number of inputs and to avoid model structure complexity. Table 4 presents the control parameters values associated to GSA algorithm including maximum number of iterations, the number of mass agents,\(\alpha\), and \(G_{0}\). GSA indeed made an optimization on the Gaussian MF and weighting coefficients in each partial description of the fuzzy-GMDH model as indicated in Fig. 11.

Table 4 Setting GSA control parameters used for fuzzy-GMDH-GSA model
Full size table
Fig. 11
figure 11

Implementation of GSA into PD’s (each neuron block) over fuzzy-GMDH topology

Full size image

5 Results and discussion

This section provides a quantitative evaluation of different developed models performance during training and testing in terms of error indicator of correlation coefficient (R), mean square error (MSE), root mean square error (RMSE), error mean and error StD in order to specify the best-fitted predictive model for approximating BTS of the rock material; some statistical performance criterions were defined and calculated for each developed model (Eqs. 35–39)

$$R = \left( {\frac{{\sum\nolimits_{i = 1}^{M} {\left( {y_{{i({\text{Actual}})}} - \bar{y}_{{({\text{Actual}})}} } \right)\left( {y_{{i({\text{Model}})}} - \bar{y}_{{({\text{Model}})}} } \right)} }}{{\sum\nolimits_{i = 1}^{M} {\left( {y_{{i({\text{Actual}})}} - \bar{y}_{{({\text{Actual}})}} } \right)^{2} {\mkern 1mu} \times {\mkern 1mu} \sum\nolimits_{i = 1}^{M} {\left( {y_{{i({\text{Model}})}} - \bar{y}_{{({\text{Model}})}} } \right)^{2} } } }}} \right)$$
(35)
$${\text{MSE}} = \frac{1}{M}\sum\limits_{i = 1}^{M} {\left( {y_{{i({\text{Model}})}} - y_{{i({\text{Actual}})}} } \right)^{2} }$$
(36)
$${\text{RMSE}} = \left( {\frac{{\sum\nolimits_{i = 1}^{M} {\left( {y_{{i({\text{Model}})}} - y_{{i({\text{Actual}})}} } \right)^{2} } }}{M}} \right)$$
(37)
$${\text{Error}}\,{\text{mean}} = \frac{{\sum\nolimits_{i = 1}^{M} {(y_{{i({\text{Actual}})}} - y_{{i({\text{Model}})}} } }}{M}$$
(38)
$${\text{Error}}\,{\text{StD}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{M} {\left( {E_{{i({\text{Model}})}} - \bar{E}_{\text{Model}} } \right)} }}{M - 1}}$$
(39)

where \(y_{{i({\text{Model}})}}\) denotes predicted value,\(y_{{i({\text{Actual}})}}\) is measured value, M is the number of dataset and \(E\) indicate the error value between observed measured value and predicted value.

Results from regression analysis have shown that predictive models must be developed to predict rock BTS, accurately. Thus, three intelligence models were proposed for estimating BTS of the rock samples. Three neurons, i.e. Rn, DD and Is50, were taken into account in input layer for the development of all models, while BTS values were considered in output layer. Many models were constructed based on several parametric simulations to select the best hybrid CFCM-FIS, GMDH and fuzzy-GMDH-GSA models, separately for each developed model. Consequently, based on calculated error performance criteria (MSE, RMSE, Error) as well as according to R values, the best-fitted model among three proposed models was selected (see Figs. 14, 17, 20). Moreover, these selected models were verified more on the basis of other performance indices (PIs) comparison, i.e. R, MSE, RMSE and Error StD values. Table 5 and Figs. 15, 16, 19 simultaneously demonstrate the overall PIs values for all developed models for both training and testing phases.

Table 5 Descriptive statistical error performance analysis of the proposed AI models
Full size table

Furthermore, Figs. 12, 15, and 18 show plotted curves between the measured rock BTS (target) and those predicted values (outputs) obtained from CFCM-FIS, GMDH and fuzzy-GMDH-GSA models, respectively, for train and test datasets, separately. Figures 13, 14, 15, 16, 18 and 19 along with the PI list expressed in Table 5 plan to show precision and verification of proposed fuzzy-GMDH-GSA model as more efficient predictive model in comparison with two other models (CFCM-FIS and GMDH) for all PIs values. In other words, the developed fuzzy-GMDH-GSA has shown relatively higher level of accuracy compared to others (highest value of R and lowest values of RMSE, MSE and Errors indices) for training and testing datasets among the three predictive models. The fuzzy-GMDH-GSA model having R of 0.90, MSE of 0.0099, RMSE of 0.099 and an Error Mean, StD of − 5.84e−17, 0.1007 can estimate relatively accurate the BTS values more efficiently than the GMDH model with a R of 0.86, a MSE of 0.012, and a RMSE of 0.110 for training datasets. In addition, the fuzzy-GMDH-GSA is also shown much better performance than the CFCM-FIS model with R of 0.87, MSE of 0.014, RMSE of 0.118 and Error Mean of − 0.021, respectively, for train stage. According to Table 5 and presented figures, the statistical performance criteria show the superiority of the fuzzy-GMDH-GSA model over the other models in estimating the tensile strength of the rock material for testing stage. The relative error values diagrams with error distribution histograms were shown for CFCM-FIS, GMDH and fuzzy-GMDH-GSA models through Figs. 13, 16 and 19, respectively, for training and testing stages. It is noted that relative error values define as the difference values between measured BTS values (target values) and predicted BTS values (model output) for each observation within the desired datasets (train and test dataset). According to computed error indices, it was concluded that fuzzy-GMDH-GSA model has capability to predict BTS with acceptable level of accuracy and reliability in terms of statistical performance criterion as well as having relatively lowest error indicators compared to other developed models for both training and testing datasets. Consequently, although the BTS could be predicted in acceptable precision rate across all of the aforementioned predictive models, however, the fuzzy-GMDH-GSA model is known as the best-fitted repressor model in this study. The rock BTS prediction through applying fuzzy-GMDH-GSA predictive model should obviously be introduced in geotechnical practical work as a novel predictive model (Figs. 17, 18, 19, 20, 21).

Fig. 12
figure 12

Plot of measured versus predicted BTS values for CFCM-FIS model in train and test stage

Full size image
Fig. 13
figure 13

Error distribution histogram and statistical error indices for CFCM-FIS model in train and test stages

Full size image
Fig. 14
figure 14

Regression plot of measured versus predicted BTS output for CFCM-FIS model in train and test stage

Full size image
Fig. 15
figure 15

Plot of measured versus predicted BTS values for GMDH model in train and test stage

Full size image
Fig. 16
figure 16

Error distribution histogram and statistical error indices for GMDH model in train and test stages

Full size image
Fig. 17
figure 17

Regression plot of measured versus predicted BTS output for GMDH model in train and test stage

Full size image
Fig. 18
figure 18

Plot of measured versus predicted BTS values for fuzzy-GMDH-GSA model in train and test stage

Full size image
Fig. 19
figure 19

Error histogram and statistical error indices for fuzzy-GMDH-GSA model in train and test stages

Full size image
Fig. 20
figure 20

Regression plot of measured versus predicted BTS output for fuzzy-GMDH-GSA model in train and test stage

Full size image
Fig. 21
figure 21

Results of both SRC and SRRC techniques for each input parameter

Full size image

It should be noted that several hybrid ANN-models were developed to forecast BTS of the rock. However, they are a hybrid ANN-based technique which are optimized by some optimization algorithms like PSO, ICA, GA and IWO. In fact, they can be used for optimizing weights and biases of ANN to avoid over-fitting of ANN during training stage. Here, in this study, approaching the implement of a complicated hybrid AI model namely, fuzzy-GMDH-GSA has been introduced for solving problem of BTS of rock material. Innovation of the present study compared to previous works performed in the field of application of AI algorithms (e.g. PSO-ANN, GA-ANN, ANFIS–PSO/ICA, and GMDH) in predicting BTS of rocks is that the integrated hybrid structure of fuzzy-GMDH model utilizes the inherent properties of FIS concepts and GMDH algorithm at the same time. In fact, the benefits of the hybrid fuzzy-GMDH-GSA network can be attributed to the low volume of computation per neuron, self-organizing hybrid model compared to other AI methods such as ANFIS. The advantage of the hybrid fuzzy-GMDH-GSA model is the simplicity of performability, time-consuming and cost-effective rather than experimental rock BTS tests. Also compared to ANN’s, ANFIS and GMDH algorithms, the developed fuzzy-GMDH-GSA structure has overall lower computational volume and time-performance. Our proposed methods do not act as black-box against old ANNs and the users are able to control over hybrid fuzzy-GMDH-GSA.

As explained before, the block rock samples were collected from the face of a water transfer tunnel constructed in Malaysia which is a tropical country. Then, these block samples were transferred to the laboratory in order to conduct rock index tests. We tested DD, Is50, Rn, and BTS on all samples in the laboratory and established a database to develop predictive intelligence models. As a fact in field of rock mechanics, the established database is only for the specific rock mass properties in the transfer tunnel with specific input and output parameters, ranges and rock type. Therefore, finding a series of data with these properties (rock type, inputs and their ranges, tropical area) is very difficult in the literature. Due to this reason, it is not possible to compare our results with those presented already in the literature. However, it should be noted that testing section of datasets was applied in order to evaluate models development. By using these data which are not involved in training section, we are able to see how model development is successful during modelling development process.

6 Sensitivity analysis

Sensitivity analysis (SA) examines the relationship between a model’s assumptions, which may be applied in a computer-based system, and its model inputs. Finding a relation between model output and input needs more than a point output derivative together with their inputs. Considering the multivariate nature of the model inputs and their uncertainty ranges, they have a deep impact on the systems specially hybrid systems. Such an approach is applicable to a variety of methods, including model quality assurance and the literature describes some SA strategies, and some inter-comparative studies are also available. This research highlights the effectiveness of the standardized regression coefficients (SRC) and the non-parametric regression-based techniques such as the standardized rank regression coefficient (SRRC). When working with this model, it is common to utilize SA estimators that provide a global sensitivity calculation, where the effects of a model input on a model output are averaged on both the parameter distribution itself and the distribution of all the remaining parameters (global SA techniques). Nonetheless, every model has unknown input parameters; likewise, the extent of uncertainty would probably vary from parameter to parameter and a comprehensive analysis of the model response over the entire range of inputs.

Both SRC and SRRC have been applied on the model inputs to investigate their effects on the system output. Figure 21 shows results of both SRC and SRRC techniques for each input parameter on BTS of the rock. As can be seen in this figure, considering the results of both techniques, Is50 receives the deepest impact on BTS of the rock, whereas, Rn is the input parameter with the lowest effect on the BTS of the rock.

7 Conclusions

The main goal of this study was to propose a new AI hybrid model for prediction of BTS of the rock samples. To do that, the fuzzy-GMDH structure was combined and improved in a parallel process through applying GSA optimization method in order to receive higher prediction performance compared to CFCM-FIS and GMDH predictive models. The modelling of this study was done using 3 model inputs (Rn, DD and Is50) and one output (BTS). The outcomes of all predictive models were compared according to several evaluation criteria including R, MSE, RMSE, error mean and error StD and the best predictive technique was selected based on them. After computation of the results, the developed fuzzy-GMDH-GSA model achieved a higher level of modelling efficiency in predicting BTS of the rock compared to other applied predictive models. R, MSE, RMSE, error mean and error StD values of (0.90, 0.008, 0.087, − 0.017, and 0.087), (0.86, 0.011, 0.105, 0.035, and 0.101) and (0.86, 0.007, 0.085, − 0.024 and 0.083) were obtained for testing datasets of fuzzy-GMDH-GSA, GMDH, and CFCM-FIS models, respectively. The results indicated that fuzzy-GMDH-GSA model can predict BTS more accurately than the other implemented models. In fact, the benefits of the hybrid fuzzy-GMDH-GSA network can be attributed to the low volume of computation per neuron, self-organizing hybrid model compared to other AI methods such as ANFIS and GMDH. The advantage of the hybrid fuzzy-GMDH-GSA model is the simplicity of implementation, time-consuming and cost-effective rather than experimental rock BTS tests. Additionally, by performing sensitivity analysis through the use of SRC and SRRC techniques, Is50 was the most effective input parameter on BTS of the rock. The finding of the current study provides a new hybrid AI method for predicting aims that other researchers, students and designers are able to utilize it with caution in preliminary stage of their studies or projects.