1 Introduction

The fundamental period of vibration is a critical parameter for the seismic design of structures in accordance with the modal superposition method. Nevertheless, the so far available in the literature proposals for its estimation are often conflicting, making their use uncertain. The majority of these proposals are usually based on deterministic methods using experimental or analytical data, and they do not take into account the presence of infill walls (with or without opening, in the structure), even though infill walls increase the stiffness and mass of the structure and, thus, lead to significant changes in the fundamental period [7, 9, 10].

The lack of a reliable and robust method for the prediction of the value of the fundamental period of structures is mainly due to the large number of parameters affecting its nonlinear behavior. To the best of our knowledge, the available proposals in the literature, which are based on analytical semi-empirical formulas, depict considerable variation [9, 10, 13, 15], thus revealing the need for further investigation and refinement of the proposals. As the deterministic methods have failed to offer reliable predictions in the last two decades, soft computing techniques, such as the artificial neural networks models, have started to contribute to the problems’ solutions in a significant way.

Artificial neural network (ANN) models are receiving increased attention in the last decades, while they have been used by many researchers for a variety of engineering applications. The basic strategy for developing ANN models for material behavior is to train ANN models on the results of a series of experiments in relation to that material. If the experimental results contain the relevant information about the material behavior, then the trained ANN models will contain sufficient information about the material’s behavior, enabling them to qualify as a material model. It should be noticed that the achieved optimum ANN model is valid for structures with values of geometrical and mechanical characteristics (input parameters) within the range of the values in the data sets used for the ANN model training and development. Such trained ANN models are not only able to reproduce the experimental results, but can also approximate the results of other experiments through their generalization capability.

In the field of civil engineering, the use of artificial neural networks has been widely adopted for a plethora of structural engineering problems, such as the determination of concrete mechanical properties. Specifically, the use of ANNs and fuzzy logic models has been used for the prediction of the compressive strength of concrete [14, 28, 29, 35, 36, 42, 43]. ANNs have been also used for the modeling of special cases of concrete materials, such as the soilcrete materials [8, 11] and for concrete containing fly ash [41]. In the same direction, that is for the prediction of concrete compressive strength, the use of evolutionary ANNs has been proposed and applied as well [39]. The application of ANNs has also been used for the estimation of mechanical properties of masonry materials [32, 44]. Furthermore, ANNs have been successfully used for the modeling of the masonry failure criterion under plane stress [6, 37]. Soft computing techniques (such as the imperialist competitive algorithms) have also been proposed for the prediction of the corrosion current density in reinforced concrete [38]. Besides the modeling of the materials mechanical properties, ANNs have been also successfully applied for the determination of the crack pattern of reinforced concrete buildings [12, 24, 30, 34]. Detailed and in-depth state-of-the-art relevant works can be found in Adeli [1] and Asteris and Kolovos [5].

In this context, the main objective of the present work is to utilize the artificial bee colony algorithm in order to optimize artificial neural networks weights (as a new optimization algorithm) aiming to specify the fundamental period in Infilled RC Frame Structures. For the development of the artificial neural network models, the number of storeys, the number of spans, the span length, the infill wall panel stiffness, and the percentage of openings within the infill panel are used as input parameters, whereas the value of vibration period is considered as output parameter. It is worth noticing that the center for each one opening is identified through the center of the infill wall panels. For this case, we have the great reduction in stiffness.

2 Comprehensive literature review of estimation methods of the fundamental period of structures

A plethora of methodological approaches have been proposed for the estimation of the fundamental period of vibration (T) of reinforce concrete (RC) frame structures with/or without infill walls. Worldwide codes and several research works provide simple empirical formulas. In most cases, the methodological approaches and mathematical expressions (formulae) are simply related to the overall height of the buildings. The most common expression for the calculation of the fundamental period of vibration T is [3]:

$$T = C_{\text{t}} \cdot H^{3/4}$$
(1)

where H is the total height of the building (in meters) and Ct is a coefficient depending on the structural typology. The above expression was adopted for the first time in 1978 by the Applied Technology Council [3] for reinforced concrete moment-resisting frames. The determination of the coefficient Ct was based on the measurements of the periods of buildings during the San Fernando earthquake (1971). A regression analysis of the experimental data led to a value of 0.075 for Ct. Eurocode 8 [19] and Uniform Building Code [26], among others, adopt the same expression, while building codes from different nations adopt similar expressions assigning different values to Ct. Among these, the New Zealand Seismic Code (New Zealand Society of Earthquake Engineering, [33]) states a value of 0.09 for reinforced concrete frames, 0.14 for structural steel and 0.06 for other types of structures.

The Uniform Building Code (UBC) proposed formula has been updated in FEMA-450 [20] based on the study by Goel and Chopra [22] as well as on the measured period of concrete moment-resisting frame buildings, monitored during the California earthquakes (including the 1994 Northridge earthquake). Based on the lower bound of the data presented by Goel and Chopra [22], FEMA proposed an expression (similar to Eq. [1]) for RC frames that provides a conservative estimate of the base shear, namely:

$$T = C_{\text{r}} H_{n}^{x}$$
(2)

where Hn is the height of the structure (in meters), Cr is equal to 0.0466, and x is 0.9.

Several researchers have proposed refined semi-empirical expressions for the fundamental period of RC frame structures based on the height related formula (Table 1). In 2004, Crowley and Pinho [15] indicated the importance of developing region-specific simplified period-height formulae. Based on the assessment of 17 existing RC frames (representative of the European building stock), they proposed a period-height formula for displacement-based design. The simple relationships presented in Table 1 are valid for RC buildings without masonry infills. The examined RC frames corresponded to actual buildings from five different south European countries designed and built between 1930 and 1980 according to older design codes. Later in 2006, Crowley and Pinho [16] using eigenvalue analysis studied the elastic and yield period of existing European RC buildings of varying height. Their study led to a simplified period-height expression for the assessment of existing RC buildings considering the presence of masonry infills.

Table 1 Expressions for the evaluation of the fundamental period of vibration
Full size table

Guler et al. [23] proposed a relationship derived by ambient vibration tests and elastic numerical analyses obtaining similar results to those by Hong and Hwang [25]. Detailed and in-depth state-of-the-art relevant works can be found in Asteris et al. [8] and Asteris and Kolovos [5].

The main disadvantage available in the literature proposals for the estimation of the fundamental period of structures is that they often conflict one another, thus, making their use uncertain. Moreover, these proposals do not take into account parameters that crucially affect the fundamental period’s value such as the number of spans, the span length, the infill wall panel stiffness, and the percentage of openings in infill walls. This considerable variation on the predicted value of the period of vibration reveals the need for further investigation and refinement of the code provisions and proposals.

3 Introducing the artificial bee colony algorithm (ABC)

3.1 Behavior of the real bee

Tereshko [40] proposed a model of foraging behavior of a honeybee colony based on reaction–diffusion equations. This model, leading to the emergence of collective intelligence of honeybee swarms, consists of three essential components: food sources, employed foragers, and unemployed foragers; in addition, two leading modes of honeybee colony behavior are defined: one is the recruitment of a food source and the other is the source abandonment. Tereshko explains his model’s main components as follows:

  • Food sources In order to select a food source, a forager bee evaluates several properties related to the food source, such as distance from the hive, richness of the energy, nectar taste, and ease or difficulty of extracting this energy. For the sake of simplicity, the quality of a food source can be represented by only one variable (although it depends on various aforementioned parameters) [27].

  • Employed foragers An employed forager is occupied at a specific food source, which she is currently exploiting. She carries information of this specific source and shares it with other bees waiting in the hive. The information includes the distance, direction and profitability of food source [27].

3.2 Honey bee performance

In the ABC algorithm, food source location represents a possible solution to the optimization problem and food source nectar amount corresponds to the quality (fitness) of the associated solution [27]. The basic idea behind bee colony optimization (BCO) is to build a multi-agent system (colony of artificial bees), which will search for good solutions of various combinatorial optimization problems, by adopting the principles used by honey bees during nectar collection process. An artificial bee colony usually consists of a small number of individuals. Artificial bees explore the search space looking for feasible solutions. In order to find the best possible solution, autonomous artificial bees collaborate and exchange information. Using collective knowledge and information sharing, artificial bees concentrate on the more promising areas and slowly abandon the less promising ones. Step by step, artificial bees collectively improve the solutions. The BCO search is running in iterations until some predefined stopping criterion is satisfied. The number of the employed bees or the onlooker bees equals to the number of solutions in the population. At the first step, ABC generates an initial randomly distributed population (C = 0) of SN solutions (food source positions), where SN denotes the size of employed bees or onlooker bees. Each solution \({\mathbf{x}}_{{\mathbf{i}}}\) (i = 1, 2, …., SN) is a D-dimensional vector. Here, D is the number of optimization parameters. After the initialization, the population of the locations (solutions) is subjected to repeated cycles, C = 1, 2, …, MCN (maximum cycle number); of search processes of employed bees, a bee produces an amount of nectar from the new source (the new solution) [27].

If the new nectar amount is higher than that of the previous, the bee memorizes the new position and forgets the old one. In the opposite case, the bee remembers the previous one. Once all employed bees complete the search process, information of food sources and location data is shared with onlooker bees. An onlooker bee evaluates the nectar information taken from all employed bees and chooses a food source with a probability related to the nectar amount [27]. The employed bee, for instance, modifies the source location in her memory and checks the nectar amount of the candidate source. If the nectar amount is higher than that of the previous one, the bee memorizes the new position and forgets the old one. The main steps of the algorithm are as follows [27]:

  1. 1.

    Initialize population

  2. 2.

    Reiteration

  3. 3.

    Positioning employed bees on food sources

  4. 4.

    Positioning onlooker bees on food sources depending on nectar amounts

  5. 5.

    Sending the scouts to search area for discovering new food sources

  6. 6.

    Memorizing the best food source found so far

  7. 7.

    Until requirements are met.

4 Materials and methods

4.1 Experimental details and database

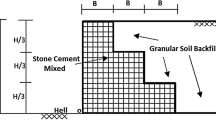
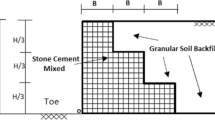
The database used herein consists of 4026 data sets obtained from literature [4]. Specifically, a total of 4026 infilled plane reinforced concrete frames (Fig. 1) have been investigated; the quantitative outcomes of these cases are included in the FP4026 Research Database [4]. The number of storeys ranged from 1 to 22 and was investigated by upgrading the number of storeys by unit increments. The storey height for all buildings was kept constant and equal to 3.0 m. The number of spans varied between 2, 4 and 6. For each case, four different span lengths have been considered, namely 3.0 m, 4.5 m, 6.0 m and 7.5 m. In the perpendicular direction, the span length was constant and equal to 5 m for all cases. All the buildings have been designed in accordance with Eurocodes 2 and 8 [17, 18].

Fig. 1
figure 1

Cross section details of an infilled RC frame [4]

Full size image

The building parameters used for the development of the model are listed in Table 2. In total, 4026 different cases of infilled RC frames were analyzed in order to investigate the influence of several parameters on the fundamental period of a frame structure. The 4026 values of the fundamental period of all cases of infilled frames studied are presented in Asteris [4].

Table 2 Building parameters [4]
Full size table

Each input training vector p is of dimension 1 × 5 and comprises the values of the five infilled frame parameters (R = 5), namely the Number of Storeys, the number of Spans, the Length of Spans, the Opening Percentage and the Masonry Wall Stiffness (Et). The corresponding output training vectors are of dimension 1 × 1 and consist of the Fundamental Period. Their mean values together with the minimum and maximum values are listed in Table 3.

Table 3 Research data
Full size table

4.2 Research methodology

In the present study, we use a back-propagation neural network (BPNN). A BPNN is a feed-forward, multilayer network, i.e., information flows only from the input toward the output with no back loops and the neurons of the same layer are not connected to each other, but they are connected with all the neurons of the previous and subsequent layer. A BPNN has a standard structure that can be written as

$${\mathbf{N}} - {\mathbf{H}}_{1} - {\mathbf{H}}_{2} - \cdots - {\mathbf{H}}_{{{\mathbf{NHL}}}} - {\mathbf{M}}$$
(3)

where \(N\) is the number of input neurons (input parameters); \(H_{i}\) is the number of neurons in the \(i{\text{th}}\) hidden layer for \(i = 1, \ldots ,{\text{NHL}}\), where \({\text{NHL }}\) is the number of hidden layers and M is the number of output neurons (output parameters).

Each BPNN model was trained with over 2817 datasets out of a total of 4025 datasets, (70% of the total data) and the validation and testing of the trained ANN were performed with the remaining 1208 datasets. More specifically, 604 datasets (15%) were used for the validation of the trained ANN and 604 (15%) datasets were used for the testing (estimating the Pearson’s correlation coefficient \(R^{2}\)).

The number of nodes in the hidden layer was obtained using the following empirical formula [21]

$$\varvec{N}_{{\mathbf{H}}} \le 2{\mathbf{N}} + 1$$
(4)

where \(N_{\text{H}}\) is the maximum number of nodes in hidden layers and \(N\) is the number of inputs. The number of obtained effective inputs equals 5, and the maximum number of nodes in the hidden layer is 11.

In order to find the training algorithm that is more suitable to tackle the nonlinear behavior of the SCC’s compressive strength, the performance of various optimization techniques such as the quasi-Newton, Resilient, One-step secant, Gradient descent with momentum and adaptive learning rate and the Levenberg–Marquardt method has been investigated. It should be mentioned that all the ANNs under investigation (which are presented in detail in the next section) have been investigated by means of all the aforementioned training algorithms. Among these algorithms, the best—by far—ANN prediction of the output parameter was achieved by using the Levenberg–Marquardt algorithm as implemented by levmar via the MATLAB trainlm function. This algorithm appears to be optimum for training moderate-sized (up to several hundred neurons per layer) feed-forward neural networks dealing with non-linear problems [31]. It should also be noted that the Hyperbolic tangent sigmoid transfer function (MATLAB tansig function) has been used as activation function. Furthermore, the rng MATLAB function has been used in order to control random number generation.

To assign the optimized weight of any artificial neural network model, the bee colony is used as a new meta-heuristic algorithm in civil engineering. Table 4 indicates the optimized structure of each model along with the characteristics of the bee colony algorithm.

Table 4 Characteristics of bee colony algorithm and FF neural network
Full size table

According to the results, it is inferred that the feed-forward model (the weights of which are optimized via bee colony algorithm) is optimized with the 5–6–5–1 structure (Fig. 2); furthermore, properties of 10 bees, 5 bee sources and 50 optimized replications offered the best results in the desired models.

Fig. 2
figure 2

A 5–6–5–1 feed-forward BPNN

Full size image

Figure 3 shows the FF–ABC network cost graph. In Figs. 4 and 5, performance of the artificial neural network has been presented in three phases of training, validation and testing.

Fig. 3
figure 3

Cost graph for 50 replications in ABC_FF model, as the best model

Full size image
Fig. 4
figure 4

Best validation performance in artificial neural network model

Full size image
Fig. 5
figure 5

The training state for the artificial neural network model

Full size image

Figure 6 depicts the comparison of the exact experimental values with the predicted values of the optimum NN model with topology 5–6–5–1. These results clearly show that the values of the fundamental period of infilled frame structures predicted from the multilayer feed-forward neural network are very close to the values of the “exact” period.

Fig. 6
figure 6

The Pearson’s correlation coefficient \(R^{2}\) of the ‘exact’ and of the predicted values of the period for the FF–ABC–NN model (5–6–5–1)

Full size image

4.3 Final values of weights of the NN model

It is common practice, in the majority of the published articles on NNs Models, for authors to present the architecture of the optimum NN model without any information about the final values of NN weights. Any architecture without the values of final values of NN model weights has very little value for others researchers and practicing engineers. In order to be useful, a proposed NN architecture should be accompanied by the (quantitative) values of weights. Thus, the NN model can be readily implemented in an MS-Excel file, available to anyone interested in the problem of modeling.

To this end, in Table 5 the final weights for both hidden layers and bias are presented. By employing the properties defined in Table 3 and using the weights and bias values between different layers of ANN, the value of the fundamental period can be estimated (predicted).

Table 5 Final values of weights and bias of the optimum FF–ABC–NN model 5–6–5–1
Full size table

4.4 Model validation

Three different statistical parameters were employed to evaluate the performance of the derived FF–ABC–NN model as well as the available formulae in the literature, including the root-mean-square error (RMSE), the mean absolute percentage error (MAPE), and the Pearson Correlation Coefficient \(R^{2}\). Lower RMSE and MAPE values are indicative of more accurate prediction results. Higher \(R^{2}\) values demonstrate an increased fit between the analytical and predicted values. The aforementioned statistical parameters are calculated by the following expressions [2]:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {x_{i} - y_{i} } \right)^{2} }$$
(5)
$${\text{MAPE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {\frac{{x_{i} - y_{i} }}{{x_{i} }}} \right|$$
(6)
$$R^{2} = 1 - \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{i} - y_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{i} - \bar{x}} \right)^{2} }}} \right)$$
(7)

where n denotes the total number of datasets, and \(x_{i}\) and \(y_{i}\) represent the predicted and target values, respectively.

The advantages of the derived FF–ABC–NN model compared to the code provisions and other research formulae for training, validation, test and all data set are shown in Table 6. It is clearly shown that the FF–ABC–NN present a high correlation coefficient \(R^{2}\) between the predicted and the exact period, a low root-mean-square error (RMSE) and a low mean absolute percentage error (MAPE), consistent with the above results. It is worth noting that the values 0.9939, 0.9942, 0.9933 and 0.9939 of the Pearson Correlation Coefficient \(R^{2}\) are higher than those presented in the relative literature.

Table 6 Statistical results of FF–ABC–NN and results available in the literature formulae
Full size table

Moreover, in Fig. 7 the results from the eigenvalue analysis of the 4025 examined structures (mentioned as “Exact”) have been compared with the predicted results from the proposed FF–ABC–NN model. Additionally, the “Exact” results are also compared with the empirical expressions of EC8 [18], FEMA-450 [20] and Goel and Chopra [22]. These results clearly show that the values of the fundamental periods of infilled frame structures predicted from the artificial bee colony-based neural network model offer a much better fit than the values of the fundamental periods predicted by code provisions.

Fig. 7
figure 7

Comparison of the proposed FF–ABC–NN model (5–6–5–1) with formulae from the literature

Full size image

5 Conclusions

In this work, the artificial bee colony algorithm, which is a new, simple and robust optimization algorithm, has been used to train feed-forward artificial neural networks for the prediction of the fundamental period of vibration of infilled frame reinforced concrete structures. The obtained results show that artificial bee colony algorithm can be successfully applied to train feed-forward neural networks. Specifically, the artificial bee colony algorithm can serve as a powerful tool in optimizing the weights of artificial neural networks models. Furthermore, the proposed FF–ABC–NN model seemed to fit the data better than other models and formulae available in the literature, as demonstrated by the high correlation \(R^{2}\) coefficient between the predicted and the exact period, as well as by the low root-mean-square error (RMSE) and mean absolute percentage error (MAPE).