A new multi-criteria group decision-making approach based on q-rung orthopair fuzzy interaction Hamy mean operators

Abstract

The recently proposed q-rung orthopair fuzzy set (q-ROFS) is a powerful and effective tool to describe uncertainty and vagueness, and Hamy mean (HM) has a significant advantage of capturing the interrelationship among aggregated arguments. In order to take full advantage of q-ROFS and HM, and consider the interactions between membership and non-membership degrees at the same time, in this paper, we propose a family of q-rung orthopair fuzzy Hamy mean operators based on interaction operations. First, we define interaction operational rules for q-rung orthopair fuzzy numbers. Based on the new operational rules, q-rung orthopair fuzzy interaction HM and q-rung orthopair fuzzy interaction weighted HM operators are proposed. Further, we propose a dual Hamy mean (DHM) operator and extend it to accommodate q-rung orthopair fuzzy environment. Based on interaction operational rules and DHM, q-rung orthopair fuzzy interaction DHM operator and its weighted form are also developed. Then, a novel multi-attribute group decision-making approach based on proposed operators is introduced. Finally, a numerical instance, as well as some comparative analyses, is provided to illustrate the validity and advantages of the new approach.

1 Introduction

MAGDM plays an important role in modern decision science, and it has been widely used in economics, management and the other fields in recent years. Its essence is the process of ranking the alternatives and selecting an optimal scheme among a set of alternatives with respect to a list of attribute values. Thus, how to effectively aggregate attribute values is a core issue of any MAGDM methods. On the other hand, due to the subjective nature of human thinking in real decision-making problems, decision makers’ evaluations over alternatives are always imprecise and fuzzy. To deal with this kind of uncertainty or impreciseness, Yager [1] introduced a new tool, called Pythagorean fuzzy set (PFS), characterized by a membership degree and a non-membership degree. Compared with Atanassov’s intuitionistic fuzzy set (IFS) [2], the lax constraint of PFS that the square sum of membership and non-membership degrees is less than or equal to one provides decision makers more freedom to express their assessments. Due to its higher capacity of modeling the fuzziness of information, quite a few of achievements on PFS have been done, such as correlation coefficients between Pythagorean fuzzy numbers (PFNs) [3], similarity measures between PFNs [4,5,6], distance measures between PFNs [7, 8], TOPSIS and TODIM approaches [9,10,11], combination of PFNs and other fuzzy sets [12,13,14] and future directions [15]. In addition, more scholars have focused on Pythagorean fuzzy MAGDM methods based on aggregation operators. For instance, Ma and Xu [16] proposed symmetric Pythagorean fuzzy weighted geometric and averaging operators. Garg [17, 18] and Ragman et al. [19] introduced some Pythagorean fuzzy Einstein operational laws and then proposed some new Pythagorean fuzzy Einstein aggregation operators. Considering these aggregation operators do not take into account the interaction between membership and non-membership degrees of PFNs, Wei [20] and Gao et al. [21] proposed Pythagorean fuzzy interaction aggregation operators. To capture the interrelationship between PFNs, Liang et al. [22, 23], Zhang et al. [24], Wei and Lu [25], Qin [26], Yang and Pang [27] extended some existing operators, such as Bonferroni mean (BM), Maclaurin symmetry mean (MSM) and generalized Maclaurin symmetry mean to PFSs.

Recently, Yager [28] generalized IFS and PFS and proposed the concept of q-ROFS. The constraint of q-ROFS is that the sum of the qth power of membership degree and the qth power of non-membership degree is less than or equal to one. Evidently, the larger the rung q, the more orthopairs satisfy the bounding constraint and thus the larger the fuzzy information space that can be expressed by q-ROFSs. This feature makes q-ROFSs more powerful and useful than IFS and PFS in the aspect of dealing with vagueness and fuzzy information. For instance, a decision maker provides 0.9 and 0.7 as the membership and non-membership degrees, respectively. Given 0.9 + 0.7 > 1 and 0.9² + 0.7² > 1, the evaluation attribute value (0.9, 0.7) cannot be expressed by IFSs and PFSs. In this case, when q = 4, we can get 0.9⁴ + 0.7⁴ < 1 and the evaluation value of attributes can be expressed by q-ROFSs. Therefore, by adjusting the value of parameter q, q-ROFSs allow decision makers to independently assign values to membership degree and non-membership degree. Based on these advantages of q-ROFSs, Liu and Wang [29], Liu and Liu [30], and Wei [31] successively extended existing operators, such as arithmetic and geometric operators, BM operator and Heronian mean to the q-ROFSs. Meanwhile, Peng et al. [32] proposed a new exponential operational law on q-ROFNs and then applied it to derive the q-rung orthopair fuzzy weighted exponential aggregation operator. Liu et al. [33] propose a new method based on the q-rung orthopair fuzzy extended Bonferroni mean (q-ROFEBM) operator and entropy measure for dealing with heterogeneous relationships among attributes and unknown attribute weight information.

However, owing to the increased complications of modern decision-making problems, the following MAGDM issues should be considered. (1) The aforementioned q-rung orthopair fuzzy aggregation operators are based on the algebraic operational rules proposed by Liu and Wang [29]. Nevertheless, the traditional algebraic operational rules of q-ROFNs proposed by Liu and Wang [29] do not consider the interaction between membership and non-membership degrees. For instance, let a_i = (u_i, v_i), (i = 1, 2,…, n) be a collection of q-ROFNs. If a_k = (u_k, 0), and $u_{k} \ne 0$, then by traditional algebraic operational rules [29], we derive $u_{{a_{i} \times a_{k} }} = 0$, which means the non-membership degrees of the product result of $u_{{a_{i} }}$ and $u_{{a_{k} }}$ will always be zero if $v_{k} = 0$. Moreover, all the aggregation operators for q-ROFNs based on the algebraic operational rules are also unsuitable for all the circumstances. Taking the q-ROFWA(a₁, a₂,…, a_n) operator in the literature [29] as an example, we will get $v_{{q - {\text{ROFWA}}(a_{1} ,a_{2} , \ldots ,a_{n} )}} = 0$ if $v_{k} = 0.$ Obviously, $v_{{a_{i} }} \left( {i = 1,2, \ldots ,n,i \ne k} \right)$ will have no influence of the final aggregation results, which is somewhat counterintuitive. Therefore, there is need to improve the operational laws of q-ROFNs. (2) In most decision-making problems, some of the attributes are often correlated so that the interrelationships among them should be taken into account. An issue with Liu’s [30] and Wei’s [31] operators is that they can only consider the interrelationship between any two arguments. Thus, we should pay attention to the aggregation technologies that can account for the interrelationships among multiple attributes.

Obviously, the interaction operational laws proposed by He et al. [34, 35] can address the first issue mentioned above by considering the interactions between membership and non-membership degrees. Therefore, we first develop new interaction operational laws of q-ROFNs. For the second issue, we note that the Hamy mean (HM) introduced by Hara et al. [36] is an effective information aggregation technology. Compared with the Bonferroni mean (BM) and Heronian mean [37, 38], HM is more powerful and useful as it takes into account of the interrelationships among multiple arguments. In addition, Qin [39], Liu and You [40] point out that HM can be regarded as an extension of MSM from the perspective of mathematical structure. Hence, we use HM to aggregate q-rung orthopair fuzzy information. Based on the above comprehensive analysis, the goal of this paper is to develop q-rung orthopair fuzzy aggregation operators by combining HM operators with interaction operational laws and then apply them to solve MAGDM problems. Therefore, we propose q-rung orthopair fuzzy interaction weighted Hamy mean operators and its dual form and develop a new MAGDM method under the q-rung orthopair fuzzy environment to deal with the complex MAGDM problems mentioned above.

The main contributions of this paper are three aspects. First, interaction operational rules of q-ROFNs are provided. The proposed operational rules take the interaction among membership and non-membership degrees into account. Thus, they can reasonably handle situations in which the membership or non-membership degrees equal to zero values and exhibit more powerfulness and flexibility than existing operational rules of q-ROFNs. Second, novel q-rung orthopair fuzzy aggregation operators are proposed. More concretely, we not only propose q-rung orthopair fuzzy interaction Hamy mean operator but also propose DHM and extend it to q-ROFSs. The proposed operators not only take the interaction among membership and non-membership degrees and the interrelationship among multiple aggregated q-ROFNs into consideration, but also demonstrate high generality than exiting q-rung orthopair fuzzy aggregation operators. Third, a novel approach to MAGDM with q-rung orthopair fuzzy information is proposed. Compared with the existing MAGDM methods, the novel method has wider and more flexible applicable scope.

The rest of this paper is organized as follows. Section 3 briefly recalls basic concepts of the q-ROFS and HM and then proposes interaction operational laws on q-ROFNs and the dual form of HM in Sect. 4. In Sect. 4, we develop new q-rung orthopair fuzzy aggregation operators, such as the q-ROFIHM operator and the q-ROFIWHM operator. In Sect. 5, we further develop the q-ROFIDHM and the q-ROFIWDHM operators. In Sect. 6, we introduce a novel approach to MAGDM problems based on the proposed operators. In Sects. 7 and 8, a numerical example is provided to show the validity and advantages of the proposed method.

2 Preliminaries

In this section, we introduce basic concepts, such as q-ROFS, operational laws on q-ROFNs, HM and DHM.

2.1 q-Rung orthopair fuzzy set and improved operational rules

Definition 1

[28] Let X be an ordinary fixed set, a q-ROFS A defined on X is given by

$$ A = \left\{ {\left\langle {x,\mu_{A} \left( x \right),v_{A} \left( x \right)} \right\rangle \;\left| {x \in X} \right.} \right\} , $$

(1)

where $\;\mu_{A} \left( x \right)$ and $\;v_{A} \left( x \right)$ represent the membership degree and non-membership degree, respectively, satisfying $\;\mu_{A} \left( x \right) \in \left[ {0,1} \right]$,$\;v_{A} \left( x \right) \in \left[ {0,1} \right]$ and $\;0 \le \mu_{A} \left( x \right)^{q} + v_{A} \left( x \right)^{q} \le 1$, $\left( {q \ge 1} \right)$. The indeterminacy degree is defined as $\pi_{A} \left( x \right) = \left( {\mu_{A} \left( x \right)^{q} + v_{A} \left( x \right)^{q} - \mu_{A} \left( x \right)^{q} v_{A} \left( x \right)^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} .$ For convenience, $\left( {\mu_{A} \left( x \right),v_{A} \left( x \right)} \right)$ is called a q-ROFN by Liu and Wang [29], which can be denoted by $A = \left( {\mu_{A} ,v_{A} } \right)$.

Liu and Wang [29] also proposed operational laws for q-ROFNs as follows.

Definition 2

[29] Let $a = \left( {\mu ,v} \right),$$a_{1} = \left( {\mu_{1} ,v_{1} } \right)$, and $a_{2} = \left( {\mu_{2} ,v_{2} } \right)$ be three q-ROFNs, and $\lambda$ be a positive real number, then

• 1.
  $$ a_{2} \oplus a_{2} = \left( {\left( {u_{1}^{q} + u_{2}^{q} - u_{1}^{q} u_{2}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,v_{1} v_{2} } \right) $$
• 2.
  $$ a_{2} \otimes a_{2} = \left( {\mu_{1} \mu_{2} ,\left( {v_{1}^{q} + v_{2}^{q} - v_{1}^{q} v_{2}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right) $$
• 3.
  $$ \lambda a = \left( {\left( {1 - \left( {1 - \mu^{q} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,v^{\lambda } } \right) $$
• 4.
  $$ a^{\lambda } = \left( {\mu^{\lambda } ,\left( {1 - \left( {1 - v^{q} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right) $$

However, the above operational laws do not consider some special cases. For instance, let $a_{1} = \left( {\mu_{1} ,v_{1} } \right)$ and $a_{2} = \left( {\mu_{2} ,v_{2} } \right)$ be two q-ROFNs, if $v_{1} = 0$ and $v_{2} \ne 0$ or $v_{1} \ne 0$ and $v_{2} = 0$, according the above operational laws, the non-membership of the addition of $a_{1}$ and $a_{2}$ is zero. Obviously, if one of the non-memberships is zero, then the result of non-membership of addition will be zero no matter what other values are. In order to overcome this situation, we define new operational laws for q-ROFNs that are shown as follows.

Definition 3

Let $a = \left( {\mu ,v} \right)$,$a_{1} = \left( {\mu_{1} ,v_{1} } \right)$ and $a_{2} = \left( {\mu_{2} ,v_{2} } \right)$ be any three q-ROFNs and $\lambda$ be a positive real number, then interaction operational laws on q-ROFNs are defined as:

• 1. $a_{1} \oplus a_{2} = \left\langle {\left. {\left( {1 - \left( {1 - \mu_{1}^{q} } \right)\left( {1 - \mu_{2}^{q} } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {\left( {1 - \mu_{1}^{q} } \right)\left( {1 - \mu_{2}^{q} } \right) - \left( {1 - \mu_{1}^{q} - v_{1}^{q} } \right)\left( {1 - \mu_{2}^{q} - v_{2}^{q} } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle } \right.$

• 2. $a_{1} \otimes a_{2} = \left\langle {\left. {\left( {\left( {1 - v_{1}^{q} } \right)\left( {1 - v_{2}^{q} } \right) - \left( {1 - \mu_{1}^{q} - v_{1}^{q} } \right)\left( {1 - \mu_{2}^{q} - v_{2}^{q} } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {1 - \left( {1 - v_{1}^{q} } \right)\left( {1 - v_{2}^{q} } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle } \right.$

• 3. $\lambda a = \left\langle {\left. {\left( {1 - \left( {1 - \mu^{q} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {\left( {1 - \mu^{q} } \right)^{\lambda } - \left( {1 - \mu^{q} - v^{q} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle } \right.$

• 4. $a^{\lambda } = \left\langle {\left. {\left( {\left( {1 - v^{q} } \right)^{\lambda } - \left( {1 - \mu^{q} - v^{q} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {1 - \left( {1 - v^{q} } \right)^{\lambda } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle } \right.$

To compare two q-ROFNs, Liu and Wang [29] proposed a comparison method for q-ROFNs.

Definition 4

[29] Let $a = \left( {\mu ,v} \right)$ be a q-ROFN, then the score function of a is defined as $S\left( a \right) = \mu^{q} - v^{q}$, and the accuracy of a is defined as $H\left( a \right) = \mu^{q} + v^{q}$. For any two q-ROFNs, $a_{1} = \left( {\mu_{1} ,v_{1} } \right)$ and $a_{2} = \left( {\mu_{2} ,v_{2} } \right)$. Then

• 1. If $S\left( {a_{1} } \right) > S\left( {a_{2} } \right)$, then $a_{1} > a_{2}$;

• 2. If $S\left( {a_{1} } \right) = S\left( {a_{2} } \right)$, then

  • If $H\left( {a_{1} } \right) > H\left( {a_{2} } \right)$, then $a_{1} > a_{2}$;

  • If $H\left( {a_{1} } \right) = H\left( {a_{2} } \right)$, then $a_{1} = a_{2}$.

3 Hamy mean and dual Hamy mean

Hamy mean (HM) was firstly proposed by Hara et al. [36] for crisp numbers. It can consider the interrelationships among arguments.

Definition 5

[36] Let $a_{i} (i = 1,2, \ldots ,n)$ be a collection of crisp numbers, and $k = 1,2, \ldots ,n$, if

$$ {\text{HM}}^{\left( k \right)} \left( {\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{n} } \right) = \frac{{\sum\nolimits_{{1 \le i_{1} < \cdots < i_{n} }} {\left( {\prod\nolimits_{j = 1}^{k} {a_{{i_{j} }} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } }}{{C_{n}^{k} }} $$

(2)

then $HM^{\left( k \right)}$ is called the Hamy mean, where $\left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right)$ traversal all the k-tuple combinations of $\left( {1,2, \ldots ,n} \right)$ and $C_{n}^{k}$ is the binomial coefficient.

From Eq. (2), it is clear that the HM satisfies the following properties:

• 1. ${\text{HM}}^{\left( k \right)} \left( {0,0, \ldots ,0} \right) = 0$

• 2. ${\text{HM}}^{\left( k \right)} \left( {a,a, \ldots ,a} \right) = a$

• 3. ${\text{HM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \le {\text{HM}}^{\left( k \right)} \left( {b_{1} ,b_{2} , \ldots ,b_{n} } \right)$, if $a_{i} \le b_{i}$ for all i

• 4. ${ \hbox{min} }_{i} \left( {a_{i} } \right) \le {\text{HM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \le { \hbox{max} }_{i} \left( {a_{i} } \right)$

From the above properties, we know the HM is a Schur-convex and monotonic function when aggregating numerical information. Based on the theory of majorization, there exists a dual form of the HM such that it satisfies Schur convexity and monotonic as well. Therefore, we propose the DHM as follows:

Definition 6

Let $a_{i} = \left( {u_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$ be a collection of crisp numbers, and $k = 1,2, \ldots ,n$, if

$$ {\text{DHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\frac{{\sum\nolimits_{j = 1}^{k} {a_{{i_{j} }} } }}{k}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} $$

(3)

then ${\text{DHM}}^{\left( k \right)}$ is called the dual Hamy mean, where $\left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right)$ traversal all the k-tuple combinations of $\left( {1,2, \ldots ,n} \right)$ and $C_{n}^{k}$ is the binomial coefficient.

In particular, if k = 1, based on the definition of DHM, the DHM reduces to the geometric mean as follows:

$$ {\text{DHM}}^{\left( 1 \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left( {\prod\limits_{{1 \le i_{1} \le n}} {a_{{i_{{1^{\prime } }} }} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} $$

(4)

if k = n, based on the definition of DHM, the DHM reduces to the arithmetic operator as follows:

$$ {\text{DHM}}^{\left( n \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \frac{{\sum\nolimits_{{1 \le i_{1} < n}} {a_{{i_{{1^{\prime } }} }} } }}{n} $$

(5)

Moreover, it is easy to prove that the DHM operator satisfies the following properties:

• 1. ${\text{DHM}}^{\left( k \right)} \left( {0,0, \ldots ,0} \right) = 0$

• 2. ${\text{DHM}}^{\left( k \right)} \left( {a,a, \ldots ,a} \right) = a$

• 3. ${\text{DHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \le {\text{DHM}}^{\left( k \right)} \left( {b_{1} ,b_{2} , \ldots ,b_{n} } \right)$, i.e., DHM is monotonic, if $a_{i} \le b_{i}$ for all i

• 4. ${ \hbox{min} }_{i} \left( {a_{i} } \right) \le {\text{DHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \le { \hbox{max} }_{i} \left( {a_{i} } \right)$

4 q-Rung orthopair fuzzy interaction Hamy mean aggregation operators

In this section, based on interaction operational laws of q-ROFNs, we extend the HM to q-rung orthopair fuzzy environment and propose a q-rung orthopair fuzzy interaction Hamy mean (q-ROFIHM) operator and its weight form (q-ROFIWHM).

4.1 q-ROFIHM operator

Definition 7

Let $a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$ be a collection of q-ROFNs, and $k = 1,2, \ldots ,n$, then the q-ROFIHM operator is defined as

$$ q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{k} a_{{i_{j} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} }}{{C_{n}^{k} }} $$

(6)

where $\left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right)$ traversal all the k-tuple combinations of $\left( {1,2, \ldots ,n} \right)$ and $C_{n}^{k}$ is the binomial coefficient.

Based on the new operational rules for q-ROFNs in Sect. 2, the following theorem can be obtained.

Theorem 1

Let $a_{i} = \left( {\mu_{i} ,v_{i} } \right)$ $(i = 1,2, \ldots ,n)$ be a collection of q-ROFNs, and $k = 1,2, \ldots ,n$ , then the aggregated value by the q-ROFIHM operator is still a q-ROFN and

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left\langle {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} } \right., \\ & \quad \left. {\left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} } \right\rangle \\ \end{aligned} $$

(7)

Proof

According to the operations for q-ROFNs, we can get

$$ \begin{aligned} & \mathop \otimes \limits_{j = 1}^{k} a_{{i_{j} }} { = }\left( {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)} - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)} } \right)^{1/q} ,\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)} } \right)^{1/q} } \right) \\ & \left( {\mathop \otimes \limits_{j = 1}^{k} a_{{i_{j} }} } \right)^{1/k} { = }\left( {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)^{1/q} ,\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)^{1/q} } \right) \\ \end{aligned} $$

Then $\begin{aligned} & \mathop \oplus \limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \limits_{j = 1}^{k} a_{{i_{j} }} } \right)^{1/k} = \left( {\left( {1 - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{1/q} } \right. , \\ & \quad \left. {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{1/q} } \right) \\ \end{aligned}$

Subsequently, we have

$$ \begin{aligned} & \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \limits_{j = 1}^{k} a_{{i_{j} }} } \right)^{1/k} }}{{C_{n}^{k} }} = \left\langle {\left( {1 - \left( {\prod\nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\nolimits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} } \right. \\ & \quad \left. {\left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} } \right\rangle \\ \end{aligned} $$

According to the above process, Eq. (7) is kept.

(2) In the following, we prove that Eq. (7) is a q-ROFN. It needs to meet two conditions:

• i. $0 \le \mu \le 1,\;0 \le v \le 1;$

• ii. $0 \le \mu^{q} + v^{q} \le 1.$

Let

$$ \begin{aligned} \mu & = \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} \\ v & = \left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} \\ \end{aligned} $$

We prove the condition (1) as follows:

We know

$$ \mu_{i} \in \left[ {0,1} \right],v_{i} \in \left[ {0,1} \right],\;{\text{and}}\;0 \le \mu_{i}^{q} + \nu_{i}^{q} \le 1. $$

So we have

$$ 0 \le \prod\limits_{j = 1}^{k} {\left( {1 - \nu_{i}^{q} } \right)^{1/k} } \le 1,\;{\text{and}}\;0 \le \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{1/k} } \le 1. $$

Then

$$ 0 \le 1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \le 1. $$

And

$$ 0 \le \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} \le 1. $$

We get

$$ 0 \le \mu = \left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} \le 1. $$

So far, $0 \le \mu \le 1$ is proved. Similarly, we have $0 \le v \le 1.$

And then, we will prove the condition (2):

$$ \mu^{q} + v^{q} = 1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} . $$

We have proved that $0 \le \prod\nolimits_{j = 1}^{n} {\left( {1 - \mu_{i}^{q} - \nu_{i}^{q} } \right)^{1/k} } \le 1.$

So $0 \le 1 - \left( {\prod\nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\nolimits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{{1/k} \mathord{\left/ {\vphantom {{1/k} k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} \le 1.$

So far, $0 \le \mu^{q} + v^{q} \le 1$ holds, too, which means the aggregated value obtained by the q-ROFIHM operator is also a q-ROFN. Therefore, the proof of Theorem 1 is complete.□

Example 1

Let $a_{1} = \left( {0.9,0.3} \right),a_{2} = \left( {0.7,0.6} \right),a_{3} = \left( {0.6,0.8} \right)$ be three q-ROFNs, then we utilize the q-ROFIHM operator (suppose k = 2) to aggregate them and get a comprehensive value. Steps are shown as follows:

$$ \begin{aligned} & q - {\text{ROFIHM}}^{(k)} \left( {a_{1} ,a_{2} ,a_{3} } \right) = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{k} a_{{i_{j} }} } \right)^{1/k} }}{{C_{n}^{k} }} \\ & \quad { = }\left\langle {\left( {1 - \left( \begin{aligned} \left( {1 - \left( {1 - 0.3^{3} } \right)^{1/2} \times \left( {1 - 0.6^{3} } \right)^{1/2} + \left( {1 - 0.9^{3} - 0.3^{3} } \right)^{1/2} \times \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{1/2} } \right) \hfill \\ \times \left( {1 - \left( {1 - 0.3^{3} } \right)^{1/2} \times \left( {1 - 0.8^{3} } \right)^{1/2} + \left( {1 - 0.9^{3} - 0.3^{3} } \right)^{1/2} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{1/2} } \right) \hfill \\ \times \left( {1 - \left( {1 - 0.6^{3} } \right)^{1/2} \times \left( {1 - 0.8^{3} } \right)^{1/2} + \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{1/2} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{1/2} } \right) \hfill \\ \end{aligned} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{3}^{2} }}} \right. \kern-0pt} {C_{3}^{2} }}}} } \right)^{1/3} ,} \right. \\ & \quad \left( {\left( \begin{aligned} \left( {1 - \left( {1 - 0.3^{3} } \right)^{1/2} \times \left( {1 - 0.6^{3} } \right)^{1/2} + \left( {1 - 0.9^{3} - 0.3^{3} } \right)^{1/2} \times \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \times \left( {1 - \left( {1 - 0.3^{3} } \right)^{1/2} \times \left( {1 - 0.8^{3} } \right)^{1/2} + \left( {1 - 0.9^{3} - 0.3^{3} } \right)^{1/2} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \times \left( {1 - \left( {1 - 0.6^{3} } \right)^{1/2} \times \left( {1 - 0.8^{3} } \right)^{1/2} + \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{1/2} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \end{aligned} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{3}^{2} }}} \right. \kern-0pt} {C_{3}^{2} }}}} } \right. \\ & \quad - \left. {\left. {\left( {\left( {\left( {1 - 0.9^{3} - 0.3^{3} } \right) \times \left( {1 - 0.7^{3} - 0.6^{3} } \right) \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)} \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{3}^{2} }}} \right. \kern-0pt} {C_{3}^{2} }}}} } \right)^{1/3} } \right\rangle \\ & \quad = \left( {0.7530, \, 0.6422} \right) \\ \end{aligned} $$

In the following, we present desirable properties of the q-ROFIHM operator.

Theorem 2

(Idempotency). Let$a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$be a collection of q-ROFNs, if all the q-ROFNs are equal, i.e.,$a_{i} = a$for all i, then

$$ q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = a. $$

(8)

Proof

Since $a_{i} = a$ for all i, we have

$$ \begin{aligned} q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) & = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{k} a_{{i_{j} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} }}{{C_{n}^{k} }} = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{k} a} \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} }}{{C_{n}^{k} }} \\ & \quad { = }\frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {a^{k} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} }}{{C_{n}^{k} }} = \frac{1}{{C_{n}^{k} }}C_{n}^{k} a = a. \\ \end{aligned} $$

□

Theorem 3

(Commutativity) Let$a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$be a collection of q-ROFNs, and$\left( {\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} } \right)$is any permutation of$\left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right),$then

$$ q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = q - {\text{ROFIHM}}^{\left( k \right)} \left( {\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} } \right) $$

(9)

Proof

Since $a_{i} = a$ for all i, we have

$$ \begin{aligned} q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) &= \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{k} a_{{i_{j} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} }}{{C_{n}^{k} }} \\ & = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{k} \tilde{a}_{{i_{j} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} }}{{C_{n}^{k} }} = q - {\text{ROFIHM}}^{\left( k \right)} \left( {\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} } \right). \\ \end{aligned} $$

□

By assigning different values to the parameters k and q, special cases can be obtained accordingly.

Case 1

if k = 1, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{1} a_{{i_{j} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 1}} \right. \kern-0pt} 1}}} }}{n} \\ & \quad = \left\langle {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \prod\limits_{j = 1}^{1} {\left( {1 - v_{{i_{j} }}^{q} } \right)} + \prod\limits_{j = 1}^{1} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,} \right. \\ & \quad \left. {\left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{1} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 1}} \right. \kern-0pt} 1}}} } + \prod\limits_{j = 1}^{1} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{1} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 1}} \right. \kern-0pt} 1}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ & \quad = \left\langle {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{q} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right.,\quad \left. {\left( {\left( {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{q} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} - \left( {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{q} - v_{{i_{1} }}^{q} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ & \quad = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < n}} a_{{i_{1`} }} }}{n}{ = }\frac{{\mathop \oplus \nolimits_{i = 1}^{n} a_{{i_{`} }} }}{n} = q - {\text{ROFIA}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the q-rung orthopair fuzzy interaction averaging (q-ROFIA) operator.

Case 2

if k = n, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left\langle {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{n} \le n}} {\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } + \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)} } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right., \\ & \quad \left. {\left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } + \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)} } \right) - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{n} \le n}} {\left( {\prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)} } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ & \quad = \left\langle {\left( {1 - \left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } + \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right., \\ & \quad \left. {\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } + \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ & \quad = \left\langle {\left( {\prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right.,\left. {\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ & \quad = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{n} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{n} a_{{i_{j} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} }}{{C_{n}^{n} }} = \left( {\mathop \otimes \nolimits_{i = 1}^{n} a_{i} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} = q - {\text{ROFIG}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the q-rung orthopair fuzzy interaction geometric (q-ROFIG) operator.

Case 3

if q = 1, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left\langle {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }} - v_{{i_{j} }} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right., \\ & \quad \left. {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }} - v_{{i_{j} }} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }} - v_{{i_{j} }} } \right)^{1/k} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right\rangle \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the intuitionistic fuzzy interaction Hamy mean (IFIHM) operator.

Case 4

if q = 2, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left\langle {\sqrt {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } } \right., \\ & \quad \left. {\sqrt {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } } \right\rangle \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the Pythagorean fuzzy interaction Hamy mean (PFIHM) operator.

Case 5

if k = 1, q = 1, based on the definition of q-ROFIHM operator, we have

$$ q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left\langle {1 - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right.,\left. {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{{}} - v_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right\rangle $$

In this case, the q-ROFIHM operator reduces to the intuitionistic fuzzy weighted interaction geometric (IFWIG) operator.

Case 6

if k = n, q = 1, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\& = \left\langle {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - v_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{{}} - v_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } ,} \right.\left. {1 - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - v_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right\rangle \\ & \quad = {\text{IFWGIA}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the intuitionistic fuzzy weighted geometric interaction averaging (IFWGIA) operator defined by He et al. [34].

Case 7

if k = 1, q = 2, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned}& q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\& = \left\langle {\sqrt {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } } \right.,\left. {\sqrt {\prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } } \right\rangle \\ & = {\text{PFIWA}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the Pythagorean fuzzy interaction weighted averaging (PFIWA) operator defined by Wei [20].

Case 8

if k = n, q = 2, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\& = \left\langle {\sqrt {\prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } } \right.,\left. {\sqrt {1 - \prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } } \right\rangle \\ & = {\text{PFIWG}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the Pythagorean fuzzy interaction weighted geometric (PFIWG) operator defined by Wei [20].

4.2 q-ROFIWHM operator

In many situations, the importance of each argument is not equal and thus needs to be assigned different weights. However, the q-ROFIHM operator does not consider the importance of the aggregated arguments. To overcome the shortcoming, we introduce its weighted form (q-ROFIWHM).

Definition 8

Let $a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$ be a collection of q-ROFNs, $w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{\text{T}}$ be the weight vector of $a_{i}$, satisfying $w_{i} \in \left[ {0,1} \right]$ and $\sum\nolimits_{i = 1}^{n} {w_{i} } = 1$, and $k = 1,2, \ldots ,n$. Then the q-ROFIWHM operator is defined as

$$ q - {\text{ROFIWHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{k} \left( {a_{{i_{j} }} } \right)^{{w_{{i_{j} }} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} }}{{C_{n}^{k} }} $$

(10)

where $\left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right)$ traversal all the k-tuple combinations of $\left( {1,2, \ldots ,n} \right)$ and $C_{n}^{k}$ is the binomial coefficient.

Similarly, we can obtain the following aggregated value by the q-ROFIWHM operator according to the operational rules of q-ROFNs given in Definition 2.

Theorem 4

Let$a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$be a collection of q-ROFNs and$k = 1,2, \ldots ,n$, then the aggregated value by the q-ROFIWHM operator is also a q-ROFNs and

$$ \begin{aligned} & q - {\text{ROFIWHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left\langle {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right., \\ & \quad \left. {\left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ \end{aligned} $$

(11)

Proof

Because $\left( {a_{{i_{j} }} } \right)^{{w_{{i_{j} }} }} = \left\langle {\left. {\left( {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{w_{{i_{j} }} }} - \left( {1 - \mu_{{i_{j} }}^{q} - \nu_{{i_{j} }}^{q} } \right)^{{w_{{i_{j} }} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {1 - \left( {1 - v_{{i_{j} }}^{q} } \right)^{{w_{{i_{j} }} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle } \right.$, we can replace $\mu_{{i_{j} }}$ in Eq. (7) with $\left( {\left( {1 - v_{{i_{j} }}^{q} } \right)^{{w_{{i_{j} }} }} - \left( {1 - \mu_{{i_{j} }}^{q} - \nu_{{i_{j} }}^{q} } \right)^{{w_{{i_{j} }} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}$ and $\nu_{{i_{j} }}$ in Eq. (7) with $\left( {1 - \left( {1 - v_{{i_{j} }}^{q} } \right)^{{w_{{i_{j} }} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}}$, then we can get Eq. (11).

Example 2

In Example 1, if the input arguments $a_{1} ,a_{2} ,a_{3}$ have a different importance, then we select the q-ROFIWHM operator to aggregate. Here, we assume that the weight of each argument is $w_{1} = 0.27$,$w_{2} = 0.39$ and $w_{3} = 0.34$, then

$$ \begin{aligned} & q - {\text{ROFIWHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} ,a_{3} } \right) = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < \ldots < i_{k} \le n}} \left( {\mathop \otimes \nolimits_{j = 1}^{k} \left( {a_{{i_{j} }} } \right)^{{w_{{i_{j} }} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} }}{{C_{n}^{k} }} \\ & \quad \left\langle {\left( {1 - \left( \begin{aligned} \left( {1 - \left( {1 - 0.3^{3} } \right)^{{{{0.27} \mathord{\left/ {\vphantom {{0.27} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.6^{3} } \right)^{{{{0.39} \mathord{\left/ {\vphantom {{0.39} 2}} \right. \kern-0pt} 2}}} + \left( {1 - 0.9^{3} - 0.3^{3} } \right)^{{{{0.27} \mathord{\left/ {\vphantom {{0.27} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{{{{0.39} \mathord{\left/ {\vphantom {{0.39} 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \times \left( {1 - \left( {1 - 0.3^{3} } \right)^{{{{0.27} \mathord{\left/ {\vphantom {{0.27} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.8^{3} } \right)^{{{{0.34} \mathord{\left/ {\vphantom {{0.34} 2}} \right. \kern-0pt} 2}}} + \left( {1 - 0.9^{3} - 0.3^{3} } \right)^{{{{0.27} \mathord{\left/ {\vphantom {{0.27} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{{{{0.34} \mathord{\left/ {\vphantom {{0.34} 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \times \left( {1 - \left( {1 - 0.6^{3} } \right)^{{{{0.39} \mathord{\left/ {\vphantom {{0.39} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.8^{3} } \right)^{{{{0.34} \mathord{\left/ {\vphantom {{0.34} 2}} \right. \kern-0pt} 2}}} + \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{{{{0.39} \mathord{\left/ {\vphantom {{0.39} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{{{{0.34} \mathord{\left/ {\vphantom {{0.34} 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \end{aligned} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{3}^{2} }}} \right. \kern-0pt} {C_{3}^{2} }}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} ,} \right. \\ & \quad \left( {\left( \begin{aligned} \left( {1 - \left( {1 - 0.3^{3} } \right)^{{{{0.27} \mathord{\left/ {\vphantom {{0.27} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.6^{3} } \right)^{{{{0.39} \mathord{\left/ {\vphantom {{0.39} 2}} \right. \kern-0pt} 2}}} + \left( {1 - 0.9^{3} - 0.3^{3} } \right)^{{{{0.27} \mathord{\left/ {\vphantom {{0.27} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{{{{0.39} \mathord{\left/ {\vphantom {{0.39} 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \times \left( {1 - \left( {1 - 0.3^{3} } \right)^{{{{0.27} \mathord{\left/ {\vphantom {{0.27} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.8^{3} } \right)^{{{{0.34} \mathord{\left/ {\vphantom {{0.34} 2}} \right. \kern-0pt} 2}}} + \left( {1 - 0.9^{3} - 0.3^{3} } \right)^{{{{0.27} \mathord{\left/ {\vphantom {{0.27} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{{{{0.34} \mathord{\left/ {\vphantom {{0.34} 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \times \left( {1 - \left( {1 - 0.6^{3} } \right)^{{{{0.39} \mathord{\left/ {\vphantom {{0.39} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.8^{3} } \right)^{{{{0.34} \mathord{\left/ {\vphantom {{0.34} 2}} \right. \kern-0pt} 2}}} + \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{{{{0.39} \mathord{\left/ {\vphantom {{0.39} 2}} \right. \kern-0pt} 2}}} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{{{{0.34} \mathord{\left/ {\vphantom {{0.34} 2}} \right. \kern-0pt} 2}}} } \right) \hfill \\ \end{aligned} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{3}^{2} }}} \right. \kern-0pt} {C_{3}^{2} }}}} } \right. \\ & & \quad - \left. {\left. {\left( {\left( {\left( {1 - 0.9^{3} - 0.3^{3} } \right)^{0.27} \times \left( {1 - 0.7^{3} - 0.6^{3} } \right)^{0.39} \times \left( {1 - 0.6^{3} - 0.8^{3} } \right)^{0.34} } \right)} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{3}^{2} }}} \right. \kern-0pt} {C_{3}^{2} }}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} } \right\rangle \\ & \quad = \left( {0.5938, \, 0.4753} \right) \\ \end{aligned} $$

5 q-Rung orthopair fuzzy interaction dual Hamy mean aggregation operators

In this section, based on interaction operational laws of q-ROFNs and proposed dual HM in Sect. 3, we develop the q-rung orthopair fuzzy interaction dual Hamy mean operator (q-ROFIDHM) and its weighted form (q-ROFIWDHM).

5.1 q-ROFIDHM operator

Definition 9

Let $a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$ be a collection of q-ROFNs, and $k = 1,2, \ldots ,n$, then the q-ROFIDHM operator is defined as

$$ q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left( {\mathop \otimes \limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} a_{{i_{j} }} }}{k}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} $$

(12)

where $\left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right)$ traversal all the k-tuple combinations of $\left( {1,2, \ldots ,n} \right)$ and $C_{n}^{k}$ is the binomial coefficient.

Based on the interaction operational laws for q-ROFNs, the following theorem can be obtained.

Theorem 5

Let $a_{i} = \left( {\mu_{i} ,v_{i} } \right)$ $(i = 1,2, \ldots ,n)$ be a collection of q-ROFNs, and $k = 1,2, \ldots ,n$ , then the aggregated value by the q-ROFIDHM operator is still a q-ROFN and

$$ \begin{aligned} & q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,} \right. \\ & \quad \left. {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ \end{aligned} $$

(13)

Proof

According to the interaction operational laws for q-ROFNs, we can get

$$ \begin{aligned} & \mathop \oplus \limits_{j = 1}^{k} a_{{i_{j} }} { = }\left( {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)} - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right) \\ & \frac{{\mathop \oplus \nolimits_{j = 1}^{k} a_{{i_{j} }} }}{k}{ = }\left( {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right) \\ \end{aligned} $$

Then $\begin{aligned} \mathop \otimes \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} a_{{i_{j} }} }}{k} & = \left( {\left. {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right),} \right. \\ & \quad \left( {1 - \prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} \\ \end{aligned}$

Subsequently, we have

$$ \begin{aligned} & \left( {\mathop \otimes \limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} a_{{i_{j} }} }}{k}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} \\ & \quad = \left\langle {\left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,} \right. \\ & \quad \left. {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ \end{aligned} $$

Therefore, Eq. (13) holds, which completes the proof.□

In the following, we discuss some desirable properties of the q-ROFIDHM operator.

Theorem 6

(Idempotency) Let$a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$be a collection of q-ROFNs, if all the q-ROFNs are equal, i.e.,$a_{i} = a$for all i, then

$$ q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = a. $$

(14)

Proof

Since $a_{i} = a$ for all i, we have

$$ \begin{aligned} q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) & \quad = \left( {\mathop \otimes \limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} a_{{i_{j} }} }}{k}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} = \left( {\mathop \otimes \limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} a}}{k}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} \\ & \quad = \left( {\mathop \otimes \limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} a} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} = \left( {a^{{C_{n}^{k} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} = a. \\ \end{aligned} $$

□

Theorem 7

(Commutativity). Let$a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$be a collection of q-ROFNs, and$\left( {\tilde{a}_{1} ,\tilde{a}_{2} , \cdots \tilde{a}_{n} } \right)$is any permutation of$\left( {a_{1} ,a_{2} , \cdots a_{n} } \right),$then

$$ q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = q - {\text{ROFIDHM}}^{\left( k \right)} \left( {\tilde{a}_{1} ,\tilde{a}_{2} , \ldots \tilde{a}_{n} } \right) $$

(15)

Proof

$$ \begin{aligned} & q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left( {\mathop \otimes \limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} a_{{i_{j} }} }}{k}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} \\ & \quad = \left( {\mathop \otimes \limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} \tilde{a}_{{i_{j} }} }}{k}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} = q - {\text{ROFIHM}}^{\left( k \right)} \left( {\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} } \right). \\ \end{aligned} $$

□

In the following, we discuss some cases with the changes to the parameters k and q.

Case 1

if k = 1, based on the definition of q-ROFIDHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\left( {\left( {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \nu_{{i_{1} }}^{q} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} - \left( {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{q} - v_{{i_{1} }}^{q} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} ,} \right.\left. {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \nu_{{i_{1} }}^{q} } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ & \quad = \left( {\mathop \otimes \nolimits_{{1 \le i_{1} \le n}} a_{{i_{1`} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} = q - {\text{ROFIG}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIDHM operator reduces to the q-rung orthopair fuzzy interaction geometric (q-ROFIG) operator.

Case 2

if k = n, based on the definition of q-ROFIDHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\left( {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right.,\left. {\left( {\prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 q}} \right. \kern-0pt} q}}} } \right\rangle \\ & \quad = \left( {\mathop \otimes \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} a_{{i_{j} }} }}{n}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{n} }}} \right. \kern-0pt} {C_{n}^{n} }}}} = \frac{{\mathop \oplus \nolimits_{{1 \le i_{1} < n}} a_{{i_{1`} }} }}{n} = q - {\text{ROFIA}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIDHM operator reduces to the q-rung orthopair fuzzy interaction averaging (q-ROFIA) operator.

Case 3

if q = 1, based on the definition of q-ROFIDHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIDHM}}^{(k)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }} - v_{{i_{j} }} } \right)^{1/k} } } \right)} } \right)^{{1/C_{n}^{k} }} } \right. \\ & \quad - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }} - v_{{i_{j} }} } \right)^{1/k} } } \right)} } \right)^{{1/C_{n}^{k} }} , \\ & \quad \left. {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }} } \right)^{1/k} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }} - v_{{i_{j} }} } \right)^{1/k} } } \right)} } \right)^{{1/C_{n}^{k} }} } \right\rangle . \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the intuitionistic fuzzy interaction dual Hamy mean (IFIDHM) operator.

Case 4

if q = 2, based on the definition of q-ROFIDHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\sqrt {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } } \right.. \\ & \qquad \left. {\sqrt {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } } \right\rangle \\ \end{aligned} $$

In this case, the q-ROFIDHM operator reduces to the Pythagorean fuzzy interaction dual Hamy mean (PFIDHM) operator.

Case 5

if k = 1, q = 1, based on the definition of q-ROFIDHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \nu_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{{}} - v_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right.,\left. {1 - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \nu_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right\rangle \\ & \quad = {\text{IFWGIA}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIDHM operator reduces to the intuitionistic fuzzy weighted geometric interaction averaging (IFWGIA) operator defined by He et al. [26].

Case 6

If k = n, q = 1, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {1 - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right.,\left. {\prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{{1 \le i_{1} \le n}} {\left( {1 - \mu_{{i_{1} }}^{{}} - v_{{i_{1} }}^{{}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } \right\rangle \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the intuitionistic fuzzy weighted interaction geometric (IFWIG) operator.

Case 7

if k = 1, q = 2, based on the definition of q-ROFIHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\sqrt {\prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } } \right.,\left. {\sqrt {1 - \prod\limits_{j = 1}^{n} {\left( {1 - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } } \right\rangle \\ & \quad = {\text{PFIWG}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIHM operator reduces to the Pythagorean fuzzy interaction weighted geometric (PFIWA) operator defined by Wei [20].

Case 8

if k = n, q = 2, based on the definition of q-ROFIDHM operator, we have

$$ \begin{aligned} & q - {\text{ROFIDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\sqrt {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } ,\left. {\sqrt {\prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{{i_{j} }}^{2} - v_{{i_{j} }}^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}}} } } } \right\rangle } \right. \\ & \quad = {\text{PFIWA}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ \end{aligned} $$

In this case, the q-ROFIDHM operator reduces to the Pythagorean fuzzy interaction weighted averaging (PFIWA) operator defined by Wei [20].

5.2 q-ROFIWDHM operator

Similarly, the q-ROFIDHM operator does not consider the importance of the input arguments. To overcome the limitation of the q-ROFIDHM operator, we propose its weighted form (q-ROFIWDHM).

Definition 10

Let $a_{i} = \left( {\mu_{i} ,v_{i} } \right)$$(i = 1,2, \ldots ,n)$ be a collection of q-ROFNs, $w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{\text{T}}$ be the weight vector of $a_{i}$, satisfying $w_{i} \in \left[ {0,1} \right]$ and $\sum\nolimits_{i = 1}^{n} {w_{i} } = 1$, and $k = 1,2, \ldots ,n$. Then the q-ROFIWDHM operator is defined as:

$$ q - {\text{ROFIWDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \left( {\mathop \otimes \nolimits_{{1 \le i_{1} < \cdots < i_{k} \le n}} \frac{{\mathop \oplus \nolimits_{j = 1}^{k} \left( {w_{{i_{j} }} \otimes a_{{i_{j} }} } \right)}}{k}} \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} $$

(16)

where $\left( {i_{1} ,i_{2} , \ldots ,i_{k} } \right)$ traversal all the k-tuple combinations of $\left( {1,2, \ldots ,n} \right)$ and $C_{n}^{k}$ is the binomial coefficient.

Similarly, we can obtain the following theorem according to the interaction operational rules of q-ROFNs.

Theorem 8

Let $a_{i} = \left( {\mu_{i} ,v_{i} } \right)$ $(i = 1,2, \ldots ,n)$ be a collection of q-ROFNs and $k = 1,2, \ldots ,n$ , then the aggregated value by the q-ROFIWDHM is also a q-ROFN and

$$ \begin{aligned} & q - {\text{ROFIWDHM}}^{\left( k \right)} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) \\ & \quad = \left\langle {\left( {\left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right.} \right. \\ & \quad \left. { - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {\prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} , \\ & \quad \left. {\left( {1 - \left( {\prod\limits_{{1 \le i_{1} < \cdots < i_{k} \le n}} {\left( {1 - \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } + \prod\limits_{j = 1}^{k} {\left( {1 - \mu_{{i_{j} }}^{q} - v_{{i_{j} }}^{q} } \right)^{{{{w_{{i_{j} }} } \mathord{\left/ {\vphantom {{w_{{i_{j} }} } k}} \right. \kern-0pt} k}}} } } \right)} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {C_{n}^{k} }}} \right. \kern-0pt} {C_{n}^{k} }}}} } \right)^{1/q} } \right\rangle \\ \end{aligned} $$

(17)

The proof of Theorem 8 is similar to that of Theorem 4, which is omitted here.

6 A novel approach to MAGDM problems based on the proposed operators

In this section, we shall apply the proposed aggregation operators to solve MAGDM problems under q-rung orthopair fuzzy environment.

6.1 Description of a typical MAGDM problem with q-rung orthopair fuzzy information

The q-ROFS is an effective tool to describe indeterminacy of decision makers. Therefore, it is widely used in MAGDM problems. A typical q-rung orthopair fuzzy MAGDM problem can be described as: Let $X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{m} } \right\}$ be a collection of alternatives, $G = \left\{ {G_{1} ,G_{2} , \ldots ,G_{n} } \right\}$ be n attributes and $D = \left\{ {D_{1} ,D_{2} , \ldots ,D_{t} } \right\}$ be a collection of decision makers. For attribute $G_{j} \left( {j = 1,2, \ldots ,n} \right)$ of alternative $x_{i} \left( {i = 1,2, \ldots ,m} \right)$, decision maker $D_{s}$ is required to utilize a q-ROFN to express his/her evaluation value, which can be denoted as $a_{ij}^{s} = \left( {\mu_{ij}^{s} ,v_{ij}^{s} } \right)$. Finally, several q-rung orthopair fuzzy decision matrices can be obtained, which can be denoted as $A^{s} = \left( {a_{ij}^{s} } \right)_{m \times n}$. Weight vector of decision makers is $\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{t} } \right)^{\text{T}}$, satisfying $\lambda_{s} \in \left[ {0,1} \right]\left( {s = 1,2, \ldots ,t} \right)$ and $\sum\nolimits_{s = 1}^{t} {\lambda_{s} } = 1$. Weight vector of the attributes is $w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{\text{T}}$, satisfying $w_{j} \in \left[ {0,1} \right]\left( {j = 1,2, \ldots ,n} \right)$ and $\sum\nolimits_{j = 1}^{n} {w_{j} } = 1$.

6.2 An algorithm to q-rung orthopair fuzzy MAGDM problems

Step 1

In decision-making problems, attributes can be classified into two types: the benefit type and the cost type. Therefore, the original decision matrix can be normalized to eliminate the impact of different attribute types. We can normalize the decision matrix by the following equation,

$$ a_{ij}^{s} = \left( {u_{ij}^{s} ,v_{ij}^{s} } \right)\left\{ \begin{aligned} \left( {\mu_{ij}^{s} ,v_{ij}^{s} } \right)\quad G_{j} \in I_{1} \hfill \\ \left( {v_{ij}^{s} ,\mu_{ij}^{s} } \right)\quad G_{j} \in I_{2} \hfill \\ \end{aligned} \right., $$

(18)

where $I_{1}$ and $I_{2}$ represent the benefit attribute type and the cost attribute type, respectively.

Step 2

Utilize the q-ROFIWHM operator

$$ a_{ij} = q - {\text{ROFIWHM}}^{\left( k \right)} \left( {a_{ij}^{1} ,a_{ij}^{2} , \ldots ,a_{ij}^{t} } \right) $$

(19)

or the q-ROFIWDHM operator

$$ a_{ij} = q - {\text{ROFIWDHM}}^{\left( k \right)} \left( {a_{ij}^{1} ,a_{ij}^{2} , \ldots ,a_{ij}^{t} } \right) $$

(20)

to fuse all attribute values to collective information $a_{ij}^{{}}$ with respect to each alternative for each decision maker.

Step 3

Utilize the q-ROFIWHM operator

$$ a_{i} = q - {\text{ROFIWHM}}^{\left( k \right)} \left( {a_{i1} ,a_{i2} , \ldots ,a_{\text{in}} } \right), $$

(21)

or the q-ROFIWDHM operator

$$ a_{i} = q - {\text{ROFIWDHM}}^{\left( k \right)} \left( {a_{i1} ,a_{i2} , \ldots ,a_{\text{in}} } \right), $$

(22)

to determine the overall evaluation value of each alternative $a_{i} \left( {i = 1,2, \ldots ,m} \right).$

Step 4

According to Definition 4, calculate the score value and accuracy degree of the overall evaluation value $a_{i} \left( {i = 1,2, \ldots ,m} \right).$

Step 5

Rank the alternatives and select the best one.

7 Numerical example

In this section, an application of the proposed approach is illustrated by a practical example about the “Location Selection” problem (cited from Liu et al. [41]).

Example 3

A company plans to select a best company location. After primary evaluation, there are five possible locations of the company remaining on the candidate list. They can be denoted by $X = \left\{ {x_{1} ,x_{2} ,x_{3} ,x_{4} ,x_{5} } \right\}.$ Three decision makers $D_{s} \left( {s = 1,2,3} \right)$ whose weight vector is $\lambda = \left( {0.35,0.45,0.2} \right)^{\text{T}}$ are invited to assess the five possible companies from four attributes which are defined as follows: the cost of rent (G₁), the convenience of transportation (G₂), the cost of labor (G₃) and the environmental impact (G₄). Suppose that the weight vector of the attributes is $w = \left( {0.25,0.1,0.3,0.35} \right)^{\text{T}}$. The decision makers $D_{s} \left( {s = 1,2,3} \right)$ are required to evaluate the companies $x_{i} \left( {i = 1,2,3,4,5} \right)$ with respect to the attributes $G_{j} \left( {j = 1,2,3,4} \right)$ by the q-ROFNs. Therefore, three decision matrices $A^{s} = \left( {a_{ij}^{s} } \right)_{5 \times 4} \left( {s = 1,2,3} \right)$ can be obtained, which are shown in Tables 1, 2 and 3. Then, we apply the proposed MAGDM approach to address the “Location Selection” problem:

Table 1 Decision matrix A¹ by expert D₁

Table 2 Decision matrix A² by expert D₂

Table 3 Decision matrix A³ by expert D₃

8 The decision-making process

(1) The decision-making steps based on the q-ROFIWHM operator

• Step 1 Normalize the decision-making matrices. As all the attributes are benefit attributes, they do not need to be normalized.

• Step 2 For each alternative $x_{i}$, aggregate each attribute value G_j provided by decision makers D_s. Here we utilize Eq. (19) to aggregate and we assume $q = 3$ and $k = 1$. Therefore, we can get an integration decision matrix as shown in Table 4.

  Table 4 Integration decision matrix

• Step 3 Calculate the collective evaluation value of each alternative by Eq. (21). We assume $q = 3$ and $k = 2$, then we get

  $$ \begin{aligned} a_{1} & = \left( {0.2086,0.1744} \right),\quad a_{2} = \left( {0.2640,0.1288} \right),\quad a_{3} = \left( {0.2346,0.1640} \right), \\ a_{4} & = \left( {0.2470,0.1628} \right),\quad a_{5} = \left( {0.2282,0.1560} \right) \\ \end{aligned} $$

• Step 4 Calculate the scores of collective evaluation values, we have

  $$ \begin{aligned} s\left( {a_{1} } \right) & = 0.0038,\quad s\left( {a_{2} } \right) = 0.0163,\quad s\left( {a_{3} } \right) = 0.0082, \\ s\left( {a_{4} } \right) & = 0.0107,\quad s\left( {a_{5} } \right) = 0.0081. \\ \end{aligned} $$

• Step 5 Rank the alternatives. According to the score values of overall assessments of alternatives, the ranking result of corresponding alternatives is $x_{2} \succ x_{4} \succ x_{3} \succ x_{5} \succ x_{1}$. Therefore,$x_{2}$ is the best company location.

(2) The decision-making steps based on the q-ROFIWDHM operator

• Step 1 Normalize the decision-making matrices. As all the attributes are benefit attributes, they do not need to be normalized.

• Step 2 For each alternative $x_{i}$, aggregate each attribute value $G_{i}$ provided by decision makers $D_{s}$. Here we utilize Eq. (20) to aggregate and we assume $q = 3$ and $k = 1$.

  Therefore, we can get the integration decision matrix shown in Table 5.

  Table 5 Integration decision matrix

• Step 3 Calculate the collective evaluation value of each alternative by Eq. (22). We assume $q = 3$ and $k = 2$, then we get

  $$ \begin{aligned} a_{1} & = \left( { 0. 2 0 5 9 , 0. 1 7 8 2} \right),\quad a_{2} = \left( { 0. 2 6 2 2 , 0. 1 3 5 9} \right),\quad a_{3} = \left( { 0. 2 3 0 6 , 0. 1 6 8 0} \right), \\ a_{4} & = \left( {{ 0} . 2 4 5 2 , 0. 1 6 6 8} \right),\quad a_{5} = \left( { 0. 2 2 5 9 , 0. 1 6 0 8} \right) \\ \end{aligned} $$

• Step 4 Calculate the scores of collective evaluation values, we have

  $$ \begin{aligned} & s\left( {a_{1} } \right) = 0.0031,\quad s\left( {a_{2} } \right) = 0.0155,\quad s\left( {a_{3} } \right) = 0.0075, \\ & s\left( {a_{4} } \right) = 0.0101,\quad s\left( {a_{5} } \right) = 0.0074. \\ \end{aligned} $$

• Step 5 The ranking order of the alternatives is $x_{2} \succ x_{4} \succ x_{3} \succ x_{5} \succ x_{1}$, which means $x_{2}$ is the best alternative.

Therefore, the ranking results based on the q-ROFIWHM operator and the q-ROFIWDHM operator for dealing with Example 3 are the same. Thus, the best alternative is $x_{2}$.

8.1 The influence of parameters k and q on the results

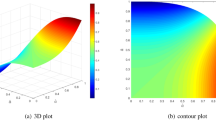
To reflect the influence of parameters q on the ranking results, we use the proposed q-ROFIWHM and q-ROFIWDHM operators to analyze the variation tendency of score values with the change of parameter q for the above MAGDM problem. MATLAB software is used for this process, and results are shown in Table 6, Figs. 1 and 2.

Table 6 Ranking results by using different parameters q in the q-ROFIWHM operator

Fig. 1

Score values of the alternatives when $q \in \left( {1,10} \right)$ based on the q-ROFIWHM operator

Fig. 2

Score values of the alternatives when $q \in \left( {1,10} \right)$ based on the q-ROFIWDHM operator

Figure 1 shows the variation tendency of the score values of alternatives obtained by the q-ROFIWHM operator. For more clarity, we take the results of Fig. 1 as examples to illustrate the score values of alternatives in Fig. 1, which is shown in Table 6. For example, we can get $S\left( {a_{1} } \right) = 0.0001$, $S\left( {a_{2} } \right) = 0.0057$, $S\left( {a_{3} } \right) = 0.0032$, $S\left( {a_{4} } \right) = 0.0041,$$S\left( {a_{5} } \right) = 0.0028$ when q = 5 and k = 2 in the q-ROFIWHM operator. From Table 6 and Fig. 1, we can see that the scores of alternatives are different when assigning different parameters q to the q-ROFIWHM operator. However, the ranking results are always $x_{2} \succ x_{4} \succ x_{3} \succ x_{5} \succ x_{1}$. In addition, the score values of alternatives obtained by the q-ROFIWHM operator become smaller as q increases on [1, 10]. Furthermore, when the parameter q is less than 3, the score values of alternatives have a sharply change. Then, as the value of q becomes greater and greater, the score values are very close to a fixed value, no matter the value of q. Therefore, the parameter q can be viewed as decision makers’ attitude. The more the optimistic decision makers are, the smaller the value assigned to q, and the more the pessimistic decision makers are, the greater the value assigned to q.

Similarly, Fig. 2 illustrates the variation tendency of the score values of alternatives obtained by the q-ROFIWDHM operator as assigned different values of q. From Fig. 2, we find that with different parameters q in the q-ROFIWDHM operator, the scores vary. Specifically, score values of alternatives by utilizing the q-ROFIWDHM operator become greater as q increases on [1, 1.853] while the values become smaller as q increases on (1.853, 10]. However, no matter what the parameters q are, the ranking results are always $x_{2} \succ x_{4} \succ x_{5} \succ x_{1} \succ x_{3}$. Furthermore, x₂ is always the best alternative, as with the q-ROFIWHM operator. Moreover, the score values change smoothly as q increases on (1.853, 10], and then are also very close to a fixed value when q becomes greater and greater.

In the following, based on the q-ROFIWHM and q-ROFIWDHM operators, we investigate the influence of parameter k on the score values and final ranking results. Here, we take $q = 3$ in the q-ROFIWHM and q-ROFIWDHM operators. Details are shown in Tables 7 and 8.

Table 7 Ranking results by using the different parameters k in the q-ROFIWHM operator

Table 8 Ranking results by using different parameters k in the q-ROFIWDHM operator

As shown in Tables 7 and 8, the scores of overall values are different when utilizing different parameters k. When k = 2, 3, it produces the same ranking result $x_{2} \succ x_{4} \succ x_{3} \succ x_{5} \succ x_{1}$, whereas the ranking results are different, i.e., $x_{2} \succ x_{4} \succ x_{5} \succ x_{3} \succ x_{1}$ when k = 1, 4. This is because the method (k = 1, k = 4) does not take into account the interrelationship among the attributes, and thus, the ranking result is not same as those obtained by the method when k = 2, 3, when attributes are interrelated. This also illustrates that our method is very flexible in the process of aggregation and can deal with MAGDM problems where the interrelationships exist among attributes according to different parameters.

Moreover, from Table 7, we find that the more the interrelationships among arguments are taken into account, the smaller the score values of overall assessments will become, which is the difference between q-ROFIWHM operator and q-ROFIWDHM operator. Therefore, decision makers can appropriately select the value of k according to their preference and actual needs.

8.2 Comparative analysis

In order to illustrate the advantages of proposed method, we use some existing MAGDM methods to solve Example 3. Considering proposed method is based on q-ROFIWHM or q-ROFIWDHM operator that combines interaction operational rules with HM under q-rung orthopair fuzzy environment, to analyze the advantages of the proposed method, we select the following MAGDM methods as reference approaches to solve Example 3.

• (1) Comparing with the methods proposed by Xu [42], Ma and Xu [16], and Liu and Wang [29]

In this subsection, we utilize Xu’s method [42] based on intuitionistic fuzzy weighted averaging (IFWA) operator, Ma and Xu’s method [16] based on the Pythagorean fuzzy weighted averaging (PFWA) operator, and Liu and Wang’s method [29] based on the q-rung orthopair fuzzy weighted averaging (q-ROFWA) operator to solve Example 3. Results are shown in Table 9.

Table 9 Ranking results based on different methods for Example 3

The ranking results obtained by our method based on q-ROFIWHM and q-ROFIWDHM operators (k = 1) are the same as the ones obtained by methods proposed by Xu [42], Ma and Xu [16], and Liu and Wang [29], i.e., $x_{2} \succ x_{4} \succ x_{5} \succ x_{3} \succ x_{1}$, which can be easily explained since they do not take interrelationships among attributes into account. This fact also verifies the validity of the new method (k = 1).

However, the ranking results obtained by Xu’s method [42], Ma and Xu’s method [16], and Liu and Wang’s method [29] are different from ones produced by our approach based on q-ROFIWHM and q-ROFIWDHM operators when k = 2. The reason is that the former three methods aggregate attribute values by using simple weighted averaging operators that are based on algebraic operational laws. Additionally, they do not consider interrelationships among attributes. Thus, our proposed approach is more reasonable than the approaches presented in the studies [16, 29, 42].

• (2) Comparing He et al.’s method [34] and Wei’s method [20]

In this subsection, we utilize He et al.’s method [34] based on intuitionistic fuzzy weighted geometric interaction averaging (IFWGIA) operator and Wei’s method [20] based on the Pythagorean fuzzy interaction weighted average (PFIWA) operator to solve the above example. Results are shown in Table 10.

Table 10 Ranking results based on different methods for Example 3

From Table 10, we can find that the ranking results obtained by our method based on q-ROFIWHM and q-ROFIWDHM operators (k = 2) are $x_{2} \succ x_{4} \succ x_{3} \succ x_{5} \succ x_{1}$, whereas He et al.’s method [34] based on IFWGIA operator and Wei’s method [14] based on PFIWA operator produce a different ranking result, i.e., $x_{2} \succ x_{4} \succ x_{5} \succ x_{3} \succ x_{1}$. The reason is that IFWGIA and PFIWA operators only consider the interaction operational rules but ignore the interrelationships between attributes. Our proposed approach based on q-ROFIWHM and q-ROFIWDHM operators not only adopts interaction operational laws, which can avoid the unreasonable influence if one of the non-memberships being zero, but also capture the interrelationship among attributes. Therefore, the ranking results obtained by the proposed approach are more reasonable than the ones obtained by He et al.’s method [34] and Wei’s method [20].

If there are no interrelationships between arguments, in this situation, the proposed method based on the q-ROFIWHM and q-ROFIWDHM operators (k = 1) will produce the same results as He et al.’s method [34] and Wei’s method [20]. In order to test this conclusion, we utilize the proposed approach based on the q-ROFIWHM and q-ROFIWDHM operators (k = 1) to solve the MAGDM problem in Example 3. The ranking result is $x_{2} \succ x_{4} \succ x_{5} \succ x_{3} \succ x_{1}$, which is the same as that obtained by He et al.’s method [34] and Wei’s method [20]. Thus, our approach based on the q-ROFIWHM and q-ROFIWDHM operators is more flexible than He et al.’s method [34] and Wei’s method [20].

• (3) Comparing with the methods proposed by Xu and Yager [43], Liang et al. [22], Liu and Liu [30], Qin and Liu [44], and Wei and Lu [25]

In this subsection, we utilize Xu and Yager’s method [43] based on weighted intuitionistic fuzzy Bonferroni mean (WIFBM) operator, Liang et al.’s method [22] based on weighted Pythagorean fuzzy Bonferroni mean (WPFBM) operator, Liu and Liu’s method [30] based on q-rung orthopair fuzzy Bonferroni mean operator, Qin and Liu’s method [44] based on intuitionistic fuzzy Maclaurin symmetric mean (IFMSM) operator, and Wei and Lu’s method [25] based on Pythagorean fuzzy Maclaurin symmetric mean (PFMSM) operator, to solve the above example. Results are shown in Table 11.

Table 11 Ranking results based on different methods for Example 3

From Table 11, we can easily find that the proposed method based on q-ROFIWHM and q-ROFIWDHM operators (k = 2), Xu and Yager’s method [43], Liang et al.’s method [22], Liu and Liu’s method [30], Qin and Liu’s method [44], and Wei and Lu’s method [25] produce the same ranking results, i.e., $x_{2} \succ x_{4} \succ x_{3} \succ x_{5} \succ x_{1}$. The reason is they are based on HM, BM and MSM operators, respectively, and thus can capture the interrelationship between attributes. This fact also further verifies that the new method is effective when k = 2. However, they (WIFBM, WPFBM, q-ROFWBM, WIFMSM and PFWMSM operations) are all based on algebraic operations that will get unreasonable result if one of the membership or non-membership degrees is zero. Since our approach based on q-ROFIWHM and q-ROFIWDHM operators adopts the interaction operational rules defined in Sect. 2, it can overcome the shortcomings of methods proposed by Xu and Yager [43], Liang et al. [22], Liu and Liu [30], Qin and Liu [44], and Wei and Lu [25] and thus can derive more reasonable ranking results.

As aforementioned above, the ranking results obtained by these methods are the same, which cannot reflect the advantages of our method very well. To further illustrate the main advantages of our method, we do a further analysis by adjusting some of the data in the above example.

Example 4

From Example 3, we know that all non-memberships of attributes in Tables 1, 2 and 3 are nonzero values. Thus, we change the non-membership value of some elements in decision matrix $D_{k}$ in Example 3 to zero, that is, the value of $a_{44}^{1}$ is changed from $(0.3,0.6)$ into $(0.3,0.0),$ the value of $a_{41}^{2}$ is changed from $(0.5,0.4)$ into $(0.5,0.0),$ the value of $a_{42}^{3}$ is changed from $(0.5,0.3)$ into $(0.5,0.0)$, and the value of $a_{43}^{3}$ is changed from $(0.3,0.5)$ into $(0.3,0.0)$, respectively. Then we solve the MAGDM problem by using the methods proposed by Xu and Yager [43], Liang et al. [22], Liu and Liu [30], Qin and Liu [44], and Wei and Lu [25] and the proposed approach, respectively. The score values and ranking results produced by above approaches are shown in Table 12.

Table 12 Ranking results based on different methods for Example 4

In Example 4, we adjust the data $a_{44}^{1}$ from $(0.3,0.6)$ to $(0.3,0.0),$$a_{41}^{2}$ from $(0.5,0.4)$ to $(0.5,0.0),$$a_{42}^{3}$ from $(0.5,0.3)$ to $(0.5,0.0)$ and $a_{43}^{3}$ from $(0.3,0.5)$ to $(0.3,0.0)$, respectively. From Table 12, we can find that the best alternative obtained by WIFBM, WPFBM, q-ROFWBM, WIFMSM and PFWMSM operators is all changed from $x_{2}$ into $x_{4}$ while the ranking results obtained by our proposed approach are unchanged. For the above results, we can provide an explanation as follows. Methods based on WIFBM, WPFBM, q-ROFWBM, WIFMSM and PFWMSM operators use the traditional operational laws and thus cannot consider the special situation in which membership or non-membership degree of some attribute values is zero. According to the traditional operational laws, the non-membership of collective evaluation value of alternative $x_{4}$ is always zero no matter the other values. Thus, scores of $x_{4}$ increase by WIFBM, WPFBM, q-ROFWBM, WIFMSM and PFWMSM operations when we change some non-membership degrees of alternative $x_{4}$. However, our approach based on q-ROFIWHM and q-ROFIWDHM operators considers the interaction operations that can reduce the unreasonable effect on ranking results when the non-membership value of some alternatives is zero.

Thus, the proposed approach is more reasonable than the methods proposed by Xu and Yager [43], Liang et al. [22], Liu and Liu [30], Qin and Liu [44], and Wei and Lu [25] in solving practical decision-making problems where the membership or non-membership values of some alternatives are zero.

• (4) Comparing the methods proposed by He et al. [45] and Yang and Pang [27]

In this subsection, we utilize He et al.’s method [45] based on intuitionistic fuzzy interaction Bonferroni means (WIFIBM) operator, Yang and Pang’s method [27] based on Pythagorean fuzzy interaction Maclaurin symmetric mean (PFIWMSM) operator, to solve the above example. Results are shown in Table 13.

Table 13 Ranking results based on different methods for Example 4

From Table 13, we can see that proposed method based on q-ROFIWHM and q-ROFIWDHM operators (k = 2), He et al.’s method based on WIFIBM operator [45] and Yang and Pang’s method based on PFIWMSM operator [27] produce the same ranking result, i.e., $x_{2} \succ x_{4} \succ x_{3} \succ x_{5} \succ x_{1}$. The reason is both of these three methods are not only based on interaction operational rules, but also consider the interrelationship of attributes.

However, Yang and Pang’s method [27] and He et al.’s method [45] also have some limitations. That is, they are based on the IFNs and PFNs and thus cannot deal with the situation where the sum or square sum of the membership degree and the non-membership degree is bigger than 1, whereas the proposed method in this paper is more powerful as they are based on q-ROFNs.

To further explain the advantages of the proposed approach in modeling fuzzy information comparing WIFIBM and PFIWMSM operators proposed in the studies [27, 45], we give another real-life example.

Example 5

At present, in China, large hospitals are overcrowded, and the burden of disease is getting heavier. As the part of China’s 13th Five-Year Plan (2016-2020) for deepening medical and health system reform, the hierarchical medical treatment system (HMTS) aims to provide an effective response to the challenges of insufficient and unbalanced medical resources in China. Through the implementation of HMTS, patients are divided into different levels of hospitals according to the urgency of diseases instead of all patients rushing to large hospitals. However, the HMTS in China has not been effectively carried out and remains to be further perfected. To push forward implementation of the system, four patients with lung diseases, denoted by x_i (i = 1, 2, 3, 4), need to be distributed into different levels of hospitals. The four patients are diagnosed from four symptoms (attributes): G₁: vital signs, including heart rate, blood pressure and so on; G₂: body temperature; G₃: the frequency of cough; and G₄: the frequency of hemoptysis. The weight vector of the attribute is w = (0.5, 0.25, 0.35, 0.25)^T. Suppose that the doctor gives the rating values for the four patients with respect to the symptoms by using q-ROFNs, and the decision matrix is shown in Table 14.

Table 14 Decision matrix of Example 5

Then we solve the MADM problem and compare the ranking results obtained by He et al.’s method [45], Yang and Pang’s method [27] and proposed approach (Suppose $k = 2,q = 3$). Details are shown in Table 15.

Table 15 Ranking results based on different methods for Example 5

In Example 5, the elements a₂₂ and a₄₃ are (0.8, 0.7) and (0.9, 0.6), respectively. Table 15 shows that He et al.’s method [45], Yang and Pang’s method [27] cannot solve the above problem as the membership degree and non-membership degree do not satisfy the constraint conditions of IFNs and PFNs. However, the proposed approach based on the q-ROFIWHM and q-ROFIWDHM operators can still work as (0.8, 0.7) and (0.9, 0.6) can be represented by q-ROFNs by adjusting the value of q. According to the calculation results above, the fourth patient’s condition is the most serious, which means that she should be treated in grade III, class A hospitals. Meanwhile, the third patient should be treated in local hospitals since his condition is not so serious.

Therefore, the applicable range of our approach is wider than He et al.’s method based on the WIFIBM operator [45], and Yang and Pang’s method based on PFIWMSM operator [27].

• (5) Summary about the proposed operators’ superiorities

To further illustrate the advantages of proposed aggregation operators, we present the characteristics of proposed operators and operators in the studies [16, 20, 22, 25, 27, 29, 30, 34, 42,43,44,45]. Results are shown in Table 16.

Table 16 Characteristics of different aggregation operators

From Table 16, we can find proposed operators have the following superiorities compared with the existing operators introduced in the studies [16, 20, 22, 25, 27, 29, 30, 34, 42,43,44,45]:

• (1) From the point view of operational laws, the IFWA, PFWA, q-ROFWA, WIFBM, WPFBM, q-ROFWBM, IFWMSM and WPFMSM operators in the studies [16, 22, 25, 29, 30, 42,43,44,44] use traditional operational rules and thus cannot avoid the unreasonable situation if one of the membership or non-membership degrees is zero. Moreover, IFWA, PFWA and q-ROFWA operators cannot consider the interrelationship among attributes, whereas WIFBM, WPFBM, q-ROFWBM, WIFMSM, PFWMSM operators in the studies [22, 25, 30, 43, 44] and the proposed operators in this paper consider interrelationships of attributes.

• (2) From the point view of aggregation operators, although WIFBM, WPFBM and q-ROFWBM [22, 25, 30, 43, 44] can consider the interrelationship of the attributes, they only capture the interrelationship between two attributes, whereas the q-ROFIWHM and q-ROFIWDHM operators proposed in this paper can capture the interrelationships among the multi-input attributes according to different parameters k. Moreover, our approaches based on q-ROFIWHM and q-ROFIWDHM operators adopt the interaction operational laws that can avoid the unreasonable effect on ranking result when the membership or non-membership value of some alternatives is zero, which is the same as IFWGIA and PFIWA operators [20, 34]. However, IFWGIA and PFIWA operators [20, 34] are special cases of proposed q-ROFIWHM (k = n, q = 1) and q-ROFIWDHM (k = 1, q = 2) operators, respectively.

• (3) From the point view of information expression, the scope of application of our approach is very wide. Although WIFIBM operator [45] and PFIWMSM operator [27] cannot only capture the interrelationship of attributes but also adopt the interaction operational laws, it can only solve MAGDM problems expressed by IFNs and PFNs. Moreover, compared with WIFIBM operator [45] and PFIWMSM operator [27], the proposed q-ROFIWHM and q-ROFIWDHM operators are more functional as they can capture the interrelationship among multi-input arguments. Additionally, decision makers can appropriately select the values of k, q in the q-ROFIWHM and q-ROFIWDHM operators according to actual needs.

In summary, because the proposed method can combine the interaction operational laws with the HM and extend them to deal with q-ROFNs, our approach provides a flexible and general tool to deal with MAGDM problems. Based on the comparisons and analysis above, our method is more functional and powerful than existing methods based on WA, BM and MSM operators.

9 Conclusions

The recently proposed q-ROFS can dynamically adjust the range of indication of decision information by changing a parameter q based on the different hesitation degrees. In order to better integrate fuzzy information, we have combined the interaction operational rules with the HM mean and have extended them to the q-rung orthopair fuzzy environment and propose q-rung orthopair fuzzy interaction weighted Hamy mean operator and its dual form. Further, based on the proposed operators, we establish a novel approach to MAGDM problems in which attribute values take the form of q-ROFNs. Finally, we give a practical example to illustrate the applicability and advantages of the new approach. The experimental results show that the novel MAGDM method outperforms the existing MAGDM methods for dealing with MAGDM problems.

Compared with existing methods, the major advantage of the proposed MAGDM approach is it can not only accommodate situations in which the input arguments are q-ROFNs and consider the interrelationships among multi-input arguments, but also avoid the unreasonable effect on ranking result when the membership or non-membership value of some alternatives is zero. Furthermore, the proposed method has a strong practicability and dependability and can be further applied to various practical decision-making problems, such as pilot hospital selection, healthcare management, supplier selection and emergency decision-making.

For future study, it is worth integrating the HM with other classical t-conorm and t-norm, such as Frank t-norm and t-conorm [46], and Dombi t-norm and t-conorm [47], and further considering the interaction among the criteria by using the Choquet integral. In addition, further research can extend the proposed operators to other fuzzy sets, such as interval-valued intuitionistic fuzzy set [48], interval-valued Pythagorean fuzzy set [49], intuitionistic fuzzy soft set [50, 51] and triangular Atanassov’s intuitionistic fuzzy set [52], and further apply these to the fields of recommendation systems, cluster analysis and so on.