Novel score functions of generalized orthopair fuzzy membership grades with application to multiple attribute decision making

Abstract

The notion of generalized orthopair fuzzy sets, as a natural extension of both intuitionistic fuzzy sets and Pythagorean fuzzy sets, provides a more flexible framework for expressing and processing uncertain information. In intelligent decision making based on generalized orthopair fuzzy sets, it is a pivotal issue to compare or rank q-rung orthopair membership grades. In this work, we investigate the ranking issue of q-rung orthopair membership grades from a geometric point of view. We propose the regular Minkowski distance of q-rung orthopair membership grades which strengthens or extends some useful distance measures in the literature. By virtue of the regular Minkowski distance, we define a generic class of novel score functions called the Minkowski score function of q-rung orthopair membership grades. This new type of score functions not only extends the existing notions such as the expectation score function, but also overcomes the difficulty that Hamming (or Euclidean) distance-based score functions cannot distinguish those intuitionistic fuzzy values with identical expectation score (or ideal positive degree). We examine several critical properties of the Minkowski score function of q-rung orthopair membership grades. By taking advantage of the q-rung orthopair fuzzy weighted averaging (or geometric) operator and the Minkowski score function, a flexible approach is developed to support multiple attribute decision making with generalized orthopair fuzzy soft information. Finally, a benchmark problem is used for comparison with several existing methods to verify the cogency and feasibility of the proposed method.

1 Introduction

The process of decision making is considered as a creative human activity based on cognition, which aims at ranking a list of alternatives or choosing the best one(s) among them. In multiple attribute decision making (MADM), all the alternatives are evaluated via several complex and sometimes conflicting attributes. The assessment of alternatives describes their performance from various standpoints. In MADM process, many scholars have strained to reconcile the contradictory goals and striven for compromise solutions (Ishizaka and Nemery 2013). At the same time, the information related to decision making problems in the real world is often incomplete or uncertain due to a lack of data, time, or cognitive capability. In response to this, it is of vital importance to explore MADM under an uncertain environment (Xu 2004).

Fuzzy set theory initially established by Zadeh (1965) provides a helpful tool to describe and deal with uncertainty based on the viewpoint of gradualness. However, fuzzy set theory only considers the membership grade of an element with respect to a fuzzy set. The non-membership grade of an element is regarded as the complement of the membership grade and thus totally determined by it. Atanassov (1986) put forward the notion named intuitionistic fuzzy set (IFS), which takes both membership and non-membership grades into consideration. This concept extends fuzzy sets in a meaningful way and it can be used to capture uncertainty caused by hesitancy in human cognition (Yager 2016). In the case of IFSs, the sum of the degrees of non-membership and membership of every element with respect to an IFS lies between 0 and 1. For simplicity, Xu and Yager (2006) referred to an ordered pair comprised of the membership degree and non-membership degree as an intuitionistic fuzzy value (IFV). In fact, IFVs serve as basic information granules for uncertain information processing under an intuitionistic fuzzy environment. decision making based on IFSs and their extensions has received considerable attention in recent years (Chen and Chu 2020; Chen and Huang 2017; Ouyang and Pedrycz 2016; Zou et al. 2021). In particular, Chen and Randyanto (2013) brought forward a useful similarity measure between IFVs and extended it to a similarity measure of intuitionistic fuzzy sets. They also considered the applications of their similarity measures to both medical diagnosis and pattern recognition. Using the TOPSIS method and similarity measures between IFVs, a multicriteria decision making method was developed in Chen et al. (2016). Chen and Chang (2016) presented intuitionistic fuzzy geometric averaging operators, and developed a fuzzy MADM method based on the transformation between IFVs and right-angled triangular fuzzy numbers. Zeng et al. (2019) put forth a helpful score function of IFVs and a modified VIKOR method by virtue of the proposed score function. Liu et al. (2020a) introduced the notion of weighted partitioned Maclaurin symmetric mean operators for intuitionistic fuzzy numbers and applied it to intuitionistic fuzzy multiattribute group decision making problems. Yager (2014) proposed a novel notion called Pythagorean fuzzy sets (PFSs) to expand the value space of IFVs. In PFSs, the sum of the squares of the non-membership and membership grades of every object with respect to a PFS is no more than one. Furthermore, Yager (2017) put forward q-rung orthopair fuzzy sets (q-ROFSs), which can adjust the constraint on the degrees of non-membership and membership in terms of a parameter q. Note that q-ROFSs are also known as generalized orthopair fuzzy sets (GOFSs). In the case of GOFSs, the sum of the qth powers of the membership and non-membership degrees is bounded by one. Following the term coined by Yager (2017), we refer to an ordered pair composed of the membership degree and non-membership degree of an element with respect to a q-ROFS as a q-rung orthopair membership grade (q-ROMG). Clearly, the value space of valid q-ROMGs expands whenever the rung q increases.

To deal with uncertainty in a general manner, Molodtsov (1999) put forward a fundamental concept called soft sets. The definition of soft set not only involves the object domain, but also a parameter space related to the domain of objects (Feng et al. 2016). Yang and Yao (2020) put forth two convincing semantics for soft set theory, namely the semantics of multi-context and possible-world, respectively. As pointed out by Yang and Yao (2020), the multi-context semantics suggests that soft sets are suitable for modelling uncertain concepts expressed by different crisp sets under distinct contexts. In addition, the possible-world semantics indicates that soft sets can also be used to characterize the uncertainty entailed by insufficient information. In this case, a soft set provides a collection of alternative representations of a concept in various possible worlds, and only one of them is the actual case if all information is completely available (Yang and Yao 2020). It is interesting to see that there are abundant connections among soft sets, rough sets and fuzzy sets (Alcantud 2016; Alcantud et al. 2020; Feng et al. 2011). Fuzzy soft sets initiated in Maji et al. (2001a) are hybrid structures integrating fuzzy sets and soft sets in a meaningful way. The concept of intuitionistic fuzzy soft sets (IFSSs) was presented by Maji et al. (2001b). This hybrid structure was successfully used to describe and handle MADM problems in an intuitionistic fuzzy environment (Ali et al. 2019; Feng et al. 2020). Xiao and Ding (2019) introduced divergence measure of Pythagorean fuzzy sets and applied this measure to medical diagnosis. Peng et al. (2015) put forth the Pythagorean fuzzy soft set (PFSS) model which combines Pythagorean fuzzy sets with soft sets. Zhan et al. (2020) introduced the notion of covering-based Pythagorean fuzzy rough sets (CPFRSs) and presented two different TOPSIS methods based on the CPFRS model. Akram and Ali (2020) developed two useful hybrid models to support decision making by combining Pythagorean fuzzy sets, bipolar soft sets and rough sets. By combining soft sets with generalized orthopair fuzzy sets, Hussain et al. (2020) introduced the generalized orthopair fuzzy soft set (GOFSS) model to further expand the scope of intuitionistic fuzzy soft sets and Pythagorean fuzzy soft sets. Akram and Shahzadi (2020) proposed six types of generalized orthopair fuzzy aggregation operators by applying Yager’s t-norm and t-conorm operations. Garg and Chen (2020) introduced neutrality aggregation operators of q-ROFSs and discussed their application to multiple attribute group decision making.

In MADM based on GOFSs, q-ROMGs quantify the performance of alternatives and can be viewed as the most elementary components. Therefore, ranking q-ROMGs plays a fundamental role in solving MADM problems under a generalized orthopair fuzzy environment. In fact, q-ROMGs can be considered as the generalized orthopair fuzzy counterpart of real numbers in the unit interval [0, 1]. As we know, the unit interval forms a linearly ordered set. Thus, any two real numbers in [0, 1] can be compared or ranked conveniently. However, as pointed out by Ali (2018), the set $L_q^*$ of all q-ROMGs only forms a complete lattice instead of a linearly ordered set under the usual order of q-ROMGs. This makes the comparing and ranking of q-ROMGs more complicated and challenging. As a particular case, the IFV ranking problem has attracted more and more attentions in recent years. Sophisticated methods have been developed to quantify the difference between the information carried by IFVs. From a geometric point of view, Xing et al. (2018) proposed a method in which IFVs are considered as points in Euclidean space, and the preference grade of an IFV is characterized in terms of the Euclidean distance between the IFV and the positive ideal IFV. The method is essentially based on the intuition that a better IFV should be relatively closer to the positive ideal IFV. Their IFV ranking method overcomes the drawbacks such as the inadmissibility, non-robustness, and indifference problem of several existing methods. Nonetheless, it cannot distinguish different IFVs if they have the same ideal positive degree. Later on, Du (2018) proposed the Minkowski distance of q-ROMGs and discussed its application to MADM. Although the Minkowski distance of q-ROMGs is useful in applications, it does not reflect the effect of the parameter q on the ranking of q-ROMGs.

Motivated by the issues mentioned above, a new distance measure called the regular Minkowski distance of q-ROMGs is proposed in this study. We present a score function called Minkowski score function for ranking q-ROMGs based on the regular Minkowski distance between q-ROMGs. More specifically, this Minkowski score function is defined as the regular Minkowski distance between any given q-ROMG and the negative ideal orthopair $\alpha _*=(0,1)$. It is worth noting that our new score function generalizes both the ideal positive degree in Xing et al. (2018) and the expectation score function of IFVs in Feng et al. (2019a, b) to the more general case of q-ROMGs based on the regular Minkowski distance. Meanwhile, our new score function simplifies the ideal positive degree of IFVs. In addition, it also overcomes the difficulty that Hamming (or Euclidean) distance-based score functions cannot distinguish those IFVs with identical expectation score (or ideal positive degree). For other useful notions not discussed in the study, the readers are referred to Akram et al. (2020a, b); Liu et al. (2020b); Akram et al. (2020c); Liu et al. (2018).

The main contributions of this work can be summarized as follows:

• 1. The regular Minkowski distance of q-ROMGs is presented, which includes not only the parameter p for specifying particular type of the distance, but also the parameter q indicating the specific rung of the q-ROMGs. For any two different q-ROMGs, both parameters can affect the regular Minkowski distance between them. This feature can help enhance the distance measure presented by Du (2018).

• 2. Based on the proposed regular Minkowski distance, the Minkowski score function of q-ROMGs is proposed and its related properties are discussed in detail. Particularly, it is proved that with the enlargement of the parameter p, the value of Minkowski score function depends more heavily on the non-membership degree.

• 3. A flexible approach to MADM under a generalized orthopair fuzzy environment is proposed by taking advantages of the Minkowski score function and the q-ROFWA (or q-ROFWG) operator. A benchmark problem is used for comparison with some existing methods to show the validity and feasibility of the presented approach.

The remainder of our study is arranged in the following way. Some fundamental notions such as intuitionistic fuzzy sets, Pythagorean fuzzy sets and generalized orthopair fuzzy sets are recalled in Sect. 2. In Sect. 3, we define the Minkowski score function of q-ROMGs and point out some special cases of it. Moreover, a series of fundamental properties of Minkowski score function are investigated in detail. In Sect. 4, we propose a new approach to solve MADM problems in a q-rung orthopair fuzzy soft setting. In addition, a case study on a benchmark problem is conducted to verify the feasibility of our approach and compare it with the methods presented by Du (2018) and Liu and Wang (2018). Finally, conclusions are given in Sect. 5.

2 Preliminaries

Throughout the whole paper, let ${\mathcal {V}}$ denote the universe of discourse, which is a nonempty set.

A fuzzy set $\mu$ in ${\mathcal {V}}$ is a mapping $\mu :{\mathcal {V}}\rightarrow [0,1]$, where $\mu (\nu )$ specifies the degree to which $\nu$ belongs to the fuzzy set $\mu$ for all $\nu \in {\mathcal {V}}$. Alternatively, it can be represented as $\mu =\{(\nu ,\mu (\nu ))\mid \nu \in {\mathcal {V}}\}$. In what follows, the collection of all fuzzy sets in ${\mathcal {V}}$ will be denoted by $\mathcal {FS}({\mathcal {V}})$.

Definition 1

(Atanassov 1986) An intuitionistic fuzzy set I in ${\mathcal {V}}$ is defined as

$$\begin{aligned} I=\{(\nu ,{\hat{I}}(\nu ), \check{I}(\nu ))\mid \nu \in {\mathcal {V}}\}, \end{aligned}$$

where the mappings ${\hat{I}}:{\mathcal {V}}\rightarrow [0,1]$ and $\check{I}:{\mathcal {V}}\rightarrow [0,1]$ specify the membership grade ${\hat{I}}(\nu )$ and non-membership grade $\check{I}(\nu )$, such that

$$\begin{aligned}0\le {\hat{I}}(\nu )+\check{I}(\nu )\le 1\end{aligned}$$

The hesitancy degree of $\nu$ to I is given by ${\tilde{I}}(\nu )=1-({\hat{I}}(\nu )+\check{I}(\nu ))$. In what follows, $\mathcal {IFS}({\mathcal {V}})$ denotes the collection of all IFSs in ${\mathcal {V}}$.

Definition 2

(Yager 2014) A Pythagorean fuzzy set P in ${\mathcal {V}}$ is defined as

$$\begin{aligned} P=\{(\nu ,{\hat{P}}(\nu ),\check{P}(\nu ))\mid \nu \in {\mathcal {V}}\}, \end{aligned}$$

where $\check{P}:{\mathcal {V}}\rightarrow [0,1]$ and ${\hat{P}}:{\mathcal {V}}\rightarrow [0,1]$ are called the non-membership function and membership function of the Pythagorean fuzzy set P, respectively. It is required that $0\le ({\hat{P}}(\nu ))^2+(\check{P}(\nu ))^2\le 1$ for all $\nu \in {\mathcal {V}}$.

We refer to ${\tilde{P}}(\nu )=\sqrt{1-({\hat{P}}(\nu ))^2-(\check{P}(\nu ))^2}$ as the hesitancy degree of $\nu$ to P. In the following, $\mathcal {PFS}({\mathcal {V}})$ denotes the collection of all PFSs in ${\mathcal {V}}$.

Definition 3

(Yager 2017) Let $q\ge 1$. A generalized orthopair fuzzy set G (also called q-rung orthopair fuzzy set) on ${\mathcal {V}}$ is defined as

$$\begin{aligned} G=\{(\nu ,{\hat{G}}(\nu ),\check{G}(\nu ))\mid \nu \in {\mathcal {V}}\}, \end{aligned}$$

where $\check{G}(\nu )$ and ${\hat{G}}(\nu )$ are the non-membership grade and membership grade of $\nu$ in G, respectively. It is required that

$$\begin{aligned}0\le ({\hat{G}}(\nu ))^q+(\check{G}(\nu ))^q\le 1\end{aligned}$$

for all $\nu \in {\mathcal {V}}.$

The hesitancy degree of $\nu$ to G is defined as

$$\begin{aligned}{\tilde{G}}(\nu )=\left( 1-({\hat{G}}(\nu ))^q-(\check{G}(\nu ))^q\right) ^{1/q}.\end{aligned}$$

Hereinafter, the class of all q-rung orthopair fuzzy sets in ${\mathcal {V}}$ is denoted by $\mathcal {GOFS}_{q}({\mathcal {V}})$.

Recently, Ali (2018) pointed out that q-rung orthopair fuzzy sets can be viewed as L-fuzzy sets with respect to the complete lattice $(L_q^*,\le _{L_q^*})$, where

$$\begin{aligned}L_q^*=\{(a,b)\in [0,1]^2 \mid a^q+b^q\le 1\},\end{aligned}$$

and the corresponding lattice order $\le _{L_q^*}$ is defined as

$$\begin{aligned} (a_1,b_1)\le _{L_q^*}(a_2,b_2)\Leftrightarrow (a_1\le a_2)\wedge (b_1\ge b_2) \end{aligned}$$

(1)

for all $(a_1,b_1),(a_2,b_2)\in L_q^*$.

Each ordered pair $(a,b)\in L_q^*$ was originally named as q-rung orthopair membership grade (q-ROMG) by Yager (2017), which is also known as q-rung orthopair fuzzy number. To avoid confusion with the term fuzzy number, we would like to use Yager’s original term in the following. For convenience, $L_1^*$ is simply denoted by $L^*$ and its elements are called intuitionistic fuzzy values. Similarly, ordered pairs in $L_2^*$ are called Pythagorean fuzzy values (PFVs).

Definition 4

(Feng et al. 2019a, b) Let $A=({\hat{a}}, \check{a})\in L^*$. The mapping $\delta :L^*\rightarrow [0,1]$ given by

$$\begin{aligned} \delta (A)=\delta _A=\frac{{\hat{a}}-\check{a}+1}{2} \end{aligned}$$

is called the expectation score function of IFVs.

Assume that $A=({\hat{a}}, \check{a}), C=({\hat{c}}, \check{c})\in L_q^*$ and $\lambda >0$. Then some basic operations of q-ROMGs can be defined as follows:

• $A \vee C=(\max \{{\hat{a}},{\hat{c}}\},\min \{\check{a},\check{c}\})$;

• $A \wedge C=(\min \{{\hat{a}},{\hat{c}}\},\max \{\check{a},\check{c}\})$;

• $A^c=(\check{a},{\hat{a}})$;

• $A\oplus C=\left( \left( {\hat{a}}^q+{\hat{c}}^q-{\hat{a}}^q{\hat{c}}^q\right) ^{1/q}, \check{a}\check{c}\right)$;

• $\lambda A= \left( \left( 1-(1-{\hat{a}}^q)^\lambda \right) ^{1/q}, \check{a}^\lambda \right)$;

• $A\otimes C=\left( {\hat{a}}{\hat{c}}, \left( \check{a}^q+\check{c}^q-\check{a}^q\check{c}^q\right) ^{1/q}\right) ;$

• $A^{\lambda }= \left( {\hat{a}}^\lambda , \left( 1-(1-\check{a}^q)^\lambda \right) ^{1/q}\right)$.

It is easy to see that $L^*\subseteq L_q^*\subseteq L_{q+1}^*$ for any $q\ge 2$. Moreover, Ali (2018) gave a more insightful observation as follows:

Theorem 1

(Ali 2018) The lattice $L^*$ is a sublattice of $L_q^*$ for each $q\ge 1$.

Obviously, Atanassov’s IFSs are q-ROFSs with $q=1$ and Yager’s PFSs are q-ROFSs with $q=2$.

Theorem 2

(Yager 2017) If A is a $q_1$-ROFS on ${\mathcal {V}}$ and if $q_2 > q_1$, then A is also a $q_2$-ROFS on ${\mathcal {V}}$.

In other words, we have

$$\begin{aligned} q_1\le q_2 \Rightarrow \mathcal {GOFS}_{q_1}({\mathcal {V}})\subseteq \mathcal {GOFS}_{q_2}({\mathcal {V}})\end{aligned}$$

for all $q_1, q_2\ge 1$.

Definition 5

(Liu and Wang 2018) Let $C=({\hat{c}},\check{c})\in L_q^*$ ($q\ge 1$). The mapping $s:L_q^*\rightarrow [-1,1]$ given by

$$\begin{aligned} s(C)=s_C={\hat{c}}^q-\check{c}^q \end{aligned}$$

(2)

is called the score function of q-ROMGs.

Definition 6

(Liu and Wang 2018) Let $C=({\hat{c}},\check{c})\in L_q^*$ ($q\ge 1$). The mapping $h:L_q^*\rightarrow [0,1]$ given by

$$\begin{aligned} h(C)=h_C={\hat{c}}^q+\check{c}^q \end{aligned}$$

(3)

is called the accuracy function of q-ROMGs.

With the help of the score and accuracy functions of q-ROMGs, Liu and Wang (2018) proposed an effective way of comparing q-ROMGs. Their initial idea can be further simplified to give the following notion.

Definition 7

Assume that $A=({\hat{a}},\check{a}),C=({\hat{c}},\check{c}) \in L_q^*$ ($q\ge 1$). We can define a binary relation $\le ^{(s,h)}_q$ on $L_q^*$ in the following way:

$$\begin{aligned} A \le ^{(s,h)}_q C \Leftrightarrow (s_A < s_C)\vee (s_A = s_C\wedge h_A \le h_C). \end{aligned}$$

It can be shown that $\le ^{(s,h)}_q$ is a total order on $L_q^*$, which is named as the Liu-Wang lexicographic order of q-ROMGs hereinafter.

Suppose that A and C are q-ROFSs. Yager (2017) put forth the following basic notions:

$\bullet$:

$A\sqcup C=\{(\nu ,\max \{{\hat{A}}(\nu ),{\hat{C}}(\nu )\},\min \{\check{A}(\nu ),\check{C}(\nu )\})\mid \nu \in {\mathcal {V}}\}$;

$\bullet$:

$A\sqcap C=\{(\nu ,\min \{{\hat{A}}(\nu ),{\hat{C}}(\nu )\},\max \{\check{A}(\nu ),\check{C}(\nu )\})\mid \nu \in {\mathcal {V}}\}$;

$\bullet$:

$A^{c}=\{(\nu ,\check{A}(\nu ),{\hat{A}}(\nu ))\mid \nu \in {\mathcal {V}}\}$;

$\bullet$:

$A\sqsubseteq C$ if and only if ${\hat{A}}(\nu )\le {\hat{C}}(\nu )$ and $\check{A}(\nu )\ge \check{C}(\nu )$ for all $\nu \in {\mathcal {V}}$.

Suppose that $E_{{\mathcal {V}}}$ is the set of all parameters associated with objects in the universe of discourse ${\mathcal {V}}$. Conventionally, we refer to $E_{{\mathcal {V}}}$ as the parameter space and simply write it as E. We also refer to $({\mathcal {V}},E)$ as a soft universe. Depending on the needs in real life applications, parameters usually include characteristics, properties or attributes of objects in the universe ${\mathcal {V}}$.

Definition 8

(Hussain et al. 2020) Let $q\ge 1$. A q-rung orthopair fuzzy soft set  (q-ROFSS) over ${\mathcal {V}}$ is an ordered pair ${\mathfrak {G}}=({\widetilde{F}},A)$, where $A\subseteq E$ and the mapping ${\widetilde{F}}:A\rightarrow \mathcal {GOFS}_{q}({\mathcal {V}})$ is called the approximate function of ${\mathfrak {G}}$.

When q is known from the context, we simply call a q-rung orthopair fuzzy soft set as a generalized orthopair fuzzy soft set (GOFSS). The collection of all generalized orthopair fuzzy soft sets over the soft universe $({\mathcal {V}},E)$ with a fixed rung $q\ge 1$ is denoted by $\mathcal {GOFSS}^{E}_{q}({\mathcal {V}})$ hereinafter.

By a poset $(P,\leqslant )$, we mean a set P together with a partial order $\leqslant$ on it. In particular, when $\leqslant$ is a total order, we refer to $(P,\leqslant )$ as a chain.

Definition 9

Assume that $(A,\leqslant _A)$ and $(C,\leqslant _C)$ are two posets. An order homomorphism is a mapping $\varTheta :A\rightarrow C$ such that

$$\begin{aligned}\alpha \leqslant _A \gamma \Rightarrow \varTheta (\alpha )\leqslant _C \varTheta (\gamma )\end{aligned}$$

for all $\alpha ,\gamma \in A$.

An order homomorphism $\varTheta :A\rightarrow C$ is said to be an order isomorphism if it is bijective and $\varTheta ^{-1}:C\rightarrow A$ is an order homomorphism as well.

For a positive integer n, the set $\{1,2,\ldots ,n\}$ is written as [n] in the sequel. Liu and Wang (2018) introduced the following useful operators for the aggregation of q-ROMGs.

Definition 10

(Liu and Wang 2018) Let $q\ge 1$ and $A_i=({\hat{a}}_i,\check{a}_i)\in L_q^*$ ($i\in [n]$). The q-rung orthopair fuzzy weighted averaging (q-ROFWA) operator of dimension n is a mapping $\mho ^{w}:(L_q^*)^n\rightarrow L_q^*$ defined as

$$\begin{aligned} \mho ^{w}(A_1,A_2,\ldots ,A_n)=w_1A_1\oplus w_2A_2\oplus \cdots \oplus w_nA_n, \end{aligned}$$

where $w=(w_1,w_2,\ldots ,w_n)^T$ is the weight vector with $0\le w_i\le 1$ ($i\in [n]$) and $\sum _{i=1}^n w_i=1$.

According to Liu and Wang (2018), the aggregation result of q-ROFWA operator can be obtained by

$$\begin{aligned} \mho ^{w}(A_1,A_2,\ldots ,A_n)=\left( \left( 1-\prod _{k=1}^n(1-{\hat{a}}_k^q)^{w_k}\right) ^{1/q}, \prod _{k=1}^n\check{a}_k^{w_k}\right) . \end{aligned}$$

(4)

Definition 11

(Liu and Wang 2018) Let $q\ge 1$ and $A_i=({\hat{a}}_i,\check{a}_i)\in L_q^*$ ($i\in [n]$). The q-rung orthopair fuzzy weighted geometric (q-ROFWG) operator of dimension n is a mapping $\varOmega ^{w}:(L_q^*)^n\rightarrow L_q^*$ given by

$$\begin{aligned} \varOmega ^{w}(A_1,A_2,\ldots ,A_n)=A_1^{w_1}\otimes A_2^{w_2}\otimes \cdots \otimes A_n^{w_n}, \end{aligned}$$

where $w=(w_1,w_2,\ldots ,w_n)^T$ is the weight vector with $0\le w_i\le 1$ ($i\in [n]$) and $\sum _{i=1}^n w_i=1$.

Liu and Wang (2018) proved that the aggregation result of q-ROFWG operator can be obtained as follows:

$$\begin{aligned} \varOmega ^{w}(A_1,A_2,\ldots ,A_n)=\left( \prod _{k=1}^n{\hat{a}}_k^{w_k}, \left( 1-\prod _{k=1}^n(1-\check{a}_k^q)^{w_k}\right) ^{1/q}\right) . \end{aligned}$$

(5)

3 Minkowski score functions

Definition 12

(Du 2018) Let $A =({\hat{a}}, \check{a}),C=({\hat{c}}, \check{c})\in L_q^*$ with $q\ge 1$. For $p\ge 1$, the Minkowski distance between A and C is defined as

$$\begin{aligned} D_p(A,C)=\left( \frac{\left| {\hat{a}}-{\hat{c}}\right| ^p+\left| \check{a}-\check{c}\right| ^p}{2}\right) ^{\frac{1}{p}}. \end{aligned}$$

(6)

In particular, $D_1(A,C)$ and $D_2(A,C)$ are called the Hamming distance and Euclidean distance between A and C, respectively. Based on the Euclidean distance, Xing et al. (2018) presented a useful measure for evaluating the preference degree of IFVs as follows:

Definition 13

(Xing et al. 2018) Assume that $C=({\hat{c}}, \check{c})\in L^*$ and $\alpha ^*=(1,0)$. Then

$$\begin{aligned} P(C)=1-D_2(C,\alpha ^*)=1-\left( \frac{(1-{\hat{c}})^2+\check{c}^2}{2}\right) ^{\frac{1}{2}} \end{aligned}$$

(7)

is called the ideal positive degree (IPD) of C.

Remark 1

Based on a geometric perspective, one can see that the closer an IFV $C=({\hat{c}}, \check{c})$ is to the positive ideal IFV $\alpha ^*=(1,0)$, the better it is among all the IFVs in $L^*$ and it should have a greater IPD. In particular, it is easy to see that $P(\alpha ^*)=1$. Thus, intuitively, $\alpha ^*$ can be regarded as the best IFV in $L^*$ since it has the maximum IPD.

Definition 14

Let $p,q\ge 1$ and $A =({\hat{a}}, \check{a}),C=({\hat{c}}, \check{c})\in L_q^*$. Then

$$\begin{aligned} M^q_p(A,C)=\left( \frac{\left| {\hat{a}}^q-{\hat{c}}^q\right| ^p+\left| \check{a}^q-\check{c}^q\right| ^p}{2}\right) ^{\frac{1}{p}} \end{aligned}$$

(8)

is called the regular Minkowski distance between A and C.

We simply write $M^1_p(A,C)$ as $M_p(A,C)$ in the sequel. It is easy to see that $M^1_p(A,C)=M_p(A,C)=D_p(A,C)$. That is, $M^q_p(A,C)$ reduces to the Minkowski distance of two IFVs in $L^*$ when $q=1$.

Remark 2

It is necessary to highlight the difference between the regular Minkowski distance defined above and the Minkowski distance presented by Du (2018). Note first that Du’s Minkowski distance is well defined and has been proven to be useful in applications.

At the same time, it is worth noting that the vital information carried by the parameter q is simply ignored in Eq. (6). More specifically, for any $A=({\hat{a}},\check{a}), C=({\hat{c}},\check{c})\in L_q^*$ and $p,q\ge 1$, the Minkowski distance $D_p(A,C)$ between A and C will remain unchanged even if the parameter q is altered. Hence, the Minkowski distance in Du (2018) cannot reflect the impact of the parameter q on the ranking of q-ROMGs. In contrast, the regular Minkowski distance of q-ROMGs includes not only the parameter p for specifying the particular type of distances, but also the parameter q indicating the specific rung of q-ROMGs. For any two different q-ROMGs A and C, both parameters p, q can affect their regular Minkowski distance $M^q_p(A,C)$. In particular, the regular Minkowski distance between two q-ROMGs might change when the distance parameter p is fixed but the rung parameter q is changed. This feature can help enhance the distance measure given by Du (2018). To demonstrate this, we present an example as follows.

Example 1

Assume that

$$\begin{aligned}A=({\hat{a}},\check{a})=(0.7,0.6)\end{aligned}$$

and

$$\begin{aligned}C=({\hat{c}},\check{c})=(0.8,0.7).\end{aligned}$$

Obviously, A, C can be viewed as both 3-ROMGs and 4-ROMGs. Note first that Du’s Minkowski distance

$$\begin{aligned} D_3(A,C)= & {} \left( \frac{\left| {\hat{a}}-{\hat{c}}\right| ^p+\left| \check{a}-\check{c}\right| ^p}{2}\right) ^{\frac{1}{p}}\\= & {} \left( \frac{\left| 0.7-0.8\right| ^3+\left| 0.6-0.7\right| ^3}{2}\right) ^{\frac{1}{3}}=0.1\end{aligned}$$

will not change whenever we compute this value in $L_3^*$ or $L_4^*$. However, if we regard A, C as 3-ROMGs and set $p=3$. Using Eq. (8), we can compute the regular Minkowski distance of A and C in $L_3^*$ as follows:

$$\begin{aligned} \begin{aligned} M^3_3(A,C)&=\left( \frac{\left| {\hat{a}}^3-{\hat{c}}^3\right| ^3+\left| \check{a}^3-\check{c}^3\right| ^3}{2}\right) ^{\frac{1}{3}}\\&=\left( \frac{\left| 0.7^3-0.8^3\right| ^3+\left| 0.6^3-0.7^3\right| ^3}{2}\right) ^{\frac{1}{3}}\\&=0.1509. \end{aligned} \end{aligned}$$

Meanwhile, for $p=3$ we can also take A, C as 4-ROMGs and calculate the regular Minkowski distance of them in $L_4^*$ as follows:

$$\begin{aligned} \begin{aligned} M^4_3(A,C)&=\left( \frac{\left| {\hat{a}}^4-{\hat{c}}^4\right| ^3+\left| \check{a}^4-\check{c}^4\right| ^3}{2}\right) ^{\frac{1}{3}}\\&= \left( \frac{\left| 0.7^4-0.8^4\right| ^3+\left| 0.6^4-0.7^4\right| ^3}{2}\right) ^{\frac{1}{3}}\\&=0.1460. \end{aligned} \end{aligned}$$

It is clear that $M^3_3(A,C)\ne M^4_3(A,C)$.

The following result further reveals a close connection between the regular Minkowski distance of q-ROMGs and the Minkowski distance of IFVs proposed by Du (2018).

Proposition 1

Let $p,q\ge 1$ and $A=({\hat{a}},\check{a}), C=({\hat{c}},\check{c})\in L_q^*$. Then

$$\begin{aligned}M^q_p(A,C)=D_p(A',C')\end{aligned}$$

where $A'=({\hat{a}}^q,\check{a}^q)$ and $C'=({\hat{c}}^q,\check{c}^q)$.

Proof

Straightforward. $\square$

Remark 3

It is worth noting that $\chi '=({\hat{x}}^q,\check{x}^q)\in L^*$ for any q-ROMG $\chi =({\hat{x}},\check{x})\in L_q^*$ with $q\ge 1$. Given $A=({\hat{a}},\check{a})$ and $C=({\hat{c}},\check{c})$ in $L_q^*$, we can first transform them into two IFVs $A'=({\hat{a}}^q,\check{a}^q)$ and $C'=({\hat{c}}^q,\check{c}^q)$. After this process of regularization, it suffices to compute Du’s Minkowski distance between the two IFVs $A'$ and $C'$ by Eq. (6), which coincides with the regular Minkowski distance between A and C in $L_q^*$. For this reason, the distance given by Eq. (8) is named as “regular” Minkowski distance.

Using the regular Minkowski distance, Definition 13 can be extended to a more general case of q-ROMGs in the following way:

Definition 15

Assume that $p,q\ge 1$, $\alpha _*=(0,1)$ and $A=({\hat{a}},\check{a})\in L_q^*$. The mapping $M^q_p:L_q^*\rightarrow [0,1]$ given by

$$\begin{aligned} M^q_p(A)=M^q_p(A,\alpha _*)=\left[ \frac{{\hat{a}}^{qp}+(1-\check{a}^{q})^p}{2}\right] ^{\frac{1}{p}} \end{aligned}$$

(9)

is called the Minkowski score function (MSF) of q-ROMGs.

When $p=1$, Eq. (9) can be simplified as

$$\begin{aligned} M^q_1(A)=\frac{{\hat{a}}^{q}-\check{a}^{q}+1}{2}=\frac{s(A)+1}{2}, \end{aligned}$$

(10)

which is said to be the Hamming score function (HSF) of q-ROMGs. For convenience, $M^1_p(A)$ is simply denoted by $M_p(A)$. It should be noted that

$$\begin{aligned}M_1(A)=\frac{{\hat{a}}-\check{a}+1}{2}=\delta (A).\end{aligned}$$

The above result reveals that the MSF $M^q_p(A)$ of q-ROMGs coincides with the expectation score function $\delta (A)$ of IFVs when $p=q=1$.

When $p=2$, Eq. (9) can be simplified as:

$$\begin{aligned} M^q_2(A)=\left[ \frac{{\hat{a}}^{2q}+(1-\check{a}^{q})^2}{2}\right] ^{\frac{1}{2}}, \end{aligned}$$

(11)

which is said to be the Euclidean score function (ESF) of q-ROMGs. In particular,

$$\begin{aligned} M_2(A)=\left( \frac{{\hat{a}}^2+(1-\check{a})^2}{2}\right) ^{\frac{1}{2}} \end{aligned}$$

(12)

is the ESF of IFVs.

Proposition 2

Let $A=({\hat{a}},\check{a})\in L^*$. Then

$$\begin{aligned}M_2(A)=1-P(A^c)\end{aligned}$$

where $A^c=(\check{a},{\hat{a}})$ is the complement of $A=({\hat{a}},\check{a})$.

Proof

Straightforward. $\square$

Remark 4

The above result reveals an inner connection between the ESF value $M_2(A)$ of an IFV $A\in L^*$ and the IPD $P(A^c)$ of its complement. It shows that when $q=1$ the ESF $M_2(A)$ given by Eq. (12) and the IPD P(A) in Xing et al. (2018) can be regarded as a pair of dual notions. In other words, Definition 15 extends the IPD of IFVs to a more general case based on the regular Minkowski distance of q-ROMGs. By comparing Eq. (7) with Eq. (12), it is clear that $M_2(A)$ also simplifies the calculation of P(A).

By considering both the score function and non-membership grade of q-ROMGs, we introduce the following notion, which is called the nonmembership score order (NSO) of q-ROMGs hereinafter.

Definition 16

Assume that $A=({\hat{a}},\check{a}),C=({\hat{c}},\check{c})\in L_q^*$ ($q\ge 1$). We can define a binary relation $\le ^{(s,f)}_q$ on $L_q^*$ in the following way:

$$\begin{aligned} A \le ^{(s,f)}_q C \Leftrightarrow (s_A \le s_C)\wedge (\check{a} \ge \check{c}). \end{aligned}$$

(13)

The NSO $\le ^{(s,f)}_q$ is an extension of the lattice order $L_q^*$ as shown below.

Proposition 3

Let $A=({\hat{a}},\check{a}),C=({\hat{c}},\check{c})\in L_q^*$. Then

$$\begin{aligned}A\le _{L_q^*}C\Rightarrow A\le ^{(s,f)}_q C,\end{aligned}$$

where $q\ge 1$.

Proof

By Eq. (1), we have ${\hat{a}}\le {\hat{c}}$ and $\check{a}\ge \check{c}$. Thus, ${\hat{a}}^{q} \le {\hat{c}}^{q}$, $\check{a}^{q} \ge \check{a}^{q}$ since $q\ge 1$ and ${\hat{a}}, \check{a}, {\hat{c}}, \check{c}\ge 0$. This implies that

$$\begin{aligned} s_A={\hat{a}}^{q}-\check{a}^{q}\le {\hat{c}}^{q}-\check{c}^{q}=s_C. \end{aligned}$$

Note also that $\check{a}\ge \check{c}$. By Eq. (13), it follows that $A\le ^{(s,f)}_q C$, as required. □

The following example demonstrates that the converse of the above implication, namely

$$\begin{aligned}A\le ^{(s,f)}_q C \Rightarrow A\le _{L_q^*}C,\end{aligned}$$

is not true in general.

Example 2

Suppose that

$$\begin{aligned}A=({\hat{a}},\check{a})=(0.8,0.7)\end{aligned}$$

and

$$\begin{aligned}C=({\hat{c}},\check{c})=(0.6,0.3)\end{aligned}$$

are q-ROMGs in $L_3^*$. By Eq. (2), we have

$$\begin{aligned}s_A={\hat{a}}^{q}-\check{a}^{q}=0.8^3-0.7^3=0.169\end{aligned}$$

and

$$\begin{aligned}s_C={\hat{c}}^{q}-\check{c}^{q}=0.6^3-0.3^3=0.189.\end{aligned}$$

It is clear that $s_A < s_C$ and $\check{a} > \check{c}$. Thus, by Eq. (13), we can see that $A\le ^{(s,f)}_3 C$ holds. However, note also that ${\hat{a}}>{\hat{c}}$. This implies that $A\le _{L_q^*}C$ does not hold. Therefore, the implication

$$\begin{aligned}A\le ^{(s,f)}_q C \Rightarrow A\le _{L_q^*}C,\end{aligned}$$

does not hold in general. In other words, the NSO $\le ^{(s,f)}_q$ is a strict extension of the lattice order $L_q^*$.

Next, we examine several vital properties of the MSF of q-ROMGs.

Proposition 4

Let $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$. Then

$$\begin{aligned}M_p^q(A)=0\Leftrightarrow A=(0,1).\end{aligned}$$

Proof

By Definition 15 and Eq. (9), we have

$$\begin{aligned}M^q_p(A)=\left[ \frac{{\hat{a}}^{qp}+(1-\check{a}^{q})^p}{2}\right] ^{\frac{1}{p}}.\end{aligned}$$

If $M^q_p(A)=0$, then ${\hat{a}}^{qp}+(1-\check{a}^{q})^p=0$. Note also that ${\hat{a}}\ge 0$ and $\check{a}\le 1$. Thus ${\hat{a}}^{qp}\ge 0$ and $(1-\check{a}^{q})^p \ge 0$ since $p,q\ge 1$. We can get ${\hat{a}}^{qp}=0$ and $(1-\check{a}^{q})^p=0$. It follows that $A=({\hat{a}},\check{a})=(0,1)$. Conversely, if $A=(0,1)$, then ${\hat{a}}=0$ and $\check{a}=1$. Hence, it is easy to see that $M_p^q(A)=0$. □

Proposition 5

Let $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$. Then

$$\begin{aligned}M_p^q(A)=1\Leftrightarrow A=(1,0).\end{aligned}$$

Proof

The proof is omitted since it is similar to what has been done for Proposition 4. □

It should be noted that even for the same $q\ge 1$, MSFs with different parameter p might not be logically equivalent when we use them to compare q-ROMGs. This can be seen from the following example.

Example 3

Suppose that

$$\begin{aligned}A=({\hat{a}},\check{a})=(0.8,0.6)\end{aligned}$$

and

$$\begin{aligned}C=({\hat{c}},\check{c})=(0.7,0.5)\end{aligned}$$

are q-ROMGs in $L_2^*$. At first, by setting $p=2$ and using Eq. (11), we have

$$\begin{aligned} M_2^2(A)= & {} \left[ \frac{{\hat{a}}^4+(1-\check{a}^2)^2}{2}\right] ^{\frac{1}{2}}=\left[ \frac{0.8^4+(1-0.6^2)^2}{2}\right] ^{\frac{1}{2}}\\= & {} 0.6400 \end{aligned}$$

and

$$\begin{aligned} M_2^2(C)= & {} \left[ \frac{{\hat{c}}^4+(1-\check{c}^2)^2}{2}\right] ^{\frac{1}{2}}=\left[ \frac{0.7^4+(1-0.5^2)^2}{2}\right] ^{\frac{1}{2}}\\= & {} 0.6335. \end{aligned}$$

It is clear that $M_2^2(A)=0.6400>0.6335=M_2^2(C)$. Thus, if we compare A, C by means of the ESF of 2-ROMGs, then A is superior to C .

Moreover, the MSF values of the 2-ROMGs A and C can be calculated by setting $p=3$ in Eq. (9). That is,

$$\begin{aligned} M_3^2(A)= & {} \left[ \frac{{\hat{a}}^6+(1-\check{a}^2)^3}{2}\right] ^{\frac{1}{3}}=\left[ \frac{0.8^6+(1-0.6^2)^3}{2}\right] ^{\frac{1}{3}}\\= & {} 0.6400\end{aligned}$$

and

$$\begin{aligned} M_3^2(C)= & {} \left[ \frac{{\hat{c}}^6+(1-\check{c}^2)^3}{2}\right] ^{\frac{1}{3}}=\left[ \frac{0.7^6+(1-0.5^2)^3}{2}\right] ^{\frac{1}{3}}\\= & {} 0.6461.\end{aligned}$$

Obviously, $M_3^2(A)=0.6400<0.6461=M_3^2(C)$. Hence, we deduce that A is inferior to C if we compare them using the MSF of 2-ROMGs with $p=3$.

From the above discussion, it can be seen that the comparison results might be completely opposite when q is fixed but p is changed.

In addition, for any chosen but fixed $p\ge 1$, the comparison results derived from the same MSF could be different when we change the parameter q of the q-ROMGs under our consideration.

Example 4

Suppose that

$$\begin{aligned}A=({\hat{a}},\check{a})=(0.80,0.61)\end{aligned}$$

and

$$\begin{aligned}C=({\hat{c}},\check{c})=(0.85,0.65).\end{aligned}$$

It is clear that A, C can be viewed as both 3-ROMGs and 4-ROMGs. Firstly, let us take A, C as 3-ROMGs and set $p=3$. Using Eq. (9), we can compute the MSF values of A and C as follows:

$$\begin{aligned} M_3^3(A)= & {} \left[ \frac{{\hat{a}}^9+(1-\check{a}^3)^3}{2}\right] ^{\frac{1}{3}}=\left[ \frac{0.80^9+(1-0.61^3)^3}{2}\right] ^{\frac{1}{3}}\\= & {} 0.6680 \end{aligned}$$

and

$$\begin{aligned} M_3^3(C)= & {} \left[ \frac{{\hat{c}}^9+(1-\check{c}^3)^3}{2}\right] ^{\frac{1}{3}}=\left[ \frac{0.85^9+(1-0.65^3)^3}{2}\right] ^{\frac{1}{3}}\\= & {} 0.6743.\end{aligned}$$

It is clear that $M_3^3(A)=0.6680<0.6743=M_3^3(C)$. Thus, if A, C is compared in $L_3^*$ by using the MSF with $p=3$, then A is inferior to C.

Second, we can also take A, C as 4-ROMGs and calculate their MSF values with $p=3$ as follows:

$$\begin{aligned} M_3^4(A)= & {} \left[ \frac{{\hat{a}}^{12}+(1-\check{a}^4)^3}{2}\right] ^{\frac{1}{3}}=\left[ \frac{0.80^{12}+(1-0.61^4)^3}{2}\right] ^{\frac{1}{3}}\\= & {} 0.7075 \end{aligned}$$

and

$$\begin{aligned} M_3^4(C)= & {} \left[ \frac{{\hat{c}}^{12}+(1-\check{c}^4)^3}{2}\right] ^{\frac{1}{3}}=\left[ \frac{0.85^{12}+(1-0.65^4)^3}{2}\right] ^{\frac{1}{3}}\\= & {} 0.7036. \end{aligned}$$

Obviously, $M_3^4(A)=0.7075>0.7036=M_3^4(C)$. Hence, if A, C is compared in $L_4^*$ by virtue of the MSF with $p=3$, then A is superior to C.

As shown above, the comparison results might be completely opposite when p is fixed but q is changed.

It is important to see that the MSF is an order homomorphism from the complete lattice $(L_q^*,\le _{L_q^*})$ to the complete lattice $([0,1],\le )$, as shown below.

Proposition 6

Let $p,q\ge 1$ and $A,C\in L_q^*$. Then

$$\begin{aligned}A\le _{L_q^*}C\Rightarrow M_p^q(A)\le M_p^q(C),\end{aligned}$$

where $\le _{L_q^*}$ is the lattice order of the complete lattice $(L_q^*,\le _{L_q^*})$.

Proof

Assume that $A=({\hat{a}},\check{a})$ and $C=({\hat{c}},\check{c})$ are two q-ROMGs such that $A\le _{L_q^*}C$. According to Eq. (1), it can be seen that ${\hat{a}}\le {\hat{c}}$ and $\check{a}\ge \check{c}$. Thus, ${\hat{a}}^{qp} \le {\hat{c}}^{qp}$ and $(1-\check{a}^q)^p\le (1-\check{c}^q)^p$ since $p,q\ge 1$. This implies that

$$\begin{aligned} M_p^q(A)=\left[ \frac{{\hat{a}}^{qp}+(1-\check{a}^{q})^p}{2}\right] ^{\frac{1}{p}}\le \left[ \frac{{\hat{c}}^{qp}+(1-\check{c}^{q})^p}{2}\right] ^{\frac{1}{p}}=M_p^q(C), \end{aligned}$$

which completes the proof. □

The following example demonstrates that the converse of the implication in Proposition 6 does not hold in general.

Example 5

Suppose that $A=({\hat{a}},\check{a})=(0.3,0.6), C=({\hat{c}},\check{c})=(0.1,0.2)$ are two IFVs. Then assume that $p=2$, by Eq. (12), we have

$$\begin{aligned} M_2(A)= & {} \left( \frac{{\hat{a}}^2+(1-\check{a})^2}{2}\right) ^{\frac{1}{2}}\\= & {} \left( \frac{0.3^2+(1-0.6)^2}{2}\right) ^{\frac{1}{2}}=0.3536\end{aligned}$$

and

$$\begin{aligned} M_2(C)= & {} \left( \frac{{\hat{c}}^2+(1-\check{c})^2}{2}\right) ^{\frac{1}{2}}\\= & {} \left( \frac{0.1^2+(1-0.2)^2}{2}\right) ^{\frac{1}{2}}=0.5701. \end{aligned}$$

Thus it is easy to see that $M_2(A)< M_2(C)$. However, one can find that $A\le _{L_q^*}C$ does not hold since ${\hat{a}}>{\hat{c}}$. Consequently, the implication

$$\begin{aligned}M_p^q(A)\le M_p^q(C)\Rightarrow A\le _{L_q^*}C,\end{aligned}$$

does not hold in general.

It should be noted that $A\le ^{(s,h)}_q C\Rightarrow M_p^q(A)\le M_p^q(C)$ does not hold, as illustrated below.

Example 6

Suppose that $A=({\hat{a}},\check{a})=(0.8,0.6),C=({\hat{c}},\check{c})=(0.7,0.5)$ are two 2-ROMGs. On the one hand, using Eq. (2) and Eq. (3), we have

$$\begin{aligned} s(A) &= {\hat{a}}^q-\check{a}^q=0.8^2-0.6^2=0.28, \ h(A)\\ &= {\hat{a}}^q+\check{a}^q=0.8^2+0.6^2=1\end{aligned}$$

and

$$\begin{aligned} s(C)= & {} {\hat{c}}^q-\check{c}^q=0.7^2-0.5^2=0.24, \ h(C)\\= & {} {\hat{c}}^q+\check{c}^q=0.7^2+0.5^2=0.74.\end{aligned}$$

According to Definition 7, we can get $C\le ^{(s,h)}_2A$ due to $s(A)>s(C)$.

On the other hand, it has been shown that $M_3^2(C)>M_3^2(A)$ in Example 3. Hence, $A\le ^{(s,h)}_q C$ cannot imply $M_p^q(A)\le M_p^q(C)$ in general.

The MSF is an order homomorphism from $\left( L_q^*,\le ^{(s,f)}_q\right)$ to $([0,1],\le )$, as revealed by the following result.

Proposition 7

Let $p,q\ge 1$ and $A,C\in L_q^*$. Then

$$\begin{aligned}A\le ^{(s,f)}_q C\Rightarrow M_p^q(A)\le M_p^q(C),\end{aligned}$$

where $\le ^{(s,f)}_q$ is the NSO of q-ROMGs.

Proof

By Definition 15 and Eq. (9), we have $p,q \ge 1$ and

$$\begin{aligned} M^q_p(A)= & {} \left[ \frac{{\hat{a}}^{qp}+(1-\check{a}^{q})^p}{2}\right] ^{\frac{1}{p}},\\M^q_p(C)\\= & {} \left[ \frac{{\hat{c}}^{qp}+(1-\check{c}^{q})^p}{2}\right] ^{\frac{1}{p}}.\end{aligned}$$

If we compare $M^q_p(A)$ and $M^q_p(C)$ we just need to compare ${\hat{a}}^{qp}+(1-\check{a}^{q})^p$ and ${\hat{c}}^{qp}+(1-\check{c}^{q})^p$, because both of them are greater than 0. From Eq. (13), we can get $\check{a}\ge \check{c}$ and $s_A\le s_C$, so $1-\check{a}^q\le 1-\check{c}^q$ because $\check{a}\ge \check{c}\ge 0$ and $q\ge 1$. According to Eq. (2), we can get ${\hat{a}}^q-\check{a}^q\le {\hat{c}}^q-\check{c}^q$, then ${\hat{a}}^q-{\hat{c}}^q\le \check{a}^q-\check{c}^q$ (or ${\hat{a}}^q-{\hat{c}}^q\le (1-\check{c}^q)-(1-\check{a}^q)$). There are two cases which need to be discussed.

Case 1: If ${\hat{a}}^q-{\hat{c}}^q\le 0\le (1-\check{c}^q)-(1-\check{a}^q)$, then according to Eq. (1) and Proposition 6, it is easy to get that $M^q_p(A)\le M^q_p(C)$ for each $p\ge 1$.

Case 2: If $0\le {\hat{a}}^q-{\hat{c}}^q\le (1-\check{c}^q)-(1-\check{a}^q)$, then we can get

$$\begin{aligned}{\hat{c}}^q\le {\hat{a}}^q\le 1-\check{a}^q\le 1-\check{c}^q\end{aligned}$$

since ${\hat{a}}^q\le 1-\check{a}^q$ and ${\hat{c}}^q\le 1-\check{c}^q$. Note also that ${\hat{a}}^q+(1-\check{a}^q)\le {\hat{c}}^q+(1-\check{c}^q)$. Then we have

$$\begin{aligned}&{\hat{a}}^{qp}+(1-\check{a}^{q})^p\\&\quad \le {\hat{c}}^{qp}+(1-\check{c}^{q})^p\end{aligned}$$

since $x^p$ ($p\ge 1$) is a convex function on [0, 1]. Thus, we have

$$\begin{aligned}M_p^q(A)\le M_p^q(C).\end{aligned}$$

To sum up, we conclude that the MSF is an order homomorphism from $\left( L_q^*,\le ^{(s,f)}_q\right)$ to $([0,1],\le )$. □

Proposition 8

Let $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$. Then

$$\begin{aligned}0\le M_p^q(A)\le 1.\end{aligned}$$

Proof

According to Eq. (1), it can be seen that

$$\begin{aligned}(0,1)\le _{L_q^*} A \le _{L_q^*} (1,0), \end{aligned}$$

where $A=({\hat{a}},\check{a})\in L_q^*$. From Proposition 6, it follows that

$$\begin{aligned}M_p^q(0,1)\le M_p^q(A) \le M_p^q(1,0).\end{aligned}$$

Note also that $M_p^q(0,1)=0$ and $M_p^q(1,0)=1$. Thus, we have $0\le M_p^q(A)\le 1$, which completes the proof. □

Proposition 9

Let $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$ with ${\tilde{a}}=0$. Then

$$\begin{aligned}M_p^q(A)={\hat{a}}^q,\end{aligned}$$

where ${\tilde{a}}$ is the hesitancy degree of the q-ROMG A.

Proof

According to the definition of hesitancy degree, ${\tilde{a}}=\left( 1-{\hat{a}}^q-\check{a}^q\right) ^{1/q}$. Thus, for every $A=({\hat{a}},\check{a})\in L_q^*$ with ${\tilde{a}}=0$, we can get ${\hat{a}}^q=1-\check{a}^q$. From Definition 15 and Eq. (9), it follows that

$$\begin{aligned} M_p^q(A)= & {} \left[ \frac{{\hat{a}}^{qp}+(1-\check{a}^{q})^p}{2}\right] ^{\frac{1}{p}}\\= & {} \left[ \frac{{\hat{a}}^{qp}+{\hat{a}}^{qp}}{2}\right] ^{\frac{1}{p}}={\hat{a}}^q, \end{aligned}$$

completing the proof. □

Theorem 3

Let $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$. Then

$$\begin{aligned} \lim _{p\rightarrow \infty } M_p^q(A)=\lim _{p\rightarrow \infty }\left[ \frac{{\hat{a}}^{qp}+(1-\check{a}^{q})^p}{2}\right] ^{\frac{1}{p}}=1-\check{a}^q.\end{aligned}$$

Proof

Let $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$. Consider two vectors $\alpha =({\hat{a}}^{q},\check{a}^{q})^T$ and $\delta =(0,1)^T$. The p-norm of the vector $\alpha -\delta$ is defined as

$$\begin{aligned} \parallel \alpha -\delta \parallel _p= & {} \left( \mid {\hat{a}}^{q}-0\mid ^{p}+\mid \check{a}^{q}-1\mid ^{p}\right) ^{\frac{1}{p}} \\= & {} \left[ {\hat{a}}^{qp}+\left( 1-\check{a}^{q}\right) ^{p}\right] ^{\frac{1}{p}}. \end{aligned}$$

By calculation, we have

$$\begin{aligned} \begin{aligned} \lim _{p\rightarrow \infty }M_p^q(A)&=\lim _{p\rightarrow \infty }\left[ \frac{{\hat{a}}^{qp}+(1-\check{a}^{q})^p}{2}\right] ^{\frac{1}{p}}\\&=\lim _{p\rightarrow \infty }\left[ {\hat{a}}^{qp}+(1-\check{a}^{q})^p\right] ^{\frac{1}{p}}\cdot \lim _{p\rightarrow \infty }\left( \frac{1}{2}\right) ^{\frac{1}{p}}\\&=\lim _{p\rightarrow \infty }\left[ {\hat{a}}^{qp}+(1-\check{a}^{q})^p\right] ^{\frac{1}{p}}\\&=\lim _{p\rightarrow \infty }\parallel \alpha -\delta \parallel _p\\&=\parallel \alpha -\delta \parallel _{\infty }\\&=\max \{{\hat{a}}^{q}, 1-\check{a}^{q}\}. \end{aligned} \end{aligned}$$

Note also that ${\hat{a}}^q+\check{a}^q \le 1$. It follows that

$$\begin{aligned}\lim _{p\rightarrow \infty } M_p^q(A)=\max \{{\hat{a}}^{q}, 1-\check{a}^{q}\}=1-\check{a}^q.\end{aligned}$$

This completes the proof. □

The following result regrading the MSF of IFVs can be easily obtained from Theorem 3 by taking $q=1$.

Corollary 1

Let $p\ge 1$ and $A=({\hat{a}},\check{a})\in L^*$. Then

$$\begin{aligned}\lim _{p\rightarrow \infty } M_p(A)=\lim _{p\rightarrow \infty }\left[ \frac{{\hat{a}}^{p}+(1-\check{a})^p}{2}\right] ^{\frac{1}{p}}=1-\check{a}.\end{aligned}$$

Fig. 1

The HSF of 3-ROMGs

Fig. 2

The ESF of 3-ROMGs

Fig. 3

The MSF of 3-ROMGs with $p=5$

Fig. 4

The MSF of 3-ROMGs with $p=10$

Fig. 5

The MSF of 3-ROMGs with $p=100$

Remark 5

The graphic illustration of the HSF and ESF of 3-ROMGs is shown in Figs. 1 and 2. In a similar fashion, Figs. 3,  4 and  5, respectively, give the graphic illustration of the MSF of 3-ROMGs with $p=5$, $p=10$ and $p=100$. From Figs. 1 and  2, it is easy to observe that the HSF and ESF values of 3-ROMGs depend on non-membership degree and membership degree. As shown in Figs. 3,  4 and  5, the MSF values of 3-ROMGs depend more heavily on the non-membership degree rather than the membership degree, when the parameter p increase from $p=5$ to $p=100$. Therefore, the parameter p in the definition of MSFs can reflect the emphasis that decision-makers would like to put on the non-membership degree. That is to say, with the aid of the newly proposed MSF of q-ROMGs in this study, the decision-makers are able to make more flexible decisions by setting different values of parameter p. Evidently, Theorem 3 reveals that the greater the value of parameter p is, the more emphasis the decision-makers would like to put on the degree of non-membership. Note also that a consequence with regard to IFVs (i.e., Corollary 1) follows immediately from Theorem 3. This means that our result can be easily applied to decision making with intuitionistic fuzzy information as well.

Proposition 10

Let $p,q\ge 1$. The MSF $M^q_p:L_q^*\rightarrow [0,1]$ is a surjection.

Proof

For each $s\in [0,1]$, we consider the q-ROMG

$$\begin{aligned}A=({\hat{a}},\check{a})=(\root q \of {s},\root q \of {1-s}).\end{aligned}$$

Obviously, the hesitancy degree of A is

$$\begin{aligned}{\tilde{a}}=\left( 1-{\hat{a}}^q-\check{a}^q\right) ^{1/q}=0.\end{aligned}$$

By Proposition 9, it follows that $M_p^q(A)={\hat{a}}^q=s$. Hence, the MSF $M_p^q$ is surjective. □

Proposition 11

Assume that $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$. Then the MSF $M_p^q(A)$ is a non-decreasing function with respect to ${\hat{a}}$.

Proof

For any $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$, we can get ${\hat{a}}^{qp}\ge 0$, $(1-\check{a}^q)^p\ge 0$ and ${\hat{a}}^{qp-1}\ge 0$ since ${\hat{a}} \ge 0$ and $\check{a} \le 1$. Then according to Definition 15 and Eq. (9), we have

$$\begin{aligned}M_p^q(A)=\left[ \frac{{\hat{a}}^{qp}+(1-\check{a}^{q})^p}{2}\right] ^{\frac{1}{p}}=\left[ \frac{{\hat{a}}^{qp}+{\hat{a}}^{qp}}{2}\right] ^{\frac{1}{p}}={\hat{a}}^q.\end{aligned}$$

The partial derivative function of $M_p^q$ with respect to ${\hat{a}}$ is

$$\begin{aligned}\frac{\partial M_p^q(A)}{\partial {\hat{a}}}=\frac{q\cdot {\hat{a}}^{qp-1}}{2}\left( \frac{{\hat{a}}^{qp}+(1-\check{a}^q)^p}{2}\right) ^{\frac{1-p}{p}}\ge 0.\end{aligned}$$

Hence, $M_p^q(A)$ is non-decreasing with respect to ${\hat{a}}$. □

Proposition 12

Assume that $p,q\ge 1$ and $A=({\hat{a}},\check{a})\in L_q^*$. Then the MSF $M_p^q(A)$ is a non-increasing function with respect to $\check{a}$.

Proof

The proof is omitted since it is similar to what has been done for Proposition 11. □

4 A generalized orthopair fuzzy soft MADM method

In this section, we propose an approach to MADM based on the MSF under a generalized orthopair fuzzy environment. To facilitate our discussion below, let us first denote the universe of discourse by ${\mathcal {V}}=\{ \nu _1, \nu _2,\ldots , \nu _m\}$. All the attributes associated with the alternatives in ${\mathcal {V}}$ constitute the parameter set $E=\{e_1,e_2,\ldots ,e_n\}$. A group of specialists are requested to assess all the alternatives in ${\mathcal {V}}$ based on the attributes in E. After the assessment, a q-ROFSS ${\mathfrak {Q}}=({\widetilde{U}},A)$ is constructed with the evaluations of specialists.

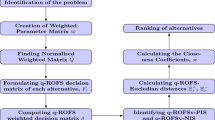
4.1 An algorithm for MADM

By taking advantages of the MSF and the q-ROFWA (or q-ROFWG) operator, a MADM approach is presented as follows:

Algorithm 1

Step 1. Specify $q\ge 1$ and construct a q-ROFSS ${\mathfrak {Q}}=({\widetilde{U}},A)$ over ${\mathcal {V}}=\{ \nu _1, \nu _2,\ldots , \nu _m\}$ with the collected data of the decision making problem to be solved. For simplicity, we denote the approximate function of ${\mathfrak {Q}}$ by

$$\begin{aligned}{\widetilde{U}}(e_j)( \nu _i)=({\hat{u}}_{ij},\check{u}_{ij}),\end{aligned}$$

where $j\in [n]$ and $i\in [m]$.

Step 2. Determine the weight vector $w=(w_1,w_2,\ldots ,w_n)^T$.

Step 3. Using the weight vector w to calculate the overall generalized orthopair fuzzy preference grade (OGOFPG) $Q(\nu _i)$ of the alternative $\nu _i$ in two cases based on two different operators:

$\bullet$ Case 1: (q-ROFWA based aggregation)

According to Definition 10 and Eq. (4), the OGOFPG $Q( \nu _i)$ of $\nu _i$ can be obtained as follows:

$$\begin{aligned} \begin{aligned} Q( \nu _i)&=\mho ^{w}({\widetilde{U}}(e_1)( \nu _i),{\widetilde{U}}(e_2)( \nu _i),\ldots ,{\widetilde{U}}(e_n)( \nu _i))\\&=\left( \left( 1-\prod _{j=1}^n\left( 1-\left( {\hat{u}}_{ij}\right) ^q\right) ^{w_j}\right) ^{1/q}, \prod _{j=1}^n\left( \check{u}_{ij}\right) ^{w_j}\right) \\&=\left( {\hat{Q}}(\nu _i), \check{Q}(\nu _i)\right) , \end{aligned} \end{aligned}$$

for $i\in [m]$.

$\bullet$ Case 2: (q-ROFWG based aggregation)

According to Definition 11 and Eq. (5), the OGOFPG $Q( \nu _i)$ of $\nu _i$ can be obtained as follows:

$$\begin{aligned} \begin{aligned} Q( \nu _i)&=\varOmega ^{w}({\widetilde{U}}(e_1)( \nu _i),{\widetilde{U}}(e_2)( \nu _i),\ldots ,{\widetilde{U}}(e_n)( \nu _i))\\&=\left( \prod _{j=1}^n\left( {\hat{u}}_{ij}\right) ^{w_j}, \left( 1-\prod _{j=1}^n\left( 1-\left( \check{u}_{ij}\right) ^q\right) ^{w_j}\right) \right) \\&=\left( {\hat{Q}}(\nu _i),\check{Q}(\nu _i)\right) , \end{aligned} \end{aligned}$$

for $i\in [m]$.

Step 4. Specify the parameter $p\ge 1$.

Step 5. Calculate the MSF value $M_p^q\left( Q( \nu _i)\right)$ of the OGOFPG $Q( \nu _i)$ by Eq. (9). That is,

$$\begin{aligned} M_p^q\left( Q( \nu _i)\right) =\left[ \frac{({\hat{Q}}(\nu _i))^{qp}+(1-(\check{Q}(\nu _i))^{q})^p}{2}\right] ^{\frac{1}{p}} \end{aligned}$$

for $i\in [m]$.

Step 6. Rank $\nu _i$ ($i\in [m]$) according to the descending order of the MSF values $M_p^q\left( Q(\nu _i)\right)$.

4.2 A case study

To verify the ranking method proposed above, a practical MADM example originally raised by Liu and Wang (2018) is revisited. Assume that an investor intends to choose a company for investment. Five companies in ${\mathcal {V}}=\{\nu _1,\nu _2,\nu _3,\nu _4,\nu _5\}$ can be taken into consideration as potential options. The experts evaluate these five companies according to six criteria in $E=\{e_1,e_2,e_3,e_4,e_5,e_6\}$. The meaning of the criterion $e_j\ (1 \le j \le 6)$ (Liu and Wang 2018) has been completed as follows:

• $e_1$ means the technical ability;

• $e_2$ means the expected benefit;

• $e_3$ means the competitive power on the market;

• $e_4$ means the ability of undertaking risks;

• $e_5$ means the management capability;

• $e_6$ means the positive social-political impact.

For the sake of comparison, the evaluations used to construct the q-ROFSS are adopted verbatim from Liu and Wang (2018). As shown in Table 1, these results can be expressed by a 3-rung orthopair fuzzy soft set ${\mathfrak {Q}}=({\widetilde{U}},E)$ over ${\mathcal {V}}$. From Table 1, the assessment result of the company $\nu _1$ with respect to the criterion $e_1$ is given by the 3-ROMG ${\widetilde{U}}(e_1)(\nu _1)=(0.5, 0.2)$. The attribute weight vector is

$$\begin{aligned} w= & {} (w_1,w_2,w_3,w_4,w_5,w_6)^T\\= & {} (0.20,0.10,0.30,0.15,0.15,0.10)^T. \end{aligned}$$

Table 1 3-Rung orthopair fuzzy soft set ${\mathfrak {Q}}=({\widetilde{U}},E)$

We now demonstrate how Algorithm 1 can be used to solve the above problem in two different cases.

Case 1 (Decision process using q-ROFWA and MSF):

In this case, we calculate the OGOFPGs $Q(\nu _i)=\left( {\hat{Q}}(\nu _i),\check{Q}(\nu _i)\right)$ of alternative $\nu _i\ (i=1,2,\ldots ,5)$ using the q-ROFWA operator ($q=3$). The OGOFPG $Q(\nu _1)$ can be obtained by Eq. (4) and all the results are listed in Table 2.

By setting $p=1$, $p=2$, $p=3$, we can calculate the HSF value $M^3_1(Q(\nu _i))$, the ESF values $M^3_2(Q(\nu _i))$ and $M^3_3(Q(\nu _i))$ of the OGOFPGs $Q(\nu _i)$, respectively. For instance, the scores of $Q(\nu _1)$ can be calculated as

$$\begin{aligned}M^3_1(Q(\nu _1))=\frac{({\hat{Q}}(\nu _1))^{3}-(\check{Q}(\nu _1))^{3}+1}{2}=0.6507,\\M^3_2(Q(\nu _1))=\left[ \frac{({\hat{Q}}(\nu _1))^{6}+\left( 1-(\check{Q}(\nu _1))^3\right) ^2}{2}\right] ^{\frac{1}{2}}=0.7276,\\M^3_3(Q(\nu _1))=\left[ \frac{({\hat{Q}}(\nu _1))^{9}+\left( 1-(\check{Q}(\nu _1))^3\right) ^3}{2}\right] ^{\frac{1}{3}}=0.7843.\end{aligned}$$

The other results are shown in Table 2. According to the descending order of MSF values, the rankings of $\nu _i\ (i=1,2,\ldots ,5)$ are shown in Table 4.

Table 2 3-ROFWA-based OGOFPGs $Q(\nu _i)$ and MSF values with $p=1,2,3$

Case 2 (Decision process using q-ROFWG and MSF):

In this case, we obtain the OGOFPGs $G(\nu _i)=({\hat{G}}(\nu _i),\check{G}(\nu _i))$ of alternative $\nu _i\ (i=1,2,\ldots ,5)$ using the q-ROFWG $(q=3)$ operator (Liu and Wang 2018). All the results can be computed by Eq. (5) and are listed in Table 3. Similar to Case 1, we can calculate the MSF value $M^3_p(Q(\nu _i))$ of the the OGOFPGs $G(\nu _i)\ (i=1,2,\ldots ,5)$ by setting parameter $p=1$, $p=2$ and $p=3$, respectively. We also calculate the score $s(G(\nu _i))$ and accuracy $h(G(\nu _i))$ of the OGOFPGs $G(\nu _i)\ (i=1,2,\ldots ,5)$ (In particular, some of score values $s(G(\nu _i))$ have been corrected based on the results obtained by Liu and Wang (2018)). All results are shown in Table 3. As in Case 1, several rankings of $\nu _i\ (i=1,2,\ldots ,5)$ based on MSF values are shown in Table 4.

Table 3 3-ROFWG-based OGOFPGs $G(\nu _i)$ and MSF values with $p=1,2,3$

4.3 A comparative analysis among different methods

To further validate the cogency of the newly proposed approach, we compare the ranking results with those obtained in other literature. All the ranking results obtained by different methods are summarized in Table 4. In view of these results, the following issues deserve to be emphasized:

Table 4 Ranking results given by different methods

First, we can find that there are three distinct ranking results derived from various decision making approaches, and the difference among these results is not significant. In fact, almost all rankings indicate that $\nu _1$ is the best company and $\nu _5$ is the worst one. As shown in Table 4, the six rankings derived from two Minkowski-type distance-based methods only have minor divergence with regard to the ranking of $\nu _3$ and $\nu _4$. Particularly, all three results obtained from Minkowski-type distance-based method 1 in Du (2018) are completely consistent. Nonetheless, by taking the parameter $p=5$, Minkowski-type distance-based method 2 in (Du 2018) results in a slightly different ranking. This shows that Du’s Minkowski-type distance-based method is not sensitive to the variation of parameter p.

Secondly, note that the ranking results based on the ESF values $M^3_2(Q(\nu _i))$ are different from those rankings based on the HSF value $M^3_1(Q(\nu _i))$ in general. This is due to the fact that the MSFs with different parameter p are essentially not equivalent for comparing q-ROMGs as shown in Sect. 3. Nevertheless, it is interesting to see that the ranking results derived from the MSFs with different parameter p might also be identical in some cases. For instance, the ranking based on q-ROFWA and $M^3_2(Q(\nu _i))$ coincides with the ranking obtained by virtue of q-ROFWA and $M^3_3(Q(\nu _i))$.

Lastly, note that the ranking obtained by q-ROFWA and $\le _{(s,h)}$ is identical to the one based on the HSF value $M^3_1(Q(\nu _i))$. Meanwhile, the ranking obtained by q-ROFWG and $\le _{(s,h)}$ is identical to the one based on the HSF value $M^3_1(G(\nu _i))$. Since all the scores $s(Q(\nu _i))$ ($1\le i \le 5$) are different, only the score function is used when comparing $Q(\nu _i)$ or $G(\nu _i)$. Furthermore, it is easy to observe that the HSF given by Eq. (2) and the score function given by Eq. (10) are equivalent for comparing q-ROMGs. Therefore, the ranking approaches proposed by Liu and Wang (2018) can be seen as special cases of the newly proposed Algorithm 1 in this situation.

In view of the above discussion, it can be concluded that our new approach provides a general and flexible way of handling MADM problems under a generalized orthopair fuzzy environment.

5 Conclusion

We have investigated how to compare and rank q-ROMGs in the complete lattice $L_q^*$ from a geometric perspective. We proposed the regular Minkowski distance of q-ROMGs and related it to some useful distance measures in Du (2018) and Xing et al. (2018). By using the regular Minkowski distance, we defined the MSF of q-ROMGs, whose rationale depends on the idea that a q-ROMG farther from the negative ideal q-ROMG should possess a greater score value. It has been revealed that the MSF extends the IPD in Xing et al. (2018) and the expectation score function in Feng et al. (2019a, b) to a more general case of q-ROMGs. We also showed that our new score functions can overcome the difficulty that Hamming (or Euclidean) distance-based score functions fail to distinguish the IFVs with identical expectation score (or IPD). We investigated several important properties of MSFs and examined the influence of parameters p, q on the values of MSFs. It has been shown that the parameter p in the definition of MSFs can reflect the emphasis that decision-makers would like to put on the non-membership degree of q-ROMGs. In fact, it has been found that the MSF value depends more heavily on the non-membership degree with the enlargement of the parameter p. In addition, when two different q-ROMGs are indiscernible since they have the same MSF value, the parameter p can be adjusted to make them eventually distinguishable. This enables the decision-makers to make more flexible decisions in practical MADM applications by setting different values of the parameter p. With the help of the MSF and the q-ROFWA (or q-ROFWG) operator, we also developed a generalized orthopair fuzzy soft MADM method. Based on a benchmark problem, a brief comparative analysis has been made between our method and several well-known approaches, which demonstrate that the newly proposed approach provides a more general and flexible way for solving q-ROFSS based MADM problems. In the future, we will further explore the applications of MSFs and develop new MADM methods based on generalized orthopair fuzzy soft sets.