MAGDM based on triangular Atanassov’s intuitionistic fuzzy information aggregation

Abstract

Triangular Atanassov’s intuitionistic fuzzy number (TAIFN) has better ability to model fuzzy ill-defined quantity. The information aggregation of TAIFNs is of great importance in multi-attribute group decision-making (MAGDM). In this paper, some arithmetic aggregation operators for TAIFNs are defined, with the triangular Atanassov’s intuitionistic fuzzy weighted average (TAIFWA) operator, ordered weighted average (TAIFOWA) operator and hybrid weighted average (TAIFHWA) operator included. Then we further investigate the Atanassov’s triangular intuitionistic fuzzy generalized ordered weighted average (TAIFGOWA) operator and generalized hybrid weighted average (TAIFGHWA) operator. Some desirable and useful properties of these operators, such as idempotence, monotonicity and boundedness, are also discussed. For the MAGDM with TAIFNs and incomplete attribute weight information, a multi-objective programming model is constructed by minimizing total deviation between all alternatives and fuzzy positive ideal solution, which is transformed into a linear goal programming. Consequently, the attribute weights are objectively derived. Thereby, an innovated MAGDM method is proposed on the basis of the TAIFWA and TAIFGHWA operators. Finally, a green supplier selection example is provided to illuminate the practicability of the proposed method in this paper.

1 Introduction

Multiple attribute decision-making (MADM) and multiple attribute group decision-making (MAGDM) have been extensively applied in a variety of real-life decision problems. With the influence of subjective factors, sometimes decision maker (DM) relies on intuition and experience to evaluate the attributes in decision problems. It is very difficult for DM to give precise assessment information on the attributes of alternatives. Furthermore, DM usually has a certain degree of hesitation during the evaluation process. Consequently, Atanassov [1] initially proposed Atanassov’s intuitionistic fuzzy sets (AIFSs) that is more flexible and practical than fuzzy set in dealing with ambiguity and uncertainty [2–5].

Similar to the fuzzy number, Atanassov’s intuitionistic fuzzy number (AIFN) is a particular AIFS defined on the set of real numbers. There are several typical AIFNS, such as triangular AIFN (ATIFN) [6–15], trapezoidal AIFN (TrAIFN) [16–23] and interval-valued TrAIFN (IVTrAIFN) [24–26]. Compared with the AIFSs, TAIFNs can express decision information in different dimensions and reflect the assessment information more comprehensively [6–15]. Therefore, it is very meaningful and valuable to apply TAIFNs to MAGDM problems. Hence, in this paper, we mainly focus on TAIFN and do not discuss the TrAIFN and IVTrAIFN.

At present, the research on TAIFNs has made some progresses. Shu and Cheng [6] characterized the membership and non-membership degrees of AIFS using triangular fuzzy numbers and put forward the concept of TAIFN. Li [7] improved the operation laws of TAIFNs defined in [6]. Nan et al. [8] studied matrix game problem in which the payments are TAIFNs. Li [9] defined the values and ambiguities for a TAIFN, developed a new ranking method on the basis of the ratio of the value index to the ambiguity index which is incorporated in MADM with TIFNs. Li et al. [10] investigated the cut sets and the values and ambiguities of TAIFNs, thereby proposed a ranking method of TAIFNs to solve MADM problems. Wan et al. [11] extended the classical VIKOR method for MAGDM using TIFNs. According to the possibility theory of fuzzy sets, Wan et al. [12] introduced the possibility mean, variance and covariance of TAIFNs. Wan [13] further proposed the MADM method on the basis of the possibility variance coefficient of TIFNs. Wan and Dong [14] developed the possibility-based method for MAGDM with incomplete weight information in the context of TAIFNs. Wang et al. [15] proposed some operation laws for TAIFNs, which are employed in fault analysis of a printed circuit board assembly system.

The aforementioned research mainly focuses on operation laws, ranking method, possibility mean, variance and covariance of TAIFNs. There is less investigation on the information fusion operators of TAIFNs. Information aggregation is an important link for MAGDM. The information fusion operators of TAIFNs are the useful tools for integrating all attributes of alternative into an individual overall value. Up to now, a great number of aggregation operators have been proposed and applied to decision-making field, such as ordered weighted average (OWA) operator [27], generalized ordered weighted average (GOWA) operator [28], fuzzy generalized ordered weighted average (FGOWA) operator [29], hybrid average (HA) operator [30], fuzzy generalized hybrid average (FGHA) operator [31], quasi-arithmetic mean operators [32], to name a few. For more details, readers can refer to the review literature [33] and the newest monograph [34]. Therefore, this paper defines some weighted arithmetic average operators and generalized ordered weighted average operators of TAIFNs and proposes a new approach to solving the MAGDM problems with TAIFNs and incomplete attribute weight information. The main works and features of this paper are presented as follows:

• 1. Define some triangular intuitionistic fuzzy aggregation operators, i.e., the triangular Atanassov’s intuitionistic fuzzy weighted average (TAIFWA) operator, ordered weighted average (TAIFOWA) operator and hybrid weighted average (TAIFHWA) operator.

• 2. Develop two triangular Atanassov’s intuitionistic fuzzy generalized ordered weighted average operators, i.e., triangular Atanassov’s intuitionistic fuzzy generalized ordered weighted average (TAIFGOWA) operator and triangular Atanassov’s intuitionistic fuzzy generalized hybrid weighted average (TAIFGHWA) operator.

• 3. Determine objectively the attribute weights through constructing multi-objective programming model which can be transformed into a linear goal programming one to solve.

• 4. Propose a new approach to MAGDM with TIFNs and incomplete attribute weight information.

The rest of this paper is organized as follows. In Sect. 2, we review the basic concepts, distance and ranking method of TAIFNs. Section 3 introduces some triangular intuitionistic fuzzy arithmetic aggregation operators and generalized ordered weighted average operators and discusses some desirable properties in detail. Section 4 proposes a new approach to solving the MAGDM problems with TAIFNs and incomplete attribute weight information. In Sect. 5, we provide a green supplier selection example to illuminate the proposed method. Some conclusion remarks are made in the last section.

2 Triangular Atanassov’s intuitionistic fuzzy numbers

In this section, we give some concepts of TAIFNs, involving the definition, operation laws, Hamming distance and ranking method.

2.1 Review on TAIFNs

Definition 1

[9] A TAIFN $\tilde{a} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,a,\bar{a});w_{{\tilde{a}}} ,u_{{\tilde{a}}} } \right)$ is a special AIFS on the set R of real numbers, whose membership and non-membership functions are, respectively, defined as follows:

$$ \mu_{{\tilde{a}}} (x) = \left\{ {\begin{array}{lll} {\frac{{x - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}{{a - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }}w_{{\tilde{a}}} ,} & {\text{if}} & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \le x\, < \,a} \\ {w_{{\tilde{a}}} ,} & {\text{if}} & {x = a} \\ {\frac{{\bar{a} - x}}{{\bar{a} - a}}w_{{\tilde{a}}} ,} & {\text{if}} & {a\,<\,x\, \le \, \bar{a}} \\ {0,} & {\text{if}} & {x\,< \,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \,{\text{or}} \,x\, >\, \bar{a}} \\ \end{array} } \right., $$

and

$$ \nu_{{\tilde{a}}} (x) = \left\{ {\begin{array}{lll} {\frac{{a - x + (x - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} )u_{{\tilde{a}}} }}{{a - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} }},} & {\text{if}} & {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \le x < a} \\ {u_{{\tilde{a}}} ,} & {\text{if}} & {x = a} \\ {\frac{{x - a + (\bar{a} - x)u_{{\tilde{a}}} }}{{\bar{a} - a}},} & {\text{if}} & {a < x \le \bar{a}} \\ {1,} & {\text{if}} & {x < \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}\, {\text{or}} \,x > \bar{a}} \\ \end{array} } \right., $$

which are depicted in Fig. 1, and the values $w_{{\tilde{a}}}$ and $u_{{\tilde{a}}}$ mean the maximum degree of membership and the minimum degree of non-membership, such that $0 \le w_{{\tilde{a}}} \le 1$, $0 \le u_{{\tilde{a}}} \le 1$ and $w_{{\tilde{a}}} + u_{{\tilde{a}}} \le 1$. $\pi_{{\tilde{a}}} (x) = 1 - w_{{\tilde{a}}} (x) - u_{{\tilde{a}}} (x)$ is called an intuitionistic fuzzy index of an element x in $\tilde{a}$.

Fig. 1

The membership function and non-membership function of TAIFN

If $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} \ge 0$ and at least one of $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}$, a and $(i = 1,2)$ is not equal to 0, then the TAIFN $\tilde{a} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,a,\bar{a});w_{{\tilde{a}}} ,u_{{\tilde{a}}} } \right)$ is positive and denoted by $\tilde{a} \ge 0$ [9]. In the sequel, we only use positive TAIFNs. Denote the set of all positive TAIFNs by Ω.

Definition 2

[9] Let $\tilde{a}_{i} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} ,a_{i} ,\bar{a}_{i} );w_{{\tilde{a}_{i} }} ,u_{{\tilde{a}_{i} }} } \right)$ (i = 1, 2) be two TAIFNs and $\lambda \ge 0$. Then the operation laws for TAIFNs are defined as:

• 1. $\tilde{a}_{1} + \tilde{a}_{2} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} ,a_{1} + a_{2} ,\bar{a}_{1} + \bar{a}_{2} );w_{{\tilde{a}_{1} }} \wedge w_{{\tilde{a}_{2} }} ,u_{{\tilde{a}_{1} }} \vee u_{{\tilde{a}_{2} }} } \right),$

• 2. $\tilde{a}_{1} \tilde{a}_{2} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} ,a_{1} a_{2} ,\bar{a}_{1} \bar{a}_{2} );w_{{\tilde{a}_{1} }} \wedge w_{{\tilde{a}_{2} }} ,u_{{\tilde{a}_{1} }} \vee u_{{\tilde{a}_{2} }} } \right),$

• 3. $\lambda \tilde{a}_{1} = \left( {(\lambda \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} ,\lambda a_{1} ,\lambda \bar{a}_{1} );w_{{\tilde{a}_{1} }} ,u_{{\tilde{a}_{1} }} } \right),$

• 4. $\tilde{a}_{1}^{\lambda } = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1}^{\lambda } ,a_{1}^{\lambda } ,\bar{a}_{1}^{\lambda } );w_{{\tilde{a}_{1} }} ,u_{{\tilde{a}_{1} }} } \right),$

where “$\wedge$” and “$\vee$” represent min and max operators, respectively.

Definition 3

Let $\tilde{a}_{1} = ((\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} ,a_{1} ,\bar{a}_{1} );w_{{\tilde{a}_{1} }} ,u_{{\tilde{a}_{1} }} )$ and $\tilde{a}_{2} = ((\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} ,a_{2} ,\bar{a}_{2} );w_{{\tilde{a}_{2} }} ,u_{{\tilde{a}_{2} }} )$ be two TAIFNs. The Hamming distance between $\tilde{a}_{1}$ and $\tilde{a}_{2}$ is defined as

$$ d(\tilde{a}_{1} ,\tilde{a}_{2} ) = \tfrac{1}{6}[|(1 + w_{{\tilde{a}_{1} }} - u_{{\tilde{a}_{1} }} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} - (1 + w_{{\tilde{a}_{2} }} - u_{{\tilde{a}_{2} }} )\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} | + |(1 + w_{{\tilde{a}_{1} }} - u_{{\tilde{a}_{1} }} )a_{1} - (1 + w_{{\tilde{a}_{2} }} - u_{{\tilde{a}_{2} }} )a_{2} |{\kern 1pt} {\kern 1pt} + |(1 + w_{{\tilde{a}_{1} }} - u_{{\tilde{a}_{1} }} )\bar{a}_{1} - (1 + w_{{\tilde{a}_{2} }} - u_{{\tilde{a}_{2} }} )\bar{a}_{2} |]. $$

2.2 The ranking method of TAIFNs

Definition 4

[9] Let $\tilde{a} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,a,\bar{a});w_{{\tilde{a}}} ,u_{{\tilde{a}}} } \right)$ be a TAIFN. Then the membership function average index $S(\tilde{a})$ and the non-membership function average index $H(\tilde{a})$ of $\tilde{a}$ are defined by

$$ S(\tilde{a}) = {{w_{{\tilde{a}}} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} + 2a + \bar{a})} \mathord{\left/ {\vphantom {{w_{{\tilde{a}}} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} + 2a + \bar{a})} 4}} \right. \kern-0pt} 4}, $$

(1)

and

$$ H(\tilde{a}) = {{(1 - u_{{\tilde{a}}} )(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} + 2a + \bar{a})} \mathord{\left/ {\vphantom {{(1 - u_{{\tilde{a}}} )(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} + 2a + \bar{a})} 4}} \right. \kern-0pt} 4}, $$

(2)

respectively.

Li [9] presented an order relation among two TAIFNs, which is specified in Definition 5.

Definition 5

[9] Let $\tilde{a}_{1}$ and $\tilde{a}_{2}$ be two TAIFNs. $S(\tilde{a}_{i} ) = {{w_{{\tilde{a}_{i} }} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} + 2a_{i} + \bar{a}_{i} )} \mathord{\left/ {\vphantom {{w_{{\tilde{a}_{i} }} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} + 2a_{i} + \bar{a}_{i} )} 4}} \right. \kern-0pt} 4}$ and $H(\tilde{a}_{i} ) = {{(1 - u_{{\tilde{a}_{i} }} )(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} + 2a_{i} + \bar{a}_{i} )} \mathord{\left/ {\vphantom {{(1 - u_{{\tilde{a}_{i} }} )(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} + 2a_{i} + \bar{a}_{i} )} 4}} \right. \kern-0pt} 4}$ are the membership and non-membership function average indexes of $\tilde{a}_{i}$ (i = 1, 2), respectively. Then

• 1. if $S(\tilde{a}_{1} ) < S(\tilde{a}_{2} )$, then $\tilde{a}_{1}$ is smaller than $\tilde{a}_{2}$, denoted by $\tilde{a}_{1} < \tilde{a}_{2}$;

• 2. if $S(\tilde{a}_{1} ) = S(\tilde{a}_{2} )$, then

  • a) if $H(\tilde{a}_{1} ) = H(\tilde{a}_{2} )$, then $\tilde{a}_{1}$ and $\tilde{a}_{2}$ represent the same amount, i.e., $\tilde{a}_{1}$ is equal to $\tilde{a}_{2}$, denoted by $\tilde{a}_{1} = \tilde{a}_{2}$;

  • b) if $H(\tilde{a}_{1} ) < H(\tilde{a}_{2} )$ then $\tilde{a}_{1} < \tilde{a}_{2}$.

Theorem 1

For two TAIFNs $\tilde{a}_{i} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} ,a_{i} ,\bar{a}_{i} );w_{{\tilde{a}_{i} }} ,u_{{\tilde{a}_{i} }} } \right)$ $(i = 1,2)$, if

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} \le \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} ,a_{1} \le a_{2} ,\bar{a}_{1} \le \bar{a}_{2} ,w_{{\tilde{a}_{1} }} \le w_{{\tilde{a}_{2} }} ,u_{{\tilde{a}_{1} }} \ge u_{{\tilde{a}_{2} }} , $$

(3)

then $\tilde{a}_{1} \le \tilde{a}_{2}$, where the symbol ≤ means smaller than or equal to.

Proof

Since $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} \le \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} ,a_{1} \le a_{2} ,\bar{a}_{1} \le \bar{a}_{2} ,w_{{\tilde{a}_{1} }} \le w_{{\tilde{a}_{2} }} ,u_{{\tilde{a}_{1} }} \ge u_{{\tilde{a}_{2} }}$, we have

$$ {{w_{{\tilde{a}_{1} }} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} + 2a_{1} + \bar{a}_{1} )} \mathord{\left/ {\vphantom {{w_{{\tilde{a}_{1} }} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} + 2a_{1} + \bar{a}_{1} )} 4}} \right. \kern-0pt} 4} \le {{w_{{\tilde{a}_{2} }} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} + 2a_{2} + \bar{a}_{2} )} \mathord{\left/ {\vphantom {{w_{{\tilde{a}_{2} }} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} + 2a_{2} + \bar{a}_{2} )} 4}} \right. \kern-0pt} 4},\,{{(1 - u_{{\tilde{a}_{1} }} )(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} + 2a_{1} + \bar{a}_{1} )} \mathord{\left/ {\vphantom {{(1 - u_{{\tilde{a}_{1} }} )(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{1} + 2a_{1} + \bar{a}_{1} )} 4}} \right. \kern-0pt} 4} \le {{(1 - u_{{\tilde{a}_{2} }} )(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} + 2a_{2} + \bar{a}_{2} )} \mathord{\left/ {\vphantom {{(1 - u_{{\tilde{a}_{2} }} )(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{2} + 2a_{2} + \bar{a}_{2} )} 4}} \right. \kern-0pt} 4}. $$

Namely, $S(\tilde{a}_{1} ) \le S(\tilde{a}_{2} )$, $H(\tilde{a}_{1} ) \le H(\tilde{a}_{2} )$. Thus, $\tilde{a}_{1} \le \tilde{a}_{2}$.

Theorem 1 shows that Eq. (3) may be viewed as a sufficient condition of $\tilde{a}_{1} \le \tilde{a}_{2}$.

3 Some triangular Atanassov’s intuitionistic fuzzy aggregation operators

In this part, motivated by existing achievements [29–34], we develop some triangular Atanassov’s intuitionistic fuzzy arithmetic aggregation operators and discuss some useful properties of them. Then, two new generalized aggregation operators for TAIFNs are further investigated.

3.1 Some triangular Atanassov’s intuitionistic fuzzy arithmetic aggregation operators

Definition 6

A triangular Atanassov’s intuitionistic fuzzy weighted average operator is a mapping TAIFWA: $\varOmega^{n} \to \varOmega$ and

$$ {\text{TAIFWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \left( {\left( {\sum\limits_{i = 1}^{n} {w_{i} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} } ,\sum\limits_{i = 1}^{n} {w_{i} a_{i} } ,\sum\limits_{i = 1}^{n} {w_{i} \bar{a}_{i} } } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}_{i} }} , \vee_{i = 1}^{n} u_{{\tilde{a}_{i} }} } \right), $$

(4)

in which $w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{\text {T}}$ is the weighting vector of $\tilde{a}_{i}$ (i = 1, 2,…,n), satisfying $0 \le w_{i} \le 1$ (i = 1, 2,…,n) and $\sum\nolimits_{i\,=\,1}^{n} {w_{i} = 1}$. In particular, if $w_{i} = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}$, then the TAIFWA operator is called the triangular Atanassov’s intuitionistic fuzzy arithmetic average (TAIFAA) operator.

Definition 7

A triangular Atanassov’s intuitionistic fuzzy ordered weighted average operator is a mapping TAIFOWA: $\varOmega^{n} \to \varOmega$ and

$$ {\text{TAIFOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \sum\limits_{i = 1}^{n} {w_{i} \tilde{a}_{(i)} } = \left( {\left( {\sum\limits_{i = 1}^{n} {w_{i} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} } ,\sum\limits_{i = 1}^{n} {w_{i} a_{(i)} } ,\sum\limits_{i = 1}^{n} {w_{i} \bar{a}_{(i)} } } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}_{(i)} }} , \vee_{i = 1}^{n} u_{{\tilde{a}_{(i)} }} } \right), $$

(5)

where $\varvec{w} = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{\text{T}}$ is the weighting vector associated with TAIFOWA, satisfying $0 \le w_{i} \le 1\,(i = 1,2, \ldots ,n)$ and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, $((1),(2), \ldots ,(n))$ is a permutation of (i = 1, 2,…,n) such that $\tilde{a}_{(i - 1)} \ge \tilde{a}_{(i)}$ for all i.

Definition 8

A triangular Atanassov’s intuitionistic fuzzy hybrid weighted average operator is a mapping TAIFHWA: $\varOmega^{n} \to \varOmega$ and

$$ {\text{TAIFHWA}}_{\omega ,w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \sum\limits_{i = 1}^{n} {w_{i} \tilde{b}_{(i)} } = \left( {\left( {\sum\limits_{i = 1}^{n} {w_{i} \left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}_{(i)} } \right)} ,\sum\limits_{i = 1}^{n} {w_{i} \left( {b_{(i)} } \right)} ,\sum\limits_{i = 1}^{n} {w_{i} \left( {\bar{b}_{(i)} } \right)} } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}_{(i)} }} , \vee_{i = 1}^{n} u_{{\tilde{a}_{(i)} }} } \right), $$

(6)

where $w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{\text {T}}$ is the weighting vector associated with TAIFHWA, satisfying $0 \le w_{i} \le 1$ (i = 1, 2,…,n) and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, $\varvec{\omega}= (\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} )^{\text{T}}$ is the weighting vector of $\tilde{a}_{i}$ (i = 1, 2,…,n), satisfying $0 \le \omega_{i} \le 1$ (i = 1, 2,…,n) and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, $\tilde{b}_{i}$ is a TAIFN obtained by weighting the $\tilde{a}_{i}$, i.e., $\tilde{b}_{i} = n\omega_{i} \tilde{a}_{i}$, $\left( {(1),(2), \ldots ,(n)} \right)$ is a permutation of $(1,2, \ldots ,n)$ such that $\tilde{b}_{(1)} \ge \tilde{b}_{(2)} \ge \cdots \ge \tilde{b}_{(n)}$.

The weighting vector $\varvec{w} = (w_{1} ,w_{2} , \ldots ,w_{n} )^{\text{T}}$ associated with TAIFHWA (or TAIFOWA) can be obtained by the fuzzy linguistic quantifier [27] as follows:

$$ w_{i} = Q(\tfrac{i}{n}) - Q(\tfrac{i - 1}{n})\,(i = 1,2, \ldots ,n) $$

(7)

where Q is the fuzzy linguistic quantifier and

$$ Q(t) = \left\{ {\begin{array}{ll} {0,} \quad & {t < \xi } \\ {(t - \xi )/(\eta - \xi ),} \quad & {\xi \le t < \eta } \\ {1,} \quad & {t \ge \eta } \\ \end{array} } \right. $$

with $\xi ,t,\eta \in [0,1]$. For the criteria “at least half,” “most” and “as many as possible,” the parameter pair $(\xi ,\eta )$ takes the values (0, 0.5), (0.3, 0.8) and (0.5,1), respectively.

3.2 Some generalized ordered weighted average operators of TAIFNs

In this section, the TAIFOWA operator is further generalized to develop two new generalized aggregation operators for TIFNs, which are totally inspired by Merigó and Casanovas [29, 31, 32].

Definition 9

A triangular Atanassov’s intuitionistic fuzzy generalized ordered weighted average operator is a mapping TAIFGOWA: $\varOmega^{n} \to \varOmega$ and

$$ \begin{aligned} & {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \left( {\sum\limits_{i = 1}^{n} {w_{i} (\tilde{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } \\ & \quad = \left( {\left( {\left( {\sum\limits_{i = 1}^{n} {w_{i} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\sum\limits_{i = 1}^{n} {w_{i} (a_{(i)} )^{\lambda } } } \right)^{1/\lambda } ,\,\left( {\sum\limits_{i = 1}^{n} {w_{i} (\bar{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}_{(i)} }} , \vee_{i = 1}^{n} u_{{\tilde{a}_{(i)}}}}\right),\\ \end{aligned} $$

(8)

where $\lambda \in (0, + \infty )$ is a parameter, $\varvec{w} = (w_{1} ,w_{2} , \ldots ,w_{n} )^{\text{T}}$ is the weighting vector associated with TAIFGOWA, satisfying $0 \le w_{i} \le 1$ (i = 1, 2,…,n) and $\sum\nolimits_{i = 1}^{n} {w_{i} } = 1$, $\left( {(1),(2), \ldots ,(n)} \right)$ is a permutation of $(1,2, \ldots ,n)$ such that $\tilde{a}_{(i - 1)} \ge \tilde{a}_{(i)}$ for all i.

The TAIFGOWA operator has some useful properties which are listed in the following propositions.

Proposition 1

(Idempotence) Let $\tilde{a}_{i} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} ,a_{i} ,\bar{a}_{i} );w_{{\tilde{a}_{i} }} ,u_{{\tilde{a}_{i} }} } \right)$ (i = 1, 2,…,n) be a group of TAIFNs. If all $\tilde{a}_{i}$ $(i = 1,2, \ldots ,n)$ are equal, i.e., $\tilde{a}_{1} = \tilde{a}_{2} = \cdots = \tilde{a}_{n} = \tilde{a}$ , then ${\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \tilde{a}$.

Proof

According to Definition 9, for $\tilde{a}_{i} = \tilde{a}$ (i = 1, 2,…,n), we have

$$ \begin{aligned} &{\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \left( {\left( {\left({\sum\limits_{i = 1}^{n} {w_{i} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\sum\limits_{i = 1}^{n} {w_{i} (a_{(i)} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\sum\limits_{i = 1}^{n} {w_{i} (\bar{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}_{(i)} }} , \vee_{i = 1}^{n} u_{{\tilde{a}_{(i)} }} } \right) \\ & \quad = \left( {\left( {\left( {\sum\limits_{i = 1}^{n} {w_{i} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\sum\limits_{i = 1}^{n} {w_{i} (a)^{\lambda } } } \right)^{1/\lambda } ,\left( {\sum\limits_{i = 1}^{n} {w_{i} (\bar{a})^{\lambda } } } \right)^{1/\lambda } } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}}} , \vee_{i = 1}^{n} u_{{\tilde{a}}} } \right) \\ \end{aligned} $$

Note that $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, so

$$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \left( {(((\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} )^{\lambda } )^{1/\lambda } ,((a)^{\lambda } )^{1/\lambda } ,((\bar{a})^{\lambda } )^{1/\lambda } );w_{{\tilde{a}}} ,u_{{\tilde{a}}} } \right) = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a} ,a,\bar{a});w_{{\tilde{a}}} ,u_{{\tilde{a}}} } \right) = \tilde{a}. $$

Proposition 2

(Monotonicity) Let $\tilde{a}_{i} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} ,a_{i} ,\bar{a}_{i} );w_{{\tilde{a}_{i} }} ,u_{{\tilde{a}_{i} }} } \right)$ and $\tilde{a}^{\prime}_{i} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}^{\prime}_{i} ,a^{\prime}_{i} ,\bar{a}^{\prime}_{i} );w_{{\tilde{a}^{\prime}_{i} }} ,u_{{\tilde{a}^{\prime}_{i} }} } \right)$ be two collections of TAIFNs, and $((1),(2), \ldots ,(n))$ is a permutation of $(1,2, \ldots ,n)$ such that $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} \le \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a^{\prime}}_{(i)}$, $a_{(i)} \le a^{\prime}_{(i)}$, $\bar{a}_{(i)} \le \bar{a}^{\prime}_{(i)}$, $w_{{\tilde{a}_{(i)} }} \le w_{{\tilde{a}^{\prime}_{(i)} }}$, $u_{{\tilde{a}_{(i)} }} \ge u_{{\tilde{a}^{\prime}_{(i)} }}$ for all $i$ (i = 1, 2,…,n), then

$$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) \le {\text{TAIFGOWA}}_{w} (\tilde{a}^{\prime}_{1} , \ldots ,\tilde{a}^{\prime}_{n} ). $$

Proof

Since $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} \le \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a^{\prime}}_{(i)}$, $a_{(i)} \le a^{\prime}_{(i)}$, $\bar{a}_{(i)} \le \bar{a}^{\prime}_{(i)}$, $w_{{\tilde{a}_{(i)} }} \le w_{{\tilde{a}^{\prime}_{(i)} }}$, $u_{{\tilde{a}_{(i)} }} \ge u_{{\tilde{a}^{\prime}_{(i)} }}$, we get

$$ \begin{aligned} & \left( {\sum\limits_{i = 1}^{n} {w_{i} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } \le \left( {\sum\limits_{i = 1}^{n} {w_{i} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)}^{{\prime }} )^{\lambda } } } \right)^{1/\lambda } , \\ & \left( {\sum\limits_{i = 1}^{n} {w_{i} (a_{(i)} )^{\lambda } } } \right)^{1/\lambda } \le \left( {\sum\limits_{i = 1}^{n} {w_{i} (a_{(i)}^{{\prime }} )^{\lambda } } } \right)^{1/\lambda } , \\ & \left( {\sum\limits_{i = 1}^{n} {w_{i} (\bar{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } \le \left( {\sum\limits_{i = 1}^{n} {w_{i} (\bar{a}_{(i)}^{{\prime }} )^{\lambda } } } \right)^{1/\lambda } , \\ & \quad \mathop \wedge \limits_{i} w_{{\tilde{a}_{(i)} }} \le \mathop \wedge \limits_{i} w_{{\tilde{a}^{\prime}_{(i)} }} ,{\kern 1pt} {\kern 1pt} \mathop \vee \limits_{i} u_{{\tilde{a}_{(i)} }} \ge \mathop \vee \limits_{i} u_{{\tilde{a}^{\prime}_{(i)} }} . \\ \end{aligned} $$

Therefore, according to Eqs. (3) and (8), we have

$$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) \le {\text{TAIFGOWA}}_{w} (\tilde{a}^{\prime}_{1} , \ldots ,\tilde{a}^{\prime}_{n} ). $$

Proposition 3

(Boundedness) Let $\tilde{a}_{i} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} ,a_{i} ,\bar{a}_{i} );w_{{\tilde{a}_{i} }} ,u_{{\tilde{a}_{i} }} } \right)$ (i = 1, 2,…,n) be a group of TAIFNs. If

$$ \tilde{a}^{ - } = \left( {(\mathop {\hbox{min} }\limits_{i} \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} } \right\},\mathop {\hbox{min} }\limits_{i} \left\{ {a_{i} } \right\},\mathop {\hbox{min} }\limits_{i} \left\{ {\bar{a}_{i} } \right\});\mathop \wedge \limits_{i} w_{{\tilde{a}_{i} }} ,\mathop \vee \limits_{i} u_{{\tilde{a}_{i} }} } \right),\,\tilde{a}^{ + } = \left( {(\mathop {\hbox{max} }\limits_{i} \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} } \right\},\mathop {\hbox{max} }\limits_{i} \left\{ {a_{i} } \right\},\mathop {\hbox{max} }\limits_{i} \left\{ {\bar{a}_{i} } \right\});\mathop \vee \limits_{i} w_{{\tilde{a}_{i} }} ,\mathop \wedge \limits_{i} u_{{\tilde{a}_{i} }} } \right), $$

then

$$ \tilde{a}^{ - } \le {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) \le \tilde{a}^{ + } . $$

Proof

For any $\tilde{a}_{i} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} ,a_{i} ,\bar{a}_{i} );w_{{\tilde{a}_{i} }} ,u_{{\tilde{a}_{i} }} } \right)$ (i = 1, 2,…,n), we have

$$ \begin{aligned} \mathop {\hbox{min} }\limits_{i} \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} } \right\} & \le \left( {\sum\limits_{i = 1}^{n} {w_{i} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } \le \mathop {\hbox{max} }\limits_{i} \left\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} } \right\}, \\ \mathop {\hbox{min} }\limits_{i} \left\{ {a_{(i)} } \right\} & \le \left( {\sum\limits_{i = 1}^{n} {w_{i} (a_{(i)} )^{\lambda } } } \right)^{1/\lambda } \le \mathop {\hbox{max} }\limits_{i} \left\{ {a_{(i)} } \right\}, \\ \mathop {\hbox{min} }\limits_{i} \left\{ {\bar{a}_{(i)} } \right\} & \le \left( {\sum\limits_{i = 1}^{n} {w_{i} (\bar{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } \le \mathop {\hbox{max} }\limits_{i} \left\{ {\bar{a}_{(i)} } \right\}. \\ \end{aligned} $$

Thus, according to Eqs. (8) and (1), we get $\tilde{a}^{ - } \le {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) \le \tilde{a}^{ + }$.

Proposition 4

Let $(\dot{\tilde{a}}_{1} ,\dot{\tilde{a}}_{2} , \ldots ,\dot{\tilde{a}}_{n} )$ be an arbitrary permutation of $(\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} )$, then

$$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = {\text{TAIFGOWA}}_{w} (\dot{\tilde{a}}_{1} ,\dot{\tilde{a}}_{2} , \ldots ,\dot{\tilde{a}}_{n} ). $$

Proof

Since $(\dot{\tilde{a}}_{1} ,\dot{\tilde{a}}_{2} , \ldots ,\dot{\tilde{a}}_{n} )$ is an arbitrary permutation of $(\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} )$, $\dot{\tilde{a}}_{(i - 1)} \ge \dot{\tilde{a}}_{(i)}$ is equivalent to $\tilde{a}_{(i - 1)} \ge \tilde{a}_{(i)}$. Thus, we have

$$ {\text{TAIFGOWA}}_{w} (\dot{\tilde{a}}_{1} ,\dot{\tilde{a}}_{2} , \ldots ,\dot{\tilde{a}}_{n} ) = \left( {\sum\limits_{i = 1}^{n} {w_{i} (\dot{\tilde{a}}_{(i)} )^{\lambda } } } \right)^{1/\lambda } = \left( {\sum\limits_{i = 1}^{n} {w_{i} (\tilde{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } {\text{ = TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ). $$

Proposition 5

Let $\tilde{a}_{i} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{i} ,a_{i} ,\bar{a}_{i} );w_{{\tilde{a}_{i} }} ,u_{{\tilde{a}_{i} }} } \right)$ (i = 1, 2,…,n) be a collection of TAIFNs. Then,

• 1. when $\lambda \to 0$, it easily follows from Eq. (8) that

  $$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \prod\limits_{i = 1}^{n} {(\tilde{a}_{(i)} )^{{w_{i} }} } , $$

  which is called the ordered weighted geometric operator of TAIFNs;

• 2. when $\lambda \to 1$, it easily follows from Eq. (8) that

  $$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \sum\limits_{i = 1}^{n} {w_{i} \tilde{a}_{(i)} } , $$

  which is reduced to the TAIFOWA operator;

• 3. when $\lambda \to + \infty$ and $w_{i} \ne 0$ (i = 1, 2,…,n), by Eq. (8) it follows that

  $$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \hbox{max} \{ \tilde{a}_{i} |i = 1,2, \ldots ,n\} , $$

  which is called the max operator of TAIFNs;

• 4. if all weights are equal, i.e., $w_{i} = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}{\kern 1pt}$ (i = 1, 2,…,n), then by Eq. (8) it is easily derived that

  $$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {(\tilde{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } , $$

  (9)

  which is called the triangular Atanassov’s intuitionistic fuzzy generalized mean (TAIFGM) operator. To sum up, the TAIFGOWA operator reduces to the TAIFGM operator, if the weighting vector $\varvec{w}\,{=}\,\left( {{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n},{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}, \ldots ,{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}} \right)^{\text{T}}.$

By Eq. (8), Eq. (9) can be explicitly written as

$$ \begin{aligned} & {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) \\ & \quad = \left( {\left( {\left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {(a_{(i)} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\frac{1}{n}\sum\limits_{i = 1}^{n} {(\bar{a}_{(i)} )^{\lambda } } } \right)^{1/\lambda } } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}_{(i)} }} , \vee_{i = 1}^{n} u_{{\tilde{a}_{(i)} }} } \right). \\ \end{aligned} $$

(10)

Particularly, if λ = 1, then by Eq. (10) it is easily derived that

$$ {\text{TAIFGOWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \left({\left( { {\frac{1}{n}\sum\limits_{i = 1}^{n} {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{(i)} } } ),\frac{1}{n}\sum\limits_{i = 1}^{n} {(a_{(i)} )} ,\frac{1}{n}\sum\limits_{i = 1}^{n} {(\bar{a}_{(i)} )} } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}_{(j)} }} , \vee_{i = 1}^{n} u_{{\tilde{a}_{(i)} }} } \right), $$

which is called triangular Atanassov’s intuitionistic fuzzy simple average operator.

Propositions 1–5 show that, although the meaning of λ is not totally obvious, the TAIFGOWA operator can have different forms using different values of the parameter λ. The parameter λ can reflect some preference of DM to some degree. It can be chosen properly according to the need of real application and the DM’s preference.

Definition 10

A triangular Atanassov’s intuitionistic fuzzy generalized hybrid weighted average operator is a mapping TAIFGHWA: $\varOmega^{n} \to \varOmega$ and

$$ {\text{TAIFGHWA}}_{\omega ,w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \left( {\sum\limits_{i = 1}^{n} {w_{i} (\tilde{b}_{(i)} )^{\lambda } } } \right)^{1/\lambda } \, = \left( {\left( {\left( {\sum\limits_{i = 1}^{n} {w_{i} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{b}_{(i)} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\sum\limits_{i = 1}^{n} {w_{i} (b_{(i)} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\sum\limits_{i = 1}^{n} {w_{i} (\bar{b}_{(i)} )^{\lambda } } } \right)^{1/\lambda } } \right); \wedge_{i = 1}^{n} w_{{\tilde{a}_{(i)} }} , \vee_{i = 1}^{n} u_{{\tilde{a}_{(i)} }} } \right), $$

(11)

where $\lambda \in (0, + \infty )$ is a parameter, $\varvec{w} = (w_{1} ,w_{2} , \ldots ,w_{n} )^{\text{T}}$ is the weighting vector associated with TAIFGHWA, satisfying $0 \le w_{i} \le 1$ (i = 1, 2,…,n) and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, $\varvec{\omega}= (\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} )^{\text{T}}$ is the weighting vector of $\tilde{a}_{i}$ (i = 1, 2,…,n), satisfying $0 \le \omega_{i} \le 1\;\;\;(i = 1,2, \ldots ,n)$ and $\sum\nolimits_{i = 1}^{n} {w_{i} = 1}$, (i) indicates a permutation of i such that $\tilde{b}_{(1)} \ge \tilde{b}_{(2)} \ge \cdots \ge \tilde{b}_{(n)}$ and $\tilde{b}_{i}$ is a triangular Atanassov’s intuitionistic fuzzy number obtained by weighting the $\tilde{a}_{i}$, that is, $\tilde{b}_{i} = n\omega_{i} \tilde{a}_{i}$. In particular, if λ = 1, then the TAIFGHWA operator is called the triangular Atanassov’s intuitionistic fuzzy hybrid weighted average (TAIFHWA) operator.

By Definition 10, we can immediately get the following conclusions:

• 1. when $\lambda \to 0$, it easily follows from Eq. (11) that

  $$ {\text{TAIFGHWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \prod\limits_{i = 1}^{n} {(\tilde{b}_{(i)} )^{{w_{i} }} } , $$

  which is called the hybrid weighted geometrical operator of TAIFNs;

• 2. when $\lambda \to 1$, it easily follows from Eq. (11) that

  $$ {\text{TAIFGHWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \sum\limits_{i = 1}^{n} {w_{i} \tilde{b}_{(i)} } , $$

  which is called the hybrid weighted average operator of TAIFNs;

• 3. when $\lambda \to + \infty$ and $w_{i} \ne 0$ (i = 1, 2,…,n), it easily follows from Eq. (11) that

  $$ {\text{TAIFGHWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \hbox{max} \{ \tilde{b}_{i} |i = 1,2, \ldots ,n\} , $$

  which is called the hybrid max operator of TAIFNs;

• 4. if all weights are equal, i.e., $w_{i} = {1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0pt} n}{\kern 1pt}$ (i = 1, 2,…,n), then by Eq. (11) it is easily derived that

  $$ {\text{TAIFGHWA}}_{w} (\tilde{a}_{1} ,\tilde{a}_{2} , \ldots ,\tilde{a}_{n} ) = \left( {\tfrac{1}{n}\sum\limits_{i = 1}^{n} {(\tilde{b}_{(i)} )^{\lambda } } } \right)^{1/\lambda } , $$

  which is called generalized hybrid mean operator of TAIFNs.

4 MAGDM with TIFNs and incomplete attribute weight information

In this part, we present the MAGDM problems with TAIFNs and incomplete attribute weight information and then propose a new approach to solving such MAGDM problems using TAIFWA and TAIFGHWA operators.

4.1 Statement of MAGDM problems using TIFNs and incomplete attribute weight information

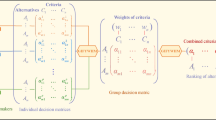
MAGDM refers to the selection or ranking alternatives associated with some attributes for a decision group. There are p DMs e _k $(k = 1,2, \ldots ,p)$ who attempt to choose one of (or rank) m alternatives A _i $(i = 1,2, \ldots ,m)$ assessed on n attributes $a_{j} (j = 1,2, \ldots ,n)$. Denote the set of DMs (or experts) by $E = \{ e_{1} ,e_{2} , \ldots ,e_{p} \}$, the set of alternatives by $A = \{ A_{1} ,A_{2} , \ldots ,A_{m} \}$ and the set of attributes by $F = \{ a_{1} ,a_{2} , \ldots ,a_{n} \}$. Assume that the rating of alternative A _i on attribute a _j given by the DM e _k is represented by a TAIFN $\tilde{a}_{ij}^{k} = \left( {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{ij}^{k} ,\,a_{ij}^{k} ,\,\bar{a}_{ij}^{k} );\,w_{{\tilde{a}_{ij}^{k} }} ,u_{{\tilde{a}_{ij}^{k} }} } \right)$ $(i = 1,2, \ldots ,m;\;j = 1,2, \ldots ,n;\;k = 1,2, \ldots ,p)$. Thus, we can get the triangular Atanassov’s intuitionistic fuzzy decision matrices $\tilde{\varvec{D}}^{k} = (\tilde{a}_{ij}^{k} )_{m \times n}$ $(k = 1,2, \ldots ,p)$, on the basis of which the MAGDM problems are usually investigated.

Suppose that t _k is the weight of expert $e_{k} \in E\,(k = 1,2, \ldots ,p)$, and it is known in advance. $\omega_{j}$ is the relative weight of attribute $a_{j} \in F\,(j = 1,2, \ldots ,n)$, satisfying the normalization condition: $\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1$ and $\omega_{j} \in [0,1]$ $(j = 1,2, \ldots ,n)$. Denote $\varLambda_{0} = \{ \omega |\sum\nolimits_{j = 1}^{n} {\omega_{j} } = 1,\omega_{j} \in [0,1]\;(j = 1,2, \ldots ,n)\}$, which is the set of all attribute weighting vectors. Usually, the information of attribute weights is incomplete. It has five basic relations, which are denoted by subsets $\varLambda_{s}$ $(s = 1,2,3,4,5)$ of $\varLambda_{0}$, respectively (see Refs. [3, 4, 35] for detail). Denote the incomplete information structure of attribute weights by $\varLambda$, which consists of several subsets $\varLambda_{s}$ $(s = 1,2,3,4,5)$.

The motivation of this paper is to select the best alternative according to the fuzzy decision matrices $\tilde{\varvec{D}}^{k}$ $(k = 1,2, \ldots ,p)$ and incomplete information structure $\varLambda$ of attribute weights.

4.2 Determining the attribute weighting vector based on goal programming model

In order to diminish the physical effect of different dimensions on the final decision results, the decision matrix $\tilde{\varvec{D}}^{k} = (\tilde{a}_{ij}^{k} )_{m \times n}$ should be normalized as $\tilde{\varvec{R}}^{k} = (\tilde{r}_{ij}^{k} )_{m \times n}$ where $\tilde{r}_{ij}^{k} = ((\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} ,r_{ij}^{k} ,\bar{r}_{ij}^{k} );w_{{\tilde{a}_{ij}^{k} }} ,u_{{\tilde{a}_{ij}^{k} }} )$, and

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{ij}^{k} /\sqrt {\sum\nolimits_{i = 1}^{m} {(\bar{a}_{ij}^{k} )^{2} } } ,r_{ij}^{k} = a_{ij}^{k} /\sqrt {\sum\nolimits_{i = 1}^{m} {(a_{ij}^{k} )^{2} } } ,\bar{r}_{ij}^{k} = \bar{a}_{ij}^{k} /\sqrt {\sum\nolimits_{i = 1}^{m} {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{ij}^{k} )^{2} } },\,{\text{ for}}\quad j \in F^{b} ; $$

(12)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} = \frac{1}{{\bar{a}_{ij}^{k} }}/\sqrt {\sum\nolimits_{i = 1}^{m} {\left( {\frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{ij}^{k} }}} \right)^{2} } } ,\,r_{ij}^{k} = \frac{1}{{a_{ij}^{k} }}/\sqrt {\sum\nolimits_{i = 1}^{m} {\left( {\frac{1}{{a_{ij}^{k} }}} \right)^{2} } } ,\bar{r}_{ij}^{k} = \frac{1}{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}_{ij}^{k} }}/\sqrt {\sum\nolimits_{i = 1}^{m} {\left( {\frac{1}{{\bar{a}_{ij}^{k} }}} \right)^{2} } } ,\,\text{for}\,\,j \in F^{c} , $$

(13)

where F ^b is the collection of benefit attributes and F ^c is the collection of cost attributes.

To derive the weights of attributes, we select the triangular Atanassov’s intuitionistic fuzzy positive ideal solution $A^{ + } = (\tilde{r}_{1}^{ + } ,\tilde{r}_{2}^{ + } , \ldots ,\tilde{r}_{n}^{ + } )$ as a reference point, where $\tilde{r}_{j}^{ + } = ((1,1,1);1,0)$ $(j = 1,2, \ldots ,n)$.

Generally, the closer the alternative to the positive ideal solution, the better the alternative is. We use Hamming distance to measure the deviation between the ideal solution and alternative. The Hamming distance between alternative A _i and A ⁺ for the DM e _k is computed as follows:

$$ \begin{aligned} & d_{k} (A_{i} ,A^{ + } ) = \tfrac{1}{6}[|(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} } - 2| + |(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} r_{ij}^{k} } - 2| \\ & \quad + |(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \bar{r}_{ij}^{k} } - 2|]. \\ \end{aligned} $$

Hence, the total deviation between all alternatives and A ⁺ for the DM e _k is $\sum\nolimits_{i = 1}^{m} {d_{k} (A_{i} ,A^{ + } )}$.

To reasonably determine the weights of attributes, we can establish the multi-objective optimization model:

$$ \begin{aligned} & \hbox{min} \left\{ \sum\limits_{i = 1}^{m} {d_{1} (A_{i} ,A^{ + } )} \, ,\sum\limits_{i = 1}^{m} {d_{2} (A_{i} ,A^{ + } )} , \ldots ,\sum\limits_{i = 1}^{m} {d_{p} (A_{i} ,A^{ + } )} \right\} . \\ & {\text{s}} . {\text{t}}.\,\varvec{\omega}\in \varLambda \\ \end{aligned} $$

(14)

Equation (14) can be converted into a single-objective programming by linear sum of DMs’ weights:

$$ \begin{aligned} & \hbox{min} \left\{ {\sum\limits_{k = 1}^{p} {[t_{k} \sum\limits_{i = 1}^{m} {d_{k} (A_{i} ,A^{ + } )} ]} } \right\} \\ & {\text{s}}.{\text{t}}.\,\varvec{\omega}\in \varLambda \\ \end{aligned} $$

(15)

To solve the above model, we can set

$$ \begin{aligned} d_{i1}^{k + } & = \tfrac{1}{2}[|(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} } - 2| + (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} } - 2], \\ d_{i1}^{k - } & = \tfrac{1}{2}[|(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} } - 2| - (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} } + 2], \\ d_{i2}^{k + } & = \tfrac{1}{2}[|(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} r_{ij}^{k} } - 2| + (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} r_{ij}^{k} } - 2], \\ d_{i2}^{k - } & = \tfrac{1}{2}[|(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} r_{ij}^{k} } - 2| - (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} r_{ij}^{k} } + 2], \\ d_{i3}^{k + } & = \tfrac{1}{2}[|(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \bar{r}_{ij}^{k} } - 2| + (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \bar{r}_{ij}^{k} } - 2], \\ d_{i3}^{k - } & = \tfrac{1}{2}[|(1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \bar{r}_{ij}^{k} } - 2| - (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \bar{r}_{ij}^{k} } + 2]. \\ \end{aligned} $$

Thus, Eq. (15) is converted into the linear goal programming model:

$$ \begin{aligned} & \hbox{min} \, Z = \tfrac{1}{6}\sum\limits_{k = 1}^{p} {[t_{k} \sum\limits_{i = 1}^{m} {\sum\limits_{l = 1}^{3} {(d_{il}^{k + } + d_{il}^{k - } )} } ]} \\ & {\text{s}} . {\text{t}} . { }\left\{ \begin{array}{l} (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} } - 2 - d_{i1}^{k + } + d_{i1}^{k - } = 0 \, (i = 1,2, \ldots ,m; \, k = 1,2, \ldots ,p) \, \hfill \\ (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} r_{ij}^{k} } - 2 - d_{i2}^{k + } + d_{i2}^{k - } = 0 \, (i = 1,2, \ldots ,m; \, k = 1,2, \ldots ,p) \, \hfill \\ (1 + \mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} - \mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} )\sum\limits_{j = 1}^{n} {\omega_{j} \bar{r}_{ij}^{k} } - 2 - d_{i3}^{k + } + d_{i3}^{k - } = 0 \, (i = 1,2, \ldots ,m; \, k = 1,2, \ldots ,p) \,\\ d_{il}^{k + } \ge 0, \, d_{il}^{k - } \ge 0, \, d_{il}^{k + } d_{il}^{k - } = 0 \, (i = 1,2, \ldots ,m; \, k = 1,2, \ldots ,p; \, l = 1,2,3)\\ \varvec{\omega}\in \Lambda \hfill \\ \end{array} \right. \\ \end{aligned} $$

(16)

By simplex method, the attribute weighting vector $\omega = (\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} )^{\text {T}}$ can be obtained.

4.3 A new approach to MAGDM using TAIFNs and incomplete attribute weight information

So, a new approach to MAGDM with TAIFNs and incomplete attribute weight information is described step by step as follows:

Step 1:

Normalized the decision matrix $\tilde{\varvec{D}}^{k} = (\tilde{a}_{ij}^{k} )_{m \times n}$ to $\tilde{\varvec{R}}^{k} = (\tilde{r}_{ij}^{k} )_{m \times n}$ by using Eqs. (12) and (13).

Step 2:

By integration of the ith row elements of the matrix $\tilde{\varvec{R}}^{k} = (\tilde{r}_{ij}^{k} )_{m \times n}$ using the TAIFWA operator, the individual comprehensive value $\tilde{r}_{i}^{k}$ of alternative A _i for the DM e _k is obtained as follows:

$$ \tilde{r}_{i}^{k} = ((\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{i}^{k} ,r_{i}^{k} ,\bar{r}_{i}^{k} );w_{{\tilde{r}_{i}^{k} }} ,u_{{\tilde{r}_{i}^{k} }} ) = {\text{TIFWA}}_{\varvec{\omega}} (\tilde{r}_{i1}^{k} ,\tilde{r}_{i2}^{k} , \ldots ,\tilde{r}_{in}^{k} ) = \left(\left(\sum\limits_{j = 1}^{n} {\omega_{j} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{ij}^{k} } ,\sum\limits_{j = 1}^{n} {\omega_{j} r_{ij}^{k} } ,\sum\limits_{j = 1}^{n} {\omega_{j} \bar{r}_{ij}^{k} } \right);\mathop \wedge \limits_{j} w_{{\tilde{r}_{ij}^{k} }} ,\mathop \vee \limits_{j} u_{{\tilde{r}_{ij}^{k} }} \right), $$

(17)

where $\varvec{\omega}= (\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} )^{\text{T}}$ is the weighting vector of attributes.

Step 3:

Determine the weights of attributes through constructing multi-objective programming.

Step 4:

Utilized the TAIFGHWA operator to integrate all the individual comprehensive values $\tilde{r}_{i}^{k}$ $(k = 1,2, \ldots ,p)$, the collective comprehensive value $\tilde{r}_{i}$ of alternative A _i is computed by

$$ \begin{aligned} & \tilde{r}_{i} = ((\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{i} ,r_{i} ,\bar{r}_{i} );w_{{\tilde{r}_{i} }} ,u_{{\tilde{r}_{i} }} ) = {\text{TAIFGHWA}}_{w,v} (\tilde{r}_{i}^{1} ,\tilde{r}_{i}^{2} , \ldots ,\tilde{r}_{i}^{p} ) \\ & & & \quad = \left( {\left( {\left( {\sum\limits_{k = 1}^{p} {w_{k} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{i}^{{{\prime }(k)}} )^{\lambda } } } \right)^{1/\lambda } ,\,\left( {\sum\limits_{k = 1}^{p} {w_{k} (r_{i}^{{{\prime }(k)}} )^{\lambda } } } \right)^{1/\lambda } ,\left( {\sum\limits_{k = 1}^{p} {w_{k} (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{i}^{{{\prime }(k)}} )^{\lambda } } } \right)^{1/\lambda } } \right);\mathop \wedge \limits_{k} w_{{\tilde{r}_{i}^{k} }} ,\mathop \vee \limits_{k} u_{{_{{\tilde{r}_{i}^{k} }} }} } \right), \\ \end{aligned} $$

(18)

where $\tilde{r}_{i}^{{{\prime }(k)}} = \left( {\left( {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{i}^{{{\prime }(k)}} ,r_{i}^{{{\prime }(k)}} ,\bar{r}_{i}^{{{\prime }(k)}} } \right);\,w_{{\tilde{r}_{i}^{{{\prime }(k)}} }} ,\,u_{{\tilde{r}_{i}^{{{\prime }(k)}} }} } \right)$ represents the kth largest TAIFN of $\tilde{r}_{i}^{{{\prime }k}} = pt_{k} \tilde{r}_{i}^{k}$ $(k = 1,2, \ldots ,p)$, ${\text{T}} = (t_{1} ,t_{2} , \ldots ,t_{p} )^{\text{T}}$ is the weighting vector of DMs, $\varvec{w} = (w_{1} ,w_{2} , \ldots ,w_{p} )^{\text{T}}$ is the weighting vector associated with TAIFGHWA.

Step 5:

According to Definition 4, calculate the membership and non-membership function average indexes for the collective comprehensive value $\tilde{r}_{i}^{k}$ to sort $\tilde{r}_{i}$ (i = 1, 2,…,m), and then generate the ranking order of alternatives.

The aforementioned decision-making process can be described by the following algorithm.

Algorithm: An approach to MAGDM with TAIFNs

Step 1: Normalize each decision matrixes by Eqs. (12) and (13); Step 2: Calculate the individual comprehensive value $\tilde{r}_{i}^{k}$ by Eq. (17); Step 3: Determine the weights of attributes by Eq. (16); Step 4: Compute the collective comprehensive value $\tilde{r}_{i}$ by Eq. (18); Step 5: Rank the alternatives by the value $\tilde{r}_{i}$ (i = 1, 2,…,m).

5 A green supplier selection example analysis

In this part, a green supplier selection example is provided to demonstrate the applicability and reasonability of the proposed method in the paper.

5.1 A green supplier selection example and the analysis process

Nowadays, global environment is a vital concern in reality, and an increasingly extensive attention is concentrated on the green production in various fields. An air-conditioning company plans to select the most appropriate green supplier for a key element in its process of manufacture. After pre-assessment, four suppliers A _i $(i = 1,2,3,4)$ are remained for further evaluation from five aspects: the product quality a ₁; the technology capability a ₂; the pollution control a ₃; the environmental management a ₄; and the profitability a ₅ (whose weighting vector is unknown). A group of DMs are asked to form a advisory committee: e ₁ is from the production department; e ₂ is from the engineering department; e ₃ is from the quality inspection department; and e ₄ is from the purchasing department (whose weighting vector is known that $\varvec{t} = ( 0. 2 0 , { 0} . 3 0 , { 0} . 3 5 , { 0} . 1 5 )^{\text{T}}$). By statistical analysis, the assessment information of the alternatives on attributes can be characterized by TAIFNs as in Tables 1, 2, 3 and 4.

Table 1 The TAIFN decision matrix by e ₁

Table 2 The TAIFN decision matrix given by e ₂

Table 3 The TAIFN decision matrix by e ₃

Table 4 The TAIFN decision matrix by e ₄

The weighting vector of attributes is unknown, but their incomplete weight information can be used to estimate. According to the experts’ comprehensions and judgments, the preference information structure $\varLambda$ of attribute weight by the experts is presented as follows:

$$ \varLambda = \{ \omega \in \varLambda_{0} |\omega_{1} > 1.2\omega_{2} {\kern 1pt} {\kern 1pt} ;\;\;0.06 < \omega_{3} - \omega_{2} < 0.12;\;\;0.21 < \omega_{4} < 0.35;\;\;\omega_{4} - \omega_{5} > \omega_{3} - \omega_{1} ;\;\;\omega_{5} < \omega_{2} \} $$

Step 1:

According to Eq. (12), the normalized decision matrices are obtained as in Tables 5, 6, 7 and 8.

Table 5 The normalized TAIFN decision matrix by e ₁

Table 6 The normalized TAIFN decision matrix by e ₂

Table 7 The normalized TAIFN decision matrix by e ₃

Table 8 The normalized TAIFN decision matrix by e ₄

Step 2:

According to Eq. (17), the individual comprehensive values of alternatives for each DM are obtained as follows:

$$ \begin{aligned} \tilde{r}_{1}^{1} & = ((0.26\omega_{1} + 0.36\omega_{2} + 0.24\omega_{3} + 0.37\omega_{4} + 0.32\omega_{5} ,0.50\omega_{1} + 0.54\omega_{2} + 0.41\omega_{3} + 0.55\omega_{4} + 0.48\omega_{5} , \\ & \quad 0.73\omega_{1} + 0.77\omega_{2} + 0.56\omega_{3} + 0.76\omega_{4} + 0.66\omega_{5} );0.4,0.5) \\ \tilde{r}_{2}^{1} & = ((0.33\omega_{1} + 0.31\omega_{2} + 0.42\omega_{3} + 0.39\omega_{4} + 0.28\omega_{5} ,0.50\omega_{1} + 0.48\omega_{2} + 0.54\omega_{3} + 0.59\omega_{4} + 0.44\omega_{5} , &\quad 0.83\omega_{1} + 0.77\omega_{2} + 0.73\omega_{3} + \, 0.86\omega_{4} + 0.63\omega_{5} );0.3,0.6) \\ \tilde{r}_{3}^{1} & = ((0.26\omega_{1} + 0.31\omega_{2} + 0.48\omega_{3} + 0.28\omega_{4} + 0.32\omega_{5} ,0.41\omega_{1} + 0.48\omega_{2} + 0.61\omega_{3} + 0.39\omega_{4} + 0.48\omega_{5} , \\ & \quad 0.62\omega_{1} + 0.69\omega_{2} + 0.81\omega_{3} + 0.81\omega_{4} + 0.71\omega_{5} );0.4,0.3) \\ \tilde{r}_{4}^{1} & = ((0.40\omega_{1} + 0.36\omega_{2} + 0.30\omega_{3} + 0.24\omega_{4} + 0.47\omega_{5} ,0.58\omega_{1} + 0.48\omega_{2} + 0.41\omega_{3} + 0.44\omega_{4} + 0.59\omega_{5} , \\ & \quad 0.93\omega_{1} + 0.77\omega_{2} + 0.56\omega_{3} + 0.60\omega_{4} + 0.78\omega_{5} );0.6,0.3) \\ \tilde{r}_{1}^{2} & = ((0.23\omega_{1} + 0.32\omega_{2} + 0.25\omega_{3} + 0.32\omega_{4} + 0.17\omega_{5} ,0.43\omega_{1} + 0.42\omega_{2} + 0.55\omega_{3} + 0.45\omega_{4} + 0.31\omega_{5} , \\ & \quad 0.71\omega_{1} + 0.68\omega_{2} + 0.91\omega_{3} + 0.57\omega_{4} + 0.52\omega_{5} );0.5,0.4) \\ \tilde{r}_{2}^{2} & = ((0.35\omega_{1} + 0.26\omega_{2} + 0.25\omega_{3} + 0.45\omega_{4} + 0.36\omega_{5} ,0.50\omega_{1} + 0.48\omega_{2} + 0.44\omega_{3} + 0.53\omega_{4} + 0.54\omega_{5} , \\ & \quad 0.80\omega_{1} + 0.68\omega_{2} + 1.00\omega_{3} + 0.61\omega_{4} + 0.70\omega_{5} );0.4,0.3) \\ \tilde{r}_{3}^{2} & = ((0.29\omega_{1} + 0.37\omega_{2} + 0.33\omega_{3} + 0.43\omega_{4} + 0.44\omega_{5} ,0.50\omega_{1} + 0.54\omega_{2} + 0.55\omega_{3} + 0.52\omega_{4} + 0.54\omega_{5} , \\ & \quad 0.71\omega_{1} + 0.76\omega_{2} + 0.91\omega_{3} + 0.63\omega_{4} + 0.71\omega_{5} );0.5,0.4) \\ \tilde{r}_{4}^{2} & = ((0.41\omega_{1} + 0.42\omega_{2} + 0.25\omega_{3} + 0.43\omega_{4} + 0.46\omega_{5} ,0.57\omega_{1} + 0.54\omega_{2} + 0.44\omega_{3} + 0.49\omega_{4} + 0.57\omega_{5} , \\ & \quad 0.80\omega_{1} + 0.76\omega_{2} + 0.76\omega_{3} + 0.63\omega_{4} + 0.71\omega_{5} );0.5,0.3) \\ \tilde{r}_{1}^{3} & = ((0.30\omega_{1} + 0.35\omega_{2} + 0.29\omega_{3} + 0.39\omega_{4} + 0.44\omega_{5} ,0.42\omega_{1} + 0.50\omega_{2} + 0.45\omega_{3} + 0.48\omega_{4} + 0.53\omega_{5} , \\ & \quad 0.75\omega_{1} + 0.79\omega_{2} + 0.69\omega_{3} + 0.64\omega_{4} + 0.65\omega_{5} );0.3,0.4) \\ \tilde{r}_{2}^{3} & = ((0.36\omega_{1} + 0.29\omega_{2} + 0.37\omega_{3} + 0.34\omega_{4} + 0.39\omega_{5} ,0.63\omega_{1} + 0.50\omega_{2} + 0.62\omega_{3} + 0.42\omega_{4} + 0.51\omega_{5} , \\ & \quad 0.94\omega_{1} + 0.99\omega_{2} + 0.92\omega_{3} + 0.59\omega_{4} + 0.65\omega_{5} );0.5,0.4) \\ \tilde{r}_{3}^{3} & = ((0.36\omega_{1} + 0.23\omega_{2} + 0.37\omega_{3} + 0.47\omega_{4} + 0.35\omega_{5} ,0.49\omega_{1} + 0.43\omega_{2} + 0.53\omega_{3} + 0.60\omega_{4} + 0.48\omega_{5} , \\ & \quad 0.75\omega_{1} + 0.69\omega_{2} + 0.81\omega_{3} + 0.74\omega_{4} + 0.64\omega_{5} \, );0.5,0.3) \\ \tilde{r}_{4}^{3} & = ((0.24\omega_{1} + 0.29\omega_{2} + 0.22\omega_{3} + 0.30\omega_{4} + 0.38\omega_{5} ,0.42\omega_{1} + 0.57\omega_{2} + 0.36\omega_{3} + 0.48\omega_{4} + 0.47\omega_{5} , \\ & \quad 0.66\omega_{1} + 0.89\omega_{2} + 0.69\omega_{3} + 0.65\omega_{4} + 0.62 \, \omega_{5} );0.4,0.5) \\ \tilde{r}_{1}^{4} & = ((0.35\omega_{1} + 0.28\omega_{2} + 0.32\omega_{3} + 0.48\omega_{4} + 0.39\omega_{5} ,0.51\omega_{1} + 0.53\omega_{2} + 0.42\omega_{3} + 0.56\omega_{4} + 0.55\omega_{5} \\ & \quad 0.94\omega_{1} + 0.80\omega_{2} + 0.68\omega_{3} + 0.68\omega_{4} + 0.76\omega_{5} );0.5,0.3) \\ \tilde{r}_{2}^{4} & = ((0.23\omega_{1} + 0.33\omega_{2} + 0.26\omega_{3} + 0.32\omega_{4} + 0.33\omega_{5} ,0.37\omega_{1} + 0.47\omega_{2} + 0.48\omega_{3} + 0.42\omega_{4} + 0.51\omega_{5} , \\ & \quad 0.56\omega_{1} + 0.71\omega_{2} + 0.68\omega_{3} + 0.54\omega_{4} + 0.73\omega_{5} \, );0.5,0.4) \\ \tilde{r}_{3}^{4} & = ((0.35\omega_{1} + 0.22\omega_{2} + 0.37\omega_{3} + 0.42\omega_{4} + 0.35\omega_{5} ,0.59\omega_{1} + 0.47\omega_{2} + 0.54\omega_{3} + 0.52\omega_{4} + 0.53\omega_{5} , \\ & \quad 0.94\omega_{1} + 0.80\omega_{2} + 0.76\omega_{3} + 0.64\omega_{4} + 0.79\omega_{5} );0.4,0.5) \\ \tilde{r}_{4}^{4} & = ((0.29\omega_{1} + 0.39\omega_{2} + 0.42\omega_{3} + 0.38\omega_{4} + 0.29\omega_{5} ,0.51\omega_{1} + 0.53\omega_{2} + 0.54\omega_{3} + 0.49\omega_{4} + 0.39\omega_{5} , \\ & \quad 0.75\omega_{1} + 0.89\omega_{2} + 0.76\omega_{3} + 0.61\omega_{4} + 0.62\omega_{5} );0.5,0.3). \\ \end{aligned} $$

Step 3:

Determine the triangular Atanassov’s intuitionistic fuzzy positive ideal solution $A^{ + } = (\tilde{r}_{1}^{ + } ,\tilde{r}_{2}^{ + } , \ldots ,\tilde{r}_{n}^{ + } )$, where $\tilde{r}_{j}^{ + } = ((1,1,1);1,0)$ $(j = 1,2, \ldots ,5)$. Then by Eq. (16), a linear goal programming model is structured:

$$ \begin{aligned} & \hbox{min} \, Z = \tfrac{1}{6}\sum\limits_{k = 1}^{4} {\left[ {t_{k} \sum\limits_{i = 1}^{4} {\sum\limits_{l = 1}^{3} {(d_{il}^{k + } + d_{il}^{k - } )} } } \right]} \\ & {\text{s}} . {\text{t}} .\left\{ \begin{aligned} & \omega_{2} > 1.2\omega_{1} {\kern 1pt} {\kern 1pt} ;\;\; 0. 0 6 { < }\omega_{3} - \omega_{2} { < 0} . 1 2 ;\;\; 0. 2 1 { < }\omega_{4} { < 0} . 3 5 ;\;\;\omega_{4} - \omega_{5} > \omega_{3} - \omega_{1} ;\;\;\omega_{2} < \omega_{5} ; \\ & 0 \le \omega_{j} \le 1,\;\sum\limits_{j = 1}^{5} {\omega_{j} } = 1;\;\;\;\;\;\;t_{1} = 0.20,\;t_{2} = 0.30,\;t_{3} = 0.35,\;t_{4} = 0.15; \\ & 0. 9\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{1}^{1} - 2 - d_{11}^{1 + } + d_{11}^{1 - } = 0,\;\; 0. 9r_{1}^{1} - 2 - d_{12}^{1 + } + d_{12}^{1 - } = 0,\; 0. 9\bar{r}_{1}^{1} - 2 - d_{13}^{1 + } + d_{13}^{1 - } = 0; \\ & 0. 7\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{2}^{1} - 2 - d_{21}^{1 + } + d_{21}^{1 - } = 0,\;\; 0. 7r_{2}^{1} - 2 - d_{22}^{1 + } + d_{22}^{1 - } = 0,\;\; 0. 7\bar{r}_{2}^{1} - 2 - d_{23}^{1 + } + d_{23}^{1 - } = 0; \\ & 1.1\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{3}^{1} - 2 - d_{31}^{1 + } + d_{31}^{1 - } = 0,\;\;1.1r_{3}^{1} - 2 - d_{32}^{1 + } + d_{32}^{1 - } = 0,\;\;1.1\bar{r}_{3}^{1} - 2 - d_{33}^{1 + } + d_{33}^{1 - } = 0; \\ & 1. 3\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{4}^{1} - 2 - d_{41}^{1 + } + d_{41}^{1 - } = 0,\;\; 1. 3r_{4}^{1} - 2 - d_{42}^{1 + } + d_{42}^{1 - } = 0,\;\; 1. 3\bar{r}_{4}^{1} - 2 - d_{43}^{1 + } + d_{43}^{1 - } = 0; \\ & 1.1\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{1}^{2} - 2 - d_{11}^{2 + } + d_{11}^{2 - } = 0,\;1.1r_{1}^{2} - 2 - d_{12}^{2 + } + d_{12}^{2 - } = 0,\;\;1.1\bar{r}_{1}^{2} - 2 - d_{13}^{2 + } + d_{13}^{2 - } = 0; \\ & 1. 1\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{2}^{2} - 2 - d_{21}^{2 + } + d_{21}^{2 - } = 0,\; 1. 1r_{2}^{2} - 2 - d_{22}^{2 + } + d_{22}^{2 - } = 0,\;\; 1. 1\bar{r}_{2}^{2} - 2 - d_{23}^{2 + } + d_{23}^{2 - } = 0; \\ & 1.1\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{3}^{2} - 2 - d_{31}^{2 + } + d_{31}^{2 - } = 0,\;1.1r_{3}^{2} - 2 - d_{32}^{2 + } + d_{32}^{2 - } = 0,\;\;1.1\bar{r}_{3}^{2} - 2 - d_{33}^{2 + } + d_{33}^{2 - } = 0; \\ & 1. 2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{4}^{2} - 2 - d_{41}^{2 + } + d_{41}^{2 - } = 0,\; 1. 2r_{4}^{2} - 2 - d_{42}^{2 + } + d_{42}^{2 - } = 0,\;\; 1. 2\bar{r}_{4}^{2} - 2 - d_{43}^{2 + } + d_{43}^{2 - } = 0; \\ & 0. 9\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{1}^{3} - 2 - d_{11}^{3 + } + d_{11}^{3 - } = 0,\; 0. 9r_{1}^{3} - 2 - d_{12}^{3 + } + d_{12}^{3 - } = 0,\;\; 0. 9\bar{r}_{1}^{3} - 2 - d_{13}^{3 + } + d_{13}^{3 - } = 0; \\ & 1.1\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{2}^{3} - 2 - d_{21}^{3 + } + d_{21}^{3 - } = 0,\;1.1r_{2}^{3} - 2 - d_{22}^{3 + } + d_{22}^{3 - } = 0,\;\;1.1\bar{r}_{2}^{3} - 2 - d_{23}^{3 + } + d_{23}^{3 - } = 0; \\ & 1.2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{3}^{3} - 2 - d_{31}^{3 + } + d_{31}^{3 - } = 0,\;1.2r_{3}^{3} - 2 - d_{32}^{3 + } + d_{32}^{3 - } = 0,\;\;1.2\bar{r}_{3}^{3} - 2 - d_{33}^{3 + } + d_{33}^{3 - } = 0; \\ & 0. 9\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{4}^{3} - 2 - d_{41}^{3 + } + d_{41}^{3 - } = 0,\; 0. 9r_{4}^{3} - 2 - d_{42}^{3 + } + d_{42}^{3 - } = 0,\;\; 0. 9\bar{r}_{4}^{3} - 2 - d_{43}^{3 + } + d_{43}^{3 - } = 0; \\ & 1.2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{1}^{4} - 2 - d_{11}^{4 + } + d_{11}^{4 - } = 0,\;1.2r_{1}^{4} - 2 - d_{12}^{4 + } + d_{12}^{4 - } = 0,\;\;1.2\bar{r}_{1}^{4} - 2 - d_{13}^{4 + } + d_{13}^{4 - } = 0; \\ & 1.1\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{2}^{4} - 2 - d_{21}^{4 + } + d_{21}^{4 - } = 0,\;1.1r_{2}^{4} - 2 - d_{22}^{4 + } + d_{22}^{4 - } = 0,\;\;1.1\bar{r}_{2}^{4} - 2 - d_{23}^{4 + } + d_{23}^{4 - } = 0; \\ & 0. 9\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{3}^{4} - 2 - d_{31}^{4 + } + d_{31}^{4 - } = 0,\; 0. 9r_{3}^{4} - 2 - d_{32}^{4 + } + d_{32}^{4 - } = 0,\;\; 0. 9\bar{r}_{3}^{4} - 2 - d_{33}^{4 + } + d_{33}^{4 - } = 0; \\ & 1. 2\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{r}_{4}^{4} - 2 - d_{41}^{4 + } + d_{41}^{4 - } = 0,\; 1. 2r_{4}^{4} - 2 - d_{42}^{4 + } + d_{42}^{4 - } = 0,\;\; 1. 2\bar{r}_{4}^{4} - 2 - d_{43}^{4 + } + d_{43}^{4 - } = 0; \, \\ & d_{il}^{k + } \ge 0, \, d_{il}^{k - } \ge 0, \, d_{il}^{k + } d_{il}^{k - } = 0 \, (i = 1,2,3,4; \, k = 1,2,3,4; \, l = 1,2,3) \\ \end{aligned} \right. \\ \end{aligned} $$

(19)

Solving Eq. (19) by Lingo software, we can obtain the weights of attributes:

$$ \omega_{1} = 0.1848,\,\omega_{2} = 0.2217,\,\omega_{3} = 0.1617,\,\omega_{4} = 0.2100,\,\omega_{5} = 0.2217. $$

By Step 2, the individual comprehensive values of alternatives for each DM are calculated as:

$$ \begin{aligned} \tilde{r}_{1}^{1} & = ((0.3153,0.5004,0.7022);0.4,0.5),\,\tilde{r}_{2}^{1} = ((0.3416,0.5076,0.7625);0.3,0.6),\, \\ \tilde{r}_{3}^{1} & = ((0.3242,0.4692,0.7261);0.4,0.3),\,\tilde{r}_{4}^{1} = ((0.3569,0.5031,0.7321);0.6,0.3), \\ \tilde{r}_{1}^{2} & = ((0.2588,0.4248,0.6642);0.5,0.4),\,\,\tilde{r}_{2}^{2} = ((0.3371,0.5010,0.7283); \, 0.4,0.3), \\ \tilde{r}_{3}^{2} & = ((0.3769,0.5300,0.7366); \, 0.5,0.4),\,\tilde{r}_{4}^{2} = ((0.4016,0.5255,0.729); \, 0.5,0.3), \\ \tilde{r}_{1}^{3} & = ((0.3594,0.4796,0.7039); \, 0. \, 3,0.4),\,\tilde{r}_{2}^{3} = ((0.3485,0.5288,0.8100); \, 0.5,0.4), \\ \tilde{r}_{3}^{3} & = ((0.3537,0.504,0.7199); \, 0.5,0.3),\,\tilde{r}_{4}^{3} = ((0.2915,0.4672,0.7049); \, 0.4,0.5), \\ \tilde{r}_{1}^{4} & = ((0.3658,0.5192,0.7724); \, 0.5,0.3),\,\,\tilde{r}_{2}^{4} = ((0.2981,0.4515,0.6462); \, 0.5,0.4), \\ \tilde{r}_{3}^{4} & = ((0.3391,0.5273,0.7836); \, 0.4,0.5),\,\,\tilde{r}_{4}^{4} = ((0.3521,0.4885,0.7244); \, 0.5,0.3). \\ \end{aligned} $$

Step 4:

Utilize the TAIFGHWA operator to calculate $\tilde{r}_{i}^{{{\prime }k}} = 4t_{k} \tilde{r}_{i}^{k}$ and acquire the ranking order of $\tilde{r}_{i}^{{{\prime }k}}$ $(i = 1,2,3,4; \, k = 1,2,3)$ by Eqs. (2) and (3). Then take the criterion “most,” the weighting vector associated with TAIFGHWA is computed using Eq. (7) as w ₁ = 0, w ₂ = 0.4, w ₃ = 0.5 and w ₄ = 0.1. We got the collective comprehensive values of alternatives A _i (i = 1, 2, 3, 4) by Eq. (18):

$$ \begin{aligned} \tilde{r}_{1} &= (((0 \times 0.311^{\lambda } + 0.4 \times 0.503^{\lambda } + 0.5 \times 0.219^{\lambda } + 0.1 \times 0.252^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,(0 \times 0.510^{\lambda } + 0.4 \times 0.671^{\lambda } + 0.5 \times 0.312^{\lambda } \\ & \quad + 0.1 \times 0.400^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\;(0 \times 0.797^{\lambda } + 0.4 \times 0.985^{\lambda } + 0.5 \times 0.463^{\lambda } + 0.1 \times 0.562^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} );0.3,0.5) \\ \tilde{r}_{2} & = (((0 \times 0.488^{\lambda } + 0.4 \times 0.405^{\lambda } + 0.5 \times 0.179^{\lambda } + 0.1 \times 0.273^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,(0 \times 0.740^{\lambda } + 0.4 \times 0.601^{\lambda } + 0.5 \times 0.271^{\lambda } \\ & \quad + 0.1 \times 0.406^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\;(0 \times 1^{\lambda } + 0.4 \times 0.874^{\lambda } + 0.5 \times 0.388^{\lambda } + 0.1 \times 0.61^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} );0.3,0.6) \\ \tilde{r}_{3} & = (((0 \times 0.495^{\lambda } + 0.4 \times 0.452^{\lambda } + 0.5 \times 0.259^{\lambda } + 0.1 \times 0.204^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,(0 \times 0.706^{\lambda } + 0.4 \times 0.636^{\lambda } + 0.5 \times 0.375^{\lambda } \\ & \quad + 0.1 \times 0.316^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\;(0 \times 1^{\lambda } + 0.4 \times 0.884^{\lambda } + 0.5 \times 0.581^{\lambda } + 0.1 \times 0.470^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} );0.4,0.5) \\ \tilde{r}_{4} & = (((0 \times 0.482^{\lambda } + 0.4 \times 0.408^{\lambda } + 0.5 \times 0.285^{\lambda } + 0.1 \times 0.211^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,(0 \times 0.631^{\lambda } + 0.4 \times 0.654^{\lambda } + 0.5 \times 0.403^{\lambda } \\ & \quad + 0.1 \times 0.293^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} ,\;(0 \times 0.875^{\lambda } + 0.4 \times 0.987^{\lambda } + 0.5 \times 0.586^{\lambda } + 0.1 \times 0.435^{\lambda } )^{{{1 \mathord{\left/ {\vphantom {1 \lambda }} \right. \kern-0pt} \lambda }}} );0.4,0.5) \\ \end{aligned} $$

Step 5:

Calculate the membership and non-membership function average indexes for $\tilde{r}_{i}$ (i = 1, 2, 3, 4), and then generate the ranking order of alternatives.

For example, when λ = 2, we get the following results:

$$ \begin{aligned} \tilde{r}_{1} & = (( 0. 0 6 5 9 , 0. 1 2 2 4 , 0. 2 6 3 7);0.3,0.5), \\ \tilde{r}_{2} & = (( 0. 0 4 4 5 , 0. 0 9 8 9 , 0. 2 0 9 0);0.3,0.6), \\ \tilde{r}_{3} & = (( 0. 0 5 9 8 , 0. 1 2 1 1 , 0. 2 5 1 7);0.4,0.5), \\ \tilde{r}_{4} & = (( 0. 0 5 5 9 , 0. 1 3 0 4 , 0. 2 9 0 0);0.4,0.5). \\ \end{aligned} $$

Thus, we obtain the membership and non-membership function average indexes:

$$ \begin{aligned} & S(\tilde{r}_{1} ) = 0.0431,\,H(\tilde{r}_{1} ) = \;0.0718;\,S(\tilde{r}_{2} ) = 0.0338,\,H(\tilde{r}_{2} ) = 0.0451; \\ & S(\tilde{r}_{3} ) = 0.0554,\,H(\tilde{r}_{3} ) = 0.0692;\,S(\tilde{r}_{4} ) = 0.0607,\,H(\tilde{r}_{4} ) = \;0.0758. \\ \end{aligned} $$

Therefore, by Definition 4, the ranking of the alternatives is A ₄ ≻ A ₃ ≻ A ₁ ≻ A ₂.

Similarly, for different parameter value λ, we can obtain the ranking order of the alternatives. The results and ranking of alternatives are presented in Table 9.

Table 9 The results for different parameter values and ranking of alternatives

From Table 9, we find that the ranking alternatives are different when parameter value λ takes different values. When $\lambda \in [0,4.27]$, the ranking is A ₄ ≻ A ₃ ≻ A ₁ ≻ A ₂ and the best is A ₄; while $\lambda \in (4.27,50]$, the ranking is A ₄ ≻ A ₁ ≻ A ₃ ≻ A ₂ and the best is A ₄; especially, when $\lambda \to + \infty$, the ranking is A ₃ ≻ A ₄ ≻ A ₂ ≻ A ₁ and the best is A ₃. The above analysis shows that the parameter λ is indeed of great importance to the decision-making. The DMs can choose different parameter λ according to their preference and requirement which well ensures the flexibility and agility of decision-making process.

5.2 Comparison analysis

Wan et al. [11] proposed the VIKOR method for MAGDM using TAIFNs. We use the method in [11] to solve the above example for illustration of the superiorities of the proposed method in this paper. By method [11], the closeness of each alternative to the ideal solution and the ranking results with different coefficient of decision mechanism λ are shown in Table 10.

Table 10 The ranking results of alternatives with different coefficient of decision mechanism

It can be seen from Table 10 that although the ranking orders obtained by method [11] are not completely the same when the coefficient of decision mechanism λ takes different values, the best candidate is always A ₂, while the best candidate by the method in this paper is A ₂ when $\lambda < + \infty$, A ₄ when λ → + ∞. In contrast with method [11], the method in this paper is featured by the following points:

• 1. The former only utilized the TAIFWA operator to obtain the group decision matrix, whereas the latter uses the TAIFWA and TAIFGHWA operators to derive the collective comprehensive values of alternatives. The TAIFGHWA operator simultaneously considers the weights of elements and the weights of the positions. Therefore, the latter is more comprehensive than the former.

• 2. Through choosing different parameter values of λ in TAIFGHWA operator, the latter is able to give different ranking orders of alternatives, which well ensures the flexibility and agility of the proposed method.

• 3. The former assumed that the attribute weighting information was completely unknown and did not consider the incomplete weight information of attribute weight. In reality, it is possible that DMs may give the incomplete weight information through using their knowledge, experience and judgment. From this point of view, the latter is closer to the actual situation than the former.

6 Conclusion

This paper defined some arithmetic aggregation operators for TIFNs including the TAIFWA operator and TAIFOWA operator. Then we further develop two triangular intuitionistic fuzzy generalized aggregation operators: TAIFGOWA operator and TAIFGHWA operator. Taking into account the incomplete attribute weight information, we propose a new approach to MAGDM with TAIFN and incomplete weight information.

The TAIFGOWA and TAIFGHWA operators are the useful extensions of the arithmetic aggregation operators of TAIFNs. The developed TAIFGOWA and TAIFGHWA operators are especially suitable for MAGDM in a variety of situations. Although a green supplier selection problem is provided to show the feasibility and effectiveness of the proposed method, it can be also applied to many real-life decision problems, such as water resource evaluation and supply chain management. However, the weights of experts are known in advance in the proposed method, which is a weakness of this paper. How to determine these weights of experts objectively will be studied in future. In addition, we will develop some new generalized geometric aggregation operators of TAIFNs and generalize some quasi-arithmetic mean operators to accommodate to the case of TAIFNs.