Group decision-making based on 2-tuple linguistic T-spherical fuzzy COPRAS method

Abstract

Data mining is a thoroughly advanced method that evaluates and makes more sense of a variety in electronic commerce (e-commerce)-related knowledge, discovering useful ideas, predicting user actions, and assisting enterprises selection in modifying competitive strategy, minimizing cost, and attaining the finest results. Data mining has already become more popular in recent years. In this research paper, we propose a multi-attribute group decision-making (MAGDM) method under T-spherical fuzzy environment for selecting an optimal data mining strategy which is an important part of modern decision-making research. The information aggregation operators play an important role in solving MAGDM problems. Some point aggregation operators based on the 2-tuple linguistic T-spherical fuzzy numbers, including 2-tuple linguistic T-spherical fuzzy point weighted averaging (2TLT-SFPWA) operator, 2-tuple linguistic T-spherical fuzzy point weighted geometric (2TLT-SFPWG) operator, 2-tuple linguistic T-spherical fuzzy generalized point weighted averaging (2TLT-SFGPWA) operator and 2-tuple linguistic T-spherical fuzzy generalized point weighted geometric (2TLT-SFGPWG) operator, are proposed which competently capture all the aspects of human opinions expressible in terms of yes, no, cessation and denial with no limitation. The proposed aggregation operators are valid and have some basic properties which are keenly analyzed. Furthermore, the complex proportional assessment (COPRAS) method is developed on the basis of 2-tuple linguistic T-spherical fuzzy point aggregation operators. Finally, a numerical example is illustrated for demonstrating the effectiveness of the proposed work along with comparative analysis which verifies the reliability and efficacy of its outcomes. In the end, we conclude some results from the numerical analysis, i.e., to balance the long-term development of e-commerce, data mining can mine massive amounts of data which boosts the growth of e-commerce in future.

1 Introduction

Multiple attribute decision-making (MADM) is the technique for selecting the optimal alternative from a finite collection of alternatives based on numerous, typically conflicting attributes (or called criteria). MAGDM is fascinating and challenging everyday problem that is important to decision theory. However, how to successfully obtain attribute information in the face of uncertainty and diversity in the decision-making environment is the main vexing challenge of MAGDM. Thus, Zadeh (1965) introduced the concept of fuzzy set (FS) to deal with real-life problems involving variability or inaccuracy. Atanassov (1986) extended the idea of FS and proposed the intuitionistic fuzzy set (IFS) which consists of membership degree (MD) and non-membership degree (NMD) to describe the unreliability of an event with a condition that the sum of the MD and NMD should not exceed 1. Yager (2014) strengthened this concept by introducing the notion of Pythagorean fuzzy set (PyFS) in which the range for assigning values to MD and NMD was increased. Yager (2016) also proposed a generalized orthopair FS commonly known as q-ROFS. Wang et al. (2019b) developed some aggregation operators for fusing q-ROF information. They extended the Muirhead mean to q-ROF environment and proposed a family of q-ROF Muirhead mean operators. Darko and Liang (2020) proposed some q-ROF Hamacher aggregation operators, i.e., the q-ROF Hamacher average operator, the weighted q-ROF Hamacher average operator, the q-ROF Hamacher Maclaurin symmetric mean operator and the weighted q-ROF Hamacher Maclaurin symmetric mean operator along with their special properties. Xing et al. (2019) developed a novel category of point weighted aggregation operators to aggregate q-ROF information. These recommended operators can divide q-ROFN membership and non-membership based on different criteria.

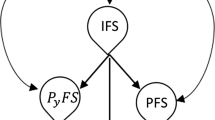
Somehow, the pairs of IFS, PyFS and q-ROFS deal with inaccuracy that occurs in real life but these duplets discuss only two dimensions of human opinion, i.e., like and dislike, although a human opinion also involves certain extent of abstinence and rejection. Cuong and Kreinovich (2014) suggested that the pair, representing an IFS or its generalized form, represents the human opinion only in terms of MD and NMD, where the abstinence degree (AD) and the refusal degree (RD) are kind of ignored, leading to the loss of knowledge. For this reason, they proposed the idea of a picture fuzzy set (PFS) in the form of triplets using MD, AD and NMD with a limitation that their sum is not greater than 1. Kahraman and Gündogdu (2018) originally presented the idea of spherical fuzzy sets (SFSs). In 2019, F.K. Gündogdu and C. Kahraman, (2019) developed a MAGDM technique, namely spherical fuzzy TOPSIS (SF-TOPSIS) method, to tackle the complex decision-making problems. Later, Kahraman et al. (2019) applied the SF-TOPSIS to choose the most appropriate site for a hospital. Mahmood et al. (2019) presented the T-spherical fuzzy set (T-SFS) with the basic operations and aggregation operators which increased the range for assigning MD, Ashraf and Abdullah (2019); Ashraf et al. (2020) put forward the decision-making strategies based on spherical fuzzy aggregation operators. Akram et al. (2020b) developed novel spherical fuzzy prioritized weighted aggregation operators to solve MAGDM problems. Ullah et al. (2020) introduced Hamacher aggregation operators based on T-spherical fuzzy numbers and discussed their basic properties. They proposed the idea of T-SF Hamacher-weighted averaging and T-SF Hamacher-weighted geometric aggregation operators to incorporate four aspects of human opinion including yes, no, abstinence and refusal with no limitations. Ashraf et al. (2019) introduced spherical fuzzy t-norms and t-conorms, developed spherical fuzzy negator and some classifications of spherical fuzzy t-norms and spherical fuzzy t-conorms to aggregate the SF information, and examined the spaces of spherical fuzzy membership grades and picture fuzzy membership grades graphically. Zeng et al. (2020) proposed new operational laws with T-SF information for Einstein geometric interaction operators and Einstein averaging interactive aggregation operators. Some fundamental characteristics and benefits of proposed aggregation operators are also discussed. Liu et al. (2020) proposed the linguistic T-SFNs, the linguistic T-spherical fuzzy weighted averaging operator, and extended multi-attributive border approximation area comparison method in the linguistic spherical fuzzy environment. Further, Akram et al. (2020a, 2021a, 2021b, 2021c), Akram et al. (2021), Naz et al. (2022a, 2022b, 2022c), Liu et al. (2022) and Zahid et al. (2022) introduced several decision-making methods under generalized fuzzy scenario.

Processing manner of 2-tuple linguistic information can effectively avoid the distortion and loss of information. Herrera and Martinez (2000a) proposed the representation model of fuzzy 2-tuple linguistic term to handle linguistic decision-making problems. In last few decades, various 2-tuple linguistic aggregation operators and decision methods have been proposed to combine the individual preference information into a collective one, such as the generalized 2-tuple linguistic Pythagorean fuzzy Heronian mean operator, 2-tuple linguistic Pythagorean fuzzy geometric Heronian mean operator and its weighted form (Deng et al. 2019). Ju et al. (2020) developed the q-ROF 2-tuple linguistic weighted averaging operator and the q-ROF 2-tuple linguistic weighted geometric operator. Furthermore, they proposed the q-ROF 2-tuple linguistic Muirhead mean operator and the q-ROF 2-tuple linguistic dual Muirhead mean operator on the basis of Muirhead mean operator and dual Muirhead mean operator. Wang et al. (2019a) proposed a concept of interval-valued q-ROF 2-tuple linguistic sets and discussed its properties. They developed some weighted averaging and geometric aggregation operators for

interval-valued q-ROF 2-tuple linguistic sets and characterized their desirable properties. On the basis of Archimedean t-norm and t-conorm, Mo and Huang (2020) developed the dual hesitant fuzzy geometric Heronian mean operator and dual hesitant fuzzy geometric weighted Heronian mean operator. Some properties and special cases are also discussed. Rong et al. (2020a) introduced the complex q-ROF 2-tuple linguistic Maclaurin symmetric mean operator, and the complex q-ROF 2-tuple linguistic dual Maclaurin symmetric mean operator along with several attractive characteristics of the developed operators. Rong et al. (2020b) proposed the hesitant fuzzy linguistic Hamy mean operator, hesitant fuzzy linguistic dual Hamy mean operator, and its weighted form along with their properties. Even though the MADM methods provide numerically significant and consistent rankings in a particular situation, the optimal solution can be presented in a different manner. The decision-makers’ task of determining the optimal conclusion in a scenario might be complicated by the random selection of the most favorable alternative. Based on the outcome, it is highly challenging to determine the capacity or capability strengths of more than 100 MADM approaches. This issue is still regarded as a riddle due to the lack of accepted standards in the literature for analyzing MADM approaches under uncertainty.

The COPRAS method, developed by Zavadskas et al. (1994), is the most valuable and suitable method to solve complex MAGDM problems. Based on the benefit and cost criteria, it gives information accurately on comparing with other existing approaches. The most crucial advantage of COPRAS method is that it portrays the ratio to the worst and the best results simultaneously. In this regard, COPRAS method was extended under several models of FS theory. To evaluate the pulmonary disease, Zheng et al. (2018) developed the hesitant fuzzy linguistic COPRAS approach. Mishra et al. (2019) introduced extended COPRAS approach to evaluate the multiple criteria decision-making problems based on hesitant FSs. Buyukozkan and Gocer (2019) presented an integrated model associated with AHP-COPRAS to evaluate the digital supply chain partner selection within Pythagorean fuzzy environment. Dorfeshan and Mousavi (2019) developed a new integrated TOPSIS-COPRAS method to determine the critical path of projects. Over the past few decades, considerable research has been done on information aggregation. The aggregation operator is a method that can combine a specified number of inputs into a single output. Yager (1988) developed a class of generalized ordered weighted average aggregation operators based on the ordered weighted average operator. Xu and Yager (2006) also developed some geometric aggregation operators. It must be noted that these aggregation operators are based on original information, therefore the uncertainty of the aggregated arguments cannot be minimized. However, in some situations, it is essential to reduce information ambiguity.

The motivations of this article are as follows:

• (1) The T-SFS has been proved to be an efficient tool in expressing DMs evaluation values in MAGDM procedure. However, the existing theories about T-SFS fail to depict uncertain information through the 2-tuple linguistic representation model. The 2-tuple linguistic model has stronger capability to describe linguistic information and it also can avoid information distortion loss in dealing with linguistic decision issues. The 2TLT-SFSs are more powerful than 2TLIFSs, 2TLPyFSs, and 2TLq-ROFs. It is more efficient to use 2TLT-SFSs to express evaluation values of the DMs in the MAGDM process.

• (2) Some effective information processing and evaluation methods need to be developed in order to aggregate the information. So in this article, we give point aggregation operators for 2TLT-SFS, which can reduce the degree of uncertainty of the information, and propose 2TLT-SFPWA operator, 2TLT-SFPWG operator, 2TLT-SFGPWA operator and 2TLT-SFGPWG operator, as effective tools to aggregate the 2TLT-SFNs. The point weighted aggregation operator is more appropriate in considering the redistribution between the different number of attributes by the variable vector and in reducing the impact of the inappropriate evaluation values by measuring the degree of hesitance between any two individuals.

• (3) In some recent publications, COPRAS method has received much attention from researchers but there is currently no progress in extending COPRAS to the 2TLT-SF domain. So, we develop a novel 2TLT-SF-COPRAS method by extending the COPRAS method into 2TLT-SFN.

In considering the aforementioned justifications and arguments, the novelty of this article is demonstrated in the following three ways:

• (1) To aggregate 2TLT-SFNs, we develop four new aggregation operators based on point operations, such as 2TLT-SFPWA operator, 2TLT-SFPWG operator, 2TLT-SFGPWA operator and 2TLT-SFGPWG operator. Desirable properties of proposed operators are also examined.

• (2) We design a novel 2TLT-SF-COPRAS method based on the 2TLT-SFPWA and 2TLT-SFPWG operators. Specifically, we utilize the 2TLT-SFPWA operator and 2TLT-SFPWG operator to fuse the evaluation preferences of the DMs. Then, with the integration of the 2TLT-SFPWA operator (2TLT-SFPWG operator) and the 2TLT-SF-COPRAS method, we appraise the alternatives.

• (3) Finally, we test the applicability of our proposed 2TLT-SF-COPRAS method by solving a problem to select the best data mining task.

In order to accomplish this, we organize the rest of our paper as follows. In Sect. 2, we review fundamental concepts associated with T-spherical fuzzy set (T-SFS), 2-tuple linguistic terms and 2TLT-SFS. In Sect. 3, depending on point operators on 2TLT-SFNs, we develop 2TLT-SFPWA operator, 2TLT-SFPWG operator, 2TLT-SFGPWA operator and 2TLT-SFGPWG operator and also discuss their properties. In Sect. 4, we give a novel technique of COPRAS method for solving MAGDM with 2TLT-SF information. In Sect. 5, a practical illustration for selecting the optimal user through data mining tasks is addressed and comparative analysis by comparing numerical results with the existing methodologies is demonstrated. Finally, Sect. 6 summarizes the paper.

2 Preliminaries

In this section, some correlative basic concepts of T-SFS, 2-tuple linguistic terms and 2TLT-SFS are recapped to facilitate the next sections.

Mahmood et al. (2019) defined the T-spherical fuzzy set as an extension of q-ROFS and SFS as follows:

Definition 1

(Mahmood et al. 2019) For any universal set L, a T-SFS is of the form

$$\begin{aligned} T=\{\langle l,{\mathfrak {a}}_{T}(l),{\mathfrak {b}}_{T}(l),{\mathfrak {c}}_{T}(l)\rangle |l\in L\}, \end{aligned}$$

(1)

where ${\mathfrak {a}}_{T},{\mathfrak {b}}_{T},{\mathfrak {c}}_{T}: L\rightarrow [0,1]$ represent the MD, abstinence degree (AD) and NMD, respectively, with the condition $0 \le {\mathfrak {a}}_{T}^q(l)+{\mathfrak {b}}_{T}^q(l)+{\mathfrak {c}}_{T}^q(l)\le 1$ for positive number $q\ge 1$, and $r(l)= \root q \of {1-({\mathfrak {a}}_{T}^q(l)+{\mathfrak {b}}_{T}^q(l)+{\mathfrak {c}}_{T}^q(l))}$ is known as the degree of refusal of l in T. To express information conveniently, the triplet $({\mathfrak {a}},{\mathfrak {b}},{\mathfrak {c}})$ is known as a T-spherical fuzzy number (T-SFN).

Definition 2

(Herrera and Martinez 2000b) Let $S=\{s_{{i}}|{i}=0,\ldots , {{k}}\}$ be a linguistic term set and $\beta \in [0, {{k}}]$ is a number value representing the aggregation result of linguistic symbolic. Then, the function $\Delta$ used to obtain the 2-tuple linguistic information equivalent to $\beta$ is defined as

$$\begin{aligned}{} & {} \Delta :[0, {{k}}]\rightarrow S\times [-0.5,0.5),\nonumber \\{} & {} \Delta (\beta )= {\left\{ \begin{array}{ll} s_{{i}}, {i}=\text {round}(\beta )\\ \alpha = \beta -{i},~\alpha \in [-0.5, 0.5), \end{array}\right. } \end{aligned}$$

(2)

where round(.) is the usual round operation, $s_{{i}}$ has the closest index label to $\beta$, and $\alpha$ is the value of the symbolic translation.

Definition 3

(Herrera and Martinez 2000b) Let $S=\{s_{{i}}|{i}=0,\ldots , {{k}}\}$ be a linguistic term set and $(s_{{i}},\alpha )$ be a 2-tuple linguistic information, then there exists an inverse function $\Delta ^{-1}$ that restores the 2-tuple linguistic information to its equivalent numerical value $\beta \in [0, {{k}}],$ where

$$\begin{aligned} \Delta ^{-1}: S\times [-0.5, 0.5)\rightarrow [0, {{k}}], \nonumber \\ \Delta ^{-1}(s_{{i}}, \alpha )= {i}+\alpha =\beta . \end{aligned}$$

(3)

Inspired by the ideas of 2-tuple linguistic term and T-SFS, Akram et al. (2022) developed the new concept of 2TLT-SFS. The mathematical representation of 2TLT-SFS is described as follows:

Definition 4

(Akram et al. 2022) Let L be a universal set. A 2TLT-SFS ${\mathfrak {T}}$ in L is defined as

$$\begin{aligned} {\mathfrak {T}}=\{\langle l,(({s_{a}(l)},\varsigma (l)),(s_{b}(l),\psi (l)),(s_{c}(l),\varphi (l)))\rangle \mid l \in L\}, \end{aligned}$$

(4)

where $({s_{a}(l)},\varsigma (l)),(s_{b}(l),\psi (l)),$ and $(s_{c}(l),\varphi (l))$ represent the MD, abstinence degree, and NMD, respectively, with the conditions $s_{a}(l), s_{b}(l), s_{c}(l) \in {\mathfrak {T}}$, $\varsigma (l), \psi (l), \varphi (l)\in [-0.5,0.5),$ $0\le \Delta ^{-1}({s_{a}(l)},\varsigma (l))\le {{k}}$, $0\le \Delta ^{-1}({s_{b}(l)},\psi (l))\le {{k}}$, $0\le \Delta ^{-1}({s_{c}(l)},\varphi (l))\le {{k}}$ and $0\le (\Delta ^{-1}({s_{a}(l)},\varsigma (l)))^q+ (\Delta ^{-1}({s_{b}(l)},\psi (l)))^q+ (\Delta ^{-1}({s_{c}(l)},\varphi (l)))^q\le {{k}}^{q}$. For convenience, we say $\gamma =(({s_{{a}}},\varsigma ),({s_{{b}}},\psi ),({s_{{c}}},\varphi ))$, a 2TLT-SFN, where $0\le \Delta ^{-1}({s_{a}},\varsigma )\le {{k}}$, $0\le \Delta ^{-1}({s_{b}},\psi )\le {{k}}$, $0\le \Delta ^{-1}({s_{c}},\varphi )\le {{k}}$ and $0\le (\Delta ^{-1}({s_{a}},\varsigma ))^q+ (\Delta ^{-1}({s_{b}},\psi ))^q+ (\Delta ^{-1}({s_{c}},\varphi ))^q\le {{k}}^{q}.$

In order to compare any two 2TLT-SFNs, their score and accuracy functions are defined as follows:

Definition 5

(Akram et al. 2022) Let $\gamma =(({s_{a}},\varsigma ),({s_{b}},\psi ),(s_{c},\varphi ))$ be a 2TLT-SFN. Then, the score function ${\mathcal {S}}$ of a 2TLT-SFN ${\gamma }$ can be represented as

$$\begin{aligned}{} & {} \textstyle {\mathcal {S}}(\gamma ) =\Delta \left\{ \frac{{k}}{2}\left( 1+\left( \frac{\Delta ^{-1}({s_{a}},\varsigma )}{{k}}\right) ^{q} -\left( \frac{\Delta ^{-1}({s_{c}},\varphi )}{{k}}\right) ^{q}\right) \right\} ,\nonumber \\ {}{} & {} {\mathcal {S}}(\gamma )\in [0, {{k}}], \end{aligned}$$

(5)

and its accuracy function ${\mathcal {H}}$ is defined as

$$\begin{aligned}{} & {} \textstyle {\mathcal {H}}(\gamma )=\Delta \left\{ {{k}}\left( \left( \frac{\Delta ^{-1}({s_{a}},\varsigma )}{{k}}\right) ^{q} +\left( \frac{\Delta ^{-1}({s_{c}},\varphi )}{{k}}\right) ^{q}\right) \right\} ,\nonumber \\ {}{} & {} {\mathcal {H}}(\gamma )\in [0,{{k}}]. \end{aligned}$$

(6)

Definition 6

(Akram et al. 2022) Let $\gamma _{1}=(({s_{{a}_1}},{\varsigma _1}),({s_{{b}_1}},{\psi _1}),({s_{{c}_1}},{\varphi _1}))$ and $\gamma _{2}=(({s_{{a}_2}},{\varsigma _2}),({s_{{b}_2}},{\psi _2}),({s_{{c}_2}},{\varphi _2}))$ be two 2TLT-SFNs; then, these two 2TLT-SFNs can be compared according to the following rules:

• (1) If ${\mathcal {S}}(\gamma _{1})>{\mathcal {S}}(\gamma _{2})$, then $\gamma _{1}\succ \gamma _{2}$;

• (2) If ${\mathcal {S}}(\gamma _{1})<{\mathcal {S}}(\gamma _{2})$, then $\gamma _{1}\prec \gamma _{2}$;

• (3) If ${\mathcal {S}}(\gamma _{1})={\mathcal {S}}(\gamma _{2})$, then

  • If ${\mathcal {H}}(\gamma _{1})>{\mathcal {H}}(\gamma _{2})$, then $\gamma _{1}\succ \gamma _{2}$;

  • If ${\mathcal {H}}(\gamma _{1})<{\mathcal {H}}(\gamma _{2})$, then $\gamma _{1}\prec \gamma _{2}$;

  • If ${\mathcal {H}}(\gamma _{1})={\mathcal {H}}(\gamma _{2})$, then $\gamma _{1} \sim \gamma _{2}$.

Definition 7

(Akram et al. 2022) Let $\gamma =((s_{a},\varsigma ),(s_{b},\psi ),(s_{c},\varphi )),$ $\gamma _1=((s_{a_1},\varsigma _1),(s_{b_1},\psi _1),(s_{c_1},\varphi _1))$ and $\gamma _2=((s_{a_2},\varsigma _2),(s_{b_2},\psi ),(s_{c_2},\varphi _2))$ be three 2TLT-SFNs, $q\ge 1$, then

• 1.
  $$\begin{aligned}{} & {} \gamma _{1}\oplus \gamma _{2}\\{} & {} \quad ={\scriptstyle \left( \begin{array}{l} \Delta \left( {{k}}\root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{a_{1}},\varsigma _{1})}{{{k}}}\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{a_{2}},\varsigma _{2})}{{{k}}}\right) ^{q}\right) }\right) , \\ \Delta \left( {{k}}\left( \frac{\Delta ^{-1}(s_{b_{1}},\psi _{1})}{{{k}}}\right) \left( \frac{\Delta ^{-1}(s_{b_{2}},\psi _{2})}{{{k}}}\right) \right) ,\\ \Delta \left( {{k}}\left( \frac{\Delta ^{-1}(s_{c_{1}},\varphi _{1})}{{{k}}}\right) \left( \frac{\Delta ^{-1}(s_{c_{2}},\varphi _{2})}{{{k}}}\right) \right) \end{array}\right) }; \end{aligned}$$
• 2.
  $$\begin{aligned}{} & {} \gamma _{1}\otimes \gamma _{2}\\{} & {} \quad ={\scriptstyle \left( \begin{array}{l} \Delta \left( {{k}}\left( \frac{\Delta ^{-1}(s_{a_{1}},\varsigma _{1})}{{{k}}}\right) \left( \frac{\Delta ^{-1}(s_{a_{2}},\varsigma _{2})}{{{k}}}\right) \right) ,\\ \Delta \left( {{k}}\root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{b_{1}},\psi _{1})}{{{k}}}\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{b_{2}},\psi _{2})}{{{k}}}\right) ^{q}\right) }\right) ,\\ \Delta \left( {{k}}\root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{c_{1}},\varphi _{1})}{{{k}}}\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{c_{2}}, \varphi _{2})}{{{k}}}\right) ^{q}\right) }\right) \end{array}\right) }; \end{aligned}$$
• 3.
  $$\begin{aligned}{} & {} \lambda \gamma \\{} & {} \quad ={\scriptstyle \left( \begin{array}{l} \Delta \left( {{k}}\root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{a},\varsigma )}{{{k}}}\right) ^{q}\right) ^{\lambda }}\right) ,\\ \Delta \left( {{k}}\left( \frac{\Delta ^{-1}(s_{b},\psi )}{{{k}}}\right) ^{\lambda }\right) ,\\ \Delta \left( {{k}}\left( \frac{\Delta ^{-1}(s_{c},\varphi )}{{{k}}}\right) ^{\lambda }\right) \end{array}\right) },~ \lambda >0; \end{aligned}$$
• 4.
  $$\begin{aligned}{} & {} \gamma ^{\lambda }\\{} & {} \quad ={\scriptstyle \left( \begin{array}{l} \Delta \left( {{k}}\left( \frac{\Delta ^{-1}(s_{a},\varsigma )}{{{k}}}\right) ^{\lambda }\right) ,\\ \Delta \left( {{k}}\root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{b},\psi )}{{{k}}}\right) ^{q}\right) ^{\lambda }}\right) ,\\ \Delta \left( {{k}}\root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{c},\varphi )}{{{k}}}\right) ^{q}\right) ^{\lambda }}\right) \end{array}\right) },~ \lambda >0. \end{aligned}$$

3 2TLT-SF point aggregation operators

In this section, we present a new class of aggregation operators to aggregate 2TLT-SF information such as the 2TLT-SFPWA operator, 2TLT-SFPWG operator, 2TLT-SFGPWA operator and 2TLT-SFGPWG operator. Moreover, we discuss some properties of the proposed operators.

3.1 2TLT-SFPWA operators

Definition 8

Let $\Omega$ be the set of all 2TLT-SFNs, and $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}), ({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs and $\xi _{{i}},\zeta _{{i}}\in [0,1]$. Then, the series of 2TLT-SFPWA operators: $\Omega ^m \rightarrow \Omega$ is defined, if

• (1) $\text {2TL}T-\text {SFPWAD}_\xi ^n(\gamma _{1},\gamma _2,\ldots ,\gamma _m) = \omega _1D^n_{\xi _{1}}(\gamma _1)\oplus \omega _2D^n_{\xi _{2}}(\gamma _2)\oplus \ldots \oplus \omega _mD^n_{\xi _{n}}(\gamma _m);$

• (2) $\text {2TL}T-\text {SFPWAF}_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) = \omega _1F^n_{\xi _{1},\zeta _{1}}( \gamma _1)\oplus \omega _2F^n_{\xi _{2},\zeta _{2}}(\gamma _2)\oplus \ldots \oplus \omega _mF^n_{\xi _{m},\zeta _{m}}(\gamma _m);$

• (3) $\text {2TL}T-\text {SFPWAG}_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $\omega _1G^n_{\xi _{1},\zeta _{1}}( \gamma _1)\oplus \omega _2G^n_{\xi _{2},\zeta _{2}}(\gamma _2)\oplus \ldots \oplus \omega _mG^n_{\xi _{m},\zeta _{m}}(\gamma _m);$

• (4) $\text {2TL}T-\text {SFPWAH}_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $\omega _1H^n_{\xi _{1},\zeta _{1}}( \gamma _1)\oplus \omega _2H^n_{\xi _{2},\zeta _{2}}(\gamma _2)\oplus \ldots \oplus \omega _mH^n_{\xi _{m},\zeta _{m}}(\gamma _m);$

• (5) $\text {2TL}T-\text {SFPWAJ}_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $\omega _1J^n_{\xi _{1},\zeta _{1}}( \gamma _1)\oplus \omega _2J^n_{\xi _{2},\zeta _{2}}(\gamma _2)\oplus \ldots \oplus \omega _mJ^n_{\xi _{m},\zeta _{m}}(\gamma _m),$

where as $\omega =(\omega _1,\omega _2,\ldots \omega _m)^T$ is the weight vector of $(\gamma _1,\gamma _2,\ldots ,\gamma _m)$, satisfying $\omega _{{i}} \in [0,1]$ and $\sum \nolimits ^m_{{i}=1} \omega _{{i}}=1$.

By the defined operational laws in Sect. 2, we can get the following Theorem.

Theorem 1

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}}, {\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs, and $\xi _{{i}}, \zeta _{{i}} \in [0,1]$, and $\xi _{{i}}+\zeta _{{i}}\le 1$, so the aggregated value by the series of 2TLT-SFPWA operators is also 2TLT-SFNs and

(1):

2TLT-SFPWAD$^n_\xi (\gamma _1,\gamma _2,\ldots ,\gamma _m)$

$$\begin{aligned}= & {} \left( \begin{array}{l} \Delta \left( k\left( 1-\prod \limits ^m _{{i}=1}\left( 1- \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},\varsigma _{{i}})}{k}\right) ^q_{\gamma _{{i}}} +\xi _{{i}}\pi ^q_{\gamma _{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}\right) ,\\ \Delta \left( k\left( \prod \limits ^m_{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}+(1-\xi _{{i}})\pi ^q_{\gamma _{{i}}}\right) ^ {\omega _{{i}}}\right) \right) ,\\ \Delta \left( k\left( \prod \limits ^m_{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}}, {\varphi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}+(1-\xi _{{i}})\pi ^q_{\gamma _{{i}}}\right) ^ {\omega _{{i}}}\right) \right) \end{array} \right) _q \end{aligned}$$

(2):

2TLT-SFPWAF$^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

$$\begin{aligned}= & {} \left( \begin{array}{l} \Delta \left( k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-{\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^q}_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}\right) ,\\ \Delta \left( k\left( \prod \limits ^m _{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) \right) ,\\ \Delta \left( k\left( \prod \limits ^m_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) \right) \end{array} \right) _q \end{aligned}$$

where

$$\begin{aligned}{} & {} \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\\{} & {} \quad =\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^q_{\gamma _{{i}}} +\xi _{{i}}\pi ^q_{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}} +\zeta _{{i}}}}}\right) ^{\frac{1}{q}}\\{} & {} \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\\{} & {} \quad =\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}+\zeta _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}} +\zeta _{{i}}}}}\right) ^{\frac{1}{q}}\\{} & {} \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _{{F^n_{\xi _{{i}}, \zeta _{{i}}}}(\gamma _{{i}})}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}}, {\varphi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}+\zeta _{{i}}\pi ^q_{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}} +\zeta _{{i}}}}}\right) ^{\frac{1}{q}}. \end{aligned}$$

(3):

2TLT-SFPWAG$^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

$$\begin{aligned} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}{\xi ^n_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^m _{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}{\zeta ^n_{{i}}}\right) ^{\frac{\omega _{{i}}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}}, {\varphi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}{\zeta ^n_{{i}}}\right) ^{\frac{\omega _{{i}}}{q}}\right) }\right) \end{array}\right) _q \end{aligned}$$

(4):

2TLT-SFPWAH$^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

$$\begin{aligned}= & {} \left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m _{{i}=1}\left( 1-\left( \frac{\Delta ^{-1} ({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^q{\xi ^n_{{i}}}\right) ^{{{\omega _{{i}}}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^m _{{i} =1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^ {\omega _{{i}}}_{{H^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^ {\omega _{{i}}}_{{H^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\right) }\right) \end{array} \right) _q \end{aligned}$$

where

$$\begin{aligned}{} & {} \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _{{H^n_{{\xi _{{i}},\zeta _{{i}}}}}(\gamma _{{i}})} =\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}\right. \\{} & {} \quad \left. +\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}\right) \left( 1-\left( 1-\zeta _{{i}}\right) ^n\right) \right. \\{} & {} \left. -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}\zeta _{{i}} \left( \Sigma ^{n-1}_{t=0}{\xi ^{n-1-t}_{{i}}}(1-\zeta _{{i}})^t\right) \right) ^{\frac{1}{q}},\\{} & {} \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _{{H^n_{{\xi _{{i}},\zeta _{{i}}}}}(\gamma _{{i}})}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}} +\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}\right) \left( 1-\left( 1-\zeta _{{i}}\right) ^n\right) \right. \\{} & {} \quad \left. -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}\zeta _{{i}} \left( \Sigma ^{n-1}_{t=0}{\xi ^{n-1-t}_{{i}}}(1-\zeta _{{i}})^t\right) \right) ^{\frac{1}{q}} \end{aligned}$$

(5):

$\text {2TL}T-\text {SFPWAJ}^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

$$\begin{aligned}= & {} \left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i} =1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{J^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i} =1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q{\xi ^n_{{i}}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i} =1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q{\xi ^n_{{i}}}\right) }\right) \end{array} \right) _q \end{aligned}$$

where

$$\begin{aligned}{} & {} \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _{{J{^n_{\xi _{{i}},\zeta _{{i}}}}}(\gamma _{{i}})}=\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}\right. \\{} & {} \quad +\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}\right) \left( 1-\left( 1-\xi _{{i}}\right) ^n\right) \\{} & {} \quad \left. -\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}\xi _{{i}} (\Sigma {^{n-1}_{t=0}}{\zeta ^{n-1-t}_{{i}}}(1-\xi _{{i}})^t)\right) ^{\frac{1}{q}}. \end{aligned}$$

Proof

We will prove Eq. 1 by the use of mathematical induction on m, and the others will prove to be equivalent. As

$$\begin{aligned}{} & {} 0\le \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k},\\{} & {} \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}, \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\le 1,\\{} & {} q\ge 1 0\le \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^q +\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q\\{} & {} +\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q\le 1, \end{aligned}$$

and

$$\begin{aligned}{} & {} {\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}}\\{} & {} \quad =\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\\{} & {} \qquad +\xi _{{i}}\pi ^q_{(\gamma _{{i}})}{\frac{1-(1-\xi _{{i}}-\zeta _{{i}})^n}{\xi _{{i}}+\zeta _{{i}}}},\\{} & {} {\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}}\\{} & {} \quad =\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\\{} & {} \qquad +\zeta _{{i}}\pi ^q_{(\gamma _{{i}})}{\frac{1-(1-\xi _{{i}}-\zeta _{{i}})^n}{\xi _{{i}}+\zeta _{{i}}}},\\{} & {} {\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}}\\{} & {} \quad =\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\\{} & {} \qquad +\zeta _{{i}}\pi ^q_{(\gamma _{{i}})}{\frac{1-(1-\xi _{{i}}-\zeta _{{i}})^n}{\xi _{{i}}+\zeta _{{i}}}} \end{aligned}$$

When $m=2$, from the operational laws, we have

$$\begin{aligned}{} & {} \text {2TL}T-\text {SFPWAF}^n_{\xi ,\zeta }(\gamma _1,\gamma _2)=\omega _1\gamma _1\oplus \omega _2\gamma _2\\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^{\omega _{1}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{1}}_{F^n_{{\xi _{1},\zeta _{1}}}({\gamma _{1}})}\right) }\right) ,\\ \Delta \left( {k\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{1}}_{F^n_{{\xi _{1},\zeta _{1}}}({\gamma _{1}})}\right) }\right) \oplus \\ \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{F^n_{{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) ^{\omega _{2}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{2}}_{F^n_{{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) }\right) ,\\ \Delta \left( {k\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{2}}_{F^n_{{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) }\right) \end{array} \right) _q \\{} & {} =\left( \begin{array}{l} \begin{array}{l} \left( \begin{array}{l} \Delta \left( k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^{\omega _{1}}\right) +1\right. \\ \left. -\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{2},\zeta _{2}}}{(\gamma _{2})}}\right) ^{\omega _{2}}\right. \\ \left. -\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{F^n_{{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^{\omega _{1}}\right) \right. \\ \left. \left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{F^n_{{\xi _{2},\zeta _{2}}}{(\gamma _{2})}}\right) ^{\omega _{2}}\right) ^{\frac{1}{q}}\right) \end{array}\right) , \\ {\Delta \left( k\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{1}}_{F^n_{{\xi _{1},\zeta _{1}}}(\gamma _{1})} \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{2}}_{{F^n_{{\xi _{2}, \zeta _{2}}}(\gamma _{2})}}\right) \right) },\\ \Delta \left( k\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}}, {\varphi _{{i}}})}{k}\right) ^{\omega _{1}}_{F^n_{{\xi _{1},\zeta _{1}}}(\gamma _{1})} \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^ {\omega _{2}}_{{F^n_{{\xi _{2},\zeta _{2}}}(\gamma _{2})}}\right) \right) \end{array} \end{array} \right) _q \\{} & {} =\left( \begin{array}{l} \Delta \left( k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^{\omega _{1}}\right. \right. \\ \left. \left. \left( {1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{2},\zeta _{2}}}(\gamma _{2})}}\right) ^{\omega _{2}}\right) ^{\frac{1}{q}}\right) ,\\ \Delta \left( k\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^{\omega _{1}}_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^{\omega _{2}} _{{F^n_{{\xi _{2},\zeta _{2}}}}{(\gamma _{2})}}\right) \right) ,\\ \Delta \left( k\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{1}}_{{F^n_{\xi _{1}, \zeta _{1}}}(\gamma _{1})}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{2}}_{{F^n_{{\xi _{2},\zeta _{2}}}}{(\gamma _{2})}}\right) \right) \end{array} \right) _q \\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^2_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right) ^ {\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^2_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^ {\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^2_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^ {\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) \end{array} \right) _q \end{aligned}$$

Consequently, the result is true for $m=2$. If Eq. 1 holds for $m=t$, i.e.,

$$\begin{aligned}{} & {} \text {2TL}T-\text {SFPWAF}^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots \gamma _{t})\\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^{t}_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^{t}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^{t}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) \end{array} \right) _q \end{aligned}$$

Next, when $m=t+1$, then from the operational laws, we have

$$\begin{aligned}{} & {} \text {2TL}T-\text {SFPWAF}^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots \gamma _{t+1})\\{} & {} \quad =\text {2TL}T-\text {SFPWAF}^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _{t})\oplus \omega _{t+1}{{F^n_{\xi ,\zeta }}{(\gamma _{t+1})}}\\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^{t}_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^{t}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^{t}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) \oplus \\ \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{t+1},\zeta _{t+1}}}{(\gamma _{t+1})}}\right) ^{\omega _{t+1}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{t+1},\zeta _{t+1}}}{(\gamma _{t+1})}}\right) }\right) ,\\ \Delta \left( {k\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{t+1},\zeta _{t+1}}}{(\gamma _{t+1})}}\right) }\right) \end{array} \right) _q \\{} & {} =\left( \begin{array}{l} \begin{array}{l} \left( \begin{array}{l} \Delta \left( k\left( 1-\prod \limits ^{t}_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right. \right. \\ \left. \left. +1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{t+1},\zeta _{t+1}}}{(\gamma _{t+1})}}\right) ^{\omega _{t+1}}\right. \right. \\ \left. \left. -\left( 1-\prod \limits ^{t}_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right) \right. \right. \\ \left. \left. \left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{t+1},\zeta _{t+1}}}{(\gamma _{t+1})}}\right) ^{\omega _{t+1}}\right) \right) ^{\frac{1}{q}}\right) \end{array}\right) ,\\ \Delta \left( {k\left( \prod \limits ^{t}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},\varphi _{{i}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}} \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{t+1},\zeta _{t+1}}}{(\gamma _{t+1})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^{t}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},\varphi _{{i}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}} \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{t+1},\zeta _{t+1}}}{(\gamma _{t+1})}}\right) }\right) \\ \end{array} \end{array} \right) _q \\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^{t+1}_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^{t+1}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^{t+1}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) \end{array} \right) _q. \end{aligned}$$

Thus, Eq. 1 holds for $m=t+1$. Hence, Eq. 1 holds for all m. $\square$

Theorem 2

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs with the weight vector $\omega =(\omega _1,\omega _2,\ldots .,\omega _m)^T$, satisfying $\omega _{{i}}\in [0,1]$ and $\sum ^m_{{i}=1}\omega _{{i}}=1$, $\alpha \succ 0$, then

• (1) $\text {2TL}T-\text {SFPWA}D_\xi ^n(\alpha \gamma _1,\alpha \gamma _2,\ldots ,\alpha \gamma _m)$ = $\alpha \text {2TL}T-\text {SFPWA}D_{\xi }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (2) $\text {2TL}T-\text {SFPWA}F_{\xi ,\zeta }^n(\alpha \gamma _1,\alpha \gamma _2,\ldots ,\alpha \gamma _m)$ = $\alpha \text {2TLT}-\text {SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (3) $\text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n(\alpha \gamma _1,\alpha \gamma _2,\ldots ,\alpha \gamma _m)$ = $\alpha \text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (4) $\text {2TL}T-\text {SFPWA}H_{\xi ,\zeta }^n(\alpha \gamma _1,\alpha \gamma _2,\ldots ,\alpha \gamma _m)$ = $\alpha \text {2TL}T-\text {SFPWA}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (5) $\text {2TL}T-\text {SFPWA}J_{\xi ,\zeta }^n(\alpha \gamma _1,\alpha \gamma _2,\ldots ,\alpha \gamma _m)$ = $\alpha \text {2TL} T-\text {SFPWA}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m).$

Proof

We will prove Eq. 2 holds for all m, and the others can be obtained corresponding. From the operational law in Sect. 2, we have

$$\begin{aligned}{} & {} \alpha \gamma _{{i}} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{i}}\right) ^\alpha \right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^\alpha _{{i}}}\right) , \Delta \left( {k\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^\alpha _{{i}}}\right) \end{array} \right) _q \end{aligned}$$

and

$$\begin{aligned}{} & {} \text {2TL}T-\text {SFPWA}F^n_{\xi ,\zeta }(\alpha \gamma _1,\alpha \gamma _2,\ldots ,\alpha \gamma _m)\\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\alpha \omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\alpha \omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\alpha \omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) \end{array} \right) _q \end{aligned}$$

and hence

$$\begin{aligned}{} & {} \alpha \text {2TL}T-\text {SFPWA}F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)\\{} & {} =\alpha \left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\alpha \omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\alpha \omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\alpha \omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) \end{array} \right) _q \\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\alpha \omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\alpha \omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\alpha \omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) }\right) \end{array} \right) _q\\{} & {} =\text {2TL}T-\text {SFPWA}F^n_{\xi ,\zeta }(\alpha \gamma _1,\alpha \gamma _2,\ldots ,\alpha \gamma _m) \end{aligned}$$

$\square$

Theorem 3

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q$ and $\gamma '_{{i}}=(({s'_{{a}_{{i}}}},{\varsigma '_{{i}}}),({s'_{{b}_{{i}}}},{\psi '_{{i}}}),({s'_{{c}_{{i}}}},{\varphi '_{{i}}}))({i}=1,2,\ldots ,m)$ be two collections of 2TLT-SFNs, and their weight vector is $\omega =(\omega _1,\omega _2,\ldots ,\omega _m)^T$, satisfying $\omega _{{i}}\in [0,1]$ and $\sum ^m_{{i}=1}\omega _{{i}}=1$, then

• (1) $\text {2TLT-SFPWA}D_\xi ^n(\gamma _1\oplus \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TLT-SFPWA}D_\xi ^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\oplus \text {2TLT-SFPWA}D_\xi ^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (2) $\text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma _1\oplus \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\oplus \text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (3) $\text {2TLT-SFPWA}G_{\xi ,\zeta }^n(\gamma _1\oplus \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TLT-SFPWA}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\oplus \text {2TLT-SFPWA}G_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (4) $\text {2TLT-SFPWA}H_{\xi ,\zeta }^n(\gamma _1\oplus \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TLT-SFPWA}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\oplus \text {2TLT-SFPWA}H_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (5) $\text {2TLT-SFPWA}J_{\xi ,\zeta }^n(\gamma _1\oplus \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TLT-SFPWA}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\oplus \text {2TLT-SFPWA}J_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m).$

Proof

We will prove Eq. 2 holds for all m, and the others can be proved corresponding. From the operational laws, we

have

$$\begin{aligned}{} & {} \gamma _{{i}}\oplus \gamma '_{{i}} =\left( \begin{array}{l} \Delta \left( k\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{\gamma _{{i}}}+\left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right) ^{q}_{\gamma '_{{i}}}\right. \right. \\ \left. \left. -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{\gamma _{{i}}}\left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right) ^{q}_{\gamma '_{{i}}}\right) ^{\frac{1}{q}}\right) ,\\ \Delta \left( k\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _{\gamma _{{i}}}\left( \frac{\Delta ^{-1}({s'_{{b}_{{i}}}},{\psi '_{{i}}})}{k}\right) _{\gamma '_{{i}}}\right) ,\\ \Delta \left( k\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _{\gamma _{{i}}}\left( \frac{\Delta ^{-1}({s'_{{c}_{{i}}}},{\varphi '_{{i}}})}{k}\right) _{\gamma '_{{i}}}\right) \end{array} \right) _q \\{} & {} \text {2TL{ T}-SFPWA}F_{\xi ,\zeta }^n(\gamma _1\oplus \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)\\{} & {} =\left( \begin{array}{l} \Delta \left( k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right. \right. \right. \\ \left. \left. \left. -\left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}} +\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right. \right. \right. \\ \left. \left. \left. \left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}} _{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\left( \frac{\Delta ^{-1}({s'_{{b}_{{i}}}},{\psi '_{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\left( \frac{\Delta ^{-1}({s'_{{c}_{{i}}}},{\varphi '_{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) }\right) \end{array} \right) _q \\{} & {} =\left( \begin{array}{l} \Delta \left( k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right. \right. \\ \left. \left. \left( 1-\left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) ^{\omega _{{i}}}\right) \right) ,\\ \Delta \left( k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right. \right. \\ \left. \left. \left( \frac{\Delta ^{-1}({s'_{{b}_{{i}}}},{\psi '_{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) \right) ,\\ \Delta \left( k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right. \right. \\ \left. \left. \left( \frac{\Delta ^{-1}({s'_{{c}_{{i}}}},{\varphi '_{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) \right) \end{array} \right) _q \end{aligned}$$

And

$$\begin{aligned}{} & {} \text {2TL{ T}-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\oplus \\{} & {} \text {2TL{ T}-SFPWA}F_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m)\\{} & {} =\left( \begin{array}{l} \Delta \left( k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right. \right. \\ \left. \left. +1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) ^{\omega _{{i}}}\right. \right. \\ \left. \left. -\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right) \right. \right. \\ \left. \left. \left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) ^{\omega _{{i}}}\right) \right) \right) ,\\ \Delta \left( k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}} \left( \frac{\Delta ^{-1}({s'_{{b}_{{i}}}},{\psi '_{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) \right) ,\\ \Delta \left( k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}} \left( \frac{\Delta ^{-1}({s'_{{c}_{{i}}}},{\varphi '_{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) \right) \end{array} \right) _q \\{} & {} =\left( \begin{array}{l} \Delta \left( k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right. \right. \\ \left. \left. \left( 1-\left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) ^{\omega _{{i}}}\right) \right) ,\\ \Delta \left( k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}} \left( \frac{\Delta ^{-1}({s'_{{b}_{{i}}}},{\psi '_{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) \right) ,\\ \Delta \left( k\left( \prod \limits ^{m}_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}} \left( \frac{\Delta ^{-1}({s'_{{c}_{{i}}}},{\varphi '_{{i}}})}{k}\right) ^{\omega _{{i}}}_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma '_{{i}})}}\right) \right) \end{array} \right) _q\\{} & {} =\text {2TL{ T}-SFPWA}F_{\xi ,\zeta }^n(\gamma _1\oplus \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m). \end{aligned}$$

$\square$

Moreover, the series of 2TLT-SFPWA operator have the following properties.

Theorem 4

(Idempotency) If $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ are equal, that is, $\gamma _{{i}}=\gamma =(({s_{{a}}},{\varsigma }),({s_{{b}}},{\psi }),({s_{{c}}},{\varphi }))$ then

• (1) $\text {2TLT-SFPWA}D_\xi ^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)=D_\xi ^n;$

• (2) $\text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)=F_{\xi ,\zeta }^n;$

• (3) $\text {2TLT-SFPWA}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)=G_{\xi ,\zeta }^n;$

• (4) $\text {2TLT-SFPWA}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)=H_{\xi ,\zeta }^n;$

• (5) $\text {2TLT-SFPWA}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)=J_{\xi ,\zeta }^n.$

Theorem 5

(Monotonicity) Let $\gamma _{{i}}=(({s_{{a}_{{i}}}}, {\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q$ and $\gamma '_{{i}}=(({s'_{{a}_{{i}}}},{\varsigma '_{{i}}}),({s'_{{b}_{{i}}}}, {\psi '_{{i}}}),({s'_{{c}_{{i}}}},{\varphi '_{{i}}}))({i}=1,2,\ldots ,m)$ be two collections of 2TLT-SFNs, if $\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) \le \left( \frac{\Delta ^{-1}({s'_{{a}_{{i}}}},{\varsigma '_{{i}}})}{k}\right)$,$\left( \frac{\Delta ^{-1} ({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) \ge \left( \frac{\Delta ^{-1}({s'_{{b}_{{i}}}},{\psi '_{{i}}})}{k}\right)$ and $\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) \ge \left( \frac{\Delta ^{-1}({s'_{{c}_{{i}}}},{\varphi '_{{i}}})}{k}\right)$ holds for all j, then

• (1) $\text {2TLT-SFPWA}D_\xi ^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le \text {2TLT-SFPWA}D_\xi ^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (2) $\text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le \text {2TL}$T$-\text {SFPWA}F_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (3) $\text {2TL}$T$-\text {SFPWA}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le \text {2TLT-SFPWA}G_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (4) $\text {2TLT-SFPWA}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le \text {2TL}$T$-\text {SFPWA}H_{\xi ,\zeta }^n (\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (5) $\text {2TLT-SFPWA}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le \text {2TLT-SFPWA}J_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m).$

Theorem 6

(Boundedness) Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs, then

• (1) $d_{D^n_\xi }^{-}\le \text {2TLT-SFPWA}D_\xi ^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le d_{D^n_\xi }^+;$

• (2) $d_{F^n_{\xi ,\zeta }}^{-}\le \text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le d_{F^n_{\xi ,\zeta }}^+;$

• (3) $d_{G^n_{\xi ,\zeta }}^{-}\le \text {2TLT-SFPWA}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le d_{G^n_{\xi ,\zeta }}^+;$

• (4) $d_{H^n_{\xi ,\zeta }}^{-}\le \text {2TLT-SFPWA}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le d_{H^n_{\xi ,\zeta }}^+;$

• (5) $d_{J^n_{\xi ,\zeta }}^{-}\le \text {2TLT-SFPWA}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\le d_{J^n_{\xi ,\zeta }}^+$ where $d^+_\Delta =\left( \max \limits _{{i}}\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _\Delta \right) \right)$, $\min \limits _{{i}}\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _\Delta \right)$, $\min \limits _{{i}}\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _\Delta \right)$ and $d^-_\Delta =\left( \min \limits _{{i}}\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _\Delta \right) \right)$, $\max \limits _{{i}}\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _\Delta \right)$,$\max \limits _{{i}}\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _\Delta \right) ,$ , $\Delta$ denotes ${D^n_\xi },{F^n_{\xi ,\zeta }},{G^n_{\xi ,\zeta }},{H^n_{\xi ,\zeta }},{J^n_{\xi ,\zeta }}$.

We have the special cases, by giving different values to the parameters $n,\omega ,q$.

Theorem 7

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}), ({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ a collection of 2TLT-SFNs, $\omega =(\omega _1,\omega _2,\ldots ,\omega _m)^T$ are the weight of $(\gamma _1,\gamma _2,\ldots ,\gamma _m)$, with $\omega _{{i}}\in [0,1]$, $q\ge 1$ and $\sum ^m_{{i}=1}\omega _{{i}}=1$, then

• (1) If $q=1$, then the series of 2TLT-SFPWA operators will all be reduced to the series of 2TLPFPWA operators.

• (2) If $q=2$, then the series of 2TLT-SFPWA operators will all be reduced to the series of 2TLSFPWA operators.

• (3) If $n=0$, then the series of 2TLT-SFPWA operators will all be reduced to the 2TLT-SFWA operator.

• (4) If $n=0$, $q=1$, then the series of 2TLT-SFPWA operators will all be reduced to a 2TLPFWA operator.

• (5) If $n=0$, $q=2$, then the series of 2TLT-SFPWA operators will all be reduced to 2TLSFWA operator.

• (6) If $n=0$, $\omega =({\frac{1}{m}},{\frac{1}{m}},\ldots ,{\frac{1}{m}})^T$, then the series of 2TLT-SFPWA operators will all be reduced to a 2TLT-SFA operator.

• (7) If $n=0$, $\omega =({\frac{1}{m}},{\frac{1}{m}},\ldots ,{\frac{1}{m}})^T$, $q=1$, then the series of 2TLT-SFPWA operators will all be reduced to a 2TLPFA operator.

• (8) If $n=0$, $\omega =({\frac{1}{m}},{\frac{1}{m}},\ldots ,{\frac{1}{m}})^T$, $q=2$, then the series of 2TLT-SFPWA operators will all be reduced to a 2TLSFA operator.

3.2 2TLT-SFPWG operators

Definition 9

Let $\Omega$ be the set of all 2TLT-SFNs, and $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs and $\xi _{{i}},\zeta _{{i}}\in [0,1]$. Then, the series of 2TL T-SFPWG operators: $\Omega ^m \rightarrow \Omega$ will define, if

• (1) $\text {2TL}T-\text {SFPWG}D_\xi ^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)=(D^n_{\xi _{1}}(\gamma _1))^{\omega _1}$ $\otimes (D^n_{\xi _{2}}(\gamma _2))^{\omega _2}\otimes \ldots \otimes (D^n_{\xi _{m}}(\gamma _m))^{\omega _m};$

• (2) $\text {2TL}T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) = (F^n_{\xi _{1},\zeta _{1}}( \gamma _1))^{\omega _1}$ $\otimes (F^n_{\xi _{2},\zeta _{2}}(\gamma _2))^{\omega _2}\otimes \ldots \otimes (F^n_{\xi _{m},\zeta _{m}}(\gamma _m))^{\omega _m};$

• (3) $\text {2TL}T-\text {SFPWG}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $(G^n_{\xi _{1},\zeta _{1}}( \gamma _1))^{\omega _1} \otimes (G^n_{\xi _{2},\zeta _{2}}(\gamma _2))^{\omega _2}\otimes \ldots \otimes (G^n_{\xi _{m},\zeta _{m}}(\gamma _m))^{\omega _m};$

• (4) $\text {2TL} T-\text {SFPWG}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $(H^n_{\xi _{1},\zeta _{1}} ( \gamma _1))^{\omega _1}\otimes (H^n_{\xi _{2},\zeta _{2}}(\gamma _2))^{\omega _2}\otimes \ldots \otimes (H^n_{\xi _{m},\zeta _{m}}(\gamma _m))^{\omega _m};$

• (5) $\text {2TL} T-\text {SFPWG}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $(J^n_{\xi _{1},\zeta _{1}}( \gamma _1)) ^{\omega _1}\otimes (J^n_{\xi _{2},\zeta _{2}}(\gamma _2))^{\omega _2}\otimes \ldots \otimes (J^n_{\xi _{m},\zeta _{m}}(\gamma _m))^{\omega _m}$

where $\omega =(\omega _1,\omega _2,\ldots \omega _m)^T$ is the weight vector of $(\gamma _1,\gamma _2,\ldots ,\gamma _m)$, satisfying $\omega _{{i}} \in [0,1]$ and $\sum \nolimits ^m_{{i}=1} \omega _{{i}}=1.$

From the operational laws defined in Definition 7, we get the following theorem.

Theorem 8

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs, taking $\xi _{{i}}, \zeta _{{i}} \in [0,1]$, and $\xi _{{i}}+\zeta _{{i}}\le 1$, then the aggregated value from the series of 2TL T-SFPWG operators is also 2TLT-SFNs and

• (1) $\text {2TL}T-\text {SFPWG}D^n_\xi (\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( \prod \limits ^m _{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}+\left( 1-\xi _{{i}}\right) \pi ^q_{(\gamma _{{i}})}\right) ^{\frac{\omega _{{i}}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( 1-\prod \limits \limits ^m _{{i}=1}\left( 1-\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q _{(\gamma _{{i}})}+\xi _{{i}}\pi ^q_{(\gamma _{{i}})}\right) \right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits \limits ^m_{{i}=1}\left( 1-\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q _{(\gamma _{{i}})}+\xi _{{i}}\pi ^q_{(\gamma _{{i}})}\right) \right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q \end{aligned}$$

• (2) $\text {2TL}T-\text {SFPWG}F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^{\omega _{{i}}}_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) }\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^q_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^ {\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q, \end{aligned}$$

  where

  $$\begin{aligned}{} & {} \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _{{{F^n_{\xi _{{i}},\zeta _{{i}}}}}(\gamma _{{i}})}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}+\xi _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}}\\{} & {} \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _{{{F^n_{\xi _{{i}},\zeta _{{i}}}}}(\gamma _{{i}})}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q_{(\gamma _{{i}})}+\zeta _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}}\\{} & {} \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _{{{F^n_{\xi _{{i}},\zeta _{{i}}}}}(\gamma _{{i}})}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q_{(\gamma _{{i}})}+\zeta _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}} \end{aligned}$$

  .

• (3) $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^ q{\xi ^n_{{i}}}\right) ^{\frac{\omega _{{i}}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q{\zeta ^n_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q{\zeta ^n_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q \end{aligned}$$

• (4) $\text {2TL}T-\text {SFPWG}H^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{\omega _{{i}}}_{H^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) }\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q_{(\gamma _{{i}})}{\xi ^n_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q_{(\gamma _{{i}})} {\xi ^n_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q \end{aligned}$$

  where

  $$\begin{aligned}{} & {} \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _{{{H^n_{\xi _{{i}},\zeta _{{i}}}}}_{(\gamma _{{i}})}}=\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right. \\{} & {} \quad + \left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right) \left( 1-\left( 1-\xi _{{i}}\right) ^n\right) \\{} & {} \left. -\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q_{(\gamma _{{i}})} \xi _{{i}}\left( \Sigma ^{n-1}_{t=0}{\zeta ^{n-1-t}_{{i}}}\left( 1-\xi _{{i}}\right) ^t \right) \right) ^{\frac{1}{q}} \end{aligned}$$

  .

• (5) $\text {2TL}T-\text {SFPWG}J^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$.

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right) }\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{J^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\zeta ^n_{{i}}\right) ^ {\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{\omega _{{i}}}_{{J^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\zeta ^n_{{i}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q, \end{aligned}$$

  where

  $$\begin{aligned}{} & {} \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _{{{J^n_{\xi _{{i}},\zeta _{{i}}}}}{(\gamma _{{i}})}}=\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right. \\{} & {} \quad + \left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right) \left( 1-\left( 1-\zeta _{{i}}\right) ^n\right) \\{} & {} \left. -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}\zeta _{{i}}\left( \Sigma {^{n-1}_{t=0}}{\xi ^{n-1-t}_{{i}}}\left( 1-\zeta _{{i}}\right) ^t\right) \right) ^{\frac{1}{q}} \end{aligned}$$

  .

Same as the 2TLT-SFPWA, we have the following properties of 2TL T-SFPWG. To save space, proofs of those properties are omitted.

Theorem 9

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}}, {\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs with the weight vector $\omega =(\omega _1,\omega _2,\ldots .,\omega _m)^T$, satisfying $\omega _{{i}}\in [0,1]$ and $\sum ^m_{{i}=1}\omega _{{i}}=1$, then

• (1) $\text {2TL} T-\text {SFPWG}D_\xi ^n(\gamma _1^\alpha ,\gamma _2^\alpha ,\ldots ,\gamma _m^\alpha )$ =($\text {2TL}T-\text {SFPWG}D_{\xi }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m))^\alpha ;$

• (2) $\text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1^\alpha ,\gamma _2^\alpha ,\ldots ,\gamma _m^\alpha )$ =($\text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m))^\alpha ;$

• (3) $\text {2TL} T-\text {SFPWG}G_{\xi ,\zeta }^n(\gamma _1^\alpha ,\gamma _2^\alpha ,\ldots ,\gamma _m^\alpha )$ =($\text {2TL} T-\text {SFPWG}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m))^\alpha ;$

• (4) $\text {2TL} T-\text {SFPWG}H_{\xi ,\zeta }^n(\gamma _1^\alpha ,\gamma _2^\alpha ,\ldots ,\gamma _m^\alpha )$ =($\text {2TL} T-\text {SFPWG}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m))^\alpha ;$

• (5) $\text {2TL} T-\text {SFPWG}J_{\xi ,\zeta }^n(\gamma _1^\alpha ,\gamma _2^\alpha ,\ldots ,\gamma _m^\alpha )$ =($\text {2TL} T-\text {SFPWG}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m))^\alpha .$

Theorem 10

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}}, {\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q$ and $\gamma '_{{i}}=(({s'_{{a}_{{i}}}},{\varsigma '_{{i}}}),({s'_{{b}_{{i}}}}, {\psi '_{{i}}}),({s'_{{c}_{{i}}}},{\varphi '_{{i}}}))_q({i}=1,2,\ldots ,m)$ be two collections of 2TLT-SFNs, then

• (1) $\text {2TL} T-\text {SFPWG}D_\xi ^n(\gamma _1\otimes \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TL} T-\text {SFPWG}D_\xi ^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\otimes \text {2TL} T-\text {SFPWG}D_\xi ^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (2) $\text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1\otimes \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\otimes \text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (3) $\text {2TL} T-\text {SFPWG}G_{\xi ,\zeta }^n(\gamma _1\otimes \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TL} T-\text {SFPWG}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\otimes \text {2TL} T-\text {SFPWG}G_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (4) $\text {2TL} T-\text {SFPWG}H_{\xi ,\zeta }^n(\gamma _1\otimes \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TL} T-\text {SFPWG}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\otimes \text {2TL} T-\text {SFPWG}H_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m);$

• (5) $\text {2TL} T-\text {SFPWG}J_{\xi ,\zeta }^n(\gamma _1\otimes \gamma '_1,\gamma _2\oplus \gamma '_2,\ldots ,\gamma _m\oplus \gamma '_m)$ = $\text {2TL} T-\text {SFPWG}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\otimes \text {2TL} T-\text {SFPWG}J_{\xi ,\zeta }^n(\gamma '_1,\gamma '_2,\ldots ,\gamma '_m).$

The 2TL T-SFPWG operators series have properties same like the 2TLT-SFPWA operators such as idempotency, monotonicity and boundedness under some defined conditions, which are omitted in order to save space. We get the special cases through giving different values to the parameters $n,\omega ,q$.

Theorem 11

Let $\gamma _{{i}} =(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}), ({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ a collection of 2TLT-SFNs, $\omega =(\omega _1,\omega _2,\ldots ,\omega _m)^T$ is the weight of $(\gamma _1,\gamma _2,\ldots ,\gamma _m)$, with $\omega _{{i}}\in [0,1], q\ge 1$ and $\sum ^m_{{i}=1}\omega _{{i}}=1$, then

• (1) If $q=1$, then the series of 2TL T-SFPWG operators will all be reduced to the series of 2TLPFPWG operators.

• (2) If $q=2$, then the series of 2TL T-SFPWG operators will all be reduced to the series of 2TLSFPWG operators.

• (3) If $n=0$, then the series of 2TL T-SFPWG operators will all be reduced to the 2TLT-SFWG operator.

• (4) If $n=0$, $q=1$, then the series of 2TL T-SFPWG operators will all be reduced to 2TLPFWG operator.

• (5) If $n=0$, $q=2$, then the series of 2TL T-SFPWG operators will all be reduced to 2TLSFWG operator.

• (6) If $n=0$, $\omega =({\frac{1}{m}},{\frac{1}{m}},\ldots ,{\frac{1}{m}})^T$, $q=1$, then the series of 2TL T-SFPWG operators will all be reduced to a 2TLT-SFG operator.

• (7) If $n=0$, $\omega =({\frac{1}{m}},{\frac{1}{m}},\ldots ,{\frac{1}{m}})^T$, $q=1$, then the series of 2TL T-SFPWG operators will all be reduced to a 2TLPFG operator.

• (8) If $n=0$, $\omega =({\frac{1}{m}},{\frac{1}{m}},\ldots ,{\frac{1}{m}})^T$, $q=2$, then the series of 2TL T-SFPWG operators will all be reduced to a 2TLSFG operator.

3.3 2TLT-SFGPWA operators

Definition 10

Let $\Omega$ be the set of all 2TLT-SFNs, and $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}), ({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs and $\xi _{{i}},\zeta _{{i}}\in [0,1],\lambda >0$. Then, the series of 2TLT-SFGPWA operators: $\Omega ^m \rightarrow \Omega$ define, if

• (1) $\text {2TL}T-\text {SFGPWA}D_\xi ^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) = (\omega _1D^n_{\xi _{1}}(\gamma _1))^{\frac{1}{\lambda }}\oplus$ $(\omega _2D^n_{\xi _{2}}(\gamma _2))^{\frac{1}{\lambda }}\oplus \ldots \oplus (\omega _mD^n_{\xi _{m}}(\gamma _m))^{\frac{1}{\lambda }};$

• (2) $\text {2TL}T-\text {SFGPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) = (\omega _1F^n_{\xi _{1},\zeta _{1}}( \gamma _1))^{\frac{1}{\lambda }}$ $\oplus (\omega _2F^n_{\xi _{2},\zeta _{2}}(\gamma _2))^{\frac{1}{\lambda }}\oplus \ldots \oplus (\omega _mF^n_{\xi _{m},\zeta _{m}} (\gamma _m))^{\frac{1}{\lambda }};$

• (3) $\text {2TL}T-\text {SFGPWA}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $(\omega _1G^n_{\xi _{1},\zeta _{1}}( \gamma _1))^{\frac{1}{\lambda }} \oplus (\omega _2G^n_{\xi _{2},\zeta _{2}}(\gamma _2))^{\frac{1}{\lambda }}\oplus \ldots \oplus (\omega _mG^n_{\xi _{m},\zeta _{m}} (\gamma _m))^{\frac{1}{\lambda }};$

• (4) $\text {2TLT-SFGPWA}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $(\omega _1H^n_{\xi _{1},\zeta _{1}}( \gamma _1))^{\frac{1}{\lambda }}\oplus (\omega _2H^n_{\xi _{2},\zeta _{2}}(\gamma _2))^{\frac{1}{\lambda }}\oplus \ldots \oplus (\omega _mH^n_{\xi _{m},\zeta _{m}}(\gamma _m))^{\frac{1}{\lambda }};$

• (5) $\text {2TLT-SFGPWA}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ = $(\omega _1J^n_{\xi _{1},\zeta _{1}}( \gamma _1))^{\frac{1}{\lambda }}\oplus (\omega _2J^n_{\xi _{2},\zeta _{2}} (\gamma _2))^{\frac{1}{\lambda }}\oplus \ldots \oplus (\omega _mJ^n_{\xi _{m},\zeta _{m}}(\gamma _m))^{\frac{1}{\lambda }}$

where $\omega =(\omega _1,\omega _2,\ldots \omega _m)^T$ is the weight vector of $(\gamma _1,\gamma _2,\ldots ,\gamma _m)$, satisfying $\omega _{{i}} \in [0,1]$ and $\sum \nolimits ^m_{{i}=1} \omega _{{i}}=1.$ From operational laws defined in Sect. 2, we get the following Theorem.

Theorem 12

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}}, {\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs, taking $\xi _{{i}}, \zeta _{{i}} \in [0,1]$, and $\xi _{{i}}+\zeta _{{i}}\le 1$, then the aggregated value by the series of 2TLT-SFGPWA operators is also 2TLT-SFNs and

• (1) $\text {2TL}T-\text {SFGPWA}D^n_\xi (\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m _{{i}=1}\left( 1-\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}+\xi _{{i}}\pi ^q_{(\gamma _{{i}})}\right) ^\lambda \right) ^ {\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits \limits ^m _{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}-\left( 1-\xi _{{i}}\right) \pi ^q _{\gamma _{{i}}}\right) ^\lambda \right) ^ {\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) }\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits \limits ^m_{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}}, {\varphi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}-\left( 1-\xi _{{i}}\right) \pi ^q_{\gamma _{{i}}}\right) ^\lambda \right) ^ {\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) }\right) \end{array} \right) _q \end{aligned}$$

• (2) $\text {2TL}T-\text {SFGPWA}F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^{q\lambda }_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^ {\omega _{{i}}}\right) ^{\frac{1}{q^\lambda }}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits ^m _{{i}=1} \left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^{q}_{F^n_{\xi _{{i}},\zeta _{{i}}} (\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^ {\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits ^m _{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^{q}_{F^n_{\xi _{{i}},\zeta _{{i}}} (\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q, \end{aligned}$$

  where

  $$\begin{aligned}{} & {} \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _{{{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}}}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{\gamma _{{i}}}+\xi _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-\left( 1-{\xi _{{i}}-\zeta _{{i}}}\right) ^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}},\\{} & {} \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}+\zeta _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-\left( 1-{\xi _{{i}}-\zeta _{{i}}}\right) ^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}}\\,~{} & {} \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^q_{\gamma _{{i}}}+\zeta _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-\left( 1-{\xi _{{i}}-\zeta _{{i}}}\right) ^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}} \end{aligned}$$

  .

• (3) $\text {2TL}T-\text {SFGPWA}G^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q\lambda }_{(\gamma _{{i}})}\xi ^{n\lambda }_{{i}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q\lambda }}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}{\zeta ^n_i}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) \\ \Delta \left( {k\left( 1-\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}{\zeta ^n_i}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q \end{aligned}$$

• (4) $\text {2TL}T-\text {SFGPWA}H^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m _{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q\lambda } _{(\gamma _{{i}})}{\xi ^{n\lambda }_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q\lambda }}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^m _{{i}=1}\left( 1-\left( 1-\prod \limits _{{i}=1}^{m}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{{H^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( 1-\left( 1-\prod \limits _{{i}=1}^{m}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{{H^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}\right) }\right) \end{array} \right) _q, \end{aligned}$$

  where $\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _{H{^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}= \left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}+\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}\right) \left( 1-\left( 1-\zeta _{{i}}\right) ^n\right) -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}\zeta _{{i}}\left( \Sigma ^{n-1}_{t=0}{\xi ^{n-1-t}_{{i}}}\left( 1-\zeta _{{i}}\right) ^t\right) \right) ^{\frac{1}{q}}$ $\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _{H{^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}= \left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}+\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}\right) \left( 1-\left( 1-\zeta _{{i}}\right) ^n\right) -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}\zeta _{{i}}\left( \Sigma ^{n-1}_{t=0}{\xi ^{n-1-t}_{{i}}}\left( 1-\zeta _{{i}}\right) ^t\right) \right) ^{\frac{1}{q}}$

• (5) $\text {2TL}T-\text {SFGPWA}J^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{{J^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\xi ^{n\lambda }_{{i}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q\lambda }}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( 1-\left( 1-\prod \limits _{{i}=1}^{m}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q\lambda }_{(\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( 1-\left( 1-\prod \limits _{{i}=1}^{m}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q\lambda }_{(\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}\right) }\right) \end{array} \right) _q, \end{aligned}$$

  where

  $$\begin{aligned}{} & {} \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _{J{^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}\\{} & {} =\left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right. \\{} & {} \left. +\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right) \left( 1-\left( 1-\xi _{{i}}\right) ^n\right) \right. \\{} & {} \left. -\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}\xi _{{i}}\left( \Sigma {^{n-1}_{t=0}}{\zeta ^{n-1-t}_{{i}}}\left( 1 -\xi _{{i}}\right) ^t\right) \right) ^{\frac{1}{q}}. \end{aligned}$$

Proof

We will prove Eq. 2 holds for all m, and similarly, we can prove the others.We will prove Eq. 2 based on the mathematical induction on m. When $m=2$, we have

$$\begin{aligned}{} & {} \omega _1\left( {{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^\lambda \\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q\lambda }_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^{\omega _{1}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^\lambda \right) ^{\frac{\omega _1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^\lambda \right) ^{\frac{\omega _1}{q}}}\right) \end{array} \right) _q \end{aligned}$$

$$\begin{aligned}{} & {} \omega _2\left( {{F^n_{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) ^\lambda \\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q\lambda }_{{F^n_{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) ^{\omega _{1}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) ^\lambda \right) ^{\frac{\omega _1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) ^\lambda \right) ^{\frac{\omega _1}{q}}}\right) \end{array} \right) _q \\ \end{aligned}$$

$$\begin{aligned}{} & {} \omega _1\gamma _1^\lambda \oplus \omega _2\gamma _2^\lambda \\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q\lambda }_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^{\omega _{1}}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q\lambda }_{{F^n_{\xi _{2},\zeta _{2}}}{(\gamma _{2})}}\right) ^{\omega _{2}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^\lambda \right) ^{\frac{\omega _1}{q}}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) ^\lambda \right) ^{\frac{\omega _2}{q}}\right) }\right) ,\\ \Delta \left( {k\left( \left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{1},\zeta _{1}}}(\gamma _{1})}\right) ^\lambda \right) ^{\frac{\omega _1}{q}}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{{F^n_{\xi _{2},\zeta _{2}}}(\gamma _{2})}\right) ^\lambda \right) ^{\frac{\omega _2}{q}}\right) }\right) \end{array} \right) _q \\{} & {} \text {2TL{ T}-SFGPWA}F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)=(\omega _1\gamma _1^\lambda \oplus \omega _2\gamma _2^\lambda )^{\frac{1}{\lambda }}\\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^2_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q\lambda }_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q^\lambda }}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits ^2 _{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits ^2_{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q \end{aligned}$$

So, result is hold for $m=2$. If Eq. 2 holds for $m=t$, that is

$$\begin{aligned}{} & {} \text {2TL{ T}-SFGPWA}F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots \gamma _{t})\\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^{t}_{{i}=1} \left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q\lambda }_{{F^n_{\xi _{{i}},\zeta _{{i}}}}{(\gamma _{{i}})}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q\lambda }}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits ^{t} _{{i}=1} \left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\left( 1-\prod \limits ^{t}_{{i}=1} \left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}}, {\varphi _{{i}}})}{k}\right) ^{q}_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q \end{aligned}$$

Then, when $m=t+1$, we have $\text {2TL}T-\text {SFGPWA} F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _{t+1}) =\text {2TLT-SFGPWA}F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots , \gamma _{t}).$ Thus, Eq. 2 is true for $m=t+1$. Hence, Eq. 2 holds for all m. $\square$

The series of 2TLT-SFGPWA operator have same properties to 2TLT-SFPWA operators such as idempotency, monotonicity and boundedness under some defined conditions, which are excluded in order to save space.

3.4 2TLT-SFGPWG operators

Definition 11

Let $\Omega$ be the set of all 2TLT-SFNs, and$\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}), ({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs and $\xi _{{i}},\zeta _{{i}}\in [0,1],\lambda \succ 0$. Then, the series of 2TLT-SFGPWG operators: $\Omega ^m \rightarrow \Omega$ define, if

• (1) $\text {2TL}T-\text {SFGPWG}D_\xi ^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) ={\frac{1}{\lambda }}\big (\big (\lambda D^n_{\xi _{1}} (\gamma _1)\big )^{\omega _1} \otimes \big (\lambda D^n_{\xi _{2}}(\gamma _2)\big )^{\omega _2}\otimes \ldots \otimes \big (\lambda D^n_{\xi _{m}}(\gamma _m)\big )^{\omega _m}\big );$

• (2) $\text {2TL}T-\text {SFGPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) ={\frac{1}{\lambda }}\big (\big (\lambda F^n_{\xi _{1},\zeta _{1}} (\gamma _1)\big )^{\omega _1} \otimes \big (\lambda F^n_{\xi _{2},\zeta _{2}}(\gamma _2)\big )^{\omega _2}\otimes \ldots \otimes \big (\lambda F^n_{\xi _{m},\zeta _{m}}(\gamma _m)\big )^{\omega _m}\big );$

• (3) $\text {2TL}T-\text {SFGPWG}G_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) = {\frac{1}{\lambda }}\big (\big (\lambda G^n_{\xi _{1},\zeta _{1}} (\gamma _1)\big )^{\omega _1} \otimes \big (\lambda G^n_{\xi _{2},\zeta _{2}}(\gamma _2)\big )^{\omega _2}\otimes \ldots \otimes \big (\lambda G^n_{\xi _{m},\zeta _{m}}(\gamma _m)\big )^{\omega _m}\big );$

• (4) $\text {2TLT-SFGPWG}H_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) = {\frac{1}{\lambda }}\big (\big (\lambda H^n_{\xi _{1},\zeta _{1}} (\gamma _1)\big )^{\omega _1} \otimes \big (\lambda H^n_{\xi _{2},\zeta _{2}}(\gamma _2)\big )^{\omega _2}\otimes \ldots \otimes \big (\lambda H^n_{\xi _{m},\zeta _{m}}(\gamma _m)\big )^{\omega _m}\big );$

• (5) $\text {2TLT-SFGPWG}J_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m) = {\frac{1}{\lambda }}\big (\big (\lambda J^n_{\xi _{1},\zeta _{1}} (\gamma _1)\big )^ {\omega _1}\otimes \big (\lambda J^n_{\xi _{2},\zeta _{2}}(\gamma _2)\big )^{\omega _2}\otimes \ldots \otimes \big (\lambda J^n_{\xi _{m},\zeta _{m}}(\gamma _m)\big )^{\omega _m}\big )$

where $\omega =(\omega _1,\omega _2,\ldots \omega _m)^T$ is the weight vector of $(\gamma _1,\gamma _2,\ldots ,\gamma _m)$, satisfying $\omega _{{i}} \in [0,1]$ and $\sum \limits ^m_{{i}=1} \omega _{{i}}=1.$

Theorem 13

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs, taking $\xi _{{i}}, \zeta _{{i}} \in [0,1]$, and $\xi _{{i}}+\zeta _{{i}}\le 1$, then the aggregated value by the series of 2TLT-SFGPWG operators are also 2TLT-SFNs and

• (1) $\text {2TL}T-\text {SFGPWG}D^n_\xi (\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\prod \limits ^m _{{i}=1} \left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})} -\left( 1-\xi _{{i}}\right) \pi ^q_{\gamma _{{i}}}\right) ^\lambda \right) ^{\omega _{{i}}}\right) \right) ^ {\frac{1}{\lambda }}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits \limits ^m _{{i}=1} \left( 1-\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}+\zeta _{{i}}\pi ^q_{\gamma _{{i}}}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) , \\ \Delta \left( {k\left( 1-\prod \limits \limits ^m _{{i}=1}\left( 1-\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q} _{(\gamma _{{i}})}+\zeta _{{i}}\pi ^q_{\gamma _{{i}}}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q \end{aligned}$$

• (2) $\text {2TL}T-\text {SFGPWG}F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \!\!\!\begin{array}{l} \Delta \left( {k\left( \!\! 1{-}\left( \!\! 1{-}\prod \limits ^m_{{i}=1}\left( \!\! 1{-}\left( \!\! 1{-}\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\!\! \right) ^{q}_{F^n_{\xi _{{i}},\zeta _{{i}}} (\gamma _{{i}})}\!\! \right) ^\lambda \right) ^{\omega _{{i}}}\!\!\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\!\!\right) ,\\ \Delta \left( \!\!{k\left( \!\! 1{-}\prod \limits ^m_{{i}=1}\left( \!\! 1{-}\left( \!\!\frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\!\! \right) ^ {q\lambda }_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\!\! \right) ^{\omega _{{i}}}\!\! \right) ^{\frac{1}{q\lambda }}}\!\! \right) ,\\ \Delta \left( \!\!{k\left( \!\! 1{-}\prod \limits ^m_{{i}=1}\left( \!\! 1{-}\left( \!\! \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\!\! \right) ^ {q\lambda }_{F^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}\!\! \right) ^{\omega _{{i}}}\!\!\right) ^{\frac{1}{q\lambda }}}\!\!\right) \end{array}\!\!\! \right) _q \end{aligned}$$

  where $\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}= \left( \left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right. \left. +\xi _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}}$, $\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) _{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})} = \left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}+\zeta _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}}$, $\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) _{{F^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})} =\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}\right. \left. +\zeta _{{i}}\pi ^q _{\gamma _{{i}}}{\frac{1-(1-{\xi _{{i}}-\zeta _{{i}}})^n}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{1}{q}}$.

• (3) 2TLT-SFGPWG$G^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}{\xi ^n_{{i}}}\right) ^\lambda \right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q\lambda }_{(\gamma _{{i}})} {\zeta ^{n\lambda }_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q\lambda }}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q\lambda }_{(\gamma _{{i}})}{\zeta ^{n\lambda }_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q\lambda }}}\right) \end{array} \right) _q \end{aligned}$$

• (4) 2TLT-SFGPWG$H^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k} \right) ^{q\lambda }_{\gamma _{{i}}}\right) ^\lambda \right) ^{\omega _{{i}}} \right) ^{\frac{1}{\lambda }}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k} \right) ^{q}_{H^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}{\zeta ^{n\lambda }_{{i}}}\right) ^{\omega _{{i}}} \right) ^{\frac{1}{q\lambda }}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k} \right) ^{q}_{H^n_{\xi _{{i}},\zeta _{{i}}}(\gamma _{{i}})}{\zeta ^{n\lambda }_{{i}}}\right) ^{\omega _{{i}}} \right) ^{\frac{1}{q\lambda }}}\right) \end{array} \right) _q \end{aligned}$$

  where $\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k} \right) _{H{^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}= \left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k} \right) ^{q}_{\gamma _{{i}}}+\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k} \right) ^{q}_{\gamma _{{i}}}\right) \left( 1-\left( 1-\zeta _{{i}}\right) ^{n}\right) -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k} \right) ^{q}_{\gamma _{{i}}}\zeta _{{i}}(\Sigma ^{n-1}_{t=0}{\xi ^{n-1-t}_{{i}}}(1-\zeta _{{i}})^t)\right) ^{\frac{1}{q}}$ $\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k} \right) _{H{^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}= \left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k} \right) ^{q}_{\gamma _{{i}}}+\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}}, {\varphi _{{i}}})}{k}\right) ^{q}_{\gamma _{{i}}}\right) \left( 1-\left( 1-\zeta _{{i}}\right) ^{n}\right) -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^{q}_{\gamma _{{i}}}\zeta _{{i}} (\Sigma ^{n-1}_{t=0}{\xi ^{n-1-t}_{{i}}}(1-\zeta _{{i}})^t)\right) ^{\frac{1}{q}}$

• (5) $\text {2TL}T-\text {SFGPWG}J^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$

  $$\begin{aligned}{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( 1 -\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q} _{{J^n_{\xi _{{i}},\zeta _{{i}}}} (\gamma _{{i}})}\right) ^{\lambda }\right) ^{\omega _{{i}}}\right) ^{\frac{1}{\lambda }}\right) ^ {\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{{i}=1}\left( 1 -\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^ {q\lambda }_{(\gamma _{{i}})}{\zeta ^{n\lambda }_{{i}}}\right) ^{\omega _{{i}}}\right) ^ {\frac{1}{q\lambda }}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m \_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q\lambda } _{(\gamma _{{i}})}{\zeta ^{n\lambda }_{{i}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q\lambda }}}\right) \end{array} \right) _q \end{aligned}$$

  where $\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) _{J{^n_{\xi _{{i}},\zeta _{{i}}}}(\gamma _{{i}})}= \Big (\Big (\frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\Big )^{q}_{(\gamma _{{i}})} +\Big (1-\Big (\frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\Big )^{q}_{(\gamma _{{i}})}\Big )\Big (1 -(1-\xi _{{i}})^n\Big )-\Big (\frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\Big )^{q} _{(\gamma _{{i}})}\xi _{{i}}\Big (\Sigma {^{n-1}_{t=0}}{\zeta ^{n-1-t}_{{i}}} \Big (1-\xi _{{i}}\Big )^t\Big )\Big )^{\frac{1}{q}}$.

Theorem 14

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}), ({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs with the weight vector is $\omega =({\frac{1}{m}},{\frac{1}{m}},\ldots .,{\frac{1}{m}})^T$, satisfying $\omega _{{i}}\in [0,1]$ and $\sum ^m_{{i}=1}\omega _{{i}}=1$, $q\ge 1$, then the operation of complement on aggregation operator is as follows:

• (1) $\left[ \text {2TLT-SFPWA}F_{\xi ,\zeta }^n (\gamma _1^\complement ,\gamma _2^\complement ,\ldots ,\gamma _m^\complement )\right] ^\complement$ $=\text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (2) $\left[ \text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1^\complement , \gamma _2^\complement ,\ldots ,\gamma _m^\complement )\right] ^\complement$ =$\text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (3) $\left[ \text {2TLT-SFGPWA}F_{\xi ,\zeta }^n(\gamma _1^\complement , \gamma _2^\complement ,\ldots ,\gamma _m^\complement )\right] ^\complement$ =$\text {2TLT-SFGPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (4) $\left[ \text {2TLT-SFGPWG}F_{\xi ,\zeta }^n(\gamma _1^\complement , \gamma _2^\complement ,\ldots ,\gamma _m^\complement )\right] ^\complement$ =$\text {2TLT-SFGPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m).$

Theorem 15

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}), ({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs with their weight vector is $\omega =({\frac{1}{m}},{\frac{1}{m}},\ldots .,{\frac{1}{m}})^T$, satisfying $\omega _{{i}}\in [0,1]$ and $\sum ^m_{{i}=1}\omega _{{i}}=1$, $q\ge 1$, $\lambda >0$, then

• (1) $\lim \limits _{n\rightarrow \infty } \text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $=\text {2TLT-SFPWA}D_{\frac{\zeta }{\xi +\zeta }}^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (2) $\lim \limits _{n\rightarrow \infty } \text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $=\text {2TL} T-\text {SFPWG}D_{\frac{\zeta }{\xi +\zeta }}^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (3) $\lim \limits _{n\rightarrow \infty } \text {2TLT-SFGPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $=\text {2TLT-SFGPWA}D_{\frac{\zeta }{\xi +\zeta }}^n(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (4) $\lim \limits _{n\rightarrow \infty }\text {2TLT-SFGPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $=\text {2TLT-SFGPWG}D_{\frac{\zeta }{\xi +\zeta }}^n(\gamma _1,\gamma _2,\ldots ,\gamma _m).$

To save space, proof of the theorem is omitted.

Theorem 16

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}),({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs, with the weight vector is $\omega =(\frac{1}{m},\frac{1}{m},\ldots ,\frac{1}{m})^T$, satisfying $\omega _{{i}}\in [0,1]$ and $\sum ^{m}_{{i}=1}\omega _{{i}=1}$, $\lambda >0$, $q\ge 1$. If $\xi _{{i}}=\frac{\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}}{\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}+\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}}, \zeta _{{i}}=\frac{\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}}{\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}+\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}}$, then

• (1) $\text {2TLT-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $=\text {2TLT-SFPWA}F_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (2) $\text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $=\text {2TL} T-\text {SFPWG}F_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (3) $\text {2TLT-SFGPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $=\text {2TLT-SFGPWA}F_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

• (4) $\text {2TLT-SFGPWG}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $=\text {2TLT-SFGPWG}F_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m).$

Proof

We proof Eq. 1 holds, and other can be proved correspondingly. From the Theorem 1, we get

$$\begin{aligned}{} & {} \text {2TL{ T}-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^m_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}}, {\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}-\xi _{{i}}\pi ^q_{\gamma _{{i}}}\frac{1 -\left( 1-{\xi _{{i}}-\zeta _{{i}}}\right) ^n}{{\xi _{{i}}+\zeta _{{i}}}}\right) ^{\omega _{{i}}} \right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}}, {\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}+\zeta _{{i}}\pi ^{q}_{\gamma _{{i}}}{\frac{1 -\left( 1-{\xi _{{i}}-\zeta _{{i}}}\right) ^n}{\xi _{{i}} +\zeta _{{i}}}}\right) ^{\frac{{\omega _{{i}}}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}}, {\varphi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}+\zeta _{{i}}\pi ^{q}_{\gamma _{{i}}}{\frac{1 -\left( 1-{\xi _{{i}}-\zeta _{{i}}}\right) ^n}{\xi _{{i}}+\zeta _{{i}}}}\right) ^{\frac{{\omega _{{i}}}}{q}}\right) }\right) \end{array} \right) _q \end{aligned}$$

Since $\xi _{{i}}=\frac{\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}}{\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})} +\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}},\zeta _{{i}}=\frac{\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}}{\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})} +\left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})}}$, we have

$$\begin{aligned}{} & {} \text {2TL{ T}-SFPWA}F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)\\{} & {} =\left( \begin{array}{l} \Delta \left( {k\left( 1-\prod \limits ^{m}_{{i}=1}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{{i}}}},{\varsigma _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})} -{\frac{\xi _{{i}}\pi ^{q}_{\gamma _{{i}}}}{\xi _{{i}}+\zeta _{{i}}}}\right) ^{\omega _{{i}}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{b}_{{i}}}},{\psi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})} +{\frac{\zeta _{{i}}\pi ^{q}_{\gamma _{{i}}}}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{\omega _{{i}}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m_{{i}=1}\left( \left( \frac{\Delta ^{-1}({s_{{c}_{{i}}}},{\varphi _{{i}}})}{k}\right) ^{q}_{(\gamma _{{i}})} +{\frac{\zeta _{{i}}\pi ^{q}_{\gamma _{{i}}}}{{\xi _{{i}}+\zeta _{{i}}}}}\right) ^{\frac{\omega _{{i}}}{q}}\right) }\right) \end{array} \right) _q\\{} & {} =\text {2TL{ T}-SFPWA}F_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m) \end{aligned}$$

$\square$

Further, we discuss the relationships and the differences between 2TLT-SFPWA, 2TLT-SFPWG, 2TLT-SFGPWA and 2TLT-SFGPWG operators. In case when $\lambda =1$, and the 2TLT-SFGPWG operator is reduced to the 2TLT-SFPWG operator in Definition 9. Contrastingly, 2TLT-SFPWA is the arithmetic aggregation operator. So, 2TLT-SFPWG operator behaved its geometric form. Similarly, 2TLT-SFGPWG operator is geometric form of 2TLT-SFGPWA operator. Since $\prod \nolimits ^m_{{i}=1}x^{\lambda _{{i}}}_{{i}}\le \sum \nolimits ^{m}_{{i}=1}\lambda _{{i}} x_{{i}}$ when $x_{{i}}>0,\lambda _{{i}}>0$, $\sum \nolimits ^{m}_{{i}=1} \lambda _{{i}}=1$, the relationship between the aggregated values obtained by the 2TLT-SFPWA, 2TLT-SFPWG, 2TLT-SFGPWA and 2TLT-SFGPWG operators is shown as follows:

Theorem 17

Let $\gamma _{{i}}=(({s_{{a}_{{i}}}},{\varsigma _{{i}}}),({s_{{b}_{{i}}}},{\psi _{{i}}}), ({s_{{c}_{{i}}}},{\varphi _{{i}}}))_q({i}=1,2,\ldots ,m)$ be a collection of 2TLT-SFNs, then

(1):

2TLT-SFPWG $F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $\le$ 2TLT-SFPWA $F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m)$;

(2):

2TLT-SFGPWG $F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $\le$ 2TLT-SFGPWA $F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

(3):

2TLT-SFPWG $F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $\le$ 2TLT-SFGPWA $F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m);$

(4):

2TLT-SFGPWG $F_{\xi ,\zeta }^n(\gamma _1,\gamma _2,\ldots ,\gamma _m)$ $\le$ 2TLT-SFPWA $F^n_{\xi ,\zeta }(\gamma _1,\gamma _2,\ldots ,\gamma _m).$

From the Theorem 17, we get that the values obtained from the 2TLT-SFPWG operators are not bigger than ones obtained by the 2TLT-SFPWA and 2TLT-SFGPWA operators. Same as the values obtained from GPFPCG operator are not bigger than the ones obtained by the 2TLT-SFPWA and 2TLT-SFGPWA operators for any $\lambda _{{i}}>0$. Thus, DMs can select the any of four different operators according to the preference and actual needs.

4 An extended COPRAS method for MAGDM within 2TLT-SF environment

The COPRAS method is a reliable approach to solve MAGDM problems. This section introduces a new extended COPRAS method based on the series of 2TLT-SFPWA and 2TLT-SFPWG operators to build the ranking procedure.

To solve the group decision-making problem, we choose a set of m alternatives $\{A_{1},A_{2},\ldots ,A_{m}\}$ and a set of n attributes $\{{{Q}}_{1},{{Q}}_{2},\ldots ,{{Q}}_{n}\}$. Let $(w_{1},w_{2},\ldots ,w_{n})^{T}$ be the weighting vector of attributes satisfying $0\le w_{j} \le 1$ and $\sum \limits _{j=1}^{n} w_{j}=1$. Suppose $\{e_{1},e_{2},\ldots ,e_{g}\}$ is the collection of DMs having weights $(\varpi _{1},\varpi _{2},\ldots ,\varpi _{g})^{T}$, satisfying $0\le \varpi _{l} \le 1$ and $\sum \nolimits _{l=1}^{g} \varpi _{l}=1$. Suppose that the lth expert has evaluated the alternative $A_{i}$ under $Q_{j}$ and provided the decision matrices with 2TLT-SFNs, $R^{l}=({r_{ij}^l})_{m\times {n}}$ $(l=1,2,\ldots ,g)$, where $r_{ij}^l = \left( ({s^{l}_{a}}_{ij},\varsigma ^{l}_{ij}), ({s^{l}_{b}}_{ij},\psi ^{l}_{ij}), ({s^{l}_{c}}_{ij},\varphi ^{l}_{ij})\right)$, $0\le \Delta ^{-1}({s^{l}_{a}}_{ij},\varsigma ^{l}_{ij})\le {{k}}$, $0\le \Delta ^{-1}({s^{l}_{b}}_{ij},\psi ^{l}_{ij})\le {{k}}$, $0\le \Delta ^{-1}({s^{l}_{c}}_{ij},\varphi ^{l}_{ij})\le {{k}}$ and $(\Delta ^{-1}({s^{l}_{a}}_{ij},\varsigma ^{l}_{ij}))^q+ (\Delta ^{-1}({s^{l}_{b}}_{ij},\psi ^{l}_{ij}))^q+ (\Delta ^{-1}({s^{l}_{c}}_{ij},\varphi ^{l}_{ij}))^q\le {{k}}^{q}$, $i={1,2,\ldots ,m}, {j=1,2,\ldots ,n}$.

The 2TLT-SF-COPRAS method is constructed to get the best choice. The computation steps are described as follows:

Step 1.:

In this step, we integrate the individual decision matrices into an aggregated decision matrix $R=(r_{ij})_{m\times {n}}$ by using (3) of Theorem 1 ((3) of Theorem 8).

$$\begin{aligned}{} & {} r_{i j}=\text {2TL{ T}-SFPWAG}^n_{\xi ,\zeta }(r_{i j}^{1},r_{i j}^{2},\ldots ,r_{i j}^{g}). \end{aligned}$$

(7)

$$\begin{aligned}{} & {} \acute{r}_{i j}=\text {2TL{ T}-SFPWGG}^n_{\xi ,\zeta }(r_{i j}^{1},r_{i j}^{2},\ldots ,r_{i j}^{g}). \end{aligned}$$

(8)

We will develop an extended COPRAS method based on the $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta } (\text {2TLT-SFPWGG}^n_{\xi ,\zeta })$, named $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS ($\text {2TL}T-\text {SFPWGG}^n_{\xi ,\zeta }$-COPRAS) method, to tackle the information in the aggregated decision matrix.

Step 2.:

Utilizing the aggregated decision matrix, we sum the values of benefit attributes. The sum of the values of the benefit attributes by using $\text {2TL}T-\text {SFPWA}G^n_{\xi ,\zeta }$ operator can be computed as follows:

$$\begin{aligned} {\mathcal {P}}_{i}= & {} \left( \begin{array}{l} \Delta \left( {k\left( 1-\left( \prod \limits ^m_{i=1;{i} \in N_{B}}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{i}}},{\varsigma _{i}})}{k}\right) _{r_{i}}^q{\xi ^n_{i}}\right) ^{\omega _{i}}\right) ^{\frac{1}{q}}\right) }\right. ,\\ \Delta \left( {k\left( \prod \limits ^m _{i=1;{i} \in N_{B}}\left( \left( \frac{\Delta ^{-1}({s_{{b}_{i}}},{\psi _{i}})}{k} \right) _{r_{i}}^q{\zeta ^n_{i}}\right) ^{\frac{\omega _{i}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m _{i=1;{i} \in N_{B}}\left( \left( \frac{\Delta ^{-1}({s_{{c}_{i}}},{\varphi _{i}})}{k} \right) _{r_{i}}^q{\zeta ^n_{i}}\right) ^{\frac{\omega _{i}}{q}}\right) }\right) \end{array} \right) _q\nonumber \\ \end{aligned}$$

(9)

The sum of the values of the benefit attributes by using $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$ operator can be computed as follows:

$$\begin{aligned} \mathcal {\acute{P}}_{i}= & {} \left( \begin{array}{l} \Delta \left( {k\left( \prod \limits ^m_{i=1;{i} \in N_{B}}\left( \left( \frac{\Delta ^{-1}({s_{{a}_{i}}},{\varsigma _{i}})}{k}\right) _{\acute{r}_{i}}^q{\xi ^n_{i}}\right) ^{\frac{\omega _{i}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{i=1;{i} \in N_{B}}\left( 1 -\left( \frac{\Delta ^{-1}({s_{{b}_{i}}},{\psi _{i}})}{k}\right) _{\acute{r}_{i}}^q{\zeta ^n_{i}}\right) ^ {\omega _{i}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{i=1;{i} \in N_{B}}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{i}}},{\varphi _{i}})}{k}\right) _{\acute{r}_{i}}^q{\zeta ^n_{i}}\right) ^{\omega _{i}}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q\nonumber \\ \end{aligned}$$

(10)

And then find the score function of ${\mathcal {P}}_{i}$ and $\mathcal {\acute{P}}_{i}$.

Step 3.:

Similarly, utilizing aggregated decision matrix, we sum the values of cost attributes. The sum of the values of the cost attributes by using $\text {2TL}T-\text {SFPWA}G^n_{\xi ,\zeta }$ operator can be computed as follows:

$$\begin{aligned} {\mathcal {R}}_{i}= & {} \left( \begin{array}{l} \Delta \left( {k\left( 1-\left( \prod \limits ^m_{i=1;{i} \in N_{C}}\left( 1-\left( \frac{\Delta ^{-1}({s_{{a}_{i}}},{\varsigma _{i}})}{k}\right) _{r_{i}}^q{\xi ^n_{i}}\right) ^{\omega _{i}}\right) ^{\frac{1}{q}}\right) }\right. ,\\ \Delta \left( {k\left( \prod \limits ^m _{i=1;{i} \in N_{C}} \left( \left( \frac{\Delta ^{-1}({s_{{b}_{i}}},{\psi _{i}})}{k}\right) _{r_{i}}^q{\zeta ^n_{i}}\right) ^ {\frac{\omega _{i}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( \prod \limits ^m _{i=1;{i} \in N_{C}}\left( \left( \frac{\Delta ^{-1}({s_{{c}_{i}}},{\varphi _{i}})}{k}\right) _{r_{i}}^q{\zeta ^n_{i}}\right) ^ {\frac{\omega _{i}}{q}}\right) }\right) \end{array} \right) _q\nonumber \\ \end{aligned}$$

(11)

The sum of the values of the cost attributes by using $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$ operator can be computed as follows:

$$\begin{aligned} \mathcal {\acute{R}}_{i}= & {} \left( \begin{array}{l} \Delta \left( {k\left( \prod \limits ^m_{i=1;{i} \in N_{C}}\left( \left( \frac{\Delta ^{-1}({s_{{a}_{i}}},{\varsigma _{i}})}{k}\right) _{\acute{r}_{i}}^q{\xi ^n_{i}}\right) ^{\frac{\omega _{i}}{q}}\right) }\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{i=1;{i} \in N_{C}}\left( 1-\left( \frac{\Delta ^{-1}({s_{{b}_{i}}},{\psi _{i}})}{k}\right) _ {\acute{r}_{i}}^q{\zeta ^n_{i}}\right) ^{\omega _{i}}\right) ^{\frac{1}{q}}}\right) ,\\ \Delta \left( {k\left( 1-\prod \limits ^m _{i=1;{i} \in N_{C}}\left( 1-\left( \frac{\Delta ^{-1}({s_{{c}_{i}}},{\varphi _{i}})}{k}\right) _{\acute{r}_{i}}^q{\zeta ^n_{i}}\right) ^{\omega _{i}}\right) ^{\frac{1}{q}}}\right) \end{array} \right) _q\nonumber \\ \end{aligned}$$

(12)

And, also find the score function of ${\mathcal {R}}_{i}$ and $\mathcal {\acute{R}}_{i}$.

Step 4.:

We determine each alternative $A_{i}(i= 1, 2, \ldots , m)$’s relative significance ${\mathcal {Q}}_{i}$ $(\mathcal {\acute{Q}}_{i})$. Obviously, the more important the alternative is, the larger the value of ${\mathcal {Q}}_{i}$ $(\mathcal {\acute{Q}}_{i})$. The relative significance ${\mathcal {Q}}_{i}$ $(\mathcal {\acute{Q}}_{i})$ can be calculated as

$$\begin{aligned} {\mathcal {Q}}_{i}= & {} {\mathcal {S}}({\mathcal {P}}_{i})+\frac{{\mathcal {S}}({\mathcal {R}}_{min})\sum \nolimits _{i=1}^{m}{\mathcal {S}}({\mathcal {R}}_{i})}{{\mathcal {S}}({\mathcal {R}}_{i})\sum \nolimits _{i=1}^{m}\frac{{\mathcal {S}}({\mathcal {R}}_{min})}{{\mathcal {S}}({\mathcal {R}}_{i})}}\nonumber \\= & {} {\mathcal {S}}({\mathcal {P}}_{i})+\frac{\sum \nolimits _{i=1}^{m}{\mathcal {S}}({\mathcal {R}}_{i})}{{\mathcal {S}}({\mathcal {R}}_{i})\sum \nolimits _{i=1}^{m}\frac{1}{{\mathcal {S}}({\mathcal {R}}_{i})}}. \end{aligned}$$

(13)

$$\begin{aligned} \mathcal {\acute{Q}}_{i}= & {} {\mathcal {S}}(\mathcal {\acute{P}}_{i})+\frac{{\mathcal {S}}(\mathcal {\acute{R}}_{min})\sum \nolimits _{i=1}^{m}{\mathcal {S}}(\mathcal {\acute{R}}_{i})}{{\mathcal {S}}(\mathcal {\acute{R}}_{i})\sum \nolimits _{i=1}^{m}\frac{{\mathcal {S}}(\mathcal {\acute{R}}_{min})}{{\mathcal {S}}(\mathcal {\acute{R}}_{i})}}\nonumber \\= & {} {\mathcal {S}}(\mathcal {\acute{P}}_{i})+\frac{\sum \nolimits _{i=1}^{m}{\mathcal {S}}(\mathcal {\acute{R}}_{i})}{{\mathcal {S}}(\mathcal {\acute{R}}_{i})\sum \nolimits _{i=1}^{m}\frac{1}{{\mathcal {S}}(\mathcal {\acute{R}}_{i})}}. \end{aligned}$$

(14)

The ${\mathcal {Q}}_{i}$ $(\mathcal {\acute{Q}}_{i})$ from Eq. (13) (Eq. (14)) reflects the satisfaction measure of each alternative.

Step 5.:

Based on the ${\mathcal {Q}}_{i}$ $(\mathcal {\acute{Q}}_{i})$, the maximal relative significance value ${\mathcal {K}}$ $(\mathcal {\acute{K}})$ can be determined. Utilize Eq. (15) (Eq. 16) to identify the value of ${\mathcal {K}}$ $(\mathcal {\acute{K}})$.

$$\begin{aligned} {\mathcal {K}}= & {} \max \limits _{1\le i\le m}{\mathcal {Q}}_{i}. \end{aligned}$$

(15)

$$\begin{aligned} \mathcal {\acute{K}}= & {} \max \limits _{1\le i\le m}\mathcal {\acute{Q}}_{i}. \end{aligned}$$

(16)

Thus, the alternative(s) with the associated maximal relative significance value is selected among the possible alternatives.

Step 6.:

Moreover, calculate the utility degree ${\mathcal {U}}_{i}$ $(\mathcal {\acute{U}}_{i})$ of each alternative utilizing the relative significance ${\mathcal {Q}}_{i}$ $(\mathcal {\acute{Q}}_{i})$. The ${\mathcal {U}}_{i}$ $(\mathcal {\acute{U}}_{i})$ can be determined by using Eq. (17) (Eq. (18)).

$$\begin{aligned} {\mathcal {U}}_{i}= & {} \left( \frac{{\mathcal {Q}}_{i}}{{\mathcal {K}}}\right) \times 100\%. \end{aligned}$$

(17)

$$\begin{aligned} \mathcal {\acute{U}}_{i}= & {} \left( \frac{\mathcal {\acute{Q}}_{i}}{\mathcal {\acute{K}}}\right) \times 100\%. \end{aligned}$$

(18)

Step 7.:

Rank the alternatives in the descending order of ${\mathcal {U}}_{i}$ $(\mathcal {\acute{U}}_{i})$. Hence, the bigger the value ${\mathcal {U}}_{i}$ $(\mathcal {\acute{U}}_{i})$, the higher is the rank of the alternative $A_{i} (i={1,2,\ldots ,m})$.

5 The problem enumerate and validity analysis

In this section, we will provide a problem enumerate and a validity analysis to verify our proposed methods.

5.1 The problem enumerate

Data mining integrated the concept and technique of databases, artificial intelligence, machine learning, statistics, and other areas. It is the methodology of searching into content’s obscured regularities from unique perspectives for categorizing it into valuable data. This information is collected and assembled in precise aspects such as data warehouses, efficient analysis, and data mining algorithms, which help in decision-making as well as other data requirements and finally reduce costs and increase earnings. It is one of the most helpful tool for researchers, businesspeople, and users which enables them to extract the required information from massive data sets. The terminology

Knowledge discovery in database also refers to data mining. The methods concerned with knowledge discovery are data cleansing, data unification, data selection, data modification, data mining, trend interpretation, and data representation. Companies employ such techniques to retrieve particular knowledge from gigantic databases in order to deal with business challenges. It mainly transforms unprocessed data into insightful knowledge. It is related to data science carried out by an individual in a particular context, with a particular set of data and with a specific goal. Various services, such as text mining, web mining, audio and video mining, picture data mining, and social media mining, are all part of this process. Simple or advanced software is used to perform these tasks. Data mining can be outsourced to have the task done quickly and cheaply. E-commerce is rapidly gaining ground in business world. If the changeover is performed appropriately, it opens the door for successful productivity, digital programs, reduced transaction costs, and enhanced client relations. Data mining technology is becoming more and more dominant in e-commerce. It has grown into a specialized area of basic and practical computer science study, especially when it comes to e-commerce. It has rich academic value and therefore will effectively fix numerous practical problems when implemented in e-commerce. When data mining innovation and e-commerce are merged, enterprises will be more likely to recognize one’s product offerings, make smarter choices, achieve a competitive edge, and have a wide variety of application opportunities. It will end up making e-commerce sites more productive and offer more advantages to companies. Web data mining for e-commerce can expose a plethora of information that is not visible to enterprises boost sales which enhances enterprise customer relationships, enhance site effectiveness, boost system performance, and grab a growing amount of customers. In this research, we will study a variety of the most advanced techniques and strategies utilized in the disciplines of e-commerce and data mining. It is obvious that e-commerce has raised and tends to generate latest research challenges in a very diverse wide range of data domains and data mining tasks. Here, the COPRAS method is utilized to evaluate the best data mining task for further research process. In this research article, we choose five different data mining tasks as a case study to show which one is more precise and better than others. A group of three DMs (users) $\{e_{1}, e_{2}, e_{3}\}$ with weighting vector $(0.24,0.42,0.34)^{T}$ were invited to evaluate the five data mining tasks namely

(1):

Classification analysis $({{\mathcal {C}}}{{\mathcal {A}}});$

(2):

Regression analysis $({{\mathcal {R}}}{{\mathcal {A}}});$

(3):

Sequence analysis $({{\mathcal {S}}}{{\mathcal {A}}});$

(4):

Prediction analysis $({{\mathcal {P}}}{{\mathcal {A}}});$

(5):

Association analysis $({{\mathcal {A}}}{{\mathcal {A}}}).$

After careful analysis, these four attributes are preferred for the evaluation: (1) Optimize enterprise resources $(\mathcal {OER})$; (2) Manage customer data $(\mathcal {MCD})$; (3) Assess business credit $(\mathcal {ABC})$; (4) Determine the abnormal events $(\mathcal {DAE})$ with the corresponding weight vector $(0.13,0.15,0.41,0.31)^{T}$. Here, $\mathcal {OER}$ and $\mathcal {ABC}$ are benefit attributes, while $\mathcal {MCD}$ and $\mathcal {DAE}$ are cost attributes. Then, the individual evaluation matrices provided by three DMs (users) $e_{1}$, $e_{2}$ and $e_{3}$, respectively, are expressed in the form of 2TLT-SF information with $n=1$, $k=8$, $q=4$, $\xi =0.4$ and $\zeta =0.5$. Generally, n and q can take any values between zero to infinity. However, in some special situations, if n takes the value of 0, then the $\text {2TL}T-\text {SFPWAG}_{\xi ,\zeta }^n$ is reduced to the $\text {2TL}T-\text {SFPWA}$ operator and thus cannot reduce the uncertainty of data. Hence, from the application point of view, we generally advise DMs to take the values of $n = 1$, $q = 4$, which can not only effectively control the uncertainty of 2TLT-SFNs, but also simplify the process of calculation. Decision matrices $R^{l}=({r_{ij}^l})_{m\times {n}}$ given by the DMs $e_{l}(l = 1, 2, 3)$ are shown in Tables 1, 2 and 3.

Table 1 2-Tuple linguistic T-spherical fuzzy decision matrix given by $e_{1}$

Table 2 2-Tuple linguistic T-spherical fuzzy decision matrix given by $e_{2}$

Table 3 2-Tuple linguistic T-spherical fuzzy decision matrix given by $e_{3}$

5.2 Decision analysis with $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS method

In this subsection, we utilize the proposed method to select the best data mining task. The detailed decision-making procedure from the extended $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS method is described as follows:

Step 1.:

We integrate the individual decision matrices given by three DMs into an aggregated decision matrix by using $\text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n$ operator according to Eq. (7). The aggregated decision matrix $R=({r_{ij}})_{m\times {n}}$ is given in Table 4.

Step 2.:

Utilizing the aggregated decision matrix, we sum the collective values of the benefit attributes from Eq. (9) and obtain the score function of ${\mathcal {P}}_{{{i}}}({{i}}= 1,2,\ldots ,5)$ for each alternative as shown in Table 5.

Step 3.:

Similarly, utilizing the aggregated decision matrix, we sum the collective values of the cost attributes from Eq. (11) and obtain the score function of ${\mathcal {R}}_{{{i}}}({{i}}= 1,2,\ldots ,5)$ for each alternative as shown in Table 6.

Step 4.:

For each alternative, we compute the relative significance ${\mathcal {Q}}_{{{i}}}$ from Eq. (13).

$$\begin{aligned} {\mathcal {Q}}_{1}= & {} 3.8167\\{} & {} +\frac{3.7744+3.9760+3.6511+3.9580+3.7713}{3.7744\left( \frac{1}{3.7744} +\frac{1}{3.9760}+\frac{1}{3.6511}+\frac{1}{3.9580}+\frac{1}{3.7713}\right) }\\{} & {} =7.6913,\\ {\mathcal {Q}}_{2}= & {} 3.9715\\{} & {} +\frac{3.7744+3.9760+3.6511+3.9580+3.7713}{3.9760\left( \frac{1}{3.7744} +\frac{1}{3.9760}+\frac{1}{3.6511}+\frac{1}{3.9580}+\frac{1}{3.7713}\right) }\\{} & {} =7.6496,\\ {\mathcal {Q}}_{3}= & {} 3.8220\\{} & {} +\frac{3.7744+3.9760+3.6511+3.9580+3.7713}{3.6511\left( \frac{1}{3.7744} +\frac{1}{3.9760}+\frac{1}{3.6511}+\frac{1}{3.9580}+\frac{1}{3.7713}\right) }\\{} & {} =7.8274,\\ {\mathcal {Q}}_{4}= & {} 3.9864\\{} & {} +\frac{3.7744+3.9760+3.6511+3.9580+3.7713}{3.9580\left( \frac{1}{3.7744} +\frac{1}{3.9760}+\frac{1}{3.6511}+\frac{1}{3.9580}+\frac{1}{3.7713}\right) }\\{} & {} =7.6813,\\ {\mathcal {Q}}_{5}= & {} 3.7827\\{} & {} +\frac{3.7744+3.9760+3.6511+3.9580+3.7713}{3.7713\left( \frac{1}{3.7744} +\frac{1}{3.9760}+\frac{1}{3.6511}+\frac{1}{3.9580}+\frac{1}{3.7713}\right) }\\{} & {} =7.6605. \end{aligned}$$

Step 5.:

Based on the ${\mathcal {Q}}_{{{i}}}$, we identify the maximum relative significance ${\mathcal {K}}$ utilizing Eq. (15). The value of ${\mathcal {K}}$ is given as

$$\begin{aligned} {\mathcal {K}}=7.8274. \end{aligned}$$

Step 6.:

Now, we calculate the utility degree ${\mathcal {U}}_{{{i}}}$ of each alternative by using Eq. (17) as follows:

$$\begin{aligned}{} & {} {\mathcal {U}}_{1}=\left( \frac{7.6913}{7.8274}\right) \times 100\%=98.26\%,~~\\{} & {} \quad {\mathcal {U}}_{2}=\left( \frac{7.6496}{7.8274}\right) \times 100\%=97.72\%,~~\\{} & {} \quad {\mathcal {U}}_{3}=\left( \frac{7.8274}{7.8274}\right) \times 100\%=100\%,\\{} & {} \quad {\mathcal {U}}_{4}=\left( \frac{7.6813}{7.8274}\right) \times 100\%=98.13\%,~~\\{} & {} {\mathcal {U}}_{5}=\left( \frac{7.6605}{7.8274}\right) \times 100\%=97.86\%. \end{aligned}$$

Step 7.:

Based on the utility degree ${\mathcal {U}}_{{{i}}}({{i}}=1,2,\ldots ,5)$, we rank the alternatives in the descending order as

$$\begin{aligned} {{\mathcal {S}}}{{\mathcal {A}}}\succ {{\mathcal {C}}}{{\mathcal {A}}}\succ {{\mathcal {P}}}{{\mathcal {A}}}\succ {{\mathcal {A}}}{{\mathcal {A}}}\succ {{\mathcal {R}}}{{\mathcal {A}}} \end{aligned}$$

. So, ${{\mathcal {S}}}{{\mathcal {A}}}$ is the best choice.

Table 4 Aggregated decision matrix by $\text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n$ operator

Table 5 Sum up values and score functions of benefit type attributes by $\text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n$ operator

Table 6 Sum up values and score functions of cost type attributes by $\text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n$ operator

5.3 Decision analysis with $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS method

In this subsection, we utilize the proposed method to select the best data mining task. The detailed decision-making procedure from the extended $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS method is described as follows:

Step 1.:

We integrate the individual decision matrices given by three DMs into an aggregated decision matrix by using $\text {2TL}T-\text {SFPWG}G_{\xi ,\zeta }^n$ operator according to Eq. (8). The aggregated decision matrix $\acute{R}=({\acute{r}_{ij}})_{m\times {n}}$ is given in Table 7.

Step 2.:

Utilizing the aggregated decision matrix, we sum the collective values of the benefit attributes from Eq. (10) and obtain the score function of $\mathcal {\acute{P}}_{{{i}}}({{i}}= 1,2,\ldots ,5)$ for each alternative as shown in Table 8.

Step 3.:

Similarly, utilizing the aggregated decision matrix, we sum the collective values of the cost attributes from Eq. (12) and obtain the score function of $\mathcal {\acute{R}}_{{{i}}}({{i}}= 1,2,\ldots ,5)$ for each alternative as shown in Table 9.

Step 4.:

For each alternative, we compute the relative significance $\mathcal {\acute{Q}}_{{{i}}}$ from Eq. (14).

Table 7 Aggregated decision matrix by$\text {2TL}T-\text {SFPWG}G_{\xi ,\zeta }^n$ operator

Table 8 Sum up values and score functions of benefit type attributes by $\text {2TL}T-\text {SFPWG}G_{\xi ,\zeta }^n$ operator

Table 9 Sum up values and score functions of cost type attributes by $\text {2TL}T-\text {SFPWG}G_{\xi ,\zeta }^n$ operator

Table 10 Relative significance and ranking results according to the parameter q by $\text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n$-COPRAS method

Table 11 Relative significance and ranking results according to the parameter q by $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS method

$$\begin{aligned} \mathcal {\acute{Q}}_{1}= & {} 4.1462\\{} & {} +\frac{4.4836+4.6820+4.3876+4.5919+4.4880}{4.4836\left( \frac{1}{4.4836} +\frac{1}{4.6820}+\frac{1}{4.3876}+\frac{1}{4.5919}+\frac{1}{4.4880}\right) }\\= & {} 8.7140,\\ \mathcal {\acute{Q}}_{2}= & {} 4.5120\\{} & {} +\frac{4.4836+4.6820+4.3876+4.5919+4.4880}{4.6820\left( \frac{1}{4.4836} +\frac{1}{4.6820}+\frac{1}{4.3876}+\frac{1}{4.5919}+\frac{1}{4.4880}\right) }\\= & {} 8.8862,\\ \mathcal {\acute{Q}}_{3}= & {} 4.4881\\{} & {} +\frac{4.4836+4.6820+4.3876+4.5919+4.4880}{4.3876\left( \frac{1}{4.4836} +\frac{1}{4.6820}+\frac{1}{4.3876}+\frac{1}{4.5919}+\frac{1}{4.4880}\right) }\\= & {} 9.1558,\\ \mathcal {\acute{Q}}_{4}= & {} 4.3278\\{} & {} +\frac{4.4836+4.6820+4.3876+4.5919+4.4880}{4.5919\left( \frac{1}{4.4836} +\frac{1}{4.6820}+\frac{1}{4.3876}+\frac{1}{4.5919}+\frac{1}{4.4880}\right) }\\= & {} 8.7879,\\ \mathcal {\acute{Q}}_{5}= & {} 4.6053\\{} & {} +\frac{4.4836+4.6820+4.3876+4.5919+4.4880}{4.4880\left( \frac{1}{4.4836} +\frac{1}{4.6820}+\frac{1}{4.3876}+\frac{1}{4.5919}+\frac{1}{4.4880}\right) }\\= & {} 9.1686. \end{aligned}$$

Step 5.:

Based on the $\mathcal {\acute{Q}}_{{{i}}}$, we identify the maximum relative significance $\mathcal {\acute{K}}$ utilizing Eq. (16). The value of $\mathcal {\acute{K}}$ is given as

$$\begin{aligned} \mathcal {\acute{K}}=9.1686. \end{aligned}$$

Step 6.:

Now, we calculate the utility degree $\mathcal {\acute{U}}_{{{i}}}$ of each alternative by using Eq. (18) as follows:

$$\begin{aligned}{} & {} \mathcal {\acute{U}}_{1}=\left( \frac{8.7140}{9.1686}\right) \times 100\%=95.04\%,~~ \\{} & {} \mathcal {\acute{U}}_{2}=\left( \frac{8.8862}{9.1686}\right) \times 100\%=96.92\%,~~ \\{} & {} \mathcal {\acute{U}}_{3}=\left( \frac{9.1558}{9.1686}\right) \times 100\%=99.86\%,\\{} & {} \mathcal {\acute{U}}_{4}=\left( \frac{8.7879}{9.1686}\right) \times 100\%=95.84\%,~~ \\{} & {} \mathcal {\acute{U}}_{5}=\left( \frac{9.1686}{9.1686}\right) \times 100\%=100\%. \end{aligned}$$

Step 7.:

Based on the utility degree $\mathcal {\acute{U}}_{i}(i=1,2,\ldots ,5)$, we rank the alternatives in the descending order as ${{\mathcal {A}}}{{\mathcal {A}}}\succ {{\mathcal {S}}}{{\mathcal {A}}}\succ {{\mathcal {R}}}{{\mathcal {A}}}\succ {{\mathcal {P}}}{{\mathcal {A}}}\succ {{\mathcal {C}}}{{\mathcal {A}}}$. So, ${{\mathcal {A}}}{{\mathcal {A}}}$ is the best choice.

5.4 Analyzing the influence of parameters on ranking results

In this subsection, we examine the influence of parameters on the ranking results of the proposed method. In this approach, n and q are two parameters, different parameter values show different risk preference attitudes of DMs in solving MAGDM problems. The proposed $\text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n$-COPRAS ($\text {2TL}T-\text {SFPWG}G_{\xi ,\zeta }^n$-COPRAS) is a technique that enables DMs to expand their decision evaluation space based on the parameters q and n. The main characteristic of our proposed operator(s) is not only the effective control of the degree of uncertainty of 2TLT-SFS but also the efficient and powerful model of practical decision-making problems for additional parameters.

5.4.1 Influence of the parameter q

To show the influence of parameter on ranking results, we utilize different values of parameter q to rank the alternatives by the proposed $\text {2TL}T-\text {SFPWA}G_{\xi ,\zeta }^n$-COPRAS and $\text {2TL}T-\text {SFPWG}G_{\xi ,\zeta }^n$-COPRAS methods. It can be seen in Tables 10 and 11 and Figs. 1 and 2, there is difference in the ranking results when parameter changes. The parameter q is very important and has major impact on the decision results. Influence of the parameter q on the relative significance and ranking results is explained by taking the fixed value of parameter $n ~(n=1)$.

Fig. 1

Ranking results $A_{{{i}}}({{i}} = 1, 2, 3, 4, 5)$ when $n= 1$ and $q=1,2,3,4,5$ based on the $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS method

Fig. 2

Ranking results $A_{{{i}}}({{i}} = 1, 2, 3, 4, 5)$ when $n= 1$ and $q=1,2,3,4,5$ based on the $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS method

5.4.2 Influence of the parameter n

In practical MAGDM problems, the value of n can be seen as the DM’s attitude parameter toward optimism and pessimism. If DMs are cautious about their decisions, then n should be given higher priority, and when decisions are uncertain, lower value of n is taken by DMs. By assigning different values to parameter n, we analyze the influence of the parameter n on relative significance and ranking results by taking fixed value of $q~(q = 4)$. We can see in Tables 12 and 13 and Figs. 3 and 4, different ranking results are derived by different values of n in the $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS and $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS methods, which also demonstrates the elasticity of our proposed methods.

Table 12 Relative significance and ranking results according to the parameter n by $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS method

Table 13 Relative significance and ranking results according to the parameter n by $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS method

Fig. 3

Ranking results $A_{{{i}}}({{i}} = 1, 2, 3, 4,5)$ when $q=4$ and $n=1,2,3,4,5$ based on the $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS method

Fig. 4

Ranking results $A_{{{i}}}({{i}} = 1, 2, 3, 4,5)$ when $q=4$ and $n=1,2,3,4,5$ based on the $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS method

5.5 Validity analysis of the developed method

For further illustration of the effectiveness and advantages of the proposed method in this paper, we compare it with the other methods. Detailed evaluation results gained by using different MAGDM methods are given in Table 14, in which we used linguistic picture fuzzy point weighted average COPRAS (LPFPWA-COPRAS), linguistic picture fuzzy point weighted geometric COPRAS (LPFPWG-COPRAS), linguistic spherical fuzzy point weighted average COPRAS (LSFPWA-COPRAS), linguistic spherical fuzzy point weighted geometric COPRAS (LSFPWG-COPRAS), 2-tuple linguistic T-spherical fuzzy point weighted average COPRAS ($\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS), and 2-tuple linguistic T-spherical fuzzy point weighted geometric COPRAS ($\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS) methods.

Table 14 Comparison of decision results by utilizing different methods

To explain the effectiveness of the proposed method in modeling fuzzy information, we present the characteristics of the proposed operators. We can see that the ranking results of the above methods are slightly different; however, the best alternative is ${{\mathcal {S}}}{{\mathcal {A}}}$ or ${{\mathcal {A}}}{{\mathcal {A}}}$. This verifies that the developed $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS and $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS methods are reasonable and useful for MAGDM problems with 2TLT-SFNs and provide the powerful information in MAGDM.

(1):

From the aspect of data articulation, it is obvious that the valuable feature of our techniques is that they provide a diverse range of applications since they not only tackle problems that the existing methods can but also handle a few more circumstances that they are incapable to handle. The method proposed in this work is a very efficient tool for solving aggregated decision-making problems in the dynamic decision-making today’s environment.

(2):

Some commonly utilized weighted aggregation operators, including 2TLT-SFWA and 2TLT-SFWG, are special examples of the proposed operators when $n = 0$. As a result, compared to all of those presented in the latest research, our approaches are more comprehensive and versatile. Furthermore, based on the parameters, the proposed operators can include almost all of the geometric and arithmetic aggregation operators for 2TLIFNs, 2TLPyFNs, and 2TLq-ROFNs. As a result, the proposed method is more efficient and general.

(3):

To reflect either positive or negative perspectives, DMs can employ the appropriate point weighted aggregation operators from the perspective of actual needs. In addition to the other operators, our techniques also take into consideration other aspects that indicate the DM’s interests, enabling them to choose different aspects in accordance with their risk preferences.

5.6 Advantages of the proposed work

Different aggregation operators have different functions, and the DMs can choose suitable aggregation operators according to the real decision-making environment. Our extended method therefore has some benefits and superiorities when compared to other methods. The merits of our developed approach are summarized as follows:

• Proposed methods are preferable to others because they effectively handle the redistribution of the multi-input arguments. Moreover, they have monotonicity with respect to the parameter n and can effect the risk attitude of the DMs. Thus, we can conclude that the proposed methods are significantly strong and have more comprehensive applications. The 2TLT-SFS can tackle practical problems both quantitatively and qualitatively. Therefore, proposed approach is clear and has less loss of data.

• $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS and $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS methods can provide more versatile and robust information fusion and make it more feasible to tackle MAGDM problems. From the point view of aggregation operators, we note that the existing methods are only based on the original information, and thus cannot control the uncertainty degree, while our method can redistribute the MD, AD and NMD in 2TLT-SFNs according to different principles and thus can get more intensive and objective information from the original 2TLT-SFS.

• Proposed methods consider both the benefit attributes and the cost attributes which provide more precise information compared with simply handling benefit attributes or cost attributes. Also, it increases the success rate of given data and the precision of decision results as well.

6 Conclusions

In this article, we covered some commonly used data mining tasks as well as some applications of these tasks toward e-commerce utilizing the 2TLT-SFS which increases the range for assigning MD, AD and NMD. The 2-tuple linguistic term can best describe the information given by the DMs. Some novel 2TLT-SF point weighted aggregation operators, such as 2TLT-SFPWA operator, 2TLT-SFPWG operator, 2TLT-SFGPWA operator and 2TLT-SFGPWG operator, have been put forward for aggregating 2TLT-SFNs. As COPRAS method interprets the ratio to the worst and the best results, therefore, an extended 2TLT-SF point weighted COPRAS method for MAGDM under the 2TLT-SF environment was proposed. Subsequently, a novel approach to MAGDM based on $\text {2TL}T-\text {SFPWAG}^n_{\xi ,\zeta }$-COPRAS method and $\text {2TL}T-\text {SFPWG}G^n_{\xi ,\zeta }$-COPRAS method has been presented under 2TLT-SF circumstances. Further, a numerical instance related to the data mining tasks toward e-commerce has been presented to demonstrate the validity of the set forward concepts in MAGDM. Comparison analysis has been conducted, and the superiorities have been illustrated. As we have observed, q and n parameters of the aggregation operator also influence the rankings of the alternative. In addition to accommodating 2TLT-SFNs, the 2TLT-SFPWA and 2TLT-SFPWG operators have been distinguished from other operators by including the redistribution phenomenon among their attributes. In future, by utilizing point operators along with different applications of data mining such as artificial intelligence, science and engineering, automation, dynamic pricing, transportation, loan payment prediction, targeted marketing, financial crimes detection and many more will be extended to (1) 2-tuple linguistic complex interval-valued T-spherical fuzzy sets; (2) 2-tuple linguistic complex simplified interval-valued T-spherical fuzzy sets; and (3) 2-tuple linguistic complex hesitant T-spherical fuzzy sets. Although e-commerce is an ideal application, exploratory research is still required to enhance the marketing strategies of data mining, therefore, it is expected to be as famous and trendy as other relevant technologies in future study of decision-making.