Multiple attribute decision-making based on cubical fuzzy aggregation operators

Abstract

The picture fuzzy set, briefly as; PFS and its extensions, spherical fuzzy set (SFS), and T-spherical fuzzy set (T-SFS) are all effective tools to express uncertain and incomplete cognitive information with membership, neutral membership, and non-membership degrees. The cubical fuzzy set (CFS) introduced in this paper, carries out uncertain and imprecise information smartly in exercising decision-making than PFS and SFS. Cubical fuzzy set (CFS)is an extension of the picture fuzzy set and spherical fuzzy set. In CFS, the membership grades satisfy the condition ${0}\le {\mu } ^{3}(x)+{\eta }^{3}\left( {x}\right) +{\nu }^{3}\left( {x}\right) \le {1}$ instead of ${0}\le {\mu } ^{2}({x})+{\eta }^{2}\left( {x}\right) +{\nu } ^{2}\left( {x}\right) \le {1}$, which is the condition of a spherical fuzzy set (SFS). In the course of this article, we first devise some operations on CFS, discuss the basic properties, and propose the cubical fuzzy arithmetic and geometric aggregation operators. We introduce the concept of cubical fuzzy weighted average (CFWA) operator, cubical fuzzy ordered weighted average (CFOWA) operator, and cubical fuzzy hybrid average (CFHA) operator. In the second section, we develop cubical fuzzy weighted geometric (CFWG) operator, cubical fuzzy ordered weighted geometric (CFOWG) operator, and cubical fuzzy hybrid geometric (CFHG) operator. We define the distance measure between two CFSs and study some of its properties. In the last section, the developed operators are utilized to devise approaches for solving multiple attribute decision-making problems (MADM) in a cubical fuzzy environment. A practical example of enterprise resource planning (ERP) system selection is given to verify the developed approach and to demonstrate the practicality and effectiveness of the proposed operators.

1 Introduction

The theory of fuzzy sets (FSs) (Zadeh 1965) is a very powerful tool Zadeh (1996), which has successfully been applied in many fields Abdulai and Turunen (2021), Calvo and Recasens (2021) and Garcia-Pardo et al. (2021). Different types of fuzzy set extensions have been introduced to deal with the uncertainty and fuzziness of data Atanassov (1986), Cuong and Kreinovich (2013), Yager (2013a) and Senapati and Yager (2020). In the orthopair fuzzy set the membership grades of an element x are pairs of values $\left( {\mu }\left( {x}\right) ,{\nu }\left( {x}\right) \right)$ in the unit interval, indicating the membership and nonmembership respectively in the fuzzy set Yager (2016). Atanassov’s intuitionistic fuzzy sets (IFSs) ( Atanassov 2012, 1989) and the second kind of intuitionistic fuzzy sets ( Atanassov and Vassilev 2013) are some examples of orthopair fuzzy sets. The idea of the second kind of IFS has been followed by Parvathi and Vassilev Vassilev et al. (2008). In the case of IFSs, the sum of membership and nonmembership is bounded by one and for the second kind, known as Pythagorean fuzzy sets (PFSs), the sum of the squares of the membership and nonmembership is bounded by one Yager (2013a), Rahman et al. (2017). Yagėr generalized the idea in Yager (2016) and introduced a general class of such types of sets called the q-rung orthopair fuzzy sets (q-ROFSs). The biggest advantage of this class of fuzzy sets is that, in q-ROFSs, the sum of qth power of the membership and nonmembership is bounded by one. Yager pointed out that the space of acceptable orthopairs increases directly with an increase in q which gives the users more freedom to express their belief about membership grades. On the other hand, in a cubical fuzzy set, the membership grades of an element x are in the unit triplet $\left( {\mu }({x} ),{\eta }({x}),{\nu }({x})\right) ,$ in which ${\mu }({x})$ indicates support for membership, ${\eta }({x})$ indicates neutral membership, and ${\nu }({x})$ indicates support in against membership. Two known subclasses of cubical fuzzy sets are Coung’s picture fuzzy sets (PFS) Cuong and Kreinovich (2013) and spherical fuzzy sets (SFS) Ashraf and Abdullah (2019). In PFSs the sum of the grades for support, neutral support, and against support is bounded by one, while in SFSs the square sum of these grades is bounded by 1. Cuong’s construction of PFSs has a remarkable reputation, but once again, the condition on membership grades ${\mu }({x})$, ${\eta }({x})$, and ${\nu }({x})$ restricts a decision-maker in assigning membership values. To resolve this problem and give more freedom to a decision-maker, Ashraf et. al, applied the same concept (as by Yager for the Pythagorean fuzzy set) and introduced a new structure known as the spherical fuzzy set (SFS). In SFSs the space of membership degrees ${\mu }({x})$, ${\eta }({x})$, and ${\nu }({x})$ is larger as compared to that of PFSs and the membership grades satisfy the condition ${0\le \mu }^{2}({x} )+{\eta }^{2}({x})+{\nu }^{2}({x}){\le 1}.$ In addition to that, PFSs and SFSs have their unique importance in situations where opinion is not only constrained to yes or no but there is some sort of abstinence or refusal. Decision-making could be a suitable example, in the case when each expert has three different classes of opinions about an alternative. Another and the most suitable example could be the voting process where three types of voters can occur who vote in favor or vote against or refuse to vote. In SFS, the decision-makers are still restricted to assigning values in the decision process because of the restrictions on the grades of memberships that $0\le \mu ^{2}(x)+\eta ^{2}(x)+\nu ^{2}(x)\le 1$ should be satisfied, and the decision-makers are restricted to a particular domain. For example, if we consider $\mu (x)=0.8,$ $\eta (x)=0.5$ and $\nu (x)=0.6,$ which implies that $\mu (x)+\eta (x)+\nu (x)=1.9\nleq 1$ and definitely it does not satisfy the condition of PFS. Further, we have $\left( 0.8\right) ^{2}+\left( 0.5\right) ^{2}+\left( 0.6\right) ^{2} =1.25\nleq 1.$ But if we consider $\left( 0.8\right) ^{3}+\left( 0.5\right) ^{3}+\left( 0.6\right) ^{3}=0.853<1,$ which is an appropriate reason to define another class of fuzzy sets that has more ability in capturing the uncertainties and therefore, we defined cubical fuzzy set. This is to mention here that the CFSs have more potential to deal with uncertainties than PFSs and SFSs and are capable to deal with higher levels of fuzziness. Decision-making problems have been extensively studied by several researchers all over the world and characterized several aspects of daily life problems, e.g., (see Xu and Zhang 2013; Yager and Abbasov 2013 and Yager 2013b; Manoj et al. 1998). For the applications of FSs in different aspects of man-machine learning and other databases, we refer (see Chen and Huang 2003; Chen 1996; Chen and Jong 1997; Manoj et al. 1998).

The objectives of this article are as follows: (1) To introduce the cubical fuzzy set (CFS), cubical fuzzy numbers (CFNs), and their operational identities. (2) To define the score, accuracy, and certainty functions to compare cubical fuzzy numbers. (3) To propose cubical fuzzy aggregation operators and investigate their operational rules. (4) To demonstrate a MADM method based on the proposed operators in the environment of cubical fuzzy information. The article is arranged as follows. Section 2 reviews basic ideas related to PFSs and SFSs and their properties. Section 3, gives comprehensive details about CFSs and their operational properties. Finally, in Sect. 4, a decision-making method has been established based on these operators, for ranking the alternatives by utilizing cubical fuzzy information. The proposed method has also been demonstrated with the help of a descriptive example for investigating its stability, reliability, and effectiveness. Lastly, some comparisons of the proposed and existing methods are demonstrated.

2 Preliminaries

Some basic ideas associated with PFS and SFS are reviewed here. Also, a few more concepts are discussed which are utilized in the sequential discussions.

Definition 1

Cuong and Kreinovich (2013) A PFS A over the universe ${\ddot{U}}$ is an object of the form,

$$\begin{aligned} A=\{ {\varepsilon },{\mu }_{{A}}({\varepsilon }),{\eta }_{{A}}({\varepsilon }),{\nu }_{{A} }({\varepsilon })|{\varepsilon \in {\ddot{U}}}\}, \end{aligned}$$

where ${\mu }_{A}({\varepsilon }),$ ${\eta }_{A} ({\varepsilon }),$ ${\nu }_{A}({\varepsilon })\in [0,$ 1] are respectively called the “degree of positive membership, neutral membership, and negative membership of A ”. Also $0\le {\mu }_{A}({\varepsilon })+{\eta }_{A}({\varepsilon })+{\nu }_{A} ({\varepsilon }){\le }1$ for all ${\varepsilon } {\in {\ddot{U}}}$. For ${\varepsilon }\in {{\ddot{U}}}$, $\pi _{A}({\varepsilon })=1-\left( {\mu }_{A}({\varepsilon })+{\eta }_{A}({\varepsilon })+{\nu }_{A} ({\varepsilon })\right) ,$ is known as the degree of refusal membership of ${\varepsilon }$ in A.

Definition 2

Ashraf and Abdullah (2019) The spherical fuzzy set defined on a non-empty set ${{\ddot{U}} }$ is a structure of the form given below

$$\begin{aligned} A=\left\{ \left\langle {\varepsilon },{\mu }_{A}\left( {\varepsilon }\right) ,{\eta }_{A}\left( {\varepsilon }\right) ,{\nu }_{A}\left( {\varepsilon }\right) \right\rangle :{\varepsilon }\in {{\ddot{U}}}\right\}, \end{aligned}$$

such that ${\mu }_{A}:{{\ddot{U}}}\longrightarrow [{0},$ 1],  ${\eta }_{A}:{{\ddot{U}}} \longrightarrow {[0},$ 1],  and ${\nu }_{A}:{{\ddot{U}} }\longrightarrow {[0},$ 1],  respectively are called the degree of membership, degree of neutral membership, and degree of nonmembership of every ${\varepsilon }\in {{\ddot{U}}}$to the set A and ${0} \le \left( {\mu }_{A}\left( {\varepsilon }\right) \right) ^{2}+\left( {\eta }_{A}\left( {\varepsilon }\right) \right) ^{2}+\left( {\nu }_{A}\left( {\varepsilon }\right) \right) ^{2}{\le 1},$ $\forall$ ${\varepsilon }\in {{\ddot{U}}}$. For any ${\varepsilon }\in {{\ddot{U}}}$ and a spherical fuzzy set A, 

$$\begin{aligned} \pi _{A}({\varepsilon })=\sqrt{{1}-\left( {\mu }_{A}\left( {\varepsilon }\right) \right) ^{2}-\left( {\eta }_{A}\left( {\varepsilon }\right) \right) ^{2}-\left( {\nu }_{A}\left( {\varepsilon }\right) \right) ^{2}} \end{aligned}$$

is known as the degree of refusal of ${\varepsilon }$ to A. Ashraf et al. Ashraf and Abdullah (2019), also defined the following operations on SFSs.

Definition 3

Ashraf and Abdullah (2019) For two SFSs $S_{1}$ and $S_{2}$ over the same universe ${\ddot{U}}$, the inclusion, union, intersection, and complement are defined as follows:

• (i) $S_{1}\subseteq S_{2}$ if $\mu _{S_{1} }\left( \varepsilon \right) \le \mu _{S_{2}}\left( \varepsilon \right) ,$ $\eta _{S_{1}}\left( \varepsilon \right) \le \eta _{S_{2}}\left( \varepsilon \right)$ and $\nu _{S_{1}}\left( \varepsilon \right) \ge \nu _{S_{2}}\left( \varepsilon \right) ,$ $\forall$ $\varepsilon \in {\ddot{U}}$

• (ii) $S_{1}=S_{2}$ if $S_{1}\subseteq S_{2}$ and $S_{2}\subseteq S_{1}$

• (iii) $S_{1}\cap S_{2} =\left( \varepsilon ,\min \left\{ \mu _{S_{1}}\left( \varepsilon \right) ,\mu _{S_{2} }\left( \varepsilon \right) \right\} ,\min \left\{ \eta _{S_{1}}\left( \varepsilon \right) ,\eta _{S_{2}}\left( \varepsilon \right) \right\} ,\max \left\{ \nu _{S_{1}}\left( \varepsilon \right) ,\nu _{S_{2}}\left( \varepsilon \right) \right\} |\varepsilon \in {\ddot{U}} \right)$

• (iv) $S_{1}\cup S_{2} =\left( \varepsilon ,\max \left\{ \mu _{S_{1}}\left( \varepsilon \right) ,\mu _{S_{2}}\left( \varepsilon \right) \right\} ,\min \left\{ \eta _{S_{1}}\left( \varepsilon \right) ,\eta _{S_{2}}\left( \varepsilon \right) \right\} ,\min \left\{ \nu _{S_{1}}\left( \varepsilon \right) ,\nu _{S_{2}}\left( \varepsilon \right) \right\} |\varepsilon \in {\ddot{U}}\right)$

• (v) $S_{1}^{c}=\left( x,\left( \nu _{S_{1}}(\varepsilon ),\eta _{S_{1}} (\varepsilon ),\mu _{S_{1}}(\varepsilon )\right) |\varepsilon \in {\ddot{U}}\right) .$

Definition 4

Assume that ${{\ddot{U}}}$ is a universe of discourse. A cubical fuzzy set (CFS) denoted by C, is a structure of the form

$$\begin{aligned} {C}=\left\{ \left\langle \left\langle {\varepsilon } ,{f}_{{C}}\left( {\varepsilon }\right) ,{g} _{{C}}\left( {\varepsilon }\right) ,{h}_{{C} }\left( {\varepsilon }\right) \right\rangle :{\varepsilon } \in {{\ddot{U}}}\right\rangle \right\} \end{aligned}$$

where $f_{{C}}:{{\ddot{U}}}\longrightarrow [0,1],$ $g_{{C}}:{{\ddot{U}}}\longrightarrow {[0},1],$ and $h_{{C}}:{{\ddot{U}}}\longrightarrow {[0},$ 1],  respectively are known as the degrees of membership, neutral membership, and non-membership of each element of ${{\ddot{U}}}$ to the set C such that ${0\le }\left( {f}_{{C}}\left( {x} \right) \right) ^{3}+\left( {g}_{{C}}\left( {x} \right) \right) ^{3}+\left( {h}_{{C}}\left( {x} \right) \right) ^{3}{\le 1,}$ for all ${\varepsilon } \in {{\ddot{U}}}$.

For any ${\varepsilon }\in {{\ddot{U}}}$ and a CFS C,  $\pi _{C}({\varepsilon })=\sqrt[3]{1-\left( f_{{C}}\left( {\varepsilon }\right) \right) ^{3}-\left( g_{{C}}\left( {\varepsilon }\right) \right) ^{3}-\left( h_{{C}}\left( {\varepsilon }\right) \right) ^{3}}$ is known as the degree of refusal of x to C. For simplicity we shall use the symbol ${C} =\left( f_{{C}},g_{{C}},h_{{C}}\right)$ for the CFS $\left\{ \left\langle \left\langle {\varepsilon },f_{{C}}\left( {\varepsilon }\right) ,g_{{C}}\left( {\varepsilon }\right) ,h_{{C}}\left( {\varepsilon }\right) \right\rangle :{\varepsilon }\in {{\ddot{U}}}\right\rangle \right\}$ and call it a cubical fuzzy element (CFE).

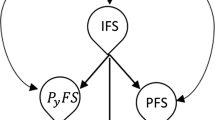
For a better understanding of the concept of a CFS, we give an illustration to accept the proposed notion. Suppose that a person is asked to give his preference degree to an alternative ${x}_{i}$ corresponding to a criterion $C_{j}.$ Let the person has allowed the degree to which the alternative ${x}_{i}$ satisfy the criterion $C_{j}$ as 0.8,  the degree when ${x}_{i}$ remains neutral in the criterion $C_{j}$ as 0.5 and similarly when ${x}_{i}$ dissatisfies $C_{j}$ as 0.6. Definitely, $0.8+0.5+0.6\nleq 1$, which does not follow the condition of PFSs. Also, $\left( 0.8\right) ^{2}+\left( 0.5\right) ^{2}+\left( 0.6\right) ^{2} =0.64+0.25+0.36=1.25\nleq 1,$ which does not obey the condition of SFS. But, we can have $\left( 0.8\right) ^{3}+\left( 0.5\right) ^{3}+\left( 0.6\right) ^{3}=0.512+0.125+0.216=0.853<1$ which is an appropriate reason to accept the notion of CFS. This is to mention that the CFSs have more potential to capture the uncertainties than picture fuzzy sets and spherıcal fuzzy sets, and are capable to deal with information involving high levels of fuzziness (Fig. 1).

Fig. 1

Range of the cubical fuzzy set

We shall mention here that the membership grades related to a CFS are cubical membership grades (CMGs).

Theorem 1

The space of CMGs is larger than the spaces of spherical membership grades (S MGs) and picture membership grades (PMGs).

Proof

For any three real numbers $a,b,c\in [0,$ 1], we get ${a}^{3}{\le a}^{2}{\le a},$ ${b}^{3}{\le b}^{2}{\le b,~}$and ${c}^{3}{\le c}^{2}{\le c}.$ Thus

$$\begin{aligned} {a+b+c\le 1\Longrightarrow a}^{2}{+b}^{2}{+c} ^{2}{\le 1\Longrightarrow a}^{3}{+b}^{3}{+c} ^{3}{\le 1}. \end{aligned}$$

Therefore ${\text {PMG}\subseteq \text {SMG}\subseteq \text {CMG}}.$ $\square$

There are CMGs that are neither PMGs nor SMGs. Consider a point $\left( \frac{\sqrt[3]{3}}{2},\frac{\sqrt[3]{2}}{2},\frac{\sqrt[3]{3}}{2}\right) ,$ we have $\left( \frac{\sqrt[3]{3}}{2}\right) ^{3}+\left( \frac{\sqrt[3]{2} }{2}\right) ^{3}+\left( \frac{\sqrt[3]{3}}{2}\right) ^{3}=1$ and it is a CMG. But $\left( \frac{\sqrt[3]{3}}{2}\right) ^{2}+\left( \frac{\sqrt[3]{2}}{2}\right) ^{2}+\left( \frac{\sqrt[3]{3}}{2}\right) ^{2} =0.3605+0.3149+0.3605=1.0359>1$ and $\frac{\sqrt[3]{3}}{2} +\frac{\sqrt[3]{2}}{2}+\frac{\sqrt[3]{3}}{2}=0.7212+0.6299+0.7212=2.0723> 1.$ Therefore $\left( \frac{\sqrt[3]{3}}{2}{,}\frac{\sqrt[3]{2}}{2}{,}\frac{\sqrt[3]{3}}{2}\right)$ is neither a PMG nor a SMG.

3 Set operations on cubical fuzzy sets

Definition 5

Let $C=\left( f_{{C}},g_{{C}},h_{{C}}\right) ,$ ${C}_{1}=\left( f_{{C}_{1}},g_{{C}_{1}},h_{{C} _{1}}\right) ,$ and ${C}_{2}=\left( f_{{C}_{2}},g_{{C} _{2}},h_{{C}_{2}}\right) ,$ be any three CFSs, then their set operations are defined as follows:

• (i) $C_{1}\cap C_{2}=\left( \min \left\{ f_{c_{1}},f_{c_{2}}\right\} ,\min \left\{ g_{c_{1}},g_{c_{2}}\right\} ,\max \left\{ h_{c_{1}},h_{c_{2}}\right\} \right) ,$

• (ii) $C_{1}\cup C_{2}=\left( \max \left\{ f_{c_{1}},f_{c_{2}}\right\} ,\min \left\{ g_{c_{1}},g_{c_{2}}\right\} ,\min \left\{ h_{c_{1}},h_{c_{2}}\right\} \right) ,$

• (iii) $C_{1}\subseteq C_{2}$ if and only if $f_{c_{1}}\le f_{c_{2}},$ $g_{c_{1}}\le g_{c_{2}}$ and $h_{c_{1}}\ge h_{c_{2}}$ $\left( iv\right)$ $C^{c}=\left( h_{c},g_{c},f_{c}\right)$.

Definition 6

Let $C=\left( f_{C},g_{C},h_{C}\right) ,$ $C_{1}=\left( f_{C_{1}},g_{C_{1} },h_{C_{1}}\right) ,$ and $C_{2}=\left( f_{C_{2}},g_{C_{2}},h_{C_{2} }\right) ,$ be any three CFSs, and $\lambda >0,$ then some operations are defined as follows:

• (i) $C_{1}\boxplus C_{2}=\left( \sqrt[3]{f_{C_{1}}^{3}+f_{C_{2}}^{3}-f_{C_{1}}^{3}f_{C_{2}}^{3}},g_{C_{1} }.g_{C_{2}},h_{C_{1}}.h_{C_{2}} \right)$

• (ii) $C_{1}\boxtimes C_{2}=\left( f_{C_{1}}.f_{C_{2}},g_{C_{1}}.g_{C_{2}} ,\sqrt[3]{h_{C_{1}}^{3}+h_{C_{2}}^{3}-h_{C_{1}}^{3}.h_{C_{2}}^{3}} \right)$

• (iii) $\lambda C=\left( \sqrt[3]{1-\left( 1-f_{C}^{3}\right) ^{\lambda }},g_{C}^{\lambda } ,h_{C}^{\lambda } \right)$

• (iv) $C^{\lambda }=\left( f_{C}^{\lambda },g_{C}^{\lambda },\sqrt[3]{1-\left( 1-h_{C} ^{3}\right) ^{\lambda }}\right) .$

Theorem 2

For three CFSs $C=\left( f_{C},g_{C},h_{C}\right) ,$ $C_{1}=\left( f_{C_{1}},g_{C_{1}},h_{C_{1}}\right) ,$ and $C_{2}=\left( f_{C_{2}} ,g_{C_{2}},h_{C_{2}}\right) ,$ the following properties are valid:

• (i) $C_{1}\boxplus C_{2}=C_{2}\boxplus C_{1}.$

• (ii) $C_{1}\boxtimes C_{2}=C_{2}\boxtimes C_{1}.$

• (iii) $\lambda \left( C_{1}\boxplus C_{2}\right) =\lambda C_{1}\boxplus \lambda C_{2},\lambda >0.$

• (iv) $\left( \lambda _{1}+\lambda _{2}\right) C$ $\mathcal {=}$ $\lambda _{1}C\boxplus \lambda _{2}C,$ $\lambda _{1},\lambda _{2}>0.$

• (v) $\left( C_{1}\boxtimes C_{2}\right) ^{\lambda } =C_{1}^{\lambda }\boxtimes C_{2}^{\lambda },$ $\lambda >0.$

• (vi) $C^{\lambda _{1}}\boxtimes C^{\lambda _{2}}=C^{\lambda _{1}+\lambda _{2}},$ $\lambda _{1},\lambda _{2}>0.$

Proof

(i) $C_{1}{\boxplus }C_{2}=\left( \sqrt[3]{{f}_{C_{1} }^{3}+{f}_{C_{2}}^{3}-{f}_{C_{1}}^{3}{f}_{C_{2}}^{3} },{g}_{C_{1}}.{g}_{C_{2}},{h}_{C_{1}}.{h}_{C_{2} }\right)$ $=\left( \sqrt[3]{f_{C_{2}}^{3}+f_{C_{1}}^{3} -{f}_{C_{2}}^{3}.{f}_{C_{1}}^{3}}{,g}_{C_{2}} {.g}_{C_{1}}{,h}_{C_{2}}.{h}_{C_{1}}\right) =C_{2}{\boxplus }C_{1}.$ (ii) $C_{1}\boxtimes C_{2}=\left( f_{C_{1}}.f_{C_{2}},g_{C_{1}}.g_{C_{2}},\sqrt[3]{{h}_{C_{1}} ^{3}{+h}_{C_{2}}^{3}{-h}_{C_{1}}^{3}{.h}_{C_{2}}^{3} }\right)$ $=\left( f_{C_{2}}.f_{C_{1}},g_{C_{2}}.g_{C_{1}} ,\sqrt[3]{{h}_{C_{2}}^{3}{+h}_{C_{1}}^{3}{-h}_{C_{2}} ^{3}{.h}_{C_{1}}^{3}}\right) =C_{2}\boxtimes C_{1}.$ (iii) $\lambda \left( C_{1}{\boxplus }C_{2}\right) =\lambda \left( \sqrt[3]{{f}_{C_{1}}^{3}{+f}_{C_{2}}^{3}{-f}_{C_{1}} ^{3}{f}_{C_{2}}^{3}}{,g}_{C_{1}}{.g}_{C_{2}} {,h}_{C_{1}}{.h}_{C_{2}}\right)$ $=\left( \sqrt[3]{{1-}\left( 1-{f}_{C_{1}}^{3}{-f}_{C_{2}} ^{3}{+f}_{C_{1}}^{3}{f}_{C_{2}}^{3}\right) ^{\lambda }},\left( {g}_{C_{1}}{.g}_{C_{2}}\right) ^{\lambda },\left( {h}_{C_{1}}{.h}_{C_{2}}\right) ^{\lambda }\right)$ $=\left( \sqrt[3]{{1-}\left( 1-f_{C_{1}}^{3}\right) ^{\lambda }\left( 1-f_{C_{2}}^{3}\right) ^{\lambda }},\left( g_{C_{1} }.g_{C_{2}}\right) ^{\lambda },\left( {h}_{C_{1}}{.h}_{C_{2} }\right) ^{\lambda }\right) ;$ $\lambda C_{1}{\boxplus }\lambda C_{2}=\left( \sqrt[3]{1-\left( {1-}f_{C_{1}}^{3}\right) ^{\lambda } },g_{C_{1}}^{\lambda },h_{C_{1}}^{\lambda }\right) {\boxplus }\left( \sqrt[3]{{1-}\left( 1-f_{C_{2}}^{3}\right) ^{\lambda }},g_{C_{2} }^{\lambda },h_{C_{2}}^{\lambda }\right)$ $=\left( \sqrt[3]{1-\left( 1-f_{C_{1}}^{3}\right) ^{\lambda }\left( 1-f_{C_{2}}^{3}\right) ^{\lambda } },{g}_{C_{1}}^{\lambda }{.g}_{C_{2}}^{\lambda }{,h}_{C_{1} }^{\lambda }{.h}_{C_{2}}^{\lambda }\right) =\lambda \left( C_{1}{\boxplus }C_{2}\right) .$ (iv) $\left( {\lambda }_{1}{+\lambda }_{2}\right) C\mathcal {=}\left( {\lambda } _{1}{+\lambda }_{2}\right) \left( f_{C},g_{C},h_{C}\right) =\left( \sqrt[3]{{1-}\left( {1-f}_{C}^{3}\right) ^{\lambda _{1} +\lambda _{2}}},g_{C}^{\lambda _{1}+\lambda _{2}},h_{C}^{\lambda _{1}+\lambda _{2} }\right)$ $=\left( \sqrt[3]{1-\left( 1-f_{C}^{3}\right) ^{\lambda _{1}}\left( 1-f_{C}^{3}\right) ^{\lambda _{2}}},g_{C}^{\lambda _{1}+\lambda _{2}},h_{C}^{\lambda _{1}+\lambda _{2}}\right)$ $=\left( \sqrt[3]{1-\left( 1-f_{C}^{3}\right) ^{\lambda _{1}}},g_{C}^{\lambda _{1} },h_{C}^{\lambda _{1}}\right) \boxplus \left( \sqrt[3]{1-\left( 1-f_{C} ^{3}\right) ^{\lambda _{2}}},g_{C}^{\lambda _{2}},h_{C}^{\lambda _{2}}\right) =\lambda _{1}C\boxplus \lambda _{2}C.$ (v) $\left( C_{1}\boxtimes C_{2}\right) ^{\lambda }=\left( f_{C_{1}}.f_{C_{2}},g_{C_{1}}.g_{C_{2} },\sqrt[3]{h_{C_{1}}^{3}+h_{C_{2}}^{3}-h_{C_{1}}^{3}.h_{C_{2}}^{3}}\right) ^{\lambda }$ $=\left( \left( f_{C_{1}}.f_{C_{2}}\right) ^{\lambda },\left( g_{C_{1}}.g_{C_{2}}\right) ^{\lambda },\sqrt[3]{1-\left( 1-h_{C_{1}}^{3}-h_{C_{2}}^{3}+h_{C_{1}}^{3}.h_{C_{2}}^{3}\right) ^{\lambda } }\right)$ $=\left( f_{C_{1}}^{\lambda }.f_{C_{2}}^{\lambda },g_{C_{1} }^{\lambda }.g_{C_{2}}^{\lambda },\sqrt[3]{1-\left( 1-h_{C_{1}}^{3}\right) ^{\lambda }\left( 1-h_{C_{2}}^{3}\right) ^{\lambda }}\right)$ $=\left( f_{C_{1}}^{\lambda },g_{C_{1}}^{\lambda },\sqrt[3]{1-\left( 1-h_{C_{1}}^{3}\right) ^{\lambda }}\right) \boxtimes \left( f_{C_{2} }^{\lambda },g_{C_{2}}^{\lambda },\sqrt[3]{1-\left( 1-h_{C_{2}}^{3}\right) ^{\lambda }}\right) =C_{1}^{\lambda }\boxtimes C_{2}^{\lambda }.$ (vi) $C^{\lambda _{1}}{\boxtimes }C^{\lambda _{2}}=\left( f_{C}^{\lambda _{1} },g_{C}^{\lambda _{1}},\sqrt[3]{1-\left( 1-h_{C}^{3}\right) ^{\lambda _{1}} }\right) \boxtimes \left( f_{C}^{\lambda _{2}},g_{C}^{\lambda _{2}} ,\sqrt[3]{1-\left( 1-h_{C}^{3}\right) ^{\lambda _{2}}}\right)$ $=\left( f_{C}^{\lambda _{1}+\lambda _{2}},g_{C}^{\lambda _{1} +\lambda _{2}},\sqrt[3]{1-\left( 1-h_{C}^{3}\right) ^{\lambda _{1}+\lambda _{2}}}\right) =C^{\left( \lambda _{1}+\lambda _{2}\right) }.$ $\square$

Theorem 3

For four CFSs $C=\left( f_{C},g_{C},h_{C}\right) ,$ $C_{1}=\left( f_{C_{1} },g_{C_{1}},h_{C_{1}}\right) ,$ $C_{2}=\left( f_{C_{2}},g_{C_{2}},h_{C_{2} }\right)$, and $C_{3}=\left( f_{C_{3}},g_{C_{3}},h_{C_{3}}\right) ,$ the following properties are valid: (i) $C_{1}{\cap } C_{2}{=}C_{2}{\cap }C_{1}.$ (ii) $C_{1}{\cup }C_{2}{=}C_{2}{\cup }C_{1}.$ (iii) $C_{1}{\cap }\left( C_{2}{\cap }C_{3}\right) {=}\left( C_{1}{\cap }C_{2}\right) {\cap }C_{3}.$ (iv) $C_{1}{\cup }\left( C_{2}{\cup }C_{3}\right) {=}\left( C_{1}{\cup } C_{2}\right) {\cup }C_{3}.$ (v) ${\lambda }\left( C_{1}{\cup }C_{2}\right) {=\lambda }C_{1}{\cup \lambda }C_{2}.$ (vi) $\left( C_{1}{\cup }C_{2}\right) ^{\lambda }{=}C_{1}^{\lambda }{\cup }C_{2}^{\lambda }.$

Proof

We shall only prove (i), (iii) and (v). Let $C=\left( {f} _{C}{,g}_{C}{,h}_{C}\right) ,$ $C_{1}=\left( {f} _{C_{1}}{,g}_{C_{1}}{,h}_{C_{1}}\right) ,$ $C_{2}=\left( {f}_{C_{2}}{,g}_{C_{2}}{,h}_{C_{2}}\right)$, and $C_{3}=\left( f_{C_{3}},g_{C_{3}},h_{C_{3}}\right) ,$ be four CFSs and $\lambda >0.$ By Definitions 5 and 6, we obtain (i) $C_{1}\cap C_{2}=\left( \min \left\{ f_{c_{1}},f_{c_{2}}\right\} ,\min \left\{ g_{c_{1}},g_{c_{2}}\right\} ,\max \left\{ h_{c_{1}},h_{c_{2} }\right\} \right)$ $=\left( \min \left\{ f_{c_{2}},f_{c_{1} }\right\} ,\min \left\{ g_{c_{2}},g_{c_{1}}\right\} ,\max \left\{ h_{c_{2} },h_{c_{1}}\right\} \right) =C_{2}{\cap }C_{1}.$ (ii) $C_{1}{\cap }\left( C_{2}{\cap }C_{3}\right) =\left( f_{C_{1}},g_{C_{1}},h_{C_{1}}\right) {\cap \min }\left( \left\{ f_{C_{2}},f_{C_{3}}\right\} ,\min \left\{ g_{C_{2}},g_{C_{3} }\right\} ,\max \left\{ h_{C_{2}},h_{C_{3}}\right\} \right)$ $=\min \left\{ f_{C_{1}},\min \left\{ f_{C_{2}},f_{C_{3}}\right\} \right\} ,\min \left\{ g_{C_{1}},\min \left\{ g_{C_{2}},g_{C_{3}}\right\} \right\} ,\max \left\{ h_{C_{1}},\max \left\{ h_{C_{2}},h_{C3}\right\} \right\}$ $=\left( \min \left\{ \min \left\{ f_{C_{1} },f_{C_{2}}\right\} ,f_{C_{3}}\right\} ,\min \left\{ \min \left\{ g_{C_{1} },g_{C_{2}}\right\} ,g_{C_{3}}\right\} ,\max \left\{ \max \left\{ h_{C_{1} },h_{C_{2}}\right\} ,h_{C_{3}}\right\} \right)$ $=\left( \min \left\{ f_{C_{1}},f_{C_{2}}\right\} ,\min \left\{ g_{C_{1}},g_{C_{2} }\right\} ,\max \left\{ h_{C_{1}},h_{C_{2}}\right\} \right) \cap \left( f_{C_{3}},g_{C_{3}},h_{C_{3}}\right) =\left( C_{1}{\cap }C_{2}\right) {\cap }C_{3}$ $\left( v\right)$ $\lambda \left( C_{1}\cup C_{2}\right) =\lambda \left( \max \left\{ f_{C_{1}},f_{C_{2}}\right\} ,\min \left\{ g_{C_{1}},g_{C_{2}}\right\} ,\min \left\{ h_{C_{1}},h_{C_{2} }\right\} \right)$ $=\left( \sqrt[3]{1-\left( 1-\max \left\{ f_{C_{1}}^{3},f_{C_{2}}^{3}\right\} \right) ^{\lambda }},\min \left\{ g_{C_{1}}^{\lambda },g_{C_{2}}^{\lambda }\right\} ,\min \left\{ h_{C_{1} }^{\lambda },h_{C_{2}}^{\lambda }\right\} \right) .$ $\lambda C_{1} \cup \lambda C_{2}=\left( \sqrt[3]{1-\left( 1-f_{C_{1}}^{3}\right) ^{\lambda }},g_{C_{1}}^{\lambda },h_{C_{1}}^{\lambda }\right) {\cup }\left( \sqrt[3]{1-\left( 1-f_{C_{2}}^{3}\right) ^{\lambda }},g_{C_{2} }^{\lambda },h_{C_{2}}^{\lambda }\right)$ $=\left( \max \left\{ \sqrt[3]{{1-}\left( {1-}f_{C_{1}}^{3}\right) ^{\lambda } },\sqrt[3]{1-\left( 1-f_{C_{2}}^{3}\right) ^{\lambda }}\right\} ,\min \left\{ g_{C_{1}}^{\lambda },g_{C_{2}}^{\lambda }\right\} ,\min \left\{ h_{C_{1}}^{\lambda },h_{C_{2}}^{\lambda }\right\} \right) =\lambda \left( C_{1}\cup C_{2}\right) .$ The remaining assertions can be proved analogously. $\square$

Theorem 4

For three CFSs, $C=\left( f_{C},g_{C},h_{C}\right) ,$ $C_{1}=\left( f_{C_{1}},g_{C_{1}},h_{C_{1}}\right) ,$ and $C_{2}=\left( f_{C_{2}} ,g_{C_{2}},h_{C_{2}}\right) ,$ the following properties are valid: $\left( i\right)$ $\left( C_{1}{\cap }C_{2}\right) ^{c}=C_{2} ^{c}{\cup }C_{1}^{c}.$ $\left( ii\right)$ $\left( C_{1}{\cup }C_{2}\right) ^{c}=C_{2}^{c}{\cap }C_{1}^{c}.$ $\left( iii\right)$ $\left( C_{1}{\boxplus }C_{2}\right) ^{c}=C_{1}^{c}{\boxtimes }C_{2}^{c}.$ $\left( iv\right)$ $\left( C_{1}{\boxtimes }C_{2}\right) ^{c}=C_{1}^{c}{\boxplus }C_{2}^{c}.$ $\left( v\right)$ $\left( C^{c}\right) ^{\lambda }=\left( \lambda C\right) ^{c}.$ $\left( vi\right)$ $\lambda \left( C^{c}\right) =\left( C^{\lambda }\right) ^{c}.$

Proof

We provĕ (i), (iii) and (v). For any three CFSs C,  $C_{1},$ and $C_{2}$ and $\lambda >{0},$ according to Definition 5 and Definition 6, we can obtain (i) $\left( C_{1}{\cap }C_{2}\right) ^{c}=\left( \min \left\{ f_{C_{1}},f_{C_{2}}\right\} ,\min \left\{ g_{C_{1} },g_{C_{2}}\right\} ,\max \left\{ h_{C_{1}},h_{C_{2}}\right\} \right) ^{c}$ $=\left( \max \left\{ h_{C_{1}},h_{C_{2}}\right\} ,\min \left\{ g_{C_{1}},g_{C_{2}}\right\} ,\min \left\{ f_{C_{1}},f_{C_{2}}\right\} \right)$ $=\left( h_{C_{1}},g_{C_{1}},f_{C_{1}}\right) \cup \left( h_{C_{2,}}g_{C_{2}},f_{C_{2}}\right) =C_{1}^{c}\cup C_{2}^{c}.$ (iii) $\left( C_{1}{\boxplus }C_{2}\right) ^{c}=\left( \sqrt[3]{f_{C_{1}}^{3}+f_{C_{2}}^{3}-f_{C_{1}}^{3}.f_{C_{2}}^{3} },g_{C_{1}}.g_{C_{2}},h_{C_{1}}.h_{C_{2}}\right) ^{c}$ $=\left( h_{C_{1}}.h_{C_{2}},g_{C_{1}}.g_{C_{2}},\sqrt[3]{f_{C_{1}}^{3}+f_{C_{2}} ^{3}-f_{C_{1}}^{3}.f_{C_{2}}^{3}}\right) =\left( h_{C_{1}},g_{C_{1} },f_{C_{1}}\right) {\boxtimes }\left( h_{C_{2}},g_{C_{2}},f_{C_{2} }\right) =C_{1}^{c}{\boxtimes }C_{2}^{c}.$ (v) $\left( C^{c}\right) ^{\lambda }=\left( h_{C},g_{C},f_{C}\right) ^{\lambda }=\left( h_{C}^{\lambda },g_{C}^{\lambda },\sqrt[3]{1-\left( 1-f_{C} ^{3}\right) ^{\lambda }}\right) =\left( \sqrt[3]{1-\left( 1-f_{C} ^{3}\right) ^{\lambda }},g_{C}^{\lambda },h_{C}^{\lambda }\right) ^{c}=\left( \lambda C\right) ^{c}.$ The remaining assertions can be proved analogously. $\square$

Theorem 5

For three CFSs $C=\left( f_{C},g_{C},h_{C}\right) ,$ $C_{1}=\left( f_{C_{1}},g_{C_{1}},h_{C_{1}}\right) ,$ and $C_{2}=\left( f_{C_{2}} ,g_{C_{2}},h_{C_{2}}\right) ,$ the following properties are valid. $\left( i\right)$ $\left( C_{1}{\cap }C_{2}\right) \boxplus C_{3}=\left( C_{1}\boxplus C_{3}\right) {\cap }\left( C_{2}\boxplus C_{3}\right) .$ $\left( ii\right)$ $\left( C_{1}{\cup } C_{2}\right) \boxplus C_{3}=\left( C_{1}\boxplus C_{3}\right) {\cup }\left( C_{2}\boxplus C_{3}\right) .$ $\left( iii\right)$ $\left( C_{1}{\cap }C_{2}\right) \boxtimes C_{3}=\left( C_{1}\boxtimes C_{3}\right) {\cap }\left( C_{2}\boxtimes C_{3}\right) .$ $\left( iv\right)$ $\left( C_{1}{\cup }C_{2}\right) \boxtimes C_{3}=\left( C_{1}\boxtimes C_{3}\right) {\cup }\left( C_{2}\boxtimes C_{3}\right) .$

Proof

We will present the proofs of (i) and (iii). For the three CFSs $C_{1},$ $C_{2},$ and $C_{3},$ according to Definitions 5 and 6, we obtain$\left( i\right)$ $\left( C_{1}\cap C_{2}\right) \boxplus C_{3}=\left( \min \left\{ f_{C_{1}},f_{C_{2}}\right\} ,\min \left\{ g_{C_{1}},g_{C_{2} }\right\} ,\max \left\{ h_{C_{1}},h_{C_{2}}\right\} \right) \boxplus \left( f_{C_{3}},g_{C_{3}},h_{C_{3}}\right)$ $=\left( \sqrt[3]{\min \left\{ f_{C_{1}}^{3},f_{C_{2}}^{3}\right\} +f_{C_{3}}^{3}-f_{C_{3}}^{3}.\min \left\{ f_{C_{1} }^{3},f_{C_{2}}^{3}\right\} },\min \left\{ g_{C_{1}},g_{C_{2}}\right\} .g_{C_{2}},\max \left\{ h_{C_{1}},h_{C_{2}}\right\} .h_{C_{3}}\right)$ $=\left( \sqrt[3]{\left( 1-f_{C_{3}}^{3}\right) \min \left\{ f_{C_{1}}^{3},f_{C_{2}}^{3}\right\} +f_{C_{3}}^{3}},\min \left\{ g_{C_{1} }.g_{C_{3}},g_{C_{2}}.g_{C_{3}}\right\} ,\max \left\{ h_{C_{1}}.h_{C_{3} },h_{C_{2}}.h_{C_{3}}\right\} \right) ;$ $\left( C_{1}\boxplus C_{3}\right) \cap \left( C_{2}\boxplus C_{3}\right) =\left( \sqrt[3]{f_{C_{1}}^{3}+f_{C_{3}}^{3}-f_{C_{1}}^{3}.f_{C_{3}}^{3}},g_{C_{1}}.g_{C_{3} },h_{C_{1}}.h_{C_{3}}\right) \cap$ $\left( \sqrt[3]{f_{C_{2}}^{3}+f_{C_{3}}^{3}-f_{C_{2}}^{3}.f_{C_{3}}^{3} },g_{C_{2}}.g_{C_{3}},h_{C_{2}}.h_{C_{3}}\right)$ $=\left( \begin{array}{c} \min \left\{ \sqrt[3] {f_{C_{1}}^{3}+f_{C_{3}}^{3}-f_{C_{1}}^{3}.f_{C_{3}}^{3} },\sqrt[3] {f_{C_{2}}^{3}+f_{C_{3}}^{3}-f_{C_{2}}^{3}.f_{C_{3}}^{3}}\right\} ,\min \left\{ g_{C_{1}}.g_{C_{3}},g_{C_{2}}.g_{C_{3}}\right\} ,\\ \max \left\{ h_{C_{1}}.h_{C_{3}},h_{C_{2}}.h_{C_{3}}\right\} \end{array} \right)$ $=\left( \begin{array}{c} \min \left\{ \sqrt[3]{\left( 1-f_{C_{3}}^{3}\right) f_{C_{1}}^{3}+f_{C_{3} }^{3}},\sqrt[3]{\left( 1-f_{C_{3}}^{3}\right) f_{C_{2}}^{3}+f_{C_{3}}^{3} }\right\} ,\min \left\{ g_{C_{1}}.g_{C_{3}},g_{C_{2}}.g_{C_{3}}\right\} ,\\ \max \left\{ h_{C_{1}}.h_{C_{3}},h_{C_{2}}.h_{C_{3}}\right\} \end{array} \right)$ $=\left( \sqrt[3]{\left( 1-f_{C_{3}}^{3}\right) \min \left\{ f_{C_{1}}^{3},f_{C_{2}}^{3}\right\} +f_{C_{3}}^{3}},\min \left\{ g_{C_{1}}.g_{C_{3}},g_{C_{2}}.g_{C_{3}}\right\} ,\max \left\{ h_{C_{1} }.h_{C_{3}},h_{C_{2}}.h_{C_{3}}\right\} \right) .$ So $\left( C_{1}{\cap }C_{2}\right) \boxplus C_{3}=\left( C_{1}\boxplus C_{3}\right) {\cap }\left( C_{2}\boxplus C_{3}\right) .$ (ii) $\left( C_{1}\cap C_{2}\right) \boxtimes C_{3}=\left( \min \left\{ f_{C_{1}},f_{C_{2}}\right\} ,min\left\{ g_{C_{1} },g_{C_{2}}\right\} ,\max \left\{ h_{C_{1}},h_{C_{2}}\right\} \right) \boxtimes \left( f_{C_{3}},g_{C_{3}},h_{C_{3}}\right)$ $=\left( \min \left\{ f_{C_{1}},f_{C_{2}}\right\} .f_{C_{3}},\min \left\{ g_{C_{1} },g_{C_{2}}\right\} .g_{C_{3}},\sqrt[3]{max\left\{ h_{C_{1}}^{3},h_{C_{2} }^{3}\right\} +h_{C_{3}}^{3}-h_{C_{3}}^{3}\max \left\{ h_{C_{1}}^{3} ,h_{C_{2}}^{3}\right\} }\right)$ $=\left( \min \left\{ f_{C_{1} }.f_{C_{3}},f_{C_{2}}.f_{C_{3}}\right\} ,\min \left\{ g_{C_{1}}.g_{C_{3} },g_{C_{2}}.g_{C_{3}}\right\} ,\sqrt[3]{\left( 1-h_{C_{3}}^{3}\right) \max \left\{ h_{C_{1}}^{3},h_{C_{2}}^{3}\right\} +h_{C_{3}}^{3}}\right) ;$ $\left( C_{1}\boxtimes C_{3}\right) \cap \left( C_{2}\boxtimes C_{3}\right) =\left( f_{C_{1}}.f_{C_{3}},g_{C_{1}}.g_{C_{3}},\sqrt[3]{h_{C_{1}}^{3}+h_{C_{3}}^{3}-h_{C_{1}}^{3},h_{C_{3}}^{3}}\right) \cap$

$\left( f_{C_{2}}.f_{C_{3}},g_{C2}.g_{C_{3}},\sqrt[3]{h_{C_{2}}^{3}+h_{C_{3} }^{3}-h_{C_{2}}^{3},h_{C_{3}}^{3}}\right)$ $=\left( \begin{array}{c} \min \left\{ f_{C_{1}}.f_{C_{3}},f_{C_{2}}.f_{C_{3}}\right\} ,\min \left\{ g_{C_{1}}.g_{C_{3}},g_{C2}.g_{C_{3}}\right\} ,\\ \max \left\{ \sqrt[3]{h_{C_{1}}^{3}+h_{C_{3}}^{3}-h_{C_{1}}^{3},h_{C_{3}}^{3} }, \sqrt[3]{h_{C_{2}}^{3}+h_{C_{3}}^{3}-h_{C_{2}}^{3},h_{C_{3}}^{3}}\right\} \end{array} \right)$ $=\left( \min \left\{ f_{C_{1}}.f_{C_{3}},f_{C_{2} }.f_{C_{3}}\right\} ,\min \left\{ g_{C_{1}}.g_{C_{3}},g_{C_{2}}.g_{C_{3} }\right\} ,\sqrt[3]{\left( 1-h_{C_{3}}^{3}\right) \max \left\{ h_{C_{1} }^{3},h_{C_{2}}^{3}\right\} +h_{C_{3}}^{3}}\right) .$ Thus $\left( C_{1}\cap C_{2}\right) \boxtimes C_{3}=\left( C_{1}\boxtimes C_{3}\right) \cap \left( C_{2}\boxtimes C_{3}\right) .$ Similarly, we can prove the other assertions. $\square$

In order to rank CFEs, we define score function of the CFEs.

Definition 7

Let $C=\left( f_{C},g_{C},h_{C}\right)$ be a CFE, then the score function of C can be defined as $sc\left( C\right) =f_{c} ^{3}-h_{c}^{3}\in [-1,1].$ In particular score $sc\left( C\right) =\left\{ \begin{array}{c} 1, if C=\left( 1,0,0\right) \\ -1, if C=\left( 0,0,1\right) \end{array} \right.$ In the Definitions 8 and 9, we define a new relation between cubical fuzzy elements.

Definition 8

Let $C_{1}=\left( f_{C_{1}},g_{C_{1}},h_{C_{1}}\right) ,$ and $C_{2}=\left( f_{C_{2}},g_{C_{2}},h_{C_{2}}\right)$ be any two CFEs and let score$\left( C_{1}\right)$ and score$\left( C_{2}\right)$ be the respective scores of $C_{1}$ and $C_{2},$ then (i) If $sc\left( C_{1}\right) <sc\left( C_{2}\right) ,$ then $C_{1}<C_{2}.$ (ii) If $sc\left( C_{1}\right) >sc\left( C_{2}\right) ,$ then $C_{1}>C_{2}$ Let $C_{1}=\left( 0.93,0.30,0.50\right)$ and $C_{2}=\left( 0.85,0.45,0.65\right)$ be any two CFSs, then by Definition 7, sc$\left( C_{1}\right) =\left( 0.93\right) ^{3}-\left( 0.50\right) ^{3}=0.6793$ and score$\left( C_{2}\right) =\left( 0.85\right) ^{3}-\left( 0.65\right) ^{3}=0.3395.$ Since sc$\left( C_{1}\right) >$ sc $\left( C_{2}\right) ,$ by Definition 8, we get $C_{1}>C_{2}.$ To provide a comparison of the family of CFEs,  the efficiency of the score function is accepted in this field. Sometimes it cannot be applied to have an appropriate decision in which a better CFE can be selected.

Let $C_{1}=\left( \frac{\sqrt[3]{4}}{2},\frac{1}{2},\frac{\sqrt[3]{4}}{2}\right)$ and $C_{2}=\left( 0.8,0.4,0.8\right)$, then score$\left( C_{1}\right) =$ score$\left( C_{2}\right) =0$ and hence final conclusion can not be drawn from the comparison of CFEs. To rectify this drawback, we define the accuracy function for CFEs.

Definition 9

Let $C=\left( f_{C},g_{C},h_{C}\right) ,$ be a CFE, then the accuracy function of C is defined as, acc$\left( C\right)$ $=f_{C}^{3}+h_{C}^{3}\in [0,1]$. We now give a complete criterion for the ranking of CFEs.

Definition 10

Let $C_{1}=\left( f_{C_{1}},g_{C_{1}},h_{C_{1}}\right) ,$ and $C_{2}=\left( f_{C_{2}},g_{C_{2}},h_{C_{2}}\right)$ be any two CFEs and let sc$\left( C_{i}\right)$ and acc$\left( C_{i}\right)$ $\left( i=1,2\right)$ be the respective scores and accuracies of $C_{1}$ and $C_{2},$ then (I) If $sc\left( C_{1}\right) <sc\left( C_{2}\right) ,$ then $C_{1}<C_{2}.$ (II) If $sc\left( C_{1}\right) >sc\left( C_{2}\right) ,$ then $C_{1}>C_{2}.$ (III) If $sc\left( C_{1}\right) =sc\left( C_{2}\right) ,$ then (i) If $acc\left( C_{1}\right) <acc\left( C_{2}\right) ,$ then $C_{1}<C_{2}.$ (ii) If $acc\left( C_{1}\right) >acc\left( C_{2}\right) ,$ then $C_{1}>C_{2}.$ (iii) If $acc\left( C_{1}\right) =acc\left( C_{2}\right) ,$ then $C_{1}\sim C_{2}.$

Definition 11

Let $C=\left( f_{C},g_{C},h_{C}\right) ,$ be a CFE, then the certainty function of C is defined as, cr$\left( C\right)$ $=f_{C}^{3}\in [0,1].$

Definition 12

Let $C_{1}=\left( f_{C_{1}},g_{C_{1}},h_{C_{1}}\right) ,$ and $C_{2}=\left( f_{C_{2}},g_{C_{2}},h_{C_{2}}\right)$ be any two CFEs and let sc$\left( C_{i}\right)$ and cr$\left( C_{i}\right)$ $\left( i=1,2\right)$ be the respective scores and certainties of $C_{1}$ and $C_{2},$ then (I) If $sc\left( C_{1}\right) <sc\left( C_{2}\right) ,$ then $C_{1}<C_{2}.$ (II) If $sc\left( C_{1}\right) >sc\left( C_{2}\right) ,$ then $C_{1}>C_{2}.$ (III) If $sc\left( C_{1}\right) =sc\left( C_{2}\right) ,$ then (i) If $cr\left( C_{1}\right) <cr\left( C_{2}\right) ,$ then $C_{1}<C_{2}.$ (ii) If $cr\left( C_{1}\right) >cr\left( C_{2}\right) ,$ then $C_{1}>C_{2}.$ (iii) If $cr\left( C_{1}\right) =cr\left( C_{2}\right) ,$ then $C_{1}\sim C_{2}.$

4 Comparison of proposed and existing operations

In this section, we compare the proposed operations of CFEs with the existing operations defined in Mahmood et al. (2019), for spherical fuzzy numbers (SFNs). In Mahmood et al. (2019), Mahmood et al., proposed the following operations for SFNs. Let ${\widetilde{S}}_{1}=\{ \mu _{S_{1}},\eta _{S_{1}},\upsilon _{S_{1}}\}$ and ${\widetilde{S}}_{2}=\{ \mu _{S_{2}},\eta _{S_{2}},\upsilon _{S_{2}}\}$ be two SFNs with $\xi >0$. Then,

• (1) ${\widetilde{S}}_{1}\otimes {\widetilde{S}}_{2}=\left\{ \left( \mu _{S_{1} }+\eta _{S_{1}}\right) \left( \mu _{S_{2}}+\eta _{S_{2}}\right) -\eta _{S_{1} }\eta _{S_{2}},\eta _{S_{1}}\eta _{S_{2}},\sqrt{1-\left( 1-\upsilon _{S_{1}} ^{2}\right) \left( 1-\upsilon _{S_{2}}^{2}\right) }\right\} ;$

• (2) ${\widetilde{S}}_{1}\oplus {\widetilde{S}}_{2}=\left\{ \sqrt{1-\left( 1-\mu _{S_{1}}^{2}\right) \left( 1-\mu _{S_{2}}^{2}\right) },\eta _{S_{1}} \eta _{S_{2}},\left( \upsilon _{S_{1}}+\eta _{S_{1}}\right) \left( \upsilon _{S_{2}}+\eta _{S_{2}}\right) -\eta _{S_{1}}\eta _{S_{2}}\right\} ;$

• (3) $\xi {\widetilde{S}}_{1}=\left\{ \sqrt{1-\left( 1-\mu _{S_{1}}^{2}\right) ^{\xi }},\eta _{S_{1}}^{\xi },\left( \upsilon _{S_{1}}+\eta _{S_{1}}\right) ^{\xi }-\eta _{S_{1}}^{\xi }\right\} ;$

• (4) ${\widetilde{S}}_{1}^{\xi }=\left\{ \left( \mu _{S_{1}}+\eta _{S_{1}}\right) ^{\xi }-\eta _{S_{1}}^{\xi },\eta _{S_{1}}^{\xi },\sqrt{1-\left( 1-\upsilon _{S_{1}}^{2}\right) ^{\xi }}\right\} .$ The above operation rules (1) and (2) for SFS, have some deficiencies, for example if we consider two SFSs, ${\widetilde{F}}_{1}=\{1,0,0\}$ and ${\widetilde{F}}_{2}=\{0.5,0.5,0.7\},$ then using (1), we have

$$\begin{aligned}&{\widetilde{S}}_{1}\otimes {\widetilde{S}}_{2} =\left\{ 1,0,0\right\} \otimes \{0.7,0.5,0.5\}\\&\quad =\left\{ \left( 1+0\right) \left( 0.7+0.5\right) -(0)(0.5),\sqrt{1-(1-0^{2})(1-0.5^{2})}\right\} \\&\quad =\left\{ 1.2,0.0,0.5\right\} . \end{aligned}$$

By constraint condition of SFS, we have $\mu _{S}^{2}+\eta _{S}^{2}+\upsilon _{S}^{2}=(1.2)^{2}+(0)^{2}+(0.5)^{2}=1.69\nleq 1,$ and the basic condition of SFS is not satisfied. Similarly, if we consider

$$\begin{aligned} {\widetilde{S}}_{1}\boxplus {\widetilde{S}}_{2}&=\left\{ 0,0,1\right\} \boxtimes \{0.7,0.5,0.5\} \\&=\left\{ \sqrt{1-(1-0^{2})(1-0.5^{2})},(0)(0.5),\left( 1+0\right) \left( 0.7+0.5\right) -(0)(0.5)\right\} \\&\quad =\left\{ 0.5,0.0,1.2\right\} . \end{aligned}$$

By basic condition of SFS, we get $\mu _{S}^{2}+\eta _{S}^{2}+\upsilon _{S} ^{2}=(0.5)^{2}+(0)^{2}+(1.2)^{2}=1.69\nleq 1,$ and the constraint condition of SFS is not satisfied. On the other hand, if we apply our proposed operations of multiplication and addition developed in section 4, for above two SFNs, we get

$$\begin{aligned} S_{1}\boxtimes S_{2}&=\left( \mu _{S_{1}}.\mu _{S_{2}},\eta _{S_{1}} .\eta _{S_{2}},\sqrt[3]{1-\left( 1-\upsilon _{S_{1}}^{3}\right) \left( 1-\upsilon _{S_{2}}^{3}\right) }\right) \\&=\left( (1)(0.7),(0)(0.5),\sqrt[3]{1-(1-(0)^{3})(1-(0.5)^{3}}\right) =\left( 0.7,0,0.5\right) \end{aligned}$$

By the condition of cubical fuzzy set, $\mu _{S}^{3}+\eta _{S}^{3}+\upsilon _{S}^{3}=\left( 0.7\right) ^{3}+(0)^{3}+\left( 0.5\right) ^{3} =0.343+0+0.125=0.468<1,$ and the condition of CFS is satisfied. Similarly,

$$\begin{aligned} S_{1}\boxplus S_{2}&=\left( \sqrt[3]{1-(1-\mu _{S_{1}}^{3})(1-\mu _{S_{2} }^{3})},\eta _{S_{1}}.\eta _{S_{2}},\upsilon _{S_{1}}.\upsilon _{S_{2}}\right) \\&=\left( \sqrt[3]{1-(1-0^{3})(1-0.5^{3})},(0)(0.5),(1)(0.7)\right) =\left( 0.5,0,0.7\right) \end{aligned}$$

By the condition of cubical fuzzy set, $\mu _{S}^{3}+\eta _{S}^{3}+\upsilon _{S}^{3}=\left( 0.5\right) ^{3}+(0)^{3}+\left( 0.7\right) ^{3} =0.125+0+0.343=0.468<1,$ and the condition of CFS is satisfied. It is concluded that the proposed operations of addition and multiplication of CFEs are better than the existing operation of spherical fuzzy sets.

5 Cubical fuzzy arithmetic aggregation operators

5.1 Cubical fuzzy weighted averaging operators

We are now in the position to define some arithmetic aggregation operators based on cubical fuzzy information, like cubical fuzzy weighted averaging (CFWA) operator, cubical fuzzy ordered weighted averaging (CFOWA) operator, and cubical fuzzy hybrid averaging (CFHA) operator.

Definition 13

Let $C_{\hat{\jmath }}=\left( {f}_{C_{\hat{\jmath }}}{,g} _{C_{\hat{\jmath }}}{,h}_{C\hat{\jmath }}\right)$ $\left( \hat{\jmath }={1,2,...,n}\right)$ be a family of cubical fuzzy elements (CFEs) and ${\omega }=\left( {\omega }_{1}{,\omega } _{2}{,...,\omega }_{n}\right) ^{T}$ be the weight vector of $C_{\hat{\jmath }}$ $\left( {\hat{\jmath }=1,2,...,n}\right)$ with ${\omega }_{\hat{\jmath }}{>0}$, ${\displaystyle \sum \limits _{_{\hat{\jmath }}=1}^{n}} {\omega }_{\hat{\jmath }}{=1}.$ Then the cubical fuzzy weighted average (CFWA) operator is a mapping $CFWA_{\omega }:C^{n}\longrightarrow C$ such that

$$\begin{aligned} CFWA_{\omega }\left( C_{1},C_{2},...,C_{n}\right) = {\displaystyle \bigoplus \limits _{_{\hat{\jmath }}=1}^{n}} \left( \omega _{_{\hat{\jmath }}}C_{_{\hat{\jmath }}}\right) \end{aligned}$$

(1)

Theorem 6

The aggregated value by CFWA operator is again a CFE and is given by,

$$\begin{aligned} CFWA_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) = {\displaystyle \bigoplus \limits _{j=1}^{n}} \left( \omega _{_{\hat{\jmath }}}C_{_{\hat{\jmath }}}\right) \end{aligned}$$

$$\begin{aligned} =\left( \sqrt[3]{{1-} {\displaystyle \prod \limits _{_{\hat{\jmath }}=1}^{n}} \left( 1-f_{{\mathcal {C}}_{_{\hat{\jmath }}}}^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{_{\hat{\jmath }}=1}^{n}} \left( g_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( h_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}\right) \end{aligned}$$

(2)

Proof

By mathematical induction on n, $\left( I\right)$ When $n=2$,

$$\begin{aligned} C{FWA}_{\omega }\left( C_{1}{,}C_{2}\right) ={\omega }_{1}C_{1}{\oplus \omega }_{2}C_{2}. \end{aligned}$$

By Theorem 2, we know that both ${\omega }_{1}C_{1}$ and ${\omega }_{2}C_{2}$ are CFEs and the value ${\omega }_{1}C_{1}{\oplus \omega }_{2}C_{2},$ is also a CFE. From the operational laws of CFEs, we have

$$\begin{aligned} {\omega }_{1}C_{1}&=\left( \sqrt[3]{1-\left( 1-f_{{\mathcal {C}}_{1} }^{3}\right) ^{\omega _{1}}}{,}\left( g_{{\mathcal {C}}_{1}}\right) ^{\omega _{1}}{,}\left( h_{{\mathcal {C}}_{1}}\right) ^{\omega _{1} }\right) ,\\ {\omega }_{2}C_{2}&=\left( \sqrt[3]{1-\left( 1-f_{{\mathcal {C}}_{2} }^{3}\right) ^{\omega _{2}}},\left( g_{{\mathcal {C}}_{2}}\right) ^{\omega _{2} },\left( h_{{\mathcal {C}}_{2}}\right) ^{\omega _{2}}\right) . \end{aligned}$$

Then

$$\begin{aligned} \text {CFWA}_{\omega }\left( C_{1}{,}C_{2}\right)&={\omega } _{1}C_{1}{\oplus \omega }_{2}C_{2}\\&=\left( \sqrt[3]{1-\left( 1-f_{{\mathcal {C}}_{1}}^{3}\right) ^{\omega _{1}}},\left( g_{{\mathcal {C}}_{1} }\right) ^{\omega _{1}},\left( h_{{\mathcal {C}}_{1}}\right) ^{\omega _{1} }\right) \oplus \left( \sqrt[3]{1-\left( 1-f_{{\mathcal {C}}_{2}}^{3}\right) ^{\omega _{2}} },\left( g_{{\mathcal {C}}_{2}}\right) ^{\omega _{2}},\left( h_{{\mathcal {C}} _{2}}\right) ^{\omega _{2}}\right) \\&=\left( \begin{array}{l} \sqrt[3]{ \begin{array}{l} {1-}\left( 1-f_{{\mathcal {C}}_{1}}^{3}\right) ^{\omega _{1}} {+1-}\left( 1-f_{{\mathcal {C}}_{2}}^{3}\right) ^{\omega _{2}} -\left( {1} -\left( 1-f_{{\mathcal {C}}_{1}}^{3}\right) ^{\omega _{1}}\right) .\left( 1-\left( 1-f_{{\mathcal {C}}_{2}}^{3}\right) ^{\omega _{2}}\right) \end{array} }, \left( g_{{\mathcal {C}}_{1}}\right) ^{\omega _{1}}{.}\left( g_{{\mathcal {C}}_{2}}\right) ^{\omega _{2}}{,} \left( h_{{\mathcal {C}}_{1} }\right) ^{\omega _{1}}{.}\left( h_{{\mathcal {C}}_{2}}\right) ^{\omega _{2}} \end{array} \right) \\&=\left( \begin{array}{l} \sqrt[3]{1-\left( 1-f_{{\mathcal {C}}_{1}}^{3}\right) ^{\omega _{1}}\left( 1-f_{{\mathcal {C}}_{2}}^{3}\right) ^{\omega _{2}}},\left( g_{{\mathcal {C}}_{1} }\right) ^{\omega _{1}}.\left( g_{{\mathcal {C}}_{2}}\right) ^{\omega _{2}}, \left( h_{{\mathcal {C}}_{1}}\right) ^{\omega _{1}}.\left( h_{{\mathcal {C}}_{2} }\right) ^{\omega _{2}} \end{array} \right) \\&=\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{2}} \left( 1-f_{{\mathcal {C}}_{j}}^{3}\right) ^{\omega _{j}}\left( 1-f_{{\mathcal {C}}_{j}}^{3}\right) ^{\omega j}}, {\displaystyle \prod \limits _{j=1}^{2}} \left( g_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{2}} \left( h_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}\right) . \end{aligned}$$

$\left( II\right)$ Assume that for $n=k$, Eq. (2) holds, i.e.,

$$\begin{aligned} \text {CFWA}_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{k}\right) = {\displaystyle \bigoplus \limits _{j=1}^{k}} \left( \omega _{j}{\mathcal {C}}_{j}\right) =\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{k}} \left( 1-f_{{\mathcal {C}}_{j}}^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{j=1}^{k}} \left( g_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{k}} \left( h_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}\ \right) \end{aligned}$$

And for ${n=k+1}$, by the operational laws of cubical fuzzy elements,

$$\begin{aligned} \text {CFWA}_{\omega }\left( C_{1}{,}C_{2}{,...,} C_{k+1}\right)&= {\displaystyle \bigoplus \limits _{j=1}^{k+1}} \left( {\omega }_{j}C_{j}\right) \\&={\omega }_{1}C_{1}{\oplus \omega }_{2}C_{2}{\oplus ,...,\oplus \omega }_{k}C_{k}{\oplus \omega }_{k+1}C_{k+1} \\&=\left( \begin{array}{l} \sqrt[3]{ \begin{array}{c} {1-} {\displaystyle \prod \limits _{j=1}^{k}} \left( 1-f_{{\mathcal {C}}_{j}}^{3}\right) ^{\omega _{j}}{+1-}\left( {1-f}_{{\mathcal {C}}_{j}}^{3}\right) ^{\omega _{k+1}}-\left( 1- {\displaystyle \prod \limits _{j=1}^{k}} \left( 1-f_{{\mathcal {C}}_{j}}^{3}\right) ^{\omega _{j}}\right) \left( 1-\left( 1-f_{{\mathcal {C}}_{j}}^{3}\right) ^{\omega _{k+1}}\right) \end{array} },\\ {\displaystyle \prod \limits _{j=1}^{k}} \left( g_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}.\left( g_{{\mathcal {C}} _{k+1}}\right) ^{\omega _{k+1}}, {\displaystyle \prod \limits _{j=1}^{k}} \left( h_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}.\left( h_{{\mathcal {C}} _{k+1}}\right) ^{\omega _{k+1}} \end{array} \right) \\&=\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{k+1}} \left( 1-f_{{\mathcal {C}}_{j}}^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{j=1}^{k+1}} \left( g_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{k+1}} \left( h_{{\mathcal {C}}_{j}}\right) ^{\omega _{j}}\right) , \end{aligned}$$

Therefore Eq. (2) holds for $n=k+1$, thus from (I) and (II), we conclude that Eq. (2) holds for all n. Following are some properties of the CFWA operator. $\square$

Theorem 7

(Idempotency) If for all $C_{j}\left( j=1,2,...,n\right)$, $C_{j}=C$, then

$$\begin{aligned} {CFWA}_{\omega }\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2},...,{\mathcal {C}} _{n}\right) ={\mathcal {C}}. \end{aligned}$$

Theorem 8

(Boundedness) Let $C_{j}{=}\left( {f}_{{\mathcal {C}}_{j} }{,g}_{{\mathcal {C}}_{j}}{,h}_{{\mathcal {C}}_{j}}\right)$ $\left( \hat{\jmath }=1,2,...,n\right)$ be a family of cubical fuzzy elements (CFEs) and $C^{-}=$min$_{1\le j\le n}\left\{ C_{j}\right\} ,$$C^{+} =$max$_{{1\le j\le n}}\left\{ C_{j}\right\} .$ Then,

$$\begin{aligned} C^{-}{\le }C{FWA}_{\omega }\left( C_{1}{,}C_{2} {,...,}C_{n}\right) \le C^{+}. \end{aligned}$$

Theorem 9

(Monotonicıty) Let $C_{j}$ $\left( {j=1,2,...,n}\right)$ and $C_{j}^{^{\prime }}$ $\left( \hat{\jmath }=1,2,...,n\right)$ be two set of CFEs. If ${\mathcal {C}}_{j}\le {\mathcal {C}}_{j}^{^{\prime }}$ $\forall$ j, then

$$\begin{aligned} CFWA_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) {\le }CFWA_{\omega }\left( C_{1}^{^{\prime }}{,}C_{2}^{^{\prime } }{,...,}C_{n}^{^{\prime }}\right) . \end{aligned}$$

5.2 Cubical fuzzy ordered weighted averaging operator

Next, we define Cubical fuzzy ordered weighted averaging (CFOWA) operator.

Definition 14

Let $C_{j}=\left( {f}_{{\mathcal {C}}_{j}}{,g}_{{\mathcal {C}}_{j} }{,h}_{{\mathcal {C}}_{j}}\right)$ $\left( j={1,2,...,n}\right)$ be a family of cubical fuzzy elements (CFEs). Then the CFOWA operator of dimension n is a mapping $\text {CFOWA}_{\omega }:C^{n}{\longrightarrow }C$ defined by,

$$\begin{aligned} \text {CFOWA}_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) = {\displaystyle \bigoplus \limits _{j=1}^{n}} \left( \omega _{j}C_{\sigma \left( j\right) }\right) \end{aligned}$$

(3)

such that, ($\left( {\sigma }\left( 1\right) {,\sigma }\left( 2\right) {,\sigma }\left( 3\right) {,...,\sigma }\left( n\right) \right)$ is a permutation of $\left( {1,2,...,n}\right)$ with $C_{\sigma \left( j-1\right) }{\ge }C_{\sigma \left( j\right) }$ $\forall$ $j=\left( 2,...,n\right) .$

Theorem 10

The aggregated value by the CFOWA operator is again a CFE, where

$$\begin{aligned}&CFWA_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) = {\displaystyle \bigoplus \limits _{j=1}^{n}} \left( \omega _{j}{\mathcal {C}}_{\sigma \left( j\right) }\right) \nonumber \\&\quad =\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{n}} \left( 1-f_{{\mathcal {C}}_{\sigma \left( j\right) }}^{3}\right) ^{\omega _{j} }}{,} {\displaystyle \prod \limits _{j=1}^{n}} \left( g_{{\mathcal {C}}_{\sigma \left( j\right) }}\right) ^{\omega _{j} }{,} {\displaystyle \prod \limits _{j=1}^{n}} \left( h_{{\mathcal {C}}_{\sigma \left( j\right) }}\right) ^{\omega _{j} }\right) . \end{aligned}$$

(4)

It can be easily verified that the CFOWA operator satisfies all the properties discussed for the CFWA operator. i.e.,

Theorem 11

(Idempotency) If all $C_{\hat{\jmath }}$ $\left( {j=1,2,...,n}\right)$ are equal i.e., if $C_{j}{=}C$ for all j, then

$$\begin{aligned} C{FOWA}_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) {=}C. \end{aligned}$$

Theorem 12

(Boundedness) Let $C_{j}{=}\left( {f}_{{\mathcal {C}}_{j} }{,g}_{{\mathcal {C}}_{j}}{,h}_{{\mathcal {C}}_{j}}\right)$ $\left( {j=1,2,...,n}\right)$ be a family of cubical CFEs and $C^{-}=$ min$_{1\le j\le n}\left\{ C_{j}\right\} ,$$C^{+}{=}$ max$_{1\le j\le n}\left\{ {\mathcal {C}}_{j}\right\} .$ Then,

$$\begin{aligned} C^{-}{\le }C{FOWA}_{\omega }\left( C_{1}{,} C_{2}{,...,}C_{n}\right) {\le }C^{+}. \end{aligned}$$

Theorem 13

(Monotonicıty) Let $C_{j}$ and $C_{j}^{^{\prime }}$ where ${j=1,2,...,n,}$ be two sets of CFEs. If $C_{j}{\le } C_{j}^{^{\prime }}$ $\forall$ j, then

$$\begin{aligned} CFOWA_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) \le CFWA_{\omega }\left( C_{1}^{^{\prime }}{,}C_{2}^{^{\prime } }{,...,}C_{n}^{^{\prime }}\right) . \end{aligned}$$

5.3 Cubical fuzzy hybrid averaging operator

From Definitions 13 and 14, it is clear that the CFWA operator only weights the cubical fuzzy elements, whereas the CFOWA operator weights the ordered positions of the CFEs instead of weighting the arguments themselves. Hence, in both CFWA and CFOWA operators, the weights represent two different aspects. But each of them considers only one aspect. In the following definition, we shall propose the cubical fuzzy hybrid averaging operator.

Definition 15

A cubical fuzzy hybrid averaging (CFHA) operator is a mapping $\text {CFHA}_{w,\omega }:C^{n}{\longrightarrow }C$ defined as,

$$\begin{aligned} \text {CFHA}_{w,\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) = {\displaystyle \bigoplus \limits _{j=1}^{n}} \left( w_{j}{\widetilde{C}}_{\sigma \left( j\right) }\right) \end{aligned}$$

(5)

such that ${w}=\left( {w}_{1}{,w}_{2}{,...,w} _{n}\right) ^{T}$ is an associated weighting vector, with $w_{j}\in [0,$ 1], ${\displaystyle \sum \limits _{j=1}^{n}} {w}_{j}=1$, and $\widetilde{{\mathcal {C}}}_{\sigma \left( j\right) }$ is the j-th largest element of the cubical fuzzy elements $\widetilde{{\mathcal {C}}}_{j}$ $\left( \widetilde{{\mathcal {C}}}_{j}{=}\left( {n\omega }_{j}\right) C_{j},\text { }j=1,2,...,n\right) ,$ $\omega =\left( {\omega }_{1}{,\omega }_{2}{,...,\omega }_{n}\right) ^{T}$ is the weighting vector of the cubical fuzzy arguments $C_{j}$ $\left( {j=1,2,...,n}\right)$ and ${\omega } _{j}{\in }\left[ 0,\text { }1\right] ,$ ${\displaystyle \sum \limits _{\hat{\jmath }=1}^{n}} {\omega }_{j}{=1,}$ where n is a blanching coefficient. If ${w=}\left( {1/n,1/n,...,1/n}\right) ^{T}$ then CFHA is reduced to cubical fuzzy weighted average CFWA operator. Also, if ${\omega =}\left( {1/n,1/n,...,1/n}\right) ^{T}$ then CFHA is reduced to cubical fuzzy ordered weighted average (CFOWA) operator.

Theorem 14

The aggregated value by using the CFHA operator is also a CFE, where

$$\begin{aligned}&CFWA_{w,\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) = {\displaystyle \bigoplus \limits _{j=1}^{n}} \left( w_{j}{\widetilde{C}}_{\sigma \left( j\right) }\right) \nonumber \\&\quad =\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{n}} \left( 1-f_{{\widetilde{C}}_{\sigma \left( j\right) }}^{3}\right) ^{w_{j}}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( g_{{\widetilde{C}}_{\sigma \left( j\right) }}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( h_{{\widetilde{C}}_{\sigma \left( j\right) }}\right) ^{w_{j}}\right) . \end{aligned}$$

(6)

6 Cubical fuzzy geometric aggregation operators

Here, we present some geometric aggregation operators in the environment of CFS, like cubical fuzzy weighted geometric (CFWG) operator, cubical fuzzy ordered weighted geometric (CFOWG) operator, and cubical fuzzy hybrid geometric (CFHG) operator.

6.1 Cubical fuzzy weighted geometric operator

Definition 16

Let $C_{j}{=}\left( {f}_{{\mathcal {C}}_{j}}{,g} _{{\mathcal {C}}_{j}}{,h}_{{\mathcal {C}}_{j}}\right)$ $\left( {j=1,2,...,n}\right)$ be a family CFEs. Then the cubical fuzzy weighted geometric ( CFWA) operator is a mapping $CFWG_{\omega }:C^{n}{\longrightarrow }C$ defined as,

$$\begin{aligned} \text {CFWG}_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) = {\displaystyle \bigotimes \limits _{j=1}^{n}} \left( C_{j}\right) ^{\omega _{j}} \end{aligned}$$

(7)

where $\omega =\left( {\omega }_{1}{,\omega }_{2} {,...,\omega }_{n}\right) ^{T}$ be the weight vector of $C_{j}$ $\left( {j=1,2,...,n}\right) ,$ and $\omega _{j}>0$, ${\displaystyle \sum \limits _{j=1}^{n}} {\omega }_{j}=1.$

Theorem 15

The aggregated value by using the CFWG operator is also a CFE and

$$\begin{aligned}&CFWG_{w}\left( C_{1},C_{2},...,C_{n}\right) = {\displaystyle \bigotimes \limits _{j=1}^{n}} \left( C_{j}\right) ^{w_{j}}\nonumber \\&\quad =\left( {\displaystyle \prod \limits _{j=1}^{n}} \left( f_{c_{j}}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( g_{c_{j}}\right) ^{w_{j}},\sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{n}} \left( 1-h_{c_{j}}^{3}\right) ^{w_{j}}}\right) . \end{aligned}$$

(8)

Proof

We use mathematical induction to prove the result. (I) When n=2, we have $CFWG_{w}\left( C_{1},C_{2}\right) =\left( C_{1}\right) ^{w_{1}}\otimes \left( C_{2}\right) ^{w_{2}}$ By theorem 2, we know that both $\left( C_{1}\right) ^{w_{1}}$ and $\left( C_{2}\right) ^{w_{2}}$ are CFEs and so $\left( C_{1}\right) ^{w_{1}} \otimes \left( C_{2}\right) ^{w_{2}}$ is also a CFE. From the operational laws of CFEs we have,

$$\begin{aligned} \left( C_{1}\right) ^{w_{1}}&=\left( \left( f_{c_{1}}\right) ^{w_{1} },\left( g_{c_{1}}\right) ^{w_{1}},\sqrt[3]{1-\left( 1-h_{c_{1}} ^{3}\right) ^{w_{1}}}\right) ;\\ \left( C_{2}\right) ^{w_{2}}&=\left( \left( f_{c_{2}}\right) ^{w_{2} },\left( g_{c_{2}}\right) ^{w_{2}},\sqrt[3]{1-\left( 1-h_{c_{2}} ^{3}\right) ^{w_{2}}}\right) , \end{aligned}$$

then

$$\begin{aligned}&CFWG_{w}\left( C_{1},C_{2}\right) =\left( C_{1}\right) ^{w_{1}} \otimes \left( C_{2}\right) ^{w_{2}} \\&\quad =\left( \begin{array}{c} \left( f_{c_{1}}\right) ^{w_{1}}.\left( f_{c_{2}}\right) ^{w_{2}},\left( g_{c_{1}}\right) ^{w_{1}}.\left( g_{c_{2}}\right) ^{w_{2}},\\ \sqrt[3]{1-\left( 1-h_{c_{1}}^{3}\right) ^{w_{1}}+1-\left( 1-h_{c_{2}} ^{3}\right) ^{w_{2}}-\left( 1-\left( 1-h_{c_{1}}^{3}\right) ^{w_{1} }\right) \left( 1-\left( 1-h_{c_{2}}^{3}\right) ^{w_{2}}\right) } \end{array} \right) \\&\quad =\left( \left( f_{c_{1}}\right) ^{w_{1}}.\left( f_{c_{2}}\right) ^{w_{2} },\left( g_{c_{1}}\right) ^{w_{1}}.\left( g_{c_{2}}\right) ^{w_{2} },\sqrt[3]{1-\left( 1-h_{c_{1}}^{3}\right) ^{w_{1}}\left( 1-h_{c_{2}} ^{3}\right) ^{w_{2}}}\right) \\&\quad =\left( {\displaystyle \prod \limits _{j=1}^{2}} \left( f_{c_{j}}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{2}} \left( g_{c_{j}}\right) ^{w_{j}},\sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{2}} \left( 1-h_{c_{j}}^{3}\right) ^{w_{j}}}\right) \end{aligned}$$

(II) Suppose that for $n=k$ Eq. 8 holds, i.e.,

$$\begin{aligned}&CFWG_{w}\left( C_{1},C_{2},...,C_{k}\right) = {\displaystyle \bigotimes \limits _{j=1}^{k}} \left( C_{j}\right) ^{w_{j}} \\&\quad =\left( {\displaystyle \prod \limits _{j=1}^{k}} \left( f_{c_{j}}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{k}} \left( g_{c_{j}}\right) ^{w_{j}},\sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{k}} \left( 1-h_{c_{j}}^{3}\right) ^{w_{j}}}\right) \end{aligned}$$

Then for $n=k+1$ by the operational laws of CFEs,

$$\begin{aligned}&CFWG_{w}\left( C_{1},C_{2},...,C_{k+1}\right) = {\displaystyle \bigotimes \limits _{j=1}^{k+1}} \left( C_{j}\right) ^{w_{j}}=\left( {\displaystyle \bigotimes \limits _{j=1}^{k}} \left( C_{j}\right) ^{w_{j}}\right) \otimes \left( C_{k+1}\right) ^{w_{k+1}}\\&\quad \left( {\displaystyle \prod \limits _{j=1}^{k}} \left( f_{c_{j}}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{k}} \left( g_{c_{j}}\right) ^{w_{j}},\sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{k}} \left( 1-h_{c_{j}}^{3}\right) ^{w_{j}}}\right) \otimes \\&\quad \left( \left( f_{c_{k+1}}\right) ^{w_{k+1}},\left( g_{c_{k+1}}\right) ^{w_{k+1}},\sqrt[3]{1-\left( 1-h_{c_{k+1}}^{3}\right) ^{w_{k+1}}}\right) \\&\quad \left( \begin{array}{c} {\displaystyle \prod \limits _{j=1}^{k}} \left( f_{c_{j}}\right) ^{w_{j}}.\left( f_{c_{k+1}}\right) ^{w_{k+1}}, {\displaystyle \prod \limits _{j=1}^{k}} \left( g_{c_{j}}\right) ^{w_{j}}.\left( g_{c_{k+1}}\right) ^{w_{k+1}},\\ \sqrt[3]{ \begin{array}{c} 1- {\displaystyle \prod \limits _{j=1}^{k}} \left( 1-h_{c_{j}}^{3}\right) ^{w_{j}}+1-\left( 1-h_{c_{k+1}}^{3}\right) ^{w_{k+1}}-\\ \left( 1- {\displaystyle \prod \limits _{j=1}^{k}} \left( 1-h_{c_{j}}^{3}\right) ^{w_{j}}\right) \left( 1-\left( 1-h_{c_{k+1}}^{3}\right) ^{w_{k+1}}\right) \end{array} } \end{array} \right) \\&\quad \left( \begin{array}{c} {\displaystyle \prod \limits _{j=1}^{k}} \left( f_{c_{j}}\right) ^{w_{j}}.\left( f_{c_{k+1}}\right) ^{w_{k+1}}, {\displaystyle \prod \limits _{j=1}^{k}} \left( g_{c_{j}}\right) ^{w_{j}}.\left( g_{c_{k+1}}\right) ^{w_{k+1}},\\ \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{k}} \left( 1-h_{c_{j}}^{3}\right) ^{w_{j}}.\left( 1-h_{c_{k+1}}^{3}\right) ^{w_{k+1}}} \end{array} \right) \\&\quad \left( {\displaystyle \prod \limits _{j=1}^{k+1}} \left( f_{c_{j}}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{k+1}} \left( g_{c_{j}}\right) ^{w_{j}},\sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{k+1}} \left( 1-h_{c_{j}}^{3}\right) ^{w_{j}}}\right) \end{aligned}$$

Thus Eq. 8 holds for $n=k+1.$ Therefore, from $\left( I\right)$ and $\left( II\right)$ we conclude that Eq. 8 holds for all n. $\square$

The following properties of the CFWG operator can easily be proved.

Theorem 16

$\left( \text {Idempotency}\right)$ If all ${\mathcal {C}}_{j}$ $\left( j=1,2,...,n\right)$ are equal i.e., ${\mathcal {C}}_{j}={\mathcal {C}}$ $\forall$ j, then

$$\begin{aligned} CFWG_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) =C. \end{aligned}$$

Theorem 17

$\left( \text {Boundedness}\right)$ Let ${\mathcal {C}}_{j}=\left( {f}_{{\mathcal {C}}_{j}}{,g}_{{\mathcal {C}}_{j}}{,h} _{{\mathcal {C}}_{j}}\right)$ $\left( {j=1,2,...,n}\right)$ be a family of CFEs and let

$$\begin{aligned} {\mathcal {C}}^{-}=\text {min}_{1\le j\le n}\left\{ C_{j}\right\} ,{\mathcal {C}}^{+}=\text {max}_{1\le j\le n}\left\{ {\mathcal {C}} _{j}\right\} \end{aligned}$$

Then

$$\begin{aligned} C^{-}{\le }C{FWG}_{\omega }\left( C_{1}{,}C_{2} {,...,}C_{n}\right) {\le }C^{+}. \end{aligned}$$

Theorem 18

$\left( \text {Monotonicity}\right)$ Let $C_{j}$ $\left( {j=1,2,...,n}\right)$ and ${\mathcal {C}}_{j}^{^{\prime }}$ $\left( {j=1,2,...,n}\right)$ be two set of CFEs. If $C_{j}{\le }C_{j}^{^{\prime }}$ $\forall$ j, then

$$\begin{aligned} CFWG_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) \le CFWG_{\omega }\left( C_{1}^{^{\prime }}{,}C_{2}^{^{\prime } }{,...,}C_{n}^{^{\prime }}\right) . \end{aligned}$$

6.2 Cubical fuzzy ordered weighted geometric operator

Definition 17

Let $C_{j}=\left( {f}_{{\mathcal {C}}_{j}}{,g}_{{\mathcal {C}}_{j} }{,h}_{{\mathcal {C}}_{j}}\right)$ $\left( {j=1,2,...,n}\right)$ be a family of CFEs. The cubical fuzzy ordered weighted geometric (CFOWG) operator of dimension n is a mapping $\text {CFOWG}_{\omega }:{\mathcal {C}}^{n}\longrightarrow {\mathcal {C}}$ given by,

$$\begin{aligned} \text {CFOWG}_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) = {\displaystyle \bigotimes \limits _{j=1}^{n}} \left( C_{\sigma \left( j\right) }\right) ^{\omega _{j}} \end{aligned}$$

(9)

such that $\left( {\sigma }\left( 1\right) {,\sigma }\left( 2\right) {,\sigma }\left( 3\right) {,...,\sigma }\left( n\right) \right)$ is a permutation of $\left( 1,2,...,n\right)$ where ${\mathcal {C}}_{\sigma \left( j-1\right) }\ge {\mathcal {C}}_{\sigma \left( j\right) }$ $\forall$ ${j=2,...,n}$.

Theorem 19

The aggregated value by using the CFOWG operator is also a CFE and

$$\begin{aligned}&CFOWG_{w}\left( C_{1},C_{2},...,C_{n}\right) = {\displaystyle \bigotimes \limits _{j=1}^{n}} \left( C_{\sigma \left( j\right) }\right) ^{w_{j}} \nonumber \\&\quad =\left( {\displaystyle \prod \limits _{j=1}^{n}} \left( f_{c_{\sigma \left( j\right) }}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( g_{c_{\sigma \left( j\right) }}\right) ^{w_{j}},\sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{n}} \left( 1-h_{c_{\sigma \left( j\right) }}^{3}\right) ^{w_{j}}}\right) . \end{aligned}$$

(10)

Theorem 20

(Idempotency) If all $C_{j}$ $\left( {j=1,2,...,n}\right)$ are equal i.e., if $C_{j}=C$ $\ \forall$ j, then

$$\begin{aligned} CFWOG_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) ={\mathcal {C}}. \end{aligned}$$

Theorem 21

(Boundedness) Let ${\mathcal {C}}_{j}=\left( {f}_{{\mathcal {C}}_{j} }{,g}_{{\mathcal {C}}_{j}}{,h}_{{\mathcal {C}}_{j}}\right)$ $\left( {j=1,2,...,n}\right)$ be a family of CFEs and let

$$\begin{aligned} C^{-}={min}_{{1\le j\le n}}\left\{ C_{j}\right\} ,C^{+}={max}_{{1\le j\le n}}\left\{ C_{j}\right\} . \end{aligned}$$

Then

$$\begin{aligned} C^{-}\le C{FOWG}_{\omega }\left( C_{1}{,}C_{2}{,...,} C_{n}\right) {\le }C^{+}. \end{aligned}$$

Theorem 22

(Monotonicıty) Let $C_{j}$ $\left( {j=1,2,...,n}\right)$ and $C_{j}^{^{\prime }}$ $\left( {j=1,2,...,n}\right)$ be two set of C FEs, if $C_{j}{\le }C_{j}^{^{\prime }}$, $\forall$ j, then

$$\begin{aligned} C{FOWG}_{\omega }\left( C_{1}{,}C_{2}{,...,}C_{n}\right) {\le }C{FOWG}_{\omega }\left( C_{1}^{^{\prime }}{,} C_{2}^{^{\prime }}{,...,}C_{n}^{^{\prime }}\right) . \end{aligned}$$

6.3 Cubical fuzzy hybrid geometric operator

From Definitions 16 and 17, we note that the CFWG operator only weighs the CFEs themselves whereas the CFOWG operator weighs the ordered positions of the CFEs instead of weighting their arguments. This means that in each case the weight represents two different aspects in CFWG and CFOWG operators. But both operators take only one of them. To resolve this problem, we now introduce the cubical fuzzy hybrid geometric (CFHG) operator.

Definition 18

A cubical fuzzy hybrid geometric (CFHG) operator is a mapping $\text {CFHG}_{w,\omega }:C^{n}{\longrightarrow }C$, such that

$$\begin{aligned} \text {CFHG}_{w,\omega }\left( C_{1}{,}C_{2}{,...,} C_{n}\right) = {\displaystyle \bigotimes \limits _{j=1}^{n}} \left( {\widetilde{C}}_{\sigma \left( j\right) }\right) ^{w_{j}} \end{aligned}$$

(11)

where $w=\left( w_{1},w_{2},..,w_{n}\right) ^{T}$ is the associated weighting vector, with $w_{j}\in [0,$ 1], ${\displaystyle \sum \limits _{j=1}^{n}} w_{j}=1$, and $\widetilde{{\mathcal {C}}}_{\sigma \left( j\right) }$ is the j-th largest element of the cubical fuzzy arguments $\widetilde{{\mathcal {C}}}_{j}$ $\left( {\widetilde{C}}_{j}=\left( C_{j}\right) ^{n\omega _{j}},\text { }{j=1,2,...,n}\right) ,$ $\omega =\left( {\omega } _{1}{,\omega }_{2}{,...,\omega }_{n}\right) ^{T}$ is the weighting vector of cubical fuzzy arguments $C_{j},$ $\left( {j=1,2,...,n}\right) ,$ and $\omega _{j}\in \left[ 0,\text { }1\right] ,$ ${\displaystyle \sum \limits _{j=1}^{n}} \omega _{j}=1$, and n is the blanching coefficient. If $w=\left( {1/n,1/n,...,1/n}\right) ^{T}$ then CFHG is reduced to CFWG operator; if $\omega =\left( {1/n,1/n,...,1/n}\right) ^{T}$ then CFHG is reduced to CFOWG operator.

Theorem 23

The aggregated value by using the CFHG operator is also a CFE and

$$\begin{aligned}&CFHG_{w}\left( C_{1},C_{2},...,C_{n}\right) = {\displaystyle \bigotimes \limits _{j=1}^{n}} \left( {\widetilde{C}}_{\sigma \left( j\right) }\right) ^{w_{j}}\nonumber \\&\quad =\left( {\displaystyle \prod \limits _{j=1}^{n}} \left( f_{{\widetilde{c}}_{\sigma \left( j\right) }}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( g_{{\widetilde{c}}_{\sigma \left( j\right) }}\right) ^{w_{j}} ,\sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{n}} \left( 1-h_{{\widetilde{c}}_{\sigma \left( j\right) }}^{3}\right) ^{w_{j}} }\right) . \end{aligned}$$

(12)

7 Distance between cubical fuzzy sets and models for multiple attribute decision making with cubical fuzzy information

7.1 Distance between cubical fuzzy sets

Definition 19

Let ${\mathcal {C}}_{1}=\left( {f}_{{\mathcal {C}}_{1}}{,g} _{{\mathcal {C}}_{1}}{,h}_{{\mathcal {C}}_{1}}\right) ,$ and ${\mathcal {C}} _{2}=\left( {f}_{{\mathcal {C}}_{2}}{,g}_{{\mathcal {C}}_{2} }{,h}_{{\mathcal {C}}_{2}}\right)$ be any two CFSs. Then the distance between ${\mathcal {C}}_{1}$ and ${\mathcal {C}}_{2}$, denoted by $d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2}\right)$ is defined by

$$\begin{aligned} d\left( C_{1}{,}C_{2}\right) =\sqrt[3]{\frac{1}{2}\left[ \left( {f}_{{\mathcal {C}}_{1}}^{3}{-f}_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( {g}_{{\mathcal {C}}_{1}}^{3}{-g}_{{\mathcal {C}}_{2}} ^{3}\right) ^{2}+\left( {h}_{{\mathcal {C}}_{1}}^{3}{-h} _{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( {\pi }_{{\mathcal {C}}_{1}} ^{3}{-\pi }_{{\mathcal {C}}_{2}}^{3}\right) ^{2}\right] }. \end{aligned}$$

(13)

If ${\mathcal {C}}_{1}=\left( 0.8,0.5,0.6\right) ,$ and ${\mathcal {C}}_{2}=\left( 0.9,0.4,0.5\right)$ be any two CFSs. Then the distance between ${\mathcal {C}}_{1}$ and ${\mathcal {C}}_{2}$ is

$$\begin{aligned} d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2}\right)&=\sqrt[3]{\frac{1}{2}\left[ \begin{array}{l} \left( \left( 0.8\right) ^{3}-\left( 0.9\right) ^{3}\right) ^{2}+\left( \left( 0.5\right) ^{3}-\left( 0.4\right) ^{3}\right) ^{2}+\left( \left( 0.6\right) ^{3}-\left( 0.5\right) ^{3}\right) ^{2} +\left( \left( 0.5277\right) ^{3}-\left( 0.4344\right) ^{3}\right) ^{2} \end{array} \right] }\\&=0.3172154638. \end{aligned}$$

Based on Definition 19, in the following, we can derive some properties of the distance between two CFEs.

Theorem 24

Let ${\mathcal {C}}_{1}=\left( f_{{\mathcal {C}}_{1}},g_{{\mathcal {C}}_{1} },h_{{\mathcal {C}}_{1}}\right) ,$ and ${\mathcal {C}}_{2}=\left( f_{{\mathcal {C}} _{2}},g_{{\mathcal {C}}_{2}},h_{{\mathcal {C}}_{2}}\right)$ be any two CFSs. Then

(i) ${d}\left( C_{1}{,}C_{2}\right) {=d}\left( C_{2}{,}C_{1}\right) ;$

(ii) $d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2}\right) =0$ if and only if ${\mathcal {C}}_{1}={\mathcal {C}}_{2};$

(iii) $0\le d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2}\right) \le \sqrt{2}.$

Proof

From Definition 19, we know that $f_{{\mathcal {C}}_{1}},g_{{\mathcal {C}}_{1} },h_{{\mathcal {C}}_{1}},f_{{\mathcal {C}}_{2}},g_{{\mathcal {C}}_{2}},h_{{\mathcal {C}} _{2}}\in \left[ 0,\text { }1\right] ,$ ${f}_{{\mathcal {C}}_{1}} ^{3}{+g}_{{\mathcal {C}}_{1}}^{3}{+h}_{{\mathcal {C}}_{1}} ^{3}{\le 1}$ and ${f}_{{\mathcal {C}}_{2}}^{3}{+g} _{{\mathcal {C}}_{2}}^{3}{+h}_{{\mathcal {C}}_{2}}^{3}{\le 1}$ then, (i)

$$\begin{aligned} d\left( C_{1}{,}C_{2}\right)&=\sqrt[3]{\frac{1}{2}\left[ \left( f_{{\mathcal {C}}_{1}}^{3}-f_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( g_{{\mathcal {C}}_{1}}^{3}-g_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( h_{{\mathcal {C}}_{1}}^{3}-h_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( \pi _{{\mathcal {C}}_{1}}^{3}-\pi _{{\mathcal {C}}_{2}}^{3}\right) ^{2}\right] }\\&=\sqrt[3]{\frac{1}{2}\left[ \left( f_{{\mathcal {C}}_{2}}^{3}-f_{{\mathcal {C}} _{1}}^{3}\right) ^{2}+\left( g_{{\mathcal {C}}_{2}}^{3}-g_{{\mathcal {C}}_{1}} ^{3}\right) ^{2}+\left( h_{{\mathcal {C}}_{2}}^{3}-h_{{\mathcal {C}}_{1}} ^{3}\right) ^{2}+\left( \pi _{{\mathcal {C}}_{2}}^{3}-\pi _{{\mathcal {C}}_{1}} ^{3}\right) ^{2}\right] } =d\left( {\mathcal {C}}_{2},{\mathcal {C}}_{1}\right) . \end{aligned}$$

(ii)

$$\begin{aligned} d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2}\right)&=\sqrt[3]{\frac{1}{2}\left[ \left( f_{{\mathcal {C}}_{1}}^{3}-f_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( g_{{\mathcal {C}}_{1}}^{3}-g_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( h_{{\mathcal {C}}_{1}}^{3}-h_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( \pi _{{\mathcal {C}}_{1}}^{3}-\pi _{{\mathcal {C}}_{2}}^{3}\right) ^{2}\right] }=0\\&\Longleftrightarrow \left( f_{{\mathcal {C}}_{1}}^{3}-f_{{\mathcal {C}}_{2}} ^{3}\right) ^{2}=0,\left( g_{{\mathcal {C}}_{1}}^{3}-g_{{\mathcal {C}}_{2}} ^{3}\right) ^{2}=0,\left( h_{{\mathcal {C}}_{1}}^{3}-h_{{\mathcal {C}}_{2}} ^{3}\right) ^{2}=0,\left( \pi _{{\mathcal {C}}_{1}}^{3}-\pi _{{\mathcal {C}}_{2} }^{3}\right) ^{2}=0\\&\Longleftrightarrow f_{{\mathcal {C}}_{1}}^{3}=f_{{\mathcal {C}}_{2}} ^{3},g_{{\mathcal {C}}_{1}}^{3}=g_{{\mathcal {C}}_{2}}^{3},h_{{\mathcal {C}}_{1}} ^{3}=h_{{\mathcal {C}}_{2}}^{3},\pi _{{\mathcal {C}}_{1}}^{3}=\pi _{{\mathcal {C}}_{2} }^{3}\Longleftrightarrow {\mathcal {C}}_{1}={\mathcal {C}}_{2}. \end{aligned}$$

$\square$

Theorem 25

Let ${\mathcal {C}}_{i}=\left( f_{{\mathcal {C}}_{i}},g_{{\mathcal {C}}_{i} },h_{{\mathcal {C}}i}\right) ,$ $\left( i=1,2,3\right)$ be three CFSs, if ${\mathcal {C}}_{1}\subseteq {\mathcal {C}}_{2}\subseteq {\mathcal {C}}_{3},$ then $d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2}\right) \le d\left( {\mathcal {C}} _{1},{\mathcal {C}}_{3}\right)$ and $d\left( {\mathcal {C}}_{2},{\mathcal {C}} _{3}\right) \le d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{3}\right) .$

Proof

If ${\mathcal {C}}_{1}\subseteq {\mathcal {C}}_{2}\subseteq {\mathcal {C}}_{3},$ then $f_{{\mathcal {C}}_{1}}^{3}\le f_{{\mathcal {C}}_{2}}^{3}\le f_{{\mathcal {C}}_{3} }^{3},$ $g_{{\mathcal {C}}_{1}}^{3}\le g_{{\mathcal {C}}_{2}}^{3}\le g_{{\mathcal {C}}_{3}}^{3}$ and $h_{{\mathcal {C}}_{1}}^{3}\ge h_{{\mathcal {C}}_{2} }^{3}\ge h_{{\mathcal {C}}_{3}}^{3}.$ By Definition 19, we get:

$$\begin{aligned} d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2}\right)&=\sqrt[3]{\frac{1}{2}\left[ \left( f_{{\mathcal {C}}_{1}}^{3}-f_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( g_{{\mathcal {C}}_{1}}^{3}-g_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( h_{{\mathcal {C}}_{1}}^{3}-h_{{\mathcal {C}}_{2}}^{3}\right) ^{2}+\left( \pi _{{\mathcal {C}}_{1}}^{3}-\pi _{{\mathcal {C}}_{2}}^{3}\right) ^{2}\right] }\\&\le \sqrt[3]{\frac{1}{2}\left[ \left( f_{{\mathcal {C}}_{1}}^{3} -f_{{\mathcal {C}}_{3}}^{3}\right) ^{2}+\left( g_{{\mathcal {C}}_{1}} ^{3}-g_{{\mathcal {C}}_{3}}^{3}\right) ^{2}+\left( h_{{\mathcal {C}}_{1}} ^{3}-h_{{\mathcal {C}}_{3}}^{3}\right) ^{2}+\left( \pi _{{\mathcal {C}}_{1}} ^{3}-\pi _{{\mathcal {C}}_{3}}^{3}\right) ^{2}\right] } =d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{3}\right) . \end{aligned}$$

Similarly, we can prove that $d\left( {\mathcal {C}}_{1},{\mathcal {C}}_{2}\right) \le d\left( {\mathcal {C}}_{2},{\mathcal {C}}_{3}\right) .$ $\square$

7.2 Models for multiple attribute decision making with cubical fuzzy information

This section is devoted to introduce a model for MADM problems based on CFWA and $\ CFWG$ operators in the environment of CFSs. Let $A=\{A_{1} ,A_{2},...,A_{m}\}$ be a set of alternatives that are to be evaluated by the experts, $G=\{G_{1},G_{2},...,G_{n}\}$ be the set of parameters under the considerations, and $\omega =(\omega _{1},\omega _{2},...,\omega _{n})$ be the weighting vector associated with the parameters $G_{j}$ $\left( j=1,2,...,n\right)$, with $\omega _{j}\in [0,$ 1],  ${\displaystyle \sum \limits _{j=1}^{n}} \omega _{j}=1.$ Assume that ${\widetilde{M}}=\left( m\right) _{m\times n}=\left( f_{ij},g_{ij},h_{ij}\right) _{m\times n}$ is the cubical fuzzy decision matrix, where $f_{ij},~g_{ij}$ and $h_{ij}$ respectively represent the degree of positive, neutral and nonmembership that the alternative $A_{i}$ satisfies the attribute $G_{j}$ of an expert. Also $f_{ij}\in \left[ 0,\text { }1\right] ,$ $g_{ij}\in \left[ 0,\text { }1\right]$ and $h_{ij}\in \left[ 0,\text { }1\right] ,$ $\left( f_{ij}\right) ^{3}+\left( g_{ij}\right) ^{3}+\left( h_{ij}\right) ^{3}\le 1,$ $i=1,2,...,m$, $j=1,2,...,n$. Following are the steps to be followed during the process. Step 1. Collect the data about each alternative in terms of CFNs and summarize it in the form of cubical fuzzy matrix ${\widetilde{M}}=\left( m\right) _{m\times n}=\left( f_{ij},g_{ij},h_{ij}\right) _{m\times n}$. Step 2. Normalize the data by converting cost type parameters into benefit type parameters if any. Step 3. Calculate the overall preferences ${\mathcal {C}}_{i}$ $\left( i=1,2,...,m\right)$ of the alternative $A_{i}$ by applying the (CFWA) operator,

$$\begin{aligned} {\widetilde{m}}_{i}&=\text {CFWA}_{\omega }\left( {\widetilde{m}}_{i1},\widetilde{m}_{i2},...,{\widetilde{m}}_{in}\right) = {\displaystyle \bigoplus \limits _{j=1}^{n}} \left( \omega _{j}{\widetilde{m}}_{ij}\right) \\ \\&=\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{n}} \left( 1-f_{ij}^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( g_{ij}\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( h_{ij}\right) ^{\omega _{j}}\right) ; i&=1,2,...,m. \end{aligned}$$

Or (CFWG) operator

$$\begin{aligned} {\widetilde{m}}_{i}&=\text {CFWG}_{\omega }\left( {\widetilde{m}}_{i1},\widetilde{m}_{i2},...,{\widetilde{m}}_{in}\right) = {\displaystyle \bigotimes \limits _{j=1}^{n}} \left( {\widetilde{m}}_{ij}\right) ^{\omega _{j}}\nonumber \\&=\left( {\displaystyle \prod \limits _{j=1}^{n}} \left( f_{ij}\right) ^{w_{j}}, {\displaystyle \prod \limits _{j=1}^{n}} \left( g_{ij}\right) ^{w_{j}},\sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{n}} \left( 1-h_{ij}^{3}\right) ^{w_{j}}}\right) ; i=1,2,...,m. \end{aligned}$$

(14)

Step 4. Calculate the scores $S\left( {\mathcal {C}}_{i}\right)$ $\left( i=1,2,...,n\right)$ of the overall cubical fuzzy numbers ${\widetilde{m}}_{i}$ $\left( i=1,2,...,m\right)$ and utilize the accuracy function if required. Rank the alternatives $A_{i}$ and $A_{j}$ in accordance with the accuracy degrees $\text {acc}$(${\widetilde{m}}_{i}$) and $\text {acc}({\widetilde{m}}_{j}).$ Step 5. Rank all the alternatives $A_{i}$ $\left( i=1,2,...,m\right)$ and select the best one(s) in accordance with score$\left( {\widetilde{m}}_{i}\right)$ $\left( i=1,2,...,n\right) .$

8 Numerical example and comparative analysis

8.1 Numerical example

We assume a practical example of MADM problems to illustrate the application of the developed approaches. Suppose a particular organization wants to implement an enterprise resource planning (ERP) system (adapted from Xu and Yager (2006)). First, a team of experts is appointed that consists of the CEO and two senior representatives from the user department. By collecting all possible information about ERP vendors and systems, the project team chooses five potential ERP systems $A_{i}$ $\left( \imath =1,2,...,5\right)$ as candidates. The company employs some external professional organizations to aid this decision-making. The team of experts chooses four different parameters under which the alternatives are to be evaluated as function and technology $\left( G_{1}\right)$, strategic fitness $\left( G_{2}\right)$, vendor’s ability $\left( G_{3}\right)$, and vendor’s reputation $\left( G_{4}\right)$. These possible ERP systems $A_{i}$ $(i=1,2,...,5)$ are to be evaluated using the CFNs by the experts under the set of four parameters whose associated weighting vector is $\omega =(0.2,0.1,0.3,0.4)$. To select the most desirable ERP systems, we utilize the above step-wise procedure using CFWA, CFWG operators. Step 1 The CFNs are summarized in the cubical fuzzy matrix ${\widetilde{M}}=\left( {\widetilde{m}}_{ij}\right) _{5\times 4}$ shown in Table 1

Table 1 Cubical fuzzy decision matrix

Step 2 Since, the data is already in normalized form thus step 2 is skipped Step 3 From Table 1, aggregate all cubical fuzzy numbers ${\widetilde{m}}_{\imath j}$ $\left( j=1,2,...,n\right)$ by using the CFWA or CFWG operator to derive the overall cubical fuzzy elements ${\widetilde{m}}_{i}$ $\left( i=1,2,...,m\right)$ of the alternative $A_{i}$. The aggregated results by using CFWA and CFWG operators are shown in Table 2.

Table 2 Aggregated results of ERP systems by CFWA and CFWG operator

Step 4 From Table 2, the calculated score values of ERP systems are given in Table 3.

Table 3 The scores values of the ERP systems

Table 4 Ordering of the ERP systems

Finally, Table 4 shows that the best alternative (ERP system) is $A_{1}.$ Moreover, $A_{5}$ can be selected as the best one if $A_{1}$ is not available. Based on CFWA (CFWG) operator, in the following, we use the cubical fuzzy hybrid average (CFHA) operator to compute the best ERP system.

8.2 By CFHA operator

The following steps of CFHA operator have been performed for the selection of the best ERP system(s). Step 1$^{^{\prime }}.$ Utilize the CFHA operator given in Theorem 14 on Table 1, to collect the relative importance ERP system by supposing the weight vector $w=\left( 0.2575,0.3316,0.1292,0.1397,0.1420\right) ^{T}.$ From $\overset{\cdot }{{\widetilde{m}}}_{ij}=4w_{j}m_{ij},$ we have

$$\begin{aligned} \overset{\cdot }{{\widetilde{m}}}_{11}&=\left( \sqrt[3]{1-\left( 1-\left( 0.83\right) ^{3}\right) ^{4\times 0.2575}},\left( 0.53\right) ^{4\times 0.2575},\left( 0.63\right) ^{4\times 0.2575}\right) =\left( 0.8351,0.5200,0.6213\right) ,\\ \overset{\cdot }{{\widetilde{m}}}_{21}&=\left( \sqrt[3]{1-\left( 1-\left( 0.89\right) ^{3}\right) ^{4\times 0.2575}},\left( 0.39\right) ^{4\times 0.2575},\left( 0.49\right) ^{4\times 0.2575}\right) =\left( 0.8944,0.3791,0.4796\right) ,\\ \overset{\cdot }{{\widetilde{m}}}_{31}&=\left( \sqrt[3]{1-\left( 1-\left( 0.82\right) ^{3}\right) ^{4\times 0.2575}},\left( 0.22\right) ^{4\times 0.2575},\left( 0.42\right) ^{4\times 0.2575}\right) =\left( 0.8252,0.2102,0.4092\right) ,\\ \overset{\cdot }{{\widetilde{m}}}_{41}&=\left( \sqrt[3]{1-\left( 1-\left( 0.60\right) ^{3}\right) ^{4\times 0.2575}},\left( 0.20\right) ^{4\times 0.2575},\left( 0.80\right) ^{4\times 0.2575}\right) =\left( 0.6052,0.1905,0.7946\right) \end{aligned}$$

Similarly, we can get the other weighted arguments. By using the score function we can get the ordered weighted decision matrix given in Table 5.

Table 5 Cubical fuzzy ordered weighted decision matrix

Therefore, by CFHA operator, we get the aggregated value $\left( {\widetilde{m}}_{i}\right)$ of each alternative $A_{i}$ $\left( i=1,2,...,5\right) ,$ we have

$$\begin{aligned} {\widetilde{m}}_{1}&=\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{4}} \left( 1-\left( \overset{\cdot }{{\widetilde{f}}}_{\sigma \left( 1j\right) }\right) ^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{g}}}_{\sigma \left( 1j\right) }\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{h}}}_{\sigma \left( 1j\right) }\right) ^{\omega _{j}}\right) \\&=\left( \begin{array}{c} \sqrt[3]{1-\left( 1-\left( 0.89\right) ^{3}\right) ^{0.2}\times \left( 1-\left( 0.82\right) ^{3}\right) ^{0.1}\times \left( 1-\left( 0.83\right) ^{3}\right) ^{0.3}\times \left( 1-\left( 0.60\right) ^{3}\right) ^{0.4}},\\ \left( 0.39\right) ^{0.2}\left( 0.22\right) ^{0.1}\left( 0.53\right) ^{0.3}\left( 0.20\right) ^{0.4},\left( 0.49\right) ^{0.2}\left( 0.42\right) ^{0.1}\left( 0.63\right) ^{0.3}\left( 0.80\right) ^{0.4} \end{array} \right) \\&=\left( 0.7891,0.3091,0.6329\right) . \\ {\widetilde{m}}_{2}&=\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{4}} \left( 1-\left( \overset{\cdot }{{\widetilde{f}}}_{\sigma \left( 2j\right) }\right) ^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{g}}}_{\sigma \left( 2j\right) }\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{h}}}_{\sigma \left( 2j\right) }\right) ^{\omega _{j}}\right) \\&=\left( \begin{array}{c} \sqrt[3]{1-\left( 1-\left( 0.80\right) ^{3}\right) ^{.2}\times \left( 1-\left( 0.63\right) ^{3}\right) ^{0.1}\times \left( 1-\left( 0.43\right) ^{3}\right) ^{0.3}\times \left( 1-\left( 0.43\right) ^{3}\right) ^{0.4}},\\ \left( 0.50\right) ^{0.2}\left( 0.23\right) ^{0.1}\left( 0.63\right) ^{0.3}\left( 0.23\right) ^{0.4},\left( 0.30\right) ^{0.2}\left( 0.43\right) ^{.1}\left( 0.33\right) ^{0.3}\left( 0.63\right) ^{0.4} \end{array} \right) \\&=\left( 0.3789,0.3091,0.6329\right) . \\ {\widetilde{m}}_{3}&=\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{4}} \left( 1-\left( \overset{\cdot }{{\widetilde{f}}}_{\sigma \left( 3j\right) }\right) ^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{g}}}_{\sigma \left( 3j\right) }\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{h}}}_{\sigma \left( 3j\right) }\right) ^{\omega _{j}}\right) \\&=\left( \begin{array}{c} \sqrt[3]{1-\left( 1-\left( 0.91\right) ^{3}\right) ^{0.2}\times \left( 1-\left( 0.11\right) ^{3}\right) ^{0.1}\times \left( 1-\left( 0.24\right) ^{3}\right) ^{0.3}\times \left( 1-\left( 0.27\right) ^{3}\right) ^{0.4}},\\ \left( 0.21\right) ^{0.2}\left( 0.91\right) ^{0.1}\left( 0.85\right) ^{0.3}\left( 0.17\right) ^{0.4},\left( 0.11\right) ^{0.2}\left( 0.21\right) ^{0.1}\left( 0.65\right) ^{0.3}\left( 0.87\right) ^{0.4} \end{array} \right) \\&=\left( 0.5902,0.3634,0.4305\right) . \\ {\widetilde{m}}_{4}&=\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{4}} \left( 1-\left( \overset{\cdot }{{\widetilde{f}}}_{\sigma \left( 4j\right) }\right) ^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{g}}}_{\sigma \left( 4j\right) }\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{h}}}_{\sigma \left( 4j\right) }\right) ^{\omega _{j}}\right) \\&=\left( \begin{array}{c} \sqrt[3]{1-\left( 1-\left( 0.85\right) ^{3}\right) ^{0.2}\times \left( 1-\left( 0.84\right) ^{3}\right) ^{0.1}\times \left( 1-\left( 0.35\right) ^{3}\right) ^{0.3}\times \left( 1-\left( 0.20\right) ^{3}\right) ^{0.4}},\\ \left( 0.25\right) ^{0.2}\left( 0.24\right) ^{0.1}\left( 0.85\right) ^{0.3}\left( 0.89\right) ^{0.4},\left( 0.45\right) ^{0.2}\left( 0.44\right) ^{0.1}\left( 0.25\right) ^{0.3}\left( 0.39\right) ^{0.4} \end{array} \right) \\&=\left( 0.6464,0.3399,0.4572\right) . \\ {\widetilde{m}}_{5}&=\left( \sqrt[3]{1- {\displaystyle \prod \limits _{j=1}^{4}} \left( 1-\left( \overset{\cdot }{{\widetilde{f}}}_{\sigma \left( 5j\right) }\right) ^{3}\right) ^{\omega _{j}}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{g}}}_{\sigma \left( 5j\right) }\right) ^{\omega _{j}}, {\displaystyle \prod \limits _{j=1}^{4}} \left( \overset{\cdot }{{\widetilde{h}}}_{\sigma \left( 5j\right) }\right) ^{\omega _{j}}\right) \\&=\left( \begin{array}{c} \sqrt[3]{1-\left( 1-\left( 0.90\right) ^{3}\right) ^{0.2}\times \left( 1-\left( 0.68\right) ^{3}\right) ^{0.1}\times \left( 1-\left( 0.45\right) ^{3}\right) ^{0.3}\times \left( 1-\left( 0.11\right) ^{3}\right) ^{0.4}},\\ \left( 0.15\right) ^{.2}\left( 0.58\right) ^{0.1}\left( 0.87\right) ^{0.3}\left( 0.21\right) ^{0.4},\left( 0.32\right) ^{0.2}\left( 0.28\right) ^{0.1}\left( 0.35\right) ^{0.3}\left( 0.91\right) ^{0.4} \end{array} \right) \\&=\left( 0.6355,0.5972,0.3554\right) . \end{aligned}$$

Table 6 The ordering of the score values corresponding to these aggregated values are

Step 3$^{^{\prime }}$. According to the score functions shown in Table 6 and the comparison formula of score functions, the ordering of the ERP systems is shown below.

$$\begin{aligned} A_{1}>A_{5}>A_{4}>A_{3}>A_{2}. \end{aligned}$$

As we can see, depending on the aggregation operators used, the ordering of the ERP systems is slightly different, but the best ERP system is $A_{1}$.

8.3 Comparative analysis

In this section, we compare our proposed operators with those that already exist in the literature. We select the most relevant aggregation operators. In Mahmood et al. (2019), spherical fuzzy sets and their application have been completely studied. Here we consider the spherical fuzzy aggregation operators developed in Mahmood et al. (2019) and compare our proposed operators. In Mahmood et al. (2019), the decision matrix in Table 7 was taken and applied the weighted spherical fuzzy averaging and geometric operator to get the aggregated values of the proposed alternatives as given in Table 8. The rating values of SFWA/SFWG and proposed operators are given in Table 9. The ranking of alternatives obtained by SFWA/SFWG and proposed operators are given in Table 10. The accuracy values of CFWA/CFWG operators are given in Table 11. The certainty values of CFWA/CFWG operators are given in Table 12. On the other hand, if we drop the abstinence degree from each triplet of cubical fuzzy information given in Table 1, then Table 1, is reduced to Fermatean fuzzy (FF) information and which is discussed in Example 1.

Table 7 Spherical fuzzy decision matrix

Table 8 Aggregated values by (SFWA/SFWG)

Table 9 Score values of SFWA/SFWG operators

Table 10 Ranking orders

Table 11 Accuracy values

Table 12 Certainty values

Example 1

Reconsider the cubical fuzzy information matrix given in Table 1 and drop the abstinence degree from each triplet of CFN. The reduced decision matrix consists of FF information, given in Table 12.

Table 13 Fermatean fuzzy decision matrix

To obtain aggregated FFNs, we apply FFWA and FFWG operators in Table 13, and the aggregated FFNs are given in Table 14. Using the score function, the score values of the alternatives are given in Table 15.

Table 14 Aggregated values of alternatives using FFWA and FFWG operators

Table 15 Score values of alternatives using FFWA and FFWG operators

The ranking order of alternatives are shown in Table 16.

Table 16 The ranking order of alternatives

9 Conclusion

In this paper, we proposed the concept of cubical fuzzy information and studied the basic properties of this notion. we investigated the MADM problem based on the aggregation operators with cubical fuzzy information. Then, we developed some aggregation operators for aggregating cubical fuzzy information, including CFWA operator, CFWG operator, CFOWA operator, CFOWG operator, CFHWA operator, and CFHWG operator. The special cases of these proposed operators are studied. Further, we have utilized these operators to develop some approaches to solve the cubical fuzzy MADM problems. Finally, a practical example for the selection of an ERP system is given to verify the developed approach and to demonstrate its practicality and effectiveness. In the future, we shall continue working on the extension and application of the developed operators to other domains.