Assessment of Hydropower Plants in Pakistan: Muirhead Mean-Based 2-Tuple Linguistic T-spherical Fuzzy Model Combining SWARA with COPRAS

Abstract

In the study of group decision-making, the most important issue is how to coordinate opinions from different decision experts (DEs) to reach a consensus under uncertainty. To tackle uncertainties surrounding multi-attribute group decision-making (MAGDM) problems in real-life scenes, we introduce 2-tuple linguistic T-spherical fuzzy sets (2TLT-SFSs) which generalize T-spherical fuzzy sets by means of 2-tuple linguistic terms. The 2TLT-SFS model enables the degrees of membership, abstention, and non-membership to be expressed by linguistic terms. This makes it more flexible and descriptive to model the attitudes of DEs in MAGDM applications. Due to the fact that multi-input arguments are interconnected and DEs have a lot of options perception, we also define Muirhead mean (MM) aggregation operators (AOs) to facilitate the fusion of 2TLT-SF information. With the aid of 2TLT-SFSs and MM AOs, the main goal of this research is to present a general MAGDM framework by integrating the step-wise weight assessment ratio analysis (SWARA) with the complex proportional assessment (COPRAS). Firstly, the MM, weighted MM, dual MM, and weighted dual MM operators are adapted to the 2TLT-SF environment, which put forward several new notions such as the 2-tuple linguistic T-spherical fuzzy Muirhead mean (2TLT-SFMM), 2-tuple linguistic T-spherical fuzzy weighted Muirhead mean (2TLT-SFWMM), 2-tuple linguistic T-spherical fuzzy dual Muirhead mean (2TLT-SFDMM), and 2-tuple linguistic T-spherical fuzzy weighted dual Muirhead mean (2TLT-SFWDMM) operators. Meanwhile, some properties regarding idempotency, monotonicity, boundedness, and specializations of the proposed operators are analyzed. Secondly, an integrated 2TLT-SF-MAGDM framework is established. In the proposed decision framework, the 2TLT-SF-SWARA method is utilized to identify the subjective weights of decision attributes, and the 2TLT-SF-COPRAS approach is used to rank alternatives. Lastly, a case study concerning hydropower plants assessment is presented to demonstrate that the suggested scheme is feasible and effective. Furthermore, sensitivity and comparison analyses are conducted to show the robustness and superiority of the proposed method.

1 Introduction

1.1 Historical Perspective

A group decision-making approach is one in which a panel of specialists collaborates to obtain an agreement on a solution to a particular issue from a collection of possibilities. With the fast evolution of social and industrial practices, as well as the complexities of decision-making (DM) [1, 2] concerns, more and more experts are being welcomed to take part in the decision procedure in order to accumulate robust and efficient knowledge, group DM has thus become extremely relevant and has drawn the interest of several more scholars. Figure 1 illustrates the graphical representation of DM strategy.

Fig. 1

Decision-making analysis strategy

It is difficult for decision experts (DEs) to express their assessments using crisp values to indicate the complexity of human activities and the uncertainties of evaluated objects in real-world multiple attribute decision-making (MADM) [3,4,5,6] problems. Zadeh [7] introduced the fuzzy set (FS) theory, which gives DEs a mathematical tool to quantitatively describe gradualness-caused uncertainty. Later, several generalizations of FSs [8,9,10,11] have been introduced and applied to MAGDM [12,13,14,15,16,17,18,19], which makes it more convenient for DEs for dealing with uncertainty in DM. Yager [20] proposed a more general FS named the q-rung orthopair fuzzy set (q-ROFS) to unify several existing generalized FSs by setting a parameter q. More specifically, when $q = 1$, $q = 2$, and $q=3$, the q-ROFS reduces to the intuitionistic FS (IFS), Pythagorean FS (PyFS), and Fermatean FS, respectively. Furthermore, the value range of the q-ROFS extends when the parameter q is increased, providing experts or DEs have more flexibility in presenting their assessment information in complex DM situations. The q-ROFS serves as an efficient approach for dealing with complicated fuzzy data, and it is specified by three factors: a membership degree (MD), a non-membership degree (NMD), and an indeterminacy degree. More specifically, a q-ROFS A in L can be written as: $A=\{\langle \ell ,p(\ell ),l(\ell )\rangle |\ell \in L\}$, where $p_{A}$ and $l_{A}$ indicate the MD and NMD degrees with a restriction that $0 \le p^q(\ell )+l^q(\ell )\le 1$. Furthermore, Mahmood et al. [21] observed that a q-ROFS $A=\{\langle \ell ,p(\ell ),l(\ell )\rangle |\ell \in L\}$ can be extended to $T=\{\langle \ell , p(\ell ),n(\ell ),l(\ell )\rangle |\ell \in L\}$ by considering the abstention degree (AD) in addition to the MD and NMD degrees, with a restriction that $0 \le p^q(\ell )+n^q(\ell )+l^q(\ell )\le 1$. Such a powerful extension of the q-ROFS is known as the T-spherical fuzzy set (T-SFS). The preceding discussion of q-ROFSs and T-SFSs has shown that T-SFSs have a stronger capability than q-ROFSs to tackle problems in MADM scenarios when there is uncertainty. Garg et al. [22] defined several weighted averaging and geometric power AOs by utilizing the advantages of T-SFSs. Karaaslan and Dawood [23] introduced the Dombi operations on complex T-SFSs. Based on Dombi operations, they defined some AOs, developed a MADM method under the complex T-SFSs environment and presented an algorithm for the proposed method. Ju et al. [24] investigated the MAGDM problems with incomplete weight information under T-SF environment. By utilizing the concepts of score functions and distance measurements for complicated T-SF information, Wang and Chen [25] proposed an innovative T-SF ELECTRE (Elimination Et Choice Translating Reality) strategy to tackle complex assessment problems.

Real numbers or linguistic terms are required to interpret assessment techniques. Furthermore, due to the incredible ambiguity of MADM conflicts and the uncertainty that people face when making decisions, it is difficult to precisely and quantitatively describe and analyze many possibilities, such as evaluating emergency response capacity and categorization of real images. In complex and dynamic practical DM, FSs, and obtained fuzzy numbers have some limitations. The use of fuzzy numbers as evaluation information, in specific, is measurable, but in methodology, people prefer to use qualitative phrases. When someone makes a prediction, linguistic-level language is definitely used. When a doctor diagnoses a patient, for example, the doctor may make a “very critical,” “not too critical,” or “better” decision based on the patient’s disease. A FS or derived fuzzy numbers cannot represent people’s linguistic DM information. Using a picture fuzzy set, a q-ROFS, or a T-SFS to illustrate emotional impact in language evaluation information is ineffective. People can also provide language evaluation information faster than a fuzzy number. To resolve this concern, Zadeh [26] first established linguistic variables, and Xu [27] then extended the discrete linguistic term set (LTS) to the continuous LTS. Herrera, Herrera, and Martinez [28, 29] established a theory of 2TL terms in some cases, evaluating natural language or other narrative language forms.

Zhao et al. [30] introduced an improved TODIM technique based on 2TL neutrosophic sets and cumulative prospect theory as a novel approach to MAGDM issues. Depending on existing research studies, Zhang et al. [31] enhanced the TODIM approach as well as cumulative prospect theory under the 2TL-PyFSs. By assessing the reliability of the information, Chai et al. [32] introduced the notion of Z-uncertain probabilistic linguistic variables (Z-UPLVs). The operating rules, normalizing, distance and similarity measurements, and Z-UPLV comparative technique was then introduced. Under the dual probabilistic LTSs, Saha et al. [33] used the ideas of consistency and similarity amongst DEs to establish the DEs’ subjective and objective weights, correspondingly. Wu et al. [34] established a taxonomy of current distributed linguistic conceptions as well as a complete view of the evolution of distributed linguistic conceptions in DM. The fundamental aspects and implementations of distributed linguistic pattern recognition in DM, such as distance measurement, distributed linguistic preference relations, aggregation techniques, and distributed linguistic MADM models, were then discussed.

As a result, in cases where the information given is unclear, and non-probabilistic, linguistic modeling appears logical and has yielded important results in a variety of domains. Linguistics modeling applications can be seen in Fig. 2.

Fig. 2

Linguistic modeling applications

Accumulation of assessment data is a critical stage in the MADM, and AOs have become more crucial in this way. In real-life applications, moreover, attributes are interconnected but not distinct. Regarding that, some researchers focus on AOs capable of capturing the interdependence of input arguments in MADM problems. Various AOs have been progressively proposed to capture the interrelationship between any two input arguments. Nevertheless, there may be several circumstances in which multi-input arguments collaborate with each other in MADM problems rather than three or two arguments. As a consequence, it is critical to develop more general and long-lasting operators for capturing interrelationships among any number of input arguments. The MM [35] and dual MM [36] operators appear to be the best choice for evaluating the interrelationships of multi-input arguments via a parameter vector, and it is a generalization of some emerging AOs like averaging, geometric, geometric Bonferroni mean (BM), geometric Maclaurin symmetric mean (MSM), Heronian mean and so on. Garg et al. [37] proposed the MM and dual MM operators under the complex interval-valued q-ROF environment to more efficiently represent DEs evaluation information in complicated MAGDM processes. Under the cubic q-ROF linguistic set (Cq-ROFLS) environment to quantify the uncertainty in the information, Garg et al. [38] introduced the Cq-ROFL-MM, Cq-ROFL weighted MM, and Cq-ROFL dual MM operators to aggregate the different pairs of the preferences. Deng et al. [39] extended the MM and dual MM operators with 2TL picture fuzzy numbers (2TLPFNs) to define the 2TLPFMM, the 2TLPFWMM, the 2TLPFDMM, and the 2TLPFWDMM operators. Fahmi and Amin [40] constructed some bipolar neutrosophic fuzzy (BNF) operators including BNF prioritized MM weighted averaging, BNF prioritized MM ordered weighted averaging, BNF prioritized MM weighted geometric, BNF prioritized MM ordered weighted geometric, BNF prioritized MM hybrid weighted averaging, and BNF prioritized MM hybrid weighted geometric operators by utilizing the prioritized MM AOs. Du and Liu [41] devised a DM strategy to cope with probabilistic linguistic (PL) MADM issues by extending dual MM operators to the PL preference environment. They defined PL dual MM operators such as PL dual MM operator and PL weighted dual MM operator by studying the interconnections between multi-input arguments of PL terms.

Moreover, different MADM methods [42,43,44] are used to aggregate data from recent decades, and one of the advanced methods in this field are SWARA and COPRAS. The weight values of the attribute are essential components of the MADM methodology. The objective and subjective weights are used to determine the requirements of the attribute. To quantify the subjective weights, we utilize data provided by DEs [45] to construct decision matrices, which in turn are used to quantify the objective weights. SWARA is a novel methodology which was developed by Kersuliene et al. [46] for generating the weighted evaluation ratios required for establishing subjective attributes weights. This method is slightly less complicated than other methods for measuring weights. Over the years, studies have incorporated various MADM innovations, which have then been built upon by past study to solve increasingly difficult decision issues in our everyday lives. For every evaluation, there are the following key components: (a) alternatives; (b) attribute; (c) relative importance (importance/value) of each attribute; (d) measurement of the options’ quality relative to the attribute, and (e) means for differentiating between different options. The goal of the MADM strategy is to choose the best alternative among a number of reasonable options, all subject to varying degrees of competitiveness. In place of traditional methods, which consider for conflict computing, a compliance with article for data testing, called COPRAS, was innovated by Zavadskas et al. [47]. Extending the COPRAS methodology to deal with increasingly ambiguous and complicated MADM problems is currently under investigation. Furthermore, the combined form of these two methods has also been researched by many scholars. Alipour et al. [48] introduced a combined methodology for selecting fuel cell and hydrogen component suppliers based on entropy, SWARA, and COPRAS methodologies in a PyF environment. To determine shipbuilding enterprise suppliers, Ziquan et al. [49] developed a novel technique depending on the IF-SWARA and COPRAS methodologies, which is an innovative research topic. Mishra et al. [50] presented a combined approach based on the SWARA and COPRAS methods for the determination of optimal alternatives. In the combined approach, weights of attributes were determined by the SWARA method, and the ranking order of bioenergy production technology alternatives was decided by the COPRAS method using IFSs. Rosiana et al. [51] enhanced the Rough method SWARA and the COPRAS to assess the performance of third-party logistics providers. Ansari et al. [52] employed a MADM framework using fuzzy SWARA and fuzzy COPRAS to analyze the risks and the solutions to mitigate sustainable remanufacturing supply chain.

1.2 Motivational Description

The overall aim of this research study is to identify the hydropower plants that may help Pakistan to reduce their poor electricity output. After collecting various data from DEs, the MAGDM approach is used to determine the most acceptable hydropower plants. The selection of attributes is a crucial part of MAGDM. There are two categories of attributes: favorable attributes and non-favorable attributes, depending on whether they are useful or useless in determining the appropriate hydropower plants for generating electricity. DEs who take into account membership, abstention, and non-membership degrees think clearly when they use the 2TLT-SFS in this type of MAGDM technique. Furthermore, adopting the 2TLT-SFWMM operator and 2TLT-SFWDMM operator allow DEs to make more informed judgments on their significant and 2TLT-SF ideas. The attributes weights of the MAGDM approach are calculated using 2TLT-SF-SWARA, an innovative weight-calculating algorithm. It has many processes. The 2TLT-SF-SWARA technique calculates appropriate weights, which explains why it is often used for that objective importance. The 2TLT-SF-COPRAS approach is also implemented to assess alternatives by classifying the applicable attribute into favorable and non-favorable types. As a result, it prioritizes the alternatives based on their important values and numerical applicability. In particular, the outcomes of the 2TLT-SF-SWARA-COPRAS approach are comparable to those of the 2TLT-SF-EDAS, 2TLT-SF-CODAS, 2TLT-SF-TOPSIS, 2TL spherical FS, and 2TL picture FS approaches in this article. All these techniques are significant MAGDM fundamental approaches. These approaches could be used to do a parameter analysis of variations in the weight values of the specified alternatives in terms of the kind of hydropower plants and the amount of energy generated, and their outcomes could be examined accordingly.

1.3 Contributions and Structure

This research has contributed to the exploration of MAGDM under uncertainty in the following aspects:

• The 2TLT-SFS is introduced as a new generalization in FS theory to tackle the complexities in numerical data combing the 2TL terms and T-SFS.

• The 2TLT-SFMM operator, 2TLT-SFWMM operator, 2TLT-SFDMM operator, and 2TLT-SFWDMM operator are proposed by the integration of 2TLT-SFS and MM operators.

• A MAGDM innovation for hydropower plants assessment in Pakistan based on the 2TLT-SFWMM and 2TLT-SFWDMM operators is established.

• An assessment framework of the hydropower plants selection scheme using the proposed MAGDM innovation is constructed.

The remainder of this research paper is structured as follows: In Sect. 2, the basic concepts of the 2TL representation model, the description of T-SFSs, MM, and dual MM operators with weighted forms are summarized; in Sect. 3 the basic review of 2TLT-SFS with operational laws is presented; in Sect. 4, the 2TLT-SFMM, 2TLT-SFWMM, 2TLT-SFDMM, and 2TLT-SFWDMM operators are constructed; in Sect. 5, based on the initiated weighted AOs, a MAGDM innovation is constructed; in Sect. 6, to demonstrate the usefulness of the strategy provided in this research work, a case study on hydropower plants selection in Pakistan is given; in Sect. 7, the concluding remarks and potential directions for future research are summarized.

2 Preliminaries

In this part, some basic concepts such as 2TL terms, T-SFSs, and MM operators are recapped to facilitate the discussion in subsequent parts.

2.1 2-Tuple Linguistic Representation Model

Definition 1

[28] Let $S=\{s_{\epsilon }|\epsilon =0, 1,\ldots , \tau \}$ be an LTS with odd cardinality, where $s_{\epsilon }$ indicates a possible linguistic term for a linguistic variable. Let $s_{\epsilon }, s_{k}$ be two linguistic terms, then we have the following:

• (i) The set is ordered: $s_{\epsilon }>s_{k}$, if and only if $\epsilon >k.$

• (ii) Max operator: $\max (s_{\epsilon }, s_{k})=s_{\epsilon },$ if and only if $\epsilon \ge k$.

• (iii) Min operator: $\min (s_{\epsilon }, s_{k})=s_{\epsilon },$ if and only if $\epsilon \le k$.

• (iv) Negative operator: Neg$(s_{\epsilon })=s_{k}$ such that $k=\tau -\epsilon .$

The 2TL representation model depends on the idea of symbolic translation, introduced by Herrera and Martinez [29]. It is useful for representing the linguistic assessment information by means of a 2-tuple $(s_{\epsilon },\upsilon _{\epsilon })$, where $s_{\epsilon }$ is a linguistic term from the predefined LTS S and $\upsilon _{\epsilon }$ is the value of symbolic translation with $\upsilon _{\epsilon }\in [-0.5, 0.5)$.

Definition 2

[29] Let $S=\{s_0, s_1, s_2, \ldots , s_\tau \}$ be an LTS and $\varrho \in [0, \tau ]$ be an aggregation result of the indices of some linguistic terms from S, i.e., the result of a symbolic aggregation operation. Let $\epsilon =\text {round}(\varrho )$ and $\upsilon = \varrho -\epsilon$ be two values with $\epsilon \in [0, \tau ]$ and $\upsilon \in [-0.5, 0.5)$. Then $\upsilon$ is called a symbolic translation.

Definition 3

[29] Let $S=\{s_0, s_1, s_2, \ldots , s_\tau \}$ be an LTS and $\varrho \in [0, \tau ]$ be a value representing the result of a symbolic aggregation operation. Then the function $\Delta$ used to obtain the 2TL information equivalent to $\varrho$ is defined as:

$$\begin{aligned} \Delta :[0, \tau ]\rightarrow S\times [-0.5,0.5), \end{aligned}$$

$$\begin{aligned} \Delta (\varrho )=(s_{\epsilon }, \upsilon ), \text{ with } {\left\{ \begin{array}{ll} s_{\epsilon }, &{}\epsilon =\text {round}(\varrho ),\\ \upsilon =\varrho -\epsilon , &{}\upsilon \in [-0.5, 0.5). \end{array}\right. } \end{aligned}$$

(1)

Definition 4

[29] Let $S=\{s_0, s_1, s_2, \ldots , s_\tau \}$ be an LTS and $(s_{\epsilon },\upsilon _{\epsilon })$ be a 2-tuple. There exists a function $\Delta ^{-1}$ restoring the 2-tuple $(s_{\epsilon },\upsilon _{\epsilon })$ to its equivalent numerical value $\varrho \in [0, \tau ]$ where

$$\begin{aligned} \Delta ^{-1}: S\times [-0.5, 0.5)\rightarrow [0, \tau ],\nonumber \\ \Delta ^{-1}(s_{\epsilon }, \upsilon )= \epsilon +\upsilon =\varrho . \end{aligned}$$

(2)

2.2 T-spherical Fuzzy Set

Mahmood et al. [21] defined the T-SFS as an extension of q-ROFS and SFS as follows:

Definition 5

[21] For any universal set L, a T-SFS is of the form

$$\begin{aligned} T=\{\langle \ell ,p(\ell ),n(\ell ),l(\ell )\rangle |\ell \in L\}, \end{aligned}$$

where $p,n,l: L\rightarrow [0,1]$ represent the MD, AD and NMD, respectively, with the condition $0 \le p^q(\ell )+n^q(\ell )+l^q(\ell )\le 1$ for positive number $q\ge 1$, and $r(\ell )= \root q \of {1-(p^q(\ell )+n^q(\ell )+l^q(\ell ))}$ is known as the degree of refusal of $\ell$ in T. To express information conveniently, the triplet (p, n, l) is known as a T-spherical fuzzy number (T-SFN).

A T-SFN is a generalized form of an existing fuzzy numbers and it reduces to:

• (i) Spherical fuzzy number; by taking q as 2.

• (ii) Picture fuzzy number; by taking q as 1.

• (iii) q-rung orthopair fuzzy number; by taking n as zero.

• (iv) Pythagorean fuzzy number; by taking n as zero and q as 2.

• (v) Intuitionistic fuzzy number; by taking n as zero and q as 1.

• (vi) Fuzzy number; by taking n and l as zero and q as 1.

2.3 The MM Operator and Its Weighted Forms

Let $[{\mathfrak {n}}]=\{1,2, \ldots , {\mathfrak {n}}\}$, $\mathbf {\eth }=(\eth _1,\eth _2,\ldots ,\eth _{{\mathfrak {n}}})$ and $\{{\mathfrak {a}}_{\epsilon }\mid \epsilon \in [{\mathfrak {n}}]\}$ be a set of non-negative numbers. Then we can define the following operators:

• 1. MM [35]:

  $$\begin{aligned}&\text {MM}^{\mathbf {\eth }}({\mathfrak {a}}_{1},{\mathfrak {a}}_{2},\ldots ,{\mathfrak {a}}_{{\mathfrak {n}}})\\&\qquad =\left( \frac{1}{\mathfrak {n!}}\sum \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}{{\mathfrak {a}}}_{\varrho (\epsilon )}^{\mathbf {\eth }_{\epsilon }}\right) ^{{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}; \end{aligned}$$

• 2. Weighted MM [35]:

  $$\begin{aligned}&\text {WMM}^{\mathbf {\eth }}_{\varkappa }({\mathfrak {a}}_{1},{\mathfrak {a}}_{2},\ldots , {\mathfrak {a}}_{{\mathfrak {n}}})\\&\quad =\left( \frac{1}{\mathfrak {n!}}\sum \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\prod \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\left( {\mathfrak {n}}\varkappa _{\varrho (\epsilon )}{\mathfrak {a}}_{\varrho (\epsilon )}\right) ^{\mathbf {\eth }_{\epsilon }} \right) ^{{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1} \mathbf {\eth }_{\epsilon }}}}; \end{aligned}$$

• 3. Dual MM [36]:

  $$\begin{aligned}&\text {DMM}^{\mathbf {\eth }}({\mathfrak {a}}_{1},{\mathfrak {a}}_{2},\ldots ,{\mathfrak {a}}_{{\mathfrak {n}}})\\&\quad =\frac{1}{\sum \nolimits _{{\epsilon }=1}^{{\mathfrak {n}}}\mathbf {\eth }_{\epsilon }}\left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\sum \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\mathbf {\eth }_{\epsilon }{{\mathfrak {a}}}_{\varrho (\epsilon )}\right) ^{\frac{1}{\mathfrak {n!}}}; \end{aligned}$$

• 4. Weighted dual MM [36]:

  $$\begin{aligned}&\text {WDMM} ^{\mathbf {\eth }}_{\varkappa }({\mathfrak {a}}_{1},{\mathfrak {a}}_{2},\ldots ,{\mathfrak {a}}_{{\mathfrak {n}}})\\&\quad ={\frac{1}{\sum \nolimits _{{\epsilon }=1}^{{\mathfrak {n}}}\mathbf {\eth }_{\epsilon }}} \left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\sum \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\mathbf {\eth }_{\epsilon } {{\mathfrak {a}}_{\varrho (\epsilon )}}^{{\mathfrak {n}}\varkappa _{\varrho (\epsilon )}}\right) ^{\frac{1}{\mathfrak {n!}}}, \end{aligned}$$

where $\varrho =\left( \begin{array}{cccc} 1 \,\,&{}\,\, 2 \,\,&{}\,\, \cdots \,\,&{}\,\, {\mathfrak {n}}\\ \varrho (1) \,\,&{}\,\, \varrho (2) \,\,&{}\,\, \cdots \,\,&{}\,\, \varrho ({\mathfrak {n}}) \end{array} \right)$ denotes any permutation of $[{\mathfrak {n}}]$ and ${\mathbb {S}}_{{\mathfrak {n}}}$ is the symmetric group on ${\mathfrak {n}}$ symbols.

3 2-Tuple Linguistic T-spherical Fuzzy Set

We introduce the 2TLT-SFS with its operational rules as a new advancement of FS theory, in this part. Inspired by the ideas of 2TL terms and T-SFSs, we develop the new concept of 2TLT-SFS by combining both the advantages of 2TL terms and T-SFS. The newly proposed set has flexibility due to the q-th power of MD, AD, and NMD. The mathematical representation of 2TLT-SFS is described as follows:

Definition 6

Let $S=\{s_{\jmath }|\jmath =0, 1,\ldots , \tau \}$ be a LTS with odd cardinality. If $(({s_{p}},\wp ),({s_{n}},\aleph ),(s_{l},\pounds ))$ is defined for $s_{p}, s_{n},s_{l} \in S,~ \wp ,\aleph ,\pounds \in [-0.5,0.5)$, where $({s_{p}},\wp ),({s_{n}},\aleph ), and (s_{l},\pounds )$ represent the MD, AD and NMD by 2TLSs. A 2TL T-spherical fuzzy set is defined as:

$$\begin{aligned} \aleph =\{\langle \ell ,(({s_{p}}(\ell ),\wp (\ell )),(s_{n}(\ell ),\aleph (\ell )),(s_{l}(\ell ),\pounds (\ell ))) \rangle | \ell \in L \} \end{aligned}$$

(3)

where $0\le \Delta ^{-1}({s_{p}}(\ell ),\wp (\ell ))\le \tau , 0\le \Delta ^{-1}({s_{n}}(\ell ),\aleph (\ell ))\le \tau , 0\le \Delta ^{-1}(s_{l}(\ell ),\pounds (\ell ))\le \tau ,$ and $0\le (\Delta ^{-1}({s_{p}}(\ell ),\wp (\ell )))^{q} + (\Delta ^{-1}({s_{n}}(\ell ),\aleph (\ell )))^{q} + (\Delta ^{-1}(s_{l}(\ell ),\pounds (\ell )))^{q} \le \tau ^{q}.$

For convenience, we say ${\Upsilon ^{\star }}=(({s_{{p}}},\wp ),({s_{{n}}},\aleph ),({s_{{l}}},\pounds ))$, a 2TLT-SFN, where $0\le \Delta ^{-1}({s_{p}},\wp )\le \tau$, $0\le \Delta ^{-1}({s_{n}},\aleph )\le \tau$, $0\le \Delta ^{-1}({s_{l}},\pounds )\le \tau$ and $0\le (\Delta ^{-1}({s_{p}},\wp ))^q+ (\Delta ^{-1}({s_{n}},\aleph ))^q+ (\Delta ^{-1}({s_{l}},\pounds ))^q\le \tau ^q.$

The conversion of a linguistic term into a linguistic 2-tuple consists of adding a value 0 as symbolic translation:

$$\begin{aligned} \Delta ({s_{{p}_{\jmath }}},{s_{{n}_{\jmath }}},{s_{{l}_{\jmath }}}) = (({s_{{p}_\jmath }},0),({s_{{n}_\jmath }},0),({s_{{l}_\jmath }},0)). \end{aligned}$$

(4)

To compare any two 2TLT-SFNs, their score value and accuracy value are defined as follows:

Definition 7

Let ${\Upsilon ^{\star }}=(({s_{p}},\wp ),({s_{n}},\aleph ),(s_{l},\pounds ))$ be a 2TLT-SFN. Then the score function $\mathfrak {g}^{\star }$ of a 2TLT-SFN ${{\Upsilon ^{\star }}}$, can be represented as

$$\begin{aligned}&\mathfrak {g}^{\star }({\Upsilon ^{\star }})=\Delta \left( \frac{\tau }{2}\left( 1+\left( \frac{\Delta ^{-1}({s_{p}},\wp )}{\tau }\right) ^{q}-\left( \frac{\Delta ^{-1}({s_{l}},\pounds )}{\tau }\right) ^{q}\right) \right) ,\nonumber \\&\quad \mathfrak {g}^{\star }({\Upsilon ^{\star }})\in [0, \tau ], \end{aligned}$$

(5)

and its accuracy function $\beth$ is defined as

$$\begin{aligned}&\beth ({\Upsilon ^{\star }})=\Delta \left( \tau \left( \left( \frac{\Delta ^{-1}({s_{p}},\wp )}{\tau }\right) ^{q}+\left( \frac{\Delta ^{-1}({s_{l}},\pounds )}{\tau }\right) ^{q}\right) \right) ,\nonumber \\&\qquad \beth ({\Upsilon ^{\star }})\in [0,\tau ]. \end{aligned}$$

(6)

3.1 Operational Laws for 2TLT-SFNs Based on Algebraic Operations

In this subpart, we will put forward the novel operational laws based on the 2TLT-SFNs, such as addition, multiplication, scalar multiplication, power, and ranking rules.

Definition 8

Let ${\Upsilon ^{\star }}=((s_{p},\wp ),(s_{n},\aleph ),(s_{l},\pounds )),$ ${\Upsilon ^{\star }_1}=((s_{p_{1}},\wp _{1}),(s_{n_{1}},\aleph _{1}),(s_{l_{1}},\pounds _{1}))$ and ${\Upsilon ^{\star }_2}=((s_{p_{2}},\wp _{2}),(s_{n_{2}},\aleph _{2}),(s_{l_{2}},\pounds _{2}))$ be three 2TLT-SFNs, $q\ge 1$, then

• 1.
  $$\begin{aligned}&{\Upsilon ^{\star }_{1}}\oplus {\Upsilon ^{\star }_{2}} ={\left( \begin{array}{l} \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{p_{1}},\wp _{1})}{\tau }\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{p_{2}},\wp _{2})}{\tau }\right) ^{q}\right) }\right) ,\\ \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{n_{1}},\aleph _{1})}{\tau }\right) \left( \frac{\Delta ^{-1}(s_{n_{2}},\aleph _{2})}{\tau }\right) \right) , \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{l_{1}},\pounds _{1})}{\tau }\right) \left( \frac{\Delta ^{-1}(s_{l_{2}},\pounds _{2})}{\tau }\right) \right) \end{array}\right) }; \end{aligned}$$
• 2.
  $$\begin{aligned}&{\Upsilon ^{\star }_{1}}\otimes {\Upsilon ^{\star }_{2}}={\left( \begin{array}{l} \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{p_{1}},\wp _{1})}{\tau }\right) \left( \frac{\Delta ^{-1}(s_{p_{2}},\wp _{2})}{\tau }\right) \right) ,\\ \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{n_{1}},\aleph _{1})}{\tau }\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{n_{2}}, \aleph _{2})}{\tau }\right) ^{q}\right) }\right) ,\\ \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{l_{1}},\pounds _{1})}{\tau }\right) ^{q}\right) \left( 1-\left( \frac{\Delta ^{-1}(s_{l_{2}}, \pounds _{2})}{\tau }\right) ^{q}\right) }\right) \end{array}\right) }; \end{aligned}$$
• 3.
  $$\begin{aligned}&\lambda {\Upsilon ^{\star }}\\&\quad =\left( \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{p},\wp )}{\tau }\right) ^{q}\right) ^{\lambda }}\right) ,\right. \\&\qquad \left. \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{n},\aleph )}{\tau }\right) ^{\lambda }\right) ,\right. \\&\qquad \quad \left. \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{l},\pounds )}{\tau }\right) ^{\lambda }\right) \right) ,~ \lambda >0; \end{aligned}$$
• 4.
  $$\begin{aligned}&{\Upsilon ^{\star }}^{\lambda }\\&\quad =\left( \Delta \left( \tau \left( \frac{\Delta ^{-1}(s_{p},\wp )}{\tau }\right) ^{\lambda }\right) ,\right. \\&\qquad \left. \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{n},\aleph )}{\tau }\right) ^{q}\right) ^{\lambda }}\right) ,\right. \\&\qquad \quad \left. \Delta \left( \tau \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}(s_{l},\pounds )}{\tau }\right) ^{q}\right) ^{\lambda }}\right) \right) ,\\&~ \lambda >0. \end{aligned}$$

Definition 9

Let ${\Upsilon ^{\star }_{1}}=(({s_{{p}_1}},{\wp _1}),({s_{{n}_1}},{\aleph _1}),({s_{{l}_1}},{\pounds _1}))$ and ${\Upsilon ^{\star }_{2}}=(({s_{{p}_2}},{\wp _2}),({s_{{n}_2}},{\aleph _2}),({s_{{l}_2}},{\pounds _2}))$ be two 2TLT-SFNs, then these two 2TLT-SFNs can be compared according to the following rules:

• (1) If $\mathfrak {g}^{\star }({\Upsilon ^{\star }_{1}})>\mathfrak {g}^{\star }({\Upsilon ^{\star }_{2}})$, then ${\Upsilon ^{\star }_{1}}>{\Upsilon ^{\star }_{2}}$;

• (2) If $\mathfrak {g}^{\star }({\Upsilon ^{\star }_{1}})=\mathfrak {g}^{\star }({\Upsilon ^{\star }_{2}})$, then

  • If $\beth ({\Upsilon ^{\star }_{1}})>\beth ({\Upsilon ^{\star }_{2}})$, then ${\Upsilon ^{\star }_{1}}> {\Upsilon ^{\star }_{2}}$;

  • If $\beth ({\Upsilon ^{\star }_{1}})=\beth ({\Upsilon ^{\star }_{2}})$, then ${\Upsilon ^{\star }_{1}} \sim {\Upsilon ^{\star }_{2}}$.

4 The 2TLT-SF Muirhead Mean Aggregation Operators

In this part, we expand the application criteria of the MM operator to the 2TLT-SF environment and introduce several novel AOs based on the 2TLT-SF operations to aggregate data. This part is concerned with the introduction of four novel AOs including the 2TLT-SFMM operator, the 2TLT-SFWMM operator, the 2TLT-SFDMM operator, and the 2TLT-SFWDMM operator. Moreover, we analyze their properties, as well as special cases. The proposed AOs satisfy the basic properties of aggregation including idempotency, monotonicity, and boundedness.

4.1 The 2TLT-SFMM Operator

Utilizing the Def. 6 and the novel operational rules of Def. 8, we develop the definition of 2-tuple linguistic T-spherical fuzzy Muirhead mean (2TLT-SFMM) operator as follows:

Definition 10

Let ${\Upsilon ^{\star }_{\epsilon }}=\left( \left( s_{p_{\epsilon }},\wp _{\epsilon }\right) ,\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) , \left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) \right) ~\left( {\epsilon }=1,2,\ldots ,{\mathfrak {n}}\right)$ be a collection of 2TLT-SFNs and $\mathbf {\eth }=(\mathbf {\eth }_{1},\mathbf {\eth }_{2},\ldots , \mathbf {\eth }_{{\mathfrak {n}}}) \in {\mathbb {R}}^{{\mathfrak {n}}}$ be a parameters vector, then the 2TLT-SFMM operator is given as

$$\begin{aligned}&\text {2TL}T\text {-SFMM}^{\mathbf {\eth }}({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\nonumber \\&\quad =\left( \frac{1}{\mathfrak {n!}}\oplus _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\otimes _{{\epsilon }=1}^{{\mathfrak {n}}}{\Upsilon ^{\star }}_{\varrho (\epsilon )}^{\mathbf {\eth }_{\epsilon }}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}. \end{aligned}$$

(7)

Theorem 1

Let ${\Upsilon ^{\star }_{\epsilon }}=\left( \left( s_{p_{\epsilon }},\wp _{\epsilon }\right) ,\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) ,\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) \right) ~\left( {\epsilon }=1,2,\ldots ,{\mathfrak {n}}\right)$ be a collection of 2TLT-SFNs and $\mathbf {\eth }=(\mathbf {\eth }_{1},\mathbf {\eth }_{2},\ldots , \mathbf {\eth }_{{\mathfrak {n}}}) \in {\mathbb {R}}^{{\mathfrak {n}}}$ be a vector of parameters. Then their aggregated result by applying the 2TLT-SFMM operator is also a 2TLT-SFN, and

$$\begin{aligned}&\text {2TL}T\text {-SFMM}^{\mathbf {\eth }}({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\nonumber \\&=\left( \begin{array}{l} \Delta \left( \tau \left( \root q \of {1-\left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }},\wp _{\epsilon }\right) }{\tau }\right) ^{q\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )}\right) \right) ^{\frac{1}{\mathfrak {n!}}}}\right) ^{{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}\right) ,\\ \Delta \left( \tau \left( \root q \of {1-\left( 1-\left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }}, \aleph _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )}\right) ^{\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}\right) ^{{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1} \mathbf {\eth }_{\epsilon }}}}}\right) \right) ,\\ \Delta \left( \tau \left( \root q \of {1-\left( 1-\left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}} \left( 1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}\right) ^{{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}}\right) \right) \end{array}\right) . \end{aligned}$$

(8)

Proof

By utilizing the novel operational laws of 2TLT-SFNs (see Def. 8), we have

$$\begin{aligned}&{{\Upsilon ^{\star }}}^{\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )}=\left( \begin{array}{l}\left( \Delta \left( \tau \left( \left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }},\wp _{\epsilon }\right) }{\tau } \right) ^{\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )}\right) \right) \right) ,\\ \Delta \left( \tau \left( \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{{\mathbf {\eth }_{\epsilon }}}}\right) \right) ,\\ \Delta \left( \tau \left( \root q \of {1-\left( 1-\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{{\mathbf {\eth }_{\epsilon }}}}\right) \right) \end{array}\right) , \\&\otimes _{{\epsilon }=1}^{{\mathfrak {n}}}{{\Upsilon ^{\star }}}^{\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )}=\left( \begin{array}{l}\Delta \left( \tau \left( \prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }}, \wp _{\epsilon }\right) }{\tau }\right) ^{\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )}\right) \right) ,\\ \Delta \left( \tau \left( \root q \of {1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{{\mathbf {\eth }_{\epsilon }}}}\right) \right) ,\\ \Delta \left( \tau \left( \root q \of {1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{{\mathbf {\eth }_{\epsilon }}}} \right) \right) \end{array}\right) . \end{aligned}$$

Moreover,

$$\begin{aligned}&\oplus _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\otimes _{{\epsilon }=1}^{{\mathfrak {n}}}{{\Upsilon ^{\star }}}^{\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )} =\left( \begin{array}{l}\Delta \left( \tau \left( \root q \of {1-\prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }},\wp _{\epsilon }\right) }{\tau }\right) _{\varrho (\epsilon )}^{q\mathbf {\eth }_{\epsilon }}\right) } \right) \right) ,\\ \Delta \left( \tau \left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\root q \of {1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{\mathbf {\eth }_{\epsilon }}}\right) \right) ,\\ \Delta \left( \tau \left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\root q \of {1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{\mathbf {\eth }_{\epsilon }}}\right) \right) \end{array}\right) . \end{aligned}$$

And,

$$\begin{aligned}&\frac{1}{\mathfrak {n!}}\oplus _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\otimes _{{\epsilon }=1}^{{\mathfrak {n}}}{{\Upsilon ^{\star }}}^{\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )}=\left( \begin{array}{l}\Delta \left( \tau \left( \root q \of {1-\left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }},\wp _{\epsilon }\right) }{\tau }\right) _{\varrho (\epsilon )}^{q\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}} \right) \right) ,\\ \left( \Delta \left( \tau \left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\root q \of {1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )}\right) ^{\mathbf {\eth }_{\epsilon }}}\right) ^{\frac{1}{\mathfrak {n!}}} \right) \right) ,\\ \left( \Delta \left( \tau \left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\root q \of {1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{\mathbf {\eth }_{\epsilon }}}\right) ^{\frac{1}{\mathfrak {n!}}}\right) \right) \end{array}\right) . \end{aligned}$$

Therefore,

$$\begin{aligned}&\left( \frac{1}{\mathfrak {n!}}\oplus _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\otimes _{{\epsilon }=1}^{{\mathfrak {n}}}{{\Upsilon ^{\star }}}^{\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )}\right) ^{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}\\&\quad =\left( \begin{array}{l}\Delta \left( \tau \left( \left( \root q \of {1-\left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }},\wp _{\epsilon }\right) }{\tau }\right) ^{q\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )} \right) \right) ^{\frac{1}{\mathfrak {n!}}}}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}\right) \right) ,\\ \Delta \left( \tau \left( \root q \of {1-\left( 1-\left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )}\right) ^{\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}\right) ^{{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}}\right) \right) ,\\ \Delta \left( \tau \left( \root q \of {1-\left( 1-\left( \prod _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )}\right) ^{\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}\right) ^{{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}}\right) \right) \end{array}\right) . \end{aligned}$$

$\square$

4.1.1 Some Fundamental Properties and Special Cases of 2TLT-SFMM Operator

Theorem 2

Let ${\Upsilon ^{\star }}_{\epsilon }=((s_{p_{\epsilon }},\wp _{\epsilon }),(s_{n_{\epsilon }},\aleph _{\epsilon }),(s_{l_{\epsilon }},\pounds _{\epsilon }))$ and ${\Upsilon ^{\star }}'_{\epsilon }=((s_{p_{\epsilon }}',\wp _{\epsilon }'),(s_{n_{\epsilon }}',\aleph _{\epsilon }'),(s_{l_{\epsilon }}',\pounds _{\epsilon }'))(\epsilon =1,2,\ldots ,{\mathfrak {n}})$ be two sets of 2TLT-SFNs; then the 2TLT-SFMM operator has the following properties:

• 1. (Idempotency) If all ${\Upsilon ^{\star }_{\epsilon }}$ $(\epsilon = 1, 2, \ldots , n )$ are equal, i.e., ${\Upsilon ^{\star }_{\epsilon }}= {\Upsilon ^{\star }}$ for all $\epsilon$, then

  $$\begin{aligned} \text {2TL}T\text {-SFMM}^{\mathbf {\eth }}({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})={\Upsilon ^{\star }}. \end{aligned}$$

• 2. (Monotonicity) Let ${\Upsilon ^{\star }_{\epsilon }}$ and $\acute{{\Upsilon ^{\star }}}_{\epsilon }$ $(\epsilon =1,2,\ldots ,{\mathfrak {n}})$ be two sets of 2TLT-SFNs; if $(s_{p_{\epsilon }},\wp _{\epsilon }) \ge (s'_{p_{\epsilon }},\wp '_{\epsilon })$, $(s_{n_{\epsilon }},\aleph _{\epsilon }) \le (s'_{n_{\epsilon }},\aleph '_{\epsilon })$, and $(s_{l_{\epsilon }},\pounds _{\epsilon }) \le (s'_{l_{\epsilon }},\pounds '_{\epsilon })$ for all $\epsilon$, then

  $$\begin{aligned}&\text {2TL}T\text {-SFMM}^{\mathbf {\eth }}({\Upsilon ^{\star }}_{1}, {\Upsilon ^{\star }}_{2},\ldots , {\Upsilon ^{\star }}_{{\mathfrak {n}}})\ge \text {2TL}T\text {-SFMM}\\&^{\mathbf {\eth }}({\Upsilon ^{\star }}'_{1},{\Upsilon ^{\star }}'_{2},\ldots ,{\Upsilon ^{\star }}'_{{\mathfrak {n}}}). \end{aligned}$$

• 3. (Boundedness) Let ${\Upsilon ^{\star }_{\epsilon }}(\epsilon =1,2,\ldots ,{\mathfrak {n}})$ be any set of 2TLT-SFNs, suppose

  $$\begin{aligned} {\Upsilon ^{\star }}^{-}= & {} \min _{\epsilon } {\Upsilon ^{\star }_{\epsilon }} = \left( \min _{\epsilon } (s_{p_{\epsilon }},\wp _{\epsilon }),\max _{\epsilon } (s_{n_{\epsilon }},\aleph _{\epsilon }),\right. \\&\left. \max _{\epsilon }(s_{l_{\epsilon }},\pounds _{\epsilon })\right) , \end{aligned}$$

   

  $$\begin{aligned} {\Upsilon ^{\star }}^{+}= & {} \max _{\epsilon } {\Upsilon ^{\star }_{\epsilon }} = \left( \max _{\epsilon } (s_{p_{\epsilon }},\wp _{\epsilon }),\min _{\epsilon } (s_{n_{\epsilon }},\aleph _{\epsilon }),\right. \\&\left. \min _{\epsilon }(s_{l_{\epsilon }},\pounds _{\epsilon })\right) . \end{aligned}$$

  Then,

  $$\begin{aligned}&{\Upsilon ^{\star }}^{-}\le \text {2TL}T\text {-SFMM}^{\mathbf {\eth }}({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\le {\Upsilon ^{\star }}^{+}. \end{aligned}$$

Theorem 3

Now, with regard to parameters $\mathbf {\eth }$ and q, we can describe certain specific cases of the 2TLT-SFMM operator.

• Case 1. When $\mathbf {\eth } =(1,0,\ldots ,0)$, the 2TLT-SFMM operator converts to the 2TLT-SF arithmetic averaging operator.

• Case 2. When $\mathbf {\eth } =(\lambda ,0,\ldots ,0)$, the 2TLT-SFMM operator converts to the 2TLT-SF generalized arithmetic averging operator.

• Case 3. When $\mathbf {\eth }=(1,1,0,\ldots ,0)$, the 2TLT-SFMM operator converts to the 2TLT-SF-BM operator.

• Case 4. When $\mathbf {\eth }=(\overbrace{1, 1, \ldots , 1}^{k} ,\overbrace{0, 0, \ldots , 0}^{{\mathfrak {n}}-k})$, the 2TLT-SFMM operator converts to the 2TLT-SF-MSM operator.

• Case 5. When $\mathbf {\eth } =(1,1,\ldots ,1)$, the 2TLT-SFMM operator converts to the 2TLT-SF geometric averging operator.

• Case 6. When $\mathbf {\eth } =(\frac{1}{{\mathfrak {n}}},\frac{1}{{\mathfrak {n}}},\ldots ,\frac{1}{{\mathfrak {n}}})$, the 2TLT-SFMM operator converts to the 2TLT-SF geometric averging operator.

• Case 7. When $q =2$, the 2TLT-SFMM operator converts to the 2TLT-SF Pythagorean fuzzy Muirhead mean operator.

• Case 8. When $q =1$, the 2TLT-SFMM operator converts to the 2TLT-SF intuitionistic fuzzy Muirhead mean operator.

4.2 The 2TLT-SFWMM Operator

There is no attention paid to the correlation among every given information and the significance of every individual given information in the proposed 2TLT-SFMM operator; instead, just the input factor $\mathbf {\eth }$ is taken into account. The significance of aggregating information is considered in order to handle real-world issues and we present the 2TLT-SFWMM operator to account for this. Utilizing the Def. 6 and the novel operational rules of Def. 8, we develop the definition of 2-tuple linguistic T-spherical fuzzy weighted Muirhead mean (2TLT-SFWMM) operator as follows:

Definition 11

Let ${\Upsilon ^{\star }_{\epsilon }}=\left( \left( s_{p_{\epsilon }},\wp _{\epsilon }\right) ,\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) ,\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) \right) \left( {\epsilon }=1,2,\ldots ,{\mathfrak {n}}\right)$ be a set of 2TLT-SFNs with weighting vectors $\varkappa =(\varkappa _{1},\varkappa _{2},\ldots ,\varkappa _{{\mathfrak {n}}})^{T}$, satisfying $\varkappa _{\epsilon }\in [0, 1],$ $\sum \limits _{\epsilon =1}^{{\mathfrak {n}}} \varkappa _{\epsilon }=1$ and $\mathbf {\eth }= (\mathbf {\eth }_{1}, \mathbf {\eth }_{2}, \ldots \mathbf {\eth }_{{\mathfrak {n}}})\in {\mathbb {R}}^{{\mathfrak {n}}}$, then the 2TLT-SFWMM operator is described as follows:

$$\begin{aligned}&\text {2TL}T\text {-SFWMM}^{\mathbf {\eth }}_{\varkappa }({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\nonumber \\&\quad = \left( \frac{1}{\mathfrak {n!}}\oplus _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\otimes ^{{\mathfrak {n}}}_{{\epsilon }=1}\left( {\mathfrak {n}}\varkappa _{\varrho (\epsilon )}{\Upsilon ^{\star }}_{\varrho (\epsilon )}\right) ^{\mathbf {\eth }_{\epsilon }}\right) ^{{\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1} \mathbf {\eth }_{\epsilon }}}}. \end{aligned}$$

(9)

By utilizing the novel operational laws of 2TLT-SFNs (see Def. 8), we can obtain Theorem 4.

Theorem 4

Let ${\Upsilon ^{\star }_{\epsilon }} =\left( \left( s_{p_{\epsilon }},\wp _{\epsilon }\right) ,\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) ,\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) \right) ~\left( {\epsilon }=1,2,\ldots ,{\mathfrak {n}}\right)$ be a set of 2TLT-SFNs, then their aggregated result by using the 2TLT-SFWMM operator is also a 2TLT-SFN, and

$$\begin{aligned}&\text {2TL}T\text {-SFWMM}^{\mathbf {\eth }}_{\varkappa }({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\nonumber \\&\quad = \left( \begin{array}{l}\Delta \left( \tau \left( \left( \root q \of {1-\left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }},\wp _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )} \right) ^{{\mathfrak {n}}\varkappa _{\varrho (\epsilon )}}\right) ^{\mathbf {\eth }_{\epsilon }} \right) \right) ^{\frac{1}{\mathfrak {n!}}}}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}\right) \right) , \\ \Delta \left( \tau \left( \root q \of {1-\left( 1- \left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-{\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }}, \aleph _{\epsilon }\right) }{\tau }\right) ^{q{\mathfrak {n}}\varkappa _{\varrho (\epsilon )}}_{\varrho _{(\epsilon )}}}\right) ^{\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}}\right) \right) ,\\ \Delta \left( \tau \left( \root q \of {1-\left( 1- \left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-{\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }}, \pounds _{\epsilon }\right) }{\tau }\right) ^{q{\mathfrak {n}}\varkappa _{\varrho (\epsilon )}}_{\varrho _{(\epsilon )}}}\right) ^{\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}}\right) \right) \end{array}\right) . \end{aligned}$$

(10)

4.2.1 Some Fundamental Properties and Special Cases of 2TLT-SFWMM Operator

The properties of monotonicity and boundedness are fulfilled by 2TLT-SFWMM, but the property of idempotency is not satisfied.

Now, with regard to parameters $\mathbf {\eth }$ and q, the 2TLT-SFWMM operator has the same certain specific cases as Theorem 3.

4.3 The 2TLT-SFDMM Operator

Utilizing the Def. 6 and the novel operational rules of Def. 8, we develop the definition of 2-tuple linguistic T-spherical fuzzy dual Muirhead mean (2TLT-SFDMM) operator as follows:

Definition 12

Let ${\Upsilon ^{\star }_{\epsilon }}=\left( \left( s_{p_{\epsilon }},\wp _{\epsilon }\right) ,\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) ,\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) \right) ~\left( {\epsilon }=1,2,\ldots ,{\mathfrak {n}}\right)$ be a set of 2TLT-SFNs and parameters vector are $\mathbf {\eth }=(\mathbf {\eth }_{1},\mathbf {\eth }_{2},\ldots ,\mathbf {\eth }_{{\mathfrak {n}}})\in {\mathbb {R}}^{{\mathfrak {n}}}$, and

$$\begin{aligned}&\text {2TL}T\text {-SFDMM}^{\mathbf {\eth }} ({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\nonumber \\&\quad = \frac{1}{\sum \nolimits _{{\epsilon }=1}^{{\mathfrak {n}}}\mathbf {\eth }_{\epsilon }}\left( \otimes _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\oplus _{{\epsilon }=1}^{{\mathfrak {n}}}\mathbf {\eth }_{\epsilon }{\Upsilon ^{\star }}_{\varrho (\epsilon )}\right) ^{\frac{1}{\mathfrak {n!}}}. \end{aligned}$$

(11)

By utilizing the novel operational laws of 2TLT-SFNs (see Def. 8), we can obtain Theorem 5.

Theorem 5

Let ${\Upsilon ^{\star }_{\epsilon }}=\left( \left( s_{p_{\epsilon }},\wp _{\epsilon }\right) ,\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) ,\left( s_{l_{\epsilon }}, \pounds _{\epsilon }\right) \right) ~\left( {\epsilon }=1,2,\ldots ,{\mathfrak {n}}\right)$ be a set of 2TLT-SFNs, then their aggregated result by applying the 2TLT-SFDMM operator is also a 2TLT-SFN, then

$$\begin{aligned}&\text {2TL}T\text {-SFDMM}^{\mathbf {\eth }} ({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\nonumber \\&=\left( \begin{array}{l}\Delta \left( \tau \left( \root q \of {1-\left( 1-\left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }},\wp _{\epsilon }\right) }{\tau }\right) ^{q} _{\varrho (\epsilon )}\right) ^{\mathbf {\eth }_k}\right) \right) ^{\frac{1}{\mathfrak {n!}}}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1} \mathbf {\eth }_{\epsilon }}}}}\right) \right) ,\\ \Delta \left( \tau \left( \left( \root q \of {1-\left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) }{\tau }\right) ^{q\mathbf {\eth } _{\epsilon }}_{\varrho (\epsilon )}\right) \right) ^{\frac{1}{\mathfrak {n!}}}} \right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}\right) \right) ,\\ \Delta \left( \tau \left( \left( \root q \of {1-\left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) }{\tau }\right) ^{q\mathbf {\eth }_{\epsilon }}_{\varrho (\epsilon )}\right) \right) ^{\frac{1}{\mathfrak {n!}}}} \right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}\right) \right) \end{array}\right) . \end{aligned}$$

(12)

4.3.1 Some Fundamental Properties and Special Cases of 2TLT-SFDMM Operator

The 2TLT-SFDMM operator has the same properties as Theorem 2.

Theorem 6

Now, with regard to parameters $\mathbf {\eth }$ and q, we can describe certain specific cases of the 2TLT-SFDMM operator.

• Case 1. When $\mathbf {\eth } =(1,0,\ldots ,0)$, the 2TLT-SFDMM operator converts to the 2TLT-SF geometric operator.

• Case 2. When $\mathbf {\eth } =(\lambda ,0,\ldots ,0)$, the 2TLT-SFDMM operator converts to the 2TLT-SF generalized geometric operator.

• Case 3. When $\mathbf {\eth }=(1,1,0,\ldots ,0)$, the 2TLT-SFDMM operator converts to the 2TLT-SF geometric BM operator.

• Case 4. When $\mathbf {\eth }=(\overbrace{1, 1, \ldots , 1}^{k} ,\overbrace{0, 0, \ldots , 0}^{{\mathfrak {n}}-k})$, the 2TLT-SFDMM operator converts to the 2TLT-SF dual MSM operator.

• Case 5. When $\mathbf {\eth } =(1,1,\ldots ,1)$, the 2TLT-SFDMM operator converts to the 2TLT-SF arithmetic averging operator.

• Case 6. When $\mathbf {\eth } =(\frac{1}{{\mathfrak {n}}},\frac{1}{{\mathfrak {n}}},\ldots ,\frac{1}{{\mathfrak {n}}})$, the 2TLT-SFDMM operator converts to the 2TLT-SF arithmetic averging operator.

• Case 7. When $q =2$, the 2TLT-SFDMM operator converts to the 2TLT-SF Pythagorean fuzzy dual MM operator.

• Case 8. When $q =1$, the 2TLT-SFDMM operator converts to the 2TLT-SF intuitionistic fuzzy dual MM operator.

4.4 The 2TLT-SFWDMM Operator

There is no attention paid to the correlation among every given information and the significance of every individual given information in the proposed 2TLT-SFDMM operator; instead, just the input factor $\mathbf {\eth }$ is taken into account. The significance of aggregating information is considered in order to handle real-world issues and we present the 2TLT-SFWDMM operator to account for this. Utilizing the Def. 6 and the novel operational rules of Def. 8, we develop the definition of 2-tuple linguistic T-spherical fuzzy weighted dual Muirhead mean (2TLT-SFWDMM) operator as follows:

Definition 13

Let ${\Upsilon ^{\star }_{\epsilon }}=\left( \left( s_{p_{\epsilon }},\wp _{\epsilon }\right) ,\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) ,\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) \right) \left( {\epsilon }=1,2,\ldots ,{\mathfrak {n}}\right)$ be a set of 2TLT-SFNs with weighting vectors $\varkappa =(\varkappa _{1},\varkappa _{2},\ldots ,\varkappa _{{\mathfrak {n}}})^{T}$, satisfying $\varkappa _{\epsilon }\in [0, 1],$ $\sum \nolimits _{\epsilon =1}^{{\mathfrak {n}}} \varkappa _{\epsilon }=1$ and $\mathbf {\eth }= (\mathbf {\eth }_{1}, \mathbf {\eth }_{2}, \ldots \mathbf {\eth }_{{\mathfrak {n}}})\in {\mathbb {R}}^{{\mathfrak {n}}}$, then the 2TLT-SFWDMM operator is describe as follows:

$$\begin{aligned}&\text {2TL}T\text {-SFWDMM}^{\mathbf {\eth }}_{\varkappa }({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\nonumber \\&\quad ={\frac{1}{\sum \nolimits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}\left( \otimes _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\oplus ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }({\Upsilon ^{\star }}_{\varrho (\epsilon )})^{{\mathfrak {n}}\varkappa _{\varrho (\epsilon )}}\right) ^{\frac{1}{\mathfrak {n!}}}. \end{aligned}$$

(13)

By utilizing the novel operational laws of 2TLT-SFNs (see Def. 8), we can obtain Theorem 7.

Theorem 7

Let ${\Upsilon ^{\star }_{\epsilon }}= \left( \left( s_{p_{\epsilon }},\wp _{\epsilon }\right) ,\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) ,\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) \right) ~\left( {\epsilon }=1,2,\ldots ,{\mathfrak {n}}\right)$ be a set of 2TLT-SFNs, then aggregated result by applying the 2TLT-SFWDMM operation is also a 2TLT-SFN, and

$$\begin{aligned}&\text {2TL}T\text {-SFWDMM}^{\mathbf {\eth }}_{\varkappa }({\Upsilon ^{\star }}_{1},{\Upsilon ^{\star }}_{2},\ldots ,{\Upsilon ^{\star }}_{{\mathfrak {n}}})\nonumber \\&=\left( \begin{array}{l} \Delta \left( \tau \left( \root q \of {1-\left( 1-\left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( \frac{\Delta ^{-1}\left( s_{p_{\epsilon }}, \wp _{\epsilon }\right) }{\tau }\right) ^{q{\mathfrak {n}}\varkappa _{\varrho (\epsilon )}}_{\varrho (\epsilon )}\right) ^{\mathbf {\eth }_{\epsilon }} \right) \right) ^{\frac{1}{\mathfrak {n!}}}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1}\mathbf {\eth }_{\epsilon }}}}}\right) \right) ,\\ \Delta \left( \tau \left( \left( \root q \of {1- \left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}\left( s_{n_{\epsilon }},\aleph _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )}\right) ^{{\mathfrak {n}}\varkappa _{\varrho (\epsilon )}}\right) ^{\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1 }\mathbf {\eth }_{\epsilon }}}}\right) \right) ,\\ \Delta \left( \tau \left( \left( \root q \of {1- \left( \prod \limits _{\varrho \in {\mathbb {S}}_{{\mathfrak {n}}}}\left( 1-\prod \limits _{{\epsilon }=1}^{{\mathfrak {n}}}\left( 1-\left( 1-\left( \frac{\Delta ^{-1}\left( s_{l_{\epsilon }},\pounds _{\epsilon }\right) }{\tau }\right) ^{q}_{\varrho (\epsilon )}\right) ^{{\mathfrak {n}}\varkappa _{\varrho (\epsilon )}}\right) ^{\mathbf {\eth }_{\epsilon }}\right) \right) ^{\frac{1}{\mathfrak {n!}}}}\right) ^{{\frac{1}{\sum \limits ^{{\mathfrak {n}}}_{{\epsilon }=1 }\mathbf {\eth }_{\epsilon }}}}\right) \right) \end{array}\right) . \end{aligned}$$

(14)

4.4.1 Some Fundamental Properties and Special Cases of 2TLT-SFWDMM Operator

The properties of monotonicity and boundedness are fulfilled by 2TLT-SFWDMM, but the property of idempotency is not satisfied.

Now, with regard to parameters $\mathbf {\eth }$ and q, the 2TLT-SFWDMM operator has the same certain specific cases as Theorem 6.

5 The 2TLT-SF-SWARA-COPRAS Method

Under the 2TLT-SF environment, this part develops an interconnected framework that combines the SWARA and COPRAS models. The SWARA and COPRAS methods play a vital role in the MAGDM environment. The relative importance and initial assessment of alternatives for each attribute are evaluated by the DEs opinion throughout the SWARA model, which utilizes the weighting scheme. Afterward, each attribute’s relative weight is calculated. Finally, the overall ranking and rating of the attributes is determined by the following strategy characteristics:

• (1) The attributes are monetary in the natural environment.

• (2) The attributes are independent of each other.

In the SWARA method, the relative importance $\Bbbk _{\epsilon }$ of the $\epsilon ^{th}$ attribute is determined as the input information based on the idea of the DEs. Additionally, the COPRAS method is used to assess the maxima and minima index values, and the effect of maxima and minima indexes of attributes on the assessment of the results is considered separately. Accordingly, the following features are considered for this method:

• (1) It is a compensatory method.

• (2) The qualitative attributes are converted into quantitative attributes.

Thus, an interconnected 2TLT-SF-SWARA-COPRAS framework is introduced in order to assess subjective attributes in weight and to assess the priority order of alternatives. The following is a description of the framework’s key steps:

Phase 1.:

Establish the attributes as well as the alternatives.

The goal of the MAGDM process is to choose the best alternative from a set of m alternatives $\gimel =\{\gimel _{1},\gimel _{2},\ldots ,\gimel _{m}\}$ under the attribute set $\hbar =\{\hbar _{1},\hbar _{2},\ldots ,\hbar _{n}\}$. Assume a group of DEs appointed to serve on a panel $E=\{e_{1},e_{2},\ldots ,e_{\Lambda }\}$, which was formulated in order to find the optimal alternative(s). Let $\eta =\left( \eta _{\kappa \epsilon }^{\lambda }\right) , \kappa = 1(1)m, \epsilon = 1(1)n$ be the linguistic decision matrix provided by the DEs, where $\eta _{\kappa \epsilon }^{\lambda }$ shows the assessed values of an alternative $\eta _{\kappa }$ over attribute $\hbar _{\epsilon }$ in the form of linguistic values for $\lambda ^{th}$ expert.

Phase 2.:

Construct the aggregated 2TLT-SF decision matrix.

We stimulate the 2TLT-SFWMM and 2TLT-SFWDMM operators to obtain the decision matrix subsequently, we achieve $R =\left( \eta _{\lambda \epsilon }\right) _{\Lambda \times n}$ from Eqs. (10) and (14).

Phase 3.:

Utilize the SWARA model for determining the weights of attributes.

SWARA examines pairwise directly higher to lower-ranked attributes after rating the attribute. Following that, a relative rate is determined, as well as the weight for addressing MAGDM issues is estimated and assessed. The following steps are used to estimate attributes weights using SWARA:

Phase 3.1.:

Determine the measurements for 2TLT-SF information. Score values $\mathfrak {g}^{\star }(\eta _{\lambda \epsilon })$ of 2TLT-SFNs acquired by Eq. (5) are estimated by Def. 7.

Phase 3.2.:

Quantify the attribute’s priority ranking. The attributes are organized from the highest to the lowest ranked attribute according to the DE’s priorities.

Phase 3.3.:

Assess the relative importance of the valuation of the score. The attribute that’s also favored in the second rank is used to calculate relative importance, and the attribute $\epsilon$ and attribute $\epsilon -1$ are used to calculate consecutive relative importance.

Phase 3.4.:

Make a calculation of the relative factor. The factor $\Bbbk _\epsilon$ is provided as:

$$\begin{aligned} \Bbbk _{\epsilon }=\left\{ \begin{array}{cc} 1,&{} \quad \epsilon =1\\ {\mathfrak {s}}_{\epsilon }+1, &{} \quad \epsilon >1. \\ \end{array}\right. \end{aligned}$$

(15)

Here ${\mathfrak {s}}_{\epsilon }$ represents the relative importance of score value [46].

Phase 3.5.:

Calculate the approximate weights. The weight that has been reassessed, $\Im _{\epsilon }$, is described as:

$$\begin{aligned} \Im _{\epsilon }=\left\{ \begin{array}{cc} 1,&{} \quad \epsilon =1\\ \frac{\Im _{\epsilon -1}}{\Bbbk _{\epsilon }},&{} \quad \epsilon >1. \\ \end{array}\right. \end{aligned}$$

(16)

Phase 3.6.:

Determine the weights for each attribute. The following formula is used to determine the attributes weights:

$$\begin{aligned} \varkappa _{\epsilon }=\frac{\Im _{\epsilon }}{\sum _{\epsilon =1}^{n}\Im _{\epsilon }}. \end{aligned}$$

(17)

Phase 4.:

Calculate the assessment values of the favorable-type and non-favorable-type attributes.

Each alternative is defined throughout the designed model in terms of its total of maxima $\breve{\alpha }_{\kappa }$ (favorable type) and minima $\breve{\beta }_{\kappa }$ (non-favorable type); i.e., maxima and minima, respectively, produce the optimal outcomes. In such circumstances, $\breve{\alpha }_{\kappa }$ and $\breve{\beta }_{\kappa }$ can be obtained as described below.

Let $\Delta =\{1,2,\ldots ,{\mathfrak {l}}\}$ be a favorable-type attribute. Afterward, for every alternative, we compute the greatest possible index value in contexts of 2TLT-SFNs, as follows:

$$\begin{aligned} \breve{\alpha }_{\kappa }=\oplus _{\epsilon =1}^{{\mathfrak {l}}}\varkappa _{\epsilon }\eta _{\kappa \epsilon }, ~ \kappa =1(1)m. \end{aligned}$$

(18)

Let $\nabla =\{{\mathfrak {l}}+1,{\mathfrak {l}}+2,\ldots ,n\}$ be a non-favorable-type attribute. Afterward, for every alternative, we assess the index value in contexts of 2TLT-SFNs as follows:

$$\begin{aligned} \breve{\beta }_{\kappa }=\oplus _{\epsilon ={\mathfrak {l}}+1}^{n}\varkappa _{\epsilon }\eta _{\kappa \epsilon }, ~ \kappa =1(1)m. \end{aligned}$$

(19)

Here ${\mathfrak {l}}$ represents favorable types and n represents the attributes.

Phase 5.:

Further, we calculate the relative degree $\Gamma _{\kappa }$ of each alternative $\gimel _{\kappa }(\kappa =1(1)m)$. Obviously, the bigger the value of $\Gamma _{\kappa }$, the higher the importance of the alternative. The $\Gamma _{\kappa }$ can be obtained as follows:

$$\begin{aligned} \Gamma _{\kappa }=\mathfrak {g^{\star }}(\breve{\alpha }_{\kappa })+\frac{\min _{\kappa }\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })\sum \nolimits _{\kappa =1}^{p}\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })}{\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })\sum \nolimits _{\kappa =1}^{p}\frac{\min _{\kappa }\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })}{\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })}}, \quad \kappa =1(1)m.\nonumber \\ \end{aligned}$$

(20)

Here, $\mathfrak {g^{\star }}(\breve{\alpha }_{\kappa })$ is the score value of $\breve{\alpha }_{\kappa }$ and $\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })$ is the score value of $\breve{\beta }_{\kappa }$. Eq. (20) can be simplified as:

$$\begin{aligned} \Gamma _{\kappa }=\mathfrak {g^{\star }}(\breve{\alpha }_{\kappa })+\frac{\sum \nolimits _{\kappa =1}^{p}\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })}{\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })\sum \nolimits _{\kappa =1}^{p}\frac{1}{\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })}}, \quad \kappa =1(1)m.\nonumber \\ \end{aligned}$$

(21)

The $\Gamma _{\kappa }$ from Eq. (21) reflects the satisfaction measure of each alternative. Based on the $\Gamma _{\kappa }$, maximal value $\mathfrak {g^{\star }}$ can be determined.

Phase 6.:

Calculate the summary of priority.

$$\begin{aligned} \mathfrak {g^{\star }}=\max _{\kappa }\Gamma _{\kappa }, ~~~\kappa =1(1)m. \end{aligned}$$

(22)

Thus, the alternative(s) with the associated maximal relative degree is selected among the possible alternatives. Moreover, we can ascertain the utility degree ${\mathscr {U}}_{\kappa }$ of each alternative with the aid of the $\Gamma _{\kappa }$. The ${\mathscr {U}}_{\kappa }$ can be determined by using the formula below:

$$\begin{aligned} {\mathscr {U}}_{\kappa }=\left( \frac{\Gamma _{\kappa }}{\Gamma _{\max }}\right) \times 100\%, ~~~\kappa =1(1)m. \end{aligned}$$

(23)

Hence, the bigger the value ${\mathscr {U}}_{\kappa }$, the higher is the rank of the alternative $\gimel _{\kappa }$.

The description about the steps of proposed model is given in the following flowchart (see Fig. 3).

Fig. 3

The flowchart of developed MAGDM approach

Fig. 4

The capacity and service date of 9 hydropower plants in Pakistan

6 Numerical Illustration

The most appropriate alternative is selected based on the combination of weighted attributes and the data provided by the DEs in the MAGDM environment. To validate our model, we tackle the problem of selecting the best hydropower plants to overcome the minimum supply of electricity in Pakistan.

6.1 The Problem Description

Pakistan has extensive hydropower resources, and the government is passionate about serving private investors in boosting the hydropower system in the country. Pakistan has approximately 60,000 MW of hydropower resources, the majority of which are located in Punjab, Gilgit-Baltistan, Khyber Pakhtunkhwa, Azad Jammu, and Kashmir. Electricity is a stimulant for a country’s socio-economic status raise. Furthermore, approximately 70% of Pakistan’s population now has reliable electricity. Pakistan possessed a very small power framework of only 60 MW capacity for its 31.5 million people when it achieved independence. When WAPDA was established in 1958, the total national hydropower capacity was increased to 119 MW. Pakistan was granted access to 142 MAF (Indus 93, Jhelum 23, and Chenab 26) of surface water with the agreement of the Indus Basin Water Treaty in 1960. Although, there is plenteous hydropower capacity that has yet to be recognized. Pakistan’s hydropower resources are primarily concentrated in mountainous areas in the country’s northwestern region. The hydropower resources in the south, which are restricted, primarily consist of small to medium-sized strategies based on barrages and canal falls. Pakistan’s hydropower resources are divided into six sectors: (1) Punjab (1698 MW); (2) Gilgit-Baltistan (50,000 MW); (3) Khyber Pakhtunkhwa (30,000 MW); (4) Balochistan (1292 MW); (5) Azad Jammu and Kashmir (1036 MW); (6) Sindh (2402 MW). In this research article, we choose the nine hydropower plants of Pakistan as a case study to show which hydropower plants produce the largest amount of electricity in Pakistan.

Further, the detailed description about the nine hydropower plants in Pakistan is illustrated in Fig. 4.

Following an initial assessment, let $\{\gimel _{1},\gimel _{2},\ldots ,\gimel _{9}\}$ be a set of nine hydropower plants in Pakistan and let $\{\hbar _{1},\hbar _{2},\hbar _{3},\hbar _{4}\}$ be a set of four attributes with weighting vector $\varkappa =(0.2412, 0.2668, 0.2427, 0.2493)^{T}$. Suppose, nine hydropower plants are evaluated by four engineers $E=\{e_{1},e_{2},e_{3},e_{4}\}$ (Civil engineers, mechanical engineers, electrical engineers, and system engineers), with weighting vector $\varpi =(0.2 ,0.4 ,0.3, 0.1)^{T}$ for choosing the best hydropower plants to provide the best electrical supply in the country. In order to quantify each LTS $S^{9}$={ $s^{9}_{0}$ : extremely poor, $s^{9}_{1}$ : very poor, $s^{9}_{2}$ : poor, $s^{9}_{3}$ : slightly poor, $s^{9}_{4}$ : fair, $s^{9}_{5}$ : slightly good, $s^{9}_{6}$ : good, $s^{9}_{7}$ : very good, $s^{9}_{8}$ : extremely good }, four engineers $E_{e} (e = 1, 2, 3, 4)$ provide their opinions. Based on their experience, each decision engineer has an opinion for the selection of best hydropower plants. These hydropower plants are:

• (1) Mangla hydropower plant ($\gimel _{1}$);

• (2) Warsak hydropower plant ($\gimel _{2}$);

• (3) Tarbela hydropower plant ($\gimel _{3}$);

• (4) Neelum-Jhelum hydropower plant ($\gimel _{4}$);

• (5) Ghazi-Barotha hydropower plant ($\gimel _{5}$);

• (6) Chashma Barrage hydropower plant ($\gimel _{6}$);

• (7) Gomal Zam hydropower plant ($\gimel _{7}$);

• (8) Satpara hydropower plant ($\gimel _{8}$);

• (9) Darawat hydropower plant ($\gimel _{9}$).

Further details about the nine hydropower plants of Pakistan can be seen in Fig. 5. The nine above described hydropower plants are evaluated according to four attributes, including:

• 1. Renewable ($\hbar _{1}$);

• 2. Providing flood control ($\hbar _{2}$);

• 3. Irrigation support ($\hbar _{3}$);

• 4. Clean drinking water ($\hbar _{4}$).

In order to avoid the risk of flooding and over-filling of water, engineers should evaluate the effective qualities of hydropower plants concerning all attributes in conjunction with their interaction in the hydropower plants center and identify the most suitable hydropower plants to provide the best electrical supply, according to the guidelines of engineers. Each decision engineer uses the 2TLT-SFNs to assess each hydropower plant’s ability to control the shortage supply of electricity in Pakistan. Following the engineers’ recommendations, the 2TLT-SFNs for the selection of the best hydropower plants are recorded in Table 1.

Fig. 5

Graphical representation of 9 hydropower plants in Pakistan

Table 1 The assessing matrix with 2TLT-SFNs by four engineers

6.2 The Outcomes of a Case Study

In order to choose the most desirable hydropower plants, the 2TLT-SFWMM and 2TLT-SFWDMM operators are used to solve the MAGDM problem with 2TLT-SFNs, which involves the following computing steps:

6.2.1 Decision-Making Procedure Based on the 2TLT-SFWMM Operator

On the basis of the 2TLT-SFNs matrix (see Table 1) and by utilizing Eq. (10), the collective 2TLT-SF assessing matrix is computed. The aggregated outcomes are listed in Table 2.

Table 2 Collective 2TLT-SF assessing matrix by the 2TLT-SFWMM operator

Compute the weights of attributes $\varkappa _{\epsilon }(\epsilon =1,2,3,4)$ with the help of the 2TLT-SF-SWARA method and by utilizing Eqs. (15) to (17) as listed in Table 3.

Table 3 Assessed values of attributes weights by utilizing the 2TLT-SF-SWARA method

Construct the assessing matrix (see Table 4) of favorable and non-favorable-type attributes by utilizing Eqs. (10), (18), and (19).

Table 4 Assessing values of favorable and non-favorable-type attributes by 2TLT-SFWMM operator

Calculate the scoring outcomes of hydropower plants for favorable ($\mathfrak {g^{\star }}(\breve{\alpha }_{\kappa })$) and non-favorable ($\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })$) type attributes by utilizing Eq. (5) and establishing the ranking order by using the 2TLT-SF-COPRAS method. The evaluation outcomes are listed in Table 5.

Table 5 Assessing outcomes of hydropower plants and ranking order by utilizing the 2TLT-SF-COPRAS method

The ranking of nine hydropower plants by utilizing the 2TLT-SFWMM operator is shown in Fig. 6.

6.2.2 Decision-Making Procedure Based on the 2TLT-SFWDMM Operator

On the basis of the 2TLT-SFNs matrix (see Table 1) and by utilizing Eq. (14), the collective 2TLT-SF assessing matrix is computed. The aggregated outcomes are listed in Table 6.

Fig. 6

The graphical interpretation about the ranking of 9 hydropower plants

Table 6 Collective 2TLT-SF assessing matrix by the 2TLT-SFWDMM operator

Table 7 Assessed values of attributes weights by utilizing the 2TLT-SF-SWARA method

Table 8 Assessing values of favorable and non-favorable-type attributes by 2TLT-SFWDMM operator

Table 9 Assessing outcomes of hydropower plants and ranking order by utilizing the 2TLT-SF-COPRAS

Compute the weights of attributes $\varkappa _{\epsilon }(\epsilon =1,2,3,4)$ with the help of the 2TLT-SF-SWARA method and by utilizing Eqs. (15) to (17) as listed in Table 7.

Construct the assessing matrix (see Table 8) of favorable and non-favorable-type attributes by utilizing Eqs. (14), (18), and (19).

Calculate the scoring outcomes of hydropower plants for favorable ($\mathfrak {g^{\star }}(\breve{\alpha }_{\kappa })$) and non-favorable ($\mathfrak {g^{\star }}(\breve{\beta }_{\kappa })$) type attributes by utilizing Eq. (5) and establishing the ranking order by using the 2TLT-SF-COPRAS method. The evaluation outcomes are listed in Table 9.

The ranking of nine hydropower plants by utilizing the 2TLT-SFWDMM operator is shown in Fig. 7.

6.3 Sensitivity Analysis

6.3.1 Effects of Parameters $\mathbf {\eth }$ and q on the Ranking Outcomes by 2TLT-SFWMM Operator

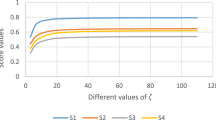
When aggregating data, it should be observed that the parameters $\mathbf {\eth }$ and q of the 2TLT-SFWMM operator serve as an essential role in determining the outcomes. As an initial step, in order to investigate the impact of the parameter $\mathbf {\eth }$ on the aggregation results, we vary the value of the parameter $\mathbf {\eth }$ in Phase 2 of the developed MAGDM approach. The desirable outcomes of hydropower plants are depicted in Table 10 (Suppose $q = 4$). From Table 10, we can also see that the hydropower plants are ranked in order of importance as parameter $\mathbf {\eth }$ take different values by utilizing the 2TLT-SFWMM operator. That parameter $\mathbf {\eth }$ indicates the degree of interrelations among attributes due to the alternate order of hydropower plants. The interrelationship pattern of attributes changes by using the 2TLT-SFWMM operator, as the engineer chooses alternate values of the $\mathbf {\eth }$ parameter. Thus, the ranking orders of hydropower plants differ from one another in terms of importance.

We examine the impact of the parameter q on the aggregated outcomes by experimenting with various values of the parameter q in Phase 4 of the developed MAGDM approach. The desirable outcomes of hydropower plants are depicted in Table 11 (Suppose $\mathbf {\eth } = (1,1,1,1)$). We can also see that the hydropower plants are ranked in order of importance as parameter q take different values by utilizing the 2TLT-SFWMM operator. So as the parameter q varies, the ranking order of hydropower plants shifts, while the best hydropower plants remains unchanged in the procedure. During the DM process, the engineer must choose the optimal hydropower plants with the variation of the parameter q for effectively modeling the 2TLT-SF data. On the basis of the attributes’ evaluating values, the parameter q can be set to the lowest integer that meets the inequality’s requirements as $0\le (\Delta ^{-1}({s_{p}(\ell )},\wp (\ell )))^q+ (\Delta ^{-1}({s_{n}(\ell )},\aleph (\ell )))^q+ (\Delta ^{-1}({s_{l}(\ell )},\pounds (\ell )))^q\le \tau ^q$.

6.3.2 Effects of Parameters $\mathbf {\eth }$ and q on the Ranking Outcomes by 2TLT-SFWDMM Operator

When aggregating data, it should be observed that the parameters $\mathbf {\eth }$ and q of the 2TLT-SFWDMM operator serve as an essential role in determining the outcomes. As an initial step, in order to investigate the impact of the parameter $\mathbf {\eth }$ on the aggregation results, we vary the value of the parameter $\mathbf {\eth }$ in Phase 2 of the developed MAGDM approach. The desirable outcomes of hydropower plants are depicted in Table 12 (Suppose $q = 4$). From Table 12, we can also see that the hydropower plants are ranked in order of importance as parameter $\mathbf {\eth }$ take different values by utilizing the 2TLT-SFWDMM operator. That parameter $\mathbf {\eth }$ indicates the degree of interrelations among attributes due to the alternate order of hydropower plants. The interrelationship pattern of attributes changes by using the 2TLT-SFWDMM operator, as the engineer chooses alternate values of the $\mathbf {\eth }$ parameter. Thus, the ranking orders of hydropower plants differ from one another in terms of importance.

We examine the impact of the parameter q on the aggregated outcomes by experimenting with various values of the parameter q in Phase 4 of the developed MAGDM approach. The desirable outcomes of hydropower plants are depicted in Table 13 (Suppose $\mathbf {\eth } = (1,1,1,1)$). We can also see that the hydropower plants are ranked in order of importance as parameter q take different values by utilizing the 2TLT-SFWDMM operator. So as the parameter q varies, the ranking order of hydropower plants shifts, while the best hydropower plants remains unchanged in the procedure. During the DM process, the engineer must choose the optimal hydropower plants with the variation of the parameter q for effectively modeling the 2TLT-SF data. On the basis of the attributes’ evaluating values, the parameter q can be set to the lowest integer that meets the inequality’s requirements as $0\le (\Delta ^{-1}({s_{p}(\ell )},\wp (\ell )))^q+ (\Delta ^{-1}({s_{n}(\ell )},\aleph (\ell )))^q+ (\Delta ^{-1}({s_{l}(\ell )},\pounds (\ell )))^q\le \tau ^q$.

Fig. 7

The graphical interpretation about the ranking of 9 hydropower plants

Table 10 Score functions and ranking outcomes according to the parameter $\mathbf {\eth }$ by 2TLT-SFWMM operator

Table 11 Score functions and ranking outcomes according to the parameter q by 2TLT-SFWMM operator

Table 12 Score functions and ranking outcomes according to the parameter $\mathbf {\eth }$ by 2TLT-SFWDMM operator

Table 13 Score functions and ranking outcomes according to the parameter q by 2TLT-SFWDMM operator

6.4 Comparative Analysis

6.4.1 Comparative Analysis with Different MAGDM Methods

We compare the new method 2TLT-SF-SWARA-COPRAS predicated on 2TLT-SFNs and 2TLT-SFWMM (2TLT-SFWDMM) operator with different methodologies to accurately reflect the reasonability and effectiveness of the new method introduced in this research paper. However, there are some minor differences in the ordering of judgments, as shown in Figs. 8, 9, 10, 11, 12 and 13, it is useful to note that the best decisions are consistently different. In rationality, each method has both upsides and downsides. To rank the hydropower plants, the 2TLT-SF-SWARA-EDAS method computes the distances of hydropower plants from the average ratings of attributes. The 2TLT-SF-SWARA-CODAS method is used to determine the worthiness of hydropower plants by using the Euclidean distance as the primary criterion and the Hamming distance as the secondary criterion, both are calculated by using the distance from the negative ideal point. The 2TLT-SF-SWARA-TOPSIS method is based on an analysis of all of the problems of hydropower plants. Moreover, it is discovered that the score function values of the hydropower plants under different assessments differ only slightly. In general, the four methods can efficiently and successfully select the best hydropower plants. Furthermore, the proposed 2TLT-SF-SWARA-COPRAS methodology needs to take into account the influence factors of DEs and the uncertainty in DM, resulting in more credible ranking results.

Fig. 8

2TLT-SFWMM-SWARA-EDAS [53]

Fig. 9

2TLT-SFWDMM-SWARA-EDAS [53]

Fig. 10

2TLT-SFWMM-SWARA-CODAS [54]

Fig. 11

2TLT-SFWDMM-SWARA-CODAS [54]

Fig. 12

2TLT-SFWMM-SWARA-TOPSIS [55]

Fig. 13

2TLT-SFWDMM-SWARA-TOPSIS [55]

Fig. 14

2TLSFWMM-SWARA-COPRAS [56]

Fig. 15

2TLSFWDMM-SWARA-COPRAS [56]

Fig. 16

2TLPFWMM-SWARA-COPRAS [57]

Fig. 17

2TLPFWDMM-SWARA-COPRAS [57]

6.4.2 Comparative Analysis with Different Generalized Fuzzy Sets

We compare the new method 2TLT-SF-SWARA-COPRAS predicated on 2TLT-SFNs and 2TLT-SFWMM (2TLT-SFWDMM) operator with different extensions of FSs to accurately reflect the reasonability and effectiveness of the new method introduced in this research paper. However, there are some minor differences in the ordering of judgments, as shown in Figs. 14, 15, 16 and 17, it is useful to note that the best decisions are consistently different. In rationality, each extension of FS has both upsides and downsides. To rank the hydropower plants evaluating values, the parameter q can be set to the lowest integer that meets the inequality’s requirements as $0\le (\Delta ^{-1}({s_{p}(\ell )},\wp (\ell )))^2+ (\Delta ^{-1}({s_{n}(\ell )},\aleph (\ell )))^2+ (\Delta ^{-1}({s_{l}(\ell )},\pounds (\ell )))^2\le \tau ^2$ and $0\le \Delta ^{-1}({s_{p}(\ell )},\wp (\ell ))+ \Delta ^{-1}({s_{n}(\ell )},\aleph (\ell ))+ \Delta ^{-1}({s_{l}(\ell )},\pounds (\ell ))\le \tau$ for 2TLSFS, and 2TLPFS, respectively. Moreover, it is discovered that the score function values of the hydropower plants under different assessments differ slightly. In general, these two generalized FSs can be efficiently and successfully applied to the selection of the best hydropower plants.

7 Concluding Remarks

The interpretation area for assessment data in several existing extensions of FSs is restricted, making it difficult to cope with the problem of assessing hydropower plants under a complicated situation, which is full of uncertainties. To overcome this difficulty, we have employed a new generalization of FSs, termed as 2TLT-SFSs. Based on the 2TLT-SFWMM and 2TLT-SFWDMM operators, a general framework has been developed for MAGDM with 2TLT-SF information. The 2TLT-SFS permits the total of the membership, abstinence, and non-membership grades to be larger than one while their q-th power sum to be less than or equal to one. It is perceived that the approach proposed in this work gives a vast range for expressing assessment data, which facilitates DEs in evaluating hydropower plant plans efficiently and flexibly. The suggested 2TLT-SF decision framework combines SWARA with COPRAS in the assessment process, with 2TLT-SF-SWARA being used to determine the subjective weights of attributes and 2TLT-SF-COPRAS being used to evaluate hydropower plants strategies. A realistic case study on the assessment of hydropower plants in Pakistan was used to demonstrate the practicality and validity of the suggested technique. The experimental findings suggest that using our technique to establish the finalized hydropower plants selection scheme depending on the ranking outcomes is acceptable and adequate. Moreover, using the data from the preceding example, the impact of parameters q and $\mathbf {\eth }$ on the assessment outcomes was investigated extensively. Even though the parameters of the model have a substantial influence on the selecting outcomes, the efficient strategy remains constant, demonstrating that the approach provided in this research study is quite robust. Furthermore, the outcomes of an analysis of different approaches demonstrate that this approach has substantial benefits in terms of exploring multi-layer diverse relationships between attributes and reducing the influence of immense importance of assessment information.

Moreover, there are some limitations to this approach that should be taken into account in future studies. The presence of ambiguity and unpredictability in the structure of the qualitative attribute makes quantitative measurement complicate. This research focuses entirely on the aggregation of the 2TLT-SFNs by utilizing MM AOs. Future research will include a variety of assessment knowledge on the aggregation of the 2TLT-SFNs by utilizing different AOs such as Hamy mean, MSM, Heronian mean, BM, and Hamacher. Therefore, this research will continue to expand in DM environment. The DM approach based on the 2TLT-SF-SWARA-COPRAS method has complicated assessments due to the involvement of two steps aggregation: (1) for benefit attributes; (2) for cost attributes. Additionally, if there are considerable variability in weights and/or performance evaluations, the 2TLT-SF-SWARA-COPRAS approach may become unreliable. This research also related to a collection of data with a relationship among them, which indicated that the selection of simulated data is not addressed in our suggested research.

Furthermore, this technique may be integrated with other soft computing or uncertainty modeling tools, such as probability sets [58], language sets [59], hesitant fuzzy sets [60], cloud models [61], and so on, to increase the technique’s versatility and broaden the range for expression of assessment information. To integrate the complicated assessment data, various traditional operators including the Einstein operator [62], Frank operator [63], and Choquet integrals operator [64] can also be extended to aggregate 2TLT-SF information.