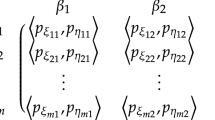Solution of matrix games with payoffs of single-valued trapezoidal neutrosophic numbers

Abstract

Single-valued neutrosophic numbers (SVNNs) are very much useful to express uncertain environments. In real-life problems, there are many situations where players of a matrix game can not assess their payoffs by using ordinary fuzzy sets or intuitionistic fuzzy sets. In these situations, single-valued trapezoidal neutrosophic numbers (SVTNNs) play a vital role in game theory, as it includes indeterminacy in the information besides truth and falsity. The objectives of this paper are to explore matrix games with SVTNN payoffs and to investigate two different solution methodologies. To solve such games, a pair of neutrosophic mathematical programming problems have been formulated. In the first approach, the two neutrosophic mathematical programming models are converted into interval-valued multi-objective programming problems by using a new ranking order relation of SVTNNs. Finally, the reduced problems are solved using the weighted average approach and utilizing LINGO 17.0 software. It is worth mentioning that the values of the game for both the players are obtained in SVTNN forms, which is desirable. In the second approach, each neutrosophic mathematical programming model is transformed into a crisp one by using the idea of $\alpha$-weighted possibility mean value for SVTNNs. A market share problem and another numerical example are illustrated to show the validity and applicability of the proposed approaches.

1 Introduction

Matrix game theory Owen (1982) gives a mathematical framework to conceive strategies that help to overcome real-life conflicting situations. There are various kinds of mathematical games Roy and Mula (2016); Das and Roy (2013); Roy and Maiti (2020); Seikh et al. (2021); Bhaumik and Roy (2021) which have been extensively studied and successfully applied in many fields. Many of the real-life situations are uncertain due to the imprecision of data, asymmetric information, and conflict of interest between opponents in the same field of business. The fuzzy set (FS) was the first to successfully encounter the uncertainty which is not due to the randomness of an event. FS represents each element with a grade of belongingness, called membership value which lies in between 0 and 1. In the literature, matrix games with fuzzy pay-offs have been extensively studied and analyzed by numerous researchers. Campos et al. (1992) used a linear programming approach to solve fuzzy matrix games by defining a ranking function of fuzzy numbers. Bector and Chandra (2005) used fuzzy linear programming duality to solve matrix games with fuzzy goals and fuzzy pay-offs. Li (2012) explored a fast approach to find fuzzy values of fuzzy matrix games. Li (2013) designed an effective approach to solving fuzzy matrix games. Li (2016) evolved several methods to solve matrix games with payoffs as triangular fuzzy numbers. Xia (2019) presented a solution methodology with cross-evaluated payoffs. Verma and Kumar (2020) proposed the Mehar method for fuzzy matrix games. Seikh et al. (2015c) implemented an $\alpha$-cut based approach to solve fuzzy matrix games. Recently, Jana and Roy (2018) analyzed the solution approach of matrix games with generalized trapezoidal fuzzy payoffs. Very recently, Seikh et al. (2020) developed a methodology to solve matrix games with hesitant fuzzy payoffs. Some recent references on fuzzy matrix games are Bhaumik et al. (2020); Jana and Roy (2019); Seikh et al. (2021a, 2021c); Karmakar et al. (2021); Xue et al. (2020).

In FS, the degree of membership of the elements cannot provide any additional information regarding the incomplete concept of the elements. Atanassov (1999) generalized the idea of FS to intuitionistic fuzzy set (IFS). The non-membership grade $\nu _A(a)\in [0,1]$ is also attached with the membership grade $\mu _A(a)\in [0,1]$ for each element $a\in A$ in a universe such that $0\le \mu _A(a)+\nu _A(a)\le 1$. IFS describes uncertainty more precisely and descriptively than FS, as IFS considers both complete and incomplete imprecise data.

Nan et al. (2014) proposed a solution methodology to study matrix games with payoffs of triangular intuitionistic fuzzy numbers (TIFNs). Li (2014) developed effective methodologies to solve matrix games with intuitionistic fuzzy payoffs. Seikh et al. (2015a, 2015b, 2016) proposed different approaches to solve matrix games with intuitionistic fuzzy payoffs. Applying robust ranking method, Bhaumik et al. (2017) analyzed the matrix game with pay-offs expressed by TIFNs. Xing and Qiu (2019) used the accuracy function method to solve a matrix game where the payoffs are considered as TIFN. Roy and Bhaumik (2018) considered matrix games with payoffs as triangular type-2 intuitionistic fuzzy numbers.

However, in reality, the available information always contains some imprecise data which consists of conflicting, unpredictable, and indeterminate information. The FS can not express the false membership information and the IFS fails to control the indeterminacy of information. Neutrosophic sets (NSs) Smarandache (1998) considers the degree of indeterminacy $\omega _A(a)\in [0,1]$ together with the degree of membership and non-membership function. Therefore, the NSs can capture more realistic data than that of FS and IFS. The NSs are represented by degree of truth ($\mu$), degree of indeterminacy ($\omega$), and degree of falsity ($\nu$) which are independent and $0\le \mu ,~\omega ,~\nu \le 1$ provided $0\le \mu +\omega +\nu \le 3$. NS becomes the classical set when $\omega =0$, $\mu , ~\nu$ either 0 or 1 and $\mu +\omega +\nu =1$; the FS when $\omega =0$, $0\le \mu ,~\omega ,~\nu \le 1$ and $\mu +\omega +\nu =1$; the IFS when $0\le \mu ,~\omega ,~\nu \le 1$ and $0<\mu +\omega +\nu <1$. Therefore, one can conclude that the NS is a generalization of the classical set, FS and IFS.

For realistic applications, Wang et al. (2010) introduced the concept of a single-valued neutrosophic set (SVNS) which is a special form of NS. SVNS depicts the variables which are entirely appropriate for human speculation because of the blemish of information that human gets or sees from the outer world. For instance, for a given proposition, “The smartphone company X would be the best seller”, in this circumstance human brain surely can not create an exact answer as far as yes or no. Indeterminacy is the segment of ignorance of the value of the proposition between truth and lie. For that reason, the three components of the NS are very much suitable to exhibit the indeterminacy and inconsistency in the information. Hence, the application of SVNS theory has been growing quickly in many research areas Biswas et al. (2016); Ye (2014a, 2014b); Sodenkamp et al. (2018); Wei and Wei (2018). Selvachandran et al. (2018) presented a modified TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) with maximizing deviation method based on the SVNS model. Garg (2020) defined some new distance measures under the SVNS environment and developed an algorithm for single-valued neutrosophic decision making based on TOPSIS method.

Later, Ye (2015) introduced the concept of single-valued trapezoidal neutrosophic set (SVTNS) by combining the concept of trapezoidal fuzzy numbers and single-valued neutrosophic set. SVTNNs are considered as a special type of SVTNSs, which have appealing interpretations and can be easily specified and implemented by the decision-maker. Ye (2015) also developed some operational rules, score functions, and accuracy functions for SVTNN. Deli and Subas (2017) was first to define the concept of the cut sets of SVNSs and applied to SVTNNs. They also explored a ranking method of SVNNs based on the values and ambiguities of SVNN.

In matrix games, due to the lack of information in the available data, the degree of indeterminacy plays a vital role while assessing the payoff values. Therefore, the notion of FS or IFS fails to describe the elements of the pay-off matrix. For example, suppose a company is going to launch a new item in the market, and the marketing manager wants to estimate the sales amount of the item. The sales amount of the new item depends on various uncertain parameters such as production cost, the demand for the product, the capacity of supply, selling price, etc. But, the company wants to know whether ‘the guaranteed sales amount would be $\$$120 per day or less’ before starting its production. Then some experts are consulted for their opinions about the guaranteed sales amount. The existence of this uncertain guaranteed sales amount always contains some knowledge of ‘neutral’ (indeterminate/unknown) thought besides ‘truth/membership’ and ‘falsehood/non-membership’ components that lie in FS/IFS. This situation can not be revealed by FS or IFS and NS serves better the purpose. So, there are many uncertain situations where players can assess pay-offs of the matrix game problems in SVTNN forms. However, in the literature, there is a fewer number of investigations in matrix games with neutrosophic payoffs. Bhaumik et al. (2021) analyzed a matrix game with multiple objectives and solved the problem under a single-valued neutrosophic environment in a linguistic approach. Bhaumik et al. (2021) proposed a new ranking approach based on the $(\alpha , \beta , \gamma )$-cut of single-valued triangular neutrosophic number and used to solve bi-matrix games. Deli (2019) used the concept of pure strategies to apply neutrosophic sets to two-person matrix games. However, there is no investigation on matrix games with SVTNNs as payoffs. This useful requirement influences us to investigate the matrix game with SVTNN payoffs.

In this paper, we have studied matrix games with pay-offs represented by SVTNNs. Firstly, a pair of neutrosophic mathematical programming problems have been formulated to get the optimal value and optimal strategies for the players. We solve these problems by using two different solution methodologies. In the first approach, we define a new ranking order relation between two SVTNNs based on the $(\rho , \sigma , \tau )$-cut set of SVTNNs. Using this new ranking order relation, the two neutrosophic mathematical programming problems are converted into interval-valued multi-objective linear programming problems. Then we solve the reduced problems using the weighted average approach. In the second approach, each neutrosophic mathematical programming problem is transformed into a crisp one by using the ranking method depending on the $\alpha$-weighted possibility mean value (WPMV) for SVTNN. The transformed crisp problems are solved by the simplex method using LINGO 17.0 software. The key contributions of this paper are augmented as under.

• (i) A new ranking order relation on SVTNNs is proposed by considering the $(\rho , \sigma , \tau )$-cut set of SVTNNs.

• (ii) Based on this proposed ranking order relation, the matrix game with SVTNN payoffs is solved. The optimal values of the game for both the players are obtained in the SVTNN forms, which is desirable.

• (iii) Since the solution methodology is based on ($\rho , \sigma , \tau$)-cut set of SVTNNs, for different values of $\rho , \sigma , \tau$ give different optimal solutions. However, the most likely values of gain-floor of Player-I and loss-ceiling of Player-II are also obtained.

• (iv) Based on $\alpha$-WPMV of SVTNN, another solution approach is proposed. In this approach, we obtained the optimal strategies of each player.

• (v) A real-life market share problem and another numerical example are illustrated to check the applicability and validity of the proposed approaches.

The paper unfolds as follows. Some basic preliminaries related to SVNS, SVTNSs, and cut sets of SVTNSs are recalled in Sect. 2. Also, a new ranking order relation of SVTNNs and the concept of $\alpha$-WPMV of SVTNN is described in Sect. 2. The idea of SVTNN matrix games is conceptualized in Sect. 3. Section 4 is dedicated to the model formulation and the solution process of the SVTNN matrix game and the development of the algorithm. In Sect. 5, a market share problem and another example are illustrated with two proposed approaches. The results are discussed and analyzed to verify the validity of the proposed approaches. Section 6 concludes the paper.

2 Preliminaries

In this section, some basic definitions and preliminaries are recalled.

Definition 2.1

(SVNS) Wang et al. (2010) A set ${\tilde{S}}$ = $\{\langle \xi , ({\Gamma _{{\tilde{S}} }}(\xi ), {\Upsilon _{{\tilde{S}}}}(\xi ), {\Lambda _{{\tilde{S}}}}(\xi )) \rangle | \xi \in \Omega , {\Gamma _{{\tilde{S}}}}(\xi ),{\Upsilon _{\tilde{S}}}(\xi ),{\Lambda _{{\tilde{S}}}}(\xi )$ $\in [0, 1]\}$ is said to be a SVNS over a universe $\Omega$, where $\Gamma _{{\tilde{S}}} : \Omega \rightarrow [0,1]$, $\Upsilon _{{\tilde{S}}}:\Omega \rightarrow [0,1]$ and $\Lambda _{{\tilde{S}}}: \Omega \rightarrow [0,1]$ are called respectively truth- membership function, indeterminacy-membership function and falsity-membership function such that $0\le {\Gamma _{{\tilde{S}}}}(\xi )+ {\Upsilon _{{\tilde{S}}}}(\xi )+$ ${\Lambda _{{\tilde{S}}(\xi ) }}\le 3$.

Definition 2.2

(SVTNN) Subas (2015) A SVTNN ${\tilde{M}}= \langle (t,u,v,w);\ell ,m,n\rangle$ is a unique SVNS on $\mathfrak {R}$ (depicted in Fig. 1), whose truth-membership ($\Gamma _{{\tilde{M}}}$), indeterminacy-membership ($\Upsilon _{{\tilde{M}}}$) and falsity-membership function ($\Lambda _{{\tilde{M}}}$) are respectively defined as

$$\begin{aligned} \Gamma _{{\tilde{M}}}(\xi )= & {} \left\{ \begin{array}{ll} \frac{(\xi -t)\ell }{(u-t)},&{}~~t \le \xi \le u;\\ \ell ,&{}~~u \le \xi \le v;\\ \frac{(w-\xi )t}{(w-v)},&{}~~v \le \xi \le w;\\ 0,&{}~~\text{ otherwise }\end{array}\right. \\ \Upsilon _{{\tilde{M}}}(\xi )= & {} \left\{ \begin{array}{ll} \frac{(u-\xi + m(\xi -t))}{(u-t)},&{}~~t \le \xi \le u;\\ m,&{}~~u \le \xi \le v;\\ \frac{(\xi -v+m(w-\xi )}{(w-v)},&{}~~v \le \xi \le w;\\ 1,&{}~~\text{ otherwise }\end{array}\right. \\ \Lambda _{{\tilde{M}}}(\xi )= & {} \left\{ \begin{array}{ll} \frac{(u-\xi + n(\xi -t))}{(u-t)},&{}~~t \le \xi \le u;\\ n,&{}~~u \le \xi \le v;\\ \frac{(\xi -v+n(w-\xi )}{(w-v)},&{}~~v \le \xi \le w;\\ 1,&{}~~\text{ otherwise }\end{array}\right. \end{aligned}$$

where $\ell ,m,n$ represents the degree of truth, the degree of indeterminacy and the degree of falsity, respectively and $0 \le \ell ,m,n\le 1$, $0\le \ell +m+n \le 3$.

Fig. 1

Rough sketch of a SVTNN ${\tilde{M}}= \langle (t,u,v,w);\ell ,m,n\rangle$

Definition 2.3

(Operations on SVTNNs) Subas (2015) Let ${\tilde{M}}=\langle (t_1, u_1 , v_1 , w_1 );\ell _1, m_1,n_1 \rangle$ and $\tilde{ M^*}=\langle (t_2, u_2 , v_2 , w_2 );\ell _2,m_2, n_2\rangle$ be two SVTNNs and $\lambda$ is a scalar. The basic arithmetic operations between ${\tilde{M}}$ and $\tilde{ M^*}$ are described as

• 1. ${\tilde{M}}+\tilde{ M^*}=\langle (t_1+t_2,~u_1+u_2,~v_1+v_2,~w_1+w_2);\min \{\ell _1,\ell _2\}, \max \{m_1,m_2\},\max \{n_1,n_2\}\rangle$;

• 2. ${\tilde{M}}-\tilde{ M^*}=\langle (t_1-w_2,~u_1-v_2,~v_1-u_2,~w_1-t_2);\min \{\ell _1,\ell _2\}, \max \{m_1,m_2\},\max \{n_1,n_2\}\rangle$;

• 3. ${\tilde{M}}\times \tilde{M^*}=\langle (t_1 t_2,u_1u_2,v_1v_2,w_1w_2);\min \{\ell _1,\ell _2\}, \max \{m_1,m_2\},\max \{n_1,n_2\}\rangle$;

• 4. $\lambda {\tilde{M}}=\left\{ \begin{array}{ll} \langle (\lambda t_1,\lambda u_1, \lambda v_1, \lambda w_1); \ell _1, m_1,n_1\rangle ,&{}~\text{ if }~\lambda \ge 0;\\ \langle (\lambda w_1,\lambda v_1, \lambda u_1, \lambda t_1); \ell _1, m_1,n_1\rangle ,&{}~\text{ if }~\lambda \le 0. \end{array}\right.$

2.1 Concepts of cut sets of SVTNNs

Definition 2.4

Deli and Subas (2017) Let ${\tilde{M}}$= $\langle (t,u,v,w);\ell , m,n\rangle$ be a SVTNN. Then, $\rho$-cut set, $\sigma$-cut set and $\tau$-cut set of $\tilde{M}$ are denoted by ${\hat{M}}_{\rho }$, ${\hat{M}}_{\sigma }$ and ${\hat{M}}_{\tau }$ respectively, where

$$\begin{aligned}&{\hat{M}}_{\rho }=\{\xi :\Gamma _{{\tilde{M}}}(\xi )\ge \rho \}\subseteq \mathfrak {R},~ 0\le \rho \le \ell ; \\&{\hat{M}}_{\sigma }=\{\xi :\Upsilon _{{\tilde{M}}}(\xi )\le \sigma \}\subseteq \mathfrak {R}, ~m \le \sigma \le 1; \\&{\hat{M}}_{\tau }=\{\xi :\Lambda _{{\tilde{M}}}(\xi )\le \tau \}\subseteq \mathfrak {R}, ~ n\le \tau \le 1. \end{aligned}$$

Definition 2.5

Deli and Subas (2017) A $(\rho ,\sigma ,\tau )$-cut set of a SVTNN ${\tilde{M}}$= $\langle (t,u,v,w);\ell , m,n\rangle$ is defined by ${\hat{M}}_{\rho ,\sigma ,\tau }=\{\xi :\Gamma _{{\tilde{M}}}(\xi )\ge \rho , \Upsilon _{{\tilde{M}}}(\xi )\le \sigma , \Lambda _{{\tilde{M}}}(\xi )\le \tau \}\subseteq \mathfrak {R},$ where $0\le \rho \le \ell$, $m \le \sigma \le 1$, $n \le \tau \le 1$ and $0\le \rho + \sigma + \tau \le 3$.

Definition 2.6

(Interval number) Moore (1979) An interval $\hat{I}\subseteq \mathfrak {R}$ is defined by $\hat{I}=[I_{l},~ I_{r}]=\{x\in \mathfrak {R}:I_l\le x \le I_r\}$, where $I_l$ and $I_r$ are two endpoints of $\hat{I}$. Here $\hat{I_c}= \frac{I_{l}+ I_{r}}{2}$ is defined to be the center of $\hat{I}=[I_{l},~ I_{r}]$.

From Definitions 2.1, 2.4, it follows that ${\hat{M}}_{\rho }$, ${\hat{M}}_{\sigma }$ and ${\hat{M}}_{\tau }$ are closed intervals as follows:

${\hat{M}}_{\rho }=[ M_{l\rho },~ M_{r\rho }]=[t+\rho (u-t)/\ell ,~w-\rho (w-v)/\ell ]$,

${\hat{M}}_{\sigma }=[M_{l\sigma },~ M_{r\sigma }]=[\{(1-\sigma )u+(\sigma -m)t\}/(1-m),~\{(1-\sigma )v+(\sigma -m)w\}/(1-m)]$, and

${\hat{M}}_{\tau }=[ M_{l\tau },~ M_{r\tau }]=[\{(1-\tau )u+(\tau -n)t\}/(1-n),~\{(1-\tau )v+(\tau -n)w\}/(1-n)]$.

Theorem 2.1

Assume that ${\tilde{M}}$ = $\langle (t,u,v,w);\ell , m,n\rangle$ is any SVTNN. For any values $\rho \in [0,\ell ]$, $\sigma \in [m,1]$ and $\tau \in [n,1]$ such that $0\le \rho +\sigma +\tau \le 3$, then ${\hat{M}}_{\rho ,\sigma ,\tau }$=${\hat{M}}_{\rho }\cap {\hat{M}}_{\sigma }\cap {\hat{M}}_{\tau }$ is valid.

Proof

The proof can be easily derived from Definitions (2.4), (2.5). $\square$

2.2 Ranking order relation of SVTNNs

In this section, we develop a new ranking order relation between two SVTNNs

Definition 2.7

Let ${\tilde{M}}=\langle (t_1, u_1 , v_1 , w_1 );\ell _1, m_1,n_1 \rangle$ and $\tilde{ M^*}=\langle (t_2, u_2 , v_2 , w_2 );\ell _2,m_2, n_2\rangle$ be two SVTNNs and ${\hat{M}}_{\rho }$ (or ${\hat{M}}^*_{\rho }$), ${\hat{M}}_{\sigma }$ (or ${\hat{M}}^*_{\sigma }$) and ${\hat{M}}_{\tau }$ (or ${\hat{M}}^*_{\tau }$) are respectively the $\rho$- cut set, $\sigma$- cut set and $\tau$- cut set of ${\tilde{M}}$ (or ${\tilde{M}}^*$). Then

• (i) ${\tilde{M}} \preceq {\tilde{M}}^*$ i.e., ${\tilde{M}}$ is approximately smaller than ${\tilde{M}}^*$ if and only if ${\hat{M}}_{\rho }\le _{I} {\hat{M}}^*_{\rho }$, ${\hat{M}}_{\sigma }\le _{I} {\hat{M}}^*_{\sigma }$ and ${\hat{M}}_{\tau }\le _{I} {\hat{M}}^*_{\tau }$ for any $\rho \in [0,\min \{\ell _1,\ell _2\}]$, $\sigma \in [\max \{m_1,m_2\},1]$, $\tau \in [\max \{n_1,n_2\},1]$, where $0\le \rho +\sigma +\tau \le 3$.

• (ii) ${\tilde{M}} \succeq {\tilde{M}}^*$ i.e., ${\tilde{M}}$ is approximately bigger than ${\tilde{M}}^*$ if and only if ${\hat{M}}_{\rho }\ge _{I} {\hat{M}}^*_{\rho }$, ${\hat{M}}_{\sigma }\ge _{I} {\hat{M}}^*_{\sigma }$ and ${\hat{M}}_{\tau }\ge _{I} {\hat{M}}^*_{\tau }$ for any $\rho \in [0,\min \{\ell _1,\ell _2\}]$, $\sigma \in [\max \{m_1,m_2\},1]$, $\tau \in [\max \{n_1,n_2\},1]$, where $0\le \rho +\sigma +\tau \le 3$.

The symbols“$\preceq$” and “$\succeq$” are the neutrosophic version of the order relations “$\le$” and “$\ge$”, which express the linguistic interpretation “Approximately less than or equal to” and “Approximately greater than or equal to”, respectively.

2.3 Weighted possibility mean value of SVTNNs

Definition 2.8

Garai et al. (2020) Let ${\tilde{M}}= \langle (t,u,v,w);\ell ,m,n\rangle$ be a SVTNN. Then

• (i) $\Pi _{\Gamma }({\tilde{M}})=\frac{(t+2u+2v+w)}{6} \ell ^2$ is the possibility mean value (PMV) of the truth-membership function $({\Gamma }_{{\tilde{M}}})$,

• (ii) $\Pi _{\Upsilon }({\tilde{M}})$=$\frac{(t+2u+2v+w)}{6}$ $(1-{m})^2$ is the PMV of the indeterminacy- membership function ${\Upsilon }_{{\tilde{M}}}$,

• (iii) $\Pi _{\Lambda }({\tilde{M}})$=$\frac{(t+2u+2v+w)}{6}$ $(1-{n})^2$ is the PMV of the falsity-membership function ${\Lambda }_{\tilde{M}}$.

Then, the $\alpha$-weighted possibility mean value (WPMV) of SVTNN ${\tilde{M}}$ is defined as

$$\begin{aligned} \Pi _{\alpha }({\tilde{M}})= & {} \alpha ~ \Pi _{\Gamma }({\tilde{M}}) + (1-\alpha )~ \Pi _{\Upsilon }({\tilde{M}}) + (1-\alpha )~ \Pi _{\Lambda }({\tilde{M}})\\= & {} \frac{(t+2u+2v+w)}{6}\\&\big [\alpha ~\ell ^2+(1-\alpha ) ~(1-m)^2+(1-\alpha ) ~(1-n)^2\big ], \end{aligned}$$

where $\alpha \in [0,1]$ is a weight, which indicates the decision maker’s viewpoint or desire information.

For particular value of $\alpha =0$, the $\alpha$-WPMV of ${\tilde{M}}$ is obtained as

$$\begin{aligned} \Pi _{0}({\tilde{M}})= & {} \Pi _{\Upsilon }({\tilde{M}}) + \Pi _{\Lambda }({\tilde{M}})\\= & {} \frac{(t+2u+2v+w)}{6} \big [(1-m)^2+(1-n)^2\big ], \end{aligned}$$

and for $\alpha =1$, the $\alpha$-WPMV of ${\tilde{M}}$ is reduced to

$$\begin{aligned} \Pi _{1}({\tilde{M}})= & {} \Pi _{\Gamma }({\tilde{M}}) \\= & {} \frac{(t+2u+2v+w)}{6} {\ell ^2}. \end{aligned}$$

Based on $\alpha$-WPMV of SVTNN, the ranking order relation between SVTNN is given below.

Let ${\tilde{M}}$ and $\tilde{ M^*}$ be two SVTNNs and $\Pi _{\alpha }({\tilde{M}})$ and $\Pi _{\alpha }({\tilde{M}}^*)$ are the $\alpha$-WPMV of ${\tilde{M}}$ and ${\tilde{M}}^*$, respectively. Then,

• 1. if $\Pi _{\alpha }({\tilde{M}})> \Pi _{\alpha }({\tilde{M}}^*)$, then ${\tilde{M}}$ is bigger than ${\tilde{M}}^*$, denoted by ${\tilde{M}} \succ {\tilde{M}}^*$;

• 2. if $\Pi _{\alpha }({\tilde{M}})< \Pi _{\alpha }({\tilde{M}}^*)$, then ${\tilde{M}}$ is smaller than ${\tilde{M}}^*$, denoted by ${\tilde{M}} \prec {\tilde{M}}^*$;

• 3. if $\Pi _{\alpha }({\tilde{M}})= \Pi _{\alpha }({\tilde{M}}^*)$ then

• (a) if $\Pi _{\Gamma }({\tilde{M}}) > \Pi _{\Gamma }({\tilde{M}}^*)$ then ${\tilde{M}} \succ {\tilde{M}}^*$;

• (b) when $\Pi _{\Gamma }({\tilde{M}})= \Pi _{\Gamma }({\tilde{M}}^*)$, if $\Pi _{\Upsilon }({\tilde{M}})> \Pi _{\Upsilon }({\tilde{M}}^*)$, then $\tilde{M} \succ {\tilde{M}}^*$;

• (c) when $\Pi _{\Gamma }({\tilde{M}})= \Pi _{\Gamma }({\tilde{M}}^*)$ and $\Pi _{\Upsilon }({\tilde{M}})= \Pi _{\Upsilon }({\tilde{M}}^*)$, if $\Pi _{\Lambda }({\tilde{M}})> \Pi _{\Lambda }({\tilde{M}}^*)$,then ${\tilde{M}} \succ {\tilde{M}}^*$;

• 4. if $\Pi _{\alpha }({\tilde{M}})= \Pi _{\alpha }({\tilde{M}}^*)$, $\Pi _{\Gamma }({\tilde{M}})= \Pi _{\Gamma }({\tilde{M}}^*)$, $\Pi _{\Upsilon }({\tilde{M}})= \Pi _{\Upsilon }({\tilde{M}}^*)$, $\Pi _{\Lambda }({\tilde{M}})=\Pi _{\Lambda }({\tilde{M}}^*)$,then ${\tilde{M}} \approx {\tilde{M}}^*$, i.e., two SVTNNs are neutrosophically equal.

3 Matrix Games with Pay-offs of SVTNNs

Let the pure strategies $\delta _h$ and $\gamma _k$ are chosen by Player-I and II with probabilities $u_h$ and $v_k$ respectively, for $h\in \bigtriangleup _1$ and $k\in \bigtriangleup _2$ where $\bigtriangleup _1=\{1,2,\ldots ,p\}$ and $\bigtriangleup _2=\{1,2,\ldots ,q\}$. If $\sum \nolimits _{h=1}^p u_h=1$ and $\sum \nolimits _{k=1}^q v_k=1$ for $(\mathbf{u}, \mathbf{v}) \in \mathfrak {R}^p_{+} \times \mathfrak {R}^q_{+}$ where $\mathbf{u}= (u_1,u_2,\ldots ,u_p)$ and $\mathbf{v}=(v_1,v_2,\ldots ,v_q)$, then $\mathbf{u}$ and $\mathbf{v}$ are called the mixed strategies for Player-I and II, respectively.

Let the sets of all mixed strategies for Player-I and II are denoted by U and V respectively, where

$$\begin{aligned} U= & {} \Big \{{\mathbf{u}}=(u_1,u_2,\ldots ,u_p)\in \mathfrak {R}^p_{+}: \sum \limits _{h=1}^p u_h=1\Big \},~\\ V= & {} \Big \{{\mathbf{v}}=(v_1,v_2,\ldots ,v_q)\in \mathfrak {R}^q_{+}: \sum \limits _{k=1}^q v_k=1\Big \}. \end{aligned}$$

Let us consider the payoff matrix ${\tilde{N}}=({\tilde{n}}_{hk})_{p\times q}$ for Player-I, where ${\tilde{n}}_{hk}=\langle (t_{hk},u_{hk},v_{hk},w_{hk})$ $;\ell _{hk},m_{hk},n_{hk}\rangle$ is a SVTNN. Here, ${\tilde{n}}_{hk}$ represents the payoff for Player-I. Then, the matrix game with SVTNN payoffs is represented by $\{U,V,{\tilde{N}}\}$. From this, the two-person matrix game $\{U,V,{\tilde{N}}\}$ with payoffs of SVTNNs is supposed to call as a SVTNN matrix game ${\tilde{N}}$.

For the choice of mixed strategy $({\mathbf{u}},{\mathbf{v}})\in U\times V$ by Player-I and II, the expected payoff $\tilde{E}({\mathbf{u}},{\mathbf{v}})$ for Player- I will be calculated as

$$\begin{aligned} {\tilde{E}}({\mathbf{u}},{\mathbf{v}})= & {} {\mathbf{u}}^T\tilde{N}{\mathbf{v}}=\sum \limits _{h=1}^{p}\sum \limits _{k=1}^{q} {\tilde{n}}_{hk} u_{h} v_{k}\\= & {} \sum \limits _{h=1}^{p}\sum \limits _{k=1}^{q} \langle (t_{hk},u_{hk},v_{hk},w_{hk});\ell _{hk},m_{hk},n_{hk}\rangle u_{h} v_{k}\\= & {} \Big \langle \Big (\sum \limits _{h=1}^{p}\sum \limits _{k=1}^{q}t_{hk}~u_{h} v_{k},\sum \limits _{h=1}^{p}\sum \limits _{k=1}^{q}u_{hk}~ u_{h} v_{k},\sum \limits _{h=1}^{p}\sum \limits _{k=1}^{q}\\&v_{hk}~u_{h}v_{k},\sum \limits _{h=1}^{p}\sum \limits _{k=1}^{q}w_{hk}~ u_{h} v_{k}\Big ); \\&\qquad \min \limits _{h,k} \ell _{hk},\max \limits _{h,k} m_{hk},\max \limits _{h,k}n_{hk}\Big \rangle \end{aligned}$$

and similarly, the expected pay-off for Player-II is given by $-{\tilde{E}}({\mathbf{u}},{\mathbf{v}})= {\mathbf{u}}^T(-{{\tilde{N}}}){\mathbf{v}}$. Both ${\tilde{E}}({\mathbf{u}},{\mathbf{v}})$ and $-\tilde{E}({\mathbf{u}},{\mathbf{v}})$ are SVTNNs.

Irrespective of the use of best strategies of the players, the maximum guaranteed gain (or the minimum possible loss) is the value of the game for Player-I (or Player-II). Following Owen (1982), if for some $(\mathbf{{u^0}},\mathbf{{v^0}})\in U \times V$, such that

$$\begin{aligned} {{\mathbf{u}}^0}^T {\tilde{N}} {\mathbf{v}}^0 = \max \limits _{{\mathbf{u}}\in U}\min \limits _{\mathbf{v}\in V}\{\mathbf{{u}^T}{\tilde{N}} {\mathbf{v}}\} = \min \limits _{\mathbf{v}\in V} \max \limits _{{\mathbf{u}}\in U} \{\mathbf{{u}^T}{\tilde{N}} {\mathbf{v}}\} , \end{aligned}$$

then ${\mathbf{u}}^0$ and ${\mathbf{v}}^0$ are called optimal strategies for Player-I and II, respectively and $\mathbf{{u^0}}^T {\tilde{N}} \mathbf{{v^0}}$ is the value of SVTNN matrix game ${\tilde{N}}$.

Definition 3.1

(Reasonable solution of a SVTNN matrix game) Let $\tilde{\theta }$ and $\tilde{\phi }$ be two SVTNNs. If for some $(\bar{\mathbf {u}}, \bar{\mathbf {v}})\in {U}\times {V}$, the relation $\bar{\mathbf {u}}{\tilde{N}} {\mathbf{v}}\succeq \tilde{\theta }$ and $\mathbf{u}{\tilde{N}} \bar{\mathbf {v}}\preceq \tilde{\phi }$ hold for any $\mathbf{u}\in U$ and ${\mathbf{v}}\in V$, then $(\bar{\mathbf {u}},\bar{\mathbf {v}},\tilde{\theta },\tilde{\phi })$ is said to be a reasonable solution of $\tilde{N}$; $\tilde{\theta }$ and $\tilde{\phi }$ are called reasonable values and $\bar{\mathbf {u}}\in {U}$ and $\bar{\mathbf {v}}\in {V}$ are called reasonable strategies for Player-I and Player-II, respectively.

It is to be noted that the reasonable solution, which is defined in the above definition, is not the solution of the SVTNN matrix game. The concept of the solution of the SVTNN matrix game is given in the following definition.

Definition 3.2

(Solution of a SVTNN matrix game) Let $\Theta$ and $\Phi$ are the sets of reasonable values $\tilde{\theta }$ and $\tilde{\phi }$ for Player-I and II respectively. If for some ${\tilde{\theta }}^*\in \Theta$ and ${\tilde{\phi }}^*\in \Phi$, there do not exist ${\tilde{\theta }}'\in \Theta ({\tilde{\theta }}'\ne {\tilde{\theta }}^*)$ and ${\tilde{\phi }}'\in \Phi ({\tilde{\phi }}'\ne {\tilde{\phi }}^*)$ such that ${\tilde{\theta }}^*\preceq {\tilde{\theta }}'$ and ${\tilde{\phi }}^*\succeq {\tilde{\phi }}'$, then $(\mathbf{u}^*, \mathbf{v}^*, {\tilde{\theta }}^*, {\tilde{\phi }}^*)$ is said to be a optimal solution of ${\tilde{N}}$; $\mathbf{u}^*$(or $\mathbf{v}^*)$ is called a maximin (or minimax) strategy for Player-I (or Player-II) ; ${\tilde{\theta }}^*$ and ${\tilde{\phi }}^*$ are represented as Player-I’s gain floor and Player-II’s loss ceiling respectively.

4 Model formulation and solution procedure

Following Definitions (3.1) and (3.2), the maximin strategy ($\mathbf{u}^*\in U$) for Player-I and minimax strategy ($\mathbf{v}^*\in V$) for Player-II can be obtained by solving the neutrosophic mathematical programming models (1) and (2), respectively as follows:

$$\begin{aligned}&\max ~\tilde{\theta }=\langle (t_{\tilde{\theta }},u_{\tilde{\theta }},v_{\tilde{\theta }},w_{\tilde{\theta }});\ell _{\tilde{\theta }},m_{\tilde{\theta }},n_{\tilde{\theta }}\rangle \nonumber \\ \text{ subject } \text{ to }&\sum \limits _{h=1}^{p} {\tilde{n}}_{hk}~ u_h~\succeq \tilde{\theta },~ k\in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} u_h=1,~u_h\ge 0,~ h\in \bigtriangleup _1 \end{aligned}$$

(1)

and

$$\begin{aligned}&\min ~\tilde{\phi }=\langle (t_{\tilde{\phi }},u_{\tilde{\phi }},v_{\tilde{\phi }},w_{\tilde{\phi }});\ell _{\tilde{\phi }},m_{\tilde{\phi }},n_{\tilde{\phi }}\rangle \nonumber \\ \text{ subject } \text{ to }&\sum \limits _{k=1}^{q} {\tilde{n}}_{hk} ~ v_k\preceq \tilde{\phi },~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} v_k=1,~v_k\ge 0,~ k \in \bigtriangleup _2. \end{aligned}$$

(2)

It can be easily proved by the following theorem that Player-I’s gain floor can not exceed Player-II’s loss ceiling.

Theorem 4.1

Suppose ${\tilde{\theta }}^*$ and ${\tilde{\phi }}^*$ are Player-I’s gain floor and Player-II’s loss ceiling, respectively, then ${\tilde{\theta }}^* \preceq {\tilde{\phi }}^*$ is valid.

Proof

It follows from problems (1) and (2) that

$$\begin{aligned} {\tilde{\theta }}^*= & {} \sum \limits _{k=1}^{q} {\tilde{\theta }}^* v_k \preceq \sum \limits _{k=1}^{q}\left( \sum \limits _{h=1}^{p}{\tilde{n}}_{hk}~ u_h \right) v_k\\= & {} \sum \limits _{h=1}^{p} \left( \sum \limits _{k=1}^{q}{\tilde{n}}_{hk}~ v_k \right) u_h \preceq \sum \limits _{h=1}^{p} {\tilde{\phi }}^*u_h={\tilde{\phi }}^* \end{aligned}$$

i.e., ${\tilde{\theta }}^*\preceq {\tilde{\phi }}^*$. $\square$

The proposed mathematical models (1) and (2) are solved by two different approaches. In Approach-I, the game problem is solved using the new ranking method defined in Sect. 2.2. In Approach-II, the ranking method based on the weighted possibility mean value of SVTNN is used to solve the game problem, which is discussed in Sect. 2.3. Two approaches are considered to compare the obtained results. The utilization of these two approaches is as follows.

4.1 Proposed approach-I

Using Definition 2.5, Problem (1) is converted into the interval-valued multi-objective linear programming problem as follows:

$$\begin{aligned}&\max ~\Big \{\hat{\theta }_\rho , \hat{\theta }_\sigma , \hat{\theta }_\tau \Big \}\nonumber \\ \text{ subject } \text{ to }&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_\rho ~\ge _{I}~ \hat{\theta }_\rho ,~ k \in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_\sigma ~\ge _{I}~ \hat{\theta }_\sigma ,~ k \in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_\tau ~\ge _{I}~ \hat{\theta }_\tau ,~ k \in \bigtriangleup _2 \nonumber \\&\sum \limits _{h=1}^{p} u_h=1,~u_h\ge 0,~ h \in \bigtriangleup _1 \end{aligned}$$

(3)

According to Definition (2.4), Problem (3) can be rewritten as follows:

$$\begin{aligned}&\max ~\Big \{\Big [\theta _{l\rho },~ \theta _{r\rho }\Big ],\Big [\theta _{l\sigma },~ \theta _{r\sigma }\Big ],\Big [\theta _{l\tau },~\theta _{r\tau } \Big ]\Big \}\nonumber \\ \text{ subject } \text{ to }&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{l\rho }~\ge ~ \theta _{l\rho } ,~ ~\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{r\rho }~\ge ~ \theta _{r\rho } ,~ k \in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{l\sigma }~\ge ~ \theta _{l\sigma } ,~ ~\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{r\sigma }~\ge ~ \theta _{r\sigma } ,~ k \in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{l\tau }~\ge ~ \theta _{l\tau } ,~ ~\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{r\tau }~\ge ~\theta _{r\tau } ,~ k \in \bigtriangleup _2 \nonumber \\&\sum \limits _{h=1}^{p} u_h=1,~u_h\ge 0,~ h \in \bigtriangleup _1 \end{aligned}$$

(4)

The three objective functions of Problem (4) may be considered with equal weights i.e., their importance are same. Therefore, the three objective functions of Problem (4) are aggregated. Then objective function of Problem (4) may be written as

$$\begin{aligned} \max ~\Big \{\Big [\frac{\theta _{l\rho }+\theta _{l\sigma }+\theta _{l\tau }}{3},~\frac{ \theta _{r\rho }+ \theta _{r\sigma }+\theta _{r\tau }}{3}\Big ]\Big \}, \end{aligned}$$

which is an interval-valued objective function.

Now, according to Ishibuchi and Tanaka (1990), the maximization problem $\max \{\hat{I}=[I_{l},~ I_{r}] |\hat{I}\in \hat{\Psi }_1\}$ is equivalent to $\max \{\{I_{l},~ I_{c}\}|\hat{I}\in \hat{\Psi }_1\},$ where $I_{c}$ is the center of $\hat{I}$ and $\hat{I}$ should satisfy the set of constraints $\hat{\Psi }_1$.

Then, the transformed maximization problem with interval-valued objective function is converted into the bi-objective programming problem as

$$\begin{aligned} \max ~\Big \{\frac{\theta _{l\rho }+\theta _{l\sigma }+\theta _{l\tau }}{3},~\frac{\theta _{l\rho }+\theta _{r\rho }+\theta _{l\sigma }+ \theta _{r\sigma }+\theta _{l\tau }+\theta _{r\tau }}{6}\Big \}. \end{aligned}$$

There are several methods to solve bi-objective programming problem. In this paper, we use the weighted average method. Then, the above bi-objective programming problem can be written as

$$\begin{aligned}&\max \Big \{\chi \Big (\frac{\theta _{l\rho }+\theta _{l\sigma }+\theta _{l\tau }}{3}\Big )+(1-\chi )\\&\quad \Big (\frac{\theta _{l\rho }+ \theta _{r\rho }+\theta _{l\sigma }+ \theta _{r\sigma }+\theta _{l\tau }+\theta _{r\tau }}{6}\Big )\Big \}, \end{aligned}$$

where $\chi \in [0,1].$ For simplicity, we choose $\chi =0.5$ throughout the paper.

Therefore, Problem (4) is transformed to the following Problem (5) as follows.

$$\begin{aligned}&\max \left\{ \frac{1}{2}\left( \frac{\theta _{l\rho }+ \theta _{l\sigma }+ \theta _{l\tau }}{3}\right. \right. \nonumber \\&\qquad \left. \left. +\frac{ \theta _{l\rho }+ \theta _{r\rho }+\theta _{l\sigma }+ \theta _{r\sigma }+\theta _{l\tau }+\theta _{r\tau }}{6}\right) \right\} \nonumber \\ \text{ subject } \text{ to }&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{l\rho }~\ge ~ \theta _{l\rho } ,~ ~\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{r\rho }~\ge ~ \theta _{r\rho } ,~ k \in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{l\sigma }~\ge ~ \theta _{l\sigma } ,~ ~\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{r\sigma }~\ge ~ \theta _{r\sigma } ,~ k \in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{l\tau }~\ge ~ \theta _{l\tau } ,~ ~\nonumber \\&\sum \limits _{h=1}^{p} ({\tilde{n}}_{hk}~ u_h)_{r\tau }~\ge ~ \theta _{r\tau } ,~ k \in \bigtriangleup _2 \nonumber \\&\sum \limits _{h=1}^{p} u_h=1,~u_h\ge 0,~ h \in \bigtriangleup _1 \end{aligned}$$

(5)

For given values of $\rho \in [0, \min \limits _{h,k}{\ell _{hk}}]$, $\sigma \in [\max \limits _{h,k} m_{hk},1]$, and $\tau \in [\max \limits _{h,k} n_{hk},1]$ and applying the simplex method, the optimal solution of Problem (5) will be obtained as $( \mathbf{u^*},~\theta _{l\rho },~ \theta _{r\rho },~\theta _{l\sigma },~ \theta _{r\sigma },$ $\theta _{l\tau },~\theta _{r\tau })$. Here $\mathbf{u^*}$ is the maximin strategy and $\theta _{l\rho },~ \theta _{r\rho },~ \theta _{l\sigma },~ \theta _{r\sigma },~\theta _{l\tau },~\theta _{r\tau }$ are the corresponding upper and lower bounds of $\rho$-cut sets, $\sigma$-cut sets and $\tau$-cut sets of the Player-I’s gain floor ($\tilde{\theta }^*$). In the sense of Theorem (2.1), a ($\rho ,\sigma ,\tau$)-cut set ($\hat{\theta }^*_{\rho ,\sigma ,\tau }$) of $\tilde{\theta }^*$ can be obtained where $\hat{\theta }^*_{\rho ,\sigma ,\tau }$=$\hat{\theta }_{\rho }\cap \hat{\theta }_{\sigma }\cap \hat{\theta }_{\tau }$=$[\theta _{l\rho },~\theta _{r\rho }]\cap [\theta _{l\sigma },~ \theta _{r\sigma }]\cap [\theta _{l\tau },~\theta _{r\tau }]=[\max \{\theta _{l\rho },\theta _{l\sigma },\theta _{l\tau }\}, \min \{ \theta _{r\rho }, \theta _{r\sigma },\theta _{r\tau }\}]$.

By using $\hat{\theta }^*_{\rho ,\sigma ,\tau }$, we can approximate the value of $\tilde{\theta }^*$ for different values of $\rho ,~ \sigma , ~\tau$. The interval $\hat{\theta }^*_{\rho ,\sigma ,\tau }$ becomes the most likely value of $\tilde{\theta }^*$, for the value $\rho =\min \limits _{h,k} {\ell _{hk}}$, $\sigma =\max \limits _{h,k}{m_{hk}}$ and $\tau =\max \limits _{h,k}{n_{hk}}$.

As previous, Problem (2) can be converted into the following interval-valued programming problem (6) as follows.

$$\begin{aligned}&\min ~\Big \{\hat{\phi }_\rho , ~\hat{\phi }_\sigma ,~ \hat{\phi }_\tau \Big \}\nonumber \\ \text{ subject } \text{ to }&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_\rho ~\le _{I}~ \hat{\phi }_\rho ,~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_\sigma ~\le _{I}~ \hat{\phi }_\sigma ,~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_\tau ~\le _{I}~ \hat{\phi }_\tau ,~ h \in \bigtriangleup _1 \nonumber \\&\sum \limits _{k=1}^{q} v_k=1,~v_k\ge 0,~ k \in \bigtriangleup _2 \end{aligned}$$

(6)

According to Definition 2.4, Problem (6) can be written as

$$\begin{aligned}&\min ~\Big \{\Big [\phi _{l\rho },~ \phi _{r\rho }\Big ],\Big [\phi _{l\sigma },~ \phi _{r\sigma }\Big ],\Big [\phi _{l\tau },~\phi _{r\tau } \Big ]\Big \}\nonumber \\ \text{ subject } \text{ to }&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{l\rho }~\le ~ \phi _{l\rho } ,~ ~\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{r\rho }~\le ~ \phi _{r\rho } ,~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{l\sigma }~\le ~ \phi _{l\sigma } ,~ ~\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{r\sigma }~\le ~ \phi _{r\sigma } ,~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{l\tau }~\le ~ \phi _{l\tau } ,~ ~\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{r\tau }~\le ~ \phi _{r\tau } ,~ h \in \bigtriangleup _1 \nonumber \\&\sum \limits _{k=1}^{q} v_k=1,~v_k\ge 0,~ k \in \bigtriangleup _2 \end{aligned}$$

(7)

The three objective functions of the above equation may be regarded with equal weight, i.e., they have the same importance. Therefore, the objective functions of Problem (7) are aggregated and reduce to the interval-valued objective function as

$$\begin{aligned} \min ~\Big \{\Big [\frac{\phi _{l\rho }+\phi _{l\sigma }+\phi _{l\tau }}{3},~\frac{ \phi _{r\rho }+ \phi _{r\sigma }+\phi _{r\tau }}{3}\Big ]\Big \}. \end{aligned}$$

Now, according to Ishibuchi and Tanaka (1990), the minimization problem with the objective functions as interval numbers,

$$\begin{aligned} \min \{\hat{I}=[I_{l},~ I_{r}]~|~\hat{I}\in \hat{\Psi }_2\} \end{aligned}$$

is equivalent to the problem

$$\begin{aligned} \min \{\{I_{r},~ I_{c}\}|\hat{I}\in \hat{\Psi }_2\}, \end{aligned}$$

where $I_{c}$ is the center of $\hat{I}$ and $\hat{I}$ should satisfy the set of constraints $\hat{\Psi }_2$.

Then, following Ishibuchi and Tanaka (1990), the above reduced interval-valued objective function is converted to the bi-objective function as

$$\begin{aligned}&\min ~\Big \{\frac{\phi _{l\rho }+\phi _{l\sigma }+\phi _{l\tau }+ \phi _{r\rho }+ \phi _{r\sigma }+ \phi _{r\tau }}{6},~\nonumber \\&\qquad \frac{ \phi _{r\rho }+ \phi _{r\sigma }+\phi _{r\tau }}{3}\Big \}. \end{aligned}$$

Now, in a similar fashion as previous, Problem (7) can be transformed to the following Problem (8) as follows.

$$\begin{aligned}&\min \Big \{\frac{1}{2}\Big (\frac{\phi _{l\rho }+\phi _{l\sigma }+\phi _{l\tau }+ \phi _{r\rho }+\phi _{r\sigma }+\phi _{r\tau }}{6}\nonumber \\&\qquad +\frac{\phi _{r\rho }+\phi _{r\sigma }+\phi _{r\tau }}{3}\Big )\Big \}\nonumber \\ \text{ subject } \text{ to }&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{l\rho }~\le ~ \phi _{l\rho } ,~ ~\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{r\rho }~\le ~ \phi _{r\rho } ,~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{l\sigma }~\le ~ \phi _{l\sigma } ,~ ~\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{r\sigma }~\le ~ \phi _{r\sigma } ,~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{l\tau }~\le ~ \phi _{l\tau } ,~ ~\nonumber \\&\sum \limits _{k=1}^{q} ({\tilde{n}}_{hk}~ v_k)_{r\tau }~\le ~ \phi _{r\tau } ,~ h \in \bigtriangleup _1 \nonumber \\&\sum \limits _{k=1}^{q}v_k=1,~v_k\ge 0,~ k \in \bigtriangleup _2 \end{aligned}$$

(8)

By solving Problem (8) for specific values of $\rho \in [0, \min \limits _{h,k}{\ell _{hk}}]$, $\sigma \in [\max \limits _{h,k} m_{hk},1]$, and $\tau \in [\max \limits _{h,k} n_{hk},1]$, the optimal solution $( \mathbf{v^*},~\phi _{l\rho },~ \phi _{r\rho },~\phi _{l\sigma },~ \phi _{r\sigma },~\phi _{l\tau },~ \phi _{r\tau })$ will be obtained. Here $\mathbf{v^*}$ is the minimax strategy and $\phi _{l\rho },~ \phi _{r\rho },~\phi _{l\sigma },~ \phi _{r\sigma },~\phi _{l\tau },~\phi _{r\tau }$ are the corresponding upper and lower bounds of $\rho$-cut sets, $\sigma$-cut sets and $\tau$-cut sets of the Player-II’s loss ceiling ($\tilde{\phi }^*$). According to Theorem (2.1), $\hat{\phi }^*_{\rho ,\sigma ,\tau }$=$[\phi _{l\rho },~ \phi _{r\rho }]\cap ~[\phi _{l\sigma }, \phi _{r\sigma }]\cap [\phi _{l\tau },~\phi _{r\tau }]=[\max \{\phi _{l\rho },\phi _{l\sigma },\phi _{l\tau }\}, \min \{ \phi _{r\rho }, \phi _{r\sigma },\phi _{r\tau }\}].$ For the value $\rho =\min \limits _{h,k} {\ell _{hk}}$, $\sigma =\max \limits _{h,k}{m_{hk}}$ and $\tau =\max \limits _{h,k}{n_{hk}}$, the interval $\hat{\phi }^*_{\rho ,\sigma ,\tau }$ is the most likely value of $\tilde{\phi }^*$.

4.2 Proposed approach-II

The definition of $\alpha$-WPMV of SVTNN was given by Garai et al. (2020), which is discussed in Sect. 2.3. We use this concept of $\alpha$-WPMV of SVTNN to develop this second approach. Using $\alpha$-WPMV of SVTNNs, Problem (1) and Problem (2) reduce to the corresponding Problem (9) and Problem (10), respectively as follows.

$$\begin{aligned}&\max ~\{\Pi _{\alpha }(\tilde{\theta })\},\nonumber \\ \text{ subject } \text{ to }&\Pi _{\alpha }\left( \sum \limits _{h=1}^{p}{\tilde{n}}_{hk}~ u_h\right) ~\ge \Pi _{\alpha }(\tilde{\theta }) ,~k \in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} u_h=1,~u_h\ge 0,~ h \in \bigtriangleup _1 \end{aligned}$$

(9)

and

$$\begin{aligned}&\min ~\{\Pi _{\alpha }(\tilde{\phi })\}, \nonumber \\ \text{ subject } \text{ to }&\Pi _{\alpha }\left( \sum \limits _{k=1}^{q} {\tilde{n}}_{hk} \right) ~ v_k \le \Pi _{\alpha }(\tilde{\phi }),~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} v_k=1,~v_k\ge 0,~k \in \bigtriangleup _2. \end{aligned}$$

(10)

Assuming $P_1=\Pi _{\alpha }(\tilde{\theta })$ and $P_2=\Pi _{\alpha }(\tilde{\phi })$, Problem (9) and Problem (10) transform to the corresponding Problem (11) and Problem (12) as follows.

$$\begin{aligned}&\max ~\{P_1\} \nonumber \\ \text{ subject } \text{ to }&\Pi _{\alpha }\left( \sum \limits _{h=1}^{p}{\tilde{n}}_{hk}~ u_h \right) ~\ge P_1 ,~ k \in \bigtriangleup _2\nonumber \\&\sum \limits _{h=1}^{p} u_h=1,~u_h\ge 0,~ h \in \bigtriangleup _1 \end{aligned}$$

(11)

$$\begin{aligned}&\min ~\{P_2\} \nonumber \\ \text{ subject } \text{ to }&\Pi _{\alpha }\left( \sum \limits _{k=1}^{q} {\tilde{n}}_{hk} \right) ~ v_k \le P_2,~ h \in \bigtriangleup _1\nonumber \\&\sum \limits _{k=1}^{q} v_k=1,~v_k\ge 0,~ k \in \bigtriangleup _2 \end{aligned}$$

(12)

Now solving Problem (11) and Problem (12) for given value of $\alpha \in [0,1]$, we can obtain the crisp values of the optimal gain and optimal loss for Player-I and Player-II and the optimal strategies for each player.

4.2.1 Algorithm

The algorithm for solving SVTNN matrix games by the two proposed approaches is abstracted as follows.

Algorithm for Approach-I:
Step-1:	Consider a matrix game with payoffs of SVTNNs.
Step-2:	To solve the game, two neutrosophic mathematical programming models are formulated.
Step-3:	Using ($\rho , \sigma , \tau$)-cut set based ranking order relation of SVTNNs as described in Sect. 2.2, the formulated models are converted to corresponding interval-valued multi-objective programming problems.
Step-4:	The objective functions of the multi-objective programming problems are aggregated by considering equal weights of the objective functions and reduced to the corresponding interval-valued objective function.
Step-5:	Following Ishibuchi and Tanaka (1990), interval-valued objective function is transformed into bi-objective problem.
Step-6:	Using the weighted average method, bi-objective problems are reduced into corresponding crisp LPP.
Step-7:	Taking weight value 0.5, the reduced crisp LPP are solved to obtain optimal strategies $\mathbf{u^*}$ and $\mathbf{v^*}$ for Player-I and II respectively and the cut sets of gain floor and loss ceiling.

Algorithm for Approach-II:
Step-1:	Consider a matrix game with payoffs of SVTNNs.
Step-2:	To solve the game, two neutrosophic mathematical programming models are formulated.
Step-3:	Using $\alpha$-WPMV as described in Sect. 2.3, the formulated problems are transformed into corresponding crisp problems.
Step-4:	Solving the reduced crisp problems using simplex method, the optimal strategies and the $\alpha$- WPMV of the Player-I’s gain floor and Player-II’s loss ceiling are obtained.

The corresponding algorithmic flowchart of the proposed Approach-I and Approach-II is presented in Fig. 2.

Fig. 2

Algorithmic flowchart of Approach-I and Approach-II

5 Numerical examples

In this section, we consider a market share problem and another numerical example. The problems are solved with proposed solution approaches (Approach-I and Approach-II). The obtained results are discussed and analyzed.

5.1 Example 1: a market share problem

Suppose that two online merchants $M_1$ and $M_2$ sell smartphones in a selected market area where the demand for smartphones is fixed, i.e. when the total selling amount of $M_1$ increases then the total selling amount of $M_2$ decreases and same for the alternate case also. Merchants $M_1$ and $M_2$ consider two strategies to increase their total selling amount in the targeted market: Strategy I is ‘to reduce the price rate’ of the smartphone and strategy II is ‘to extend the storage capacity’ of the smartphone. This situation of extending the sales amount of each merchant may be considered as a matrix game where $M_1$ and $M_2$ may be assumed respectively as Player-I and Player-II. As there always exists uncertainty in the marketing industry, the sales amount of smartphones can not be predicted precisely by the marketing research department (MRD) of the merchants. MRD can roughly calculate the sales amount with an indeterminacy degree, along with the membership and non-membership degree of the sales amount. To come out from this unsettled situation, SVTNNs are applied to express the sales amount of smartphones. The pay-off matrix ${\tilde{N}}$ for merchant $M_1$ is given as follows:

Here $\langle (175,177,180,190);0.6,0.3,0.4\rangle$ from ${\tilde{N}}$ represents the sales amount of the Merchant $M_1$, when both of the merchants use the strategy I simultaneously. According to the MRD, it is approximately equal to the interval [177,180] positively by 60$\%$ and unable to say by 40$\%$. MRD has indeterminacy to say that the sales amount would fall in the interval by 30$\%$. Other SVTNNs in ${\tilde{N}}$ have also similar explanations.

5.1.1 The solution procedure

(i) Computational results obtained by Approach-I

According to Problem (5) and Problem (8), two linear programming models (13) and (14) are obtained as follows:

$$\begin{aligned}&\max \Big \{\frac{1}{2}\Big (\frac{\theta _{l\rho }+\theta _{l\sigma }+\theta _{l\tau }}{3}\nonumber \\&+\frac{\theta _{l\rho }+ \theta _{r\rho }+\theta _{l\sigma } + \theta _{r\sigma }+\theta _{l\tau }+\theta _{r\tau }}{6}\Big )\Big \}\nonumber \\ \text{ subject } \text{ to }&(0.6-\rho )(175u_1+125u_2)+\rho (177u_1+128u_2)\nonumber \\&\ge 0.6~ \theta _{l\rho },\nonumber \\&(0.6-\rho )(190u_1+140u_2)+\rho (180u_1+132u_2)\nonumber \\&\ge 0.6~ \theta _{r\rho },\nonumber \\&(0.5-\rho )(150u_1+175u_2)+\rho (153u_1+185u_2)\nonumber \\&\ge 0.5~ \theta _{l\rho },\nonumber \\&(0.5-\rho )(158u_1+200u_2)+\rho (156u_1+195u_2)\nonumber \\&\ge 0.5~ \theta _{r\rho },\nonumber ;\\&(1-\sigma )(177u_1+128u_2)+(\sigma -0.3)(175u_1+125u_2)\nonumber \\&\ge 0.7~\theta _{l\sigma },\nonumber \\&(1-\sigma )(180u_1+132u_2)+(\sigma -0.3)(190u_1+140u_2)\nonumber \\&\ge 0.7~\theta _{r\sigma },\nonumber \\&(1-\sigma )(153u_1+185u_2)+(\sigma -0.4)(150u_1+175u_2)\nonumber \\&\ge 0.6~\theta _{l\sigma },\nonumber \\&(1-\sigma )(156u_1+195u_2)+(\sigma -0.4)(158u_1+200u_2)\nonumber \\&\ge 0.6~\theta _{r\sigma },\nonumber \\&(1-\tau )(177u_1+128u_2)+(\tau -0.5)(175u_1+125u_2)\nonumber \\&\ge 0.5~\theta _{l\tau },\nonumber \\&(1-\tau )(180u_1+132u_2)+(\tau -0.5)(190u_1+140u_2)\nonumber \\&\ge 0.5~\theta _{r\tau },\nonumber \\&(1-\tau )(153u_1+185u_2)+(\tau -0.5)(150u_1+175u_2)\nonumber \\&\ge 0.5~\theta _{l\tau },\nonumber \\&(1-\tau )(153u_1+195u_2)+(\tau -0.5)(158u_1+200u_2)\nonumber \\&\ge 0.5~\theta _{r\tau },\nonumber \\&u_1+u_2=1,~u_1\ge 0,~u_2\ge 0. \end{aligned}$$

(13)

Table 1 Maximin strategies and the $(\rho ,\sigma ,\tau )$-cut sets of the gain-floor for Player-I

Table 2 Minimax strategies and the $(\rho ,\sigma ,\tau )$-cut set of the loss-ceiling for Player-II

and

$$\begin{aligned}&\min \Big \{\frac{1}{2}\Big (\frac{\phi _{l\rho }+\phi _{l\sigma }+\phi _{l\tau }+ \phi _{r\rho }+ \phi _{r\sigma }+\phi _{r\tau }}{6}\nonumber \\&\qquad +\frac{\phi _{r\rho }+\phi _{r\sigma }+\phi _{r\tau }}{3}\Big )\Big \}\nonumber \\ \text{ subject } \text{ to }&(0.5-\rho )(175v_1+150v_2)+\rho (177v_1+153v_2)\nonumber \\&\qquad \le 0.5~ \phi _{l\rho },\nonumber \\&(0.5-\rho )(190v_1+158v_2)+\rho (180v_1+156v_2)\nonumber \\&\qquad \le 0.5~ \phi _{r\rho },\nonumber \\&(0.5-\rho )(125v_1+175v_2)+\rho (128v_1+185v_2)\nonumber \\&\qquad \le 0.5~ \phi _{l\rho },\nonumber \\&(0.5-\rho )(140v_1+200v_2)+\rho (132v_1+195v_2)\nonumber \\&\qquad \le 0.5~ \phi _{r\rho },\nonumber \\&(1-\sigma )(177v_1+153v_2)+(\sigma -0.3)(175v_1+150v_2)\nonumber \\&\qquad \le 0.7~\phi _{l\sigma },\nonumber \\&(1-\sigma )(180v_1+156v_2)+(\sigma -0.3)(190v_1+158v_2)\nonumber \\&\qquad \le 0.7~\phi _{r\sigma },\nonumber \\&(1-\sigma )(128v_1+185v_2)+(\sigma -0.4)(125v_1+175v_2)\nonumber \\&\qquad \le 0.6~\phi _{l\sigma },\nonumber \\&(1-\sigma )(132v_1+195v_2)+(\sigma -0.4)(140v_1+200v_2)\nonumber \\&\qquad \le 0.6~\phi _{r\sigma },\nonumber \\&(1-\tau )(177v_1+153v_2)+(\tau -0.4)(175v_1+150v_2)\nonumber \\&\qquad \le 0.6~\phi _{l\tau },\nonumber \\&(1-\tau )(180v_1+156v_2)+(\tau -0.4)(190v_1+158v_2)\nonumber \\&\qquad \le 0.6~\phi _{r\tau },\nonumber \\&(1-\tau )(128v_1+185v_2)+(\tau -0.5)(125v_1+175v_2)\nonumber \\&\qquad \le 0.5~\phi _{l\tau },\nonumber \\&(1-\tau )(132v_1+195v_2)+(\tau -0.5)(140v_1+200v_2)\nonumber \\&\qquad \le 0.5~\phi _{r\tau },\nonumber \\&v_1+v_2=1,~v_1\ge 0,~v_2\ge 0. \end{aligned}$$

(14)

Solving Problem (13) and Problem (14) for $\rho \in [0,0.5]$, $\sigma \in [0.4,1]$ and $\tau \in [0.5,1]$, the upper and lower bounds of $\rho$-cut sets, $\sigma$-cut sets, and $\tau$-cut sets of the Player-I’s gain floor ($\tilde{\theta }^*$) and Player-II’s loss ceiling ($\tilde{\phi }^*$) can be obtained respectively. According to Theorem 2.1, the $(\rho ,\sigma ,\tau )$-cut sets, $\hat{\theta }^*_{\rho ,\sigma ,\tau }$ and $\hat{\phi }^*_{\rho ,\sigma ,\tau }$ for $\tilde{\theta }^*$ and $\tilde{\phi }^*$ respectively, can be obtained. The corresponding maximin strategies $\mathbf{u}^*$ and minimax strategies $\mathbf{v}^*$ for the players are obtained as shown in Tables 1 and 2.

Table 3 Optimal strategies and $\alpha$-WPMV of gain floor and loss ceiling

Fig. 3

Picture representation of gain floor and loss ceiling for the game problem ${\tilde{N}}$

(ii) Computational results obtained by Approach-II

According to Problem (11) and Problem (12), the following Problem (15) and Problem (16) are obtained respectively.

$$\begin{aligned}&\max ~\{P_1\} \nonumber \\ \text{ subject } \text{ to }&(1079 u_1+ 785 u_2)(0.74-0.38 \alpha )/6~\ge ~ P_1 ,\nonumber \\&(926~ u_1+ 1135~ u_2)(0.61-0.36 ~\alpha )/6~\ge ~ P_1 ,\nonumber \\&u_1+u_2~=1,~u_1~\ge ~ 0,~u_2~\ge ~0. \end{aligned}$$

(15)

and

$$\begin{aligned}&\min ~\{P_2\} \nonumber \\ \text{ subject } \text{ to }&(1079 v_1+ 926 v_2)(0.98-0.73 \alpha )/6 ~ \le P_2 ,\nonumber \\&(785 v_1+ 1135 v_2)(0.61-0.36 \alpha )/6 \le P_2,\nonumber \\&v_1+v_2=1,~v_1\ge 0,~v_2\ge 0. \end{aligned}$$

(16)

The above reduced problems (15) and (16) are solved for given weight $\alpha \in [0,1]$ by simplex method using LINGO 17.0 software and we can obtain the maximin strategy $\mathbf{u^*}(\alpha )$, the PMV $P_1^*(\alpha )$ of the gain floor for the merchant $M_1$ as well as the minimax strategy $\mathbf{v^*}(\alpha )$, the possibility mean value $P_2^*(\alpha )$ of the merchant $M_2$, depicted in following Table 3.

Table 4 $\alpha$-WPMV of $\tilde{\theta }^*$ and $\tilde{\phi }^*$ obtained by Approach-I for various $\alpha \in [0,1]$

Table 5 Maximin strategies and the $(\rho ,\sigma ,\tau )$-cut sets of the gain-floor for Player-I

Table 6 Minimax strategies and the $(\rho ,\sigma ,\tau )$-cut set of the loss-ceiling for Player-II

5.1.2 Discussion on the results

From Tables 1 and 2, the following observations are enlisted.

• (i) $\hat{\theta }^*_{\rho ,\sigma ,\tau }=[162.3306,166.0041]$ is the smallest interval ranges for the $(\rho , \sigma , \tau )-$cut-set of the gain-floor $\tilde{\theta }^*$ of Player-I for $\rho =0.5$, $\sigma =0.4$, and $\tau =0.5$.

• (ii) $\hat{\phi }^*_{\rho ,\sigma ,\tau }=[163.7586,$ 166.7586] is the smallest interval ranges for the $(\rho , \sigma , \tau )-$cut-set of the loss-ceiling $\tilde{\phi }^*$ of Player-II for $\rho =0.5$, $\sigma =0.4$, and $\tau =0.5$.

• (iii) It is clear that the larger the $\rho (\in [0,0.5])$ values and the smaller the $\sigma ( \in [0.4,1])$, and $\tau ( \in [0.5,1])$ values, $\hat{\theta }^*_{\rho ,\sigma ,\tau }$ (or $\hat{\phi }^*_{\rho ,\sigma ,\tau }$) are becoming smaller. Specifically, when $\rho =0$, $\sigma =1$ and $\tau =1$, the ($\rho , \sigma , \tau$)-cut sets of the gain floor and the loss ceiling are the intervals [158.3333,172] and [161.413,172.6087], respectively, These are the largest interval in range i.e., the value of the gain floor (or loss ceiling) never falls outside of the interval [158.3333,172] (or [161.413,172.6087]). These are the most likely value of the gain-floor and loss ceiling.

• (iv) The approximate values of the gain floor and the loss ceiling are as follows: $\tilde{\theta }^*=\langle (158.3333,162.3306,166.0041,172 );0.5,0.4,0.5 \rangle$ and $\tilde{\phi }^*=\langle (161.413,163.7586, 166.7586,172.6087);0.5,0.4,0.5\rangle$, which are depicted as in Fig. 3a and b, respectively.

• (v) $\tilde{\theta }^*$ represents that the sales amount of smartphones for the merchant $M_1$ is not less than 158.3333 units and is positively in the interval [162.3306,166.0041] by 50$\%$. It is unable to convince about the sales amount lie in the interval [162.3306,166.0041] by 50$\%$. It is indeterminate to assume that the sales amount is in the interval [162.3306,166.0041] by 40$\%$. In this case, strategies I and II are chosen with probability 0.7084189 and 0.2715811, respectively.

• (vi) $\tilde{\phi }^*$ represents the sales amount of smartphones for the merchant $M_2$ and confirms that the sales amount is not greater than 172.6087 units and it is positively in the interval [163.7586,166.7586] by 50$\%$ and unable to convince about the sales amount lie in the interval [163.7586,166.7586] by 50$\%$. It is indeterminate to assume that the sales amount is in the interval [163.7586,166.7586] by 40$\%$. In this case, strategies I and II are chosen with probability 0.4482759 and 0.5517241 respectively.

Table 3 shows the $\alpha$-WPMV $P_1^*(\alpha )$ (or $P_2^*(\alpha ))$ for various values of $\alpha \in [0,1]$ and the corresponding optimal strategies. From Table 3, it follows that $P_1^*(\alpha )$ (or $P_2^*(\alpha ))$ is a non-increasing function of the parameter $\alpha \in [0,1]$. To compare the results obtained by the two proposed approaches, Table 4 is framed. Table 4 presents the $\alpha -$WPMV of $\tilde{\theta }^*$ and $\tilde{\phi }^*$ obtained by Approach-I for various $\alpha \in [0,1]$. From Tables 3 and 4, it is clear that the PMV of the gain floor (or loss ceiling) obtained by Approach-I is lower than the PMV obtained by the Approach-II for various values of $\alpha \in [0,1]$. This implies the fact that the gain floor (or loss ceiling) represented by SVTNN obtained by Approach-I is smaller than the same obtained by the Approach-II. Again, by the Approach-I, the gain-floor (or loss-ceiling) of the matrix game ${\tilde{N}}$ can be framed in SVTNN form, which is desirable, whereas the Approach-II provides the gain-floor (or loss-ceiling) of the matrix game $\tilde{N}$ in crisp values. So, Approach-I is more reliable than Approach-II.

5.2 Example 2

Let us consider a simple numerical example where each player has two pure strategies and the SVTNN pay-off matrix ${\tilde{R}}$ for Player-I is given as follows:

$$\begin{aligned} {\tilde{R}}= & {} \begin{array}{l} \hbox {I}\\ \hbox {II} \end{array} \left( \begin{array}{ll} \qquad \quad \text{ I } &{} \qquad \quad \text{ II }\\ \langle (55,57,60,70);0.7,0.3,0.4\rangle &{}\quad \langle (30,33,36,38);0.6,0.3,0.4\rangle \\ \langle (35,38,42,47);0.8,0.2,0.4\rangle &{} \quad \langle (55,65,75,80);0.6,0.5,0.4\rangle \\ \end{array}\right) . \end{aligned}$$

As previous, the matrix game ${\tilde{R}}$ is solved by Approach-I. The upper and lower bounds of $\rho$-cut sets, $\sigma$-cut sets, and $\tau$-cut sets of $\tilde{\theta }^*$ and $\tilde{\phi }^*$ are obtained respectively, for $\rho \in [0,0.6]$, $\sigma \in [0.5,1]$ and $\tau \in [0.4,1]$. $\hat{\theta }^*_{\rho ,\sigma ,\tau }$ and $\hat{\phi }^*_{\rho ,\sigma ,\tau }$ and the corresponding maximin strategies $\mathbf{u}^*$ and minimax strategies $\mathbf{v}^*$ for the players are obtained and gathered in Tables 5 and 6.

Table 7 Optimal strategies and $\alpha$-WPMV of gain floor and loss ceiling

From Tables 5 and 6, it follows that $\hat{\theta }^*_{\rho ,\sigma ,\tau }=[48.0588,51.5294]$ and $\hat{\phi }^*_{\rho ,\sigma ,\tau }=[46.1539,$ 58.6769] are the smallest interval range for the $(\rho , \sigma , \tau )-$cut-set of $\tilde{\theta }^*$ and $\tilde{\phi }^*$ respectively, for $\rho =0.6$, $\sigma =0.5$, and $\tau =0.4$. Also it is clear that for $\rho =0$, $\sigma =1$ and $\tau =1$, the ($\rho , \sigma , \tau$)-cut sets of the gain floor and the loss ceiling are the intervals [43.8889,57.2222] and [46.1539,58.6769], respectively. These are the largest interval in range i.e., the value of the gain floor (or loss ceiling) never falls outside of the interval [43.8889,57.2222](or [46.1539,58.6769]). These are the most likely value of the gain-floor and loss ceiling. The approximate values of the gain floor and the loss ceiling are respectively $\tilde{\theta }^*=\langle (43.8889,48.0588,51.5294,57.2222 );0.6,0.5,0.4 \rangle$ and $\tilde{\phi }^*=\langle (46.1539,49.421,54.5564,58.6769);0.6,0.5,0.4\rangle$. The proposed Approach-II is also applied for the SVTNN matrix game ${\tilde{R}}$ as described in Sect. 4.2. The $\alpha$-WPMV of the optimal values for the players and the corresponding optimal strategies are obtained for various values of the parameter $\alpha$. Obtained results are shown in Table 7 for different values of $\alpha \in [0,1]$.

6 Conclusion

The SVTNN is a very useful tool to tackle uncertainty in decision-making problems. This paper uses SVTNNs to represent the imprecise payoffs so that players can consider the neutrality of the elements better. In this paper, two different solution procedures are established to solve a new matrix game where the payoffs are represented by SVTNNs. Two neutrosophic mathematical programming models are formulated to obtain the optimal values and optimal strategies for the players. First, in Approach-I, ($\rho ,\sigma ,\tau$)-cut set based ranking order relations of the SVTNNs is used to transform the defined problems into multi-objective interval-valued linear programming problems. These problems are solved to obtain the ($\rho ,\sigma ,\tau$)-cut set of the gain floor ($\tilde{\theta }^*$) and loss ceiling ($\tilde{\phi }^*$). Second, in Approach-II, we have used the concept of $\alpha$-WPMV of SVTNNs, and each neutrosophic mathematical programming model is transformed into crisp problems with the parameter $\alpha$. The proposed approaches are illustrated by solving a market share problem and another example, which implies the validity and effectiveness of the proposed approaches.

The limitation of the proposed Approach-I is that it does not find the solution to the game problem directly, as it considers the construction of different cut sets and considers a large number of in-equations. Also, Approach-I gives a wide range of the optimal values which is difficult for the decision-maker to take the appropriate decision for optimum value. But the obtained results are obtained in SVTNN form, which is desirable. Though Approach-II gives the solution of the SVTNN matrix game problem directly, it depends on the value of the parameter $\alpha$, which is difficult for the decision-maker to choose the best solution.

The proposed methods are indeed able to solve SVTNN matrix games. Moreover, the concept of this work is readily applicable to other games such as two-person non-zero-sum games, multi-objective matrix game problems, and so on. Although the discussed approaches are applied to solve a market share problem, the proposed approaches may be applied in solving many problems in management science, war science, economics, advertising, and so on.