Matrix games with linguistic intuitionistic fuzzy Payoffs : Basic results and solution methods

Abstract

Game theory has found successful applications in different areas to handle competitive situations among different persons or organizations. Several extensions of ordinary game theory have been studied by the researchers to accommodate the uncertainty and vagueness in terms of payoffs and goals. Matrix games with payoffs represented by interval numbers, fuzzy numbers, and intuitionistic fuzzy numbers have considered only the quantitative aspects of the problems. But in many situations, qualitative information plays a crucial role in representing the payoffs of a game problem. This work presents a valuable study on matrix games with payoff represented by linguistic intuitionistic fuzzy numbers (LIFNs). First, the paper defines some new operational-laws for LIFNs based on linguistic scale function (LSF) and studies their properties in detail. Next, we define a new aggregation operator called ‘generalized linguistic intuitionistic fuzzy weighted average (GLIFWA)’operator for aggregating LIFNs. Several properties and special cases of GLIFWA operator are also discussed. The LSF provides an ability to consider the different semantic situations in a single formulation during the aggregation process. Further, the paper introduces some basic results of matrix games with payoffs represented by LIFNs. We develop solution methods using a pair of auxiliary linear/nonlinear-programming models derived from a pair of nonlinear bi-objective programming models. Finally, a real-life numerical example is considered to demonstrate the validity and applicability of the developed methods.

1 Introduction

The theory of fuzzy sets (FSs), proposed by Zadeh (1975), provides an efficient tool to deal with uncertainty and fuzziness occurred in many organizational decision making and game-related problems. In fuzzy sets, Zadeh associated a degree of membership (DM) to each element of the set, which lies in the interval [0, 1]. Here, the degree of non-membership (DNM) can be directly obtained by $\left( {1 - {\text{DM}}} \right)$. In 1986, Atanassov (1986) generalized the idea of fuzzy sets by introducing the notion of the intuitionistic fuzzy set (IFS). In general, an IFS describes two kinds of fuzziness (agreement and disagreement) simultaneously, making it an efficient tool for describing real-life decision making situations more comprehensively. In past three decades, IFS theory has been successful applied to solve many complex problems related to different areas including medical diagnosis(De et al. 2001; Vlachos and Sergiadis 2007; Maheshwari and Srivastava 2016), pattern recognition(Vlachos and Sergiadis 2007; Dengfeng and Chuntian 2002; Hung and Yang 2008), decision making(Verma and Sharma 2012, 2013, 2014, 2015; Verma 2021), and image registration(Chaira 2011; Chaira and Panwar 2014).

Game theory (GT) is an important research topic of operation research that provides a mathematical framework to study cooperation and conflict between rational, intelligent decision-makers. After the pioneering work of von Neumann and MorgensternVon Neumann and Morgenstern (1953), GT has been achieved great success in multiple disciplines, and fields (Leng and Parlar 2005; Jaeger 2008; Kapliński and Tamošaitiene 2010; Madani 2010; McFadden et al. 2012; Sanchez-Soriano 2013; Muggy and Heier Stamm 2014; Nagurney et al. 2017). In the past, a wide range of studies have been carried out to solve matrix games with crisp/precise payoffs. It means that the information about the game is entirely known by the players. But in realistic situations, the information about the payoffs is not entirely known by the players due to the presence of uncertainty or insufficient information about the problem data. Firstly, fuzzy games were studied by Aubin (1981) and Butnariu (1978). Campos (1989) explored the zero-sum fuzzy matrix game with a single payoff, and the max-min problem was solved using the fuzzy mathematical programming (FMP) method. Further, Sakawa and Nishizaki (1994) studied zero-sum fuzzy matrix games with multi-objectives. Since then, several studies have been reported in the literature on matrix games and bimatrix games with fuzzy payoffs and/or fuzzy goals(Vidyottama et al. 2004; Vijay et al. 2005). Maeda (2003) defined three types of min-max equilibrium strategies of matrix games with fuzzy payoffs. In 2005, Bector et al. (2004) used the fuzzy linear programming duality approach to solve matrix games with fuzzy goals. Later, Bector et al. (2004) proved the duality result for linear programming problems with fuzzy parameters and utilized them to solve zero-sum matrix games with fuzzy payoffs. Cevikel and Ahlatolu (2010) developed two models for studying two-person zero-sum matrix games with fuzzy payoffs and fuzzy goals. They also proved that the fuzzy relation approach and the max-min solution approach are equivalent.

Atanassov (1995), firstly discussed a matrix game problem with IFS. In 2009, Li and Nan (2009) formulated a non-linear programming method for solving the matrix games with payoffs represented by IFSs. Li (2010) developed a mathematical programming approach to get the solution of matrix games with interval-valued intuitionistic fuzzy payoffs. Aggarwal et al. (2012) explored the application of intuitionistic fuzzy linear programming to matrix games with intuitionistic fuzzy goals. Later on, Aggarwal et al. (2012) discussed the applications of intuitionistic fuzzy sets to matrix games with fuzzy goals and fuzzy payoffs. Xia (2018) developed a generalized approach for solving interval-valued intuitionistic fuzzy matrix games using aggregation operators based on Archimedean t-conorm and t-norm. Khan et al. (2017) gave an approach to solve matrix games with intuitionistic fuzzy goals by resolving hesitancy degree from each goal. Recently, Naqvi et al. (2019) designed a solution procedure for intuitionistic fuzzy matrix games by using Tanaka and Asai’s approach. Up to now, several attempt have been made to develop solutions for intuitionistic fuzzy matrix games (Seikh et al. 2015; Bhaumik et al. 2017; Nan et al. 2017; Verma and Kumar 2018).

Fuzzy and intuitionistic fuzzy matrix games have been widely used to solve many real-life decision-making problems related to different application areas. However, in many real-world situations, the payoffs of a matrix game cannot be expressed in term of numerical values but maybe assessed easily by linguistic terms (Zadeh 1975). For example: suppose two insurance companies plan to launch new competing medical insurance policies for the university employees. They select the time to introduce the insurance policies, and options are 1 month, 2 month, and 3 month from now. Since companies do not have sufficient information about the market share, the payoffs cannot be quantified in numerical values but maybe assessed easily by using linguistic terms such as ‘good ’, ‘very good ’and ‘poor ’. In 2006, Arfi (2006) studied game theory based on linguistic fuzzy logic by defining the notions of linguistic fuzzy domination and the Nash equilibrium. Following this work, Singh et al. (2020) developed the linguistic linear programming (LLP) model and then utilized it to solve a two-person zero-sum matrix game with 2-tuple linguistic payoffs. Firstly, Zadeh (1975) conceptualized the idea of the linguistic variable to represent human thinking and cognition more realistically. After that, various computational models were proposed to deal with linguistic information. In the fuzzy theory, this methodology is known as ‘computing with words’(CW), which is based on fuzzy logic and fuzzy linguistic approach. In 2000, Herrera and Martínez (2000) proposed a new and useful representation model for CW, which is called the 2-tuple linguistic model.

In IFSs, the DM and the DNM are represented by numerical values. However, there are many situations in which a decision-maker cannot describe his/her preferences corresponding to DM and DNM in terms of numerical values. Also, intuitionistic fuzzy sets are incapable of representing qualitative information. In 2014, Zhang (2014) introduced the theory of linguistic intuitionistic fuzzy sets (LIFSs), which provides an efficient tool to deal with uncertain qualitative information by representing DM and DNM in terms of linguistic variables, respectively. Chen et al. (2015) formulated some aggregation operators for aggregating a collection of linguistic intuitionistic fuzzy numbers (LIFNs). Garg and Kumar (2018) used a set pair analysis approach to develop some new aggregation operators for LIF information. Peng et al. (2018) generalized the Heronian mean operator for LIFSs using Frank operations. Further, Verma (2020) developed the idea of linguistic trapezoidal fuzzy intuitionistic fuzzy sets and discussed its application in multiple attribute group decision-making problems.

It is worth mentioning that the LIFN is a very prominent tool to describe qualitative information more efficiently. So far, the discussed literature reveals that there is no study of matrix games under a linguistic intuitionistic fuzzy environment. Additionally, the existing methods cannot solve the matrix game problems with qualitative information more precisely. Therefore, the main objective of this work is to develop the basic theory and solution method for matrix games with linguistic intuitionistic fuzzy payoffs. The present study makes some novel and valuable contributions to the ongoing research in linguistic intuitionistic fuzzy modeling and matrix games to achieve the objective. First, the paper defines some new operational laws for LIFNs based on the linguistic scale function (LSF) approach and discusses their properties in detail. Note that the linguistic scale function (LSF) approach provides an ability to consider the expert’s semantic intention under different semantic environments during the operational process. Then, we define a new aggregation operator called ‘generalized linguistic intuitionistic fuzzy weighted average (GLIFWA)’operator for aggregating different LIFNs. Some properties and special cases of the proposed operator are also studied. Note that the GLIFWA operator has a flexible parameter to consider the decision-makers’ attitudinal character during the information aggregation process. Next, this paper introduces the novel concept of matrix games with payoffs represented by LIFNs. By utilizing the developed aggregation operator, the work presents the mathematical formulation of the matrix games with payoffs represented by LIFNs and the solution methods for them. Finally, we consider a real-life numerical example to demonstrate the application of the developed methods.

The rest of the paper is organized as follows: Sect. 2 presents some preliminary results on linguistic variables (LVs), LIFSs, the LSF, and the conventional matrix game. Section 3 defines some new operational laws for LIFNs with LSF and discusses their properties in detail. Next, we propose the generalized linguistic intuitionistic fuzzy weighted average operator and discuss its properties and special cases. In Sect. 4 we formulate the matrix games with payoffs represented by LIFNs and the concept of solutions. Section 5 proves that each matrix game with payoffs represented by LIFNs has a solution which is obtained by solving the auxiliary linear/nonlinear-programming models derived from a pair of nonlinear bi-objective programming models. A numerical example is considered to demonstrate the solution steps and flexibility of the given approach in Sect. 6. The work is concluded with some potential future directions for research in Sect. 7.

2 Preliminaries

This section briefly reviews some basic results related to LVs, LIFSs, LSF and conventional matrix game, which will be used for further development of the paper.

2.1 Linguistic variable

Definition 1

Let $\widehat{\mathbb {P}}=\left\{ p_{d} |d=0,1,\ldots ,2t\right\}$ be a totally ordered discrete linguistic term set (LTS) with the odd cardinality. Any level $p_{d}$ represents a possible value for a linguistic variable and t is a positive integer. The LTS $\widehat{\mathbb {P}}$ should satisfy the following properties (Herrera and Martínez 2000):

• (i) Order relation: If $p_{i} \le p_{j} \Leftrightarrow i\le j$

• (ii) Negation operator: $neg\left( p_{d} \right) =p_{2t-d}$

• (iii) Maximum operator: $\max \left( p_{i},p_{j} \right) =p_{i} \Leftrightarrow i\ge j$

• (iv) Minimum Operator: $\min \left( p_{i} ,p_{j} \right) =p_{i}\Leftrightarrow i\le j$.

For example, a set of seven linguistic terms can be represented as:

$$\begin{aligned} \widehat{\mathbb {P}}=\left\{ \begin{array}{l} p_{0} =\text {very dissatisfied (VD)},p_{1} =\text {moderately dissatisfied (MD)},p_{2} =\text { slightly dissatisfied (SD)},\\ p_{3} =\text {neither satisfied nor dissatisfied (NSND)}, p_{4} =\text {slightly satisfied(SS)}, p_{5} =\text {moderately satisfied (MS)}, \\ p_{6} =\text {very satisfied (VS)}\end{array}\right\} \end{aligned}$$

To avoid the information loss, Xu (2007) defined the extended continuous LTS $\widehat{\mathbb {P}}_{\left[ 0,2t\right] } =\left\{ p_{d}| p_{0} \le p_{d} \le p_{2t} ,d\in \left[ 0,2t\right] \right\}$, where, if $p_{d} \in \widehat{\mathbb {P}}$, then $p_{d}$ is called the original linguistic term (OLT), otherwise, $p_{d}$ is known as the virtual linguistic term (VLT).

2.2 Intuitionistic fuzzy set

Definition 2

Atanassov (1986) Let a set ${\mathfrak {U}}$ be universe of discourse. An IFS $\mathfrak {J}$ in ${\mathfrak {U}}$ is given by

$$\begin{aligned} \mathfrak {J}=\left\{ \left\langle u,{\xi _{\mathfrak {J}} \left( u\right) },{\eta _{\mathfrak {J}} \left( u\right) }\right\rangle |u \in {\mathfrak {U}}\right\} , \end{aligned}$$

(1)

where ${\xi _{\mathfrak {J}} \left( u\right) },{\eta _{\mathfrak {J}} \left( u\right) } \in \left[ 0,1\right]$, satisfying $0\le \xi _\mathfrak {J} \left( u\right) +\eta _{\mathfrak {J}} \left( u\right) \le 1 \, \forall \, u\in {\mathfrak {U}}$. The numbers ${\xi _{\mathfrak {J}} \left( u\right) }$ and ${\eta _{\mathfrak {J}} \left( u\right) }$ represent, respectively, the DM and DNM of an element $u\in {\mathfrak {U}}$ to the IFS $\mathfrak {J}$. The degree of hesitancy of ${u} \in \mathfrak {U}$ to $\mathfrak {J}$ is defined as ${\psi _{\mathfrak {J}} \left( u\right) }=1- \xi _{\mathfrak {J}}\left( u\right) - \eta _{\mathfrak {J}} \left( u\right)$. Usually, the pair $\left\langle \xi _{\mathfrak {J}}\left( u\right) , \eta _{\mathfrak {J}} \left( u\right) \right\rangle$ is called an intuitionistic fuzzy number (IFN) and it is simplified as $\delta =\left\langle \xi _{\delta }, \eta _{\delta } \right\rangle$.

2.3 Linguistic Intuitionistic fuzzy set

Zhang (2014) forwarded the notion of IFSs to linguistic environment and proposed the concept of linguistic intuitionistic fuzzy sets (LIFSs) to represent qualitative information more precisely. It can be defined as follows:

Definition 3

Zhang (2014) Let ${\mathfrak {U}}$ be a set of universe of discourse and $\widehat{\mathbb {P}}_{\left[ 0,2t\right] } =\left\{ p_{d} |p_{0} \le p_{d} \le p_{2t}, d\in \left[ 0,2t\right] \right\}$ be an extended continuous LTS. A LIFS $\mathfrak {L}$ in ${\mathfrak {U}}$ is given by

$$\begin{aligned} \mathfrak {L}=\left\{ \left\langle u,p_{\xi _{\mathfrak {L}} \left( u\right) },p_{\eta _{\mathfrak {L}} \left( u\right) }\right\rangle |u \in {\mathfrak {U}}\right\} , \end{aligned}$$

(2)

where $p_{\xi _{\mathfrak {L}} \left( u\right) },p_{\eta _{\mathfrak {L}} \left( u\right) } \in \widehat{\mathbb {P}}_{\left[ 0,2t\right] }$, satisfying $0\le \xi _\mathfrak {L} \left( u\right) +\eta _{\mathfrak {L}} \left( u\right) \le 2t\, \forall \, u\in {\mathfrak {U}}$. The LTs $p_{\xi _{\mathfrak {L}} \left( u\right) }$ and $p_{\eta _{\mathfrak {L}} \left( u\right) }$ represent, respectively, the DM and DNM of an element $u\in {\mathfrak {U}}$ to the LIFS $\mathfrak {L}$. The degree of hesitancy of ${u} \in \mathfrak {U}$ to the set $\mathfrak {L}$ can be calculated as $p_{\psi _{\mathfrak {L}} \left( u\right) }=p_{{ 2t- {\xi _{\mathfrak {L}} \left( u\right) }- {\eta _{\mathfrak {L}} \left( u\right) }}}$. For a given element $u\in \mathfrak {U}$, the pair $\left\langle {p}_{\xi _{\mathfrak {L}} \left( u\right) } ,{p}_{\eta _{\mathfrak {L}} \left( u\right) } \right\rangle$ is called a linguistic intuitionistic fuzzy number (LIFN), which can be simply denoted by $\Upsilon =\left\langle p_{\xi }, p_{\eta } \right\rangle$.

Definition 4

(Zhang 2014) (Set-theoretic operations) Let ${\Upsilon } =\left\langle p_{\xi }, p_{\eta } \right\rangle$, ${\Upsilon }_1 =\left\langle p_{\xi _{1}}, p_{\eta _{1}} \right\rangle$ and ${\Upsilon }_2 =\left\langle p_{\xi _{2}}, p_{\eta _{2}} \right\rangle$ be three LIFNs, then

• (i) ${{\Upsilon }_{1}}\subseteq {{\Upsilon }_{2}}$ if ${p_{\xi _{1}}} \le {p_{\xi _{2}}}$ and ${p_{\eta _{1}}}\ge {p_{\eta _{2}}}$;

• (ii) ${{\Upsilon }_{1}}= {{\Upsilon }_{2}}$ if and only if ${{\Upsilon }_{1}}\subseteq {{\Upsilon }_{2}}$ and ${{\Upsilon }_{2}}\subseteq {{\Upsilon }_{1}}$ ;

• (iii) ${\Upsilon }^{C}=\left\langle p_{\eta }, p_{\xi } \right\rangle$;

• (iv) ${{\Upsilon }_{1}}{\cup }{{\Upsilon }_{2}}= \left\langle \max \left( {{p}_{{\xi }_{1}}},{{p}_{{\xi }_{2}}} \right) ,\min \left( {p}_{{\eta }_{1}},{p}_{{{\eta }_{2}}} \right) \right\rangle$;

• (v) ${{\Upsilon }_{1}}{\cap }{{\Upsilon }_{2}}= \left\langle \min \left( {{p}_{{\xi }_{1}}},{{p}_{{\xi }_{2}}} \right) ,\max \left( {p}_{{\eta }_{1}},{p}_{{{\eta }_{2}}} \right) \right\rangle$.

Definition 5

(Zhang 2014) (Algebraic operations) Let ${\Upsilon } =\left\langle p_{\xi }, p_{\eta } \right\rangle$, ${\Upsilon }_1 =\left\langle p_{\xi _{1}}, p_{\eta _{1}} \right\rangle$ and ${\Upsilon }_2 =\left\langle p_{\xi _{2}}, p_{\eta _{2}} \right\rangle$ be three LIFNs, then the algebraic operations of the LIFNs are defined as follows:

• (i) ${{\Upsilon }_{1}}{{\oplus }} {{\Upsilon }_{2}} =\left\langle p_{\xi _{1}+\xi _{2}-\frac{\xi _{1}\xi _{2}}{2t} }, p_{\frac{{\eta _{1}}{\eta _{2}}}{2t}}\right\rangle$;

• (ii) ${{\Upsilon }_{1}}{{\otimes }} {{\Upsilon }_{2}} =\left\langle p_{\frac{{\xi _{1}}{\xi _{2}}}{2t}}, p_{\eta _{1}+\eta _{2}-\frac{\eta _{1}\eta _{2}}{2t} }\right\rangle$;

• (iii) $\lambda {{*}}{\Upsilon }=\left\langle p_{2t{{\left( 1-\left( 1-\frac{\xi }{2t }\right) ^\lambda \right) }}},p_{2t\big (\frac{\eta }{2t}\big )^\lambda }\right\rangle$;

• (iv) ${\Upsilon }^{{\wedge }}\lambda =\left\langle p_{2t\big (\frac{\xi }{2t}\big )^\lambda }, p_{2t{{\left( 1-\left( 1-\frac{\eta }{2t }\right) ^\lambda \right) }}}\right\rangle$.

Definition 6

(Zhang 2014) Let $\Upsilon =\left\langle {p_{\xi },p_{\eta }} \right\rangle$ be a LIFN, the score and accuracy values of $\Upsilon$ can be defined as

$$\begin{aligned} \mathcal {S}\left( \Upsilon \right) ={{p}_{{\left( \frac{{{2t}}+\xi -\eta}{2} \right) }}} \;\;\;\text {and} \;\;\; \mathcal {A}\left( \Upsilon \right) ={{p}_{{{\xi+\eta}}}}. \end{aligned}$$

(3)

Based on these values, an order relation between two LIFNs ${{\Upsilon }_{1}}=\left\langle {{p}_{{{\xi }_{{_{1}}}}}},{{p}_{{{\eta }_{{_{1}}}}}} \right\rangle$ and ${{\Upsilon }_{2}}=\left\langle {{p}_{{{\xi }_{{_{2}}}}}},{{p}_{{{\eta }_{{_{2}}}}}} \right\rangle$, is given as Zhang (2014):

• (i) If $\mathcal {S}\left( {\Upsilon _{1}} \right) >\mathcal {S}\left( {{\Upsilon }_{2}} \right)$ then, ${{\Upsilon }_{1}}\succ {{\Upsilon }_{2}}$;

• (ii) If $\mathcal {S}\left( {{\Upsilon }_{1}} \right) =\mathcal {S}\left( {{\Upsilon }_{2}} \right)$, then

  • (a) $\mathcal {A}\left( {{\Upsilon }_{1}} \right) >\mathcal {A}\left( {{\Upsilon }_{2}} \right)$, then ${{\Upsilon }_{1}}\succ {{\Upsilon }_{2}}$;

  • (b) $\mathcal {A}\left( {{\Upsilon }_{1}} \right) =\mathcal {A}\left( {{\Upsilon }_{2}} \right)$, then ${{\Upsilon }_{1}}={{\Upsilon }_{2}}$.

Zhang (2014) also defined the following arithmetic and geometric aggregation operators for aggregating a set n LIFNs ${\Upsilon }_i =\left\langle p_{\xi _{i}}, p_{\eta _{i}} \right\rangle$   $\left( i=1,2,\ldots ,n \right)$ with weight vector $w=\left( w_{1},w_{2},\ldots ,w_{n} \right) ^T$ of ${\Upsilon }_i$, satisfying $w_{i}>0$ and $\sum _{i=1}^{n}w_{i}=1$.

• (a) Linguistic intuitionistic fuzzy weighted average (LIFWA) operator

  $$\begin{aligned} LIFWA\left( \Upsilon _{1}, \Upsilon _{2},\ldots ,\Upsilon _{n}\right) =\left( w_{1}*\Upsilon _{1}\right) \oplus \left( w_{2}*\Upsilon _{2}\right) \oplus \cdots \oplus \left( w_{n}*\Upsilon _{n}\right) =\left\langle p_{2t\left( 1-\prod _{i=1}^{n} \left( 1-\frac{\xi _{i}}{2t}\right) ^{w_{i}} \right) },p_{2t\left( \prod _{i=1}^{n} \left( \frac{\eta _{i}}{2t} \right) ^{w_{i}}\right) } \right\rangle , \end{aligned}$$

  (4)

• (b) Linguistic intuitionistic fuzzy weighted geometric (LIFWG) operator

  $$\begin{aligned} LIFWG\left( \Upsilon _{1}, \Upsilon _{2},\ldots ,\Upsilon _{n}\right) =\left( {\Upsilon _{1}}^{{\wedge }}{w_{1}}\right) \otimes \left( {\Upsilon _{2}}^{{\wedge }}{w_{2}}\right) \otimes \cdots \otimes \left( {\Upsilon _{n}}^{{\wedge }}{w_{n}}\right) =\left\langle p_{\left( 2t\prod _{i=1}^{n} \left( \frac{\xi _{i}}{2t} \right) ^{w_{i}}\right) },p_{2t\left( 1-\prod _{i=1}^{n} \left( 1-\frac{\eta _{i}}{2t}\right) ^{w_{i}} \right) } \right\rangle . \end{aligned}$$

  (5)

It is worth mentioning that the operational rules given in Def. 5 were developed with the assumption that the absolute semantic gap (ASG) between any two LTs is always equal. However, in many practical situations, as the subscript of the LT expends from the middle to both ends, decision maker may feel that the ASG will increase or decrease, not always be equal. Also, the LIFWA and LIFWG operators cannot accommodate the semantic translation requirements of different decision makers (DMs). To cope with this issue, Wang et al. (2014) proposed the concept of LSF by motivating the notion of numerical scale (Dong et al. 2009). It provides an efficient tool to convert LT into an equivalent real number and vice-versa with considering the semantic changes of DMs under different semantic environments.

2.4 Linguistic scale function

Definition 7

Let $\widehat{\mathbb {P}}=\left\{ {p_{d}}|d=0,1,\ldots ,2t \right\}$ be a discrete LTS with the odd cardinality and ${\kappa _{d}}\in \left[ 0,1 \right]$ be a real number, then the LSF $\varphi$ can be defined as

$$\begin{aligned} \varphi :{p_{d}}\rightarrow {\kappa _{d}} \left( d=0,1,\ldots ,2t \right) , \end{aligned}$$

(6)

where $\varphi$ is a strictly monotonically increasing function with respect to subscript d.

The LSF $\varphi$ satisfies the following properties: (a) $\varphi \left( {p_{0}} \right) =0$, $\varphi \left( {p_{2t}} \right) =1$ (b) $\varphi \left( {p_{{{d}_{1}}}} \right) \ge \varphi \left( {p_{{{d}_{2}}}} \right) \text { if and only if }{{d}_{1}}\ge {{d}_{2}}$.

According to Wang et al. (2014) , we have the following three different linguistic scale functions, given as

• (i) When the ASG between two adjacent LTs remains unchanged.

  $$\begin{aligned} {{\varphi }_{1}}\left( {p_{d}} \right) ={\kappa _{d}}=\frac{d}{2t},\, (d=0,1,\ldots ,2t). \end{aligned}$$

  (7)

• (ii) When the ASG between two semantics of the adjacent LTs is increasing with the extension from $p_{t}$ to both ends of LTS.

  $$\begin{aligned} {{\varphi }_{2}}\left( {p_{d}}\right) ={\kappa _{d}}= {\left\{ \begin{array}{ll} \frac{\varrho ^t-\varrho ^{t-d}}{2(\varrho ^t-1)},&{} d=0,1,\ldots ,t\\ \frac{\varrho ^t+\varrho ^{d-t}-2}{2(\varrho ^t-1)} &{} d=t+1,t+2,\ldots ,2t. \end{array}\right. } \end{aligned}$$

  (8)

  where $\varrho >1$ is a threshold value, which can be determined by a subjective method according to the specific problem. If the LTS is a set of seven terms, then $\varrho \in [1.37,1.40]$ .

• (iii) When the ASG between two semantics of the adjacent LTs is decreasing with the extension from $p_{t}$ to both ends of LTS.

  $$\begin{aligned} {{\varphi }_{3}}\left( {p_{d}}\right) ={\kappa _{d}}= {\left\{ \begin{array}{ll} \frac{t^\rho -\left( {t-d}\right) ^\rho }{2t^\rho },&{} d=0,1,\ldots ,t\\ \frac{t^{\tau }+\left( {d-t}\right) ^\tau }{2t^\tau } &{} d=t+1,t+2,\ldots ,2t. \end{array}\right. } \end{aligned}$$

  (9)

  where $\rho ,\tau \in [ 0,1]$ are determined according to the specific problem. If the LTS is a set of seven terms, then $\rho =\tau =0.8$.

In order to avoid an information loss during calculation process, the LSF can be further generalized to an extended continuous LTS as follows:

Definition 8

Let ${{\widehat{\mathbb {P}}}_{\left[ 0,2t \right] }}=\left\{ {p_{d}}|{p_{0}}\le {p_{d}}\le {p_{2t}},d\in \left[ 0,2t \right] \right\}$ be an extended continuous LTS and ${\kappa _{d}}\in \left[ 0,1 \right]$ be a real number, then the linguistic scale function (LSF) ${{\varphi }^{*}}$ can be defined as

$$\begin{aligned} {{\varphi }^{*}}:{{\widehat{\mathbb {P}}}_{\left[ 0,2t \right] }}\rightarrow {\kappa _{d}}, \end{aligned}$$

(10)

where ${{\varphi }^{*}}$ is also a strictly monotonically increasing and continuous function, and its inverse is denoted by ${{\varphi }^{*}}^{-1}$.

Example 1

Let ${{\widehat{\mathbb {P}}}_{\left[ 0,8 \right] }}=\left\{ {p_{d}}|d\in \left[ 0,8 \right] \right\}$ be a continuous LTS, then the inverse corresponding to the LSFs $\varphi _{1}^{*}$ ,$\varphi _{2}^{*}$ and $\varphi _{3}^{*}$ can be obtained as follows:

• 1. ${{\varphi }_{1}^{*}} (p_{d})=\kappa _{d}=\frac{d}{8}, \, d=[0,8]$, then ${\varphi }_{1}^{*-1}(\kappa _d) =p_{8\times {\kappa _{d}}}(\kappa _{d}\in [0,1])$.

• 2. ${{\varphi }_{2}^{*}}\left( {p_{d}}\right) ={\kappa _{d}}= {\left\{ \begin{array}{ll} \frac{\varrho ^4-\varrho ^{4-d}}{2\times (\varrho ^4-1)},&{} d=0\le d\le 4\\ \frac{\varrho ^4+\varrho ^{d-4}-2}{2\times (\varrho ^4-1)} &{} d=4< d\le 8, \end{array}\right. }$ then

  $$\begin{aligned} {{\varphi }_{2}^{*-1}}\left( {\kappa _{d}}\right) ={p_{d}}= {\left\{ \begin{array}{ll} p_{4-log_{\varrho }[{\varrho }^4-(2{\varrho }^4-2){\kappa _{d}}]}, &{} \kappa _{d} \in [0,0.5]\\ p_{4+log_{\varrho }[(2{\varrho }^4-2){\kappa _{d}-{\varrho }^4+2}]} &{} \kappa _{d} \in (0.5,1] \end{array}\right. }. \end{aligned}$$

• 3. ${{\varphi }_{3}^{*}}\left( {p_{d}}\right) ={\kappa _{d}}= {\left\{ \begin{array}{ll} \frac{4^\rho -(4-d)^{\rho }}{2\times 4^{\rho }},&{} d=0\le d\le 4\\ \frac{4^\tau +(d-4)^{\tau }}{2\times 4^{\tau }} &{} d=4< d\le 8, \end{array}\right. }$ then

  $$\begin{aligned} {{\varphi }_{3}^{*-1}}\left( {\kappa _{d}}\right) ={p_{d}}= {\left\{ \begin{array}{ll} p_{4-\left[ 4^{\rho }-2\times 4^{\rho }\times {\kappa _{d}} \right] ^\frac{1}{\rho }} , &{} \kappa _{d} \in [0,0.5]\\ p_{4+\left[ 2\times 4^{\tau }\times {\kappa _{d}}-4^{\tau } \right] ^\frac{1}{\tau }} &{} \kappa _{d} \in (0.5,1] \end{array}\right. }. \end{aligned}$$

2.5 A two-person zero-sum matrix game

This subsection recalls some preliminaries from standard non-cooperative matrix game theory.

Definition 9

(Barron 2008) A two-person zero-sum matrix game $\mathfrak {G}$ is a triplet $\left( \mathbb {S}^m,\mathbb {S}^n,\mathcal {A} \right)$, where

• 1. $\mathbb {S}^m=\left( \alpha _1,\alpha _2,\ldots ,\alpha _m \right)$ is a finite set of m possible strategies for person I;

• 2. $\mathbb {S}^n=\left( \beta _1,\beta _2,\ldots ,\beta _n \right)$ is a finite set of n possible strategies for person II;

• 3. $\mathcal {A}=\left( a_{ij}\right) _{m\times n}$ is a real matrix representing the payoffs of person I against person II, and $-\mathcal {A}$ is taken as the payoff matrix for person II.

Definition 10

(Barron 2008) A matrix game $\mathfrak {G}$ with $\mathcal {A}=\left( a_{ij}\right) _{m\times n}$ has the maximin value and the minimax value , respectively, given as

$$\begin{aligned} \left. \begin{array}{l} \aleph ^{-}=\max _{i=1,2,\ldots ,m}\min _{j=1,2,\ldots ,m}\left( a_{ij}\right) \\ \aleph ^{+}=\min _{j=1,2,\ldots ,m}\max _{i=1,2,\ldots ,n}\left( a_{ij}\right) \end{array}.\right\} \end{aligned}$$

(11)

Here $\aleph ^{-}$ (person I’s gain floor) is the minimum payoff that person I is assured to receive and $\aleph ^{+}$(person II’s loss ceiling) is the maximum payoff that person II can loose. A game $\mathfrak {G}$ has value if and only if $\aleph ^{-}=\aleph ^{+}$. The strategies $i^{*}$ and $j^{*}$, giving the payoffs $a_{i^{*}j^{*}}=\aleph ^{-}=\aleph ^{+}$, are optimal strategies for person I and person II, respectively. In addition, $a_{ij^{*}}\le a_{i^{*}j^{*}}\le a_{i^{*}j}$ $\forall i=1,2,\ldots ,m; j\, j=1,2,\ldots ,n$, and $\left( i^{\star },j^{\star }\right)$ is called the saddle point of game $\mathfrak {G}$.

Definition 11

(Barron 2008) A mixed strategy is an ordered pair of vectors $\left( x,y\right) \in \mathbb {S}^m\times \mathbb {S}^n$, where

$$\begin{aligned} \mathbb {S}^m&=\left\{ \left( x_{1},x_{2},\ldots ,x_{m} \right) : x_{i}\ge 0, i=1,2,\ldots ,n; \sum _{i=1}^{m} x_{i}=1\right\} ; \\ \mathbb {S}^n&=\left\{ \left( y_{1},y_{2},\ldots ,y_{n} \right) : y_{j}\ge 0, j=1,2,\ldots ,m; \sum _{j=1}^{n}y_{j}=1\right\} . \end{aligned}$$

Here, $x_{i}$ denotes the probability of person I choosing strategy $\alpha _{i}$ and $y_{j}$ is the probability of person II selecting strategy $\beta _{j}$ .

In the next section, we define some new operational laws of LIFNs based on LSF and analyze a number of desirable properties associated with them in detail. We also develop a new generalized arithmetic aggregation operator for LIFNs using new operational laws of LIFNs.

3 New operational laws and aggregation operator for LIFNs based on LSF

3.1 New operational laws of LIFNs based on LSF

Definition 12

Let ${\Upsilon } =\left\langle p_{\xi }, p_{\eta } \right\rangle$, ${\Upsilon }_1 =\left\langle p_{\xi _{1}}, p_{\eta _{1}} \right\rangle$ and ${\Upsilon }_2 =\left\langle p_{\xi _{2}}, p_{\eta _{2}} \right\rangle$ be three LIFNs, $\varphi ^*$ be a LSF, $\varphi ^{*-1}$ be the inverse function of $\varphi ^*$ and $\lambda >0$. Then, new operational laws are defined as follows:

• (i) ${{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}} = \left\langle {{\varphi ^{*-1} \left( \varphi ^*\left( {p_{\xi _{1}}}\right) +\varphi ^*\left( {p_{\xi _{2}}}\right) -\varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) \right) }}, {{\varphi ^{*-1}\left( \varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) }}\right\rangle ;$

• (ii) ${{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}} = \left\langle {{\varphi ^{*-1} \left( \varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) \right) }}, {{\varphi ^{*-1}\left( \varphi ^*\left( {p_{\eta _{1}}}\right) +\varphi ^*\left( {p_{\eta _{2}}}\right) - \varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) }}\right\rangle ;$

• (iii) $\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }} = \left\langle {{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda \right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda \right) }}\right\rangle ;$

• (iv) ${\Upsilon }^{\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda \right) }}\right\rangle .$

Example 2

Let ${\Upsilon }=\left\langle p_{2},p_{3}\right\rangle$, ${\Upsilon }_1=\left\langle p_{4},p_{2}\right\rangle$ and ${\Upsilon }_2=\left\langle {p_{5}},{p_{1}} \right\rangle$ be three LIFNs defined on ${{\widehat{\mathbb {P}}}_{\left[ 0,8 \right] }}$ and $\lambda =3$. Then, using the new operational laws mentioned in Def. 12 with different LSFs, we get the results as shown in Table 1.

Table 1 The values of various operational laws of LIFNs based on different LSFs

Theorem 1

Let ${\Upsilon }_1 =\left\langle p_{\xi _{1}}, p_{\eta _{1}} \right\rangle$ and ${\Upsilon }_2 =\left\langle p_{\xi _{2}}, p_{\eta _{2}} \right\rangle$ be two LIFNs. If ${\Upsilon }_3 ={{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}}$ and ${\Upsilon }_4 ={{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}$. Then, both ${\Upsilon }_3$ and ${\Upsilon }_4$ are also LIFNs.

Proof

Since ${\Upsilon }_3 ={{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}}=\left\langle p_{\xi _{3}}, p_{\eta _{3}} \right\rangle$. From Def. 12, we have

$$\begin{aligned} p_{\xi _{3}}&=\varphi ^{*-1} \left( \varphi ^*\left( {p_{\xi _{1}}}\right) +\varphi ^*\left( {p_{\xi _{2}}}\right) -\varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) \right) ; \end{aligned}$$

(12)

$$\begin{aligned} p_{\eta _{3}}&=\varphi ^{*-1}\left( \varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) . \end{aligned}$$

(13)

Since $p_{\xi _{i}}, p_{\eta _{i}} \in {{\widehat{\mathbb {P}}}_{\left[ 0,2t \right] }}$ and $\xi _{i}+\eta _{i}\le 2t \,\,\text {for} \, i=1,2$, then $\varphi ^*\left( p_{\xi _{i}}\right)$, $\varphi ^*\left( p_{\eta _{i}}\right) \in \left[ 0,1 \right]$ and $\varphi ^*\left( p_{\xi _{i}}\right) + \varphi ^*\left( p_{\eta _{i}}\right) \le 1 \, \text {for} \, i=1,2$. Using these results, we have

$$\begin{aligned} 0 \le \varphi ^*\left( {p_{\xi _{1}}}\right) +\varphi ^*\left( {p_{\xi _{2}}}\right) -\varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) \le 1 \,\, \text {and} \,\, 0 \le \varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \le 1. \end{aligned}$$

Therefore

$$\begin{aligned}&\varphi ^{*-1}\left( \varphi ^*\left( {p_{\xi _{1}}}\right) +\varphi ^*\left( {p_{\xi _{2}}}\right) -\varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) \right) ,\\&\varphi ^{*-1}\left( \varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) \in {{\widehat{\mathbb {P}}}_{\left[ 0,2t \right] }}. \end{aligned}$$

By using Eqs. (12) and (13), we get

$$\begin{aligned}&\varphi ^{*}\left( p_{\xi _{3}}\right) + \varphi ^{*}\left( p_{\eta _{3}}\right) = \varphi ^*\left( {p_{\xi _{1}}}\right) +\varphi ^*\left( {p_{\xi _{2}}}\right) -\varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) + \varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \\&\quad \le \varphi ^*\left( {p_{\xi _{1}}}\right) +\varphi ^*\left( {p_{\xi _{2}}}\right) -\varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) + \left( 1-\varphi ^*\left( {p_{\xi _{1}}}\right) \right) \left( 1- \varphi ^*\left( {p_{\xi _{2}}}\right) \right) =1. \end{aligned}$$

which shows that ${\Upsilon }_3$ is a LIFN. Similarly, we can prove that ${\Upsilon }_4$ is also a LIFN.

This completes the proof of Theorem. $\square$

Theorem 2

Let ${\Upsilon } =\left\langle p_{\xi }, p_{\eta } \right\rangle$ be a LIFN and $\lambda > 0$. If ${\Upsilon }_1 =\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }}$ and ${\Upsilon }_2 ={{\Upsilon }}^{\overset{\blacktriangle }{\wedge }} \lambda$, then, both ${\Upsilon }_1$ and ${\Upsilon }_2$ are also LIFNs.

Proof

Since ${\Upsilon _{1}}={\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }}}=\left\langle p_{\xi _{1}}, p_{\eta _{1}} \right\rangle$. Using Def. 12, we get

$$\begin{aligned} p_{\xi _{1}}&={{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda \right) }}; \end{aligned}$$

(14)

$$\begin{aligned} p_{\eta _{1}}&= {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda \right) }}. \end{aligned}$$

(15)

Also $p_{\xi }, p_{\eta } \in {{\widehat{\mathbb {P}}}_{\left[ 0,2t \right] }}$ and ${\xi } + {\eta }\le 2t$, then $\varphi ^*\left( p_{\xi }\right)$, $\varphi ^*\left( p_{\eta }\right) \in \left[ 0,1 \right]$ and $\varphi ^*\left( p_{\xi }\right) +\varphi ^*\left( p_{\eta }\right) \le 1$. It gives

$$\begin{aligned} 0\le {{1 -\left( 1- \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda }}\le 1;\, 0\le {{ \left( \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda }} \le 1. \end{aligned}$$

Therefore

$$\begin{aligned} {{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda \right) }}}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda \right) }} \in {{\widehat{\mathbb {P}}}_{\left[ 0,2t \right] }}. \end{aligned}$$

From Eqs. (14) and (15), we have

$$\begin{aligned} \varphi ^{*}\left( p_{\xi _{1}}\right) + \varphi ^{*}\left( p_{\eta _{1}}\right) ={{1 -\left( 1- \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda }}+ {{ \left( \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda }} \le {{1 -\left( 1- \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda }}+ {{ \left( 1-\varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda }}=1. \end{aligned}$$

which confirms that ${\Upsilon }_1$ is a LIFN. Similarly, we can prove that ${\Upsilon }_2$ is also a LIFN.

This proves the Theorem. $\square$

Remark 1

In the following, let us examine the $\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }}$ and ${\Upsilon }^{\overset{\blacktriangle }{\wedge }}\lambda$ for some special cases of $\lambda$ and ${\Upsilon }$.

• (i) If ${\Upsilon } =\left\langle p_{\xi }, p_{\eta } \right\rangle =\left\langle p_{2t}, p_{0} \right\rangle$, then

  $$\begin{aligned}&\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }} = \left\langle {{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{2t}}\right) \right) ^\lambda \right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{0}}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{2t}, p_{0} \right\rangle ;\\&{\Upsilon }^{\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{2t}}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{0}}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{2t}, p_{0} \right\rangle . \end{aligned}$$

• (ii) If ${\Upsilon } =\left\langle p_{\xi }, p_{\eta } \right\rangle =\left\langle p_{0}, p_{2t} \right\rangle$, then

  $$\begin{aligned}&\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }} = \left\langle {{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{0}}\right) \right) ^\lambda \right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{2t}}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{0}, p_{2t} \right\rangle ;\\&{\Upsilon }^{\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{0}}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{2t}}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{0}, p_{2t} \right\rangle . \end{aligned}$$

• (iii) If $\lambda \rightarrow 0$, then

  $$\begin{aligned}&\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }} = \left\langle {{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda \right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{0}, p_{2t} \right\rangle ;\\&{\Upsilon }^{\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{2t}, p_{0} \right\rangle . \end{aligned}$$

• (iv) If $\lambda \rightarrow +\infty$, then

  $$\begin{aligned}&\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }} = \left\langle {{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda \right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{2t}, p_{0} \right\rangle ;\\&{\Upsilon }^{\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\xi }}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\eta }}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{0}, p_{2t} \right\rangle . \end{aligned}$$

• (v) If ${\Upsilon } =\left\langle p_{\xi }, p_{\eta } \right\rangle =\left\langle p_{0}, p_{0} \right\rangle$, then

  $$\begin{aligned}&\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }} = \left\langle {{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{0}}\right) \right) ^\lambda \right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{0}}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{0}, p_{0} \right\rangle ;\\&{\Upsilon }^{\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{0}}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{0}}\right) \right) ^\lambda \right) }}\right\rangle =\left\langle p_{0}, p_{0} \right\rangle . \end{aligned}$$

Theorem 3

Let ${\Upsilon }_1 =\left\langle p_{\xi _{1}}, p_{\eta _{1}} \right\rangle$ and ${\Upsilon }_2 =\left\langle p_{\xi _{2}}, p_{\eta _{2}} \right\rangle$ and ${\Upsilon }_3 =\left\langle p_{\xi _{3}}, p_{\eta _{3}} \right\rangle$ be three LIFNs, then new operational laws of LIFNs satisfy the following properties:

• (a) ${{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}}={{\Upsilon }_{2}}{\overset{\blacktriangle }{\oplus }}{{\Upsilon }_{1}}$;

• (b) ${{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}={{\Upsilon }_{2}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{1}}$;

• (c) $\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}}\right) {\overset{\blacktriangle }{\oplus }}{{\Upsilon }_{3}} ={{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }}\left( {{\Upsilon }_{2}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{3}}\right)$;

• (d) $\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}\right) {\overset{\blacktriangle }{\otimes }}{{\Upsilon }_{3}} ={{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }}\left( {{\Upsilon }_{2}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{3}}\right)$.

Proof

The proof follows directly from Definition 12. $\square$

Theorem 4

Let ${\Upsilon } =\left\langle p_{\xi }, p_{\eta } \right\rangle$, ${\Upsilon }_1 =\left\langle p_{\xi _{1}}, p_{\eta _{1}} \right\rangle$ and ${\Upsilon }_2 =\left\langle p_{\xi _{2}}, p_{\eta _{2}} \right\rangle$,${\Upsilon }_3 =\left\langle p_{\xi _{3}}, p_{\eta _{3}} \right\rangle$ be four LIFNs and $\lambda ,\lambda _{1},\lambda _{2}>0$, then

• (a) $\left( \lambda {\overset{\blacktriangle }{*}} {{\Upsilon }_{1}}\right) {\overset{\blacktriangle }{\oplus }} \left( \lambda {\overset{\blacktriangle }{*}} {{\Upsilon }_{2}}\right) =\lambda {\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}}\right)$;

• (b) $\left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}\lambda \right) {\overset{\blacktriangle }{\otimes }} \left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}\lambda \right) =\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}\right) ^ {\overset{\blacktriangle }{\wedge }}\lambda$;

• (c) $\left( \lambda _{1} {\overset{\blacktriangle }{*}} {{\Upsilon }}\right) {\overset{\blacktriangle }{\oplus }} \left( \lambda _{2} {\overset{\blacktriangle }{*}} {{\Upsilon }}\right) =\left( \lambda _{1}+\lambda _{2}\right) {\overset{\blacktriangle }{*}} {{\Upsilon }}$;

• (d) $\left( {{\Upsilon }}^{\overset{\blacktriangle }{\wedge }}\lambda _{1} \right) {\overset{\blacktriangle }{\otimes }} \left( {{\Upsilon }}^{\overset{\blacktriangle }{\wedge }}\lambda _{2} \right) ={{\Upsilon }}^ {\overset{\blacktriangle }{\wedge }}\left( \lambda _{1}+\lambda _{2}\right)$;

• (e) $\lambda _{1}{\overset{\blacktriangle }{*}}\left( \lambda _{2} {\overset{\blacktriangle }{*}} {{\Upsilon }}\right) =\left( \lambda _{1}\lambda _{2}\right) {\overset{\blacktriangle }{*}}{\Upsilon }$;

• (f) $\left( {{\Upsilon }}^{\overset{\blacktriangle }{\wedge }}\lambda _{1} \right) ^{\overset{\blacktriangle }{\wedge }}\lambda _{2}={{\Upsilon }}^ {\overset{\blacktriangle }{\wedge }}\left( \lambda _{1}\lambda _{2}\right)$;

• (g) ${{\Upsilon }_{1}^{C}} {\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}^{C}} =\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}\right) ^{C}$;

• (h) ${{\Upsilon }_{1}^{C}} {\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}^{C}} =\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}}\right) ^{C}$;

• (i) $\left( {{\Upsilon }^{C}}\right) ^ {\overset{\blacktriangle }{\wedge }} {\lambda }=\left( {{\lambda }{\overset{\blacktriangle }{*}}{\Upsilon }}\right) ^{C}$;

• (j) ${\lambda }{\overset{\blacktriangle }{*}}\left( {{\Upsilon }^{C}}\right) =\left( {{\Upsilon }^{\overset{\blacktriangle }{\wedge }} {\lambda }}\right) ^{C}$.

Proof

Here, we shall prove only (a), (b) and (g), the proofs of the other statements can be obtained similarly.

(a) Utilizing the operational laws given in Def. 12, we have

$$\begin{aligned}&\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }_{1}} = \left\langle {{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\xi _{1}}}\right) \right) ^\lambda \right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta _{1}}}\right) \right) ^\lambda \right) }}\right\rangle ,\\&\lambda {\overset{\blacktriangle }{*}} {{\Upsilon }_{2}} = \left\langle {{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\xi _{2}}}\right) \right) ^\lambda \right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta _{2}}}\right) \right) ^\lambda \right) }}\right\rangle , \end{aligned}$$

and

$$\begin{aligned} {{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}} = \left\langle {{\varphi ^{*-1} \left( \varphi ^*\left( {p_{\xi _{1}}}\right) +\varphi ^*\left( {p_{\xi _{2}}}\right) -\varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi_{2}}}\right) \right) }}, {{\varphi ^{*-1}\left( \varphi ^*\left( {p_{\eta_{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) }}\right\rangle . \end{aligned}$$

Therefore, we get

$$\begin{aligned} \left( \lambda {\overset{\blacktriangle }{*}} {{\Upsilon }_{1}}\right) {\overset{\blacktriangle }{\oplus }} \left( \lambda {\overset{\blacktriangle }{*}} {{\Upsilon }_{2}}\right) = \left\langle {{\varphi ^{*-1} \left( 1-\left( 1-\varphi ^*\left( {p_{\xi _{1}}}\right) \right) ^{\lambda } \left( 1-\varphi ^*\left( {p_{\xi _{2}}}\right) \right) ^{\lambda }\right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta _{1}}}\right) \right) ^{\lambda } \left( \varphi ^*\left( {p_{\eta _{2}}}\right) \right) ^{\lambda } \right) }}\right\rangle , \end{aligned}$$

(16)

and

$$\begin{aligned} \lambda {\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}}\right) = \left\langle {{\varphi ^{*-1} \left( 1-\left( 1-\varphi ^*\left( {p_{\xi _{1}}}\right) \right) ^{\lambda } \left( 1-\varphi ^*\left( {p_{\xi _{2}}}\right) \right) ^{\lambda }\right) }}, {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\eta _{1}}}\right) \right) ^{\lambda } \left( \varphi ^*\left( {p_{\eta _{2}}}\right) \right) ^{\lambda } \right) }}\right\rangle . \end{aligned}$$

(17)

Hence, from (16) and (17), we get

$$\begin{aligned} \left( \lambda {\overset{\blacktriangle }{*}} {{\Upsilon }_{1}}\right) {\overset{\blacktriangle }{\oplus }} \left( \lambda {\overset{\blacktriangle }{*}} {{\Upsilon }_{2}}\right) =\lambda {\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}} {\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}}\right) . \end{aligned}$$

(b) From operational laws defined in Def. 12, we know

$$\begin{aligned}&{\Upsilon _{1}}^ {\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\xi _{1}}}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\eta _{1}}}\right) \right) ^\lambda \right) }}\right\rangle ;\\&{\Upsilon _{2}}^ {\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\xi _{2}}}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\eta _{2}}}\right) \right) ^\lambda \right) }}\right\rangle ; \end{aligned}$$

and

$$\begin{aligned} {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}} = \left\langle {{\varphi ^{*-1} \left( \varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) \right) }}, {{\varphi ^{*-1}\left( \varphi ^*\left( {p_{\eta _{1}}}\right) +\varphi ^*\left( {p_{\eta _{2}}}\right) - \varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) }}\right\rangle . \end{aligned}$$

Therefore, we get

$$\begin{aligned} \left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}\lambda \right) {\overset{\blacktriangle }{\otimes }} \left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}\lambda \right) = \left\langle {{\varphi ^{*-1} \left( \left( \varphi ^*\left( {p_{\xi _{1}}}\right) \right) ^{\lambda } \left( \varphi ^*\left( {p_{\xi _{2}}}\right) \right) ^{\lambda } \right) }}, {{\varphi ^{*-1} \left( 1-\left( 1-\varphi ^*\left( {p_{\eta _{1}}}\right) \right) ^{\lambda } \left( 1-\varphi ^*\left( {p_{\eta _{2}}}\right) \right) ^{\lambda }\right) }}\right\rangle , \end{aligned}$$

(18)

and

$$\begin{aligned} \left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}\right) ^ {\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1} \left( \left( \varphi ^*\left( {p_{\xi _{1}}}\right) \right) ^{\lambda } \left( \varphi ^*\left( {p_{\xi _{2}}}\right) \right) ^{\lambda } \right) }}, {{\varphi ^{*-1} \left( 1-\left( 1-\varphi ^*\left( {p_{\eta _{1}}}\right) \right) ^{\lambda } \left( 1-\varphi ^*\left( {p_{\eta _{2}}}\right) \right) ^{\lambda }\right) }}\right\rangle . \end{aligned}$$

(19)

Hence, Eqs. (18) and (19) gives

$$\begin{aligned} \left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}\lambda \right) {\overset{\blacktriangle }{\otimes }} \left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}\lambda \right) =\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}\right) ^ {\overset{\blacktriangle }{\wedge }}\lambda . \end{aligned}$$

(g) Using operational laws given in Defs. 4 and 12, we have

$$\begin{aligned} {{\Upsilon }_{1}^{C}} {\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}^{C}} = \left\langle {{\varphi ^{*-1} \left( \varphi ^*\left( {p_{\eta _{1}}}\right) +\varphi ^*\left( {p_{\eta _{2}}}\right) -\varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) }}, {{\varphi ^{*-1}\left( \varphi ^*\left( {p_{\xi_{1}}}\right) \varphi ^*\left( {p_{\xi_{2}}}\right) \right) }}\right\rangle , \end{aligned}$$

(20)

and

$$\begin{aligned} \left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}\right) ^{C} = \left\langle {{\varphi ^{*-1} \left( \varphi ^*\left( {p_{\eta _{1}}}\right) +\varphi ^*\left( {p_{\eta _{2}}}\right) -\varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) }}, {{\varphi ^{*-1}\left( \varphi ^*\left( {p_{\xi_{1}}}\right) \varphi ^*\left( {p_{\xi_{2}}}\right) \right) }}\right\rangle . \end{aligned}$$

(21)

From Eqs. (20) and (21), we obtain

$$\begin{aligned} {{\Upsilon }_{1}^{C}} {\overset{\blacktriangle }{\oplus }} {{\Upsilon }_{2}^{C}} =\left( {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }} {{\Upsilon }_{2}}\right) ^{C}. \end{aligned}$$

Hence proved. $\square$

Theorem 5

Let ${\Upsilon }_1 =\left\langle p_{\xi _{1}}, p_{\eta _{1}} \right\rangle$ and ${\Upsilon }_2 =\left\langle p_{\xi _{2}}, p_{\eta _{2}} \right\rangle$ be two LIFNs, then the following results are true:

• (a) $\left( {{\Upsilon }_{1}}\cup {{\Upsilon }_{2}} \right) {\overset{\blacktriangle }{\oplus }} \left( {{\Upsilon }_{1}}\cap {{\Upsilon }_{2}} \right) = {{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }}{{\Upsilon }_{2}}$;

• (b) $\left( {{\Upsilon }_{1}}\cup {{\Upsilon }_{2}} \right) {\overset{\blacktriangle }{\otimes }} \left( {{\Upsilon }_{1}}\cap {{\Upsilon }_{2}} \right) = {{\Upsilon }_{1}}{\overset{\blacktriangle }{\otimes }}{{\Upsilon }_{2}}$.

Proof

In the following, we shall prove only (a) part, and (b) can be proved similarly.

$$\begin{aligned}&\left( {{\Upsilon }_{1}}\cup {{\Upsilon }_{2}} \right) {\overset{\blacktriangle }{\otimes }} \left( {{\Upsilon }_{1}}\cap {{\Upsilon }_{2}} \right) \\&\quad =\left\langle {{\varphi ^{*-1} \left( \varphi ^*\left( {\max \left( p_{\xi _{1}}, p_{\xi _{2}}\right) }\right) +\varphi ^*\left( {{\min \left( p_{\xi _{1}}, p_{\xi _{2}}\right) }}\right) -\varphi ^*\left( {\max \left( p_{\xi _{1}}, p_{\xi _{2}}\right) }\right) \varphi ^*\left( {\min \left( p_{\xi _{1}}, p_{\xi _{2}}\right) }\right) \right) }}\right. ,\\ \left. {{\varphi ^{*-1}\left( \varphi ^*\left( {{\min \left( p_{\eta _{1}}, p_{\eta _{2}}\right) }}\right) \varphi ^*\left( {{\max \left( p_{\eta _{1}}, p_{\eta _{2}}\right) }}\right) \right) }}\right\rangle \\&=\left\langle \varphi ^{*-1} \left( \left( {\max \left( \varphi ^*\left( p_{\xi _{1}}\right) , \varphi ^*\left( p_{\xi _{2}}\right) \right) }\right) +\left( \min \left( \varphi ^*\left( p_{\xi _{1}}\right) , \varphi ^*\left( p_{\xi _{2}}\right) \right) \right) \right. \right. \\&\quad \left. \left. -\left( {\max \left( \varphi ^*\left( p_{\xi _{1}}\right) ,\varphi ^*\left( p_{\xi _{2}}\right) \right) }\right) \left( {\min \left( \varphi ^*\left( p_{\xi _{1}}\right) ,\varphi ^*\left( p_{\xi _{2}}\right) \right) }\right) \right) ,\right. \\&\quad {\left. \varphi ^{*-1}\left( \left( {{\min \left( \varphi ^*\left( p_{\eta _{1}}\right) ,\varphi ^*\left( p_{\eta _{2}}\right) \right) }}\right) \left( {{\max \left( \varphi ^*\left( p_{\eta _{1}}\right) , \varphi ^*\left( p_{\eta _{2}}\right) \right) }}\right) \right) \right\rangle }\\&\quad {=\left\langle {{\varphi ^{*-1} \left( \varphi ^*\left( {p_{\xi _{1}}}\right) +\varphi ^*\left( {p_{\xi _{2}}}\right) -\varphi ^*\left( {p_{\xi _{1}}}\right) \varphi ^*\left( {p_{\xi _{2}}}\right) \right) }}, {{\varphi ^{*-1}\left( \varphi ^*\left( {p_{\eta _{1}}}\right) \varphi ^*\left( {p_{\eta _{2}}}\right) \right) }}\right\rangle }\\&\quad {={{\Upsilon }_{1}}{\overset{\blacktriangle }{\oplus }}{{\Upsilon }_{2}.}}. \end{aligned}$$

This completes the proof. $\square$

3.2 Generalized weighted arithmetic aggregation operator for LIFNs with LSF

In this subsection, we formulate a generalized linguistic intuitionistic fuzzy weighted average operator by using the new operational laws defined in Def. 12 in order to aggregate a collection of n LIFNs ${\Upsilon }_{i} =\left\langle p_{\xi _{i}}, p_{\eta _{i}} \right\rangle , \left( i=1,2,\ldots ,n\right)$. Let $\Xi$ be the collection of all LIFNs.

Definition 13

Let ${\Upsilon }_{i} =\left\langle p_{\xi _{i}}, p_{\eta _{i}} \right\rangle , \left( i=1,2,\ldots ,n\right)$ be a collection of n LIFNs and $GLIFWA: \Xi ^{n} \rightarrow \Xi$, if

$$\begin{aligned} GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) = \left( \left( w_{1}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) \right) {\overset{\blacktriangle }{\oplus }} \left( {w_{2}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) {\overset{\blacktriangle }{\oplus }}\ldots {\overset{\blacktriangle }{\oplus }} \left( {w_{n}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{n}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) \right) ^{\overset{\blacktriangle }{\wedge }}{\frac{1}{\lambda }} , \end{aligned}$$

(22)

then GLIFWA is called the generalized linguistic intuitionistic fuzzy weighted average operator, where $\lambda >0$, $w=\left( w_{1},w_{2},\ldots , w_{n} \right) ^T$ is a weight vector of ${\Upsilon }_{i}$ with ${w}_{i}>0$ and $\sum \nolimits _{i=1}^{n}{w}_{i}=1$.

Theorem 6

Let ${\Upsilon }_{i} =\left\langle p_{\xi _{i}}, p_{\eta _{i}} \right\rangle , \left( i=1,2,\ldots ,n\right)$ be a collection of n LIFNs. Then, the aggregated value by using the GLIFWA operator is also a LIFN and is given by

$$\begin{aligned}&GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) \nonumber \\&= \Bigg \langle \varphi ^{*-1}\left( \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) ^{\frac{1}{\lambda }} \right) , \varphi ^{*-1}\left( 1- \left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) ^{\frac{1}{\lambda }} \right) \Bigg \rangle . \end{aligned}$$

(23)

Proof

The first result follows quickly from Definition 12 and Theorem 1. In the following, we first prove

$$\begin{aligned}&\left( w_{1}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) \right) {\overset{\blacktriangle }{\oplus }} \left( {w_{2}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) {\overset{\blacktriangle }{\oplus }}\ldots {\overset{\blacktriangle }{\oplus }} \left( {w_{n}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{n}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) \nonumber \\&\quad =\Bigg \langle \varphi ^{*-1} \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) , \varphi ^{*-1}\left( \prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) \Bigg \rangle . \end{aligned}$$

(24)

by using the principle of mathematical induction on n.

First, let $n=2$, by using the operational laws of LIFNs listed in Def. 12, we get

$$\begin{aligned}&{\Upsilon _{1}}^{\overset{\blacktriangle }{\wedge }}\lambda = \left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\xi _{1}}}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\eta _{1}}}\right) \right) ^\lambda \right) }}\right\rangle ,\\&{\Upsilon _{2}}^{\overset{\blacktriangle }{\wedge }}\lambda =\left\langle {{\varphi ^{*-1}\left( \left( \varphi ^*\left( {p_{\xi _{2}}}\right) \right) ^\lambda \right) }},{{\varphi ^{*-1}\left( 1 -\left( 1- \varphi ^*\left( {p_{\eta _{2}}}\right) \right) ^\lambda \right) }}\right\rangle . \end{aligned}$$

then

$$\begin{aligned} \left( w_{1}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) \right) {\overset{\blacktriangle }{\oplus }} \left( {w_{2}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) = \Bigg \langle \varphi ^{*-1} \left( 1-\prod _{i=1}^{2}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) , \varphi ^{*-1}\left( \prod _{i=1}^{2}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) \Bigg \rangle . \end{aligned}$$

That is, Eq. (24) true for $n=2$.

Next, suppose that Eq. (24) holds for $n=k$, i.e.,

$$\begin{aligned}&\left( w_{1}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) \right) {\overset{\blacktriangle }{\oplus }} \left( {w_{2}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) {\overset{\blacktriangle }{\oplus }}\ldots {\overset{\blacktriangle }{\oplus }} \left( {w_{k}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{k}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) \nonumber \\&\quad =\Bigg \langle \varphi ^{*-1} \left( 1-\prod _{i=1}^{k}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) , \varphi ^{*-1}\left( \prod _{i=1}^{k}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) \Bigg \rangle . \end{aligned}$$

(25)

When $n=k+1$, based on the operational laws mentioned in Def. 12, we have

$$\begin{aligned}&\left( w_{1}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) \right) {\overset{\blacktriangle }{\oplus }} \left( {w_{2}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) {\overset{\blacktriangle }{\oplus }}\ldots {\overset{\blacktriangle }{\oplus }} \left( {w_{k+1}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{k+1}}^{\overset{\blacktriangle }{\wedge }}{\lambda }\right) }\right) \nonumber \\&\quad {=\Bigg \langle \varphi ^{*-1} \left( 1-\prod _{i=1}^{k}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) , \varphi ^{*-1}\left( \prod _{i=1}^{k}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) \Bigg \rangle }\nonumber \\&\quad {{\overset{\blacktriangle }{\oplus }}\Bigg \langle \varphi ^{*-1} \left( 1-\left( 1-\left( \varphi ^{*}\left( p_{\xi _{k+1}} \right) \right) ^{\lambda } \right) ^{w_{k+1}} \right) , \varphi ^{*-1}\left( \left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{k+1}} \right) \right) ^{\lambda } \right) ^{w_{k+1}} \right) \Bigg \rangle }\nonumber \\&\quad {=\Bigg \langle \varphi ^{*-1} \left( 1-\prod _{i=1}^{k+1}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) , \varphi ^{*-1}\left( \prod _{i=1}^{k+1}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) \Bigg \rangle .} \end{aligned}$$

(26)

Hence it is clear that the Eq. (24) holds for $n=k+1$. Therefore, by the principle of mathematical induction, the result given in Eq. (24) is true for all $n \in Z^{+}$. Then

$$\begin{aligned}&GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) \\&\quad = \left( \Bigg \langle \varphi ^{*-1} \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) , \varphi ^{*-1}\left( \prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) \Bigg \rangle \right) ^{\overset{\blacktriangle }{\wedge }}{\frac{1}{\lambda }}\\&{= \Bigg \langle \varphi ^{*-1}\left( \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) ^{\frac{1}{\lambda }} \right) , \varphi ^{*-1}\left( 1- \left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}} \right) \right) ^{\lambda } \right) ^{w_{i}} \right) ^{\frac{1}{\lambda }} \right) \Bigg \rangle .} \end{aligned}$$

This completes the proof of theorem. $\square$

Based on Definition 14, we can easily prove some desirable properties of the GLIFWA operator.

Theorem 7

Let ${\Upsilon }_{i} =\left\langle p_{\xi _{i}}, p_{\eta _{i}} \right\rangle , \left( i=1,2,\ldots ,n\right)$ be a collection of n LIFNs and $w=\left( w_{1},w_{2},\ldots , w_{n} \right) ^T$ be the weighting vector of ${\Upsilon }_{i}$ with ${w}_{i}>0$ and $\sum \limits _{i=1}^{n}{w}_{i}=1$, then we have the following properties:

• (a) (Idempotency) If ${\Upsilon }_{i} =\Upsilon =\left\langle p_{\xi }, p_{\eta } \right\rangle \; \forall \; i$, then

  $$\begin{aligned} GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) =\left\langle p_{\xi }, p_{\eta } \right\rangle . \end{aligned}$$

• (b) (Monotonicity) Let ${\Upsilon }_{i}^{'} =\left\langle p_{\xi _{i}^{'}}, p_{\eta _{i}^{'}} \right\rangle \left( i=1,2,\ldots ,n\right)$ be a collection of LIFNs such that $p_{\xi _{i}^{'}}\ge p_{\xi _{i}}$ and $p_{\eta _{i}^{'}}\le p_{\eta _{i}} \;\forall \;i$, then

  $$\begin{aligned} GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) \le GLIPFWA\left( {\Upsilon }_{1}^{'},{\Upsilon }_{2}^{'},\ldots ,{\Upsilon }_{n}^{'} \right) . \end{aligned}$$

• (c) (Boundedness) If ${\Upsilon }^{\blacktriangle } =\left\langle \max \limits _{i}\left( p_{\xi _{i}}\right) ,\min \limits _{i}\left( p_{\eta _{i}}\right) \right\rangle$ and ${\Upsilon }^{\blacktriangledown } =\left\langle \min \limits _{i}\left( p_{\xi _{i}}\right) ,\max \limits _{i}\left( p_{\eta _{i}}\right) \right\rangle$ are two LIFNs , then

  $$\begin{aligned} {\Upsilon }^{\blacktriangledown } \le GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) \le {\Upsilon }^{\blacktriangle }. \end{aligned}$$

Proof

(a) By Theorem 6, we have

$$\begin{aligned}&GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) =GLIFWA\left( {\Upsilon },{\Upsilon },\ldots ,{\Upsilon } \right) \\&\quad = \Bigg \langle \varphi ^{*-1}\left( \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi } \right) \right) ^{\lambda } \right) ^{w_{i}} \right) ^{\frac{1}{\lambda }} \right) , \varphi ^{*-1}\left( 1- \left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta } \right) \right) ^{\lambda } \right) ^{w_{i}} \right) ^{\frac{1}{\lambda }} \right) \Bigg \rangle \\&\quad = \Bigg \langle \varphi ^{*-1}\left( \left( 1-\left( 1-\left( \varphi ^{*}\left( p_{\xi } \right) \right) ^{\lambda } \right) \right) ^{\frac{1}{\lambda }} \right) , \varphi ^{*-1}\left( 1+\left( \left( 1- \varphi ^{*}\left( p_{\eta } \right) \right) ^{\lambda } \right) ^{\frac{1}{\lambda }} \right) \Bigg \rangle =\left\langle p_{\xi }, p_{\eta } \right\rangle = \Upsilon . \end{aligned}$$

(b) Since $p_{\xi _{i}^{'}}\ge p_{\xi _{i}}$ and ${p_{\eta _{i}^{'}}}\le p_{\eta _{i}}$ for all i, then

$$\begin{aligned}&\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i} \le \prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}}\right) \right) ^{\lambda }\right) ^{w_i}\nonumber \\&\Rightarrow 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i} \ge 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}}\right) \right) ^{\lambda }\right) ^{w_i}\nonumber \\&\Rightarrow \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i}\right) ^{\frac{1}{\lambda }} \ge \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}}\right) \right) ^{\lambda }\right) ^{w_i} \right) ^{\frac{1}{\lambda }}\nonumber \\&\Rightarrow \varphi ^{*-1}\left( \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i}\right) ^{\frac{1}{\lambda }}\right) \ge \varphi ^{*-1}\left( \left( \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}}\right) \right) ^{\lambda }\right) ^{w_i} \right) ^{\frac{1}{\lambda }}\right) \right) , \end{aligned}$$

(27)

and

$$\begin{aligned}&\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i} \le \prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}}\right) \right) ^{\lambda }\right) ^{w_i}\nonumber \\&\Rightarrow 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i} \ge 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}}\right) \right) ^{\lambda }\right) ^{w_i}\nonumber \\&\Rightarrow \left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i}\right) ^{\frac{1}{\lambda }} \ge \left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}}\right) \right) ^{\lambda }\right) ^{w_i} \right) ^{\frac{1}{\lambda }}\nonumber \\&\Rightarrow \varphi ^{*-1}\left( 1-\left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i}\right) ^{\frac{1}{\lambda }} \right) \le \varphi ^{*-1}\left( 1-\left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}}\right) \right) ^{\lambda }\right) ^{w_i} \right) ^{\frac{1}{\lambda }} \right) . \end{aligned}$$

(28)

Therefore, according to Definition 6, we obtain

$$\begin{aligned}&\left\langle \varphi ^{*-1}\left( \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i}\right) ^{\frac{1}{\lambda }}\right) ,\varphi ^{*-1}\left( 1-\left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}^{'}}\right) \right) ^{\lambda } \right) ^{w_i}\right) ^{\frac{1}{\lambda }} \right) \right\rangle \nonumber \\&\quad \ge \left\langle \varphi ^{*-1}\left( \left( \left( 1-\prod _{i=1}^{n}\left( 1-\left( \varphi ^{*}\left( p_{\xi _{i}}\right) \right) ^{\lambda }\right) ^{w_i} \right) ^{\frac{1}{\lambda }}\right) \right) ,\varphi ^{*-1}\left( 1-\left( 1-\prod _{i=1}^{n}\left( 1-\left( 1- \varphi ^{*}\left( p_{\eta _{i}}\right) \right) ^{\lambda }\right) ^{w_i} \right) ^{\frac{1}{\lambda }} \right) \right\rangle , \end{aligned}$$

(29)

that is,

$$\begin{aligned} GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) \le GLIPFWA\left( {\Upsilon }_{1}^{'},{\Upsilon }_{2}^{'},\ldots ,{\Upsilon }_{n}^{'} \right) . \end{aligned}$$

(c) It directly follows from part (b).

This completes the proof. $\square$

Example 3

Let ${\Upsilon }_{1} =\left\langle p_{4}, p_{3} \right\rangle ,{\Upsilon }_{2} =\left\langle p_{1}, p_{5} \right\rangle ,{\Upsilon }_{3} =\left\langle p_{2}, p_{3} \right\rangle ,{\Upsilon }_{4} =\left\langle p_{3}, p_{1} \right\rangle$ and ${\Upsilon }_{5} =\left\langle p_{2}, p_{4} \right\rangle$ be five LIFNs derived from ${{\widehat{\mathbb {P}}}_{\left[ 0,8 \right] }}=\left\{ {p_{d}}|d\in \left[ 0,8 \right] \right\}$. Further assume that $w=\left( 0.20,0.10,0.15, 0.25,0.30 \right) ^T$ represents the weight vector associated with LIFNs ${\Upsilon }_{i}\left( i=1,2,\ldots ,5 \right)$. Hence, the aggregated values based on developed GLIFWA aggregation operator mention in Eq. (23) by taking different LSFs are summarized in Table 2.

Table 2 Aggregated values based on GLIFWA aggregation operator with different LSF

Now, we investigate some special cases of the proposed GLIFWA operator.

SC1.:

If ${\lambda }=1$, then GLIFWA operator becomes the linguistic intuitionistic fuzzy weighted averaging (LIFWA) operator.

$$\begin{aligned} GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) = \left( w_{1}{\overset{\blacktriangle }{*}}{{\Upsilon }_{1}}\right) {\overset{\blacktriangle }{\oplus }} \left( {w_{2}{\overset{\blacktriangle }{*}}{{\Upsilon }_{2}}}\right) {\overset{\blacktriangle }{\oplus }}\ldots {\overset{\blacktriangle }{\oplus }} \left( {w_{n}{\overset{\blacktriangle }{*}}{{\Upsilon }_{n}}}\right) . \end{aligned}$$

(30)

SC2.:

If ${\lambda }=2$, then GLIFWA operator is reduced to the quadratic linguistic intuitionistic fuzzy weighted averaging (QLIFWA) operator.

$$\begin{aligned} GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) = \left( \left( w_{1}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}{2}\right) \right) {\overset{\blacktriangle }{\oplus }} \left( {w_{2}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}{2}\right) }\right) {\overset{\blacktriangle }{\oplus }}\ldots {\overset{\blacktriangle }{\oplus }} \left( {w_{n}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{n}}^{\overset{\blacktriangle }{\wedge }}{2}\right) }\right) \right) ^{\overset{\blacktriangle }{\wedge }}{\frac{1}{2}}. \end{aligned}$$

(31)

SC3.:

When ${\lambda }=3$, then GLIFWA operator reduces to the cubic linguistic intuitionistic fuzzy weighted averaging (CLIFWA) operator.

$$\begin{aligned} GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) = \left( \left( w_{1}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}{3}\right) \right) {\overset{\blacktriangle }{\oplus }} \left( {w_{2}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}{3}\right) }\right) {\overset{\blacktriangle }{\oplus }}\ldots {\overset{\blacktriangle }{\oplus }} \left( {w_{n}{\overset{\blacktriangle }{*}}\left( {{\Upsilon }_{n}}^{\overset{\blacktriangle }{\wedge }}{3}\right) }\right) \right) ^{\overset{\blacktriangle }{\wedge }}{\frac{1}{3}}. \end{aligned}$$

(32)

SC4.:

If ${\lambda }\rightarrow 0$, then GLIFWA operator becomes the linguistic intuitionistic fuzzy weighted geometric (LIFWG) operator.

$$\begin{aligned} GLIFWA\left( {\Upsilon }_{1},{\Upsilon }_{2},\ldots ,{\Upsilon }_{n} \right) = \left( {{\Upsilon }_{1}}^{\overset{\blacktriangle }{\wedge }}{w_{1}}\right) {\overset{\blacktriangle }{\otimes }} \left( {{{\Upsilon }_{2}}^{\overset{\blacktriangle }{\wedge }}{w_{2}}}\right) {\overset{\blacktriangle }{\otimes }}\ldots {\overset{\blacktriangle }{\otimes }}\left( {{{\Upsilon }_{n}}^{\overset{\blacktriangle }{\wedge }}{w_{n}}}\right) . \end{aligned}$$

(33)

SC5.:

If ${\lambda }=1$ and $\varphi ^{*}=\varphi _{1}^{*}$, then GLIFWA operator is reduced into the LIFWA operator mentioned in Eq. (4) .

SC6.:

If ${\lambda }\rightarrow 0$ and $\varphi ^{*}=\varphi _{1}^{*}$, then GLIFWA operator becomes the LIFWG operator given in Eq. (5) .

4 Matrix games with linguistic intuitionistic fuzzy payoffs and solutions

Suppose that ${\tilde{{\mathcal{A}}}}$ denotes a matrix game with payoffs represent by LIFNs. Let $\mathbb {S}^m=\left( \alpha _{1},\alpha _{2},\ldots ,\alpha _{m} \right)$ and $\mathbb {S}^n=\left( \beta _{1},\beta _{2},\ldots ,\beta _{n} \right)$ be two finite sets of pure strategies for person I and person II, respectively and $\widehat{\mathbb {P}}_{\left[ 0,2t\right] } =\left\{ p_{d}| p_{0} \le p_{d} \le p_{2t} ,d\in \left[ 0,2t\right] \right\}$ be a continuous LTS with odd cardinality. Here, t is a positive integer. If person I chooses a pure strategy $\alpha _{i}\in \mathbb {S}^{m}$ and person II selects a pure strategy $\beta _{j}\in \mathbb {S}^{n}$, then at the outcome $\left( \alpha _{i}, \beta _{j} \right)$, the person I gains a payoff represented by LIFN $\Upsilon _{ij} = \left\langle p_{\xi _{ij}},p_{\eta _{ij}}\right\rangle$ with the conditions $p_{\xi _{ij}},p_{\eta _{ij}} \in \widehat{\mathbb {P}}_{\left[ 0,2t\right] }$ and $0\le {\xi _{ij}}+{\eta _{ij}}\le 2t$. On the other hand, person II gains a negation of LIFS $\Upsilon _{ij} = \left\langle p_{\xi _{ij}},p_{\eta _{ij}}\right\rangle$, i.e. $\Upsilon _{ij}^C = \left\langle p_{\eta _{ij}},p_{\xi _{ij}}\right\rangle$. Thus the matrix game${\tilde{{\mathcal{A}}}}$ can be expressed as

Let $R^n$ denotes the n-dimensional Euclidean space and $R^{n}_{+}=\left\{ z | z \in R^{n}, z \ge 0\right\}$. Let $x_{i}\,\left( i=1,2,\ldots ,m \right)$ and $y_{j}\,\left( i=1,2, \ldots ,n \right)$ be the probabilities for the persons I and II, respectively, to choose the pure strategies $\alpha _{i}$ and $\beta _{j}$, respectively. The probability vectors $x=\left( x_{1},x_{2},\ldots ,x_{m} \right) ^{T}\,\in R^{m}_{+}$ and $y=\left( y_{1},y_{2},\ldots ,y_{n} \right) ^{T}\,\in R^{n}_{+}$ are said to be the mixed strategies for persons I and II, respectively, if they satisfy $x^{T}e_{m}=1$ and $y^{T}e_{n}=1$ with $e_{m}=\left( 1,1,\ldots ,1 \right) \in R^{m}_{+}$ and $e_{n}=\left( 1,1,\ldots ,1 \right) \in R^{n}_{+}$, respectively. Further, let $X=\left\{ x|x \in R^{m}_{+}, x^{T}e_{m}=1\right\}$ and $Y=\left\{ y|y \in R^{n}_{+}, y^{T}e_{n}=1\right\}$ be the mixed strategy spaces for the persons I and II, respectively. Then, a matrix game with payoffs represented by LIFNs in mixed strategies can be shown by $\mathfrak {LIFG}=\left( {\mathbb {S}}^{m},X,{\mathbb {S}}^{n},Y,\widehat{\mathbb {P}}_{\left[ 0,2t\right] }, {\tilde{{\mathcal{A}}}} \right)$, which is usually called the matrix game ${\tilde{{\mathcal{A}}}}=\left( \Upsilon _{ij}\right) _{m\times n}$ with payoffs represented by LIFNs.

Suppose person I chooses a mixed strategy $x\in X$ and person II chooses a mixed strategy $y \in Y$, then the expected payoff for person I is obtained as

Then, by using the GLIFFWA operator defined in Eq. (28) with $\lambda =1$, the expected value $\mathfrak { E}(x,y)$ can be expressed as

$$\begin{aligned} \mathfrak { E}\left( x,y\right) = \Bigg \langle \varphi ^{*-1} \left( 1-\prod _{j=1}^{n}\prod _{i=1}^{m}\left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{x_{i}y_{j}} \right) , \varphi ^{*-1}\left( \prod _{j=1}^{n}\prod _{i=1}^{m}\left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{x_{i}y_{j}} \right) \Bigg \rangle =\left\langle p_{\xi _{xy}}, p_{\eta _{xy}}\right\rangle . \end{aligned}$$

(34)

Without loss of generality, let us assume that the person I is a maximizing person and person II is a minimizing person. Then, based on the maximin and minmax principles of the persons I and II, respectively, if there exists a pair of mixed strategies $\left( x^{\star },y^{\star }\right) \,\left( x^{\star }\in X,y^{\star }\in Y \right)$ such that

$$\begin{aligned} x^{\star T}{\tilde{{\mathcal{A}}}} y^{\star }=\max _{x\in X}\min _{y\in Y}\left\{ x^{ T}{\tilde{{\mathcal{A}}}} y \right\} =\min _{y\in Y}\max _{x\in X}\left\{ x^{ T}{\tilde{{\mathcal{A}}}} y \right\} , \end{aligned}$$

(35)

then, $x^{\star }$ and $y^{\star }$ are known as optimal strategies for persons I and II, respectively and $x^{\star T}{\tilde{{\mathcal{A}}}} y^{\star }$ is called the value of the matrix game with LIFNs.

Definition 14

Let $\bar{\Upsilon }$ and $\bar{\bar{\Upsilon }}$ be two LIFNs. If there exist $\bar{x}\in X$ and $\bar{y}\in Y$ such that ${\bar{x}}^{ T}{\tilde{{\mathcal{A}}}} y \supseteq \bar{\Upsilon }$ and ${x}^{T}{\tilde{{\mathcal{A}}}} \bar{y} \subseteq \bar{\bar{\Upsilon }}$ for any $x \in X,\, y \in Y$, then $\left( \bar{x},\bar{y}, \bar{\Upsilon }, \bar{\bar{\Upsilon }} \right)$ is called the fesiable soluation of the matrix game ${\tilde{{\mathcal{A}}}}$ with LIFN payoffs,$\bar{\Upsilon }$ and $\bar{\bar{\Upsilon }}$ are known as the feasible values for the person I and II, respectively, and $\bar{x}$ and $\bar{y}$ are called feasible strategies for the persons I and II, respectively.

Definition 15

Let ${\mathcal {M}}_{1}$ and ${\mathcal {M}}_{2}$ be the sets of all feasible values for the persons I and II, respectively. Assume that there exist ${\Upsilon }^\star \in {\mathcal {M}}_{1}$ and ${{\Upsilon }^{\star \star }} \in {\mathcal {M}}_{2}$. If there do no exist $\bar{\Upsilon } \in {\mathcal {M}}_{1}$ and $\bar{\bar{\Upsilon }} \in {\mathcal {M}}_{2}$ such that $\bar{\Upsilon }\supseteq {\Upsilon }^\star$and $\bar{\bar{\Upsilon }} \subseteq {{\Upsilon }^{\star \star }}$, with $\bar{\Upsilon }\ne {\Upsilon }^\star$and $\bar{\bar{\Upsilon }} \ne {{\Upsilon }^{\star \star }}$, then $\left( x^{\star },y^{\star },{\Upsilon }^\star ,{\Upsilon }^{\star \star } \right)$ is called the solution of the matrix game $\tilde{\mathcal {A}}$ with LIFN payoffs. In addition, $x^{\star }$ is called a maximin strategy for person I and $y^{\star }$ is called a minimax strategy for person II; ${\Upsilon }^\star$ and ${\Upsilon }^{\star \star }$ are called the values of the matrix game $\tilde{\mathcal {A}}$ with LIFN payoffs for person I and II, respectively.

5 Mathematical-programming models for matrix games with payoffs represented by LIFNs

The minimum expected gain $\Psi$ for person I can be given as:

$$\begin{aligned} \Psi =\left\langle p_{\xi _{\Psi } }, p_{\eta _{\Psi } }\right\rangle =\min _{y\in Y} \mathfrak { E}\left( x,y\right) = \left\langle \min _{y\in Y}\left( p_{\xi _{xy}}\right) ,\max _{y\in Y}\left( p_{\eta _{xy}}\right) \right\rangle . \end{aligned}$$

Note that here $\Psi$ is the function of x only. Then, to maximize the value of $\Psi$, the person I will select a mixed strategy $x^{\star }\in X$, i.e.,

$$\begin{aligned} \Psi ^{\star }=\left\langle p_{\xi _{\Psi ^{\star }} }, p_{\eta _{\Psi ^{\star }} }\right\rangle =\max _{x\in X}\min _{y\in Y} \mathfrak { E}\left( x,y\right) = \left\langle \max _{x\in X}\min _{y\in Y}\left( p_{\xi _{xy}}\right) ,\min _{x\in X}\max _{y\in Y}\left( p_{\eta _{xy}}\right) \right\rangle . \end{aligned}$$

Such a mixed strategy $x^{\star }$ is called the maximin strategy for person I and $\Psi ^{\star }$ is called the gain floor for person I.

The maximum expected loss $\Omega$ for person II is represented as:

$$\begin{aligned} \Omega =\left\langle p_{\xi _{\Omega } }, p_{\eta _{\Omega } }\right\rangle =\max _{x\in X} \mathfrak { E}\left( x,y\right) = \left\langle \max _{x\in X}\left( p_{\xi _{xy}}\right) ,\min _{x\in X}\left( p_{\eta _{xy}}\right) \right\rangle . \end{aligned}$$

It is worth mentioning that here $\Omega$ is the function of y only. Then, to minimize the value of $\Omega$, the person II will choose a mixed strategy $y^{\star }\in Y$, i.e.,

$$\begin{aligned} \Omega ^{\star }=\left\langle p_{\xi _{\Omega ^{\star }} }, p_{\eta _{\Omega ^{\star }} }\right\rangle =\min _{y\in Y}\max _{x\in X} \mathfrak { E}\left( x,y\right) = \left\langle \min _{y\in Y}\max _{x\in X}\left( p_{\xi _{xy}}\right) ,\max _{y\in Y}\min _{x\in X}\left( p_{\eta _{xy}}\right) \right\rangle . \end{aligned}$$

The mixed strategy $y^{\star }$ is called the minimax strategy for person II and $\Psi ^{\star }$ is called the loss ceiling for person II.

Theorem 8

Let $\Psi ^{\star }$ and $\Omega ^{\star }$ be the gain floor and the loss ceiling for persons I and II, respectively, then we have $\Psi ^{\star }\subseteq\Omega ^{\star }$.

Proof

From Eq. (34), we know that $\mathfrak { E}\left( x,y \right)$ is a LIFN. Then

$$\begin{aligned} p_{\xi _{xy}}, p_{\eta _{xy}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] }\,\,\, \text {and}\,\,\, 0 \le {\xi _{xy}}+{\eta _{xy}}\le 2t \end{aligned}$$

(36)

Hence

$$\begin{aligned} \max _{x\in X}\min _{y\in Y}\left( p_{\xi _{xy}}\right) , \min _{x\in X}\max _{y\in Y}\left( p_{\eta _{xy}}\right) \in \widehat{\mathbb {P}}_{\left[ 0,2t\right] } \end{aligned}$$

(37)

Using Eq. (36), it can be easily obtained that

$$\begin{aligned} 0 \le {\xi _{xy}}+\min _{y\in Y}\left( {\eta _{xy}}\right) \le {\xi _{xy}}+\max _{y\in Y}\left( {\eta _{xy}}\right) \le 2t. \end{aligned}$$

Thus, we have

$$\begin{aligned} 0 \le \min _{y\in Y}\left( {\xi _{xy}}\right) +\min _{y\in Y}\left( {\eta _{xy}}\right) \le {\xi _{xy}}+\max _{y\in Y}\left( {\eta _{xy}}\right) \le 2t. \end{aligned}$$

It follows that

$$\begin{aligned} 0 \le \min _{y\in Y}\left( {\xi _{xy}}\right) +\min _{x\in X}\min _{y\in Y}\left( {\eta _{xy}}\right) \le \min _{y\in Y}\left( {\xi _{xy}}\right) +\min _{x\in X}\max _{y\in Y}\left( {\eta _{xy}}\right) \le {\xi _{xy}}+\min _{x\in X}\max _{y\in Y}\left( {\eta _{xy}}\right) \le 2t. \end{aligned}$$

Therefore, we have

$$\begin{aligned} 0 \le \max _{x\in X}\min _{y\in Y}\left( {\xi _{xy}}\right) +\min _{x\in X}\min _{y\in Y}\left( {\eta _{xy}}\right) \le \max _{x\in X}\min _{y\in Y}\left( {\xi _{xy}}\right) +\min _{x\in X}\max _{y\in Y}\left( {\eta _{xy}}\right) \le \max _{x\in X} \left( {\xi _{xy}}\right) +\min _{x\in X}\max _{y\in Y}\left( {\eta _{xy}}\right) \le 2t, \end{aligned}$$

which gives

$$\begin{aligned} 0 \le \max _{x\in X}\min _{y\in Y}\left( {\xi _{xy}}\right) +\min _{x\in X}\max _{y\in Y}\left( {\eta _{xy}}\right) \le 2t. \end{aligned}$$

(38)

Eqs. (37) and (38) show that $p_{\xi _{\Psi ^{\star }}}, p_{\eta _{\Psi ^{\star }} } \in \widehat{\mathbb {P}}_{\left[ 0,2t\right] }$ and $0\le {\xi _{\Psi ^{\star }}}+{\eta _{\Psi ^{\star }} }\le 2t$. Hence $\Psi ^{\star }$ is a LIFN. Similarly, we can also prove that $\Omega ^{\star }$ is a LIFN.

For any $x\in X$ and $y\in Y$, we have

$$\begin{aligned} \min _{y\in Y}\left( p_{\xi _{xy}}\right) \le \left( p_{\xi _{xy}}\right) \le \max _{x\in X}\left( p_{\xi _{xy}}\right) . \end{aligned}$$

Hence

$$\begin{aligned} \min _{y\in Y}\left( p_{\xi _{xy}}\right) \le \min _{y\in Y}\max _{x\in X}\left( p_{\xi _{xy}}\right) . \end{aligned}$$

Therefore, we get

$$\begin{aligned} \max _{x\in X}\min _{y\in Y}\left( p_{\xi _{xy}}\right) \le \min _{y\in Y}\max _{x\in X}\left( p_{\xi _{xy}}\right) \Rightarrow p_{{\xi }_{\Psi ^{\star }}} \le p_{{\xi }_{\Omega ^{\star }}}. \end{aligned}$$

(39)

On the other hand, for any $x\in X$ and $y\in Y$, we have

$$\begin{aligned} \max _{y\in Y}\left( p_{\eta _{xy}}\right) \ge \left( p_{\eta _{xy}}\right) \ge \min _{x\in X}\left( p_{\eta _{xy}}\right) . \end{aligned}$$

Hence

$$\begin{aligned} \max _{y\in Y}\left( p_{\eta _{xy}}\right) \ge \max _{y\in Y}\min _{x\in X}\left( p_{\eta _{xy}}\right) . \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \min _{x\in X}\max _{y\in Y}\left( p_{\eta _{xy}}\right) \ge \max _{y\in Y}\min _{x\in X}\left( p_{\eta _{xy}}\right) \Rightarrow p_{{\eta }_{\Psi ^{\star }}} \ge p_{{\eta }_{\Omega ^{\star }}}. \end{aligned}$$

(40)

Using the inequalities given in Eqs. (39) and (40), we can conclude that

$$\begin{aligned} \Psi ^{\star }\subseteq \Omega ^{\star }. \end{aligned}$$

This completes the proof. $\square$

The maximin strategy $x^{\star }$ and the gain floor $\Psi ^{\star }=\left\langle p_{\xi _{\Psi ^{\star }} }, p_{\eta _{\Psi ^{\star }} }\right\rangle$ for person I can be obtained by solving the following nonlinear bi-objective programming model:

$$\begin{aligned}&\left( \mathbf{MOD} 1 \right) \quad \max \left\{ p_{\xi _{\Psi }} \right\} , \min \left\{ p_{\eta _{\Psi }} \right\} \nonumber \\&\quad s.t. {\left\{ \begin{array}{ll} p_{\xi _{xy}} \ge p_{\xi _{\Psi }},&{} \text {for any}\,\, \,y\in Y\\ p_{\eta _{xy}} \le p_{\eta _{\Psi }}, &{} \text {for any}\,\, \,y\in Y\\ p_{\xi _{{xy}}}, p_{\eta _{{xy}}},p_{\xi _{\Psi }}, p_{\eta _{\Psi }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Psi }+\eta _{\Psi }\le 2t,0\le \xi _{{xy}}+\eta _{{xy}}\le 2t\\ x_{i}\ge 0, \,\,\sum _{i=1}^{m}x_{i}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(41)

where $p_{\xi _{\Psi }}=\displaystyle \min _{y\in Y} \left( p_{\xi _{{xy}}}\right)$,  $p_{\eta _{\Psi }}=\displaystyle \max _{y\in Y} \left( p_{\eta_{{xy}}}\right)$.

Then according to the Def. 4 and Eq. (34), we have

$$\begin{aligned}&{\left\{ \begin{array}{ll} p_{\xi _{xy}} \ge p_{\xi _{\Psi }} \\ p_{\eta _{xy}} \le p_{\eta _{\Psi }} \end{array}\right. } \Leftrightarrow {\left\{ \begin{array}{ll} \varphi ^{*-1} \left( 1-\prod _{j=1}^{n}\prod _{i=1}^{m}\left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{x_{i}y_{j}} \right) \ge p_{\xi _{\Psi }} \\ \varphi ^{*-1}\left( \prod _{j=1}^{n}\prod _{i=1}^{m}\left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{x_{i}y_{j}}\right) \le p_{\eta _{\Psi }} \end{array}\right. }\nonumber \\&\Leftrightarrow {\left\{ \begin{array}{ll} \prod _{j=1}^{n}\prod _{i=1}^{m}\left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{x_{i}y_{j}} \le 1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) \\ \prod _{j=1}^{n}\prod _{i=1}^{m}\left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{x_{i}y_{j}} \le \varphi ^{*}\left( p_{\eta _{\Psi }} \right) . \end{array}\right. } \end{aligned}$$

(42)

which are equivalent to the following inequalities:

$$\begin{aligned} \Leftrightarrow {\left\{ \begin{array}{ll} \sum _{j=1}^{n}\sum _{i=1}^{m}{x_{i}y_{j}} \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) \le \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right) \\ \sum _{j=1}^{n}\sum _{i=1}^{m}{x_{i}y_{j}}\ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \le \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right) . \end{array}\right. } \end{aligned}$$

(43)

except for $p_{\xi _{\Psi }}=p_{2t}$, $p_{\eta _{\Psi }}=p_{0}$, $p_{\xi _{ij}}=p_{2t}$ and $p_{\eta _{ij}}=p_{0}$.

Since $\varphi ^{*}$ is a strictly monotonically increasing function, then we have

$$\begin{aligned}&\max \left\{ p_{\xi _{\Psi }} \right\} \Leftrightarrow \max \left\{ \varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right\} \Leftrightarrow \min \left\{ { 1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) } \right\} \Leftrightarrow \min \left\{ { \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right) } \right\} \text {for any}\,\, p_{\xi _{\Psi }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\&\quad { \min \left\{ p_{\eta _{\Psi }} \right\} \Leftrightarrow \min \left\{ \varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right\} \Leftrightarrow \min \left\{ \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right) \right\} \text {for any}\,\, p_{\eta _{\Psi }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] }.} \end{aligned}$$

Utilizing the weighted averaging operator Harsanyi (1955), the objective function of (MOD-1) can be written as:

$$\begin{aligned} \min \left\{ \theta \ln \left( {1-{\varphi ^{*}\left( p_{\xi _{\Psi }}\right) }}\right) +\left( 1-\theta \right) \left( {{\ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right) } }\right) \right\} , \end{aligned}$$

(44)

where $\theta \in [0, 1]$ reflects the person’s attitudinal character, which is provided by the persons according to the situation.

Combining Eq. (44)) with Eq. (43), then (MOD 1) can be expressed as

$$\begin{aligned}&\left( \mathbf{MOD} 2 \right) \quad \min \left\{ \theta \ln \left( {1-{\varphi ^{*}\left( p_{\xi _{\Psi }}\right) }}\right) +\left( 1-\theta \right) \left( {{\ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right) } }\right) \right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \sum _{j=1}^{n}\sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {x_{i}y_{j}} \\ \qquad \qquad \le \theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right) \, \, \text {for any}\,\, \,y\in Y\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}},p_{\xi _{\Psi }}, p_{\eta _{\Psi }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Psi }+\eta _{\Psi }\le 2t,0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ x_{i}\ge 0, \,\,\sum _{i=1}^{m}x_{i}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(45)

except for $p_{\xi _{\Psi }}=p_{2t}$, $p_{\eta _{\Psi }}=p_{0}$, $p_{\xi _{ij}}=p_{2t}$ and $p_{\eta _{ij}}=p_{0}$.

Further let $\mathfrak {R}_{1}=\theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right)$, then (Model 2) can be rewritten as

$$\begin{aligned}&\left( \mathbf{MOD} 3 \right) \quad \min \left\{ \mathfrak {R}_{1} \right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \sum _{j=1}^{n}\sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {x_{i}y_{j}} \le \mathfrak {R}_{1} \, \, \text {for any}\,\, \,y\in Y\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ \mathfrak {R}_{1}\le 0, x_{i}\ge 0, \,\,\sum _{i=1}^{m}x_{i}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(46)

Since Y is a finite and compact convex set, so, we can consider only the extreme points of the set. Therefore, (MOD-3) can be modified as follows:

$$\begin{aligned}&\left( \mathbf{MOD} 4 \right) \quad \min \left\{ \mathfrak {R}_{1} \right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {x_{i}} \le \mathfrak {R}_{1}, \, \, j=1,2,\ldots ,n\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ \mathfrak {R}_{1}\le 0, x_{i}\ge 0, \,\,\sum _{i=1}^{m}x_{i}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(47)

Similarly, the minimax strategy $y^{\star }$ and the loss ceiling $\Omega ^{\star }=\left\langle p_{\xi _{\Omega ^{\star }} }, p_{\eta _{\Omega ^{\star }} }\right\rangle$ for person II can be generated by solving the following nonlinear bi-objective programming model given as follows:

$$\begin{aligned}&\left( \mathbf{MOD} 5 \right) \quad \min \left\{ p_{\xi _{\Omega }} \right\} , \max \left\{ p_{\eta _{\Omega }} \right\} \nonumber \\&s.t. {\left\{ \begin{array}{ll} p_{\xi _{xy}} \le p_{\xi _{\Omega }},&{} \text {for any}\,\, \,x\in X\\ p_{\eta _{xy}} \ge p_{\eta _{\Omega }}, &{} \text {for any}\,\, \,x\in X\\ p_{\xi _{{xy}}}, p_{\eta _{{xy}}},p_{\xi _{\Omega }}, p_{\eta _{\Omega }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Omega }+\eta _{\Omega }\le 2t,0\le \xi _{{xy}}+\eta _{{xy}}\le 2t\\ y_{i}\ge 0, \,\,\sum _{j=1}^{n}y_{j}=1, j=1,2,\ldots ,n \end{array}\right. } \end{aligned}$$

(48)

where $p_{\xi _{\Omega }}=\displaystyle \max _{x\in X} \left( p_{\xi _{{xy}}}\right)$,  $p_{\eta _{\Omega }}=\displaystyle \min _{x\in X} \left( p_{\eta_{{xy}}}\right)$.

Then according to the Def. 4 and Eq. (34), we have

$$\begin{aligned}&{\left\{ \begin{array}{ll} p_{\xi _{xy}} \le p_{\xi _{\Omega }} \\ p_{\eta _{xy}} \ge p_{\eta _{\Omega }} \end{array}\right. } \Leftrightarrow {\left\{ \begin{array}{ll} \varphi ^{*-1} \left( 1-\prod _{j=1}^{n}\prod _{i=1}^{m}\left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{x_{i}y_{j}} \right) \le p_{\xi _{\Omega }} \\ \varphi ^{*-1}\left( \prod _{j=1}^{n}\prod _{i=1}^{m}\left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{x_{i}y_{j}}\right) \ge p_{\eta _{\Omega }} \end{array}\right. }\nonumber \\&\Leftrightarrow {\left\{ \begin{array}{ll} \prod _{j=1}^{n}\prod _{i=1}^{m}\left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{x_{i}y_{j}} \ge 1-\varphi ^{*}\left( p_{\xi _{\Omega }}\right) \\ \prod _{j=1}^{n}\prod _{i=1}^{m}\left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{x_{i}y_{j}} \ge \varphi ^{*}\left( p_{\eta _{\Omega }} \right) , \end{array}\right. } \end{aligned}$$

(49)

which are equivalent to the following inequalities:

$$\begin{aligned} \Leftrightarrow {\left\{ \begin{array}{ll} \sum _{j=1}^{n}\sum _{i=1}^{m}{x_{i}y_{j}} \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) \ge \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Omega }}\right) \right) \\ \sum _{j=1}^{n}\sum _{i=1}^{m}{x_{i}y_{j}}\ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \ge \ln \left( \varphi ^{*}\left( p_{\eta _{\Omega }} \right) \right) . \end{array}\right. } \end{aligned}$$

(50)

except for $p_{\xi _{\Omega }}=p_{2t}$, $p_{\eta _{\Omega }}=p_{0}$, $p_{\xi _{ij}}=p_{2t}$ and $p_{\eta _{ij}}=p_{0}$.

Since $\varphi ^{*}$ is a strictly monotonically increasing function, then we have

$$\begin{aligned}&\min \left\{ p_{\xi _{\Omega }} \right\} \Leftrightarrow \min \left\{ \varphi ^{*}\left( p_{\xi _{\Omega }}\right) \right\} \Leftrightarrow \max \left\{ { 1-\varphi ^{*}\left( p_{\xi _{\Omega }}\right) } \right\} \Leftrightarrow \max \left\{ { \ln \left( 1-\varphi ^{*}\left( p_{\Omega _{\Psi }}\right) \right) } \right\} \text {for any}\,\, p_{\xi _{\Omega }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\&\quad { \max \left\{ p_{\eta _{\Psi }} \right\} \Leftrightarrow \max \left\{ \varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right\} \Leftrightarrow \max \left\{ \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right) \right\} \text {for any}\,\, p_{\eta _{\Omega }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] }.} \end{aligned}$$

Using the weighted averaging operator Harsanyi (1955), the objective function of (MOD-5) can be represented as:

$$\begin{aligned} \max \left\{ \theta \ln \left( {1-{\varphi ^{*}\left( p_{\xi _{\Omega }}\right) }}\right) +\left( 1-\theta \right) {{\ln \left( \varphi ^{*}\left( p_{\eta _{\Omega }} \right) \right) }} \right\} . \end{aligned}$$

(51)

Combining Eq. (51)) with Eq. (50), then (MOD 5) can be formulated as

$$\begin{aligned}&\left( \mathbf{MOD} 6 \right) \quad \max \left\{ \theta \ln \left( {1-{\varphi ^{*}\left( p_{\xi _{\Omega }}\right) }}\right) +\left( 1-\theta \right) {{\ln \left( \varphi ^{*}\left( p_{\eta _{\Omega }} \right) \right) } } \right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \sum _{j=1}^{n}\sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {x_{i}y_{j}} \\ \qquad \qquad \ge \theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Omega }}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Omega }} \right) \right) \, \, \text {for any}\,\, \,x\in X\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}},p_{\xi _{\Omega}}, p_{\eta _{\Omega}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Omega}+\eta _{\Omega}\le 2t,0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ y_{j}\ge 0, \,\,\sum _{j=1}^{n}x_{i}=1,\, j=1,2,\ldots ,n \end{array}\right. } \end{aligned}$$

(52)

except for $p_{\xi _{\Omega }}=p_{2t}$, $p_{\eta _{\Omega }}=p_{0}$, $p_{\xi _{ij}}=p_{2t}$ and $p_{\eta _{ij}}=p_{0}$.

Besides, let $\mathfrak {R}_{2}=\theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Omega }}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Omega }} \right) \right)$, then (Mod 6) can be rewritten as

$$\begin{aligned}&\left( \mathbf{MOD} 7 \right) \quad \max \left\{ \mathfrak {R}_{2} \right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \sum _{j=1}^{n}\sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {x_{i}y_{j}} \ge \mathfrak {R}_{2} \, \, \text {for any}\,\, \,x\in X\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ \mathfrak {R}_{2}\le 0, y_{j}\ge 0, \,\,\sum _{j=1}^{n}y_{j}=1,\, j=1,2,\ldots ,n \end{array}\right. } \end{aligned}$$

(53)

Since X is a finite and compact convex set, so, we can consider only the extreme points of the set. Therefore, (MOD-7) can be modified as follows:

$$\begin{aligned}&\left( \mathbf{MOD} 8 \right) \quad \max \left\{ \mathfrak {R}_{2} \right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {y_{j}} \ge \mathfrak {R}_{2}, \, \, i=1,2,\ldots ,m\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ \mathfrak {R}_{2}\le 0, y_{j}\ge 0, \,\,\sum _{j=1}^{n}y_{j}=1,\, i=1,2,\ldots ,n \end{array}\right. } \end{aligned}$$

(54)

Theorem 9

For any $\theta \in \left[ 0,1\right]$, the matrix game $\tilde{\mathcal {A}}$ with payoffs represented by LIFNs always has a solution $(x^{\star }, y^{\star }, {{x^{\star }}^T}A{y^{\star }})$.

Proof

For any given $\theta \in \left[ 0,1\right]$, the (MOD 4) and (MOD 8) given in Eqs. (47) and (54), respectively, are a pair of dual-primal linear programming models corresponding to the matrix game with the payoff matrix

$$\begin{aligned} \left( \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right) _{m\times n} \end{aligned}$$

(55)

According to the minimax theorem for matrix games Barron (2008),the (MOD 4) and (MOD 8) always have optimal solutions, which are represented by $\left( x^{\star },\Psi ^{\star }\right)$ and $\left( y^{\star },\Omega ^{\star }\right)$, respectively, where $\Psi ^{\star }=\Omega ^{\star }$. Hence,the matrix game $\tilde{\mathcal {A}}$ with payoffs represented by LIFNs always has a solution $(x^{\star }, y^{\star }, {{x^{\star }}^T}A{y^{\star }})$. $\square$

Theorem 10

$\mathfrak {R}_{1}$ and $\mathfrak {R}_{2}$ are monotonic and nondecreasing functions of $\theta \in [0, 1]$.

Proof

Since $\mathfrak {R}_{1}=\theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right)$ with $p_{\xi _{\Psi }}, p_{\eta _{\Psi }} \in \widehat{\mathbb {P}}_{\left[ 0,2t\right] }$. Then, the partial derivative of $\mathfrak {R}_{1}$ with respect to $\theta$ is calculated as follows:

$$\begin{aligned} \frac{d\mathfrak {R}_{1}}{d\theta }=\ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) \right) -\ln \left( \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \right) =\ln \left( \frac{1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) }{\varphi ^{*}\left( p_{\eta _{\Psi }} \right) }\right) \end{aligned}$$

(56)

Since $p_{\xi _{\Psi }}, p_{\eta _{\Psi }} \in \widehat{\mathbb {P}}_{\left[ 0,2t\right] }$, which satisfies ${\xi _{\Psi }}+ p_{{\Psi }} \le 2t$, then $\varphi ^{*}\left( p_{\xi _{\Psi }} \right) , \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \in \left[ 0,1 \right]$ and $\varphi ^{*}\left( p_{\xi _{\Psi }} \right) + \varphi ^{*}\left( p_{\eta _{\Psi }} \right) \le 1$. Therefore $\left( \frac{1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) }{\varphi ^{*}\left( p_{\eta _{\Psi }} \right) }\right) \ge 1, \, \text {except for } \varphi ^{*}\left( p_{\eta _{\Psi }} \right) =0$. Hence

$$\begin{aligned} \ln \left( \frac{1-\varphi ^{*}\left( p_{\xi _{\Psi }}\right) }{\varphi ^{*}\left( p_{\eta _{\Psi }} \right) }\right) \ge 0 \Rightarrow \frac{d\mathfrak {R}_{1}}{d\theta }\ge 0, \end{aligned}$$

which clearly shows that the $\mathfrak {R}_{1}$ is a monotonic and nondecreasing function of $\theta \in [0, 1]$. Similarly, we can prove that $\mathfrak {R}_{2}$ is a monotonic and nondecreasing function of $\theta \in [0, 1]$. $\square$

Theorem 11

Assume that $(x^{\star },\mathfrak {R}_{1}^{\star })$ and $(y^{\star },\mathfrak {R}_{2}^{\star })$ are optimal solutions of (MOD 4) and (MOD 8) with $0<\theta <1$, respectively. Then, $(x^{\star },\Psi ^{\star })$ and $(y^{\star },\Omega ^{\star })$ are Pareto optimal/noninferior solutions of (MOD 1) and (MOD 5), where $\Psi ^{\star }=\left\langle p_{\xi _{\Psi ^{\star }} }, p_{\eta _{\Psi ^{\star }} }\right\rangle$ and $\Omega ^{\star }=\left\langle p_{\xi _{\Omega ^{\star }} }, p_{\eta _{\Omega ^{\star }} }\right\rangle$ are the LIFNs, respectively.

Proof

Let us suppose $(x^{\star },\Psi ^{\star })$ is not a Pareto optimal/noninferior solution of (MOD 1), then there exists an optimal solution $(x^{\bullet },\Psi ^{\bullet })$, where $x^{\bullet } \in X$ and $\Psi ^{\bullet }=\left\langle p_{\xi _{\Psi ^{\bullet }} }, p_{\eta _{\Psi ^{\bullet }} }\right\rangle$ such that

$$\begin{aligned} s.t. {\left\{ \begin{array}{ll} \varphi ^{*-1} \left( 1-\prod _{j=1}^{n}\prod _{i=1}^{m}\left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{x_{i}^{\bullet }y_{j}} \right) \ge p_{\xi _{\Psi ^{\bullet }}},&{} \text {for any}\,\, \,y\in Y\\ \varphi ^{*-1}\left( \prod _{j=1}^{n}\prod _{i=1}^{m}\left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{x_{i}^{\bullet }y_{j}}\right) \le p_{\eta _{\Psi ^{\bullet }}} , &{} \text {for any}\,\, \,y\in Y\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}},p_{\xi _{\Psi ^{\bullet }}}, p_{\eta _{\Psi ^{\bullet }}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Psi ^{\bullet }}+\eta _{\Psi ^{\bullet }}\le 2t,0\le \xi _{{ij}}+\eta _{{ij}}\le 2t\\ {x_{i}^{\bullet }}\ge 0, \,\,\sum _{i=1}^{m}{x_{i}^{\bullet }}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(57)

$p_{\xi _{\Psi ^{\bullet }}}\ge p_{\xi _{\Psi ^{\star }}}$, $p_{\eta _{\Psi ^{\bullet }}}\le p_{\eta _{\Psi ^{\star }}}$, and at least one of which is strictly valid.

As $0<\theta <1$, then we have

$$\begin{aligned} s.t.{\left\{ \begin{array}{ll} \sum _{j=1}^{n}\sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {{x_{i}^{\bullet }}y_{j}} \\ \qquad \qquad \le \theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi ^{\bullet }}}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi ^{\bullet }}} \right) \right) \, \, \text {for any}\,\, \,y\in Y\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}},p_{\xi _{\Psi ^{\bullet }}}, p_{\eta _{\Psi ^{\bullet }}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Psi ^{\bullet }}+\eta _{\Psi ^{\bullet }}\le 2t,0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ {x_{i}^{\bullet }}\ge 0, \,\,\sum _{i=1}^{m}{x_{i}^{\bullet }}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(58)

and

$$\begin{aligned} \theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi ^{\bullet }}}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi ^{\bullet }}} \right) \right) < \theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi ^{\star }}}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi ^{\star }}} \right) \right) . \end{aligned}$$

(59)

Since Y is a finite and compact convex set, it makes sense to consider only the extreme points of the set Y, thus, Eq. (58) is reduced into the following:

$$\begin{aligned} s.t.{\left\{ \begin{array}{ll} \sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {{x_{i}^{\bullet }}} \\ \qquad \qquad \le \theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi ^{\bullet }}}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi ^{\bullet }}} \right) \right) , \, \, j=1,2,\ldots ,n\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}},p_{\xi _{\Psi ^{\bullet }}}, p_{\eta _{\Psi ^{\bullet }}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Psi ^{\bullet }}+\eta _{\Psi ^{\bullet }}\le 2t,0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ {x_{i}^{\bullet }}\ge 0, \,\,\sum _{i=1}^{m}{x_{i}^{\bullet }}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(60)

Let $\mathfrak {R}_{1}^{\bullet }=\theta \ln \left( 1-\varphi ^{*}\left( p_{\xi _{\Psi ^{\bullet }}}\right) \right) +\left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{\Psi ^{\bullet }}} \right) \right)$, then

$$\begin{aligned} s.t.{\left\{ \begin{array}{ll} \sum _{i=1}^{m} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) \right] {{x_{i}^{\bullet }}} \le \mathfrak {R}_{1}, \, \, j=1,2,\ldots ,n\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ \mathfrak {R}_{1}^{\bullet }\le 0, {x_{i}^{\bullet }}\ge 0, \,\,\sum _{i=1}^{m}{x_{i}^{\bullet }}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(61)

It means $\left( x^{\bullet },\mathfrak {R}_{1}^{\bullet }\right)$ is an optimal solution of (MOD 4), Eq. (59) gives $\mathfrak {R}_{1}^{\bullet }<\mathfrak {R}_{1}^{\star }$. Therefore, there exists a contradiction with the fact that $\left( x^{\star }, \mathfrak {R}_{1}^{\star }\right)$ is the optimal solution of (MOD 4). Hence, $\left( x^{\star }, \Psi ^{\star }\right)$ is a Pareto optimal/noninferior solution of (MOD-1). Similarly, we can prove that $\left( y^{\star }, \Omega ^{\star }\right)$ is a Pareto optimal/noninferior solution of (MOD-5).

It is worth mentioning that if $p_{\xi _{ij}}=p_{2t}$ and $p_{\eta _{ij}}=p_{0}$, then $\ln \left( 1-\varphi ^{*}\left( p_{\xi _{ij}}\right) \right) \rightarrow -\infty$ and $\ln \left( \varphi ^{*}\left( p_{\eta _{ij}}\right) \right) \rightarrow -\infty$. In this situation, the (MOD 4) and (MOD 8) have no sense. Thus, we can rewrite the (MOD 4) and (MOD 8) as the following nonlinear-programming models:

$$\begin{aligned}&\left( \mathbf{MOD} 9 \right) \quad \min \left\{ \left( {1-{\varphi ^{*}\left( p_{\xi _{\Psi }}\right) }}\right) ^{\theta } \left( {{ \varphi ^{*}\left( p_{\eta _{\Psi }} \right) } }\right) ^{\left( 1-\theta \right) } \right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \prod _{i=1}^{m} \left[ \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{\theta } \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{\left( 1-\theta \right) }\right] ^{x_{i}} \\ \qquad \qquad \le \left( {1-{\varphi ^{*}\left( p_{\xi _{\Psi }}\right) }}\right) ^{\theta } \left( {{ \varphi ^{*}\left( p_{\eta _{\Psi }} \right) } }\right) ^{\left( 1-\theta \right) } \, \, \text {for any}\,\, \,y\in Y\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}},p_{\xi _{\Psi }}, p_{\eta _{\Psi }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Psi }+\eta _{\Psi }\le 2t,0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ x_{i}\ge 0, \,\,\sum _{i=1}^{m}x_{i}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(62)

and

$$\begin{aligned}&\left( \mathbf{MOD} 10 \right) \quad \max \left\{ \left( {1-{\varphi ^{*}\left( p_{\xi _{\Omega }}\right) }}\right) ^{\theta } \left( {{ \varphi ^{*}\left( p_{\eta _{\Omega }} \right) } }\right) ^{\left( 1-\theta \right) } \right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \prod _{j=1}^{n} \left[ \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{\theta } \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{\left( 1-\theta \right) }\right] ^{y_{j}} \\ \qquad \qquad \ge \left( {1-{\varphi ^{*}\left( p_{\xi _{\Omega }}\right) }}\right) ^{\theta } \left( {{ \varphi ^{*}\left( p_{\eta _{\Omega }} \right) } }\right) ^{\left( 1-\theta \right) } \, \, \text {for any}\,\, \,x\in X\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}},p_{\xi _{\Omega }}, p_{\eta _{\Omega }}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \xi _{\Omega }+\eta _{\Omega }\le 2t,0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ y_{j}\ge 0, \,\,\sum _{j=1}^{n}y_{j}=1,\, j=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(63)

Further assume that

$$\begin{aligned} \mathfrak {I}_{1}&= \left( {1-{\varphi ^{*}\left( p_{\xi _{\Psi }}\right) }}\right) ^{\theta } \left( {{ \varphi ^{*}\left( p_{\eta _{\Psi }} \right) } }\right) ^{\left( 1-\theta \right) } \end{aligned}$$

(64)

$$\begin{aligned} \mathfrak {I}_{2}&= \left( {1-{\varphi ^{*}\left( p_{\xi _{\Omega }}\right) }}\right) ^{\theta } \left( {{ \varphi ^{*}\left( p_{\eta _{\Omega }} \right) } }\right) ^{\left( 1-\theta \right) }. \end{aligned}$$

(65)

Using Eqs. (64) and (65), the (MOD 9) and (MOD 10) are transformed into the nonlinear-programming models given by:

$$\begin{aligned}&\left( \mathbf{MOD} 9 \right) \quad \min \left\{ \mathfrak {I}_{1}\right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \prod _{i=1}^{m} \left[ \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{\theta } \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{\left( 1-\theta \right) }\right] ^{x_{i}} \le \mathfrak {I}_{1} \, \, \text {for any}\,\, \,y\in Y\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \mathfrak {I}_{1}\le 1, 0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ x_{i}\ge 0, \,\,\sum _{i=1}^{m}x_{i}=1,\, i=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(66)

and

$$\begin{aligned}&\left( \mathbf{MOD} 10 \right) \quad \max \left\{ \mathfrak {I}_{2}\right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \prod _{j=1}^{n} \left[ \left( 1- \varphi ^{*}\left( p_{\xi _{ij}} \right) \right) ^{\theta } \left( \varphi ^{*}\left( p_{\eta _{ij}} \right) \right) ^{\left( 1-\theta \right) }\right] ^{y_{j}} \ge \mathfrak {I}_{2} \, \, \text {for any}\,\, \,x\in X\\ p_{\xi _{{ij}}}, p_{\eta _{{ij}}}\in \widehat{\mathbb {P}}_{\left[ 0,2t\right] },\\ 0\le \mathfrak {I}_{2}\le 1,,0\le \xi _{{ij}}+\eta _{{ij}}\le 2t,\\ y_{j}\ge 0, \,\,\sum _{j=1}^{n}y_{j}=1,\, j=1,2,\ldots ,m \end{array}\right. } \end{aligned}$$

(67)

From Eqs. (47), (54), (66), and (67), we have $\mathfrak {I}_{1}^{\star }=\mathfrak {I}_{2}^{\star }$ and $\mathfrak {I}_{1}^{\star }=e^{\mathfrak {R}_{1}^{\star }}, \mathfrak {I}_{2}^{\star }=e^{\mathfrak {R}_{2}^{\star }}$, where $\left( x^{\star },\mathfrak {R}_{1}^{\star }\right)$ and $\left( y^{\star },\mathfrak {R}_{2}^{\star }\right)$ are the optimal solutions of (MOD 4) and (MOD 8) and $\left( x^{\star },\mathfrak {I}_{1}^{\star }\right)$ and $\left( y^{\star },\mathfrak {I}_{2}^{\star }\right)$ are the optimal solutions of (MOD 9) and (MOD 10) , respectively.

In the next section, we consider a real-life numerical example to demonstrate the solution procedure.

6 Application

Example 4

Let us suppose two companies $\complement _{1}$ and $\complement _{2}$ produce three-dimensional (3D) printers.It is assumed that the demand amount of the 3D printers in the targeted market basically is fixed. It means the market share of one company is increased while the other is decreased. In order to achieve their goal, these two companies have to choose their marketing strategies very carefully. The company $\complement _{1}$ has three options: (i) to reduce the price of their 3D printers $\left( \alpha _{1}\right)$ (ii) to up-to-date the technology $\left( \alpha _{2}\right)$ and (iii) to give some advertisements in print media and sell their 3D printers at a reasonable price $\left( \alpha _{3}\right)$. The company $\complement _{2}$ has three options as well: (i) to sell their 3D printers at a low price with free home delivery $\left( \beta _{1}\right)$ (ii) to provide a money-back voucher with their 3D printers and sell at the current price $\left( \beta _{2}\right)$ and (iii) to give an advertisement on the broadcast media and sell at a reasonable price $\left( \beta _{3}\right)$. Note that both the companies have limited amount of money, so, they can choose one option only. Thus, this competitive decision problem may be regarded as a matrix game, i.e., the companies $\complement _{1}$ and $\complement _{2}$ are regarded as persons I and II, respectively. The payoffs correspond to how much market share a company can expect to receive will depend on the option as selected by the respective company. Due to very limited information and unpredictable nature of the market, the payoffs can not be quantified in numerics. Based on to the experts’ opinions, the payoff matrix ${\tilde{{\mathcal{A}}}}$ for the company $\complement _{1}$ is formed by using the LIFNs defined on LTS

$$\begin{aligned} \widehat{\mathbb {P}}=\left\{ \begin{array}{l} p_{0} =\text {very very low (VVL)}, p_{1} =\text {very low (VL)}, p_{2} =\text {moderately low (ML)},\\ p_{3} =\text { slightly low (SL)},p_{4} =\text {average (Avg)}, p_{5} =\text {slightly high (SH)},\\ p_{6} =\text {moderately high (MH)}, p_{7} =\text {very high (VH)}, p_{8} =\text { very very high (VVH)}\end{array}\right\} , \end{aligned}$$

as follows:

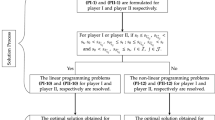
Solution steps: Utilizing the (MOD 4) and (MOD 8) given in Eqs. (47) and (54), the linear-programming models are constructed as follows:

$$\begin{aligned}&\min \left\{ \mathfrak {R}_{1}\right\} \nonumber \\&\quad s.t.{\left\{ \begin{array}{ll} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{7} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{1} \right) \right) \right] {x_{1}}+\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{2} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{6} \right) \right) \right] {x_{2}} \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{1} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{2} \right) \right) \right] {x_{3}} \le \mathfrak {R}_{1},\\ \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{6} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{2} \right) \right) \right] {x_{1}}+\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{7} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{1} \right) \right) \right] {x_{2}}\\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{1} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{7} \right) \right) \right] {x_{3}} \le \mathfrak {R}_{1},\\ \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{1} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{2} \right) \right) \right] {x_{1}}+\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{6} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{2} \right) \right) \right] {x_{2}}\\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{7} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{1} \right) \right) \right] {x_{3}} \le \mathfrak {R}_{1},\\ x_{i}\ge 0,\, i=1,2,3\, \text {and} \,x_{1}+x_{2}+x_{3}=1. \end{array}\right. } \end{aligned}$$

(68)

and

$$\begin{aligned}&\min \left\{ \mathfrak {R}_{2}\right\} \nonumber \\&\quad s.t.{\left\{ \begin{array}{ll} \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{7} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{1} \right) \right) \right] {y_{1}}+\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{6} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{2} \right) \right) \right] {y_{2}} \\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{1} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{2} \right) \right) \right] {y_{3}} \ge \mathfrak {R}_{2},\\ \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{2} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{6} \right) \right) \right] {y_{1}}+\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{7} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{1} \right) \right) \right] {y_{2}}\\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{6} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{2} \right) \right) \right] {y_{3}} \ge \mathfrak {R}_{2},\\ \left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{1} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{2} \right) \right) \right] {y_{1}}+\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{1} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{7} \right) \right) \right] {y_{2}}\\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\left[ \theta \ln \left( 1- \varphi ^{*}\left( p_{7} \right) \right) + \left( 1-\theta \right) \ln \left( \varphi ^{*}\left( p_{1} \right) \right) \right] {y_{3}} \ge \mathfrak {R}_{2},\\ y_{j}\ge 0,\, j=1,2,3\, \text {and} \,y_{1}+y_{2}+y_{3}=1. \end{array}\right. } \end{aligned}$$

(69)

Taking a specific LSF as per the semantic situation and assume different values of $\theta \in (0, 1)$, we can solve the optimization models given in Eqs. (68) and (69) by the existing methods for linear programming problems. The obtained optimal solutions and corresponding expected values of the models mentioned in Eqs. (68) and (69) are summarized in Tables 3, 4 and 5, respectively.

Table 3 Optimal solutions of the models given in Eqs. (68) and (69) and the corresponding expected payoffs with $\varphi ^{\star }=\varphi _{1}^{\star }$

Table 4 Optimal solutions of the models given in Eqs. (68) and (69) and the corresponding expected payoffs with $\varphi ^{\star }=\varphi _{2}^{\star }$

Table 5 Optimal solutions of the models given in Eqs. (68) and (69) and the corresponding expected payoffs with $\varphi ^{\star }=\varphi _{3}^{\star }$

Further, corresponding to the models given in Eqs. (66) and (67), the non-linear programming models are constructed as follows:

$$\begin{aligned}&\min \left\{ \mathfrak {I}_{1}\right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \left( \left( 1- \varphi ^{*}\left( p_{7} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{1} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{1}}\left( \left( 1- \varphi ^{*}\left( p_{2} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{6} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{2}}\left( \left( 1- \varphi ^{*}\left( p_{1} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{2} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{3}} \le \mathfrak {I}_{1},\\ \left( \left( 1- \varphi ^{*}\left( p_{6} \right) \right) ^ \theta \left( \varphi ^{*}\left( p_{2} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{1}}\left( \left( 1- \varphi ^{*}\left( p_{7} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{1} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{2}}\left( \left( 1- \varphi ^{*}\left( p_{1} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{7} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{3}} \le \mathfrak {I}_{1},\\ \left( \left( 1- \varphi ^{*}\left( p_{1} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{2} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{1}}\left( \left( 1- \varphi ^{*}\left( p_{6} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{2} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{2}}\left( \left( 1- \varphi ^{*}\left( p_{7} \right) \right) ^ \theta \left( \varphi ^{*}\left( p_{1} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {x_{3}} \le \mathfrak {I}_{1},\\ x_{i}\ge 0,\, i=1,2,3\, \text {and} \,x_{1}+x_{2}+x_{3}=1. \end{array}\right. } \end{aligned}$$

(70)

and

$$\begin{aligned}&\min \left\{ \mathfrak {I}_{2}\right\} \nonumber \\&s.t.{\left\{ \begin{array}{ll} \left( \left( 1- \varphi ^{*}\left( p_{7} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{1} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{1}}\left( \left( 1- \varphi ^{*}\left( p_{6} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{2} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{2}}\left( \left( 1- \varphi ^{*}\left( p_{1} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{2} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{3}} \ge \mathfrak {I}_{1},\\ \left( \left( 1- \varphi ^{*}\left( p_{2} \right) \right) ^ \theta \left( \varphi ^{*}\left( p_{6} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{1}}\left( \left( 1- \varphi ^{*}\left( p_{7} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{1} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{2}}\left( \left( 1- \varphi ^{*}\left( p_{6} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{2} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{3}} \ge \mathfrak {I}_{1},\\ \left( \left( 1- \varphi ^{*}\left( p_{1} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{2} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{1}}\left( \left( 1- \varphi ^{*}\left( p_{1} \right) \right) ^\theta \left( \varphi ^{*}\left( p_{7} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{2}}\left( \left( 1- \varphi ^{*}\left( p_{7} \right) \right) ^ \theta \left( \varphi ^{*}\left( p_{1} \right) \right) ^{\left( 1-\theta \right) }\right) ^ {y_{3}} \ge \mathfrak {I}_{1},\\ y_{j}\ge 0,\, j=1,2,3\, \text {and} \,y_{1}+y_{2}+y_{3}=1. \end{array}\right. } \end{aligned}$$

(71)

Choosing a specific LSF according to the semantic situation and assume different values of $\theta \in (0, 1)$, the optimization models given in Eqs. (70) and (71) can be solved by using the non-linear programming methods. Tables 6, 7, 8 shown the obtained optimal solutions and corresponding expected values of the models mentioned in Eqs. (70) and (71), respectively.

Table 6 Optimal solutions of the models given in Eqs. (70) and (71) and the corresponding expected payoffs with $\varphi ^{\star }=\varphi _{1}^{\star }$

Table 7 Optimal solutions of the models given in Eqs. (70) and (71) and the corresponding expected payoffs with $\varphi ^{\star }=\varphi _{2}^{\star }$

Table 8 Optimal solutions of the models given in Eqs. (70) and (71) and the corresponding expected payoffs with $\varphi ^{\star }=\varphi _{3}^{\star }$

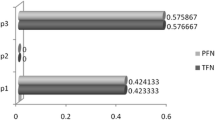
The results presented in the Tables 3, 4, 5, 6, 7, 8 clearly show that as the values of parameter $\theta$ and the LFS change, we obtain different mixed strategies corresponding to the persons I and II, respectively. It is important to note that the values of $\mathfrak {R}_{1}^{\star }$, $\mathfrak {R}_{2}^{\star }$, $\mathfrak {I}_{1}^{\star }$ and $\mathfrak {I}_{2}^{\star }$ are monotonic and nondecreasing with respect to $\theta$. Also the maximin strategies $x^{\star }$ and minimax strategies $y^{\star }$ obtained by the models mentioned in Eqs. (68) and (69) are, respectively, similar as those obtained by the models given in Eqs. (70) and (71), i.e., $\mathfrak {I}_{1}^{\star }=e^{\mathfrak {R}_{1}^{\star }}$ and $\mathfrak {I}_{2}^{\star }=e^{\mathfrak {R}_{2}^{\star }}$, with $p_{\xi _{ij}}\ne p_{2t}$ and $p_{\eta _{ij}}\ne p_{0}$ $\left( i,j=1,2,3 \right)$. It is interesting to note the the developed approach provide an ability to the decision-makers to consider different semantic situation in a single formulation.

7 Conclusions

In this paper, we have studied matrix games with payoffs represented by LIFNs. First, paper has defined some new operational laws for LIFNs based on LSF and proved several properties associated with them. Second, we have designed a new generalized aggregation operator for LIFNs. The work has also studied the properties and special cases of the proposed aggregation operator in detail. Next, we have developed some basic concepts for matrix games with payoffs represented by LIFNs.The maximin and minimax strategies for I and II persons have been defined and obtained by solving a pair of linear/nonlinear-programming models derived from two auxiliary nonlinear bi-objective programming models. The linguistic scaling function based aggregation operator has been used to calculate the expected value of the game to consider different semantic situations under different environment. Finally, a real-life numerical example has been given to illustrate the solution steps and effectiveness of the method.

In future work, we will utilize the developed aggregation operator in other problems including supplier selection, faculty requirement, and ERP software selection. We will also study the matrix games with linguistic interval-valued intutionistic fuzzy payoffs.