Modified approaches to solve matrix games with payoffs of single-valued trapezoidal neutrosophic numbers

Abstract

Seikh and Dutta (Soft Comput 26: 921–936, 2022) claimed that there does not exist any approach to solve single-valued trapezoidal neutrosophic (SVTrN) matrix games (matrix games in which each payoff is represented by a SVTrN number). To fill this gap, Seikh and Dutta, firstly, proposed SVTrN non-linear programming problems (NLPPs) corresponding to Player-I and Player-II. Then, Seikh and Dutta proposed two different approaches to transform the proposed SVTrN NLPPs into crisp linear programming problems (CLPPs). Finally, Seikh and Dutta claimed that an optimal solution of the transformed CLPPs also represents an optimal solution of SVTrN NLPPs. Brikaa (Soft Comput 26: 9137–9139, 2022) pointed out that a mathematically incorrect result is considered in Seikh and Dutta’s first approach to transform SVTrN NLPPs into CLPPs. Therefore, the transformed CLPPs are not equivalent to SVTrN NLPPs. Hence, it is mathematically incorrect to assume that an optimal solution of the transformed CLPPs also represents an optimal solution of SVTrN NLPPs. Brikaa also proposed an approach to transform the SVTrN NLPPs into CLPPs. In this paper, it is pointed out that on solving the CLPPs, obtained by Brikaa’s approach corresponding to SVTrN NLPPs of Player-I and Player-II, different optimal value is obtained. Also, it is pointed out that on solving the CLPPs, obtained by Seikh and Dutta’s second approach corresponding to SVTrN NLPPs of Player-I and Player-II, a different optimal value is obtained. However, in the actual case, the obtained optimal value should be the same as in the literature; it is proved that the CLPPs corresponding to Player-I and Player-II represent a primal–dual pair. This indicates that neither the CLPPs, obtained by Brikaa’s approach nor the CLPPs, obtained by Seikh and Dutta’s second approach, are equivalent to the SVTrN NLPPs of Player-I and Player-II. Hence, it is inappropriate to use the CLPPs, obtained by Brikaa’s approach as well as Seikh and Dutta’s second approach to find an optimal solution for the SVTrN NLPPs of Player-I and Player-II. Also, Brikaa’s approach as well as Seikh and Dutta’s second approach is modified to transform SVTrN NLPPs into their equivalent CLPPs. Furthermore, it is proved that the CLPPs corresponding to SVTrN NLPPs of Player-I and Player-II, obtained by the proposed modified approaches, represent a primal–dual pair. Finally, the correct result of a SVTrN matrix game, considered by Seikh and Dutta to illustrate their approaches, is obtained by the proposed modified approaches.

1 Introduction

In the last few years, several methods are proposed in the literature to solve matrix games under various extensions of fuzzy environment (see, Chen et al. 2023; Jana and Roy 2023; Karmakar and Seikh 2023; Liu and Hu 2023; Naqvi et al. 2023; Sharma et al. 2023; Singla et al. 2023; Verma et al. 2023 and references therein).

In this section, some recently proposed methods to solve matrix games under various extensions of fuzzy environment are discussed.

Jana and Roy (2019) pointed out that there does not exist any method to solve matrix games with dual hesitant fuzzy payoffs. To fill this gap, Jana and Roy (2019) proposed an approach to solve matrix games with dual hesitant fuzzy payoffs.

Seikh et al. (2020) pointed out that there does not exist any method to solve matrix games with triangular hesitant fuzzy payoffs. To fill this gap, Seikh et al. (2020) proposed a method to solve matrix games with triangular hesitant fuzzy payoffs.

Yang and Song (2020) proposed the concept of triangular dual hesitant fuzzy numbers and a method to solve matrix games with triangular dual hesitant fuzzy payoffs.

Bhaumik and Roy (2021), firstly, proposed the concept of the intuitionistic interval-valued hesitant fuzzy set by integrating the concept of an interval-valued intuitionistic fuzzy set (Atanassov and Gargov 1989) and the concept of a hesitant fuzzy set (Torra 2010). Then, Bhaumik and Roy (2021) proposed some arithmetic operations of intuitionistic interval-valued hesitant fuzzy sets as well as a ranking function to transform an intuitionistic interval-valued hesitant fuzzy set into its equivalent real number. Finally, using the proposed arithmetic operations and the proposed ranking function, Bhaumik and Roy (2021) proposed a method to solve matrix games with intuitionistic interval-valued hesitant fuzzy payoffs.

Jangid and Kumar (2021), firstly, proposed a ranking method for comparing two single-valued triangular neutrosophic numbers. Then, using the proposed comparing method, Jangid and Kumar (2021) proposed an approach to solve matrix games with single-valued triangular neutrosophic payoffs.

Verma (2021) pointed out that some mathematically incorrect results are considered in Li and Hong’s (2013) method to solve constrained matrix games with trapezoidal fuzzy payoffs. So, it is inappropriate to use Li and Hong’s (2013) method. Verma (2021) also proposed an approach for solving constrained matrix games with trapezoidal fuzzy payoffs.

Verma and Aggarwal (2021a) pointed out that there does not exist any method in the literature to solve matrix games with linguistic intuitionistic fuzzy payoffs. To fill this gap, Verma and Aggarwal (2021a) proposed a method to solve matrix games with linguistic intuitionistic fuzzy payoffs.

Verma and Aggarwal (2021b) pointed out that there does not exist any method to solve matrix games with 2-tuple intuitionistic fuzzy linguistic payoffs. To fill this gap, Verma and Aggarwal (2021b) proposed a method to solve matrix games with 2-tuple intuitionistic fuzzy linguistic payoffs.

Xue et al. (2021) pointed out that there does not exist any method to solve matrix games with hesitant fuzzy linguistic payoffs. To fill this gap, Xue et al. (2021) proposed a method to solve matrix games with hesitant fuzzy linguistic payoffs.

Yang et al. (2021) pointed out that much computational effort is required to apply existing approaches (Li and Liu 2015; Li and Nan 2009) for solving matrix games and bi-matrix games with intuitionistic fuzzy payoffs. To reduce the computational effort, Yang et al. (2021) proposed an approach to solve matrix games and bi-matrix games with intuitionistic fuzzy payoffs.

Brikaa et al. (2022) pointed out that some mathematically incorrect results are considered in Yang and Song’s (2020) method. So, it is inappropriate to use Yang and Song’s (2020) method. Brikaa et al. (2022) also proposed an approach (named Mehar approach) to solve matrix games with triangular dual hesitant fuzzy payoffs.

Yang and Xu (2022), firstly, proposed the concept of a probabilistic triangular intuitionistic hesitant fuzzy set. Then, Yang and Xu (2022) proposed some arithmetic operations of probabilistic triangular intuitionistic hesitant fuzzy sets. Finally, using the proposed arithmetic operations, Yang and Xu (2022) proposed a matrix game-based method to solve multi-attribute decision-making problems under a probabilistic triangular intuitionistic hesitant fuzzy environment.

Seikh and Dutta (2022) pointed out that there does not exist any method to solve matrix games with SVTrN payoffs. To fill this gap, Seikh and Dutta (2022) proposed two different approaches, based upon two different ranking methods for comparing SVTrN numbers, to solve matrix games with SVTrN payoffs.

Brikaa (2022) pointed out that a mathematically incorrect result is considered in Seikh and Dutta’s (2022) first approach. Therefore, it is inappropriate to use Seikh and Dutta’s (2022) first approach. Brikaa (2022) also proposed an approach by modifying Seikh and Dutta’s (2022) first approach to solve matrix games with SVTrN payoffs.

In this paper,

• (i) It is pointed out that some mathematically incorrect results are also considered in

  • (a) Brikaa’s (2022) approach.

  • (b) Seikh and Dutta’s (2022) second approach.

    So, it is inappropriate to use Brikaa’s (2022) approach and Seikh and Dutta’s (2022) second approach.

• (ii) A modified approach is proposed corresponding to Brikaa’s (2022) approach.

• (iii) A modified approach is proposed corresponding to Seikh and Dutta’s (2022) second approach.

• (iv) The correct results of the existing SVTrN matrix games (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929) are obtained by both the modified approaches.

This paper is organized as follows. In Sect. 2, existing approaches (Brikaa 2022; Seikh and Dutta 2022) to solve SVTrN matrix games are discussed. In Sect. 3, it is pointed out that the existing approaches (Brikaa 2022; Seikh and Dutta 2022) are not valid. In Sect. 4, reason for the invalidity of the existing approach (Brikaa 2022) is discussed. In Sect. 5, reason for the invalidity of the existing approach (Seikh and Dutta 2022) is discussed. In Sect. 6, modified approaches, corresponding to the existing approaches (Brikaa 2022; Seikh and Dutta 2022) are proposed. In Sect. 7, it is proved that the proposed modified approaches are valid. In Sect. 8, correct result of the existing SVTrN matrix game (Seikh and Dutta 2022) is obtained by the proposed modified approaches. Section 9 concludes the study.

2 Existing approaches

Based on the existing results (Bector and Chandra 2005, Sect. 1.4, pp. 6–7), it can be easily concluded that if in the payoff matrix $A={\left({a}_{ij}\right)}_{m\times n}$ of a matrix game, ${a}_{ij}$ represents the payoff of Player-I corresponds to the ith strategy of Player-I and the jth strategy of Player-II, $m$ represents the number of strategies of Player-I and $n$ represents the number of strategies of Player-II. Then,

(i) The optimal probability ${u}_{i}, i=\mathrm{1,2},\dots ,m$ for selecting the ith strategy by Player-I can be obtained by solving the crisp NLPP (P1) or its equivalent CLPP (P2).

Problem (P1)

$$Maximize\left\{\begin{array}{c} Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}{a}_{ij}{u}_{i}\right){v}_{j}\right\}\\ {\text{Subject to}} \\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0,j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$${\sum }_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P2)

$$Maximize \left\{\theta \right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{a}_{ij}{u}_{i}\ge \theta , j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, \quad i=\mathrm{1,2},\dots ,m.$$

(ii) The optimal probability ${v}_{j}, j=\mathrm{1,2},\dots ,n$ for selecting the ${j}{\text{th}}$ strategy by Player-II can be obtained by solving the crisp NLPP (P3) or its equivalent CLPP (P4).

Problem (P3)

$$Minimize\left\{\begin{array}{l} Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}{a}_{ij}{v}_{j}\right){u}_{i}\right\}\\ {\text{Subject to}} \\ {\sum }_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0,i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Problem (P4)

$$Minimize \left\{\phi \right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{a}_{ij}{v}_{j}\le \phi , i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, \quad j=\mathrm{1,2},\dots ,n.$$

In the same direction, Seikh and Dutta (2022) claimed that if in the payoff matrix $\widetilde{A}={\left(\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle \right)}_{m\times n}$ of a SVTrN matrix game, the SVTrN number $\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle$ represents the payoff of Player-I corresponding to the ${i}{\text{th}}$ strategy of Player-I and the ${j}{\text{th}}$ strategy of Player-II, $m$ represents the number of strategies of Player-I and $n$ represents the number of strategies of Player-II. Then,

(i) The optimal probability ${u}_{i}, i=\mathrm{1,2},\dots ,m$ for selecting the ${i}{\text{th}}$ strategy by Player-I can be obtained by solving the SVTrN NLPP (P5) or its equivalent CLPP.

Problem (P5)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right\}\\ {\text{Subject to}} \\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

(ii) The optimal probability ${v}_{j}, j=\mathrm{1,2},\dots ,n$ for selecting the ${j}{\text{th}}$ strategy by Player-II can be obtained by solving the SVTrN NLPP (P6) or its equivalent CLPP.

Problem (P6)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right\}\\ {\text{Subject to}} \\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Seikh and Dutta (2022) proposed two different approaches to transform the SVTrN NLPPs (P5) and (P6) into CLPPs. Hence, Seikh and Dutta (2022) proposed two different approaches to find the optimal probability ${u}_{i}, i=\mathrm{1,2},\dots ,m$ for selecting the ${i}{\text{th}}$ strategy by Player-I as well as to find the optimal probability ${v}_{j}, j=\mathrm{1,2},\dots ,n$ for selecting the ${j}{\text{th}}$ strategy by Player-II.

Brikaa (2022) pointed out that a mathematically incorrect result is considered in Seikh and Dutta’s (2022) first approach. Therefore, CLPPs, obtained by Seikh and Dutta’s (2022) first approach, are not equivalent to the SVTrN NLPPs (P5) and (P6). Brikaa (2022) also proposed an approach by modifying Seikh and Dutta’s (2022) first approach to transform the SVTrN NLPP into CLPPs. Hence, Brikaa (2022) proposed an approach to find the optimal probability ${u}_{i}, i=\mathrm{1,2},\dots ,m$ for selecting the ${i}{\text{th}}$ strategy by Player-I as well as to find the optimal probability ${v}_{j}, j=\mathrm{1,2},\dots ,n$ for selecting the ${j}{\text{th}}$ strategy by Player-II.

In this section, firstly, the ranking methods, used in Seikh and Dutta’s (2022) approaches to compare SVTrN numbers, are discussed. Then, Brikaa’s (2022) approach is discussed. Finally, Seikh and Dutta’s (2022) second approach is discussed.

2.1 Ranking methods

In this section, the ranking methods, used in Seikh and Dutta’s (2022) approaches to compare SVTrN numbers, are discussed.

2.2 Ranking method used in Seikh and Dutta’s first approach

In Seikh and Dutta’s (2022) first approach, the following ranking method is used to compare two SVTrN numbers.

Let ${\widetilde{A}}_{1}=\Bigg\langle \left({A}_{11},{A}_{12},{A}_{13},{A}_{14}\right);{l}_{1},{m}_{1},{n}_{1}\Bigg\rangle$ and ${\widetilde{A}}_{2}=\Bigg\langle \left({A}_{21},{A}_{22},{A}_{23},{A}_{24}\right);{l}_{2},{m}_{2},{n}_{2}\Bigg\rangle$ be two SVTrN numbers. Then, for a specific value of $\rho \in \left[0,\mathit{minimum }\left\{{l}_{1},{l}_{2}\right\}\right],$ $\sigma \in \left[\mathit{maximum }\left\{{m}_{1},{m}_{2}\right\}, 1\right],\tau \in \left[\mathit{maximum }\left\{{n}_{1},{n}_{2}\right\}, 1\right]$,

${\widetilde{A}}_{1}\preccurlyeq {\widetilde{A}}_{2}$ if ${\left({\widetilde{A}}_{1}\right)}_{\rho }\le {\left({\widetilde{A}}_{2}\right)}_{\rho },{\left({\widetilde{A}}_{1}\right)}_{\sigma }\le {\left({\widetilde{A}}_{2}\right)}_{\sigma }$ and ${\left({\widetilde{A}}_{1}\right)}_{\tau }\le {\left({\widetilde{A}}_{2}\right)}_{\tau }$i.e.,$\left[{\left({A}_{1}\right)}_{l\rho },{\left({A}_{1}\right)}_{r\rho }\right]\le \left[{\left({A}_{2}\right)}_{l\rho }, \right. \left.{\left({A}_{2}\right)}_{r\rho }\right],$ $\left[{\left({A}_{1}\right)}_{l\sigma },{\left({A}_{1}\right)}_{r\sigma }\right]\le \left[{\left({A}_{2}\right)}_{l\sigma },{\left({A}_{2}\right)}_{r\sigma }\right]$ and

$$\left[{\left({A}_{1}\right)}_{l\tau },{\left({A}_{1}\right)}_{r\tau }\right]\le \left[{\left({A}_{2}\right)}_{l\tau },{\left({A}_{2}\right)}_{r\tau }\right]$$

i.e., ${\left({A}_{1}\right)}_{l\rho }\le {\left({A}_{2}\right)}_{l\rho },{\left({A}_{1}\right)}_{r\rho }\le {\left({A}_{2}\right)}_{r\rho }$, ${\left({A}_{1}\right)}_{l\sigma }\le {\left({A}_{2}\right)}_{l\sigma },{\left({A}_{1}\right)}_{r\sigma }\le {\left({A}_{2}\right)}_{r\sigma },{\left({A}_{1}\right)}_{l\tau }\le {\left({A}_{2}\right)}_{l\tau }$ and

$${\left({A}_{1}\right)}_{r\tau }\le {\left({A}_{2}\right)}_{r\tau }$$

where,

$${\left({A}_{i}\right)}_{l\rho }=\frac{\left({l}_{i}-\rho \right){A}_{i1}+\rho {A}_{i2}}{{l}_{i}}, {\left({A}_{i}\right)}_{r\rho }=\frac{\left({l}_{i}-\rho \right){A}_{i4}+\rho {A}_{i3}}{{l}_{i}},{\left({A}_{i}\right)}_{l\sigma }=\frac{\left(1-\sigma \right){A}_{i2}+\left(\sigma -{m}_{i}\right){A}_{i1}}{{1-m}_{i}},$$

$${\left({A}_{i}\right)}_{r\sigma }=\frac{\left(1-\sigma \right){A}_{i3}+\left(\sigma -{m}_{i}\right){A}_{i4}}{1-{m}_{i}}, {\left({A}_{i}\right)}_{l\tau }=\frac{\left(1-\tau \right){A}_{i2}+\left(\tau -{n}_{i}\right){A}_{i1}}{{1-n}_{i}},{\left({A}_{i}\right)}_{r\tau }=\frac{\left(1-\tau \right){A}_{i3}+\left(\tau -{n}_{i}\right){A}_{i4}}{1-{n}_{i}}; i=\mathrm{1,2}.$$

2.3 Ranking method used in Seikh and Dutta’s second approach

In Seikh and Dutta’s (2022) second approach, the following ranking method is used to compare two SVTrN numbers.

Let ${\widetilde{A}}_{1}=\Bigg\langle \left({A}_{11},{A}_{12},{A}_{13},{A}_{14}\right);{l}_{1},{m}_{1},{n}_{1}\Bigg\rangle$ and ${\widetilde{A}}_{2}=\Bigg\langle \left({A}_{21},{A}_{22},{A}_{23},{A}_{24}\right);{l}_{2},{m}_{2},{n}_{2}\Bigg\rangle$ be two SVTrN numbers. Then, for a specific value of $\alpha \in \left[\mathrm{0,1}\right]$,

${\widetilde{A}}_{1}\preccurlyeq {\widetilde{A}}_{2}$ if ${\Pi }_{\alpha }\left({\widetilde{A}}_{1}\right)\le {\Pi }_{\alpha }\left({\widetilde{A}}_{2}\right).$

where,

$${\Pi }_{\alpha }\left({\widetilde{A}}_{i}\right)=\frac{\left({A}_{i1}+2\left({A}_{i2}+{A}_{i3}\right)+{A}_{i4}\right)}{6}\left[\alpha \left({{l}_{i}}^{2}\right)+\left(1-\alpha \right){\left(1-{m}_{i}\right)}^{2}+\left(1-\alpha \right){\left(1-{n}_{i}\right)}^{2}\right]; i=\mathrm{1,2}.$$

2.4 Brikaa’s approach

Brikaa (2022) proposed the following approach to find the optimal probability ${u}_{i}, i=\mathrm{1,2},\dots ,m$ for selecting the ${i}{\text{th}}$ strategy by Player-I, the optimal probability ${v}_{j}, j=\mathrm{1,2},\dots ,n$ for selecting the ${j}{\text{th}}$ strategy by Player-II, the crisp value of the game (minimum expected gain) of Player-I and the crisp value of the game (maximum expected loss) of Player-II.

Step 1: Find an optimal solution ${{\theta }_{l\rho },\theta }_{r\rho },{\theta }_{l\sigma },{\theta }_{r\sigma },{\theta }_{l\tau },{\theta }_{r\tau }, {u}_{i},i=\mathrm{1,2},\dots ,m$ and the corresponding optimal value $\frac{1}{2}\left(\frac{{\theta }_{l\rho }+{\theta }_{l\sigma }+{\theta }_{l\tau }}{3}+\frac{{{\theta }_{l\rho }+\theta }_{r\rho }+{\theta }_{l\sigma }+{\theta }_{r\sigma }+{\theta }_{l\tau }+{\theta }_{r\tau }}{6}\right)$ of the CLPP (P7) for some specific values of $\rho \in \left[0, {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}\right],\sigma \in [{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}, 1]$ and $\tau \in \left[{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}, 1\right].$

Problem (P7)

$$Maximize \left\{\frac{1}{2}\left(\frac{{\theta }_{l\rho }+{\theta }_{l\sigma }+{\theta }_{l\tau }}{3}+\frac{{{\theta }_{l\rho }+\theta }_{r\rho }+{\theta }_{l\sigma }+{\theta }_{r\sigma }+{\theta }_{l\tau }+{\theta }_{r\tau }}{6}\right)\right\}$$

Subject to

$$\left({minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\}-\rho \right)\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i}+\rho \sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i}\ge \left({minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\}\right) {\theta }_{l\rho }, j=\mathrm{1,2},\dots ,n,$$

$$\left({minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\}-\rho \right)\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}+\rho \sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i}\ge \left({minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\}\right){\theta }_{r\rho }, j=\mathrm{1,2},\dots ,n,$$

$$\left(1-\sigma \right)\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i}+\left(\sigma -{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\}\right)\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i}\ge \left(1-{maximum }_{1\le i\le m}\right.\left.\left\{{m}_{ij}\right\}\right){\theta }_{l\sigma }, j=\mathrm{1,2},\dots ,n,$$

$$\left(1-\sigma \right)\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i}+\left(\sigma -{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\}\right)\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\ge \left(1-{maximum }_{1\le i\le m}\right.\left.\left\{{m}_{ij}\right\}\right){\theta }_{r\sigma }, j=\mathrm{1,2},\dots ,n,$$

$$\left(1-\tau \right)\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i}+\left(\tau -{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\right)\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i}\ge \left(1-{maximum }_{1\le i\le m}\right.\left.\left\{{n}_{ij}\right\}\right){\theta }_{l\tau }, j=\mathrm{1,2},\dots ,n,$$

$$\left(1-\tau \right)\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i}+\left(\tau -{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\right)\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\ge \left(1-{maximum }_{1\le i\le m}\right.\left.\left\{{n}_{ij}\right\}\right){\theta }_{r\tau }, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Step 2: Find an optimal solution ${\phi }_{l\rho },{\phi }_{l\sigma },{\phi }_{l\tau },{\phi }_{r\rho },{\phi }_{r\sigma },{\phi }_{r\tau }, {v}_{j}, j=\mathrm{1,2},...,n$ and the corresponding optimal value $\frac{1}{2}\left(\frac{{\phi }_{l\rho }+{\phi }_{l\sigma }+{\phi }_{l\tau }+{\phi }_{r\rho }+{\phi }_{r\sigma }+{\phi }_{r\tau }}{6}+\frac{{\phi }_{r\rho }+{\phi }_{r\sigma }+{\phi }_{r\tau }}{3}\right)$ of the CLPP (P8) for some specific values of $\rho \in \left[0, {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}\right],$$\sigma \in [{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}, 1]$ and $\tau \in \left[{maximum}_{\begin{array}{l}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}, 1\right].$

Problem (P8)

$$Minimize \left\{\frac{1}{2}\left(\frac{{\phi }_{l\rho }+{\phi }_{l\sigma }+{\phi }_{l\tau }+{\phi }_{r\rho }+{\phi }_{r\sigma }+{\phi }_{r\tau }}{6}+\frac{{\phi }_{r\rho }+{\phi }_{r\sigma }+{\phi }_{r\tau }}{3}\right)\right\}$$

Subject to

$$\left({minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\}-\rho \right)\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j}+\rho \sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j}\le \left({minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\}\right){\phi }_{l\rho },i=\mathrm{1,2},\dots ,m,$$

$$\left({minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\}-\rho \right)\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}+\rho \sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j}\le \left({minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\}\right){\phi }_{r\rho },i=\mathrm{1,2},\dots ,m,$$

$$\left(1-\sigma \right)\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j}+\left(\sigma -{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\}\right)\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j}\le \left(1-{maximum }_{1\le j\le n}\right.\left.\left\{{m}_{ij}\right\}\right){\phi }_{l\sigma }, i=\mathrm{1,2},\dots ,m,$$

$$\left(1-\sigma \right)\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j}+\left(\sigma -{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\}\right)\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\le \left(1-{maximum }_{1\le j\le n}\right.\left.\left\{{m}_{ij}\right\}\right){\phi }_{r\sigma }, i=\mathrm{1,2},\dots ,m,$$

$$\left(1-\tau \right)\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j}+\left(\tau -{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\right)\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j}\le \left(1-{maximum }_{1\le j\le n}\right.\left.\left\{{n}_{ij}\right\}\right){\phi }_{l\tau }, i=\mathrm{1,2},\dots ,m,$$

$$\left(1-\tau \right)\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j}+\left(\tau -{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\right)\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\le \left(1-{maximum }_{1\le j\le n}\right.\left.\left\{{n}_{ij}\right\}\right){\phi }_{r\tau }, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1,{v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 3: The optimal values of ${u}_{i},i=\mathrm{1,2},\dots ,m,$ obtained in Step 1, represents the optimal probability for selecting the ${i}{\text{th}}$ strategy by Player-I and the optimal values of ${v}_{j},j=\mathrm{1,2},\dots ,n,$ obtained in Step 2, represents the optimal probability for selecting the ${j}{\text{th}}$ strategy by Player-II for the considered SVTrN matrix game.

Step 4: The optimal value $\frac{1}{2}\left(\frac{{\theta }_{l\rho }+{\theta }_{l\sigma }+{\theta }_{l\tau }}{3}+\frac{{{\theta }_{l\rho }+\theta }_{r\rho }+{\theta }_{l\sigma }+{\theta }_{r\sigma }+{\theta }_{l\tau }+{\theta }_{r\tau }}{6}\right),$ obtained in Step 1, represents the crisp value of the game (minimum expected gain) of Player-I and the optimal value $\frac{1}{2}\left(\frac{{\phi }_{l\rho }+{\phi }_{l\sigma }+{\phi }_{l\tau }+{\phi }_{r\rho }+{\phi }_{r\sigma }+{\phi }_{r\tau }}{6}+\frac{{\phi }_{r\rho }+{\phi }_{r\sigma }+{\phi }_{r\tau }}{3}\right),$ obtained in Step 2, represents the crisp value of the game (maximum expected loss) of Player-II.

2.5 Seikh and Dutta’s second approach

Using Seikh and Dutta’s (2022) second approach, the optimal probability ${u}_{i}, i=\mathrm{1,2},\dots ,m$ for selecting the ${i}{\text{th}}$ strategy by Player-I, the optimal probability ${v}_{j}, j=\mathrm{1,2},\dots ,n$ for selecting the ${j}{\text{th}}$ strategy by Player-II, the crisp value of the game (minimum expected gain) of Player-I and the crisp value of the game (maximum expected loss) of Player-II can be obtained as follows:

Step 1: Find an optimal solution ${\Omega }_{1}, {u}_{i},i=\mathrm{1,2},\dots ,m$ of the CLPP (P9) for some specific values of $\alpha \in \left[0, 1\right].$

Problem (P9)

$$Maximize \left\{{\Omega }_{1}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{\gamma }_{j}\left(\frac{{a}_{ij1}+2{a}_{ij2}+2{a}_{ij3}+{a}_{ij4}}{6}\right){u}_{i}\ge {\Omega }_{1}, j=\mathrm{1,2},\dots ,n$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

where,

$${\gamma }_{j}=\left[\alpha {\left({minimum}_{ 1\le i\le m}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ 1\le i\le m}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ 1\le i\le m}\left\{{n}_{ij}\right\}\right)}^{2}\right].$$

Step 2: Find an optimal solution ${\Omega }_{2}, {v}_{j}, j=\mathrm{1,2},...,n$ of the CLPP (P10) for some specific values of $\alpha \in \left[0, 1\right].$

Problem (P10)

$$Minimize \left\{{\Omega }_{2}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{\gamma }_{i}\left(\frac{{a}_{ij1}+2{a}_{ij2}+2{a}_{ij3}+{a}_{ij4}}{6}\right){v}_{j}\le {\Omega }_{2}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

where,

$${\gamma }_{i}=\left[\alpha {\left({minimum}_{ 1\le j\le n}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ 1\le j\le n}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ 1\le j\le n}\left\{{n}_{ij}\right\}\right)}^{2}\right].$$

Step 3: The optimal value of ${u}_{i},i=\mathrm{1,2},\dots ,m,$ obtained in Step 1, represents the optimal probability for selecting the ${i}{\text{th}}$ strategy by Player-I and the optimal value of ${v}_{j}, j=\mathrm{1,2},\dots ,n,$ obtained in Step 2, represents the optimal probability for selecting the ${j}{\text{th}}$ strategy by Player-II for the considered SVTrN matrix game.

Step 4: The optimal value of ${\Omega }_{1},$ obtained in Step 1, represents the crisp value of the game (minimum expected gain) of Player-I and the optimal value of ${\Omega }_{2},$ obtained in Step 2, represents the crisp value of the game (maximum expected loss) of Player-II.

3 Invalidity of existing approaches

Based on the existing results (Bector and Chandra 2005, Sect. 1.4, pp. 6–7), it can be easily concluded that the CLPPs (P2) and (P4), corresponding to Player-I and Player-II respectively, represent a primal–dual pair. Therefore,

• (i) If Brikaa’s (2022) approach is valid then, the CLPPs (P7) and (P8), corresponding to Player-I and Player-II respectively, should represent a primal–dual pair. Hence, on solving the CLPPs (P7) and (P8), the same optimal value, representing crisp value of the game, should be obtained. However, in this section, with the help of a numerical example, it is shown that the optimal value of the CLPP (P7) is not equal to the optimal value of the CLPP (P8). Therefore, Brikaa’s (2022) approach is not valid.

• (ii) If Seikh and Dutta’s (2022) approach is valid then, the CLPPs (P9) and (P10), corresponding to Player-I and Player-II respectively, should represent a primal–dual pair. Hence, on solving the CLPPs (P9) and (P10), the same optimal value, representing crisp value of the game, should be obtained. However, in this section, with the help of a numerical example, it is shown that the optimal value of the CLPP (P9) is not equal to the optimal value of the CLPP (P10). Therefore, Seikh and Dutta’s (2022) second approach is not valid.

3.1 Invalidity of Brikaa’s approach

In this section, with the help of a numerical example, it is shown that the optimal value of the CLPP (P7) is not equal to the optimal value of the CLPP (P8). Therefore, Brikaa’s (2022) approach is not valid.

Seikh and Dutta (2022, Sect. 5.1, Example 1, p. 929) considered the payoff matrix.

$$\widetilde{A}=\left(\begin{array}{ll}\Bigg\langle \left(175, 177, 180, 190\right);\mathrm{0.6,0.3,0.3}\Bigg\rangle & \Bigg\langle \left(150, 153, 156, 158\right);\mathrm{0.5,0.2,0.3}\Bigg\rangle \\ \Bigg\langle \left(125, 128, 132, 140\right);\mathrm{0.9,0.1,0.5}\Bigg\rangle & \Bigg\langle \left(175, 185, 195, 200\right);\mathrm{0.5,0.4,0.5}\Bigg\rangle \end{array}\right)$$

of a SVTrN matrix game to illustrate their proposed approaches.

It can be easily verified that for the considered SVTrN matrix game, the CLPPs (P7) and (P8) are transformed into the CLPPs (P11) and (P12) respectively.

Problem (P11)

$$Maximize \left\{\frac{1}{2}\left(\frac{{\theta }_{l\rho }+{\theta }_{l\sigma }+{\theta }_{l\tau }}{3}+\frac{{\theta }_{l\rho }+{\theta }_{r\rho }+{\theta }_{l\sigma }+{\theta }_{r\sigma }+{\theta }_{l\tau }+{\theta }_{r\tau }}{6}\right)\right\}$$

Subject to

$$\left(0.6-\rho \right)\left(175{u}_{1}+125{u}_{2}\right)+\rho \left(177{u}_{1}+128{u}_{2}\right)\ge 0.6 {\theta }_{l\rho },$$

$$\left(0.6-\rho \right)\left(190{u}_{1}+140{u}_{2}\right)+\rho \left(180{u}_{1}+132{u}_{2}\right)\ge 0.6{ \theta }_{r\rho },$$

$$\left(0.5-\rho \right)\left(150{u}_{1}+175{u}_{2}\right)+\rho \left(153{u}_{1}+185{u}_{2}\right)\ge 0.5 {\theta }_{l\rho },$$

$$\left(0.5-\rho \right)\left(158{u}_{1}+200{u}_{2}\right)+\rho \left(156{u}_{1}+195{u}_{2}\right)\ge 0.5{ \theta }_{r\rho },$$

$$\left(1-\sigma \right)\left(177{u}_{1}+128{u}_{2}\right)+\left(\sigma -0.3\right)\left(175{u}_{1}+125{u}_{2}\right)\ge 0.7{\theta }_{l\sigma },$$

$$\left(1-\sigma \right)\left(180{u}_{1}+132{u}_{2}\right)+\left(\sigma -0.3\right)\left(190{u}_{1}+140{u}_{2}\right)\ge 0.7{\theta }_{r\sigma },$$

$$\left(1-\sigma \right)\left(153{u}_{1}+185{u}_{2}\right)+\left(\sigma -0.4\right)\left(150{u}_{1}+175{u}_{2}\right)\ge 0.6{\theta }_{l\sigma },$$

$$\left(1-\sigma \right)\left(156{u}_{1}+195{u}_{2}\right)+\left(\sigma -0.4\right)\left(158{u}_{1}+200{u}_{2}\right)\ge 0.6{\theta }_{r\sigma },$$

$$\left(1-\tau \right)\left(177{u}_{1}+128{u}_{2}\right)+\left(\tau -0.5\right)\left(175{u}_{1}+125{u}_{2}\right)\ge 0.5{\theta }_{l\tau },$$

$$\left(1-\tau \right)\left(180{u}_{1}+132{u}_{2}\right)+\left(\tau -0.5\right)\left(190{u}_{1}+140{u}_{2}\right)\ge 0.5{\theta }_{r\tau },$$

$$\left(1-\tau \right)\left(153{u}_{1}+185{u}_{2}\right)+\left(\tau -0.5\right)\left(150{u}_{1}+175{u}_{2}\right)\ge 0.5{\theta }_{l\tau },$$

$$\left(1-\tau \right)\left(153{u}_{1}+195{u}_{2}\right)+\left(\tau -0.5\right)\left(158{u}_{1}+200{u}_{2}\right)\ge 0.5{\theta }_{r\tau },$$

$${u}_{1}+{u}_{2}=1, {u}_{1}\ge 0, {u}_{2}\ge 0.$$

Problem (P12)

$$Minimize \left\{\frac{1}{2}\left(\frac{{\phi }_{l\rho }+{\phi }_{r\rho }+{\phi }_{l\sigma }+{\phi }_{r\sigma }+{\phi }_{l\tau }+{\phi }_{r\tau }}{6}+\frac{{\phi }_{r\rho }+{\phi }_{r\sigma }+{\phi }_{r\tau }}{3}\right)\right\}$$

Subject to

$$\left(0.5-\rho \right)\left(175{v}_{1}+150{v}_{2}\right)+\rho \left(177{v}_{1}+153{v}_{2}\right)\le 0.5 {\phi }_{l\rho },$$

$$\left(0.5-\rho \right)\left(190{v}_{1}+158{v}_{2}\right)+\rho \left(180{v}_{1}+156{v}_{2}\right)\le 0.5 {\phi }_{r\rho },$$

$$\left(0.5-\rho \right)\left(125{v}_{1}+175{v}_{2}\right)+\rho \left(128{v}_{1}+185{v}_{2}\right)\le 0.5 {\phi }_{l\rho },$$

$$\left(0.5-\rho \right)\left(140{v}_{1}+200{v}_{2}\right)+\rho \left(132{v}_{1}+195{v}_{2}\right)\le 0.5 {\phi }_{r\rho },$$

$$\left(1-\sigma \right)\left(177{v}_{1}+153{v}_{2}\right)+\left(\sigma -0.3\right)\left(175{v}_{1}+150{v}_{2}\right)\le 0.7 {\phi }_{l\sigma },$$

$$\left(1-\sigma \right)\left(180{v}_{1}+156{v}_{2}\right)+\left(\sigma -0.3\right)\left(190{v}_{1}+158{v}_{2}\right)\le 0.7 {\phi }_{r\sigma },$$

$$\left(1-\sigma \right)\left(128{v}_{1}+185{v}_{2}\right)+\left(\sigma -0.4\right)\left(125{v}_{1}+175{v}_{2}\right)\le 0.6 {\phi }_{l\sigma },$$

$$\left(1-\sigma \right)\left(132{v}_{1}+195{v}_{2}\right)+\left(\sigma -0.4\right)\left(140{v}_{1}+200{v}_{2}\right)\le 0.6 {\phi }_{r\sigma },$$

$$\left(1-\tau \right)\left(177{v}_{1}+153{v}_{2}\right)+\left(\tau -0.4\right)\left(175{v}_{1}+150{v}_{2}\right)\le 0.6 {\phi }_{l\tau },$$

$$\left(1-\tau \right)\left(180{v}_{1}+156{v}_{2}\right)+\left(\tau -0.4\right)\left(190{v}_{1}+158{v}_{2}\right)\le 0.6 {\phi }_{r\tau },$$

$$\left(1-\tau \right)\left(128{v}_{1}+185{v}_{2}\right)+\left(\tau -0.5\right)\left(125{v}_{1}+175{v}_{2}\right)\le 0.5 {\phi }_{l\tau },$$

$$\left(1-\tau \right)\left(132{v}_{1}+195{v}_{2}\right)+\left(\tau -0.5\right)\left(140{v}_{1}+200{v}_{2}\right)\le 0.5 {\phi }_{r\tau },$$

$${v}_{1}+{v}_{2}=1, {v}_{1}\ge 0, {v}_{2}\ge 0.$$

It can be easily verified that.

• (i) The results, shown in Table 1, are obtained on solving the CLPP (P11).

• (ii) The results, shown in Table 2, are obtained on solving the CLPP (P12).

Table 1 Optimal solution and the corresponding optimal value for Player-I

Table 2 Optimal solution and the corresponding optimal value for Player-II

It is obvious from the results, shown in Tables 1 and 2, the optimal value of the CLPP (P11) is not equal to the optimal value of the CLPP (P12). For example, for $\rho =0, \sigma =1,\tau =1,$ the optimal value of the CLPP (P11) is $161.75$ and the optimal value of the CLPP (P12) is $169.8098$.

This clearly indicates that Brikaa’s (2022) approach is not valid.

3.2 Invalidity of Seikh and Dutta’s second approach

In this section, with the help of a numerical example, it is shown that the optimal value of the CLPP (P9) is not equal to the optimal value of the CLPP (P10). Hence, Seikh and Dutta’s (2022) second approach is not valid.

Seikh and Dutta (2022, Sect. 5.1, Example 1, p. 929) considered the payoff matrix.

$$\widetilde{A}=\left(\begin{array}{cc}\Bigg\langle \left(175, 177, 180, 190\right);\mathrm{0.6,0.3,0.3}\Bigg\rangle & \Bigg\langle \left(150, 153, 156, 158\right);\mathrm{0.5,0.2,0.3}\Bigg\rangle \\ \Bigg\langle \left(125, 128, 132, 140\right);\mathrm{0.9,0.1,0.5}\Bigg\rangle & \Bigg\langle \left(175, 185, 195, 200\right);\mathrm{0.5,0.4,0.5}\Bigg\rangle \end{array}\right)$$

of a SVTrN matrix game to illustrate their proposed approaches.

Seikh and Dutta (2022) claimed that for the considered SVTrN matrix game, the CLPPs (P9) and (P10) are transformed into the CLPPs (P13) (Seikh and Dutta 2022, Sect. 5.1.1, Problem 15, p. 931) and (P14) (Seikh and Dutta 2022, Sect. 5.1.1, Problem 16, p. 931) respectively.

Problem (P13)

$$Maximize \left\{{\Omega }_{1}\right\}$$

Subject to

$$\frac{\left(1079{u}_{1}+785{u}_{2}\right)\left(0.74-0.38\alpha \right)}{6}\ge {\Omega }_{1},$$

$$\frac{\left(926{u}_{1}+1135{u}_{2}\right)\left(0.61-0.36\alpha \right)}{6}\ge {\Omega }_{1},$$

$${u}_{1}+{u}_{2}=1, {u}_{1}\ge 0,{u}_{2}\ge 0.$$

Problem (P14)

$$Minimize \left\{{\Omega }_{2}\right\}$$

Subject to

$$\frac{\left(1079{v}_{1}+926{v}_{2}\right)\left(0.98-0.73\alpha \right)}{6}\le {\Omega }_{2},$$

$$\frac{\left(785{v}_{1}+1135{v}_{2}\right)\left(0.61-0.36\alpha \right)}{6}\le {\Omega }_{2},$$

$${v}_{1}+{v}_{2}=1, {v}_{1}\ge 0,{v}_{2}\ge 0.$$

Seikh and Dutta (2022) further claimed that on solving the CLPPs (P13) and (P14), the existing results (Seikh and Dutta 2022, Sect. 5.1.1, Table 3, p. 932), shown in Table 3, are obtained.

Table 3 Optimal values of $\left({u}_{1},{u}_{2},{\Omega }_{1}\right)$ for Player-I and $\left({v}_{1},{v}_{2},{\Omega }_{2}\right)$ for Player-II

It is obvious from the results, shown in Table 3, the optimal value of the CLPP (P13) is not equal to the optimal value of the CLPP (P14). For example, for $\alpha =0.1,$ the optimal value of CLPP (P13) i.e., ${\Omega }_{1}$ is $102.4294$ and the optimal value of CLPP (P14) i.e., ${\Omega }_{2}$ is $139.9803$.

This clearly indicates that Seikh and Dutta’s (2022) second approach is not valid.

4 Reason for the invalidity of Brikaa’s approach

It is obvious from Sect. 3.1 that Brikaa’s (2022) approach is not valid. The reason for the invalidity of Brikaa’s (2022) approach is that in Brikaa’s (2022) approach some mathematically incorrect results are considered to transform the SVTrN NLPPs (P5) and (P6) into the CLPPs (P7) and (P8) respectively. To point out the mathematically incorrect results, considered in Brikaa’s (2022) approach, there is a need to discuss the transformation method, used in Brikaa’s (2022) approach, to transform the SVTrN NLPPs (P5) and (P6) into the CLPPs (P7) and (P8) respectively. Therefore, in this section, firstly, the transformation method, used in Brikaa’s (2022) approach, is discussed. Then, the mathematically incorrect results, considered in the transformation method, are discussed.

4.1 Transformation method used in Brikaa’s approach

In Brikaa’s (2022) approach, the following method is used to transform the SVTrN NLPPs (P5) and (P6) into the CLPPs (P7) and (P8) respectively.

Step 1: According to the first ranking method, discussed in Sect. 2.1.1, to find an optimal solution of the SVTrN NLPPs (P5) and (P6) is equivalent to find an optimal solution of the interval-valued NLPPs (P15) and (P16) respectively.

Problem (P15)

$$Maximize \left\{\begin{array}{c}Minimize\left\{{\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)}_{\rho }\right\}\\ Minimize\left\{{\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)}_{\sigma }\right\}\\ Minimize\left\{{\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)}_{\tau }\right\}\\ {\text{Subject to}} \\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P16)

$$Minimize \left\{\begin{array}{c}Maximize\left\{{\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)}_{\rho }\right\}\\ Maximize\left\{{\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)}_{\sigma }\right\}\\ Maximize\left\{{\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)}_{\tau }\right\} \\ {\text{Subject to}} \\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 2: Using the expressions (1) and (2), to find an optimal solution of the interval-valued NLPPs (P15) and (P16) is equivalent to find an optimal solution of the interval-valued NLPPs (P17) and (P18) respectively.

$${\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)}_{k}=\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{v}_{j}; k=\rho ,\sigma ,\tau $$

(1)

$${\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)}_{k}=\sum\limits_{i=1}^{m}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{u}_{i}; k=\rho ,\sigma ,\tau $$

(2)

Problem (P17)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\rho }{v}_{j}\right\}\\ Minimize\left\{\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\sigma }{v}_{j}\right\}\\ Minimize\left\{\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\tau }{v}_{j}\right\}\\ {\text{Subject to}} \\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P18)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\rho }{u}_{i}\right\}\\ Maximize\left\{\sum\limits_{i=1}^{m}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\sigma }{u}_{i}\right\}\\ Maximize\left\{\sum\limits_{i=1}^{m}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\tau }{u}_{i}\right\} \\ {\text{Subject to}} \\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 3: Since

$$\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{v}_{j}$$

is a convex linear combination of

$${\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k},j=\mathrm{1,2},\dots ,n;k=\rho ,\sigma ,\tau $$

and

$$\sum\limits_{i=1}^{m}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{u}_{i}$$

is a convex linear combination of

$${\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}, i=\mathrm{1,2},...,m; k=\rho ,\sigma ,\tau. $$

So, to find an optimal solution of the interval-valued NLPPs (P17) and (P18) is equivalent to find an optimal solution of the interval-valued NLPPs (P19) and (P20) respectively.

Problem (P19)

$$Maximize \left\{\begin{array}{c}{Minimum}_{1\le j\le n}\left\{{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\rho }\right\}\\ \begin{array}{c}{Minimum}_{1\le j\le n}\left\{{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\sigma }\right\}\\ {Minimum}_{1\le j\le n}\left\{{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\tau }\right\}\end{array}\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P20)

$$Minimize \left\{\begin{array}{c}{Maximum}_{1\le i\le m}\left\{{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\rho }\right\}\\ {Maximum}_{1\le i\le m}\left\{{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\sigma }\right\}\\ {Maximum}_{1\le i\le m}\left\{{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\tau }\right\}\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 4: Assuming,

$${Minimum}_{1\le j\le n}{\left\{\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right\}}_{k}={\widetilde{\theta }}_{k};$$

$k=\rho ,\sigma ,\tau$ and

$${Maximum}_{1\le i\le m}\left\{{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}\right\}={\widetilde{\phi }}_{k}; k=\rho ,\sigma ,\tau ,$$

to find an optimal solution of the interval-valued NLPPs (P19) and (P20) is equivalent to find an optimal solution of the interval-valued NLPPs (P21) and (P22) respectively.

Problem (P21)

$$Maximize \left\{{\widetilde{\theta }}_{\rho }, {\widetilde{\theta }}_{\sigma }, {\widetilde{\theta }}_{\tau }\right\}$$

Subject to

$${\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}\ge {\widetilde{\theta }}_{k}, k=\rho ,\sigma ,\tau ; \quad j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, \quad i=\mathrm{1,2},\dots ,m.$$

Problem (P22)

$$Minimize \left\{{\widetilde{\phi }}_{\rho }, {\widetilde{\phi }}_{\sigma }, {\widetilde{\phi }}_{\tau }\right\}$$

Subject to

$${\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}\le {\widetilde{\phi }}_{k}, k=\rho ,\sigma ,\tau ;$$

$$i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 5: Using the expression (3), to find an optimal solution of the interval-valued NLPPs (P21) and (P22) is equivalent to find an optimal solution of the interval-valued NLPPs (P23) and (P24) respectively.

$${\left({\widetilde{\beta }}_{ij}\right)}_{k}=\left[{\left({\beta }_{ij}\right)}_{lk},{\left({\beta }_{ij}\right)}_{rk}\right]; k=\rho ,\sigma ,\tau $$

(3)

Problem (P23)

$$Maximize \left\{\left[{\theta }_{l\rho },{\theta }_{r\rho }\right],\left[{\theta }_{l\sigma },{\theta }_{r\sigma }\right],\left[{\theta }_{l\tau },{\theta }_{r\tau }\right]\right\}$$

Subject to

$$\left[\begin{array}{c}{\left(\begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\right)}_{lk},\\ {\left(\begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\right)}_{rk}\end{array}\right]\ge \left[{\theta }_{lk},{\theta }_{rk}\right],k=\rho ,\sigma ,\tau ;j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P24)

$$Minimize \left\{\left[{\phi }_{l\rho },{\phi }_{r\rho }\right],\left[{\phi }_{l\sigma },{\phi }_{r\sigma }\right],\left[{\phi }_{l\tau },{\phi }_{r\tau }\right]\right\}$$

Subject to

$$\left[\begin{array}{c}{\left(\begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\right)}_{lk},\\ {\left(\begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\right)}_{rk}\end{array}\right]\le \left[{\phi }_{lk},{\phi }_{rk}\right],$$

$$k=\rho ,\sigma ,\tau ;i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 6: Using the expression (4), to find an optimal solution of the interval-valued NLPPs (P23) and (P24) is equivalent to find an optimal solution of the interval-valued NLPPs (P25) and (P26) respectively.

$$\left[{\left({\beta }_{ij}\right)}_{lk},{\left({\beta }_{ij}\right)}_{rk}\right]\ge \left[{\left({\gamma }_{ij}\right)}_{lk},{\left({\gamma }_{ij}\right)}_{rk}\right]\Rightarrow {\left({\beta }_{ij}\right)}_{lk}\ge {\left({\gamma }_{ij}\right)}_{lk},{\left({\beta }_{ij}\right)}_{rk}\ge {\left({\gamma }_{ij}\right)}_{rk}; k=\rho ,\sigma ,\tau $$

(4)

Problem (P25)

$$Maximize \left\{\left[{\theta }_{l\rho },{\theta }_{r\rho }\right],\left[{\theta }_{l\sigma },{\theta }_{r\sigma }\right],\left[{\theta }_{l\tau },{\theta }_{r\tau }\right]\right\}$$

Subject to

$${\left(\begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\right)}_{lk}\ge {\theta }_{lk},k=\rho ,\sigma ,\tau ;j=\mathrm{1,2},\dots ,n,$$

$${\left(\begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\right)}_{rk}\ge {\theta }_{rk},k=\rho ,\sigma ,\tau ; j=\mathrm{1,2},\dots ,n,\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P26)

$$Minimize \left\{\left[{\phi }_{l\rho },{\phi }_{r\rho }\right],\left[{\phi }_{l\sigma },{\phi }_{r\sigma }\right],\left[{\phi }_{l\tau },{\phi }_{r\tau }\right]\right\}$$

Subject to

$${\left(\begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\right)}_{lk}\le {\phi }_{lk}, k=\rho ,\sigma ,\tau ;$$

$$i=\mathrm{1,2},\dots ,m,$$

$${\left(\begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\right)}_{rk}\le {\phi }_{rk}, k=\rho ,\sigma ,\tau ;i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 7: Using the expressions (5) to (10), to find an optimal solution of the interval-valued NLPPs (P25) and (P26) is equivalent to find an optimal solution of the interval-valued NLPPs (P27) and (P28) respectively.

$${\left(\Bigg\langle \left({A}_{i1},{A}_{i2},{A}_{i3},{A}_{i4}\right);{l}_{i},{m}_{i},{n}_{i}\Bigg\rangle \right)}_{l\rho }=\frac{\left({l}_{i}-\rho \right){A}_{i1}+\rho {A}_{i2}}{{l}_{i}}$$

(5)

$${\left(\Bigg\langle \left({A}_{i1},{A}_{i2},{A}_{i3},{A}_{i4}\right);{l}_{i},{m}_{i},{n}_{i}\Bigg\rangle \right)}_{r\rho }=\frac{\left({l}_{i}-\rho \right){A}_{i4}+\rho {A}_{i3}}{{l}_{i}}$$

(6)

$${\left(\Bigg\langle \left({A}_{i1},{A}_{i2},{A}_{i3},{A}_{i4}\right);{l}_{i},{m}_{i},{n}_{i}\Bigg\rangle \right)}_{l\sigma }=\frac{\left(1-\sigma \right){A}_{i2}+\left(\sigma -{m}_{i}\right){A}_{i1}}{{1-m}_{i}}$$

(7)

$${\left(\Bigg\langle \left({A}_{i1},{A}_{i2},{A}_{i3},{A}_{i4}\right);{l}_{i},{m}_{i},{n}_{i}\Bigg\rangle \right)}_{r\sigma }=\frac{\left(1-\sigma \right){A}_{i3}+\left(\sigma -{m}_{i}\right){A}_{i4}}{1-{m}_{i}}$$

(8)

$${\left(\Bigg\langle \left({A}_{i1},{A}_{i2},{A}_{i3},{A}_{i4}\right);{l}_{i},{m}_{i},{n}_{i}\Bigg\rangle \right)}_{l\tau }=\frac{\left(1-\tau \right){A}_{i2}+\left(\tau -{n}_{i}\right){A}_{i1}}{{1-n}_{i}}$$

(9)

$${\left(\Bigg\langle \left({A}_{i1},{A}_{i2},{A}_{i3},{A}_{i4}\right);{l}_{i},{m}_{i},{n}_{i}\Bigg\rangle \right)}_{r\tau }=\frac{\left(1-\tau \right){A}_{i3}+\left(\tau -{n}_{i}\right){A}_{i4}}{1-{n}_{i}}$$

(10)

Problem (P27)

$$Maximize \left\{\left[{\theta }_{l\rho },{\theta }_{r\rho }\right],\left[{\theta }_{l\sigma },{\theta }_{r\sigma }\right],\left[{\theta }_{l\tau },{\theta }_{r\tau }\right]\right\}$$

Subject to

$$\left({minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\}-\rho \right)\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i}+\rho \sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i}\ge \left({minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\}\right){\theta }_{l\rho },$$

$$j=\mathrm{1,2},\dots ,n,$$

$$\left({minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\}-\rho \right)\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}+\rho \sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i}\ge \left({minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\}\right){\theta }_{r\rho },$$

$$j=\mathrm{1,2},\dots ,n,$$

$$\left(1-\sigma \right)\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i}+\left(\sigma -{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\}\right)\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i}\ge \left(1-{maximum }_{1\le i\le m}\right.$$

$$\left.\left\{{m}_{ij}\right\}\right){\theta }_{l\sigma }, j=\mathrm{1,2},\dots ,n,$$

$$\left(1-\sigma \right)\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i}+\left(\sigma -{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\}\right)\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\ge \left(1-{maximum }_{1\le i\le m}\right.$$

$$\left.\left\{{m}_{ij}\right\}\right){\theta }_{r\sigma }, j=\mathrm{1,2},\dots ,n,$$

$$\left(1-\tau \right)\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i}+\left(\tau -{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\right)\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i}\ge \left(1-{maximum }_{1\le i\le m}\right.$$

$$\left.\left\{{n}_{ij}\right\}\right){\theta }_{l\tau }, j=\mathrm{1,2},\dots ,n,$$

$$\left(1-\tau \right)\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i}+\left(\tau -{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\right)\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\ge \left(1-{maximum }_{1\le i\le m}\right.$$

$$\left.\left\{{n}_{ij}\right\}\right){\theta }_{r\tau }, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P28)

$$Minimize \left\{\left[{\phi }_{l\rho },{\phi }_{r\rho }\right],\left[{\phi }_{l\sigma },{\phi }_{r\sigma }\right],\left[{\phi }_{l\tau },{\phi }_{r\tau }\right]\right\}$$

Subject to

$$\left({minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\}-\rho \right)\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j}+\rho \sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j}\le \left({minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\}\right){\phi }_{l\rho },i=\mathrm{1,2},\dots ,m,$$

$$\left({minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\}-\rho \right)\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}+\rho \sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j}\le \left({minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\}\right){\phi }_{r\rho },i=\mathrm{1,2},\dots ,m,$$

$$\left(1-\sigma \right)\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j}+\left(\sigma -{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\}\right)\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j}\le \left(1-{maximum }_{1\le j\le n}\right.\left.\left\{{m}_{ij}\right\}\right){\phi }_{l\sigma }, i=\mathrm{1,2},\dots ,m,$$

$$\left(1-\sigma \right)\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j}+\left(\sigma -{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\}\right)\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\le \left(1-{maximum }_{1\le j\le n}\right.\left.\left\{{m}_{ij}\right\}\right){\phi }_{r\sigma }, i=\mathrm{1,2},\dots ,m,$$

$$\left(1-\tau \right)\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j}+\left(\tau -{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\right)\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j}\le \left(1-{maximum }_{1\le j\le n}\right.\left.\left\{{n}_{ij}\right\}\right){\phi }_{l\tau }, i=\mathrm{1,2},\dots ,m,$$

$$\left(1-\tau \right)\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j}+\left(\tau -{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\right)\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\le \left(1-{maximum }_{1\le j\le n}\right.\left.\left\{{n}_{ij}\right\}\right){\phi }_{r\tau }, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 8: Applying the concept of Ishibuchi and Tanaka (1990), to find an optimal solution of the interval-valued NLPPs (P27) and (P28) is equivalent to find an optimal solution of the bi-objective NLPPs (P29) and (P30) respectively.

Problem (P29)

$$Maximize\left\{\frac{{\theta }_{l\rho }+{\theta }_{l\sigma }+{\theta }_{l\tau }}{3},\frac{{{\theta }_{l\rho }+\theta }_{r\rho }+{\theta }_{l\sigma }+{\theta }_{r\sigma }+{\theta }_{l\tau }+{\theta }_{r\tau }}{6}\right\}$$

Subject to

Constraints of the Problem (P27).

Problem (P30)

$$Minimize\left\{\frac{{{\phi }_{l\rho }+\phi }_{r\rho }+{\phi }_{l\sigma }+{\phi }_{r\sigma }+{\phi }_{l\tau }+{\phi }_{r\tau }}{6},\frac{{\phi }_{r\rho }+{\phi }_{r\sigma }+{\phi }_{r\tau }}{3}\right\}$$

Subject to

Constraints of the Problem (P28).

Step 9: Using the weighted average method, to find an optimal solution of the bi-objective NLPPs (P29) and (P30) is equivalent to find an optimal solution of the CLPPs (P7) and (P8) respectively.

4.2 Mathematically incorrect results considered in Brikaa’s approach

Brikaa’s (2022) approach is not valid as the following two mathematically incorrect results are considered in it.

4.2.1 First mathematically incorrect result

It is obvious that in Step 2 of Brikaa’s (2022) approach, discussed in Sect. 4.1, the expression (1) i.e., ${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{k}=$

$$\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{v}_{j};k=\rho ,\sigma ,\tau $$

is used to transform the interval-valued NLPP (P15) into the interval-valued NLPP (P17).

However, the expression (1) is mathematically incorrect and the expression (11) represents the mathematically correct form of the expression (1). So, the interval-valued NLPP (P15) is not equivalent to the interval-valued NLPP (P17).

$${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{k}=\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{v}_{j};k=\rho ,\sigma ,\tau $$

(11)

The following clearly indicates that the above claim is valid.

$\mathrm{Assuming }\,k=\rho ,$

$${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{k}=\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},\right.$$

$${n}_{ij}\Bigg\rangle {\left.{u}_{i}{v}_{j}\right)}_{\rho }=\Bigg\langle \left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}{v}_{j}\right);{minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},$$

$${{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\Bigg\rangle }_{\rho }$$

$$=\Bigg\langle \left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}{v}_{j}\right);{l,m,n\Bigg\rangle }_{\rho }$$

where,

$$l={minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},m={maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},n={maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}$$

$$=\left[\frac{\left(l-\rho \right)\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i}{v}_{j}+\rho \sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i}{v}_{j}}{l},\frac{\left(l-\rho \right)\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}{v}_{j}+\rho \sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i}{v}_{j}}{l}\right]$$

$$=\left[\frac{\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij1}\left(l-\rho \right){u}_{i}{v}_{j}+\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij2}\rho {u}_{i}{v}_{j}}{l},\frac{\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij4}\left(l-\rho \right){u}_{i}{v}_{j}+\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij3}\rho {u}_{i}{v}_{j}}{l}\right]$$

$$=\sum\limits_{j=1}^{n}\left[\frac{\sum\limits_{i=1}^{m}{a}_{ij1}\left(l-\rho \right){u}_{i}+\sum\limits_{i=1}^{m}{a}_{ij2}\left(l-\rho \right){u}_{i}}{l},\frac{\sum\limits_{i=1}^{m}{a}_{ij4}\left(l-\rho \right){u}_{i}+\sum\limits_{i=1}^{m}{a}_{ij3}\left(l-\rho \right){u}_{i}}{l}\right]{v}_{j}$$

$$=\sum\limits_{j=1}^{n}{\left(\Bigg\langle \left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);l,m,n\Bigg\rangle \right)}_{\rho } {v}_{j}$$

$$=\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\rho }{v}_{j}$$

So, ${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{\rho }=$

$$\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\rho }{v}_{j}$$

Similarly, it can be easily proved that

$${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{\sigma }=$$

$$\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\sigma }{v}_{j}$$

and

$${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{\tau }=\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{\tau }{v}_{j}.$$

Hence,

$${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{k}=$$

$$\sum\limits_{j=1}^{n}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{v}_{j};k=\rho ,\sigma ,\tau $$

Furthermore, it is obvious that in Step 2 of Brikaa’s (2022) approach, discussed in Sect. 4.1, the expression (2) i.e.,

$${\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)}_{k}=\sum\limits_{i=1}^{m}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{u}_{i}; k=\rho ,\sigma ,\tau $$

is used to transform the interval-valued NLPP (P16) into interval-valued NLPP (P18).

While, it can be easily verified that the expression (2) is mathematically incorrect and the expression (12) represents the mathematically correct form of the expression (2). So, the interval-valued NLPP (P16) is not equivalent to the interval-valued NLPP (P18).

$${\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)}_{k}=\sum\limits_{i=1}^{m}{\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}{u}_{i};k=\rho ,\sigma ,\tau .$$

(12)

4.2.2 Second mathematically incorrect result

It is a well-known fact that if ${a}_{j},j=\mathrm{1,2},\dots ,n$ are $n$ real numbers. Then,

$\theta ={Minimum}_{1\le j\le n}\left\{{a}_{j}\right\}$ (i) will be one of the real numbers ${a}_{j},j=\mathrm{1,2},\dots ,n$. Therefore, the expression (13) is valid.

$${a}_{j}\ge \theta ,j=\mathrm{1,2},\dots ,n$$

(13)

$\phi ={Maximum}_{1\le i\le m}\left\{{a}_{i}\right\}$ (ii) will be one of the real numbers ${a}_{i}, i=\mathrm{1,2},\dots ,m.$ Therefore, the expression (14) is valid.

$${a}_{i}\le \phi ,i=\mathrm{1,2},\dots ,m$$

(14)

In the same direction, in Step 4 of Brikaa’s (2022) approach, it is assumed that if $\Bigg\langle \left({a}_{j1},{a}_{j2},{a}_{j3},{a}_{j4}\right);{l}_{j},{m}_{j},{n}_{j}\Bigg\rangle , j=\mathrm{1,2},\dots ,n$ are $n$ SVTrN numbers. Then,

(i)

$${\widetilde{\theta }}_{k}={Minimum}_{1\le j\le n}\left\{\left(\Bigg\langle \left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\right.\right.$$

$$\left.{\left.{minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\Bigg\rangle \right)}_{k}\right\};k=\rho ,\sigma ,\tau $$

will be one of the intervals

$$\left(\Bigg\langle \left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\right.$$

$${\left.{minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\Bigg\rangle \right)}_{k},j=\mathrm{1,2},\dots ,n.$$

Therefore, the expression (15) is valid

$${\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}\left({a}_{ij1}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij2}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij3}\right){u}_{i},\sum\limits_{i=1}^{m}\left({a}_{ij4}\right){u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{ {l}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum }_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}\ge {\widetilde{\theta }}_{k}, j=\mathrm{1,2},\dots ,n$$

(15)

(ii)

$${\widetilde{\phi }}_{k}={Maximum}_{1\le i\le m}\left\{\left(\Bigg\langle\left(\sum _{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum _{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum _{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum _{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\right.\right.$$

$$\left.{\left.{minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\Bigg\rangle \right)}_{k}\right\};k=\rho ,\sigma ,\tau $$

will be one of the intervals $\left(\Bigg\langle \left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\right.$ ${\left.{minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\Bigg\rangle \right)}_{k},k=\rho ,\sigma ,\tau, \;i=\mathrm{1,2},\dots ,m$.

Therefore, the expression (16) is valid.

$${\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}\left({a}_{ij1}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij2}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij3}\right){v}_{j},\sum\limits_{j=1}^{n}\left({a}_{ij4}\right){v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{ {l}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum }_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}_{k}\le {\widetilde{\phi }}_{k}, k=\rho ,\sigma ,\tau,\;i=\mathrm{1,2},\dots ,m$$

(16)

However, the following example clearly indicates that neither the expression (15) nor the expression (16) is valid.

Let $\widetilde{M}=\Bigg\langle \left(\mathrm{2,4},\mathrm{8,10}\right);\mathrm{0.6,0.5,0.4}\Bigg\rangle$ and $\widetilde{N}=\Bigg\langle \left(\mathrm{1,5},\mathrm{7,9}\right);\mathrm{0.6,0.5,0.4}\Bigg\rangle$ be two SVTrN numbers. Then,

$${\widetilde{M}}_{\rho }=\left[{M}_{l\rho },{M}_{r\rho }\right]=\left[2+\frac{2\rho }{0.6},10-\frac{2\rho }{0.6}\right],{\widetilde{N}}_{\rho }=\left[{N}_{l\rho },{N}_{r\rho }\right]=\left[1+\frac{4\rho }{0.6},9-\frac{2\rho }{0.6}\right].$$

Substituting $\rho =0.6; {\widetilde{M}}_{0.6}=\left[\mathrm{4,8}\right],{\widetilde{N}}_{0.6}=\left[\mathrm{5,7}\right]$ Therefore, $Minimum\left\{{\widetilde{M}}_{0.6},{\widetilde{N}}_{0.6}\right\}=Minimum\left\{\left[\mathrm{4,8}\right],\left[\mathrm{5,7}\right]\right\}=\left[Minimum \left\{\mathrm{4,5}\right\}, Minimum\left\{\mathrm{8,7}\right\}\right]=\left[\mathrm{4,7}\right]$

$$Maximum\left\{{\widetilde{M}}_{0.6},{\widetilde{N}}_{0.6}\right\}=Maximum\left\{\left[\mathrm{4,8}\right],\left[\mathrm{5,7}\right]\right\}=\left[Maximum \left\{\mathrm{4,5}\right\}, Maximum\left\{\mathrm{8,7}\right\}\right]=\left[\mathrm{5,8}\right]$$

It is obvious that $Minimum\left\{{\widetilde{M}}_{0.6},{\widetilde{N}}_{0.6}\right\}\ne {\widetilde{M}}_{0.6}, Minimum\left\{{\widetilde{M}}_{0.6},{\widetilde{N}}_{0.6}\right\}\ne {\widetilde{N}}_{0.6}$ and $Maximum\left\{{\widetilde{M}}_{0.6},{\widetilde{N}}_{0.6}\right\}\ne {\widetilde{M}}_{0.6}, Maximum\left\{{\widetilde{M}}_{0.6},{\widetilde{N}}_{0.6}\right\}\ne {\widetilde{N}}_{0.6}$.

Similarly, it can be easily verified that $Minimum\left\{{\widetilde{M}}_{0.5},{\widetilde{N}}_{0.5}\right\}\ne {\widetilde{M}}_{0.5}, Minimum\left\{{\widetilde{M}}_{0.5},{\widetilde{N}}_{0.5}\right\}\ne {\widetilde{N}}_{0.5}$ and $Maximum\left\{{\widetilde{M}}_{0.5},{\widetilde{N}}_{0.5}\right\}\ne {\widetilde{M}}_{0.5}, Maximum\left\{{\widetilde{M}}_{0.5},{\widetilde{N}}_{0.5}\right\}\ne {\widetilde{N}}_{0.5}$ and $Minimum\left\{{\widetilde{M}}_{0.4},{\widetilde{N}}_{0.4}\right\}\ne {\widetilde{M}}_{0.4}, Minimum\left\{{\widetilde{M}}_{0.4},{\widetilde{N}}_{0.4}\right\}\ne {\widetilde{N}}_{0.4}, Maximum\left\{{\widetilde{M}}_{0.4},{\widetilde{N}}_{0.4}\right\}\ne {\widetilde{M}}_{0.4},Maximum\left\{{\widetilde{M}}_{0.4},{\widetilde{N}}_{0.4}\right\}\ne {\widetilde{N}}_{0.4}$.

5 Reason for the invalidity of Seikh and Dutta’s second approach

It is obvious from Sect. 3.2 that Seikh and Dutta’s (2022) second approach is not valid. The reason for the invalidity of Seikh and Dutta’s (2022) second approach is that in Seikh and Dutta’s (2022) second approach some mathematically incorrect results are considered to transform the SVTrN NLPPs (P5) and (P6) into the CLPPs (P9) and (P10) respectively. To point out the mathematically incorrect results, considered in Seikh and Dutta’s (2022) second approach, there is a need to discuss the transformation method, used in Seikh and Dutta’s (2022) second approach, to transform the SVTrN NLPPs (P5) and (P6) into the CLPPs (P9) and (P10) respectively. Therefore, in this section, firstly, the transformation method, used in Seikh and Dutta’s (2022) second approach, is discussed. Then, the mathematically incorrect result, considered in the transformation method, is discussed.

5.1 Transformation method used in Seikh and Dutta’s second approach

In Seikh and Dutta’s (2022) second approach, the following method is used to transform the SVTrN NLPPs (P5) and (P6) into the CLPPs (P9) and (P10) respectively.

Step 1: According to the second-ranking method, discussed in Sect. 2.1.2, to find an optimal solution of the SVTrN NLPPs (P5) and (P6) is equivalent to find an optimal solution of the crisp NLPPs (P31) and (P32) respectively.

Problem (P31)

$$Maximize \left\{\begin{array}{c}Minimize \left\{{\Pi }_{\alpha }\left(\sum\nolimits_{j=1}^{n}\left(\sum\nolimits_{i=1}^{m}\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\rangle {u}_{i}\right){v}_{j}\right)\right\}\\ {\text{Subject to}} \\ \sum_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\nolimits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P32)

$$Minimize \left\{\begin{array}{c}Maximize \left\{{\Pi }_{\alpha }\left(\sum\nolimits_{i=1}^{m}\left(\sum\nolimits_{j=1}^{n}\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\rangle {v}_{j}\right){u}_{i}\right)\right\}\\ {\text{Subject to}} \\ \sum\nolimits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0,i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\nolimits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0,j=\mathrm{1,2},\dots ,n.$$

Step 2: Using the expressions (17) and (18), to find an optimal solution of the crisp NLPPs (P31) and (P32) is equivalent to find an optimal solution of the crisp NLPPs (P33) and (P34) respectively.

$${\Pi }_{\alpha }\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)=\sum\limits_{j=1}^{n}{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right){v}_{j}$$

(17)

$${\Pi }_{\alpha }\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)=\sum\limits_{i=1}^{m}{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right){u}_{i}$$

(18)

Problem (P33)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right){v}_{j}\right\}\\ {\text{Subject to}}\\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P34)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right){u}_{i}\right\}\\ {\text{Subject to}}\\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 3: Since,

$$\sum\limits_{j=1}^{n}{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right){v}_{j}$$

is a convex linear combination of

$${\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right), j=\mathrm{1,2},\dots ,n$$

and

$$\sum\limits_{i=1}^{m}{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right){u}_{i}$$

is a convex linear combination of

$${\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right), i=\mathrm{1,2},\dots ,m$$

. So, to find an optimal solution of the crisp NLPPs (P33) and (P34) is equivalent to find an optimal solution of the crisp NLPPs (P35) and (P36) respectively.

Problem (P35)

$$Maximize \left\{{Minimum}_{1\le j\le n}\left\{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)\right\}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P36)

$$Minimize \left\{{Maximum}_{1\le i\le m}\left\{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)\right\}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 4: Assuming

$${Minimum}_{1\le j\le n}\left\{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)\right\}={\Omega }_{1};$$

$${Maximum}_{1\le i\le m}\left\{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)\right\}={\Omega }_{2},$$

to find an optimal solution of the crisp NLPPs (P35) and (P36) is equivalent to find an optimal solution of the CLPPs (P37) and (P38) respectively.

Problem (P37)

$$Maximize \left\{{\Omega }_{1}\right\}$$

Subject to

$${\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\nolimits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\nolimits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\nolimits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\nolimits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)\ge {\Omega }_{1}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P38)

$$Minimize \left\{{\Omega }_{2}\right\}$$

Subject to

$${\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)\le {\Omega }_{2}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 5: Using the expressions (19) and (20), to find an optimal solution of the CLPPs (P37) and (P38) is equivalent to find an optimal solution of the CLPPs (P39) and (P40), respectively.

$${\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{ 1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{ 1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{ 1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)={\upgamma }_{j}\left(\frac{\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i}+2\left(\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i}+\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i}\right)+\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}}{6}\right)$$

(19)

where,

$${\gamma }_{j}=\left[\alpha {\left({minimum}_{ 1\le i\le m}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ 1\le i\le m}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ 1\le i\le m}\left\{{n}_{ij}\right\}\right)}^{2}\right]$$

$${\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{ 1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{ 1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{ 1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)={\upgamma }_{i}\left(\frac{\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j}+2\left(\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j}+\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j}\right)+\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}}{6}\right)$$

(20)

where,

$${\gamma }_{i}=\left[\alpha {\left({minimum}_{ 1\le j\le n}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ 1\le j\le n}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ 1\le j\le n}\left\{{n}_{ij}\right\}\right)}^{2}\right]$$

Problem (P39)

$$Maximize \left\{{\Omega }_{1}\right\}$$

Subject to

$${\upgamma }_{j}\left(\frac{\sum\nolimits_{i=1}^{m}{a}_{ij1}{u}_{i}+2\left(\sum\nolimits_{i=1}^{m}{a}_{ij2}{u}_{i}+\sum\nolimits_{i=1}^{m}{a}_{ij3}{u}_{i}\right)+\sum\nolimits_{i=1}^{m}{a}_{ij4}{u}_{i}}{6}\right)\ge {\Omega }_{1}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (P40)

$$Minimize \left\{{\Omega }_{2}\right\}$$

Subject to

$${\upgamma }_{i}\left(\frac{\sum\nolimits_{j=1}^{n}{a}_{ij1}{v}_{j}+2\left(\sum\nolimits_{j=1}^{n}{a}_{ij2}{v}_{j}+\sum\nolimits_{j=1}^{n}{a}_{ij3}{v}_{j}\right)+\sum\nolimits_{j=1}^{n}{a}_{ij4}{v}_{j}}{6}\right)\le {\Omega }_{2}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 6: Using the expressions (21) and (22), to find an optimal solution of the CLPPs (P39) and (P40) is equivalent to find an optimal solution of the CLPPs (P9) and (P10).

$$\frac{\sum\nolimits_{i=1}^{m}{a}_{ij1}{u}_{i}+2\left(\sum\nolimits_{i=1}^{m}{a}_{ij2}{u}_{i}+\sum\nolimits_{i=1}^{m}{a}_{ij3}{u}_{i}\right)+\sum\nolimits_{i=1}^{m}{a}_{ij4}{u}_{i}}{6}=\sum\nolimits_{i=1}^{m}\left(\frac{{a}_{ij1}+2{a}_{ij2}+2{a}_{ij3}+{a}_{ij4}}{6}\right){u}_{i}$$

(21)

$$\frac{\sum\nolimits_{j=1}^{n}{a}_{ij1}{v}_{j}+2\left(\sum\nolimits_{j=1}^{n}{a}_{ij2}{v}_{j}+\sum\nolimits_{j=1}^{n}{a}_{ij3}{v}_{j}\right)+\sum\nolimits_{j=1}^{n}{a}_{ij4}{v}_{j}}{6}=\sum\nolimits_{j=1}^{n}\left(\frac{{a}_{ij1}+2{a}_{ij2}+2{a}_{ij3}+{a}_{ij4}}{6}\right){v}_{j}$$

(22)

5.2 Mathematically incorrect result considered in Seikh and Dutta’s second approach

Seikh and Dutta’s (2022) second approach is not valid as the following mathematically incorrect result is used in it.

It is obvious that in Step 2 of Seikh and Dutta’s (2022) second approach, discussed in Sect. 5.1, the expression (17) i.e.,

$${\Pi }_{\alpha }\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)$$

$$=\sum\limits_{j=1}^{n}\left({\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right)\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)\right){v}_{j}$$

is used to transform the crisp NLPP (P31) into the crisp NLPP (P33).

However, the expression (17) is mathematically incorrect and the expression (23) represents the mathematically correct form of the expression (17). So, the crisp NLPP (P31) is not equivalent to the crisp NLPP (P33).

$${\Pi }_{\alpha }\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)=\sum\limits_{j=1}^{n}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right){v}_{j}$$

(23)

where

$${\gamma }_{j}=\left[\alpha {\left({minimum}_{1\le i\le m}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\right)}^{2}\right]$$

and

$$\gamma =\left[\alpha {\left({minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}\right)}^{2},\left(1-\alpha \right){\left(1-{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}\right)}^{2},\left(1-\alpha \right){\left(1-{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\right)}^{2}\right]$$

The following clearly indicates that the above claim is valid.

$${\Pi }_{\alpha }\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)=={\Pi }_{\alpha }\left(\Bigg\langle \left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i}{v}_{j},\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}{v}_{j}\right);\right.$$

$$\left.{minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\Bigg\rangle \right)$$

$$=\gamma \left(\frac{\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i}{v}_{j}+2\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i}{v}_{j}+\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i}{v}_{j}\right)+\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}{v}_{j}}{6}\right)$$

$$=\gamma \sum\limits_{j=1}^{n}\left(\frac{\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i}+2\left(\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i}+\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i}\right)+\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}}{6}\right){v}_{j}$$

$$=\sum\limits_{j=1}^{n}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right){v}_{j}$$

Hence,

$${\Pi }_{\alpha }\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)=\sum\limits_{j=1}^{n}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right){v}_{j}$$

Furthermore, it is obvious that in Step 2 of Seikh and Dutta’s (2022) second approach, discussed in Sect. 5.1, the expression (18) i.e.,

$${\Pi }_{\alpha }\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)=\sum\limits_{i=1}^{m}{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right){u}_{i}$$

is used to transform the crisp NLPP (P32) into crisp NLPP (P34).

While, it can be easily verified that the expression (18) is mathematically incorrect and the expression (24) represents the correct form of the expression (18). So, the crisp NLPP (P32) is not equivalent to the crisp NLPP (P34).

$${\Pi }_{\alpha }\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)=\gamma \sum\limits_{i=1}^{m}\left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j} ,\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{i}}\right){u}_{i}$$

(24)

6 Proposed modified approaches

It is obvious from Sects. 4.2 and 5.2 that neither Brikaa’s (2022) approach nor Seikh and Dutta’s (2022) second approach is valid. In this section, an approach by modifying Brikaa’s (2022) approach as well as an approach by modifying Seikh and Dutta’s (2022) second approach is proposed. The origin of the CLPPs, used in the proposed modified approaches, is discussed in Appendix A and Appendix B.

6.1 Proposed modified approach-I

The following modified approach, corresponding to Brikaa’s (2022) approach, is proposed to find the optimal strategies ${u}_{i}, i=\mathrm{1,2},\dots ,m$ of Player-I, the optimal strategies ${v}_{j}, j=\mathrm{1,2},\dots ,n$ of Player-II, the crisp value of the game (minimum expected gain) of Player-I and the crisp value of the game (maximum expected loss) of Player-II.

Step 1: Find an optimal solution $\theta , {u}_{i}, i=\mathrm{1,2},\dots ,m$ of the CLPP (P41) for some specific values of $\rho \in \left[0, {minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}\right],\sigma \in [{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}, 1]$ and $\tau \in \left[{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}, 1\right].$

Problem (P41)

$$Maximize \left\{\theta \right\}$$

Subject to

$$\sum\limits_{i=1}^{m}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){u}_{i}\ge \theta , j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

where

$${\left({b}_{ij}\right)}_{l\rho }=\frac{\left({minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}-\rho \right){a}_{ij1}+\rho \left({a}_{ij2}\right)}{{minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}}, {\left({b}_{ij}\right)}_{r\rho }=\frac{\left({minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}-\rho \right){a}_{ij4}+\rho \left({a}_{ij3}\right)}{{minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}},$$

$${\left({b}_{ij}\right)}_{l\sigma }=\frac{\left(1-\sigma \right){a}_{ij2}+\left(\sigma -{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}\right){a}_{ij1}}{1-{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}},{\left({b}_{ij}\right)}_{r\sigma }=\frac{\left(1-\sigma \right){a}_{ij3}+\left(\sigma -{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}\right){a}_{ij4}}{1-{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}},$$

$${\left({b}_{ij}\right)}_{l\tau }=\frac{\left(1-\tau \right){a}_{ij2}+\left(\tau -{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\right){a}_{ij1}}{1-{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}}\mathrm{and }{\left({b}_{ij}\right)}_{r\tau }=\frac{\left(1-\tau \right){a}_{ij3}+\left(\tau -{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\right){a}_{ij4}}{1-{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}}.$$

Step 2: Find an optimal solution $\phi , {v}_{j}, j=\mathrm{1,2},...,n$ of the CLPP (P42) for some specific values of $\rho \in \left[0, {minimum}_{\begin{array}{l}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}\right],\sigma \in [{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}, 1]$ and $\tau \in \left[{maximum}_{\begin{array}{l}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}, 1\right].$

Problem (P42)

$$Minimize \left\{\phi \right\}$$

Subject to

$$\sum\limits_{j=1}^{n}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){v}_{j}\le \phi , i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

where,

${\left({b}_{ij}\right)}_{l\rho },{\left({b}_{ij}\right)}_{l\sigma },{\left({b}_{ij}\right)}_{l\tau },{\left({b}_{ij}\right)}_{r\rho },{\left({b}_{ij}\right)}_{r\sigma },{\left({b}_{ij}\right)}_{r\tau }$ are the same as defined in Step 1.

Step 3: The optimal value of ${u}_{i},i=\mathrm{1,2},\dots ,m,$ obtained in Step 1, represents the optimal probability for selecting the ${i}{\text{th}}$ strategy by Player-I and the optimal value of ${v}_{j},j=\mathrm{1,2},\dots ,n,$ obtained in Step 2, represents the optimal probability for selecting the ${j}{\text{th}}$ strategy by Player-II for the considered SVTrN matrix game.

Step 4: The optimal value of $\theta ,$ obtained in Step 1, represents the crisp value of the game (minimum expected gain) of Player-I and the optimal value of $\phi ,$ obtained in Step 2, represents the crisp value of the game (maximum expected loss) of Player-II.

6.2 Proposed modified approach-II

The following modified approach, corresponding to Seikh and Dutta’s (2022) second approach, is proposed to find the optimal strategies ${u}_{i}, i=\mathrm{1,2},\dots ,m$ of Player-I, find the optimal strategies ${v}_{j}, j=\mathrm{1,2},\dots ,n$ of Player-II, the crisp value of the game (minimum expected gain) of Player-I and the crisp value of the game (maximum expected loss) of Player-II.

Step 1: Find an optimal solution ${\Omega }_{1}, {u}_{i},i=\mathrm{1,2},\dots ,m$ of the CLPP (P43) for some specific values of $\alpha \in \left[0, 1\right].$

Problem (P43)

$$Maximize \left\{{\Omega }_{1}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}\gamma \left(\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}\right){u}_{i}\ge {\Omega }_{1}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

where,

$$\gamma =\left[\alpha {\left({minimum}_{\begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ \begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ \begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\right)}^{2}\right]$$

Step 2: Find an optimal solution ${\Omega }_{2}, {v}_{j}, j=\mathrm{1,2},...,n$ of the CLPP (P44) for some specific values of $\alpha \in \left[0, 1\right].$

Problem (P44)

$$Minimize \left\{{\Omega }_{2}\right\}$$

Subject to.

$$\sum\limits_{j=1}^{n}\gamma \left(\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}\right){v}_{j}\le {\Omega }_{2}, i=\mathrm{1,2},\dots ,m$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

where,

$$\gamma =\left[\alpha {\left({minimum}_{\begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ \begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ \begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\right)}^{2}\right]$$

Step 3: The optimal value of ${u}_{i},i=\mathrm{1,2},\dots ,m,$ obtained in Step 1, represents the optimal probability for selecting the ${i}{\text{th}}$ strategy by Player-I and the optimal value of ${v}_{j}, j=\mathrm{1,2},\dots ,n,$ obtained in Step 2, represents the optimal probability for selecting the ${j}{\text{th}}$ strategy by Player-II for the considered SVTrN matrix game.

Step 4: The optimal value of ${\Omega }_{1},$ obtained in Step 1, represents the crisp value of the game (minimum expected gain) of Player-I and the optimal value of ${\Omega }_{2},$ obtained in Step 2, represents the crisp value of the game (maximum expected loss) of Player-II.

7 Validity of the proposed modified approaches

In this section, it is proved that the proposed modified approaches are valid.

7.1 Validity of the proposed modified approach-I

It is pertinent to mention that the proposed modified approach-I will be valid only if.

• (i) The CLPPs (P41) and (P42) are equivalent to the interval-valued NLPPs (P15) and (P16), respectively.

• (ii) The CLPPs (P41) and (P42) represent the primal–dual pair.

Statement (i) is proved in Appendix A whereas; statement (ii) is proved in this section.

Replacing the unrestricted decision variables $\theta$ and $\phi$ with ${\theta }_{1}-{\theta }_{2}$ and ${\phi }_{1}-{\phi }_{2}$ respectively, where ${\theta }_{1}\ge 0, {\theta }_{2}\ge 0,{\phi }_{1}\ge 0, {\phi }_{2}\ge 0,$ the CLPPs (P41) and (P42) are transformed into the CLPPs (P41_1) and (P42_1) respectively.

Problem (P41_1)

$$Maximize \left\{{\theta }_{1}-{\theta }_{2}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){u}_{i}\ge {\theta }_{1}-{\theta }_{2}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}\le 1, \sum\limits_{i=1}^{m}{u}_{i}\ge 1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m,$$

$${\theta }_{1}\ge 0, {\theta }_{2}\ge 0.$$

Problem (P42_1)

$$Minimize \left\{{\phi }_{1}-{\phi }_{2}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){v}_{j}\le {\phi }_{1}-{\phi }_{2}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}\le 1, \sum\limits_{j=1}^{n}{v}_{j}\ge 1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n,$$

$${\phi }_{1}\ge 0,{\phi }_{2}\ge 0.$$

Converting the sign of all the constraints of the CLPP (P41_1) into $\le$, it is transformed into the CLPP (P41_2) and converting the sign of all the constraints of the CLPP (P42_1) into $\ge$, it is transformed into the CLPP (P42_2).

Problem (P41_2)

$$Maximize \left\{{\theta }_{1}-{\theta }_{2}\right\}$$

Subject to

$$-\sum\limits_{i=1}^{m}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){u}_{i}\le -{\theta }_{1}+{\theta }_{2}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}\le 1,-\sum\limits_{i=1}^{m}{u}_{i}\le -1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m,$$

$${\theta }_{1}\ge 0, {\theta }_{2}\ge 0.$$

Problem (P42_2)

$$Minimize \left\{{\phi }_{1}-{\phi }_{2}\right\}$$

Subject to

$$-\sum\limits_{j=1}^{n}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){v}_{j}\ge -{\phi }_{1}+{\phi }_{2}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}\ge 1,-\sum\limits_{j=1}^{n}{v}_{j}\ge -1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n,$$

$${\phi }_{1}\ge 0,{\phi }_{2}\ge 0.$$

Assuming ${\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }={A}_{ij}$ and ${\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }={B}_{ij}$, the CLPP (P41_2) is transformed into the CLPP (P41_3) and the CLPP (P42_2) is transformed into the CLPP (P42_3).

Problem (P41_3)

$$Maximize \left\{{\theta }_{1}-{\theta }_{2}\right\}$$

Subject to

$$-\sum\limits_{i=1}^{m}\frac{1}{12}\left(3{A}_{ij}+{B}_{ij}\right){u}_{i}\le -{\theta }_{1}+{\theta }_{2}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}\le 1,-\sum\limits_{i=1}^{m}{u}_{i}\le -1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m,$$

$${\theta }_{1}\ge 0, {\theta }_{2}\ge 0.$$

Problem (P42_3)

$$Minimize \left\{{\phi }_{1}-{\phi }_{2}\right\}$$

Subject to

$$-\sum\limits_{j=1}^{n}\frac{1}{12}\left(3{A}_{ij}+{B}_{ij}\right){v}_{j}\ge -{\phi }_{1}+{\phi }_{2}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}\ge 1,-\sum\limits_{j=1}^{n}{v}_{j}\ge -1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n,$$

$${\phi }_{1}\ge 0,{\phi }_{2}\ge 0.$$

The CLPP (P41_4) and the CLPP (P42_4) represent the matrix form of the CLPP (P41_3) and the CLPP (P42_3) respectively.

Problem (41_4)

$$Maximize \left\{CX\right\}$$

Subject to

$$AX\le b,X\ge 0.$$

Problem (42_4)

$$Minimize \left\{{b}^{T}Y\right\}$$

Subject to

$${A}^{T}Y\ge {C}^{T},Y\ge 0.$$

where,

$$C={\left[0, 0,\dots ,0, 1,-1 \right]}_{1\times \left(m+2\right)},X={\left[\begin{array}{c}0\\ 0\\ .\\ .\\ 0\\ {\theta }_{1}\\ {\theta }_{2}\end{array}\right]}_{\left(m+2\right)\times 1}, b={\left[\begin{array}{c}0\\ 0\\ .\\ .\\ 0\\ 1\\ -1\end{array}\right]}_{\left(n+2\right)\times 1},Y={\left[\begin{array}{c}0\\ 0\\ .\\ .\\ 0\\ {\phi }_{1}\\ {\phi }_{2}\end{array}\right]}_{\left(n+2\right)\times 1}$$

$$A={\left[\begin{array}{llllll}-\frac{1}{12}\left(3{{A}_{11}+B}_{11 }\right)& -\frac{1}{12}\left(3{{A}_{21}+B}_{21 }\right)& \dots & -\frac{1}{12}\left(3{{A}_{m1}+B}_{m1 }\right)& 1& -1\\ -\frac{1}{12}\left(3{{A}_{12}+B}_{12 }\right)& -\frac{1}{12}\left(3{{A}_{22}+B}_{22 }\right)& \dots & -\frac{1}{12}\left(3{{A}_{m2}+B}_{m2 }\right)& 1& -1\\ ...& \dots & \dots & \dots & \dots & \dots \\ -\frac{1}{12}\left(3{{A}_{1n}+B}_{1n }\right)& -\frac{1}{12}\left(3{{A}_{2n}+B}_{2n }\right)& \dots & -\frac{1}{12}\left(3{{A}_{mn}+B}_{mn }\right)& 1& -1\\ 1& 1& \dots & 1& 0& 0\\ -1& -1& \dots & -1& 0& 0\end{array}\right]}_{\left(n+2\right)\times \left(m+2\right)}$$

The CLPP (P41_4) and the CLPP (P42_4) represent the primal–dual pair and hence, the CLPPs (P41) and (P42) represent the primal–dual pair.

7.2 Validity of the proposed modified approach-II

It is pertinent to mention that the proposed modified approach-II will be valid only if.

• (i) The CLPPs (P43) and (P44) are equivalent to the crisp NLPPs (P31) and (P32) respectively.

• (ii) The CLPPs (P43) and (P44) represent the primal–dual pair.

Statement (i) is proved in Appendix B whereas; statement (ii) is proved in this section.

Replacing the unrestricted decision variables ${\Omega }_{1}$ and ${\Omega }_{2}$ with ${\Omega }_{11}-{\Omega }_{12}$ and ${\Omega }_{21}-{\Omega }_{22}$ respectively, where ${\Omega }_{11}\ge 0,{\Omega }_{12}\ge 0,{\Omega }_{21}\ge 0,{\Omega }_{22}\ge 0$ the CLPPs (P43) and (P44) are transformed into the CLPPs (P43_1) and (P44_1) respectively.

Problems (P43_1)

$$Maximize \left\{{\Omega }_{11}-{\Omega }_{12}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}\gamma \left(\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}\right){u}_{i}\ge {\Omega }_{11}-{\Omega }_{12}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}\le 1,\sum\limits_{i=1}^{m}{u}_{i}\ge 1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m,$$

$${\Omega }_{11}\ge 0, {\Omega }_{12}\ge 0.$$

Problems (P44_1)

$$Minimize \left\{{\Omega }_{21}-{\Omega }_{22}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}\gamma \left(\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}\right){v}_{j}\le {\Omega }_{21}-{\Omega }_{22}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}\le 1, \sum\limits_{j=1}^{n}{v}_{j}\ge 1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n,$$

$${\Omega }_{21}\ge 0, {\Omega }_{22}\ge 0.$$

Converting the sign of all the constraints of the CLPP (P43_1) into $\le$, it is transformed into the CLPP (P43_2) and converting the sign of all the constraints of the CLPP (P44_1) into $\ge$, it is transformed into the CLPP (P44_2).

Problem (P43_2)

$$Maximize \left\{{\Omega }_{11}-{\Omega }_{12}\right\}$$

Subject to

$$-\sum\limits_{i=1}^{m}\gamma \left(\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}\right){u}_{i}\le -{\Omega }_{11}+{\Omega }_{12}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}\le 1, -\sum\limits_{i=1}^{m}{u}_{i}\le -1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m,$$

$${\Omega }_{11}\ge 0, {\Omega }_{12}\ge 0.$$

Problem (P44_2)

$$Minimize \left\{{\Omega }_{21}-{\Omega }_{22}\right\}$$

Subject to

$$-\sum\limits_{j=1}^{n}\gamma \left(\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}\right){v}_{j}\ge -{\Omega }_{21}+{\Omega }_{22}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}\ge 1, -\sum\limits_{j=1}^{n}{v}_{j}\ge -1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n,$$

$${\Omega }_{21}\ge 0, {\Omega }_{22}\ge 0.$$

Assuming $\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}={D}_{ij}$, the CLPP (P43_2) is transformed into the CLPP (P43_3) and the CLPP (P44_2) is transformed into the CLPP (P44_3).

Problem (P43_3)

$$Maximize \left\{{\Omega }_{11}-{\Omega }_{12}\right\}$$

Subject to

$$-\sum\limits_{i=1}^{m}\gamma \left({D}_{ij}\right){u}_{i}\le -{\Omega }_{11}+{\Omega }_{12}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}\le 1, -\sum\limits_{i=1}^{m}{u}_{i}\le -1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m,$$

$${\Omega }_{11}\ge 0, {\Omega }_{12}\ge 0.$$

Problem (P44_3)

$$Minimize \left\{{\Omega }_{21}-{\Omega }_{22}\right\}$$

Subject to

$$-\sum\limits_{j=1}^{n}\gamma \left({D}_{ij}\right){v}_{j}\ge -{\Omega }_{21}+{\Omega }_{22}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}\ge 1, -\sum\limits_{j=1}^{n}{v}_{j}\ge -1, {v}_{j}\ge 0, \quad j=\mathrm{1,2},\dots ,n,$$

$${\Omega }_{21}\ge 0, {\Omega }_{22}\ge 0.$$

The CLPPs (P43_4) and (P44_4) represent the matrix form of the CLPPs (P43_3) and (P44_3), respectively.

Problem (43_4)

$$Maximize \left\{CX\right\}$$

Subject to

$$AX\le b,X\ge 0.$$

Problem (44_4)

$$Minimize \left\{{b}^{T}Y\right\}$$

Subject to

$${A}^{T}Y\ge {C}^{T},Y\ge 0.$$

where,

$$C={\left[0, 0,\dots ,0, 1,-1 \right]}_{1\times \left(m+2\right)},X={\left[\begin{array}{c}0\\ 0\\ .\\ .\\ 0\\ {\Omega }_{11}\\ {\Omega }_{12}\end{array}\right]}_{\left(m+2\right)\times 1}, b={\left[\begin{array}{c}0\\ 0\\ .\\ .\\ 0\\ 1\\ -1\end{array}\right]}_{\left(n+2\right)\times 1},Y={\left[\begin{array}{l}0\\ 0\\ .\\ .\\ 0\\ {\Omega }_{21}\\ {\Omega }_{22}\end{array}\right]}_{\left(n+2\right)\times 1},$$

$$A={\left[\begin{array}{llllll}{-\gamma D}_{11}& {-\gamma D}_{21}& \dots & {-\gamma D}_{m1}& 1& -1\\ {-\gamma D}_{12}& {-\gamma D}_{22}& \dots & {-\gamma D}_{m2}& 1& -1\\ ...& \dots & \dots & \dots & \dots & \dots \\ {-\gamma D}_{1n}& {-\gamma D}_{2n}& \dots & {-\gamma D}_{mn}& 1& -1\\ 1& 1& \dots & 1& 0& 0\\ -1& -1& \dots & -1& 0& 0\end{array}\right]}_{\left(n+2\right)\times \left(m+2\right)}.$$

The CLPPs (P43_4) and (P44_4) represent the primal–dual pair and hence, the CLPPs (P43) and (P44) represent the primal–dual pair.

8 Correct results of the existing SVTrN matrix game

As discussed in Sect. 3, the results of the existing SVTrN matrix game (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929), obtained by Brikaa (2022) as well as obtained by Seikh and Dutta (2022), are not correct. In this section, the correct results are obtained by the proposed modified approaches.

8.1 Correct results by the proposed modified approach-I

Using the proposed modified approach-I, the correct results of the existing SVTrN matrix game (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929) can be obtained as follows:

According to the proposed modified approach-I,

• (i) An optimal solution ${u}_{i}, i=\mathrm{1,2},\dots ,m$ of the CLPP (P41) represents the optimal probability for selecting the ${i}{\text{th}}$ strategy by Player-I.

• (ii) An optimal solution ${v}_{j}, j=\mathrm{1,2},\dots ,n$ of the CLPP (P42) represents the optimal probability for selecting the ${j}{\text{th}}$ strategy by Player-II.

Since, for the existing SVTrN matrix game (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929), the CLPPs (P41) and (P42) are transformed into the CLPPs (P45) and (P46) respectively. So, to find an optimal solution for Player-I and to find an optimal solution for Player-II of the existing SVTrN matrix game (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929), there is a need to solve the CLPPs (P45) and (P46) respectively.

Problem (P45)

$$Maximize \left\{\theta \right\}$$

Subject to

$$\frac{1}{12}\left(3\left(\frac{\left(0.5-\rho \right)\left(175{u}_{1}+125{u}_{2}\right)+\rho \left(177{u}_{1}+128{u}_{2}\right)}{0.5}+\frac{\left(1-\sigma \right)\left(177{u}_{1}+128{u}_{2}\right)+\left(\sigma -0.4\right)\left(175{u}_{1}+125{u}_{2}\right)}{1-0.4}+\left.\frac{\left(1-\tau \right)\left(177{u}_{1}+128{u}_{2}\right)+\left(\tau -0.5\right)\left(175{u}_{1}+125{u}_{2}\right)}{1-0.5}\right)+\left(\frac{\left(0.5-\rho \right)\left(190{u}_{1}+140{u}_{2}\right)+\rho \left(180{u}_{1}+132{u}_{2}\right)}{0.5}+\right.\right.\right.$$

$$\frac{\left(1-\sigma \right)\left(180{u}_{1}+132{u}_{2}\right)+\left(\sigma -0.4\right)\left(190{u}_{1}+140{u}_{2}\right)}{1-0.4}+\left.\left.\frac{\left(1-\tau \right)\left(180{u}_{1}+132{u}_{2}\right)+\left(\tau -0.5 \right)\left(190{u}_{1}+140{u}_{2}\right)}{1-0.5}\right)\right)\ge \theta ,$$

$$\frac{1}{12}\left(3\left(\frac{\left(0.5-\rho \right)\left(150{u}_{1}+175{u}_{2}\right)+\rho \left(153{u}_{1}+185{u}_{2}\right)}{0.5}+\frac{\left(1-\sigma \right)\left(153{u}_{1}+185{u}_{2}\right)+\left(\sigma -0.4\right)\left(150{u}_{1}+175{u}_{2}\right)}{1-0.4}+\left.\frac{\left(1-\tau \right)\left(153{u}_{1}+185{u}_{2}\right)+\left(\tau -0.5\right)\left(150{u}_{1}+175{u}_{2}\right)}{1-0.5}\right)+\left(\frac{\left(0.5-\rho \right)\left(158{u}_{1}+200{u}_{2}\right)+\rho \left(156{u}_{1}+195{u}_{2}\right)}{0.5}+\right.\right.\right.$$

$$\frac{\left(1-\sigma \right)\left(156{u}_{1}+195{u}_{2}\right)+\left(\sigma -0.4\right)\left(158{u}_{1}+200{u}_{2}\right)}{1-0.4}+\left.\left.\frac{\left(1-\tau \right)\left(156{u}_{1}+195{u}_{2}\right)+\left(\tau -0.5 \right)\left(158{u}_{1}+200{u}_{2}\right)}{1-0.5}\right)\right)\ge \theta ,$$

$${u}_{1}+{u}_{2}=1,{u}_{1}\ge 0, {u}_{2}\ge 0.$$

Problem (P46)

$$Minimize \left\{\phi \right\}$$

Subject to

$$\frac{1}{12}\left(3\left(\frac{\left(0.5-\rho \right)\left(175{v}_{1}+150{v}_{2}\right)+\rho \left(177{v}_{1}+153{v}_{2}\right)}{0.5}+\frac{\left(1-\sigma \right)\left(177{v}_{1}+153{v}_{2}\right)+\left(\sigma -0.4\right)\left(175{v}_{1}+150{v}_{2}\right)}{1-0.4}+\left.\frac{\left(1-\tau \right)\left(177{v}_{1}+153{v}_{2}\right)+\left(\tau -0.5\right)\left(175{v}_{1}+150{v}_{2}\right)}{1-0.5}\right)+\left(\frac{\left(0.5-\rho \right)\left(190{v}_{1}+158{v}_{2}\right)+\rho \left(180{v}_{1}+156{v}_{2}\right)}{0.5}+\right.\right.\right.$$

$$\frac{\left(1-\sigma \right)\left(180{v}_{1}+156{v}_{2}\right)+\left(\sigma -0.4 \right)\left(190{v}_{1}+158{v}_{2}\right)}{1-0.4}+\left.\left.\frac{\left(1-\tau \right)\left(180{v}_{1}+156{v}_{2}\right)+\left(\tau -0.5 \right)\left(190{v}_{1}+158{v}_{2}\right)}{1-0.5}\right)\right)\le \phi ,$$

$$\frac{1}{12}\left(3\left(\frac{\left(0.5-\rho \right)\left(125{v}_{1}+175{v}_{2}\right)+\rho \left(128{v}_{1}+185{v}_{2}\right)}{0.5}+\frac{\left(1-\sigma \right)\left(128{v}_{1}+185{v}_{2}\right)+\left(\sigma -0.4\right)\left(125{v}_{1}+175{v}_{2}\right)}{1-0.4}+\left.\frac{\left(1-\tau \right)\left(128{v}_{1}+185{v}_{2}\right)+\left(\tau -0.5\right)\left(125{v}_{1}+175{v}_{2}\right)}{1-0.5}\right)+\left(\frac{\left(0.5-\rho \right)\left(140{v}_{1}+200{v}_{2}\right)+\rho \left(132{v}_{1}+195{v}_{2}\right)}{0.5}+\right.\right.\right.$$

$$\frac{\left(1-\sigma \right)\left(132{v}_{1}+195{v}_{2}\right)+\left(\sigma -0.4 \right)\left(140{v}_{1}+200{v}_{2}\right)}{1-0.4}+\left.\left.\frac{\left(1-\tau \right)\left(132{v}_{1}+195{v}_{2}\right)+\left(\tau -0.5 \right)\left(140{v}_{1}+200{v}_{2}\right)}{1-0.5}\right)\right)\le \phi ,$$

$${v}_{1}+{v}_{2}=1,{v}_{1}\ge 0, {v}_{2}\ge 0.$$

It can be easily verified that an optimal solution, shown in Table 4, is obtained on solving the CLPPs (P45) and (P46) corresponding to Player-I and Player-II respectively.

Table 4 An optimal solution of the CLPPs (P45) and (P46)

On substituting the obtained optimal values of ${u}_{1},{u}_{2},{v}_{1}$ and ${v}_{2}$ in the expression (25), the SVTrN numbers (representing the value of the game corresponding to different values of $\left(\rho ,\sigma ,\tau \right)$) are obtained.

$$\Bigg\langle \left(175, 177, 180, 190\right);\mathrm{0.6,0.3,0.3}\Bigg\rangle {u}_{1}{v}_{1}+\Bigg\langle \left(125, 128, 132, 140\right);\mathrm{0.9,0.1,0.5}\Bigg\rangle {u}_{2}{v}_{1}+\Bigg\langle \left(150, 153, 156, 158\right);\mathrm{0.5,0.2,0.3}\Bigg\rangle {u}_{1}{v}_{2}+\Bigg\langle \left(175, 185, 195, 200\right);\mathrm{0.5,0.4,0.5}\Bigg\rangle {u}_{2}{v}_{2}$$

(25)

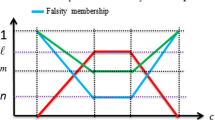
For example, on substituting ${u}_{1}=0.6625, {u}_{2}=0.3375, {v}_{1}=0.3691$ and ${v}_{2}=0.6309$ in the expression (25), the SVTrN number $\Bigg\langle \left(158.3222, 162.5681, 167.1832, 172.5256\right);\mathrm{0.5,0.4,0.5}\Bigg\rangle$ (shown in Fig. 1), representing the value of the game corresponding to $\left(\rho ,\sigma ,\tau \right) =(\mathrm{0,1},1)$, is obtained.

Fig. 1

SVTrN number (Value of the game) corresponding to $\left(\rho ,\sigma ,\tau \right) =(\mathrm{0,1},1)$

The SVTrN number $\Bigg\langle \left(158.3222, 162.5681, 167.1832, 172.5256\right);\mathrm{0.5,0.4,0.5}\Bigg\rangle$ represents that the value of the game is not less than $158.3222$ and not more than $172.5256$. The truth- membership value, the indeterminacy-membership value and the falsity-membership value for the value of game lying in the interval $[162.5681, 167.1832]$ are $0.5, 0.4$ and $0.5$ respectively.

8.2 Correct results by the proposed modified approach-II

Using the proposed modified approach-II, the correct results of the existing SVTrN matrix game (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929) can be obtained as follows:

According to the proposed modified approach-II,

• (i) An optimal solution ${u}_{i}, i=\mathrm{1,2},\dots ,m$ of the CLPP (P43) represents the optimal probability for selecting the ${i}{\text{th}}$ strategy by Player-I.

• (ii) An optimal solution ${v}_{j}, j=\mathrm{1,2},\dots ,n$ of the CLPP (P44) represents the optimal probability for selecting the ${j}{\text{th}}$ strategy by Player-II.

Since, for the existing SVTrN matrix game (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929), the CLPPs (P43) and (P44) are transformed into the CLPPs (P47) and (P48), respectively. So, to find an optimal solution for Player-I and to find an optimal solution for Player-II of the existing SVTrN matrix game (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929), there is a need to solve the CLPPs (P47) and (P48), respectively.

Problem (P47)

$$Maximize \left\{{\Omega }_{1}\right\}$$

Subject to.

$$\frac{\left(1079{u}_{1}+785{u}_{2}\right)\left(0.61-0.36\alpha \right)}{6}\ge {\Omega }_{1},$$

$$\frac{\left(926{u}_{1}+1135{u}_{2}\right)\left(0.61-0.36\alpha \right)}{6}\ge {\Omega }_{1},$$

$${u}_{1}+{u}_{2}=1, {u}_{1}\ge 0,{u}_{2}\ge 0.$$

Problem (P48)

$$Minimize\left\{{\Omega }_{2}\right\}$$

Subject to.

$$\frac{\left(1079{v}_{1}+926{v}_{2}\right)\left(0.61-0.36\alpha \right)}{6}\le {\Omega }_{2},$$

$$\frac{\left(785{v}_{1}+1135{v}_{2}\right)\left(0.61-0.36\alpha \right)}{6}\le {\Omega }_{2},$$

$${v}_{1}+{v}_{2}=1, {v}_{1}\ge 0,{v}_{2}\ge 0.$$

It can be easily verified that an optimal solution, shown in Table 5, is obtained on solving the CLPPs (P47) and (P48) corresponding to Player-I and Player-II respectively.

Table 5 An optimal solution of the CLPPs (P47) and (P48)

It is obvious from Table 5 that corresponding to all considered values of $\alpha$, ${u}_{1}=0.6958, {u}_{2}= 0.3042, {v}_{1}=0.4155$ and ${v}_{2}= 0.5845$ is obtained. On substituting the obtained optimal values of ${u}_{1}, {u}_{2}, {v}_{1}$ and ${v}_{2}$ in the expression (25), the SVTrN number $\Bigg\langle \left(158.5129, 162.4684, 166.8394, 172.4441\right);\mathrm{0.5,0.4,0.5}\Bigg\rangle$ (shown in Fig. 2), representing the value of the game corresponding to different values of $\alpha$, is obtained.

Fig. 2

SVTrN number (Value of the game) corresponding to different values of α

The SVTrN number $\Bigg\langle \left(158.5129, 162.4684, 166.8394, 172.4441\right);\mathrm{0.5,0.4,0.5}\Bigg\rangle$ represents that the value of the game is not less than $158.5129$ and not more than $172.4441$. The truth-membership value, the indeterminacy-membership value and the falsity-membership value for the value of game lying in the interval [162.4684, 166.8394] are $0.5, 0.4$ and $0.5$ respectively.

8.3 Validity of obtained results

It is obvious from Table 4 and Table 5 that corresponding to all the values of.

• (i) $\rho ,\sigma ,\tau$, the optimal value of $\theta$(minimum expected gain of Player-I) is the same as the optimal value of $\phi$ (maximum expected loss of Player-II).

• (ii) $\alpha$, the optimal value of ${\Omega }_{1}$ (minimum expected gain of Player-I) is the same as the optimal value of ${\Omega }_{2}$ (maximum expected loss of Player-II).

Hence, the obtained results are valid.s

9 Conclusions

It is pointed out that some mathematically incorrect results are considered in Brikaa’s (2022) approach as well as in Seikh and Dutta’s (2022) second approach to solve SVTrN matrix games. So, it is inappropriate to use Brikaa’s (2022) approach as well as Seikh and Dutta’s (2022) second approach to solve SVTrN matrix games. Also, a modified approach corresponding to Brikaa’s (2022) approach and a modified approach corresponding to Seikh and Dutta’s (2022) second approach are proposed. Furthermore, it is proved that the proposed modified approaches are valid. Finally, the correct result of the existing SVTrN matrix game (Seikh and Dutta 2022, Sect. 5.1, Example 1, p. 929) is obtained by the proposed modified approaches.

The proposed modified approaches cannot be used to solve SVTrN-constrained matrix games, SVTrN bi-matrix games and SVTrN-constrained bi-matrix games. In the future, one may propose approaches to solve these types of games by generalizing the proposed modified approaches. Also, the proposed modified approaches may be applied to solve real-life problems (Abbasi et al. 2021, 2023; Li et al. 2017, 2021; Yu et al. 2022).

Appendices

Appendix A

It is obvious from Sect. 6.1 that the base of the first proposed modified approach is the CLPPs (P41) and (P42). These CLPPs are obtained as follows:

Step 1: Using the expressions (11) and (12) (named as expressions (E.1) and (E.2), respectively), proved in Sect. 4.2.1, to find an optimal solution of the interval-valued NLPPs (P15) and (P16) is equivalent to find an optimal solution of the interval-valued NLPPs (A-1) and (A-2) respectively.

$${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{k}=\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}{\left({\widetilde{b}}_{ij}\right)}_{k}{u}_{i}\right){v}_{j}; k=\rho ,\sigma ,\tau $$

(E.1)

$${\left(\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}{v}_{j}\right)}_{k}=\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}{\left({\widetilde{b}}_{ij}\right)}_{k}{v}_{j}\right){u}_{i}; k=\rho ,\sigma ,\tau $$

(E.2)

where,

$${\widetilde{b}}_{ij}=\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{minimum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\},{maximum}_{\begin{array}{c}1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\Bigg\rangle $$

Problem (A-1)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}{\left({\widetilde{b}}_{ij}\right)}_{\rho }{u}_{i}\right){v}_{j}\right\}\\ Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}{\left({\widetilde{b}}_{ij}\right)}_{\sigma }{u}_{i}\right){v}_{j}\right\}\\ Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}{\left({\widetilde{b}}_{ij}\right)}_{\tau }{u}_{i}\right){v}_{j}\right\} \\ {\text{Subject to}} \\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (A-2)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}{\left({\widetilde{b}}_{ij}\right)}_{\rho }{v}_{j}\right){u}_{i}\right\}\\ Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}{\left({\widetilde{b}}_{ij}\right)}_{\sigma }{v}_{j}\right){u}_{i}\right\}\\ Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}{\left({\widetilde{b}}_{ij}\right)}_{\tau }{v}_{j}\right){u}_{i}\right\} \\ {\text{Subject to}} \\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 2: Using the expression (E.3) to find an optimal solution of the interval-valued NLPPs (A-1) and (A-2) is equivalent to find an optimal solution of the interval-valued NLPPs (A-3) and (A-4) respectively.

$${\left({\widetilde{b}}_{ij}\right)}_{k}=\left[{\left({b}_{ij}\right)}_{lk},{\left({b}_{ij}\right)}_{rk}\right];k=\rho ,\sigma ,\tau $$

(E.3)

Problem (A-3)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\left[{\left({b}_{ij}\right)}_{l\rho },{\left({b}_{ij}\right)}_{r\rho }\right]{u}_{i}\right){v}_{j}\right\}\\ Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\left[{\left({b}_{ij}\right)}_{l\sigma },{\left({b}_{ij}\right)}_{r\sigma }\right]{u}_{i}\right){v}_{j}\right\}\\ Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\left[{\left({b}_{ij}\right)}_{l\tau },{\left({b}_{ij}\right)}_{r\tau }\right]{u}_{i}\right){v}_{j}\right\}\\ {\text{Subject to}} \\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (A-4)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\left[{\left({b}_{ij}\right)}_{l\rho },{\left({b}_{ij}\right)}_{r\rho }\right]{v}_{j}\right){u}_{i}\right\}\\ Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\left[{\left({b}_{ij}\right)}_{l\sigma },{\left({b}_{ij}\right)}_{r\sigma }\right]{v}_{j}\right){u}_{i}\right\}\\ Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\left[{\left({b}_{ij}\right)}_{l\tau },{\left({b}_{ij}\right)}_{r\tau }\right]{v}_{j}\right){u}_{i}\right\}\\ {\text{Subject to}} \\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 3: Aggregating the objective function of the interval-valued NLPPs (A-3) and (A-4), to find an optimal solution of the interval-valued NLPPs (A-3) and (A-4) is equivalent to find an optimal solution of the interval-valued NLPPs (A-5) and (A-6) respectively.

Problem (A-5)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\left[\frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }}{3},\frac{{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{3}\right]{u}_{i}\right){v}_{j}\right\}\\ {\text{Subject to}}\\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (A-6)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\left[\frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }}{3},\frac{{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{3}\right]{v}_{j}\right){u}_{i}\right\}\\ {\text{Subject to}}\\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 4: To find an optimal solution of the interval-valued NLPPs (A-5) and (A-6) is equivalent to find an optimal solution of the crisp bi-objective NLPPs (A-7) and (A-8) respectively.

Problem (A-7)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\left\{\begin{array}{c}\frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }}{3},\\ \frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{l\tau }+{\left({b}_{ij}\right)}_{r\tau }}{6}\end{array}\right\}{u}_{i}\right){v}_{j}\right\}\\ {\text{Subject to}}\\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (A-8)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\left\{\begin{array}{c}\frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }}{3},\\ \frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{l\tau }+{\left({b}_{ij}\right)}_{r\tau }}{6}\end{array}\right\}{v}_{j}\right){u}_{i}\right\}\\ {\text{Subject to}}\\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 5: Using the weighted average method, to find an optimal solution of the crisp bi-objective NLPPs (A-7) and (A-8) is equivalent to find an optimal solution of the crisp NLPPs (A-9) and (A-11) or the equivalent crisp NLPPs (A-10) and (A-12) respectively.

Problem (A-9)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\frac{1}{2}\left(\begin{array}{c}\frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }}{3}+\\ \frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{l\tau }+{\left({b}_{ij}\right)}_{r\tau }}{6}\end{array}\right){u}_{i}\right){v}_{j}\right\}\\ {\text{Subject to}}\\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (A-10)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){u}_{i}\right){v}_{j}\right\}\\ {\text{Subject to}}\\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (A-11)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\frac{1}{2}\left(\begin{array}{c}\frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }}{3}+\\ \frac{{\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{l\tau }+{\left({b}_{ij}\right)}_{r\tau }}{6}\end{array}\right){v}_{j}\right){u}_{i}\right\}\\ {\text{Subject to}}\\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Problem (A-12)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){v}_{j}\right){u}_{i}\right\}\\ {\text{Subject to}}\\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 6: Since

$$\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){u}_{i}\right){v}_{j}$$

is a convex linear combination of

$$\sum\limits_{i=1}^{m}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){u}_{i}, j=\mathrm{1,2},\dots ,n$$

and

$$\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){v}_{j}\right){u}_{i}$$

is a convex linear combination of

$$\sum\limits_{j=1}^{n}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){v}_{j}, i=\mathrm{1,2},\dots ,m$$

. So, to find an optimal solution of the crisp NLPPs (A-10) and (A-12) is equivalent to find an optimal solution of the CLPPs (A-13) and (A-14).

Problem (A-13)

$$Maximize \left\{{Minimum}_{1\le j\le n}\left\{\sum\limits_{i=1}^{m}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){u}_{i}\right\}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0.$$

Problem (A-14)

$$Minimize \left\{{Maximum}_{1\le i\le m}\left\{\sum\limits_{j=1}^{n}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){v}_{j}\right\}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 7: Assuming

$${Minimum}_{1\le j\le n}\left\{\sum\limits_{i=1}^{m}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){u}_{i}\right\}=\theta $$

and

$${Maximum}_{1\le i\le m}\left\{\sum\limits_{j=1}^{n}\left(\frac{3\left({\left({b}_{ij}\right)}_{l\rho }+{\left({b}_{ij}\right)}_{l\sigma }+{\left({b}_{ij}\right)}_{l\tau }\right)+{\left({b}_{ij}\right)}_{r\rho }+{\left({b}_{ij}\right)}_{r\sigma }+{\left({b}_{ij}\right)}_{r\tau }}{12}\right){v}_{j}\right\}=\phi $$

to find an optimal solution of the CLPPs (A-13) and (A-14) is equivalent to find an optimal solution of the CLPPs (P41) and (P42) respectively.

Appendix B

It is obvious from Sect. 6.2 that the base of the second proposed modified approach is the CLPPs (P43) and (P44). These CLPPs are obtained as follows:

Step 1: Using the expressions (23) and (24) (named as (F.1) and (F.2) respectively) proved in Sect. 5.2, to find an optimal solution of the crisp NLPPs (P31) and (P32) is equivalent to find an optimal solution of the crisp NLPPs (B-1) and (B-2), respectively.

$${\Pi }_{\alpha }\left(\sum\limits_{j=1}^{n}\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {u}_{i}\right){v}_{j}\right)=$$

$$\sum\limits_{j=1}^{n}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right){v}_{j}$$

(F.1)

$${\Pi }_{\alpha }\left(\sum\limits_{i=1}^{m}\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle {v}_{j}\right){u}_{i}\right)=$$

$$\sum\limits_{i=1}^{m}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{i}}\right){u}_{i}$$

(F.2)

where,

${\gamma }_{i}=\left[\alpha {\left({minimum}_{1\le j\le n}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\right)}^{2}\right],$ ${\gamma }_{j}=\left[\alpha {\left({minimum}_{1\le i\le m}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\right)}^{2}\right]$ and

$$\gamma =\left[\alpha {\left({minimum}_{\begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{l}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ \begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{m}_{ij}\right\}\right)}^{2}+\left(1-\alpha \right){\left(1-{maximum}_{ \begin{array}{c} 1\le i\le m\\ 1\le j\le n\end{array}}\left\{{n}_{ij}\right\}\right)}^{2}\right]$$

Problem (B-1)

$$Maximize \left\{\begin{array}{c}Minimize\left\{\sum\limits_{j=1}^{n}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right){v}_{j}\right\}\\ {\text{Subject to}}\\ \sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n\end{array}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (B-2)

$$Minimize \left\{\begin{array}{c}Maximize\left\{\sum\limits_{i=1}^{m}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{i}}\right){u}_{i}\right\}\\ {\text{Subject to}}\\ \sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m\end{array}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 2: Since,

$$\sum\limits_{j=1}^{n}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right){v}_{j}$$

is a convex linear combination of

$$\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right), j=\mathrm{1,2},\dots ,n$$

and

$$\sum\limits_{i=1}^{m}\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{i}}\right){u}_{i}$$

is a convex linear combination of

$$\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{i}}\right), i=\mathrm{1,2},\dots ,m$$

. So, to find an optimal solution of the crisp NLPPs (B-1) and (B-2) is equivalent to find an optimal solution of the crisp NLPPs (B-3) and (B-4), respectively.

Problem (B-3)

$$Maximize \left\{{Minimum}_{1\le j\le n}\left\{\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right)\right\}\right\}$$

Subject to

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (B-4)

$$Minimize \left\{{Maximum}_{1\le i\le m}\left\{\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{i}}\right)\right\}\right\}$$

Subject to

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 3: Assuming,

$${Minimum}_{1\le j\le n}\left\{\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right)\right\}={\Omega }_{1}$$

and

$${Maximum}_{1\le i\le m}\left\{\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{i}}\right)\right\}={\Omega }_{2}$$

to find an optimal solution of the crisp NLPPs (B-3) and (B-4) is equivalent to find an optimal solution of the CLPPs (B-5) and (B-6), respectively.

Problem (B-5)

$$Maximize \left\{{\Omega }_{1}\right\}$$

Subject to

$$\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{i=1}^{m}{a}_{ij1}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij2}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij3}{u}_{i},\sum\limits_{i=1}^{m}{a}_{ij4}{u}_{i}\right);\\ {minimum}_{1\le i\le m}\left\{{l}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{m}_{ij}\right\},{maximum}_{1\le i\le m}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{j}}\right)\ge {\Omega }_{1}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (B-6)

$$Minimize \left\{{\Omega }_{2}\right\}$$

Subject to

$$\gamma \left(\frac{{\Pi }_{\alpha }\left(\Bigg\langle \begin{array}{c}\left(\sum\limits_{j=1}^{n}{a}_{ij1}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij2}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij3}{v}_{j},\sum\limits_{j=1}^{n}{a}_{ij4}{v}_{j}\right);\\ {minimum}_{1\le j\le n}\left\{{l}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{m}_{ij}\right\},{maximum}_{1\le j\le n}\left\{{n}_{ij}\right\}\end{array}\Bigg\rangle \right)}{{\gamma }_{i}}\right)\le {\Omega }_{2}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 4: To find an optimal solution of the crisp NLPPs (B-5) and (B-6) is equivalent to find an optimal solution of the CLPPs (B-7) and (B-8) respectively.

Problem (B-7)

$$Maximize \left\{{\Omega }_{1}\right\}$$

Subject to

$$\gamma \left(\frac{{\Pi }_{\alpha }\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle \right){u}_{i}}{{\gamma }_{j}}\right)\ge {\Omega }_{1}, j=\mathrm{1,2},\dots ,n,$$

$$\sum\limits_{i=1}^{m}{u}_{i}=1, {u}_{i}\ge 0, i=\mathrm{1,2},\dots ,m.$$

Problem (B-8)

$$Minimize \left\{{\Omega }_{2}\right\}$$

Subject to

$$\gamma \left(\frac{{\Pi }_{\alpha }\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle \right){v}_{j}}{{\gamma }_{i}}\right)\le {\Omega }_{2}, i=\mathrm{1,2},\dots ,m,$$

$$\sum\limits_{j=1}^{n}{v}_{j}=1, {v}_{j}\ge 0, j=\mathrm{1,2},\dots ,n.$$

Step 5: Using the expressions (F.3) and (F.4), to find an optimal solution of the crisp NLPPs (B-7) and (B-8) is equivalent to find an optimal solution of the CLPPs (B-43) and (B-44) respectively.

$$\frac{{\Pi }_{\alpha }\left(\sum\limits_{i=1}^{m}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle \right){u}_{i}}{{\gamma }_{j}}=\sum\limits_{i=1}^{m}\left(\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}\right){u}_{i}$$

(F.3)

$$\frac{{\Pi }_{\alpha }\left(\sum\limits_{j=1}^{n}\Bigg\langle \left({a}_{ij1},{a}_{ij2},{a}_{ij3},{a}_{ij4}\right);{l}_{ij},{m}_{ij},{n}_{ij}\Bigg\rangle \right){v}_{j}}{{\gamma }_{i}}=\sum\limits_{j=1}^{n}\left(\frac{{a}_{ij1}+2\left({a}_{ij2}+{a}_{ij3}\right)+{a}_{ij4}}{6}\right){v}_{j}$$

(F.4)