1 Introduction

Clustering is one of the most important tools in data mining. The major goal of clustering is to seek a grouping which makes the intra-group similarity large, but inter-group similarity small. However, using different methods or same method with different parameters on the same dataset will have different results. The basic challenge in clustering is choosing a suitable algorithm for one dataset. Strehl and Ghosh (2003) proposed clustering ensemble which combines independent clustering results rather than finds the best ones. Clustering ensemble, known as clustering aggregation and consensus clustering, is characterized by high robustness, stability, novelty, scalability and parallelism (Yu et al. 2014; Lv et al. 2016; Jia et al. 2011; Ma et al. 2018). In addition, clustering ensemble has advantages in privacy protection and knowledge reuse. It only needs to access clustering solutions rather than original data, so it provides privacy protection for original data (Akbari et al. 2015). Clustering ensemble uses the results from single clustering algorithms to form the final partition; that is to say, it can reuse knowledge (Wang et al. 2010).

Although clustering ensemble has many advantages, not all clustering solutions make positive contributions to the final result (Yu et al. 2016). Many existing clustering ensemble algorithms combine all clustering solutions; however, we find that only merging partial solutions produces better result. And the method using partial solutions is selective clustering ensemble (SCE) (Hong et al. 2009). Hadjitodorov proposed to select solutions according to diversity or quality (Hadjitodorov et al. 2006). Furthermore, Alizadeh presented to consider diversity and quality simultaneously for selecting solutions (Alizadeh et al. 2014). Jia et al. (2011), Yu et al. (2014) and Yu et al. (2014) regarded solutions as features of dataset and selected solutions with clustering algorithms or feature selection algorithms. These SCE algorithms have two limitations. (1) They did not consider which diversity would benefit the clustering ensemble. Hadjitodorov et al. (2006) considered solutions in low diversity being good, while Kuncheva and Hadjitodorov (2004) supported high diversity. (2) Some methods did not take into account how to make sure the selected solutions are in high quality while considering diversity.

In order to address the limitations of traditional SCE algorithms, we first propose a multiple clustering and selecting approach (MCAS), which adopts multiple clustering and selecting algorithms to select solutions. Then, we design a method, MCAS with direct combining (MCAS_DC), to integrate the selected solutions gotten by MCAS into a unified set of selected solutions. In addition, we improve MCAS_DC with a clustering and selecting algorithm and produce MCAS with clustering combining (MCAS_CC). Next, we adopt Normalized Cut algorithm (Ncut) as consensus function to produce final result. Finally, a set of experiments are used to compare different SCE algorithms with our methods over multiple datasets. The experiments on ten UCI machine learning datasets show that the proposed methods outperform most SCE algorithms.

The contribution of this paper is twofold. First, we propose a MCAS approach based on different selection approaches, which not only provides diverse solutions, but also guarantees the quality of selected solutions. Second, a combining strategy is designed to merge the selected solutions and MCAS_CC is proposed to improve MCAS_DC, which refine the clustering solution more accurately.

The remainder of this paper is organized as follows. Section 2 gives a brief survey of SCE. Section 3 presents the framework of our methods. Section 4 evaluates the performance of the proposed methods on UCI machine learning datasets. Section 5 draws conclusions and describes our future works.

2 Related works

Clustering ensemble mainly includes two steps: diversity generation and consensus function.

In the first stage, the generation of diverse clustering solutions includes four methods. (1) Heterogeneous ensemble is appropriate for low-dimensional data and this method uses different clustering algorithms, such as KMeans (KM), spectral clustering (SC) (Liu et al. 2017) and self-organizing map (SOM) (Strehl and Ghosh 2003). (2) Homogeneous ensemble is also suitable for low-dimensional data and it changes basic parameters of one algorithm, for example, KM with different initial centers, SC with different k values and SOM with different original weighting vectors (Fred and Jain 2002; Topchy et al. 2003). (3) Subsampling or resampling of original data is appropriate for big dataset (Alizadeh et al. 2013). (4) Using feature subset of data or projecting data into random subspace is suitable for high-dimensional data (Topchy et al. 2003; Bertoni and Valentini 2006).

The second stage in clustering ensemble is combining these solutions to obtain final accurate result, and it mainly includes four methods. (1) Voting approach: It solves the inconsistency of labels and assigns data to cluster which has more votes than other clusters (Zhou and Tang 2006). (2) Pairwise approach: It mainly creates co-association matrix according to pairwise similarity before clustering (Fred and Jain 2002, 2005). (3) Graph-based approach: It produces final partition by creating graph and cutting edges of graph and (Strehl and Ghosh 2003; Ma et al. 2019, 2020). (4) Feature-based approach: It considers clustering solutions as new features of original data and clusters these data with new features (Yu et al. 2016).

In addition, there are other consensus functions, such as locally adaptive clustering algorithm, genetic algorithm and kernel methods (Wang et al. 2014; Rong et al. 2019; Hong and Kwonga 2008; Rong et al. 2019). Yousefnezhad et al. (2017) and Minaei-Bidgoli (2016) proposed a kind of ensemble clustering-based wisdom of crowds theory, which is used for pairwise constraint clustering, and consider the independency, decentralization and diversity for selection.

In many methods, SCE is short of a unified definition; thereby, we introduce the concept mentioned in Muhammad et al. (2016). SCE selects solutions from solutions library according to some benchmark and merges them to improve the accuracy of final partition. Considering quality and diversity simultaneously, we get the following theorem to explain SCE.

Theorem 1

If \(R=L^q\cap L^d\), \(R\ne \varnothing \) and \(C_r\in R\), then combining \(C-{C_r}\) performs better than combining C, where \(C=\{C_1,C_2,\ldots ,C_m\}\) is solutions library, \(L^q \subset R\) is composed of solutions which have lower quality than average quality \(\bar{Q}\) of all solutions, \(L^d \subset R\) is composed of solutions which have lower diversity than average diversity \(\bar{D}\) of all solutions and \(C-{C_r}\) is a subset of R and composed of all solutions except \(C_r\).

Proof

The average quality of \(C-{C_r}\) is

$$\begin{aligned} \overline{Q^{C-C_r}} = \frac{m\bar{Q}-Q^{C_r}}{m-1} = \bar{Q}+\frac{\bar{Q}-Q^{C_r}}{m-1}, \end{aligned}$$
(1)

where \(Q^{C_r}\) is the quality of solution \(C_r\). According to the define of \(C_r\), \(Q^{C_r}< \bar{Q}\) then

$$\begin{aligned} \overline{Q^{C-C_r}} > \bar{Q}. \end{aligned}$$
(2)

In the same way, the average diversity of \(C-{C_r}\) is

$$\begin{aligned} \overline{D^{C-C_r}} = \frac{m\bar{D}-D^{C_r}}{m-1} = \bar{D}+\frac{\bar{D}-D^{C_r}}{m-1}, \end{aligned}$$
(3)

where \(D^{C_r}\) is the diversity of solution \(C_r\). According to the define of \(C_r\), \(D^{C_r}< \bar{D}\) then

$$\begin{aligned} \overline{D^{C-C_r}} > \bar{D}. \end{aligned}$$
(4)

According to (2) and (4), we can conclude that combining the solutions subset \(C-C_r\) performs better than combining all solutions in library C considering quality and diversity. A good solution has a higher diversity relative to inter-cluster and higher quality relative to intra-cluster. So a good SCE algorithm selects solutions not only considering quality of solutions to reduce the influences of the ones in low quality, but also considering the solutions which are different from others for avoiding redundancy.

Hadjitodorov studied the relationship between diversity of solutions and final partition and found that solutions in high diversity are better than the ones in low diversity (Hadjitodorov et al. 2006). However, Kuncheva found that the relationship between diversity and quality is not linear and median diversity is better than the ones in high diversity (Kuncheva and Hadjitodorov 2004). Fern took into account diversity and quality simultaneously and proposed three SCE algorithms (Fern and Lin 2008). Alizadeh et al. (2014), Naldi and Carvalho (2013), Nazari et al. (2019), Ali et al. (2019) and Wu et al. (2014) put forward new selecting strategies based on quality or diversity.

Meng regarded solutions as features of dataset and clustered this dataset with affinity propagation algorithm (Meng et al. 2016), while (Azimi and Fern 2009; Ma et al. 2015; Zhang et al. 2015; Soltanmohammadi et al. 2016; Ma et al. 2018) adopted feature selection algorithms to select features of the dataset which regards solutions as features of dataset for selecting solutions. Wei (2005) used a bagging algorithm for the purpose of selecting solutions and adopted a spectral clustering algorithm as the consensus function (Zhang and Cao 2014). In addition, Dai et al. (2015), Faceli et al. (2010) and Yang et al. (2017) presented other SCE algorithms.

For extremely large-scale datasets, (Huang et al. 2019) focus on scalability and robustness by using ultra-scalable spectral clustering and ultra-scalable ensemble clustering, which demonstrated the scalability and robustness. Bagherinia et al. (2020) propose a new fuzzy clustering ensemble framework combining the reliability-based weighted and graph-based fuzzy consensuses function and get performance clustering robustness.

3 Multiple clustering and selecting algorithms with combining strategy for SCE

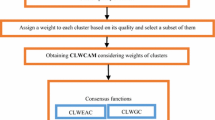
Figure 1 provides a flowchart of multiple clustering and selecting algorithms (MCAS) with combining strategy for selective clustering ensemble. First, m different clustering algorithms are used to produce solutions library \(C=\{C_1,C_2,\ldots ,C_m\}\). Then, MCAS adopts \(m'\) clustering and selecting algorithms to run on library C and each one gets a subset of solutions. Next, a combining strategy combines these subsets and produces final selected solutions. Finally, a consensus function is used to get the final partition about original dataset.

Fig. 1
figure 1

A flowchart of multiple clustering and selecting algorithms with combining strategy for selective clustering ensemble

Full size image

3.1 Diversity generation

The first step of MCAS with combining strategy for SCE is to get solutions library \(C=\{C_1,C_2,\ldots ,C_m\}\), which consists of many diverse solutions about original dataset. KMeans, as the most common clustering algorithm, has been widely used in clustering ensemble (Xu et al. 2016). However, like most traditional clustering algorithms, KMeans is only applied to convex sphere sample space. So when the sample space is not convex, it is easy to fall into local optimum. Therefore, in order to avoid this problem, we use spectral clustering (Huang et al. 2015). Spectral clustering algorithm not only can cluster non-convex dataset, but also can cluster high-dimensional data. Due to the fact that spectral clustering algorithm is easy to implement and has a good prospect, it has been widely used in many fields, such as video segmentation, speech recognition and image segmentation.

In this paper, we use KMeans to generate half of the solutions library and spectral clustering algorithm to produce the other half. KMeans clusters data according to distance, while spectral clustering explores the connection structures between data in depth. Applying KMeans and spectral clustering simultaneously is better than using KMeans and spectral clustering separately. Because they can complement each other and generate solutions from different aspects with a comprehensive exploration of data. As future study, we intend to explore for methods that generate diverse solutions.

3.2 MCAS with combining strategy

Each solution in solutions library is represented by cluster labels. \(C_i=\{c^i_{x_1},c^i_{x_2},\ldots ,\)\( c^i_{x_n}\}(i=1,2,\ldots ,m)\) and \(c^i_{x_j}\) is the cluster label of data \(x_j\) in solution \(C_i\). It cannot be directly used for the next operation. For example, solutions \(\{1,1,1,2,2,3,3,3\}\) and \(\{2,2,2,3,3,1,1,1\}\) are in different means of expression, but they represent the same partition. So it is necessary to solve the problem of cluster label inconsistency before applying MCAS. In this paper, we use the method proposed by Wei (2005). For matching clusters, the method uses the criterion that the amount of covered data by clusters which have corresponding relationship is maximum.

After solving the problem of cluster label inconsistency, we view the solutions library C as a new dataset and a solution is a piece of data which has n attributes. Then, multiple clustering and selecting algorithms are used to select solutions from C. These clustering and selecting algorithms we used in this paper are KMeans selection (KMS), expectation maximization selection (EMS), hierarchical clustering selection (HCS) and farthest-first selection(FFS) (Yu et al. 2016; Hu et al. 2016; Devi and Deepika 2016). Next, two combining strategies are proposed: direct combining (DC) and clustering combining (CC). These two combining strategies are used to combine the solutions gotten by MCAS to get the final selected solutions.

The multiple clustering and selecting algorithms we used mainly include two steps. First, it clusters solutions library C for the purpose that the solutions in the same cluster have more similar diversity than those in different clusters. And the second step is selecting one solution which has the highest quality from each cluster. In this paper, we introduce two important indexes to measure the quality of each solution and diversity between two solutions.

$$\begin{aligned}&{\hbox {quality}}(C_i)=\frac{1}{m}\sum _{j=1}^m NMI(C_i,C_j), \end{aligned}$$
(5)
$$\begin{aligned}&{\hbox {diversity}}(C_i,C_j)=1-NMI(C_i,C_j), \end{aligned}$$
(6)

where NMI\((C_i,C_j)\) denotes the NMI value between solutions \(C_i\) and \(C_j\) (\(C_i,C_j\in C\) and \(C=\{C_1,C_2,\ldots ,C_m\}\) is solutions library). Using these two steps, MCAS meets the requirements of quality and diversity in SCE. Compared with using single clustering and selecting algorithm, the reason we use multiple clustering and selecting algorithms is that it avoids the weakness of single clustering and selecting algorithm.

KMeans selection (KMS) is an algorithm that partitions solutions based on diversity and selects solutions according to quality. First, it selects K solutions from C as initial centroids. Next, it assigns each solution to the cluster with similar solutions until all solutions are assigned to the clusters. Then, according to the solutions in the clusters, the centroid of each cluster is updated. Repeat the above assignment and update until the clusters do not change anymore. Finally, the solution in each cluster that has the highest quality is selected by KMS. The pseudo-code of KMS is described in Algorithm 1.

figure a

Expectation maximization selection (EMS) clusters solutions iteratively in two steps and selects solutions according to quality. First, EMS gives k a random value and assigns all solutions into k clusters randomly. Then, E-step calculates the maximum likelihood estimator of k using existing partition of solutions. Next, M-step calculates the values of k by maximizing the maximum likelihood value obtained in E-step. The two steps continue until the value of k converges. Finally, EMS selects the solution that has the highest quality in each cluster. EMS, described in Algorithm 2, is simple and stable.

figure b

At first, hierarchical clustering selection (HCS) regards each solution as a cluster that only has one solution and creates adjacency matrix about clusters based on solutions’ diversity. Next, it combines the two clusters that have more similar diversity than others. Then, it updates the adjacency matrix about clusters according to the solutions’ diversity. Repeat the operations of combining clusters and update adjacency matrix until only k clusters are remained. Finally, the solution in each cluster that has the highest quality is selected by HCS. This method is described in Algorithm 3.

figure c

Farthest-first selection (FFS) first labels the solutions according to diversity from 1 to m, and the one that is most dissimilar with others is labeled earlier. Repeat the above process of labeling until all solutions are labeled. Next, FFS constructs a minimum spanning tree, and for any solution, its parents are solutions that are more similar to it than others. Then, it cuts the maximum edge based on diversity until only k subtrees are generated. Finally, FFS selects the solution that has the highest quality from each subtree. The specific process of FFS is described in Algorithm 4.

figure d

After selecting four subsets of C with MCAS, how to get the optimized subset is the most critical issue that needs to be solved. In this paper, we present two combining strategies: direct combining (DC) and clustering combining (CC). Direct combining (DC), as the name indicates, is directly combining solutions in each subset to obtain a new subset \(S_\mathrm{DC}=S_{kms}\cup S_{ems}\cup S_{hcs}\cup S_{ffs}\). Clustering combining (CC) is based on \(S_\mathrm{DC}\) and KMS. It takes \(S_\mathrm{DC}\) as input of KMS, clusters \(S_\mathrm{DC}\) according to diversity among solutions and selects solutions with the highest quality in each cluster. The selected solutions by KMS are \(S_\mathrm{CC}\). In the future, we will study on comparing other clustering and selecting algorithms as combining strategy.

3.3 Consensus function

The third step of MCAS with combining strategy for SCE is consensus function. In this paper, we use normalized cut (Ncut) (He and Zhang 2016) as the consensus function to acquire the final result. Before applying Ncut, a consensus matrix W is constructed and the value in W of data \(x_i\) and \(x_j\) is

$$\begin{aligned} w_{ij}=\frac{T_{ij}}{|S|}, \end{aligned}$$
(7)

where \(T_{ij}\) is the amount of times that data \(x_i\) and \(x_j\) appear together in all selected solutions and |S| is the number of selected solutions in subset \(S_\mathrm{DC}\) or \(S_\mathrm{CC}\). Then, Ncut draws a graph \(G=(X,W)\). The vertices of the graph are data in dataset X, and the edge of two vertices is the corresponding value in W. Ncut starts with a binary segmentation. It divides graph into two subgraphs \(X_1\) and \(X_2\), and repeat the above process on subgraphs until K subgraphs are obtained.

The objective function \(\Pi (X_1,X_2)\) of minimizing irrelevancies of \(X_1\) and \(X_2\) is defined as follows:

$$\begin{aligned}&\Pi (X_1,X_2)=\frac{{\hbox {cut}}(X_1,X_2)}{{\hbox {assoc}}(X_1,X)}+\frac{{\hbox {cut}}(X_1,X_2)}{{\hbox {assoc}}(X_2,X)}, \end{aligned}$$
(8)
$$\begin{aligned}&{\hbox {cut}}(X_1,X_2)=\sum _{x_i\in X_1,x_j\in X_2} w_{ij}, \end{aligned}$$
(9)
$$\begin{aligned}&{\hbox {assoc}}(X_1,X)=\sum _{x_i\in X_1,x_l\in X} w_{il}, \end{aligned}$$
(10)

where cut(\(X_1,X_2)\) is sum of the weights about edges that connect vertices between \(X_1\) and \(X_2\) and assoc(\(X_2,X)\) is sum of weights about edges that connect vertices in \(X_1\). This optimization problem is NP hard, and it can be solved by searching approximate solution in true value field. If this problem is formulated with generalized eigenvalues, the result of Ncut is the eigenvector that corresponds to the second small eigenvalue of pairwise similarity matrix.

In summary, Algorithm 5 provides pseudo-code of our proposed MCAS with combining strategy for SCE.

figure e

3.4 Complexity analysis

As Fig. 1 shows, the proposed MCAS_DC and MCAS_CC algorithms include four steps: (1) original cluster generated by different clustering algorithms; (2) clustering and selecting algorithms executed including KMeans, EMS, HCS and FFS; (3) DC and CC combining strategy used to combine the selected subset; and (4) Ncut as a consensus function to get the final result. The complexity of each step is given in the following.

Step 1 There are m original results required; half of them are generated by KMeans clustering and the other half are generated by spectral clustering.

The KMeans clustering time complexity is \(O(i*n*k)\) and the space complexity is O(n), where i is the iterate times, n is the size of dataset and k is the cluster number. The spectral clustering time complexity is \(O(n^3)\), and the space complexity is \(O(n^2)\).

The total time complexity is \(O(m*(i*n*k + n^3))\) and the space complexity is \(O(m*(n+ n^2))\), where m is the number of original clustering solutions.

Step 2 Select K subsets from the \(C=\{C_1,C_2,\ldots ,C_m\}\) original solutions. There are four methods.

KMeans The time complexity is \(O(I*m*K)\), and each iteration should calculate function (6). So, the time complexity is \(O(I*m*K*m^2)\) and the space complexity also is O(n), where \(I \ll i\) is the iterate times and \(K<k\) is the cluster number.

EMS The complexity is same, as KMeans as procedure is same. So, the time complexity is \(O(I*m*K*m^2)\) and the space complexity also is O(n).

HCS The time complexity is \(O(m^2)\) and the space complexity also is O(n).

FFS The time complexity is \(O(m*K*m^2)\) and the space complexity also is O(n).

Steps 3 Combine the selected subsets. For MCAS_DC, \(S_\mathrm{DC}=S_{kms}\cup S_{ems}\cup S_{hcs}\cup S_{ffs}\). The time complexity is O(1), and the space complexity is O(m). For MCAS_CC, using clustering algorithm combine \(4*K\) solution with K , so the time complexity is \(O(I^\prime *4K*K*4K*4K)\), where \(I^\prime \) is the iterate times, and the space complexity is O(m).

Steps 4 Adopt Ncut as consensus function to get the final result. The time complexity is O(K*K*K), and the space complexity is O(K*K).

The total time complexity is sum up above four steps, so it is: \(O(m*(i*n*k + n^3))\) + \(O(I*m*K*m^2)\) + \(O(I*m*K*m^2)\) + \(O(m^2)\) + \(O(m*K*m^2)\) + \(O(I^\prime *4K*K*4K*4K)\) + O(K*K*K).

As \(I^\prime < I \ll i\), \(K < k\), \(m \ll n\), \(K < m\), so the time complexity can be reduced to \(O(m*n^3)\).

The space complexity is: \(O(m*(n+ n^2))\) + O(n) +O(n) + O(n) + O(n) + O(m) + O(m) + O(K*K) and can be reduced to \(O(m*n^2)\).

So, the whole algorithm’s complexity depends on the spectral clustering of the first step. Our proposed methods MCAS_DC and MCAS_CC are in the same level with SCE.

4 Experiments

The proposed methods, multiple clustering and selecting with direct combining strategy (MCAS_DC) and multiple clustering and selecting with clustering combining strategy (MCAS_CC), are tested on ten UCI machine learning datasets shown in Table 1. The number of classes, features and data amount are diverse enough in order to reflect the advantages and disadvantages of our methods. It is worth noting that all of the datasets are labeled with supervised classification information, but this label information is only used to evaluate our methods, but not in our methods.

Table 1 Summary of ten UCI machine learning datasets (where k denotes the number of classes, n denotes the amount of data and d denotes the number of features)
Full size table
Fig. 2
figure 2

Comparison of single and multiple CAS algorithms for SCE. EMS, KMS, FFS and HCS are four single CAS algorithms: expectation maximization selection, KMeans selection, farthest-first selection and hierarchical clustering selection for CAS operation, respectively. MCAS_DC and MCAS_CC are our proposed SCE algorithms that use MCAS with direct combining (DC) and clustering combining (CC). a–j are, respectively, NMI values of six SCE algorithms on ten UCI datasets of 20-time running

Full size image
Fig. 3
figure 3

Relationship between MCAS for SCE and qualities of basic clustering solutions. Basic denotes the average NMI among basic clustering solutions. MCAS_DC and MCAS_CC are our proposed SCE algorithms that use MCAS with direct combining (CC) and clustering combining (CC). a–j are, respectively, NMI values of those on ten UCI datasets of 20-time running

Full size image
Fig. 4
figure 4

Relationship between selection proportion and algorithm performance. Original is clustering ensemble algorithm using all clustering solutions. MCAS_DC and MCAS_CC are our proposed SCE algorithms that use MCAS with direct combining (DC) and clustering combining (CC). a–j are, respectively, NMI values of those on ten UCI datasets of different selection proportions. When the selection proportion is \(10\%\), it means the number of selected solutions is \(100\times 10\%=10\)

Full size image
Table 2 p value according to t test on ten UCI datasets of three SCE algorithms compared with MCAS_DC and MCAS_CC
Full size table

In the step of diversity generation, the number of clusters is randomly selected from \([2,\sqrt{n}]\) and the error is set as 1e-5 in KMeans and spectral clustering. The m in Fig. 1 is consistent from 50 solutions generated by KMeans and 50 solutions generated by spectral clustering. In the step of MCAS with combining strategy, the number \(m'\) of selected solutions is from 10 to 100 with step 10. In the step of consensus function, the number of clusters for Ncut is the real class number k of dataset.

The external evaluation indexes are used to measure our proposed methods. We use normalized mutual information (NMI), adjusted Rand index (ARI) and joint index (JI) as evaluating indicators to calculate the difference between the results of our methods and the real partition of original dataset. Because these indexes produce similar results and trends compared with the real partition of dataset, we only show the result of NMI about 20-time running.

4.1 The comparison between single CAS algorithm and MCAS with combining strategy

In this experiment, we compare four single clustering and selecting algorithms, namely KMS, EMS, HCS and FFS, and two proposed MCASs with combining strategy, namely MCAS_DC, MCAS_CC. Figure 2 shows the NMI values of six SCE algorithms. It can be seen that MCAS_DC and MCAS_CC provide better results than four single CAS algorithms, especially on Ecoli, Glass Identification, Lung Cancer, Seeds, Soybean, Wine and Yeast datasets. Though our algorithms sometimes are slightly inferior to some single CAS algorithms on datasets Breast Cancer, Iris and Statlog, they are overall better than single CAS algorithm. The possible reasons are as follows. (1) We consider different solutions as a piece of data in new dataset, cluster the new dataset to ensure high diversity and select solutions with high quality from each cluster to prune redundant solutions. (2) There is not a single CAS algorithm that works well on all datasets. For example, KMS only gets better results on Lung Cancer and Statlog, while EMS achieves the best result only on Iris. This encourages us to use multiple clustering and selecting algorithms and design a combining strategy to combine the solutions selected by MCAS. In summary, the performance of MCAS with combining strategy is obviously better than that of single CAS algorithm.

4.2 The effect of solutions quality

To illustrate the relationship between the basic clustering solutions and the performance of MCAS_DC and MCAS_CC, we compare the NMI of our methods and the average NMI of basic solutions. Here, basic clustering solutions are the original solutions generated in the first step. The basic clustering solutions consist of KMeans generating 50 solutions and spectral clustering generating 50 solutions.

As shown in Fig. 3, the quality of basic solutions has positive influence on our algorithms. For instance, on Breast Cancer, the basic clustering solution has higher NMI in the first and eleventh runnings, and correspondingly, MCAS_DC and MCAS_CC have better performance in these runnings. It can be seen that basic solutions have higher NMI on Ecoli, Seeds, Soybean and Wine than on Glass, Lung Cancer and Yeast, so the performance of MCAS_DC and MCAS_CC on the first four datasets is better than that on the last three datasets. This is mainly because when the quality of basic solutions is good, MCAS_DC and MCAS_CC can ensure the selected solutions have the optimal trade-off between quality and diversity. In general, better the quality of basic clustering solutions, better the performance of MCAS_DC and MCAS_CC.

4.3 The effect of selection proportion

In order to study the relation between the selection proportion and the performance of our proposed algorithms, we make a set of experiments, and Fig. 4 shows the result of using all and partial solutions. When the selection proportion is \(10\%\), it means that the amount of selected solutions is \(100\times 10\%=10\). The result of selective clustering ensemble is better than using all solutions, but the appropriate selection proportion for different datasets is not same. For example, \(10\%\), \(20\%\), \(30\%\), \(40\%\) and \(50\%\) are, respectively, suitable for Iris, Yeast, Statlog, Ecoli and Seeds. In the future, studying the suitable selection proportion is a good direction. From Fig. 4, we can observe that it is possible to obtain better results on all datasets by choosing a subset of solutions than using all solutions, which is described in Sect. 2. Not all solutions are effective for creating subset of solutions, and pruning useless solutions can improve the performance of final result. Therefore, it is worth to research how to choose appropriate selection proportions for different datasets.

4.4 The comparison of different selective clustering ensemble algorithms

In this experiment, we compare our two algorithms with three common SCE algorithms [SCE based on Quality which is named as HCES (Akbari et al. 2015), Diversity which is named as HCSS (Jia et al. 2011) and Feature Selection which is named as SELSCE (Yu et al. 2014)] on ten UCI datasets of 20-time running. A pairwise two-sided t-test is used to analyze how better MCAS_DC and MCAS_CC are than other three SCE algorithms (Hung 2015). The p value in t-test measures the difference between two algorithms, and it represents the probability of the two compared sample sets coming from the same variance distribution. The smaller the p, the better the MCAS_DC and MCAS_CC in performance. And 0.05 is considered as a typical threshold of statically significant. The p values of three SCE algorithms compared with MCAS_DC and MCAS_CC on ten UCI datasets are reported in Table 2, and in the table, the bold values lower than 0.05 denote MCAS_DC or MCAS_CC has obvious advantage compared with others.

Table 2 shows MCAS_DC and MCAS_CC have better performances in most cases. It can be summed up from Table 2 that MCAS_DC is significantly superior to other SCE algorithms on at least five of ten datasets and MCAS_CC is better than other SCE algorithms on at least six datasets. If using all solutions, the ones in low quality will reduce the final result. And some similar solutions will increase the complexity of algorithms. Therefore, they will be filtered out by our proposed MCAS. The three SCE algorithms only select solutions form one aspect and do not think quality and diversity simultaneously. On dataset Breast Cancer, Seeds and Statlog, although MCAS_DC and MCAS_CC do not clearly beat other SCE algorithms, they edged out them by a slight advantage. It is mainly because in the process of generating diverse basic solutions, the number of classes k ranges in \([2,\sqrt{n}]\), and the real class numbers on the three datasets are relatively smaller than k. This decreases the quality of solutions and has a bad influence on final result.

From Fig. 3, it shows MCAS_CC sometimes is better than MCAS_DC, sometimes is not. We calculate the p value with the different NMIs according to each dataset to verify the advantage of MCAS_CC. We can see from the last column of Table 2 that MCAS_CC is better, but not obviously better than MCAS_DC. Generally speaking, MCAS_DC which lacks a clustering and selecting process is a good choice when the requirement of time complexity is high. Conversely, MCAS_CC is the best when considering accuracy.

5 Conclusion

In this paper, we study the problem of SCE and propose a MCAS approach taking quality and diversity into account. We also present two combining strategies, direct combining and clustering combining. We implement a throughout study of MCAS_DC and MCAS_CC on ten UCI datasets and draw several conclusions. (1) Multiple CAS algorithms work better than single CAS algorithm. (2) If the quality of basic solutions is generally good, the performance of MCAS_DC and MCAS_CC is also good. (3) The suitable selection proportion that has the best final result is not same on different datasets. (4) Our proposed algorithms, MCAS_DC and MCAS_CC, overmatch common SCE algorithms. MCAS_DC is the best choice considering algorithm complexity; otherwise, MCAS_CC is a good choice.

Considering the experiments in this paper, our future studies are mainly on the following aspects. First, we are going to study more single clustering and selecting algorithms and integrate them into our methods. Second, a comprehensive research about selection proportion on different datasets is a good direction. Third, MCAS_CC uses KMS algorithm as clustering and selecting algorithm and in the future we will explore other combining strategy. In addition, there is always priori information in real life, so how to use this knowledge to help us is one of the worth topics.