1 Introduction

Online social networking has become one of the most popular activities on the web. With the rapid growth of social networks, such as Twitter and Facebook, a large amount of social network data has been collected and maintained by the social network service providers. More and more researchers find that it is a great opportunity to obtain useful information from these social network data, such as the user behavior, community growth, disease spreading, etc. Social network service providers also want to publish these data for analysis in order to adjust its strategy to provide more attracting services. However, publication of the social network data should not reveal any private information of individuals [1, 2].

Privacy preservation in relational data publishing has been studied extensively. A variety of privacy models as well as anonymization algorithms have been developed (e.g., \(k\)-anonymity [3], \(l\)-diversity [4], \(t\)-closeness [5]). It is more challenging to anonymize the social network data than the relational data [6], techniques tackling the relational data can not be applied to social networks data straightforwardly. Researchers have adapted these techniques to address privacy issues in privacy preservation of social network data publishing, which can be broadly categorized into clustering-based approaches, and graph-modification-based approaches.

The clustering-base approaches partition a social network into groups of nodes and replace them with super nodes, which associated with properties such as the number of nodes and connections. Alternatively, in the graph-modification-based approaches, the structure of the original network is slightly modified, usually by inserting/deleting edges/vertices, to achieve a certain desired level of anonymity. Recent observations show that both of these approaches severely suffer from the same problem: if data is anonymized up to an acceptable degree the results become highly distorted compared to the original networks, thus, severely affecting their utility for analysis purposes [7]. Detailed information is lost in the social networks anonymized by the clustering-based approaches, one should sample a group of graphs by generating substructures in place of super nodes based on the reported properties. The second is modifying connections in the graph-modification-based approaches to fulfill the anonymization criteria (e.g., degree \(k\)-anonymity). The key problem related to these methods is that they usually focus on achieving the anonymization objectives and disgard the crucial need of preserve the original structural semantics of the network; hence, the outcome is a significant decrease in the utility of the results.

In this paper, we consider such structural semantics in the anonymization process by using concepts from the social network analysis theory [8]. In particular, we leverage the notion of community structure and shortest path length between vertices to protect the utility of the social network. As we demonstrate in this paper, the approach shows significant improvements in maintaining the structural measurements of the social networks such as transitivity, average clustering coefficient (ACC) and average path length (APL), etc., all of which have direct effect on the usefulness of the anonymity results.

The rest of the paper is organized as follows. Section 2 briefly reviews related works on social network anonymization. We described the problem addressed in this paper in Sect. 3. Our novel algorithm is proposed in Sect. 4 and the experimental results are given in Sect. 5. Finally, we conclude in Sect. 6.

2 Related work

To protect the privacy information in the social network, the simplest method is to publish a naive anonymized version of the network, e.g., by replacing the identifying information of the nodes with random synthetic identifiers. Backstrom et al. [9] pointed out that as unique small random sub-graphs are embedded in the network, the adversary may perform a family of active or passive attacks on the naive anonymized social network, thus, privacy will be disclosure with high probability. To address the privacy issues, several graph anonymization approaches are proposed [10–16]. Most of the existing approaches are based on the \(k\)-anonymity principle [3]. We category the state-of-the-art social network anonymization approaches into two categories: clustering-based approaches and graph-modification-based approaches.

The clustering-based approaches classify the vertices and edges into groups, in which there is at least \(k\) vertices to guarantee \(k\)-anonymity. Then each group will be generalized into a super-node, along with some structural properties of the group. As the vertices in the same super-node are not distinguishable, the adversary can not disclosure a vertex with probability higher than 1/\(k\). Hay et al. [13] proposed a heuristic approach in which nodes are grouped into partitions through a maximum likelihood approach to fit the original social network as much as possible. Campan and Truta [10] brought up a greedy approach, which partition nodes into groups in order to disturb structural information and generalization information as little as possible. However, detailed information is lost in the published social network. To use the published social network for analysis or data mining, one should sample a group of graphs by generating substructures in place of super nodes based on the reported properties. Then the analysing work can be finished by analysis each sampled graph and computing the average results. Since a user should do the sampling, the utility of the published graph does not have any guarantee and this user could never know how many samplings can guarantee to get a well enough result.

In the modification-based approaches, new edges, nodes are added or removed to ensure the network meeting desired privacy requirements. Hay et al. [17] proposed the \(k\)-candidate anonymity model, which randomly adds some edges then followed by deleting the same number of edges to resist identity disclosure. Liu and Terzi [14] brought up the concept of \(k\)-degree anonymous. A graph satisfies \(k\)-degree anonymous if each vertex in the graph has the same degree as at least \(k-1\) other vertices, and proposed a two-step algorithm to make a graph satisfying \(k\)-degree anonymous through adding edges. Lu et al. [18] proposed a fast greedy algorithm that anonymizes the social network by simultaneously adding edges and anonymizing the degree sequence, thus avoided the realizability-test which is necessary in [14]. Instead of adding edges to make the graph \(k\)-degree anonymous, Chester et al. [12] proposed a method to achieve it by adding vertices, and proposed a schema to confine that the number of vertices added were as less as possible. Zhou and Pei [6] considered \(k\)-neighborhood anonymous model: for every node, there exist at least other \(k-1\) nodes sharing isomorphic neighborhoods. \(k\)-automorphism [16], \(k\)-symmetry [15] and \(k\)-isomorphism [11] are proposed to prevent adversary with sub-graph background knowledge.

Our approach belongs to the graph-modification category. In our approach, we modify the graph by adding edges to the graph and similar vertices will also be added if necessary. Particularly, when modifying the graph, we employ the notion of community structure, which is a central organizing principle for social network, to confine the selection of the candidates. And the experimental results show that the utility of the published social network is preserved very well.

3 Problem description

In this section, we present the background of the social network anonymization problem, and then formulate the problem we tackle in this paper.

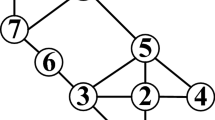
In this paper, a social network is modeled as an undirected unlabeled graph \(G(V, E)\), where \(V\) is a set of vertices representing individuals in the social network. \(E\) is a set of edges corresponding to the relationships between individuals. We use \(n\) to denote the number of vertices in graph \(G\). In this paper, we use words graph and social network, node and vertex, edge and connections interchangeably. Figure 1 shows an example of social network graph.

Fig. 1
figure 1

An example of social network

Full size image

In a published social network graph, an adversary could re-identify a node by performing structural queries. Structural queries refer to the activity that the adversary searches in the published social network graph with some priority knowledge about the victim such as the number of friends of the victim in the social network or the connections among some friends and the victim. If the candidate size of a structural query is one, then the victim will be identified identically. In this paper, we tackle the situation that the adversary has degree information as background knowledge. For example, if the adversary knows that the victim exists in the example social network and has four friends, then the adversary can conclude that node 3 must be the vertex that represents the victim.

In this paper, we utilize the \(k\)-degree anonymous model to resist the structure attack from adversary with degree information as background knowledge.

Definition 1

\(k\)-Degree anonymous [14]: a graph is said to be \(k\)-degree anonymous when each vertex in the graph has the same degree as at least \(k-1\) other vertices. In other words, any vertex cannot be identified with probability higher than 1/\(k\) if the adversary has the degree information of the graph.

In order to keep the utility of the published graph, when generating the \(k\)-degree anonymous graph, it is necessary to add as few noise edges and vertices as possible and the added edges should connect vertices that are not far away from each other with respect to the community structure and the path length.

Community structure is a central organizing principle of social network and it is a core graph topological feature which has a strong correlation with other important features (e.g., transitivity and betweenness). We consider the community structure of the social network when adding edges to the graph. Recent studies [25, 26] suggest that the communities of social networks often exhibit hierarchical organization (i.e. the large communities further contain small communities). So two vertices in the graph can be in the same community at different levels, the higher the level is, the bigger the community size is. We use the Louvain method [19], which is a heuristic algorithm based on modularity optimization [20] to get the hierarchical community structure of the graph. Initially every vertex belongs to a separate community, and vertices are moved between communities iteratively in a way that maximized the vertices local contribution to the overall modularity score. When a consensus is reached, i.e. no single move would increase the modularity score, every community in the original graph is shrunk to a single vertex and the process continues on the next level. The algorithm stops when it is not possible to increase the modularity any more after shrinking the communities to vertices.

The distance between two nodes \(u\), \(v\) is the shortest path length between \(u\) and \(v\) in the original graph. The social distance between all connectable pairs of a graph is measured by average path length (\(APL\)).

$$\begin{aligned} \textit{APL}=\frac{\sum \nolimits _{(u,v)\in \textit{RP}}{\textit{SPL}(u,v)}}{|\textit{RP}|} \end{aligned}$$
(1)

where \(RP\) denotes all reachable pair vertices, and \(\textit{SPL}(u, v)\) means the shortest path length between vertex \(u\) and \(v\). It is a measure of the efficiency of information or mass transport on a network.

We design a two-phase approach to transform the social network to its \(k\)-degree anonymous version. In the first step, we compute a target degree for each node so that it makes the original graph \(k\)-degree anonymous. In the second step, we change each vertexs degree to its target degree by adding edges/vertices.

Next, we first introduce two data structures we use in the rest of this paper, and then give the formal description the two steps in our algorithm. We adapted the concept of “degree sequence” used in [14] to record not only the degree information but also the identity information of vertices in the social network.

Definition 2

Given a graph \(G\), its degree sequence is a sequence of \(n\) 2-tuple: \([({{V}_{1}},{{d}_{{{V}_{1}}}}),({{V}_{2}},{{d}_{{{V}_{2}}}}), \ldots ({{V}_{n}},{{d}_{{{V}_{n}}}})]\) where \({{d}_{{{V}_{i}}}}\) is the degree of vertex\({{V}_{i}}\).

We use \(d[i]\) to represent node \({{V}_{i}}\)’s corresponding tuple in \(d\). For example, the degree sequence of the graph in Fig. 1 is \(d=[(3, 4), (2,3), (5,3), (7,3), (8,3)\), \( (1,2), (4,2), (6,2), (9,2)]\). In it, \(d[1]=(3,4)\) represents node \(3\) and its degree in the graph.

We call the degree sequence of the \(k\)-degree anonymous version graph the \(k\)-degree anonymous sequence, denoted as \(d^{'}\).

Definition 3

\(k\)-Degree anonymous sequence: a degree sequence \(d^{'}\) is a \(k\)-degree anonymous sequence if \(d^{'}\) satisfies the following constraints: \(d^{'}\) can be divided into a group of subsequences \([[(V_{1},d_{{V}_{1}}),\ldots , (V_{i},d_{{V}_{i}})],[(V_{i+1},d_{{V}_{i+1}}),\ldots ,(V_{k},d_{{V}_{k}})], \ldots , [(V_{w},d_{{V}_{w}}),\ldots (V_{n}, d_{{V}_{n}})]]\), such that there are at least \(k\) elements, and all elements share the same degree for any subsequence \([(V_{i+1}, d_{{V}_{i+1}}),\ldots ,(V_{k}, d_{{V}_{k}})]\) in \(d\). We also call \(d^{'}\) the target degree sequence of the original degree sequence d. For example, \(d^{'} = [(3, 4), (2, 4), (5, 3), (7, 3), (8, 3), (1, 2), (4, 2),\) \((6, 2), (9, 2)]\) is a target degree sequence, which is the \(k\)-anonymous version of the degree sequence of the graph in Fig. 1.

Formally, our objective is to transform the graph G to a graph that is \(k\)-degree anonymous, and at the same time, the utility of the graph is well preserved.

Problem definition: given a graph \(G(V, E)\), \(U(G)\) is the utility of the graph \(G\), the privacy requirement \(k\), our objective is to publish anonymized graph \(G^{'}\), such that: (1) \(G^{'}\) is \(k\)-degree anonymous; (2) the difference between \(U(G^{'})\) and \(U(G)\) is minimized.

4 Proposed KDVEM approach

In order to transform a graph to its \(k\)-degree anonymous version, we proposed a heuristic algorithm named \(k\)-degree anonymity with vertex and edge modification algorithm (KDVEM), we utilize the community structure of the social network and path length between vertices when finding candidates to increase the degree of a vertex. The proposed algorithm performs modification to the original network \(G(V, E)\) in order to turn it into a \(k\)-degree anonymous graph. Instead of only modifying edges of the graph, we utilize both edge modification and node modification. However, node modification is performed only when edge modification cant fulfill the anonymity task. The KDVEM algorithm is a two-step approach: in the first step, we first get degree sequence of the original graph, and then the target degree sequence is generated with the greedy_partition algorithm. Vertexs degree will be modified to its target degree by adding edges and vertices in the second step. In the process of adding edges and vertices to the original graph, the community structure of the social network is used to reduce the distortion on the utility of the published social network.

4.1 The greedy_partition algorithm

We use the greedy_partition algorithm (Algorithm 1) to generate \(k\)-degree anonymous sequence of the original graph. All vertices will be divided into groups and vertices in the same group shall be adjusted to have the same degree. Our greedy_partition algorithm tends to put the vertices with similar degree into the same group to reduce the degree changes.

figure a

While there are more than \(k\) vertices remaining in the degree sequence \(d\), the vertex with the largest degree is selected as the seed, and two costs are calculated:\({{C}_{new}}\), is the cost of creating a new group with the seed and its nearest \(k-1\) other vertices, we recorded these \(k\) vertices with variable \({{p}_{new}}\). \({{C}_{merge}}\), is the cost of merging the seed into the nearest existing group, recorded with \({{p}_{merge}}\). If \({{C}_{merge}}\) is smaller, the seed vertex is merged into the nearest existing group, and will be removed up from the degree sequence. Otherwise, a new group with the seed vertex and its nearest \(k-1\) other vertices is created, and all vertices in the new group will be removed from the degree sequence. For the first seed, as there are no groups exist, so the \({{C}_{merge}}\) cost is infinite.

$$\begin{aligned} {{C}_{merge}}&= \left\{ \begin{array}{ll} {\min _{p\in P}}({d^p} - {d_v}), &{}\quad \text {if } P \ne \varnothing \\ \infty , &{}\quad \text {if } P=\varnothing \end{array} \right. \end{aligned}$$
(2)
$$\begin{aligned} {{C}_{new}}&=\min \left( \sum \limits _{w\in U}({d}_{v}-{d}_{w})\right) . \end{aligned}$$
(3)

When there is less than \(k\) vertices remained in the degree sequence, its not enough to form a group, which needs to have at least \(k\) elements to guarantee \(k\)-anonymity, so the vertices will be dispersed into their nearest groups.

The target degree of vertices in the same group is set to the largest degree of vertex in the group, and the vertices will be adjusted to the target degree in the graph modification step.

Complexity For degree sequences of size \(n\), the running time of the greedy_partition algorithmis O\((nk)\); for every node \(i\), the greedy_partition algorithm looks ahead at O\((k)\) other nodes in order to make the decision to merge the node with the previous group or to start a new group. Since there are n nodes, the total running time is O\((nk)\).

4.2 The graph_modification algorithm

Once the target degree sequence \(d^{'}\) is ready, we use Algorithm 2 to transform G to its \(k\)-anonymous graph \(G^{'}\). We recorded the communities of vertices with variable \(id\_communities\), which is dictionary. The key is the identifier of a vertex, and the value is a tuple, the elements of the tuple are the members of the community at different level. The community_multilevel method in igraph package [21] offers not only how vertices are separated into communities, but also exact history of how vertices are joined into larger communities with the parameter return_levels set True. We also treat the whole graph as a community, the highest level community, all vertices in the graph belong to it.

figure b

The anonymized degree sequence \(d\) indicates which node should modify its degree. For a vertex with \(d{{'}_{v}}-{{d}_{v}}>0\), it means that the vertex should increase its degree by \(d{{'}_{v}}-{{d}_{v}}>0\), we maintain a set \(V^{+}\) to record the vertices that should increase the degree.

For each vertex \(v\) in \(V^{+}\), we should increase its degree to make its degree be identical with its target degree. We first try to increase its degree by connecting the vertex with candidates that exists in the original graph. And the candidates are selected according to the following criteria: (1) the candidate should increase its degree, and the edge \((v,candidate)\) doesnt exist in the original graph; (2) the candidate vertex will be shrunk to the same community as low level as possible with the vertex; (3) if more than one vertex satisfies the above two criteria, then the vertex that has the shortest path length is selected. This process is undertaken by the Algorithm 3, find_candidates algorithm. We get the candidates within the communities at each level, and also sort the candidates by the social distance between the candidate and the vertex in ascending order.

figure c

After modifying the graph through adding edges, if there exists vertices still need to increase its degree, we try to modify the graph through adding vertices to the graph follow the step of [22] to guarantee that the degree of vertices in the original graph is equal to its target degree.

Complexity From line 2 to line 8 takes O\((n)\) to get the vertices that need to increase its degree to the traget degree; for line 9 to line 27 the worst case is O(\(n^{2}\)), the size of \(V^{+}\) is limited in \((n - n/k)\), where \(n/k\) denotes the number of anonymous groups, and the first node in each group will not adjust its degree. Practically, the size of \(V^{+}\) is very small compared with \(n\), so our graph_modification runs very fast.

4.3 \(k\)-Degree anonymity with vertex and edge modification

KDVEM algorithm combines the greedy_partition, graph_modification algorithms. The main idea of the proposed algorithm is to distort the community structure of the social network as less as possible, so the utility of the published social network is preserved well. The graph is transformed so that there are at least \(k\) vertices in each group, and all vertices in the same group have the same degree.

figure d

KDVEM first computes the degree sequence \(d\) of \(G\) in the descending order of degree. Then vertices are partitioned into anonymization groups in the greedy_partition step. There are at least \(k\) vertices in each group, so the \(k\)-anonymity principle is satisfied, and all vertices in the same group will be assigned the largest degree in the group as the target degree. The greedy_partition algorithm pass the target degree sequence \(d\) to the graph_modification step, in which vertices get its target degree through modifying the graph. The complete algorithm is described in Algorithm 4.

Complexity As pointed out in [19], the complexity of the multivelve method is linear on typical and sparse data, and the social network is exactly with spare property. The complexity of calulating \(allPairPathLength\) is O(\(n^{3}\)) by employing Floyed method, however, we can calculate it before running the KDVEM method, so the total complexity is O\((k*n)\).

5 Experiments and results

5.1 Experimental setup

In this section, we report the empirical result to evaluate the performance of our proposed approach. We compare our approach to the priority approach [14] proposed by Liu and Terzi, the FKDA [18] approach proposed by Lu et al., and the approach proposed by Chester et. al. which we call it VertexAdd [22]. All of the experiments have been implemented using Python. We vary the value of \(k\) in the range {2–10, 15, 20, 25, 50}. Due to the random choice of a node for operation of priority approach, we run the algorithm 10 times on each dataset and compute the average value of the measures. The experiments were conducted on Intel Xeon 2.53 GHz machine with 16 GB RAM running with Windows Server 2008 R2 Enterprise.

5.2 Datasets

In this experiment, we exam the algorithms on five real datasets: ca-HepTh [23], ca-CondMat [23], email-Enron [24], ca-AstroPh [23] and ca-GrQc [23].

The ca-HepTh, ca-CondMat, ca-AstroPh and ca-GrQc datasets are co-author citation networks of High Energy Physics Theory, Condensed Matter, Astro Physics and General Relativity respectively. The email-Enron is a network of Enron employees who have communicated by the Enron email. These five datasets are available at http://snap.stanford.edu/data/index.html.

Table 1 presents the original statistics properties of these datasets, including transitivity, ACC, and APL. All the graphs are simple, undirected, and unlabeled.

Table 1 Structural properties of datasets
Full size table

5.3 Evaluation measures

In order to evaluate the effectiveness of the proposed approach, we consider three important social network analysis measures: the transitivity, ACC, and APL, which has been described in Sect. 3. These measures are calculated on the outputs of both the anonymized and the original graphs.

We calculate the transitivity of the graph, which is the count of triangles and triples in the whole graph.

$$\begin{aligned} Transitivity=\frac{3*\Delta }{\Lambda } \end{aligned}$$
(4)

where \(\Delta \) is the number of triangles, and \(\Lambda \) is the number of connected triples.

We also calculate the average clustering coefficient. The clustering coefficient of a vertex is the fraction of possible triangles through the vertex that exist:

$$\begin{aligned} {{c}_{u}}=\frac{2T(u)}{\deg (u)(\deg (u)-1)} \end{aligned}$$
(5)

where \(T(u)\) is the number of triangles through node \(u\) and \(deg(u)\) is the degree of \(u\). Then the average clustering coefficient of a graph is defined as the average clustering coefficient of all the vertices.

5.4 Results

Figures 2a, 3a, 4a, 5a and 6a show the transitivity of the anonymized and original graphs as a function of \(k\). The horizontal constant lines represent the transitivity values of the original graphs.

The transitivity value of the anonymized graph tends to become smaller on ca-HepTh, ca-CondMat, ca-AstroPh and ca-GrQc, but larger on email-Enron. This is because the original transitivity measures of these four datasets are relatively higher. When adding edges to transform the graph to the \(k\)-degree anonymous version, triangles form slower than connected triples, just the reverse on email-Enron dataset.

Fig. 2
figure 2

Results on ca-HepTh

Full size image
Fig. 3
figure 3

Results on ca-CondMat

Full size image
Fig. 4
figure 4

Results on email-Enron

Full size image
Fig. 5
figure 5

Results on ca-AstroPh

Full size image
Fig. 6
figure 6

Results on ca-GrQc

Full size image

Figures 2b, 3b, 4b, 5b and 6b list the average clustering coefficient of the anonymized graphs as a function of \(k\) on the five graphs. The horizontal constant lines represent the ACC values of the original graphs.

From the figures, we can observe that the change of ACC on five datasets of all algorithms is quite low except the priority method, and the priority change very much on all the five datasets.

Figures 2c, 3c, 4c, 5c and 6c detail the average path length between vertex pairs of the anonymized graphs as a function of \(k\). The horizontal constant lines represent the APL values of the original graphs.

All figures show the trend that the average path length becomes shorter after the anonymization, this is because new edges are added to the original graph, and vertices having a bigger shortest path length are becoming smaller.

As the performance of our proposed approach with these of FKDA and VertexAdd is very close, we quantified the relative performance of these four approaches, in terms of the number of times they are first, second, third and fourth in each of the 15 case shown in Figs. 2, 3, 4, 5 and 6. If two methods gave a tie, for example, for first position for a given case, both methods were awarded one point for first position. It’s shown in Tables 2 and 3.

As we can see from Table 2, our KDVEM approach performs best on the ACC metric, FKDA outstands on the transitivity metric and VertexAdd approach preserves best on the APL metric. It’s hard to say which metric is more important than other metrics, so we took the three metrics equally and averaged the ranking score of the three metrics. It’s our KDVEM approach get the first place, so we think our KDVEM approach is better than the other three approaches on these metrics.

As we can see from Table 3, our KDVEM approach ranks first on the ca-CondMat dataset and ca-AstroPh dataset. By looking back on the Table 1, we hypothesizes that social networks with transitivity around 0.3 and ACC around 0.65 have some unique characters and our approach performe better on social network with these characters. We leave the verification task as a future work.

Table 2 Relative performance by metric
Full size table
Table 3 Relative performance by dataset
Full size table

To sum up, on the five datasets, with varying \(k\), our algorithm performs better than the other three algorithms. The whole experimental results clearly verify that our approach, which utilizes the notion of community structure in social network, can preserve more utility of the social network.

6 Conclusion

Privacy and utility are two main sides of social network anonymization. The utility of the anonymized social network will be inevitable decreased, as distortion are introduced in the anonyming process to guarantee the privacy from being breached. In this paper, we proposed a heuristic \(k\)-degree anonymization algorithm that anonymizes a graph by modifying the graph through adding edges and vertices. The utility of the published graph is well preserved with the help of community structure in the graph when adding edges to the graph. We have demonstrated our approach using a spectrum of experimental evaluation on real world datasets and we have shown that the algorithm we proposed preserves the utility very well. Especially there are many communities and the interaction between communities are relatively low.

As a future work, we plan to compare the performance of graph anonymization approaches that modify the graph through adding edges and adding vertices. We also plan to further investigate the problem of improving the utility of stronger privacy model, such as \(k\)-neighborhood, \(k\)-isomorphism, et al. Moreover, we plan to quantify the utility of the social network, in order to provide more guiding on the modification of graph to achieve \(k\)-anonymous. We are also intended to check the performance of our approach on the large social networks, such as Facebook, Twitter, et al.