1 Introduction

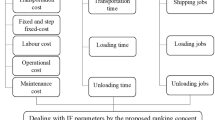
The classical transportation problem was discovered by Hitchcock (1941) as a special type of LPP that involves certain constrains. The main aim of solving the transportation problem is to minimize the total transportation cost that involves in the flow of commodity from wholesalers to consumers in the presence of some restrictions in the form of constraints. The constraints are generally considered over two features: availability of the sources and requirement of the consumer. In this highly competitive era, the purpose of organizations is to forge ways for creating and delivering values to customers. It has been observed that sometimes in transportation problem (TP), an additional cost is incurred along with the variable cost; this additional cost is called set-up cost or fixed cost. The TP that involves fixed cost is often referred to as fixed charge transportation problem (FCTP).

In FCTP, the commodities can be supplied from each origin to any destination at a shipping cost (unit cost of shipping commodity from plant to consumer) plus a fixed cost or set-up cost for opening that route or distribution center. In FCTP, it is a matter of fact that the amount which can flow by a particular route bears a fixed charge for that particular route. Further, when the route is occluding, in this case it is expressed by limiting its capacity to zero. In general, the FCTP is formulated as a 0–1 integer programming problems.

Earlier, the practitioners consider FCTP as a single stage problem, but with the need of time, it is extended to two-stage FCTP and multistage FCTP. With all these advancements in the formulation of FCTP, there arises a need to develop adequate algorithms to solve these problems. These problems have immense assortment of classical applications that have been chronicle in scheduling and facility location problem. Two of the most common among these problems are

  1. (1)

    In making plant location decision, where there is a need for opening the facility.

  2. (2)

    In transportation problems where there are fixed charges associated with transportation costs for transporting goods from source to destination.

The fixed charge includes toll charges on highways, landing fees at the airport, set-up cost in production systems or construction cost of roads.

In such type of complex decision-making problems, the available parameters for the system cannot be known exactly due to inadequate information, depletion of evidence and oscillating financial marketing conditions. For example, the provided data of transportation systems such as resources, demands and conveyance capacities may not be always absolute. The cost of the transportation depends on price of the fuel, charges of labor and taxes by government, and these factors vary with time. Fuzzy set theory introduced by Zadeh (1963) is extensively used and progressively applied to deal with these kinds of uncertainties.

In this paper, we have studied a two-stage FCTP with fuzzy demands, supplies and capacities. We have considered three objective functions (or goals), viz. minimization of total cost involved in the whole transportation process, maximization of the total quantity of items shipped and minimization of the total deterioration that occurs during the transportation. Fuzzy linguistic relations or preferences among the goals are studied as fuzzy relations for the transportation decision planning problem. We have used the approach studied by Aköz and Petrovic (2007), for dealing with the linguistic relations. An extension for the approach is also proposed for some nonlinear membership functions, i.e., exponential and hyperbolic membership functions. The main contributions of this study are stated as follows:

  1. 1.

    The two-stage FCTP with multiple objectives and fuzzy parameters is studied for the first time considering linguistic preferences among the objective functions.

  2. 2.

    For addressing the inequality relations among various supply and demand constraints of the proposed transportation problem, ranking fuzzy number approach is applied.

  3. 3.

    The fuzzy linguistic relations for the proposed problem is studied along with the application of some nonlinear membership functions to model the aspiration levels for the objective functions.

The rest of the paper is organized as follows: In Sect. 2, a brief literature on the existing work is discussed and research gap is identified. In Sect. 3, we have formulated a two-stage fixed charge transportation problem with fuzzy parameters. In Sect. 4, we have discussed solution methodology for solving the proposed model. In Sect. 5, a numerical experiment is conducted to show the validation and effectiveness of the model. In Sect. 6, results are discussed and finally, in Sect. 7, conclusion about the study is given.

2 Literature review

The FCTP is a distinctive case of fixed cost linear programming problem, formally introduced by Hirsch and Dantig (1968). It is also a special case of fixed charge network optimization problems, which plays a vital role in many distribution and network design problem (Nemhauser and Wolsey 1988). FCTP is much more difficult to solve in comparison with the linear problems. This is shown by Guisewite and Pardalos (1990) that most of the minimization network optimization problems with concave objective function, which includes fix charge, are NP hard. There are different solution approaches to solve these problems, (Balakrishnan et al. 1997; Ghiani et al. 2004) focuses on Branch and Bound, Lagrange relaxation and heuristic approach. Some other NP hard problems such as clustering problems also solved efficiently using the heuristic approaches (Abualigah and Khader 2017; Abualigah et al. 2017a, 2018c).

Several algorithms have been proposed for exact and approximate solution of FCTP, but exact solution algorithms are not useful in practical situations, because their required computational time is usually excessive (Sun et al. 1998). Murty (1968) contributed to introduce the idea of ranking extreme points in the establishment of general fixed charge problems. Geoffrion and Graves (1974) were the first to formulate the two-stage transportation problem and they have applied the Bender’s decomposition approach to solve the distribution problem.

Fixed charge solid transportation problem (FCSTP) has been studied by Yang and Liu (2007); in this study, all the quantities are taken as fuzzy numbers and different kind of mathematical models have been constructed on the basis of credibility theory. To solve these models they used tabu search algorithm and fuzzy simulation technique. Yang and Feng (2007) in their study presented a bi-criteria FCSTP and constructed three kind of goal programming models (namely, expected value goal programming model, chance constraint goal programming model and dependent chance constraint goal programming model) and then, hybrid algorithm was applied to solve these models. Jawahar and Balaji (2009) proposed a genetic algorithm to solve two-stage transportation problem, in which they have considered unit transportation cost along with the fix cost associated with each route. The study of fuzzy uncertainty is not limited to model decision planning models only. Some authors have also studied the involvement of fuzzy uncertainty in other complex mathematical problems such as, uncertainty differential equations (Arqub et al. 2016), fuzzy boundary value problems (Arqub et al. 2017), fuzzy Fredholm–Volterra integrodifferential equations (Arqub 2017).

After the developments and advancements in metaheuristic techniques, it has been widely adopted to solve FCTP. In their study, Gen and Li (1999) solved the bi-criteria FCTP with the help of genetic algorithm based on spanning tree representation. A solid transportation problem with discounted cost, fixed charge and vehicle cost was studied by Ojha et al. (2010). They considered available discount on items in the form of all unit discount or incremental quality discount or combination of these two, and the price depends upon the flow of commodity from source to destination. A model was presented by Molla-Alizadeh-Zavardehi et al. (2011) considering a two-stage model for fixed charge capacitated transportation problem (FCCTP). They have adopted artificial immune technique and genetic algorithm with prufer numbers to solve their model. Kundu et al. (2014) studied two types of FCTP with type-2 fuzzy parameters, they applied CV- based reduction method to convert type-2 fuzzy variables into type-1, and for complete defuzzification, centroid method was used.

Giri et al. (2014) studied FCSTP, considering flow of multiple items. In their study, two aspects of the problem were covered by them. In first aspect, they considered fully fuzzy fixed charge multi-item solid transportation problem (i.e., direct costs, fixed charges, supply of plant, demand of customer, capacity of conveyance and transported quantities are all fuzzy). In the second aspect, the decision variables (i.e., transported quantities) were considered as crisp numbers. Pramanik et al. (2015) studied two-stage supply chain network for FCTP with Gaussian type-2 fuzzy numbers. Zhang et al. (2016) proposed a FCTP under uncertain environment and discussed hybrid intelligent and tabu search algorithm to solve their problem. They have also compared their work with the existing methodologies for solving uncertain FCTP. Sadeghi-Moghaddam et al. (2017) proposed solution techniques for FCTP using two different metaheuristic approaches (i.e., priority-based representation and spanning tree-based prufer numbers). Hajiaghaei-Keshteli et al. (2018) presented a new metaheuristic approach named as keshtel algorithm for solving FCTP. Majumder et al. (2018) presented a multi-item FCSTP involving some budget constraints.

3 Fuzzy multi-objective model for two-stage FCTP

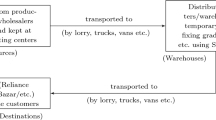
The FCTP formulated in this study is a two-stage transportation decision planning problem. The problem initiates with the establishment of the plants and the flow of commodities between plants to customers. The FCTP consist two types of costs, direct cost and fixed cost. Direct costs are unit transportation cost to transport product from source to destination, while the fixed cost is associated with different routes. During the first stage, the flow of items is considered from the manufacturing sites (plants) to the distribution centers, whereas in the second stage, the products are considered to be shipped from the distribution centers to the customers.

For the formulation of the model, we have employed the following nomenclature:

Nomenclature

Indices set

\( i \)

Index of plants \( i = 1,2, \ldots ,p \)

\( j \)

Index of distribution centers \( j = 1,2, \ldots ,q \)

\( k \)

Index of customers \( k = 1,2, \ldots ,r \)

Parameters

\( C_{ij} \, \)

Cost per unit transportation from plant \( i \) to distribution center \( j \)

\( F_{ij} \)

Fixed charge associated from plant \( i \) to distribution center \( j \)

\( A_{jk} \)

Cost per unit of transportation from distribution center \( j \) to customer \( k \)

\( B_{jk} \)

Fixed charge associated with shipment from distribution center \( j \) to customer \( k \)

\( \widetilde{\text{SUP}}_{i} \)

Fuzzy supply available at plant \( i \)

\( \widetilde{\text{CAP}}_{j} \)

Fuzzy capacity available at distribution center \( j \)

\( \widetilde{\text{DEM}}_{k} \)

Fuzzy demand required by the customer \( k \)

\( T_{ij} \)

Total transportation time from plant \( i \) to distribution center \( j \)

\( T_{jk} \)

Total transportation time from distribution center \( j \) to customer \( k \)

\( D_{ij} \)

Per thousand numbers of items deterioration during the transportation from plant \( i \) to distribution center \( j \)

\( D_{jk} \)

Per thousand numbers of items deterioration during the transportation from distribution center \( j \) to customer \( k \)

Decision variables

\( P_{ij} \)

Quantity to be shipped from plant \( i \) to distribution center \( j \)

\( Q_{jk} \)

Quantity to be shipped from distribution center \( j \) to customer \( k \)

3.1 Model formulation

A multi-objective two-stage transportation problem involving two types of transportation costs (viz. unit transportation cost and fixed charge cost) is considered in this study.

The first objective function is to minimize the total transportation cost, second is to maximize the total product transported during the whole transportation process, and the third one is to minimize the total product deterioration during the transportation process.

In this problem the supply of plant, the capacity of distribution center and the demand of customers are all assumed to be fuzzy quantities.

3.1.1 Objective functions

The first objective function (1) as discussed earlier, deals with the minimization of the total cost incurred in the whole transportation process. The objective function (1) combines the varying and fixed costs for both the stages of the transportation process

$$ {\text{Min}}\,Z_{1} = \sum\limits_{i\, = \,1}^{p} {\sum\limits_{j\, = \,1}^{q} {C_{ij} P_{ij} + \sum\limits_{i\, = \,1}^{p} {\sum\limits_{j\, = \,1\,}^{q} {F_{ij} \delta_{ij} + \sum\limits_{j\, = \,1}^{q} {\sum\limits_{k\, = \,1}^{r} {A_{jk} Q_{jk} + \sum\limits_{j\, = \,1}^{q} {\sum\limits_{k\, = \,}^{r} {B_{jk} \lambda_{jk} } } } } } } } } $$
(1)

The second objective function (2) is considered to be the maximization of the total products shipped at both stages of the transportation process. Since, the demand of the products should be less than or equal to the availability of the products, the cost minimization models generally give transportation scheme with a lot of products left at the suppliers. To reduce the left over products at the suppliers, the second objective function (2) is formulated as a contrasting or conflicting objective to objective function (1).

$$ Max\,Z_{2\,} = \sum\limits_{i\, = \,1}^{p} {\sum\limits_{j\, = \,1}^{q} {P_{ij} } } + \sum\limits_{j = \,1}^{q} {\sum\limits_{k = \,1}^{r} {Q_{jk} } } $$
(2)

Many times, transportation of the products leads to some sort of deteriorations or defects in the products. The deterioration majorly depends upon the selection of the mode of transportation as well the route chosen for the transportation. A good transportation scheme is the one that minimizes the total defects during the transportation along with optimizing the other factors. The third objective function (3) is formulated so as to minimize the total deterioration of the products during the transportation process.

$$ {\text{Min}}\,Z_{3} = \sum\limits_{i\, = \,1}^{p} {\sum\limits_{j\, = \,1}^{q} {D_{ij} P_{ij} + \sum\limits_{j\, = \,1}^{q} {\sum\limits_{k\, = \,1}^{r} {D_{jk} Q_{jk} } } } } $$
(3)

3.1.2 Constraints

The constraint (4) ensures that the quantity shipped from plant \( i \) to distribution center \( j \) should be less than or equal to the supply capacity of the plant \( i \).

$$ \sum\limits_{j\, = \,1}^{p} {P_{ij} \le \widetilde{\text{SUP}}_{i} } ;\quad i = 1,2, \ldots ,p $$
(4)

The constraint (5) ensures that the total amount received by the distribution center should be equal to the demand of the customers.

$$ \sum\limits_{j\, = \,1\,}^{q} {Q_{jk} = \widetilde{\text{DEM}}_{k} ;\quad k = 1,2, \ldots ,q} $$
(5)

The constraint (6) ensures that the flow of commodity at stage one takes place only if \( P_{ij} \, > \,0 \). The amount

$$ P_{ij} \, \le \,t_{ij} \delta_{ij} \,\, $$
(6)

Provide that \( t_{ij} = { \hbox{min} }\{ \widetilde{\text{SUP}}_{i} ,\;\widetilde{\text{CAP}}_{j} \} \)

where, \( \delta_{ij} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad {\text{if}}\,P_{ij} = 0} \hfill \\ 1 \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \)

whereas, constraint (7) ensures that the flow of the commodity at stage two should not exceed the minimum possible amount of commodity available for the shipment.

$$ Q_{jk} \, = \,W_{jk} \lambda_{jk} $$
(7)

Provided that \( W_{jk} = \hbox{min} \,\{ \widetilde{\text{CAP}}_{j} ,\;\widetilde{\text{DEM}}_{k} \} \)

where, \( \lambda_{jk} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad {\text{if}}\;Q_{jk} = 0} \hfill \\ 1 \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \)

The constraint (8) represents the restriction that the supply capacity at plant \( i \) must be greater than or equal to the demand of the customer \( k \).

$$ \sum\limits_{i\, = \,1}^{p} {\widetilde{\text{SUP}}_{i} \ge \sum\limits_{k\, = \,1}^{r} {\widetilde{\text{DEM}}_{k} } } $$
(8)

The constraint (9) ensures the flow conservation of the system, i.e., amount shipped by the plant is equal to the amount received by the customers.

$$ \sum\limits_{i\, = \,1}^{p} {P_{ij} \, = \,\sum\limits_{k\, = \,1}^{r} {Q_{jk} } } $$
(9)

The constraint (10) ensures the nonnegativity restriction for the decision variables.

$$ P_{ij} \ge 0\quad {\text{and}}\quad Q_{jk} \ge 0 $$
(10)

4 Solution methodology

4.1 Conversion of fuzzy constraints

In this study, we have adopted the method given by Jiménez et al. (2007), proposed to deal with the linear programming problems involving coefficients that are fuzzy in nature. The method permitted the interactive participation of decision maker at each step of the problem. The decision makers are allowed to express their opinion in the form of linguist terms. Díaz-Madroñero (2014a, b) extended this approach for material requirement problem that involves integrity and equality conditions.

Let us consider the following multi-objective linear programming problem with fuzzy parameters only in constraints

$$ \left\{ {\begin{array}{*{20}l} {{\text{Min}}\;\;Z = f(x)} \hfill \\ {{\text{sub}}\,{\text{to}}\;\;g(x) = \left\{ {x \in R^{n} /\tilde{a}_{i} x \le \tilde{b}_{i} ;\quad i = 1,2, \ldots ,m,\,\,x \ge 0} \right\}} \hfill \\ \end{array} } \right. $$
(11)

where \( \tilde{a}_{i} \) and \( \tilde{b}_{j} \) represent fuzzy parameters involved in the constraints.

For defining the possibility distribution of fuzzy parameters, fuzzy trapezoidal number of the form \( \left( {a_{1} ,\,a_{2} ,\,a_{3} ,\,a_{4} } \right) \) is taken into consideration for characterization. The expected interval of fuzzy trapezoidal number is denoted by \( {\text{EI}}(\tilde{a}) \) and it can be defined as

$$ {\text{EI}}(\tilde{a}) = \left[ {E_{1}^{a} ,\,E_{2}^{a} } \right] = \left[ {\frac{1}{2}\left( {a_{1} + a_{2} } \right),\,\frac{1}{2}\left( {a_{3} + a_{4} } \right)} \right] $$
(12)

The expected value of a fuzzy number, denoted as \( {\text{EV}}(\tilde{a}) \), is the half point of its expected interval (Heilpern 1992).

$$ {\text{EV}}(\tilde{a}) = \frac{{E_{1}^{a} \, + \,E_{2}^{a} }}{2}\quad {\text{and}}\quad = \frac{1}{4}\left( {a_{1} + a_{2} + a_{3} + a_{4} } \right) $$
(13)

By applying the approach introduced by Jiménez (1996), the fuzzy relation has been used to compare the fuzzy numbers. The relationship for two fuzzy numbers \( \tilde{a}_{1} \) and \( \tilde{a}_{2} \), the degree \( \alpha \) in which \( \tilde{a}_{1} \) is greater than \( \tilde{a}_{2} \) can be defined as follows

$$ \mu (\tilde{a}_{1} ,\tilde{a}_{2} ) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad {\text{if}}\;E_{2}^{{a_{1} }} - E_{1}^{{a_{2} }} < 0} \hfill \\ {\frac{{E_{2}^{{a_{1} }} - E_{1}^{{a_{2} }} }}{{E_{2}^{{a_{1} }} - E_{1}^{{a_{2} }} - (E_{1}^{{a_{1} }} - E_{2}^{{a_{2} }} )}}} \hfill & {\quad {\text{if}}\; 0\in \left[ {E_{ 1}^{{a_{1} }} - E_{2}^{{a_{2} }} ,E_{2}^{{a_{1} }} - E_{1}^{{a_{2} }} } \right]} \hfill \\ 1 \hfill & {\quad {\text{if}}\;E_{1}^{{a_{1} }} - E_{2}^{{a_{2} }} > 0} \hfill \\ \end{array} } \right. $$
(14)

where in the above relation \( [E_{1}^{{a_{1} }} ,\,E_{2}^{{a_{1} }} ] \) and \( [E_{1}^{{a_{2} }} ,\,E_{2}^{{a_{2} }} ] \) are the expected intervals for the given fuzzy numbers \( \tilde{a}_{1} \) and \( \tilde{a}_{2} \). If \( \mu \left( {\tilde{a}_{1} ,\tilde{a}_{2} } \right) \ge \alpha \), it is said that \( \tilde{a}_{1} \) is bigger than or equal to \( \tilde{a}_{2} \) by at least a degree \( \alpha \) and it can be represented as \( \tilde{a}_{1\,} \ge {}_{\alpha }\tilde{a}_{2} \).

On applying approach discussed by Jiménez et al. (2007) the multi-objective problem (11) can be easily converted into crisp equivalent parametric problem as follows:

$$ \left\{ {\begin{array}{*{20}l} {{\text{Min}}\,\,Z = f(x)} \hfill \\ {{\text{sub}}\,{\text{to}}\,\,\left[ {(1 - \alpha )E_{1}^{{a_{i} }} + \alpha E_{2}^{{a_{i} }} } \right]x \le \alpha E_{1}^{{b_{i} }} + (1 - \alpha )E_{2}^{{b_{i} }} ;\quad i = 1,2, \ldots ,m,} \hfill \\ {x \ge 0\quad {\text{and}}\quad \alpha \in \left[ {0,1} \right]} \hfill \\ \end{array} } \right. $$
(15)

where \( \alpha \) is the feasibility degree of the decision to which at least all the constrains must be satisfied. Therefore, by applying the above discussed approach to the two-stage multi-objective fixed charge transportation problem formulated in Sect. 3.1, and by considering trapezoidal fuzzy numbers, we obtain the following parametric model in which parameter \( \alpha \) represents the degree of fulfillment of fuzziness.

Equation (1)–(3)

subject to

$$ \sum\limits_{j\, = \,1}^{q} {P_{ij} \le \frac{\alpha }{2}\frac{{{\text{SUP}}_{i} 1 + {{{\text{SUP}}_{i} }}2}}{2}} + \left( {1 - \frac{\alpha }{2}} \right)\frac{{{\text{SUP}}_{i} 3 + {{{\text{SUP}}_{i} }}4}}{2} $$
(16)

Provided that \( P_{ij} \, \le \,\tilde{t}_{ij} \delta_{ij} \)

Where \( \tilde{t}_{ij} = \hbox{min} \,\{ \widetilde{\text{SUP}}_{i} ,\,\widetilde{\text{CAP}}_{j} \} \)

$$ \sum\limits_{j\, = \,1}^{q} {Q_{jk} \le \frac{\alpha }{2}\frac{{{\text{DEM}}_{k} 1 + {\text{DEM}}_{k} 2}}{2} + \left( {1 - \frac{\alpha }{2}} \right)\frac{{{\text{DEM}}_{k} 3 + {\text{DEM}}_{k} 4}}{2}} $$
(17)

Provided that \( Q_{jk} \, \le W_{jk} \lambda_{jk} \)

Where \( \tilde{W}_{jk\,} = \hbox{min} \,\{ \widetilde{\text{CAP}}_{j} ,\,\widetilde{\text{DEM}}_{k} \} \)

$$ \sum\limits_{i\, = \,1}^{p} {\left\{ {\frac{\alpha }{2}\frac{{{\text{SUP}}_{i} 1 + {\text{SUP}}_{i} 2}}{2} + \left( {1 - \frac{\alpha }{2}} \right)\frac{{{\text{SUP}}_{i} 3 + {\text{SUP}}_{i} 4}}{2}} \right\} \ge \sum\limits_{k\, = \,1}^{r} {\left\{ {\frac{\alpha }{2}\frac{{{\text{DEM}}_{k} 1 + {\text{DEM}}_{k} 2}}{2} + \left( {1 - \frac{\alpha }{2}} \right)\frac{{{\text{DEM}}_{k} 3 + {\text{DEM}}_{k} 4}}{2}} \right\}} } $$
(18)

and Eqs. (8)–(10)

4.2 Fuzzy goal programming

Fuzzy goal programming approach is a very widely used technique to deal with the multi-objective optimization problems. For the first time Zimmermann (1978) introduced this technique. As its name indicates, fuzzy aspiration levels for each objective function are established with the help of decision makers’ preferences or some upper and lower bounds. With the maximization of the aspiration levels as objective function, a parameter or degree (say \( \alpha \)) is taken into consideration up to which the constraints are fulfilled. So, the solution set which is achieved when all constraints fulfilled a degree \( \alpha \) is represented as \( F_{\alpha } (x) \). Several values can be assigned for this, by keeping in mind decision maker preferences, as;

$$ \alpha = \left\{ {0.1,\,0.2,\,0.3,\,0.4,\,0.5,\,0.6,\,0.7,\,0.8,\,0.9,\,1} \right\} $$
(19)

For formulating the fuzzy aspiration level for \( n^{th} \) objective function, upper and lower limits \( \overline{Z}_{n} \) and \( \underline{Z}_{n} \) are considered by the DM. The membership function for the fuzzy sets is given as follows

  1. (a)

    Linear membership function

The elements in the linear membership functions follow pattern of a linear function. The linear membership function is mathematically expressed as Eq. (20) and diagrammatically as Fig. 1.

$$ \psi_{n} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad {\text{if}}\,\,Z_{n} \le \underline{Z}_{n} } \hfill \\ {\frac{{\overline{Z}_{n} - Z_{n} }}{{\overline{Z}_{n} - \underline{Z}_{n} }}} \hfill & {\quad {\text{if}}\,\,\underline{Z}_{n} \le Z_{n} \le \overline{Z}_{n} } \hfill \\ 0 \hfill & {\quad {\text{if}}\,\,Z_{n} \ge \overline{Z}_{n} } \hfill \\ \end{array} } \right. $$
(20)
Fig. 1
figure 1

Representation of linear membership function

Full size image
  1. (b)

    Exponential membership function

The exponential membership function is expressed as in Eq. (21) and is represented in Fig. 2.

$$ \psi_{n} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,\,Z_{n} \le \underline{Z}_{n} } \hfill \\ {\frac{{{\text{e}}^{{ - h\omega_{n} (x)}} - {\text{e}}^{ - h} }}{{1 - {\text{e}}^{ - h} }}} \hfill & {{\text{if}}\,\,\underline{Z}_{n} < Z_{n} < \overline{Z}_{n} } \hfill \\ 0 \hfill & {{\text{if}}\,\,Z_{n} \ge \overline{{Z_{n} }} } \hfill \\ \end{array} } \right. $$
(21)

where \( \omega_{n} (x) = \frac{{\underline{Z}_{n} - Z_{n} }}{{\underline{Z}_{n} - \overline{Z}_{n} }},\quad n = 1,2, \ldots ,N\,\;{\text{and}}\,\;h \) is a nonzero parameter.

Fig. 2
figure 2

Representation of exponential membership function

Full size image
  1. (c)

    Hyperbolic membership function

The mathematical function for the hyperbolic membership function is denoted by Eq. (22) and represented as in Fig. 3.

$$ \psi_{n} (x) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {\quad {\text{if}}\,\,Z_{n} \le \underline{Z}_{n} } \hfill \\ {\frac{1}{2} + \frac{1}{2}\frac{{{\text{e}}^{{\{ (\overline{Z}_{n} + \underline{Z} )/2 - Z_{n} \} \delta_{n} }} - {\text{e}}^{{ - \{ (\overline{Z}_{n} + \underline{Z} )/2 - Z_{n} \} \delta_{n} }} }}{{{\text{e}}^{{\{ (\overline{Z}_{n} + \underline{Z} )/2 - Z_{n} \} \delta_{n} }} + {\text{e}}^{{ - \{ (\overline{Z}_{n} + \underline{Z} )/2 - Z_{n} \} \delta_{n} }} }}} \hfill & {\quad {\text{if}}\,\,\underline{Z}_{n} < Z_{n} < \overline{Z}_{n} } \hfill \\ 0 \hfill & {\quad {\text{if}}\,\;Z_{n} \ge \overline{{Z_{n} }} } \hfill \\ \end{array} } \right. $$
(22)

where \( \delta_{n} \, = \,\frac{6}{{\overline{Z}_{n} \, - \,\underline{Z}_{n} }} \)

Fig. 3
figure 3

Representation of hyperbolic membership function

Full size image

The membership functions represented in (20), (21) and (22) are used in this paper to establish the aspiration levels for the objective functions.

4.3 Fuzzy linguistic relations among goals

After determining the fuzzy aspiration levels as given in Sect. 4.2, the objective functions or goals are considered with imprecise preference relations rather than with weights (representing priority or importance of that goal). Aköz and Petrovic (2007) introduced this approach of establishing the preferences of the objective functions in linguistic terms. This approach is quite realistic than assigning some crisp values in the form of weights to prioritize the objective functions. The fuzzy linguistic approach is mainly developed to deal with two main difficulties that arises while using weighted fuzzy goal programming approach

  1. (1)

    The relation between solution and weights is not same as expected.

  2. (2)

    Difficulties arise at the time of assigning weights to different goals.

A fuzzy binary relation \( \tilde{R}(n,m) \) is used to define the imprecise preferences among the goals by a membership function. These membership functions define the degree of satisfaction of fuzzy linguistic relations. To express these fuzzy relations, linguistic terms may be use such as—\( \tilde{R}_{1} (n,m) \) as ‘nth goal is slightly important than mth goal’; \( \tilde{R}_{2} (n,m) \) as ‘nth goal is moderately important than mth goal’; and \( \tilde{R}_{3} (n,m) \) as ‘nth goal is significantly more important than mth goal.

The membership function related to these linguistic terms are given as follows:

$$ \psi_{{\tilde{R}_{1} (n,m)}} = \left\{ {\begin{array}{*{20}l} {\psi_{n} - \psi_{m} + 1} \hfill & {\quad {\text{if}}\,\, - 1 \le \psi_{n} - \psi_{m\,} \le 0} \hfill \\ 1 \hfill & {\quad {\text{if}}\,\,0 \le \psi_{n} - \psi_{m} \le 1} \hfill \\ \end{array} } \right. $$
(23)
$$ \psi_{{\tilde{R}_{2} (n,m)}} = \frac{{\psi_{n} - \psi_{m} + 1}}{2}\quad {\text{if}}\;\; - 1 \le \psi_{n} - \psi_{m} \le 1 $$
(24)
$$ \psi_{{\tilde{R}_{3} (n,m)}} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad {\text{if}}\;\; - 1 \le \psi_{n} - \psi_{m} \le 0} \hfill \\ {\psi_{n} - \psi_{m} } \hfill & {\quad {\text{if}}\;\;0 \le \psi_{n} - \psi_{m} \le 1} \hfill \\ \end{array} } \right. $$
(25)

In order to incorporate the preferences of the goals assigned by the DM, a new function for the maximization of achievement of the goals is defined. This achievement function is the sum of satisfaction degree of the fuzzy linguistic relations and fuzzy goals achievement degrees. Hence, fuzzy hierarchy goal programming is formulated as follows

$$ {\text{Max}}\,\,\,\eta \left( {\sum\limits_{{{\text{n}} = 1}}^{\text{K}} {\psi_{n} } } \right) + (1 - \eta )\left( {\sum\limits_{n\, = \,1}^{K} {\sum\limits_{m\, = \,1}^{K} {b_{nm} \psi_{{\tilde{R}(n,m)}} } } } \right) $$
(26)
$$ \psi_{n} \le 1\quad \forall K $$
(27)
$$ \psi_{m} \ge 0\quad \forall \,K $$
(28)
$$ \psi_{n} - \psi_{m} + 1 \ge \psi_{{\tilde{R}_{1} (n,m)}} \quad \forall \,b_{nm} = 1 $$
(29)
$$ \frac{{\psi_{n} - \psi_{m} + 1}}{2} \ge \psi_{{R_{2} (n,m)}} \quad \forall \,b_{nm} = 1 $$
(30)
$$ \psi_{n} - \psi_{m} \ge \psi_{{\tilde{R}_{3} (n,m)}} \quad \forall \,b_{nm} = 1 $$
(31)
$$ 0 \le \psi_{{\tilde{R}(n,m)\,}} \le 1 $$
(32)
$$ ax \le b $$
(33)
$$ x \ge 0 $$
(34)
$$ \eta \,\, \in \,\,[0,1] $$
(35)

where, \( b_{nm} \) is a binary variable and takes value 1 if an fuzzy linguistic relation is considered between nth and mth goals, and 0 otherwise.

And \( \psi_{n} \) is the membership functions (linear, exponential and hyperbolic) of nth objective and \( \psi_{{\tilde{R}(n,m)}} \) the fuzzy reference relation level between objectives n and m. Here, \( \eta \) is a parameter that is allowed to take values between 0 and 1. With decrease in the value of \( \eta \), fuzzy linguistic preferences of the goal achieve more importance; therefore, more solutions can be obtained that satisfy these preferences.

In the multi-objective two-stage FCTP problem formulated in this paper, it is considered that second objective function (2) is slightly more important than the third objective function (3) (i.e., type 1 relationship \( \tilde{R}_{1} \) between objectives 2nd and 3rd), first objective (1) is moderately important than the second objective (2) (i.e., here exist second type of relationship \( \tilde{R}_{2} \) between objective 2nd and 3rd), first objective function (1) is significantly more important than third objective function (3) (i.e., here exist type three relation between 1st and 3rd objective).

Hence, by assigning different values to \( \alpha \), as represented in Eq. (19), we can obtain different models. Now for the different values of parameter \( \eta \), different solutions can be obtained.

Based on the goal programming model (26)–(35), equivalent model for the initial problem (1)–(10) can be given as follows

$$ {\text{Max}}\,\,\,\eta \,\left( {\psi_{1} + \psi_{2} + \psi_{3} } \right) + (1 - \eta )\left( {\psi_{{\tilde{R}_{1} (2,3)}} + \psi_{{\tilde{R}_{2} (1,2)}} + \psi_{{\tilde{R}_{3} (1,3)}} } \right) $$
(36)
$$ \psi_{1} \le 1 $$
(37)
$$ \psi_{2} \le 1 $$
(38)
$$ \psi_{3} \le 1 $$
(39)
$$ \psi_{1} - \psi_{3} + 1 \ge \psi_{{\tilde{R}_{1} (2,3)}} $$
(40)
$$ \frac{{\psi_{1} - \psi_{2} + 1}}{2} \ge \psi_{{\tilde{R}_{2} (1,2)}} $$
(41)
$$ \psi_{1} - \psi_{3} \ge \psi_{{\tilde{R}_{3} (1,3)\,}} $$
(42)
$$ 0 \le \psi_{{\tilde{R}_{1} (2,3)}} \le 1 $$
(43)
$$ 0 \le \psi_{{\tilde{R}_{2} (1,2)}} \le 1 $$
(44)
$$ 0 \le \psi_{{\tilde{R}_{3} (1,3)}} \le 1 $$
(45)
$$ {\text{Eq}}\;(16){-}\left( {18} \right) \, \& {\text{ Eq}}. (9) - (10) $$
(46)

4.4 Stepwise procedure for the problem

Step 1:

A multiple objective two-stage FCTP is formulated with fuzzy constraint parameters as represented by (1)–(10)

Step 2:

For converting the fuzzy constraint equations to their equivalent crisp form, the approach by Jiménez et al. (2007) is adopted, as explained in Sect. 4.1

Step 3:

Fuzzy aspiration levels for the objective functions are established in the form of linear, exponential and hyperbolic membership functions, represented by (20), (21) and (22), respectively

Step 4:

Membership functions for the fuzzy linguistic preferences are established as given by Eqs. (23), (24) and (25)

Step 5:

Final fuzzy goal programming model is formulated as given by model (36)–(46)

Step 6:

The model (36)–(46) is solved for different membership functions and for different values of \( \eta \) and \( \alpha \)

5 Numerical illustration

In this section, we have studied a numerical problem to show the efficiency of the proposed model. In this problem we have considered a double-staged transportation scenario where at the first stage, the products are shipped from the suppliers to the distributers, whereas at the second stage, the products are transported from the distributers and finally reaches the customers. Three objective functions are considered for the described numerical problem viz. minimization of total cost, maximization of the total items transported and minimization of the total defects that occur during the transportation.

Let us consider a logistic firm that deals with the operation of transporting goods from the suppliers to the customers. There are ten different suppliers that are shipping the manufactured products to seven different distributers. Once the product reaches the distributers, they deal with the further shipment of the products to fifteen different customers. The associated unit fixed and varying transportation costs for each possible routes at the first and second stage is presented in Tables 1, 2, 3 and 4, respectively.

Table 1 Fixed cost for the transportation of unit product from suppliers to distributers
Full size table
Table 2 Fixed cost for the transportation of unit product from distributers to customers
Full size table
Table 3 Varying cost for the transportation of unit product from suppliers to distributers
Full size table
Table 4 Varying cost for the transportation of unit product from distributers to customers
Full size table

The associated fixed and varying costs acts as coefficients for the first objective as explained in Sect. 3, whereas the second objective involves only the decision variables and no coefficients associated with it. The third objective function deals with the minimization of total defects that occur during transportation. Tables 5 and 6 show the number of defects per thousand products during transportation at first and second stage, respectively.

Table 5 Defect rate (per thousand) in product transported from suppliers to distributers
Full size table
Table 6 Defect rate (per thousand) in products transported from distributers to customers
Full size table

The availability of products at the suppliers, capacities at the distributers and demand of customers are all considered to be trapezoidal fuzzy numbers. All the data involved in the constraints are considered keeping in view that it does not affect the flow of the products at the consecutive stages. Tables 7, 8 and 9 represent the availabilities, capacities and demands at the three consecutive nodes, respectively.

Table 7 Fuzzy data for the availabilities at different suppliers
Full size table
Table 8 Fuzzy data for the capacities of the different distributers
Full size table
Table 9 Fuzzy data for the demands of different customers
Full size table

6 Result and discussion

The multi-objective decision planning model given by Eqs. (36)–(46) is solved for the given data, the results are explained and evaluated in this section. The nonlinear problem obtained is coded in AMPL and solved by Knitro 10.3.0 solver through NEOS server. The results are obtained for the different values of \( \eta \) and \( \alpha \) that are recorded and analyzed.

For the model with linear membership function, the values of the objective function (\( Z \)) are given in Table 10. It is clear from Table 10 that, the value of (\( Z \)) increases with increase in the value of \( \eta \), whereas there is no significant change in values with increase in the values of \( \alpha \). This increase is because of the increase in values of associated weights (\( \eta \)), which is directly influencing the values of the membership functions of the three objective functions. Hence, value of the objective function (\( Z \)) is highest for the highest value degree of feasibility (\( \alpha \)) and weights (\( \eta \)). For the compromise values of the first objective function (\( Z_{1} \)), the cost decreases with increase in the relative weight (\( \eta \)) and increases with the increase in the feasibility degree (\( \alpha \)) as given in Table 11. The best value (minimum) for the first objective function is attained at the \( \alpha \) = 0.1 and \( \alpha \) = 0.9. This trend is noticed because the increment in the assigned weight value (\( \eta \)) gives more preference to the sum of the membership functions for the objective functions and less importance to the degree of feasibility. Similarly, Tables 12 and 13 represent the compromise values of the second and third objective functions, respectively. The second objective function (\( Z_{2} \)) is of maximization type and it remains unchanged with change in the value of \( \eta \), where its value decreases with increase in the value of \( \alpha \). For the third objective function (\( Z_{3} \)), the best compromise value is obtained at \( \alpha \) = 0.9 and \( \eta \) = 0.5. Figure 4 represents the change in the values of objective functions or goals at different values of \( \eta \) and \( \alpha \).

Table 10 Compromise value of \( Z \) for linear membership function
Full size table
Table 11 Compromise value of \( Z_{1} \) for linear membership function
Full size table
Table 12 Compromise value of \( Z_{2} \) for linear membership function
Full size table
Table 13 Compromise value of \( Z_{3} \) for linear membership function
Full size table
Fig. 4
figure 4

Representation of objective function and goals for linear membership function

Full size image

Table 14 represents the values of objective function (\( Z \)) for the exponential membership functions. Similarly, the values of first, second and third objective functions are given in Tables 15, 16 and 17, respectively, for different values of \( \eta \) and \( \alpha \). At \( \eta \) = 0.9, the value of \( Z \) becomes stable for each value of \( \alpha \),whereas for other values of \( \eta \), the value of \( Z \) is not exactly stable, but almost unchanged for any change in \( \alpha \). The compromise value of first objective or goal (\( Z_{1} \)) is minimum at \( \eta \) = 0.1 and \( \alpha \) = 0.9, which is the best value for that goal. With increase in \( \eta \), the value of \( Z_{1} \) increases less significantly up to \( \eta \) = 0.5, and it increases with a remarkable rate when \( \eta \) = 0.9. This pattern is seen because of the involvement of exponential membership function. The best value of \( Z_{2} \) is achieved at \( \alpha \) = 0.9 and is same for all the values of \( \eta \). Similarly, the best compromise value for the third objective (\( Z_{3} \)) is obtained at \( \eta \) = 0.1 and \( \alpha \) = 0.7. The pattern of variation in the values of objective functions for the exponential membership function is represented in Fig. 5.

Table 14 Compromise value of \( Z \) for exponential membership function
Full size table
Table 15 Compromise value of \( Z_{1} \) for exponential membership function
Full size table
Table 16 Compromise value of \( Z_{2} \) for exponential membership function
Full size table
Table 17 Compromise value of \( Z_{3} \) for exponential membership function
Full size table
Fig. 5
figure 5

Representation of objective function and goals for exponential membership function

Full size image

For the hyperbolic membership function, the values of the objective function and goals are, respectively, given in Tables 18, 19, 20 and 21. The objective function value (\( Z \)) is increasing with increase in the value of \( \eta \) where it is unchanged with every change in the value of \( \alpha \). For the minimization type objective function (\( Z_{1} \)), the compromise value is worst near \( \eta \) = 0.5 and best near \( \eta \) = 0.9, whereas the value (\( Z_{1} \)) not changing in a regular pattern with change in the value of \( \alpha \). The compromise value of second objective function (\( Z_{2} \)) is increasing slightly with increase in the value of \( \alpha \), while it is not in regular pattern with respect to the change in the value of parameter \( \eta \). Similarly, the compromise value of third objective function (\( Z_{3} \)) is not following any pattern with increase and decrease in the values of \( \eta \) and \( \alpha \). The diagrammatic representation of the compromise values of the objective function and goals for hyperbolic function is shown in Fig. 6.

Table 18 Compromise value of \( Z \) for hyperbolic membership function
Full size table
Table 19 Compromise value of \( Z_{1} \) for hyperbolic membership function
Full size table
Table 20 Compromise value of \( Z_{2} \) for hyperbolic membership function
Full size table
Table 21 Compromise value of \( Z_{3} \) for hyperbolic membership function
Full size table
Fig. 6
figure 6

Representation of objective function and goals for hyperbolic membership function

Full size image

7 Conclusion

In this paper, a transportation planning decision model with fixed charge and two-stage is studied in formulating the problem. The proposed model is formulated with three objectives (or goals) that are to be considered simultaneously. The first objective function is for the minimization of total transportation cost at both the stages. Maximization of the total quantity of the products to be shipped from the manufacturing plant to the distributers and from the distributers to the customers is considered as the second objective function, whereas the minimization of the total deterioration that may occur during the whole transportation process is taken as the third objective. The availabilities, capacities and the demand are all assumed to be uncertain and more specifically trapezoidal fuzzy numbers. Fuzzy linguistic relations or preferences are also studied and formulated between the three conflicting objective functions. The fuzzy linguistic preferences are discussed in details, and a fuzzy goal programming-based solution technique is also studied. We have also studied the effect on the optimal planning model when different linear and nonlinear membership functions (exponential and hyperbolic) are applied. The efficiency of the proposed model and the solution methodology is tested by solving the model carrying a simulated data set. A sensitivity analysis is also done for the change in the various parameters of the model. In this paper, we have used only linear membership functions for the fuzzy linguistic relations; however, in future the model could be extended by using nonlinear membership functions for fuzzy relations among the objectives. Also, some efficient heuristic and metaheuristic approaches such as krill herd algorithm (Abualigah et al. 2017b, c, 2018a, b) could be used in future for obtaining the compromise solution to the discussed problem.