Fully fuzzy multi-item two-stage fixed charge four-dimensional transportation problems with flexible constraints

Abstract

In real-life transportation problems (TPs), the demands, availabilities, transportation capacities, transportation costs, and fixed charges are uncertain. For this reason, the transported amounts from sources to destinations become uncertain. When the parameters and the decision variables of a problem are fuzzy in nature, the environment is termed ‘fully fuzzy’. Nowadays, with the development of infrastructure for transportation, TPs are developed with several conveyances and routes between sources and destinations. Till now, this type of TPs, i.e., four-dimensional TPs (4DTPs), did not receive much attention. Considering this type of practical problem, a fully fuzzy multi-item two-stage fixed charge 4DTP (FF-MITSFC-4DTP) with breakability during the transportation is considered. The problem consists of the models without and with flexible constraints. Two different methods, the modified graded mean integrated value method (MGMIVM) and an algorithm based on the order relation of fuzzy numbers, are, respectively, used to convert the fully fuzzy models without and with flexibility into respective equivalent deterministic problems. The defuzzified deterministic problems are solved using the generalized reduced gradient (GRG) method through Lingo (18.0) software. The efficiency of the methods is illustrated by solving a real-life problem numerically and comparing the results with an existing model. Results of particular TPs of different dimensions and without breakability are obtained and compared. Some managerial insights are discussed. A sensitivity analysis is presented. The novelty of this investigation is that, for the first time, real-life multi-item two-stage fully fuzzy 4DTPs with flexible constraints for minimum cost and their appropriate solution methodologies are presented.

1 Introduction

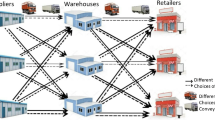
In developing countries like India, Srilanka, etc., some retail marts such as Big Bazar, Metro cash and carry, Reliance Fresh, etc. (in India) do the bulk business of home and consumer durables including cookeries, fruits, vegetables, etc. They apply the ‘farm to fork’ theory, i.e., procure from farmers/producers/artisans/local wholesalers directly or centrally by merchandising departments and sell directly to the consumers removing middlemen, providing benefits to both customers and producers. They follow the following supply chain management (SCM) system (cf. Fig. 1).

Fig. 1

SCM followed by Retail Marts in India

Nowadays, big merchants/individual companies doing the business of the items like ceramic products, marble items, shoes, etc., also follow the above SCM procedure. In this process, the procured amounts (availabilities), customers’ requirements at outlets (demands), conveyances’ capacities, and transported amounts from collecting centers to warehouses and from warehouses to outlets are uncertain, which may be considered imprecise in nature.

Moreover, with the development of infrastructures throughout the world, there are several connecting routes between different places in a country for travel and transportation. So far, the availability of multi-routes was ignored for research in the transportation system (TS). All these above facts motivated us to consider the proposed model, FF-MITSFC-4DTP, which mimics the earlier mentioned SCM procedures (cf. Fig. 1) of some national/international retail marts in developing countries in the context of present available infrastructural facilities.

The basic TPs are normally designed to minimize transportation costs/time where the products are transported from various sources to different destinations under availability and demand constraints. Hitchcock (1941) initially developed the 2DTP, which was later modified by Koopmans (1949). In most real-life situations, products are delivered from sources to destinations by different conveyances like trucks, goods trains, cargo flights, etc. When various conveyances are available and introduced in TP, it is called a solid TP (STP) or 3DTP. Haley (1962) discussed STP, but Shell (1955) first introduced the concept.

Along with source, destination, and choice of conveyances, if the choice of different paths/routes between sources and destinations is considered, the problem becomes a four-dimensional TPs/4DTPs. There may be different paths for transporting products from a source to a destination in real-life scenarios. Some may be very good and smooth among various routes, some terrible and rough, some good in condition with many humps, etc. So, for breakable/damageable products, different paths cause damage to the products in different percentages. Also, different routes may have different fixed charges (e.g., toll tax, public collections). Except for these, weight-based transportation costs may vary for different paths. These scenarios affect the total minimum cost or maximum profit of a TS.

In a TP, from suppliers to retailers, often there may be a need for a warehouse to stock the items between these two. So, warehouse plays a vital role in a TS. This type of problem, where warehouses are present, is called two-stage TP.

Apart from the regular variable transportation cost, which generally depends on the products’ quantity, fixed transportation costs like toll tax, permit fees, etc., are also collected. This type of TP is called fixed charge TP (FCTP).

The input data for a problem may not always be precisely known. If some parameters are vague, the issues are dealt with by the fuzzy set theory. Zadeh (1965) first presented the concept of fuzzy set theory. Nowadays, this idea is used in several problems (Chen et al. 2009; Chen and Wang, 2010; Shen et al, 2013; Chen and Phuong, 2017). Recently, Ammar and Emsimir (2021) worked on fuzzy integer linear programming problems with fully rough intervals.

Nowadays, in the volatile market, transportation parameters such as demands at destinations, availabilities at sources, vehicles’ transportation capacities, and fixed charges are not precisely defined. These may be defined imprecisely using fuzzy numbers. To meet the imprecise demands of this type of TPs, the transported amounts from sources to destinations can not be deterministic, which is normally considered by the investigators. In this case, the transported amounts are also imprecise in a fuzzy sense, which has been considered by very few investigators.

If all the parameters, including decision variables of a TP, are fuzzy, then the problem is called a ‘fully fuzzy’ TP. Some authors (Jalil et al. 2017; Ebrahimnejad 2019) considered single-stage, two/three-dimensional fully fuzzy TPs for a single item. Ziqan et al. (2021) investigated fully fuzzy linear systems with trapezoidal and hexagonal fuzzy numbers.

In an imprecise environment, availability, demand, and conveyance capacity constraints may be considered as a matter of degree and can be partially relaxed if necessary to ensure the feasibility of the problem. These types of constraints are called flexible constraints.

Till now, none considered two-stage 4DTPs with flexible constraints in a fully fuzzy environment considering multi-item, fixed charge, and breakabilities. To fill up this vacuum, an FF-MITSFC-4DTP is formulated and solved in this paper. To deal with this type of model, difficulty arises in the defuzzification processes of the decision variables. Here, two types of defuzzification methods are presented, i.e., MGMIVM and a method using the order relation for comparing fuzzy numbers, where the flexibility of constraints is considered.

In our proposed investigation, FF-MITSFC-4DTPs without and with flexible constraints are formulated and defuzzified using two different methods. The first method—MGMIVM, is applied to defuzzify the problem without flexible constraints. The second method is to solve the problem with flexible constraints, defuzzified by an algorithm based on the order relation of triangular fuzzy numbers. The deterministic models are solved by the GRG method using Lingo (18.0) software and illustrated through a real-life two-stage transportation problem. Results from these two procedures are compared. An existed problem by Ezzati et al. (2015) is solved, taking the constraints of this problem as flexible, and it is shown that the proposed method gives better results than the previous one. Also, the proposed model has been solved by the Ezzati et al. (2015) method, compared with the proposed method, and supremacy of our method is established. The importance of different route considerations is mentioned, i.e., the necessity of 4DTP formulation is established. Moreover, some managerial insights in the case of FF-MITSFC-4DTP are drawn.

In the existing literature, there are some 2DTPs (considering sources and destinations only), 3DTPs (considering sources, destinations, and conveyances only), and LP problems under a fully fuzzy environment. But consideration of different routes between sources and destinations is very important for the TS. Choice of appropriate routes for transportation reduces the breakability of the materials, transportation cost, etc. For this reason, 4DTPs are required to be developed, taking sources, destinations, conveyances, and routes into consideration to represent the real-life TPs. Moreover, in some TPs, transportation constraints are imprecisely satisfied. Till now, none considered fully fuzzy 4DTP/FF-MITSFC-4DTP along with/without flexible constraints. Contributions of the present investigation are as follows:

• For the first time, FF-MITSFC-4DTPs are formulated with and without flexible constraints for minimum cost.

• Two appropriate methods are presented to transform the fully fuzzy problems into deterministic ones.

• Real-life examples are solved to illustrate the proposed models, and some particular models are derived.

• Some managerial insights are presented.

• The importance of the consideration of different routes for transportation is laid down.

• The efficiencies of the proposed methods are presented in two ways by solving (1) an existing model (Ezzati et al. 2015) by our method and (2) the proposed model by an existing method (Ezzati et al. 2015) and then comparing the results.

The rest of this paper is organized as follows: Sect. 2 describes a brief literature review related to this work. In Sect. 3, we describe the problem with all notations and assumptions. Section 4 describes different solution techniques for the proposed problem. In Sect. 5, the flowchart of the optimization procedure is given. A numerical example is explained to illustrate the problem in Sect. 6. In Sect. 7, we have discussed the numerical results and some managerial insights. In Sect. 8, the overall conclusion with limitations and some future research scopes are presented. Some preliminaries and an algorithm are presented in the Appendices, which are used to formulate and solve the problems.

2 Literature review

2.1 Development of the basic TP to 4DTP

Hitchcock (1941) first presented a traditional TP, i.e., 2DTP. But in real-life situations, there are many choices of conveyances available for transportation. Now, a question arises that which conveyance should be used for cost minimization/profit maximization. Schell (1955) proposed an STP, i.e., 3DTP, which included conveyance capacity limitation. Subsequently, Haley (1962) generalized the idea of STP. Nowadays, due to the improvement of infrastructure for transportation, most of the cities are connected with more than one path/route. Again, the question arises: which route should be used for economical transportation? Taking this real-life scenario into consideration, Bera et al. (2018) extended the STP to a 4DTP.

2.2 Payment of fixed charge

Nowadays, in developing countries, toll taxes are collected for the maintenance and development of the roads (National Highways (NHs) in India). These toll taxes and other route collections (festival collections, local collections, etc.) are termed as ‘fixed charge’ and play a vital role in minimizing the total transportation costs. In this regard, Hirsch and Dantzig (1968) proposed a fixed charged TP. In many cases, fixed charges are uncertain, so they may be considered as uncertain parameters in an imprecise sense. Many researchers have considered fixed charges in different ways. Giri et al. (2015) assumed the fixed charge as a fuzzy number, Kundu et al. (2014) considered a type-2 fuzzy number, and Bera et al. (2018) considered it as a rough interval. Mollanoori et al. (2019) considered two different types of fixed charge in a single TP. The first part is up to a specific range of amounts, and then another one is applied for the rest part.

2.3 Consideration of breakability

The breakability of items also plays a significant role in a TP. When the products are transported through a very rough surface, there may be a chance for the products to be broken. The damage rates increase if the products are made of mud, ceramic, glass, or other breakable materials. The products’ breakability depends on the type/choice of route, distance from the source to destination, product’s material, etc. So, breakability should be considered in the formulation of a TP. Ojha et al. (2010) formulated a multi-objective STP with random breakability. Baidya et al. (2015) considered deterministic breakability in multi-stage TP. Halder et al. (2017) presented a 4DTP for breakable substitutable items in a fuzzy environment. Bera et al. (2020) solved a fixed charge 4DTP for the breakable items under hybrid random type-2 uncertain environments.

2.4 Development of fuzzy TPs

In a problem, if some parameters are uncertain, then the uncertainties can be handled using fuzzy numbers. Zadeh (1965) first presented the concept of fuzzy set theory. Mendel (2016) used interval type-2 fuzzy set in their problem. Mondal et al. (2018) presented non-linear interval-valued fuzzy numbers and their applications. Ashraf et al. (2019) proposed a multi-objective type-2 fuzzy reliability redundancy allocation problem. Melin and Sánchez (2019) described the optimization of type-1, interval type-2, and general type-2 fuzzy inference systems. Chakraborty et al. (2021) used hexagonal fuzzy numbers in the inventory management problem.

2.5 Development of fully fuzzy TPs

In the above-mentioned fuzzy TPs, the parameters such as cost, availabilities, etc., are considered fuzzy, but not the decision variable, i.e., the amounts of items to be transported. If in a TP, the decision variables are also considered fuzzy along with the parameters, the environment is called fully fuzzy. Numerous works exist in the literature where a fully fuzzy environment is considered for 2DTPs (Ezzati et al. 2015; Yang et al. 2015; Dhanasekar et al. 2017; Maheswari and Ganeshan 2018; Mishra et al. 2018). Investigators used different methods to solve these problems. Further, some researchers (Giri et al. 2015; Jalil et al. 2017) have considered 3DTPs with fixed charge in a fully fuzzy environment. Yang et al. (2015) solved a fully fuzzy linear programming problem with consideration of flexible constraints. Recently, Ebrahimnejad et al. (2019) discussed a fully fuzzy linear programming problem. Pérez-Cañedo et al. (2020) solved a fully fuzzy multi-objective linear programming problem using an epsilon-constraint method.

A gist of the literature reviews is given in Table 1.

Table 1 Comparison with related works

3 FF-MITSFC-4DTP model

3.1 Notations

We use the following notations to formulate the models.

$\tilde{}$ :	Denotes fuzzy (${\tilde{A}}$ means that A is fuzzy)
$\precsim$, $\succsim$:	Denote flexibility of $\le$ and $\ge$ types constraints, respectively
$\oplus$, $\otimes$:	Denote addition and multiplication of two fuzzy numbers
	Indices
i	Index for the suppliers; $i=1,2,\ldots ,I$
j	Index for warehouses; $j=1,2,\ldots ,J$
k	Index for the retailers; $k=1,2,\ldots ,K$
u	Index for conveyances, available for transporting products from supplier to warehouse; $u=1,2,\ldots ,U$
v	Index for conveyances, available for transporting products from warehouse to retailer; $v=1,2,\ldots ,V$
p	Index for different paths; $p=1,2,\ldots ,P$
m	Index for different products; $m=1,2,\ldots ,M$
	Parameters
${\tilde{c}}_{ijupm}$	Unit transportation cost, to transport product m from supplier i to warehouse j through the conveyance u along path p
${\tilde{f}}_{ijup}$	Fixed charge for the conveyance u along path p from supplier i to warehouse j
$\tilde{c^{\prime }}_{jkvpm}$	Unit transportation cost, to transport product m from warehouse j to retailer k through the conveyance v along path p
$\tilde{f^{\prime }}_{jkvp}$	Fixed charge for the conveyance v along path p from warehouse j to retailer k
${\tilde{Q}}_{im}$	Availability of product m at supplier i
${\tilde{D}}_{km}$	Demand for product m at retailer k
${\tilde{E}}_{u}$, $\tilde{E^{\prime }}_v$	Capacities of the conveyances u and v, respectively
${\tilde{\lambda }}_{ijupm}$	Rate of breakability of product m during transportation from supplier i to warehouse j through conveyance u via path p
$\tilde{\lambda ^{\prime }}_{jkvpm}$	Rate of breakability of product m during transportation from warehouse j to retailer k through conveyance v via path p
	Decision variables
${\tilde{x}}_{ijupm}$	Quantity of product m dispatched by supplier i for warehouse j through conveyance u via path p
$y_{ijup}$	Binary decision variable for fixed charge, if transported from supplier i to warehouse j through conveyance u via path p then $y_{ijup}$=1, otherwise 0
$\tilde{x^{\prime }}_{jkvpm}$	Quantity of product m dispatched by warehouse j for retailer k through conveyance v via path p
$y^{\prime }_{jkvp}$	Binary decision variable for fixed charge, if transported from warehouse j to retailer k through conveyance v via path p then $y^{\prime }_{jkvp}$=1, otherwise 0

3.2 Assumptions

To construct the model, we assume the following:

• 1. This is a two-stage TP, i.e., first, the products are sent from suppliers to the warehouse for screening/storage and then transported to the retailers as per demands.

• 2. There is enough space to store the products in the warehouses.

• 3. Items are breakable, and the breakability depends on the material of the products, conveyances, and routes.

• 4. Several conveyances and routes are available for transportation from suppliers to warehouses and warehouses to retailers.

3.3 Description of the model

Mimicking the two-stage SCM system of national and international retail marts (cf. Fig. 1), i.e., following ‘procurement at collection centers (sources) $\rightarrow$ storage at distribution centers (warehouses) $\rightarrow$ outlets for sale (retailers/destinations)’ we formulate a two-stage fully fuzzy problem. In this problem, after buying the breakable products from manufacturers/suppliers (sources), the products are sent to the warehouses for storage and screening and then the good products are transported to the retailers (destinations) for sale (cf. Fig. 2).

The proposed cost minimization models with the above assumptions and notations are formulated in a fully fuzzy environment. Let there are I suppliers, J warehouses, K retailers to transport M types of products through P paths. U and V different types of conveyances are available from suppliers to warehouses and warehouses to retailers, respectively. Here, the availabilities, demands, capacities and transported amounts, transportation costs, and fixed charges are imprecise and represented by fuzzy numbers. The problem is to find the transported amounts from sources to warehouses and warehouses to destinations so that total transportation cost is minimum, satisfying the availability, demand, and conveyances’ capacities constraints.

Fig. 2

Two-stage 4DTP

3.4 Mathematical formulation

3.4.1 Model-A: FF-MITSFC-4DTP without flexible constraint

The problem is formulated considering Fig. 2, where all the parameters and decision variables are triangular fuzzy numbers. Formulation of the objective function is as follows:

Total cost = transportation and fixed charge cost from suppliers to warehouses + transportation and fixed charge cost from warehouses to retailers.

This total cost is minimized subject to some constraints.

$$\begin{aligned} \mathrm{{Min }} {\tilde{Z}}&=\sum _{ijupm}{\tilde{c}}_{ijupm}\otimes {\tilde{x}}_{ijupm}\oplus \sum _{ijup}{\tilde{f}}_{ijup}y_{ijup} \nonumber \\&\qquad \oplus \sum _{jkvpm}\tilde{c^{\prime }}_{jkvpm}\otimes \tilde{x^{\prime }}_{jkvpm}\oplus \sum _{jkvp}\tilde{f^{\prime }}_{jkvp}y^{\prime }_{jkvp}, \end{aligned}$$

(1)

$$\begin{aligned} \qquad \text {s.t.} \sum _{jup}{\tilde{x}}_{ijupm}\le {\tilde{Q}}_{im} \quad \forall \, i,m, \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{jvp}(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}\ge {\tilde{D}}_{km} \quad \forall \, k,m, \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{ijpm}(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}\le {\tilde{E}}_{u} \quad \forall \, u,\end{aligned}$$

(4)

$$\begin{aligned}&\sum _{jkpm}(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}\le \tilde{E^{\prime }}_v \quad \forall \, v, \end{aligned}$$

(5)

$$\begin{aligned}&\sum _{iupm}(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}= \sum _{kvpm}\tilde{x^{\prime }}_{jkvpm} \quad \forall \, j, \end{aligned}$$

(6)

$$\begin{aligned}&y_{ijup}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \sum _{m}{\tilde{x}}_{ijupm} > 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, i, j, u, p, \end{aligned}$$

(7)

$$\begin{aligned}&y^{\prime }_{jkvp}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \sum _{m}\tilde{x^{\prime }}_{jkvpm} > 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, j, k, v, p,\end{aligned}$$

(8)

$$\begin{aligned}&{\tilde{x}}_{ijupm}, \ \tilde{x^{\prime }}_{jkvpm} \ge 0 \quad \forall \, i,j,k,u,v,p,m. \end{aligned}$$

(9)

In the model, constraints (2) and (3) are the availability and demand constraints, respectively. Constraints (4) and (5) define the maximum capacities of conveyances at different stages. Constraint (6) equalizes the total downloaded and uploaded products at warehouses. Constraints (7) and (8), the binary decision variables are defined. Constraint (9) furnishes the non-negativity of decision variables.

3.4.2 Model-B: FF-MITSFC-4DTP with flexible constraint

The descriptions of Model-B’s objective function and constraints are the same as Model-A. In this model, the constraints are considered flexible, represented by the symbols ‘$\precsim$’ and ‘$\succsim$’ instead of ‘$\le$’ and ‘$\ge$’, respectively. The corresponding objective function is ${\tilde{Z}}^{f}$ (say). The model is as follows:

$$\begin{aligned} {\left. \begin{aligned}&\mathrm{{Min}} \tilde{Z^f}=\mathrm{{Min}} {\tilde{Z}}\\ \text {s.t. }&\sum _{jup}{\tilde{x}}_{ijupm}\precsim {\tilde{Q}}_{im} \quad \forall \, i,m \\&\sum _{jvp}(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}\succsim {\tilde{D}}_{km} \quad \forall \, k,m \\&\sum _{ijpm}(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}\precsim {\tilde{E}}_{u} \quad \forall \, u \\&\sum _{jkpm}(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}\precsim \tilde{E^{\prime }}_v \quad \forall \, v \\&\sum _{iupm}(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}\simeq \sum _{kvpm}\tilde{x^{\prime }}_{jkvpm} \quad \forall \, j \\&y_{ijup}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \sum _{m}{\tilde{x}}_{ijupm} \succ 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, i, j, u, p \\&y^{\prime }_{jkvp}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \sum _{m}\tilde{x^{\prime }}_{jkvpm} \succ 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, j, k, v, p\\&{\tilde{x}}_{ijupm}, \ \tilde{x^{\prime }}_{jkvpm} \succsim 0 \quad \forall \, i,j,k,u,v,p,m \end{aligned}\right\} }. \end{aligned}$$

(10)

4 Solution methodology

The fuzzy numbers ${\tilde{c}}_{ijupm}$, ${\tilde{x}}_{ijupm}$, ${\tilde{f}}_{ijup}$, $\tilde{c^{\prime }}_{jkvpm}$, $\tilde{x^{\prime }}_{jkvpm}$, $\tilde{f^{\prime }}_{jkvp}$, ${\tilde{Q}}_{im}$, ${\tilde{D}}_{km}$, ${\tilde{E}}_{u}$, ${\tilde{E}}^{\prime }_{v}$, ${\tilde{\lambda }}_{ijupm}$, and $\tilde{\lambda ^{\prime }}_{jkvpm}$ are considered as triangular fuzzy numbers in the form ${\tilde{A}}=(A^1, A^2, A^3)$.

4.1 Defuzzification of Model-A: MGMIVM

Taking expected value (modified graded mean integrated value) on both sides, the crisp form of the Model-A is:

$$\begin{aligned} {\left. \begin{aligned}&\mathrm{{Min}}~ EV[{\tilde{Z}}]=EV[\sum _{ijupm}{\tilde{c}}_{ijupm}\otimes {\tilde{x}}_{ijupm}\oplus \sum _{ijup}{\tilde{f}}_{ijup}y_{ijup}\\& \oplus \sum _{jkvpm}\tilde{c^{\prime }}_{jkvpm}\otimes \tilde{x^{\prime }}_{jkvpm}\oplus \sum _{jkvp}\tilde{f^{\prime }}_{jkvp}y^{\prime }_{jkvp}] \\ \text {s.t.} ~~&EV[\sum _{jup}{\tilde{x}}_{ijupm}] \le EV[{\tilde{Q}}_{im}] \quad \forall \, i,m \\&EV[\sum _{jvp}(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}]\ge EV[{\tilde{D}}_{km}] \quad \forall \, k,m \\&EV[\sum _{ijpm}(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}]\le EV[{\tilde{E}}_{u}] \quad \forall \, u\\&EV[\sum _{jkpm}(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}]\le EV[\tilde{E^{\prime }}_v] \quad \forall \, v \\&EV[\sum _{iupm}(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}]= EV[\sum _{kvpm}\tilde{x^{\prime }}_{jkvpm}] \quad \forall \, j \\&y_{ijup}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ EV[\sum _{m}{\tilde{x}}_{ijupm}]> 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, i, j, u, p \\&y^{\prime }_{jkvp}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ EV[\sum _{m}\tilde{x^{\prime }}_{jkvpm}] > 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, j, k, v, p\\&EV[{\tilde{x}}_{ijupm}], \ EV[\tilde{x^{\prime }}_{jkvpm}] \ge 0 \quad \forall \, i,j,k,u,v,p,m \end{aligned}\right\} }. \end{aligned}$$

(11)

Let ${\tilde{Z}}=(Z^1, Z^2, Z^3)$. Then, using Definition 4, we can write $EV[{\tilde{Z}}] = \frac{Z^1+4Z^2+Z^3}{6}$, where

$$\begin{aligned}&(\text {Z}^1, \text {Z}^2, \text {Z}^3) \equiv \text {(1st, 2nd, 3rd) component of}~ \\&\sum _{ijupm} \left( {\tilde{c}}_{ijupm}\otimes {\tilde{x}}_{ijupm}\right) \oplus \sum _{ijup} \left( {\tilde{f}}_{ijup}\right) y_{ijup}\\ \oplus&\sum _{jkvpm} \left( \tilde{c^{\prime }}_{jkvpm}\otimes \tilde{x^{\prime }}_{jkvpm}\right) \oplus \sum _{jkvp} \left( \tilde{f^{\prime }}_{jkvp}\right) y^{\prime }_{jkvp}. \end{aligned}$$

Using Definition 3, we get the components of

$$ \tilde{c}_{{ijupm}} \otimes \tilde{x}_{{ijupm}} = \left\{ {\begin{array}{*{20}c} {(c_{{ijupm}}^{1} x_{{ijupm}}^{1} ,c_{{ijupm}}^{2} x_{{ijupm}}^{2} ,c_{{ijupm}}^{3} x_{{ijupm}}^{3} ),} & {{\text{if}}\;c_{{ijupm}}^{1} \ge 0} \\ {(c_{{ijupm}}^{1} x_{{ijupm}}^{3} ,c_{{ijupm}}^{2} x_{{ijupm}}^{2} ,c_{{ijupm}}^{3} x_{{ijupm}}^{3} ),} & {{\text{if}}\;c_{{ijupm}}^{1} < 0} \\ {} & {{\text{and}}\,\,c_{{ijupm}}^{3} \ge {\text{0}}} \\ {(c_{{ijupm}}^{1} x_{{ijupm}}^{3} ,c_{{ijupm}}^{2} x_{{ijupm}}^{2} ,c_{{ijupm}}^{3} x_{{ijupm}}^{1} ),} & {{\text{if}}\;c_{{ijupm}}^{3} < 0} \\ \end{array} } \right.\quad \forall {\mkern 1mu} i,j,u,p,m. $$

Similarly, we can write the components of $\tilde{c^{\prime }}_{jkvpm}\otimes \tilde{x^{\prime }}_{jkvpm}$.

Now, using Definition 4, we can write $EV[{\tilde{x}}_{ijupm}]$, $EV[\tilde{x^{\prime }}_{jkvpm}]$, $EV[{\tilde{Q}}_{im}]$, $EV[{\tilde{D}}_{km}]$, $EV[{\tilde{E}}_{u}]$, $EV[\tilde{E^{\prime }}_{v}]$ as $EV[{\tilde{A}}]=\frac{A^1+4A^2+A^3}{6}$, where ${\tilde{A}}=(A^1,A^2,A^3)$.

$$\begin{aligned}&EV[(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}] =\frac{1}{6}[\{x^{\prime 1}_{jkvpm}-\text {3rd component}\\&\text {of }(\tilde{\lambda ^{\prime }}_{jkvpm}\otimes \tilde{x^{\prime }}_{jkvpm})\}\nonumber +4\{x^{\prime 2}_{jkvpm}-\text {2nd component of}\\&(\tilde{\lambda ^{\prime }}_{jkvpm}\otimes \tilde{x^{\prime }}_{jkvpm})\} +\{x^{\prime 3}_{jkvpm}-\text {1st component of}\\&(\tilde{\lambda ^{\prime }}_{jkvpm}\otimes \tilde{x^{\prime }}_{jkvpm})\}]. \end{aligned}$$

Similarly, $EV[(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}]$ can also be written.

All the parameters and decision variables in the proposed model are non-negative. So, Eq. (11) can be rewritten in the deterministic form

$$\begin{aligned} \mathrm{{Min}} Z & = \frac{1}{6}[Z^1+4Z^2+Z^3] \\ & = \sum _{ijupm}\frac{c^1_{ijupm}x^1_{ijupm}+4c^2_{ijupm}x^2_{ijupm}+c^3_{ijupm}x^3_{ijupm}}{6} \\&\qquad + \sum _{ijup} \frac{f^{1}_{ijup}+4f^{2}_{ijup}+f^{3}_{ijup}}{6} \, \, y_{ijup}\\&\qquad + \sum _{jkvpm}\frac{c^{\prime 1} _{ijupm}x^{\prime 1}_{ijupm}+4c^{\prime 2}_{ijupm}x^{\prime 2}_{ijupm}+c^{\prime 3}_{ijupm}x^{\prime 3}_{ijupm}}{6}\\&\qquad + \sum _{jkvp}\frac{f^{\prime 1}_{jkvp}+4f^{\prime 2}_{jkvp}+f^{\prime 3}_{jkvp}}{6}\, \, y^{\prime }_{jkvp} \\&\text {s.t.}\\&\sum _{jup}\frac{1}{6}[x^{1}_{ijupm}+4x^{2}_{ijupm}+x^{3}_{ijupm}] \le \frac{1}{6}[Q^{1}_{im}+4Q^{2}_{im}+Q^{3}_{im}] \quad \forall \, i,m \\&\sum _{jvp}\frac{1}{6}[\{x^{\prime 1}_{jkvpm}-\lambda ^{\prime 3}_{jkvpm} x^{\prime 3}_{jkvpm}\} +4\{x^{\prime 2}_{jkvpm}-\lambda ^{\prime 2}_{jkvpm} x^{\prime 2}_{jkvpm}\}\\&\qquad +\{x^{\prime 3}_{jkvpm}-\lambda ^{\prime 1}_{jkvpm} x^{\prime 1}_{jkvpm}\}] \ge \frac{1}{6}[D^{1}_{km}+4D^{2}_{km}+D^{3}_{km}] \quad \forall \, k,m \\&\sum _{ijpm}\frac{1}{6}[\{x^{1}_{ijupm}-\lambda ^{3}_{ijupm} x^{3}_{ijupm}\} +4\{x^{2}_{ijupm}-\lambda ^{2}_{ijupm} x^{2}_{ijupm}\}\\&\qquad +\{x^{3}_{ijupm}-\lambda ^{1}_{ijupm} x^{1}_{ijupm}\}] \le \frac{1}{6}[E^{1}_{u}+4E^{2}_{u}+E^{3}_{u}] \quad \forall \, u\\&\sum _{jkpm}\frac{1}{6}[\{x^{\prime 1}_{jkvpm}-\lambda ^{\prime 2}_{jkvpm} x^{\prime 2}_{jkvpm}\} +4\{x^{\prime 2}_{jkvpm}-\lambda ^{\prime 3}_{jkvpm} x^{\prime 3}_{jkvpm}\}\\&\qquad +\{x^{\prime 3}_{jkvpm}-\lambda ^{\prime 1}_{jkvpm} x^{\prime 1}_{jkvpm}\}] \le \frac{1}{6}[E^{\prime 1}_{v}+4E^{\prime 2}_{v}+E^{\prime 3}_{v}] \quad \forall \, v \\&\sum _{iupm}\frac{1}{6}[\{x^{1}_{ijupm}-\lambda ^{3}_{ijupm} x^{3}_{ijupm}\} +4\{x^{2}_{ijupm}-\lambda ^{2}_{ijupm} x^{2}_{ijupm}\}\\&\qquad +\{x^{3}_{ijupm}-\lambda ^{1}_{ijupm} x^{1}_{ijupm}\}]\\&= \frac{1}{6}\sum _{kvpm}[x^{\prime 1}_{jkvpm}+4x^{\prime 2}_{jkvpm}+x^{\prime 3}_{jkvpm}] \quad \forall \, j \\&y_{ijup}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \frac{1}{6}\sum _{m}[x^{1}_{ijupm}+4x^{2}_{ijupm}+x^{3}_{ijupm}]> 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, i, j, u, p \\&y^{\prime }_{jkvp}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \frac{1}{6}\sum _{m}[x^{\prime 1}_{jkvpm}+4x^{\prime 2}_{jkvpm}+x^{\prime 3}_{jkvpm}] > 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, j, k, v, p\\&\frac{1}{6}[x^{1}_{ijupm}+4x^{2}_{ijupm}+x^{3}_{ijupm}] \ge 0 \quad \forall \, i,j,u,p,m\\&\frac{1}{6}[x^{\prime 1}_{jkvpm}+4x^{\prime 2}_{jkvpm}+x^{\prime 3}_{jkvpm}] \ge 0 \quad \forall \, j,k,v,p,m. \end{aligned}$$

4.2 Defuzzification of Model-B: Algorithm based on fuzzy order relation

Here, Model-B is made deterministic using an Algorithm, which is given in Appendix-B. We apply the method-MGMIVM on the objective function and equality constraint. But for the flexible constraints, Theorem 1 is used to reduce it to deterministic form. Then, Model-B can be written for $\alpha _k$, $k = 0, 1, \ldots , n$ as,

$$\begin{aligned} {\left. \begin{aligned}&\mathrm{{Min}}~ Z(\tilde{x}) \\& = \sum _{ijupm}\frac{c^1_{ijupm}x^1_{ijupm}+4c^2_{ijupm}x^2_{ijupm}+c^3_{ijupm}x^3_{ijupm}}{6}\\ &\qquad + \sum _{ijup} \frac{f^{1}_{ijup}+4f^{2}_{ijup}+f^{3}_{ijup}}{6} \, \, y_{ijup}\\&\qquad + \sum _{jkvpm}\frac{c^{\prime 1} _{ijupm}x^{\prime 1}_{ijupm}+4c^{\prime 2}_{ijupm}x^{\prime 2}_{ijupm}+c^{\prime 3}_{ijupm}x^{\prime 3}_{ijupm}}{6}\\&\qquad + \sum _{jkvp}\frac{f^{\prime 1}_{jkvp}+4f^{\prime 2}_{jkvp}+f^{\prime 3}_{jkvp}}{6}\, \, y^{\prime }_{jkvp} \\&\frac{2Q^2_{im}+Q^3_{im}-\sum \limits _{jup}x^{1}_{ijupm}-2\sum \limits _{jup}x^{2}_{ijupm}}{Q^3_{im}-Q^1_{im}-\sum \limits _{jup}x^{1}_{ijupm}-2\sum \limits _{jup}x^{2}_{ijupm}}\ge \alpha _k \quad \forall \, i,m\\&\frac{ { 2\sum \limits _{jvp}(x^{\prime 2}_{jkvpm}-\lambda ^{\prime 2}_{jkvpm}x^{\prime 2}_{jkvpm})+\sum \limits _{jvp}(x^{\prime 3}_{jkvpm}- \lambda ^{\prime 1}_{jkvpm}x^{\prime 1}_{jkvpm})-D^{1}_{km}-2D^2_{km} }}{{ 2\sum \limits _{jvp}(x^{\prime 3}_{jkvpm}-\lambda ^{\prime 1}_{jkvpm}x^{\prime 1}_{jkvpm})-\sum \limits _{jvp}(x^{\prime 1}_{jkvpm} -\lambda ^{\prime 3}_{jkvpm}x^{\prime 3}_{jkvpm})+D^3_{km}-D^1_{km}}} \ge \alpha _k \quad \forall \, k,m\\&\frac{ { 2E^2_u+E^3_u-\sum \limits _{ijpm}(x^1_{ijupm}-\lambda ^3_{ijupm}x^3_{ijupm})- 2\sum \limits _{ijpm}(x^2_{ijupm}-\lambda ^2_{ijupm}x^2_{ijupm}) }}{ { E^3_u-E^1_u+\sum \limits _{ijpm}(x^3_{ijupm}-\lambda ^1_{ijupm}x^1_{ijupm}) -\sum \limits _{ijpm}(x^1_{ijupm}-\lambda ^3_{ijupm}x^3_{ijupm}) }} \ge \alpha _k \quad \forall \, u\\&\frac{ { 2E^{\prime 2}_v+E^{\prime 3}_v-\sum \limits _{jkpm}(x^{\prime 1}_{jkvpm}-\lambda ^{\prime 3}_{jkvpm}x^{\prime 3}_{jkvpm}) -2\sum \limits _{jkpm}(x^{\prime 2}_{jkvpm}-\lambda ^{\prime 2}_{jkvpm}x^{\prime 2}_{jkvpm})}}{{ E^{\prime 3}_u-E^{\prime 1}_u-\sum \limits _{jkpm}(x^{\prime 3}_{jkvpm}-\lambda ^{\prime 1}_{jkvpm}x^{\prime 1}_{jkvpm}) -\sum \limits _{jkpm}(x^{\prime 1}_{jkvpm}-\lambda ^{\prime 3}_{jkvpm}x^{\prime 3}_{jkvpm})}} \ge \alpha _k \quad \forall \, v\\&\sum \limits _{iupm}\frac{1}{6}[\{x^{1}_{ijupm}-\lambda ^{3}_{ijupm} x^{3}_{ijupm}\} +4\{x^{2}_{ijupm}-\lambda ^{2}_{ijupm} x^{2}_{ijupm}\}\\&\qquad +\{x^{3}_{ijupm}-\lambda ^{1}_{ijupm} x^{1}_{ijupm}\}]\\&= \frac{1}{6}\sum \limits _{kvpm}[x^{\prime 1}_{jkvpm}+4x^{\prime 2}_{jkvpm}+x^{\prime 3}_{jkvpm}] \quad \forall \, j \\&y_{ijup}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \frac{1}{6}\sum \limits _{m}[x^{1}_{ijupm}+4x^{2}_{ijupm}+x^{3}_{ijupm}]> 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, i, j, u, p \\&y^{\prime }_{jkvp}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \frac{1}{6}\sum \limits _{m}[x^{\prime 1}_{jkvpm}+4x^{\prime 2}_{jkvpm}+x^{\prime 3}_{jkvpm}] > 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, j, k, v, p\\&\frac{1}{6}[x^{1}_{ijupm}+4x^{2}_{ijupm}+x^{3}_{ijupm}] \ge 0 \quad \forall \, i,j,u,p,m\\&\frac{1}{6}[x^{\prime 1}_{jkvpm}+4x^{\prime 2}_{jkvpm}+x^{\prime 3}_{jkvpm}] \ge 0 \quad \forall \, j,k,v,p,m. \end{aligned}\right\} } \end{aligned}.$$

The n + 1 crisp problems are solved for $\alpha _0, \alpha _1, \ldots , \alpha _n$, and say $\tilde{x^*}_{\alpha _k}$ is the solution for $\alpha _k, k=0, 1, \ldots , n$. Then, we find the optimal solutions $Z(\tilde{x^*}_{\alpha _0})$, $Z(\tilde{x^*}_{\alpha _1})$, ..., $Z(\tilde{x^*}_{\alpha _n})$.

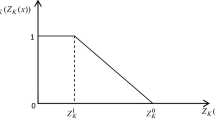
The membership function of $Z({\tilde{x}})$ is

$$\begin{aligned}&\mu (Z({\tilde{x}}))=&{\left\{ \begin{array}{ll} 1 &{} \text {if} \quad EV(Z({\tilde{x}}))< EV(Z({\tilde{x}}^{*}_{\alpha _0})) \\ \frac{EV(Z({\tilde{x}}^{*}_{\alpha _n}))-EV(Z({\tilde{x}}))}{EV(Z({\tilde{x}} ^{*}_{\alpha _n}))-EV(Z({\tilde{x}}^{*}_{\alpha _0}))} &{} \text {if} \quad EV(Z({\tilde{x}}^{*}_{\alpha _0})) \le EV(Z({\tilde{x}}))\le EV(Z({\tilde{x}}^{*}_{\alpha _n}))\\ 0 &{} \text {if} \quad EV(Z({\tilde{x}})) > EV(Z({\tilde{x}}^{*}_{\alpha _n})). \end{array}\right. } \end{aligned}$$

(12)

Calculating $\beta _k=2\alpha _k-1$ and $\mu (Z(\tilde{x^*}_{\alpha _k}))$ for $k=0,1,\ldots ,n$, we find $\mathrm{{min}}_k\{|\beta _k-\mu (Z(\tilde{x^*}_{\alpha _k}))|\}$.

Suppose $\mathrm{{min}}_k\{|\beta _k-\mu (Z(\tilde{x^*}_{\alpha _k}))|\}$=$|\beta _{k_0}-\mu (Z(\tilde{x^*}_{\alpha _{k_0}}))|$. Then we find the optimal solution as $\tilde{x^*}$=$\tilde{x^*_{\alpha _{k_0}}}$.

4.3 Some particular cases of Model-A and Model-B

FF-MITSFC-3DTP This is a particular case of FF-MITSFC-4DTP, where only one possible path (the first one, say) is considered between all sources and destinations (FF-MITSFC-3DTP) and solved using above mentioned two methods.

FF-MITSFC-4DTP without breakability As a particular case of FF-MITSFC-4DTP, a situation is considered where there is no breakage of items. Since there is no loss of items, the total transportation cost should be less than the case with breakability.

FF-MITSFC-3DTP without breakability In this particular case of FF-MITSFC-4DTP, only one possible path (the first one) is considered between all sources and destinations, and there is no breakage of items.

5 Flowchart of optimization procedure

The GRG technique is used to solve the deterministic forms of Models A and B of the FF-MITSFC-4DTP using Lingo (18.0).

Flowchart The flowchart of the optimization process is depicted in Fig. 3.

Fig. 3

Flowchart of the optimum solution procedure

6 Numerical illustration

In this section, we solve our proposed FF-MITSFC-4DTP problem by two above explained methods for without and with flexibility constraints taking real-life data in Experiment-1. In Experiment-2, we solve an existing problem of Ezzati et al. (2015), taking the constraints as flexible and solve it using the above-mentioned method for flexible constraints. In Experiment-3, we compare our method with an existing method (Ezzati et al. 2015) to show the advantages of our methods.

6.1 Experiment-1: Application of proposed methods in a real-life problem

A businessman, Mr. Kailash Biswas, has two stationary shops at Bankura and Raipur in West Bengal, a state in India. He bought ceramic plates and cups from two wholesale houses at Dhanbad and Midnapur, two cities in India. He first stores the items at warehouses located at Jamshedpur and Bardhaman, and then later, he transports the items from warehouses to his retail stores as required as per demands (cf. Fig. 4).¹ The products are breakable, and the breakabilities of the items on different paths are different. The products—plates and cups—may be damaged for the rough nature of paths or any other reason. Two different paths are available from each source to destination, and two types of conveyances, truck, and LCV, are available for transporting the products from sources to destinations. Different toll taxes are collected for different types of vehicles and roads. In some routes, the public also collects some money for local reasons, which are included in fixed charges and toll taxes. Also, the products have dissimilar breakabilities for different routes and conveyances. Here, the aim is to decide the right quantity of the product, the best path, and conveyance to get the minimum total transportation cost. The data for the toll taxes and conveyances’ capacities² are taken from the internet. All other informations are collected from his business.

Fig. 4

Locations of suppliers, warehouses and retailers of MITSFC-4DTP

6.1.1 Input data of Models A and B

For the FF-MITSFC-4DTPs, the input data (Models A and B) for the parameters of objective function and constraints are specified in Tables 2 and 3.

Table 2 Values of breakabilities (${\tilde{\lambda }}_{ijupm}$, ${\tilde{\lambda }}^{\prime }_{jkvpm}$), unit transportation costs (${\tilde{c}}_{ijupm}$, ${\tilde{c}}^{\prime }_{jkvpm}$) and fixed charges (${\tilde{f}}_{ijup}$, ${\tilde{f}}^{\prime }_{jkvp}$) of Models A and B

Table 3 Values of availabilities (${\tilde{Q}}_{im}$), demands (${\tilde{D}}_{km}$) and conveyance capacities (${\tilde{E}}_u$, ${\tilde{E}}^{\prime }_{v}$) for Models A and B

6.1.2 Experimental results

Solution of Model-A Model-A, i.e., the FF-MITSFC-4DTP (without flexible constraint) given by Eqs. (1)–(9) is defuzzified by the MGMIV method and then solved using the GRG method (through Lingo 18.0).

Solution of Model-B To solve Model-B, i.e., FF-MITSFC-4DTP (with flexible constraints), given by equation (10), we take $n=10$ and then $\alpha _k=\frac{1}{2}+\frac{k}{20}$ for $k=0, 1, \ldots , n$. Then using the above-mentioned method for flexible constraints, we find the values of $EV(Z({\tilde{x}}^*_{\alpha _k}))$, which are given in Table 4.

The membership function of $Z({\tilde{x}})$ is

$$\begin{aligned} & \mu (Z({\tilde{x}})) = \nonumber \\ & {\left\{ \begin{array}{ll} 1 & {} \text {if} \quad EV(Z({\tilde{x}}))< 235.8474 \\ \frac{305.0721-EV(Z({\tilde{x}}))}{305.0721-235.8474} &{} \text {if} \quad 235.8474 \le EV(Z({\tilde{x}}))\le 305.0721\\ 0 &{} \text {if} \quad EV(Z({\tilde{x}})) > 305.0721. \end{array}\right. } \end{aligned}$$

(13)

Table 4 Values of $|\beta _k-\mu (Z_k({\tilde{x}}))|$

Then from Table 4, $|\beta _k-\mu (Z_k({\tilde{x}}))|$ is calculated, and it is clear that $\alpha _8$ = 0.9 gives the minimum value of that. Let the optimal value of $Z(x^*_{\alpha _8})$=($Z^l, Z^2, Z^3$). Now using the MGMIV of triangular fuzzy number and then GRG technique (through Lingo 18.0), we get the optimal value $241.59 (c.f. Table 5).

The experimental results for optimum solutions for both models (i.e., min cost and the values of decision variables) are given in Table 5.

Table 5 Optimal results of different models

Solution of particular cases Some particular cases of Models-A and B (FF-MITSFC-3DTP, FF-MITSFC-4DTP without breakability and FF-MITSFC-3DTP without breakability) are derived to the deterministic form using above mentioned methods for both types of constraints (with and without flexibility) and solve by the GRG method and compared the results. For the 3DTP case, we consider only one path (the first one), which means there is no choice of multiple paths. For without breakability case, ${\tilde{\lambda }}_{ijupm}$ and $\tilde{\lambda ^{\prime }}_{jkvpm}$ are considered as zero. All the results, i.e., minimum transportation cost and transported amounts, are given in Table 5. The comparison of the optimal values is given in Table 6.

Table 6 Comparison of optimal result

The pictorial comparison of different cases of FF-MITSFC-4DTP is shown in Fig. 5.

Fig. 5

Comparison of results

6.2 Experiment-2: Application of proposed methods in an existing model and, hence, the comparison

Ezzati et al. (2015) solved a maximization LP as an example. To illustrate the efficiency of our methods, we solve this problem considering the constraints with and without flexibility and compare the results.

Problem of Ezzati et al. (2015) A corporation has ($25,$30,$40) million available for the coming year to allocate to its four subsidiaries. Because of commitments to the stability of personnel employment and for other reasons, the corporation has established a minimal level of funding for each subsidiary. These funding levels are ($2,$3,$5) million, ($4,$5,$6) million, ($5,$8,$9) million and ($7,$8,$14) million respectively. Each subsidiary has the opportunity to conduct various projects with the funds it receives. A rate of return (as a percent of investment) has been established for each project. In addition, certain projects permit only limited investment. The data of each project are given in Table 7. What is the best allocation to the four subsidiaries such that the maximum return is achieved for the corporation?

Table 7 Data of problem of Ezzati et al. (2015) Example 4.3 (in U.S. dollar)

Solution Taking the constrains of the problem as flexible, we can write the problem as

$$\begin{aligned} \text {max }&(5,7,8) {\tilde{x}}_{11} \oplus (3,5,6) {\tilde{x}}_{12}\\&\quad \oplus (4,8,9) {\tilde{x}}_{13} \oplus (3,5,7) {\tilde{x}}_{21} \oplus (4,7,8) {\tilde{x}}_{22}\\&\oplus (8,9,10) {\tilde{x}}_{23} \oplus (7,10,11) {\tilde{x}}_{31}\\&\quad \oplus (6,8,10) {\tilde{x}}_{32} \oplus (4,7,8) {\tilde{x}}_{33} \oplus \\&(4,6,8) {\tilde{x}}_{41} \oplus (3,5,7) {\tilde{x}}_{42} \oplus (7,9,11) {\tilde{x}}_{43}\\&\sum _{i=1}^{4}\sum _{j=1}^{3}{\tilde{x}}_{ij}\simeq (25,30,40),\\&\quad \sum _{j=1}^{3}{\tilde{x}}_{1j}\succsim (2,3,5), \sum _{j=1}^{3}{\tilde{x}}_{2j}\succsim (4,5,6),\\&\sum _{j=1}^{3}{\tilde{x}}_{3j}\succsim (5,8,9), \sum _{j=1}^{3}{\tilde{x}}_{4j}\succsim (7,8,14),\\&{\tilde{x}}_{11}\precsim (4,6,7), {\tilde{x}}_{12}\precsim (3,5,6), {\tilde{x}}_{13} \precsim (8,9,10),\\&{\tilde{x}}_{21}\precsim (5,7,8), {\tilde{x}}_{22}\precsim (8,10,11), {\tilde{x}}_{23}\precsim (3,4,5),\\&{\tilde{x}}_{31}\precsim (4,5,7), {\tilde{x}}_{32}\precsim (2,3,6), {\tilde{x}}_{33}\precsim (4,7,9),\\&{\tilde{x}}_{41}\precsim (4,6,7), {\tilde{x}}_{42}\precsim (4,5,9), {\tilde{x}}_{43}\precsim (2,4,5). \end{aligned}$$

We take $n=10$ and then $\alpha _k=\frac{1}{2}+\frac{k}{20}$ for $k=0, 1, \ldots , n$. Then solve the problem and find the values of $EV(Z({\tilde{x}}^*_{\alpha _k}))$.

The membership function of $Z({\tilde{x}})$ is

$$\begin{aligned}&\mu (Z({\tilde{x}}))= \nonumber \\&{\left\{ \begin{array}{ll} 0 &{} \text {if}\,\,EV(Z({\tilde{x}}))< 246.6111 \\ \frac{EV(Z({\tilde{x}}))-246.6111}{296.8333-246.6111} &{} \text {if}\,\,246.6111 \le EV(Z({\tilde{x}}))\le 296.8333\\ 1 &{} \text {if}\,\, EV(Z({\tilde{x}})) > 296.8333. \end{array}\right. } \end{aligned}$$

(14)

Then calculating $|\beta _k-\mu (Z_k({\tilde{x}}))|$, from Table 8, it is clear that the maximum value is found for $\alpha =0.7$ (as $|\beta _k-\mu (Z_4({\tilde{x}}))|$ is minimum). Let the optimal $Z(x^*_{\alpha _4})$=($Z^l$, $Z^2$, $Z^3$). Now using MGMIV of triangular fuzzy number, we get the optimal value $261.77 > $Z_\mathrm{{max}}^{\mathrm{{Ezzati's ~ method}}}$ = EV[(133,245,362)] = $245.83.

Table 8 Values of $|\beta _k-\mu (Z_k({\tilde{x}}))|$ for the problem of Ezzati et al. (2015)

6.3 Experiment-3: Solution of proposed model using the existing method—Ezzati’s method (Ezzati et al. 2015) and, hence, the comparison

Following Ezzati et al. (2015), the FF-MITSFC-4DTP without flexibility can be reduced to the following problem adding slack and surplus variables.

$$\begin{aligned} {\left. \begin{aligned} \mathrm{{Min}} {\tilde{Z}}=&\sum _{ijupm}{\tilde{c}}_{ijupm}\otimes {\tilde{x}}_{ijupm}\oplus \sum _{ijup}{\tilde{f}}_{ijup}y_{ijup} \\&\oplus \sum _{jkvpm}\tilde{c^{\prime }}_{jkvpm}\otimes \tilde{x^{\prime }}_{jkvpm}\oplus \sum _{jkvp}\tilde{f^{\prime }}_{jkvp}y^{\prime }_{jkvp} \\ \text {s.t.}&\sum _{jup}{\tilde{x}}_{ijupm}+{\tilde{s}}_1 = {\tilde{Q}}_{im} \quad \forall \, i,m \\&\sum _{jvp}(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}-{\tilde{s}}_2 = {\tilde{D}}_{km} \quad \forall \, k,m\\&\sum _{ijpm}(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}+{\tilde{s}}_3 = {\tilde{E}}_{u} \quad \forall \, u\\&\sum _{jkpm}(1-\tilde{\lambda ^{\prime }}_{jkvpm})\otimes \tilde{x^{\prime }}_{jkvpm}+{\tilde{s}}_4= \tilde{E^{\prime }}_v \quad \forall \, v \\&\sum _{iupm}(1-{\tilde{\lambda }}_{ijupm})\otimes {\tilde{x}}_{ijupm}= \sum _{kvpm}\tilde{x^{\prime }}_{jkvpm} \quad \forall \, j \\&y_{ijup}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \sum _{m}{\tilde{x}}_{ijupm} \succ 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, i, j, u, p \\&y^{\prime }_{jkv}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \sum _{m}\tilde{x^{\prime }}_{jkvpm} \succ 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, j, k, v, p\\&{\tilde{x}}_{ijupm}, \ \tilde{x^{\prime }}_{jkvpm} \succeq 0 \quad \forall \, i,j,k,u,v,p,m \end{aligned}\right\} }, \end{aligned}$$

where the fuzzy numbers ${\tilde{s}}_l$=$(s^1_l,s^2_l,s^3_l)$, l=1, 2, 3, 4.

First, we express the fuzzy parameters and decision variables of the problem as a triangular fuzzy number and then applying the algorithm given by Ezzati et al. (2015), we get the form of the problem as

$$\begin{aligned} \mathrm{{Min}} Z^1 & =\sum _{ijupm}c^2_{ijupm}x^2_{ijupm}+ \sum _{ijup}f^2_{ijup} y_{ijup} \\ & \quad + \sum _{jkvpm}c^{\prime 2}_{jkvpm}x^{\prime 2}_{jkvpm}+ \sum _{jkvp}f^{\prime 2}_{jkvp}y^{\prime }_{jkvp}, \end{aligned}$$

(15)

$$\begin{aligned} \mathrm{{Max}} Z^2 & =\sum _{ijupm}c^3_{ijupm}x^3_{ijupm}+ \sum _{ijup}f^3_{ijup} y_{ijup} \\ & \quad + \sum _{jkvpm}c^{\prime 3}_{jkvpm}x^{\prime 3}_{jkvpm}+ \sum _{jkvp}f^{\prime 3}_{jkvp}y^{\prime }_{jkvp} -(\sum _{ijupm}c^1_{ijupm}x^1_{ijupm} \nonumber \\&+ \sum _{ijup}f^1_{ijup} y_{ijup}+ \sum _{jkvpm}c^{\prime 1}_{jkvpm}x^{\prime 1}_{jkvpm}+ \sum _{jkvp}f^{\prime 1}_{jkvp}y^{\prime }_{jkvp}), \end{aligned}$$

(16)

$$\begin{aligned} \mathrm{{Min}} Z^3 & =\sum _{ijupm}c^3_{ijupm}x^3_{ijupm}+ \sum _{ijup}f^3_{ijup} y_{ijup} \\ & \quad + \sum _{jkvpm}c^{\prime 3}_{jkvpm}x^{\prime 3}_{jkvpm}+ \sum _{jkvp}f^{\prime \prime 3}_{jkvp}y^{\prime }_{jkvp} +(\sum _{ijupm}c^1_{ijupm}x^1_{ijupm} \\ & \quad + \sum _{ijup}f^1_{ijup} y_{ijup}+ \sum _{jkvpm}c^{\prime \prime 1}_{jkvpm}x^{\prime 1}_{jkvpm}+ \sum _{jkvp}f^{\prime 1}_{jkvp}y^{\prime }_{jkvp}), \end{aligned}$$

(17)

$$\begin{aligned} {\left. \begin{aligned} \text {s.t.}&\sum _{jup}x^1_{ijupm}+s^1_1= Q^1_{im} , \sum _{jup}x^2_{ijupm} +s^2_1= Q^2_{im} ,\\&\sum _{jup}x^3_{ijupm} +s^3_1= Q^3_{im} \quad \forall \, i,m\\&\sum _{jvp}(x^{\prime 1}_{jkvpm}-\lambda ^{\prime 3}_{jkvpm}x^{\prime 3}_{jkvpm}) -s^1_2= D^1_{km},\\&\sum _{jvp}(x^{\prime 2}_{jkvpm}-\lambda ^{\prime 2}_{jkvpm}x^{\prime 2}_{jkvpm}) -s^2_2= D^2_{km}, \\&\sum _{jvp}(x^{\prime 3}_{jkvpm}-\lambda ^{\prime 1}_{jkvpm}x^{\prime 1}_{jkvpm}) -s^3_2= D^3_{km} \quad \forall \, k,m \\&\sum _{ijpm}(x^1_{ijupm}-\lambda ^3_{ijupm}x^3_{ijupm}) +s^1_3= E^1_{u} ,\\&\sum _{ijpm}(x^2_{ijupm}-\lambda ^2_{ijupm}x^2_{ijupm}) +s^2_3= E^2_{u}, \\&\sum _{ijpm}(x^3_{ijupm}-\lambda ^1_{ijupm}x^1_{ijupm}) +s^3_3= E^3_{u} \quad \forall \, u\\&\sum _{jkpm}(x^{\prime 1}_{jkvpm}-\lambda ^{\prime 3}_{jkvpm}x^{\prime 3}_{jkvpm}) +s^1_4= E^{\prime 1}_v ,\\&\sum _{jkpm}(x^{\prime 2}_{jkvpm}-\lambda ^{\prime 2}_{jkvpm}x^{\prime 2}_{jkvpm}) +s^2_4= E^{\prime 2}_v ,\\&\sum _{jkpm}(x^{\prime 3}_{jkvpm}-\lambda ^{\prime 1}_{jkvpm}x^{\prime 1}_{jkvpm}) +s^3_4= E^{\prime 3}_v \quad \forall \, v \\&\sum _{iupm}(x^1_{ijupm}-x^3_{ijupm}\lambda ^3_{ijupm})= \sum _{kvpm}x^{\prime 1}_{jkvpm},\\&\sum _{iupm}(x^2_{ijupm}-x^2_{ijupm}\lambda ^2_{ijupm})= \sum _{kvpm}x^{\prime 2}_{jkvpm}, \\&\sum _{iupm}(x^3_{ijupm}-x^1_{ijupm}\lambda ^1_{ijupm})= \sum _{kvpm}x^{\prime 3}_{jkvpm} \quad \forall \, j \\&y_{ijup}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \sum _{m}x^3_{ijupm}> 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, i, j, u, p \ \\&y^{\prime }_{jkvp}= {\left\{ \begin{array}{ll} 1, &{} \text {if} \ \sum _{m}x^{\prime 3}_{jkvpm} > 0\\ 0,&{} \text {otherwise}\\ \end{array}\right. } \quad \forall \, j, k, v, p\\&x^2_{ijupm}-x^1_{ijupm}\ge 0 ~ x^3_{ijupm}-x^2_{ijupm}\ge 0,\\&x^1_{ijupm}\ge 0 \quad \forall \, i,j,u,p,m \\&x^{\prime 2}_{jkvpm}-x^{\prime 1}_{jkvpm}\ge 0 ~ x^{\prime 3}_{jkvpm}-x^{\prime 2}_{jkvpm}\ge 0 \\&x^{\prime 1}_{jkvpm} \ge 0 \quad \forall \, j,k,v,p,m \end{aligned}\right\} }. \end{aligned}$$

(18)

Now, we solve the above problem with objective (15) and constraints (18). If there is a unique optimal solution, then stop. Otherwise, take an optimal solution, say $Z^{1*}$. In the next step, solve the second objective (16) with all previous constraints and add another constraint $\sum _{ijupm}c^2_{ijupm}x^2_{ijupm}+ \sum _{ijup}f^2_{ijup} y_{ijup}+ \sum _{jkvpm}c^{\prime 2}_{jkvpm}x^{\prime 2}_{jkvpm}+ \sum _{jkvp}f^{\prime 2}_{jkvp}y^{\prime }_{jkvp}=Z^{1*}.$ If an optimal solution is found, say stop, otherwise solve the third objective with all the previous step constraints with one extra constraint $\sum _{ijupm}c^3_{ijupm}x^3_{ijupm}+ \sum _{ijup}f^3_{ijup} y_{ijup}+ \sum _{jkvpm}c^{\prime 3}_{jkvpm}x^{\prime 3}_{jkvpm}+ \sum _{jkvp}f^{\prime 3}_{jkvp}y^{\prime }_{jkvp} -(\sum _{ijupm}c^1_{ijupm}x^1_{ijupm}+ \sum _{ijup}f^1_{ijup} y_{ijup}+ \sum _{jkvpm}c^{\prime 1}_{jkvpm}x^{\prime 1}_{jkvpm}+ \sum _{jkvp}f^{\prime 1}_{jkvp}y^{\prime }_{jkvp})=Z^{2*}$, which gives the optimal solution.

The deterministic forms are solved by the GRG technique using LINGO 18.0, and we get the minimum deterministic cost $337.38, which is larger than $319.35 (minimum cost using MGMIVM and GRG).

7 Discussion of computational results and managerial insights

7.1 Optimum results of FF-MITSFC-4DTP

In Table 5, the decision variable $x_{11222}$ = 73.72 means 73.72 kg of the second product is transported from the first supplier to the first warehouse through the second conveyance and second path. All the other decision variables, whose values are not mentioned in the table, are considered to be zero.

From Table 5, it is observed that in the case of cost minimization, the model with flexibility constraints gives a better optimal result than the model without flexibility constraints. This agrees with the definition of flexibility. In the method for flexibility constraint, if the value of n is taken as a large number, the solution will be more accurate. This is as per expectation.

7.2 Importance of routes

In Table 5, $x_{11222}$ = 73.72 but $x_{11212}$ = 0, i.e., source, destination, product, and conveyance, all are the same; only the route is different. No transportation takes place through the first route, but through the second route, the product is transported. Now we investigate the reason behind it. 73.72 kg of the second product is transported from the first source to the first destination through the second conveyance. If the products are transported through the first route, the total transportation cost will be 73.72 x (0.40, 0.45, 0.50) + (44, 54, 64) = 73.72 x 0.45 + 54 = $ 87.17. But on the second route, the total transportation cost is 73.72 x (0.35, 0.40, 0.45) + (38, 48, 58) = 73.72 x 0.4 + 48 = $ 77.49. As the second route demands minimum transportation cost, so transportation is made through the second route.

Also, from the result’s comparison (cf. Table 6 and Fig. 5), it is clear that always the 4DTP model gives lower total transportation cost than the 3DTP model as expected. Since in 4DTP, the decision-maker has many route options to transport the products, he can choose the route with lower transportation cost. So this is obvious.

7.3 Effect of breakability

From Table 6, it is seen that, for each model, 4DTP, and 3DTP with breakability, the total transportation cost is higher than without breakability. For Model-A, the minimum cost (without breakability) is $307.2 < $325.59 (with breakability), and for Model-B, the minimum cost is $232.69 (without breakability) < $241.59 (with breakability). That comparison can be seen more clearly in Fig. 5 in the bar diagram. This result is obvious and as per expectation.

7.4 Sensitivity analysis

For sensitivity analysis, we investigate the change of total transportation cost for the change of demand. For this, we take an equal modified graded mean integrated value of demands. The resultant total transportation costs for different demands are given in Table 9 for both types of constraints—with flexibility and without flexibility. In Fig. 6, the total transportation cost linearly increases for increasing demands in both cases—without flexibility constraints and with flexibility constraints.

Table 9 Demand vs total transportation cost

Fig. 6

Changes in total transportation cost for change of demands

7.5 Managerial insights

In most real-life cases, the products need to be stored at warehouses before sending those to retailers or customers, e.g., nowadays Flipkart, Amazon, etc., online shopping companies follow this procedure. India has a vast market for this type of company. So, they have suppliers for different products all over India, and the products are stored or transported to nearby located warehouses or storehouses before delivering to the retailers. With the development of infrastructures in India, there are many paths and conveyances for transportation of the products between different locations along with different toll taxes at different routes for different conveyances. Hence, the FF-MITSFC-4DTP is a perfect model for finding minimum total transportation cost and optimal distribution system. Since the problem is considered in a fully fuzzy environment with flexible constraints, the problem is applicable when the data are vague or imprecise. So, E-commerce companies can utilize our models and techniques to adjust the supply and distribution system.

8 Conclusions

This study investigates FF-MITSFC-4DTPs and some particular models without and with flexible constraints. The supplies, demands, capacities of conveyances, unit transportation costs, transported amounts, and fixed charges for transportation are assumed fuzzy. For the first time, FF-MITSFC-4DTPs with and without flexible constraints are solved by two different methods developed for this purpose. The MGMIVM and an algorithm based on fuzzy order relation are used to convert the fully fuzzy problems into deterministic ones. Some particular models also have been solved. The efficiency of the proposed methods is illustrated through a comparison of the results of an existing model. The importance of the consideration of different routes for transportation, i.e., formulation as 4DTP, is laid down.

In the present model and method, there are a lot of scopes for future extension. The existing 4DTP can be formulated as fully interval-valued fuzzy multi-item two-stage fixed charge 4DTP with flexible constraints and solved using the interval-valued fuzzy set theory following Turksen (1986), Chen et al. (1997), Chen (1997), Chen and Hsiao (2000), Chen et al. (2012), etc. The other TPs, having new constraints, e.g., budget constraints, discount constraints, restrictions on space at warehouses, can be solved by these methods. Though the model has been developed with a triangular fuzzy number, it can be developed for other types of fuzzy numbers, such as trapezoidal fuzzy numbers, parabolic fuzzy numbers, etc.

The limitations of the present investigation are the following. The proposed model is formulated for a single objective (i.e., cost minimization). It can be formulated as a multi-objective one with time minimization, fuel cost minimization, etc. Moreover, the proposed model has been illustrated with two sources, two warehouses, and two retailers. It can also be solved for a large set of data.

Appendices

Appendices

(A) Preliminary

In this section, to gain a better understanding of the proposed method, some of the necessary definitions and examples related to fully fuzzy variables concepts are presented. In detail, the defuzzification processes of fully fuzzy variables are properly illustrated for the proposed method.

Definition 1

A fuzzy number ${\tilde{u}}$ is a convex normalized fuzzy set ${\tilde{u}}$ of the real line $\mathrm I\!R$, with membership function $\mu _{{\tilde{u}}}:\mathrm I\!R \rightarrow [0,1]$, satisfying the following conditions:

• (i) There exists exactly one interval $I \in \mathrm I\!R$ such that $\mu _{{\tilde{u}}}(x)=1$, $\forall x \in I$.

• (ii) The membership function $\mu _{{\tilde{u}}}(x)$ is piecewise continuous.

Definition 2

A triangular fuzzy number (TFN) ${\tilde{u}}$ is specified by three parameters $(x^1, x^2, x^3)$ and is defined by its continuous membership function $\mu _{{\tilde{u}}}(x):X \rightarrow [0,1]$ as follows: $\mu _{{\tilde{u}}}(x)= {\left\{ \begin{array}{ll} \frac{x-x^1}{x^2-x^1},&{} \text {for } x^1 \le x \le x^2 \\ \frac{x^3-x}{x^3-x^2},&{} \text {for } x^2 \le x \le x^3 \\ 0,&{} \text {otherwise}.\\ \end{array}\right. }$

Definition 3

(Kauffman and Gupta 1991) The arithmetic operations between two triangular fuzzy numbers are:

• (i) $k\ge 0, ~ k{\tilde{u}}=(kx^1,kx^2,kx^3)$,

• (ii) $k\le 0, ~ k{\tilde{u}}=(kx^3,kx^2,kx^1)$,

• (iii) ${\tilde{u}} \oplus {\tilde{v}}=(x^1+y^1,x^2+y^2, x^3+y^3)$,

• (iv) ${\tilde{u}} \ominus {\tilde{v}}=(x^1-y^3,x^2-y^2, x^3-y^1)$,

• (v) If ${\tilde{v}}=(y^1, y^2, y^3)$ is non-negative,

  $$\begin{aligned} {\tilde{u}}\otimes {\tilde{v}}=&{\left\{ \begin{array}{ll} (x^1y^1,x^2y^2,x^3y^3), &{} \text {if} \ x^1 \ge 0\\ (x^1y^3,x^2y^2,x^3y^3), &{} \text {if} \ x^1< 0, x^3 \ge 0\\ (x^1y^3,x^2y^2,x^3y^1), &{} \text {if} \ x^3 < 0. \end{array}\right. } \end{aligned}$$

Definition 4

(Yang et al. 2015) Let ${\tilde{u}}=(x^1,x^2,x^3) \in TF(\mathrm I\!R)$ be a triangular fuzzy number. Then, MGMIV of ${\tilde{u}}$, i.e., $EV({\tilde{u}})=\frac{1}{6}(x^1+4x^2+x^3)$.

Definition 5

(Yang et al. 2015) Flexible constraint is one in which satisfaction is a matter of degree and can be partially relaxed if necessary, so as to ensure the flexibility of the problem. Mathematically, it is defined as follows:

Let ${\tilde{u}}$ and ${\tilde{v}}$ be two arbitrary fuzzy numbers. Then, the order relation between fuzzy numbers is defined as:

• (i) ${\tilde{u}} \succeq {\tilde{v}}$ if and only if $P({\tilde{u}}, {\tilde{v}}) \ge \frac{1}{2}$.

• (ii) ${\tilde{u}} \preceq {\tilde{v}}$ if and only if $P({\tilde{v}}, {\tilde{u}}) \ge \frac{1}{2}$.

• (iii) ${\tilde{u}} \simeq {\tilde{v}}$ if and only if $P({\tilde{u}}, {\tilde{v}}) = \frac{1}{2}$.

The notation ‘$\precsim$’ will be used to express the fully fuzzy linear programming with flexible constraints. First, we describe the significance of the flexible inequality ${\tilde{u}} \precsim {\tilde{v}}$. ${\tilde{u}} \preceq _\alpha {\tilde{v}}$, which means ${\tilde{u}}$ is less than ${\tilde{v}}$ in a degree of $\alpha$, if and only if $P({\tilde{v}}, {\tilde{u}})\ge \alpha$. Here, ${\tilde{u}} \preceq _\alpha {\tilde{v}}$ and ${\tilde{v}} \succeq _\alpha {\tilde{u}}$ indicate the identical thing. The flexible inequality ${\tilde{u}} \precsim {\tilde{v}}$ represents ${\tilde{u}} \preceq _\alpha {\tilde{v}}$, where $\alpha$ is a flexible parameter and $\frac{1}{2} \le \alpha \le 1$.

Theorem 1

Fuzzy order relation (Yang et al. 2015) Let ${\tilde{u}}=(x^1,x^2,x^3)$ and ${\tilde{v}}=(y^1,y^2,y^3)$ are two triangular fuzzy numbers and $\alpha \in [0,1]$. Then ${\tilde{u}}\preceq {\tilde{v}}$ if and only if $\frac{2y^2+y^3-x^1-2x^2}{y^3-y^1+x^3-x^1}\ge \alpha$.

(B) Algorithm

Fully fuzzy LPP (FFLP) without flexible constraints is described as:

$$\begin{aligned}&\mathrm{{max}}~ ~Z({\tilde{x}})= {\tilde{c}}_1 \otimes {\tilde{x}}_1 \oplus {\tilde{c}}_2 \otimes {\tilde{x}}_2 \oplus ~\ldots ~\oplus {\tilde{c}}_n \otimes {\tilde{x}}_n\\&s.t. {\left\{ \begin{array}{ll} {\tilde{a}}_{i1} \otimes {\tilde{x}}_1 \oplus {\tilde{a}}_{i2} \otimes {\tilde{x}}_2 \oplus ~\ldots ~\oplus {\tilde{a}}_{in} \otimes {\tilde{x}}_n \preceq {\tilde{b}}_i\\ {\tilde{x}}_j \in TF(R)^+,\\ i=1,2,\ldots ,m, ~ j=1,2,\ldots ,n. \end{array}\right. } \end{aligned}$$

This algorithm is followed from the research work by Yang et al. (2015) for flexible constraints.

Step 1:

Fixed a positive integer n and calculate the value of $\alpha _k$ by $\alpha = \frac{1}{2}+\frac{k}{2n}, ~~ k=0,1,\ldots ,n.$

Step 2:

If ${\tilde{c}}_j=(c^1_j,c^2_j,c^3_j)$, ${\tilde{x}}_j=(x^1_j,x^2_j,x^3_j)$, ${\tilde{a}}_{ij}=(a^1_{ij},a^2_{ij},a^3_{ij})$, ${\tilde{b}}_j=(b^1_i,b^2_i,b^3_i)$, $i=1,2,\ldots ,m,$ $j=1,2,\ldots ,n$ Then FFLP can be written as:

$$\begin{aligned}&\mathrm{{max }}~~ (f^1(X),f^2(X),f^3(X))\\&s.t. {\left\{ \begin{array}{ll} (g^1_i(X),g^2_i(X),g^3_i(X)) \preceq (b^1_i,b^2_i,b^3_i) \\ {\tilde{x}}_j \in TF(R)^+,\\ i=1,2,\ldots ,m, ~ j=1,2,\ldots ,n, \end{array}\right. } \end{aligned}$$

where $f^1(X)$, $f^2(X)$, $f^3(X)$, $g^1(X)$, $g^2(X)$, $g^3(X)$ are all linear functions of X=($x^1_1$, $x^2_1$, $x^3_1$, $x^1_2$, $x^2_2$, $x^3_2$, ..., $x^1_n$, $x^2_n$, $x^3_n)$.

Step 3:

Then using Definition 4 and Theorem 1, the linear crisp form will be

$$\begin{aligned}&\mathrm{{max}} ~~ \frac{1}{6}(f^1(X)+4f^2(X)+f^3(X))\\&s.t. {\left\{ \begin{array}{ll} \frac{2b^2_i+b^3_i-g^1_i(X)-2g^2_i(X)}{b^3_i-b^1_i+g^3_i(X)-g^1_i(X)}\ge \alpha \\ {\tilde{x}}_j \in TF(R)^+,\\ i=1,2,\ldots ,m, ~ j=1,2,\ldots ,n, ~ \text {for } \alpha \in [0,1]. \end{array}\right. } \end{aligned}$$

Step 4:

Solve the linear programming problem obtained in Step-2.

Step 5:

If no solution is found, then there is no solution. Otherwise, let $X^*$=($x^{1*}_1$, $x^{2*}_1$, $x^{3*}_1$, $x^{1*}_2$, $x^{2*}_2$, $x^{3*}_2$, ..., $x^{1*}_n$, $x^{2*}_n$, $x^{3*}_n)$ be a solution then the optimal solution ${\tilde{x}}^*_\alpha$ will be

$$\begin{aligned} {\tilde{x}}^*_\alpha&=({\tilde{x}}^*_\alpha ,{\tilde{x}}^*_\alpha ,\ldots ,{\tilde{x}}^*_\alpha )\\&=((x^{1*}_1,x^{2*}_1,x^{3*}_1), (x^{1*}_2,x^{2*}_2,x^{3*}_2), \ldots , (x^{1*}_n,x^{2*}_n,x^{3*}_n)). \end{aligned}$$

Taking the values of $\alpha$ as $\alpha _0$, $\alpha _1$, ..., $\alpha _n$ (chosen in step-1), solve $FFLP_{\alpha _0}$, $FFLP_{\alpha _1}$, ..., $FFLP_{\alpha _n}$.

Step 6:

Suppose $\tilde{x^*}_{\alpha _k}$ is one of the optimal solutions of $FFLP_{\alpha _k}$, k = 0, 1, ..., n. Calculate the optimal objective values $Z(\tilde{x^*}_{\alpha _0})$, $Z(\tilde{x^*}_{\alpha _1})$, ..., $Z(\tilde{x^*}_{\alpha _n})$, then $\mu (Z({\tilde{x}}))$ provide the membership functions.

Step 7:

Evaluate $\beta _k=2\alpha _k-1$ and $\mu (Z(\tilde{x^*}_{\alpha _k}))$, $k=0,1,\ldots ,n$.

Step 8:

Compute $\mathrm{{min}}_k\{|\beta _k-\mu (Z(\tilde{x^*}_{\alpha _k}))|\}$.

Step 9:

Assume $\mathrm{{min}}_k\{|\beta _k-\mu (Z(\tilde{x^*}_{\alpha _k}))|\}$=$|\beta _{k_0}-\mu (Z(\tilde{x^*}_{\alpha _{k_0}}))|$. Then the fuzzy optimal solution of FFLP is $\tilde{x^*}$=$\tilde{x^*_{\alpha _{k_0}}}$.