Intuitionistic fuzzy sustainable multi-objective multi-item multi-choice step fixed-charge solid transportation problem

Abstract

Embedding sustainability in a distribution system solves major concerns appearing during wielding a distribution process. Therefore, this study explores a novel integrated model by developing sustainability in a multi-objective multi-item multi-choice step fixed-charge solid transportation problem under an intuitionistic fuzzy environment by considering economic, customers’ satisfaction and social aspects. Uncertainty in the parameters of the proposed model is handled by treating those as triangular intuitionistic fuzzy numbers. A new ranking concept with the help of total integral values is developed to defuzzify the above mentioned uncertainty. Apart from fixed-charge, an extra charge is calculated conjointly when the load is bigger than a particular quantity of product during shipping the commodities by different transportation modes. Herein, two different equivalent models are presented from the intuitionistic fuzzy model by utilizing the ranking concept and the possibility measure, respectively, thereafter these models are further transformed into fully deterministic models by converting the multi-choice parameter into a single choice using binary variables. A new method namely, intuitionistic fuzzy game-theoretic method is originated to solve the deterministic models, and then we compare the solutions with another extended method namely, augmented Tchebycheff method for showing the superiority of the new method. The competency of our findings is clarified with an industrial-based application example. Finally, a comparison study is drawn among the other existing techniques. Lastly, managerial implications, conclusions and future scopes are depicted.

1 Introduction

Today, it is not hidden how the efficiency of a supply chain can affect the reputation of a company, also due to the increment of social and environmental regulations/issues, only considering economic aspects are not enough to answer the questions arise in real-world industrial loopholes. Consequently, network design becomes more complex than previous. However, for resolving the environmental issues, the green network or green supply chain becomes a warm topic of research trends nowadays (Das and Roy 2019; Midya et al. 2021). Exempting from the customary research trends, we explore this study by including social aspects in the transportation problem (TP), which is a well-known and important network design problem and can be solved as a linear programming problem. There is a few kinds of researches, in which social aspects are placed in a TP. Among these, Mehlawat et al. (2019) planned a three-stage fixed-charge multi-objective TP (MOTP) with economical, environmental, and social aspects. Gupta et al. (2018) formulated AHP-DEA in a multi-objective sustainable TP in the mining industry. Initially from the time of the introduction of TP by Hitchcock (1941), it had been expressed as a two-dimensional problem i.e., it has two sets, a set of sources and a set of destinations until it was extended to solid transportation problem (STP) by Shell (1955) by attaching a new set, set of conveyances. Then it turns into three-dimensional TP and gets more closer to real-world applications. After that, several research works were made on different types of STP. Chen et al. (2019) presented an STP with entropy function in uncertain environment. Again Chen et al. (2017) solved an STP under interval and fuzzy atmosphere.

Fixed-charge transportation problem (FTP) is another conventional notable variation of TP which is created by Hirsch and Dantzig (1968), in which, except variable transportation cost an extra cost namely, fixed-cost (can be occurred as toll tax, rail-way tax, landing tax, fuel cost, etc.) is considered. Again in the time of transportation through a specific route, often another cost apart from fixed-charge has to be paid due to overload of any conveyance (larger than a destined amount). As a result, an extended version of TP is revealed and FTP became step fixed-charge transportation problem (SFTP) (Kowalski and Lev 2008), which promotes the cost function of FTP into a higher stair and gets STP more closer to the real-world applications. Due to the presence of very few researches on SFTP in the literature, and its practical and realistic nature, we take into account step-fixed charge along with fixed-charge in the STP model. Then the problem turns into step fixed-charge STP (SFSTP).

In real-life situations, generally, two or multiple products are produced for getting more profit at the plants of a company, and those products are shipped to different destinations through various transportation modes. Due to this reason, we incur multiple items in the SFSTP, and that extends SFSTP into a multi-item SFSTP (MSFSTP). Several researchers studied TP with multiple items such as Liu et al. (2018) presented a single objective multi-item fixed-charge STP with uncertain parameters. Majumder et al. (2019) studied a multi-objective solid FTP in an uncertain environment with multiple items and budget constraints. Moreover, in practical problems, two- or multi-criteria are more preferable than a single criterion to handle different conflicting situations. To accommodate these criteria, multiple objective functions are treated simultaneously in an SFTP. Nowadays, the bulk of TP is constructed with multiple objectives instead of a single objective (Biswas et al. 2019; Sifaoui and Aïder 2019; Singh and Yadav 2018). Hence, to tackle such types of objective functions in industrial transporting systems, we further modify MSFSTP to multi-objective MSFSTP (M$^2$SFSTP) by considering three objective functions.

Because of market competition, prices up-down, multiple routes of transportation, etc. such situations arise when taking transportation cost as multi-choice varieties would be a better option than a single choice. Therefore, to adequate multi-choice criteria of the parameters in transporting systems, we extend M$^2$SFSTP to multi-objective multi-item multi-choice SFSTP (M$^3$SFSTP), in which multi-choice parameter is converted into single choice parameter with the help of binary variables (Maity and Roy 2016).

In the recent decades, a rapid advancement has been made due to handle uncertainty in the network design. Some of those can be categorized as uncertain (Chen et al. 2019), intuitionistic fuzzy (Ghosh et al. 2021), neutrosophic (Rizk-Allah et al. 2018), interval (Biswas et al. 2019), uncertain-interval (Sifaoui and Aïder 2019), etc. During the period of information assortment, the relying components of M$^3$SFSTP framework contain a lot of ambiguities or vagueness due to several uncontrollable factors such as incompleteness or lack of evidence, statistical analysis, data inference, etc., also, treating the parameters as the precise or wrong estimation may lead to higher losses or may even fail the whole operation. Hence, to tackle such situations, many researchers included fuzzy set (FS) in TP (El-Washed and Lee 2006), which was invented by Zadeh (1965). But FS only deals with the satisfaction case of fuzziness, and the dissatisfaction case is out of control for FS. Regarding this concern, Atanassov (1986) originated an advanced version of FS, Intuitionistic fuzzy set (IFS), which is symbolized by the membership as well as non-membership degree in such a manner that the sum of both values lies between zero and one, and can tackle the aforementioned uncertainty suitably. Some of the previous researchers placed IFS in their formulated TP such as Ebrahimnejad and Verdegay (2018), Midya et al. (2021), Roy and Midya (2019). Again, Singh and Yadav (2018) solved multi-objective programming problems in intuitionistic fuzzy environment by optimistic, pessimistic and mixed approaches. Among the various form of intuitionistic fuzzy numbers (IFNs), triangular or trapezoidal IFN is commonly used to handle vagueness. However, in the view of the previous researches, we have come to know that triangular IFN (TIFN) is very simple and flexible to provide adequate information. Based on these, TIFN is involved to overcome the ill-knowingness of M$^3$SFSTP model suitably. Although we cannot solve the intuitionistic fuzzy M$^3$SFSTP model directly, and to solve we have to convert it into an equivalent deterministic one. For this purpose, the bulk of the researchers utilized ranking or expected value, and a few of them used different chance measures such as possibility, necessity and credibility measures of IFN. Several procedures which are available in the literature can be followed to extract the crisp value of IFN such as using the ratio of value and ambiguity indices (Li 2010a), using $(\alpha ,\beta )$-cut (Nayagam et al. 2016), using centroid value (Roy and Midya 2019). Again, Midya et al. (2021) incorporated the expected value of IFN to form the deterministic STP. In contrast, we present two equivalent deterministic models corresponding to the intuitionistic fuzzy M$^3$SFSTP model, out of those, one is obtained by applying a new ranking concept and another one is obtained by utilizing the possibility measure of TIFN. Moreover, the ranking concept is introduced with the help of integral values, and it is based on DM’s optimistic and pessimistic viewpoints Liou and Wang (1992). The left and right integral values of the membership function reflect the pessimistic and optimistic viewpoint respectively, and for the non-membership function is the opposite one. The total integral values can be obtained by taking a convex combination of left and right integrals by indexes of optimisms. We define the convex combination of the total integral values of membership and non-membership function through another index of optimism as the ranking index.

The main target of this study is to reduce logistic costs and transportation time, and to increase employments. For this purpose, we examine a lot of related previous researches and locate the actual research gaps from there. Thenceforth, an extensive comparison of several features between the proposed study and preceding related studies in this direction is exhibited in Table 1. The following gaps of the previous research works are traced through this research:

(1):

Considering the existing works on sustainability, most of the previous studies took into account either only economical (Biswas et al. 2019; Roy and Midya 2019) or economical and environmental aspects (Midya et al. 2021), however, this study extends the literature by involving social aspects along with economical and customers’ satisfaction aspects in the transportation network.

(2):

Comparing with extent studies on optimization problem with IFN, many researchers (Ebrahimnejad and Verdegay 2018; Singh and Yadav 2016) generally formulated optimization problems with a single objective, which are unable to define the real-world conflicting state; also by ignoring other components such as multiple items, fixed or step fixed-charge, their models brought more dissatisfaction. On the other side, the proposed study is presented with multiple objectives regarding the above-mentioned components.

(3):

Contrasting with the available literature on the economical objective function, a good number of previous researches are built either without incorporating any extra charges except transportation cost (Chen et al. 2019) or only incorporating fixed-charge (Liu et al. 2018; Sifaoui and Aïder 2019). Notwithstanding, our proposed study is a composition of both fixed and step-fixed, and labour cost. Furthermore, to the best of our knowledge, a large number of previous researchers included the labour cost in fixed-charge, however, due to fluctuation of the workload with the market conditions, the number of requisite labours in any organization is variable. So, we treat the total labour cost as a variable in our study.

(4):

Collating with previous studies on handling uncertainty in the network design, researchers like Liu et al. (2018), Majumder et al. (2019) used uncertain parameters in FTP, however, uncertain parameters are suitable only when undesirable incidents occurred such as natural disaster, which is inconvenient in daily life transporting systems. Also, Kowalski and Lev (2008) and Mehlawat et al. (2019) considered precise parameters which are inconvenient as well. Again, for stochastic parameters in MOTP, a priori predictable periodicity or posterior frequency distribution is required. Henceforth, we overcome these drawbacks by placing TIFN in our proposed model.

(5):

Choosing the subsisting researches on the number of transportation modes, many researchers (Das and Roy 2019; Gupta et al. 2018) addressed only one kind of conveyance. However, due to the magnificent geographical dissemination, considering heterogeneous conveyances are another elementary and vital characteristic of TP as it resists late delivery, and reduces time and extra expenses.

(6):

Comparing with subsisting researches on solving procedures, intuitionistic fuzzy programming (IFP) was used by Roy and Midya (2019) and global criterion method (GCM) was used by Majumder et al. (2019) to solve a multi-objective optimization problem (MOOP), however, our proposed methods deliver better efficient solutions than two mentioned methods in fewer CPU times (according to Tables 11 and 12). Again, Mehlawat et al. (2019) used the $\epsilon$-constraint method which is more laborious and time-consuming than our proposed methods. Furthermore, Chen et al. (2017) applied goal programming (GP) for solving MOTP, but, in GP it is difficult to find a suitable efficient solution by setting proper goals, and if the goals are not set properly, it generates a worse solution. On contrary, such difficulties need not appear in our proposed methods.

Fig. 1

The framework of the proposed research work

Table 1 Some noticeable research works about miscellaneous kind of TP

To fill in the gaps in a concrete way, a novel non-linear multi-objective mixed integer programming (MOMIP) model describing a sustainable M$^3$SFSTP is offered under a two-fold (multi-choice and TIFN) uncertainty. The main goals of the network managers usually are gaining more profit by reducing various expenses (economical aspects), holding a good image to the customers (customers’ satisfaction aspects), maintaining greenness during distribution (environmental effects), maintaining a nice public image (social impacts) etc. Out of these, economic aspects gain more attention of the managers, indeed, any company with an economically inefficient network cannot survive very long, and also cannot reflect other aspects of the network. Again, customers’ satisfaction (in time or early delivery, good quality of products, discounts, etc.) helps the company to keep the customers and to maintain good relation with customers for long-term. On the other hand, social impacts help the company to achieve competitive advantages in the global market by obtaining a nice public image. Based on this consideration, we design the M$^3$SFSTP model with economical, customers’ satisfaction, and social objective functions. Moreover, to acquire efficient solutions by solving the deterministic models, we propose two solving methods, intuitionistic fuzzy game-theoretic method (IFGTM) and augmented Tchebycheff method (ATM). Out of which, IFGTM is originated for the first time in research, and ATM is an extension of the weighted Tchebycheff method. The framework of the proposed research work is depicted in Fig. 1. Hence, the main findings, which pronounce the novelties of the paper, are briefed as follows:

(i):

A unique non-linear MOMIP model is formulated, which describes an intuitionistic fuzzy M$^3$SFSTP in which transportation cost is taken as multi-choice TIFN and other parameters are chosen as TIFN.

(ii):

The formulation delivers the pieces of information regarding the required labours and newly created jobs, also it treats the labour cost as a variable, which is a novel achievement in this field.

(iii):

The overall distribution cost including fixed, step-fixed, and labour cost (economical), transportation together with loading and unloading time (customers’ satisfaction), and newly created jobs during transportation, loading and unloading (social) are considered simultaneously.

(iv):

A new ranking concept and possibility measure of TIFN are utilized to offer two equivalent crisp but multi-choice models, and then the fully deterministic models are put forward through turning the multi-choice parameter into a single choice with the help of binary variables.

(v):

Two solving methods namely IFGTM and ATM, are described to deliver the best efficient solution of M$^3$SFSTP by presenting an industrial practical problem.

(vi):

A comparative study is discussed among the proposed and existing solving techniques by calculating the degrees of closeness.

The paper is further demonstrated in the following way. The motivation for this investigation is described in Sect. 2. The basic ideas and the defuzzification technique of TIFN are discussed in Sect. 3. The description of the problem together with the related model and its deterministic versions are addressed in Sect. 4. A detailed discussion of the solving techniques is established in Sect. 5. Computational experience with a practical industrial example is shared in Sect. 6 to assess the efficiency of the proposed construction and solving techniques. Thereafter, a comparative study for some particular cases is explored in Sect. 7. Important managerial implications are described in Sect. 8. Finally, the paper is ended with Sect. 9 by describing conclusions and several future scopes of this study.

2 Motivation for this investigation

With the increment of population, the unemployment rate has been increased in the recent decade, which raises immense issues in front of developing countries like India, Pakistan etc. As a result, governments as well as organizations around the world have been undergoing pressure concerning this fact. To resolve this issue, it is essential to change the traditional logistic management and to bring forward the social impacts in the transportation system, as TP is one of the widest connecting networks in the world. Based on this fact, exempting from conventional research tendencies, we introduce a transportation network with social impacts by maximizing employments.

In practical industrial applications, DMs usually feel hesitant due to the absence of previous experiences or some unpredictable incidents to take precise decisions during allotting the components of an industrial distribution framework. Therefore, DMs choose the values of the parameters of a logistic problem depending on some professional or experts’ opinions which are generally interval value, linguistic term, uncertain, stochastic, and others. Thus indeterminacy occurs in the decision making process. For this reason, TIFN is considered here to tackle the uncertainty as well as the hesitancy obtained by the data. But, why we involve TIFN in the network system? To answer this question, we discuss the following linguistic examples.

Example 2.1

The unit shipping cost along a certain road is Rupees 10.

Example 2.2

The unit shipping cost along a certain road is around Rupees 10.

Example 2.3

The unit shipping cost along a certain road is nearly Rupees 10 and lies between Rupees 7 and Rupees 12. Also, it is not usually less than Rupees 7, if less, it is never less than Rupees 6, and not usually greater than Rupees 12, if increases, it is never greater than Rupees 14.

In Example 2.1, the mentioned unit transportation cost along a certain road is exactly Rupees 10, and it never changes whatever the situation arises. So, this is the deterministic value of the mentioned parameter. However, in a practical situation, transportation cost depends on several factors such as fuel consumption, nature and friction of the road, fuel cost, previous experiences, statistical data, etc., which are unstable and fluctuate depending on natural and unnatural causes. Therefore, it is inconvenient to always consider the mentioned parameter is exactly Rupees 10.

Example 2.2 describes that the unit transportation cost along a certain road is not exactly Rupees 10, it is more or less Rupees 10. Thus, uncertainty arises in the parameter, and so it can be handled by treating it as a fuzzy number defining a membership function for an interval containing 10. But, the other information, i.e., the inadmissible values are still unknown from this example.

On the other hand, Example 2.3 delivers more information about the value of the unit transportation cost along a definite road. From those information, one can express the mentioned parameter suitably by defining it as a TIFN using any value between 7 and 12 by taking different grades of membership function and any value between 6 and 14 by taking different grades of non-membership function. Thus, the unit transportation cost along a certain road can be delineated as a TIFN, ${\widetilde{c}}_{ijk}^p=(7,10,12;6,10,14).$ Based on this, other parameters (except capacity of conveyance) are also treated as TIFNs.

Furthermore, when transportation takes place through different routes instead of one particular route, multiple choices of unit transportation cost may be available due to different road conditions, traffic, accident, road blockage, etc., rather than a single choice to choose the best option. Then, the unit transportation cost for delivering products from sources to destinations becomes multi-choice TIFNs, $\{{\widetilde{c}}_{ijk}^{{(p)}_{(1)}},{\widetilde{c}}_{ijk}^{{(p)}_{(2)}},\ldots ,{\widetilde{c}}_{ijk}^{{(p)}_{(r)}}\}.$ For this motivation, we take into consideration the unit transportation cost as multi-choice TIFN and the remaining parameters (except capacity of conveyance) as TIFN.

3 Preliminaries

In this section, we present some basic definitions, remarks and theorems on intuitionistic fuzzy sets and intuitionistic fuzzy numbers.

Definition 3.1

(Atanassov 1986) An intuitionistic fuzzy set ${\tilde{A}}$ in a universal discourse X is a set of ordered triplet, ${\tilde{A}}=\{\langle x, \mu _{{\tilde{A}}}(x), \nu _{{\tilde{A}}^I}(x)\rangle : x\in X\}$, where the functions $\mu _{{\tilde{A}}}(x):X\rightarrow [0, 1]$ and $\nu _{{\tilde{A}}}(x):X\rightarrow [0, 1]$ represent the membership and non-membership degrees of x in ${\tilde{A}}$ respectively, and are referred to as membership and non-membership grades of ${\tilde{A}}$ respectively such that $0~\leqslant \mu _{{\tilde{A}}^I}(x)+\nu _{{\tilde{A}}}(x)\leqslant 1$, $\forall$ x in X. For every intuitionistic fuzzy set ${\tilde{A}}=\{\langle x, \mu _{{\tilde{A}}^I}(x), \nu _{{\tilde{A}}}(x)\rangle : x\in X\}$ in X, the value $\pi _{{\tilde{A}}^I}(x)=1-(\mu _{{\tilde{A}}}(x)+\nu _{{\tilde{A}}}(x))$ is called the degree of hesitancy or degree of uncertainty or degree of indeterminacy of x in ${\tilde{A}}$. If for all $x\in X, \mu _{{\tilde{A}}}(x)+\nu _{{\tilde{A}}}(x)=1$, then ${\tilde{A}}$ reduces to fuzzy set ${\tilde{A}}$ in X.

Definition 3.2

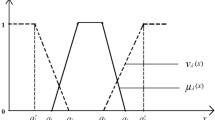
(Roy and Midya 2019) A TIFN is a special kind of IFN, represented as ${\tilde{A}}^{T}=(a_{1}, a_{2}, a_{3}; a^{\prime }_1, a_{2}, a^{\prime }_3)$, where $a^{\prime }_1 \le a_{1}\le a_{2}\le a_{3}\le a^{\prime }_3$ (see Fig. 2), whose membership and non-membership functions are defined respectively as follows:

$$\begin{aligned} \mu _{{\widetilde{A}}^{T}}(x)= & {} {\left\{ \begin{array}{ll} f_{\mu _{{\widetilde{A}}^{T}}}^{L}(x)= \dfrac{x-a_{1}}{a_{2}-a_{1}}, & a_{1} \le x \le a_{2} ,\\ ~~~~~~1,~~~~~~~~~~~~~~~x=a_{2},\\ f_{{{\widetilde{A}}^{T}}}^{R}(x)= \dfrac{a_{3}-x}{a_{3}-a_{2}}, & a_{2} \le x \le a_{3},\\ ~~~~~~0,~~~~~~~~~~~~~~~\text{ otherwise }. \end{array}\right. }\nonumber \\ \nu _{{{\widetilde{A}}^{T}}}(x)= & {} {\left\{ \begin{array}{ll} g_{\nu _{{\widetilde{A}}^{T}}}^{L}(x)= \dfrac{a_{2}-x}{a_{2}-a^{\prime }_1}, & a^{\prime }_1 \le x \le a_{2} ,\\ ~~~~~~0,~~~~~~~~~~~~~~~x=a_{2},\\ g_{\nu _{{\widetilde{A}}^{T}}}^{R}(x)= \dfrac{x-a_{2}}{a^{\prime }_3-a_{2}}, & a_{2}\le x \le a^{\prime }_3,\\ ~~~~~~1,~~~~~~~~~~~~~~~\text{ otherwise }. \end{array}\right. } \end{aligned}$$

(1)

If $a_{1} = a_{2} = a_{3} = a^{\prime }_1 = a^{\prime }_3 = a$ then ${{\widetilde{A}}^{T}}=(a_{1}, a_{2}, a_{3}; a^{\prime }_1, a_{2}, a^{\prime }_3)$ represents a real number a.

Definition 3.3

Let ${{{\widetilde{A}}^{T}}}=(a_1,a_2,a_3;a_1^{'},a_2,a_3^{'})$ be TIFN with membership and non-membership functions defined in Eq. (1), then the possibility measure for membership and non-membership function are defined in Eq. (2).

$$\begin{aligned} Pos_{\mu }({{\widetilde{A}}^{T}}\le x)= & {} {\left\{ \begin{array}{ll} 1, & x \ge a_{2} ,\\ \dfrac{x-a_1}{a_2-a_1}, & a_{1} \le x\le a_2,\\ 0, & x \le a_{1}. \end{array}\right. } \nonumber \\ Pos_{\nu }({{\widetilde{A}}^{T}}\le x)= & {} {\left\{ \begin{array}{ll} 0, & x \ge a_{2} ,\\ \dfrac{a_2-x}{a_2-a_1^{'}},& a_{1}^{'} \le x\le a_2,\\ 1, & x \le a_{1}^{'}. \end{array}\right. } \end{aligned}$$

(2)

Note: $Pos({{\widetilde{A}}^{T}}\ge x)=1-Pos({{\widetilde{A}}^{T}}< x).$

Arithmetic operation of TIFNs: Let ${{\widetilde{A}}^{T}}=(a_{1}, a_{2}, a_{3}; a^{\prime }_1, a_{2}, a^{\prime }_3)$ and ${{\widetilde{B}}^{T}}=(b_{1}, b_{2}, b_{3}; b^{\prime }_1, b_{2}, b^{\prime }_3)$ are two TIFNs then the arithmetic operations between them are given below:

(i):

${{\widetilde{A}}^{T}} \oplus {{\widetilde{B}}^{T}}= (a_{1} + b_{1}, a_{2} + b_{2}, a_{3} + b_{3}; a^{\prime }_1 + b^{\prime }_1, a_{2} + b_{2}, a^{'}_3 + b^{'}_3)$.

(ii):

${{\widetilde{A}}^{T}} \ominus {{\widetilde{B}}^{T}} = (a_{1} - b_{3}, a_{2} - b_{2}, a_{3} - b_{1}; a^{\prime }_1 - b^{\prime }_3, a_{2} - b_{2}, a^{'}_3 - b^{'}_1)$.

(iii):

Let p is a real number then,

If $p >0$, $p{{\widetilde{A}}^{T}}=(pa_{1}, pa_{2}, pa_{3}; pa^{'}_3, pa_{2}, pa^{'}_1),$

If $p<0$, $p{{\widetilde{A}}^{T}}=(pa_{3}, pa_{2}, pa_{1}; pa^{'}_3, pa_{2}, pa^{'}_1)$.

(iv):

${{\widetilde{A}}^{T}}\otimes {{\widetilde{B}}^{T}} = (\rho _1, \rho _2, \rho _3; \rho ^{'}_1, \rho _{2}, \rho ^{'}_3)$, where,

$\rho _{1}=\min \{a_{1}b_{1}, a_{1}b_{3}, a_{3}b_{1}, a_{3}b_{3}\},\rho ^{'}_1=\min \{a^{'}_1b^{'}_1, a^{'}_1b^{'}_3, a^{'}_3b^{'}_1, a^{'}_3b^{'}_3\},\rho _{2}=a_{2}b_{2}.$

$\rho _{3}=\max \{a_{1}b_{1}, a_{1}b_{3}, a_{3}b_{1}, a_{3}b_{3}\},\rho ^{'}_3=\max \{a^{'}_1b^{'}_1, a^{'}_1b^{'}_3, a^{'}_3b^{'}_1, a^{'}_3b^{'}_3\}.$

Here $\oplus$, $\ominus$ and $\otimes$ are intuitionistic fuzzy addition, subtraction and multiplication respectively.

Fig. 2

Triangular intuitionistic fuzzy number

Fig. 3

Inverse functions of TIFN

3.1 Defuzzification of TIFN

Literature survey reveals that there exist several methods for defuzzification of TIFN. However, in this subsection, we introduce a new methodology for defuzzification of TIFN by its total integral values, which is described as follows:

Methodology: Let ${{\widetilde{A}}^{T}}=(a_{1}, a_{2}, a_{3}; a^{\prime }_1, a_{2}, a^{\prime }_3)$ be a TIFN then its left and right membership and non-membership functions are given respectively in Eq. (1). The inverse functions are given by, $\displaystyle h_{\mu _{{\widetilde{A}}^{T}}}^{L}(y)=a_{1}+(a_{2}-a_{1})y$ and $\displaystyle h_{\mu _{{\widetilde{A}}^{T}}}^{R}(y)=a_{3}-(a_{3}-a_{2})y$ respectively (for membership function) and $\displaystyle k_{\nu _{{\widetilde{A}}^{T}}}^{L}(y)=a_{2}-(a_{2}-a^{'}_1)y$ and $\displaystyle k_{\nu _{{\widetilde{A}}^{T}}}^{R}(y)=a_{2}+(a^{'}_3-a_{2})y$ respectively (for non-membership function) (see Fig. 3). Then left and right integrals of membership function are given by, $I^{L}_\mu =\displaystyle \int _{0}^{1} h_{\mu _{{\widetilde{A}}^{T}}}^{L}(y)dy = \dfrac{a_{1}+a_{2}}{2}$ and $I^{R}_\mu =\displaystyle \int _{0}^{1} h_{\mu _{{\widetilde{A}}^{T}}}^{R}(y)dy = \dfrac{a_{2}+a_{3}}{2}$ respectively. Then the total integral value of membership function is given by, $I_{\mu }=\alpha \left( \dfrac{a_{1}+a_{2}}{2}\right) +(1-\alpha )\left( \dfrac{a_{2}+a_{3}}{2}\right)$, $(0\le \alpha \le 1).$ Similarly left, right and total integral values of non-membership function are given by, $I^{L}_\nu =\dfrac{a^{'}_1+a_{2}}{2}$, $I^{R}_\nu =\dfrac{a_{2}+a^{'}_3}{2}$ and $I_{\nu }=\beta \left( \dfrac{a^{'}_1+a_{2}}{2}\right) +(1-\beta )\left( \dfrac{a_{2}+a^{'}_3}{2}\right)$, $(0\le \beta \le 1)$ respectively.

Now ranking index of ${{\widetilde{A}}^{T}}$ is given by, $\mathfrak {R}({{\widetilde{A}}^{T}})={\gamma } I_{\mu } + (1-{\gamma })I_{\nu },(0 \le \alpha , \beta , \gamma \le 1),$ where $\alpha , \beta$ and $\gamma$ are the degrees of optimism of DM. When $\alpha , \beta$ and $\gamma$ all are equal to $\dfrac{1}{2}$, then $\mathfrak {R}({{\widetilde{A}}^{T}})=\dfrac{a_{1}+a_{3}+4a_{2}+a^{'}_1+a^{'}_3}{8}$.

Theorem 3.1

Ranking index of TIFN, $(i.e.,~\mathfrak {R}({{\widetilde{A}}^{T}}))$ is linear.

Proof

Let ${{\widetilde{A}}^{T}}=(a_{1}, a_{2}, a_{3}; a^{\prime }_1, a_{2}, a^{\prime }_3)$ and ${{\widetilde{B}}^{T}}=(b_{1}, b_{2}, b_{3}; b^{\prime }_1, b_{2}, b^{\prime }_3)$ are two TIFNs then we have to show that $\mathfrak {R}(c{{\widetilde{A}}^{T}}+d{{\widetilde{B}}^{T}})=c\mathfrak {R}({{\widetilde{A}}^{T}})+d\mathfrak {R}({{\widetilde{B}}^{T}})$, where c and d are two positive real numbers (say). Now, by arithmetic operations of TIFN we have,

$c{{\widetilde{A}}^{T}}=(ca_{1}, ca_{2}, ca_{3}; ca^{'}_1, ca_{2}, ca^{'}_3)$, $d{{\widetilde{B}}^{T}}=(db_{1}, db_{2}, db_{3}; db^{'}_1, db_{2}, db^{'}_3)$ and $c{{\widetilde{A}}^{T}}+d{{\widetilde{B}}^{T}}=(ca_{1}+db_{1}, ca_{2}+db_{2}, ca_{3}+db_{3}; ca^{'}_1+db^{'}_1, ca_{2}+db_{2}, ca^{'}_3+db^{'}_3)$.

Now,

$$\begin{aligned}&\mathfrak {R}(c{{\widetilde{A}}^{T}}+d{{\widetilde{B}}^{T}})\\&\quad ={\gamma }\left[ \alpha \left( \dfrac{ca_{1}+db_{1}+ca_{2}+db_{2}}{2}\right) \right. \\&\left. \qquad +(1-\alpha )\left( \dfrac{ca_{2}+db_{2}+ca_{3}+db_{3}}{2}\right) \right] \\&\qquad +(1-{\gamma })\left[ \beta \left( \dfrac{ca^{'}_1+db^{'}_1+ca_{2}+db_{2}}{2}\right) \right. \\&\left. \qquad +(1-\beta )\left( \dfrac{ca_{2}+db_{2}+ca^{'}_3+db^{'}_3}{2}\right) \right] . \\&\quad =c\left[ {\gamma }\left\{ \alpha \left( \dfrac{a_{1}+a_{2}}{2}\right) +(1-\alpha )\left( \dfrac{a_{2}+a_{3}}{2}\right) \right\} \right. \\&\left. \qquad +(1-{\gamma })\left\{ \beta \left( \dfrac{a^{'}_1+a_{2}}{2}\right) +(1-\beta )\left( \dfrac{a_{2}+a^{'}_3}{2}\right) \right\} \right] \\&\qquad +d\left[ {\gamma }\left\{ \alpha \left( \dfrac{b_{1}+b_{2}}{2}\right) +(1-\alpha )\left( \dfrac{b_{2}+b_{3}}{2}\right) \right\} \right. \\&\left. \qquad +(1-{\gamma })\left\{ \beta \left( \dfrac{b^{'}_1+b_{2}}{2}\right) +(1-\beta )\left( \dfrac{b_{2}+b^{'}_3}{2}\right) \right\} \right] .\\&\quad =c\mathfrak {R}({{\widetilde{A}}^{T}})+d\mathfrak {R}({{\widetilde{B}}^{T}}). \end{aligned}$$

Hence $\mathfrak {R}$ is linear. $\square$

Proposition 3.1

If ${{\widetilde{A}}^{T}}$ and ${{\widetilde{B}}^{T}}$ be two TIFNs, then

• 4.1.1 ${{\widetilde{A}}^{T}}\succeq {{\widetilde{B}}^{T}}\Leftrightarrow \mathfrak {R}({{\widetilde{A}}^{T}})\ge \mathfrak {R}({{\widetilde{B}}^{T}}).$

• 4.1.2 ${{\widetilde{A}}^{T}}\preceq {{\widetilde{B}}^{T}}\Leftrightarrow \mathfrak {R}({{\widetilde{A}}^{T}})\le \mathfrak {R}({{\widetilde{B}}^{T}}).$

• 4.1.3 ${{\widetilde{A}}^{T}} \approx {{\widetilde{B}}^{T}}\Leftrightarrow \mathfrak {R}({{\widetilde{A}}^{T}})= \mathfrak {R}({{\widetilde{B}}^{T}}).$

3.2 Advantages of proposed ranking concept

• The proposed concept gives a suitable defuzzified value of TIFN in its simpler form in lesser time than other existing methods, which is flexible to apply in decision-making problems.

• The proposed concept takes into account numerical values as well as membership and non-membership values of TIFNs.

• From Table 2, it can be seen that the proposed ranking concept is logical regardless of Li (2010a), and Roy and Midya (2019), as their methods give equal values in Examples 3.1, 3.2, 3.3, and Examples 3.1, 3.6 respectively. Therefore, their concepts failed to rank TIFNs mentioned in the above-mentioned examples.

• The proposed ranking concept requires easy computation on integral values, and it also considers DM’s degrees of optimism.

Table 2 Relative comparison of the proposed ranking concept with some existing concepts

4 Problem description

In this section, we formulate a novel MOMIP model that describes an M$^{3}$SFSTP with single and multi-choice TIFN parameters from an economical, customers’ satisfaction, and social frame of reference. The formulation consists of multiple suppliers/sources (plants, factories) from which multiple products are transferred to multiple destinations/demand centers (retailers, customers) via multiple modes of transportation (trucks, trains, aeroplanes). The premier targets are: (T1) to alleviate the overall transportation cost and time, and to enhance new employments, and (T2) to find the optimal quantity of shipped products and the optimal number of labours required for shipping, loading and unloading, besides, the followings affiliations are also taken into consideration: (A1) the labour cost at origins, destinations, and during transportation, (A2) toll charge, service taxes, maintenance charge of the conveyances, safety expenses, etc., entitled as fixed-cost, (A3) an extra charge, designated as step fixed-cost, which occurs due to overload of conveyances by a particular amount, (A4) the loading and unloading time of products, which increase the validity level of the allotment time. The main goal of this construction is to find the optimal quantities of the delivered product and the optimal number of requisite labours such that the requirements of all products at the demand points are satisfied by optimizing the aggregate logistic cost (economical), overall logistic time (customers’ satisfaction), and new jobs (social). The graphical network of the proposed problem can be found in Fig. 4. In order to develop the M$^{3}$SFSTP, the following assumptions are enlisted as follows:

• The shipping cost is directly proportional to the amount of delivered commodities, and homogeneous type of products are distributed via heterogeneous transportation fleet.

• Conveyances, and supply and demand centers have limited and known capacities, and in distribution centers, after receiving products, distributors deliver the products as soon as possible, so, storage cost is not considered at destinations.

• Only the unit transportation cost is treated as multi-choice TIFN and all other remaining parameters are taken as TIFN except conveyances’ capacities which are taken as crisp.

• Only variable jobs are considered instead of fixed jobs (managerial post).

Fig. 4

Graphical network of the proposed TP

Fig. 5

A notional diagram of the offered research work

4.1 Model identification

Herein, an unprecedented MOMIP model is introduced which is consisted of three objective functions and the essential constraints, to recount the M$^3$SFSTP model under intuitionistic fuzzy ambience. The construction seeks out the delivered amount of different products, requisite number of labours and new employments at the same time. A brief idea of the proposed research work is illustrated in Fig. 5. The mathematical model together with the necessary constraints are narrated as follows:

Model 1

$$\begin{aligned} \text{ minimize }~{\widetilde{Z}}_{1}^{T}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\nonumber \\&\left\{ {\widetilde{c}}_{ijk}^{(p)_{(1)}T} \text{ or }~ {\widetilde{c}}_{ijk}^{ (p)_{(2)}T} \text{ or }\ldots \text{ or }~ {\widetilde{c}}_{ijk}^{(p)_{(r)}T}\right\} x_{ijk}^{p}\nonumber \\&+\sum _{i=1}^{M}\sum _{j=1}^{N}\left[ \sum _{k=1}^{V}\sum _{p=1}^{P}\left\{ {\widetilde{f}}_{ijk}^{(p)T} y_{ijk}^{p}+{\widetilde{g}}_{ijk}^{(p)T} {\eta }_{ijk}^{p}\right\} \nonumber \right. \\&\left. +{\widetilde{lt}}_{ij}^{T}wt_{ij}+{\widetilde{ll}}_{i}^{T}wl_{i}+{\widetilde{lu}}^{T}_jwu_j\right] \nonumber \\&+\displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ \left( {\widetilde{ol}}_i^{T}+{\widetilde{ou}}_j^{T}\right) x_{ijk}^{p}\nonumber \right. \\&\left. +{\widetilde{mc}}_k^{T}y_{ijk}^{p}d_{ij}\right] \end{aligned}$$

(3)

$$\begin{aligned} \text{ minimize }~{\widetilde{Z}}_{2}^{T}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ {\widetilde{t}}_{ijk}^{(p)T}y_{ijk}^{p}+\left( {\widetilde{l}}_i^{T}+{\widetilde{ul}}^{T}_j\right) x_{ijk}^p\right] \end{aligned}$$

(4)

$$\begin{aligned} \text{ maximize }~{\widetilde{Z}}_{3}^{T}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}~\left[ {\widetilde{st}}_{ij}^{T}\left( x_{ijk}^p/e_k\right) \nonumber \right. \\&\left. +{\widetilde{sl}}_{i}^{T}\left( x_{ijk}^p/{\widetilde{a}}_i^{(p)T}\right) +{\widetilde{su}}_{j}^{T}\left( x_{ijk}^p/{\widetilde{b}}_j^{(p)T}\right) \right] \end{aligned}$$

(5)

$$\begin{aligned} \text{ subject } \text{ to }&\sum _{j=1}^{N}\sum _{k=1}^{V}x_{ijk}^{p}\le {\widetilde{a}}_{i}^{(p)T}, \nonumber \\&(i=1,2,\ldots ,M; p=1,2,\ldots ,P) \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{k=1}^{V}x_{ijk}^{p}\ge {\widetilde{b}}_{j}^{(p)T},\nonumber &\quad (j=1,2,\ldots ,N; p=1,2,\ldots ,P) \end{aligned}$$

(7)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{p=1}^{P}x_{ijk}^{p}\le e_{k},~~(k=1,2,\ldots ,V) \end{aligned}$$

(8)

$$\begin{aligned}&\sum _{k=1}^{V}\sum _{p=1}^{P}{\widetilde{mt}}_{ij}^{T}x_{ijk}^p\le wt_{ij},~~~\nonumber \quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(9)

$$\begin{aligned}&\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}{\widetilde{ml}}_{i}^{T}x_{ijk}^p\le wl_{i},~~~\nonumber\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(10)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{k=1}^{V}\sum _{p=1}^{P}{\widetilde{mu}}_{j}^{T}x_{ijk}^p\le wu_{j},~~~\nonumber\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(11)

$$\begin{aligned} y_{ijk}^{p}= & {} {\left\{ \begin{array}{ll} 1, &{} \text {if}~ x_{ijk}^{p}>0,\\ 0, &{} \text {if}~ x_{ijk}^{p}=0. \end{array}\right. } \end{aligned}$$

(12)

$$\begin{aligned} \eta _{ijk}^{p}= & {} {\left\{ \begin{array}{ll} 1,&{} \text {if}~x_{ijk}^{p}>A~(\text {fixed amount}),\\ 0,&{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

(13)

$$\begin{aligned} x_{ijk}^{p}\ge & {} 0,wt_{ij},wl_{i},wu_{j}~ \text{ are } \text{ integers. } \end{aligned}$$

(14)

In Model 1, $\{{\tilde{c}}_{ijk}^{I(p)_{(1)}T}\text{ or }~{\tilde{c}}_{ijk}^{I (p)_{(2)}T}\text{ or }\ldots \text{ or }~ {\tilde{c}}_{ijk}^{I(p)_{(r)}T}\}$ is the multi-choice cost of transportation for transporting per unit $p\mathrm{th}$ product from $i\mathrm{th}$ source to $j\mathrm{th}$ destination center via $k\mathrm{th}$ conveyance in intuitionistic fuzzy form with r choices. Equation (3) is the economical objective function, which aims to minimize variable transportation cost (first part), fixed and step-fixed cost (second part), labour cost for shipping and loading-unloading of products (third part), operational cost in sources and destinations (fourth part), and maintenance cost of vehicles (last part). Equation (4) is the satisfactory objective function which is included to maximize customers’ satisfaction by minimizing transportation and loading-unloading time. Equation (5) is the social objective function which maximizes new jobs created during shipping and loading-unloading of products. Constraints (6) state that the distributed quantity from each source must be less than or equal to its availability. Constraints (7) enunciate that the overall shipped quantity to each destination must fulfil its demand. Constraints (8) demonstrate that the overall load in each conveyance cannot go beyond its capacity. Constraints (9), (10) and (11) impose that required worker cannot surpass the available labour during transportation, in sources and in destinations respectively. Also, those constraints are included to determine the number of workers that are required for shipping, loading and unloading of products respectively. Constraints (12)–(14) define the nature of the variables of Model 1.

4.2 Deterministic equivalence of the model

In order to solve optimization problems with uncertainty either we have to convert it into its deterministic form or to develop stochastic model. As the encountered problem is with two-fold uncertainty (intuitionistic fuzzy and multi-choice), and only one scenario is taken into consideration, we propose two simple steps to reduce the uncertainty of the model by avoiding any complexity. Therefore, we solve Model 1 in three steps: Step 1, we deal with intuitionistic fuzzy parameters through two manners by presenting two equivalent models i.e., Models 2.1 and 2.2; Step 2, then by reducing multi-choice parameter into a single choice by binary variables, we get fully deterministic equivalent models i.e., Models 3.1 and 3.2; Step 3, finally, deterministic multi-objective models are resolved by multi-objective optimization technique(s). All models are described in the following way.

Step 1.1 Dealing with IF parameters by ranking concept, In the first part of Step 1, we turn the intuitionistic fuzzy M$^3$SFSTP model (Model 1) into an equivalent crisp model (Model 2.1) by applying the proposed ranking concept (see Sect. 3.1), and using Theorem 3.1 and Proposition 3.1, which is stated as follows:

Model 2.1

The objective functions with multi-choice and crisp (defuzzified) parameters are given in Eqs. (15)–(17).

$$\begin{aligned} \text{ minimize }~{Z}^{'}_{1}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\nonumber \\&\left\{ \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{(p)_{(1)}T}\right) \text{ or }~ \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{ (p)_{(2)}T}\right) \text{ or }\cdots \text{ or }~ \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{(p)_{(r)}T}\right) \right\} x_{ijk}^{p}\nonumber \\&+\sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left\{ \mathfrak {R}\left( {\widetilde{f}}_{ijk}^{(p)T}\right) y_{ijk}^{p}\nonumber \right. \left. +\mathfrak {R}\left( {\widetilde{g}}_{ijk}^{(p)T}\right) {\eta }_{ijk}^{p}\right\} \nonumber \\&+\sum _{i=1}^{M}\sum _{j=1}^{N}\left\{ \mathfrak {R}\left( {\widetilde{lt}}_{ij}^{T}\right) wt_{ij}\nonumber \right. \left. +\mathfrak {R}\left( {\widetilde{ll}}_{i}^{T}\right) wl_{i}+\mathfrak {R}\left( {\widetilde{lu}}^{T}_j\right) wu_j\right\} \nonumber \\&+ \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ \left( \mathfrak {R}\left( {\widetilde{ol}}_i^{T}\right) \nonumber \right. \right. \left. \left. +\mathfrak {R}\left( {\widetilde{ou}}_j^{T}\right) \right) x_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{mc}}_k^{T}\right) y_{ijk}^{p}d_{ij}\right] \end{aligned}$$

(15)

$$\begin{aligned} \text{ minimize }~{Z}^{'}_{2}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ \mathfrak {R}\left( {\widetilde{t}}_{ijk}^{(p)T}\right) y_{ijk}^{p}\nonumber \right. \\&\left. +\left( \mathfrak {R}\left( {\widetilde{l}}_i^{T}\right) +\mathfrak {R}\left( {\widetilde{ul}}^{T}_j\right) \right) x_{ijk}^p\right] \end{aligned}$$

(16)

$$\begin{aligned} \text{ maximize }~{Z}^{'}_{3}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ \mathfrak {R}\left( {\widetilde{st}}_{ij}^{T}\right) \left( \dfrac{x_{ijk}^p}{e_k} \right) \nonumber \right. \\&\left. +\mathfrak {R}\left( {\widetilde{sl}}_{i}^{T}\right) \left( \dfrac{ x_{ijk}^p}{\mathfrak {R}\left( {\widetilde{a}}_i^{(p)T}\right) }\right) \right] \nonumber \\&+\displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\mathfrak {R}\left( {\widetilde{su}}_{j}^{T}\right) \left( \dfrac{ x_{ijk}^p}{\mathfrak {R}\left( {\widetilde{b}}_j^{(p)T}\right) }\right) \end{aligned}$$

(17)

The respective defuzzified constraints are given as follows:

$$\begin{aligned} \text{ subject } \text{ to }&\sum _{j=1}^{N}\sum _{k=1}^{V}x_{ijk}^{p}\le \mathfrak {R}\left( {\widetilde{a}}_i^{(p)T}\right) ,~~~~\nonumber \\&(i=1,2,\ldots ,M; p=1,2,\ldots ,P) \end{aligned}$$

(18)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{k=1}^{V}x_{ijk}^{p}\ge \mathfrak {R}\left( {\widetilde{b}}_j^{(p)T}\right) ,\quad (j=1,2,\ldots ,N; p=1,2,\ldots ,P) \end{aligned}$$

(19)

$$\begin{aligned}&\sum _{k=1}^{V}\sum _{p=1}^{P}\mathfrak {R}\left( {\widetilde{mt}}_{ij}^{T}\right) x_{ijk}^p\le wt_{ij},\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(20)

$$\begin{aligned}&\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\mathfrak {R}\left( {\widetilde{ml}}_{i}^{T}\right) x_{ijk}^p\le wl_{i},\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(21)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{k=1}^{V}\sum _{p=1}^{P}\mathfrak {R}\left( {\widetilde{mu}}_{j}^{T}\right) x_{ijk}^p\le wu_{j},\quad (i=1,2,\ldots M; j=1,2,\ldots N)\nonumber \\&\quad \text{ the } \text{ constraints } (4.8),\nonumber \\&\quad \text{ the } \text{ constraints } (4.12){-}(4.14). \end{aligned}$$

(22)

Step 1.2 Dealing with IF parameters by possibility measure, In the second part of Step 1, possibility measure of TIFN (using Definition 3.3) along with the ranking concept (see Sect. 3.1) and Theorem 3.1 are employed to convert the intuitionistic fuzzy M$^3$SFSTP model (Model 1) into another equivalent deterministic model (Model 2.2), which is described as follows:

Model 2.2

The objective functions with multi-choice and crisp (defuzzified) parameters are given in Eqs. (23)–(25).

$$\begin{aligned} \text{ minimize }~{Z}^{'}_{1}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P} \left\{ \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{(p)_{(1)}T}\right) \text{ or }~ \nonumber \right. \left. \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{ (p)_{(2)}T}\right) \text{ or }\ldots \text{ or }~ \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{(p)_{(r)}T}\right) \right\} x_{ijk}^{p}\nonumber \\&+\sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\nonumber \left\{ \mathfrak {R}\left( {\widetilde{f}}_{ijk}^{(p)T}\right) y_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{g}}_{ijk}^{(p)T}\right) {\eta }_{ijk}^{p}\right\} \nonumber \\&+\sum _{i=1}^{M}\sum _{j=1}^{N}\left\{ \mathfrak {R}\left( {\widetilde{lt}}_{ij}^{T}\right) wt_{ij}\right. \nonumber \left. +\mathfrak {R}\left( {\widetilde{ll}}_{i}^{T}\right) wl_{i}+\mathfrak {R}\left( {\widetilde{lu}}^{T}_j\right) wu_j\right\} \nonumber \\&+\displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ \left( \mathfrak {R}\left( {\widetilde{ol}}_i^{T}\right) \right. \right. \nonumber \left. \left. +\mathfrak {R}\left( {\widetilde{ou}}_j^{T}\right) \right) x_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{mc}}_k^{T}\right) y_{ijk}^{p}d_{ij}\right] \end{aligned}$$

(23)

$$\begin{aligned} \text{ minimize }~{Z}^{'}_{2}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\nonumber \\&\left[ \mathfrak {R}\left( {\widetilde{t}}_{ijk}^{(p)T}\right) y_{ijk}^{p}+\left( \mathfrak {R}\left( {\widetilde{l}}_i^{T}\right) +\mathfrak {R}\left( {\widetilde{ul}}^{T}_j\right) \right) x_{ijk}^p\right] \end{aligned}$$

(24)

$$\begin{aligned} \text{ maximize }~{Z}^{'}_{3}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\nonumber \\&\left[ \mathfrak {R}\left( {\widetilde{st}}_{ij}^{T}\right) \left( \dfrac{x_{ijk}^p}{e_k} \right) +\mathfrak {R}\left( {\widetilde{sl}}_{i}^{T}\right) \left( \dfrac{ x_{ijk}^p}{\mathfrak {R}\left( {\widetilde{a}}_i^{(p)T}\right) }\right) \right] \nonumber \\&+\displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\mathfrak {R}\left( {\widetilde{su}}_{j}^{T}\right) \left( \dfrac{ x_{ijk}^p}{\mathfrak {R}\left( {\widetilde{b}}_j^{(p)T}\right) }\right) \end{aligned}$$

(25)

The respective defuzzified constraints are given as follows:

$$\begin{aligned} \text{ subject } \text{ to }&\sum _{j=1}^{N}\sum _{k=1}^{V}Pos_{\mu }(x_{ijk}^{p}\le {\widetilde{a}}_{i}^{(p)T})\ge \theta ,~~~~\nonumber \\&(i=1,2,\ldots ,M; p=1,2,\ldots ,P) \end{aligned}$$

(26)

$$\begin{aligned}&\sum _{j=1}^{N}\sum _{k=1}^{V}Pos_{\nu }(x_{ijk}^{p}\le {\widetilde{a}}_{i}^{(p)T})\le \pi ,\quad (i=1,2,\ldots ,M; p=1,2,\ldots ,P) \end{aligned}$$

(27)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{k=1}^{V}Pos_{\mu }(x_{ijk}^{p}\ge {\widetilde{b}}_{j}^{(p)T})\ge \theta ,\quad (j=1,2,\ldots ,N; p=1,2,\ldots ,P) \end{aligned}$$

(28)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{k=1}^{V}Pos_{\nu }(x_{ijk}^{p}\ge {\widetilde{b}}_{j}^{(p)T})\le \pi ,\quad (j=1,2,\ldots ,N; p=1,2,\ldots ,P) \end{aligned}$$

(29)

$$\begin{aligned}&\sum _{k=1}^{V}\sum _{p=1}^{P}Pos_{\mu }({\widetilde{mt}}_{ij}^{T}x_{ijk}^p\le wt_{ij})\ge \theta ,\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(30)

$$\begin{aligned}&\sum _{k=1}^{V}\sum _{p=1}^{P}Pos_{\nu }({\widetilde{mt}}_{ij}^{T}x_{ijk}^p\le wt_{ij})\le \pi ,\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(31)

$$\begin{aligned}&\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}Pos_{\mu }({\widetilde{ml}}_{i}^{T}x_{ijk}^p\le wl_{i})\ge \theta ,\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(32)

$$\begin{aligned}&\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}Pos_{\nu }({\widetilde{ml}}_{i}^{T}x_{ijk}^p\le wl_{i})\le \pi ,\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(33)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{k=1}^{V}\sum _{p=1}^{P}Pos_{\mu }({\widetilde{mu}}_{j}^{T}x_{ijk}^p\le wu_{j})\ge \theta ,\quad (i=1,2,\ldots M; j=1,2,\ldots N) \end{aligned}$$

(34)

$$\begin{aligned}&\sum _{i=1}^{M}\sum _{k=1}^{V}\sum _{p=1}^{P}Pos_{\nu }({\widetilde{mu}}_{j}^{T}x_{ijk}^p\le wu_{j})\le \pi ,\quad (i=1,2,\ldots M; j=1,2,\ldots N) \nonumber \\&\text{ the } \text{ constraints } (4.8),\nonumber \\&\text{ the } \text{ constraints } (4.12){-}(4.14). \end{aligned}$$

(35)

$\begin{aligned} \\&\text{ the } \text{ constraints } (8),\nonumber \\&\text{ the } \text{ constraints } (12){-}(14). \end{aligned}$

Here, $\theta$ and $\pi$ are the predefined confidence levels satisfying $0\le \theta +\pi \le 1.$

In Models 2.1 and 2.2, $\left\{ \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{(p)_{(1)}T}\right) \text{ or }~ \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{ (p)_{(2)}T}\right) \text{ or }\cdots \text{ or }~ \mathfrak {R}\left( {\widetilde{c}}_{ijk}^{(p)_{(r)}T}\right) \right\}$ is the multi-choice cost of transportation for transporting per unit $p\mathrm{th}$ product from $i\mathrm{th}$ source to $j\mathrm{th}$ destination center via $k\mathrm{th}$ conveyance in crisp form with r choices.

Step 2 Transformation of multi-choice parameter, In Step 2, binary variables (Maity and Roy 2016) are utilized for reduction of multi-choice parameter $\left( {\widetilde{c}}_{ijk}^{(p)_{(r)}T}\right)$ of Models 2.1 and 2.2 into a single choice. Thus, Models 2.1 and 2.2 are further transformed to Models 3.1 and 3.2 respectively as follows:

Model 3.1 (for Model 2.1)

The fully crisp objective functions, i.e., objective functions with single-choice and crisp (defuzzified) parameters are given in Eqs. (36)–(38).

$$\begin{aligned} \text{ minimize }~{Z}_{1}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P} \left[ {\overline{c}}_{ijk}^{(p)}x_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{f}}_{ijk}^{(p)T}\right) y_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{g}}_{ijk}^{(p)T}\right) {\eta }_{ijk}^{p}\right] \nonumber \\&+\sum _{i=1}^{M}\sum _{j=1}^{N}\left\{ \mathfrak {R}\left( {\widetilde{lt}}_{ij}^{T}\right) wt_{ij}\nonumber \right. \left. +\mathfrak {R}\left( {\widetilde{ll}}_{i}^{T}\right) wl_{i}+\mathfrak {R}\left( {\widetilde{lu}}^{T}_j\right) wu_j\right\} \nonumber \\&+\displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ \left( \mathfrak {R}\left( {\widetilde{ol}}_i^{T}\right) \nonumber \right. \right. \left. \left. +\mathfrak {R}\left( {\widetilde{ou}}_j^{T}\right) \right) x_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{mc}}_k^{T}\right) y_{ijk}^{p}d_{ij}\right] \end{aligned}$$

(36)

$$\begin{aligned} \text{ minimize }~{Z}_{2}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ \mathfrak {R}\left( {\widetilde{t}}_{ijk}^{(p)T}\right) y_{ijk}^{p}\nonumber \right. \\&\left. +\left( \mathfrak {R}\left( {\widetilde{l}}_i^{T}\right) +\mathfrak {R}\left( {\widetilde{ul}}^{T}_j\right) \right) x_{ijk}^p\right] \end{aligned}$$

(37)

$$\begin{aligned} \text{ maximize }~{Z}_{3}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\nonumber \\&\left[ \mathfrak {R}\left( {\widetilde{st}}_{ij}^{T}\right) \left( \dfrac{x_{ijk}^p}{e_k} \right) +\mathfrak {R}\left( {\widetilde{sl}}_{i}^{T}\right) \left( \dfrac{ x_{ijk}^p}{\mathfrak {R}\left( {\widetilde{a}}_i^{(p)T}\right) }\right) \right] \nonumber \\&+\displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\mathfrak {R}\left( {\widetilde{su}}_{j}^{T}\right) \left( \dfrac{ x_{ijk}^p}{\mathfrak {R}\left( {\widetilde{b}}_j^{(p)T}\right) }\right) \end{aligned}$$

(38)

$\begin{aligned} \text{ subject } \text{ to }&\text{ the } \text{ constraints } (8),\nonumber \\&\text{ the } \text{ constraints } (12){-}(14),\nonumber \\&\text{ the } \text{ constraints } (18){-}(22). \end{aligned}$Model 3.2 (for Model 2.2)

The fully crisp objective functions, i.e., objective functions with single-choice and crisp (defuzzified) parameters are given in Eqs. (39)–(41).

$$\begin{aligned} \text{ minimize }~{Z}_{1}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P} \left[ {\overline{c}}_{ijk}^{(p)}x_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{f}}_{ijk}^{(p)T}\right) y_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{g}}_{ijk}^{(p)T}\right) {\eta }_{ijk}^{p}\right] \nonumber \\&+\sum _{i=1}^{M}\sum _{j=1}^{N}\left\{ \mathfrak {R}\left( {\widetilde{lt}}_{ij}^{T}\right) wt_{ij}\nonumber \right. \left. +\mathfrak {R}\left( {\widetilde{ll}}_{i}^{T}\right) wl_{i}+\mathfrak {R}\left( {\widetilde{lu}}^{T}_j\right) wu_j\right\} \nonumber \\&+\displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\left[ \left( \mathfrak {R}\left( {\widetilde{ol}}_i^{T}\right) \nonumber \right. \right. \left. \left. +\mathfrak {R}\left( {\widetilde{ou}}_j^{T}\right) \right) x_{ijk}^{p}+\mathfrak {R}\left( {\widetilde{mc}}_k^{T}\right) y_{ijk}^{p}d_{ij}\right] \end{aligned}$$

(39)

$$\begin{aligned} \text{ minimize }~{Z}_{2}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\nonumber \\&\left[ \mathfrak {R}\left( {\widetilde{t}}_{ijk}^{(p)T}\right) y_{ijk}^{p}+\left( \mathfrak {R}\left( {\widetilde{l}}_i^{T}\right) +\mathfrak {R}\left( {\widetilde{ul}}^{T}_j\right) \right) x_{ijk}^p\right] \end{aligned}$$

(40)

$$\begin{aligned} \text{ maximize }~{Z}_{3}= & {} \displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\nonumber \\&\left[ \mathfrak {R}\left( {\widetilde{st}}_{ij}^{T}\right) \left( \dfrac{x_{ijk}^p}{e_k} \right) +\mathfrak {R}\left( {\widetilde{sl}}_{i}^{T}\right) \left( \dfrac{ x_{ijk}^p}{\mathfrak {R}\left( {\widetilde{a}}_i^{(p)T}\right) }\right) \right] \nonumber \\&+\displaystyle \sum _{i=1}^{M}\sum _{j=1}^{N}\sum _{k=1}^{V}\sum _{p=1}^{P}\mathfrak {R}\left( {\widetilde{su}}_{j}^{T}\right) \left( \dfrac{ x_{ijk}^p}{\mathfrak {R}\left( {\widetilde{b}}_j^{(p)T}\right) }\right) \end{aligned}$$

(41)

$\begin{aligned} \text{ subject } \text{ to }&\text{ the } \text{ constraints } (8),\nonumber \\&\text{ the } \text{ constraints } (12){-}(14),\nonumber \\&\text{ the } \text{ constraints } (26){-}(35). \end{aligned}$

Definition 4.1

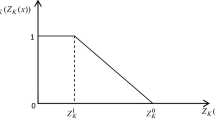
Feasible solutions $x1^{*}~\text{ and }~x2^{*}=(x1_{ijk}^{p*}~\text{ and }~x2_{ijk}^{p*}:i=1, 2,\ldots ,M;j=1, 2,\ldots ,N;k=1,2,\ldots ,V;p=1,2,\ldots ,T)$ of Models 3.1 and 3.2 respectively are said to be efficient solutions of Models 3.1 and 3.2 respectively if there do not exist any other feasible solutions $x1~\text{ and }~x2=(x1_{ijk}^{p}~\text{ and }~x2_{ijk}^{p}:i=1, 2,\ldots ,M;j=1, 2,\ldots ,N;k=1,2,\ldots ,V;p=1,2,\ldots ,T)$ of Models 3.1 and 3.2 respectively such that ${Z}_{\kappa }(x_1)\left( {Z}_{\kappa }(x_2)\right) \le {Z}_{\kappa }(x_1^{*})\left( {Z}_{\kappa }(x_2^{*})\right)$ for $\kappa =1,2,$ and ${Z}_{3}(x_1)\left( {Z}_{3}(x_2)\right) \ge {Z}_{3}(x_1^{*})\left( {Z}_{3}(x_2^{*})\right) ,$ and ${Z}_{\kappa }(x_1)\left( {Z}_{\kappa }(x_2)\right) <{Z}_{\kappa }(x_1^{*})\left( {Z}_{\kappa }(x_2^{*})\right)$ for at least one $\kappa =1,2,$ and ${Z}_{3}(x_1)\left( {Z}_{3}(x_2)\right) >{Z}_{3}(x_1^{*})\left( {Z}_{3}(x_2^{*})\right) .$

5 Solution procedure

In MOOP, there are multiple conflicting objective functions which tend to achieve optimum values. For this reason, it is difficult to select an optimal solution for which all objective functions are optimized. Therefore, we have to incorporate an efficient solution. There exist several methods in the literature such as fuzzy programming (FP) (Zimmermann 1978), intuitionistic fuzzy programming (IFP) (Angelov 1997), TOPSIS (Li 2010b), global criterion method (GCM) (Miettinen 2012), goal programming (GP) (Charnes and Cooper 1957), $\epsilon$-constraint method (Chankong and Haimes 2008), etc., which can be utilized to solve the presented deterministic models (i.e., Models 3.1 and 3.2). However, due to some drawbacks of these methods (some are mentioned previously), we implement two methods namely, IFGTM and ATM to obtain an efficient solution. The operating steps of IFGTM and ATM are briefly discussed in the following subsections.

5.1 IFGTM

Game-theoretic method (GTM) was proposed by Rao and Freiheit (1991) to solve multi-objective decision making problems, which was performed by minimizing a utility function consisting of a bargaining and a super criterion function (one can see Rao and Freiheit 1991). Inspiring from the traditional GTM, we introduce here IFGTM by the intersection of intuitionistic fuzzy and game-theoretic concept, which operates through the following steps:

(S1):

First, the best and the worst values, and the optimum point of each objective function are obtained by solving Model 3.1 and Model 3.2 respectively as single objective models by taking one objective function at a time with subject to the constraints defined in Model 3.1 and Model 3.2 respectively as, ${Z}_{\kappa }^{*}=\text{ min }~Z_{\kappa },\kappa =1,2;{Z}_{3}^{*}=\text{ max }~Z_{3},$ and ${{\widehat{Z}}}_{\kappa }=\displaystyle \max \nolimits _{\kappa ^{'}=1,2,3}~Z_{\kappa }(X_{\kappa ^{'}}),\kappa =1,2;{{\widehat{Z}}}_{3}=\min \nolimits _{\kappa ^{'}=1,2,3}~Z_{3}(X_{\kappa ^{'}})$. Here, ${Z}_{\kappa }^{*},{{\widehat{Z}}}_{\kappa }$ and $X_{\kappa }$ are the best value, the worst value and the optimum point of ${Z}_{\kappa } ~(\kappa =1,2,3)$ respectively. If all the optimum solutions $X_{\kappa },\kappa =1,2,3$ are same, then we get the efficient solution, otherwise we have to go the following steps.

(S2):

Then, the membership $(\phi _{Z_{\kappa }}(x))$ and non-membership $(\psi _{Z_{\kappa }}(x))$ functions for $Z_{\kappa }(x)$ are constructed, which are given in Eqs. (42) and (43) and displayed in Fig. 6.

$$\begin{aligned}&\phi _{Z_{\kappa }}(x)= {\left\{ \begin{array}{ll} 1, & \text{ if }~Z_{\kappa }(x)\le Z_{\kappa }^{*},\\ \dfrac{{{\widehat{Z}}}_{\kappa }-Z_{\kappa }(x)}{{{\widehat{Z}}}_{\kappa }-Z_{\kappa }^{*}}, & \text{ if }~ Z_{\kappa }^{*}\le Z_{\kappa }(x)\le {{\widehat{Z}}}_{\kappa },\\ 0, & \text{ if }~ Z_{\kappa }(x)\ge {{\widehat{Z}}}_{\kappa }, \end{array}\right. }\nonumber \\&\psi _{Z_{\kappa }}(x)= {\left\{ \begin{array}{ll} 0, & \text{ if }~Z_{\kappa }(x)\le Z_{\kappa }^{*},\\ \dfrac{Z_{\kappa }(x)-Z_{\kappa }^{*}}{{{\widehat{Z}}}_{\kappa }-Z_{\kappa }^{*}}, & \text{ if }~ Z_{\kappa }^{*}\le Z_{\kappa }(x)\le {{\widehat{Z}}}_{\kappa },\\ 1, & \text{ if }~ Z_{\kappa }(x)\ge {{\widehat{Z}}}_{\kappa }. \end{array}\right. } \end{aligned}$$

(42)

for $\kappa =1,2.$

$$\begin{aligned}&\phi _{Z_3}(x)= {\left\{ \begin{array}{ll} 0, & \text{ if }~Z_{3}(x)\le {{\widehat{Z}}}_{3},\\ \dfrac{Z_{3}(x)-{{\widehat{Z}}}_{3}}{Z_{3}^{*}-{{\widehat{Z}}}_{3}}, & \text{ if }~ {{\widehat{Z}}}_{3}\le Z_3(x)\le Z_{3}^{*},\\ 1, & \text{ if }~ Z_3(x)\ge Z_{3}^{*}, \end{array}\right. }\nonumber \\&\psi _{Z_3}(x)= {\left\{ \begin{array}{ll} 1, & \text{ if }~Z_3(x)\le {{\widehat{Z}}}_{3},\\ \dfrac{Z_{3}^{*}-Z_{3}(x)}{Z_{3}^{*}-{{\widehat{Z}}}_{3}}, & \text{ if }~ {{\widehat{Z}}}_{3}\le Z_{3}(x)\le Z_{3}^{*},\\ 0, & \text{ if }~ Z_{3}(x)\ge Z_{3}^{*}. \end{array}\right. } \end{aligned}$$

(43)

(S3):

Thenceforth, the intuitionistic fuzzy game-theoretic models (i,e., Model 4.1 and Model 4.2) are displayed below.

Fig. 6

Membership and non-membership functions for a minimization $(\kappa =1,2)$ and b maximization $(\kappa =3)$ objective functions

Model 4.1 (for Model 3.1)

In order to obtain the efficient solution, the bargaining function has to be minimized and the super criterion function has to be maximized, therefore the intuitionistic fuzzy game theoretic objective function to obtain the efficient solution of Model 3.1 is defined in Eq. (44).

$$\begin{aligned} \text{ minimize }&{\mathcal {B}}-{\mathcal {S}} \end{aligned}$$

(44)

The bargaining $({\mathcal {B}})$ and the super criterion $({\mathcal {S}})$ functions of the intuitionistic fuzzy game theoretic model for Model 3.1 are defined in Eqs. (45) and (46) respectively.

$$\begin{aligned} \text{ subject } \text{ to }&{\mathcal {B}}=\displaystyle \sum _{\kappa =1}^{2}(Z_{\kappa }-Z_{\kappa }^{*})+(Z_{3}^{*}-Z_3), \end{aligned}$$

(45)

$$\begin{aligned}&{\mathcal {S}}=\prod _{\kappa =1}^{3}\phi _{Z_{\kappa }}-\prod _{\kappa =1}^{3}\psi _{Z_{\kappa }}, \end{aligned}$$

(46)

$\begin{aligned}\\&\text{ the } \text{ constraints } (8),\nonumber \\&\text{ the } \text{ constraints } (12){-}(14),\nonumber \\&\text{ the } \text{ constraints } (18){-}(22). \end{aligned}$Model 4.2 (for Model 3.2)

The intuitionistic fuzzy game theoretic objective function to obtain the efficient solution of Model 3.2 is defined in Eq. (47).

$$\begin{aligned} \text{ minimize }&{\mathcal {B}}-{\mathcal {S}} \end{aligned}$$

(47)

The bargaining $({\mathcal {B}})$ and the super criterion $({\mathcal {S}})$ functions of the intuitionistic fuzzy game theoretic model for Model 3.2 are defined in Eqs. (48) and (49) respectively.

$$\begin{aligned} \text{ subject } \text{ to }&{\mathcal {B}}=\displaystyle \sum _{\kappa =1}^{2}(Z_{\kappa }-Z_{\kappa }^{*})+(Z_{3}^{*}-Z_3), \end{aligned}$$

(48)

$$\begin{aligned}&{\mathcal {S}}=\prod _{\kappa =1}^{3}\phi _{Z_{\kappa }}-\prod _{\kappa =1}^{3}\psi _{Z_{\kappa }}, \end{aligned}$$

(49)

$\begin{aligned}\nonumber \\&\text{ the } \text{ constraints } (8), \nonumber \\&\text{ the } \text{ constraints } (12){-}(14),\nonumber \\&\text{ the } \text{ constraints } (26){-}(35). \end{aligned}$(S4) On solving Model 4.1 and Model 4.2, we obtain the efficient solutions of Model 3.1 and Model 3.2 respectively. The flowchart of IFGTM is illustrated in Fig. 7.

Fig. 7

A conditional flowchart of IFGTM

5.2 ATM

ATM, which is suggested in this paper, is an extension of augmented weighted Tchebycheff method. The main advantage of this method is that it eliminates weakly non-dominated solutions. Efficient solutions of the deterministic models can be obtained from this method by going through the following simple steps: First, the ideal solutions of three objective functions are obtained by solving the deterministic M$^3$SFSTP models (Models 3.1 and 3.2) as single-objective multi-item SFSTP by considering one objective function at a time with subject to the constraints defined in Models 3.1 and 3.2. Then, the efficient solutions of Models 3.1 and 3.2 are derived by solving Models 5.1 and 5.2 respectively.

Model 5.1 (for Model 3.1)

Equation (50) represents the objective function of the augmented Tchebycheff program which is an additional variable and used for linearising the max-min program of Model 3.1.

$$\begin{aligned} \text{ minimize }&\Gamma \end{aligned}$$

(50)

Equations (51) and (52) define the relations between the additional variable and the Tchebycheff metric for Model 3.1.

$$\begin{aligned} \text{ subject } \text{ to }&\Gamma \ge (Z_{\kappa }-Z_{\kappa }^{*}) +\epsilon \left[ \displaystyle \sum _{\kappa =1}^{2}(Z_{\kappa }-Z_{\kappa }^{*})+(Z_{3}^{*}-Z_{3})\right] ,~~~\forall ~\kappa =1,2 \end{aligned}$$

(51)

$$\begin{aligned}&\Gamma \ge (Z_{3}^{*}-Z_{3})+\epsilon \left[ \displaystyle \sum _{\kappa =1}^{2}(Z_{\kappa }-Z_{\kappa }^{*})+(Z_{3}^{*}-Z_{3})\right] , \end{aligned}$$

(52)

$\begin{aligned}\nonumber \\&\text{ the } \text{ constraints } (8),\nonumber \\&\text{ the } \text{ constraints } (12){-}(14),\nonumber \\&\text{ the } \text{ constraints } (18){-}(22). \end{aligned}$Model 5.2 (for Model 3.2)

Equation (53) represents the objective function of the augmented Tchebycheff program which is an additional variable and used for linearising the max-min program of Model 3.2.

$$\begin{aligned} \text{ minimize }&\Gamma \end{aligned}$$

(53)

Equations (54) and (55) define the relations between the additional variable and the Tchebycheff metric for Model 3.2.

$$\begin{aligned} \text{ subject } \text{ to }&\Gamma \ge (Z_{\kappa }-Z_{\kappa }^{*})\nonumber \\&+\epsilon \left[ \displaystyle \sum _{\kappa =1}^{2}(Z_{\kappa }-Z_{\kappa }^{*})+(Z_{3}^{*}-Z_{3})\right] ,~~~\forall ~\kappa =1,2, \end{aligned}$$

(54)

$$\begin{aligned}&\Gamma \ge (Z_{3}^{*}-Z_{3}) +\epsilon \left[ \displaystyle \sum _{\kappa =1}^{2}(Z_{\kappa }-Z_{\kappa }^{*})+(Z_{3}^{*}-Z_{3})\right] , \end{aligned}$$

(55)

$\begin{aligned}\nonumber \\&\quad \text{ the } \text{ constraints } (8),\nonumber \\&\quad \text{ the } \text{ constraints } (12){-}(14),\nonumber \\&\quad \text{ the } \text{ constraints } (26){-}(35).\end{aligned}$Here, $Z_{\kappa }^{*}$ is the ideal value of the objective function $Z_{\kappa },\kappa =1,2,3,$ and $\epsilon$ is a very small number in Models 5.1 and 5.2.

Table 3 Multi-choice intuitionistic fuzzy and multi-choice crisp transportation costs (Rupees/unit) $\left( {\widetilde{c}}_{ijk}^{(p)T},\mathfrak {R}\left( {\widetilde{c}}_{ijk}^{(p)T}\right) \right)$

6 Computational experiment

This section evaluates the effectiveness of the proposed model and solution techniques by implementing an industrial application example and sharing the computational experiences.

Table 4 Intuitionistic fuzzy and crisp fixed $\left( {\widetilde{f}}_{ijk}^{(p)T},\mathfrak {R}\left( {\widetilde{f}}_{ijk}^{(p)T}\right) \right)$ and step fixed-costs (Rupees) $\left( {\widetilde{g}}_{ijk}^{(p)T},\mathfrak {R}\left( {\widetilde{g}}_{ijk}^{(p)T}\right) \right)$

Table 5 Intuitionistic fuzzy and crisp transportation times (hour) $\left( {\widetilde{t}}_{ijk}^{(p)T},\mathfrak {R}\left( {\widetilde{t}}_{ijk}^{(p)T}\right) \right)$

Table 6 Intuitionistic fuzzy and crisp supplies (unit) $\left( {\widetilde{a}}_{i}^{(p)T}, \mathfrak {R}\left( {\widetilde{a}}_{i}^{(p)T}\right) \right)$, labour costs (Rupees/number) $\left( {\widetilde{ll}}_{i}^{T}, \mathfrak {R}\left( {\widetilde{ll}}_{i}^{T}\right) \right)$, required manpowers (number/unit) $\left( {\widetilde{ml}}_{i}^{T}, \mathfrak {R}\left( {\widetilde{ml}}_{i}^{T}\right) \right)$ and loading times (hour/unit) $\left( {\widetilde{l}}_{i}^{T}, \mathfrak {R}\left( {\widetilde{l}}_{i}^{T}\right) \right)$ at source

Table 7 Intuitionistic fuzzy and crisp demands (unit) $\left( {\widetilde{b}}_{j}^{(p)T},\mathfrak {R}\left( {\widetilde{b}}_{j}^{(p)T}\right) \right)$, labour costs (Rupees/number) $\left( {\widetilde{lu}}_{j}^{T}, \mathfrak {R}\left( {\widetilde{lu}}_{j}^{T}\right) \right)$, required manpowers (number/unit) $\left( {\widetilde{mu}}_{j}^{T}, \mathfrak {R}\left( {\widetilde{mu}}_{j}^{T}\right) \right)$ and unloading times (hour/unit) $\left( {\widetilde{ul}}_{j}^{T}, \mathfrak {R}\left( {\widetilde{ul}}_{j}^{T}\right) \right)$ at destinations

Table 8 Intuitionistic fuzzy and crisp labour costs (Rupees/number) $\left( {\widetilde{lt}}_{ij}^{T},\mathfrak {R}\left( {\widetilde{lt}}_{ij}^{T}\right) \right)$, required manpowers (number/unit) $\left( {\widetilde{mt}}_{ij}^{T},\mathfrak {R}\left( {\widetilde{mt}}_{ij}^{T}\right) \right)$, created new jobs (man hour) $\left( {\widetilde{st}}_{ij}^{T},\mathfrak {R}\left( {\widetilde{st}}_{ij}^{T}\right) \right)$, and crisp conveyances capacity (unit) (${e}_{k})$

Table 9 Intuitionistic fuzzy and crisp operational costs (Rupees/unit) $\left( {\widetilde{ol}}_{i}^{T},{\widetilde{ou}}_{j}^{T},\mathfrak {R}\left( {\widetilde{ol}}_{i}^{T}\right) \mathfrak {R}\left( {\widetilde{ou}}_{j}^{T}\right) \right)$, and vehicle maintenance cost (Rupees/km.) $\left( {\widetilde{mc}}_{k}^{T},\mathfrak {R}\left( {\widetilde{mc}}_{k}^{T}\right) \right)$

Table 10 Intuitionistic fuzzy and crisp new created jobs (man hour) $\left( {\widetilde{sl}}_{i}^{T},\mathfrak {R}\left( {\widetilde{sl}}_{i}^{T}\right) \right)$ at source and at destination $\left( {\widetilde{su}}_{j},\mathfrak {R}\left( {\widetilde{su}}_{j}\right) \right)$ and distances (km.) $(d_{ij})$

6.1 Industrial example

Here, we consider a reputed marble manufacturer company, Rajasthan Marble Ltd. in India produces two types of marble namely, ‘Makrana white marble’ and ‘Abu white marble’ $(P=2)$, and wishes to transport these mentioned marbles from two production centers at Doongri and Ambaji $(M = 2)$ in the state of Rajasthan to three different places $(N = 3)$ at Kolkata, Delhi and Bhubaneswar in India via two types of transportation modes, trucks and goods trains $( V = 2)$, through highways and railways respectively. As fixed costs, toll charges of National Highway, booking charges of Railway Authority, maintenance charge and fuel cost of vehicles etc. are considered, and as step fixed-cost, an extra charge is considered due to overloading of conveyances by 15 units $(A = 15)$. Also, variable labour cost besides other costs, loading and unloading time are taken into account. Furthermore, the manager of this operation is not only concerned about making profit by minimizing overall logistic cost but also decides to take into consideration the customers’ satisfaction and social factors. Therefore, he/she sets the targets of this operation as: (i) minimize overall operational cost, (ii) minimize total expend time, and (iii) maximize total created employments. Triangular intuitionistic fuzzy parameters related to the three objective functions and the constraints, and their crisp forms are displayed in Tables 3, 4, 5, 6, 7, 8, 9 and 10. The corresponding units of all parameters are presented in these tables.

6.2 Efficiency analysis

In order to render the performances of the solution methods for solving the example we consider the degree of closeness (DOC), which was defined by El-Washed and Lee (2006) as follows:

$D_n({\delta ,\kappa })=\left[ \displaystyle \sum \nolimits _{\kappa =1}^{3}\delta _{\kappa }(1-\rho _{\kappa })^{n}\right] ^{1/n},$ where $\delta _{\kappa }$ is the weight preference of $\kappa \mathrm{th}$ objective function and $\rho _{\kappa }$ is the DOC of the compromise value of the $\kappa \mathrm{th}$ objective function to its ideal value. In our study, we assume $\displaystyle \sum \nolimits _{\kappa =1}^{3} \delta _{\kappa }=1$ and consider the following DOC: $D_1({\delta ,\kappa })=\left( 1-\displaystyle \sum \nolimits _{\kappa =1}^{3}\delta _{\kappa }\rho _{\kappa }\right) ,$ where $\rho _{\kappa }=$ (the ideal value of $Z_{\kappa })/(\text{ the } \text{ compromise } \text{ value } \text{ of }~ Z_{\kappa }),$ for $\kappa =1,2,$ and $\rho _{3}=$ (the compromise value of $Z_{3})$/(the ideal value of $Z_{3}).$ The lesser value of DOC implies more nearness of the efficient solution to the optimal solution. Thus, the method with least DOC is preferable than other methods.

Table 11 Efficient solution of Model 3.1 (the optimal solution is indicated by boldface)

Table 12 Efficient solution of Model 3.2 (the optimal solution is indicated by boldface)

Fig. 8

Components of three objective functions obtained by IFGTM

6.3 Parley of outcomes and analogy

Here, we share our experiences for solving the presented application example by the proposed two methods, described in Sect. 5, utilizing same set of given inputs. Thus, DM can choose his/her preferred solution from the outcomes of the methods.

The optimal solutions obtained by solving the example through two deterministic models (Models 3.1 and 3.2) described in Sect. 4.2 executing two proposed and two existing methods, are depicted in Tables 11 and 12 respectively. From Tables 11 and 12, it is evident that all methods produce better efficient solutions in the possibility measure model than in the ranking model, but take a little bit much CPU time (except IFGTM). By going through Tables 11 and 12, we conclude that the proposed IFGTM yields the best efficient solution in comparison with the efficient solutions obtained by other methods in least CPU time. On the other hand, the other proposed method, ATM provides less preferable solutions than IFGTM, but better solution than the existing methods in preferable CPU time. Also, from Tables 11 and 12, based on the degrees of closeness, the order for the preferable methods from the best to the worst, is concluded as: (i) IFGTM, (ii) ATM, (iii) GCM, (iv) IFP. Moreover, the illustrated results disclose that the economical, customers’ satisfaction and social objectives are optimized, and the optimum product flow and the number of labours required at plants, destinations, and during transportation are also traced. Furthermore, to provide a notion about the structures of three objective functions, we calculate the values of different segments of each objective function after obtaining the efficient solution by IFGTM. Therefore, the components of three objective functions are revealed in Fig. 8. From Fig. 8, we find that most of the portions in three objective functions are occupied by labour related aspects, which is justifiable, as the workers are active in plants, destinations as well as during transportation for loading, unloading and shipping of various products. Also, by going through Fig. 8 and the solutions of the model, organizations can reduce or increase the components of financial, customers’ satisfaction and social aspects which are larger or smaller than expectation, respectively, by sending preferable amounts of products to proper demand points via proper conveyance.

6.4 Sensitivity analysis

In this subsection, we pursue the resiliency of the compromise solution by carrying out the sensitivity analysis on the key parameters (supply, demand and capacity of conveyance) of the proposed M$^3$SFSTP. For this purpose, we employ a simple technique which was mentioned in Das and Roy (2019). The procedure is taken place based on the fact that the basic variables remains basic, but their values will change. Thus, the same steps mentioned in Das and Roy (2019) are repeated to obtain the legitimate ranges of the key parameters. For this, let us assume $\mathfrak {R}({\widetilde{a}}_{i}^{p})$ is altered to $\mathfrak {R}({\widetilde{a}}_{i}^{p*})~(i=1,2)$, $\mathfrak {R}({\widetilde{b}}_{j}^{p})$ is changed to $\mathfrak {R}({\widetilde{b}}_{j}^{p*})~(j=1,2,3)$ and $e_k$ is transformed to $e_k^{*}~(k=1,2)$. Exploring the aforementioned steps, we display the ranges of $\mathfrak {R}({\widetilde{a}}_{i}^{p*}),\mathfrak {R}({\widetilde{b}}_{j}^{p*})$ and $e_k^{*}$ in Table 13, in which the proposed model (Model 3.1) is stable and the extracted solutions remain efficient for these input parameters.

Table 13 The ranges of supply $\left( \mathfrak {R}\left( {\widetilde{a}}_{i}^{p}\right) \right)$, demand $\left( \mathfrak {R}\left( {\widetilde{b}}_{j}^{p}\right) \right)$ and conveyance capacity $(e_{k})$

7 Performance evaluation

The performances of the proposed models and methods are further analysed in this section. In order to do this, we present two existing examples which are particular cases of the proposed problem. Thereafter a stochastic optimization approach namely genetic algorithm (GA) is executed to solve the examples and results are compared with the proposed methods. Lastly, computational complexity of the methods is presented.

Example 7.1

For the first case, we consider the following particular features of the proposed problem: (F11) only one item is transferred via one type of transportation mode, (F12) fixed, step-fixed and labour costs, and loading/unloading times are not taken into consideration, (F13) all parameters are crisp in nature, (F14) three objective functions are of minimization types. With these features, the proposed problem is transferred into an MOTP. One can see Rizk-Allah et al. (2018) for more mathematical details. Hence, we pick up the example from Rizk-Allah et al. (2018), in which the following inputs are used: Supplies: $a_1=5,a_2=4,a_3=2,a_4=9$; Demands: $b_1=4,b_2=4,b_3=6,b_4=2,b_5=4;$ and the penalties of three objective functions are as follows:

$$\begin{aligned} C^{1}= & {} \begin{bmatrix} 9&{}12&{}9&{}6&{}9\\ 7&{}3&{}7&{}7&{}5\\ 6&{}5&{}9&{}11&{}3\\ 6&{}8&{}11&{}2&{}2 \end{bmatrix},~C^{2}=\begin{bmatrix} 2&{}9&{}8&{}1&{}4\\ 1&{}9&{}9&{}5&{}2\\ 8&{}1&{}8&{}4&{}5\\ 2&{}8&{}6&{}9&{}8 \end{bmatrix},\\ C^{3}= & {} \begin{bmatrix} 2&{}4&{}6&{}3&{}6\\ 4&{}8&{}4&{}9&{}2\\ 5&{}3&{}5&{}3&{}6\\ 6&{}9&{}6&{}3&{}1 \end{bmatrix}. \end{aligned}$$

Example 7.2

To investigate the validity of the possibility measure model, we consider another example with the following features: (F21) step-fixed and labour costs, and loading/unloading times are emitted, (F22) three objective functions are of minimization types, (F23) only single item is transported. With these particular features, the proposed problem becomes a multi-objective solid FTP under intuitionistic fuzzy environment. More details of this problem can be found in Roy and Midya (2019). Therefore, the whole problem and input data are lifted from Roy and Midya (2019).

Table 14 Comparative results of the proposed and other existing methods, and models

Comparison: The optimal solutions for both of the examples which are acquired by the proposed and existing methods, are displayed in Table 14. From Table 14, we elicit that, the proposed methods deliver better optimal solutions than other existing methods and the cited authors’ proposed methods for both examples as DOCs of the proposed methods are less than the existing methods. Consequently, by going through Tables 11, 12 and 14, we conclude that the proposed IFGTM is the most promising method among the mentioned methods. Furthermore, from Table 14, we observe that although the authors (Roy and Midya 2019) applied two same methods (GCM and IFP), their proposed model (ranking model) provided worse solution than our proposed possibility measure model. This fact asserts the efficiency of the possibility measure model.

7.1 Comparison with GA

In this subsection, we compare the results of the proposed methods with GA. The operators of the GA (evaluation, crossover, mutation, etc.) are considered as default, and number of population and maximum iteration are set as 100 and 200 respectively. Therefore, three examples are solved by GA and results are displayed in Table 15. From Table 15, based on the values of DOCs we see that GA has outperformed the existing methods (GCM and IFP) but has shown worse performance than the proposed methods in three examples.

Table 15 Results of three examples solved by GA

7.2 Computational complexity

In this subsection, we share the complexity in performing the numerical experiments of all examples. All the methods are coded in GAMS 31.2.0 software except GA, which is coded in MATLAB 9.10.0.1684407 on a computer with 2.10 GH CPU and 8 GB RAM. The CPU times for solving three examples by all methods are displayed in Tables 11, 12, 14 and 15. In these tables, we see that the proposed possibility measure model has taken more CPU time but produces better efficient solutions than the ranking model. Furthermore, IFGTM has taken least CPU time to produce the most preferable solution. Also, from Table 15, we see that times for solving three examples by GA are longest.

8 Managerial implication

The presented study can be applied widely in various organizations associated with logistic system and supply chain management. Organizations can build a potential network design as well as can take into account the sustainability impacts with the help of the proposed model. The proposed model can be very helpful to deal with two-fold uncertainty (multi-choice and IFN) during any logistic operation when single type uncertainty is not enough to define some parameters. Taking into account step fixed-charges together with fixed-charges, DMs will be able to operate the logistic system by transporting proper amount of products to the proper demand centers without extra expenses. Also, variable labour costs will be a beneficial factor to take decisions about appointing workers. Furthermore, loading/unloading times are also incorporated together with transportation time, which will direct the organizations to calculate more appropriate time. Thus, the model is constructed with economic (overall cost) and customers’ satisfaction (overall time) related objective functions with multiple items, which will help the organizations to maintain a reputable position in the competitive global market by gaining more profit and customers’ satisfaction. Again, the social impacts of the model will help the organization to build a nice public image by creating new employments. A draft of the usefulness of the proposed study is depicted in Fig. 9. In the real-world problems, the possibility measure model will be helpful by giving scopes to set desired satisfaction levels (i.e., $\theta$ and $\pi )$ in order to acquire the best outcome. Also, from three practical examples it is evident that, two proposed solving methods can provide better efficient solutions than existing methods with less computational burden. Once more, experts can extract more appropriate defuzzified values of IFNs by applying the proposed ranking concept without larger errors and computational complexity. Last but not the least, organizations can choose the best efficient solution as well as appropriate solution strategy by going through the outcomes and comparative studies. Also, the sensitivity analysis will help to set suitable inputs.

Fig. 9

Three aspects of the proposed model

9 Epilogue and future exploration scopes

An integrated sustainable logistic systems with economical, customers’ satisfaction and social aspects under a two-fold uncertainty has been formed in this paper. In order to perform this operation, an unprecedented MOMIP model has been formulated which describes an M$^3$SFSTP with three objective functions related to the above-mentioned aspects and multiple items under multi-choice as well as intuitionistic fuzzy environment. The formulation has also provided information about the number of required labours and the optimal quantities of delivered commodities by different conveyances during the logistic operation. Besides, some major contributions such as fixed and step-fixed charge cost, variable labour cost and constraints, loading and unloading time, and new created jobs during the whole operation has been made through this study. Thereafter, a simple form of IFN, TIFN has been envisaged to deal with the uncertainties in the parameters. Consequently, based on the total integral values, a new ranking concept has been introduced to present a deterministic model by defuzzifying the TIFN parameters. Also, the ranking concept has defuzzified TIFNs with lesser computational exertion. Moreover, possibility measure of TIFN has also been utilized to display another deterministic model. Following that, two equivalent fully crisp models have been put forward by transforming the multi-choice parameter into a single choice with the help of binary variables. A fresh and an extended solving method have been implemented to obtain the efficient solution of the stated problem. The superiority of the models and the proposed solving methods have been clarified through a practical industrial example. Furthermore, some particular cases of the narrated formulation have also been incorporated by demonstrating two existing examples. The stable ranges of some parameters have been debunked by the sensitivity analysis. Finally, discussing some decisions regarding the sustainability impacts, we have inferred that our rendered formulation and solution can assist the organizations/companies in resolving the economical, customers’ satisfaction and social issues.

Various emerging areas have not been underlined in this study, because of their exteriorities from our enforceable set. None the less, some fascinating research directions can be forwarded, for instance other sustainability aspects such as environmental, safety, vehicles efficiency (Gupta et al. 2018), fixed jobs, etc., can be encountered in our proposed M$^3$SFSTP. Beside that, different uncertainties such as type-2 fuzzy, rough, fuzzy-rough, neutrosophic, type-3 fuzzy system (Mohammadzadeh et al. 2019) etc., can be developed in our model. Also, including time windows can make the proposed model more satisfactory. Other forms of IFN such as trapezoidal, hexagonal can be used in the proposed model and apart from possibility measure, necessity or credibility measure can also be used for obtaining deterministic model. The proposed problem can be extended by integrating type-2 fuzzy control method (Mohammadzadeh and Kayacan 2020), type-2 fuzzy neural network (Mohammadzadeh and Zhang 2019) etc. Furthermore, the inclusion of fixed and step-fixed charge in M$^3$SFSTP has made it a complex problem, therefore, various heuristic, meta-heuristic and hybrid methods can be developed to solve the large scale instances of our proposed problem.