ELECTRE-IDAT for design decision-making problems with interval data and target-based criteria

Abstract

A majority of decision-making problems are accompanied by some kinds of predictions and uncertainties. Therefore, interval data are widely used instead of exact data. The elimination and choice expressing reality methods, referred to as ELECTRE, belong to the outranking methods. Despite their relative complexity, avoiding compensation between criteria is one of the main advantages of the ELECTRE methods. However, no version of ELECTRE methods has the capability to deal with both interval data and target-based criteria. Target-based criteria are applicable in many areas ranging from material selection to medical decision-making problems. Efficiency of the modified ELECTRE method (ELECTRE-IDAT) was examined through two challenging examples. Also, a sensitivity analysis was performed to show advantages of the ELECTRE-IDAT approach. Additionally, the concept of bounded criteria was explained and applicability of interval data as well as benefit, cost, and target criteria were described with a biomaterial selection problem.

1 Introduction

Due to limited available information or inadequate understanding of the problem, interval data instead of exact ratios are widely accepted for solving decision-making problems. The conventional multiple-attribute decision-making (MADM) frameworks suppose that the ratings and the importance of the criteria are known exactly, whereas this is an unrealistic assumption particularly in materials/design selection environment (Hafezalkotob and Hafezalkotob 2016; Jahan and Edwards 2013; Jahan et al. 2016). To overcome uncertainty in determining importance of criteria, different solutions were proposed (Alemi-Ardakani et al. 2016; Baradaran and Azarnia 2013; Yan et al. 2014). A significant number of real decision-making problems are accompanied by some kinds of predictions and uncertainties, for which reason the classical MADM methods are not suitable for solving them (Stanujkic et al. 2017).

Grey systems theory is a relatively new methodology that focuses on the study of problems involving poor information (Li et al. 2007). Grey numbers have a powerful capacity to express uncertainty and consequently have been extensively studied and applied to solve MADM problems that contain uncertainty. Emergence of various theories and methodologies of uncertain systems has been significant in the areas of systems science. Zadeh (1965) established fuzzy mathematics, Deng (1982) developed grey systems theory, and Pawlak (1982) advanced rough set theory. These works represent some of the most important efforts in uncertain systems research from different angles. Based on the fuzzy and the grey set theories (Fang et al. 2016; Liu et al. 2013; Liu and Forrest 2010; Liu et al. 2016a, b, 2017; Sevastianov 2007), many ordinary MADM methods have further been extended with the aim of applying fuzzy or grey numbers. Perhaps the imperfect knowledge about the criteria performances and parameter values may be represented in a more natural and easy way by interval numbers. The methods based on interval data are more suitable, when there are crisp data with high variability, or when a probabilistic data (Tavana et al. 2016) set cannot represent the existing uncertainty. Among numerous MADM methods, ELECTRE, proposed by Roy (1991), is well known and widely applied (Chatterjee et al. 2009). The elimination and choice expressing reality methods, referred to as ELECTRE, belong to the outranking methods. The outranking methods are based on the pairwise comparisons of the options. They form one of the main methods of MADM family despite their relative complexity. The ELECTRE I method is used to develop a partial ranking and choose a set of the promising alternatives. ELECTRE II is used to rank all the alternatives, and it might yield more visible solutions compared to the ELECTRE I due to considering pure concordances and discordances separately. The main advantage of the ELECTRE methods over existing MADM techniques is that they avoid compensation between criteria, which is important in material/design selection problems (Shanian and Savadogo 2006). For example, in parts of aircraft, the weak performance of the specific strength should not be compensated by good price of the material. In the past decades, considerable efforts have been made to extend the ELECTRE, and to hybridize it with other MADM methods. To the best of the author’s knowledge, there is no extension of the ELECTRE approaches addressing target-based criteria in addition to cost and benefit criteria that are considered in conventional MADM problems. Therefore, in this paper a new interval-based ELECTRE method has been proposed that effectively deal with all types of criteria.

2 Summary of current knowledge on the considered problem

Over the last decades, various decision-making methods were proposed. This section presents a brief review of the literature on normalization methods for target-based criteria, the grey-based MADM approaches and ELECTRE for interval data. Then, we will discuss research gaps of our literature study.

2.1 Brief review of normalization methods for target-based criteria

Wu (2002) proposed nominal-is-best normalization method for target criteria. One of the shortcomings of this method is that it would not work out when the target value is higher than the maximum performance rating (available alternatives). Zhou et al. (2006) suggested a ratio-based normalization method that covers all types of criteria, but the method causes an asymmetry issue in the normalized values (Jahan and Edwards 2015). Shih et al. (2007) proposed non-monotonic normalization approach that also has asymmetry issue. Jahan et al. (2011) extended VIKOR for point target-based criteria and addressed shortcomings of Limits on Properties (LOP) method (Farag 1979). Bahraminasab and Jahan (2011) used this comprehensive VIKOR for selecting the materials of a knee prosthesis. Jahan et al. (2012) developed TOPSIS with a more accurate normalization technique (Linear target-based method) to be used in selection problems involving point target-based criteria. Zeng et al. (2013) proposed a new normalization method for range target criteria in medical decision-making. Liu et al. (2014) developed a novel hybrid MADM method for material selection problem possessing interdependent and point target-based criteria. Hafezalkotob and Hafezalkotob (2015) developed the MULTIMOORA method with point target-based criteria for materials selection. Vafaei et al. (2016) assessed the most appropriate normalization technique in decision problems, specifically for the Analytical Hierarchy Process. Perez et al. (2016) proposed a new MADM method, the reference ideal method (RIM), which is based on “ideal solution”, that can occur between the minimum and maximum values (range target- based criteria). Recently, Cables et al. (2018) developed the RIM for a fuzzy multi-criteria decision-making environment. Vafaei et al. (2018) evaluated the effects of different normalization techniques on the Weighted Average (WA) or SAW (Simple Additive Weighting) and found the most suitable normalization technique. Hafezalkotob et al. (2018) applied an exponential target-based normalization method for developing Weighted Aggregated Sum Product Assessment (WASPAS) method in selection of olive harvester machines. Liao et al. (2018) introduced an enhanced target-based linear normalization formula and a target-based vector normalization formula, called Double Normalization-Based Multi-Aggregation Method (DNBMA), to deal with MADM problems considering the benefit, cost and target criteria. Table 1 shows summary of recent trends in developed normalization methods for target-based criteria. Together, these studies indicate that target-based criteria received rapid attention recently.

Table 1 Recent trend in target-based normalization methods

2.2 Brief review of grey-based MADM approaches

Several methods have been reported to solve decision-making problems involving crisp interval data. Jahanshahloo et al. (2006) extended the original TOPSIS method for decision-making problems to include interval data. An extended VIKOR method for interval data was presented by Sayadi et al. (2009), and it was shown that the interval VIKOR is better than the interval TOPSIS. In another research, Jahanshahloo et al. (2009) offered new TOPSIS method for interval data that can sort alternatives by interval efficiency. Chen (2012) compared SAW and TOPSIS based on interval-valued fuzzy sets. Dymova et al. (2013) proposed a direct interval extension of TOPSIS method to overcome shortcomings of previous methods. Li et al. (2007) described the weights and ratings of attributes for all alternatives by linguistic variables expressed in grey numbers. Also, using a grey possibility degree, the ranking order of all alternatives was determined. Zavadskas et al. (2009) used a case study to demonstrate the concept of general contractor choice on the basis of multiple attributes of efficiency with fuzzy inputs applying COPRAS-G method. Zavadskas et al. (2010a, b) proposed SAW-G method and used it for Contractor selection in construction works. Turskis and Zavadskas (2010) developed grey additive ratio assessment (ARAS-G) method for multiple criteria analysis. Zavadskas et al. (2010a, b) applied TOPSIS grey and COPRAS-G methods with attributes values determined at intervals for risk assessment of construction projects. Hashemkhani Zolfani et al. (2012) evaluated performance of rural ICT centres (telecentres) using SAW-G and TOPSIS grey. Hajiagha et al. (2012) extended LINMAP model for multi-criteria decision-making with grey numbers. Stanujkic et al. (2012) studied on grey extension of the MOORA for solving decision-making problems with interval data. Baradaran and Azarnia (2013) proposed an approach to test consistency and generate weights from grey pairwise matrices in grey AHP. Jahan and Edwards (2013) extended the VIKOR method for interval data and target-based criteria, but the range target-based criteria were not taken into account in their work. Kracka and ZAVADSKAS (2013) presented the process of effective selection of building elements for renovation which are important for energy effectiveness of buildings. Multi-criteria MOORA and MULTIMOORA methods were adapted for problems solving with interval data. Yue and Jia (2015) proposed a methodology for group decision-making problems based on TOPSIS technique, in which attribute values are characterized in hybrid form with exact values and interval data. Chithambaranathan et al. (2015) proposed a grey-based hybrid framework for evaluating the environmental performance of service supply chains by integrating grey-based method with ELECTRE and VIKOR approaches. Liu et al. (2016a, b) presented all the new models and techniques in their new book of Grey Data Analysis: Methods, Models and Applications. Hafezalkotob et al. (2016) developed the MULTIMOORA method by applying interval numbers based on the fuzzy logic concept. Zhou et al. (2017) proposed a grey stochastic MADM approach based on regret theory and TOPSIS method. Jiang et al. (2017) proposed an I-TODIM method for multi-attribute decision-making with interval numbers. Ahn (2017) developed AHP with interval preference statements. Stanujkic et al. (2017) improved the Operational Competitiveness Rating (OCRA) method based on the use of interval grey numbers. Khanzadi et al. (2017) developed a new hybrid MADM model of discrete zero-sum two-person matrix games with grey numbers as a framework to solve dispute resolution problems in construction.

These studies would have been more useful if they had focused on all types of criteria. However, the above-mentioned grey extensions are successfully used for solving a large number of different problems, such as the supplier selection (Liou et al. 2016; Xie and Xin 2014), air traffic management (Xie and Xin 2014), the supply chain performance benchmarking (Kumar Sahu et al. 2014), the selection of the inside thermal insulation (Zagorskas et al. 2014), the assessment of the structural systems of high-rise buildings (Tamošaitienė and Gaudutis 2013), the social media platform selection (Tavana et al. 2013), the market segment evaluation (Zavadskas et al. 2015), the building foundation alternatives selection (Turskis et al. 2016), the robot selection (Datta et al. 2013) and materials selection (Chauhan and Vaish 2014; Hafezalkotob et al. 2016; Jahan and Edwards 2013).

2.3 Brief review of ELECTRE method for interval data

The criteria information processing is partially compensatory in ELECTRE methods. An advantage of the ELECTRE method is that a significantly weak criterion value of an alternative cannot directly be compensated by other good criteria values. On the other hand, the solution mechanism in ELECTRE method is not as extreme as purely non-compensatory methods. Amiri et al. (2008) developed a new ELECTRE I method by applying principles of the ELECTRE technique for interval data. Although the proposed approach is interesting, complex calculations are required. In addition, it is in contradiction with basics of the classical ELECTRE method that is expected to accomplish comparisons and calculation using interval data rather than separating them to real-valued data. Vahdani et al. (2010) extended the ELECTRE I method for interval weights and data. Although for all calculations, the interval arithmetic was used, the method was limited to the interval data with no intersection. In other words, the comparison of alternatives in specifying concordance sets is not possible for the values of ratings intersect. Balali et al. (2012) proposed an interval extension of ELECTRE III. In the Balali’s paper, criterion values, weights, and veto thresholds are considered interval numbers that replace their corresponding real values in the formulas of the ELECTRE III model. However, the credibility index is not contained in the interval [0, 1], which is not meaningful. Heravi et al. (2017) used advantages of integration of utility function, ELECTRE I, and grey theory to create the new method of grey-utility-ELECTRE to rank the sustainable industrial building options focused on petrochemical projects. However, previous studies of the ELECTRE and the modified versions (Fernández et al. 2018; Govindan and Jepsen 2016) have not dealt with target criteria.

2.4 Research gaps in the present study

Reviewed studies in Sects. 2.1 and 2.2 indicate that target-based criteria and grey-based MADM approaches received increasing attention recently. Studies reviewed in Sect. 2.3 reported that in contrast to the valued outranking methods that are well documented and have been intensively used in practice, the ELECTRE methods with interval data are recent and are not well documented in the literature. Furthermore, the research to date has tended to focus on cost and benefit criteria rather than target-based criteria. Generally, the classical MADM methods deal only with cost and benefit criteria, while target criteria (Bahraminasab and Jahan 2011; Hafezalkotob and Hafezalkotob 2015, 2017; Liu et al. 2014; Perez et al. 2016; Zeng et al. 2013) are applicable in many areas including biomedical engineering, aerospace and even rehabilitation of reinforced concrete structures in the maintenance of infrastructures where the repair materials should have similar properties to the main material in some criteria. The contribution of this paper has four aspects: (1) addressing the gap in the ELECTRE literature for problems involving imperfect knowledge in shape of intersecting interval-based data; (2) extending the ELECTRE method to consider target criteria in addition to cost and benefit; (3) improving ranking capability of the ELECTRE method; and (4) showing superiority of the proposed method using test problems and sensitivity analysis.

3 ELECTRE method for interval data and target-based criteria (ELECTRE-IDAT)

3.1 Structure of data and objectives in material and design selection problems

Multi-criteria decision analysis supports designers with a comprehensive collection of approaches. Numerical values are used to express the absolute measure of a material property such as density, modulus, strength and thermal conductivity. However, the values of material properties are often imprecisely measured due to the stochastic nature of material processing operations. Material properties are usually ranged between two values; for example, the tensile strength of cobalt-chromium alloy is approximately [450, 1000] MPa. In materials selection problems, the research to date has tended to have more focus on fixed values of materials’ properties rather than ranges. The same issue arises in design selection problems. Computer-aided engineering has become a demanded tool in engineering design process, but usually there is a difference between finite element analysis (FEA) predictions and real experimental results. Therefore, after minimizing the errors in the acceptable range, designers have to rely on either simulation outputs or experimental data (Rezvani and Jahan 2015). Both approaches lead to missing some essential information in selecting optimal shapes/dimensions for the design of components, but a reasonable approach to tackle this issue could be using interval data.

Let $\left[ {x_{ij}^{L} ,x_{ij}^{U} } \right]$ be an interval value of jth criterion for ith alternative in which $x_{ij}^{L}$ and $x_{ij}^{U}$ are the lower and upper bounds of interval, respectively. Meanwhile, as shown in Table 2, $W = \left\{ {w_{1} ,w_{2} , \ldots ,w_{n} } \right\}$ is the weight vector that shows importance of criteria.

Table 2 MADM problem with interval data

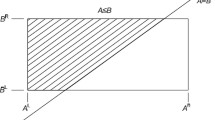
Figure 1 demonstrates ratings of alternatives for a criterion in format of interval data. Intersect between data was shown for $A_{n - 1}$ and $A_{n}$. Data belong to a universe of discourse ($A_{i} \in \left[ {A,B} \right]$).

Fig. 1

Universe of data for the criterion j and intersection between the interval data

Figure 2 shows four types of criteria in design decision-making problems. Objectives in decision matrix consist of target criteria, bounded criteria, cost, and benefit criteria.

Fig. 2

Four types of criteria in design selection problems

Target criteria are applicable in many areas, particularly in implant materials selection in which the material must possess close properties to those of human tissues. Moreover, in patch repair material selection applications, ranging from aerospace to rehabilitation of reinforced concrete structures in the maintenance of infrastructures where the repair materials should have similar properties to the main material in some criteria.

Bounded criteria are divided into upper/lower bounds for a property or design requirement. They can be converted to benefit or cost criteria through subtracting rate of alternatives from upper/lower bounds. For example, in selecting an insulating material for a flexible electrical cable, lower limit property to insulate resistance can be 10¹⁴ O.cm. Therefore, this bounded attribute will be benefit criterion if the criterion is converted from $x_{ij}$ to $x_{ij} - 10^{14} .$ Design selection problem for femoral component of knee prosthesis is another example in which a bounded criterion was used along with cost and benefit criteria (Jahan and Bahraminasab 2015). The criteria were extracted from computer simulation based on the finite element analysis of the different designs (alternatives) of femoral component. The bounded criterion, in this example, was the maximum contact slip at the femoral component–bone interface as a measure of implant micro-motion relative to the adjoining bone, which should be less than 150 μm not to cause bone loss. The benefit criterion was range of stress in critical region of femoral bone, i.e., mean stress ± STDV (standard deviation) in the region with the highest coefficient of variation in the femur as a measure of stress shielding where the mean and STDV were estimated for several random points in different regions of the bone. Although the points in each region were extremely close, every point had its own value of stress as it was located in different coordinates and experienced a slightly different stress level. Therefore, the best way to show the value of this criterion for candidate design can be using a range indicating the distribution and uncertainty of the data. Furthermore, maximum peg stress, area of cross section, and maximum stress at corner points of inner contour were also used as cost criteria. Table 3 presents these criteria, and alternatives are shown in.

Table 3 Performance metrics of different designs of femoral component of knee prosthesis

Figure 3 shows the possible location for target value in universe of data. When target value is B or A, the target criterion becomes benefit or cost, respectively. In other words, cost and benefit criteria are the special subset of target criteria.

Fig. 3

Possible location for target value (T_j) of criterion j in universe of data

3.2 Brief definition of interval numbers

Most of the MADM problems require crisp data as input. We can assume a crisp value to represent the average outcome when the degree of uncertainty is low. However, in the opposite condition (high uncertainty), it is better to report the data in a range format (Chauhan and Vaish 2014). The interval is a bounded subset of real numbers (Eq. 1), in particular $a^{L}$ or $a^{U}$ cannot be infinite here.

$$ \left( {\bar{A} = \left\lfloor {a^{L} ,a^{U} } \right\rfloor {\text{is}}\;{\text{an}}\;{\text{interval}}} \right) \Leftrightarrow \left( {\bar{A} = \left\{ {x \in R\left| {a^{L} \le x \le a^{U} } \right.} \right\}} \right) $$

(1)

Three useful functions defined on intervals are (see Eqs. 2–4)

$$ {\text{Center}}:{\text{mid}}(\bar{A}) = \frac{1}{2}\left( {a^{L} + a^{U} } \right) $$

(2)

$$ \bar{A} + \bar{B} = \left[ {a^{L} + b^{L} ,a^{U} + b^{U} } \right] $$

(3)

$$ \bar{A} - \bar{B} = \left[ {a^{L} - b^{U} ,a^{U} - b^{L} } \right] $$

(4)

To compare intervals, the quantitative indices are usually used (Sevastianov 2007). As Wang et al. (2005) explained, most of the proposed methods for interval comparison are “totally based on the midpoints of interval numbers”. Therefore, the midpoint of interval number obtained from subtraction of A and B ($\varDelta_{A - B}$) can be used for the comparison of the interval numbers. Dymova et al. (2013) clarified (Eq. 5) that the sign of midpoints in interval numbers indicates which interval is greater/lesser ($\bar{A}$ or $\bar{B}$).

$$ \left( {\varDelta_{A - B} } \right) = \frac{1}{2}\left( {\left( {a^{L} - b^{U} } \right) + \left( {a^{U} - b^{L} } \right)} \right) = \frac{1}{2}\left( {a^{L} + a^{U} } \right) - \frac{1}{2}\left( {b^{L} + b^{U} } \right) $$

(5)

Moreover, the values of abs $(\varDelta_{{\bar{A} - \bar{B}}} )$ may be treated as distances between intervals, since these values are close to the other methods either when intervals have a common area (intersect between data) or when the there is no such an area.

Furthermore, a simple heuristic method was used for comparing and ranking in order to provide the degree of possibility that an interval is greater/lesser than another one (Dymova et al. 2013; Hafezalkotob et al. 2016; Wang et al. 2005). For intervals $\bar{B} = [b^{L} ,b^{U} ]$ and $\bar{A} = [a^{L} ,a^{U} ]$, the possibilities of $\bar{B} \ge \bar{A}$ and $\bar{A} \ge \bar{B}$ are defined in Eqs. (6, 7):

$$ P(\bar{B} \ge \bar{A}) = \frac{{{\text{Max}}\left\{ {0,b^{U} - a^{L} } \right\} - {\text{Max}}\left\{ {0,b^{L} - a^{U} } \right\}}}{{a^{U} - a^{L} + b^{U} - b^{L} }} $$

(6)

$$ P(\bar{A} \ge \bar{B}) = \frac{{{\text{Max}}\left\{ {0,a^{U} - b^{L} } \right\} - {\text{Max}}\left\{ {0,a^{L} - b^{U} } \right\}}}{{a^{U} - a^{L} + b^{U} - b^{L} }} $$

(7)

In the subsequent parts of this paper, the definitions presented in this section will be used for all algebraic operations.

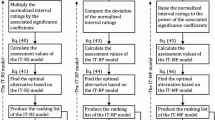
3.3 The proposed algorithmic ELECTRE-IDAT method

In the classical ELECTRE methods, the ratings of alternatives are presented by real values, but sometimes it is difficult to precisely determine the real values of ratings of alternatives with respect to criteria, and as a result, these ratings are presented by intervals. A systematic approach to modify the ELECTRE method in the presence of interval data and target-based criteria is proposed in this section.

Step 1 Convert the decision matrix into normalized values using Eqs. 8 and 9, while $i = 1,2, \ldots ,m$ and $j = 1,2, \ldots ,n$.

$$ n_{ij}^{L} = {\text{Min}}\left[ {1 - \frac{{\left| {x_{ij}^{L} - T_{j} } \right|}}{{\hbox{max} \left\{ {\left| {B - T_{j} } \right|,\left| {A - T_{j} } \right|} \right\}}},1 - \frac{{\left| {x_{ij}^{U} - T_{j} } \right|}}{{\hbox{max} \left\{ {\left| {B - T_{j} } \right|,\left| {A - T_{j} } \right|} \right\}}}} \right] $$

(8)

$$ n_{ij}^{U} = {\text{Max}}\left[ {1 - \frac{{\left| {x_{ij}^{L} - T_{j} } \right|}}{{\hbox{max} \left\{ {\left| {B - T_{j} } \right|,\left| {A - T_{j} } \right|} \right\}}},1 - \frac{{\left| {x_{ij}^{U} - T_{j} } \right|}}{{\hbox{max} \left\{ {\left| {B - T_{j} } \right|,\left| {A - T_{j} } \right|} \right\}}}} \right] $$

(9)

where the interval [A, B] is a range belonging to a universe of discourse ($x_{ij}^{L} \& x_{ij}^{U} \in \left[ {A,B} \right]$).

$$ T_{j} = \left| {\begin{array}{*{20}l} A \hfill &\quad {{\text{Less\,is\,better}}\left( {{\text{Cost\,criteria}}} \right)} \hfill \\ B \hfill &\quad {{\text{Less\,is\,better}}\left( {{\text{Cost\,criteria}}} \right)} \hfill \\ {{\text{Between}}\;A\;{\text{and}}\;B} \hfill &\quad {\text{Approaching\,to\,specific\,value}}\\&\quad {\text{is\,desirable}}\left( {{\text{Target\,criteria}}} \right) \hfill \\ \end{array} } \right. $$

Perhaps, the most serious disadvantage of vector normalization method (Eq. 10) used in the traditional version of ELECTRE is failing to remove the scales of criteria completely (Eq. 11).

$$ \begin{array}{*{20}c} {n_{ij} (x_{ij} ) = \frac{{x_{ij} }}{{\sqrt {\sum\nolimits_{i = 1}^{m} {(x_{ij} )^{2} } } }}} & \begin{aligned} i = 1,2, \ldots ,m \hfill \\ j = 1,2, \ldots ,n \hfill \\ \end{aligned} \\ \end{array} $$

(10)

$$ \varphi_{ij} = \alpha x_{ij} + \beta ,\alpha > 0 $$

(11)

Considering the vector normalization method, it can be observed in Eq. (12) that different result is achieved.

$$ n_{ij} (\varphi_{ij} ) = n_{ij} (\alpha x_{ij} + \beta ) = \frac{{\alpha x_{ij} + \beta }}{{\sqrt {\sum\nolimits_{i = 1}^{m} {(\alpha x_{ij} + \beta )}^{2} } }} $$

(12)

The equation holds true only if

$$ \beta = 0 \Rightarrow n_{ij} (\varphi_{ij} ) = n_{ij} (x_{ij} ) $$

However, there is not such an issue using the normalization method proposed in Eqs. (8, 9).

Step 2 Determine the weighted normalized interval matrix

Construct the weighted normalized interval decision matrix using Eqs. (13, 14) where $w_{j}$ is the importance of criteria $j$($W = \left\{ {w_{1} ,w_{2} , \ldots ,w_{n} } \right\}$).

$$ \begin{array}{*{20}c} {V_{ij}^{L} = w_{j} n_{ij}^{L} } & \begin{aligned} i = 1,2, \ldots ,m \hfill \\ j = 1,2, \ldots ,n \hfill \\ \end{aligned} \\ \end{array} $$

(13)

$$ \begin{array}{*{20}c} {V_{ij}^{U} = w_{j} n_{ij}^{U} } & \begin{aligned} i = 1,2, \ldots ,m \hfill \\ j = 1,2, \ldots ,n \hfill \\ \end{aligned} \\ \end{array} $$

(14)

Then, $\bar{V}_{ij} = \left\lfloor {V_{ij}^{L} ,V_{ij}^{U} } \right\rfloor$ will be weighted normalized decision matrix. The interval $\left\lfloor {V_{ij}^{L} ,V_{ij}^{U} } \right\rfloor$ will have always positive utility using the new proposed normalization method (Eqs. 8, 9).

$$ \bar{V} = \left| {\begin{array}{*{20}c} {\left[ {V_{11}^{L} ,V_{11}^{U} } \right]} & \ldots & {\left\lfloor {V_{1j}^{L} ,V_{1j}^{U} } \right\rfloor } & \ldots & {\left[ {V_{1n}^{L} ,V_{1n}^{U} } \right]} \\ . & \ldots & . & \ldots & . \\ . & \ldots & . & \ldots & . \\ . & \ldots & {\left\lfloor {V_{ij}^{L} ,V_{ij}^{U} } \right\rfloor } & \ldots & . \\ . & \ldots & . & \ldots & . \\ . & \ldots & . & \ldots & . \\ {\left[ {V_{m1}^{L} ,V_{m1}^{U} } \right]} & \ldots & {\left\lfloor {V_{mj}^{L} ,V_{mj}^{U} } \right\rfloor } & \ldots & {\left[ {V_{mn}^{L} ,V_{mn}^{U} } \right]} \\ \end{array} } \right| $$

Step 3 Specify concordance and discordance interval sets

Referring to Eqs. (6, 7) presented in Sect. 2.2 concordance and discordance interval sets for each interval pair of $k$ and $l$, alternatives can be specified ($k,l = 1,2, \ldots ,m;l \ne k$). The set of available interval indicators $(J = \left\{ {\left. j \right|j = 1,2, \ldots n} \right\})$ is divided into two different sets of concordance interval set ($S_{k,l}$) and discordance interval set ($D_{k,l}$). Concordance set of alternatives $A_{k}$ and $A_{l}$ consists of all indicators (criteria) for each of them, and $A_{k}$ is superior to $A_{l}$(Eq. 15).

$$ S_{k,l} = \left\{ {\left. j \right|\bar{V}_{kj} \ge \bar{V}_{lj} } \right\} = \left\{ {\left. j \right|\left\lfloor {V_{kj}^{L} ,V_{kj}^{U} } \right\rfloor \ge \left\lfloor {V_{lj}^{L} ,V_{lj}^{U} } \right\rfloor } \right\} $$

(15)

Table 4 Guideline for determining concordance interval sets

Table 4 and Eq. (16) help to find the concordance interval sets.

$$\begin{aligned} P(\bar{V}_{kj} \ge \bar{V}_{lj} ) & = P\left( {\left[ {V_{kj}^{L} ,V_{kj}^{U} } \right] \ge \left[ {V_{lj}^{L} ,V_{lj}^{U} } \right]} \right) \\ & = \frac{{{\text{Max}}\left\{ {0,V_{kj}^{U} - V_{lj}^{L} } \right\} - {\text{Max}}\left\{ {0,V_{kj}^{L} - V_{lj}^{U} } \right\}}}{{V_{kj}^{U} - V_{kj}^{L} + V_{lj}^{U} - V_{lj}^{L} }}\end{aligned} $$

(16)

Vice versa, the complementary subset named discordance set is a set of indicators that for each of them, we have

$$ D_{k,l} = \left\{ {\left. j \right|\left\lfloor {V_{kj}^{L} ,V_{kj}^{U} } \right\rfloor < \left\lfloor {V_{lj}^{L} ,V_{lj}^{U} } \right\rfloor } \right\} = J - S_{k,l} $$

(17)

Step 4 Calculate the concordance interval matrix

The concordance matrix for each pairwise comparison of the actions is defined as

$$ {\text{CI}} = \left| {\begin{array}{*{20}c} - &\quad {{\text{CI}}_{1,2} } &\quad {{\text{CI}}_{1,3} } &\quad \ldots &\quad {} &\quad {{\text{CI}}_{1,m} } \\ {{\text{CI}}_{2,1} } &\quad - &\quad . &\quad \ldots &\quad {} &\quad {{\text{CI}}_{2,m} } \\ {{\text{CI}}_{3,1} } &\quad . &\quad - &\quad \ldots &\quad {} &\quad {{\text{CI}}_{3,m} } \\ . &\quad . &\quad . &\quad \ldots &\quad {} &\quad . \\ . &\quad . &\quad . &\quad \ldots &\quad {} &\quad {{\text{CI}}_{m - 1,m} } \\ . &\quad . &\quad . &\quad \ldots &\quad - &\quad . \\ {{\text{CI}}_{m,1} } &\quad {{\text{CI}}_{m,2} } &\quad {{\text{CI}}_{m,3} } &\quad \ldots &\quad {{\text{CI}}_{m,m - 1} } &\quad - \\ \end{array} } \right| $$

where

$$ {\text{CI}}_{k,l} = \sum\limits_{{j \in S_{k,l} }} {W_{j} } $$

(18)

Step 5 Calculate the discordance interval matrix

The discordance matrix is defined as

$$ {\text{DI}} = \left| {\begin{array}{*{20}c} - &\quad {{\text{DI}}_{1,2} } &\quad {{\text{DI}}_{1,3} } &\quad \ldots &\quad {} &\quad {{\text{DI}}_{1,m} } \\ {{\text{DI}}_{2,1} } &\quad - &\quad . &\quad \ldots &\quad {} &\quad {{\text{DI}}_{2,m} } \\ {{\text{DI}}_{3,1} } &\quad . &\quad - &\quad \ldots &\quad {} &\quad {{\text{DI}}_{3,m} } \\ . &\quad . &\quad . &\quad \ldots &\quad {} &\quad . \\ . &\quad . &\quad . &\quad \ldots &\quad {} &\quad . \\ . &\quad . &\quad . &\quad \ldots &\quad - &\quad {{\text{DI}}_{m - 1,m} } \\ {{\text{DI}}_{m,1} } &\quad {{\text{DI}}_{m,2} } &\quad {{\text{DI}}_{m,3} } &\quad \ldots &\quad {{\text{DI}}_{m,m - 1} } &\quad - \\ \end{array} } \right| $$

where

$$ {\text{DI}}_{k,l} = \frac{{\mathop {\text{Max}}\limits_{{j \in D_{k,l} }} \left| {\left[ {V_{kj}^{L} ,V_{kj}^{U} } \right] - \left[ {V_{lj}^{L} ,V_{lj}^{U} } \right]} \right|}}{{\mathop {\text{Max}}\limits_{j \in J} \left| {\left[ {V_{kj}^{L} ,V_{kj}^{U} } \right] - \left[ {V_{lj}^{L} ,V_{lj}^{U} } \right]} \right|}} $$

(19)

Referring to Eq. (5), the distance between intervals can be measured to obtain discordance matrix elements.

Step 6 Specify the pure concordance and discordance indices using Eqs. (20, 21), respectively.

$$ \begin{aligned}&{\text{Pure\,concordance\;index}}\,\left( {C_{i} } \right) \\ &\quad= \sum\limits_{k = 1}^{m} {{\text{CI}}_{i,k} } - \sum\limits_{k = 1}^{m} {{\text{CI}}_{k,i} } \quad (i \ne k)\end{aligned} $$

(20)

$$\begin{aligned} &{\text{Pure\;discordance\;index}}\,\left( {D_{i} } \right)\\&\quad = \sum\limits_{k = 1}^{m} {{\text{DI}}_{i,k} } - \sum\limits_{k = 1}^{m} {{\text{DI}}_{k,i} } \quad (i \ne k) \end{aligned}$$

(21)

Here, an alternative with a higher net concordance and lower discordance is preferred.

Step 7 Compute the index values $E_{i}$.

Once the two indices are estimated, obtain final rankings on the basis of these indices using Eq. (22) where $C^{ - } = {\text{Min}}\;C_{i}$, $C^{ + } = {\text{Max}}\;C_{i}$, $D^{ - } = {\text{Min}}\;D_{i}$, $D^{ + } = {\text{Max}}\;D_{i}$, and γ is introduced as a weight to balance between concordance and discordance indices. The value of $\gamma$ lies in the range of 0–1, $\gamma = 0.5$ determining an average ranking from the two indices. Select the alternative with the maximum $E_{i}$.

$$ E_{i} = \left\{ {\begin{array}{*{20}l} {\left[ {\frac{{D_{i} - D^{ - } }}{{D^{ + } - D^{ - } }}} \right]} \hfill & {{\text{if}}\;C^{ + } = C^{ - } } \hfill \\ {\left[ {\frac{{C_{i} - C^{ - } }}{{C^{ + } - C^{ - } }}} \right]} \hfill & { {\text{if}}\;D^{ + } = D^{ - } } \hfill \\ {\left[ {\frac{{C_{i} - C^{ - } }}{{C^{ + } - C^{ - } }}} \right]\gamma + \left[ {\frac{{D^{ + } - D_{i} }}{{D^{ + } - D^{ - } }}} \right]\left( {1 - \gamma } \right)} \hfill & {\text{Otherwise}} \hfill \\ \end{array} } \right. $$

(22)

4 Results

4.1 Test problems to evaluate effectiveness of the proposed method

To describe the advantages of the proposed method, two challenging examples were extracted from the literature for comparison. The first one includes many intervals representing the values of ratings intersect. In the second one, there are no intersecting intervals in the columns of decision matrix.

Example 1

Suppose the problem includes three alternatives $A_{i} ,i = 1,2,3$ and four criteria $C_{j} ,j = 1,2,3,4$ presented by intervals in Table 5, where C1 and C2 are benefit criteria and C3 and C4 are cost criteria. This example was used by Dymova et al. (2013) in order to demonstrate the validity of the direct interval extension of the TOPSIS method. Since this case includes intersecting interval data (for example, see C2 for alternatives A1 and A2 which are $\left[ {10,15} \right]$ and $\left[ {8,11} \right]$ respectively), it is not possible to apply the available interval ELECTRE method proposed by Vahdani et al. (2010) in order to choose the best alternative.

Table 5 Interval decision matrix for Example 1

Using $W = (0.25,0.25,0.25,0.25)$ and the method of ELECTRE-IDAT, it was obtained that A1 > A2 > A3. The ranking order is exactly the same as that gained by Dymova et al. (2013).

Example 2

This example was adopted from Sayadi et al. (2009). It was assumed that there are three alternatives (A1, A2, and A3) and two criteria (C1, C2) with the same importance (C1 = 0.5, C2 = 0.5). The decision-maker wants to choose an alternative with minimum C1 and maximum C2. As it can be observed in Table 6, there are no intersecting intervals.

Table 6 Interval decision matrix for Example 2

Using the proposed method here, A2 > A3 > A1 was obtained. Using the compromise solution from the extended VIKOR method (Sayadi et al. 2009), the ranking was A2 > A1 > A3. Although the top-rank alternative is the same in both approaches, we can observe that there is a slight difference between the final ranking obtained by Sayadi et al. (2009) and using our method based on the ELECTRE-IDAT. This can be explained by the fact that the ELECTRE methods are in a group of non-compensatory techniques, while the VIKOR is in the group of compensatory approaches. Table 7 shows that assigning different weights to criteria (seven scenarios) leads to changes in the rankings of alternatives. However, sensitivity of the methods to changes in weight is quite different. From Figs. 4 and 5, it can be seen that changes in importance of criteria in VIKOR method have not too much effect on the ranking orders, while using ELECTRE-IDAT method, the top-rank alternative (A2) will be changed symmetrically (Fig. 4).

Table 7 A sensitivity analysis on ranking of alternatives with respect to changing the weights

Fig. 4

Strong and symmetrical sensitivity of alternatives to criteria weights in ELECTRE-IDAT method

Fig. 5

Weak sensitivity of alternatives to criteria weights in VIKOR method

Results of the above analysis indicate strong and symmetrical sensitivity of ELECTRE-IDAT method to criteria weights which is another advantage compared to VIKOR method. Nevertheless, we cannot claim that the ELECTRE-IDAT method produces a better solution because different MADM methods involve various types of underlying assumptions, and evaluation principles (Hwang and Yoon 1981). For a given problem, there are both compatibilities and incompatibilities using each model. There are no specific rules on which MADM method(s) should be used. Different MADM approaches are introduced for different decision situations (Hwang and Yoon 1981). There are many MADM methods and models, but none can be considered the “best” and/or appropriate for all situations.

4.2 Demonstrating application of the proposed method: knee prosthesis

A total knee implant usually has three main parts, including femoral component, tibial component comprised of tray and insert, and patellar component. The femoral component and the tibial tray substitute the distal femur and the proximal tibia, respectively. The tibial insert is implanted between these two components, and the patellar part replaces the posterior part of the patella for which polymers such as ultra-high molecular weight polyethylene are used to manufacture them. The insert and the patellar component both provide articular surfaces against the prosthetic femur attempting to mimic the natural knee constraints and motion. The femoral part and the tibial tray are mostly made from metals and alloys such as Co–Cr and Ti alloys and sometimes from ceramic materials including Al2O3 and ZrO2. These components are either cemented or press-fitted into place. Figure 6 shows the components of the knee prosthesis.

Fig. 6

Components of total knee implant

This example ranks the candidate materials for the femoral component of the knee implant using the proposed method. This example was taken from our previous study in which in-use and newly developed (potential) metals were considered candidate materials (Bahraminasab and Jahan 2011). The candidate metallic materials were stainless steel L316 (annealed), stainless steel L316 (cold worked), Co–Cr alloys (wrought Co–Ni-Cr–Mo), Co–Cr alloys (cast able Co–Cr–Mo), Ti alloys (pure Ti), Ti alloys (Ti–6 Al–4V), Ti–6Al–7Nb (IMI-367 wrought), Ti–6Al–7Nb (Protasul-100 hot-forged), NiTi shape memory alloy, and porous NiTi shape memory alloy. However, in the present study, only top-rank materials identified in the prior research (Bahraminasab and Jahan 2011) (see Table 8) were used for ranking with the proposed modified method. The material properties considered here as criteria include tensile strength, modulus of elasticity, ductility, corrosion resistance, wear resistance and osseointegration ability. Table 8 shows the properties of top-rank materials evaluated in the previous study. This case study includes interval data, incomplete data, linguistic terms and target criteria. Among the criteria, corrosion resistance, wear resistance, and osseointegration are linguistic terms converted into their respective fuzzy numbers and used to assign the values of the attributes on a qualitative scale. In Table 8, the interval data with infinite bound are converted into exact value equal to limited bound (for example replacing ≥ 900 with 900) meaning that the interval data with infinite bound ([a,∞], [∞,a]) are exact value equal to limited bound (a). The target criteria are density and modulus of elasticity, which should be near to those of human bone, and for all the other properties, the higher is the better.

Table 8 Properties of candidate materials for femur component materials selection

The application of the ELECTRE-IDAT described in the previous section is illustrated in this case, step by step, as follows:

Table 9 shows the normalized decision obtained based on Eqs. 8, 9. Table 10 presents the weighted normalized interval matrix. Table 11 summarizes concordance and discordance sets according to Eqs. 15–17. Tables 12 and 13 show matrix of concordance and discordance indices.

Table 9 Normalized interval matrix

Table 10 Weighted normalized interval matrix

Table 11 Concordance and discordance sets

Table 12 Matrix of concordance index

Table 13 Matrix of discordance index

Table 14 highlights the similarity of ranking in the proposed method and comprehensive VIKOR (CVIKOR) for the top and worst ranks. The differences can be explained by the effect of interval data that neglected in Bahraminasab and Jahan (2011) and logic of the proposed method compared to the CVIKOR.

Table 14 Final ranking

We considered an application to demonstrate the details of the proposed ELECTRE-IDAT method explained in the previous section. This step-by-step demonstration of the proposed method was not intended to compare our results with those of Bahraminasab and Jahan (2011). Such a comparison may be pointless as different multi-criteria decision-making methods may yield inconsistent results when applied to the same problem. Zanakis et al. (1998) explained that the inconsistency in results occurs because (1) the techniques use weights differently; (2) algorithms differ in their approach to selecting the “best” solution; (3) many algorithms attempt to scale the objective; and (4) some algorithms introduce additional parameters that affect which solution will be chosen. There is no one optimal method for a given MADM problem, and the numerical comparison is not usually enough to determine which method is the most appropriate.

In other words, our approach provides more meaningful and useful information by revealing which material is preferable, with respect to uncertainty in data, whereas previous method (CVIKOR) only can deal with crisp data.

5 Conclusion

The increasing complexity of the rapidly evolving materials and design selection problems entails making right decisions in considering a diversity of factors. The MADM supports designers with a comprehensive collection of approaches. Each material/design criterion may have special units of measurement, and relative weight. Some criteria can be measured numerically, and other criteria can only be described subjectively. Materials properties or design selection parameters vary so widely in practice. Due to uncertainty of data, in many circumstances, exact data are not enough to model the design decision-making problem. For these situations, researchers developed some structures, such as interval data, ordinal data, and fuzzy numbers. In the ELECTRE methods, a significantly weak criterion value of an alternative cannot be directly compensated by other good criteria values. This paper focused on modifying the ELECTRE method for interval data coupled with target-based criteria (ELECTRE-IDAT). Superiorities of the modified ELECTRE method demonstrated through applying that to a material selection problem including both exact and interval data as well as dealing with benefit, cost, and target criteria. This combination of findings provides some support for developing different version of the ELECTRE in the same direction.