1 Introduction

Humans are faced with situations each and every day where they have to choose among a set of options. In general, decision-makers make their choices following a set of rules and heuristic associated with their experience level, their independence degree, the type of information available, etc. In every situation it is necessary to consider that there are not unique criteria for making decisions, but that the decision-maker has to decide taking into account different decision criteria; thus, let us focus on the so-called Multi Criteria Decision Making (MCDM) problems and methods. In these circumstances, to select the most favourable alternative of the set, we must resort to operating methods that assess alternatives objectively and rationally with respect to previously established criteria and they may have associated weights reflecting their value, intensity, importance, etc.

The quality of our decisions depends directly on these methods, which must be able to synthesize large amount of information, often from different sources and therefore with different natures and different meanings. The MCDM problem resolution depends on the effectiveness, efficiency and functionality of these methods which are of great importance.

Among the wide variety of MCDM methods, in this paper we will consider those associated with compensatory strategy which take into account that the chosen alternative is superior to the other alternatives in the sum of the weighted utilities of all the criteria considered; by selecting, at the end of the process, the alternative with a higher score. In other words, we will consider methods that permit trade-offs between criteria [17]. It is important to mention that in these methods, a negative value on one attribute can be compensated by an equal or higher value on another attribute.

  • Among the compensatory methods we can consider the methods using:

  • A utility function, as is the case of the Analytical Hierarchy Process (AHP) [25], the Analytical Network Process (ANP) [26], or the SMART method [11], among others.

  • An outranking relation between alternatives, for example: the ELECTRE method [27] and the PROMETHEE method [3]. The identification of the ideal solution to perform the aggregation of information, for example: the TOPSIS method [33], the VIKOR method [22], and the Reference Ideal Method (RIM) [5].

  • Moreover, from the high level of imprecision that is reflected in the information collected in real decision problems, different MCDM methods have been extended or combined, so as to operate with fuzzy information [20], for example: The AHP method, [4, 7, 15, 28, 32], the ANP method, [16, 19, 29], the ELECTRE method and their respective variants and applications such as ELECTRE III [24], ELECTRE TRI [14, 23, 27, 30], the PROMETHEE method [2, 13], the TOPSIS method, with different variants, [1, 5, 9, 12] and the VIKOR method [8, 10, 18, 21, 31] among many others.

As can be observed, there are different MCDM methods using fuzzy numbers. These methods have as their purpose to resolve the high levels of imprecision that the information presents to confront decision making problems in different areas with a high degree of objectivity. In general, these methods consider that the best is the maximum value when it comes to profits and the worst when we consider losses.

It is also necessary to consider problems, both in the crisp as well as in the fuzzy case, where for a given criterion, “the best” should not be the maximum (profit case) or the minimum (losses case), but “the optimum” may be a value between the minimum and the maximum value. Such will be the case of the pH of a cosmetic, the temperature of a wine, the fat content in food, the age of a person to access a specific job, etc. In order to address these situations where the best is not the maximum neither the minimum value and to reach operational solutions, RIM was presented [6]. RIM is a new method based on the concept of “ideal solution value”, where this concept will be any value between the maximum and the minimum value, with this ideal solution being the main difference with the VIKOR and TOPSIS methods in which this value is the extreme value.

But RIM, as with other MCDM methods, cannot be applied directly to problems where the information is expressed imprecisely, or in other words to problems in which there is vagueness or imprecision in data and therefore will be expressed as fuzzy numbers. Therefore, the aim of this paper is to present the Fuzzy Reference Ideal Method (FRIM) that modifies, broadens and extends the original RIM. Thus, FRIM can operate in situations where the best for a particular criterion could be the maximum value, the minimum value or an intermediate value among them, it can operate with fuzzy numbers and therefore solve situations that until now had not been addressed.

Consequently, the problem to be solved has already been raised in this section and we have performed a discussion of some of the most recognized compensatory MCDM methods related to the problem, as well as the extension to operate with imprecise information. In the next section, RIM and the problems derived from operating with fuzzy numbers are presented. The third section is dedicated to developing FRIM itself, to finish by presenting a real illustrative example of the new formulation that we extract from the results of a research project that we are currently developing for a consumer organisation in Spain.

2 Background: The Reference Ideal Method (RIM)

Different MCDM reported in the literature, require a valuation matrix M, where its elements \( x_{ij} \) represent the evaluation of all alternatives \( A_{i} \), \( i\, = \,1,\,\,2,\, \ldots ,\,m \) for each one of the criteria \( C_{j} \), \( j\, = \,1,\,2, \ldots ,\,n \) and \( w_{j} \) is the weight associated with each criterion.

$$ M = \begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} \begin{aligned} w_{1} \hfill \\ C_{1} \hfill \\ \end{aligned} & \begin{aligned} w_{2} \hfill \\ C_{2} \hfill \\ \end{aligned} \\ \end{array} } & \begin{aligned} \,\, \hfill \\ \cdots \hfill \\ \end{aligned} \\ \end{array} } & \begin{aligned} w_{n} \hfill \\ C_{n} \hfill \\ \end{aligned} \\ \end{array} } & {} \\ {\begin{array}{*{20}c} {A_{1} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{2} } \\ \vdots \\ \end{array} } \\ {A_{m} } \\ \end{array} } \\ \end{array} } & {\left( {\begin{array}{*{20}c} {x_{11} } & {x_{12} } & \cdots & {x_{1n} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{m1} } & {x_{m2} } & {\,\, \cdots } & {x_{mn} } \\ \end{array} } \right)} & {} \\ {} & {} & {} \\ \end{array} $$

In this case, RIM also uses a valuation or judgments matrix and from it the calculations are performed to rank the alternatives involved in the decision-making process. Therefore, supposing the decision matrix M is known, RIM is based on identifying for each criterion \( C_{j} \), \( j\, = \,1,\,2,\, \ldots ,\,n \) the concepts of Range and Reference Ideal:

The Range \( R_{j} = \left[ {A_{j} ,B_{j} } \right] \) indicates any interval, ordered set of labels or ordered set of values that identify a domain of discourse and that is associated with each one of the criteria.

The Reference Ideal \( RI_{j} = \left[ {C_{j} ,D_{j} } \right] \), is an interval, an ordered set of labels, labels or simple values, which represent the optimal value, the maximum importance or relevance of the criterion \( C_{j} \) in a given Range.

Then, from the abovementioned concepts, RIM is based on determining the shortest distance to the Reference Ideal, considering the distance of a given rating \( x_{ij} \), to their respective \( \left[ {C_{j} ,D_{j} } \right] \), as follows:

$$ d_{\hbox{min} } \left( {x_{ij} ,\,\left[ {C_{j} ,D_{j} } \right]} \right) = \hbox{min} \left( {\left| {x_{ij} - C_{j} } \right|,\left| {x_{ij} - D_{j} } \right|} \right) $$
(1)

Once the distance matrix has been obtained, it is necessary to normalize it. This operation is performed with the aim of transforming all values to the same scale, because these values can usually represent different magnitudes and different meanings. Thus, we see that the TOPSIS, VIKOR and RIM methods have different metrics for the process.

Particularly, RIM performs normalization of any \( x_{ij} \in \left[ {A_{j} ,B_{j} } \right] \) value through the following function [12].

$$ f:x_{ij} \, \otimes \,\left[ {A,B} \right]\, \otimes \,\left[ {C,D} \right] \to \left[ {0,1} \right] $$
$$ f\left( {x_{ij} ,R_{j} ,RI_{j} } \right) = \left\{ {\begin{array}{*{20}c} 1 & {if\;x_{ij} \in \left[ {C_{j} ,D_{j} } \right]} \\ {1 - \frac{{d_{\hbox{min} } \left( {x_{ij} ,RI_{j} } \right)}}{{dist\left( {A_{j} ,C_{j} } \right)}}} & {if\;x_{ij} \in \left[ {A_{j} ,C_{j} } \right] \wedge A_{j} \ne C_{j} } \\ {1 - \frac{{d_{\hbox{min} } \left( {x_{ij} ,RI_{j} } \right)}}{{dist\left( {D_{j} ,B_{j} } \right)}}} & {if\;x_{ij} \in \left[ {D_{j} ,B_{j} } \right] \wedge D_{j} \ne B_{j} } \\ 0 & {in\,other\,case} \\ \end{array} } \right. $$
(2)

Example 1

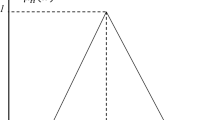
To show the behaviour of the \( f \) function, we will consider Fig. 1,

Fig. 1
figure 1

Representation of values A, B, C, D, x, y, and z in the real line

Full size image

Let us suppose \( R = \left[ {A,B} \right] = \left[ {0,10} \right] \), \( \left[ {C,D} \right] = \left[ {5,7} \right] \), and the three possibilities \( x = 2 \), \( y = 6 \) and \( z = 8 \). When calculating the \( f \) function image for the \( x,y,z \) values, we obtain:

$$ \begin{aligned} & f\left( {x,R,RI} \right) = 1 - \frac{{\hbox{min} \left( {\left| {x - C} \right|,\left| {x - D} \right|} \right)}}{{dist\left( {A,C} \right)}} = 1 - \frac{{\hbox{min} \left( {\left| {2 - 5} \right|,\left| {2 - 7} \right|} \right)}}{5} = 1 - \frac{3}{5} = \frac{2}{5} \\ & f\left( {y,R,RI} \right) = 1 \\ & f\left( {z,R,RI} \right) = 1 - \frac{{\hbox{min} \left( {\left| {z - C} \right|,\left| {z - D} \right|} \right)}}{{dist\left( {D,B} \right)}} = 1 - \frac{{\hbox{min} \left( {\left| {8 - 5} \right|,\left| {8 - 7} \right|} \right)}}{3} = 1 - \frac{1}{3} = \frac{2}{3} \\ \end{aligned} $$

As we see, RIM has been able to solve a decision problem, where “the best” can be any value \( v \in \left[ {A,B} \right] \), (not just the extremes A or B). However, when fuzzy numbers are considered, RIM presents problems; therefore in the next paragraph we will see what these problems are and how to solve them.

3 The Fuzzy Reference Ideal Method (FRIM)

Until now we have worked on a set of real numbers. However, if the values are not real ones, but fuzzy numbers, it becomes necessary to reformulate the expression (1) and therefore (2). When it is necessary to operate with fuzzy numbers the distance between two fuzzy numbers \( \tilde{X}_{ij} ,\tilde{D}_{ij} \), will be given by the vertex method distance defined in (3):

$$ dist:\tilde{X}\,x\,\tilde{Y} \to {\mathbb{R}} $$
$$ dist\left( {\tilde{X}_{ij} ,\tilde{D}_{ij} } \right) = \sqrt {\frac{1}{3}\left( {\left( {x_{1} - d_{1} } \right)^{2} + \left( {x_{2} - d_{2} } \right)^{2} + \left( {x_{3} - d_{3} } \right)^{2} } \right)} $$
(3)

Furthermore, and as we have seen before, when there is vagueness in the data, the formulation used by RIM cannot be applied directly and we will thus need to reformulate the distance measure to a fuzzy interval.

3.1 Minimal Distance to a Fuzzy Interval

As it has arisen, RIM is based on determining the shortest distance to the reference ideal, and in this case, when operated with fuzzy numbers it is possible to observe that it is not sufficient with the Euclidean distance. For this, we define the minimal distance of a fuzzy number to an interval bounded by fuzzy numbers (or a fuzzy number) through the following definition.

Definition 1

Let \( \tilde{X},\tilde{C},\tilde{D} \) be positive fuzzy numbers such that, \( \tilde{X} = \left( {x_{1} ,x_{2} ,x_{3} } \right) \), \( \tilde{C} = \left( {c_{1} ,c_{2} ,c_{3} } \right) \), \( \tilde{D} = \left( {d_{1} ,d_{2} ,d_{3} } \right) \), then the minimal distance of the value \( \tilde{X}_{ij} \) to the interval \( I\tilde{R}_{j} \) = \( \left[ {\tilde{C}_{j} ,\tilde{D}_{j} } \right] \), is given by the function \( d_{\hbox{min} }^{*} \), where:

$$ d_{\hbox{min} }^{*} :\tilde{X}_{ij} \otimes \left[ {I\tilde{R}_{j} } \right] \to {\mathbb{R}} $$
$$ d_{\hbox{min} }^{*} \left( {\tilde{X}_{ij} ,\left[ {I\tilde{R}_{j} } \right]} \right) = \hbox{min} \left( {dist\left( {\tilde{X}_{ij} ,\tilde{C}_{j} } \right),dist\left( {\tilde{X}_{ij} ,\tilde{D}_{j} } \right)} \right) $$
(4)

where, the functions \( dist\left( {\tilde{X}_{ij} ,\tilde{C}_{j} } \right) \) and \( dist\left( {\tilde{X}_{ij} ,\tilde{D}_{j} } \right) \) are calculated using the expression (3).

3.2 Normalization in FRIM

As such, RIM carries out the normalization process of the decision matrix through expression 2, which should not be used when we operate with fuzzy numbers. It may be the case that the value assigned to the variable \( \tilde{X} \) is not completely included in the Reference Ideal interval \( \left[ {\tilde{C}_{j} ,\tilde{D}_{j} } \right] \). In this case \( \tilde{X}_{ij} \cap \left[ {\tilde{C}_{j} ,\tilde{D}_{j} } \right] \ne \emptyset \). This would be the case of the \( \tilde{Y} \) value on the interval \( \left[ {\tilde{C}_{j} ,\tilde{D}_{j} } \right] \), as shown in Fig. 2.

Fig. 2
figure 2

Representation of the fuzzy Reference ideal and the fuzzy numbers \( \tilde{X} \) and \( \tilde{Y} \)

Full size image

Thus, the reformulation of (2) is expressed in the following definition.

Definition 2

Let \( \tilde{X},\,\tilde{A},\,\tilde{B},\,\tilde{C},\,\tilde{D} \) be positive fuzzy numbers such that, \( \tilde{X} = \left( {x_{1} ,\,x_{2} ,\,x_{3} } \right) \), \( \tilde{A} = \left( {a_{1} ,\,a_{2} ,\,a_{3} } \right) \), \( \tilde{B} = \left( {b_{1} ,\,b_{2} ,\,b_{3} } \right) \), \( \tilde{C} = \left( {c_{1} ,\,c_{2} ,\,c_{3} } \right) \), \( \tilde{D} = \left( {d_{1} ,\,d_{2} ,\,d_{3} } \right) \), where the interval \( \tilde{R}_{j} \) = \( \left[ {\tilde{A}_{j} ,\,\tilde{B}_{j} } \right] \) represents the range, the interval \( I\tilde{R}_{j} \) = \( \left[ {\tilde{C}_{j} ,\,\tilde{D}_{j} } \right] \) represents the Reference Ideal and \( \left[ {\tilde{C}_{j} ,\,\tilde{D}_{j} } \right]\, \subseteq \,\left[ {\tilde{A}_{j} ,\,\tilde{B}_{j} } \right] \) for each criterion \( \tilde{C}_{j} \), then the normalization function \( f^{*} \), is given by:

$$ f^{*} \left( {\tilde{X}_{ij} ,\left[ {\tilde{R}_{j} } \right],\left[ {I\tilde{R}_{j} } \right]} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\quad \tilde{X}_{ij} \in \left[ {I\tilde{R}_{j} } \right]} \hfill \\ {1 - \frac{{d_{\hbox{min} }^{*} \left( {\tilde{X}_{ij} ,\left[ {I\tilde{R}_{j} } \right]} \right)}}{{dist\left( {\tilde{A}_{j} ,\tilde{C}_{j} } \right)}}} \hfill & {if\quad \tilde{X}_{ij} \in \left[ {\tilde{A}_{j} ,\tilde{C}_{j} } \right]\, \wedge \tilde{X}_{ij} \notin \left[ {I\tilde{R}_{j} } \right] \wedge \,\,dist\left( {\tilde{A}_{j} ,\tilde{C}_{j} } \right) \ne 0\,} \hfill \\ {1 - \frac{{d_{\hbox{min} }^{*} \left( {\tilde{X}_{ij} ,\left[ {I\tilde{R}_{j} } \right]} \right)}}{{dist\left( {\tilde{D}_{j} ,\tilde{B}_{j} } \right)}}} \hfill & {if\quad \tilde{X}_{ij} \in \left[ {\tilde{D}_{j} ,\tilde{B}_{j} } \right] \wedge \tilde{X}_{ij} \notin \left[ {I\tilde{R}_{j} } \right]\, \wedge \,\,dist\left( {\tilde{D}_{j} ,\tilde{B}_{j} } \right) \ne 0} \hfill \\ 0 \hfill & {in\,\,other\,\,case} \hfill \\ \end{array} } \right. $$
(5)

where:

\( d_{\hbox{min} }^{*} \left( {\tilde{X}_{ij} ,\left[ {I\tilde{R}_{j} } \right]} \right) \) is obtained by applying (4).

\( dist\left( {\tilde{A}_{j} ,\tilde{C}_{j} } \right) \) and \( dist\left( {\tilde{D}_{j} ,\tilde{B}_{j} } \right) \) are obtained by applying (3).

Example 2

Let us suppose \( \left[ {\tilde{A}_{j} ,\,\,\tilde{B}_{j} } \right] = \left[ {\left( {0,\,\,15,\,\,35} \right),\,\,\,\left( {110,\,\,135,\,\,150} \right)} \right] \), \( \left[ {\tilde{C}_{j} ,\,\tilde{D}_{j} } \right] = \left[ {\left( {50,\,\,52,\,\,54} \right),\,\,\left( {57,\,\,60,\,\,63} \right)} \right] \) and we wish to normalize the values \( \tilde{X} = \left( {56,\,\,59,\,\,62} \right) \) and \( \tilde{Y} = \left( {59,\,\,62,\,\,65} \right) \) then:

$$ f^{*} \left( {\tilde{X},\tilde{R}_{j} ,I\tilde{R}_{j} } \right) = 1 $$

In this case the fuzzy number \( \tilde{X} \), is totally included in the interval that represents the Reference Ideal.

$$ f^{*} \left( {\tilde{Y},\tilde{R}_{j} ,I\tilde{R}_{j} } \right) = 1 - \frac{{d_{\hbox{min} }^{*} \left( {\tilde{Y},\left[ {\tilde{C}_{j} ,\tilde{D}_{j} } \right]} \right)}}{{\hbox{max} \left( {dist\left( {\tilde{A}_{j} ,\tilde{C}_{j} } \right),dist\left( {\tilde{D}_{j} ,\tilde{B}_{j} } \right)} \right)}} = 1 - \frac{2}{73} = 0.9726 $$

In this case \( \tilde{Y} \) is not completely included in the Reference Ideal with the result being near to 1.

4 Fuzzy RIM Algorithm

From the formulations showed previously, it can be considered that the FRIM algorithm stays similar to the RIM algorithm, because only step 2 changes.

Therefore, the algorithm FRIM steps are described below:

Step 1. Definition of the work context.

First, the conditions in the work context are established, and for each criterion \( C_{j} \) the following aspects are defined:

  • The Range \( \left[ {\tilde{A}_{j} ,\tilde{B}_{j} } \right] \), that from now will be denoted by \( \tilde{R}_{j} \).

  • The Reference Ideal \( \left[ {\tilde{C}_{j} ,\tilde{D}_{j} } \right] \), that from now will be denoted by \( I\tilde{R}_{j} \).

  • The weight \( w_{j} \) associated to the criterion.

Step 2. Obtain the decision matrix \( V \) in correspondence with the defined criteria. In this case, the \( \tilde{v}_{ij} \) elements represent triangular fuzzy numbers.

$$ V = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\tilde{v}_{11} } \\ {\tilde{v}_{21} } \\ \vdots \\ {\tilde{v}_{m1} } \\ \end{array} } & {\begin{array}{*{20}c} {\tilde{v}_{12} } \\ {\tilde{v}_{22} } \\ \vdots \\ {\tilde{v}_{m2} } \\ \end{array} } & {\begin{array}{*{20}c} \cdots \\ \cdots \\ \ddots \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} {\tilde{v}_{1n} } \\ {\tilde{v}_{2n} } \\ \vdots \\ {\tilde{v}_{mn} } \\ \end{array} } \\ \end{array} } \right) $$

Step 3. Normalize the decision matrix \( V \), depending on the reference ideal.

$$ N = \left( {\begin{array}{*{20}l} {f^{*} (\tilde{v}_{11} ,\tilde{R}_{1} ,I\tilde{R}_{1} )} \hfill & {f^{*} (\tilde{v}_{12} ,\tilde{R}_{2} ,\,I\tilde{R}_{2} )} \hfill & \cdots \hfill & {f^{*} (\tilde{v}_{1n} ,\tilde{R}_{n} ,\,I\tilde{R}_{n} )} \hfill \\ {f^{*} (\tilde{v}_{21} ,\tilde{R}_{1} ,\,I\tilde{R}_{1} )} \hfill & {f^{*} (\tilde{v}_{22} ,\tilde{R}_{2} ,\,I\tilde{R}_{2} )} \hfill & \cdots \hfill & {f^{*} (\tilde{v}_{2n} ,\tilde{R}_{n} ,\,I\tilde{R}_{n} )} \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {f^{*} (\tilde{v}_{m1} ,\tilde{R}_{1} ,\,I\tilde{R}_{1} )} \hfill & {f^{*} (\tilde{v}_{m2} ,\tilde{R}_{2} ,\,I\tilde{R}_{2} )} \hfill & \cdots \hfill & {f^{*} (\tilde{v}_{mn} ,\tilde{R}_{n} ,\,I\tilde{R}_{n} )} \hfill \\ \end{array} } \right) $$

where, the \( f^{*} \) function is that considered in (5).

Step 4. Calculate the weighted normalized matrix \( P \), through:

$$ P = N \otimes W = \left( {\begin{array}{*{20}l} {n_{11} \cdot w_{1} } \hfill & {n_{12} \cdot w_{2} } \hfill & \cdots \hfill & {n_{1n} \cdot w_{n} } \hfill \\ {n_{21} \cdot w_{1} } \hfill & {n_{22} \cdot w_{2} } \hfill & \cdots \hfill & {n_{2n} \cdot w_{n} } \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {n_{m1} \cdot w_{1} } \hfill & {n_{m2} \cdot w_{2} } \hfill & \cdots \hfill & {n_{mn} \cdot w_{n} } \hfill \\ \end{array} } \right) $$

Step 5. Calculate the distance to the ideal and non-ideal alternative.

$$ A_{i}^{ + } = \sqrt {\sum\limits_{j = 1}^{n} {\left( {p_{ij} - w_{j} } \right)^{2} } } \,{\text{and}}\,A_{i}^{ - } = \sqrt {\sum\limits_{j = 1}^{n} {\left( {p_{ij} } \right)^{2} } } $$

Step 6. Calculate the relative index to the reference ideal of each alternative by the following expression:

$$ I_{i} = \frac{{A_{i}^{ - } }}{{A_{i}^{ + } + A_{i}^{ - } }} ,\,{\text{where,}}\,0 \le I_{i} \le 1,i = 1,2,{ \ldots },m $$

Step 7. Rank the alternatives in descending order from the relative index \( I_{i} \). In this case, if the alternative has a relative index \( I \) near to the value 1, this indicates that it is very good. However, if this value approaches the value 0, we will interpret that the alternative should be rejected.

5 A Real Illustrative Example

The rationality of FRIM, as well as its practical importance, may be illustrated by the following real example extracted from a much broader project, to classify the different trademarks of olive oil that we are carrying out for a consumer organisation in Spain.

Olive oil is how we refer to the oil obtained from the fruit of olive trees. People have been eating olive oil for thousands of years and it is now more popular than ever, thanks to its many proven health benefits and its culinary usefulness. It is good to understand the different types or grades of olive oil to help decision makers select the appropriate uses for this healthful and flavoursome type of fat.

The basic types of olive oil are: extra virgin olive oil, virgin olive oil and pure olive oil. There are other forms, but these are blends and are not part of the formal grading process. Extra virgin is the highest quality and most expensive olive oil classification. But, as it is evident, not all trademarks of extra virgin olive oil are equal.

There are hundreds of trademarks of virgin olive oil and classifying them is an important problem, both from the economic as well as the methodological point of view, to which a large amount of resources are dedicated (http://www.bestoliveoils.com/). In situations in which the conventional methodologies (TOPSIS, VIKOR) present dysfunctions because they are unable to provide correct solutions, FRIM is shown as a rigorous methodology which perfectly resolves these solutions that are unapproachable for the other methods. For this reason FRIM is being applied to carry out the classification of olive oils that we are working on. Herein we only present this small-sized example for purely illustrative purposes.

Let us consider 8 trademarks of extra virgin olive oil that are available in supermarkets. We wish to know which the best is, considering the price, acidity, wax and qualification of tasting experts.

For each trademark measures have been taken several for each criteria, the minimum, average and maximum of the values, except those relating to the tasting of which only the final values are known, and which correspond to the mean value.

The data are collected in Table 1 and it is considered that the four criteria are equally important. The values of A are determined by minimum values for prices, while for acidity and waxes the minimum values are those given by the experience. The values of B indicate the maximum for prices and value ceilings imposed by the law for acidity and waxes. While the interval [C, D] represents the greater or lesser slack that a decision-maker is willing to admit (Tables 2 and 3).

Table 1 The decision matrix
Full size table
Table 2 The values of the range
Full size table
Table 3 The values of the Reference Ideal
Full size table

As we can see, this case cannot be resolved by TOPSIS or VIKOR methods. We detail the reasons why it is not possible through the different criteria that have been taken into account in the case proposed to illustrate the method.

  • The prices: It is logical to think that we would seek to pay as little as possible, therefore both TOPSIS and VIKOR, or indeed any other MCDM, could be applied.

  • The acidity: In this case we consider any oil as being good if its acidity is within the interval [0.16, 0.26] although by law this may reach 0.80.

  • The waxes: For this criterion, neither of the methods (TOPSIS, VIKOR) can give a solution because the optimal is the interval [50, 63], but the range possible goes from a minimum of 0 to a maximum of 150. RIM cannot be applied either because it does not work with fuzzy evaluations. Thus it must be resolved with a method such as FRIM and comparisons with other methods cannot be made since they are inapplicable.

  • The oil taste: It is easy to understand that the ideal it to achieve the maximum score by the experts, which means that both TOPSIS and VIKOR could be applied.

The following tables show the different steps of the algorithm (Tables 4, 5 and 6).

Table 4 Normalized valuation matrix
Full size table
Table 5 Weighted normalized matrix
Full size table
Table 6 Variation to the positive and negative reference ideal. Indexes calculation
Full size table

Concluding that under these criteria, the trademark with the best quality price ratio is M 5 although M 8 is very close to it.

6 Final Remarks

Since the measuring instruments are imprecise, it is necessary to work with methods that counteract this problem. In this sense, the fuzzy theory and its arithmetic give good results. On the other hand there are many problems where the best decision is not associated to the maximun or to the minimun but that the best value correspond to intermediate best value correspond to intermediate values as it the case that concerns us. Thus, to assess the quality of Virgin olive oil one of the components to consider are waxes, where the best is neither 0 nor 150, extreme values that take it. We have seen that the optimum would be a value comprised between 50 and 63.

In this paper, from the study of the Reference Ideal Method, a modification thereof is performed if the operation uses fuzzy numbers. Therefore, it has been necessary to modify RIM, because it was not possible to work directly with this method, when the fuzzy number has non-empty intersection with the Reference Ideal.

Given that RIM does not give a solution when the fuzzy number intersects with the reference ideal, a new distance has been defined and from it, the normalization function.

Triangular fuzzy numbers have been considered, but by extension the Fuzzy Reference Ideal Method (FRIM) can work with any other type of fuzzy numbers.