1 Introduction

From the mathematical aspect, chaos is defined as a pseudo-random behavior generated by nonlinear deterministic systems (Yang et al. 2006). Generally speaking, chaos has several important dynamical characteristics, namely, the sensitive dependence on initial conditions, pseudo-randomness, ergodicity, and strange attractor with self-similar fractal pattern (Yang et al. 2006, 2007, 2012; Li and Jiang 1998; Yuan and Wang 2008). Recently, chaos theory has been used to develop novel global optimization techniques, and particularly, in the specification of chaos optimization algorithms (COAs) (Li and Jiang 1998; Yang et al. 2007, 2012, 2014; Yuan and Wang 2008; Zhu et al. 2012; Hamaizia et al. 2012; Okamoto and Hirata 2013) based on the use of numerical sequences generated by means of chaotic map. Due to the dynamic properties of chaotic sequences, a lot of existing application results have demonstrated that COAs can carry out overall searches at higher speeds than stochastic ergodic searches that depend on the probabilities (Yang et al. 2012, 2014; Zhu et al. 2012; Hamaizia et al. 2012; Okamoto and Hirata 2013). Furthermore, COAs generally exhibit better numerical performance and benefits than stochastic algorithms. The main advantages of COAs include: (a) COAs escape from local minima more easily than classical stochastic optimization algorithms such as genetic algorithm (GA), simulated annealing (SA) and some meta-heuristics algorithms including particle swarm optimization (PSO), ant colony optimization algorithm (ACO), differential evolution (DE), and so on (Yang et al. 2014; b) COAs don’t depend on the strict mathematical properties of the optimization problem, such as continuity, differentiability; (c) COAs are easy to be implemented and the execution time of COAs is short (Li and Jiang 1998; Yang et al. 2007, 2012; Yuan and Wang 2008).

In addition to the development of COAs, chaos has also been integrated with meta-heuristic algorithms, such as: chaotic harmony search algorithm (Alatas 2010; Askarzadeh 2013), chaotic ant swarm optimization (Liu et al. 2013; Wan et al. 2012; Li et al. 2012), chaotic particle swarm optimization (Wu 2011; Cheng et al. 2012; Pluhacek et al. 2014), chaotic evolutionary algorithm (Ho and Yang 2012; Arunkumar and Jothiprakash 2013), chaotic genetic algorithms (Kromer et al. 2014; Ma 2012), chaos embedded discrete self organizing migrating algorithm (Davendra et al. 2014), chaotic differential evolution (Coelho and Pessoa 2011), chaotic firefly algorithm (Coelho and Mariani 2012), chaotic simulated annealing (Chen 2011; Hong 2011), chaos-based immune algorithm (Chen et al. 2011). The simulation results and applications have also shown the high efficiency, solutions diversity and global search capability of chaos-based optimization algorithms.

An essential feature of the chaotic sequence is that small change in the parameter or the starting value leads to the vastly different future behavior. Since the chaotic motions are pseudo-random and chaotic sequences are sensitive to the initial conditions, therefore, COAs’ search and converge speed are usually effected by the starting values. In view of the limitation of COAs, a kind of parallel chaos optimization algorithm (PCOA) has been proposed in our former studies (Yuan et al. 2007, 2012, 2014), and simulation results show PCOA’s superiority over original COAs. The salient feature of PCOA lies in its pseudo-parallel mechanism. In the PCOA, multiple stochastic chaos variables are simultaneously mapped onto one decision variable, so PCOA searches from diverse initial points and detracts the sensitivity of initial conditions. Although the PCOA in (Yuan et al. 2007, 2012, 2014) can easily escape from local minima, its precise exploiting capability is insufficient. Therefore, PCOA is combined with local search method, like simplex search method (SSM) and harmony search algorithm (HSA). However, this kind of hybrid PCOA with local search method is far from perfect as: the local search method has slow efficiency, the proper switch point from PCOA to local search method usually affects the search performance. In addition, parallel variables in PCOA search independently without information exchange.

To improve original PCOA, a mutative-scale pseudo-parallel chaos optimization algorithm (MPCOA) with cross and merging operation is proposed in this paper. Both cross and merging operation can exchange information within population and produce new potential parallel variables, which are different from those generated by chaotic sequences. In addition, mutative-scale search space is used to continually reduce the search space. Using cross and merging operation as well as mutative-scale strategy, MPCOA achieves a good balance between exploration and exploitation, without hybrid with local search method. The impacts of different chaotic maps and parallel numbers on the MPCOA are also discussed.

The rest of this paper is organized as follows. Section 2 briefly describes chaotic maps. The PCOA approach is introduced in Sect. 3. Section 4 gives presentation of the proposed MPCOA. The MPCOA is tested with benchmark functions and parameter identification problem in Sects. 5 and 6, respectively. Conclusions are presented in Sect. 7.

2 Chaotic map

One-dimensional maps are the simplest systems with the capability of generating chaotic behaviors. Eight well-known one-dimensional maps which yield chaotic behaviors are introduced as follows (Yuan et al. 2014; He et al. 2001; Tavazoei and Haeri 2007).

1. Logistic map: Logistic map generates chaotic sequences in (0,1). This map is also frequently used in the COAs and it is given by:

$$\begin{aligned} x _{n+1} = 4 x _{n} (1-x _{n}) \end{aligned}$$
(1)

2. Tent map: Tent chaotic map is very similar to Logistic map, which displays specific chaotic effects. Tent map generates chaotic sequences in (0,1) and it is given by:

$$\begin{aligned} x _{n+1}= {\left\{ \begin{array}{ll} x _{n} /0.7,~~ ~ x _{n} < 0.7 \\ (\frac{10}{3}) x _{n} (1-x _{n}),~~~ x _{n} \ge 0.7 \end{array}\right. } \end{aligned}$$
(2)

3. Chebyshev map: Chebyshev chaotic map is a common symmetrical region map. It is generally used in neural networks, digital communication and security problems. Chebyshev map generates chaotic sequences in [\(-\)1,1]. This map is formally given by:

$$\begin{aligned} x _{n+1} = \mathrm{cos}(5 \mathrm{cos}^{-1}x_{n}) \end{aligned}$$
(3)

4. Circle map: Circle chaotic map was proposed by Kolmogorov. This map describes a simplified model of the phase locked loop in electronics (Tavazoei and Haeri 2007). This map is formally given by:

$$\begin{aligned} x _{n+1} = x_{n}+2.5-\left( \frac{5}{2\pi }\right) \mathrm{sin}(2\pi x_{n}) ~~ ~~\mathrm{mod}~~(1) \end{aligned}$$
(4)

Circle map generates chaotic sequences in (0,1). In Eq. (4), \( x_{n+1}\) is computed mod 1.

5. Cubic map: Cubic map is one of the most commonly used maps in generating chaotic sequences in various applications like cryptography. Cubic map generates chaotic sequences in (0,1) and it is formally given by:

$$\begin{aligned} x _{n+1} =2.59 x_{n}\left( 1-x^{2}_{n}\right) \end{aligned}$$
(5)

6. Gauss map: Gauss map is also one of the very well known and commonly employed map in generating chaotic sequences in various applications like testing and image encryption. Gauss map generates chaotic sequences in (0,1), and it is formally given by:

$$\begin{aligned} x _{n+1}= {\left\{ \begin{array}{ll} 0, ~~ x _{n}=0 \\ \frac{1}{x _{n}}~~\mathrm{mod}~(1), ~ x _{n}\ne 0 \end{array}\right. } \end{aligned}$$
(6)

7. ICMIC map: Iterative chaotic map with infinite collapses (ICMIC) generates chaotic sequences in (\(-1\),1) and it is formally given by:

$$\begin{aligned} x _{n+1} = \mathrm{sin}\left( \frac{70}{x_{n}}\right) \end{aligned}$$
(7)

8. Sinusodial map: Sinusodial map generates chaotic sequences in (0,1) and it is given by:

$$\begin{aligned} x _{n+1} = \mathrm{sin}(\pi x_{n}) \end{aligned}$$
(8)

The chaotic motions of these eight chaotic maps in two-dimension space (\(x_{1}, x_{2}\)) with 200 iterations are illustrated in Fig. 1. Here, the initial values of two chaos variables are: \(x_{1}=0.152, x_{2}=0.843\). From Fig. 1, it can also be observed that the distribution or ergodic property of different chaotic maps is different. Therefore, the search performance of different chaotic maps differs from each other in view of convergence rate and accuracy (Yuan et al. 2012, 2014; He et al. 2001; Tavazoei and Haeri 2007).

Fig. 1
figure 1

Chaotic maps in two-dimension space with 200 iterations

Full size image

3 PCOA approach

The salient feature of PCOA lies in its pseudo-parallel mechanism. In the PCOA, multiple stochastic chaos variables (like population) are simultaneously mapped onto one decision variable, and the search result is the best value of parallel multiple chaos variables.

Consider an optimization problem for nonlinear multi-modal function with boundary constraints as:

$$\begin{aligned} \mathrm{min} ~~f(X)=f(x_{1},x_{2},\ldots , x_{n}), ~~x_{i}\in [L_{i}, U_{i}]. \end{aligned}$$
(9)

where \(f\) is the objective function, and \(X=(x_{1},x_{2},\ldots , x_{n}) \in R^{n}\) is a vector in the \(n\)-dimensional decision (variable) space (solution space), and the feasible solution space is \(x_{i}\in [L_{i}, U_{i}]\), where \(L_{i}\) and \(U_{i}\) represent the lower and upper bound of the \(i\)th variable, respectively. PCOA evolves a stochastic population of \(N\) candidate individuals (solutions) with \(n\)-dimensional parameter vectors. The \(N\) is the population size, meanwhile, the number of parallel candidate individuals. In the following, the subscripts \(i\) and \(j\) stand for the decision variable and parallel candidate individual, respectively.

The process of PCOA based on twice carrier wave mechanism is described as follows. The first is the raw search in different chaotic traces, while the second is refined search to enhance the search precision.

3.1 PCOA search using the first carrier wave

Step 1: Specify the maximum number of iterations \(S_{1}\) in the first carrier wave, random initial value of chaotic map \(0<\gamma ^{(0)}_{ij}<1 \), initial iterations number \(l = 0\), parallel optimum \(P^{*}_{j}=\infty \) and global optimum \(P^{*}=\infty \).

Step 2: Map chaotic map \( \gamma ^{(l)} _{ij}\) onto the variance range of decision variable by the equation:

$$\begin{aligned} x^{(l)} _{ij} = L_{i} + \gamma ^{(l)} _{ij} (U_{i} - L_{i}) \end{aligned}$$
(10)

Step 3: Compute the objective function value of \(x^{(l)}_{ij}\), then update the search result. If \( f(x_{j}^{(l)})< P^{*}_{j}\) , then parallel solution \(x^{* }_{j}= x^{(l)}_{j}\), parallel optimum \(P^{*}_{j} = f(x_{j}^{(l)})\). If \(P^{*}_{j} < P^{*} \), then global optimum \(P^{*} = P^{*}_{j}\), global solution \(X^{* }=x^{* }_{j}\). This means that the search result is the best value of parallel candidate individuals.

Step 4: Generate next value of chaotic map using one of the chaotic maps in Eqs. (1), (2), (3), (4), (5), (6), (7), (8):

$$\begin{aligned} \gamma ^{(l+1)} _{ij} = M(\gamma ^{(l)} _{ij}) \end{aligned}$$
(11)

Step 5: If \( l \ge S_{1}\) , stop the first carrier wave; otherwise \( l \longleftarrow l + 1\) , go to Step 2.

3.2 PCOA search using the second carrier wave

Step 1: Specify the maximum number of iterations \(S_{2}\) in the second carrier wave, initial iterations number \(l'= 0\), random initial value of chaotic map \(0<\gamma ^{(l')}_{ij}<1 \).

Step 2: Compute the second carrier wave by the equation:

$$\begin{aligned} x^{(l')} _{ij} = x^{*} _{j} + \lambda _{i}(\gamma ^{(l')} _{ij}-0.5 ) \end{aligned}$$
(12)

Step 3: Compute the objective function value of \(x^{(l')}_{ij}\), then update the search result. If \( f(x_{j}^{(l')})< P^{*}_{j}\) , then parallel solution \(x^{* }_{j}= x^{(l')}_{j}\), parallel optimum \(P^{*}_{j} = f(x_{j}^{(l')})\). If \(P^{*}_{j} < P^{*} \), then global optimum \(P^{*} = P^{*}_{j}\), global solution \(X^{* }=x^{* }_{j}\).

Step 4: Generate next value of chaotic map \(\gamma ^{(l'+1)} _{ij}\) as in Eq. (11).

Step 5: If \( l' \ge S_{2} \), stop the second carrier wave search process; otherwise \(\lambda _{i}\longleftarrow t\lambda _{i}\), \( l '\longleftarrow l' + 1\) , go to Step 2.

The \(\lambda \) is an adjustable parameter and adjusts small ergodic range around \(x^{*} _{j}\), and constant \(t>1\). It is difficult and heuristic to determine the appropriate value of \(\lambda _{i}\), initial value of \(\lambda _{i}\) is usually set to \(0.01 (U_{i}-L_{i})\) (Tavazoei and Haeri 2007).

4 MPCOA approach

A mutative-scale pseudo-parallel chaos optimization algorithm (MPCOA) with cross and merging operation is proposed in this section. Compared with original PCOAs, the proposed MPCOA has two obvious characteristics: (1) MPCOA doesn’t need twice carrier wave search, only one carrier wave search can reach good solutions; (2) Cross operation, merging operation and mutative-scale search space are applied in MPCOA, without hybrid with local search method.

4.1 Cross operation within population

In the original PCOAs, all parallel variables search independently according to their respective chaotic sequences without information interaction. In the proposed MPCOA, the cross operation within population will be used to find new potential solutions. The cross operation is illustrated in Fig. 2. This kind of cross operation randomly chooses two parallel variables from parallel solutions \(x^{* }_{j}\) to exchange with each other, and it may produce new potential solutions which usually are different from those generated by chaotic sequences.

Fig. 2
figure 2

Cross operation within population

Full size image

4.2 Merging operation within population

Even if original PCOAs have reached the neighborhood of global optimum, it needs to spend much computational effort to reach the optimum eventually by searching numerous points (Yuan and Wang 2008). The reason is that precise exploiting capability of PCOA is poor. For this reason, merging operation within population is employed in the MPCOA. The merging operation is illustrated in Fig. 3.

Fig. 3
figure 3

Merging operation within population

Full size image

The merging operation within population from parallel solutions \(x^{* }_{j}\) can be denoted by:

$$\begin{aligned} x_{i1}^{(M)}=\gamma _{i1}*x^{*}_{i1}+(1-\gamma _{i1})*x^{*}_{i2} \end{aligned}$$
(13)

where \(\gamma _{i1}\) is the chaotic map.

The merging operation randomly chooses two parallel variables from parallel solutions to merge, and it may produce new potential solutions for optimization problem. In essence, the merging operation is a kind of local exploiting search as shown in Eq. (13).

Both cross and merging operation within population are used as the supplement to the PCOA search. This means that if the new parallel variables after cross or merging operation have reached a better fitness than the original ones, the new parallel variables will replace the original ones. In another situation, if the new parallel variables after cross or merging operation bring a worse fitness than the original ones, the new parallel variables using cross or merging operation will be given up.

Both cross and merging operation within population are conducted at each iteration during the PCOA search procedure. Another problem is to choose how many parallel variables for cross or merging operation. The more cross or merging operation within population, the more diversity of parallel variables, while the more computing cost. In this paper, the cross operation rate is \(P_\mathrm{cross}\) = 0.1–0.5, and the merging operation rate is \(P_\mathrm{merging}\) = 0.1–0.5, i.e., about 10–50 % of parallel solutions have been executed the cross or merging operation.

4.3 Mutative-scale search

With the increase of iterations, the parallel solutions for optimization problem will be close to each other. So the precise exploiting search is the main task after certain iterations. Here, mutative-scale search using contractive search space is considered for precise exploiting search.

Mutative-scale search space is conducted by the following equations:

$$\begin{aligned} L'_{i}=x_{i}^{*}-\Phi (U_{i}-L_{i}) \end{aligned}$$
(14)
$$\begin{aligned} U'_{i}=x_{i}^{*}+\Phi (U_{i}-L_{i}) \end{aligned}$$
(15)

where \(\Phi \) represents a mutative-scale factor which is a decreasing parameter with respect to iterations \(l\) described by:

$$\begin{aligned} \Phi =\left( \frac{l_\mathrm{max}-l}{l_\mathrm{max}}\right) ^{\phi } \end{aligned}$$
(16)

where \(\phi \) is an integer usually set to 2–8.

To avoid \(L'_{i}\), \(U'_{i}\) exceeding bounds of search space \([L_{i}, U_{i}]\), the new search ranges are restricted to their bounds: If \(L'_{i}< L_{i}\), then \(L'_{i}= L_{i}\); if \(U'_{i}> U_{i}\), then \(U'_{i}= U_{i}\).

Then, the search space will be contracted for better accurate exploiting search, and the modified search space is used in the follow-up procedure as:

$$\begin{aligned} L_{i}= L'_{i} \end{aligned}$$
(17)
$$\begin{aligned} U_{i}= U'_{i} \end{aligned}$$
(18)

4.4 MPCOA implementation

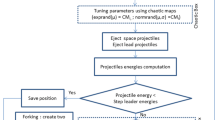
The detailed implementation of the MPCOA is presented as follows. The process of MPCOA is also illustrated in Fig. 4.

Fig. 4
figure 4

Flowchart of the proposed MPCOA approach

Full size image

Step 1: Specify the maximum number of iterations \(l_\mathrm{max}\), random initial value of chaotic map \(0<\gamma ^{(0)}_{ij}<1 \), set iterations number \(l = 0\), parallel optimum \(P^{*}_{j}=\infty \) and global optimum \(P^{*}=\infty \).

Step 2: Map chaotic map \( \gamma ^{(l)} _{ij}\) onto the variance range of decision variable as in Eq. (10).

Step 3: Compute the objective function value of \({X}^{(l)}\), then update the search result. If \( f(x_{j}^{(l)})< P^{*}_{j}\) , then parallel solution \(x^{* }_{j}= x^{(l)}_{j}\), parallel optimum \(P^{*}_{j} = f(x_{j}^{(l)})\). If \(P^{*}_{j} < P^{*} \), then global optimum \(P^{*} = P^{*}_{j}\), global solution \(X^{* }=x^{* }_{j}\).

Step 4: Execute cross operation and produce new parallel variable \(x^{(C)}_{j}\). Compute the objective function value of \(x^{(C)}_{j}\), then update the search result. If \( f(x_{j}^{(C)})< P^{*}_{j}\) , then \(x^{* }_{j}= x^{(C)}_{j}\), \(P^{*}_{j} = f(x_{j}^{(C)})\). If \(P^{*}_{j} < P^{*} \), then \(P^{*} = P^{*}_{j}\), \(X^{* }=x^{* }_{j}\).

Step 5: Execute merging operation and produce new parallel variable \(x^{(M)}_{j}\). Compute the objective function value of \(x^{(M)}_{j}\), then update the search result. If \( f(x_{j}^{(M)})< P^{*}_{j}\) , then \(x^{* }_{j}= x^{(M)}_{j}\), \(P^{*}_{j} = f(x_{j}^{(M)})\). If \(P^{*}_{j} < P^{*} \), then \(P^{*} = P^{*}_{j}\), \(X^{* }=x^{* }_{j}\).

Step 6: Conduct mutative-scale search space \([L'_{i}, U'_{i}] \) as in Eqs. (14), (15), then update the search space \([L_{i}, U_{i}] \) as in Eqs. (17), (18).

Step 7: Generate next value of chaotic map \(\gamma ^{(l+1)} _{ij}\) as in Eq. (11).

Step 8: If \( l \ge l_\mathrm{max}\) , stop the search process; otherwise \( l \longleftarrow l + 1\) , go to Step 2.

5 Benchmark functions simulation

5.1 Benchmark functions

Well-defined benchmark functions which are based on the mathematical functions can be used as objective functions to measure and test the performance of optimization algorithms. The efficiency and performance of the MPCOA are evaluated with eight common benchmark functions as in Table 1.

Table 1 Benchmark functions
Full size table

Among these benchmark functions, the former four have two or three decision variables, and the latter four have 20 decision variables. These functions are often multi-modal and several of them have many local minima, as illustrated in Fig. 5.

Fig. 5
figure 5

Benchmark functions \(f_{1}\!-\!\!f_{8}\) illustrated in two-dimension space

Full size image

5.2 Different parallel numbers \(N\) for MPCOA

Like the population size to evolutionary computing, the parallel number \(N\) in MPCOA is one parameter that a researcher has to deal with. We still largely depend on the experience or trial-and-error approach to set parameters. Generally speaking, too small parallel number \(N\) leads to similar convergence of original COAs, while too large parallel number \(N\) is computationally costly. Now we will investigate how parallel number \(N\) will influence the MPCOA performance. The parameters in the MPCOA are: \( P_\mathrm{cross}=0.5\), \( P_\mathrm{merging}=0.5\), \(\phi =6\), different parallel numbers \(N\) have been investigated, tent map in Eq. (2) is used as the chaotic map. For different optimization problems, appropriate number of maximum iterations \(l_\mathrm{max}\) of MPCOA is usually different. An appropriate \(l_\mathrm{max}\) is usually chosen with multiple runs until finding the one which yields an appropriate result. In this simulation, \(l_\mathrm{max}\) is chosen by trial with multiple runs and is labeled in Fig. 6. Convergence performance of MPCOA on benchmark functions with different parallel numbers (\(N=6,~ 12,~ 20,~ 30\)) is shown in Fig. 6.

Fig. 6
figure 6

Convergence performance of MPCOA on benchmark functions with different parallel numbers \(N\)

Full size image

The simulation results on benchmark functions obtained by MPCOA with different parallel numbers \(N\) are reported in Table 2, which shows the statistical result in 20 runs. The ‘Best’, ‘Worst’ and ‘Mean’ represent the best, the worst and the average objective function value by MPCOA in 20 runs, respectively. The ‘Rate’ represents the success rate of reaching the global optimum \(X^{*}\) with the error less than 0.01.

Table 2 Simulation results obtained by MPCOA with different parallel numbers \(N\)
Full size table

It can be seen from Fig. 6 and Table 2 that parallel number \(N\) has a direct impact on the search result of MPCOA. With the increase of parallel number \(N\), the search speed of MPCOA is faster and the search results are better. For these benchmark functions, the proposed MPCOA achieves satisfactory success rate and global optimum when \(N=30\).

5.3 Different chaotic maps for MPCOA

The performance of MPCOA using different chaotic maps described in Eqs. (1), (2), (3), (4), (5), (6), (7), (8) will be investigated here. The MPCOA parameters are: \(N=20\), \( P_\mathrm{cross}=0.5\), \( P_\mathrm{merging}=0.5\), \(\phi =6\). The simulation results on benchmark functions by the MPCOA using different chaotic maps are reported in Table 3. It can be seen from Table 3 that there is very little difference with respect to different chaotic maps for MPCOA. From Table 3, it can be seen that the sinusodial map, tent map and Gauss map show better simulation results than other maps in these tests.

Table 3 Simulation results obtained by MPCOA using different chaotic maps
Full size table

5.4 Comparison of MPCOA with other PCOAs

The proposed MPCOA is also compared with other PCOAs in Yuan et al. (2007, 2012). With the similar conditions and parameters as \( P_\mathrm{cross}=0.5\), \( P_\mathrm{merging}=0.5\), \(\phi =6\) and tent, map is used. The simulation results of success rate by these three algorithms are shown in Table 4, where ‘PCOA1’ and ‘PCOA2’ represent PCOA+CCIC and PCOA+HSA in Yuan et al. (2007) and (2012), respectively. From Table 4, one knows that with the increase of parallel number \(N\), the success rate of these PCOAs becomes higher. In each case, the MPCOA shows higher success rate than other PCOAs. The simulation results in Table 4 also verify the superiority of MPCOA compared with other PCOAs.

Table 4 The success rate by different PCOAs
Full size table

5.5 Comparison of MPCOA with other algorithms

Here, the MPCOA ( parameters are: \(N=20\), \( P_\mathrm{cross}=0.5\), \( P_\mathrm{merging}=0.5\), \(\phi =6\), sinusodial map is used) is also compared with four widely used evolutionary algorithms, they are: particle swarm optimization algorithm (PSO) (Thangaraj et al. 2011), covariance matrix adaptation evolution strategy (CMAES) (Igel et al. 2007), self-adaptive differential evolution algorithm (SaDE1) (Brest et al. 2006) and self-adaptive differential evolution algorithm (SaDE2) (Qin and Suganthan 2005). The simulation results on benchmark functions obtained by these algorithms in 30 runs are reported in Table 5. In addition to the ‘Best’ and ‘Mean’, the standard deviation of the mean objective function value (Std. Dev.) is also compared. It can be seen from Table 5 that the proposed MPCOA has achieved the best result among these algorithms in \(f_{4}\), \(f_{6}\), \(f_{7}\) and \(f_{8}\).

Table 5 Simulation results obtained by different algorithms in 30 runs
Full size table

6 Parameter identification of synchronous generator

In this section, simulations are performed to evaluate the performance of the MPCOA for parameter identification of synchronous generator. The mathematical model of synchronous generator and the fitness function for this problem are the same in Zhu et al. (2012), Yuan et al. (2012). Similar to Zhu et al. (2012), Yuan et al. (2012), 11 variables values (\(X_{d}\), \(X^{'}_{d}\), \(X^{''}_{d}\), \(T^{'}_{d0}\), \(T^{''}_{d0}\), \(K\), \(X_{q}\), \(X^{''}_{q}\), \(T^{''}_{q0}\), \(M\), \(D\)) are to be identified by optimization algorithms. The parameters of MPCOA are chosen as: \(N=20\), \( P_\mathrm{cross}=0.5\), \( P_\mathrm{merging}=0.5\), \(\phi =6\), \(l_\mathrm{max}=3,000\), Sinusodial map is used, the number of decision variables \(n=11\). Here, the relative error is used to evaluate parameter identification performance as: \(\Vert \frac{x-\hat{x}}{x}*100~\%\Vert \), where \(x\) and \(\hat{x}\) are the actual parameter value and the identified value, respectively.

Average relative errors of 11 identified variables by different algorithms repeated for 10 runs are shown in Figs. 7 and 8. The ‘COA’, ‘PCOA1’, ‘PCOA2’ and ‘MPCOA’ represent original COA, PCOA+CCIC, PCOA+HSA and proposed MPCOA, respectively. It can be seen from Figs. 7 and 8 that the MPCOA has the smallest average relative errors of these 11 variables. The parameter identification results have also verified that the proposed MPCOA has superiority over original PCOAs.

Fig. 7
figure 7

Average relative errors of 11 variables obtained by different algorithms

Full size image
Fig. 8
figure 8

Average relative errors of 11 variables obtained by different algorithms

Full size image

7 Conclusion

In the present paper, a novel MPCOA with cross and merging operation is proposed to improve original PCOA. With the increase of parallel number, MPCOA has better success rate and converge speed. Simulation results show that there is a little difference between different chaotic maps. It is observed that obvious performance improvement is possible by the MPCOA. Benchmark tests and parameter identification results have shown that the MPCOA has better performance than original PCOAs.